Collet et al. adopt a high-dimensional quantitative genetic approach using gene expression traits to test for the presence of modularity of the genotype-phenotype map, where traits contributing to the same function (functional modularity)...
Keywords: modularity, pleiotropy, genotype–phenotype map, Drosophila serrata, gene expression
Abstract
Variational modules, sets of pleiotropically covarying traits, affect phenotypic evolution, and therefore are predicted to reflect functional modules, such that traits within a variational module also share a common function. Such an alignment of function and pleiotropy is expected to facilitate adaptation by reducing the deleterious effects of mutations, and by allowing coordinated evolution of functionally related sets of traits. Here, we adopt a high-dimensional quantitative genetic approach using a large number of gene expression traits in Drosophila serrata to test whether functional grouping, defined by gene ontology (GO terms), predicts variational modules. Mutational or standing genetic covariance was significantly greater than among randomly grouped sets of genes for 38% of our functional groups, indicating that GO terms can predict variational modularity to some extent. We estimated stabilizing selection acting on mutational covariance to test the prediction that functional pleiotropy would result in reduced deleterious effects of mutations within functional modules. Stabilizing selection within functional modules was weaker than that acting on randomly grouped sets of genes in only 23% of functional groups, indicating that functional alignment can reduce deleterious effects of pleiotropic mutation but typically does not. Our analyses also revealed the presence of variational modules that spanned multiple functions.
PLEIOTROPY has the potential to generate substantial evolutionary costs that scale with the number of traits affected by each mutation. Assuming a mutation has the same magnitude effect on each trait, the probability that a mutation will be favorable decreases as the number of traits (n) influenced by a mutation increases (Fisher 1930). Under the assumption of universal pleiotropy, the rate of adaptation may also decline by a factor of n−1 (Orr 2000). Modularity has been proposed as a mechanism to reduce such potential costs of organismal complexity (Wagner 1996). Variational modules occur when phenotypic traits share genetic variance through pleiotropy, while displaying lower covariation with traits belonging to different variational modules (Wagner 1996; Schlosser and Wagner 2004; Wagner et al. 2007). Independently, functional modularity describes an architecture where traits within a functional module share a common function (Wagner et al. 2007), which implies that the effects on fitness of a trait depend on the other traits contained in its functional module. Functional integration is predicted to select for variational modularity because: (i) variational modularity reduces the range of effects of deleterious mutations, as mutations would only affect the traits belonging to the targeted functional module rather than the entire organism; (ii) all traits of a module can respond to natural selection as a unit; and (iii) it preserves the module’s function during evolutionary change (Olson and Miller 1958; Wagner and Altenberg 1996; Wagner and Mezey 2004). Several different approaches to theoretical modeling have determined that coincidence of functional and variational modules can indeed promote adaptation under some conditions (Welch and Waxman 2003; Griswold 2006; Pavlicev and Hansen 2011; Melo and Marroig 2015).
Despite the intuitive, and theoretically supported, potential evolutionary benefits of variational modules coinciding with functional modules, it is difficult to establish empirically whether functionally related sets of traits correspond to variational modules. Macroevolutionary approaches can identify evolutionary modules (sets of traits that can potentially evolve independently of other such sets) as groups of genes with conserved physical proximity, cooccurrence in the genome, or fused genes. If variational modules help preserve functional modules, selection will favor the conservation of those modules and thus evolutionary modules are also expected to coincide with functional modules (Cheverud 1984). Comparative genomic analyses of functional modules have provided some evidence that evolutionary modules are, overall, more stable between genes that interact functionally than between unrelated genes, although there are large discrepancies between modules and some functions are more conserved than others (Snel and Huynen 2004; Spirin et al. 2006; Peregrin-Alvarez et al. 2009; Moreno-Hagelsieb and Jokic 2012). Evolutionary preservation of functional modules may also cause differential rates of gene sequence evolution between functional modules. Consistent with this, Chen and Dokholyan (2006) reported that, in yeast, protein sequences and expression levels within functional modules evolve at more similar rates than between modules.
Coordinated selection that operates on functional interrelationships of traits can preserve functional modules among taxa. By comparing the topologic structure of metabolic networks among species and the environment where they live, it was found that metabolic network modularity varies with environmental conditions in bacteria (Parter et al. 2007; Kreimer et al. 2008), archae (Takemoto and Borjigin 2011), and across archae, bacteria, and eukarya (Mazurie et al. 2010), consistent with the role of natural selection in shaping variational relationships between traits belonging to functional modules (note that results using metabolic network modularity should be taken with care as the same modularity scores can be obtained with very different metabolic network structures; Zhou and Nakhleh 2012). The preservation of interactions between traits belonging to functional modules might also reflect a bias in the variation generated by mutation. However, potential biases in mutation rates within modules, and how mutation can contribute to maintaining the organization of functional modules, remain little explored.
Microevolutionary studies within species offer the opportunity to directly determine the distribution of phenotypic effects of new mutations and selection on these mutations. Identifying variational modules requires the study of many traits belonging to diverse functional modules. Morphological studies, for example, have limited use for testing the key hypothesis: statistical tests for lower covariance outside the module are relatively weak because only relationships among similar types of traits (morphology) are considered, and covariance between morphological and behavioral or physiological traits, which might contribute to a common function, are not considered. Systems biology, which involves a shift in focus from the function of individual genes in isolation to the interaction among gene products to achieve a biological function (Ideker et al. 2001; Kitano 2002; Civelek and Lusis 2014), has provided the tools to study modularity across diverse functional modules. Work in model organisms has empirically revealed the function and functional interactions of thousands of genes, valuable information that can be applied to nonmodel taxa through tools such as the database of The Gene Ontology (GO) Consortium (Ashburner et al. 2000) and the Kyoto Encyclopedia of Genes and Genomes (KEGG) pathway resources (Kanehisa et al. 2006).
Gene expression data allow questions about the distribution of variational and functional modules to be asked while considering a diverse range of biological functions. The development of high-throughput methods for the simultaneous measurement of the expression of thousands of genes has led to statistical developments allowing the identification of clusters of coexpressed genes (e.g., Eisen et al. 1998; D’haeseleer et al. 2000; Tanay et al. 2002). When gene expression has been measured within a quantitative genetic breeding design, high levels of covariance among expression traits have been found, which imply the existence of variational modules (Denver et al. 2005; Rifkin et al. 2005; Ayroles et al. 2009; Blows et al. 2015). Many studies have subsequently applied enrichment analyses to determine whether coexpressed genes were associated with the same GO terms more often than expected by chance (e.g., Ayroles et al. 2009; Blows et al. 2015; Rose et al. 2015; Storz et al. 2015). Although it appears from these studies that variational modules can predict functional group membership to some extent, it is unknown what proportion of pleiotropic covariance resides within predefined functional groups, and whether pleiotropic covariance among functional groups is of a similar magnitude to that found within functional groups. Further, the role of selection in generating these variation modules remains relatively unexplored.
Here, we adopt a high-dimensional quantitative genetic approach to directly test whether trait functional associations predict the pleiotropic covariance of gene expression traits. Using 41 mutation accumulation (M) lines of Drosophila serrata in which widespread mutational pleiotropy among small random sets of 3385 gene expression traits has been demonstrated (McGuigan et al. 2014b), we identified 13 groups of genes involved in a particular function (using GO terms and KEGG pathways), which were significantly enriched with genes that had mutational variance and that showed significant mutational covariance; the opportunity for genes to contribute to > 1 of the 13 groups was explicitly limited. Using this set of M lines and a matched set of set 30 inbred lines derived from an outbred population of D. serrata, we determined whether coexpression, which was due to pleiotropic effects of new mutations in the M lines or of alleles already present in the inbred lines, was greater within these functionally related sets of genes than it was among random sets of the same number of genes whose functions were not known. We also investigated whether we could detect pleiotropic mutations that spanned a larger array of functions. In addition to directly testing whether pleiotropic effects were stronger within functional modules, our experimental design (specifically the matched estimates of mutational and standing genetic variance) allowed us to directly estimate the strength of stabilizing selection acting against function-specific mutational pleiotropy and compare it to selection against mutational pleiotropy spanning multiple functions.
Materials and Methods
Experimental populations and data collection
We used two sets of highly inbred lines of D. serrata, which were established, maintained, and assayed in a similar way (McGuigan et al. 2014a), to measure the mutational and standing genetic covariance in sets of gene expression traits assigned to functional groups. Briefly, the first set of lines consisted of 45 M lines derived from a single inbred ancestral population. Each M line was maintained during 27 generations through full-sib inbreeding. The second set of 42 lines were derived from females collected from a wild outbred population and inbred for 15 generations of full-sib mating (G lines). As M lines were founded from a population depleted of standing genetic variance, the differences among M lines originated from mutations, filtered by relaxed selection, and M lines captured mutational variance. On the other hand, the differences among G lines originated from the natural standing genetic variance captured in the original outbred population; hence, the G lines captured standing genetic variance. We neglected the contribution of new mutations accumulated in the G lines because, as determined from the M lines, mutational variance is small relative to standing genetic variance (Table 1).
Table 1. Description of the 13 selected functional modules.
| Group | GO ID | Ontology | Term | Background | Sample (FBgn) | Sample (genes) | Enrichment (P-value) | Degree | Overlap | Genes with significant | Median | Median |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Chorion | GO:0005213 | MF | Structural constituent of chorion | 8 | 8 | 9 | 0.0011 | 1 | 0 | 3 | 0.0016 | 0.0000* |
| Amino A | GO:0000096 | BP | Sulfur amino acid metabolic process | 14 | 9 | 10 | 0.0222 | 12 | 0 | 4 | 0.0014 | 0.4453 |
| NeuroT | GO:0030594 | MF | Neurotransmitter receptor activity | 29 | 15 | 15 | 0.0245 | 10 | 0 | 5 | 0.0016 | 0.3840 |
| GT | GO:0015020 | MF | Glucuronosyltransferase activity | 25 | 15 | 17 | 0.0049 | 17 | 0 | 10 | 0.0018 | 0.6255* |
| Pro-DNA | GO:0065004 | BP | Protein–DNA complex assembly | 35 | 18 | 20 | 0.0086 | 15 | 0 | 2 | 0.0009 | 0.3198 |
| Bacterium | GO:0009617 | BP | Response to bacterium | 51 | 25 | 30 | 0.0033 | 7 | 4 | 15 | 0.0025 | 0.4621 |
| Chitin | GO:0008061 | MF | Chitin binding | 47 | 28 | 32 | 0.0001 | 2 | 0 | 10 | 0.0013 | 0.4438 |
| Sensory | GO:0007606 | BP | Sensory perception of chemical stimulus | 62 | 32 | 32 | 0.0002 | 5 | 1 | 10 | 0.0013 | 0.5777 |
| Ion Tsp | GO:0030001 | BP | Metal ion transport | 91 | 35 | 39 | 0.0373 | 12 | 2 | 10 | 0.0007 | 0.3364 |
| Heme | GO:0020037 | MF | Heme binding | 99 | 43 | 49 | 0.0037 | 2 | 1 | 24 | 0.0017 | 0.5043* |
| Cuticle | GO:0042302 | MF | Structural constituent of cuticle | 59 | 43 | 49 | < 0.0001 | 3 | 0 | 21 | 0.0014 | 0.5022 |
| Cell Fate | GO:0045165 | BP | Cell fate commitment | 133 | 59 | 65 | 0.0001 | 44 | 2 | 11 | 0.0009 | 0.2568* |
| Endopep | GO:0004252 | MF | Serine-type endopeptidase activity | 143 | 62 | 73 | 0.0004 | 7 | 3 | 31 | 0.0013 | 0.6143*** |
| Genes included in functional groups | 386 | 434 | 156 | 0.0013* | 0.4469*** | |||||||
| Biological background: genes with nonzero mutational variance that were not assigned to any of the 13 functional groups | 2397 | 2951 | 879 | 0.0011 | 0.3841 | |||||||
MF and BP describes whether the GO term is a Molecular Function or a Biological Process. Background is the count of all 8978 genes associated with FlyBase Gene IDs recognized by DAVID that are associated with the corresponding GO term. Sample (FBgn) is the number of genes that are associated with the GO term and have Hm 2> 0 when considering D. melanogaster FlyBase Gene IDs. Sample (genes) is the corresponding number of genes on the microarray; when multiple genes within the functional module correspond to the same D. melanogaster homolog, the total number of genes in the functional module, listed under Sample (genes), is larger than the number of FlyBase Gen IDs, listed under Sample (FBgn). Enrichment (P-value) is the P-value of enrichment for this term. Degree is the number of other GO terms to which a GO term relates, according to the GO term topology as revealed in Directed Acyclic Graphs. Overlap is the number of genes that can also be found in at least one other functional module. Genes with significant Hm 2 show the number of genes in the group with significant Hm 2(P-value). Median Hm 2and Hg 2 show the median mutational and broad-sense heritability, respectively, for the sampled genes of the group; median Hm 2 is calculated only for the genes that had nonzero mutational variance. Level of significance (* P < 0.05, ** P < 0.01, and *** P < 0.001) given by the median P-value of 1000 Mann–Whitney tests comparing the univariate variances of the genes of the groups to the same number genes, randomly chosen among those that were not included in any functional module. GO, gene ontology; ID, identifier; MF, molecular function; BP, biological process; DAVID, the Database for Annotation, Visualization and Integrated Discovery.
In generation 26 in the M lines and generation 14 in the G lines, we set up four replicate vials per M line and three replicate vials per G line in preparation for RNA extraction in the following generation. From these vials, 40 (M) and 60 (G) virgin male offspring were collected for each line. The use of replicate vials for each line ensured that microenvironmental variation was not confounded with the among-line (mutational or genetic) variation. Males were held in groups of five until 3 (G lines) or 4 (M lines) days after emergence, when two RNA extractions on a subsample of 20 (M lines) or 30 (G lines) males were conducted. Given the scope of this study (ratio of variance between the two treatments compared between functions and within functions), we do not expect any of these small discrepancies in handling the two sets of lines to have impacted our results. Flies were snap-frozen using liquid nitrogen; total RNA was extracted using TRIzol (Invitrogen, Carlsbad, CA) and purified using RNeasy kits (QIAGEN, Valencia, CA), all according to the manufacturers’ instructions.
As detailed in Allen et al. (2013) and McGuigan et al. (2014b), microarrays designed from a D. serrata expressed sequence tag (EST) library (Frentiu et al. 2009) were manufactured by NimbleGen (Roche); cDNA synthesis, labeling, hybridization, and microarray scanning (NimbleScan) were performed by the Centre for Genomics and Bioinformatics, Bloomington, Indiana. Microarrays contained 20K random probes plus 11,604 features from ESTs, targeted by five 60-mer oligonucleotide probes; each probe appeared twice on each array. A single sample was hybridized to each array with a single color (Cy-3). Twelve arrays appeared on each slide, and samples were randomly assigned to a slide. We performed quality control analyses with the oligo package in Bioconductor (Gentleman et al. 2005) and removed data due to poor quality or high background signal. The expression data for the 41 M lines and 30 G lines remaining after this process are analyzed below, and are available through the National Center for Biotechnology Information (NCBI)’s Gene Expression Omnibus (GEO) (Edgar et al. 2002; Barrett et al. 2011) (M: GSE49815 and G: GSE45801).
To determine which of the 11,604 phenotypes on each microarray were associated with mutational or standing genetic variation, and therefore informative for analysis of variational and functional modules, we use linear mixed model analyses to partition the variance in each expression trait. First, a linear mixed model to characterize the mutational variance in the standardized (mean = 0 and SD = 1) log10 mean expression of each probe (McGuigan et al. 2014b) was implemented within a Restricted Maximum-Likelihood framework using the function lme in R 3.1.2 (library nlme; Pinheiro and Bates 2000):
| (1) |
where SF was a fixed effect for a segregating factor observed in the M lines that must have been present in the ancestor and was therefore not a product of mutation during the experiment [see supporting information in McGuigan et al. (2014b)]. To prevent this factor from contributing to estimates of mutational (among-line) variance, we added a fixed effect to remove the mean difference in trait expression between the two groups of lines with the alternative forms of this segregating factor. Line was a random factor representing the among M line variance, Rep was a random factor nested within lines representing the two replicate extractions per line, and the residual error, ε, was the variance among the five probes per gene. To be consistent with the bivariate analyses (see below), we used the general-purpose optimization based on the Nelder–Mead algorithm (method “optim”). From the Line variance component, we calculated the broad-sense mutational heritability of gene expression for each gene according to , where t is the number of M generations, here 27 [see details in McGuigan et al. (2014b)]. Of the 11,604 gene expression traits analyzed, 3385 showed among-line variance in the M lines, with statistical support for mutational variance in 1035 traits, 533 of which remained significant at the 5% false discovery rate (FDR) threshold. Selecting genes according to a significance threshold, particularly in large data sets, is prone to limit the detection of pleiotropy (Hill and Zhang 2012). We did not wish effect size and subsequent type II error to affect the interpretation of our measure of function-specific pleiotropy. Therefore, we selected the entire subsample of 3385 genes showing nonzero mutational variance for further consideration. Second, the analysis of the G lines to estimate the standing genetic variance in each of the 3385 expression traits with nonzero mutational variance followed the same model but removed the segregating factor effect. As we detected consistent differences in mean signal intensity among the five replicate probes of each gene in the G lines, we included a fixed effect for probe when analyzing the G lines (McGuigan et al. 2014b).
EST annotation
To establish the function of the genes present on our microarrays, D. serrata ESTs were first classified as putative D. melanogaster homologs. D. melanogaster was chosen as the reference as it is a relatively well-annotated model organism that has been incorporated into many analysis tools. Homolog identifiers (IDs) were assigned following basic local alignment search tool (BLAST) analysis of the D. serrata ESTs against 12 Drosophila species’ genomes obtained from FlyBase (McQuilton et al. 2012) followed by mapping of the FlyBase gene IDs to homolog IDs from the ortholog database (Waterhouse et al. 2013), which allowed us to identify D. melanogaster homologs of the D. serrata genes even when they had a BLAST hit to a gene in a taxon other than D. melanogaster. The D. melanogaster gene’s annotations were then assigned to the D. serrata gene and used for enrichment analysis. To allow for highly divergent homologs to be identified, tblastx with a liberal e-value threshold of 10 was applied; median e-value was 1e−78. The method identified 10,843 (93%) genes on the microarray as homologs of 9500 D. melanogaster genes. For some genes, several D. serrata ESTs corresponded to a unique D. melanogaster homolog and we established that those D. serrata genes could be considered as independent (see Supplemental Material, Supplemental Information and Table S1 in File S1).
Enrichment analyses and identification of functional groups
We restricted our investigation of potential GO functions to those functional groups that were the best candidates to harbor function-specific mutational variance. If a functional group experienced a function-specific pleiotropic mutation, several (or perhaps all) of the genes that are part of that function will each exhibit univariate mutational variance. Therefore, we performed GO term and KEGG pathway enrichment analyses that detected functional groups within the 3385 genes potentially affected by mutations (nonzero mutational variance) compared to all 11,604 genes contained on the microarray. Of the 3385 variable genes, 2783 were identified as unique D. melanogaster homologs, of which 2604 were assigned a gene ID using DAVID 6.7 (Huang et al. 2009). Of the 9500 genes contained on the microarray that were assigned a unique D. melanogaster gene ID from FlyBase genes, 8978 were recognized and assigned an ID in DAVID. Therefore, we were able to apply the enrichment analysis to 2604 genes of interest (i.e., mutationally variable candidates for functional groups) against the reference background containing 8978 genes.
We did not consider enrichment on Cellular Component GO domain for two reasons. First, our goal in this paper was to identify functional modules for which we had the greatest expectation of correspondence to pleiotropic variational modules, and while both Biological Process and Molecular Function domains are likely to capture multiple functions of a single gene (He and Zhang 2006; Su et al. 2010), colocalization of gene products has a less direct link to definitions of pleiotropy. Second, gene groups identified through the Cellular Component GO domain might be more likely to be affected by Pearson’s rule of neighborhood, where geographically closer elements are more likely to be correlated than distant elements (Whiteley and Pearson 1899), which is a known source of bias in interpretations of coincidence of functional and variational modules at the phenotypic level (Mitteroecker 2009). Therefore, we only looked for enrichment in Biological Process and Molecular Function in the GO terms, and analyzed the list for GO terms and KEGG pathways with the “Functional Annotation Chart.”
Functional groups defined by GO terms typically contain a lot of genes in common with other groups because of parent–child relationships between GO terms, because the same set of genes can belong to different types of functional groups (i.e., a Molecular Function and a Biological Process), or because similar biological processes can be categorized in different regions of the GO. This is a commonly recognized problem for using analyses of GO terms to identify pleiotropic (multifunctional) genes. Most methods developed to deal with the lack of functional uniqueness or independence of GO terms use indices measuring the semantic similarity between terms that share common ancestors or children [see the comparison of methods in Harispe et al. (2014)], and more rarely the similarity between terms using their probability of sharing genes (Pritykin et al. 2015). Here, we limited gene sharing among our GO term-defined functional groups to maximize our chances of detecting a difference in pleiotropic covariance within vs. among functional groups. We achieved this using the following method. We started by selecting the group with the lowest enrichment P-value when testing mutational variance enrichment (GO term: group Cuticle, P = 3.3e−11, Table 1). Retaining this group with the lowest enrichment P-value, we then sequentially compared all groups with increasing enrichment P-values, retaining groups only if they shared < 10% of their genes with any of the previously retained (i.e., lower enrichment P-value) groups. Fourteen GO terms with low levels of gene composition overlap were selected using this process including seven molecular functions and seven biological processes, spanning structural molecule activities (two groups), metabolic processes (three groups), developmental processes (two groups), responses to stimulus (two groups), or binding (two groups) (Table 1). However, one of the 14 identified groups failed a randomization test to determine if the observed mutational covariance was above the random expectation when the mutational covariance among traits was destroyed (see Supplemental Information in File S1). We removed this group from further analysis. We further identified two independent significantly enriched KEGG pathways, but they identified the same putative functional modules as identified by the GO term enrichment analysis, and we only report GO term results here (see Supplemental Information in File S1).
We tested whether the 434 genes assigned to the 13 functional groups were a representative sample of the mutational and standing genetic variance found in the entire set of mutationally variable genes. For each functional group, we used Wilcoxon signed-rank tests to compare the mutational and standing genetic variance of the genes contained within that group to 1000 sets of the same number of genes, randomly chosen from the 2951 genes with nonzero mutational variance that were not assigned to any of our 13 studied functional groups.
Mutational and standing genetic covariance within functional groups
We determined the genetic covariance between each pair of expression traits using bivariate models within each functional group of genes in both the M and G lines separately. For each pair of genes within a functional group, we implemented the bivariate form of the model (1):
| (2) |
where and are design matrices for the line and replicate within-line random effects. We modeled the covariance structure among traits at the line () and replicate () levels, using unstructured 2 × 2 covariance matrices, and was a diagonal matrix containing the residual (among-probe) variances for each trait. The segregating factor and a probe-level fixed effect were included as before for the M line and G line analyses, respectively.
For each functional group, we used the among-Line univariate variance component (model 1) and covariance component (model 2) from the respective M and G lines to construct mutational (M) and genetic (G) variance–covariance matrices. Constructing the M and G matrices enabled us to test for the presence of shared genetic variance in any multivariate trait combination (not just pairwise combinations) in the most efficient fashion, by focusing on the presence of mutational or genetic variance in the major axes represented by the dominant eigenvectors of the respective matrices of each functional group.
Our goal was to detect whether the levels of mutational and standing genetic covariance found in our candidate functional groups were specific to that function, and exceeded the typical levels of mutational and standing genetic covariance found in traits that were not identified by the enrichment analysis as sharing the same function. To achieve this, we compared the mutational or genetic variance in the dominant eigenvectors of a matrix (mmax and m2 for mutational variance, and gmax and g2 for standing genetic variance; Table 2) of a given functional group, to the observed eigenvalues of a distribution of eigenvalues that represented biological variation characterized by the background level of mutational or genetic covariance among random sets of genes. We first created 150 data sets of 73 genes that were sampled at random from the subset of 2951 genes that showed mutational variance but were not assigned to any of the 13 functional groups under consideration. We did not know the functions of the genes included in these data sets. Thus, some of the genes included in each data set may share a common function, but it was unlikely that they all had the same function. Moreover, none of the genes included in those data sets were assigned to any of the GO terms in Table 1. Sampling was done with replacement, so that some genes were included in several of the 150 data sets. For each of the 150 created data sets, we estimated Mbb and Gbb covariance matrices (Table 2) by applying the univariate (model 1) and bivariate (model 2) mixed models, as described above. To obtain Mbb and Gbb covariance matrices of a size that matched each functional group (i.e., the number of genes in each functional group, Table 1), we randomly selected the number of genes required for each functional group from the 73 genes in each data set. Each draw of the appropriate number of genes was sampled from the set of 73 genes with replacement, creating random overlap between biological simulations of the 13 functional groups. The functional groups of the same size (groups Chitin and Sensory, and groups Heme and Cuticle) were compared to the same sample of biological background genes. A small number (seven) of the 2 × 150 = 300 Mbb and Gbb covariance matrices estimated in this fashion returned extreme outlying eigenvalues (> 1010) after diagonalization, and we removed these data sets, resulting in 143 estimates of the biological background covariance in the M and G lines for each functional group. Because several functional groups had average univariate genetic variances that were significantly higher than the genes that were not selected in any functional groups (Table 1), we could not directly compare the shared genetic variance contained in those functional groups with the biological controls. Instead, we compared the proportion of variance represented by each eigenvector, calculated by dividing each eigenvalue by the trace of the matrix, to the 95% C.I. of the proportion of variance for each vector obtained from the biological controls. This comparison was used to determine whether the genetic covariance found within functional groups was larger than among background (random) genes, independent of the level of genetic variance displayed by each gene.
Table 2. Definitions of the used mathematical terms.
| Name | Quantifies | Number of data sets/permutations | Description |
|---|---|---|---|
| Terms describing experimental variances | |||
| mmax or gmaxm2 or g2 | Eigenvectors of most (max) and second most (2) mutational (m) and genetic (g) variance | Estimated by diagonalizing the respective M or G matrix | |
| M26 G26 | Mutational (M) or standing genetic (G) covariance among functional groups | Phenotypic scores were estimated for individuals for the trait combinations described by the first and second major axes of within-function mutational or standing genetic variance for each of the 13 functional groups (i.e., 26 traits). These scores were then analyzed as per observed traits to estimate the 26 trait variance covariance matrix, which was then diagonalized. | |
| Terms used to build distributions used in estimating C.I.s | |||
| Mse Gse | Sampling error within the mutational (M) or standing genetic (G) data sets | 50 | Data shuffled among lines, disrupting the mutational or genetic covariances between traits while retaining the observed levels of variance for each individual gene expression trait |
| Mbb Gbb | Biological background levels of mutational (M) or standing genetic (G) covariance among genes for which there is no a priori expectation of functional relatedness | 143 | Uses random sets of genes taken from the list of genes that were not assigned to one of the 14 functional groups. Each of the 117 data sets was then subsampled to the same number of genes as in the respective functional group. |
| M26se G26se | Sampling error within the among functional group mutational (M26) or standing genetic (G26) covariance matrices | 50 | Data shuffled among lines, disrupting the mutational or genetic covariances between traits while retaining the observed levels of variance for each composite trait present in M26 and G26 |
Selection on pleiotropic effects within functional groups
One of the primary evolutionary advantages of modularity has been predicted to be the mitigation of the adverse effects of deleterious mutation through restricting the extent of their pleiotropic effects. We would therefore predict that selection on the genetic variance within functional groups should be weaker than selection among groups. We tested this prediction using two approaches. First, we estimated s, the selection coefficient, from our estimates of the mutational variance and standing genetic variance for gene expression, using: (Barton 1990; Houle et al. 1996). Specifically, we calculated s for the multivariate traits mmax and m2 using:
| (3) |
where was the eigenvalue of the nth eigenvector of M divided by twice the number of generations to give the per-generation input of variance (Lynch and Walsh 1998) and represents the projection of the normalized vector through the standing genetic space of G. To return s to the original log10 scale, we multiplied it by the ratio of phenotypic variances of in the G and M lines. To do this, we used the linear equation of each of the eigenvectors to generate phenotypic scores in both M and G lines. We kept the probe level of information by applying the linear equation of the eigenvectors five times; each of the five times, we randomly chose one of the five probes that targeted each trait (without replacement). We analyzed these phenotypic trait scores for the index with model (1) to estimate the phenotypic variance associated with each trait combination in the M and G lines. We repeated the same analyses for the groups of genes in the biological background. In three (out of 26) estimates for the two vectors in the observed data for the 13 functional groups, the calculation of s returned negative values, as fell within the null space of the estimated G matrix. In these three cases, we bent G using nearPD (library Matrix, R 3.1.2) to obtain the closest positive definite matrix.
To directly estimate the amount of sampling error associated with the estimates of mutational and genetic variance in s, it is necessary to take into account that the estimation of s can be inflated as a result of restricted maximum likelihood enforcing positive-definite constraints. To account for this upward bias, we applied equation (3) to random pairs of the 50 estimates of Mse and Gse for each functional group representing the amount of sampling error generated by our experimental design for a given module size (see Supplemental Information in File S1 and Table 2). We then used these 50 estimates of s representing sampling error to remove the magnitude of the inflating effect in our observed estimate of s by taking the difference between the observed estimate and the median of these 50 estimates of sampling error (McGuigan et al. 2014a).
To estimate the 95% C.I.s of s based on the biological background, we used the difference between the 143 observed biological background estimates and the corresponding median sampling error estimate obtained for each function-specific group. Since the univariate estimates of mutational and genetic variance in the functional groups were on average higher than in genes included in the biological background (Table 1), the C.I.s for the biological background could be biased if the observed ratio of tr(M)/tr(G) for a group differs from the set of 143 biological background estimates. For two groups (Chorion and Cuticle), the observed tr(M)/tr(G) was higher than the biological background. In both cases, the lower and upper 95% C.I.s for these estimates are therefore likely to be smaller in magnitude than would occur if the traces of the observed matrices matched the traces of the matrices for the biological background (as shown by the negative lower confidence interval obtained in Chorion). Therefore, for those two groups, a lower observed estimate of selection than the C.I. would be a conservative result.
As described above, estimates of s are only informative of selection operating on the major axes of mutation, but selection may act instead on other dimensions. We therefore took a second approach to test the hypothesis that mutations acting within a functional group were under weaker selection than mutations affecting functionally unrelated sets of traits. We determined the level of overlap between M and G matrices using Krzanowski’s common subspaces approach (Krzanowski 1979; Aguirre et al. 2014):
| (4) |
where and contain the two first eigenvectors of M and G as columns, respectively. The sum of the eigenvalues of the resultant matrix then ranges between 0 (complete orthogonality of the subspaces) and 2 (coincident subspaces). If selection is weak, G is not predicted to have diverged from the structure generated by mutation, and a big overlap between M and G subspaces, and thus a higher S, is expected. This approach to estimating selection does not assume that it acts directly on the eigenvectors of M, but rather on any combination of expression traits contained within the first two dimensions of M or G. Note that the upper and lower 95% random values of the sum of the eigenvalues of decrease with the size of the groups. Since we only considered the two first axes whatever the size of the group considered, it is expected that the proportion of the common subspace shared between two matrices in those two axes will be lower when those axes represent a smaller proportion of the total subspace.
Data availability
Data are archived at the NCBI’s GEO (N lines: GSE49815 and S lines: GSE54777).
Results
Mutational and standing genetic variance in genes included in functional groups
The enrichment analysis of the 3385 genes showing nonzero mutational variance identified 13 independent candidate GO terms most likely to harbor function-specific mutational covariance. Enrichment for one term (Cuticle) passed the 5% FDR threshold. A total of 434 genes were assigned to the 13 functional groups, while the remaining 2951 genes with nonzero mutational variance had functions that did not fit our criteria to belong to candidate functions. Even though the enrichment analyses did not take into account the level of mutational or genetic variance, the median standing genetic variance in 5 of the 13 functional groups was significantly higher than expected from the other genes with nonzero mutational variance that were not assigned to our candidate functional groups (Table 1). Overall, the genes assigned to the 13 functional groups had significantly higher mutational variance (median = 0.0013 vs. 0.0011, median Wilcoxon W for the 1000 tests = 103,544, median P = 0.012) and standing genetic variance (median = 0.4469 vs. 0.3841, median Wilcoxon W for the 1000 tests = 104,144, median P = 0.006) than the genes not assigned to our functional groups (Table 1).
Mutational and standing genetic covariance within functional groups
We found little support for functionally related genes being universally affected by pleiotropic mutations. The functional group “structural constituents of chorion” was the only one of the 13 functional groups in which all genes assigned to that function had mutational variance above zero (Table 1, all eight genes from the DAVID term had above-zero mutational variance). Our enrichment analysis further showed that the functional group Chorion was the only GO term of the entire DAVID 6.7 repository for which all genes showed above-zero mutational variance.
We next tested whether functional modules were enriched in function-specific mutational covariance by determining if the observed mutational covariance within a functional module exceeded that of the biological background based on random, size-matched, sets of genes whose functions were not known. Only three functional groups showed levels of mutational covariance above that found among random sets of genes (captured by Mbb) (Pro-DNA, Heme, and Cuticle: Table 3). Furthermore, we found one functional group (NeuroT) that showed lower levels of mutational covariance than random groups of genes of the same size that did not belong to a common function (Table 3). Therefore, it appears that genes within a functional module are not typically affected by pleiotropic mutations to a greater extent than functionally unrelated sets of genes (Table 3).
Table 3. Proportion of variance of the first and second eigenvectors of M and G and measures of selection within functional groups.
| Group | λmmax (C.I.) | λm2 (C.I.) | λgmax (C.I.) | λg2 (C.I.) | Krzanowski S (C.I.) | smmax (C.I.) | sm2 (C.I.) | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Chorion | 0.67 | (0.42; 0.88) | 0.37 | (0.18; 0.45) | 0.69 | *** | (0.28; 0.56) | 0.50 | *** | (0.18; 0.35) | 0.91 | (0.17; 1.31) | 1.306 | *** | (0.002; 0.177) | 0.012 | (−0.010; 0.070) | ||||
| Amino A | 0.71 | (0.41; 0.79) | 0.30 | (0.17; 0.48) | 0.42 | (0.26; 0.55) | 0.25 | (0.18; 0.33) | 0.51 | (0.14; 1.18) | 0.011 | (0.005; 0.369) | 0.010 | (−0.006; 0.089) | |||||||
| NeuroT | 0.58 | (0.35; 0.75) | 0.17 | *** | (0.18; 0.43) | 0.30 | (0.22; 0.43) | 0.22 | (0.17; 0.28) | 0.32 | (0.08; 0.94) | 0.022 | (0.005; 0.176) | 0.012 | (−0.007; 0.195) | ||||||
| GT | 0.44 | (0.35; 0.68) | 0.39 | (0.18; 0.43) | 0.25 | (0.22; 0.41) | 0.20 | (0.16; 0.27) | 0.57 | (0.08; 0.87) | 0.028 | (0.005; 0.180) | 0.022 | (−0.009; 0.075) | |||||||
| Pro-DNA | 0.66 | (0.34; 0.73) | 0.42 | * | (0.16; 0.40) | 0.34 | (0.21; 0.38) | 0.16 | (0.15; 0.26) | 0.15 | (0.07; 0.78) | 0.033 | (0.005; 0.139) | 0.031 | (−0.010; 0.096) | ||||||
| Bacterium | 0.63 | (0.31; 0.63) | 0.23 | (0.18; 0.37) | 0.30 | (0.18; 0.32) | 0.22 | (0.14; 0.22) | 0.84 | *** | (0.05; 0.61) | 0.042 | (0.008; 0.279) | 0.013 | (−0.012; 0.128) | ||||||
| Chitin | 0.56 | (0.32; 0.60) | 0.33 | (0.17; 0.36) | 0.22 | (0.18; 0.32) | 0.17 | (0.14; 0.22) | 0.27 | (0.04; 0.59) | 0.015 | (0.009; 0.218) | 0.023 | (−0.003; 0.126) | |||||||
| Sensory | 0.49 | (0.32; 0.60) | 0.23 | (0.17; 0.36) | 0.21 | (0.18; 0.32) | 0.19 | (0.14; 0.22) | 0.14 | (0.04; 0.59) | 0.024 | (0.009; 0.218) | 0.019 | (−0.003; 0.126) | |||||||
| Ion Tsp | 0.47 | (0.30; 0.60) | 0.28 | (0.17; 0.36) | 0.23 | (0.17; 0.29) | 0.18 | (0.13; 0.20) | 0.31 | (0.05; 0.55) | 0.062 | (0.012; 0.417) | 0.025 | (−0.019; 0.130) | |||||||
| Heme | 0.46 | (0.31; 0.57) | 0.40 | ** | (0.18; 0.33) | 0.17 | (0.15; 0.27) | 0.13 | (0.13; 0.18) | 0.50 | * | (0.04; 0.47) | 0.051 | (0.016; 0.443) | 0.022 | (−0.019; 0.185) | |||||
| Cuticle | 0.63 | ** | (0.31; 0.57) | 0.22 | (0.18; 0.33) | 0.23 | (0.15; 0.27) | 0.14 | (0.13; 0.18) | 0.61 | *** | (0.04; 0.47) | 0.014 | * | (0.016; 0.443) | 0.021 | (−0.019; 0.185) | ||||
| Cell fate | 0.46 | (0.30; 0.52) | 0.27 | (0.16; 0.32) | 0.19 | (0.15; 0.26) | 0.15 | (0.12; 0.18) | 0.25 | (0.04; 0.41) | 0.020 | (0.018; 0.635) | 0.037 | (−0.017; 0.238) | |||||||
| Endopep | 0.31 | (0.31; 0.52) | 0.22 | (0.17; 0.32) | 0.16 | (0.15; 0.25) | 0.13 | (0.11; 0.18) | 0.31 | (0.04; 0.38) | 0.016 | (0.012; 0.591) | 0.044 | (−0.037; 0.111] | |||||||
Within each functional group, Krzanowski S compares the two-dimensional subspaces defined by mmax and m2 in the space of M and G. C.I.s correspond to the 2.5th and 97.5th percentile eigenvalues, as a proportion, observed for the 123 Mbb and Gbb. Significance levels are: * P > 95%, ** P > 99%, and *** P is outside confidence intervals. C.I.s for two sets of two groups (Chitin and Sensory, and Heme and Cuticle) were the same as groups containing the same number of genes. Note that because there are some negative eigenvalues, the denominator used in these proportions, namely the trace, can be lower than the amount of variance found in the first two axes of M or G, resulting in sums of proportions > 1 in groups Chorion, Amino A, and Pro-DNA. Ion Tsp, .
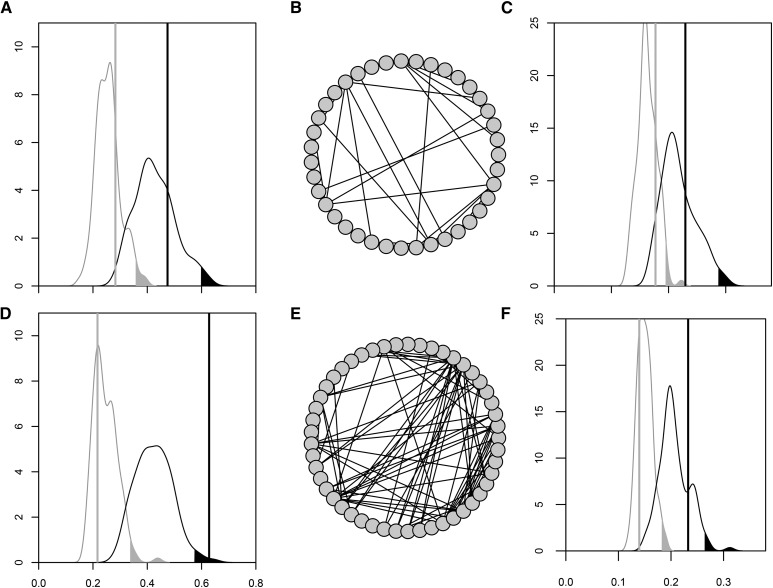
To illustrate the variation in mutational pleiotropy represented by our functional groups, the mutational covariance structure of two groups of similar size [39 and 49 genes for groups Ion Tsp and Cuticle, respectively (Table 1)] is graphically displayed in Figure 1. Most functional groups were similar to group Ion Tsp, where the mutational pleiotropy found in the first two axes did not exceed the level of pleiotropy found in random groups of genes of the same size (Figure 1A and Table 3), thus showing no sign for function-specific mutational covariance. In contrast, group Cuticle was an example of where mutational covariance exceeded the background level for mmax (Figure 1D and Table 3). The difference in mutational covariance between groups Ion Tsp and Cuticle is clearly illustrated by the difference in the frequency of pairwise mutational correlations > 0.99 within each of these functionally defined modules (Figure 1, B and E).
Figure 1.
Function-specific genetic variance in two groups of similar sizes: Ion Tsp (A–C) and Cuticle (D–F). (A and D) Proportion of the mutational variance contained in mmax and m2 against the distribution of the proportion of mutational variance in the nonfunction-specific biological background (Mbb, Table 2). mmax and m2 are represented by black and gray vertical lines, respectively. The density functions of the unspecific biological variance are represented for bbmmax (black) and bbm2 (gray) with a Gaussian smoothing kernel. The shaded area corresponds to the highest 2.5% of the distribution. (B and E) Illustration of how many strong links among pairwise traits there are within a functional group. Each circle represents a gene and the black lines represent mutational correlations between pairs of genes > 0.99 (this cutoff was chosen for the clarity of the illustration and has no role in our analyses or interpretation). (C and F) Plot as for (B and F) except graphing genetic rather than mutational variances.
Function-specific standing genetic covariance was even less common than function-specific mutational covariance. Only functional group Chorion showed higher levels of standing genetic covariance (on two axes) within the functional groups than what was seen among random sets of the same number of genes (captured by Gbb) (Table 3). In all other groups, the level of function-specific standing genetic covariance matched the typical levels of standing genetic covariance found in the biological background, as illustrated with groups Ion Tsp and Cuticle on Figure 1, C and F.
Stabilizing selection on mutational pleiotropic effects within functional modules
To test whether mutations with pleiotropic effects on functionally related sets of traits were less deleterious than mutations with pleiotropic effects on sets of random traits, we first estimated the selection coefficients (s) for both mmax and m2 for each of the 13 functional groups. One of the three s obtained after bending G (functional group Chorion) was extreme (1.306) as a consequence of the very small genetic variance in the direction of mmax; without groups with similar estimates of selection, we must consider this value as an outlier. The 25 remaining s values for mmax and m2 ranged from 0.010 to 0.062, with a median s of 0.024 and 0.022, respectively (Table 3). While these selection estimates are slightly stronger than the median reported for random sets of five expression traits (0.016; McGuigan et al. 2014a), the within functional module s was within the range of what was typically observed for the same number of randomly chosen genes (i.e., estimates fall within the 95% C.I. estimated from Gbb and Mbb; Table 3). Only one functional group, Cuticle, showed the predicted weaker within-module selection for mmax (Table 3).
Using an alternate measure of selection, which did not restrict selection to occur only along mmax or m2, three groups were revealed that showed a higher common subspace than expected (Table 3), consistent with weaker selection within these functional groups than among random sets of genes. Importantly, two of those three groups showed levels of mutational covariance higher than the 95% C.I. interval of the mutational covariance obtained in the biological background (Table 3), and the third group exhibited mutational variance close to the upper C.I. (bacterium: λmmax 0.630, upper C.I. 0.631), indicating that considerable mutational covariance was generated, which was not subsequently removed by selection.
Stabilizing selection on mutational pleiotropic effects among functional modules
Overall, mutational and genetic covariance was not typically greater than observed in the biological background, suggesting that much of the mutational covariance was not restricted to functional modules. To investigate this observation further, we estimated among-function covariance contained in the 26 trait combinations with the greatest within-function covariance (i.e., mmax and m2, or gmax and g2, within each of the 13 functional groups). This approach of reducing the within-module complexity to allow us to explore the among-module relationships is analogous to the eigengene network analysis approach developed by Langfelder and Horvath (2007).
We used the linear equations of the first two eigenvectors of M and G of each of the 13 functional groups to generate phenotypic scores for these new index traits. We applied the same univariate (model 1) and bivariate (model 2) mixed models to obtain two 26 × 26 covariance matrices (M26 and G26, Table 2), which contained any mutational or genetic covariance between functional groups that occurred among the major axes of variance within functional groups. We repeated this procedure on shuffled data to generate 50 M26se and G26se (Table 2) matrices representing sampling error to enable an assessment of the significance of the eigenvalues of M26 and G26 and the extent of covariance among functional groups (see details on how we obtained randomized distributions in the Supplemental Information in File S1 and McGuigan et al. 2014b).
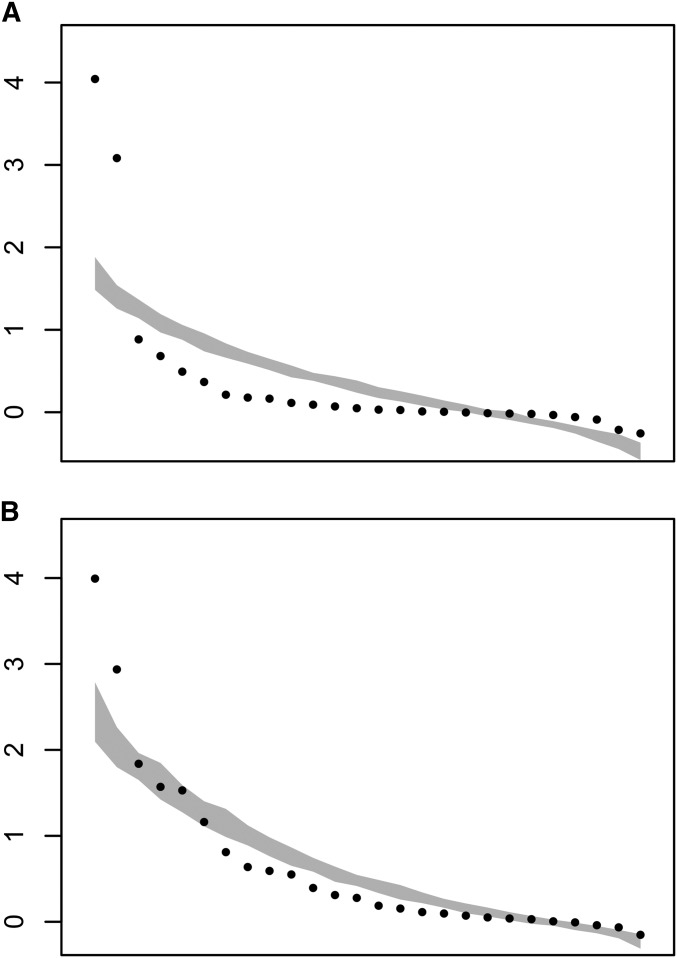
The first two eigenvalues resulting from the diagonalization of M26 exceeded the magnitude expected solely from sampling error (Figure 2A), indicating that among-functional group covariance was greater than expected from sampling error alone. These first two of the 26 eigenvalues of M26 represented 72.4% of the total mutational variance contained in the 26 traits. Therefore, most of the mutational covariance found within functional groups was also shared among the functional groups; as we explicitly limited the opportunity for the same gene to belong to different functional groups, this observation reveals strong mutational pleiotropic links among functions. For G26, again only the first two eigenvectors had eigenvalues larger than expected from sampling error (Figure 2B), but in this case only represented 40.1% of the variance included in G26. Therefore, there appears to be less pleiotropic covariance among functional groups in the standing genetic variance than that generated when new mutations first arise in the absence of selection.
Figure 2.
Spectral distribution of the mutational variance contained in M26 (A) and G26 (B) (see Table 2). The dots are the variances associated with each eigenvector in a descending order. The gray shaded area represents the 95% C.I. of the 50 simulations estimating sampling error (se).
Hine et al. (Emma Hine, Daniel E. Runcie, Katrina McGuigan, and Mark W. Blows, unpublished results) recently applied a high-dimensional Bayesian sparse factor (BSF: Runcie and Mukherjee 2013) analysis to estimate the mutational covariance across all 3385 genes in our set of 41 M lines and here we compare this broad-scale distribution of variance to our functional groups to gain further insight into the distribution of variance across traits. The BSF model identified 21 factors that displayed significant mutational heritability and explained 46% of the total estimated mutational variance. These 21 factors combined had significant contributions from 1263 of the 3385 genes. Figure 3 shows how the genes contained in each functional group analyzed here contributed significantly (average error rate < 0.005) to each high-dimensional factor. All of the 13 functional groups contained at least one gene that was significantly associated with at least one of the 21 high-dimensional factors; the 21 variational modules identified from the BSF model were typically associated with more than one functional group. This comparison indicates that genes within the functional groups are almost always part of a wider variational module, with much of the mutational variance within functional groups shared across groups within much wider variational modules, as suggested by the analysis of M26.
Figure 3.
Contribution of the genes contained in the 13 gene ontology terms functional groups to the 19 heritable phenotypic common factors identified in a Bayesian sparse factor (BSF) analysis (Hine et al., unpublished results). Each line represents a functional module (see Table 1) and each column a BSF. The number of genes within each functional module that also had a significant contribution to the BSF (5% false discovery rate) is listed, with shading from light to dark indicating few to many genes.
As modularity is expected to reduce the strength of selection acting within functional groups, the trait combinations highlighted as displaying strong covariance among functional groups are expected to be under particularly strong selection. We estimated selection against the first two axes of M26 by estimating the Krzanowski S subspace comparison of the two-dimensional subspaces of M26 and M26 in the G lines. Surprisingly, the sum of the eigenvalues of the S matrix was 1.11, considerably higher than the average S found within functional modules, suggesting that selection has had little effect on the mutational covariance that is originally widespread among functional groups.
Discussion
A genotype–phenotype map in which pleiotropic effects are relatively restricted to groups of functionally integrated traits has been predicted to be evolutionarily beneficial (Wagner 1996). Here, we provide a test of whether variational (pleiotropic) and functional modules coincide, and whether functional relationships among genes influence the strength of stabilizing selection acting on new mutations. Enrichment analyses assigned 434 mutationally variable genes to 13 independent candidate Biological Processes or Molecular Functions that also formed variational modules. In general, expressional levels of groups of genes related by function (GO terms) rarely had higher covariance than genes assigned to groups at random. Similarly, mutations jointly affecting functionally related genes were rarely under weaker selection than mutations affecting random sets of genes. Our analyses revealed widespread pleiotropic effects as we found consistent covariance among functionally unrelated traits (biological background) and we observed that pleiotropic effects spanning functional groups generate much of the mutational variance within functional groups. We now consider both the implications of these results and potential caveats on our interpretation.
Pleiotropy and selection on gene expression traits
We found weak evidence that variational modules were restricted to functional modules; in only four of 13 functional groups did covariance within functional groups exceed the background level of either mutational or genetic covariance found among random, size-matched sets of genes. Furthermore, most (72%) of the mutational covariance established within functional groups was shared among the functional groups. Again, consistent with previous analyses of these data (McGuigan et al. 2014a) and studies in other taxa (Denver et al. 2005; Lemos et al. 2005; Rifkin et al. 2005), we observed that expression traits were generally under relatively strong stabilizing (purifying) selection that typically matched levels of selection reported for life history traits (Houle et al. 1996). However, the strength of selection on mutations affecting traits within a functional group was not typically statistically distinguishable from mutations affecting random groups of genes not associated with a common function; only three of the 13 functional groups exhibited significant signatures of weaker than background stabilizing selection.
To what extent might our results reflect misidentification of functional modules? The lack of support for higher mutational or standing genetic covariance within GO terms might reflect missing or inaccurate information on gene function. GO terms are incomplete descriptions of functional groups (i.e., not all genes involved in that function have necessarily been identified), allowing the potential for strong covariance among randomly chosen genes to reflect undetected functional modules. Further, as many genes are attributed to functional groups without experimental evidence (for example, in the well-studied Arabidopsis thaliana, only 39% of annotated genes have had their function determined by experimental evidence: Rhee and Mutwil 2014), the potential exists for genes to be incorrectly assigned to functional modules (Clark and Radivojac 2011), which would result in the underestimation of covariance within putative functional modules. However, the joint analyses of coexpression and GO terms have successfully identified gene functions in many studies (e.g., Luo et al. 2007; Nayak et al. 2009; Ayroles et al. 2011; Proost and Mutwil 2017). Although we cannot exclude the possibility that current information on functional groups is so poor that functional and variational modules will not coincide, it seems likely that pleiotropy may generate covariance among functions in an unpredictable manner to a substantial extent.
Functional groups within wider variational modules
While pleiotropy clearly exists within functional groups, it is the widespread and extensive nature of pleiotropy among the GO term-defined functional groups, and among random sets of expression traits in general (McGuigan et al. 2014b; Blows et al. 2015), that is the overriding feature of the mutational and standing genetic covariance in these expression traits. The 21 variational modules of gene expression uncovered by the high-dimensional BSF model applied by Hine et al. (unpublished results) provided a very useful framework within which to interpret the mutational covariance among functional groups. At one extreme, genes from functional group NeuroT displayed within-group mutational covariance that was lower than in the biological background and only three of its genes were independently part of a wider variational module, indicating that mutations in these genes had highly specific effects. At the other extreme, genes from functional group Endopep had genes contributing to 14 of the 21 high-dimensional variational modules. The comparison of our analyses of functional group Cuticle to the 21 BSFs is of particular interest. Functional group “structural constituent of cuticle” was the only group to meet all the expectations for correspondence between variational and functional modules: (i) this was the only functional group to show significant enrichment after FDR correction; (ii) mutational variance in mmax was higher than in the biological background; and (iii) there was weaker selection on mutational variance than expected from the biological background. Group Cuticle had 19 (over one-third) genes significantly contributing to the second common factor from the Bayesian analysis. This second factor spanned multiple functions as 11 of our 13 functional groups had genes significantly contributing to it. Thus, what appeared in group Cuticle as aligned functional and variational modularity may reflect the contribution of a functional module to a larger variational module.
The sizes of the variational modules in gene expression were considerably larger than the relatively small number of genes contained by the functional groups explored here. A minimum average variational module size to explain the extent of mutational covariance among small random sets of these traits was predicted by McGuigan et al. (2014b) to be 70 genes, but it was also suggested that some variational modules were likely to be much larger than this. Analysis of the transcriptome-wide covariance structure of the standing genetic variation in the G lines indicated the presence of one variation module that affected a very large number of expression traits (Blows et al. 2015). Here, the analysis of M26 was also consistent with the existence of large variational modules.
How biologically specific a functional module is, and whether its function is essential or localized, might also help explain some of our observations. A first step toward accounting for the different roles of our 13 functional groups is to consider the structure of GO. Analyses of GO terms as directed acyclic graphs (DAGs) (or gene or protein interaction networks more generally) have identified common topological features, and highlighted the functional or evolutionary significance of certain types of nodes (genes or gene products) or edges (interactions) [reviewed in Hu et al. (2016) and Zhang et al. (2016)]. The 13 functional groups (individual GO terms) considered here varied considerably in the topology of their networks (DAGs), including in their degree (the number of other GO terms to which they relate, Table 1). Under the hypothesis that selection on function drives evolution of pleiotropy to match functional groupings, GO terms embedded within broader functional networks (i.e., with high degree) might be expected to have reduced within-term covariance compared to GO terms with more specific functions (low degree). However, the estimated Spearman’s correlation between degree and the proportion of variance associated with each of the first two axes of mutational or standing genetic variance was mainly not in the predicted direction (mmax: ρ = −0.20; m2: ρ = 0.04; gmax: ρ = 0.09; and g2: ρ = 0.02). These correlations were not statistically supported as distinct from zero (mmax: P = 0.50; m2: P = 0.90; gmax: P = 0.78; and g2: P = 0.94), but it should be noted that we had very low power given a sample size of 13. Thus, whether or not the studied GO term belonged to a broader functional module might help explain our results, but analysis of more functional modules with a range of degrees will be needed to test this robustly. It is important to remember that the effects of the genes identified in our functional groups are not restricted to this group.
Indirect evidence for the embedding of a number of functional groups within larger variational modules comes from several published studies. In humans, Pickrell et al. (2016) combined genome-wide association studies on 42 traits or diseases and identified 341 loci that associated with multiple functionally unrelated traits, highlighting that pleiotropy spanned multiple functions. When considering clusters of coexpressed genes, Allocco et al. (2004) found that in yeast, pairs of coregulated genes belong to significantly closer GO terms than randomly chosen pairs of genes. However, many coexpressed and coregulated genes belonged to very distant GO terms. Thus, although clusters of coexpression between unstudied genes and genes of known biological function have proven a powerful tool for the identification of putative function of unknown genes and of candidate genes for biological traits or functions of interest (e.g., Luo et al. 2007; Nayak et al. 2009; Ayroles et al. 2011; Proost and Mutwil 2017), there is nonetheless considerable evidence that pleiotropic variation is not strongly restricted to occur only within functional groups.
Selection on pleiotropic mutations
One of the key assumptions of theoretical predictions that variational modules should evolve to correspond to functional modules is that pleiotropic effects across functions will be associated with greater loss of fitness than pleiotropic effects within functions. Evidence for this has been equivocal, with some studies reporting that more highly connected genes, putatively highly pleiotropic genes functioning as hubs between different functional groups, are under stronger selection than genes with more functionally limited interactions (Jeong et al. 2001; Fraser et al. 2002; Krylov et al. 2003; Carter et al. 2004; Han et al. 2004; Butland et al. 2005; Zhao et al. 2007; Lin et al. 2015; Pritykin et al. 2015), while other studies have failed to detect any evidence that the strength of selection scales positively with the extent of pleiotropy, essentiality, or network position (Pál and Hurst 2003; Hahn et al. 2004; Salathé et al. 2006; Jovelin and Phillips 2009; Kopp and McIntyre 2012). Here, we also obtained mixed support for this prediction. We observed the predicated significantly weaker selection within functional groups than among random sets of genes for only 3 of the 13 functional groups. Again, variation among functional groups in their network topology could account for variation in the strength of selection acting on functional groups, with biologically more specific groups expected to more closely match this prediction. The relationship between degree and selection was in the predicted direction for two of our indices of selection (sm2: ρ = 0.38, P = 0.20 and Krzanowski S: ρ = −0.31, P = 0.30), but not for the other (smax: ρ = −0.15, P = 0.62), and in no case were we able to support a significant relationship between selection and degree. Surprisingly, our results even suggested that selection against pleiotropic mutations affecting many functions may be lower than the selection observed within functional modules. The greater similarity of the mutational and genetic subspaces that represented the among functional group covariance, compared to within functional group covariance, is inconsistent with the evolution of modularity in response to deleterious pleiotropic mutation.
Collectively, our results confirm that while focusing on individual GO terms as functional modules can to some extent predict variational modularity, it will miss many important biological connections among functional modules. Considering higher-order interactions generated by broader variational modules spanning various functions will be a necessary part of understanding the evolution of genetic covariance.
Supplementary Material
Supplemental material is available online at www.genetics.org/lookup/suppl/doi:10.1534/genetics.118.300776/-/DC1.
Acknowledgments
We thank John Stinchcombe for helpful discussions; J. Thompson, C. Oesch-Lawson, D. Petfield, O. Sissa-Zubiate, F. Frentiu, and Y.H. Ye for help with the MA experiment and data collection; and Gabriel Marroig and an anonymous reviewer for their very helpful comments on the manuscript. This work was funded by the Australian Research Council and an Agreenskills + fellowship to J.M.C.
Footnotes
Communicating editor: J. Wolf
Literature Cited
- Aguirre J. D., Hine E., McGuigan K., Blows M. W., 2014. Comparing G: multivariate analysis of genetic variation in multiple populations. Heredity 112: 21–29. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Allen S. L., Bonduriansky R., Chenoweth S. F., 2013. The genomic distribution of sex-biased genes in Drosophila serrata: X chromosome demasculinization, feminization, and hyperexpression in both sexes. Genome Biol. Evol. 5: 1986–1994. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Allocco D. J., Kohane I. S., Butte A. J., 2004. Quantifying the relationship between co-expression, co-regulation and gene function. BMC Bioinformatics 5: 18. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ashburner M., Ball C. A., Blake J. A., Botstein D., Butler H., et al. , 2000. Gene ontology: tool for the unification of biology. Nat. Genet. 25: 25–29. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ayroles J. F., Carbone M. A., Stone E. A., Jordan K. W., Lyman R. F., et al. , 2009. Systems genetics of complex traits in Drosophila melanogaster. Nat. Genet. 41: 299–307. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ayroles J. F., Laflamme B. A., Stone E. A., Wolfner M. F., Mackay T. F. C., 2011. Functional genome annotation of Drosophila seminal fluid proteins using transcriptional genetic networks. Genet. Res. 93: 387–395. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Barrett T., Troup D. B., Wilhite S. E., Ledoux P., Evangelista C., et al. , 2011. NCBI GEO: archive for functional genomics data sets-10 years on. Nucleic Acids Res. 39: D1005–D1010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Barton N. H., 1990. Pleiotropic models of quantitative variation. Genetics 124: 773–782. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Blows M. W., Allen S. L., Collet J. M., Chenoweth S. F., McGuigan K., 2015. The phenome-wide distribution of genetic variance. Am. Nat. 186: 15–30. [DOI] [PubMed] [Google Scholar]
- Butland G., Peregrin-Alvarez J. M., Li J., Yang W., Yang X., et al. , 2005. Interaction network containing conserved and essential protein complexes in Escherichia coli. Nature 433: 531–537. [DOI] [PubMed] [Google Scholar]
- Carter S. L., Brechbühler C. M., Griffin M., Bond A. T., 2004. Gene co-expression network topology provides a framework for molecular characterization of cellular state. Bioinformatics 20: 2242–2250. [DOI] [PubMed] [Google Scholar]
- Chen Y. W., Dokholyan N. V., 2006. The coordinated evolution of yeast proteins is constrained by functional modularity. Trends Genet. 22: 416–419. [DOI] [PubMed] [Google Scholar]
- Cheverud J. M., 1984. Quantitative genetics and developmental constraints on evolution by selection. J. Theor. Biol. 110: 155–171. [DOI] [PubMed] [Google Scholar]
- Civelek M., Lusis A. J., 2014. Systems genetics approaches to understand complex traits. Nat. Rev. Genet. 15: 34–48. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Clark W. T., Radivojac P., 2011. Analysis of protein function and its prediction from amino acid sequence. Proteins 79: 2086–2096. [DOI] [PubMed] [Google Scholar]
- Denver D. R., Morris K., Streelman J. T., Kim S. K., Lynch M., et al. , 2005. The transcriptional consequences of mutation and natural selection in Caenorhabditis elegans. Nat. Genet. 37: 544–548. [DOI] [PubMed] [Google Scholar]
- D’haeseleer P., Liang S., Somogyi R., 2000. Genetic network inference: from co-expression clustering to reverse engineering. Bioinformatics 16: 707–726. [DOI] [PubMed] [Google Scholar]
- Edgar R., Domrachev M., Lash A. E., 2002. Gene Expression Omnibus: NCBI gene expression and hybridization array data repository. Nucleic Acids Res. 30: 207–210. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Eisen M. B., Spellman P. T., Brown P. O., Botstein D., 1998. Cluster analysis and display of genome-wide expression patterns. Proc. Natl. Acad. Sci. USA 95: 14863–14868. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fisher R. A., 1930. The Genetical Theory of Natural Selection. Oxford University Press, Oxford. [Google Scholar]
- Fraser H. B., Hirsh A. E., Steinmetz L. M., Scharfe C., Feldman M. W., 2002. Evolutionary rate in the protein interaction network. Science 296: 750–752. [DOI] [PubMed] [Google Scholar]
- Frentiu F. D., Adamski M., McGraw E. A., Blows M. W., Chenoweth S. F., 2009. An expressed sequence tag (EST) library for Drosophila serrata, a model system for sexual selection and climatic adaptation studies. BMC Genomics 10: 40. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gentleman R., Carey V. J., Huber W., Irizarry R. A., Dudoit S. (Editors), 2005. Bioinformatics and Computational Biology Solutions Using R and Bioconductor. Springer-Verlag, New York. [Google Scholar]
- Griswold C. K., 2006. Pleiotropic mutation, modularity and evolvability. Evol. Dev. 8: 81–93. [DOI] [PubMed] [Google Scholar]
- Hahn M. W., Conant G. C., Wagner A., 2004. Molecular evolution in large genetic networks: does connectivity equal constraint? J. Mol. Evol. 58: 203–211. [DOI] [PubMed] [Google Scholar]
- Han J. D. J., Bertin N., Hao T., Goldberg D. S., Berriz G. F., et al. , 2004. Evidence for dynamically organized modularity in the yeast protein-protein interaction network. Nature 430: 88–93. [DOI] [PubMed] [Google Scholar]
- Harispe S., Sánchez D., Ranwez S., Janaqi S., Montmain J., 2014. A framework for unifying ontology-based semantic similarity measures: a study in the biomedical domain. J. Biomed. Inform. 48: 38–53. [DOI] [PubMed] [Google Scholar]
- He X. L., Zhang J. Z., 2006. Toward a molecular understanding of pleiotropy. Genetics 173: 1885–1891. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hill W. G., Zhang X. S., 2012. Assessing pleiotropy and its evolutionary consequences: pleiotropy is not necessarily limited, nor need it hinder the evolution of complexity. Nat. Rev. Genet. 13: 296. [DOI] [PubMed] [Google Scholar]
- Houle D., Morikawa B., Lynch M., 1996. Comparing mutational variabilities. Genetics 143: 1467–1483. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hu J. X., Thomas C. E., Brunak S., 2016. Network biology concepts in complex disease comorbidities. Nat. Rev. Genet. 17: 615–629. [DOI] [PubMed] [Google Scholar]
- Huang D. W., Sherman B. T., Lempicki R. A., 2009. Systematic and integrative analysis of large gene lists using DAVID bioinformatics resources. Nat. Protoc. 4: 44–57. [DOI] [PubMed] [Google Scholar]
- Ideker T., Galitski T., Hood L., 2001. A new approach to decoding life: systems biology. Annu. Rev. Genomics Hum. Genet. 2: 343–372. [DOI] [PubMed] [Google Scholar]
- Jeong H., Mason S. P., Barabasi A. L., Oltvai Z. N., 2001. Lethality and centrality in protein networks. Nature 411: 41–42. [DOI] [PubMed] [Google Scholar]
- Jovelin R., Phillips P. C., 2009. Evolutionary rates and centrality in the yeast gene regulatory network. Genome Biol. 10: R35. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kanehisa M., Goto S., Hattori M., Aoki-Kinoshita K. F., Itoh M., et al. , 2006. From genomics to chemical genomics: new developments in KEGG. Nucleic Acids Res. 34: D354–D357. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kitano H., 2002. Systems biology: a brief overview. Science 295: 1662–1664. [DOI] [PubMed] [Google Scholar]
- Kopp A., McIntyre L. M., 2012. Transcriptional network structure has little effect on the rate of regulatory evolution in yeast. Mol. Biol. Evol. 29: 1899–1905. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kreimer A., Borenstein E., Gophna U., Ruppin E., 2008. The evolution of modularity in bacterial metabolic networks. Proc. Natl. Acad. Sci. USA 105: 6976–6981. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Krylov D. M., Wolf Y. I., Rogozin I. B., Koonin E. V., 2003. Gene loss, protein sequence divergence, gene dispensability, expression level, and interactivity are correlated in eukaryotic evolution. Genome Res. 13: 2229–2235. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Krzanowski W. J., 1979. Between-groups comparison of principal components. J. Am. Stat. Assoc. 74: 703–707. [Google Scholar]
- Langfelder P., Horvath S., 2007. Eigengene networks for studying the relationships between co-expression modules. BMC Syst. Biol. 1: 54. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lemos B., Bettencourt B. R., Meiklejohn C. D., Hartl D. L., 2005. Evolution of proteins and gene expression levels are coupled in Drosophila and are independently associated with mRNA abundance, protein length, and number of protein-protein interactions. Mol. Biol. Evol. 22: 1345–1354. [DOI] [PubMed] [Google Scholar]
- Lin C. Y., Lee T. L., Chiu Y. Y., Lin Y. W., Lo Y. S., et al. , 2015. Module organization and variance in protein-protein interaction networks. Sci. Rep. 5: 9386. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Luo F., Yang Y., Zhong J., Gao H., Khan L., et al. , 2007. Constructing gene co-expression networks and predicting functions of unknown genes by random matrix theory. BMC Bioinformatics 8: 299. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lynch M., Walsh B., 1998. Genetics and Analysis of Quantitative Traits. Sinauer Associates, Sunderland, MA. [Google Scholar]
- Mazurie A., Bonchev D., Schwikowski B., Buck G. A., 2010. Evolution of metabolic network organization. BMC Syst. Biol. 4: 59. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McGuigan K., Collet J. M., Allen S. L., Chenoweth S. F., Blows M. W., 2014a Pleiotropic mutations are subject to strong stabilizing selection. Genetics 197: 1051–1062. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McGuigan K., Collet J. M., McGraw E. A., Ye Y. H., Allen S. L., et al. , 2014b The nature and extent of mutational pleiotropy in gene expression of male Drosophila serrata. Genetics 196: 911–921. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McQuilton P., St Pierre S. E., Thurmond J., FlyBase Consortium , 2012. FlyBase 101--the basics of navigating FlyBase. Nucleic Acids Res. 40: D706–D714. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Melo D., Marroig G., 2015. Directional selection can drive the evolution of modularity in complex traits. Proc. Natl. Acad. Sci. USA 112: 470–475. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mitteroecker P., 2009. The developmental basis of variational modularity: insights from quantitative genetics, morphometrics, and developmental biology. Evol. Biol. 36: 377–385. [Google Scholar]
- Moreno-Hagelsieb G., Jokic P., 2012. The evolutionary dynamics of functional modules and the extraordinary plasticity of regulons: the Escherichia coli perspective. Nucleic Acids Res. 40: 7104–7112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nayak R. R., Kearns M., Spielman R. S., Cheung V. G., 2009. Coexpression network based on natural variation in human gene expression reveals gene interactions and functions. Genome Res. 19: 1953–1962. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Olson E. C., Miller R. L., 1958. Morphological Integration. University of Chicago Press, Chicago. [Google Scholar]
- Orr H. A., 2000. Adaptation and the cost of complexity. Evolution 54: 13–20. [DOI] [PubMed] [Google Scholar]
- Pál C., Hurst L. D., 2003. Evidence for co-evolution of gene order and recombination rate. Nat. Genet. 33: 392–395. [DOI] [PubMed] [Google Scholar]
- Parter M., Kashtan N., Alon U., 2007. Environmental variability and modularity of bacterial metabolic networks. BMC Evol. Biol. 7: 169. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pavlicev M., Hansen T., 2011. Genotype-phenotype maps maximizing evolvability: modularity revisited. Evol. Biol. 38: 371–389. [Google Scholar]
- Peregrín-Alvarez J. M., Sanford C., Parkinson J., 2009. The conservation and evolutionary modularity of metabolism. Genome Biol. 10: R63. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pickrell J. K., Berisa T., Liu J. Z., Segurel L., Tung J. Y., et al. , 2016. Detection and interpretation of shared genetic influences on 42 human traits. Nat. Genet. 48: 709–717. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pinheiro J. C., Bates D. M., 2000. Mixed-Effects Models in S and S-PLUS. Springer, New York. [Google Scholar]
- Pritykin Y., Ghersi D., Singh M., 2015. Genome-wide detection and analysis of multifunctional genes. PLoS Comput. Biol. 11: e1004467. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Proost S., Mutwil M., 2017. PlaNet: comparative co-expression network analyses for plants, pp. 213–227 in Plant Genomics Databases: Methods and Protocols, edited by van Dijk A. D. J. Springer, New York. [DOI] [PubMed] [Google Scholar]
- Rhee S. Y., Mutwil M., 2014. Towards revealing the functions of all genes in plants. Trends Plant Sci. 19: 212–221. [DOI] [PubMed] [Google Scholar]
- Rifkin S. A., Houle D., Kim J., White K. P., 2005. A mutation accumulation assay reveals a broad capacity for rapid evolution of gene expression. Nature 438: 220–223. [DOI] [PubMed] [Google Scholar]
- Rose N. H., Seneca F. O., Palumbi S. R., 2015. Gene networks in the wild: identifying transcriptional modules that mediate coral resistance to experimental heat stress. Genome Biol. Evol. 8: 243–252. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Runcie D. E., Mukherjee S., 2013. Dissecting high-dimensional phenotypes with Bayesian sparse factor analysis of genetic covariance matrices. Genetics 194: 753–767. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Salathé M., Ackermann M., Bonhoeffer S., 2006. The effect of multifunctionality on the rate of evolution in yeast. Mol. Biol. Evol. 23: 721–722. [DOI] [PubMed] [Google Scholar]
- Schlosser G., Wagner G. P., 2004. Modularity in Development and Evolution. The University of Chicago Press, Chicago, London. [Google Scholar]
- Snel B., Huynen M. A., 2004. Quantifying modularity in the evolution of biomolecular systems. Genome Res. 14: 391–397. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Spirin V., Gelfand M. S., Mironov A. A., Mirny L. A., 2006. A metabolic network in the evolutionary context: multiscale structure and modularity. Proc. Natl. Acad. Sci. USA 103: 8774–8779. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Storz J. F., Bridgham J. T., Kelly S. A., Garland T., 2015. Genetic approaches in comparative and evolutionary physiology. Am. J. Physiol. Regul. Integr. Comp. Physiol. 309: R197–R214. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Su Z. X., Zeng Y. W., Gu X., 2010. A preliminary analysis of gene pleiotropy estimated from protein sequences. J. Exp. Zoolog. B Mol. Dev. Evol. 314B: 115–122. [DOI] [PubMed] [Google Scholar]
- Takemoto K., Borjigin S., 2011. Metabolic network modularity in archaea depends on growth conditions. PLoS One 6: e25874. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tanay A., Sharan R., Shamir R., 2002. Discovering statistically significant biclusters in gene expression data. Bioinformatics 18(Suppl. 1): S136–S144. [DOI] [PubMed] [Google Scholar]
- Wagner G. P., 1996. Homologues, natural kinds and the evolution of modularity. Am. Zool. 36: 36–43. [Google Scholar]
- Wagner G. P., Altenberg L., 1996. Perspective: complex adaptations and the evolution of evolvability. Evolution 50: 967–976. [DOI] [PubMed] [Google Scholar]
- Wagner G. P., Mezey J. G., 2004. The role of genetic architecture constraints in the origin of variational modularity, pp. 338–358 in Modularity in Development and Evolution, edited by Schlosser G., Wagner G. P. The University of Chicago Press, Chicago, London. [Google Scholar]
- Wagner G. P., Pavlicev M., Cheverud J. M., 2007. The road to modularity. Nat. Rev. Genet. 8: 921–931. [DOI] [PubMed] [Google Scholar]
- Waterhouse R. M., Tegenfeldt F., Li J., Zdobnov E. M., Kriventseva E. V., 2013. OrthoDB: a hierarchical catalog of animal, fungal and bacterial orthologs. Nucleic Acids Res. 41: D358–D365. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Welch J. J., Waxman D., 2003. Modularity and the cost of complexity. Evolution 57: 1723–1734. [DOI] [PubMed] [Google Scholar]
- Whiteley M. A., Pearson K., 1899. Data for the problem of evolution in man. I. A first study of the variability and correlation of the hand. Proc. R. Soc. Lond. 65: 126–151. [Google Scholar]
- Zhang X., Acencio M. L., Lemke N., 2016. Predicting essential genes and proteins based on machine learning and network topological features: a comprehensive review. Front. Physiol. 7: 75. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhao J., Ding G.-H., Tao L., Yu H., Yu Z.-H., et al. , 2007. Modular co-evolution of metabolic networks. BMC Bioinformatics 8: 311. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhou W., Nakhleh L., 2012. Convergent evolution of modularity in metabolic networks through different community structures. BMC Evol. Biol. 12: 181. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
Data are archived at the NCBI’s GEO (N lines: GSE49815 and S lines: GSE54777).