Patterns of Population Variation in Two Paleopolyploid Eudicot Lineages Suggest That Dosage-Based Selection on Homeologs Is Long-Lived

Abstract

Genes that are inherently subject to strong selective constraints tend to be overretained in duplicate after polyploidy. They also continue to experience similar, but somewhat relaxed, constraints after that polyploidy event. We sought to assess for how long the influence of polyploidy is felt on these genes’ selective pressures. We analyzed two nested polyploidy events in Brassicaceae: the At-α genome duplication that is the most recent polyploidy in the model plant Arabidopsis thaliana and a more recent hexaploidy shared by the genus Brassica and its relatives. By comparing the strength and direction of the natural selection acting at the population and at the species level, we find evidence for continued intensified purifying selection acting on retained duplicates from both polyploidies even down to the present. The constraint observed in preferentially retained genes is not a result of the polyploidy event: the orthologs of such genes experience even stronger constraint in nonpolyploid outgroup genomes. In both the Arabidopsis and Brassica lineages, we further find evidence for segregating mildly deleterious variants, confirming that the population-level data uncover patterns not visible with between-species comparisons. Using the A. thaliana metabolic network, we also explored whether network position was correlated with the measured selective constraint. At both the population and species level, nodes/genes tended to show similar constraints to their neighbors. Our results paint a picture of the long-lived effects of polyploidy on plant genomes, suggesting that even yesterday’s polyploids still have distinct evolutionary trajectories.

Introduction

Flowering plant evolution is characterized by recurrent polyploidy events. However, the genetic redundancy that these events produce is not always long-lived. Instead, polyploid genomes are subject to diploidization, whereby homeologous sequences (which are created by genome duplication events) are then removed by unequal homologous recombination, nonhomologous recombination, and chromosome loss (aneuploidy; Soltis et al. 2015). Even when duplicated regions evade such large-scale losses, the genes they encode may also be disabled by degenerative mutations or chromosomal arrangements (dysploidy; De Storme and Mason 2014) and subsequently be lost through further genetic drift (Lynch and Conery 2000).

As an example, the Arabidopsis thaliana genome retains clear evidence of at least three ancient polyploidies in its history (Maere et al. 2005), all of which are shared with its near relative Arabidopsis lyrata, which split from A. thaliana ∼5 Ma (Van de Peer et al. 2009). The most recent of these events is termed the At-α whole-genome duplication (Blanc et al. 2003; Bowers et al. 2003) and has been dated to roughly 23 Ma (Barker et al. 2009). The majority of duplicated genes created by At-α have returned to a single-copy state, a process known as fractionation (Freeling et al. 2015). Today only ∼30% of the duplicates created by At-α survive in the A. thaliana genome (Bowers et al. 2003). At-α was an allopolyploidy (Blanc et al. 2003), meaning that the two (sub)genomes that merged to form A. thaliana’s ancestor were not identical. These initial differences appear to have driven biased fractionation, which means that retention of genes from one of the subgenomes was favored over the other (Freeling 2009; Woodhouse et al. 2014).

In addition to the At-α event, relatives of A. thaliana in the tribe Brassiceae, which includes Brassica rapa (Chinese cabbage) and Brassica oleracea (broccoli and cauliflower) share a subsequent hexaploidy, the Br-α genome triplication (Lysak et al. 2005; Arias et al. 2014; Liu et al. 2014). This event occurred through two separate hybridization steps (Tang et al. 2012) ∼16 Ma and was particularly marked by its biased pattern of resolution (Cheng et al. 2012). Thus, in B. rapa, one of the three contributing subgenomes is 70% retained, the second subgenome retains 46% of its contributed duplicates, and the most fractionated subgenome retains only 36% of its genes (Wang et al. 2011). The pattern is similar in Brassica oleracea (Liu et al. 2014; Parkin et al. 2014; Cheng et al. 2016). It is believed that the least fractionated subgenome is the one contributed by the second hybridization step in the paleopolyploidy (Tang et al. 2012), meaning that a number of duplicate losses from the other two genomes had already occurred prior to this second hybridization. In a more general sense, it has been proposed that silencing of the subgenome with the higher transposable element load through factors such as differential methylation drives the overall process of biased fractionation (Schnable et al. 2011; Garsmeur et al. 2014; Edger et al. 2017).

Besides these parent-of-origin effects, duplicate loss after polyploidy is also nonrandom with respect to gene function: genes encoding transcription factors, ribosomal proteins, and kinases have survived in duplicate after many phylogenetically independent polyploidies in organisms as diverse as amoebae, plants, vertebrates, and yeasts (Seoighe and Wolfe 1998; Blanc and Wolfe 2004; Maere et al. 2005; Aury et al. 2006; Makino and McLysaght 2010; Jiang et al. 2013; Albalat and Canestro 2016; Li et al. 2016). The force driving this convergence in the retained duplicates, known as ohnologs (Wolfe 2000), is believed to be selection to maintain dosage balance among interacting gene products (Birchler et al. 2005). In other words, because complex assembly and other macromolecular associations follow the rules of biochemical kinetics (Veitia and Birchler 2015), the duplication of only some members of such complexes will tend to drive the concentration of the functional versions of them away from their selectively optimal levels (Veitia 2002; Papp et al. 2003; Maere et al. 2005; Dopman and Hartl 2007; Wapinski et al. 2007; Coate et al. 2011; Rodgers-Melnick et al. 2012; Birchler et al. 2016). However, a duplication of the entire genome will (in general) maintain the required balance (Edger and Pires 2009; Freeling 2009; Makino and McLysaght 2010; Birchler and Veitia 2014). After such an event, selection will then tend to disfavor the loss of duplicated members of such complexes. In keeping with this idea, it is known that genes encoding highly interactive proteins that are in central network positions or genes in dense regulatory pathways are prone to be dosage-sensitive (Hakes et al. 2007; Birchler and Veitia 2012) and are overretained postpolyploidy (Freeling and Thomas 2006; Birchler and Veitia 2007; Bekaert et al. 2011; Conant 2014; Conant et al. 2014).

Such functional observations lead to the question of how natural selection acts on duplicated genes. Analyses of the pattern of selective constraint seen in duplicated and single-copy genes have shown that, despite their redundancy, duplicated genes tend to actually show relatively high selective constraint, measured as a numerically small value of the ratio of nonsynonymous to synonymous substitutions; K_a/K_s (Davis and Petrov 2004; Jordan et al. 2004). Davis and Petrov (2004) used an elegant approach of looking at the selective constraint of a duplicated gene pair’s orthologs in unduplicated outgroups to show that this difference in constraint, rather than being an effect of duplication, reflects a propensity for intrinsically more constrained genes to survive in duplicate. When this tendency is coupled to the known characteristics of surviving ohnologs, such as increased essentiality and a higher propensity for having expression phenotypes (Hakes et al. 2007; Wapinski et al. 2007), it is natural to speculate that the difference in constraint between duplicates and singletons might be partly driven by retained WGD-produced duplicates in the genomes studied. And indeed, in plants, the mean K_a/K_s ratio of duplicate genes produced by small-scale duplicates is higher than that for WGD duplicates (Carretero-Paulet and Fares 2012). In fact, a relatively clear series can be drawn: recent ohnologs have higher constraint than older ones, ohnologs are more constrained than duplicates from other mechanisms, and duplicated genes are more constrained than those without duplicates (Yang and Gaut 2011). In the same vein, Scannell and Wolfe (2008) demonstrated that the ohnologs in modern bakers’ yeast were indeed drawn from a class of genes showing higher constraint in outgroup species lacking the yeast WGD. In their analysis, they also showed that the WGD did produce a relaxation of constraint (Lynch and Conery 2000), but not enough to overcome these genes’ intrinsically higher initial constraints.

Both of these studies note a temporal component to the selection acting on ohnologs (Scannell and Wolfe 2008; Yang and Gaut 2011) which has suggestive links to recent research outlining a functional progression in the evolution of polyploid genomes. In the earliest phases of the evolution of a polyploid species, there appears to be forces acting to favor the removal of duplicate copies of genes with functions in DNA repair or that are targeted to the organelles (Edger and Pires 2009; De Smet et al. 2013; Conant 2014). Selection for dosage balance is a critical force in the next phase, with potential functional partitioning or innovation occurring even later in time (Bekaert et al. 2011; Conant et al. 2014).

How long can dosage balance be maintained before the dosage constraints eventually change as genes diverge over time (Birchler and Veitia 2012)? How do selective patterns change after polyploidy? Are paleopolyploids still different from diploids in this regard? We hypothesized that genes retained in duplicate/triplicate remain under higher constraint even long after polyploidy. To test this hypothesis, we exploited the nested polyploid events in Arabidopsis and Brassica, using a different approach than previous work on these two polyploidies (Woodhouse et al. 2014). We chose the two nested polyploidies in the Brassicaceae family as our model system because of the availability of deep functional genomic resources and multiple sequenced genomes of A. thaliana, A. lyrata, B. rapa, and B. olecarea. Our goal here was to link the previous functional studies on the changing face of polyploidy through time with work on the selective constraint acting on the ohnologs. Hence, we asked whether the patterns of enhanced constraint among duplicates have continued to the present day by comparing the selective constraint seen between species to that seen in the circulating polymorphisms within two paleopolyploid species. We demonstrate that surviving ohnologs are under more stringent selective constraint even in present day populations, but that this pattern of constraint was nonetheless intrinsic to them prior to polyploidy.

Materials and Methods

Signatures of the At-α Duplication and Br-α Triplication

We obtained pairs of At-α duplicates using CoGe’s SynMap algorithm (Lyons, Pedersen, Kane, and Freeling 2008) and merged this list with the At-α duplicates reported by Bowers et al. (2003) using version 10.02 of the Arabidopsis thaliana Col-0 genome as our reference (The Arabidopsis Genome Initiative 2000). We excluded from our ohnolog lists any conflicts between the two lists and any “pairs” with more than two genes, resulting in 2,768 duplicated gene pairs that originated at the At-α event. Similarly, to identify regions created by the Brassica triplication, we used SynMap and GEvo in CoGe (Lyons, Pedersen, Kane, Alam, et al. 2008) to infer the orthologous relations of A. thaliana, B. rapa, and B. oleracea genes from the syntenic regions of the three genomes, requiring a syntenic score of 10 in a window of 60 genes. Versions 1.5 and 2.1 of the Brassica rapa (Wang et al. 2011) and Brassica oleracea TO1000 genomes (Liu et al. 2014; Parkin et al. 2014) were used, respectively.

Between-Species Divergences

We obtained maximum likelihood estimates of K_a (the number of nonsynonymous substitutions over the number of total possible nonsynonymous sites; Miyata and Yasunaga 1980) and K_s (the number of synonymous substitutions per synonymous site) using GenomeHistory (Conant and Wagner 2002) for three sets of homologous protein-coding genes pairs. We omitted pairs with K_s < 0.001 from our analysis. The first set of genes consists of ortholog pairs from A. thaliana Col-0 and A. lyrata v1.0 (Hu et al. 2011): we denote these data as At-Al K_a/K_s. We identified these pairs through an analysis of syntenic regions using the SynMap tool with the Last algorithm (Frith and Kawaguchi 2015) in CoGe (Lyons and Freeling 2008; Tang et al. 2011). We divided these pairs into orthologs from retained At-α duplicates and single copy syntenic orthologs and analyzed the distributions of K_a/K_s for each.

Our second set of homologous pairs is drawn from the comparison of B. rapa and B. oleracea, and we obtained genes that preserved synteny between the two species from the CoGe SynMap algorithm (Lyons, Pedersen, Kane, and Freeling 2008). Because of the WGT, a single ancestral syntenic locus is now represented by three syntenic loci in both B. rapa and B. oleracea, resulting in three sets of homology relationships for each B. rapa gene in B. oleracea. We binned the syntenic homologs and considered only loci that fell into three groups. The first group consisted of one-to-one ortholog pairs (Br-Bo 1:1), where the other two WGT-produced paralogs have been lost in both Brassica genomes. In the second group, we included only loci with all surviving genes from the WGT in both genomes, resulting in three-to-three homology relations (Br-Bo 3:3). For this second group, each B. rapa and B. oleracea orthologous triplet is equivalent to nine pairs of genes: we used a distance-based approach to resolve these three-to-three homology relationships. From each of the triplets, we took the B. rapa and B. oleracea gene pair with the closest K_a value and defined them to be the first pair of orthologs. Next, we found the B. rapa/B. oleracea pair with the closest K_a from the remaining two-to-two relations, defining them as the second orthologous pair. The remaining two genes were defined as the third pair of orthologs. For validation, we generated a list of the most plausible syntenic gene pairs from the SynMap results. We excluded one-to-many or many-to-many syntenic relations by starting from the largest synteny block containing members of the triplet and removing any other syntenic relationships for that pair of genes (which were necessarily in smaller synteny blocks). We found that 80.7% of our first pairs of orthologs (those closest in K_a) were in one-to-one synteny. The corresponding figures for the second and third pairs were 75.4% and 79.1%, respectively. Our third and final group contained B. rapa and B. oleracea genes that had each lost exactly one gene after triplication (Br-Bo 2:2). The ortholog pairs from these two-to-two homologous relationships were inferred using the approach just described. K_a/K_s was then computed for all the B. rapa and B. oleracea orthologous pairs (denoted Br-Bo K_a/K_s across all three groups).

Our final set of homolog pairs consists of A. thaliana genes with their B. rapa orthologs, subdivided into the two groups (surviving paralogs from the triplication and single-copy genes) just described (denoted At-Br K_a/K_s).

To assess if the selective constraint of surviving polyploid-produced duplicates differed from that of the single copy genes, we took the (nonzero) K_a/K_s values for the two groups and analyzed their distribution. We first fit separate lognormal distributions to the K_a/K_s values from the At-α duplicates and the single copy genes, computing the likelihood of observing the set of K_a/K_s values for each (L_duplicate and L_single-copy, respectively). We then fit a single log-normal distribution to the pooled K_a/K_s values from both, yielding the likelihood L_combined. We then tested the hypothesis of a difference in these distributions using a likelihood ratio test, comparing D, twice the natural log of the ratio of (L_duplicate×L_single-copy) over L_combined, to a chi-square distribution with 2 degrees of freedom (Wilks 1938):

$$D=2ln\left(\frac{L_{duplicate}{L}_{\hspace{0.17em}\text{sin}\hspace{0.17em}gle-copy}}{L_{combined}}\right)\mathrm{}\sim \mathrm{}{\chi }^2(2).$$ (1)

We performed the same analysis with the triplicated genes and single-copy genes from the comparison of B. rapa and B. oleracea.

Within-Species Variation

To quantify the actions of selection at the population level, we estimated the number of circulating synonymous and nonsynonymous polymorphisms using SNP data. For A. thaliana, we obtained polymorphism data in variant call format (VCF) from 1,135 natural inbred lines curated by the 1001 Genomes Project (Alonso-Blanco et al. 2016). SNPs in protein-coding genes were annotated as synonymous or nonsynonymous polymorphisms using SnpEff (Cingolani et al. 2012).

The B. rapa SNPs were called from the transcriptomes of 126 accessions (Qi et al. 2017), and also annotated with SnpEff. Low quality SNPs were removed with vcffilter (https://github.com/vcflib/vcflib; last accessed March 21, 2018) and VCFtools (Danecek et al. 2011): only SNPs identified in regions with read depth >10 and root mean square mapping quality >30 were used for subsequent analyses.

To normalize the number of observed SNPs per gene, we counted the number of nonsynonymous positions in each protein-coding gene showing polymorphism and divided that number by the total number of nonsynonymous changes possible in the gene. We denote this ratio as pN. Similarly, pS is the number of polymorphic synonymous positions divided by the number of possible synonymous sites (McDonald and Kreitman 1991). We then calculated the ratio of pN/pS for all possible protein-coding genes in A. thaliana and B. rapa. We removed genes with pS = 0 and pN ≤ 1; for those with pS = 0 and pN > 1, pN/pS was set to 1. We fit the distributions of pN/pS to lognormal curves as above.

Identifying Changes in Selective Constraints Prior to and Postpolyploidy

Using the syntenic orthology relations inferred for A. thaliana versus A. lyrata, A. thaliana versus B. rapa, and B. rapa versus B. oleracea that we obtained from SynMap (Lyons, Pedersen, Kane, and Freeling 2008), we linked the orthologous genes of these four species together. All four species share the At-α duplication, and the two Brassica species share the Br-α triplication. We calculated K_a/K_s for the comparison of A. thaliana and A. lyrata orthologs (At-Al), A. thaliana and B. rapa orthologs (At-Br), and B. rapa and B. oleracea orthologs (Br-Bo), respectively. At the within-species level, we calculated pN/pS for A. thaliana genes using resequencing data from 1,135 accessions (Alonso-Blanco et al. 2016) and for B. rapa from transcriptomic data on 126 accessions (Qi et al. 2017).

We partitioned each group of selective constraints into four subgroups, groups where: 1) both the Arabidopsis and Brassica lost the extra copies and returned to singleton state after the At-α duplication and the Br-α triplication, respectively, 2), Arabidopsis retained both At-α duplicates, but Brassica lost the triplicated copies returned to singleton state, 3) Arabidopsis lost the duplicated copy, but Brassica retained all three copies after the WGT, 4) Arabidopsis retained At-α duplicates and Brassica retained Br-α triplets.

We created notched boxplots for the selective constraints across the four different subgroups in R. By comparing the selective constraints in these subgroups, we could observe how selective constraints shifted after At-α WGD, before Br-α WGT, and after Br-α. We could also assess whether these changes were still preserved among populations of extant species. Nonparametric multiple comparison tests using Kruskal–Wallis tests as a pairwise basis (Siegel and Castellan 1988) were performed using the kruskalmc function in the pgirmess package in R (https://github.com/pgiraudoux/pgirmess; last accessed March 21, 2018).

To again examine the differences in functions between genes retained after polyploidy versus single copy genes, we used the gene list analysis tool from the PANTHER classification system (Mi et al. 2017) and performed overrepresentation tests of molecular function and biological process Gene Ontology (GO) terms using a list of A. thaliana genes that are orthologous to surviving triplicates in B. rapa, compared against another A. thaliana gene list that contains genes in one-to-one orthology relationships with single-copy (with respect to Br-α) genes in B. rapa.

Metabolic Network Analysis

We employed an updated version of the Arabidopsis thaliana metabolic network (de Oliveira Dal’Molin et al. 2010) that we have previously described as AraGEM v1.2 (Bekaert et al. 2012). Each node in this network represents a biochemical reaction (with associated enzyme-coding genes), and edges connect pairs of nodes with shared metabolites. We estimated the selective constraint for each node in the network by taking the average K_a/K_s or pN/pS of all the genes mapped to that reaction. To observe how the selective constraint changes from the population level to species level, we only included A. thaliana genes that both have At-Al K_a/K_s values and within-species pN/pS values. We also inferred a draft-quality B. rapa metabolic network by mapping the reactions catalyzed by A. thaliana genes onto their corresponding orthologs in B. rapa. We further refined the inferred B. rapa network by limiting it to the subset of B. rapa genes that have small nonsynonymous distances to their A. thaliana orthologs (i.e., having At-Br K_a values below the 75% percentile for the full set of genes in the network). The assumption here is that such orthologs are even more likely to retain the enzymatic function of their A. thaliana counterparts. The metabolic networks were visualized using Gephi v0.9.1 (Bastian et al. 2009) with the layout algorithm Force Atlas.

We computed three measurements of importance for the nodes in the network. The first was the node degree, that is, the number of edges connected to that node (Hakimi 1962). The next was the clustering coefficient, defined as the ratio of the number of observed connections among each triplet of nodes to the maximum number of such connections possible (Watts and Strogatz 1998). Third and finally, we computed each node’s betweenness centrality, which is the number of the network’s shortest paths passing through that node (Brandes 2001). For each statistic, we calculated the Spearman’s correlation coefficient between the nodes’ mean selective constraints and the statistic in question.

We also conducted an analysis of the similarity of the selective constraint of adjacent nodes, defining the weight of the edge connecting two nodes as the absolute value of the difference in the constraint values of those two nodes (e.g., pN/pS or K_a/K_s). To assess if adjacent nodes were more similar in constraint than expected, we generated 10,000 random networks with identical structure but randomized assignments of constraints to nodes. We compared the average and sum of the edge weights for these random networks to those of the real networks.

Results

Arabidopsis Genes Retained after At-α Polyploidy Are under Stronger Selective Constraint

We compared the between-species selective constraint, measured with the ratio of K_a/K_s, for genes retained in duplicate and those returned to single-copy after polyploidy. K_a/K_s values <1.0 suggest purifying selection against amino acid substitutions and values >1.0 are indicative of directional selection (Li 1997). We made similar comparisons using the within-species constraints estimated with the ratio pN/pS (Materials and Methods), a ratio that reports the proportion of all nonsynonymous and synonymous sites with circulating polymorphisms in a population. Thus, we calculated five groups of selective constraints: three at the species level: At-Al (A. thaliana to A. lyrata) K_a/K_s, At-Br (A. thaliana to B. rapa) K_a/K_s, and Br-Bo (B. rapa to B. oleracea) K_a/K_s; and the other two at population level: pN/pS for A. thaliana and for B. rapa. We expected that the ratio pN/pS would exceed K_a/K_s due to the circulation of low frequency, mildly deleterious polymorphisms in populations, some of which are eventually purged over the longer times represented by the between-species comparisons.

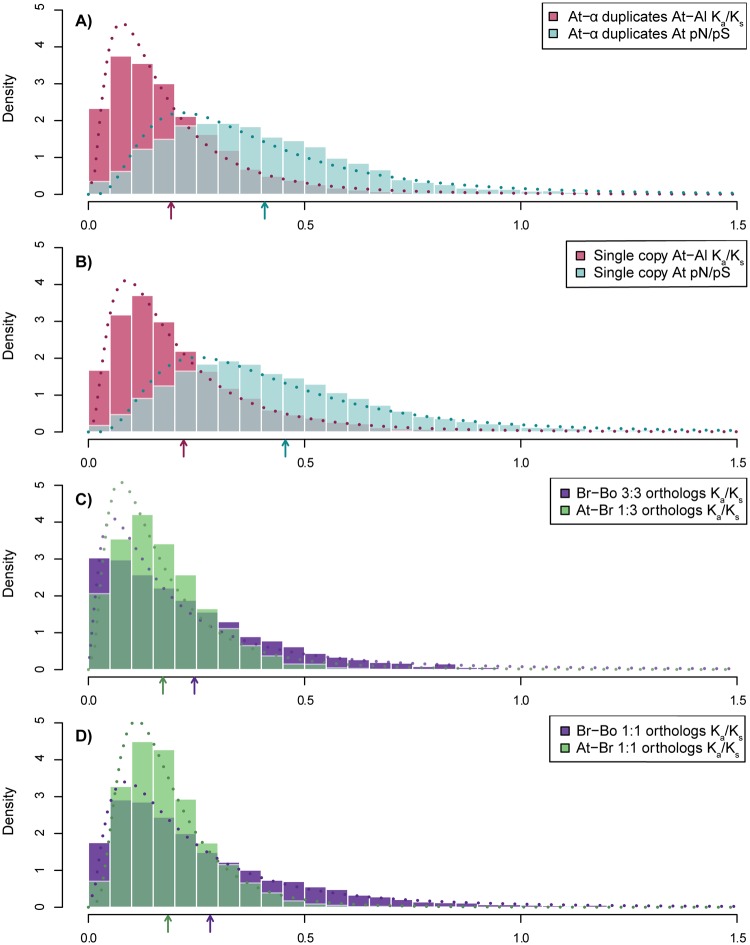
Figure 1 shows the density distributions of K_a/K_s and pN/pS for retained At-α duplicates and Br-α triplicates and for genes that returned to single copy after these polyploidy events. We fit the selective constraints to lognormal distributions and performed likelihood ratio tests to compare each pair of distributions. The distributions of selective constraint for retained duplicates/triplicates and for single copy genes are significantly different, both for the within-species population data and for between-species comparisons, with the duplicates having higher constraint in all cases (see also table 1).

Fig. 1.

—Distributions of measures of selective constraints. (A and B) Selective constraints of Arabidopsis thaliana genes that retained both At-α duplicates, and genes that returned to single copy after At-α. (A) Red: distribution of At-Al K_a/K_s for A. thaliana genes that survived At-α, blue: distribution of within-species pN/pS for corresponding retained At-α duplicates that have orthologs in A. lyrata; (B) Red: distribution of K_a/K_s for At-Al 1:1 orthologs, blue: distribution of pN/pS for the corresponding A. thaliana genes. Dotted lines: fitted lognormal density distribution curves. The distributions of K_a/K_s from retained At-α duplicates and from single-copy genes are significantly different (P < 0.00001), as are the two distributions for pN/pS (P < 0.00001). (C and D): Selective constraints of Brassica rapa genes that survived the Br-α triplication, and those of the single-copy genes, as well as the selective constraints of their A. thaliana orthologs. (C) Purple: distribution of K_a/K_s for Br-Bo orthologs that preserved three copies in both B. rapa and B. oleracea, green: distribution of K_a/K_s for At-Br orthologs where A. thaliana genes are orthologous to the same B. rapa gene set (retained triplets). (D) Purple: distribution of K_a/K_s for single copy Br-Bo orthologs, green: distribution of K_a/K_s for single copy At-Br orthologs. Dotted lines are as for (A) and (B). The distributions of K_a/K_s for Br-Bo 3:3 and Br-Bo 1:1 orthologs are significantly different (P < 0.00001); the distributions of K_a/K_s for At-Br 1:3 and At-Br 1:1 orthologs are also significantly different (P < 0.00001). Arrows mark the average selective constraint of each distribution. See also table 1.

Table 1.

Average Selective Constraints

Selective Constraints	Single-Copy Orthologs		Retained Duplicates/Triplicates		% Differencec
	Sample Sizea	Mean Valueb	Sample Sizea	Mean Valueb
At vs. Al Ka/Ksd	11,966	0.2203	4,261	0.1914	−13.13
At vs. Br Ka/Kse	5,367	0.1843	5,069	0.1724	−6.42
Br vs. Bo Ka/Ksf	7,604	0.2814	5,680	0.2454	−12.79
At 1135 ecotypes pN/pSg	14,293	0.4557	4,839	0.4078	−10.50
Br 126 accessions pN/pSh	1,316	0.1269	1,031	0.1285	1.19

Note.—See also figure 1.

^aSample size for the calculation of mean selective constraint (b): for K_a/K_s this value corresponds to the number of orthologous pairs; for pN/pS to the number of genes.

^bMean value of the measure of selective constraint in question (i.e., K_a/K_s or pN/pS, left).

^cThe difference as a percentage of the selective constraints of single copy genes.

^dThe average K_a/K_s computed between Arabidopsis thaliana and A. lyrata.

^eThe average K_a/K_s computed between A. thaliana and Brassica rapa.

^fThe average K_a/K_s computed between B. rapa and B. oleracea.

^gThe average pN/pS for A. thaliana genes with an ortholog in A. lyrata. About 1,610 genes with pS = 0 and pN ≤ 1 were removed. pN/pS values for 150 genes with pS = 0 and pN > 1 were set to 1. The total number of genes after filtering was 25,806. Only genes with orthologs in A. lyrata were included in the analysis (as noted in a).

^hThe average pN/pS for B. rapa genes with orthologs in B. oleracea. About 266 genes with pS = 0 and pN ≤ 1 were removed. pN/pS values for 129 genes with pS = 0 and pN > 1 were set to 1. The total number of genes after filtering was 5,128. Only genes with orthologs in B. oleracea were included in the analysis (as noted in a).

We also note that the separation between values of pN/pS and K_a/K_s was smaller for genes surviving in multiple copies post-WGD/WGT relative to those returned to single copy (fig. 1A and B). It takes more time for purifying selection to act on mildly deleterious polymorphisms than on more strongly deleterious ones (Hartl and Clark 1997). Hence, this observation might suggest stronger selection acting on these retained paralogs, such that, even at the population level, there is relatively fast-acting evolutionary pressure to remove deleterious variants (Cao et al. 2011). For both the within-population and the between-species comparisons of A. thaliana and A. lyrata, constraint also decreases as one moves from surviving At- α duplicates found in both genomes to At-α duplicates specific to A. thaliana to single-copy genes (supplementary fig. S1A, Supplementary Material online).

Similar patterns are seen when comparing the triplicated and single-copy genes between B. rapa and B. oleracea and for the comparison with their corresponding A. thaliana orthologs (fig. 1C and D;table 1), with both triplicated Brassica genes and their A. thaliana orthologs being more constrained. For completeness, we also considered the case of Br-Bo 2:2 pairs (i.e., both genomes retained exactly two syntenic copies after triplication; supplementary fig. S1B, Supplementary Material online). As expected, the average selective constraint of the At-Br 1:2 orthologs falls between the At-Br 1:1 and At-Br 1:3 cases. An apparently similar trend was seen in the B. rapa population data, but we lacked the statistical power to detect differences in pN/pS between the two groups when using only 126 transcriptomes for our SNP detection.

Non-WGT Orthologs of Retained Brassica Triplets Are under Strong Purifying Selection

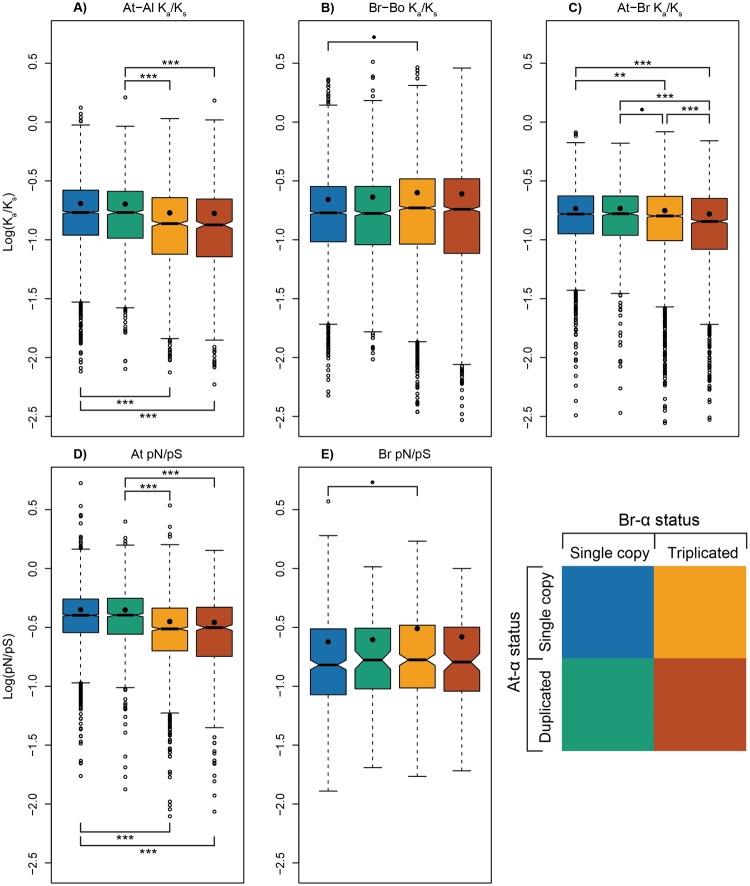
Since the Br-α triplication is specific to genus Brassica, we used the Arabidopsis genomes to estimate the patterns of selective constraint that may have acted on the Brassica genomes prior to that triplication. In particular, we can partly assess whether the ohnologs’ reduction in constraint is driven by their intrinsic properties or the polyploidy event itself. Figure 2 shows the selective constraints for the At-Al-Br-Bo syntenic orthologs in the cases where duplicates or triplicates are either lost or preserved (i.e., the four subgroups described in the Materials and Methods). The estimated constraint of the triplicated Brassica genes absent the triplication, inferred using the constraint seen between these genes’ orthologs in A. thaliana and A. lyrata (which both lack the Brassica hexaploidy), was smaller than for the corresponding single-copy genes by ∼17% (supplementary table S1, Supplementary Material online). This difference was seen regardless of whether the At-α duplicates were retained (green/red boxplots in fig. 2A and D, P < 0.0001) or lost (blue/yellow boxplots in fig. 2A and D, P < 0.0001). The WGT apparently ameliorated this difference in constraint: when comparing K_a/K_s in B. rapa and B. oleracea orthologs that are also in synteny with A. thaliana, we observed a 12% increase in the average selective constraint in the triplicated orthologs relative to the single copy pairs (fig. 2B and supplementary table S1, Supplementary Material online). This relaxation in constraint among these triplicates may be due to the redundancy they introduce (Conant and Wolfe 2008). However, when taking all Br-Bo orthologs into consideration, regardless of whether there is syntenic orthology in A. thaliana, we observed a ∼13% reduction in the K_a/K_s of the Br-Bo 3:3 genes relative to the Br-Bo 1:1 orthologs (table 1 and supplementary fig. S1B, Supplementary Material online). This apparent inconsistency is caused by the presence of a group of fast-evolving single copy Brassica genes that lack synteny with A. thaliana and that increase the average K_a/K_s value for the total set of single-copy Brassica genes.

Fig. 2.

—Notched box plots of log selective constraints among Al-At-Br-Bo syntenic orthologs. Colors indicate the loss/retention state of Arabidopsis orthologs after At-α WGD, and Brassica orthologs after Br-α WGT. “Lost”: genes returned to singleton state after polyploidy, “retained”: duplicated/triplicated copies are preserved in the genome. Subplots are boxplots of (A) log(K_a/K_s) for A. thaliana versus A. lyrata, (B) log(K_a/K_s) for B. rapa versus B. oleracea, (C) log(K_a/K_s) for A. thaliana versus B. rapa; and (D) log(pN/pS) for 1,135 A. thaliana ecotypes, (E) log(pN/pS) for 126 B. rapa accessions. The notches are 95% confidence intervals of the medians. Kruskal–Wallis multiple comparison tests were performed to evaluate significant differences across medians, P values: ***P < 0.0001, **P < 0.001, *P < 0.01, •P < 0.05. The black dots represent the log(mean) selective constraints. See also supplementary table S1, Supplementary Material online.

For those retained Br-α triplets in the B. rapa and B. oleracea (yellow and red boxplots in fig. 2), the stronger selective constraints associated with being members of a surviving At-α duplicate pair can be observed both before (fig. 2A and C) and after triplication (fig. 2B). This pattern also extends to the population level (fig. 2D and E). However, among the Brassica genes that returned to singleton state (blue and green boxplots in fig. 2), those genes deriving from surviving Arabidopsis ohnologs show a relaxation in constraint in the Brassica lineage (supplementary table S1, Supplementary Material online).

Biased fractionation allows researchers to detect three distinct subgenomes in B. rapa: the least-fractionated subgenome (LF), and the two more-fractionated subgenomes (MF1 and MF2; Wang et al. 2011; Cheng et al. 2012). It is natural to ask if our conclusions regarding selective constraint are sensitive to this fractionation pattern. As shown in supplementary figure S2, Supplementary Material online, the At-Br K_a/K_s estimates are consistent across three subgenomes. Brassica rapa and B. oleracea orthologs from the LF subgenome are slightly more constrained when compared with genes from the other two subgenomes for both the Br-Bo 1:1 and Br-Bo 3:3 cases. Thus, biased fractionation will not significantly affect our overall conclusions regarding the constraints observed for retained ohnologs and single-copy genes, but it is intriguing that genes from the more retained genome are also apparently more constrained.

Selective Constraints Are Correlated with Clustering Coefficients in the Metabolic Network

We reduced the full Arabidopsis metabolic network to include only nodes representing reactions where the enzyme-coding genes involved have A. lyrata orthologs. This simplified network contains 1,068 nodes (reactions) and 14,864 edges (representing shared metabolites between the reactions of the connected nodes). Our draft version of the inferred Brassica metabolic network contains 949 nodes and 11,499 edges. When we required that the nodes in question had estimated values for both K_a/K_s and pN/pS in B. rapa, the resulting network contains 595 nodes and 5,064 edges.

Table 2 shows the Spearman’s rank-order correlation coefficient (ρ) between a number of network statistics and the selective constraints K_a/K_s and pN/pS, respectively. Selective constraints and clustering coefficients were significantly positively correlated in both the Arabidopsis and Brassica metabolic networks, and the correlation was stronger for the between-species comparisons. This observation also holds for a further reduced subset of Brassica network, where only highly conserved B. rapa genes were included (Materials and Methods; values in parentheses in table 2). Clustering coefficient is defined as the ratio of the number of observed connections between a node’s neighbors to the maximum number of possible connections (Watts and Strogatz 1998). Only K_a/K_s for the At-Al orthology comparisons was significantly correlated with node degree, in contrast to other studies reporting either no association or the expected weak negative association (Fraser et al. 2002; Bloom and Adami 2003; Jordan et al. 2003; Hahn et al. 2004). The selective constraints showed no significant correlations with betweenness centrality (the number of shortest paths passing through the node) in the Arabidopsis network, which differs from the pattern seen in protein-interaction networks (Hahn and Kern 2005). There was a significant negative correlation between selection and betweenness centrality in the Brassica network. In general, all of the correlations observed, significant or otherwise, were numerically small, suggesting that metabolic network structure is probably not a major driver of constraint in these taxa.

Table 2.

Spearman’s Correlations of Selective Constraints and Network Statistics

Gene Setsa	Ka/Ks or pNpS	Number of Nodesb	Number of Edgesc	Selection and Node Degreed		Selection and Clustering Coefficiente		Selection and Betweenness Centralityf
				Spearman’s Correlation	P Value	Spearman’s Correlation	P Value	Spearman’s Correlation	P Value
At-Al ∩ At	At-Al Ka/Ksg	1,068	14,864	0.0856	0.002*	0.1459	0.000*	0.0067	0.443
	At pN/pSh	1,068	14,864	0.0249	0.208	0.0882	0.001*	−0.0353	0.128
Br-Bo	Br-Bo Ka/Ksi	949 (865)	11,499 (9467)	−0.0358	0.120	0.1175	0.000*	−0.1295	0.000*
				−0.0472	0.083	0.0975	0.002*	−0.1002	0.002*
Br-Bo ∩ Br	Br-Bo Ka/Ksj	595 (548)	5,064 (4455)	0.0030	0.503	0.0479	0.104	−0.1010	0.003*
				0.0149	0.392	0.0986	0.008*	−0.0910	0.010*
	Br pN/pSk	595 (548)	5,064 (4455)	0.0879	0.014*	−0.0126	0.397	0.0284	0.254
				0.1216	0.001*	0.0183	0.343	0.0757	0.040*

^*P value < 0.05.

^aMetabolic networks defined from three gene sets: 1) the Arabidopsis network with genes appearing in both the K_a/K_s and the pN/pS analyses, 2) the full Brassica network and 3) the reduced Brassica network with genes that appeared in both the K_a/K_s and the pN/pS analyses.

^bNumber of nodes in the metabolic network. Each node is a biochemical reaction.

^cNumber of edges in the metabolic network. An edge connects two nodes in the network if the reactions for those nodes share a metabolite.

^dNode degree is the number of edges connected to a node.

^eClustering coefficient is defined as the ratio of existing links connecting a node’s neighbors to each other over the maximum possible number of such links.

^fBetweenness centrality is the number of the network’s shortest paths that pass through a node.

^gThe K_a/K_s for each node, calculated by taking the average of K_a/K_s of enzyme-coding genes corresponding to the reaction of the node, computed between A. thaliana and A. lyrata.

^hThe average pN/pS for each node calculated in a similar way, for A. thaliana genes with an ortholog in A. lyrata.

ⁱThe average K_a/K_s for each node, computed between B. rapa and B. oleracea. Results for a subset of B. rapa genes for which At-Br K_a < 0.1127 are shown in parentheses.

^jThe average K_a/K_s for each node, computed between B. rapa and B. oleracea, for an intersection set of genes that appeared in both the K_a/K_s and the pN/pS analyses. Results for a subset of B. rapa genes for which At-Br K_a < 0.1127 are shown in parentheses.

^kThe average pN/pS for each node, for B. rapa genes with orthologs in B. oleracea. Results for a subset of B. rapa genes for which At-Br K_a < 0.1127 are shown in parentheses.

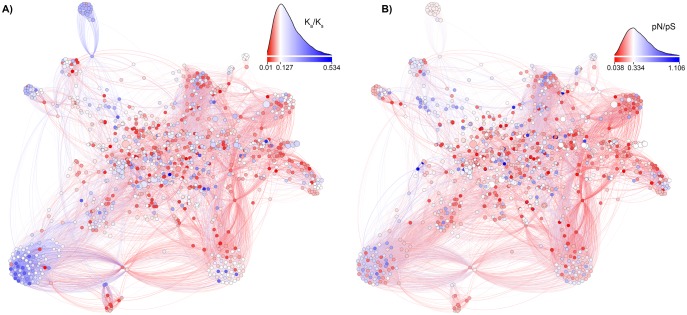
Figure 3 shows the selective constraint both between species (At-Al K_a/K_s) and within species (At pN/pS) for nodes in the Arabidopsis metabolic network. Nodes where the K_a/K_s and pN/pS are below the mean for all nodes are colored in red, and those that are less constrained than average are in blue. We observed that visually tight clusters of nodes in this diagram appear to be less constrained, leading to our analyses testing whether neighboring nodes shared similar constraints (next section).

Fig. 3.

—The distributions of selective constraints in the Arabidopsis thaliana metabolic network. Nodes represent biochemical reactions and are colored with the average selective constraints of genes encoding enzymes for each reaction. The diameter of each node is in proportion to the number of genes for the node. Edges connect two nodes if the two reactions share compounds. (A) Nodes are colored by At-Al K_a/K_s, with red indicating a K_a/K_s is below the network mean, and blue above that mean. The histogram shows the density distribution of At-Al K_a/K_s. (B) Nodes are colored by At pN/pS, with red indicating below-average constraints, and blue above. The histogram shows the density distribution of At pN/pS.

Adjacent Enzymes Share Similar Selective Constraints

We defined the weight of an edge in our network as the absolute value of the difference between the mean selective constraints (pN/pS or K_a/K_s) of its incident nodes. Supplementary table S2, Supplementary Material online, shows the sum and average edge weights of the real network and of randomized networks. At both species level and population level in A. thaliana, the sum of edge weights of the real metabolic networks is smaller than those of randomized networks, suggesting that genes under similar selective pressure tend to cluster in the network. A similar trend was seen for the comparisons between B. rapa and B. oleracea, but no significant difference was observed between the real and randomized networks for the comparison of the B. rapa populations, likely due to small sample sizes.

Discussion

As reported by others (Jordan et al. 2004; Scannell and Wolfe 2008; Yang and Gaut 2011), it is clear that polyploidy-produced duplicates are under stronger constraint than their single-copy counterparts. In a sense, this result is also not surprising, as it parallels the known functional biases of the retained ohnologs: ohnologs tend to fall into functional groups such as regulation of transcription, intracellular signal transduction and formation of multisubunit complexes (Warren et al. 2010; Wang et al. 2011; supplementary tables S3 and S4, Supplementary Material online). Such ohnologs rely on kinetic and stoichiometric balance (Birchler et al. 2016), and dosage perturbations in them can only be tolerated in a narrow range. As a result, mutations that could alter dosage are strongly selected against (Birchler and Veitia 2014; Pires and Conant 2016). It is possible that other types of mutations are equally selected against, accounting for the globally reduced selective constraints. On the other hand, there is also an interesting relationship between gene expression and selective constraint, with high gene expression strongly predicting high constraint (Drummond et al. 2005, 2006). Patterns of these kinds may drive our observations of the relaxation in selection on the Brassica triplicates (where genes from more fractionated subgenomes show relaxed constraint relative to the less fractionated subgenome), given that genes in the less fractioned subgenome also tend to show higher expression levels (Woodhouse et al. 2014).

In yeast, Scannell and Wolfe (2008) showed that a) ohnologs had intrinsically higher constraint, that b) WGD relaxed this constraint somewhat, and c) that even a relatively long time after WGD, the constraint on the ohnologs had not fully returned to the pre-WGD level. Hence, it is natural to ask two related questions: 1) can we detect both the intrinsically higher constraint and its postpolyploidy relaxation in plants as well? and 2) is the increased constraint on ohnologs acting even today for paleopolyploid species?

In answer to question #1, we have clearly shown that genes retained in duplicate/triplicate are intrinsically more constrained. When compared with the subset of Brassica single-copy genes with syntenic orthologs in A. thaliana, triplicated Brassica genes actually show less constraint than do those single copy genes. When all Brassica genes are considered, regardless of their status in Arabidopsis, the triplicated genes are on average more constrained than the single-copy genes, but still show relaxation in constraint relative to what would be predicted based on their constraint in unduplicated outgroup genomes, again arguing that intrinsic constraint did relax after the triplication. Nevertheless, speaking to question #2, we see that the balance of high intrinsic constraint relaxed by polyploidy described in question #1 is a long-lasting one: the patterns of constraints on surviving ohnologs from both At-α and Br-α are mimicked at the population level. As these population data are as near as we can come to “selection at this instant”, it appears that whatever the postpolyploidy evolution of ohnologs, they have not specialized or diverged enough to lose the characteristics that marked them as ohnologs. Our findings of the long-lived effects of polyploidy (and nested polyploidy) on a gene’s selective constraint also complement the findings of Woodhouse et al. (2014), who found that the expression differences between ohnologs due to allopolyploidy can persist even through subsequent polyploidy events.

We also see some association between selective constraint and position in the metabolic network, although these associations are weak, as has been seen in other network analyses (Bloom and Adami 2003; Jordan et al. 2003; Hahn et al. 2004; Vitkup et al. 2006). Selective constraint is correlated with clustering coefficient in the metabolic network. Higher clustering in the network means that more neighbors interact with each other, that is, there are more alternative paths connecting two reactions. Selection pressure might be relaxed in the highly clustered regions in the network because of this increased redundancy, but be relatively more stringent in less clustered parts. The fact that genes with similar selective constraints are also more likely to be neighbors in the network may describe a similar phenomenon.

We have previously suggested that postpolyploidy evolution might be seen as proceeding in phases (Bekaert et al. 2011; Conant 2014; Conant et al. 2014). Our results here suggest, however, that such phases should not be taken too literally, as the ohnologs created by polyploidy are distinct in their character at their origin and retain much of this distinctiveness, at least in their sequence evolution, long after the polyploidy events. Such a result suggests again how polyploidy continues to shape the evolution of its possessors long afterward.

Supplementary Material

Supplementary data are available at Genome Biology and Evolution online.