DNA sliding in nucleosomes via twist defect propagation revealed by molecular simulations

Abstract

While nucleosomes are highly stable structures as fundamental units of chromatin, they also slide along the DNA, either spontaneously or by active remodelers. Here, we investigate the microscopic mechanisms of nucleosome sliding by multiscale molecular simulations, characterizing how the screw-like motion of DNA proceeds via the formation and propagation of twist defects. Firstly, coarse-grained molecular simulations reveal that the sliding dynamics is highly dependent on DNA sequence. Depending on the sequence and the nucleosome super-helical location, we find two distinct types of twist defects: a locally under-twisted DNA region, previously observed in crystal structures, and a locally over-twisted DNA, an unprecedented feature. The stability of the over-twist defect was confirmed via all-atom simulations. Analysis of our trajectories via Markov state modeling highlights how the sequence-dependence of the sliding dynamics is due to the different twist defect energy costs, and in particular how nucleosome regions where defects cannot easily form introduce the kinetic bottlenecks slowing down repositioning. Twist defects can also mediate sliding of nucleosomes made with strong positioning sequences, albeit at a much lower diffusion coefficient, due to a high-energy intermediate state. Finally, we discuss how chromatin remodelers may exploit these spontaneous fluctuations to induce unidirectional sliding of nucleosomes.

INTRODUCTION

Nucleosomes are large protein–DNA complexes consisting of about ∼147 base-pairs (bp) of DNA wrapped ∼1.7 times around a histone octamer (1), and they represent the fundamental unit of chromatin organization in eukaryotic cells, enabling the genome to be efficiently packed inside the nucleus. Despite representing 75 to 90% of the whole genome (2), nucleosomal DNA cannot be directly accessed by most other DNA-binding proteins (3), raising questions about the ability of the cell to simultaneously fulfill the two roles of genome organization and transcription regulation. This apparent contradiction is resolved by the tight regulation of nucleosome positions along the genome (3). Positioning is in part encoded into the DNA sequence itself (4), which favors nucleosome assembly at sequence locations where DNA has a high intrinsic bending (5). Furthermore, nucleosome positions are dynamically regulated via the action of active chromatin remodelers, which consume ATP to displace nucleosomes to different sequence locations (6). By repositioning nucleosomes, remodelers can occlude or make accessible target regulatory sequences to the respective transcription factors (7). Remodelers are also responsible for controlling the length of the linker DNA between successive nucleosomes, ensuring their even spacing (6).

While the influence of DNA sequence on the observed in vivo nucleosome positioning patterns has been well characterized (3), with software being able to predict nucleosome affinities from DNA elasticity alone (8), there is still debate on how repositioning of nucleosomes is achieved at the molecular level (7). Most experiments focus on the activity of chromatin remodelers. However, ATP consumption is not necessary for repositioning to occur, as nucleosomes can also diffuse along the DNA sequence simply driven by thermal fluctuations (9). Moreover, spontaneous fluctuations in the nucleosome structure have been suggested to form the basis of the complex remodeling activity (1,10,11). For these reasons, a clear understanding of passive nucleosome diffusion at the molecular level is much needed, and it will be of high relevance for the understanding of active in vivo scenarios.

The nucleosome structure is stabilized, on top of global electrostatic attractions, by an extensive network of interactions between DNA and histone octamer, mainly localized at the 14 contact points where the DNA minor groove faces the octamer (12). Because of these strong interactions, repositioning via complete nucleosome disassembly and re-assembly at a different sequence location is expected to have only a minor contribution, and most models of active and passive repositioning consider some form of nucleosome sliding, where DNA can move around the histones via small intermediate steps, while maintaining most histone–DNA contacts intact (11,13,14).

Models previously suggested for nucleosome sliding can be classified into two scenarios: the rotation-uncoupled mode, where DNA sliding around a histone octamer is not accompanied by DNA rotation around its helical axis, and the rotation-coupled mode, in which DNA moves in a screw-like manner. For the former, Schiessel et al. proposed that a loop defect forms at one end of the nucleosome via partial unwrapping and it subsequently diffuses reaching the opposite end, causing a net repositioning of at least a DNA helical turn (∼10 bp) (14). On the other hand, the rotation-coupled sliding of DNA around histones was suggested to proceed via the propagation of twist defects at small steps of 1 bp (11,13). Twist defects are deformations of the DNA path that enable to accommodate different numbers, plus or minus one from the canonical number, of base pairs between any neighboring histone–DNA contact points, causing a change in the length of nucleosomal DNA from the standard 147 bp (1). In fact, defects characterized by DNA under-twisting, where the number of base pairs in one helical pitch is fewer by one, are present in crystal structures (15,16) and in solution (10), and their role in spontaneous repositioning is supported by experiments showing that sliding is suppressed after the addition of ligands that would obstruct the screw-like motion of DNA (17,18). Furthermore, the recently resolved cryo-EM structure of an active remodeler bound to the nucleosome did not reveal large-scale distortions to the canonical nucleosome conformation (19) and FRET experiments showed that repositioning can occur via small uni-directional steps (20,21), suggesting that the motion of DNA during active sliding may closely resemble the defect-mediated screw-like motion proposed for spontaneous repositioning.

Molecular dynamics simulations represent the ideal framework to address nucleosome sliding mechanisms, since they enable the direct observation of repositioning at near-atomic level. Twist defect formation has already been observed in all-atom simulations of nucleosomes (22); however, it occurred rarely and only near the nucleosome ends, whereas the study of repositioning would require defect propagation through the entire nucleosome structure. To solve the time-scale problem, we resort to coarse-graining at the level of individual residues and nucleotides. Coarse-grained MD simulations provide the optimal compromise between speed-up and accuracy, and have already been successfully applied to the study of nucleosome dynamics (5,23–28).

In particular, in two very recent studies by our (26) and de Pablo's (28) groups, MD simulations were employed to investigate the spontaneous repositioning of nucleosomes. The main result of these works was the observation of two distinct modes of sliding, coupled and uncoupled with DNA rotation, consistently with past theoretical work (11,13,14). Furthermore, the DNA sequence was found to have a large effect in favoring one mechanism versus the other. While these results are important and likely to have a wider impact for the understanding of chromatin dynamics, there were key questions left unresolved. In particular, while the rotation-uncoupled sliding mode was well-characterized, there was no clear evidence of the twist defect intermediate conformations that were suggested to mediate the rotation-coupled (or screw-like) repositioning mechanism (11,13). This was due to the absence (28) or the weakness (26) of the hydrogen bond interactions between histone octamer and DNA in the computational model, which are also necessary to stabilize twist defect conformations in the MD simulations (see Materials and Methods). In the current study, we employed an intermediate hydrogen bond strength within the range giving a nucleosome disassembly profile consistent with experiments (26), enabling us to establish the fundamental role of twist defects in nucleosome sliding.

In what follows, we first report on MD simulations of nucleosomes formed with six 2-bp periodic DNA sequences, showing that in all cases the rotation-coupled sliding proceeds via the spontaneous formation and propagation of twist defects around the nucleosome. By analyzing our MD trajectories via Markov state modeling, we characterized how the free energy costs of defect formation at the different nucleosome regions control the repositioning kinetics, and can result in highly sequence-dependent diffusion time scales, differing by almost two orders of magnitude for the considered uniform sequences. This novel type of sequence dependence adds up to the previous finding that DNA sequence may also control sliding time-scales via its intrinsic bending (11,28). Notably, our simulations reveal a form of twist defect that was previously unobserved, where local over-twisting of DNA enables to accommodate an extra base pair within one helical pitch. An all-atom MD simulation confirms the stability of this novel type of defect. In the discussion section, we further argue how the alternation of over-twisting and under-twisting across the nucleosome may facilitate the action of chromatin remodelers. Finally, we show how twist defect propagation can also mediate the spontaneous sliding of nucleosomes formed with strong positioning sequences, and since each repositioning step only corresponds to a small free energy cost, this suggests how remodelers may be able to easily displace these very stable nucleosomes.

MATERIALS AND METHODS

Coarse-grained computational model and MD simulations of the nucleosome

To investigate the molecular mechanism and the sequence-dependence of sliding, we run unbiased coarse-grained MD simulations of nucleosomes with 223 base pairs (bp) of double-stranded DNA, therefore allowing DNA repositioning up to a length equal to the ∼38 bp of linker in each direction (the initial conformation is depicted in Figure 1A, all molecular visualizations have been generated with the software VMD (29)). In the first part of our work, we consider all the six possible nucleosomal sequences with a periodicity of 2 bp, which we indicate using the repeating base step as poly-AA, AC, AG, AT, CC and CG (the complementary bases on the opposite strands being TT, GT, CT, AT, GG and CG). We note that in the literature poly-AA and poly-CC are usually referred to as poly(dA:dT) and poly(dG:dC) tracts respectively (3,30), and, despite being known for their low affinity for nucleosome formation, they can be assembled into nucleosomes (30). In the last part of the work, on the other hand, we consider nucleosomes formed by the two strong positioning sequences α-satellite and 601, as found in the respective crystal structures with PDB ids 1KX5 (16) and 3LZ0 (15). In these two cases, we use poly-CG DNA linkers to reach again the total length of 223 bp.

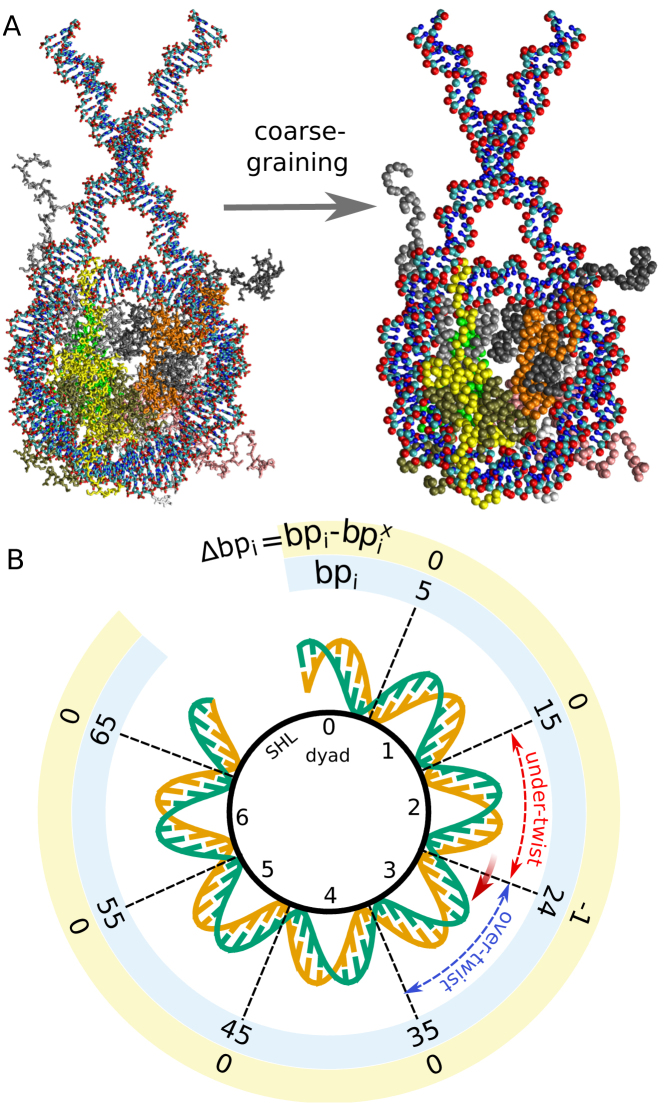
Figure 1.

Coarse-graining and defect formation. (A) All-atom (on the left) and coarse-grained (right) nucleosome structures. Histones H3 in light and dark gray, H4 in orange and light green, H2A in yellow and white, and H2B in dark green and pink. For the DNA, phosphate groups are in red, sugar groups in cyan and bases in blue. (B) Schematics of a half nucleosome structure, mechanism of defect formation and analysis method. Super-helical locations (SHLs) start from 0 at the dyad and increase by 1 every DNA turn. histone–DNA contact points are at the half-integer SHLs. For each configuration in the MD trajectories, we track the base pair indexes bp_i at the 14 histone–DNA contact points, and their value relative to the initial one observed in the 1KX5 crystal structure configuration, which we refer to as the contact indexes Δbp_i = bp_i – bp_i^X. At the beginning, when no twist defects are present, all contact indexes will be zero. If, for instance, after some time the DNA undergoes a clockwise screw-like motion by 1 base pair at contact point 2.5, then the DNA segment at SHL 2 will have a missing base pair relative to the initial structure, whereas at SHL 3 there will be an extra base pair, corresponding respectively to under-twist and over-twist defects. These defects can be quantified by the difference k between two neighboring contact indexes (respectively k = –1 and k = +1 in the example).

Following an approach similar to that of Refs. (5,23,24), the histone octamer is represented according to the AICG2+ coarse-grained model (31), whereas the DNA according to the sequence-dependent 3SPN.2C coarse-grained model (32). Notably, the ability of this force-field combination to reproduce the sequence-dependent free energies of DNA folding into nucleosomes has been confirmed (5). Furthermore, the 3SPN.2C model has been parametrized against the flexibilities of the 10 unique base steps (32), as obtained by Olson et al. (33,34), suggesting that its usage is appropriate to study detailed sequence-dependent effects at place during nucleosome repositioning. In AICG2+, we coarse-grain proteins at the level of individual amino acids, with each coarse-grained bead placed on the Cα atom of each residue; whereas in the 3SPN.2C model each nucleotide is represented by three beads corresponding to phosphate, sugar and base groups (see Figure 1A). The native structure of the histone octamer employed for the protein structured-based potential is taken from the 1KX5 crystal structure (16); flexible tails with zero occupancy in the PDB file are modeled using a sequence-dependent flexible local potential (35,36).

Histones and DNA interact via excluded volume, long-range electrostatics, and hydrogen bonds, the latter represented according to a recently developed coarse-grained potential (26). Excluded volume radii are dependent on the bead-type only and they have been obtained from a database of protein–protein and protein–DNA complexes (37) (the radii used in (37) have been further rescaled by a factor of 1.1 to prevent histone tails from inserting between the two complementary DNA strands). Electrostatics is modeled according to the Debye–Hückel theory. The charges on the Cα beads of the structured part of the histone octamer have been parametrized using the RESPAC method (38), which optimizes the coarse-grained electrostatic potential against the all-atom potential of the 1KX5 crystal structure. Since RESPAC requires the protein to maintain its native fold, this approach is only applied to the globular part of the octamer, whereas for the flexible histone tails we assigned the appropriate unit charges on ARG, LYS, ASP and GLU residues, leaving all other residues uncharged. Following the recommended practice (32,37), the intra-DNA electrostatics is generated by charges of –0.6q placed on the phosphate groups, whereas these charges are rescaled to their standard unit value for protein–DNA interactions.

Hydrogen bonds between DNA and histones were often not explicitly included in past coarse-grained models of the nucleosome (5,28). However, these interactions were shown in our previous work (26) to be necessary for obtaining stable nucleosome conformations consistent with those observed in crystal structures at high precision. In the Supporting Information (SI) Supplementary Figure S1, we further show how experimental twist-defect conformations spontaneously appear only after including hydrogen bond interactions. For the definition of hydrogen bonds between histone residues and DNA phosphate groups, we used the 1KX5 and 3LZ0 crystal structures as references. Our coarse-grained hydrogen bond potential is invariant under a screw-like motion of the DNA relative to the histone octamer, enabling the study of repositioning (see SI and (26) for more details on this potential and its validation). The energy constant ϵ of hydrogen bonds was set to 1.8k_BT, which is an intermediate value in the range resulting in a nucleosome unwrapping behavior consistent with experiments (1.2–2.4k_BT) (26). The value of ϵ employed here is larger than the one used in our previous study (26), enabling us to capture more accurately the details of the repositioning mechanism via twist defects, in particular for sequences with fast kinetics. The repositioning mechanism discussed in the results is however robust to changes in the hydrogen bond strength (see Supplementary Figure S2 for our results on poly-CG nucleosomes using ϵ = 1.2k_BT and ϵ = 2.4k_BT).

All coarse-grained MD simulations were performed with the software CafeMol 3.0 (available at http://www.cafemol.org/) (39). We prepared the initial conformations by taking the 1KX5 crystal structure and aligning the two extra 38-bp linkers to the 147-bp nucleosomal DNA. Before production runs, the coarse-grained structure was energy minimized using the steepest descent scheme. Simulations are performed integrating the equations of motion with Langevin dynamics at temperature T = 300 K. The ionic strength was set to 150 mM. All other MD settings are the default values given in CafeMol 3.0. Snapshots of the nucleosome configuration were saved every 500 time steps. For the periodic sequences, we performed 24, 24, 36, 36, 12 and 12 independent runs of 10⁷ MD time steps for poly-AC, AT, AG, CG, AA and CC respectively. To evaluate the equilibrium properties of α-satellite and 601 nucleosomes we performed a single long simulation of 10⁸ MD steps for each sequence. To investigate the repositioning kinetics of 601 nucleosomes we performed 1400 short simulations of 2 × 10⁶ to 10⁷ time steps, starting from several configurations shifted from the reference 3LZ0 crystal structure by 3, 4, 5 or 7 bp.

Twist defect analysis and generation of Markov state models

The DNA interacts with the histones mainly at the 14 contact points where the DNA minor groove faces the histone octamer (12). The nucleosomal regions are traditionally indicated by the super-helical location (SHL), corresponding to the distance in helical turns from the nucleosome symmetry axis, so that the dyad is located at SHL 0 and the SHL value changes by 1 every DNA turn, ∼10 bp (Figure 1B). Therefore, the histone–DNA contact points are located at the half-integer SHLs ±0.5, ±1.5, ±2.5, ±3.5, ±4.5, ±5.5 and ±6.5 (the terminus pair). In what follows we will indicate each contact point by the value of the corresponding SHL, e.g. the contact point 1.5 to indicate the histone–DNA contact at SHL 1.5. When the number of base pairs between two contact points increases or decreases by 1 bp relative to the reference 1KX5 nucleosome crystal structure wrapping the canonical 147 bp, we assign it a twist defect. A defect with 1 extra base pair corresponds to over-twisting of DNA at the SHL between the contact points (we term it an over-twist defect), whereas that with 1 missing base pair corresponds to under-twisting of DNA (an under-twist defect). Our terms follow from Richmond and Widom (40), although over the years different authors used different terms to refer to these two distinct types of defects (e.g. over-winding versus under-winding of DNA (41) or antikink versus kink (11)), and over-twisting may also be viewed as a DNA compression, whereas under-twisting as stretching. The missing or extra base pair will be accommodated via a structural change in the outer strand of the duplex DNA around integer SHL values, a change permitted by the lack of the constraints that are otherwise imposed by the histone–DNA contacts (12).

To evaluate the motion of DNA during sliding, we track the values of the base pair indexes at each contact point relative to the reference 1KX5 crystal structure. We call these coordinates the contact indexes Δbp_i, and in our case they are continuous variables computed from the nucleosome conformation (see SI text for the description of their calculation). Most MD simulations start in the 1KX5 conformation, where all the contact indexes will be equal to 0 and there are no twist defects. We illustrate the formation of twist defects using a hypothetical trajectory. Suppose the DNA moved by 1 bp at the contact point 2.5 toward the closest nucleosome end, whereas the DNA at the neighboring contact points did not move (Figure 1B). The contact index Δbp_2.5 takes a value close to –1, whereas the nearby contact indexes remain zero. This means that at SHL 2 there is now a missing base pair (under-twisting), accompanied by an extra base pair (over-twisting) at SHL 3. The difference between neighboring contact indexes can be used to evaluate the presence of twist defects at any SHL i: k_i = Δbp_i+1/2 – Δbp_i-1/2 (we refer to these as defect coordinates). We track the dynamics of contact indexes and defect coordinates over time to describe the repositioning pathways observed during our MD trajectories.

To generate the Markov state models (42) (MSM) of defect propagation through the nucleosome we follow an approach similar to that outlined in (43): we first performed a clustering using the list of contact indexes and then estimated the transition rates between the clusters from our MD trajectories. In our analysis we only consider the central 12 contact points (since the two weaker outer contacts show large fluctuations and do not accommodate twist defects relevant for sliding). Furthermore, for 2-bp periodic sequences we introduce the same periodicity of 2 bp in the contact indexes, since a rotation-coupled motion by 2 bp will produce exactly the same state (except for a minor change in DNA linker lengths). To do so, each contact index is represented as an angle via cosine and sine components, i.e. [cos(2πΔbp/2), sin(2πΔbp/2)].

For the 6 periodic sequences, before clustering the nucleosome conformations into discrete MSM states, the contact indexes were projected onto a lower-dimensional space defined via time-lagged independent component analysis (tICA) (44). The linear tICA projection, which is closely related to principal component analysis, can efficiently capture the slow dynamics of the system, and it is particularly well-suited to divide the conformations into the metastable cluster states which will then form the nodes of the MSM (45). The coefficients for projecting the contact indexes onto the two slowest tICA coordinates are reported in Supplementary Figure S3, showing how defect formation is automatically captured as a difference between contact indexes. The positions of typical nucleosome conformations onto two-dimensional tICA projections are shown in Supplementary Figure S4. The eight slowest tICA coordinates are sufficient to identify for all sequences the formation of metastable twist defects that play a role in nucleosome repositioning. The nucleosome conformations observed in MD are then clustered using the density peak clustering (DPC) method (46), computing the local density in the 8D tICA spaces using a Gaussian kernel with variance equal to 0.35. This method enables to automatically detect clusters corresponding to local free-energy minima (i.e. metastable states) in our complex multi-dimensional landscape, allowing to capture the detailed kinetics of the system (43,46). Depending on the considered sequences, the clustering identifies between 13 and 86 states to be used for the Markov state modeling; the cluster centers of the most populated states correspond to the same nucleosome conformations depicted in Supplementary Figure S4. In the case of 601 nucleosomes, there is no sequence periodicity, and to generate the MSM of repositioning we used the following simpler approach: we clustered all conformations using an index equal to the integer value closest to the sum of contact indexes –1.5 and +1.5, since inspection of our MD trajectories reveals that these are the slowest-changing DNA contacts and are therefore sufficient to produce a minimal model of 601 repositioning.

Markov state models were generated using the software PyEMMA 2 (45). For each periodic sequence we produced a Bayesian MSM using 24, 24, 36, 36, 12 and 12 independent trajectories (10⁷ MD steps each) and a lag time of 0.04, 0.1, 0.1, 0.02, 2 and 2 × 10⁶ time steps for poly-AC, AT, AG, CG, AA and CC, respectively. Supplementary Figure S5 shows that the implied time scales of our MSMs do not significantly change when choosing longer lag times, indicating the good quality of the results. Since all generated Markov state models display a clear separation of time scales (i.e. there are only few slow transitions in the system), we further grouped the nucleosome states into long-lived metastable basins using the Robust Perron Cluster Analysis (PCCA+) (47). The optimal number of long-lived basins to perform PCCA+ has been inferred from the gap observed in the implied time-scales of the MSMs (Supplementary Figure S5). For the 601 case, the MSM was generated from the 1400 short trajectories with different initial conditions with a lag time of 0.5 × 10⁶ steps. For each sequence, following a Bayesian approach, the reported means and standard deviations were evaluated from a sample of 100 MSMs from the corresponding ensemble of models consistent with the MD simulations (see Ref. (45) for more details). The free-energy landscapes in Figures 5 and 8C have been generated from the stationary probability distributions of the MSMs.

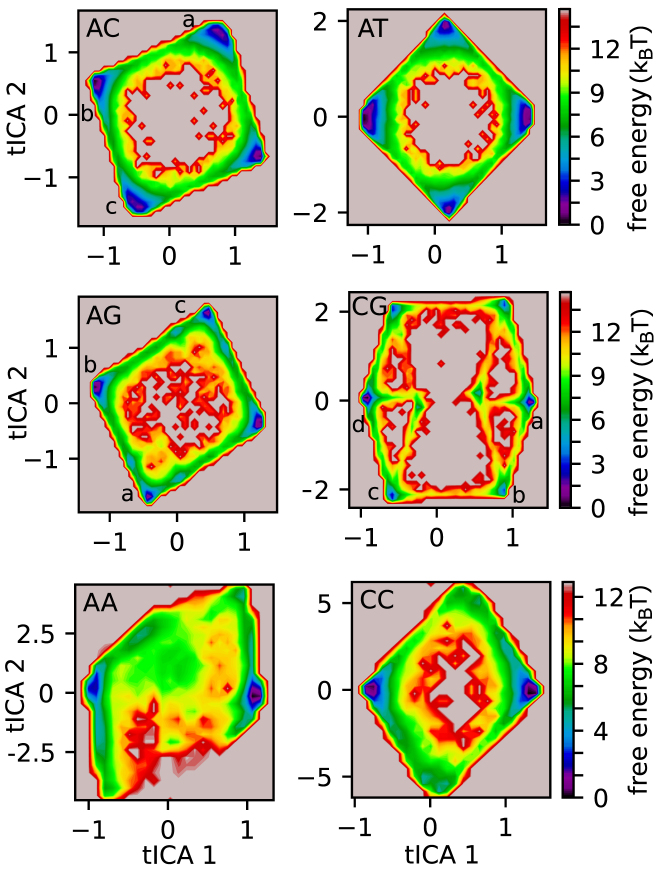
Figure 5.

Free-energy surfaces. For each 2-bp periodic DNA sequence, we show the free energy landscapes obtained via Markov state modeling along the first and second tICA coordinates. Each local minimum correspond to a long-lived metastable basin of the system (see Supplementary Figures S6 and S7). The typical nucleosome conformations and defect patterns observed in some of the basins (labeled by a, b, c or d in poly-AC, AG and CG) are represented via a set of cartoons in Figure 6.

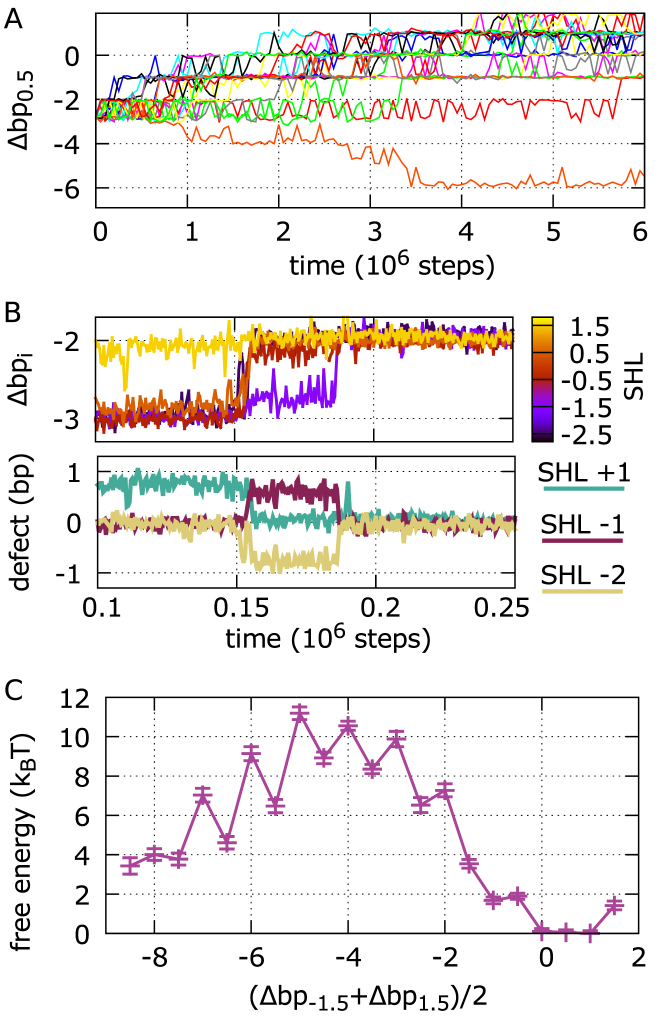
Figure 8.

Repositioning of 601 nucleosomes via defect formation. (A) Dynamics of contact index 0.5 for a sample of 20 trajectories starting from an initial configuration shifted by 3 bp from the crystal structure. In most trajectories, repositioning proceeds toward the optimal crystal structure configuration with contact indexes zero; with this shifted initial condition, out of a total of 400 MD runs, we only find 3 sliding events going in the opposite direction. (B) Dynamics of the central contact indexes during a section of a sliding trajectory (top), showing that repositioning occurs via formation or disappearance of defects at SHLs –2, –1 and +1 (bottom). (C) Free energy profile of 601 repositioning reconstructed via Markov state modeling, as a function of the average of the contact indexes at SHLs ±1.5. Integer states have no defects, while half-integer ones have DNA over-twisting at SHLs 0, –1 or +1.

RESULTS

Screw-like DNA sliding via twist defect propagation

As detailed in the Methods section, we performed coarse-grained MD simulations of nucleosomes formed with 223 bp of DNA (Figure 1A) with the 2-bp periodic sequences poly-AA, AC, AG, AT, CC and CG. In our simulations, all the sequences diffuse on the histone octamer by several base pairs within 10⁷ MD steps (Figure 2A and B). Visual inspection of the simulations suggests that the nucleosome maintains the same overall conformation even during repositioning (Figure 2A), highlighting the screw-like motion of DNA on the histone octamer (11). However, only sequences poly-AC, AG, AT and CG closely follow the DNA path observed in the crystal, with the minor grooves facing the histone octamer at the half-integer SHLs (Figure 2C). On the other hand, the homopolymeric sequences poly-AA and CC show larger structural fluctuations, and as we move from the dyad towards the nucleosome entry/exit, the DNA path becomes visibly out-of-sync with respect to the one in the crystal (Figure 2C), destabilizing the histone–DNA contacts. This difference can also be observed from the average root mean square deviation from the crystal at the different SHLs (Figure 2D); only for poly-AC, AG, AT and CG most contacts remain close to the 1KX5 reference, with root mean square deviation (rmsd) ∼2 Å, whereas poly-AA and CC display significant deviations as we move away from the dyad (rmsd up to 4 Å). These structural changes may be related to resistance of these homopolymeric sequences to be incorporated into nucleosomes (3,30). When large fluctuations away from the reference crystal structure are present, our definition of twist defects may not be appropriate, therefore for poly-AA and CC we do not analyze defect formation at SHLs further than ±2, and in all cases we do not discuss the last defects at SHLs ±6.

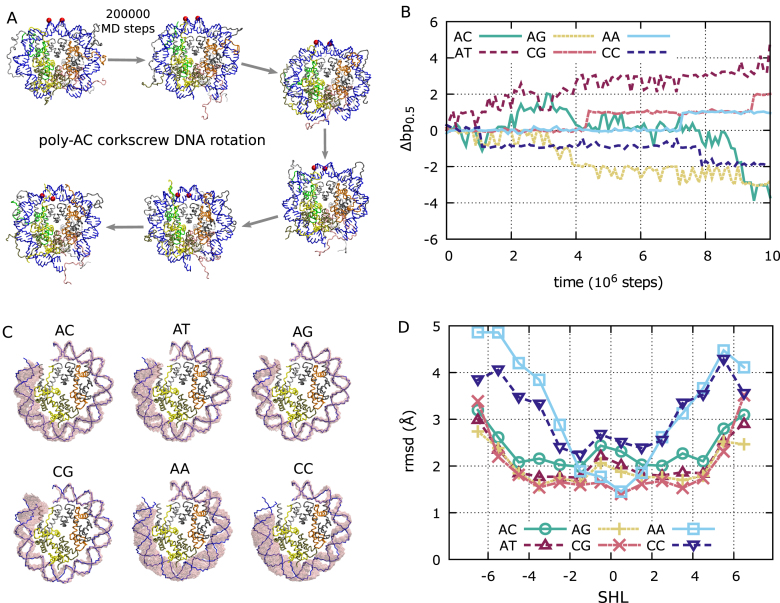
Figure 2.

Screw-like sliding of DNA. (A) Representative snapshots from a poly-AC trajectory (from 8.5 × 10⁶ to 9.5 × 10⁶ MD steps in panel B). During DNA sliding, the overall DNA path remains close to the initial crystal structure configuration. Two reference phosphates initially at the dyad are represented as red spheres, highlighting the screw-like motion of DNA. For the purpose of clarity, we only depict the central 70 bp of DNA. The histone color scheme is identical to that in Figure 1. (B) The dynamics of contact index 0.5 (next to the dyad) for representative trajectories of the six considered sequences, showing that we observe repositioning by a few base pairs within the considered time scales. (C) In pink, overlay of all DNA backbone conformations observed during the MD simulations shown in panel B. For comparison, we show in blue the DNA path in the 1KX5 crystal structure. For clarity, we only depict half of the nucleosome, from SHL = 0 to SHL = 7 (the other half of the nucleosome shows a similar behavior). (D) As a function of SHL, the average root mean square deviation from the reference 1KX5 structure of the nucleosomal regions corresponding to the 14 contact points at the half-integer SHLs.

Next, we analyzed the dynamics of the contact indexes. For all sequences that form stable nucleosomes (poly-AC, AG, AT and CG) the contact indexes reside close to integer values and move by one base pair in a stepwise fashion, indicating that the screw-like motion of DNA preserves the hydrogen bonding pattern observed in the crystal structure, with the histone residues contacting DNA phosphates progressively shifted by one base pair. Importantly, we notice that neighboring contact indexes do not always move simultaneously, indicating the formation of a twist defect between them. Examples of this behavior from the simulations are shown in Figure 3 and in the supplemental movies.

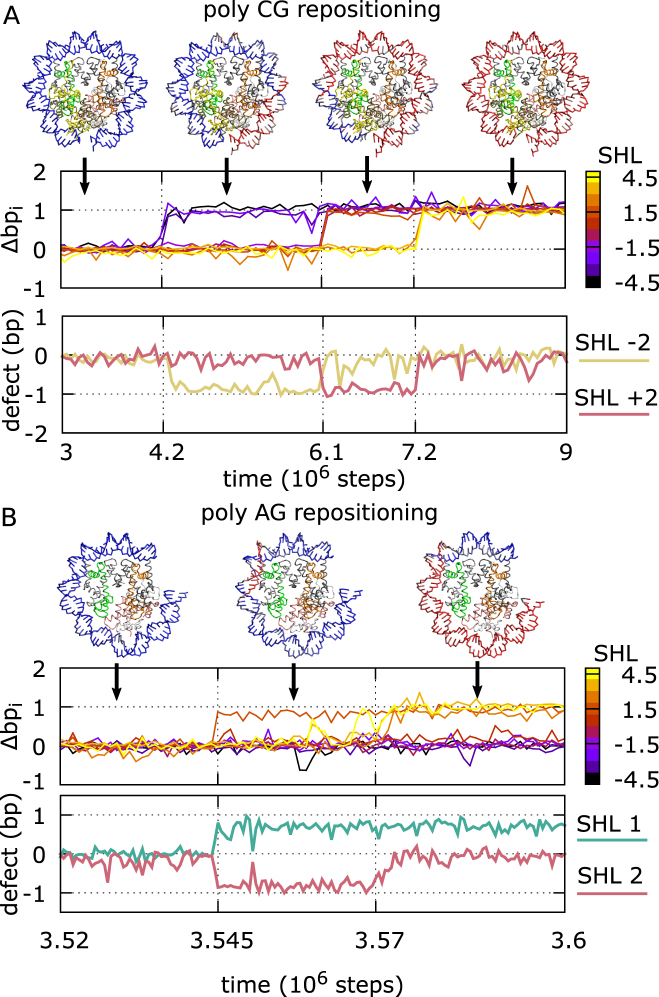
Figure 3.

Repositioning via defect propagation. Representative fragments of trajectories for the poly-CG and AG sequences, in panels A and B respectively. On the top (for each panel), nucleosome conformations during repositioning: the DNA path is initially colored in blue, and when a phosphate group moves by 1 bp in the negative SHL direction (clockwise) along the DNA backbone, we change the color of the nucleotide to red. On the center, dynamics of histone–DNA contact indexes from SHL –4.5 to 4.5 for sections of the representative trajectories. On the bottom, dynamics of the defect variables k at the SHLs where stable defects are formed.

In a trajectory for the poly-CG sequence in Figure 3A and Movie 1, at first, the contact indexes Δbp_-4.5, Δbp_-3.5, and Δbp_-2.5 move together from zero to one; this region of DNA undergoes a cooperative rotation-coupled sliding toward the closest nucleosome exit by 1 bp. We note that this motion involves the simultaneous breakage and reformation of the histone–DNA hydrogen bonds at the three contact points. At this stage, the rest of contact indexes does not move. Thus, a 1 bp gap appears between Δbp_-2.5 and Δbp_-1.5, corresponding to local DNA under-twisting at SHL –2. Later in the trajectory, the second group Δbp_-1.5, Δbp_-0.5, Δbp_0.5 and Δbp_1.5 moves together in the same direction as the previous step, not simultaneously from the third group Δbp_2.5, Δbp_3.5 and Δbp_4.5. In this period of time, the under-twist defect resides at SHL +2. Finally, the third group follows the same shift so that the defect disappears. After the third transition, the whole DNA sequence is repositioned by 1 bp. This repositioning event can be either viewed as due to three progressive rotation-coupled DNA steps in the negative SHL direction or due to the propagation DNA under-twisting in the positive SHL direction. In poly-CG nucleosomes, the same type of defects are also found at SHLs ±5 (see Figure 4A), but their dynamics is much faster than at SHLs ±2.

Figure 4.

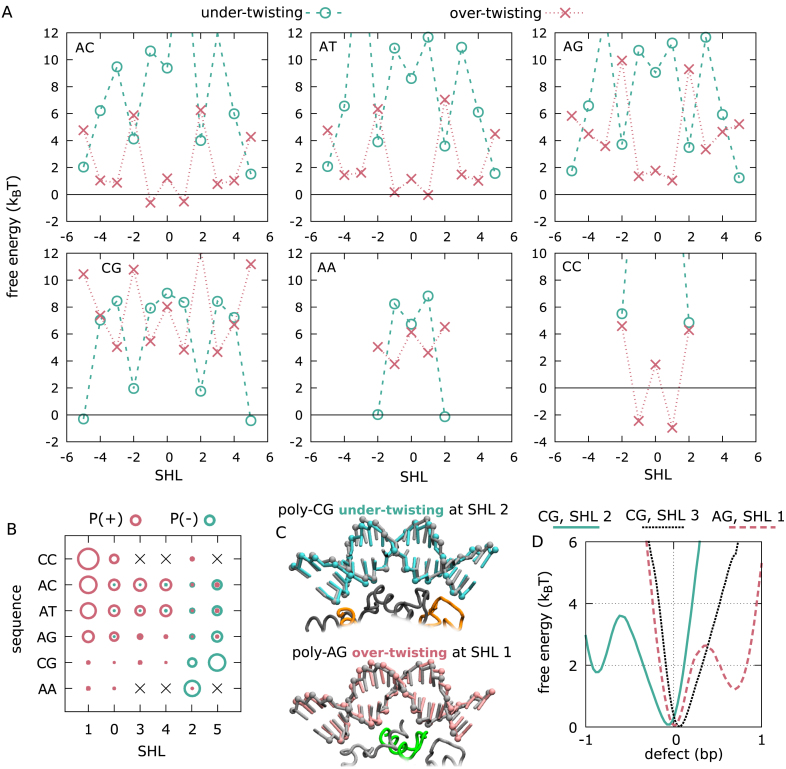
Free energy and structure of defects. (A) Free energy costs of DNA under-twisting (cyan circles) and over-twisting (pink crosses) as a function of sequence and super-helical location. For poly-AA and poly-CC sequences, we only show the results for the five central SHLs, because of the large fluctuations further away from the dyad. (B) Summary of the probabilities of under-twisting and over-twisting (proportional to the circle areas, in cyan and pink respectively) for each DNA sequence and SHL (from 0 to 5, negatives SHLs show similar behavior). Ordering is based on the propensity of the two defect types. (C) Examples of defect structures observed during our simulations: under-twisting at SHL –2 in poly-CG nucleosomes (in cyan), compared to the standard crystal structure form (black), and over-twisting at SHL 1 in poly-AG (pink), again compared to the standard form. Phosphate groups are highlighted as spheres. The missing or extra base pair is accommodated via deformations on the outer side of the DNA lacking contacts with the histones (partially shown following the color scheme of the other figures). Each DNA structure has been obtained by averaging over 100 MD frames from the representative trajectories shown in Figure 3. (D) Examples of potentials of mean force along the defect coordinates k for three representative sequences and SHLs: poly-CG at SHL 2 (cyan, solid line), where a metastable under-twist defect can form; poly-CG at SHL 3 (black, dotted line), with a unimodal distribution highlighting the absence of stable defects; poly-AG at SHL 1 (pink, dashed line), where over-twisting is metastable.

In another example, the poly-AG sequence exhibits a markedly different dynamics (Figure 3B and Movie 2). In the trajectory, repositioning is initiated by DNA motion from the internal contact point 1.5, which results in the formations of a pair of twist defects of opposite type: one at SHL 2 (under-twisting) and another at SHL 1 (over-twisting). Soon after that event, Δbp_2.5, Δbp_3.5 and Δbp_4.5 follow the movement towards the dyad from the nucleosome entry so that the defect at SHL 2 disappears. The over-twist defect at SHL 1 stays longer (Figure 3B), and it may eventually propagate to the opposite side of the nucleosome.

In general, we find that defect formation is both SHL- and sequence-dependent. Figure 4A shows the free energy costs of defect formation at the different super-helical locations for the six considered sequences. The free energy cost was estimated directly from the probabilities of forming the defects in our simulations. From these free energy curves we can identify interesting general features. Firstly, we note that under-twisting is generally the favored defect deformation at SHLs ±2 and ±5, whereas conversely over-twisting is favored at the other locations, and especially at SHLs ±1 (defect probabilities are summarized in Figure 4B). Secondly, as the DNA sequence changes from poly-CC, to AC≈AT to AG to CG to AA, under-twisting and over-twisting becomes respectively more and less favorable at every SHL (Figure 4B). Interestingly, while having to limit our analysis to the central nucleosome region only, we find that the low-affinity homopolimeric sequences poly-CC and AA (30) can be placed at the extremes of the spectrum of defect formation. Specifically, poly-AA nucleosomes rarely accommodate defects at the three central SHLs, with likely under-twisting at SHLs ±2, whereas poly-CC maintains two very stable over-twist defects at SHLs ±1, with no under-twisting observed.

In Figure 4C, we also show the average DNA conformations for two examples of defects, under-twisting in poly-CG at SHL 2 and over-twisting in poly-AG at SHL 1, in comparison with the standard DNA form in the 1KX5 crystal. The defects leave the contact-forming minor groove largely unaffected, whereas the extra or missing base pair is accommodated on the outer strand of free DNA, where the backbone takes respectively a longer or shorter path relative to the one lacking defects. The ability of the DNA to maintain the same backbone conformation near the histones (and therefore the hydrogen bonds) even in the presence of defects also explains the stability of these structures.

We have to clarify that the free energies and probabilities of under-twisting and over-twisting in Figure 4A and B are computed directly from the probabilities of the defect variable k to be respectively less than –1/2 and greater than 1/2. However, this definition does not distinguish between simple fluctuations away from the ideal reference crystal structure and actual long-lived metastable defects. Figure 4D shows three examples of free energy profiles (the potentials of mean force) along the defect variable k, corresponding to one unimodal profile centered around the standard DNA form in the 1KX5 crystal for the SHL 3 in poly-CG (where no stable defects form), and two bimodal profiles with metastable under-twist (for the SHL 2 in poly-CG) and over-twist (for the SHL 1 in poly-AG) defects. Only actual metastable defects are important to characterize the kinetics of repositioning and they are appropriately captured by our clustering procedure used to produce the Markov state models described in the next section.

Quantitative sliding dynamics by Markov state models

In order to obtain a clear and quantitative understanding of nucleosome repositioning that goes beyond the anecdotal observations from our MD trajectories and to understand better the role of DNA sequence, we constructed Markov state models (MSM) (42) of repositioning for each sequence (using the software PyEMMA 2 (45), see Materials and Methods for more details), giving us the transition probabilities between nucleosome conformations with different defect patterns. While nucleosomes can adopt many different defect configurations, the resulting MSMs display a clear separation of time scales (Supplementary Figure S5), indicating the presence of only few long-lived metastable basins, with fast transitions between states in the same basin, and slow transitions between two different basins.

The free-energy landscapes along the first and second tICA coordinates (44,45) (describing the slow dynamics of the system, see Methods) further highlight the existence of only few long-lived basins for each system (Figure 5), each of them corresponding to deep free-energy minima separated by large barriers. For poly-AC, AT, AG, CG, AA and CC, we respectively identify 4, 4, 4, 8, 2 and 2 basins, of which features are described below. On these projections, there is a perfect correspondence between the local minima and the long-lived sets identified from the MSMs via PCCA+ clustering (47) (Supplementary Figures S6 and S7, more details in Materials and Methods).

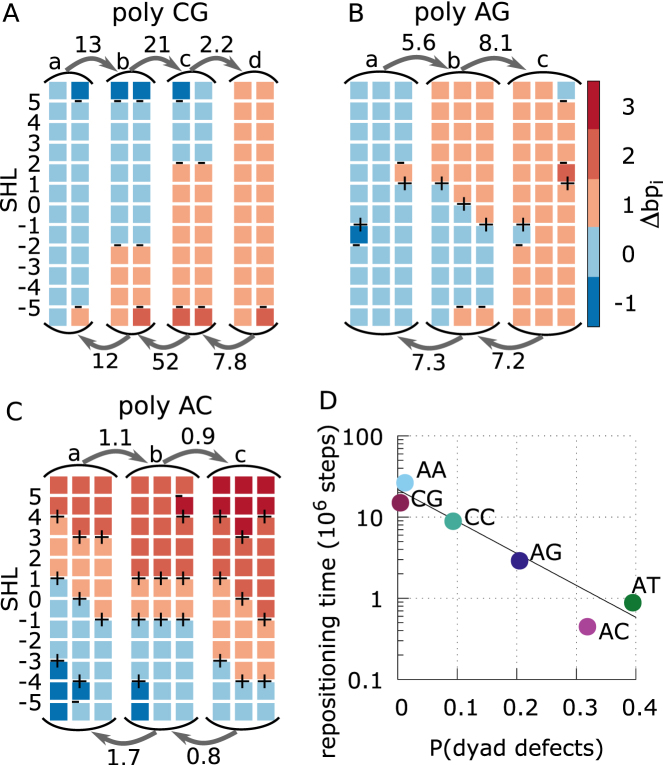
In Figure 6A–C, we describe the features of representative long-lived basins and the transitions between them along a complete repositioning pathway of 1 bp derived from the MSMs of poly-CG, AG and AC. For poly-CG, fast defect formation at SHLs ±5 allows DNA sliding at the nucleosome ends, but complete repositioning by 1 bp (from basin a to d in Figure 6A) has to proceed via two long-lived basins with DNA under-twisting at SHLs ±2 (basins b and c). The transitions between the basins are very slow because involve sliding of long DNA stretches where twist defects cannot form, so that histone–DNA hydrogen bonds have to be cooperatively broken at multiple contact points, with a significant energy barrier. This is consistent with the qualitative picture inferred from the inspection of our trajectories (Figure 3). For poly-AG, starting from the canonical nucleosome form we find fast DNA sliding at contact points ±1.5 (basins a and c in Figure 6B), with formation of a pair of defects at the neighboring SHLs (over-twisting at SHLs ±1 and under-twisting at SHLs ±2). However, repositioning proceeds via a different basin with DNA over-twisting around the dyad but no under-twisting at SHLs ±2 (basin b). The transition to this second basin is slow because the dissipation of the under-twist defect to the nearest nucleosome end involves DNA motion around SHLs ±3 and ±4, where defects have a high energy cost. For poly-AC and AT (in Figure 6C we only show the former), defect formation, specifically over-twisting, is common at most SHLs. This makes kinetics very fast at most nucleosome regions, and the only repositioning bottlenecks involve DNA motion around SHLs ±2, where the free energy cost of defects is the highest (Figure 4A). For both poly-AA and CC sequences, we identify only two long-lived basins (Supplementary Figure S7), corresponding to the same nucleosome conformations but shifted by 1 bp relative to each other. This is consistent with the high free energy cost to change the defect pattern around the dyad region (Figure 4A), which makes DNA sliding very slow.

Figure 6.

Sliding pathways and kinetics derived from Markov state models. (A–C) MSMs for poly-CG, AG, and AC (which is similar to the omitted AT case) in panels A, B and C, respectively, showing the mean first passage times (MFPTs) of the transitions between the long-lived basins of the system along a 1 bp repositioning pathway, and a sample of the most populated nucleosome conformations within each basin. The labels (a, b, c and d) on the states correspond to those indicated in the free energy landscapes of Figure 5. Each column represents a nucleosome conformation, with each colored square representing a section of 10 bps of DNA bound to a nucleosome contact point. The color of the square correspond to the contact index of that DNA section, with the DNA undergoing a screw-like rotation in the negative SHL direction as the color changes from blue towards red. The presence of under-twisting or over-twisting at each SHL is respectively indicated by the symbols – and +. MFPTs are given near the arrows in units of 10⁶ MD steps. Most basins have similar equilibrium probabilities, except for the poly-CG case, where the basins with a defect at SHL ±2 have a free energy of about 2k_BT relative the basins without defects there. (D) Repositioning times for each DNA sequence as a function of the average probability to find excited defect configurations at the three central SHLs (–1,0,1). Here we consider any deviation from the lowest energy state, which in most cases correspond to the configuration found in the 1KX5 reference. However, in the case of poly-CC, over-twist defects are the ground state at SHL ±1, and we consider instead the probability to find a non-defect (excited) state, which is expected to be relevant for repositioning.

From our Markov state modeling we see how the metastability and free energy costs of twist defects control the kinetics of repositioning. The diffusion time-scales (to reposition by 1 bp) estimated from the longest relaxation times of each MSM (Supplementary Figure S5) are 0.45, 0.88, 2.9, 9, 15 and 26 × 10⁶ MD steps respectively for poly-AC, AT, AG, CC, CG and AA sequences (relative errors are ∼7%). Therefore repositioning becomes slower as there are less low-energy metastable defects in the nucleosome. In particular, we find that the repositioning time scale clearly anti-correlates with the average probability to find an excited defect state in one of the three central SHLs (Figure 6D). The dyad nucleosome region is likely the most critical at controlling repositioning because this is where histone–DNA hydrogen bond interactions are also the strongest (48). Similarly, from Figure 6A–C we can also notice that the mean first passage times between the long-lived basins in the system increases as the length of the DNA section that undergoes a collective screw-like motion also increases. For instance, transition times between basins in poly-CG, which involve collective motion at three to four consecutive contact points, are more than one order of magnitude longer than those of poly-AC, which involve only two contacts. Interestingly, it has been found experimentally that nucleosomes formed by the α-satellite positioning sequence with an additional 16-bp poly-AA tract require a higher temperature for repositioning to occur (49). This is consistent with our results showing that the absence of defects in poly-AA nucleosomes confers the slowest repositioning kinetics amongst the uniform DNA sequences investigated.

Repositioning of positioning sequences

While our MD simulations reveal how defects control nucleosome repositioning of 2-bp periodic sequences, it is important to establish whether this mechanism can also apply to DNA sequences with a strong positioning signal, as found in real genomes (4). It has been found that positioning sequences are rich in A/T base steps periodically spaced every ∼10 bp (4); this property confers an intrinsic bending to the DNA, which in turn facilitates further folding into the nucleosome (5). Since A/T steps prefer to bend into the minor groove, when incorporated into the nucleosome they will also prefer to localize at the strong contact points where the minor groove bends inwards, interacting with the histone octamer. However, the rotation-coupled repositioning mechanism discussed here will necessarily proceed via a high-energy intermediate state where these A/T steps localize instead where the minor groove bends towards the outside, slowing down the repositioning relative to the cases discussed above (11). This high-energy state is expected to occur when the nucleosome slides by 5 base pairs from the optimal configuration, and a new low-energy state will be observed after 10 bp shift (9), where the A/T steps are again optimally aligned.

The most likely spontaneous repositioning mechanism of nucleosomes with strong positioning sequences such as 601 is still to be established without any doubt (26). MD simulations of 601 nucleosomes using a coarse-grained computational model where histone–DNA hydrogen bonds are either absent (28) or relatively weak (26) showed that these DNA sequences prefer to slide via a rotation-uncoupled motion, to avoid paying the free energy cost required by DNA rotation (5). However, employing a higher hydrogen bond strength in this study, which is an intermediate value within the range giving a nucleosome stability profile consistent with experiments (26), the rotation-coupled (or screw-like) sliding mode becomes favored over the uncoupled one, since the latter involves the breakage of a large number of histone–DNA hydrogen bonds (these results were already detailed in our previous work) (26). The new 601 nucleosome simulations presented below do not yet settle the debate over which is the preferred sliding mode. However, our main aim is to characterize if and how these strong positioning sequences may slide in nucleosomes via twist defects, since, as we will argue in the discussion section, this mechanism may be easily exploited by chromatin remodelers to displace even these very stable nucleosomes.

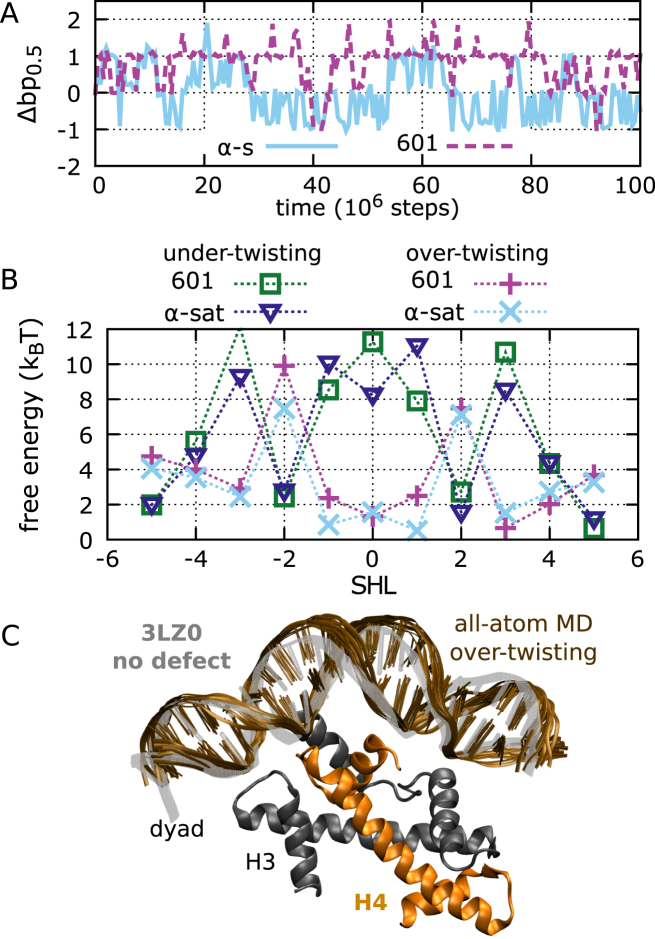
We ran MD simulations of nucleosomes using the 601 and α-satellite positioning sequences starting from the respective crystal structures with PDB ids 3LZ0 and 1KX5. From Figure 7A, we see that these nucleosomes are very stable and no significant repositioning is observed within the considered long time scales. However, in both cases twist defects are very common throughout the nucleosome, and, perhaps surprisingly, we find that the free energies of defect formation are generally lower than those observed in 2-bp periodic sequences, within 2k_BT at most super-helical locations (Figure 7B). Notably, the SHLs where under-twisting is most likely to occur are ±2 and ±5, in agreement with what observed in crystal structures (12,15–17,50) and other coarse-grained models of the nucleosome (51,48). Furthermore, we find that over-twisting is also very common, especially at SHLs ±1 (similarly to what found for the other periodic sequences). We note that while over-twisting has not been so far reported in crystal structures, DNA footprinting experiments on α-satellite nucleosomes suggested its formation near the dyad (10).

Figure 7.

Stability and defect formation in positioning sequences. (A) The dynamics of contact index 0.5 for 601 and α-satellite nucleosomes for two representative trajectories, starting from the optimal conformations found in the respective crystal structures. (B) The free-energy costs of defect formation at each SHL for 601 and α-satellite positioning sequences. (C) Structure of 601 nucleosomes around SHL –1, comparing the crystal structure with PDB id 3LZ0 (gray transparency) to the metastable form with over-twisting (brown). For the latter, we show 10 DNA frames sampled from our 100-ns all-atom MD simulation starting from a configuration back-mapped from a coarse-grained trajectory. We also show the region of the H3H4 tetramer involved in the interactions with the DNA, highlighting that the extra base pair is accommodated in the outer DNA region lacking histone contacts.

To further support the stability and importance of over-twist defects, we selected a single configuration with this type of defect at SHL –1 from a 601 trajectory, and we back-mapped the coarse-grained protein and DNA coordinates with all-atom accuracy using a reconstruction method recently developed (BioRxiv: https://doi.org/10.1101/205062, code available at http://www.cafemol.org/). This defect (shown in Figure 7C) was confirmed to be very stable during a 100 ns all-atom explicit-solvent MD simulation with the AMBER parmbsc1 force field (52) (see Supplementary Figure S8, also for more details on simulation protocol), showing that long-lived over-twisting may indeed be able to contribute to nucleosome repositioning.

To investigate further how defects contribute to the sliding of positioning sequences, we ran many (1400) MD simulations of 601 nucleosomes starting from initial configurations shifted by a few base pairs away from the reference crystal structure. We observe that for initial shifts up to 4 bp, the dynamics is clearly biased back towards the optimal conformation. However, we do occasionally find trajectories where repositioning occurs in the opposite forward direction, via the above-mentioned high-energy intermediate. For example, starting from the 3 bp shifted configuration, we find only three forward trajectories out of 400 runs that slide backwards (one such forward trajectory is depicted in Figure 8A together with 19 other backward cases). As observed in the simulations using 2-bp periodic sequences, 601 repositioning proceeds via the same screw-like rotation accompanied by the transient formation of twist defects. In particular, recurrent features are under-twisting at SHLs ±2 and over-twisting at SHLs ±1 (Figure 8B).

Using our collection of MD trajectories, we employed again Markov state modeling to reconstruct the slow dynamics of the system. This time we clustered the nucleosome conformations according to the contact indexes at SHLs ±1.5, distinguishing between states with or without defects around the dyad. In Figure 8C, we show the resulting free energy profile of 601 nucleosome repositioning as a function of the average contact index around the dyad. The profile shows an increase in free energy as we move away from the optimal conformation in the crystal, reaching a maximum of about 10k_BT for a 5 bp shift, and then decreasing again for further shifts. The estimate of our free energy barrier is consistent with what previously obtained using a different enhanced-sampling technique and a similar nucleosome coarse-grained model (5), further supporting the accuracy of our Markov state modeling. In addition to that, our approach also characterizes the system's kinetics, and shows how twist defects mediate the sliding of nucleosomes formed by high-affinity sequences. The presence of the high-energy barrier significantly increases the repositioning time scale relative to the 2-bp periodic sequences, with sliding by ∼10 bp (the distance between the two main basins separated by the barrier) occurring in ∼6 × 10¹⁰ MD steps (the longest implied time scale of the MSM, Supplementary Figure S5).

DISCUSSION

Our molecular dynamics simulations in combination with Markov state modeling enabled us to fully characterize how the energetics, kinetics and sequence-dependence of twist defect formation and propagation control the nucleosome sliding behavior, revealing important features not previously anticipated by theoretical studies of defect dynamics or by recent MD simulations of spontaneous nucleosome sliding (26,28).

Firstly, our results show a large variation in the characteristic repositioning times (by a factor of ∼60) even for simple 2-bp periodic sequences. The origin of this sequence-dependence is distinct from the one due to nucleosome affinity, which was previously recognized (11,28). In this latter case sliding of high-affinity sequences is slow relative to random sequences because of their intrinsic bending profile (5), which means that these nucleosomes are stabilized around their most favorable rotational setting (with the A/T steps located where the minor groove faces the histone octamer), and repositioning by 10 bp will proceed either via rotation-coupled sliding encountering a free energy barrier after 5 bp, or via rotation-uncoupled sliding where a free energy barrier is due to the breakage of many histone–DNA contacts (26,28). The sequence-dependent behavior observed in our 2-bp periodic sequences, on the other hand, is solely due to the differences in defect formation and propagation. As shown by our analysis via Markov state modeling, sliding of DNA is fast across the nucleosome regions where twist defects have a low energy cost and can easily propagate from one super-helical location to the neighboring one. Conversely, regions where twist defects have a high energy cost introduce kinetic bottlenecks in the sliding, since DNA motion will involve cooperative breakage of many consecutive histone–DNA contacts (e.g. see Figure 3A for poly-CG). For this reason, poly-AC and -AT, which can easily accommodate twist defects at most SHLs, are the two sequences that slide the fastest, whereas poly-CG and -AA, which do not accommodate low-energy defects at a large (∼30 bp) nucleosomal region around the dyad, are the slowest. We note that the two fastest sequences are rich in CA and TA base-pair steps, which are the most easily deformable DNA steps (33), and are also critically important for lowering the energy cost of DNA folding into nucleosomes (53). This sequence-dependent sliding behavior due to twist defects may also explain experiments showing that α-satellite nucleosomes with an incorporated long poly-AA tract diffuse slower than their fully α-satellite counterparts. This may be surprising, since from the general correlation of nucleosome affinity with sliding we would expect poly-AA tracts, which are known to have a low affinity (30), to increase the diffusivity of nucleosomes. However, these observations can be reconciled by noting that poly-AA tracts inhibit repositioning due to their low propensity to form twist defects. Therefore, our results show how the sequence-dependence of nucleosome affinity and that of nucleosome repositioning can be decoupled, and how these two may be independently regulated for biological purposes.

We would also like to comment on the conversion between the time scales of repositioning reported here, expressed in MD steps, to real times. Experimentally, starting from an initial offset, nucleosomes incorporating the α-satellite sequence slide to the optimal configuration in about 30 minutes at 37°C. Assuming this is similar to the time required to observe the sliding of 601 nucleosomes by ∼10 bp, we obtain that 10⁶ steps of our MD simulations corresponds roughly to 0.03 s. Therefore, the typical times to observe sliding by 1 bp with uniform sequences would be 0.013, 0.026, 0.09, 0.45, 0.27 and 0.8 s for poly-AC, AT, AG, CG, CC and AA sequences respectively. In these cases, sliding by an entire nucleosomal DNA length (N_bp∼147 bp) would then range between a few minutes to a few hours (for a diffusive process, time ∼N_bp²), suggesting a potential for regulation across biologically relevant time-scales. Interestingly, the repositioning time of our fastest considered sequence (poly-AC) is close to the value (0.01 s) predicted for a random sequence by a theoretical model of nucleosome sliding via twist defect formation (11), which assumed that defects can form uniformly at any SHL (similarly to poly-AC).

Another key observation of our MD simulations is that nucleosome sliding is mediated not only by nucleosome defects characterized by DNA under-twisting, which correspond to a missing base pair at one SHL and are commonly found in crystal structures (1,12,15), but also by defects characterized by DNA over-twisting, accommodating an extra base pair relative to canonical nucleosomes. While defect formation is again highly sequence-dependent, we find the nucleosome super-helical location has a strong effect in determining which type of defect will be favored: under-twisting usually occurs at SHLs ±2 and ±5, whereas over-twisting at all other SHLs, in particular at SHLs ±1. The stability of over-twisting at SHL 1 has been confirmed by our all-atom MD simulations (Figure 7C and Supplementary Figure S8), and it is also consistent with past experiments (10).

The combination of over-twisting and under-twisting allows repositioning to be initiated from an internal nucleosome location via the creation of a pair of defects of opposite type. For instance, in the poly-AG trajectory shown in Figure 3B, DNA sliding towards the dyad starts at contact point 1.5 with the generation of over-twisting at SHL 1 and under-twisting at SHL 2; repositioning over the entire nucleosomal DNA can then be completed by the diffusion of the two defects in opposite directions. Interestingly, this region overlaps with the SHL 2 binding location of the ATPase domain of chromatin remodelers (19,54). This domain is responsible for the unidirectional sliding activity and the two recent cryo-EM structures of remodelers in complex with the nucleosome (19,54) suggest that the conformational changes that occur during the ATP cycle could control twist defect formation around the binding side. The over-twist and under-twist defect types could then play together a key role in the complex remodeling activity via one or a combination of these two mechanisms: (i) powered by ATP, the ATPase domain induces DNA sliding towards the dyad from its binding location by enhancing the formation of a twist defect pair (over-twisting at SHL 1 and under-twisting at SHL 2); or (ii) the domain acts as a ratchet that blocks the annihilation of the twist defect pair after this is spontaneously generated at the binding site via thermal fluctuations. In both cases, the diffusion of the two defects in opposite directions would be sufficient to complete repositioning, inducing sliding in the direction consistent with experiments (19). Similar ideas were indeed proposed many year ago based on theoretical arguments (41), but our simulations provide further evidence and details that will be important for further characterizing the role of twist defects in active repositioning via experiments. We regard this proposed mechanism as highly attracting for offering a simple explanation of how remodelers may slide nucleosomes unidirectionally by exploiting the twist defect fluctuations that already control spontaneous sliding. Notably, this is consistent with the small repositioning steps, 1–2 bp, observed in experiments (20,21) and past experimental evidence showing how sliding by remodelers is initiated from an internal nucleosome location (6,55). We also note that recent experiments showed that the activity of remodelers can be highly sequence-dependent, specifically after the introduction of poly-AA tracts on 601 nucleosomes (56). This may be due to the sequence-dependent kinetics of twist defect formation and propagation highlighted in our study, further suggesting its potential relevance for in vivo scenarios.

Finally, our new simulations of 601 repositioning showed that when nucleosomes with strong positioning sequences undergo rotation-coupled sliding, they do so via the formation and propagation of twist defects, similarly to what observed with 2-bp periodic sequences. In particular, we find the same preference for under-twisting at SHLs ±2 and over-twisting at SHLs ±1. Therefore, the same defect-mediated active repositioning mechanism proposed above may also enable remodelers to slide very stable nucleosomes formed with positioning sequences. We finally note that while the free energy barrier of 601 screw-like sliding is rather high (∼10k_BT, Figure 8C), a single repositioning step of 1 bp costs only a couple of k_BT, which could easily be overcome by remodelers powered by ATP hydrolysis.

In the future, we aim to apply our coarse-grained model to study nucleosomes and their sliding behavior in more complex scenarios, such as under the action of remodelers (6), competing for DNA with transcription factors (3), and for gaining insights into chromatin organization (57,58).

SUPPLEMENTARY DATA

Supplementary Data are available at NAR Online.

FUNDING

JSPS KAKENHI [25251019 to S.T., 16KT0054 to S.T., 16H01303 to S.T.]; MEXT as ‘Priority Issue on Post-K computer’ (to S.T.); RIKEN Pioneering Project ‘Dynamical Structural Biology’ (to S.T.). The funders had no role in study design, data collection and analysis, decision to publish or preparation of the manuscript. Funding for open access charge: MEXT ‘Priority Issue on Post-K computer’.

Conflict of interest statement. None declared.