A Population Pharmacokinetic Model Incorporating Saturable Pharmacokinetics and Autoinduction for High Rifampicin Doses

Abstract

Accumulating evidence suggests that increasing doses of rifampicin may shorten tuberculosis treatment. The PanACEA HIGHRIF1 trial assessed safety, pharmacokinetics, and antimycobacterial activity of rifampicin at doses up to 40 mg/kg. Eighty‐three pulmonary tuberculosis patients received 10, 20, 25, 30, 35, or 40 mg/kg rifampicin daily over 2 weeks, supplemented with standard doses of isoniazid, pyrazinamide, and ethambutol in the second week. This study aimed at characterizing rifampicin pharmacokinetics observed in HIGHRIF1 using nonlinear mixed effects modeling. The final population pharmacokinetic model included an enzyme turnover model accounting for time‐dependent elimination due to autoinduction, concentration‐dependent clearance, and dose‐dependent bioavailability. The relationship between clearance and concentration was characterized by a Michaelis–Menten relationship. The relationship between bioavailability and dose was described using an E_max relationship. The model will be key in determining exposure–response relationships for rifampicin and should be considered when designing future trials and when treating future patients with high‐dose rifampicin.

Study Highlights.

WHAT IS THE CURRENT KNOWLEDGE ON THE TOPIC?

☑ The dose‐ and time‐dependent pharmacokinetics of rifampicin have been studied since its introduction to the market in 1971 based on the recommended dose of 10 mg/kg.

WHAT QUESTION DID THIS STUDY ADDRESS?

☑ The study describes the population pharmacokinetic characteristics of rifampicin given in doses of up to 40 mg/kg.

WHAT THIS STUDY ADDS TO OUR KNOWLEDGE

☑ This is the first population pharmacokinetic model describing rifampicin pharmacokinetics after doses up to 40 mg/kg. It is also the first evidence suggesting a dose‐dependent increase in bioavailability for rifampicin.

HOW THIS MIGHT CHANGE CLINICAL PHARMACOLOGY OR TRANSLATIONAL SCIENCE

☑ The presented model will enable prediction of rifampicin plasma concentrations at doses up to 40 mg/kg. It will aid in deciding the future dose of rifampicin since it allows for clinical trial simulation and can be used as input to exposure–response analyses. Furthermore, the model can be used to improve therapeutic drug monitoring with higher doses of rifampicin.

Rifampicin is a cornerstone in the treatment of pulmonary tuberculosis (TB) and reduced treatment time from 12 to 9 months by its introduction to the market in 1971.1 The currently recommended dose of the antibiotic is 10 mg/kg administered daily.2 The rationale for selecting 10 mg/kg was not achieved through current dose selection standards3 and accumulating data suggest that increasing the dose might reduce treatment time further.4, 5

The PanACEA HIGHRIF1 trial was performed to study short‐term safety, pharmacokinetics (PK), and antimycobacterial activity of higher doses of rifampicin.6 Up to 35 mg/kg of daily rifampicin was safe and an unprecedented increase in exposure was seen where the average total exposure at 35 mg/kg was almost 10 times higher than for 10 mg/kg. This more than linear increase in exposure was accompanied by a decrease in exposure with time. A higher dose of 40 mg/kg was studied in the meantime and was also safe.

The nonlinear increase in exposure of rifampicin with dose has been known since the early 1970s7 and was described in the first clinical trial that evaluated the concept of high‐dose rifampicin more recently.8 Reported reasons for the nonlinear increase in exposure include saturable biliary excretion7, 9 as well as an exposure‐dependent bioavailability (F).10 The decrease in rifampicin exposure with time is due to increased elimination by induction of enzymes and/or transporters caused by the antibiotic itself, referred to as autoinduction.9 Rifampicin activates the nuclear pregnane X receptor (PXR), which leads to increased gene transcription of several systemic and presystemic metabolizing enzymes and drug transporters.11

There are already several population PK models for rifampicin, including models that do not include any structural nonlinearity in PK parameters,12, 13 a model including structural components describing autoinduction,14 and a model including structural components for autoinduction and a nonlinear increase in exposure.10 All of these were based on the 10 mg/kg rifampicin dose. Thus, this is the first population PK analysis exploring high‐dose rifampicin with the objective of characterizing the nonlinear dose–exposure relationship and autoinduction following higher doses of rifampicin.

RESULTS

Model development was performed using rifampicin plasma concentrations from the 83 patients in the HIGHRIF1 trial,6 as summarized in Table 1. No data points were excluded on day 7, where every patient contributed 11 samples, which resulted in 913 samples. On day 14, 46 samples were excluded, as described in Supplementary Appendix S1. Of the 1,780 analyzed data points, 13.6% were below the limit of quantification (LOQ).

Table 1.

Demographics and covariates for patients included in the dataset used for modeling

Parameter	Unit	All subjects	10 mg/kg	20 mg/kg	25 mg/kg	30 mg/kg	35 mg/kg	40 mg/kg
N		83	8	15	15	15	15	15
Median weight (range)	kg	53.9 (40.2–84.2)	56.9 (46.8–64.9)	52.6 (41.8–62.7)	52.8 (40.2–67.9)	54.0 (45.7–84.2)	57.0 (40.5–74.0)	58.9 (46.7–64.8)
Median age (range)	years	31.0 (18.0–59.0)	27.5 (19.0–49.0)	27.0 (18.0–46.0)	25.0 (19.0–46.0)	40.0 (19.0–59.0)	37.0 (21.0–59.0)	34.0 (23.0–58.0)
Median body mass index (range)	kg/m2	19.4 (14.7–30.9)	20.5 (15.8–26.3)	18.6 (16.8–26.2)	19.3 (15.1–25.2)	20.9 (16.4–30.9)	19.4 (14.7–25.2)	19.4 (17.2–19.4)
Median fat free mass (range)	kg	44.6 (28.5–57.9)	44.6 (34.1–52.4)	44.3 (29.5–51.1)	44.6 (29.7–54.9)	44.6 (33.0–52.1)	45.8 (28.5–57.9)	47.1 (32.0–55.8)
Patients with male sex	n (%)	59 (71.1)	6 (75.0)	11 (73.3)	10 (66.7)	11 (73.3)	10 (66.7)	11 (73.3)
Patients with black race	n (%)	38 (45.8)	3 (37.5)	7 (46.7)	4 (26.7)	9 (60.0)	5 (33.3)	10 (66.7)
Patients with colored race	n (%)	45 (54.2)	5 (62.5)	8 (53.3)	11 (73.3)	6 (40.0)	10 (66.7)	5 (33.3)
Patients with HIV	n (%)	3 (3.6)	0 (0.0)	0 (0.0)	0 (0.0)	2 (13.3)	1 (6.7)	0 (0.0)

Structural model

The autoinduction, evident as a decrease in exposure from day 7 to 14, was accounted for using a previously developed enzyme turnover model for rifampicin14 without structural modification (Figure 1). The parameters were fixed to the previously reported estimates14 during early model development but were reestimated at a later stage, which gave a 100‐point drop in the objective function value (OFV). The parameter k_ENZ was estimated to 0.00603 h^‐1, corresponding to a half‐life of 4.79 days. The typical predicted increase in apparent clearance (CL/F) for all dose groups between days 0 and 14 are shown in Figure 2 a for the median patient in the dataset (weighing 53.9 kg and a fat‐free mass (FFM) of 44.6 kg).

Figure 1.

Schematic representation of the final rifampicin population pharmacokinetic model. The dose (Dose) goes into the absorption compartment (Abs) via a transit compartment model (Transit), where NN describes the number of transit compartments and the transfer rate between transit compartments described by the transit rate constant (k_tr), calculated as the NN+1 divided by the mean transit time (MTT). The fraction of drug that reaches Abs is dose‐dependent and increases at higher doses. The drug is absorbed from Abs to the central compartment (indicated by C_p, the plasma concentration of rifampicin) described by the absorption rate constant (k_a). The formation of enzyme is described by the first‐order enzyme degradation rate (k_ENZ, which also serves as the zero‐order formation rate of enzyme using this parameterization) but also stimulated by the presence of drug via an E_max model. The elimination of drug is described by Michaelis–Menten kinetics, which is increased proportional to A_ENZ. F₄₅₀, relative bioavailability for 450 mg; F_max, maximal increase in relative bioavailability; ED₅₀, dose corresponding to half the F_max; E_max, maximal increase in enzyme formation rate; EC₅₀, concentration corresponding to 50% of E_max; V_max, the maximal elimination rate; k_m, the C_p at which the elimination is half‐maximal; V, volume of distribution.

Figure 2.

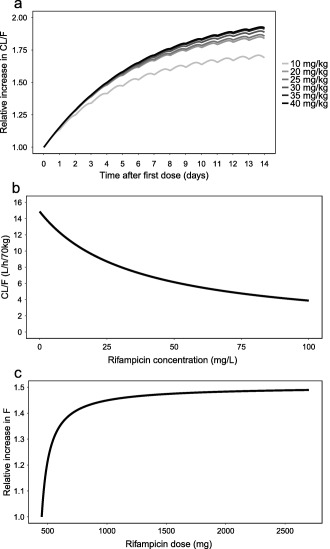
Typical model predictions from the final rifampicin population pharmacokinetic model of (a) relative increase in apparent clearance (CL/F) vs. time for a 53.9 kg patient for the different dose groups, (b) CL/F vs. rifampicin plasma concentration, and (c) relative increase in bioavailability (F) vs. rifampicin dose.

The nonlinear increase in exposure seen at the higher doses was accounted for by a concentration‐dependent CL/F and a dose‐dependent relative F. The CL/F was described by the following equation:

$$CL/F_{(C_p)}=\frac{V_{max}}{k_m+C_p}$$

where V_max is the maximal elimination rate and k_m is the rifampicin plasma concentration (C_p) at which the elimination is half‐maximal. Introducing a nonlinear CL/F in the model decreased the OFV by 92.9 points compared to having linear CL/F. The typical predicted relationship between CL/F and C_p at the preinduced state for the median patient is shown in Figure 2 b. Dividing total CL/F into two parallel elimination pathways (linear + nonlinear) gave a decreased OFV by 10.2 points. However, when the significant dose‐dependency in F was introduced into the model (see below), there was no longer any improvement in OFV upon inclusion of two elimination pathways. Hence, the final model only included one elimination pathway.

The statistically significant relationship between dose and F was described using an E_max relationship according to:

$$F=F_{450}\times (1+\frac{F_{max}\times \left(Dose-450\right)}{E{D}_{50}+\left(Dose-450\right)})$$

where F₄₅₀ is F for 450 mg, assumed to be 1. Parameters F_max and ED₅₀ are the maximal increase in F and the dose above 450 mg that corresponds to half the F_max, respectively. Inclusion of the proposed relationship reduced OFV by 28.2 points. The ED₅₀ was estimated to 67.0 mg, corresponding to a dose of 517 mg. The predicted relationship between F and dose is shown in Figure 2 c.

The distribution of rifampicin was best described using the one‐compartment disposition model. Absorption was best described by an absorption transit compartment model.

Stochastic model

The residual error model included a normally distributed additive error on log‐scale, which approximates to a constant coefficient of variance on normal scale. Interindividual variability (IIV) in k_m, apparent volume of distribution (V/F), mean transit time (MTT), number of transits (NN), absorption rate constant (k_a), and V_max was statistically significant, as well as interoccasion variability (IOV) in F, MTT, k_m, and k_a. Covariance was statistically significant between V_max and k_m. Other covariances were statistically significant, but when attempts were made to include more than one covariance simultaneously, the model became too unstable, terminated without minimization, and was not able to report any significant digits. A similar situation arose when IIV in k_ENZ was evaluated where OFV decreased by 9.91 points, but when covariance was explored using this model, it terminated without minimization. Hence, IIV in k_ENZ was excluded due to model stability issues.

Covariate model

The parameters CL/F and V/F were allometrically scaled using FFM. Sex, race, and age were not identified as influential covariates according to stratified visual predictive checks (VPCs) performed using the final model, stratified for different values, or categories for each covariate (results not shown).

Final model

The NONMEM code for the final model is given in the Supplementary Material S2. The structure of the final model is schematically represented in Figure 1 and with final parameter estimates shown in Table 2.

Table 2.

Parameter estimates from the final rifampicin population pharmacokinetic model

Parameter	Description	Estimate	90% CIa
Vmax (mg/h/70 kg)	Maximal elimination rate	525	430–564
km (mg/L)	Rifampicin concentration at which the elimination is half‐maximal	35.3	29.9–39.1
V (L/70 kg)	Volume of distribution	87.2	83.1–95.4
ka (h‐1)	Absorption rate constant	1.77	1.50–1.92
MTT (h)	Mean transit time	0.513	0.478–0.613
NN	Number of transits	23.8	20.6–26.4
Emax	Maximal increase in enzyme production rate	1.16	1.14–1.17
EC50 (mg/L)	Rifampicin concentration at which half the Emax is reached	0.0699	0.0523–0.0761
kENZ (h‐1)	First‐order rate constant for enzyme pool degradation	0.00603	0.00587–0.00622
Fmax	Maximal increase in relative bioavailability above 450 mg	0.504	0.429–0.574
ED50 (mg)	Difference in rifampicin dose from 450 mg at which half the Fmax is reached	67.0	57.1–80.5
IIV Vmax (%)b		30.0	24.7–40.9
IIV km (%)b		35.8	30.1–42.5
IIV V (%)b		7.86	6.98–9.17
IIV ka (%)b		33.8	30.1–38.4
IIV MTT (%)b		38.2	34.7–44.7
IIV NN (%)b		77.9	71.8–88.9
IOV km (%)c		18.9	16.7–21.7
IOV ka (%)c		31.4	27.7–36.9
IOV MTT (%)c		56.4	48.8–62.6
IOV F (%)c		15.7	13.4–18.0
Correlation Vmax‐km (%)		38.9	4.34–72.2
ϵ (%)	Additive error on log scale	23.6	19.3–26.4

CI, confidence interval; IIV, interindividual variability; IOV, interoccasion variability.

^a90% CI is the 90% percentile confidence interval from a nonparametric bootstrap (1,000 samples).

^bInterindividual variability expressed as coefficient of variation and in % of the parameter estimate.

^cInteroccasion variability expressed as coefficient of variation and in % of the parameter estimate.

Model evaluation

The final model described the observed continuous data and the observed proportions of samples below the LOQ well in all dose groups according to a VPC (Figure 3). Figure 4 shows posterior predictive checks performed using the final model for the noncompartmental analysis (NCA) metrics including the highest observed plasma concentration (C_max) and the area under the plasma concentration–time curve between 0 and 24 h (AUC_0‐24h). Both C_max and AUC_0‐24h were overall predicted well across all dose groups.

Figure 3.

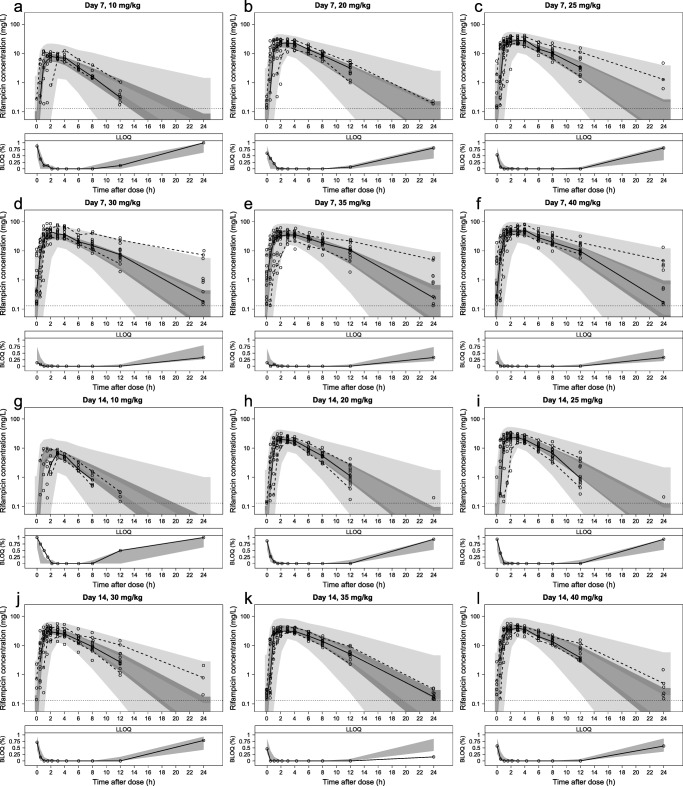
Visual predictive check for the observed rifampicin concentrations stratified on dose group and day where a–f show the day 7 observations for 10, 20, 25, 30, 35, and 40 mg/kg rifampicin, respectively, and g–l show the day 14 observations for 10, 20, 25, 30, 35, and 40 mg/kg rifampicin, respectively. Open circles are the observations. The upper and lower dashed lines are the 95th and 5th percentiles of the observed data, respectively, and the solid line is the median of the observed data. The shaded areas (top to bottom) are the 95% confidence intervals of the 95^th (light gray), median (dark gray), and 5^th (light gray) percentiles of the simulated data based on 1,000 simulations. The lower limit of quantification (indicated as LLOQ) panels show the observed proportions of samples below the limit of quantification (BLOQ) as open circles and the 95% confidence interval of the simulated proportion as a shaded gray area.

Figure 4.

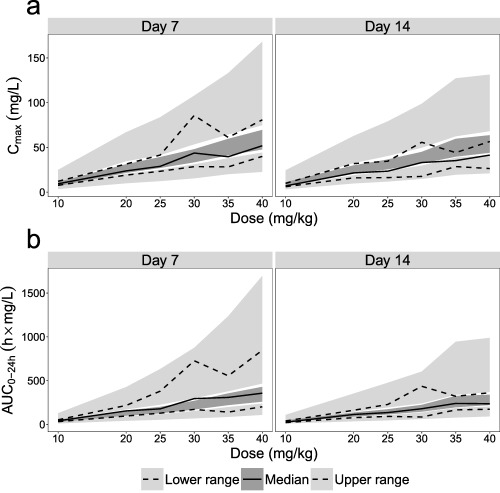
Posterior predictive checks for the noncompartmental analysis (NCA)‐based metrics including the highest observed plasma concentration (C_max) in (a) and the area under the plasma concentration–time‐curve between 0 and 24 hours (AUC_0‐24h) in (b) for the different dose groups. The upper and lower dashed lines and the solid lines are the upper range, lower range, and median, respectively, of the NCA metrics calculated from the observed dataset. The upper and lower light gray and the dark gray shaded areas are the 95% confidence intervals of the simulated upper range, lower range, and median, respectively, calculated from 1,000 simulated datasets.

Clinical trial simulation

The clinical trial simulations show that AUC_0‐24h at day 14 increased more than proportionally compared to 10 mg/kg for all dose groups (Table 3). The 90% prediction intervals overlapped with the median values for a lower and/or higher dose group for the 30, 35, and 40 mg/kg dose groups.

Table 3.

Predicted increase in exposure at day 14 compared to 10 mg/kg rifampicin

Dose group (mg/kg)	Predicted increase in median AUC0‐24h at day 14 (%)
	Median	90% prediction interval
20	239	152–343
25	330	230–460
30	525	370–708
35	667	479–914
40	760	549–1040

AUC_0‐24h, area under the plasma concentration–time curve between 0 and 24 h.

DISCUSSION

We present a population PK model based on clinical observations that includes doses of rifampicin up to 40 mg/kg. It includes components describing concentration‐ and time‐dependent elimination as well as a dose‐dependency in bioavailability. Our final model predicted the continuous concentrations and proportions of data below LOQ well across all dose arms at days 7 and 14. The model was able to predict the commonly used NCA (i.e., nonmodel‐based) metrics C_max and AUC_0‐24h. The results of this study allows for reliable predictions of rifampicin exposures at doses up to 40 mg/kg.

The capacity‐limited elimination and dose‐dependency in F may cause overexposure at higher doses, which may create safety issues. In contrast, the time‐dependent elimination leads to lower exposures over time that can lead to suboptimal treatment. Without a model taking these phenomena into account simultaneously, the exposures will be highly unpredictable.

The model predicted 1.73, 1.89, 1.91, 1.94, 1.97, and 1.99‐fold increases in CL/F for the 10, 20, 25, 30, 35, and 40 mg/kg dose groups, respectively, at steady state compared to a single dose. Previous models predicted increases of 1.8514 and 1.8910 for the 10 mg/kg dose. The predicted half‐life for the autoinduction was 4.79 days, which agrees well with the estimate from Chirehwa et al.10 of 4.5 days but is shorter than the estimate reported by Smythe et al.14 of 7.83 days. The former is probably more reliable, since it includes multiple PK sampling occasions between days 1 and 29, whereas the latter only includes data at days 0 and 28. A half‐life of 4.79 days for the autoinduction phenomenon implies that it takes 24 days (5 half‐lives) to reach the fully induced state of rifampicin autoinduction.

The current rifampicin dataset would probably not allow for full characterization of the nonlinear time‐dependency in CL/F. But by assuming the same structure as a previous enzyme turnover model for rifampicin14 it was possible to characterize the autoinduction and distinguish it from the capacity‐limited elimination.

The presented model suggests capacity‐limited elimination of rifampicin, which coincides with a previous NCA report7 and a population PK model.10 Rifampicin is eliminated through active secretion into the bile, which is known to be saturable.9 The transporter responsible for the active secretion is unknown. The maximum predicted typical CL/F at the preinduced state was 14.9 L/h/70 kg (i.e., at 0 mg/L, Figure 2 b), 3.44 times higher than the typical CL/F for a concentration of, e.g., 85.8 mg/L (highest observed rifampicin concentration in the dataset). A previous model‐based estimate of k_m is 3.35 mg/L,10 which is markedly lower than our estimate of 35.3 mg/L. The discrepancy between these estimates may exist because in contrast to the model presented here, Chirehwa et al.10 assumed a well‐stirred liver model and do not include doses above 10 mg/kg.

The final model included a dose‐dependent F, suggesting a maximal increase of 50.4% where half of the maximum increase occurs at 517 mg. There is a lack of intravenous (i.v.) vs. oral data to fully support this finding. Loos et al.15 compared 600 mg of daily i.v. and oral rifampicin during 3 weeks. Rifampicin F decreased from 90–100% at day 1 to ∼70% after 1 and 3 weeks. Thus, a time‐dependency was seen in F, which was attributed to autoinduction of nonhepatic presystemic elimination. No time‐dependency in F was explored in our study because the reported increase in F reached a maximum after 1 week15 and our dataset included observations on days 7 and 14. Loos et al.15 did not observe any dose‐dependency (since only one dose was included) and with no similar studies available, our analysis is the first evidence suggesting a dose‐dependency in F as attributed to saturation of nonhepatic presystemic elimination at high doses of rifampicin. At 10 mg/kg rifampicin, gut wall enzymes and/or transporters suppress the bioavailability of rifampicin, but at higher rifampicin doses the enzymes and/or transporters become saturated. The specific enzymes and/or transporters is unknown but may involve CYP3A4 and/or P‐glycoprotein.16

A previous PK model for rifampicin10 includes exposure‐dependency in F, but this is attributed to saturation of hepatic first‐pass elimination, as described using the well‐stirred liver model. This model was not tested on our dataset, partly because it contrasts the findings of Loos et al.15 that hepatic first‐pass elimination is not a likely cause of the reduced F of 70% for 10 mg/kg,9 as the hepatic extraction ratio of rifampicin was classified as low (0–10%),15 which is also in agreement with the interpretation by Kenny and Strates in 1981.17 No other evidence using as robust a methodology exists that can confirm the hepatic extraction ratio of rifampicin. Confirmation of the findings require a very rich study including blood and plasma measurements and urine collection following i.v. and oral doses, preferably for several rifampicin doses.

Rifampicin was assumed to be eliminated by a single elimination pathway (Figure 1). Reports on the elimination of rifampicin propose two relevant processes: metabolic transformation into desacetylrifampicin (main metabolite), and biliary excretion. The former is likely the major contributor to the elimination of rifampicin,18, 19 whereas the latter is likely to be a saturable process.7, 9 Therefore, we tested a model including two parallel (linear and nonlinear) elimination pathways. No literature data to our knowledge supports concentration‐dependency in the metabolic pathway, which would represent the linear elimination pathway and the biliary excretion would represent the nonlinear pathway. However, no model including more than one pathway was supported by the data.

Mechanistically, a model including more than one elimination pathway appears plausible, but even such a model would likely not represent the complete picture. First, describing elimination only based on hepatic elimination is theoretically wrong, since a nonnegligible fraction of rifampicin is eliminated renally.9 Second, the parent drug and the main metabolite are both cleared via biliary excretion9 and there may therefore be an intricate dependence between the elimination pathways. The final model is not intended to be viewed as the mechanistically most correct model, but a model able to describe the complex data including relatively few model parameters. The elimination of rifampicin is complex and in order to further characterize it, data including i.v., urine, and metabolite data and data from even higher doses of rifampicin may be relevant.

The PK of rifampicin was assumed to be unaffected by coadministration of isoniazid, pyrazinamide, and ethambutol. There are no data available to support any clinically significant changes of rifampicin PK by isoniazid, pyrazinamide, and ethambutol.20 In addition, as rifampicin PK is time‐dependent (autoinduction), interactions would probably have been unidentifiable using the current dataset.

Rifampicin is predicted to be a key component of future treatment regimens against TB, likely at a dose higher than 10 mg/kg.21 Thus, many patients will be treated with higher doses of rifampicin. Our model allows for better control of the exposure of rifampicin by forecasting the individual exposures of higher doses using therapeutic drug monitoring (TDM), a growing field for TB and rifamycins.22 Furthermore, the main interest is often the exposure at full autoinduction, whereas PK sampling is often performed before full induction has been reached, which can introduce bias. The model can aid in such situations by predicting the exposure at full induction based on early PK samples.

The model can be used to evaluate trial designs of future PK studies. The current study included many samples. Future trials may face stricter financial or ethical concerns that require sparser sampling and investigators must decide which sample(s) to omit from the protocol. Our model can be used to explore designs including fewer samples by simulating designs with different sampling schemes and evaluate if relevant metrics (e.g., AUC_0‐24h) can be estimated with acceptable precision and accuracy with reduced designs.

The results may further be used to make unbiased exposure–response evaluations, regarding both safety and efficacy. Markers for safety and/or efficacy are usually collected at different timepoints compared to PK samples. With time‐dependent PK there is a risk of biasing exposure–response relationships if the exposure at, e.g., day 7 are used to describe exposure–response at steady state. The model can account for such time‐dependent exposures.

For the model presented here, PK predictions following even higher doses of rifampicin would aid in the design of trials with these doses and are therefore relevant. But this poses a problem, since only one elimination pathway is included in the final model, which may not be mechanistically correct. An attribute of less mechanistic models is that prediction outside the range of the observed data requires careful consideration.23, 24 The asymptotic consequence of having only one saturable elimination pathway is that CL/F will approach a value of 0 at high concentrations, whereas in reality we postulate that a different elimination pathway takes over at a certain threshold. Therefore, predictions of exposures at doses above 40 mg/kg using the presented model should be interpreted carefully.

The developed rifampicin population PK model simultaneously accounted for exposure‐dependent autoinduction and nonlinear decrease in CL/F at higher doses of rifampicin. These findings will be important when determining rifampicin exposure–response relationships at the higher doses and should be taken into consideration when designing future clinical trials and when performing TDM with higher doses of rifampicin. The model allows for clinical trial simulations and as input for future pharmacokinetic‐pharmacodynamic modeling in order to optimize the rifampicin dose.

METHODS

Patients and study design

The data consisted of rifampicin PK data collected in the PanACEA HIGHRIF 1 trial, an open‐label phase II multiple dose‐rising trial registered at http://www.clinicaltrials.gov (NCT01392911). Prior to conducting the trial the study protocol was approved by local Ethical Review Boards and by the Medical Control Council of South Africa and was conducted according to Good Clinical Practice standards. All patients provided written informed consent before enrollment in the study. The trial included 83 adult pulmonary TB patients enrolled in Cape Town, South Africa. The patients were recruited into six consecutive cohorts where patients received 10 (n = 8, reference arm), 20, 25, 30, 35, or 40 (n = 15/arm) mg/kg daily oral rifampicin for 14 days, with an interim safety review between the subsequent treatment groups. During the first 7 days rifampicin was given as monotherapy and for the next 7 days supplemented with isoniazid, pyrazinamide, and ethambutol. Patients were sampled for rifampicin total plasma concentrations at 0, 0.5, 1, 1.5, 2, 3, 4, 6, 8, 12, and 24 h on days 7 and 14. More details on the study design is given in the original publication, which reports on the data up to 35 mg/kg.6

Data analysis

The data were analyzed using log‐transformation both sides and the nonlinear mixed effects modeling software NONMEM (v. 7.3; Icon Development Solutions, http://www.iconplc.com/technology/products/nonmem, Ellicott City, MD)25 using Laplacian conditional estimation with interaction. The M3 method26 was used to handle samples below the LOQ of 0.13 mg/L. Data handling and visualization were performed in R (v. 3.2.3; R Foundation for Statistical Computing, http://www.R-project.org, Vienna, Austria).27 Model evaluation was performed by comparing the OFV using the likelihood ratio test at the 5% significance level (decrease in OFV ≥3.84 between nested models with one added parameter) and diagnostics generated using Xpose (v. 4.5.3; Department of Pharmaceutical Biosciences, Uppsala University, http://xpose.sourceforge.net, Uppsala, Sweden)28, 29 including VPCs generated using PsN (v 4.5.2; Department of Pharmaceutical Biosciences, http://psn.sourceforge.net, Uppsala, Sweden)28, 30 using 1,000 simulations stratified on day of treatment and dose group.

Structural model building

Different disposition models were tested including the one‐ and two‐compartment disposition models. Absorption models were evaluated including first‐order absorption with and without lag time and an absorption transit compartment model.31

An enzyme turnover model for rifampicin14 was used to account for autoinduction. The change in the amount of inducing enzymes was described by:

$$\frac{d{A}_{ENZ}}{dt}=k_{ENZ}\times \left(1+\frac{E_{max}\times C_p}{E{C}_{50}+C_p}\right)-k_{ENZ}\times A_{ENZ}$$

where A_ENZ is the relative amount of enzyme, initialized to a value of 1. The parameter k_ENZ serves two purposes with the current parameterization; it is a first‐order constant for enzyme degradation and a zero‐order rate for enzyme formation. The E_max is the maximum increase in enzyme formation and EC₅₀ is the C_p that corresponds to half the E_max. The A_ENZ scaled CL/F according to:

$$CL/F_{\left(t\right)}=CL/F_{\left(C_p\right)}\times A_{ENZ}$$

In order to characterize the nonlinear increase in exposure with increased rifampicin dose, deviations from linearity were explored in F and CL/F. For F, models including linear, E_max, or sigmoidal E_max relationships between F and dose were tested. All models assumed an increase in F at doses over 450 mg (lowest dose in the dataset). The F was described by the linear, E_max, and sigmoidal E_max models, respectively, as:

$$F=F_{450}\times (1+slop{e}_F\times \left(Dose-450\right))$$

$$F=F_{450}\times (1+\frac{F_{max}\times \left(Dose-450\right)}{E{D}_{50}+\left(Dose-450\right)})$$

$$F=F_{450}\times (1+\frac{F_{max}\times {\left(Dose-450\right)}^{\gamma }}{E{D}_{50}^{\gamma }+{\left(Dose-450\right)}^{\gamma }})$$

where slope_F is a dose‐dependent linear change in F. The parameter γ is a shape parameter.

For CL/F, nonlinearity was investigated by comparing linearly decreasing and Michaelis–Menten32 relationships between CL/F and C_p to the linear model. Additional nonlinear models were tested including models with two parallel (linear + nonlinear) elimination pathways.

Stochastic model building

Different residual error models were explored including additive on log‐scale, additive on the normal scale, and a model including two components, one additive on log‐scale and one additive on normal scale.

Interindividual variability was investigated in all structural parameters except slope_F, F_max, ED₅₀, and γ. Interoccasion variability was investigated in all parameters except parameters relating to the autoinduction and slope_F, F_max, ED₅₀, and γ. Both IIV and IOV were assumed to be log‐normally distributed.

Correlations were investigated for IIVs between absorption parameters (including F) and between parameters relating to elimination (including autoinduction parameters). Correlations were investigated also between elimination parameters and V/F.

Covariate model building

Different methods for allometric scaling of CL/F and V/F were explored using different body size descriptors including total body weight,33, 34, 35, 36 FFM,33, 37 or an approach where the contributions of each of the two were estimated.37 The exponents for the allometric relationships were fixed to 0.75 and 1 for CL/F and V/F, respectively.

The impact of other covariates including age, sex, and race (classified as either “black” or “colored”) were assessed graphically by performing VPCs stratified on each covariate. Only if model misspecification was evident through our visual investigation was the relevant covariate relationship evaluated further. The HIV infection covariate was not investigated since only three patients had HIV infection.

Model evaluation

The ability of the model to predict NCA measures AUC_0‐24h and C_max was assessed by performing a posterior predictive check for days 7 and 14 using ncappc38 within R and PsN. One thousand datasets were simulated using the final model assuming the same study design and covariates as the original dataset; AUC_0‐24h and C_max were calculated from the simulated datasets, which were then compared with the same metrics calculated from the observed dataset.

A 1,000 sample bootstrap was performed in PsN28, 30 on the final model to obtain the 95% nonparametric confidence interval for all parameters for assessment of parameter uncertainty.

Clinical trial simulation

Clinical trial simulations were performed using the final model to assess the degree of overlap in the predicted increases in exposure for the different dose groups. The increase in median AUC_0‐24h compared to 10 mg/kg was calculated for each dose group for 1,000 simulated trials assuming the same protocol as the HIGHRIF1 trial. Patient covariates were sampled from the dataset used for modeling.

ACKNOWLEDGMENTS

The research leading to these results has received funding from the Swedish Research Council in addition to the Innovative Medicines Initiative Joint Undertaking (http://www.imi.europe.eu) under grant agreement n°115337, resources of which are composed of financial contribution from the European Union's Seventh Framework Programme (FP7/2007‐2013) and EFPIA companies' in kind contribution. The execution of the PanACEA HIGHRIF1 trial was supported by the European and Developing Countries Clinical Trials Partnership (EDCTP), the Netherlands‐African Partnership for Capacity Development and Clinical Interventions Against Poverty‐related Diseases (NACCAP), and the Bill and Melinda Gates Foundation.

CONFLICT OF INTEREST

The authors declared no conflict of interest.

AUTHOR CONTRIBUTIONS

U.S.H.S., R.J.S., R.E.A., A.H.D., R.D., S.H.G., and M.J.B. wrote the article; U.S.H.S., R.J.S., R.E.A., A.H.D., R.D., S.H.G., and M.J.B. designed the research; U.S.H.S., R.J.S., R.E.A., S.H.G., and M.J.B. performed the research; U.S.H.S, R.J.S., R.E.A., S.H.G., and M.J.B. analyzed the data.

Supporting information

Supplementary appendix S1 Table of excluded samples

Supplementary appendix S2 Final model code