HipMCL: a high-performance parallel implementation of the Markov clustering algorithm for large-scale networks

Abstract

Biological networks capture structural or functional properties of relevant entities such as molecules, proteins or genes. Characteristic examples are gene expression networks or protein–protein interaction networks, which hold information about functional affinities or structural similarities. Such networks have been expanding in size due to increasing scale and abundance of biological data. While various clustering algorithms have been proposed to find highly connected regions, Markov Clustering (MCL) has been one of the most successful approaches to cluster sequence similarity or expression networks. Despite its popularity, MCL’s scalability to cluster large datasets still remains a bottleneck due to high running times and memory demands. Here, we present High-performance MCL (HipMCL), a parallel implementation of the original MCL algorithm that can run on distributed-memory computers. We show that HipMCL can efficiently utilize 2000 compute nodes and cluster a network of ∼70 million nodes with ∼68 billion edges in ∼2.4 h. By exploiting distributed-memory environments, HipMCL clusters large-scale networks several orders of magnitude faster than MCL and enables clustering of even bigger networks. HipMCL is based on MPI and OpenMP and is freely available under a modified BSD license.

INTRODUCTION

Graphs and their isomorphic representations as matrices or pairs-lists are one of the principal representations of biological information on a very large scale that has emerged over the past decade (1). These graphs represent structural similarities or functional affinities, e.g. sequence homology or expression, respectively (2). Due to the rapid increase of the available information for genome structure and function, large-scale biological network clustering and analysis has become a major challenge (3). While for functional networks, where typically a whole genome is represented, scalability is easier to address (4), for sequence similarity networks (SSNs) this is not the case as thousands of genomes need to be covered. In the latter case, very large graphs stored as sparse matrices can contain the relevant homology detection across multiple genomes, which could lead to the generation of massive networks with hundreds of millions of nodes and tens of billions of edges (5). Protein family detection was first implemented by the semi-automated COG method (6) and later expanded by the fully-automated protocol TribeMCL (7) using the Markov Clustering (MCL) graph clustering algorithm (8). Yet, limitations such as high memory footprint and long running time render the clustering of large-scale networks a real challenge.

Indeed, despite the great variety of graph-based clustering algorithms available today (9,10), only a few manage to handle networks of million nodes and edges. SPICi (11) for example, is a fast, local network clustering algorithm that detects densely connected communities within a network. It is one of the fastest graph-based clustering algorithms and runs in time O(VlogV+E) and space O(E), where V and E are the number of vertices and edges in the network. While SPICi is very efficient and runs in linear time, it performs better for dense networks and not sparse ones. Louvain (12) is an efficient and easy-to-implement greedy clustering method for identifying communities in large scale networks. The method can handle networks of sizes up to 100 million nodes and billions of links. Although the exact computational complexity of the method is not known, the method seems to run in time O(VlogV). Molecular Complex Detection (MCODE) (13) detects densely connected regions in large protein–protein interaction (PPI) networks that may represent molecular complexes. The time complexity of the entire algorithm is polynomial O(VEd³) where d is the vertex size of the average vertex neighborhood in the input graph. Restricted neighborhood search clustering (RNSC) (14) uses stochastic local search. RNSC tries to achieve optimal cost clustering by assigning some cost functions to the set of clusters of a graph. It requires O(V²) memory and the complexity of a move in the naive cost function is O(V). Affinity-propagation (15) is a clustering algorithm based on the concept of ‘message passing’ between data points able to cluster 25 000 data points in a few hours or 120 000 data points in less than a day, based on all pairwise similarities on a 16GB 2.4GHz machine. The latter achieves complexity O(kV²), where k is the number of iterations.

Despite the continuous active research and the new methods that appear to serve the purpose of large-scale biological cluster detection, MCL has been one of the most successful in the field and today it comes as a core module with many Linux distributions and many visualization tools (16–24). MCL uses random walks to detect clustered structures in graphs by a mathematical bootstrapping procedure and was initially used to detect protein families in sequence similarity information, as well as protein interaction modules (25). An optimized implementation should have complexity O(Vd²), where V is the number of nodes in the graph and d is the average number of neighbors per node. MCL’s popularity stems from its remarkably robustness to graph alterations and its relatively non-parametric nature (10).

All above methods including MCL struggle to cope with the observed—and further anticipated—exponential increase of biological data volumes (26). MCL has been previously parallelized on single GPU (27), but it can only cluster relatively small networks due to memory limitations of a single GPU. This work presents HipMCL, a scalable distributed-memory parallel implementation of the MCL algorithm. In contrast to previous work, HipMCL takes advantage of the aggregate memory available in all compute nodes, clustering networks that were deemed too large to cluster using MCL. The unprecedented scalability of HipMCL stems from its use of state-of-the-art parallel algorithms for sparse matrix manipulation. HipMCL is written using MPI and OpenMP, with the principal aim to speed up graph clustering and efficiently detect clusters on a very large scale. Notably, MCL’s backbone has remained intact, thus making HipMCL a parallel implementation of the original MCL algorithm. We demonstrate the performance of HipMCL by using datasets from the Integrated Microbial Genomes (IMG) database (28).

MATERIALS AND METHODS

The markov cluster algorithm

We first review the MCL procedure here to facilitate the presentation of HipMCL. The MCL algorithm is built upon the following property of clusters in a graph: ‘random walks on the graph will infrequently go from one natural cluster to another’. The MCL algorithm does indeed simulate random walks of higher lengths on a graph. In this process, the algorithm computes the probability of random walks between pairs of vertices and prunes paths with low probability to discover natural clusters in the graph.

To capture the probability of random walks, the MCL algorithm starts with and maintains column stochastic matrices (also called Markov matrices). A column stochastic matrix is a non-negative matrix with the property that each column sums to (probability) 1. Initially, the adjacency matrix of a graph is converted into a column stochastic matrix by dividing every non-zero entry by the sum of all entries in the column where the entry belongs. The MCL algorithm then iteratively performs two operations called expansion and inflation. The expansion step performs matrix squaring, which corresponds to computing random walks of higher lengths. The inflation step computes the Hadamard power of the matrix (taking power entrywise) in order to boost the probabilities of intra-cluster walks and demote inter-cluster walks. Expansion and inflations are performed as long as there is ‘significant’ change between successive iterations. After the MCL algorithm converges, connected components of the final graph will form the final set of clusters. The inflation operation combined with the normalization for maintaining column stochasticity ensure convergence, whose properties have been studied extensively (29). The high-level description of the MCL algorithm is given below:

To reduce the memory requirement in the intermediate iterations, MCL keeps the networks sparse, by pruning low probability terms from the expanded matrices. Pruning in MCL is performed by the sequence of the following three steps:

1. Prune: first, MCL removes from the expanded matrix B entries with values smaller than a threshold. This is done early, because it is fast and speeds up subsequent steps.

2. Recover: if a column of the pruned matrix becomes very sparse, the recovery step brings back some significant non-zero entries. The goal of this step is controlling the effect of excessive pruning and keeps at least R entries in each column. Here, R is a user-provided parameter, called the recovery number. The default value of R in the current version of MCL is 1400. To perform recovery, MCL identifies the R-th largest entry in each column and then keeps the top R entries. This task is therefore a specialization of the selection problem (30), which identifies the kth largest number in a list or array.

3. Select: if a column of the pruned matrix remains too dense, the selection step prunes it further so that at most S non-zero entries remain in each column. Here, S is a user-provided parameter, called the selection number. The default value of S in the current version of MCL is 1100. To perform selection, MCL identifies the S-th largest entry in each column and then keeps the top S entries. Similar to the recovery step, the selection step is also a specialization of the k-select problem performed on every column of the matrix. Note that selection is only performed on columns where recovery is not attempted.

The number of non-zero entries in a column after pruning/recovery/select steps is at most max(R,S), where R and S are the recovery and selection number, respectively. Hence, the aforementioned steps ensure that the expanded matrix remains sparse while keeping as much information as possible.

Stijn van Dongen developed an open source implementation of the MCL algorithm available at https://micans.org/mcl/. This implementation employs multithreading to take advantage of the shared-memory parallelism available in modern multicore processors. In this paper, we use ‘MCL’ to refer to both the algorithm and its associated shared-memory parallel software.

The HipMCL algorithm

While MCL and TribeMCL have been used extensively in clustering sequence similarity and other types of information, at a large scale, MCL becomes very demanding in terms of computational and memory requirements. Consequently, existing MCL software cannot handle large datasets that have trillions of non-zero similarities across billions of protein sequences. For example, MCL is expected to take 45 days to cluster a network with ∼47 million nodes and ∼7 billion edges on a 16-core workstation with 1 terabyte of memory. The expected runtime is extrapolated based on the iterations during the first 10 days. Due to the memory limitations of a single computing node or workstation, clustering even bigger networks is not possible.

HipMCL is a distributed-memory algorithm implementation based on MCL which employs massive parallelism to cluster networks of unprecedented size. Each component of HipMCL is fully parallelized, taking advantage of both shared- and distributed-memory parallelism available on modern supercomputers (Table 1). We describe the parallelization strategies for different steps of HipMCL below.

Table 1. Computational infrastructure used for HipMCL benchmarking.

		Edison (Cray XC30 supercomputer)	Cori2 (Cray XC40 supercomputer)	In-house system
Overall system	#nodes	5586	9688	1
	#cores	134 064	658 784	8
	aggregate memory	357 terabyte	1 petabyte	1 terabyte
	max #nodes used in experiments	2025	2048	8
One computing node of the system	processor	Intel Ivy Bridge	Intel KNL	Intel Xeon
	number of cores	24	68 (272 threads)	8
	memory	64 gigabyte	112 gigabyte	1 terabyte

Data distribution and storage

Similar to MCL, HipMCL represents a network by its sparse adjacency matrix. There are two levels of parallelism available in a distributed-memory computer: parallelism within compute nodes is often handled using OpenMP threads and parallelism across compute nodes is handled using MPI processes. Since the memory of a single compute node is accessible by other threads, the matrix is only distributed across compute nodes (i.e. MPI processes). We logically view the set of MPI processes as a 2D process grid that can be indexed as P(i,j). Processes with the same row (column) index belong to the same process row (column). In our implementation, we use a √p-by-√p process grid, where p is the number of processes. Submatrices are assigned to processors according to a 2D block decomposition: processor P(i,j) stores the submatrix A_ij of dimensions (N/p) × (N/p) in its local memory, where N is the number of rows/columns in the matrix. For an illustrative example of block-distributed matrices, see section below titled: Distributed-memory parallel SpGEMM algorithm. Local submatrices are stored in a compressed format that requires storage proportional to the number of edges in the network.

Parallelizing the expansion step

Expansion is by far the most compute- and memory-intensive step of MCL (Table 2) and requires efficient parallel algorithms to make good use of hundreds of thousands of processors. To keep our discussion easy to follow, we describe parallelization of expansion in two steps: (i) designing expansion in a way that offers ample parallelism without increasing memory requirements significantly (ii) performing expansion in distributed-memory systems given the choices made in step i.

Table 2. The impact of parallelizing different steps of MCL when clustering a eukaryotic network with 3 million nodes and 359 million edges (Table 3).

	File I/O (s)	Expansion (s)	Prune (s)	Inflation (ss)	Components (s)
MCL (1 node)	600.12	1052.11	9.93	199.97	608.77
HipMCL (1024 nodes)	7.23	27.20	0.92	0.19	0.19
HipMCL speedup	83×	39×	11×	1052×	3288×

The last row shows the speedups achieved by HipMCL on 1024 nodes of Edison (Table 1). While HipMCL drastically reduces the running time of all five steps, expansion remains the most expensive step in Markov clustering. Hence, we spent the majority of our research effort to make the expansion step scalable.

Parallelism-memory trade-off in expansion

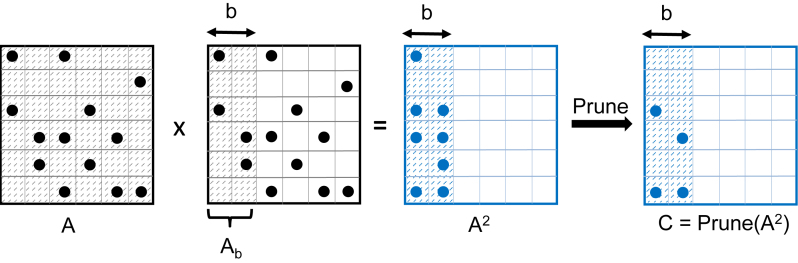
As described in the high-level description, MCL expands a column-stochastic matrix by first computing A²and then sparsifies it by pruning small entries in each column. Since the pruned version of A² requires significantly less storage, it is memory efficient to fuse expansion and pruning on a subset of columns. Figure 1 shows an example where we expand a block of b ( = 2) columns, prune these expanded columns and then move to next block of columns. Therefore, we perform the expansion and pruning in h phases where h = N/b and in each phase, we expand and prune b columns. In Figure 1, the expansion is performed in three phases. The choice of b (and h) is crucial for both computational and memory efficiency. Setting b to a small value (e.g. b = 1) saves memory by not storing many unpruned columns, but it performs a limited number of floating point operations that cannot efficiently utilize available computational power offered by large distributed-memory systems. By contrast, using a large value for b (e.g. b = N) can take advantage of many processors and truly deliver high-performance clustering for large-scale networks, but it requires a large amount of memory (Figure 1).

Figure 1.

An example of expansion and pruning of b ( = 2) columns of a column stochastic matrix A. Non-zero entries are shown with filled circles. Here, A_b is a submatrix of A, consisting all N rows and b ( = 2) columns that are currently being expanded. The product AxA_bis computed and pruned to obtain the final result for these b columns. Parts of matrices that are active in the current expansion are shown in darker shades. For comparison, MCL sets b to 1. HipMCL dynamically selects a large value for b from the range [1,N] such that the expanded columns of A² do not overflow memory. When these columns are expanded and pruned, the computation moves to the next set of b columns.

MCL takes the memory-efficient approach by expanding and pruning one column at a time (or t columns at a time when t threads are used). Therefore, in the sequential case, MCL sets b to 1 and h to N and performs N sparse matrix-sparse vector multiplications (SpMSpV). By contrast, HipMCL prefers larger blocks and fewer phases. Let A_b be a submatrix of A consisting all N rows and b columns that are being expanded in the current phase (Figure 1). Then, in a phase, HipMCL computes AxA_b by parallel sparse matrix–matrix multiplications (SpGEMM). When the entire unpruned A² can be stored in memory, HipMCL computes the entire sparse matrix-matrix product and stores it for subsequent pruning (in this case, h = 1, b = N and A_b= A). At the other extreme case with very limited memory, HipMCL can expand a matrix in N phases and imitate MCL’s column-by-column approach. However, the latter approach offers limited parallelism and diminishes the benefit of HipMCL. Hence, HipMCL selects b and h dynamically based on the available memory. Let mem(A), mem(A²) and mem(C) be the required memory to store the corresponding matrices (C is the pruned version of A²). Then, the number of phases can be estimated as follows: h = ⌈(mem(A²)/(TotalMem - mem(A) – mem(C))⌉, where TotalMem is the aggregate memory available to HipMCL. This dynamic and incremental SpGEMM enables HipMCL to expand and prune matrices as quickly as possible without overflowing the memory.

Distributed-memory parallel SpGEMM algorithm

In HipMCL, the distributed-memory SpGEMM is performed by a variant of Scalable Universal Matrix Multiplication (SUMMA) algorithm (31) adapted for sparse matrices (32). While Sparse SUMMA is prior work, we summarize it here to make the presentation self-contained. At first, we describe how Sparse SUMMA computes A² in distributed memory, assuming that the whole unpruned A² can be stored in the aggregated memory distributed across all computing nodes. The special case of computing AxA_b for any submatrix A_b will be discussed later.

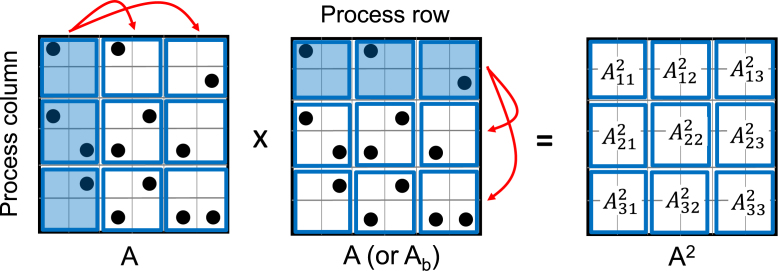
In order to compute A², Sparse SUMMA distributes input and output matrices on a √p-by-√p process grid, where p is the number of processes. Figure 2 shows an example of distributing the input and output matrices on a 3 × 3 process grid, using the same input matrix from Figure 1. To multiply distributed matrices, processes need to communicate their local submatrices. In Sparse SUMMA, this communication happens in √p stages (e.g. three stages in Figure 2). Since each stage performs similar communication and computation, we only describe the first stage using Figure 2. In the first stage, members of the first process column broadcast their local piece of A horizontally (along the process row) and members of the first process row broadcast their local piece of A vertically (along the process column). Each process then locally multiplies the received pieces of A and merges the multiplied results to its local piece of the output matrix A². Figure 2 illustrates that each process receives two (different) pieces of the input matrix and updates its local part of A². Other stages of Sparse SUMMA follow the same pattern with the exception that the ith process row and column broadcast their local submatrices in the ith stage. At the end of √p stages, each process has fully computed its local part of A², and all processes collectively store the final A².

Figure 2.

Execution of the sparse SUMMA algorithm for sparse matrix–matrix multiplication A² = A*A on a 3-by-3 process grid. We use the same input matrix from Figure 1 and denote submatrices local to different processes by blue squares. Here, we show the first stage of the sparse SUMMA algorithm where members of the first process column broadcast their local pieces of A horizontally (along the process row) and members of the first process row broadcast their local pieces of A vertically (along the process column). Broadcasting processes in the first stage are marked with blue shades and the direction of data communication is shown with red arrowheads. The rightmost figure depicts each process that locally multiplies the received parts of A and merges the multiplied results to its local part of the output matrix A².

The above computation of A² interleaves communication (broadcasting submatrices) and computation (local multiplication and merging). On a small number of nodes, the computation of A² dominates the communication cost. However, when HipMCL is run on thousands of distributed nodes, communicating data becomes expensive and may dominate the overall runtime of the expansion step, as well as the whole clustering algorithm.

The computation of AxA_b is identical to the computation of A², with the only exception that the second matrix in Figure 2 is A_b instead of A. That is, each stage of Sparse SUMMA contributes to local pieces of AxA_b. Assuming that h phases are used to compute A² from h AxA_b multiplications, the total computational cost of performing h multiplications of the form AxA_b is exactly the same as computing the whole A². However, the former approach communicates more data than the latter because over all h phases, the first input matrix in Figure 2 is needed to be communicated h times horizontally. The extra communication overhead decreases with increased node counts because the value of h decreases with the increase of total available memory. Once a subset of columns of A² is constructed, it can be sparsified immediately according to the selection, recover and pruning described below. This immediate sparsification is the crux of our approach that allows us to keep memory consumption low while still providing ample parallelism.

Parallelizing pruning, selection and recovery

Pruning non-zero entries that are below a threshold can be trivially parallelized because these pruning decisions are independent of each other. For the selection and recovery operations, we need to identify the k-th largest entry in each column of a matrix. k becomes the selection number S in the selection logic and the recovery number R in the recovery logic. We implemented a simple algorithm, called TournamentSelect (T-S), following the idea of tournament pivoting and optimization, used in solving linear systems (33). Let P(i,j) be the processor in the ith row and jth column of the 2D processor grid. Hence, j is the rank of P(i,j) in its processor column. At the beginning of T-S, each processor partially sorts each of its local columns and keeps at most k entries per column. If a column has fewer than k non-zeros, the whole column is kept. The algorithm then performs log(√p) iterations. In the r-th iteration, if the column rank j of a processor P(i,j) is divisible by 2^r, P(i,j) receives the lists from P(i,j+2^r-1) when the sending processor exists. After receiving lists from a remote partner, the receiving processor merges its current lists with the received lists and keeps the largest k entries for the next iteration. At the end of log(√p) iterations, the first processor in every processor column stores the largest k entries for the corresponding columns of the matrix. From these lists, T-S returns the k-th largest entries in every column.

Parallelizing the inflation step

The inflation step can be trivially parallelized because each non-zero entry of the matrix can be squared independently. Since the matrices are already distributed, each processor simply computes the square of its own non-zero elements. This step scales perfectly because it does not require any communication.

Distributed-memory connected component algorithm

After the MCL algorithm converges, we identify components in the final graph. These components represent clusters in the original network. For this purpose, we developed a distributed-memory parallel algorithm, following the idea of the Awerbuch-Shiloach algorithm (34). Relying on well-known graph-matrix duality, we designed our algorithm using a handful of linear-algebraic primitives and a sparse matrix vector multiplication (SpMV) is at the heart of our algorithm. Our parallel connected component algorithm is significantly different from that of MCL, both in terms of algorithmic and implementation techniques. This dual improvement made our implementation several orders of magnitude faster than MCL’s implementation, e.g. an improvement of 3000× on 1024 nodes (Table 2).

Input file indexing

HipMCL currently supports the input file format of MCL where each line specifies an edge (pairs-list), thus making it easier to efficiently read it in parallel. We first get the input size in bytes from the operating system and then assign to each thread a starting position. If the total file is S bytes, the i-th process p_i (out of p processes) moves its file cursor to location S*(i/p). If this point is in the middle of a line, it fast forward to the beginning of the next line and lets the preceding process p_i-1 read previous partial line in full.

The key to performance is to have each process open the file in binary format and read using MPI-IO functions with large buffers. In particular, we use ‘MPI_File_read_at’. The parsing of the binary data is done in memory. At this point, all the edges are stored in memory but they are not yet assigned to processes in accordance to the 2D decomposition illustrated in Figure 2. Hence, we need to repartition the edges to their correct final destinations. The simplest case is when the original labels are integers from 0 to N-1 where N is the number of vertices. All edges with source vertices in the range [i*√p, (i+1)√p) and target vertices in the range [j*√p, (j+1)√p) are assigned to process P(i,j). The re-partitioning is accomplished by an ‘MPI_Alltoallv’ operation, followed by each process building its local sparse matrix data structure independently.

In the more general case where vertex labels can be arbitrary strings, we have to first find a mapping from those strings to integers [0,N-1]. The challenge is that the data are already distributed to processes upon reading the file. Our method hashes each vertex identifier to a random number. The hashed values are partitioned to processes in a load balanced way so each vertex is assigned to a unique process. Each process sends all the vertex data it reads from the file to the process assigned to that vertex. The receiving processor then sorts the received data by its hash value and eliminates duplicates. All the processors collectively perform a prefix-sum (‘MPI_Scan’) to calculate the number of vertices owned by all the processors preceding themselves. The i-th processor renumbers the sorted local list with prefix_sum(i), 1+prefix_sum(i),2+prefix_sum(i). This numbering is precisely the mapping from labels to integers [0,N-1] we need to compute. This approach also automatically load balances the input matrix by implicitly applying a random permutation.

Implementation details

Most algorithmic components of HipMCL are based on operations from sparse linear algebra, including sparse matrix-matrix and sparse matrix-vector multiplication. To implement these operations, we relied on basic sparse matrix operations and data structures provided by the Combinatorial BLAS (CombBLAS) library (35). We have substantially modified and expanded CombBLAS to implement novel parallel algorithms needed for the expansion, pruning and connection components steps. Both HipMCL and CombBLAS are written in C++ and use standard OpenMP and MPI libraries for parallelization. We used g++ 6.1.0 to compile HipMCL on NERSC systems shown in Table 1. For experiments with MCL, we installed mcl-14–137 version from the source.

Computational infrastructure

We ran most of our experiments using two cutting-edge supercomputer systems: Edison and Cori2, hosted at the National Energy Research Scientific Computing Center (NERSC), at Lawrence Berkeley National Laboratory. In addition, we ran one experiment with MCL on a 1-terabyte-memory node using an in-house system at NERSC. We summarize the relevant information of these systems in Table 1. Notably, we did not use any library or software specific to these systems. Our software simply uses standard OpenMP and MPI libraries and can run seamlessly on any other system, including local workstations and laptops.

Datasets

In order to construct several networks to test the behaviour of HipMCL, we collected all viral, eukaryotic and archaeal proteins from the isolate genomes hosted by the IMG platform and created three domain-specific non-redundant datasets at 100% sequence similarity (April 2017). For each dataset, we used the sequence aligner LAST (36) in order to construct the all-against-all adjacency matrix by keeping all similarities above 30% and at 70% length coverage bidirectionally between the longest and shortest aligned sequences. Each produced matrix was then used as a three-column text input for HipMCL. Details for these datasets are provided in Table 3.

Table 3. Clustering quality results of HipMCL by directly comparing it to the original MCL.

Dataset	Inflation	#clusters from MCL	#clusters from HipMCL	F-score	#mismatched clusters
Eukarya |V| = 3 243 106 |E| = 359,744,161	1.4	228 965	228 965	0.99	8
	2	284 026	284 026	1.00	1
	4	446 216	446 216	1.00	1
	6	597 014	597 014	1.00	0
Archaea |V| = 1 644 227 |E| = 204 784 551	1.4	87 559	87 559	0.99	19
	2	107 207	107 207	1.00	0
	4	163 840	163 840	1.00	0
	6	222 937	222 937	1.00	0
Viruses |V| = 219,715 |E| = 4 583 048	1.4	34 519	34 519	1.00	0
	2	37 216	37 216	1.00	0
	4	41 835	41 835	1.00	0
	6	45 294	45 294	1.00	0

All experiments were run on Edison (NERSC). Column 1: |V| Vertices, |E| Edges. Column 2: The inflation value used for MCL. Column 3: The clusters produced by MCL. Column 4: The number of clusters produced by HipMCL. Column 5: The F-score comparing the results of MCL and HipMCL. As shown, results are identical. Column 6: Very few HipMCL clusters that contain slightly different number of proteins compared to the ones produced by MCL.

In order to further experiment with networks of bigger sizes and various densities, we followed the same approach to generate networks of two categories: (i) three networks containing all pairwise similarities above 30% and at 70% length coverage bidirectionally for all the predicted proteins of the isolate genomes stored in IMG (Isolates 1, 2 and 3) and (ii) similarities of proteins in Metaclust50 (https://metaclust.mmseqs.com/) dataset which contains predicted genes from metagenomes and metatranscriptomes of assembled contigs from IMG/M and NCBI. For the three isolate datasets, we used different LAST parameters as the more sensitive the LAST is, the bigger and denser the similarity matrix and vice versa, the less sensitive the LAST, the sparser the network. Isolate-1 and Isolate-2 were created by utilizing the less sensitive LAST (parameter -m 10) and by using different time snapshots of IMG (April 2016 and April 2017, respectively). The dataset Isolates-3 was created by using the more sensitive LAST (parameter -m 100). The number of vertices and edges of these larger datasets are reported in Table 4.

Table 4. Evaluation of HipMCL clustering for large-scale networks.

Network	#nodes (millions)	#edges (billions)	#clusters (millions)	HipMCL runtime (h)	Running platform
Isolate-1	47	7	1.59	1	1024 nodes on Edison
Isolate-2	69	12	3.37	1.66	1024 nodes on Edison
Isolate-3	70	68	2.88	2.41	2048 nodes on Cori2
Metaclust50	282	37	41.52	3.23	2048 nodes on Cori2

RESULTS

The performance and scalability of HipMCL was evaluated using real large biological datasets. We directly compare HipMCL with the original MCL distributed software and show that HipMCL and MCL compute virtually identical clusters, with HipMCL being 100–1000 times faster. The performance numbers we report include both the file I/O operations and the actual clustering (compute) time.

Assessment of clustering quality

HipMCL and MCL produce identical results given the same input and parameters (e.g. inflation value). For this benchmark, we used three medium-scale networks which can be clustered by both HipMCL and MCL. The properties of these networks (#nodes and #edges) are shown in Table 3.

In order to show that HipMCL is not sensitive upon parameterization compared to the original MCL distribution, we clustered each network using four different inflation values (1.4, 2, 4 and 6 respectively). Notably, the inflation parameter can be adjusted to obtain clusterings at different levels of granularity. Looking at the third and fourth column of Table 3, we confirmed that HipMCL and MCL always return the same number of clusters.

As the number of clusters is a poor indicator to directly compare two different clusterings, we use the F-score (or F-measure) to test whether the compositions of the two clusterings also match. The F-score is the harmonic mean of precision (percentage of vertices in a HipMCL cluster which are found in a MCL cluster) and recall (percentage of vertices from a MCL cluster that were recovered by a HipMCL cluster). F-score always takes values between 0 and 1, where 1 indicates a perfect match between two clusterings. The mathematical definition of F-score is further explained in the supplementary material.

Table 3 shows that the cluster composition coming from MCL and HipMCL are identical, as the F-score is always close to 1. For fine-grained clusters (obtained with higher values of the inflation parameter), HipMCL and MCL clusters match perfectly. For relatively coarse-grained clusters, we see few, yet insignificant, differences. The number of HipMCL clusters that do not match exactly to a MCL cluster is shown in the rightmost column in Table 3. Even when there is a mismatch, the number of misplaced nodes is insignificant (at most one misplaced node in the mismatched clusters in Table 3). We suspect that those minor differences, stem from different orders of floating-point summation in parallel runs. It is well documented that floating-point addition is not associative, which can affect reproducibility (37).

Runtime comparison to MCL

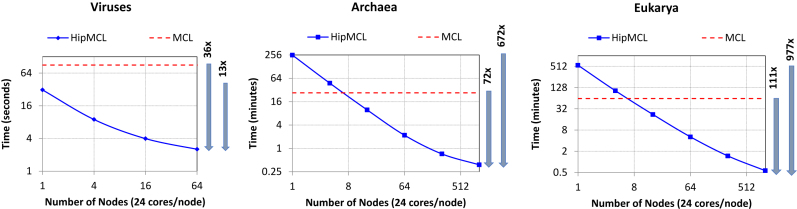
In this benchmark, we compare the runtime of HipMCL and MCL on the Edison supercomputer at NERSC. The most surprising result is the superior performance of HipMCL when running on a large number of nodes, by efficiently exploiting both the increased computational power and the increased aggregate memory of multiple nodes. Figure 3 shows the runtimes of MCL and HipMCL on the test viral, archaeal, and eukaryotic similarity networks. Notably, these smaller networks are selected so that MCL does not run out of memory and is able to successfully cluster them in a reasonable amount of time.

Figure 3.

Comparison of runtimes of the original MCL and HipMCL using three networks. Both axes are in log scale. Both MCL and HipMCL ran on Edison. MCL ran on a single compute node with 24 cores. HipMCL ran on increasing number of compute nodes to show how the clustering time reduces as we add more computing resources. HipMCL uses all 24 cores available in each node via multithreading. HipMCL ran on up to 64 nodes (1536 cores) for the smaller viruses’ network and on up to 1024 nodes (24 576 cores) for archaea and eukarya networks. The performance improvement of the highest concurrency HipMCL execution compared to single-node MCL and HipMCL executions are shown to the right of each subfigure. See text for details.

For small networks such as the viral network, HipMCL can operate significantly faster than MCL even on a single node. The faster runtime of HipMCL is partially due to the usage of a better parallel algorithm to compute sparse matrix–matrix products. However, for the archaea and eukarya networks, the memory required to store expanded matrices (before pruning) is significantly larger than the available memory on a single node. Therefore, on small concurrency, HipMCL requires many phases to operate with the given available memory, explaining the runtime of HipMCL on a single node for the archaea and eukarya networks. As we add more memory and processors, HipMCL can cluster a network very quickly as shown in the right part of each subfigure (Figure 3). For example, HipMCL can cluster the eukarya network in half a minute on 1024 nodes, which is 111 times faster than MCL. Similarly, HipMCL can cluster viruses and archaea networks 36 times and 72 times faster than MCL on 64 and 1024 nodes, respectively. HipMCL is not limited to large supercomputers and its single-node runtime is competitive to the runtime of the baseline MCL implementation.

Speedups of different steps of MCL

Table 2 shows how much time MCL and HipMCL spend for different steps of the algorithm when clustering a network representing sequence similarities of eukaryotic proteins (see Table 3) on 1 and 1024 nodes of Edison, respectively. This shows that HipMCL drastically reduces the running time of inflation and connected components by a factor of 1052× and 3288×, respectively on on 1024 nodes. File I/O time is reduced significantly (83×) within the limit of the hardware. The expansion step becomes significantly faster (39×) in HipMCL; however, it remains the most expensive step. The remarkable improvements in all five steps of MCL are based on novel parallel algorithms and efficient implementations of these algorithms on distributed-memory supercomputers.

Scalability of HipMCL

The more computing resources (processor and memory) we provide, the faster the HipMCL can cluster a network. Figure 3 shows that the runtime of HipMCL decreases almost linearly as we increase the number of nodes on Edison. Using 1024 nodes, archaeal and eukaryotic networks can be clustered 672 and 977 times faster than in a single-node. HipMCL scales better when clustering larger networks because of the availability of more work that can keep all processors busy. This can be realized in Figure 3 where the eukaryotic network scales optimally. It is also possible to achieve superlinear speedups (that is doubling the number of nodes can decrease the runtime by more than 2×) because of the synergistic effect of increased processors and memory. Overall, Figure 3 demonstrates that the clustering time of HipMCL on high concurrency can be predicted from small-scale experiments. Therefore, to cluster large-scale networks, domain scientists have the freedom to allocate resources depending on the computing budget and expected runtime.

Performance of HipMCL on larger networks

The real benefit of HipMCL lies in its ability to cluster massive networks that were impossible to cluster with the existing MCL software. Table 4 shows four networks created from proteins from isolate genomes hosted on IMG and proteins coming from metagenomes and metatranscriptomes. Of the constructed networks, the smallest one consists of 7 billion edges whereas the largest one of 68 billion edges. HipMCL was able to cluster these networks in a couple of hours using 1024/2048 computing nodes on the two supercomputers at NERSC.

Notably, none of these networks can be clustered on a single node with MCL due to memory limitations. Attempting to cluster network Isolate1 on a system with 1TB memory and 16 cores failed. MCL was able to finish only one iteration within 5 days. Based on this single finished iteration, we estimated that MCL would have taken 45 days to cluster this smallest network from Table 4. Therefore, clustering bigger networks with MCL can be impractical even with a server with quite a few terabytes of RAM.

Portability of HipMCL

The HipMCL implementation is highly portable as it is developed with C++ and standard OpenMP and MPI libraries. Hence, it can run seamlessly on any system including laptops, local workstations and large supercomputers. We have extensively tested HipMCL on Intel Haswell, Ivy Bridge and Knights Landing (KNL) processors, using a range of one to two thousand computing nodes, and with up to half a million threads across all processors. HipMCL has successfully clustered networks from thousands to billions of edges. These extensive experiments demonstrate its capability to cluster diverse classes of networks and its portability to run on diverse computing platforms.

I/O performance

Due to its fast in-memory parsing, HipMCL can read networks at rates close to the peak performance of the NERSC Lustre file systems for large inputs. In particular, HipMCL read and parsed the 1.6 Terabytes Isolate3 network data in ∼1 min using 2025 nodes (both Edison and Cori2 exhibited similar performance). HipMCL also achieves close to linear parallel scaling in terms of I/O throughput until we approach the limits of the hardware. On Edison, HipMCL’s I/O time for the Eukarya network is 300 s on one node and 7 s on 64 nodes. In contrast, MCL takes 600 s to read the same network.

DISCUSSION

HipMCL is a distributed-memory parallel implementation of MCL algorithm which can cluster large-scale networks efficiently and very rapidly. While we see that there is no barrier in the number of processors it can use to run, the memory required to store expanded matrices is significantly larger than any available memory on a single node. Since HipMCL dynamically trades parallelism with memory consumption using its memory-efficient incremental SpGEMM, it is not limited by the memory required to store expanded matrices in unpruned form. However, like MCL, HipMCL also needs to store the expanded matrix after pruning. The density of that intermediate matrix is bounded by the selection, recovery, and pruning parameters. Consider Isolate-1 from Table 4, which has ∼150 non-zeros per column as input. With the default selection parameter, the pruned expanded matrix can have at most 1100 non-zeros per column, effectively requiring seven times more intermediate memory than the input in the worst case. This property is due to the MCL algorithm itself, rather than any specific implementation. Despite this limitation, HipMCL is able to cluster networks × 1000 faster than the original MCL. Compared to the original MCL, HipMCL can easily cluster networks consisting of hundreds of millions of nodes and tens of billions of edges due to its ability to utilize distributed-memory clusters. The denser the network is, the longer it takes HipMCL to perform the file I/O and the first iteration, but density does not significantly affect the other iterations due to selection parameters.

It should be noted that despite the increase of performance at the clustering step, the input data in the form of sequence similarity matrices is still a requirement, indeed a limiting factor in most cases. Pairwise similarities are generated by sequence comparison software, such as BLAST (38) or LAST. Apart from the compute time, large disk capacity is also required. These issues are independent of HipMCL, as they require other approaches for the generation of high-quality and high-volume input datasets (39–42) for subsequent clustering and the detection of protein family clusters.

While MCL is a very established algorithm for data clustering, it should not be applied to every network blindly, as its performance is dependent on the nature and the topology of a network. In this article for example, we have demonstrated how HipMCL can efficiently cluster large scale SSNs. Other types of networks such as gene expression networks, hierarchical networks, PPI networks, networks from co-occurring terms in the literature or databases and metabolic networks must be treated accordingly. Therefore, checking several topological characteristics of a network prior to any clustering is highly encouraged. For a topological network analysis, tools like NAP (43), Stanford Network Analysis Project (SNAP) (44) as well as Cytoscape’s (23) and Gephi’s (45) network profilers can be used. One can easily calculate features such as the betweenness centrality, modularity, clustering coefficient, eccentricity, average connectivity, average density and other parameters to get a better sense of the network’s topology. For example, most hierarchical networks have clustering coefficient equal or close to zero and therefore MCL would not be a good choice, as MCL/HipMCL thrives on networks with densely connected neighborhoods. For a very dense network, other algorithms such as SPICi might be more suitable. However, calculating more complicated topological features is not always trivial when analyzing such large-scale networks. Finally, in order to get a more empirical feeling about which clustering algorithm is more suitable for a certain type of network, CLUSTEVAL (46) is a very useful evaluation platform. CLUSTEVAL offers several biological networks of various types, which were clustered by several clustering algorithms.

The scope of the present work addresses the parallelization of MCL and does not cover specific aspects of accuracy of the algorithm itself, something that have been covered extensively elsewhere. The original MCL article (7) as well as several other review articles or original papers provide extensive accuracy comparisons. For example, a direct comparison of MCL against Affinity Propagation in terms of quality and performance has been provided previously (47). MCL was directly compared against several other algorithms using PPI networks and SSNs (7). These algorithms include SPICi (11), MCUPGMA (48), SPC (49), MCODE (13), DPClus (16613608), RNSC (50) and CFinder (51). A direct, comparative assessment of four algorithms, namely MCL, RNSC (50), Super Paramagnetic Clustering (SPC) (49) and MCODE (13) was also reported (10). Finally, MCL was compared against the Spectral Clustering, Affinity Propagation (15) and RNSC (50) to show which algorithm performs better in predicting protein complexes (52). In summary, there is a great plethora of articles mentioned above, reporting detailed benchmarks of several clustering algorithms for different use cases.

To our knowledge, HipMCL is the first graph-based algorithm that can cluster massive networks efficiently using high performance computing and this indeed represents the main novelty of our work. Overall, the HipMCL implementation presented herein is expected to enable clustering and comparative analysis of very large biological datasets for the foreseeable future, tasks that even recently have seemed unattainable.

DATA AND SOFTWARE AVAILABILITY

HipMCL is based on MPI and OpenMP and is freely available under a modified BSD license at: https://bitbucket.org/azadcse/hipmcl/. Installation instructions and large datasets can be found in the relevant Wiki tab.

SUPPLEMENTARY DATA

Supplementary Data are available at NAR Online.

FUNDING

US Department of Energy (DOE) Joint Genome Institute [DE-AC02–05CH11231, in part], a DOE Office of Science User Facility; Applied Mathematics program of the DOE Office of Advanced Scientific Computing Research [DE-AC02–05CH11231, in part], Office of Science of the US Department of Energy; Exascale Computing Project (17-SC-20-SC), a collaborative effort of the U.S. Department of Energy Office of Science and the National Nuclear Security Administration. Funding for open access charge: Office of Science of the US Department of Energy [contract DE-AC02-05CH11231].

Conflict of interest statement. None declared.