Genotype-Specific Measles Transmissibility: A Branching Process Analysis

Using a branching process analysis, we characterize differences in measles transmission by estimating the association between genotype and the reproduction number among postelimination California measles cases. Genotype B3 is found to be a significant predictor of transmissibility.

Abstract

Background

Substantial heterogeneity in measles outbreak sizes may be due to genotype-specific transmissibility. Using a branching process analysis, we characterize differences in measles transmission by estimating the association between genotype and the reproduction number R among postelimination California measles cases during 2000–2015 (400 cases, 165 outbreaks).

Methods

Assuming a negative binomial secondary case distribution, we fit a branching process model to the distribution of outbreak sizes using maximum likelihood and estimated the reproduction number R for a multigenotype model.

Results

Genotype B3 is found to be significantly more transmissible than other genotypes (P = .01) with an R of 0.64 (95% confidence interval [CI], .48–.71), while the R for all other genotypes combined is 0.43 (95% CI, .28–.54). This result is robust to excluding the 2014–2015 outbreak linked to Disneyland theme parks (referred to as “outbreak A” for conciseness and clarity) (P = .04) and modeling genotype as a random effect (P = .004 including outbreak A and P = .02 excluding outbreak A). This result was not accounted for by season of introduction, age of index case, or vaccination of the index case. The R for outbreaks with a school-aged index case is 0.69 (95% CI, .52–.78), while the R for outbreaks with a non-school-aged index case is 0.28 (95% CI, .19–.35), but this cannot account for differences between genotypes.

Conclusions

Variability in measles transmissibility may have important implications for measles control; the vaccination threshold required for elimination may not be the same for all genotypes or age groups.

As a result of a successful measles vaccination program in the United States, measles was declared eliminated in 2000 [1, 2]. Measles elimination is defined as the absence of continuous measles transmission for ≥12 months in a defined geographic area [3]. However, measles remains a significant public health concern as measles importations continue to occur, resulting in limited outbreaks, small clusters, or transmission chains. While the number of measles cases continues to increase nationally, there is no direct evidence of difference in susceptible populations over the time period included in our study. Therefore, this trend may be due to an increase in the number of disease introductions rather than a change in levels of population immunity [4].

In California, 400 measles cases were reported from 1 January 2000 through 31 December 2015. The December 2014 to March 2015 measles outbreak linked to Disneyland theme parks was the largest outbreak in California since elimination, with 131 California cases, 16 cases in other states, 159 cases in a religious community in Quebec, Canada, and 1 case in Mexico [5, 6]. The majority of the California cases were unvaccinated or had unknown vaccination status; organized opposition to vaccination, the key component of measles control, remains a significant concern [7]. In addition, the outbreak linked to Disneyland theme parks is consistent with an reproduction number that is unchanged from the 2001–2011 era [6, 8], indicating that the level of population immunity may have remained roughly constant since elimination.

There may be alternative explanations for why some measles outbreaks are larger. The World Health Organization (WHO) recognizes 8 clades of measles virus, within which there are 24 recognized genotypes, of which 6 are currently circulating [9]. Measles clade B viruses (genotypes B1, B2, B3) are endemic to sub-Saharan Africa; prior to 2010, genotype B3 had been associated with frequent importations from African counties [10]. Following a measles genotype B3 outbreak in the Philippines in 2014, genotype B3 has been detected in all 6 WHO regions [11]. The 2014–2015 outbreak linked to Disneyland theme parks was an outbreak attributed to genotype B3 [5], and the Centers for Disease Control and Prevention (CDC) determined that the strain of B3 identified in this outbreak was identical to the strain associated with the Philippines outbreak [12]. The global distribution of the measles genotype B3 appeared to expand dramatically after the Philippines outbreak and was associated with record numbers of US measles cases in both 2014 and 2015.

These observations prompted consideration of whether there might be genotype-specific differences in measles transmission. Our analysis aimed to characterize differences in measles transmission by estimating the association between genotype and reproduction number among postelimination California measles cases. We also evaluated whether other variables collected during routine surveillance, such as season of introduction and age and vaccine status of the index case, may confound this relationship.

METHODS

Terms

For conciseness, we use “outbreak” to refer to clusters of size 2 and isolated cases, as well as clusters large enough to meet the CDC definition of outbreak (≥3 epidemiologically linked cases in space and time [13]). Isolated cases are part of a transmission chain where the source case(s) is either not identified or may be known but was reportable outside the jurisdiction of California. We use “index case” to refer to the progenitor case or cases, and also note that this differs from the CDC definition of the first identified case, who may be later in the transmission chain. We use R to refer to the reproduction number under vaccination [14]. Last, for clarity, we use “outbreak A” to refer to the transmission that occurred outside of Disneyland theme parks during the 2014–2015 California outbreak linked to Disneyland theme parks, as the nature of the transmission events that occurred at Disneyland theme parks is unknown [6]. See additional details under Case Ascertainment.

Case Ascertainment

Reported measles cases that met the Council of State and Territorial Epidemiologists (CSTE) case definition for confirmed measles were included in the analysis. For the majority of outbreaks, the case with the earliest rash onset date was considered the only index case for the outbreak. Additional outbreaks include 2 outbreaks with 2 and 3 contemporaneous cases, in which all were considered index cases, and outbreak A. For the latter outbreak, the case or cases who transmitted at Disneyland theme parks were never identified. Therefore, 42 cases who visited Disneyland theme parks during a 3-day period and 3 additional cases whose rash onset dates were consistent with acquiring infection during that 3-day period were all considered index cases for that outbreak. The undocumented, extreme transmission event(s) that resulted in this large number of secondary cases that occurred at or near Disneyland theme parks was omitted; only the subsequent known transmission, which likely is more typical of transmission in California [6], has been included in the estimation of the reproduction number.

Genetic Characterization

Measles virus genotypes were determined using a 450 nucleotide sequence of the nucleoprotein gene (N-450) at either the California Department of Public Health Viral and Rickettsial Disease Laboratory or the CDC Measles Virus Laboratory [15]. Outbreaks were assigned the genotype corresponding to any individual or individuals with epidemiologic linkage in that outbreak for whom genotyping was performed.

Analysis

Branching process theory [16] has been used to estimate the reproduction numbers of many subcritical diseases [17, 18]. Prior work on branching process models has outlined the approach to fitting multigenotype models that we propose for this research (eg, [19] fits a model with 2 reproduction numbers). The secondary case distribution gives the probability distribution of the number of secondary cases per case in a branching process model [19]. Specifically, assuming a negative binomial secondary case distribution, a mathematical expression for the distribution of outbreak sizes can be derived (see, [6, 19]) and is employed in our analysis. A negative binomial secondary case distribution is preferable to the limiting Poisson or geometric distributions, because it yields an empirically better fit to data [18] and accounts for heterogeneity in transmissibility [20].

Assuming a negative binomial secondary case distribution, a closed-form solution is available for the distribution of outbreak sizes when transmission is subcritical [19, 21]. The closed-form solution for the distribution of outbreak sizes can be found elsewhere [6, 20] and is a function of the number of index cases; R, the mean of the secondary case distribution; and k, the dispersion parameter, a measure of heterogeneity in transmission, with smaller values indicative of a larger variance in the secondary case distribution. (k = 1 corresponds to a geometric secondary case distribution and k = ∞ corresponds to a Poisson distribution.) Fitting this model to the distribution of outbreak sizes using maximum likelihood, we can estimate the reproduction number R [19].

P values for heterogeneity across genotype and other predictors were determined using permutation tests (1024 permutations) to determine the probability of seeing a ratio of reproduction numbers larger than was observed. Confidence intervals (CIs) for reproduction numbers were obtained by percentile bootstrap (1024 replicates). A type I error rate of 0.05 was used to test the hypothesis that genotype B3 is more transmissible than other genotypes.

It is possible that out of many genotypes one genotype would appear to give rise to larger outbreaks by chance, and in testing this genotype against all others we would be susceptible to the Texas sharpshooter fallacy [22]. To address this, we performed an additional sensitivity analysis in which we analyze the data using a multigenotype model. Specifically, we used a random-effects model to model a random effect for transmissibility by genotype. We used the distribution of outbreak sizes in equation 1, where the logit of the reproduction number R varies by genotype and is sampled from a normal distribution with mean μ and variance σ². The probability of the observed outbreaks of a given genotype for this model is the following:

$$\mathrm{Pr}(Y)={\displaystyle \prod _{g=1}^G{\displaystyle {\int }_{R=0}^{R=1}{\displaystyle \prod _{i=1}^{N_g}\mathrm{Pr}(Y_{i,g}|R,k)f(R,\mu ,\sigma )dR}}}$$ (1)

where Y is a vector of all observed outbreak sizes, G is the total number of observed genotypes, g is a specific genotype, N_g is the number of outbreaks of genotype g, Y_i,g is the size of the ith outbreak of genotype g, and $f(R,\mu ,\sigma )=\frac{1}{\sqrt{2\pi {\sigma }^2}}\frac{1}{R(1-R)}\exp \left(-\frac{{(\log \text{it }R-\mu )}^2}{2{\sigma }^2}\right)$. We then maximized the likelihood with respect to µ and σ and performed a likelihood ratio test with a model with σ equal to zero, adjusting for the fact that the null hypothesis is on the boundary [23]. We perform a similar analysis with season of outbreak.

RESULTS

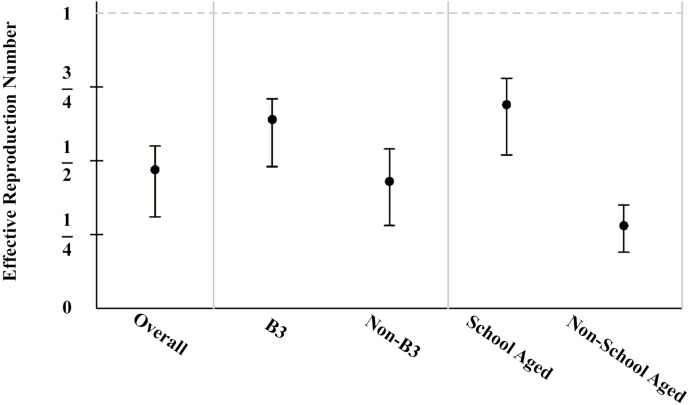
There were 400 measles cases and 165 outbreaks in California from 1 January 2000 to 31 December 2015. Table 1 summarizes the genotype data available for this study. For 2000–2015, we estimate the overall reproduction number to be 0.47 (95% CI, .31–.55). Permutation P values for the effect of genotype, season of introduction, age of the index case, and vaccine status of the index are given in Table 2. Because we find compelling evidence that genotype and age of the index case are significant predictors of measles transmissibility, we present effect estimates and confidence intervals in Table 3. These effect estimates are also summarized in Figure 1. (Parameter estimates for the random-effects models are given in Supplementary Appendix Table A1 and estimated dispersion parameters are given in Supplementary Appendix Table A3.)

Table 1.

California Measles Cases Since Elimination: Case Counts, Number of Outbreaks, and Mean Outbreak Size by Genotype

Genotype	Total Cases (Excluding Outbreak A)	Number of Outbreaks (Excluding Outbreak A)	Mean Outbreak Size (Excluding Outbreak A, per Index Case)
B3	183 (52)	21 (20)	8.71 (2.6, 2.61)
D3	4	2	2
D4	23	16	1.44
D5	16	3	5.33
D6	3	2	1.5
D7	12	4	3
D8	42	28	1.5
D9	14	8	1.75
G2	5	1	5
H1	8	8	1
No genotype	90	72	1.25 (1.25, 1.2)
Total	400 (269)	165 (164)	2.42 (1.64, 1.62)

Values for excluding outbreak A or per index case outbreak sizes are given in parentheses only when these values differ from the value including outbreak A or from the mean total outbreak size.

Table 2.

P Values for Various Predictors of Measles Transmissibility

Variable	P Value	P Value	P Value
	(Including Outbreak A)	(Excluding Outbreak A)	(Outbreaks With 1 Index Case)
Genotype (B3 vs not)	.01	.04	…
Season of introduction (winter vs not)	.01	.03	…
Age of index case (school-aged vs not)	…	…	<.001
Vaccine status of index case (vaccinated vs unvaccinated or unknown status)	…	…	.12
Random effect of genotype	.004*	.02*	…
Random effect of season	.14*	.42*	…

Starred P values are χ² likelihood ratio P values. All other P values are permutation P values.

Table 3.

Estimated Reproduction Numbers for Measles Transmission: Overall (All Outbreaks), Genotype B3 vs. Non-B3 Genotypes (Only for Genotyped Outbreaks), and School-Aged (Ages 5–18 Years) vs. Non-School Aged (Only for Outbreaks With a Single Index Case)

	Reproduction Number R (95% Confidence Interval)
Overall	0.47 (.31–.55)
B3	0.64 (.48–.71)
Non-B3	0.43 (.28–.54)
School-aged	0.69 (.52–.78)
Non-school-aged	0.28 (.19–.35)

Dispersion parameters were estimated and are included in the Supplementary Appendix.

Figure 1.

Estimated reproduction numbers for measles transmission: overall, genotype B3 vs non-B3 genotypes, and school-aged (age 5–18 years) vs non-school-aged index cases.

DISCUSSION

We evaluated whether or not differences between genotypes may be responsible for differences in observed outbreak sizes and measles transmissibility. Genotype is significantly associated with transmissibility, irrespective of type of analysis (Table 2). Prior studies [6, 8, 24] have indicated that there is not compelling evidence for declining population immunity over time during the elimination era, so we evaluated other plausible confounders in the relationship between genotype and outbreak size. Because a significant number of index cases were US residents with recent international travel, season of introduction is plausibly associated with genotype: Travel to areas with circulating B3 strains might be more common in the cooler winter months. (Supplementary Appendix Table A2 shows that it does appear that the fraction of winter B3 introductions is greater than that of other seasons.) However, while season appears significantly associated with transmissibility when comparing the winter season to all other seasons, in a random-effects model, the effect of season is nonsignificant. We think it is unlikely that age of index case or vaccine status of the index case is causally related to infecting viral genotype (see Supplementary Appendix for more information). However, school age appears to be a significant predictor of measles transmissibility, likely due to the number of contacts [25] and the potential clustering based on vaccination status, particularly among household contacts [26].

Contact investigations may have several decision points, and a better understanding of predictors of transmission could be used to minimize transmission. While routine vaccination remains the most important control measure for measles, other control measures such as home quarantine and postexposure prophylaxis are an important part of the on-the-ground response during an outbreak [27]. Contact investigations for measles and delivering postexposure prophylaxis to susceptible contacts of cases are resource intensive and divert funds and staff resources from other public health programs [28, 29]. Thus, it would be advantageous to have a marker of transmissibility that could be used to focus public health efforts, particularly in a setting of multiple cases and contact investigations competing for limited resources [27]. More accurately anticipating the number of cases during an outbreak could help improve resource and staff allocation.

Our results are consistent with prior analyses of California and US measles outbreaks. The previous estimate for the R for measles in the US between 2001 and 2011 is 0.52 (95% CI, .44–.60) [30], consistent with an overall R for California during 2000–2015 of 0.47 (95% CI, .31–.55) estimated here. The prior estimate for the R for outbreak A is 0.69 (95% CI, .48–1.04) [6] (note this estimate assumed 40 index cases), consistent with an R of 0.64 (95% CI, .48–.71) estimated here for B3 strains. Although in another study [6] the R for outbreak A was not statistically significantly higher than the R for the 2001–2011 time period (which includes outbreaks of the B3 and non-B3 genotypes), the point estimate was higher, which is consistent with the hypothesis that B3 strains are more transmissible.

This study has several strengths. Measles has been widely studied using a variety of mathematical epidemiology techniques since the 1950s [18, 31–35]. While preelimination era measles was characterized by continuous transmission with seasonal patterns in transmission [34], measles transmission in the United States is now characterized by small outbreaks following importation [3]. Branching processes are ideal for analyzing diseases that occur as isolated cases, transmission chains, and make it possible to determine whether changes in case counts are due to changes in transmissibility or changes in the numbers of introductions [30]. Thus, postelimination era dynamics favor the branching process approach we employed [17, 30].

In addition, we performed several sensitivity analyses to avoid the “Texas sharpshooter” fallacy [22]. Since outbreak A was the largest outbreak in California since elimination, this may have garnered increased, and perhaps undue, interest in the causal effects of genotype B3 and winter season on measles transmissibility. To address this possible fallacy, we omitted outbreak A and recalculated permutation P values for all predictors of interest and analyzed genotype and season as a random effect. Our result that genotype is a predictor of transmissibility was robust to inclusion or exclusion of the outbreak A and random-effects modeling. However, the effect of season is more questionable given that the P value was significant when comparing winter to all other seasons, but not in a random-effects model. Last, for outbreak A, we only included known transmission events that occurred outside of the Disneyland theme parks; this transmission was likely more typical of transmission in California [6]. In addition, if there had been a known single index case, the decision to model this outbreak as an outbreak with 45 index cases effectively reduced our statistical power to detect a difference between B3 and non-B3 genotypes; given that we did detect a significant effect, this lends credibility to the hypothesis that there are genotype-specific differences in transmissibility. We note that the number of index cases we use has been updated and thus differs from the 40 used in [6].

A weakness of this study is that we were limited by the number of California measles cases since elimination; thus, the study may have been underpowered to detect significant effects for key predictors. For example, in only 16 of 163 single-index-case outbreaks was the index case vaccinated (the remainder had unknown vaccination status or were unvaccinated). While these outbreaks were on average characterized by less transmission, we did not detect a significant effect. In addition, we cannot distinguish between biological differences between genotypes (eg, greater viral replication in the lungs for B3 strains [36]) and differences in networks in which specific genotypes may tend to circulate (eg, a larger number of contacts in networks where B3 strains tend to be introduced). While we would argue that biological differences between genotype B3 and other genotypes are plausible [36], as we did not include all possible confounders, our models cannot necessarily distinguish between competing explanations for differing transmissibility. While measles case ascertainment is thought to be high, missed cases are a possibility and could result in collider (selection) bias. For this to bias the observed association between genotype and outbreak in the observed direction, the B3 genotype would have to cause less severe disease. (Case detection would be enhanced, not diminished, during large outbreaks.) While this would be at odds with [36], the B3 genotype could cause less severe disease if the measles vaccine were less effective against this genotype. (That is, genotype B3 cases would be enriched with vaccinated and thus partially protected individuals compared with other outbreaks.) In addition, if the B3 genotype causes more severe disease, it is possible that B3 outbreaks would appear larger due to improved case finding. While we cannot rule out that genotype B3 outbreaks appear larger because genotype B3 causes more severe disease with available data, the apparent public health impact of the B3 genotype nonetheless appears to be greater than that of other genotypes.

In conclusion, we have found that genotype appears to be a significant predictor of measles transmissibility, with genotype B3 being more transmissible compared with all other genotypes combined. School age of the index case also appears to be a significant predictor of transmissibility. While we do not find compelling evidence that the relationship between genotype B3 and outbreak size is confounded by other factors, it remains to be seen whether this result could be replicated in other highly vaccinated populations. Furthermore, outbreak sizes are variable and, for example, genotype B3 outbreaks will overlap substantially in size with non-B3 outbreaks. Thus, more data are needed before one could make a firm recommendation that genotype or age of index case could be used for guiding contact investigation. The view that non-B3 outbreaks or outbreaks with index cases not of school age are of lesser public health importance is unwarranted. While high levels of population immunity achieved through routine measles vaccination remains the cornerstone of control, variability in measles transmissibility may nonetheless have important implications for measles control: the vaccination threshold required for elimination may not be the same for all genotypes or age groups.

Supplementary Data

Supplementary materials are available at Clinical Infectious Diseases online. Consisting of data provided by the authors to benefit the reader, the posted materials are not copyedited and are the sole responsibility of the authors, so questions or comments should be addressed to the corresponding author.

Notes

Acknowledgments. This work is supported by the National Institute of General Medical Sciences (NIGMS) at the National Institutes of Health (NIH) (grant number F31GM120985 to S. F. A.) and the MIDAS program at the NIGMS at the NIH (grant number U01GM087728 to T. C. P. and L. W.). The UCSF Department of Ophthalmology acknowledges support from an unrestricted grant from Research to Prevent Blindness.

Potential conflicts of interest. All authors: No reported conflicts of interest. All authors have submitted the ICMJE Form for Disclosure of Potential Conflicts of Interest. Conflicts that the editors consider relevant to the content of the manuscript have been disclosed.