Effective potential for magnetic resonance measurements of restricted diffusion

Abstract

The signature of diffusive motion on the NMR signal has been exploited to characterize the mesoscopic structure of specimens in numerous applications. For compartmentalized specimens comprising isolated subdomains, a representation of individual pores is necessary for describing restricted diffusion within them. When gradient waveforms with long pulse durations are employed, a quadratic potential profile is identified as an effective energy landscape for restricted diffusion. The dependence of the stochastic effective force on the center-of-mass position is indeed found to be approximately linear (Hookean) for restricted diffusion even when the walls are sticky. We outline the theoretical basis and practical advantages of our picture involving effective potentials.

1 INTRODUCTION

Recovering the mesoscopic structure of porous media and biological tissues via diffusion sensitized NMR methods has been an active area of research since 1960s [1, 2]. As a molecule diffuses within the medium, its magnetic moment acquires a certain phase depending upon the particle’s trajectory and the impressed magnetic field gradient profile. The total signal generated by all molecules can be expressed mathematically as

$$E=\langle e^{-i\gamma {\int }_0^t\mathrm{d}s\mathit{G}(s)·\mathit{x}(s)}\rangle ,$$ (1)

where γ is the gyromagnetic ratio while G and x denote the time-dependent magnetic field gradient and the position of the particle, respectively. The average is taken over all particle trajectories.

Conventional techniques for relating the NMR signal above to microstructural features of the medium vary from “localized” models in which the aggregate signal is envisioned to arise from isolated (e.g., restricted) compartments [3, 4] to more “global” models, which attempt to capture the medium’s disorder [5, 6]. Here, we propose to approach the problem of relating the NMR signal to microstructural features of the medium with an alternative paradigm wherein diffusion is thought to be taking place within a potential energy landscape.

When the gradient waveform, G(s), comprises two well-separated pulses of infinitesimal durations, the relationship between the NMR signal and the compartment shape is the same as that in scattering experiments. For closed pores, the signal intensity is given by E(q) = |ρ̃(q)|², i.e., the power spectrum of the equilibrium distribution of spins ρ(r). Here, the wavevector q is taken to be the time integral of each gradient pulse multiplied by γ. As the pulse duration is prolonged, the oscillatory diffraction pattern of the signal stretches towards larger q-values (q = |q|), and eventually becomes unobservable [7, 8]. This is a manifestation of the loss of information in experiments featuring long pulses; such information loss is key to our endeavour to identify an effective potential for the diffusion process.

In this Perspective, we argue that the theory of diffusion under a Hookean restoring force [9, 10, 11, 12, 7, 13] can be regarded as the effective theory of restricted diffusion for a wide class of highly relevant NMR signal acquisition scenarios. This is evident at the macroscopic scale when one considers the dependence of the signal on experimental parameters for sequences featuring long gradient pulses or plots the average effective force experienced by the particles against their mean position (center of mass of their trajectories) during the application of a long pulse. For NMR examinations of microscopic diffusion anisotropy [14, 15], the quadratic potential profile is ideally suited to represent the observable properties of small pores making up a compartmentalized medium.

2 EFFECTIVE POTENTIAL FOR RESTRICTED DIFFUSION

Here we demonstrate that, under certain experimental conditions, the influence of restricted diffusion is essentially the same as that for the Hookean potential model, which was studied in-depth recently [13]. After the theoretical grounds for the effective theory are established, we proceed with presenting simulation results that provide additional justification.

2.1 Long-pulse train

Consider a pulse sequence which consists of N rectangular gradient pulses of varying (vector) magnitudes G_n and durations δ_n. With the definition

$${\mathit{q}}_n=\gamma {\mathit{G}}_n{\delta }_n,$$ (2)

the NMR signal (1) is given by

$$E=\langle \text{exp }\{-i\sum _{n=1}^N\frac{1}{{\delta }_n}{\int }_{t_n}^{t_n+{\delta }_n}{\mathit{q}}_n·\mathit{x}(t)\mathrm{d}t\}\rangle ,$$ (3)

where t_n denotes the leading edge of the n^th pulse. Angular brackets indicate averaging over the possible trajectories x(t).

Further, introducing the stochastic center-of-mass of the particle trajectory [7] during the n^th pulse through

$${\mathit{\xi }}_n=\frac{1}{{\delta }_n}{\int }_{t_n}^{t_n+{\delta }_n}\mathit{x}(t)\mathrm{d}t,$$ (4)

the stochastic signal can be rewritten as

$$E=\langle e^{-i({\mathit{q}}_1·{\mathit{\xi }}_1+{\mathit{q}}_2·{\mathit{\xi }}_2+\dots +{\mathit{q}}_N·{\mathit{\xi }}_N)}\rangle .$$ (5)

In words, the NMR signal elicited by spatially constant gradient pulses of finite duration is sensitive to the center of mass (average position) of Brownian trajectories, rather than instantaneous coordinates. The duration of the pulses therefore serve to smear out fine spatial features.

Let p_cm(ξ, δ) denote the distribution of the center of mass during a time interval of duration δ. In the long duration regime, δ_n → ∞, the dependence on the pulse separation disappears and the signal intensity (5) factorizes, leading to

$$E={\stackrel{\sim }{p}}_{\text{cm}}({\mathit{q}}_1,{\delta }_1){\stackrel{\sim }{p}}_{\text{cm}}({\mathit{q}}_2,{\delta }_2)\dots {\stackrel{\sim }{p}}_{\text{cm}}({\mathit{q}}_N,{\delta }_N),$$ (6)

where

$${\stackrel{\sim }{p}}_{\text{cm}}(\mathit{q},\delta )=\int p_{\text{cm}}(\mathit{\xi },\delta )e^{-i\mathit{q}·\mathit{\xi }}{\mathrm{d}}^3\xi$$ (7)

is the Fourier transform of the center of mass distribution. Due to its construction (4), the random variable ξ has a distribution p_cm(ξ, δ) that approaches a Gaussian in the limit of long duration.¹ Therefore, both its Fourier transform (7) and hence the signal (6) approach Gaussians as well.

The Gaussian distribution is determined simply by its variance matrix (with its mean set to zero for convenience). The relevance of this fact here is that when a train of long pulses is employed, the signal has no means of encoding for fine features of the microscopic environment where diffusion takes place.² What survives in the signal is merely that component of the microscopic forces that provide a stable equilibrium (since the particles do not escape to infinity) for the center of mass and no more. More specifically, a Hookean force.

While restricted diffusion becomes a difficult problem to tackle in higher dimensions for all but a few special geometries, diffusion under a Hookean force is much more tractable, and it behooves one to adopt the latter model when its features are all that can be observed, as argued above. Hence we consider the case of diffusing particles subject to a (dimensionless) parabolic confining potential U(x) = (1/2)x^⊤Cx, where C is the confinement tensor [13]. Under this potential, the magnetization density evolves according to the Bloch-Torrey-Smoluchowski equation [17, 18, 13]. For this process, the center of mass distribution is Gaussian for any duration, and its Fourier transform is given by

$${\stackrel{\sim }{p}}_{\text{cm}}(\mathit{q},\delta )=e^{-\frac{1}{2}{\mathit{q}}^{\top }{\mathit{V}}_{\mathit{q}}},$$ (8)

with the variance matrix

$$\mathit{V}=2{(D\delta )}^{-2}{\mathit{C}}^{-3}(D\mathit{C}\delta +e^{-D\mathit{C}\delta }-1),$$ (9)

which is just a straightforward generalization of an expression in [7] to higher dimensions. Via Eq. (6), the signal encodes the confinement tensor, C, for the restricted region.

2.2 Insights from the one-dimensional problem

The eigenvalues of the inverse of the confinement tensor C can be associated with the square of three lengths pertaining to the overall size of a 3-dimensional region. Of course, these three lengths cannot characterize the irregular boundary of a general 3-dimensional region, as alluded to above. However, for the illustration of the size-confinement correspondence, we momentarily take up the simple 1-dimensional example of diffusion restricted by two parallel plates separated by a distance L. The variance of the center of mass position is provided by Mitra and Halperin [7] to be

$${\langle \xi {(\delta )}^2\rangle }_{\text{res}}=\frac{16L^4}{{\pi }^{6}D\delta }\sum _{n=1,3,5,\dots }^{\infty }\frac{1}{n^6}[1-\frac{1-e^{-{\pi }^2{n}^{2}D\delta /L^2}}{{\pi }^2{n}^{2}D\delta /L^2}],$$ (10)

where the subscript stands for restricted diffusion.³

In the long pulse duration regime wherein the statistics of the restricted problem approach those of the confinement problem, the variances of the center of mass position for the two problems are found by taking the long time limit of (9) and (10), respectively,

$${\langle \xi {(\delta )}^2\rangle }_{\text{con}}~\frac{2}{C^{2}D\delta },\delta \to \infty ,$$ (11)

$${\langle \xi {(\delta )}^2\rangle }_{\text{res}}~\frac{L^4}{60D\delta },\delta \to \infty .$$ (12)

Demanding that the two variances above agree results in the relation

$$C=\frac{\sqrt{120}}{L^2},$$ (13)

meaning that the confinement model with parameter C becomes the appropriate effective theory for the restriction model (the “true” theory) with length L, yielding the same observed quantities under the coarse-graining furnished by the long averaging pulse.

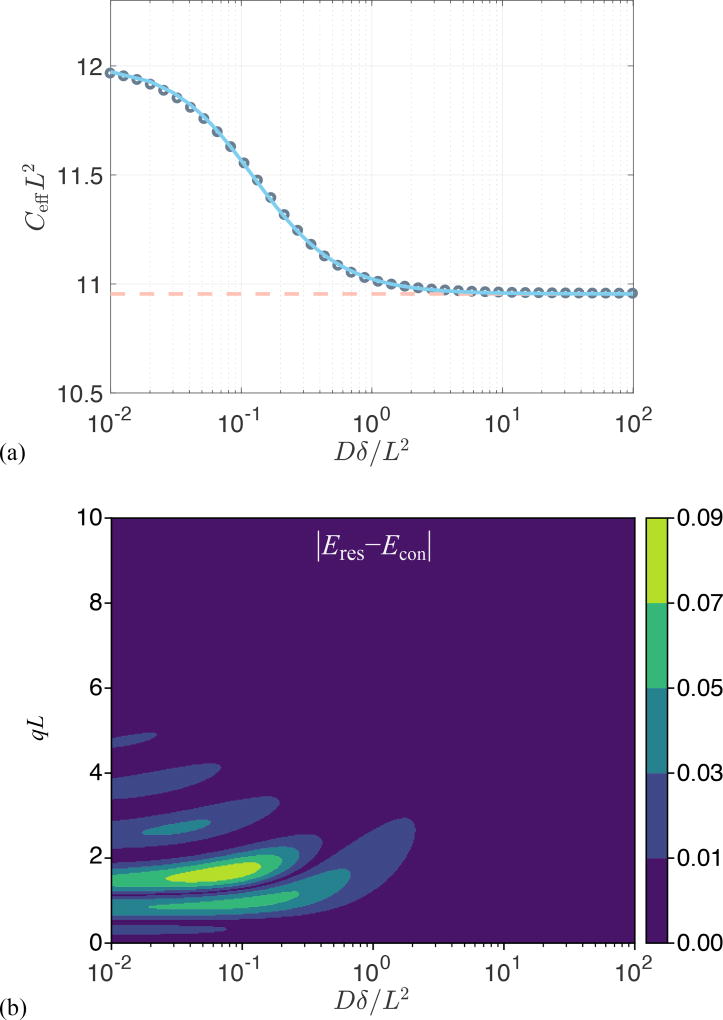
While in the above it was the long pulse duration that ensured the Gaussianity of the signal (through the center of mass distribution) for restricted diffusion, an alternative situation is one where the gradient strength is so small that qL is much smaller than unity. Because the observed signal is Gaussian for such q values, the confinement model would perfectly represent the data, yet (13) would not apply since the pulse duration is not necessarily long. If one adopts a matching scenario as above, a correspondence can be obtained numerically for general pulse durations. As shown in Figure 1a, the effective confinement value obtained by matching the variances of the center-of-mass distributions for the two problems, which is equivalent to matching the signals in an experiment employing well-separated pulses, varies within a very narrow range, namely between C = 12/L² and $C=\sqrt{120}/L^2$. Therefore, employing the asymptotic correspondence (13) in lieu of the numerical one (blue curve in Figure 1a) would still provide an acceptable estimate of L.

Figure 1.

(a) Effective dimensionless confinement value (gray circles) computed by matching the variances of the center of mass distributions in the two problems plotted vs. the dimensionless time Dδ/L². The variation in C_effL² value is well-captured (error less than 0.12%) by the expression $y=12-(12-\sqrt{120}){(\alpha x)}^{c\gamma }{[1+{(\alpha x)}^c]}^{-\gamma }$, with α = 9.495, γ = 1.210, and c = 1.266 (blue line). The dashed line indicates the asymptotic value $\sqrt{120}$. (b) The absolute value of the difference in the normalized signals implied by the two problems (restricted diffusion with separation L, and the Hookean potential with a confinement value taken to be $C=\sqrt{120}{L}^{-2}$) for a traditional Stejskal-Tanner sequence [32] with two gradient pulses whose leading edges are separated by Δ with DΔ/L² = 100. The restricted diffusion signal was computed using the multiple correlation function method [33, 34].

Contrary to the two cases above, the signal for restricted diffusion is not Gaussian for other values of q or δ. Thus, the signal profile afforded by the confinement model can only be an approximation to the true signal when the pulses are not long. To investigate the discrepancy, it is insightful to compare the signal for the restricted diffusion problem (for a slab geometry of separation L) to that for the Hookean model featuring the long-time asymptotic value (13) of the effective confinement. In Figure 1b, we show that the error (defined as the difference in the normalized signal intensities implied by the restriction and confinement pictures) is below 0.01 for a very large portion of the relevant parameter space that could be probed. Such differences are not detectable when the signal-to-noise ratio is 100 or less, thus justifying the confinement description as a reliable substitute in studies involving restricted diffusion. In fact, the most significant exception to this statement is at the peaks of the diffraction pattern, which occur roughly at qL = 3/2, 5/2, … for very short pulses (i.e., along the left edge of this figure) and at slighly larger qL values for longer durations. For long pulse durations, the diffraction pattern does not prevail, and the confinement model eventually provides an accurate description of the detectable signal.

Consider, e.g., a 4 µm pore—roughly the size of a yeast cell. Assuming a bulk diffusivity value of 2 µm²/ms, and for a pulse duration of 20 ms, which is typical for diffusion measurements via clinical scanners, the Dδ/L² value is 2.5. Thus, the signal response of the confinement picture would be indistinguishable from a much more elaborate theory involving restricted diffusion. The situation is even more favorable for smaller sized compartments. In laboratory spectrometers, however, pulse durations an order of magnitude shorter are feasible; in such scenarios, detectable differences between the restricted diffusion and confinement pictures can be encountered unless the pores are smaller. However, let us remark once more that it is only in this simplified one-dimensional scenario that there exists a single unambiguous size of the region, allowing a one-to-one correspondence to be drawn between C and L. In higher dimensions, one’s measurements have access simply to the tensor C; the actual dimensions of the region can only be speculated upon to the extent that its geometry is known.

2.3 Boundary force: simulations

The confinement model is based on a Hookean force assumption, i.e., the presence of a restoring force whose magnitude increases linearly as the particles move away from an attractive center. We shall define an effective force, F_eff, based on the impulse the particles experience during a time interval of duration δ, i.e.,

$$F_{\text{eff}}\delta ={\int }_0^{\delta }F(t)\mathrm{d}t.$$ (14)

Because the time-dependent force F(t) is proportional to −Cx(t) for particles subject to a quadratic potential, the effective force is proportional to −Cξ(δ), implying a perfectly linear dependence on the center-of-mass of each and every trajectory. On the other hand for restricted diffusion, the effective force is proportional to −ΔN/δ, where ΔN denotes the number of collisions the particle makes with the wall on the left subtracted from that with the wall on the right.

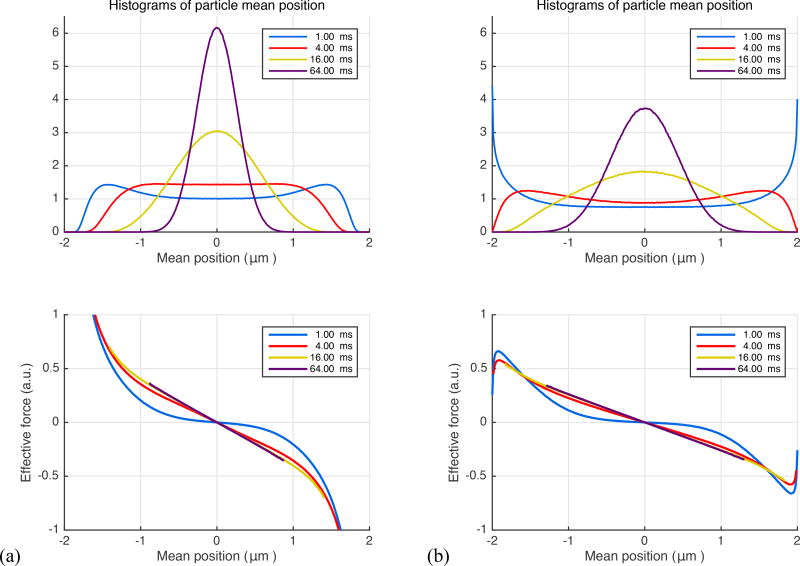
By performing random walk simulations, we investigated whether a similar (Hookean) force model could emerge for the restricted diffusion process as well. In the top panel of Figure 2a, we plot the histograms of mean particle position for different durations. As expected, the center of mass distribution approaches a Gaussian as the time is prolonged. Note that the net force is a stochastic variable just like the mean position of the trajectories. Thus, in the bottom panel of Figure 2a, we plot the average of the net effective force against the mean trajectory position. Remarkably, the effective force is linearly related to the mean position for an overwhelming portion of the particles even for moderate times. Moreover, by repeating the simulations for different L values (results not shown), we found that the slope of the curves at long durations, i.e., the effective force constant, is proportional to L⁻² just like in (13). These findings further support the idea of employing a Hookean force model as a substitute for restricted diffusion at long durations. Importantly, the Hookean model is valid even for more complicated problems, which are difficult to treat analytically. We illustrate this point by introducing stickiness to the walls of the same restricted geometry. As shown in Figure 2b, the same conclusions can be drawn for this scenario albeit for a different value of the effective confinement.

Figure 2.

(a) Random walk simulations for particles trapped between non-sticky parallel plates separated by 4 µm, diffusing with bulk diffusivity D=1.0 µm²/ms. Different curves represent different time intervals, which can be associated with durations of the pulses in NMR measurements. The distributions of the positions of the center of mass are shown at the top. The average effective force exerted on the diffusing particles plotted vs. the trajectories’ center of mass (bottom). (b) The simulations were repeated by introducing surface adsorption effect so that the particles spend, on average, 25% of the time stuck at the walls.

3 DISCUSSION & CONCLUSION

While characterizing a compartmentalized specimen or biological tissue via diffusion NMR, one is faced with the problem of determining a reliable representation of the local compartment. An accurate mathematical description of the pore shape would typically necessitate numerous parameters. However, such parameters are simply unavailable in diffusion NMR measurements featuring long gradients as a result of coarse-graining associated with the diffusion process taking place during the application of the gradients. The confinement tensor model [13] contains just the right number of parameters as dictated by the central limit theorem.

Similar to the diffusion tensor, the confinement tensor is real and symmetric, thus is described by 6 independent numbers. However, the confinement tensor model has at least one extra parameter—the bulk diffusivity, which can be scalar (isotropic) or tensorial. For the latter case, the diffusion tensor model emerges simply in the C → 0 limit [13]. It is common to express the detected NMR signal for complex specimens as the sum of contributions from Gaussian and restricted compartments [3]. Our work implies that, when appropriate acquisition parameters are employed, both these compartments could be represented by the confinement tensor model though with different confinement values.

Diffusion tensors have also been employed for representing diffusion in microscopic compartments [19, 4, 20]. Since the two models (employing diffusion and confinement tensors) have the same q dependence for traditional Stejskal-Tanner measurements performed with varying gradient vectors, their predictions of the signal would be the same, and one model cannot be preferred over the other; this was observed when the confinement tensor is employed to represent the voxel-level signal [21] similar to what is done in diffusion tensor imaging [22]. However, the diffusion tensor model is based on free diffusion, and exhibits a time-dependence which is paradoxical for a compartmentalized structure. Manifestations of the difference in time-dependencies would be observable, e.g., when the timing parameters of the measurements are varied [23]. In fact, the influence of the gradient waveform on the free-diffusion signal is fully captured [24] by a measurement tensor, referred to as the b-matrix [25]. Thus, any set of acquisitions featuring the same b-matrix would yield the same signal value if diffusion tensor model is employed. However, the quadratic potential profile would lead to qualitatively different signal profiles, approximating the response of a restricted diffusion process, which is more consistent with the underlying compartmentalized structure.

From a practical point of view, treating restricted diffusion is quite difficult even for simple geometries. For example, if we consider an ellipsoidal pore—the simplest geometry with the same number of parameters as a general confinement tensor—, the problem would be very difficult to solve analytically. We argue that doing so would also be unnecessary if long pulses are employed. The separability of the confinement model enables one to write [13] the expected signal simply in terms of the solution of the one-dimensional Hookean problem, provided that we work in a frame of reference whose axes coincide with those of the ellipsoid; in this frame, C is diagonal. Such simplicity due to separation of variables in the confinement model is valid even for more complicated shapes since the statistics of the center of mass converge to Gaussian as long as the durations of the gradient pulses are long.

We would like to note that, as shown by Bauer et al., [26] accumulation of Gaussian phase, if true, implies a propagator (not just stationary distribution) that is Gaussian. In fact, the Ornstein-Uhlenbeck propagator [27, 17, 28] associated with the quadratic potential profile is the general form following the basic properties of the process: diffusive, Markovian, stationary, with Gaussian transition probabilities [26].

In a very recent study [29], some of us considered a general potential energy landscape, U(x), in which all disturbances to otherwise free diffusion are envisioned to originate from the variations in this landscape. For this scenario, the equilibrium density of the particles is governed by Maxwell-Boltzmann statistics, i.e., ρ(x) ∝ e^−U(x), which could account for inhomogeneities in the bulk, and incorporate the effects of boundaries if needed, in a mathematically wieldy manner. We demonstrated that pulse sequences involving very short and long pulses [30, 31] could be employed to map this underlying landscape. Here, we have extended this finding to effective potential energy landscapes associated with restricted diffusion, which can be mapped without narrow pulses.

In conclusion, we have presented a new perspective in which findings of common and relevant NMR signal acquisition scenarios can be interpreted. At the heart of this perspective lies modeling the diffusion as taking place in an effective quadratic potential landscape instead of a restricted domain. We have argued that when probed via waveforms featuring long pulses, the two models become indistinguishable, and the signal should rather be taken to reflect the parameters of such an effective model. Simulations suggest that the stochastic effective force has a linear (Hookean) dependence on the average particle position. The signal for quadratic potential indeed provides a very good approximation to that for restricted diffusion in small (micron-scale) pores when examined via commonly available hardware (see Figure 1b). This observation can be generalized in a straightforward way to higher dimensions, thus making the confinement tensor model [13] relevant for applications such as clinical and pre-clinical MRI.