Abstract
The collagenous extracellular matrix (ECM) of skeletal muscle functions to transmit force, protect sensitive structures, and generate passive tension to resist stretch. The mechanical properties of the ECM change with age, atrophy, and neuromuscular pathologies, resulting in an increase in the relative amount of collagen and an increase in stiffness. Although numerous studies have focused on the effect of muscle fibrosis on passive muscle stiffness, few have examined how these structural changes may compromise contractile performance. Here we combine a mathematical model and experimental manipulations to examine how changes in the mechanical properties of the ECM constrain the ability of muscle fibers and fascicles to radially expand and how such a constraint may limit active muscle shortening. We model the mechanical interaction between a contracting muscle and the ECM using a constant volume, pressurized, fiber-wound cylinder. Our model shows that as the proportion of a muscle cross section made up of ECM increases, the muscle’s ability to expand radially is compromised, which in turn restricts muscle shortening. In our experiments, we use a physical constraint placed around the muscle to restrict radial expansion during a contraction. Our experimental results are consistent with model predictions and show that muscles restricted from radial expansion undergo less shortening and generate less mechanical work under identical loads and stimulation conditions. This work highlights the intimate mechanical interaction between contractile and connective tissue structures within skeletal muscle and shows how a deviation from a healthy, well-tuned relationship can compromise performance.
Keywords: ECM, Collagen, Muscle, Intramuscular pressure, Muscle fibrosis
1 Introduction
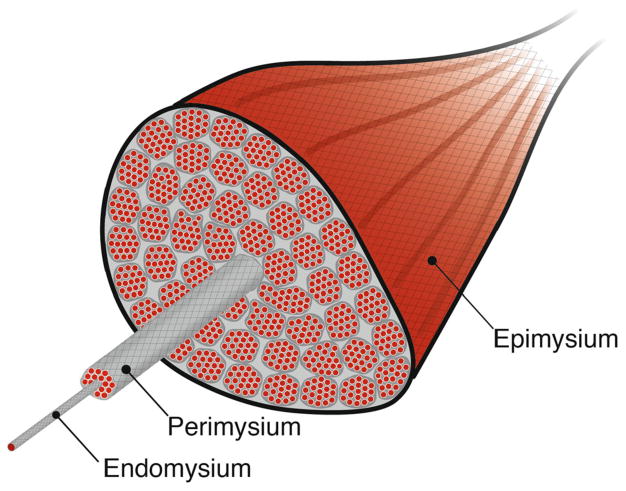
The extracellular matrix (ECM) forms the structural scaffolding of skeletal muscle. The ECM of skeletal muscle is organized into hierarchical layers, which surround muscle fibers (endomysium), muscle fascicles (perimysium), and the whole muscle (epimysium; Fig. 1). These structures serve a number of important mechanical functions. The ECM has been shown to transmit forces to adjacent fibers or fascicles through pathways acting in parallel to muscle fibers (Street 1983; Huijing et al. 1998; Huijing 1999; Maas and Huijing 2005; Huijing et al. 2007; Yucesoy 2010). The seminal work of Street (1983) showed that force can be transmitted from a muscle fiber to adjacent fibers even when longitudinal myotendinous pathways are completely disrupted. These lateral pathways have been further illuminated by the deeper understanding of the role of cytoskeletal proteins that mechanically connect the sarcomere to the extracellular matrix and allow for the transmission of force (Huijing 1999; Zhang and Gao 2014). Such non-myotendinous pathways of force have been observed at various levels of organization including between adjacent fibers and fascicles (Street 1983; Huijing 1999), two heads of the same muscle (Maas and Huijing 2005), pairs of muscle synergists (Maas and Sandercock 2010; Bernabei et al. 2015), or even along neurovascular connective tissue tracts (Huijing 2007). These myofascial interactions have important consequences for a muscle’s force–length relationship (Huijing and Baan 2003), the spatial distribution of force (Yucesoy et al. 2003), and the spatial heterogeneity of sarcomere lengths within a muscle (Yucesoy et al. 2006).
Fig. 1.
Spatial relationship between the contractile tissues and the collagenous extracellular matrix of skeletal muscle. The spatial hierarchy of skeletal muscle is delineated by connective tissue structures surrounding muscle cells or fibers (endomysium), muscle fascicles (perimysium), and the whole muscle (epimysium). The relative proportion of a muscle’s cross section made up of these connective tissue layers increases as muscles become fibrotic
In addition, to the transmission of forces, the ECM of skeletal muscle also contributes significantly to the passive elasticity and stiffness of muscle fibers and fascicles. The passive tension that develops in response to a stretch has been largely attributed to the mechanical properties of the ECM (Meyer and Lieber 2011). Since collagen is the predominate structural protein in the ECM, the amount of collagen present in the ECM is considered an important determinant of their mechanical properties. The proportion of a muscles cross section which comprised of non-contractile (extracellular) tissue has previously been used to infer the passive force–length properties of muscles (Weibel 1981). Similarly, muscles with a higher proportion of collagen within their cross section have been shown to have higher passive stiffness (Wood et al. 2014). However, some studies have shown that the direct quantitative link between the passive mechanical properties of muscles and collagen content (assessed using a hydroxyproline assay) is weak (Smith et al. 2011), suggesting that the amount of collagen alone may not fully reflect the relationship between the ECM and passive mechanical properties of muscles (Lieber and Ward 2013).
The properties of the ECM may also influence the capacity of skeletal muscles to produce mechanical work. Mechanical work is generated when muscles actively produce force during shortening. The amount a single sarcomere can shorten is assumed to be constrained entirely by the geometry of the sarcomere (Rassier et al. 1999; Gokhin and Fowler 2013). A sarcomere ceases to shorten or generate force when the ends of the sarcomere (z-bands) come in physical contact with the thick filament. Therefore, the sliding filament model defines an upper limit on the ability of sarcomeres to generate mechanical work. Based on these physical features, it is thought that the work output of a muscle can be increased by having longer fibers with more sarcomeres in series, thereby requiring less shortening from each sarcomere (Lieber and Ward 2011). However, these well-established ideas only consider the behavior of contractile elements shortening along the line of action of the muscle fiber. It has been shown that active muscle shortening must be accompanied by some radial expansion in order to retain a constant volume (Baskin and Paolini 1967). This radial expansion requires a contracting muscle fiber to interact with the collagenous network of the ECM (Purslow 1989). Recent work has also shown that an increase in muscle volume resulting in radial expansion facilitates a mechanical interaction between intramuscular fluid and the ECM, thereby contributing to the development of passive force (Sleboda and Roberts 2017). Similarly, models have shown that the radial loading of helically oriented collagen fibers of the fibers of the ECM can directly influence longitudinal force (Gindre et al. 2013). If the collagen fibers of the ECM resist the radial expansion of muscle, these mechanical interactions may also limit the ability of a muscle fiber to shorten and generate mechanical work before reaching the physical limits of the sarcomere.
The mechanical properties of the ECM are likely to determine whether the radial expansion of muscles is restricted (Gindre et al. 2013). The amount and orientation of collagen fibers within the ECM have been shown to determine its mechanical properties (Wood et al. 2014; Trotter and Purslow 1992; Smith et al. 2011; Lieber and Ward 2013). Collagen orientations vary from 0°(circumferential) to 90°(longitudinal) at rest (Trotter and Purslow 1992) and dynamically change as a muscle changes length (Purslow 1989). Although the ECM is structurally complex and the architecture of collagen highly variable, the distribution of collagen angles within the ECM has been shown to be biased toward more circumferential orientations. The mean collagen angle is about 30°at rest (Purslow and Trotter 1994) and becomes more circumferential as a muscle fiber shortens (Trotter and Purslow 1992). The mechanical and architectural features of the collagen within the ECM are consistent with the idea that these connective tissue structures may resist radial expansion and therefore limit muscle shortening and work production.
The mechanical properties of the ECM are not constant and have been shown to remodel in response to changing mechanical conditions or in response to pathologies (Kjaer 2004; Lieber and Ward 2013). The remodeling of the ECM has been documented in response to varying exercise regimes (Gosselin et al. 1998; Kjaer et al. 2006), extended unloading (Järvinen et al. 2002), neuromuscular pathologies (Smith et al. 2011), and aging (Alnaqeeb et al. 1984; Gao et al. 2008; Ramaswamy et al. 2011). Much of the remodeling response is characterized by a substantial increase in the collagen content of the ECM and described broadly as muscle fibrosis (Lieber and Ward 2013). In addition, the increased collagen content associated with aging can be accompanied by an increase in the collagen cross-linking which further increases the stiffness of the ECM (Gosselin et al. 1998; Wood et al. 2014). Regardless of the cause or underlying mechanism associated with this remodeling, fibrosis can result in a fundamental change in the mechanical properties of the ECM. As a result, muscles with a fibrotic phenotype may face increased resistance to radial expansion and may therefore be constrained in their ability to shorten and generate mechanical work.
This study aims to determine whether constraining radial expansion limits the ability of skeletal muscle to generate mechanical work. Here we used a combination of experimental and computational approaches to explore the effects of constraints to radial expansion on muscle work. We predict that if radial expansion is necessary for muscle shortening, then restricting it will reduce a muscle’s work capacity. The broad goal of this work is to explore the conditions under which the collagen within the ECM would constrain muscle shortening and limit the ability of muscles to generate mechanical work.
2 Materials and methods
2.1 Mathematical model
Our mathematical model consisted of a pressurized cylinder, which represented a muscle fiber or fascicle surrounded by a layer of helical fibers representing the collagenous extracellular matrix. The dimensions of the model are all relative such that the formulation can be modified for cylinders of any size or shape. In order to simplify some of the anatomical complexity of the muscle ECM, we assumed that the initial collagen fiber orientation (angle) was homogeneous. Therefore, we interpreted the initial orientation of the collagen as the average orientation characterized by morphological studies (Purslow 1989). The primary goal of the model was to determine how changes in the stiffness of the extracellular matrix affected the ability of a muscle fiber or fascicle to shorten.
In our simulations, the muscle fiber shortened longitudinally while expanding radially in order to maintain a constant volume. The amount of radial expansion and the change in the surface area of the muscle fiber were determined by the amount of muscle fiber shortening.
| (1) |
| (2) |
where Rf was the radius of the muscle fiber, Rf0 was the initial radius of the muscle fiber, εf was the muscle fiber strain in the longitudinal direction, SAf was the surface area of the muscle fiber, and Lf was the length of the muscle fiber.
The length and strain of the collagen fibers surrounding the muscle were based on equations describing the geometry of a helix (Gindre et al. 2013). The collagen fibers were modeled as a helix that wraps around the muscle fiber. The orientation of the helix (pitch and pitch angle) was allowed to change as the dimensions of the muscle fiber change; however, the number of coils remained constant. Therefore, not all of the radial expansion required a direct stretch applied to collagen fibers as some of the radial expansion was accommodated by a change in helix geometry. The arc length of the collagen fiber was defined using the following equations:
| (3) |
| (4) |
| (5) |
| (6) |
where p was the pitch (distance between coils) of the helix and ϕ0 and ϕ were the initial and instantaneous pitch angle of the helix, respectively. Lc was the arc length of the collagen helix, N was the number of coils, and r0 was the initial radius of the helix. Equations 3–6 are then used to calculate the strain and in turn the force required to stretch fibers surrounding the muscle fiber. The strain of the collagen fiber and resistive force of the collagen fiber were defined as:
| (7) |
| (8) |
where εc was the strain of the collagen fiber and Lc and Lc0 were the instantaneous and initial arc lengths of the collagen fiber, respectively. We calculated the resistive force of the collagen (Fc) using the Young’s modulus of collagen (Ec), cross-sectional area of the ECM (CSAecm), and the strain of the collagen fiber (εc).
In our simulations, we varied the resistance of the ECM to radial expansion by varying the cross-sectional area of the surrounding collagen relative to the cross-sectional area of the muscle fiber. This approach allowed us to input into the model empirical data from studies that have quantified the relative proportion of a muscle cross section that is composed of collagen/ECM versus contractile muscle cells with values ranging from 2 to 20% (Lieber and Ward 2013; Smith and Barton 2014; Wood et al. 2014). In addition, our simulations allowed us to vary the initial orientation of collagen fibers to explore the effect of collagen pitch angle on collagen strain.
Our simulations predict the maximum strain of the muscle fiber (longitudinal) by comparing the forces resisting radial expansion and the radial forces produced by the muscle. Since there are no direct measures of the radial forces produced by contracting muscle fibers, we used intramuscular pressure to estimate radial forces. We defined radial forces as:
| (9) |
where Fr was the radial force produced by the muscle fiber, Pmax was the maximum intramuscular pressure, and SAf was the surface area of the muscle fiber. To quantify the conditions under which the extracellular collagenous network is likely to limit the capacity of muscle fibers to shorten and produce work, we compared the maximum internal radial force generated by the muscle and the instantaneous force required to stretch the surrounding collagen. We used published values of intramuscular pressure (Ward et al. 2007; Winters et al. 2009) and the surface area of the muscle fiber to calculate maximum radial force (Eq. 9). We also used published values of the Young’s modulus of elasticity (Svensson et al. 2010) for collagen fibers and the cross-sectional area of the ECM (Lieber and Ward 2013; Smith and Barton 2014) to calculate the force required to stretch the collagen (Eq. 8). We assume that when the force required to stretch the surrounding collagen exceeded the maximum radial force of the muscle during contraction (Fr ≤ Fc), then the virtual muscle ceased to shorten.
2.2 Experimental Constraints on Radial Expansion
The palmaris longus (PL) muscles of four leopard frogs (Rana pipiens) were used for the experimental aspects of the study. A sample size of 4 was supported by a power analysis performed at α = 05 and 1 − β = 0. The PL is a biarticular muscle spanning the elbow and wrist. The PL has a slender cylindrical shape and lacks any internal tendinous inscriptions, making it an ideal muscle for testing the hypothesis that radial constraint can limit muscle work. All procedures described below were approved by the Institutional Animal Care and Use Committee at the University of California, Irvine.
We used an in vitro muscle preparation to examine how the presence of a physical constraint that limits radial expansion affects muscle shortening and the capacity of the muscle to generate mechanical work. Frogs were euthanized with a double pithing protocol, before the palmaris longus was isolated from surrounding tissue. The isolated muscle was placed in an aerated amphibian Ringer’s solution (100 mM NaCl, 2.5 mM KCl, 2.5 mM NaHCO3, 1.6 mM CaCl, 10.5 mM Dextrose). Kevlar thread was used to tie one end of the muscle to a fixed clamp controlled with a three-axis micromanipulator, while the other end was attached to the lever arm of a dual-mode servomotor (305C LR, Aurora Scientific, Ontario, CA, USA). The micromanipulator was used to set the initial length of the muscle, while the servomotor allowed us to regulate force and measure force and length throughout the contraction. To constrain the radial expansion of the muscle during a contraction, we constructed small perforated tubes made of fiber-reinforced polypropylene, fitted to the diameter of the muscle, and placed them around the muscle. The tubes were rigid particularly compared to the expected radial forces of the muscle. Contractions with the physical constraint in place were compared to control contractions without the constraint. The muscle preparation was imaged from above at 100 frames/s using a Phantom Miro M120 (Vision Research, NJ, USA) high-speed camera.
The muscle was maximally activated using field stimulation with platinum plates and an S48 Grass stimulator (Grass Inc, RI, USA). We constructed a force–length curve by performing a series of twitches (0.2-ms pulse duration, 50 V) at varying lengths to estimate the optimal muscle length for producing maximal force. The twitch force–length curve is shifted to longer lengths relative to the tetanic force–length curve (Holt and Azizi 2014). Therefore to determine the maximum isometric force (Fmax), a tetanic isometric contraction (train duration 400ms, stimulation frequency 100 pps, amplitude 50 V) was performed at a length 10% shorter than the optimal length of the twitch force–length curve. A series of isotonic contractions at loads corresponding to 25 and 50% of Fmax were used to quantify the shortening behavior of the muscle and fascicles against comparable loads during both constrained and unconstrained contractions. For these isotonic contractions, the muscle was set to a length corresponding to the optimal length of the twitch force–length curve so that the muscle would shorten through the plateau region of the tetanic force–length curve. During these isotonic contractions, the muscle was stimulated for 400 ms (stimulation frequency 100 pps, amplitude 50V) and the servomotor regulated force and allowed the muscle to shorten at a speed corresponding to the prescribed force level. The order of constrained and unconstrained trials were randomize in order to avoid any confounding effects of muscle fatigue. A tetanic contraction at the end of the experiment always produced more than 90% (average across all preps was 95.7%) of the original force, indicating little loss of muscle force throughout the experiments. The force, length, and shortening velocity data from the servomotor were recorded at 4000 Hz using a DAQ (National Instruments USB 6212, Austin, TX, USA) and Igor Pro software program (IGOR Pro v. 6.1.2.1; Wavemetrics, OR, USA). Force and velocity were used to calculate instantaneous power, and the time integral of power was used to calculate mechanical work over the 400-ms period of stimulation.
A paired t test was used to compare shortening and work over the same period of stimulation during constrained and control contractions at each of the two force levels (25 and 50% of Fmax) using JMP software (SAS Inc., NC, USA).
3 Results
3.1 Model results
We modeled the mechanical interactions of a contracting muscle fiber and the surrounding collagen as a pressurized, fiber-wound cylinder that shortened longitudinally and expanded radially to maintain a constant volume. As the muscle fiber shortened and expanded radially, the collagen fibers surrounding the muscle fibers were reoriented and stretched to accommodate that radial expansion (Fig. 2a). Consistent with previous work on fiber-wound systems, we allowed the collagen to change orientation as the dimensions of the muscle fiber changed (Purslow 2002; Kier 2012; Gindre et al. 2013). However, in many cases the change in orientation was not sufficient to accommodate the radial expansion and therefore required the collagen fibers to stretch. Not surprisingly, our results showed that the strain applied to collagen fibers was greatest when the initial orientation of the collagen fibers (ϕ0) was more circumferential (0°) rather than longitudinal (90°) (Fig. 2b). We showed that when ϕ0 > 45°, collagen fibers experienced less than 5% strain even when the muscle fiber shortened by as much as 25% (Fig. 2b). However, when ϕ0 was low and collagen fibers were oriented more circumferentially, the strain applied to collagen fibers increased rapidly during muscle shortening (Fig. 2b).
Fig. 2.
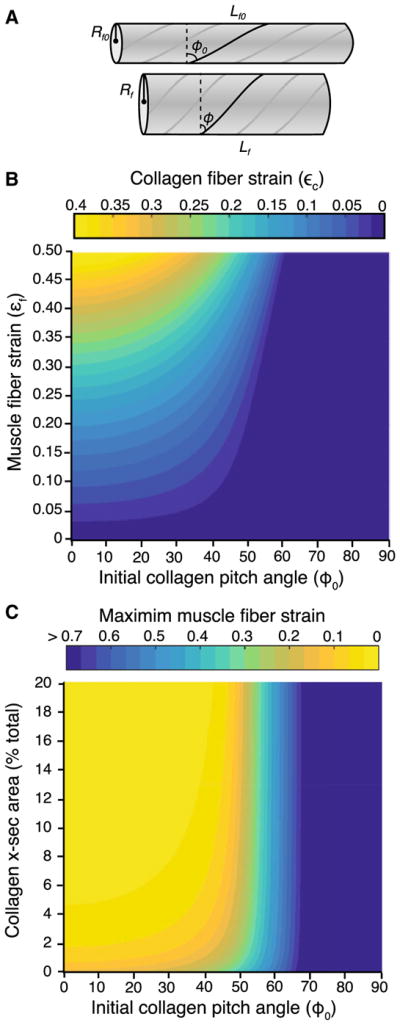
a Fiber-wound cylinder model used to probe the interactions between a contracting muscle fiber and the surrounding collagen. We treat the muscle a constant volume cylinder surrounded by collagen. The surrounding collagen of the ECM is modeled as a helix which changes orientation and stretches as the muscle shortens and expands radially. In our model, Lf0 and Rf0 are the initial length and radius of the muscle fiber, Lf and Rf are the instantaneous length and radius of the contracting muscle fiber, and ϕ0 and ϕ are the initial and instantaneous pitch angle of the helix, respectively. b The relationship between muscle fiber shortening and the stretch applied to the collagen fibers of the ECM. When the initial orientation of collagen is longitudinal (high ϕ0), little stretch is applied to the collagen fibers even when the muscle shortens by 50% of its initial length. However, when the initial orientation of collagen is circumferential (low ϕ0), even modest amounts of muscle fiber shortening where strain is below 20% require significant collagen stretch. Please note that strain in the muscle fibers indicates shortening, whereas the strain of the collagen indicates lengthening. c Increased stiffness of the ECM restricts muscle shortening. As the force required to stretch the collagen surrounding a muscle fiber increases, the force produced to expand the fiber radially becomes insufficient and the muscle fiber is unable to shorten. To drive these simulations, the maximum intramuscular pressure was set at 20 mmHg and the Young’s modulus of collagen was set at 550 MPa. The stiffness of the ECM was varied by changing the proportion of the muscle cross section made up of connective tissues. We explored this variable through a broad but physiologically realistic range (2–20%). Results show that the muscle fiber is constrained when the proportion of connective tissue increases and when the orientation of collagen is more circumferential (ϕ0 < 45°)
We predicted that the muscle fiber will cease to shorten when the force resisting radial expansion exceeded the radial force being produced by the fiber (Fr ≤ Fc). Our simulations showed that when ϕ0 > 60°, muscle fiber strain is not limited by the properties of the ECM (Fig. 2c). The collagenous ECM is likely to constrain the ability of muscle fibers to shorten under two conditions. First, when the initial orientation of the collagen fibers was more circumferential (ϕ0 < 40°), the maximum muscle fiber strain was limited. Second, when we simulated a fibrotic muscle by increasing the proportion of the cross section composed of collagen, the force required to radially expand the muscle fiber became exceedingly high. In our simulations, we used variation in the collagen component of muscle within a physiologically realistic range from 2% (healthy phenotype) to 20% (highly fibrotic phenotype) to show that a muscle’s ability to shorten and perform mechanical work is compromised by increased ECM stiffness (Fig. 2c). For example, if we started with an initial collagen angle of 45°, even a modest increase in collagen content to approximately 5% of the cross section resulted in a muscle that was unable to shorten by more than 20%.
3.2 Constraint experiments
We compared the contractile and mechanical output of a muscle during contractions with and without the presence of a radial constraint. We found that the presence of a physical constraint had little effect on the force output of a muscle. The maximum isometric force (Fmax) of the muscle was 1.66N (±0.36 SD) for the unconstrained and 1.58 N (±0.30 SD) for the constrained condition. This corresponded to an average maximum isometric stress of 17.1 and 16.3 N/cm2 for the unconstrained and constrained conditions, respectively. Neither maximum isometric force nor stress differed between the two conditions (p = 0.681; p = 0.518).
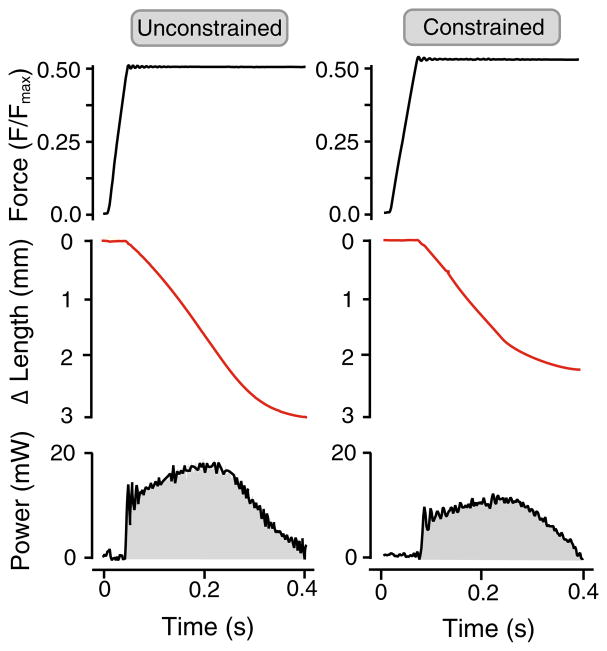
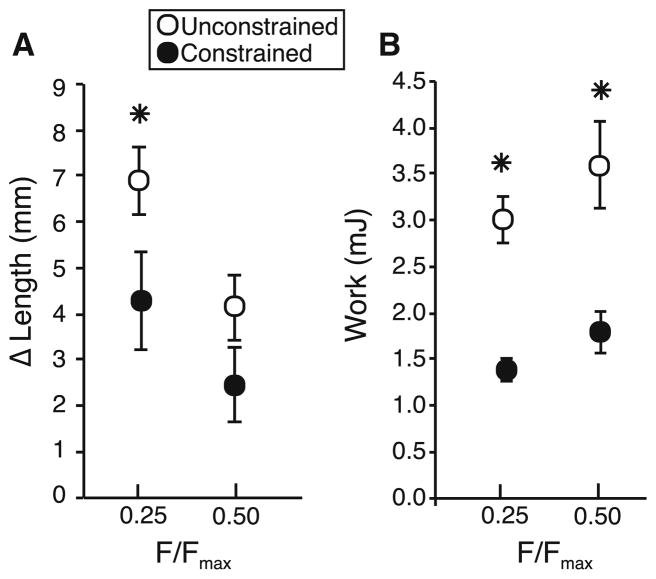
We quantified the amount of shortening that occurred during a 400-ms contraction at a force corresponding to 25 or 50% of Fmax (Fig. 3). We find that the presence of a physical constraint that restricted the radial expansion of a muscle reduced the amount of shortening. At 50% Fmax, the unconstrained muscle shortened by 4.12 mm(±0.70 SD), while the constrained muscle shortened by 2.45 mm(±0.81 SD). However, this difference was not statistically significant (p = 0.066) (Fig. 4). At 25% Fmax, the unconstrained muscle shortened by 6.88 mm (±0.74 SD) and differed significantly (p = 0.03) from the constrained muscle which shortened by 4.29 mm (±1.08 SD) (Fig. 4).
Fig. 3.
Representative contractions of active muscle shortening with and without the presence of a physical constraint that limits radial expansion. The same muscle is used for both contractions, and the muscle is contracting against a load that corresponds to 50% of its maximum isometric force. The muscle shortens less during the 400-ms period of stimulation when the constraint is in place. The reduced shortening also reduces the mechanical work output of the muscle as indicated by the shaded area under the power–time plot
Fig. 4.
Summary data of muscle shortening and muscle work. Data are shown at 25 and 50% of Fmax and in the presence (black) and absence (white) of a physical constraint that limits radial expansion in the muscle. a During 400 ms of stimulation, the muscle undergoes less shortening when radial expansion is physically constrained. While the difference is statistically significant at 25% of Fmax (p = 0.030), the trend is not statistically significant at 50% of Fmax (p = 0.066). b The work output of the muscle is significantly lower when radial expansion is constrained. n = 4 and data are shown as mean ± S.E.M
Restriction of radial expansion also changed the work output of the muscle. The work generated over 400ms of active isotonic contraction decreased with the presence of a physical constraint. At 50% Fmax, the unconstrained muscle produced 3.60 mJ (±1.43 SD) of mechanical work and differed significantly (p = 0.041) from the constrained muscle which produced 1.79 mJ (±0.89 SD) of work. Similarly, at 25% Fmax the unconstrained muscle produced 3.01 mJ (±1.02 SD) of mechanical work and differed significantly (p = 0.024) from the constrained muscle which produced 1.38 mJ (±0.48 SD) of work (Fig. 4).
4 Discussion
Here we used a combination of experimental and modeling approaches to examine how resistance to radial expansion can compromise the ability of muscle to do work. Our experimental results demonstrate that constraints to radial expansion limit muscle shortening and work (Fig. 4). Our modeling results suggest that the resistance to radial expansion provided by connective tissues may affect the work muscle can do and that pathological changes associated with muscle fibrosis may reduce muscle work. The implications of these findings are that the mechanical properties of the connective tissue structures within a muscle can directly influence contractile performance in both healthy and pathological conditions.
In this study, we aimed to isolate resistance to radial expansion and to explicitly explore its effect on the ability of muscles to generate mechanical work in healthy and pathological conditions. The direct experimental comparison of muscle shortening and work in a single muscle in constrained and unconstrained conditions allows us to demonstrate that resistance to radial expansion is an important determinant of muscle performance. The use of a mathematical model with realistic healthy and pathological connective tissue properties enables us to determine that the increased resistance to radial expansion reduces a muscle capacity to generate work independent of any other changes. Remodeling of the ECM with age (Ramaswamy et al. 2011) and disease (Smith and Barton 2014) is often associated with an increase in collagen content (as a proportion of the cross section) and in turn a large decreases in specific force. Therefore, muscles with increased collagen content likely face both a reduction in specific force and shortening capacity, such that the mechanical work output is potentially more compromised than our results indicate (Fig. 4).
The significance of a reduction in a muscle’s ability to shorten depends on the muscle’s mechanical function in vivo. For example, movements where in-series elasticity allows a muscle to function as a strut and undergo little length change (e.g., running, hopping) may be far less affected by the constraints highlighted in our study (Roberts et al. 1997; Biewener et al. 1998). In contrast, movements that require muscles to shorten significantly and generate mechanical work (e.g., jumping, acceleration) may face a relatively larger drop in performance when radial expansion is constrained (Azizi and Roberts 2010; Astley and Roberts 2012). This distinction is supported by our results. The presence of a physical constraint has a more substantial effect when the muscle is contracting against a smaller load (Fig. 4a). This difference is likely due to the fact that at 25% of maximum isometric force, the muscle shortens at a higher velocity than at 50%, which results in more shortening over the 400-ms period of stimulation. The difference between our 25 and 50% Fmax trials is consistent with the idea that a radial constraint may only affect performance during behaviors with substantial muscle shortening. Furthermore, the fact that we did not observe a significant difference in maximum isometric force in the presence of a constraint suggests that constraining radial expansion primarily affects a muscle’s ability to shorten. Therefore, functional assessments of muscle health, which rely solely on force generation, may overlook deficiencies in the capacity of muscles to shorten and generate mechanical work.
The impact of reduced muscle shortening on work output also depends on where a muscle operates on the force–length curve. If the initial length of a muscle corresponds to the descending limb of the force–length curve, then a reduction in muscle shortening may significantly reduce work output since the force capacity of the muscle increases or remains near maximum as the muscle shortens. However, if the initial length of a muscle corresponds to the ascending limb of the force–length curve, continued shortening may have limited effect on work output since force drops off steeply as the muscle shortens and continued shortening will result in relatively little work. Interestingly, recent work has shown that muscles powering behaviors that require significant mechanical work tend to operate on the descending limb and plateau of force–length curve in order to improve their force profile as the muscle undergoes significant shortening (Azizi and Roberts 2010; Azizi 2014). Therefore, it is likely that behaviors requiring significant mechanical work are most susceptible to structural changes in the ECM that constrain radial expansion.
The initial orientation of collagen fibers in the ECM has a significant effect on how they resist dimensional changes in an actively contracting muscle fiber. Our results show that a circumferential orientation of collagen can resist radial expansion during muscle shortening (Fig. 2). Previous studies have suggested that a more longitudinal orientation of collagen resists a stretch applied a muscle fiber (Purslow 1989; Gindre et al. 2013). Interestingly, the initial orientation of the collagen layer only provides a snapshot, since the orientation of collagen changes dynamically as the muscle changes length. As a muscle is stretched, the orientation of collagen fibers in perimysium and endomysium becomes more longitudinal, therefore resisting muscle stretch (Purslow 1989; Gindre et al. 2013). In fact, it has been suggested that the exponential relationship between length and force in a passive muscle may in part be explained by the changes in the collagen orientation as fiber alignment becomes more longitudinal (Purslow 1989). Similarly, as a muscle actively shortens, the orientation of collagen fibers in the perimysium and endomysium becomes more circumferential which provides greater resistance to radial expansion (Gindre et al. 2013). Since the mechanical impact of the ECM depends strongly on the change in collagen orientation, it is important that our model predictions are consistent with previously published empirical results. Using X-ray diffraction, Purslow (1989) quantified the angular change in the orientation of collagen in the perimysium and found that as a muscle fascicle shortened by 75%, the mean angle of the collagen fibers changed from 70° to about 20° (note: angles are relative to the circumferential axis). Similar results have also been presented for the endomysium (Purslow and Trotter 1994). Our model makes nearly identical predictions as 75% muscle shortening shifts the pitch angle of the collagen from 70° to about 17°. Similar to previous work, our model predicts that at longer lengths, the perimysium likely resists longitudinal stretch (Purslow 1989). However, our results also indicate that the perimysium can in fact limit radial expansion and limit shortening under some conditions. Whereas the ability to generate mechanical work in healthy muscles may well be limited by the geometry of the sarcomere, fibrotic muscles may face significantly greater resistance to shortening and may be limited by the mechanical properties of the ECM.
The mechanical properties of intramuscular connective tissues may restrict a muscle’s operating length. It has been previously suggested that as a muscle a stretched, collagen fibers of the ECM shifts to a more longitudinal orientation, thereby functioning to resist muscle fiber stretch at relatively long lengths (Purslow 1989). The increased passive resistance may prevent muscles from operating at lengths where muscles develop significant passive tension. Our model predicts that as a muscle shortens significantly, the collagen fibers shift to a more circumferential orientation which restricts radial expansion and limits further shortening. Taken together, these ideas suggest that intramuscular connective tissues may function to passively restrict the operating length of a muscle to intermediate lengths where active force production is optimal.
A number of recent studies have begun to focus on the role of off-axis (transverse) loading in skeletal muscle. Loading in the transverse direction in a muscle has been shown to affect the ability of muscles to generate force during isometric contractions (Siebert et al. 2014b). Such a drop in force is thought to result from the additional work done by the muscle against the transverse load, which decreases the work done on a longitudinal load (Siebert et al. 2014a). The change in the force capacity of the muscle may also be due to a reorientation of force producing muscle fibers within a pennate muscle in response to transverse loading (Azizi et al. 2008). More recent work suggests that a drop in the force capacity of a muscle during transverse loading may relate more to changes in internal pressure resulting in changes in the lattice spacing of myofibrils (Siebert et al. 2016). In addition, the development of fluid pressure inside a muscle has been shown to interact with surrounding collagen fibers to contribute to longitudinal forces (Sleboda and Roberts 2017). Continued focus on transverse loading will advance our understanding of how structures like intramuscular connective tissues, aponeuroses, adjacent muscles, or skeletal elements may influence muscle performance.
While fibrotic muscles may face a significant challenge in shortening and producing mechanical work, there may be ways to compensate for such constraints. In this paper, we have modeled the maximum radial force produced by a contracting muscle by keeping the maximum intramuscular pressure constant (set to 20 mmHg), while we alter the stiffness of the ECM. Therefore, we have increased the resistance to radial expansion by increasing the collagen fibers surrounding the muscle fibers without increasing the radial force (Eqs. 8, 9). It is, however, likely that the intramuscular pressure inside a fibrotic muscle increases, allowing muscle fibers to undergo more radial expansion than predicted by our model. Intramuscular pressure has been shown to increase significantly in patients with compartment syndrome reaching nearly 80 mmHg (Lynch et al. 2009). However, this increase is not a result of changes in the extracellular connective tissues but is associated with acute trauma such as hemorrhage or edema (Lynch et al. 2009), which increase the internal resting pressure inside a muscle compartment. To our knowledge, there are no studies to date that have measured intramuscular pressure in a fibrotic muscle, and therefore, we cannot rule out the possibility that increased IMP compensates for the increased resistance to radial expansion. Future work using pathological variation in the ECM (Smith et al. 2011; Gao et al. 2008; Järvinen et al. 2002) or experimental manipulations of ECM stiffness (Yucesoy et al. 2012; Turkoglu and Yucesoy 2016) will provide direct tests of the hypotheses generated by our study.
The orientation of collagen fibers has a significant effect on radial constraint imposed by the ECM, and a shift toward a more longitudinal orientation would likely allow muscles to shorten without constraint (Gindre et al. (2013); Fig. 2c). It is therefore possible that a shift in the mean orientation of collagen fibers allows fibrotic muscle to accommodate the increased resistance to radial expansion. In fact, there is some indirect evidence to support the idea that collagen orientation determines the mechanical properties of the ECM. Recent work has shown that collagen content alone, usually quantified through a hydroxyproline assay, is not an accurate predictor of passive stiffness in muscles from patients with cerebral palsy (Smith et al. 2011) or in mdx mice (Smith and Barton 2014). In addition, Gillies and Lieber (2011) highlighted the importance of collagen architecture by documenting the presence of robust, longitudinal collagen “cables,” which contribute disproportionately to longitudinal stiffness. It is therefore plausible that in addition to an increase in collagen content, the mean orientation of collagen becomes more longitudinal, increasing longitudinal stiffness while retaining the muscle’s capacity to shorten and produce mechanical work. A better understanding of the relationship between IMP and collagen architecture in fibrotic muscle will provide important insight into these mechanical constraints.
Our results combined with previous studies suggest that the forces applied to the ECM can be spatially complex. It is now well established that a stretch applied to a passive muscle is likely to load the collagen fibers of the ECM (Purslow and Trotter 1994). A number of studies have also shown that active forces generated by sarcomeres are transmitted to the ECM creating myofascial pathways that mechanically link muscle fibers, fascicles, and synergistic muscles that seemingly operate in parallel (Yucesoy 2010). In addition, the movement of muscle fibers and fascicles can result in shear stress and strain in the ECM (Purslow 2002). Shearing between adjacent muscle fibers and fascicles has often been attributed to local heterogeneity in strain which can arise from spatial variation in fiber architecture (Pappas et al. 2002; Blemker et al. 2005; Azizi 2014) or regional variation in myofascial force transmission (Pamuk et al. 2016). It is worth noting that in our experiments, the addition of a physical constraint aimed at restricting radial expansion may also mechanically alter myofascial force transmission pathways. This could result in an increase in the spatial heterogeneity of sarcomere lengths during the contraction. Given that our experiments are conducted in a whole muscle, we cannot distinguish between different mechanisms that could result in less muscle shortening when radial expansion is restricted. It is possible that the presence of a radial constraint affects all sarcomeres equally, causing sarcomeres to shorten less thereby resulting in less muscle shortening. It is also possible that the presence of the radial constraint has a more spatially heterogeneous effect on force transmission pathways such that some sarcomeres shorten more, while others lengthen resulting in an overall decrease in muscle shortening. The differences between these patterns are not trivial as heterogeneity in sarcomere strain can result in instability and increase the likelihood of muscle damage (Patel et al. 2004). Future studies aimed at distinguishing between these mechanisms will advance our understanding of how changes in the mechanical properties of the ECM might increase susceptibility to muscle damage.
In this study, we combined modeling and experiments to show that the ability of muscle fibers to shorten actively can be compromised by increased stiffness of the ECM. Our experiments confirm that when a muscle is restricted from radially expanding, its ability to actively shorten and produce mechanical work is compromised (Figs. 3, 4). Our model shows that the stiffness of ECM and the orientation of collagen fibers determine the structural resistance to radial expansion (Fig. 2). This work highlights the intimate mechanical interaction between contractile and connective tissue structures within skeletal muscle and highlights how a deviation from a healthy, well-tuned relationship can compromise performance.
Acknowledgments
The authors are grateful to Dr. Tom Roberts, Dr. Nicole Danos, Dr. Angela Horner, and David Sleboda for insightful conversations. This work has been supported by the National Science Foundation Grant #1436476 and National Institute of Health Grant # AR055295.
Footnotes
Compliance with ethical standards
Conflict of interest The authors declare no competing interests.
References
- Alnaqeeb MA, Alzaid NS, Goldspink G. Connective-tissue changes and physical-properties of developing and aging skeletal-muscle. J Anat. 1984;139(DEC):677–689. [PMC free article] [PubMed] [Google Scholar]
- Astley HC, Roberts TJ. Evidence for a vertebrate catapult: elastic energy storage in the plantaris tendon during frog jumping. Biol Lett. 2012;8(3):386–389. doi: 10.1098/rsbl.2011.0982. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Azizi E. Locomotor function shapes the passive mechanical properties and operating lengths of muscle. Proc R Soc B Biol Sci. 2014;281(1783):20132914. doi: 10.1098/rspb.2013.2914. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Azizi E, Brainerd EL, Roberts TJ. Variable gearing in pennate muscles. Proc Natl Acad Sci USA. 2008;105(5):1745–1750. doi: 10.1073/pnas.0709212105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Azizi E, Roberts TJ. Muscle performance during frog jumping: influence of elasticity on muscle operating lengths. Proc R Soc B Biol Sci. 2010;277(1687):1523–1530. doi: 10.1098/rspb.2009.2051. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Baskin RJ, Paolini PJ. Volume change and pressure development in muscle during contraction. Am J Physiol. 1967;213(4):1025–1030. doi: 10.1152/ajplegacy.1967.213.4.1025. [DOI] [PubMed] [Google Scholar]
- Bernabei M, van Dieën JH, Baan GC, Maas H. Significant mechanical interactions at physiological lengths and relative positions of rat plantar flexors. J Appl Physiol. 2015;118(4):427–436. doi: 10.1152/japplphysiol.00703.2014. [DOI] [PubMed] [Google Scholar]
- Biewener AA, Konieczynski DD, Baudinette RV. In vivo muscle force-length behavior during steady-speed hopping in tammar wallabies. J Exp Biol. 1998;201(11):1681–1694. doi: 10.1242/jeb.201.11.1681. [DOI] [PubMed] [Google Scholar]
- Blemker SS, Pinsky PM, Delp SL. A 3D model of muscle reveals the causes of nonuniform strains in the biceps brachii. J Biomech. 2005;38(4):657–665. doi: 10.1016/j.jbiomech.2004.04.009. [DOI] [PubMed] [Google Scholar]
- Gao YX, Kostrominova TY, Faulkner JA, Wineman AS. Age-related changes in the mechanical properties of the epimysium in skeletal muscles of rats. J Biomech. 2008;41(2):465–469. doi: 10.1016/j.jbiomech.2007.09.021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gillies AR, Lieber RL. Structure and function of the skeletal muscle extracellular matrix. Muscle Nerve. 2011;44:318–331. doi: 10.1002/mus.22094. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gindre J, Takaza M, Moerman KM, Simms CK. A structural model of passive skeletal muscle shows two reinforcement processes in resisting deformation. J Mech Behav Biomed Mater. 2013;22:84–94. doi: 10.1016/j.jmbbm.2013.02.007. [DOI] [PubMed] [Google Scholar]
- Gokhin DS, Fowler VM. A two-segment model for thin filament architecture in skeletal muscle. Nat Rev Mol Cell Biol. 2013;14(2):113–119. doi: 10.1038/nrm3510. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gosselin LE, Adams C, Cotter TA, McCormick RJ, Thomas DP. Effect of exercise training on passive stiffness in locomotor skeletal muscle: role of extracellular matrix. J Appl Physiol. 1998;85(3):1011–1016. doi: 10.1152/jappl.1998.85.3.1011. [DOI] [PubMed] [Google Scholar]
- Holt NC, Azizi E. What drives activation-dependent shifts in the force-length curve? Biol Lett. 2014;10(9):20140651–20140651. doi: 10.1098/rsbl.2014.0651. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huijing PA. Muscle as a collagen fiber reinforced composite: a review of force transmission in muscle and whole limb. J Biomech. 1999;32:329–345. doi: 10.1016/s0021-9290(98)00186-9. [DOI] [PubMed] [Google Scholar]
- Huijing PA. Epimuscular myofascial force transmission between antagonistic and synergistic muscles can explain movement limitation in spastic paresis. J Electromyogr Kinesiol. 2007;17(6):708–724. doi: 10.1016/j.jelekin.2007.02.003. [DOI] [PubMed] [Google Scholar]
- Huijing PA, Baan GC. Myofascial force transmission: muscle relative position and length determine agonist and synergist muscle force. J Appl Physiol. 2003;94(3):1092–1107. doi: 10.1152/japplphysiol.00173.2002. [DOI] [PubMed] [Google Scholar]
- Huijing PA, Baan GC, Rebel GT. Non-myotendinous force transmission in rat extensor digitorum longus muscle. J Exp Biol. 1998;201(Pt 5):683–691. [PubMed] [Google Scholar]
- Huijing PA, van de Langenberg RW, Meesters JJ, Baan GC. Extramuscular myofascial force transmission also occurs between synergistic muscles and antagonistic muscles. J Electromyogr Kinesiol. 2007;17(6):680–689. doi: 10.1016/j.jelekin.2007.02.005. [DOI] [PubMed] [Google Scholar]
- Järvinen TAH, Józsa L, Kannus P, Järvinen TLN, Järvinen M. Organization and distribution of intramuscular connective tissue in normal and immobilized skeletal muscles. An immunohistochemical, polarization and scanning electron microscopic study. J Muscle Res Cell Motil. 2002;23(3):245–254. doi: 10.1023/a:1020904518336. [DOI] [PubMed] [Google Scholar]
- Kier WM. The diversity of hydrostatic skeletons. J Exp Biol. 2012;215(Pt 8):1247–1257. doi: 10.1242/jeb.056549. [DOI] [PubMed] [Google Scholar]
- Kjaer M. Role of extracellular matrix in adaptation of tendon and skeletal muscle to mechanical loading. Physiol Rev. 2004;84(2):649–698. doi: 10.1152/physrev.00031.2003. [DOI] [PubMed] [Google Scholar]
- Kjaer M, Magnusson P, Krogsgaard M, Moller JB, Olesen J, Heinemeier K, Hansen M, Haraldsson B, Koskinen S, Esmarck B, Langberg H. Extracellular matrix adaptation of tendon and skeletal muscle to exercise. J Anat. 2006;208(4):445–450. doi: 10.1111/j.1469-7580.2006.00549.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lieber RL, Ward SR. Skeletal muscle design to meet functional demands. Philos Trans R Soc B Biol Sci. 2011;366(1570):1466–1476. doi: 10.1098/rstb.2010.0316. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lieber RL, Ward SR. Cellular mechanisms of tissue fibrosis. 4. Structural and functional consequences of skeletal muscle fibrosis. Am J Physiol Cell Physiol. 2013;305(3):C241–C252. doi: 10.1152/ajpcell.00173.2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lynch JE, Lynch JK, Cole SL, Carter JA, Hargens AR. Noninvasive monitoring of elevated intramuscular pressure in a model compartment syndrome via quantitative fascial motion. J Orthop Res. 2009;27(4):489–494. doi: 10.1002/jor.20778. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Maas H, Huijing PA. Myofascial force transmission in dynamic muscle conditions: effects of dynamic shortening of a single head of multi-tendoned rat extensor digitorum longus muscle. Eur J Appl Physiol. 2005;94(5–6):584–592. doi: 10.1007/s00421-005-1367-7. [DOI] [PubMed] [Google Scholar]
- Maas H, Sandercock TG. Force transmission between synergistic skeletal muscles through connective tissue linkages. J Biomed Biotechnol. 2010;2010(1):575672–575679. doi: 10.1155/2010/575672. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Meyer GA, Lieber RL. Elucidation of extracellular matrix mechanics from muscle fibers and fiber bundles. J Biomech. 2011;44(4):771–773. doi: 10.1016/j.jbiomech.2010.10.044. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pamuk U, Karakuzu A, Ozturk C, Acar B, Yucesoy CA. Combined magnetic resonance and diffusion tensor imaging analyses provide a powerful tool for in vivo assessment of deformation along human muscle fibers. J Mech Behav Biomed Mater. 2016;63:207–219. doi: 10.1016/j.jmbbm.2016.06.031. [DOI] [PubMed] [Google Scholar]
- Pappas GP, Asakawa DS, Delp SL, Zajac FE, Drace JE. Nonuniform shortening in the biceps brachii during elbow flexion. J Appl Physiol. 2002;92(6):2381–2389. doi: 10.1152/japplphysiol.00843.2001. [DOI] [PubMed] [Google Scholar]
- Patel TJ, Das R, Fridén J, Lutz GJ, Lieber RL. Sarcomere strain and heterogeneity correlate with injury to frog skeletal muscle fiber bundles. J Appl Physiol. 2004;97(5):1803–1813. doi: 10.1152/japplphysiol.00505.2003. [DOI] [PubMed] [Google Scholar]
- Purslow PP. Strain-induced reorientation of an intramuscular connective tissue network: implications for passive muscle elasticity. J Biomech. 1989;22(1):21–31. doi: 10.1016/0021-9290(89)90181-4. [DOI] [PubMed] [Google Scholar]
- Purslow PP. The structure and functional significance of variations in the connective tissue within muscle. Comp Biochem Physiol A Mol Integr Physiol. 2002;133(4):947–966. doi: 10.1016/s1095-6433(02)00141-1. [DOI] [PubMed] [Google Scholar]
- Purslow PP, Trotter JA. The morphology and mechanical properties of endomysium in series-fibred muscles: variations with muscle length. J Muscle Res Cell Motil. 1994;15(3):299–308. doi: 10.1007/BF00123482. [DOI] [PubMed] [Google Scholar]
- Ramaswamy KS, Palmer ML, van der Meulen JH, Renoux A, Kostrominova TY, Michele DE, Faulkner JA. Lateral transmission of force is impaired in skeletal muscles of dystrophic mice and very old rats. J Physiol Lond. 2011;589(5):1195–1208. doi: 10.1113/jphysiol.2010.201921. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rassier DE, MacIntosh BR, Herzog W. Length dependence of active force production in skeletal muscle. J Appl Physiol (Bethesda, MD: 1985) 1999;86(5):1445–1457. doi: 10.1152/jappl.1999.86.5.1445. [DOI] [PubMed] [Google Scholar]
- Roberts TJ, Marsh RL, Weyand PG, Taylor CR. Muscular force in running turkeys: the economy of minimizing work. Science. 1997;275(5303):1113–1115. doi: 10.1126/science.275.5303.1113. [DOI] [PubMed] [Google Scholar]
- Siebert T, Rode C, Till O, Stutzig N, Blickhan R. Force reduction induced by unidirectional transversal muscle loading is independent of local pressure. J Biomech. 2016;49(7):1156–1161. doi: 10.1016/j.jbiomech.2016.02.053. [DOI] [PubMed] [Google Scholar]
- Siebert T, Till O, Blickhan R. Work partitioning of transversally loaded muscle: experimentation and simulation. Comput Methods Biomech Biomed Eng. 2014a;17(3):217–229. doi: 10.1080/10255842.2012.675056. [DOI] [PubMed] [Google Scholar]
- Siebert T, Till O, Stutzig N, Günther M, Blickhan R. Muscle force depends on the amount of transversal muscle loading. J Biomech. 2014b;47(8):1822–1828. doi: 10.1016/j.jbiomech.2014.03.029. [DOI] [PubMed] [Google Scholar]
- Sleboda DA, Roberts TJ. Incompressible fluid plays a mechanical role in the development of passive muscle tension. Biol Lett. 2017;13(1):20160630. doi: 10.1098/rsbl.2016.0630. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Smith LR, Barton ER. Collagen content does not alter the passive mechanical properties of fibrotic skeletal muscle in mdx mice. Am J Physiol Cell Physiol. 2014;306(10):C889–C898. doi: 10.1152/ajpcell.00383.2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Smith LR, Lee KS, Ward SR, Chambers HG, Lieber RL. Hamstring contractures in children with spastic cerebral palsy result from a stiffer extracellular matrix and increased in vivo sarcomere length. J Physiol Lond. 2011;589(10):2625–2639. doi: 10.1113/jphysiol.2010.203364. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Street SF. Lateral transmission of tension in frog myofibers: a myofibrillar network and transverse cytoskeletal connections are possible transmitters. J Cell Physiol. 1983;114(3):346–364. doi: 10.1002/jcp.1041140314. [DOI] [PubMed] [Google Scholar]
- Svensson RB, Hassenkam T, Grant CA, Magnusson SP. Tensile properties of human collagen fibrils and fascicles are insensitive to environmental salts. Biophys J. 2010;99(12):4020–4027. doi: 10.1016/j.bpj.2010.11.018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Trotter JA, Purslow PP. Functional morphology of the endomysium in series fibered muscles. J Morphol. 1992;212(2):109–122. doi: 10.1002/jmor.1052120203. [DOI] [PubMed] [Google Scholar]
- Turkoglu AN, Yucesoy CA. Simulation of effects of botulinum toxin on muscular mechanics in time course of treatment based on adverse extracellular matrix adaptations. J Biomech. 2016;49(7):1192–1198. doi: 10.1016/j.jbiomech.2016.03.002. [DOI] [PubMed] [Google Scholar]
- Ward SR, Davis J, Kaufman KR, Lieber RL. Relationship between muscle stress and intramuscular pressure during dynamic muscle contractions. Muscle Nerve. 2007;36(3):313–319. doi: 10.1002/mus.20828. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Weibel E. Stereological methods. vol. 1. Practical methods for biological morphometry. J Microsc. 1981;121(1):131–132. [Google Scholar]
- Winters TM, Sepulveda GS, Cottler PS, Kaufman KR, Lieber RL, Ward SR. Correlation between isometric force and intramuscular pressure in rabbit tibialis anterior muscle with an intact anterior compartment. Muscle Nerve. 2009;40(1):79–85. doi: 10.1002/mus.21298. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wood LK, Kayupov E, Gumucio JP, Mendias CL, Claflin DR, Brooks SV. Intrinsic stiffness of extracellular matrix increases with age in skeletal muscles of mice. J Appl Physiol. 2014;117(4):363–369. doi: 10.1152/japplphysiol.00256.2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yucesoy CA. Epimuscular myofascial force transmission implies novel principles for muscular mechanics. Exerc Sport Sci Rev. 2010;38(3):128–134. doi: 10.1097/JES.0b013e3181e372ef. [DOI] [PubMed] [Google Scholar]
- Yucesoy CA, Emre Arikan Ö, Ateş F. BTX-A administration to the target muscle affects forces of all muscles within an intact compartment and epimuscular myofascial force transmission. J Biomech Eng. 2012;134(11):111002. doi: 10.1115/1.4007823. [DOI] [PubMed] [Google Scholar]
- Yucesoy CA, Koopman BHFJM, Baan GC, Grootenboer HJ, Huijing PA. Effects of inter- and extramuscular myofascial force transmission on adjacent synergistic muscles: assessment by experiments and finite-element modeling. J Biomech. 2003;36(12):1797–1811. doi: 10.1016/s0021-9290(03)00230-6. [DOI] [PubMed] [Google Scholar]
- Yucesoy CA, Maas H, Koopman BHFJM, Grootenboer HJ, Huijing PA. Mechanisms causing effects of muscle position on proximo-distal muscle force differences in extra-muscular myofascial force transmission. Med Eng Phys. 2006;28(3):214–226. doi: 10.1016/j.medengphy.2005.06.004. [DOI] [PubMed] [Google Scholar]
- Zhang C, Gao Y. The role of transmembrane proteins on force transmission in skeletal muscle. J Biomech. 2014;47(12):3232–3236. doi: 10.1016/j.jbiomech.2014.07.014. [DOI] [PMC free article] [PubMed] [Google Scholar]