Directed nucleation and growth by balancing local supersaturation and substrate/nucleus lattice mismatch

Significance

The energy barrier for a classical heterogeneous crystal nucleation can be controlled by the energy contributions from the substrate/nucleus interface and local supersaturation. Exerting control over crystal growth thus requires modifying either one of these terms. We here introduce a strategy to modulate the contributions of both parameters simultaneously using substrates containing different crystal structures of calcium carbonate. Based on a theoretical analysis, we program both the positioning and growth direction of carbonate salts on preselected polymorphs. These findings may hold relevance for understanding, mimicking, and ultimately expanding upon nature’s mineralization strategies and for developing functional microscale materials.

Abstract

Controlling nucleation and growth is crucial in biological and artificial mineralization and self-assembly processes. The nucleation barrier is determined by the chemistry of the interfaces at which crystallization occurs and local supersaturation. Although chemically tailored substrates and lattice mismatches are routinely used to modify energy landscape at the substrate/nucleus interface and thereby steer heterogeneous nucleation, strategies to combine this with control over local supersaturations have remained virtually unexplored. Here we demonstrate simultaneous control over both parameters to direct the positioning and growth direction of mineralizing compounds on preselected polymorphic substrates. We exploit the polymorphic nature of calcium carbonate (CaCO₃) to locally manipulate the carbonate concentration and lattice mismatch between the nucleus and substrate, such that barium carbonate (BaCO₃) and strontium carbonate (SrCO₃) nucleate only on specific CaCO₃ polymorphs. Based on this approach we position different materials and shapes on predetermined CaCO₃ polymorphs in sequential steps, and guide the growth direction using locally created supersaturations. These results shed light on nature’s remarkable mineralization capabilities and outline fabrication strategies for advanced materials, such as ceramics, photonic structures, and semiconductors.

Spurred by the recent advancement in techniques such as microfabrication and electron microscopy, there has been tremendous advancement in understanding and controlling both biological and artificial mineralization processes (1–4). Unlike homogeneous nucleation, heterogeneous nucleation allows for an effective strategy to control the local nucleation energy barrier by modifying the chemical and structural characteristics between the nascent nucleus and substrates (5–12). Alternatively, a local increase of the supersaturation can onset nucleation (13–15)––an approach broadly utilized by natural systems through ion channels that deliver crystallizing components to the specific site where nucleation should occur––but this approach has hardly been explored in artificial systems. Only recently, such local supersaturations were created using an ion-binding biomimetic matrix (4). However, little or no work has been done to develop principles that allow for simultaneous control over the local supersaturation and interfacial free energy for directing the nucleation position, let alone the growth (15).

While virtually all previous studies have been aimed at avoiding polymorphism (16), we here use the ability of compounds to organize in different crystal forms to rationally control both local supersaturations in the vicinities of different polymorphs and subtle variations in the lattice mismatch between the substrate and the nucleus. An ideal model system to test this strategy is the crystallization of BaCO₃ selectively on top of different polymorphs of CaCO₃. CaCO₃ is the most abundant biomineral and can be found in three anhydrous polymorphs that all occur in living organisms (17–23). At room temperature calcite is the most stable polymorph, followed by aragonite and finally vaterite as the least stable structure. To demonstrate the ability to tune the positioning of BaCO₃ on top of these polymorphs and its growth direction, we analyze and exploit local variations of supersaturations induced by the difference in the dissolution rate of CaCO₃ polymorphs. Additionally, the crystal structures of calcite, aragonite, and vaterite are different from each other, and only aragonite resembles that of BaCO₃ (23). This variation in crystal structures allows for direct evaluation of the effects of the lattice mismatch on templated nucleation of BaCO₃ on selected CaCO₃ polymorphs modulated by the local supersaturation gradients.

Results and Discussion

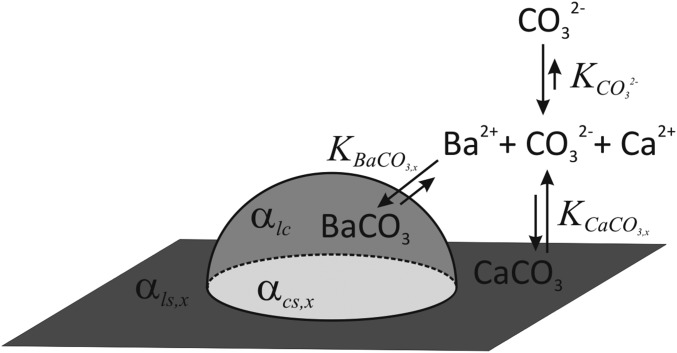
To understand the unique interplay between the interfacial free energy that arises from the lattice mismatch and supersaturation in this system, we analyze a solution containing Ba²⁺ ions in which an influx of CO₃²⁻ causes the templated nucleation of BaCO₃ on a CaCO₃ substrate with crystal structure x (Fig. 1). According to classical nucleation theory (13–15), the energy barrier to form a critical nucleus, Δg_n, can be described as a function of the local supersaturation σ and the interfacial free energy α according to

$$\mathrm{\Delta }{g}_n\propto \frac{{\alpha }_x^3}{{\sigma }_x^2}.$$ [1]

Fig. 1.

Nucleation of BaCO₃ on a CaCO₃ substrate. The energy barrier for nucleation is determined by (i) the contributions of the interfacial free energies arising from the lattice mismatch between liquid-crystal α_lc, liquid-substrate α_ls,x, and substrate-crystal α_cs,x, and (ii) the local supersaturation, which depends on the concentration of ions in the solution, the influx of CO₃²⁻, the crystallization rate of BaCO₃, and dissolution rate of CaCO₃, k_BaCO3, and k_CaCO3,x, respectively, for a specific crystal structure x. By controlling the influx of the CO₃²⁻, the balance can be shifted from the major contribution from the lattice mismatch at high [CO₃²⁻]_bulk to a local supersaturation-dominated process controlled by the differences in the solubility of CaCO₃ polymorphs at low [CO₃²⁻]_bulk. Note that the hemispherical representation is chosen for illustrative purposes and will depend on the specific nucleation conditions.

The lattice mismatch between the BaCO₃ nucleus and the underlying substrate directly contributes to the interfacial energy penalties, which include an energy contribution due to the difference in chemical bonding, and a strain-energy contribution from the interface and the nucleate volume that arises from the incoherent ordering at the interface. Although analytical expressions of each energy contribution are hard to achieve due to the complexity of the system, both energy contributions should decrease as the substrate/nucleus interface becomes more crystallographically aligned and coherent.

The energy gain resulting from the chemical potential energy is directly related to the supersaturation of BaCO₃. In case the substrate has a higher solubility than the nucleating compound, and the rate of dissolution of the substrate is higher than the rate of growth of the nucleating crystal (Fig. 1), the supersaturation in BaCO₃ can be expressed as

$$\sigma =\ln \left(\frac{k_{{\text{BaCO}}_3}\left[{\text{Ba}}^{2+}\right]{\left[{\text{CO}}_3^{2-}\right]}_{bulk}}{k_{{\text{BaCO}}_3}\left[{\text{Ba}}^{2+}\right]-k_x+k_x^{\prime }{\left[{\text{Ca}}^{2+}\right]}_s}\right),$$ [2]

with k_BaCO3 the crystallization rate constant of BaCO_3, [CO₃²⁻]_bulk the concentration of carbonate in the bulk solution, [Ca²⁺]_s the Ca²⁺ concentration close to the surface of the CaCO₃ crystal, k_x the dissolution rate constant of CaCO₃ for a specific polymorph x, and k_x′ = k_CaCO3,x/K_{sp_CaCO3,x} where K_{sp_CaCO3,x} is the solubility product of a specific polymorph x of CaCO₃ (see SI Appendix and refs. 24–27). We assume k_vaterite > k_aragonite > k_calcite and K_sp,vaterite > K_sp,aragonite > K_sp,calcite, which implies that both the dissolution rate and solubility of vaterite are higher than those for aragonite and calcite. In case of ample availability of Ba²⁺, the free-energy barrier Δg_n for nucleation on a specific polymorph of CaCO₃ is controlled by the interplay of: (i) the concentration of carbonate in the bulk solution, (ii) the polymorph-dependent lattice mismatch with the CaCO₃ substrate, and (iii) the substrate solubility equilibrium. We therefore expect that the choice of the positioning of the nucleation can be tuned by the subtle changes in relative contributions of these parameters. Below we consider various scenarios where the impact of these parameters is analyzed and exploited to direct the nucleation and growth of BaCO₃.

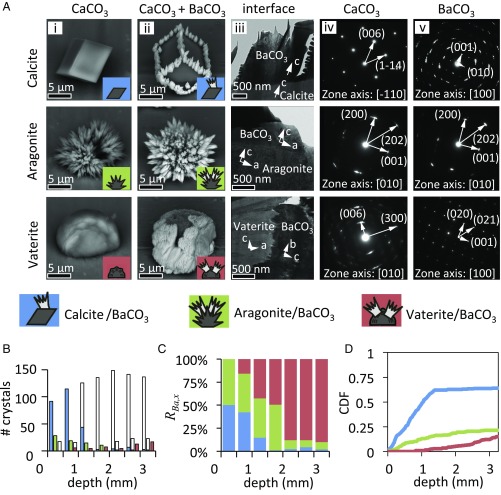
To evaluate the effects of lattice mismatch in the carbonate system studied here, we characterized the crystallographic relationships of BaCO₃ grown on top of calcite, aragonite, and vaterite as substrate crystals. The overgrown BaCO₃ crystals can be easily differentiated from the underlying CaCO₃ crystals in backscatter electron microscopy due to their electron density difference (Fig. 2 A, i and ii). Through focused ion-beam (FIB) milling, electron-transparent transmission electron microscopy (TEM) samples were prepared at the interfaces of nucleus and substrates, from which the morphological and crystallographic characteristics were evaluated (Fig. 2 A, iii–v). BaCO₃ exhibit good alignment with calcite and aragonite due to sharing the same c axes, while vaterite showed no crystallographic alignment (Fig. 2A and SI Appendix). This lack of orientation matching thus indicates a higher interfacial free energy for nucleation on vaterite compared with calcite and aragonite. A qualitative estimation of the lattice mismatch shows that BaCO₃ has a slightly smaller lattice mismatch in both a and b directions on calcite as the substrate in comparison with aragonite as the substrate (SI Appendix, section 8) (12). Therefore, when all three polymorphs are present as crystallization substrates, BaCO₃ will selectively first nucleate on calcite, followed by aragonite, but not on vaterite for the same supersaturation levels. On the other hand, substrate solubility should favor the nucleation of BaCO₃ on vaterite over crystallization on aragonite, and least on calcite, due to significant local supersaturation occurring on the surfaces of the dissolving vaterite at low values of bulk carbonate content. The relative contributions of these two factors can be easily tuned by varying [CO₃²⁻]_bulk, according to Eqs. 1 and 2. For high values of the [CO₃²⁻]_bulk the lattice mismatch is expected to dominate the crystallization position, whereas for low values of [CO₃²⁻]_bulk the solubility equilibrium of the substrate will increase the supersaturation in the vicinity of the least stable polymorphs.

Fig. 2.

Polymorph-selective nucleation of BaCO₃ on different CaCO₃ polymorphs. (A) Backscatter electron microscopy images were used to highlight the difference between BaCO₃ (appearing light) on different polymorphs of CaCO₃ (appearing dark). The lattice mismatches were estimated by measuring the crystallographic alignment of BaCO₃ on calcite, aragonite, and vaterite (SI Appendix). (A, i) Different polymorphs of CaCO₃. (A, ii) BaCO₃ crystals on top of the different polymorphs of CaCO₃. (A, iii–v) TEM imaging and corresponding selected-area electron diffraction at the interfaces revealed crystallographic alignment of BaCO₃ on top of calcite and aragonite, whereas no crystallographic alignment was found on vaterite. (B–D) Three representations of statistical data of CaCO₃ overgrowth. (B) Total number of various polymorphs of CaCO₃ crystals as a function of depth: calcite (left bar), aragonite (middle bar), and vaterite (right bar). The number of the overgrown CaCO₃ crystals in each category are shown as filled bars: calcite-BaCO₃ (blue), aragonite-BaCO₃ (green), and vaterite-BaCO₃ (red). (C) Polymorph ratio based on data in Fig. 2B, highlighting that close to the meniscus BaCO₃ nucleation only occurs on calcite and aragonite, and deeper in the solution––only on vaterite. (D) CDF of the overgrown crystals as a function of depth.

These differences in lattice mismatches, in combination with external control over the local supersaturation, allow us to selectively nucleate BaCO₃ on a predetermined polymorph of CaCO₃.

To probe the influence of [CO₃²⁻]_bulk, we developed a method to fabricate mixed polymorphic substrates containing all three polymorphs of CaCO₃ (typically, calcite 79 ± 8%, aragonite 14 ± 5%, and vaterite 7 ± 3%) by crystallizing CaCO₃ on an aluminum plate (see SI Appendix for details and setup). We vertically positioned the substrate containing all three CaCO₃ polymorphs in the reaction solution. As carbonate from the air entered the solution from the top, a [CO₃²⁻] gradient was created along the substrate, thus allowing for a continuous combinatorial screening of the influence of the [CO₃²⁻]_bulk on the overgrowth of the CaCO₃ polymorphs. To quantify the results, we manually counted each polymorph as a function of the depth (Fig. 2B). We define the polymorph overgrowth ratio R_Ba,x for a specific CaCO₃ polymorph x as R_Ba,x = (n_Ba,x/n_x)/Σ_x′(n_Ba,x′/n_x′), with n_x denoting the total number of CaCO₃ crystals of a specific polymorph x; n_Ba,x the number of CaCO₃ crystals of this polymorph that have been overgrown with BaCO₃, and the sum in the nominator running over all possible polymorphs (Fig. 2C). Additionally, we compute the cumulative distribution function (CDF) for each overgrown polymorph as a function of the depth in the solution (Fig. 2D).

Close to the meniscus (0.0–0.5 mm), the [CO₃²⁻]_bulk is the highest, which minimizes the effect of the local carbonate supersaturation due to polymorph dissolution. The lattice mismatch thus dominates the nucleation position, and BaCO₃ only nucleates on calcite and aragonite, with no nucleation on vaterite, which is expected as the lack of crystallographic alignment on vaterite results in a disadvantageous lattice mismatch. Deeper in the solution (0.5–2.0 mm), the lower [CO₃²⁻]_bulk decreases the local supersaturation around the calcite and aragonite crystals, and fewer of them become overgrown with BaCO₃. The lower [CO₃²⁻]_bulk also increases the dissolution of the least stable polymorph following Eq. 2, thus locally increasing the supersaturation around the vaterite crystals. Since the solubility of BaCO₃ is approximately 10-fold lower than that of CaCO₃ polymorphs (K_{sp_BaCO3} << K_{sp_CaCO3,x}), the increase in CO₃²⁻ concentration around the dissolving vaterite crystals onsets the nucleation of BaCO₃. Below 2.0 mm the supersaturation is too low for nucleation on either calcite or aragonite crystals even though the lattice mismatch is favorable for these substrates. The stability-dependent dissolution completely dominates the nucleation and all vaterite crystals become overgrown. Dissolving vaterite crystals even increases the local CO₃²⁻ concentration to such an extent that crystallization of BaCO₃ may occur on an accidental calcite and aragonite crystal grown in close proximity to vaterite (SI Appendix, Fig. S2B). It should be noted that a similar trend is found for the overgrowth of CaCO₃ polymorphs with SrCO₃ instead of BaCO₃ (SI Appendix, Fig. S3), demonstrating that these principles can readily be extended to other systems. Furthermore, precise control over the spatial location and polymorphism of the CaCO₃ substrates may be gained using patterned self-assembled monolayers (11).

To create more complex shapes beyond the simple morphology of BaCO₃ crystals, we introduce silica to the reaction. The resulting BaCO₃/SiO₂ structures can straightforwardly be sculpted in a rich palette of microshapes such as vases, spirals, and corals by externally modulating the reaction conditions, such as pH and temperature (28–31). The formation of these various shapes and their orientation is highly sensitive to and nearly fully determined by the concentrations of the reacting species in the vicinity of the developing structures, and can therefore act as an ideal model system to test the sensitivity of the nucleation events described above. Recently, we have also shown that precise control of the shape could lead to functional shapes such as those that can be used in photonics (31). In particular, by integrating a fluorescent dye as a light source in the nucleating barium carbonate seed crystal, effective waveguiding and beamsplitting through the rationally designed microarchitectures were achieved. While in this previous work no control over the position of these structures was obtained, the present study can introduce the ability to precisely control the location of the nucleation of these microstructures. Moreover, we anticipated that akin to chemotaxis, the creation of the local gradient in supersaturation induced by specific polymorphs of CaCO₃ that are placed in the immediate vicinity of the nucleating microstructures may be used to steer the growth of these structures in predetermined directions.

The precipitation of BaCO₃/SiO₂ structures starts with the formation of a BaCO₃ crystal, which to a good approximation is not affected by the SiO₂. Hence we can assign the nucleation position in a manner analogous to how we directed the nucleation of BaCO₃ (Fig. 3 A and B). Indeed, we find the same trend: preferred nucleation on calcite and aragonite at low immersion depths, whereas nucleation on vaterite only occurs deeper in the solution. Importantly, the ratio between the overgrown aragonite and calcite crystals in the top of the substrate gradually increases, with aragonite crystals being selectively overgrown at 0.75–1.5 mm (Fig. 3B), likely due to the growing contribution of the increase in local supersaturation from the dissolving calcium carbonate in the BaCO₃/aragonite system over the BaCO₃/calcite, as the bulk concentration in CO₂ goes down. It should be noted that the silica hampers the nucleation of BaCO₃. As a result, we observe a zone (2.0–5.0 mm) where the local supersaturation is insufficient to grow BaCO₃/SiO₂ structures and only below 5.0 mm is the local supersaturation sufficiently high to induce nucleation on vaterite. More complex shapes can be grown by rationally adjusting the reaction conditions, as exemplified by the SrCO₃/SiO₂ stems in Fig. 3C that selectively nucleated on calcite and aragonite and were opened into vases using a CO₂ pulse and subsequently decorated with serrated edges using temperature modulations.

Fig. 3.

Polymorph-selective nucleation of BaCO₃/SiO₂ and CaCO₃/PAA microstructures. (A) Backscatter SEM images of BaCO₃/SiO₂ grown on (A, i) calcite, (A, ii) aragonite, and (A, iii) vaterite. (B) Polymorph ratio showing that BaCO₃/SiO₂ structures can selectively nucleate on CaCO₃ polymorphs by controlling the depth of immersion (see also SI Appendix). (Inset, Top Right) A more detailed polymorph ratio for the depth of 0–0.75 mm. (C) SrCO₃/SiO₂ stems that were opened into vases and decorated with serrated edges that selectively nucleated on calcite (blue arrow) and aragonite (green arrow) while vaterite (red arrow) is left empty. (D) CaCO₃/PAA spirals selectively nucleate on vaterite crystals. (E) Sequential nucleation steps can be used to first grow CaCO₃/PAA spirals (dark) on vaterite (dark) and subsequently place BaCO₃ spirals (light) on aragonite while leaving calcite empty.

The ability to control nucleation on preselected polymorphs can also be used for positioning different materials on assigned polymorphs in sequential steps. We demonstrated this by first growing CaCO₃ spirals in the presence of polyaspartic acid (PAA) (32, 33). As these spirals are composed of vaterite nanocrystals, they selectively form on vaterite in the presence of all three polymorphs independent of the depth (Fig. 3D). With both the calcite and aragonite crystals still available, we subsequently positioned BaCO₃/SiO₂ spirals on the aragonite crystals while leaving the calcite crystals bare (Fig. 3E) at a depth of 1.5 mm.

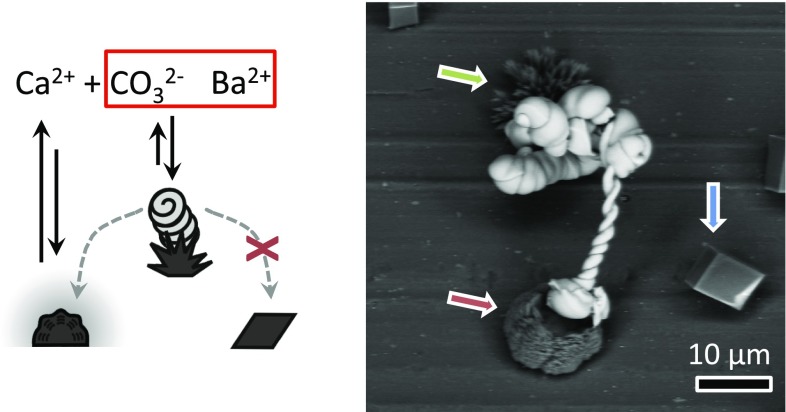
Due the sensitivity of the BaCO₃/SiO₂ coprecipitation to local gradients, one can further define the growth direction of these sophisticated structures, e.g., spirals, toward locally positioned carbonate sources. We ascertained this by growing BaCO₃/SiO₂ spirals on a substrate containing the mixture of CaCO₃ polymorphs at a depth of ∼1.5 mm. According to Fig. 3B, at this depth the nucleation of BaCO₃ preferentially occurs on aragonite whereas neighboring vaterite gradually dissolves, thus causing a local increase in [CO₃²⁻] that could attract the growth front of the BaCO₃/SiO₂ structure and induce its directional chemotaxis. Indeed, we observed that BaCO₃/SiO₂ spirals first formed on aragonite, and subsequently grew only toward nearby dissolving vaterite, while not being influenced by neighboring calcite (Fig. 4). It should be noted that in the absence of silica, we also found that dissolving vaterite crystals could induce sufficient carbonate concentrations to induce nucleation on nearby calcite and vaterite crystals (SI Appendix, Fig. S2B). Selectively lowering the relative energy barrier for nucleation on one polymorph and creating a nearby local supersaturation by dissolving another polymorph thus provides simultaneous control over both the nucleation on preselected polymorphs and growth direction.

Fig. 4.

Polymorph-specific nucleation and oriented, directional growth. The balance between the local supersaturation and lattice mismatch can be controlled by the influx of CO₂ such that nucleation of a BaCO₃/SiO₂ microstructure first occurs at aragonite (green arrow) and subsequently grows toward the carbonate source released from the nearby dissolving vaterite (red arrow) while leaving nearby calcite unaffected (blue arrow). The dashed arrow in the schematic on the Left represents the direction of growth.

Summary and Conclusions

In conclusion, we have introduced a strategy to control the polymorph-specific positioning of mineralizing compounds and their directional growth using substrates with polymorphic mixtures as crystallization templates. The power of our approach is that merely the influx of carbonate allows us to manipulate the local concentrations of the crystallizing ions within a landscape of different interfacial energies. Therefore, by simultaneously controlling the concentration of carbonate from the bulk solution, the polymorph-dependent interfacial energy contribution from the lattice mismatch, and the substrate solubility, we are able to elicit unusual mineralization pathways unachievable by separate control over these individual parameters. In contrast with commonly used nucleation techniques that are based on lowering of the interfacial free energy only, we can therefore also nucleate selectively on substrates that have an unfavorable crystallographic alignment. Additionally, we can sequentially position different materials on assigned polymorphs and steer the growth of these structures in directions predetermined by the location of neighboring dissolving species. These concepts can perfect our ability to control nucleation and growth of nanostructured materials and may elucidate mechanisms that regulate nano- and microscale phenomena in biomineralization processes.

Methods

Crystallization of CaCO₃ Polymorphic Substrates.

For the crystallization of mixed polymorphs of CaCO₃, 0.032 g of CaCl₂ was dissolved in 15 mL water in a 50- or 100-mL beaker. An aluminum slide (∼15 × 15 × 1 mm), or aluminum-coated microscope glass slide, was vertically positioned in the solution and the beaker was placed in a closed desiccator with freshly ground (NH₄)₂CO₃ following the method developed by Addadi et al. (6). After ∼30–45 min, the slide was removed from the solution, washed twice with water, and then washed with acetone and dried in the air. For details see SI Appendix, section 1.

Overgrowth of a CaCO₃ Polymorph Mixture with BaCO₃.

In a 50- or 100-mL beaker, we dissolved 0.074 g BaCl₂ in 15 mL water and adjusted the pH to 11.9 using NaOH. A previously prepared slide with a mixture of calcite, aragonite, and vaterite (see above) was positioned at a 90° angle in the solution such that a half of the previously overgrown area (shown schematically as a green line in SI Appendix, Fig. S2A, Left) was submerged. A Petri dish was loosely placed on the beaker, allowing for the CO₂ from the air to enter the beaker. After ∼30–45 min, the slide was removed from the solution, washed twice with water, and then washed with acetone and subsequently dried. Optical microscopy and SEM were used to analyze the slide and quantify the crystallization of the BaCO₃ on the CaCO₃ mixture. For details see SI Appendix, section 2 and for overgrowth with SrCO₃ see SI Appendix, section 3.

Overgrowth of a CaCO₃ Polymorph Mixture with BaCO₃/SiO₂ Microstructures.

In a 50- or 100-mL beaker, we dissolved 0.074 g of BaCl₂ and 0.016 g of Na₂SiO₃ in 15 mL water. To grow stem, vase, and coral-shaped structures, the pH was adjusted to pH 11.9 whereas for growth helices the pH was adjusted to 11.1 (30). A previously prepared slide with a mixture of calcite, aragonite, and vaterite (see above) was positioned at 90° in the solution such that half of the previously overgrown area was submerged in the solution. A Petri dish was loosely placed on the beaker such that CO₂ from the air could enter the beaker. After ∼45–120 min, the slide was removed from the solution, washed twice with water, and then washed with acetone and dried in the air. Optical microscopy and SEM were used to analyze the results.

Overgrowth of a CaCO₃ Polymorph Mixture with CaCO₃/PAA Microstructures.

In a 50- or 100-mL beaker, we dissolved 0.032 g of CaCl₂ and between 60 and 120 μg/mL poly (α,l-aspartate) (Sigma-Aldrich) in 15 mL water. A previously prepared slide with a mixture of calcite, aragonite, and vaterite (see above) was positioned at 90° in the solution such that half of the previously overgrown area was submerged. The beaker was placed in a closed desiccator with freshly ground (NH₄)₂CO₃ and placed in an oven at 45 °C. After ∼45–120 min, the slide was removed from the solution, washed twice with water, and then washed with acetone and dried in the air. Optical microscopy, Raman microscopy, and SEM were used to analyze the slide.

FIB/TEM Procedure.

Samples were coated with Au (∼5 nm) to reduce charging effects before FIB milling with a Helios Nanolab 660 dual-beam electron microscope (FEI). Typical TEM sample preparation procedure was as follows: (i) a platinum protective layer (∼0.5 μm) was first laid down on top of the desired structure; (ii) another platinum protective layer (∼1.5 μm) was further deposited on top of the rectangular region where the TEM slab was to be milled out; (iii) two sides of the coated structure were milled away by FIB, leaving the slab of specimen (thickness: ∼1.5 μm); (iv) the slab was then cut through by FIB and transferred to a copper TEM grid by an Omniprobe and welded securely with platinum deposition; (v) the lift-out lamellar of specimen was sequentially thinned by FIB at 30-, 16-, 5-, and 2-kV ion beam voltages. Final cleaning at 2 kV and 28 pA is important to obtain a clean surface and minimize damage. TEM imaging was carried out using a JEOL 2011 operated at 120 kV. See SI Appendix, sections 6–8 for detailed figures, analysis of the crystal structure, and calculation of the crystallographic mismatch.