Significance
Liquid–liquid phase separation plays an important role in diverse processes, such as the organization of cellular subcompartments, the encapsulation of active agents, or the synthesis of complex emulsions. Demixing liquids usually leads to spinodal-type patterns with no characteristic length scale. Here we show that phase separation in the wake of an immiscibility front can give macroscopic patterns in which a particular length scale is arrested. These patterns are reminiscent of Turing patterns in driven systems but occur by a different mechanism in which the speed of the immiscibility front controls their spacing. This offers a general route toward self-organization with programmable features. Here we tune the spacing of patterns in “Russian-doll” emulsions as well as stripes in rectangular capillaries.
Keywords: multilayered emulsion, Allen–Cahn, Cahn–Hilliard, spinodal decomposition, self-organization
Abstract
Miscible liquids can phase separate in response to a composition change. In bulk fluids, the demixing begins on molecular-length scales, which coarsen into macroscopic phases. By contrast, confining a mixture in microfluidic droplets causes sequential phase separation bursts, which self-organize into rings of oil and water to make multilayered emulsions. The spacing in these nonequilibrium patterns is self-similar and scale-free over a range of droplet sizes. We develop a modified Cahn–Hilliard model, in which an immiscibility front with stretched exponential dynamics quantitatively predicts the spacing of the layers. In addition, a scaling law predicts the lifetime of each layer, giving rise to a stepwise release of inner droplets. Analogously, in long rectangular capillaries, a diffusive front yields large-scale oil and water stripes on the time scale of hours. The same theory relates their characteristic length scale to the speed of the front and the rate of mass transport. Control over liquid–liquid phase separation into large-scale patterns finds potential material applications in living cells, encapsulation, particulate design, and surface patterning.
One can distinguish two broad classes of nonequilibrium patterns arising from instabilities (1, 2). The first are known as Turing-type patterns (3, 4), which occur in driven systems when a linear instability on a given length scale is stabilized by nonlinear effects to create a pattern on that same spatial scale. Examples include reaction–diffusion patterns in chemical and biological systems (5–7) and Rayleigh–Bénard or Taylor–Couette patterns in hydrodynamics (8). Patterns of this type are generated by dynamical instabilities that propagate with, for example, a moving front (9) or a temperature quench (10). In both cases, the length scale is initially set by the pattern-forming instability and the magnitude depends on the balance between the deterministic reaction and the stochastic diffusion force (11). The linear instability provides the fastest growing modes and can lead to steady-state structures that resemble those in equilibrium, such as crystal lattices with defects, but the nonequilibrium patterns require an energy input, or source term.
By contrast, in the second class of patterns, a mixture of liquids in a single phase undergoes bulk phase separation (12–14), which entails constantly evolving length scales and time scales that eventually separate into macroscopic phases (15). Surprisingly, the same experiment in a microfluidic droplet can result in long-lived patterns (16–18), stabilized on mesoscopic length scales. For example, a miscible droplet of diethylphthalate (DEP) oil, water, and ethanol (19) demixes upon contact with the aqueous phase, according to the phase diagram shown in Fig. S1, to give alternating layers of oil and water (20), as shown in Fig. 1. Empirically, the patterns depend on the initial composition, viscosity, and the interfacial tension (21, 22). The mechanism for the sorting of the oil and water phases into well-defined patterns requires elucidation. Here, we develop a model to explain the emerging length scales as a function of experimental parameters in both microfluidic droplets and inside long capillaries. In the experiments, we gain control over the patterns by varying the quench rate and composition, with results that are in good agreement with theoretical predictions. A practicable consequence is that the stepwise release time of each layer in the pattern could be tuned by its size, given a choice of surfactant to stabilize the layers.
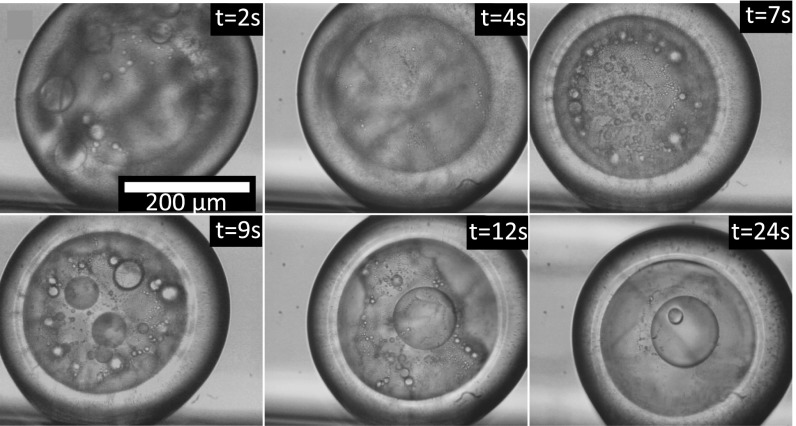
Fig. 1.
Pattern formation in demixing ternary liquids. Snapshots of a movie (see Movie S1) showing the sequential bursts of phase separation of a miscible droplet of water: DEP: ethanol (0.15:0.47:0.38) upon contact with the continuous phase with wt F127 surfactant into four alternating layers of oil and water.
Fig. 1 shows the temporal evolution of phase separation bursts and ordering that create a quadruple emulsion of alternating layers of oil and water (see Movie S1). Upon contact with an aqueous solution of wt F127 pluronic, the ethanol leaks out of the ternary droplet, as shown by the measured volume change over time in Fig. S2. This loss of ethanol from the droplet into the aqueous phase drives phase separation when the ethanol concentration drops below a critical value . Since ethanol is equally soluble in oil and water, we shall model the system as a binary mixture of oil and water, where the ethanol concentration plays the role of quench control parameter. We can model the energetics of this mixture as a switch from a single to a double-well Ginzburg–Landau potential according to the -type energy functional,
| [1] |
where gives the relative concentration of water to oil at time and position x, is the microscopic width of the interface between oil and water, and is a function that specifies the miscible region where and and the immiscible region where and (see Supporting Information for details).
In bulk liquids, the system’s evolution on the energy landscape (Eq. 1) toward equilibrium is described by the mass-conserving Cahn–Hilliard (CH) equation (15), in which the liquids separate into macroscopic phases via spinodal decomposition. In our case, this picture is changed by the finite geometry as well as by mixing effects inside the droplets. The droplets extruded from the microfluidic device experience a shear interaction with the continuous fluid that carries them away, causing a self-circulation flow with velocities on the order of several millimeters per second (23). This process is different from the standard diffusive law predicted by the Epstein–Plesset theory (24). The interfacial tension gradient within the droplet effectively scoops small droplets of oil or water toward the miscible region and results in transport that is faster than diffusive on the length scale of the droplet. A detailed theoretical treatment would couple the CH equation with the Navier Stokes equations (25), which could only be solved numerically from the start. Instead, here we adopt a simplified description in which the CH equation is modified at short length scales to capture fast transport. The dynamics of is assumed to be relaxational, as opposed to diffusive, using the chemical potential as the driving force. The faster-than-diffusive transport effectively carries mass instantaneously across the entire droplet, which can be described by the nonlocal Allen–Cahn equation (26),
| [2] |
where is the spatial average of inside the droplet (see Supporting Information for details). Once the motion of the immiscibility front is specified, the only fitting parameters in the model are the interfacial length , which can be set to in the sharp interface limit, and the relaxation time . It is important to note that while the standard Allen–Cahn equation does not conserve mass, the nonlocal equation Eq. 2 does, due to the term .
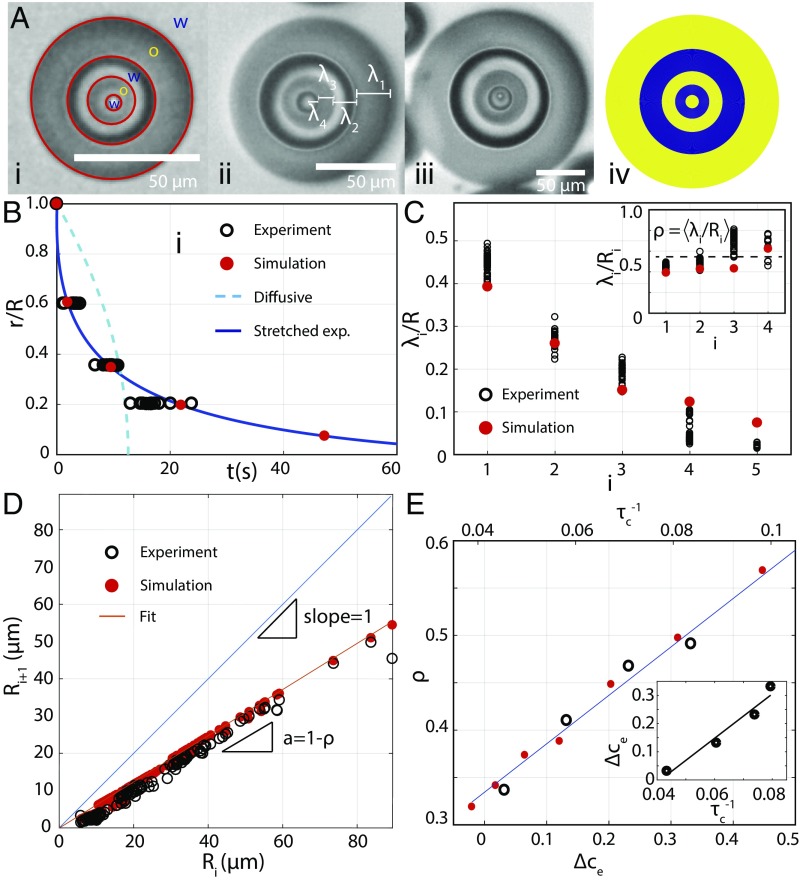
In the experiments, we measure the spacing between consecutive layers indexed by , as shown in Fig. 2A, for a given initial composition of water, oil (DEP), and ethanol (0.12:0.52:0.36). We find that increasing the size of the mother droplet recreates patterns that are independent of scale over a range of droplet sizes (Fig. 2 A, i–iii), except that an additional small droplet is stabilized in the center of a m droplet (Fig. 2 A, iii) to make quintuple emulsions, also shown in the corresponding simulation in iv and in Movie S2. To compare these experimental results with the model, we need to specify the dynamics of ethanol leakage. As mentioned above, due to shear-mixing, we empirically determine the speed of the immiscibility front in Fig. 2B. To this end, we measure the positions and times of the creation of the layers in the experiments, and we use these data to estimate the location of the immiscibility front where . The best fit shows that this front is spherically symmetric with a radius that shrinks according to a stretched exponential with exponent
| [3] |
where s is a characteristic relaxation time independent of the droplet radius . Solving Eq. 2 with Eqs. 1 and 3, assuming if (that is, ) and if (that is, ), reproduces the spatiotemporal location of the phase separation bursts, in rather good agreement with the data in Fig. 2B. This result provides supporting evidence that fast mass transfer occurs on length scales that are longer than the largest droplet radius. Moreover, both the experiment and the model show that the spacing between the layers decreases with toward the center, over a range of sizes of the mother droplet, as shown in Fig. 2C. This spacing can be rescaled by the radius of the outer boundary of each layer to give a roughly constant ratio , independent of layer number, as shown in Fig. 2, Inset. This rescaling implies a linear relationship between consecutive radii in droplets of all sizes, with a slope , all of the way down to the minimum droplet size with m that can be stabilized, as shown in Fig. 2D. Indeed, this test of self-similarity can be seen visually in the experimental data (i–iii) and in the model (iv) in Fig. 2A. The only remaining adjustable parameter in the model is the relaxation time in Eq. 2, whose value is obtained to be s by fitting to the data in Fig. 2C. The relaxation time turns out to be seven times faster than the ethanol leakage time in this case. This separation of time scales controls the sizes of the scale-free pattern. To further test the model, we vary the concentration difference inside and outside the droplet to modify the speed of ethanol leakage. We find that self-similarity is preserved in all cases, but the characteristic spacing between the layers, , increases with , as shown in Fig. 2E. Analogously, if we increase the leakage rate in the model, consistent with a steeper ethanol gradient at the droplet interface, we recover the same trend as in the experiments. The value of is then used to relate in the model and in experiments to obtain an approximately linear relation, as shown in the Inset of Fig. 2D. Therefore, the patterns are governed by the interplay between the speed at which the immiscibility front () moves inside the system and the rate at which phase separation and the associated mass transport occurs.
Fig. 2.
Comparison of the model with experiments. (A) Droplets of different sizes create self-similar multiple emulsions (i–iii), except that one extra small droplet fits into the largest mother droplet (iii), simulated in iv. (B) The radial position of layers as a function of time reveals a stretched exponential rather than a diffusive (Epstein–Plesset theory) time course for the immiscibility front. (C) Layer spacing decreases toward the center of the droplets for all droplet sizes in excellent agreement with the model. Rescaling the spacing by the layer radius gives a constant ratio , shown in the Inset, as a signature of self-similarity. (D) Consecutive radii of the layers collapse onto a straight line for all droplet sizes, whose slope gives the ratio of lengths in C. (E) Adding ethanol to the continuous phase decreases and gives rise to a finer spacing of the layers . This effect is well captured by a linear correspondence with the leakage rate in the model, shown in the Inset.
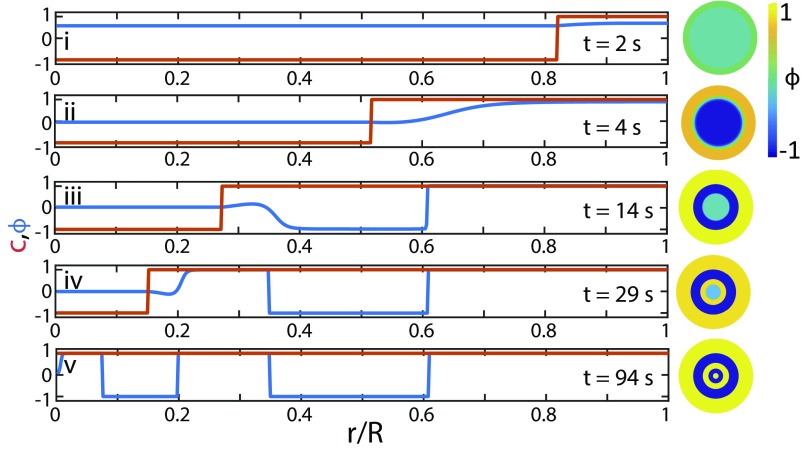
In the model, the mechanism of pattern formation is captured by the spatiotemporal evolution of composition along the radial distance as shown in Fig. 3. As ethanol leaks out, the uniform miscible mixture first reaches the critical concentration at the outer edge of the droplet (i and ii). The most abundant oil phase begins to phase-separate via spinodal decomposition and the immiscible region propagates inwards. To conserve mass, excess water moves toward the center, where the interfacial tension is the lowest. This process increases the water content of the inner droplet until it crosses over to the water-rich side of the phase diagram. Following further ethanol loss, the innermost droplet separates into a water-rich layer (iii), and this process repeats until the front reaches the center (iv and v). In this case, the model generates a quintuple, metastable emulsion, which quantitatively reproduces the experimentally observed layered pattern in Fig. 2A. Previous models based on the standard CH equation with a moving phase-separation front (27–29) have been used to explain pattern formation for example in the context of alloy manufacturing (30) or Liesegang rings (31, 32). In comparison with ours, these models tend to predict patterns whose length scale is tied up to the microscopic interfacial length and they fail to properly reproduce the mass-transport processes ahead of the front.
Fig. 3.
Numerical simulations reproduce the formation of layers in the wake of an immiscibility front. As the front (red line) moves inside the droplet and the ethanol concentration drops below , the potential switches to a double well, causing the volume fraction (blue line) to alternate between oil and water-rich regions along the radial distance.
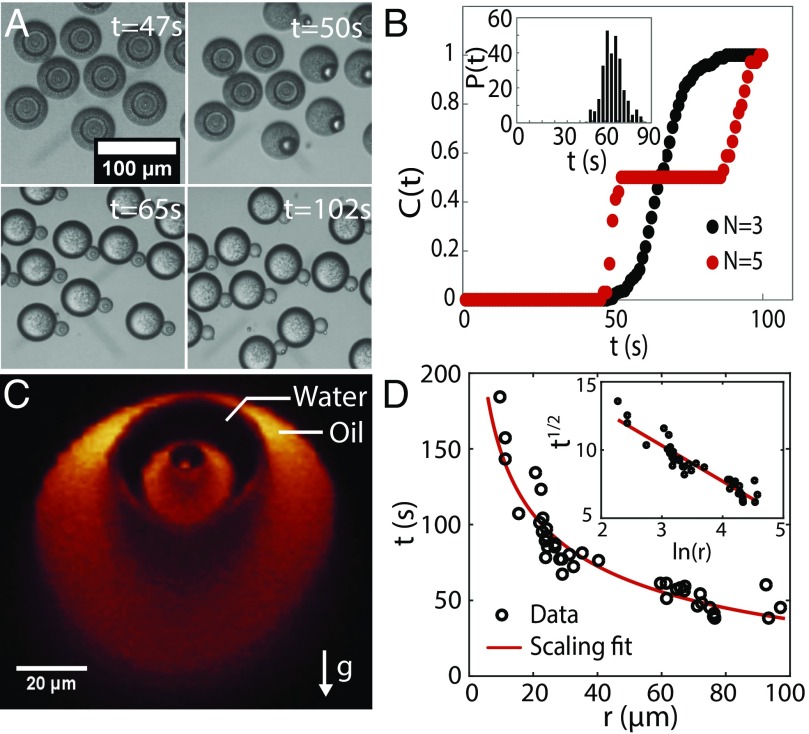
In addition to the length scale, the lifetime of the multiple emulsions can be tuned. The droplet stability is controlled by the surfactant concentration and flow rate, as shown in Fig. S3. Below F127 surfactant in the aqueous phase, the multiple emulsions become unstable and release their inner layers, as shown in Fig. 4A and Movie S3. The measured release times are plotted in the cumulative distribution in Fig. 4B for a triple and a quintuple emulsion stabilized with a low concentration of pluronic surfactant. The quintuple emulsion undergoes two bursts of events associated with the release of the large outer and then the small inner oil layers, which are separated by a time delay. The narrow histogram of release times , shown in Fig. 4B, Inset, is indicative of a stochastic process with a much shorter characteristic time than the lifetime. These results indicate that the lifetime of each layer is controlled by its size.
Fig. 4.
Timed-release of inner layers of a multiple emulsion made from a water, DEP, ethanol (0.15:0.47:0.38) mixture in the presence of wt F127 surfactant. (A) Snapshots of a movie (see Movie S3) showing the sequential release of inner layers into the continuous phase. (B) Cumulative distribution of inner layers released into the outer aqueous phase versus time for a single burst of events in a triple emulsion and two bursts for the quintuple emulsion from A. A histogram of the release times for the triple emulsion is given in Inset. (C) A confocal image of the cross-section of a z stack of a quintuple emulsion, labeled with Nile Red dye. (D) Lifetime of inner layers versus their size. The fit represents the time at which the buoyancy force begins to dominate, given by the relation , which implies that ln (r) is linear in , as shown in Inset.
The lifetime is set by a balance between the buoyancy force caused by gravity, which scales with , and the inward force centering the droplets due to the surface tension gradient, which is proportional to . Fig. 4C shows that the inner droplets, strongly stabilized by surfactants, are not centered because gravity pushes the oil down and the water up after the ethanol has leaked out. During the stretched exponential leakage, the surface tension force that centers the droplets diminishes over time until it equals the buoyancy force so that the release time in the absence of strong surfactants occurs when the buoyancy force starts to dominate, ; here is a fit parameter with the dimension of the length that encompasses the surface tension, the acceleration of gravity, etc. Repeating experiments over a range of sizes reveals that the data in Fig. 4D are in good agreement with the predicted scaling law. Moreover, the Fig. 4D, Inset shows that the scaling is linear in ln (r), with a fit that gives the proportionality constant m and s, consistent with the highest leakage rate s−1 in Fig. 2D on a time scale that is just four times faster than phase separation. These data lend additional support to the assumption that ethanol leakage follows a stretched exponential decay, which drives the centering of the layers.
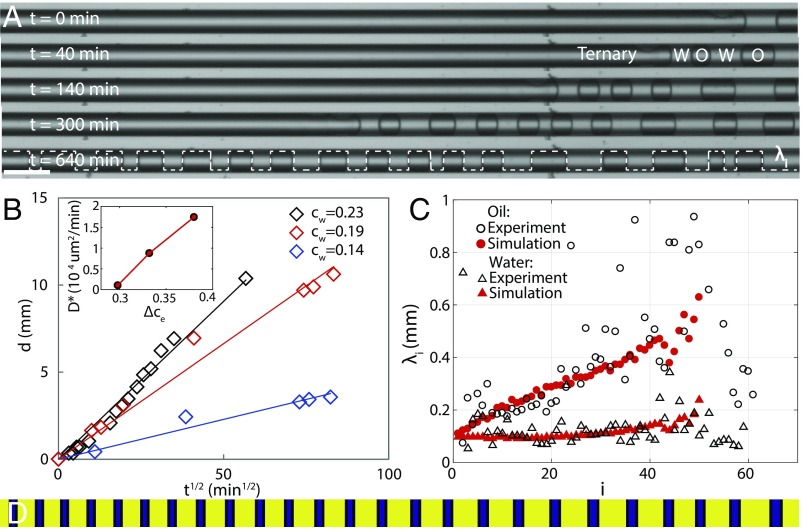
Pattern formation can also be driven by a diffusive front by simply placing the ternary mixture of water:DEP:ethanol (0.145:0.475:0.38) in a rectangular capillary (50μm × 50μm × 3 cm), in contact with the aqueous phase. The slow leakage of ethanol triggers a wave of phase separation (see Movie S4), leaving behind stripes of alternating layers of oil and water over tens of hours, as shown in the snapshots in Fig. 5A. The final ratio of stripe lengths between oil and water agrees with the initial composition, as measured by the ratio of the total sum of all oil and water stripes. The appearance of consecutive stripes in space and time, which traces the immiscibility front , follows the square root of time in Fig. 5B, consistent with a diffusive drive for phase separation. Changing the initial composition results in different slopes of the lines, corresponding to the effective diffusion constants shown in Inset. This diffusion constant depends on the relative concentrations of ethanol inside and outside the capillary, and it can be predicted by solving the diffusion equation in one dimension with an absorbing boundary condition at the end of the capillary. We obtain that the immiscibility front where follows
| [4] |
where we set , erfinv denotes the inverse of the error function, and m2/s is the bare diffusion coefficient of ethanol. Since we do not know the distance to the spinodal line for each composition, we fit to obtain the experimental in the Inset in Fig. 5B and find that .
Fig. 5.
Striped patterns in a capillary. (A) The ternary mixture in a cm-long capillary slowly phase separates to form alternating layers of oil and water at the boundary with the aqueous phase. (Scale bar, m.) (B) The immiscibility front is followed as a function of time for three ternary mixtures. The slopes of the linear fits give for each composition, as shown in Inset, consistent with the prediction Eq. 4. (C) Spacing of the water and oil layers in a phase-separated capillary shows good agreement between experiments and theory. (D) Simulation of the modified CH equation (Eq. 5) showing the formation of alternating layers of oil and water in the confinement of a capillary.
In this case, it is unphysical to assume that faster-than-diffusive mass transport occurs over the effectively infinite capillary. Mass is conserved by allowing fast transport in a finite region that extends a phenomenological distance ahead of the immiscibility front. In practice, this is implemented by assuming that again obeys a nonlocal Allen–Cahn equation
| [5] |
if and otherwise. Here denotes the spatial average of over the growing region and is the relaxation time (see Supporting Information for details about Eq. 5 and its connection with Eq. 2). The relaxational dynamics in Eq. 5 is consistent with a change of mobility in the standard CH equation and effectively captures the fast transport due to the interfacial tension gradient caused by the varying ethanol concentration along the capillary. This dependence is shown in Fig. S4, measured using the pendant drop method. It turns out that the solutions of Eq. 5 are rather insensitive to and to the precise definition of , given in the Supporting Information. Using the law (Eq. 4) to describe the diffusive motion of the immiscibility front and as input in Eq. 5, we find that the fitting parameter min reproduces the lengths of both oil and water stripes as a function of the layer number, as shown in Fig. 5C and Movies S5 and S6. The results were obtained with mm, but they do not vary for in the range mm for the conditions of our experiment. Notice that the vast difference between the values of used in the droplet and the capillary experiments indicates that this parameter is set by the leakage mechanism of ethanol, which is observed to be different in both sets of experiments. Advective effects in the droplets are absent in the capillary, but it remains an open question to explain how these effects lead to the law in Eq. 3 rather than the diffusive relation in Eq. 4.
The relaxation time is three orders of magnitude slower than in the case of shear-mixed droplets. The model captures the narrowing of stripes from the entrance of the capillary (at ) to their disappearance at very well. The large scatter in the data arises from other phenomena that begin to occur over these long time scales, such as the coalescence of consecutive oil layers. The periodic structure creates a macroscopic pattern that spans a centimeter, as shown in Fig. 5D. Even though the length of the pattern is determined by the dynamics, its scale can be captured from the following dimensional analysis,
| [6] |
This gives mm, which roughly corresponds to the sum of an oil and water stripe pair at the opening of the capillary in Fig. 5D. This result confirms that the characteristic length scale of the stripes is set by the dynamical interplay between the speed of ethanol leakage and that of phase separation/mass transfer and lies between the interfacial length and the longer length . Both emulsion droplets and capillaries demonstrate that liquid–liquid phase separation in confinement leads to controllable patterns in the wake of phase separation. The modified CH model offers us predictive power over those patterns, which may turn out to be useful in programmable coatings or the encapsulation of active ingredients into multiple layers (33–35).
Materials and Methods
Ternary mixtures used in this study consist of water (Millipore), ethanol ( purity, Sigma Aldrich), and DEP ( purity, Sigma Aldrich) with various compositions. Droplets of sizes between 40 and 300 m in diameter were prepared by flowing the ternary phase through a glass microfluidic channel into an aqueous solution of pluronic F127 surfactant (Sigma Aldrich, wt% unless otherwise indicated) using a homebuilt microfluidic device. This device consists of a square, tapered glass capillary (VitroCom) inserted into a round capillary in a coaxial geometry. Both are encased by another square glass capillary. The flow rate of the disperse phase was controlled with Harvard syringe pumps and was L/h unless otherwise indicated. The outer flow rate was controlled using air pressure with pressures varying from to psi thus controlling the droplet size.
Phase separation experiments in capillaries were performed by dipping a capillary into a ternary mixture for 5 s and subsequently into a solution of F127 for 20 s to fill the remainder of the capillary. The ends were closed with a Norland optical adhesive. Both the multiple emulsions and droplets and the striped capillaries are observed using a bright-field Olympus microscope equipped with a Thorlabs camera.
Supplementary Material
Acknowledgments
The authors gratefully acknowledge theoretical insights by the late Maxime Clusel, to whom this work is dedicated. We thank Mike Cates and Amy Novick-Cohen for insightful comments and Martin Haase for Movie S2. This work was primarily supported by the Materials Research Science and Engineering Center (MRSEC) program of the National Science Foundation under Award DMR-1420073. J.B. acknowledges support by the National Science Foundation under Grant DMR-1710163.
Footnotes
The authors declare no conflict of interest.
This article is a PNAS Direct Submission.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1716330115/-/DCSupplemental.
References
- 1.Cross MC, Hohenberg PC. Pattern formation outside of equilibrium. Rev Mod Phys. 1993;65:851–1112. [Google Scholar]
- 2.van Saarloos W. Front propagation into unstable states. Phys Rep. 2003;386:29–222. [Google Scholar]
- 3.Turing AM. The chemical basis of morphogenesis. Phil Trans R Soc B. 1952;237:37–72. [Google Scholar]
- 4.Ball P. Forging patterns and making waves from biology to geology: A commentary on Turing (1952) ‘the chemical basis of morphogenesis’. Phil Trans R Soc B. 2015;370:20140218. doi: 10.1098/rstb.2014.0218. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Hyman AA, Simons K. Beyond oil and water—Phase transitions in cells. Science. 2012;337:1047–1049. doi: 10.1126/science.1223728. [DOI] [PubMed] [Google Scholar]
- 6.Weber SC, Brangwynne CP. Inverse size scaling of the nucleolus by a concentration-dependent phase transition. Curr Biol. 2015;25:641–646. doi: 10.1016/j.cub.2015.01.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Feric M, et al. Coexisting liquid phases underlie nucleolar subcompartments. Cell. 2016;165:1686–1697. doi: 10.1016/j.cell.2016.04.047. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Schatz MF, Neitzel PG. Experiments on thermocapillary instabilities. Ann Rev Fluid Mech. 2001;33:93–127. [Google Scholar]
- 9.Rabani E, Reichman DR, Geissler PL, Brus LE. Drying-mediated self-assembly of nanoparticles. Nature. 2003;426:271–274. doi: 10.1038/nature02087. [DOI] [PubMed] [Google Scholar]
- 10.Cates ME, Vollmer J, Wagner A, Vollmer D. Phase separation in binary fluid mixtures with continuously ramped temperature. Philos Trans A Math Phys Eng Sci. 2003;361:793–804. doi: 10.1098/rsta.2002.1165. [DOI] [PubMed] [Google Scholar]
- 11.Hohenberg P, Krekhov A. An introduction to the Ginzburg-Landau theory of phase transitions and nonequilibrium patterns. Phys Rep. 2015;572:1–42. [Google Scholar]
- 12.Sitnikova NL, Sprik R, Wegdam G, Eiser E. Spontaneously formed trans-anethol/water/alcohol emulsions: Mechanism of formation and stability. Langmuir. 2005;21:7083–7089. doi: 10.1021/la046816l. [DOI] [PubMed] [Google Scholar]
- 13.Lu Z, et al. Universal nanodroplet branches from confining the Ouzo effect. Proc Natl Acad Sci USA. 2017;114:10332–10337. doi: 10.1073/pnas.1704727114. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Hajian R, Hardt S. Formation and lateral migration of nanodroplets via solvent shifting in a microfluidic device. Microfluid Nanofluidics. 2015;19:1281–1296. [Google Scholar]
- 15.Cahn JW, Hilliard JE. Free energy of a nonuniform system. I. Interfacial free energy. J Chem Phys. 1958;28:258–267. [Google Scholar]
- 16.Choi CH, Weitz DA, Lee CS. One step formation of controllable complex emulsions: From functional particles to simultaneous encapsulation of hydrophilic and hydrophobic agents into desired position. Adv Mater. 2013;25:2536–2541. doi: 10.1002/adma.201204657. [DOI] [PubMed] [Google Scholar]
- 17.Zarzar LD, et al. Dynamically reconfigurable complex emulsions via tunable interfacial tensions. Nature. 2015;518:520–524. doi: 10.1038/nature14168. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Tan H, et al. Evaporation-triggered microdroplet nucleation and the four life phases of an evaporating Ouzo drop. Proc Natl Acad Sci USA. 2016;113:8642–8647. doi: 10.1073/pnas.1602260113. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Bendová M, Řehák K, Matouš J, Novák JP. Liquid + liquid equilibrium in the ternary systems water + ethanol + dialkyl phthalate (dimethyl, diethyl, and dibutyl phthalate) at 298.15 K. J Chem Eng Data. 2001;46:1605–1609. [Google Scholar]
- 20.Haase MF, Brujic J. Tailoring of high-order multiple emulsions by the liquid–liquid phase separation of ternary mixtures. Angew Chem Int Ed Engl. 2014;53:11793–11797. doi: 10.1002/anie.201406040. [DOI] [PubMed] [Google Scholar]
- 21.Zhao CX, Middelberg A. Microfluidic mass-transfer control for the simple formation of complex multiple emulsions. Angew Chem Int Ed Engl. 2009;48:7208–7211. doi: 10.1002/anie.200902485. [DOI] [PubMed] [Google Scholar]
- 22.Deng NN, et al. Wetting-induced formation of controllable monodisperse multiple emulsions in microfluidics. Lab Chip. 2013;13:4047–4052. doi: 10.1039/c3lc50638j. [DOI] [PubMed] [Google Scholar]
- 23.Wang C, Nguyen NT, Wong TN. Optical measurement of flow field and concentration field inside a moving nanoliter droplet. Sens Actuators A Phys. 2007;133:317–322. [Google Scholar]
- 24.Epstein PS, Plesset MS. On the stability of gas bubbles in liquid-gas solutions. J Chem Phys. 1950;18:1505–1509. [Google Scholar]
- 25.Hohenberg PC, Halperin BI. Theory of dynamic critical phenomena. Rev Mod Phys. 1977;49:435–479. [Google Scholar]
- 26.Rubinstein J, Sternberg P. Nonlocal reaction–diffusion equations and nucleation. IMA J Appl Math. 1992;48:249–264. [Google Scholar]
- 27.Ball RC, Essery RLH. Spinodal decomposition and pattern formation near surfaces. J Phys: Cond Mat. 1990;2:10303. [Google Scholar]
- 28.Foard EM, Wagner AJ. Enslaved phase-separation fronts in one-dimensional binary mixtures. Phys Rev E. 2009;79:056710. doi: 10.1103/PhysRevE.79.056710. [DOI] [PubMed] [Google Scholar]
- 29.Goh R, Scheel A. Hopf bifurcation from fronts in the Cahn-Hilliard equation. Arch Rat Mech Anal. 2015;217:1219–1263. [Google Scholar]
- 30.Langer JS. Instabilities and pattern formation in crystal growth. Rev Mod Phys. 1980;52:1–28. [Google Scholar]
- 31.Liesegang R. Ueber einige eigenschaften von gallerten. Naturwissenschaftliche Wochenschrift. 1896;11:353–362. [Google Scholar]
- 32.Stern KH. The Liesegang phenomenon. Chem Rev. 1954;54:79–99. [Google Scholar]
- 33.Mitragotri S, Lahann J. Physical approaches to biomaterial design. Nat Mater. 2009;8:15–23. doi: 10.1038/nmat2344. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Hu SH, Chen SY, Gao X. Multifunctional nanocapsules for simultaneous encapsulation of hydrophilic and hydrophobic compounds and on-demand release. ACS Nano. 2012;6:2558–2565. doi: 10.1021/nn205023w. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Zhao CX. Multiphase flow microfluidics for the production of single or multiple emulsions for drug delivery. Adv Drug Deliv Rev. 2013;65:1420–1446. doi: 10.1016/j.addr.2013.05.009. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.