Coordination to lanthanide ions distorts binding site conformation in calmodulin

Significance

Calmodulin is essential to life in all eukaryotic cells and serves as a popular model for ion binding and activation in proteins. Calmodulin transduces complex calcium signals and acts on hundreds of effector proteins, but the sensitivity and complexity of this process make it difficult to characterize. Much work uses lanthanides as luminescent calcium substitutes to study ion binding and activation in calmodulin and other proteins. Using ultrafast 2D IR spectroscopy, we show that lanthanide ions perturb the finely tuned structure and dynamics of calmodulin’s binding sites. The temporal and spatial resolution of our measurements opens a new window into the study of protein−ion binding and demonstrates that seemingly innocuous ligand substitutions can significantly alter protein conformation.

Abstract

The Ca²⁺-sensing protein calmodulin (CaM) is a popular model of biological ion binding since it is both experimentally tractable and essential to survival in all eukaryotic cells. CaM modulates hundreds of target proteins and is sensitive to complex patterns of Ca²⁺ exposure, indicating that it functions as a sophisticated dynamic transducer rather than a simple on/off switch. Many details of this transduction function are not well understood. Fourier transform infrared (FTIR) spectroscopy, ultrafast 2D infrared (2D IR) spectroscopy, and electronic structure calculations were used to probe interactions between bound metal ions (Ca²⁺ and several trivalent lanthanide ions) and the carboxylate groups in CaM’s EF-hand ion-coordinating sites. Since Tb³⁺ is commonly used as a luminescent Ca²⁺ analog in studies of protein−ion binding, it is important to characterize distinctions between the coordination of Ca²⁺ and the lanthanides in CaM. Although functional assays indicate that Tb³⁺ fully activates many Ca²⁺-dependent proteins, our FTIR spectra indicate that Tb³⁺, La³⁺, and Lu³⁺ disrupt the bidentate coordination geometry characteristic of the CaM binding sites’ strongly conserved position 12 glutamate residue. The 2D IR spectra indicate that, relative to the Ca²⁺-bound form, lanthanide-bound CaM exhibits greater conformational flexibility and larger structural fluctuations within its binding sites. Time-dependent 2D IR lineshapes indicate that binding sites in Ca²⁺−CaM occupy well-defined configurations, whereas binding sites in lanthanide-bound-CaM are more disordered. Overall, the results show that binding to lanthanide ions significantly alters the conformation and dynamics of CaM’s binding sites.

Calmodulin (CaM) is the major calcium-sensing protein in eukaryotic cells (1–5). CaM has one of the mostly highly conserved sequences of any protein (6), shows remarkable conformational flexibility, and regulates hundreds of effectors (7). For example, most of the modulatory effects of Ca²⁺ on ion channel proteins are mediated by CaM (8, 9). It is essential to a variety of cellular functions, including cell growth, synaptic transmission, motor control, secretion, and differentiation, among others (3–5, 10–14). Due to its importance, stability, and small size (148 residues), CaM is commonly used as a model protein in studies of ion binding (3, 15).

Ca²⁺ Sensing and Coordination Geometry in CaM

Ca²⁺ binding in CaM exposes a core of buried hydrophobic surfaces through which CaM interacts and controls over 300 target proteins (16–22). CaM is highly sensitive to Ca²⁺ and modulates protein function differently in response to variations in the timing and amplitude of intracellular Ca²⁺ signals (3, 23). Rather than operating as a two-state on/off switch, CaM functions as an intricate molecular transducer that must transition through an ensemble of distinct but interrelated conformations to modulate a wide range of effector proteins. In such a finely balanced and sensitive system, even small structural perturbations at the ion binding sites may be amplified into global changes in conformation that alter target recognition and selectivity, or the efficacy of target activation by CaM. Since the signals encoded by CaM are highly time-dependent, conformational distortions that alter the dynamics of ion capture and release by CaM’s binding sites are particularly important.

CaM coordinates Ca²⁺ via four similar but unique EF-hand binding sites (Fig. 1), which are helix–loop–helix structural domains found in a large family of Ca²⁺-binding proteins (24, 25). The EF-hand sites in CaM coordinate Ca²⁺ in a pentagonal bipyramidal geometry. In all four binding sites, a coordinating water, a backbone amide C=O group, a bidentate glutamate carboxylate group, and two monodentate aspartate carboxylate groups occupy six of the binding positions. In two of the binding sites, the last position is occupied by a third monodentate aspartate carboxylate group. In the other two sites, the last position is occupied by an asparagine side-chain C=O.

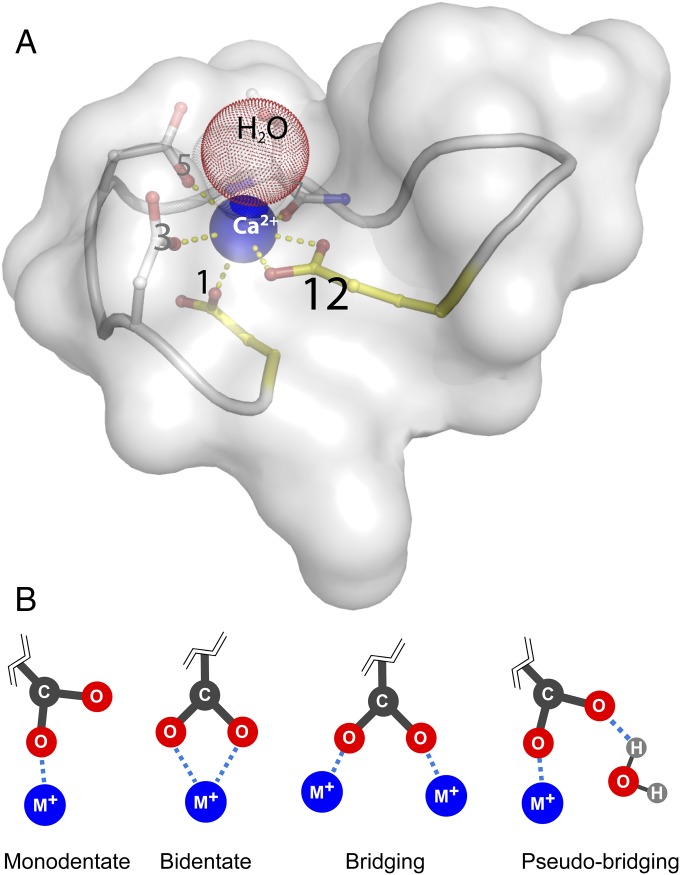
Fig. 1.

(A) Schematic of EF-hand binding sites showing the highly conserved aspartate residue at position 1 and the highly conserved glutamate residue at position 12. Bidentate coordination of Ca²⁺ by the glutamate residue at position 12 is unique among the EF-hands. Model was created from PDB ID 1CLL. A semitransparent surface of a single EF-loop is shown to illustrate that Ca²⁺ (blue sphere) sits in a crowded structure. Carbon atoms are white, nitrogen atoms are blue, and oxygen atoms are red. For simplification, only residue side chains that coordinate Ca²⁺ are represented as sticks, whereas the backbone is depicted as a ribbon. Key positions 1 and 12 are colored yellow. A water, small red sphere (H₂O), is often found immediately above the ion. The yellow dashes facilitate viewing the connections between the coordinating oxygens and Ca²⁺. CaM’s four binding sites are shown individually in detail in Fig. 2. (B) Ion coordination modes of carboxylate groups. (Left to Right) monodentate, bidentate, bridging, and pseudobridging.

Although the sequences of CaM’s four EF-hand binding sites differ from one another (Fig. 2), the aspartate and glutamate residues at positions 1 and 12 are present in all four binding sites and are highly conserved across species (6) and in other EF-hand proteins (26). The position 12 glutamate residue is of special interest since it alone coordinates ions in bidentate geometry (27, 28). All other coordination participants bind through one oxygen atom in monodentate or pseudobridging geometry (Figs. 1 and 2).

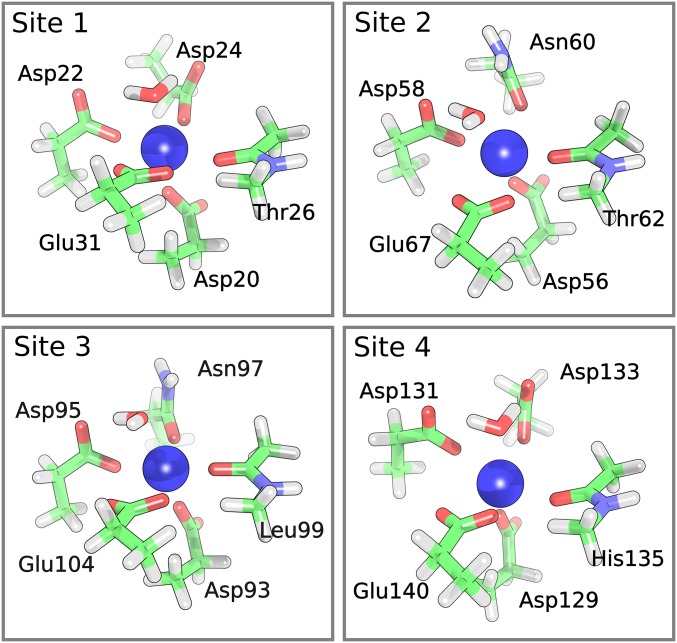
Fig. 2.

Pruned binding sites of Ca²⁺−CaM. Initial configurations were extracted from the crystal structure (PDB ID: 1CLM). Hydrogen atoms were geometry optimized using density functional theory (see Vibrational Assignments of Ca²⁺−CaM Binding Site Residues). Calculated residue frequencies are shown in Table S4.

Despite extensive investigations by many laboratories into Ca²⁺ sensing and signaling by CaM, quantitative understanding of the energetic and structural effects of metal ion binding on CaM function is incomplete. For example, recent work has shown that estimates of thermodynamic parameters for Ca²⁺ binding to CaM are neither accurate nor unique when constrained by fitting typical binding data, due to effective compensations between the parameters (29–32). In fact, the parameter uncertainties are so large that the published binding studies provide almost no information on site affinities or cooperative interactions in CaM. Similarly, the complete sequence of structural changes starting with Ca²⁺ binding to the EF hands and proceeding to CaM core exposure is not known (33–35).

Probing Ion-Dependent Binding Conformations with Infrared Spectroscopy

Carboxylate and amide carbonyl C=O stretching frequencies are highly sensitive to changes in their electrostatic and molecular environments and report structural perturbations with angstrom-level spatial sensitivity and subpicosecond temporal precision (36–38). Similarly, the C=O stretching vibrations of carbonyl groups arranged along the protein backbone, termed amide I vibrations, report on changes to global protein conformation. These vibrations can be probed with infrared spectroscopy to reveal small changes in the dynamics of CaM’s binding sites and global structure. For example, our measurements of EDTA spectroscopic shifts attending the coordination of different ions indicate that infrared spectroscopy can easily detect changes in metal ion coordination radius of less than 0.1 Å (Frequency Assignment of EDTA Spectral Features, Fig. S1, and Table S1), whereas NMR and X-ray crystal structures routinely report uncertainties more than 10 times greater (39, 40).

Infrared spectroscopy is thus an ideal method for study of both structural and dynamic aspects of CaM function. Fourier transform infrared (FTIR) spectroscopy has long been applied to questions of protein structure, in general (41, 42), and ion coordination by CaM and other proteins (43–47). However, FTIR spectroscopy lacks the time resolution necessary to probe dynamic biological processes such as ion sensing.

Ultrafast 2D infrared (2D IR) spectroscopy has helped map fast protein dynamics that have remained opaque to other experimental methods (48–61), and has recently been used to measure temperature-mediated changes in the secondary structure of apo-CaM and Ca²⁺−CaM (62). Our 2D IR spectrometer is described in detail in Two-Dimensional IR Spectrometer and Fig. S2, as are our methods for analyzing 2D IR data (Two-Dimensional IR Data Collection and Analysis and Fig. S3). The infrared analog of 2D NMR, 2D IR spectroscopy uses midinfrared laser pulses to measure a sample’s infrared absorption spectrum after it has been irradiated by a pair of excitation pulses. In this way, 2D IR spreads spectral information over two frequency axes and allows for interrogation of fast relaxation, energy exchange (61, 63–65), and conformational changes in proteins (66, 67). Additionally, 2D IR’s subpicosecond time resolution is sufficient to probe even the fastest structural rearrangements in biomolecules. Thus, 2D IR spectroscopy offers several advantages over conventional IR absorption spectroscopy, including greater time resolution, the ability to observe energy transfer between a molecule’s vibrational modes, and the capacity to resolve the orientation of molecular vibrations (68, 69).

Here, we use FTIR and 2D IR spectroscopy to study coordination of Ca²⁺ and three trivalent lanthanide ions (La³⁺, Tb³⁺, and Lu³⁺, collectively abbreviated as Ln³⁺) by CaM. Together, FTIR and 2D IR provide the subangstrom spatial resolution and subpicosecond temporal resolution necessary to probe subtle changes to binding and conformational dynamics. Ln³⁺ ions, particularly Tb³⁺ (70–77), are commonly used as luminescent substitutes for Ca²⁺, and bind to Ca²⁺ binding sites in proteins almost without exception (70). They serve as site-specific affinity probes, and as spectroscopic rulers to measure distances between binding sites (71). However, the fine distinctions between Ca²⁺- and Ln³⁺-occupied binding site structures, and possible differences in the global structure and activity of CaM bound by these metals, remain unresolved. While progress toward characterizing ion-dependent changes in binding site structure has been made using NMR spectroscopy (78, 79), work using these methods has been unable to characterize important structural details such as the mode of ion coordination by binding site carboxylate groups. Investigations of ion-dependent CaM activation show that even the minor structural changes induced by ion substitution can influence the behavior of CaM and its targets (80, 81). Our results indicate that the binding site structures of Ca²⁺- and Ln³⁺-bound CaM are distinct, suggesting that the mechanism of CaM activation by Ca²⁺ and Ln³⁺ ions may also differ.

Results

Experimental Strategy.

The overall objective of the research was to use FTIR and 2D IR spectroscopy to detect and characterize the perturbations to CaM binding site structure and dynamics, and to global CaM conformation, due to ion coordination. The Ln³⁺ ions (La³⁺, Tb³⁺, Lu³⁺) used in the study were selected for several reasons: (i) Ln³⁺ ions closely resemble the native Ca²⁺ ion in numerous physical and chemical properties, including chemical hardness, ionic radius, coordination number, and electrostatic coordination character (70); (ii) Ln³⁺ ions bind to and activate most of the Ca²⁺-binding proteins on which they have been tested (70); and (iii) the Ln³⁺ ions chosen span the width of the lanthanide series, sampling the maximum ionic radius range while holding ionic charge constant. As such, the (La³⁺, Tb³⁺, Lu³⁺) series allowed both controlled variation of ionic radius and comparison between native and nonphysiological ion binding. The perturbations effected by using different Ln³⁺ ions are subtler than the changes to ion binding sites that can be achieved using site-directed mutagenesis, which alters the chemical nature or the size and structure of amino acid side chains.

One of the challenges posed by interpreting spectra of CaM is the featureless and highly overlapped nature of protein infrared lineshapes, which arise from C=O vibrations inhabiting hundreds of slightly different environments (82). To aid the interpretation of CaM’s monodentate carboxylate features, we used EDTA as a simple model for spectroscopic interpretation. EDTA coordinates metal ions through four carboxylate groups, each of which assumes monodentate coordination geometry. Because of its small size and high symmetry (Fig. S1), EDTA has a simple infrared spectrum and is computationally tractable. We used electronic structure calculations of EDTA bound to the Ln³⁺ series and to a series of divalent metal cations (Sr²⁺, Ca²⁺, Mg²⁺) to interpret and assign spectral features in the carboxylate region of CaM spectra.

Infrared spectroscopy (both FTIR and 2D IR) of CaM’s carboxylate and carbonyl groups allows sensitive investigation of binding site structure and dynamics and overall protein conformation, since the C=O stretching vibration of both functional groups is highly sensitive to the local environment. Spectroscopic shifts of these vibrations can report on atomic displacements smaller than 0.1 Å and on processes occurring on timescales as short as 100 fs. The carboxylate and carbonyl absorptions are separate but proximal to one another along the infrared spectrum.

CaM contains 37 glutamate and aspartate residues, 14 of which participate in ion binding (Fig. S4). Since CaM’s ion binding sites contain a high proportion of glutamate and aspartate residues, absorptions in the carboxylate region (1,525 cm⁻¹ to 1,600 cm⁻¹) provide localized information about the binding sites and ion coordination (45, 83–85). Contribution of the nonbinding aspartate and glutamate residues to ion-dependent infrared features is minor because (i) the nonbinding carboxylate groups are highly solvent-exposed and (ii) the environment of these groups is not expected to change with ion binding. Therefore, infrared signatures of the nonbinding carboxylates will be both broad and invariant relative to binding site absorptions.

Since every residue contains a carbonyl group along the protein backbone, absorptions by the carbonyl groups occurring in the amide I region (1,600 cm⁻¹ to 1,680 cm⁻¹) provide information about CaM’s global structure (41, 63, 86–88). The combination of carboxylate and amide I infrared absorptions provides a critical link between the structure of the ion binding site and the global structural changes induced by ion binding in CaM.

FTIR Spectroscopy of EDTA.

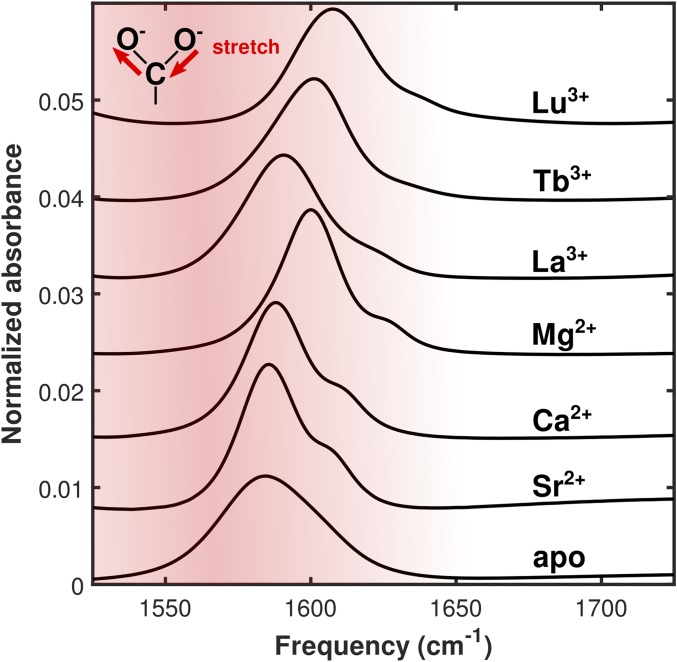
FTIR spectra show ion-dependent shifts in the position of EDTA’s carboxylate asymmetric stretching absorption (Fig. 3). The absorption is centered at 1,584 cm⁻¹ in the unbound molecule and blue-shifts (increases in frequency) with decreasing divalent cation radius to 1,586 cm⁻¹, 1,588 cm⁻¹, and 1,600 cm⁻¹ as EDTA is bound to Sr²⁺, Ca²⁺, and Mg²⁺, respectively. Similarly, the absorption blue-shifts with decreasing lanthanide ion radius to 1,592 cm⁻¹, 1,604 cm⁻¹, and 1,608 cm⁻¹ with binding to La³⁺, Tb³⁺, and Lu³⁺, respectively.

Fig. 3.

FTIR spectra of EDTA bound to the series of ions used in this study. The absorption assigned to the carboxylate asymmetric stretching mode blue-shifts as ionic radius is decreased and as ionic charge is increased.

FTIR Spectroscopy of CaM.

FTIR spectra show distinctions between apo, Ca²⁺-bound, and Ln³⁺-bound CaM (Fig. 4). The broad 1,575 cm⁻¹ side-chain absorption in the apo spectrum splits into a 1,580 cm⁻¹ peak with a strong shoulder at 1,553 cm⁻¹ upon Ca²⁺ binding. In the Ln³⁺ spectra, these features are broadened and blue-shifted. While intensity remains roughly constant at 1,570 cm⁻¹ across the Ln³⁺ series, absorption strengthens with decreasing ionic radius (La³⁺ → Tb³⁺ → Lu³⁺) in the region between 1,570 cm⁻¹ and 1,610 cm⁻¹, suggesting that absorptions in the side-chain region become blue-shifted (increased in frequency).

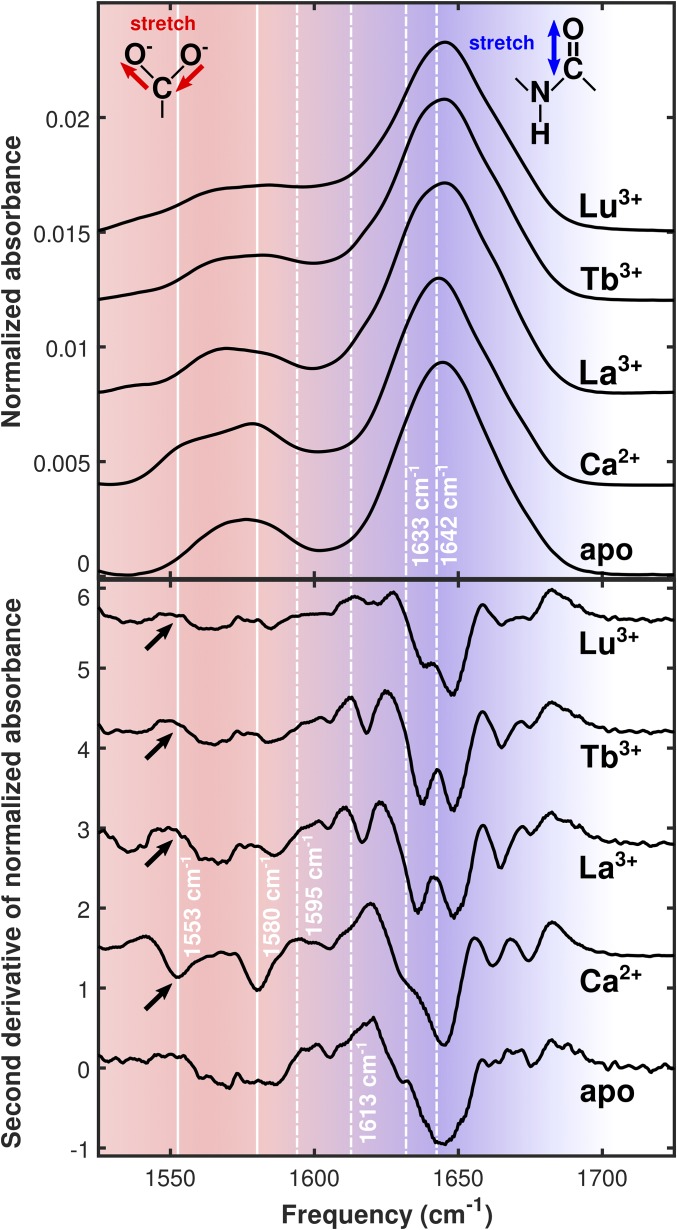
Fig. 4.

(Top) FTIR spectra of apo-CaM and CaM bound to the series of ions used in this study. (Bottom) Second derivative plots of the FTIR spectra. Solid white lines highlight peaks corresponding to different modes of carboxylate ion coordination in Ca²⁺−CaM. The bidentate glutamate peak is visible in the Ca²⁺-bound spectrum at 1,553 cm⁻¹, while the monodentate peak is visible at 1,580 cm⁻¹. Large, broad absorptions around 1,640 cm⁻¹ are amide I modes in the protein backbone. Dashed white lines drawn at 1,595 cm⁻¹, 1,613 cm⁻¹, 1,633 cm⁻¹, and 1,642 cm⁻¹ highlight 2D IR cross-peak locations. Black arrows indicate the expected locations of absorption features arising from carboxylate groups in the bidentate coordination configuration.

Second derivative FTIR spectra highlight several significant features of the data. The broad absorption between 1,550 cm⁻¹ and 1,600 cm⁻¹ in the apo spectrum sharpens to two distinct peaks at 1,553 cm⁻¹ and 1,580 cm⁻¹ in the Ca²⁺ spectrum (Fig. 4, solid lines). These peaks disappear and are replaced by two broader features centered around 1,564 cm⁻¹ and 1,585 cm⁻¹ in the Ln³⁺ spectra. Both the apo and Ca²⁺ samples show a strong, broad amide I absorption centered at 1,644 cm⁻¹ with a shoulder at 1,630 cm⁻¹. These features are replaced by two strong, broad absorptions centered around 1,637 cm⁻¹ and 1,648 cm⁻¹ in the Ln³⁺ spectra. A sharp absorption at 1,618 cm⁻¹, not present in the apo or Ca²⁺ spectra, is clearly visible in the La³⁺ and Tb³⁺ spectra. This feature appears strongly attenuated and symmetrically split in the Lu³⁺ spectrum. All samples show a sharp, weak absorption at 1,606 cm⁻¹ and a pair of absorptions between 1,660 cm⁻¹ and 1,680 cm⁻¹. This pair, present at 1,662 cm⁻¹ and 1,674 cm⁻¹ in the Ca²⁺ spectrum, is slightly blue-shifted to 1,665 cm⁻¹ and 1,675 cm⁻¹ in the Ln³⁺ spectra.

Two-Dimensional IR Spectroscopy.

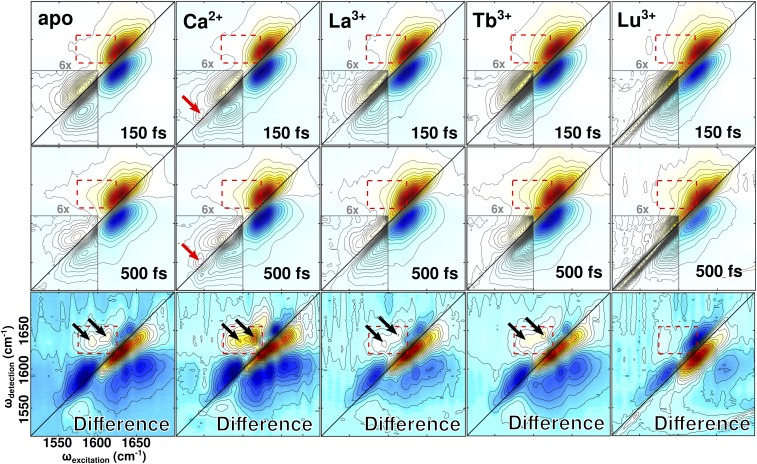
The 2D IR spectra of CaM (Fig. 5) provide a frequency-to-frequency correlation map of the protein’s molecular vibrations. A guide to 2D IR data analysis and interpretation is included in Two-Dimensional IR Data Collection and Analysis and Fig. S3. The apo and Ca²⁺ spectra show the amide I and side-chain absorptions to be centered around 1,640 cm⁻¹ and 1,580 cm⁻¹. As CaM is coordinated with Ln³⁺ ions of progressively smaller ionic radius, the side-chain absorption appears to blue-shift and gradually recede under the envelope of the amide I absorption.

Fig. 5.

The 2D IR spectra of apo-CaM, Ca²⁺−CaM, and Ln³⁺−CaM. Spectra were collected at t₂ delays of 150 fs and 500 fs. Difference spectra show the result of subtracting the 150-fs spectrum from the 500-fs spectrum. Spectra are each normalized to the strongest feature and displayed using 32 equally spaced contours. (Insets) Contouring in the carboxylate region further divides each original contour into six finer subcontours to highlight weak spectral features that are otherwise obscured. Regions where cross-peaks occur or are expected to occur are highlighted with red dashed boxes. The locations of the bidentate glutamate absorptions, present only in Ca²⁺−CaM, are marked with solid red arrows. The locations of observed cross-peaks are marked with solid black arrows. Some scatter is visible in the low-frequency region of the Lu³⁺−CaM spectra, but does not interfere with interpretation of the relevant spectral features.

Comparison of spectra taken at t₂ values of 150 fs and 500 fs show that side-chain vibrational excitations decay faster than do amide I excitations. The ratio of maximum carboxylate amplitude to maximum amide I amplitude at different t₂ values provides a measure of how quickly carboxylate vibrations in CaM’s binding sites decay relative to amide I vibrations in CaM’s backbone. By analyzing these ratios in combination with estimates of amide I vibrational relaxation extracted directly from pump-probe measurements (Calculation of CaM Binding Site Vibrational Relaxation and Fig. S5), we calculated decay constants for both the amide I and carboxylate vibrations (Table 1). Amide I vibrational excitation is longer lived than carboxylate excitation in all cases. Vibrational relaxation in the carboxylate region is slowest in Ca²⁺−CaM. A more detailed discussion of decay constant calculations is provided in Calculation of CaM Binding Site Vibrational Relaxation.

Table 1.

Ratio of carboxylate/amide I ground-state bleach signal amplitudes (arbitrary units) at different t₂ values and calculated time constants for the amide I and carboxylate vibrations

Sample	(SCOO−/SAmI) 150 fs	(SCOO−/SAmI) 500 fs	Ratio	τAmI, fs	τCOO−, fs
apo	0.17	0.069	0.41	590	230
Ca2+	0.15	0.095	0.63	670	360
La3+	0.19	0.079	0.42	670	250
Tb3+	0.25	0.13	0.52	670	300

S_COO− is the peak spectroscopic amplitude of the carboxylate ground-state bleach, normalized to the strongest feature in the 2D IR spectrum. S_AmI is the peak spectroscopic amplitude of the normalized amide I ground-state bleach. Ratio is the quotient of the amplitude ratios at 150 fs and 500 fs. Ratios were calculated using the maximum value for each peak at each t₂ delay; τ_AmI is the time constant for decay of the amide I vibration; τ_COO− is the time constant for decay of the carboxylate vibration. These metrics were not calculated for Lu³⁺-bound forms of the protein because the side-chain absorptions could not be separated from the amide I band in spectra of the Lu³⁺-bound samples. Additional parameters are available in Table S2.

Comparison of spectra taken at t₂ values of 150 fs and 500 fs also shows ion-dependent changes in carboxylate region lineshapes. Both apo-CAM and Ca²⁺−CaM spectra contain a distinct carboxylate peak centered around 1,580 cm⁻¹. This peak is elongated along the diagonal at 150 fs but shows time-dependent antidiagonal broadening, becoming rounder in the 500-fs spectrum. In spectra of Ln³⁺−CaM, separation of the carboxylate peak is less distinct and diagonal elongation of the carboxylate peak is more severe at both 150 fs and 500 fs. The Ln³⁺-carboxylate peaks show less time-dependent antidiagonal broadening than do their counterparts in the apo-CAM and Ca²⁺−CaM spectra.

Cross-peaks, which reflect vibrational energy transfer between oscillators that absorb at different frequencies, appear in the apo, Ca²⁺-, La³⁺-, and Tb³⁺-bound spectra and are visible in the (500 fs to 150 fs) difference spectra (Fig. 5, black arrows). While the same cross-peaks occur in each of these four spectra, they are most intense in the Ca²⁺−CaM spectra. Table 2 provides the frequencies and intensities of the cross-peaks. No cross-peaks were visible in the Lu³⁺-bound spectrum.

Table 2.

Cross-peak data from 2D IR spectra

Sample	ωexc,1	ωdet,1	I1	ωexc,2	ωdet,2	I2
apo	1,593	1,633	0.30	1,613	1,642	0.31
Ca2+	1,597	1,637	0.44	1,614	1,641	0.64
La3+	1,596	1,633	0.22	1,613	1,644	0.20
Tb3+	1,597	1,633	0.26	1,613	1,643	0.28

Each spectrum contains two cross-peaks, the lower-frequency of which is subscripted “1” and the higher-frequency of which is subscripted “2”. Parameters included for each pair of cross-peaks: I, the normalized peak intensity of the cross-peak relative to the strongest feature in the spectrum; ω_det, the detection frequency at which the peaks appear (cm⁻¹); ω_exc, the excitation frequency at which the cross-peak appears (cm⁻¹). No cross-peaks were visible in the Lu³⁺ spectrum.

Discussion

EDTA as a Model for Interpretation of Vibrational Modes in CaM’s Binding Sites.

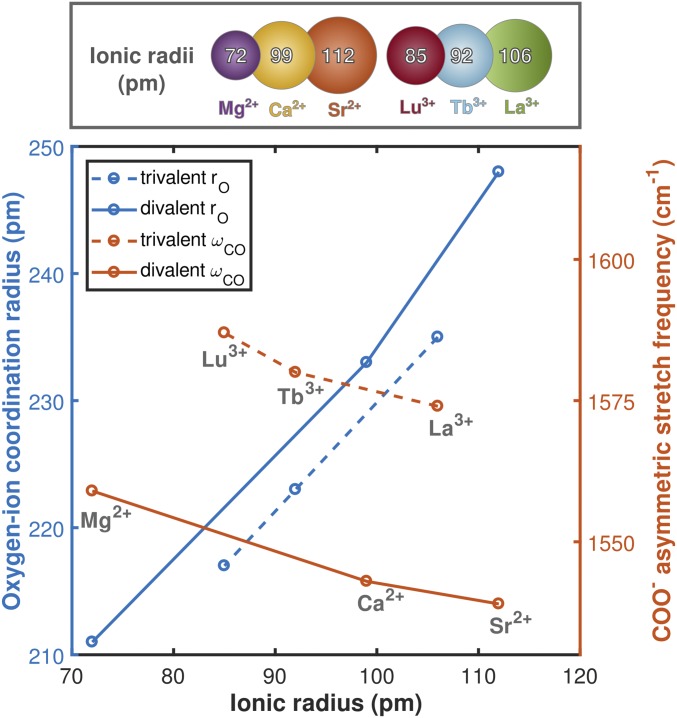
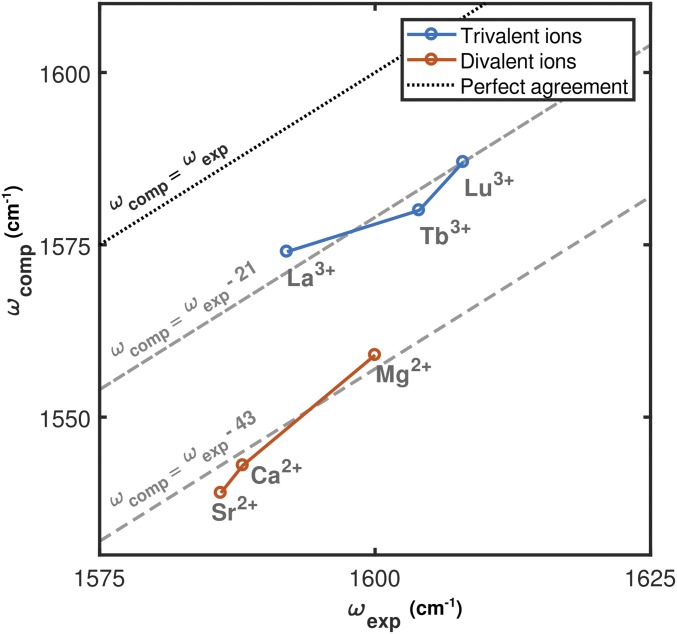
We used EDTA as a simple spectroscopic model for interpreting CaM frequencies and lineshapes. The experimentally observed spectroscopic shifts of monodentate carboxylate asymmetric stretching modes in EDTA (Fig. 3) agree with predictions derived from density functional theory (DFT) calculations (Fig. 6). Both experiment and simulation indicate that these modes blue-shift (increase in frequency) as ionic radius is decreased and ionic charge is increased. Comparison of computed EDTA asymmetric stretch frequencies with those measured spectroscopically indicates that the simulations accurately reproduce charge- and radius-dependent trends in the frequencies of the carboxylate asymmetric stretching modes (Fig. 7). These results suggest that coordination to Ln³⁺ ions results in more compact ion binding configurations in which coordinating oxygens are closer to the metal ion than in the Ca²⁺-bound case.

Fig. 6.

(Bottom) Carboxylate asymmetric stretching frequencies and oxygen ion coordination radii derived from DFT calculations of EDTA bound to a series of metal ions. Coordination radii increase, and carboxylate asymmetric stretching frequencies decrease, as a function of ionic radius. A comparison between experimental and calculated frequencies is provided in Fig. 7. (Top) The six-coordinate ionic radii of the species used are included for comparison. Ca²⁺ in the CaM binding site is seven-coordinate, but we use six-coordinate radii for comparison because seven-coordinate ionic radii have not been accurately measured for some of the ions used in this study.

Fig. 7.

Comparison of computed EDTA asymmetric stretch frequencies with those measured spectroscopically. The computational frequency is calculated as the average of the three lowest vibrational modes. These modes have similar intensities and frequencies (Table S1). Experimental frequencies are extracted from Gaussian fits to the FTIR spectra. Computational results capture the spectroscopic shifts associated with both decreasing ionic radius and increasing ionic charge.

Configuration-Dependent Behavior of Binding-Mediated Spectroscopic Shifts.

The manner in which a vibrational mode’s infrared absorption shifts due to ion binding is dependent on the binding configuration. The amide I modes of carbonyl groups, which can only bind in the monodentate configuration, are expected to red-shift (decrease in frequency) as ionic radius is decreased or ionic charge is increased (60). This can be considered a consequence of the positively charged ion withdrawing electron density from the C=O bond and thus decreasing the resonant frequency of the vibration. The asymmetric stretching modes of carboxylate groups bound in the bidentate configuration behave in the same manner (85, 89). Conversely, the asymmetric stretching modes of carboxylate groups bound in the monodentate configuration are expected to blue-shift (increase in frequency) as ionic radius is decreased or ionic charge is increased. This behavior is observed in both the experimental (Fig. 3) and computational (Fig. 6) investigations of EDTA included in the present work. We expect blue-shifting of the carboxylate asymmetric stretching mode to be accompanied by red-shifting of the carboxylate symmetric stretching mode, but do not analyze the latter in this work.

Vibrational Assignments and Binding Site Coordination Geometry.

Previous work has investigated ion binding in CaM and other proteins that coordinate metal cations using similar binding site architectures (25). These include studies of CaM itself (44, 86) and studies of CaM-like proteins in the EF-hand family such as troponin-C (47, 86) and parvalbumin (43, 46). Ion-coordinating carboxylates in proteins produce absorption features between 1,550 cm⁻¹ and 1,590 cm⁻¹ (25, 43, 44, 46, 90). More specifically, absorptions around 1,550 cm⁻¹ correspond to glutamate side chains in bidentate coordination geometry, whereas absorptions between 1,560 cm⁻¹ and 1,590 cm⁻¹ correspond to monodentate or pseudobridging carboxylates (25, 43, 44, 46, 90).

Based on the previous literature, we assign the 1,553 cm⁻¹ and 1,580 cm⁻¹ absorptions in the Ca²⁺−CaM FTIR spectrum (Fig. 4, solid lines) to bidentate and monodentate carboxylates, respectively (Fig. 1). The 1,553 cm⁻¹ feature is also clearly visible in the Ca²⁺−CaM 2D IR spectra (Fig. 5, red arrows). These assignments are supported by spectroscopic measurements (83, 91) and electronic structure calculations performed on model systems (45, 89), and by X-ray crystal structures of CaM (44, 92, 93).

As expected, the 1,553 cm⁻¹ absorption feature associated with bidentate carboxylate ion coordination in Ca²⁺−CaM is absent in the apo-CaM FTIR spectrum, where it is replaced by a single broad absorption spanning most of the 1,550 cm⁻¹ to 1,590-cm⁻¹ carboxylate window. In spectra of Ln³⁺−CaM, this feature is expected to red-shift (decrease in frequency) due to increased ion charge (89). While the Ln³⁺−CaM FTIR spectra do indeed include absorption features around 1,535 cm⁻¹, they are significantly broader and weaker than the 1,553 cm⁻¹ feature present in the CaM−Ca²⁺ spectrum. This effect is especially pronounced in the Tb³⁺ and Lu³⁺ spectra. Furthermore, any trace of the bidentate peak is absent from the Ln³⁺ 2D IR spectra (Fig. 5). Therefore, we conclude that bidentate carboxylate binding configurations are either absent from Ln³⁺−CaM or significantly more disordered in Ln³⁺−CaM than in Ca²⁺−CaM. Our study of EDTA provides a tentative explanation for Ln³⁺-induced disruption of bidentate ion coordination by the glutamate carboxylate group. Contraction of the binding site caused by Ln³⁺ coordination may place steric or electrostatic constraints on the carboxylate group that make bidentate coordination less favorable, forcing the side chain to reorient. Collapse of the binding site may also lead to greater structural disorder relative to the native configuration. This would explain why absorption features in Ln³⁺−CaM spectra are weaker and broader than their counterparts in Ca²⁺−CaM spectra.

The 1,580 cm⁻¹ monodentate peak in Ca²⁺−CaM is replaced by a single broad absorption spanning the 1,560 cm⁻¹ to 1,590-cm⁻¹ monodentate carboxylate window in the apo-CaM FTIR spectrum. In spectra of Ln³⁺−CaM, this peak is expected to blue-shift (increase in frequency) due to greater ion charge. This effect, opposite the shift expected for bidentate carboxylates, is predicted by DFT calculations that employ EDTA as a spectroscopic model (Fig. 6 and Table S1). The Ln³⁺−CaM spectra show two new features in the monodentate carboxylate region: one around 1,565 cm⁻¹ and another around 1,585 cm⁻¹. The 1,585 cm⁻¹ peak may be attributed to blue-shifting of the 1,580 cm⁻¹ feature present in the Ca²⁺−CaM spectrum (Fig. 4) in agreement with DFT predictions. We note that, unlike monodentate carboxylate absorptions in EDTA, the 1,585 cm⁻¹ Ln³⁺−CaM features do not exhibit significant ion-dependent spectral shifts. We tentatively assign this invariance to the larger size and greater structural heterogeneity of CaM’s binding sites, which may make individual oxygen ion radii less sensitive to small changes in the ionic radius of the bound ion. The 1,565 cm⁻¹ feature is more difficult to assign. It is both higher in frequency than the Ca²⁺−CaM bidentate peak at 1,553 cm⁻¹ (which should be red-shifted to lower frequency by Ln³⁺ binding) and lower in frequency than the Ca²⁺−CaM monodentate peak (which should be blue-shifted to higher frequency by Ln³⁺ binding). Thus, we tentatively assign this feature to either monodentate or pseudobridging carboxylate configurations that are unique to Ln³⁺−CaM.

The 1,565 cm⁻¹ and 1,585 cm⁻¹ Ln³⁺−CaM peaks are weaker and broader than the 1,580 cm⁻¹ feature in the Ca²⁺−CaM spectrum. They are strongest in the La³⁺−CaM spectrum and become progressively broader and weaker, while retaining their positions, in the Tb³⁺−CaM and Lu³⁺−CaM spectra. Keeping this and the above discussion in mind, we conclude that transitions between the three Ln³⁺−CaM species do not induce significant binding site reconfiguration, but subtly affect structural disorder in the binding site since the absorption features in the Ln³⁺−CaM spectra change in broadness and intensity but do not significantly shift.

Overall, the FTIR data support three conclusions: (i) Binding to Ln³⁺ ions eliminates or significantly destabilizes the bidentate ion coordination characteristic of the Ca²⁺-bound position 12 glutamate residue, (ii) binding to Ln³⁺ ions introduces monodentate and/or pseudobridging configurations among the binding sites’ carboxylate side chains that are more disordered than their Ca²⁺-bound counterparts, and (iii) ionic charge exerts a stronger influence on binding site configuration than does ionic radius.

Subpicosecond Relaxation and Energy Exchange in CaM’s Binding Sites.

Measurements of vibrational relaxation in all CaM samples show that the side-chain vibrational modes relax 20 to 40% more rapidly than do the backbone amide I modes. The rate of carboxylate relaxation is weakly dependent on the bound ion and is slowest in Ca²⁺−CaM. The faster relaxation rates observed in apo-CaM and Ln³⁺−CaM may be attributed, in part, to greater binding site disorder and structural flexibility than is present in Ca²⁺−CaM. Since the Ca²⁺−CaM binding sites sample fewer configurations than do their Ln³⁺-bound and apo counterparts, they less frequently inhabit structural states that efficiently couple and exchange energy into their surroundings.

Since CaM’s binding sites are ordered and each contain several carboxylate groups in close proximity, we considered the possibility that ion-dependent vibrational coupling could perturb the carboxylate asymmetric stretching modes used to probe the binding site environment. We used a simple transition dipole coupling model in combination with published structures of Ca²⁺−CaM and estimates of Ln³⁺-induced binding site contraction derived from our EDTA studies to calculate the likely extent of ion-dependent coupling in the binding site (Estimation of Carboxylate Vibrational Coupling in CaM’s Binding Sites). The calculations show that coupling is unlikely to significantly affect the vibrational modes we employ as probes.

The 2D IR spectra show time- and ion-dependent changes in carboxylate region lineshapes. These lineshapes provide a measure of static and dynamic structural disorder. Antidiagonal broadening gives rise to rounder peaks and reflects loss of correlation between excitation and detection frequencies. On subpicosecond timescales, this loss of correlation indicates rapid conformational interconversion characteristic of fast, local structural fluctuations or energy transfer within a single structure. The subpicosecond antidiagonal broadening present in the apo-CAM and Ca²⁺−CaM carboxylate spectra (Fig. 5, Insets) suggests the presence of one dominant binding site configuration.

In comparison with the apo-CAM and Ca²⁺−CaM results, 2D IR spectra of Ln³⁺−CaM show more severe diagonal broadening and less pronounced time-dependent antidiagonal broadening. The persistence of diagonal elongation reflects retention of correlation between excitation and detection frequencies. On subpicosecond timescales, this retention indicates the presence of multiple, distinct structures that do not undergo conformational interconversion or energy transfer within 500 fs. Thus, the persistence of diagonal elongation in the Ln³⁺−CaM carboxylate spectra (Fig. 5, Insets) indicates that Ln³⁺ binding causes CaM’s binding sites to splinter into multiple distinct configurations that do not readily interconvert. In view of vibrational relaxation results (Table 1), the manifold of configurations occupied by Ln³⁺−CaM binding sites is more efficient at coupling and exchanging energy with the surroundings than the well-defined configurations assumed by Ca²⁺−CaM binding sites.

The 2D IR difference spectra show the growth of two cross-peaks (Fig. 5, difference spectra, black arrows) from 150 fs to 500 fs as a result of energy transfer within the binding site. We used electronic structure calculations and frequency analysis of the binding sites (Vibrational Assignments of Ca²⁺−CaM Binding Site Residues) to assign the cross-peaks. In the first cross-peak, we assign excitation frequencies around 1,595 cm⁻¹ to monodentate carboxylates, and detection frequencies around 1,633 cm⁻¹ to backbone C=O groups present in the binding sites. In the second cross-peak, we assign excitation frequencies around 1,615 cm⁻¹ to asparagine side chains within the binding site and detection frequencies around 1,642 cm⁻¹ to backbone C=O groups in the binding sites (Table S4).

The cross-peaks are most intense in the Ca²⁺−CaM spectrum. They also appear in the apo-CaM, La³⁺−CaM, and Tb³⁺−CaM spectra at approximately the same locations as the Ca²⁺−CaM cross-peaks. Since cross-peaks reflect the degree of vibrational coupling and energy transfer between specific subsets of residues, they will be strongest when the interacting residues are in close proximity and have well-defined relative positions. The exceptional strength of the cross-peaks in Ca²⁺−CaM indicates that the binding sites are more compact and rigid in Ca²⁺−CaM than they are in apo-CaM or Ln³⁺−CaM. This finding agrees with the conclusions supported by the FTIR spectra.

Overall, the 2D IR data suggest that Ln³⁺-bound CaM experiences measurably greater structural disorder than does Ca²⁺−CaM. Distinctions in dynamic behavior are more nuanced. (i) Binding sites in apo-CaM and Ln³⁺−CaM exhibit less structural stability and more local disorder than do binding sites in Ca²⁺−CaM as reflected by faster rates of vibrational relaxation of features in the carboxylate region. (ii) Binding sites in apo-CaM and Ca²⁺−CaM occupy well-defined configurations whereas binding sites in Ln³⁺−CaM occupy a manifold of configurations as reflected by 2D IR lineshapes. (iii) Binding sites in apo-CaM and Ln³⁺−CaM are characterized by weaker intramolecular contacts and a smaller degree of structural rigidity than are Ca²⁺−CaM’s binding sites as reflected by cross-peaks in the 2D IR spectra. So stark is this distinction that both La³⁺−CaM and Tb³⁺−CaM more closely resemble apo-CaM than Ca²⁺−CaM from the perspective of the cross-peaks.

Conclusion

Ion binding of CaM to Ca²⁺ and to a series of Ln³⁺ ions was studied with IR spectroscopy and DFT calculations and modeled using experiments and simulations of ion binding in EDTA. The ion binding sites of CaM were found to be distorted, relative to binding with the protein’s native Ca²⁺ ion, by coordination with the lanthanides.

Experimental findings include the following: (i) Disappearance of the FTIR peak at 1,553 cm⁻¹ strongly suggests that bidentate ion binding present in Ca²⁺-bound CaM is absent or unmeasurably fleeting in Ln³⁺-bound forms. (ii) Appearance of new, broader, and higher-frequency side-chain FTIR peaks in Ln³⁺−CaM suggests new binding site configurations characterized by greater structural disorder and purely monodentate and/or pseudobridging metal coordination. (iii) Similarity of the Ln³⁺−CaM spectra indicates that ionic charge, not ionic radius, is the most important determinant of binding site configuration and structural stability. (iv) Interpretation of CaM FTIR spectra using EDTA suggests that coordination to Ln³⁺ ions causes binding site contraction. (v) Binding site vibrational relaxation in Ca²⁺−CaM and Ln³⁺−CaM indicates that Ln³⁺-bound binding sites exhibit shorter vibrational lifetimes due to greater structural flexibility and disorder. (vi) The 2D IR lineshapes indicate that binding of Ln³⁺ causes CaM’s binding sites to assume multiple configurations, whereas binding sites in Ca²⁺-CaM assume a single dominant conformation. (vii) The 2D IR cross-peak strengths indicate that the binding sites are more compact and rigid in Ca²⁺−CaM than in Ln³⁺−CaM.

Taken together, the experimental findings form a coherent picture of the structural and dynamic changes that attend CaM’s coordination to the lanthanides. CaM’s structure and kinetic behavior—notably including finely tuned rates of ion capture and release—are strongly conserved and specific to Ca²⁺. Upon lanthanide binding, this carefully tuned structure is distorted. Oxygen ion radii contract, and the compressed, more tightly bound geometries of the Ln³⁺-associated coordination sites either totally exclude bidentate coordination by the position 12 glutamate or cause it to become unstable. Similarly, the relatively stable and well-defined binding site structures anchored by Ca²⁺ coordination are disrupted in the presence of Ln³⁺ ions and splinter into multiple distinct configurations.

Since CaM structure and ion capture/release behavior is specific to Ca²⁺, the notion that CaM may be more disordered when binding Ln³⁺ than when binding Ca²⁺ is not necessarily at odds with studies that have shown CaM to have higher affinity for Tb³⁺ than for Ca²⁺ (75). The greater degree of order in Ca²⁺−CaM likely reflects structural optimization, tuned for functionally advantageous Ca²⁺ capture and release rates and conformational response to Ca²⁺, rather than energetic favorability. Similarly, the disruption of bidentate ion binding in Ln³⁺−CaM does not necessarily entail weaker binding in the coordination site. To the contrary, the greater number of geometric constraints imposed by bidentate coordination may mean that the opposite is true.

Thus, while Tb³⁺ may appear to fully activate CaM in experiments that do not test the protein’s full range of function, it is likely that the structural and dynamic disruptions attending Ln³⁺ binding inhibit or destroy aspects of CaM’s behavior that are important to conformational transduction of complex Ca²⁺ signals. This result may hold true for biophysical studies of other proteins that make use of nonnative ions, and demonstrates that the use of apparently innocuous substitutions may significantly perturb ion affinity, binding behavior, and activation.

Materials and Methods

FTIR and 2D IR spectroscopy were used to measure variations in vibrational frequencies and couplings in CaM bound to Ca²⁺ and to a series (La³⁺, Tb³⁺, Lu³⁺) of Ln³⁺ ions. Vibrational assignments were guided by ion-specific FTIR spectroscopy and DFT of the model ion-chelating compound EDTA.

CaM Preparation.

Recombinant, tagless CaM in the pET21a vector (Millipore Sigma) was expressed in BL21(DE3) cells (New England Biolabs). CaM was purified using established methods (94), but adding a final fractionation step off a preparative grade C18 column with an acetonitrile gradient for protein elution. Concentrated CaM solutions (2 mL) were dialyzed against a series of 1-L solutions for 8 h to 12 h each. The CaM was first dialyzed against two exchanges of 5 mM EDTA (>99%; Sigma-Aldrich) and 50 mM MOPS [3-(N-morpholino) propanesulfonic acid] (99%; Acros Organics) in 18-MΩ water at pH 7.4 to remove any calcium from the original solution. Next, it was dialyzed against two exchanges of 50 mM MOPS in ultrapure water at pH 7.4 to remove EDTA, whose absorption spectrum overlaps with the amide I and side-chain bands of interest to this study. Finally, it was dialyzed against two exchanges of ultrapure water.

The dialyzed CaM solution was flash frozen in LN₂ and lyophilized. The lyophilized product was deuterated by incubation in pure D₂O (99.9% isotopic purity; Cambridge Isotope Laboratories) at 50 °C for 2 h before being flash frozen and lyophilized again. The lyophilized, deuterated CaM was finally dissolved in a 50-mM solution of deuterated MOPS in D₂O adjusted to an uncorrected pH* of 6.3 with DCl (99 atom% D; Sigma-Aldrich) and NaOD (99 atom% D; Sigma-Aldrich). This pH was chosen because it was found to allow both CaM and lanthanide salts to dissolve. Lower pH values cause CaM to aggregate and precipitate, while higher values precipitate lanthanide hydroxides.

The CaM/MOPS solution was combined in equal proportion with solutions of anhydrous CaCl₂ (>97%; Sigma-Aldrich), LaCl₃ (99.9%; Alfa Aesar), TbCl₃ (99.9%; Alfa Aesar), and LuCl₃ (99.9%; Alfa Aesar) in 50 mM MOPS/D₂O to yield final samples of 1.1 mM in CaM, 5 mM in calcium or lanthanide ion to ensure saturation in all binding sites, and 50 mM in MOPS, in D₂O at an uncorrected pH reading of 6.3.

EDTA Preparation.

EDTA was used as received and prepared at 10 mg/mL concentration in D₂O at an uncorrected pH* reading of 11 to deprotonate the molecule’s carboxylate groups. Solutions equimolar in EDTA and the chloride salt of the given ion were used for FTIR measurements.

FTIR Spectroscopy.

FTIR measurements were taken using a Bruker Vertex 70 spectrometer with a deuterated triglycine sulfate detector at 2 cm⁻¹ resolution. The sample was held between two CaF₂ windows separated by a 50-μm Teflon spacer. The sample area was purged with dry (−100 °F dew point) air.

Two-Dimensional IR Spectroscopy.

The 2D IR measurements were taken using a custom-built 2D IR spectrometer as described in detail in Two-Dimensional IR Spectrometer and Fig. S2. In short, ∼100-fs midinfrared laser pulses probe the time-dependent IR absorption spectrum of the sample following excitation by a pair of pump pulses. Analogous to 2D NMR, 2D IR thus spreads the IR frequency information across two axes and allows for measurement of energy transfer and vibrational relaxation.

Computational Methods.

Detailed descriptions of carboxylate coupling estimation (Estimation of Carboxylate Vibrational Coupling in CaM’s Binding Sites), computational methods (Computational Methods), and assignment of EDTA spectral features are provided in Frequency Assignment of EDTA Spectral Features. Briefly, geometry optimization and vibrational assignment of EDTA bound to a series of ions were performed using DFT. Similarly, the vibrational frequencies of carboxylates and carbonyls in CaM’s four binding sites were examined using geometries extracted from the crystal structure (PDB ID: 1CLM).