Re-defining "learning" in statistical learning: what does an online measure reveal about the assimilation of visual regularities?

Abstract

From a theoretical perspective, most discussions of statistical learning (SL) have focused on the possible “statistical” properties which are the object of learning. Much less attention has been given to defining what “learning” is in the context of “statistical learning”. One major difficulty is that SL research has been monitoring participants’ performance in laboratory settings with a strikingly narrow set of tasks, where learning is typically assessed offline, through a set of 2-alternative-forced-choice questions, which follow a brief visual or auditory familiarization stream. Is that all there is to characterizing SL abilities? Here we adopt a novel perspective for investigating the processing of regularities in the visual modality. By tracking online performance in a self-paced SL paradigm, we focus on the trajectory of learning. In a set of three experiments we show that this paradigm provides a reliable and valid signature of SL performance, and offers important insights for understanding how statistical regularities are perceived and assimilated in the visual modality. This demonstrates the promise of integrating different operational measures to our theory of statistical learning.

In the last two decades, statistical learning (SL) has become a major theoretical construct in cognitive science. Since the seminal demonstration of Saffran and her colleagues (1996) that infants display remarkable sensitivity to transitional probabilities of syllabic segments, a large and constantly growing number of studies have focused on documenting the human ability of exploiting statistical cues to discover regularities in their environment (see Frost, Armstrong, Siegelman, & Christiansen, 2015, for a review). Following this work, SL has been commonly defined as the ability to extract the statistical properties of sensory input in time and space (e.g., Frost et al., 2015; Romberg & Saffran, 2010; Schapiro & Turk-Browne, 2015). Unsurprisingly, therefore, most experimental manipulations and theoretical discussions of SL have focused on the possible “statistical” properties which are the object of perception and assimilation (e.g., Fiser & Aslin, 2001; Newport & Aslin, 2004; Thiessen, Kronstein, & Hufnagle, 2013). Most studies have thus differed in the type of statistical contingencies embedded in their input, aiming to chart whether or not, or to what extent these contingencies affect human performance. Interestingly, much less attention has been given to defining what “learning” is in the context of “statistical learning”. The present paper aims to address this gap.

As in any exploration in the cognitive or psychological sciences, a critical step in theory development is the operationalization of the theoretical construct of interest. The goal of successful operationalization is to minimize the distance between the theoretical definition of a construct and its corresponding operational proxy. Ideally, the operational measure does not leave out critical aspects of the theoretical construct, but also does not extend to cover unrelated ones. This is important, because with time, the theoretical and operational definitions are typically taken to be the two sides of the same coin, and are often even used interchangeably. As we will argue, in the context of SL, narrowing the gap between the “Statistical Learning ability” and its operational definition is far from being trivial.

One major difficulty is that SL research has been monitoring participants’ performance in laboratory settings with a strikingly narrow set of tasks (see Armstrong, Frost, & Christiansen, 2017, for discussion). Typically, the to-be-learned regularities (i.e., co-occurrence of elements, their transitional probabilities, etc.) are embedded in a sensory input for a relatively brief familiarization phase, and their “learning” is assessed in a subsequent test phase (typically a series of two-alternative-forced-choice (2-AFC) questions). By this approach, there is evidence for learning if the mean performance of a sample of participants is significantly above chance. From an individual differences perspective, “good” statistical learners are those who obtain a high score in the test, and “bad” statistical learners are those who perform at chance or close to it. Here we ask: is this all there is to characterizing statistical learning ability? Note that this question is not confined just to characterizing “good” or “poor” individual learners. It permeates to understanding SL as an ongoing process of assimilating various types of statistical properties. For if two learning conditions result in similar score in the post-familiarization test-score, they are implicitly taken to be equal in terms of the complexity they impose on participants, with all resulting theoretical implication (e.g., Arciuli, von Koss Torkildsen, Stevens, & Simpson, 2014). In contrast, if they result in different test scores, the magnitude of the test-score difference is taken to represent the difference in complexity between condition possibly suggesting different mechanisms (e.g., Bogaerts, Siegelman, & Frost, 2016). Are these implicit assumptions necessarily true?

The main aim of the present research is to expand the theoretical scope of “learning” in SL, by exploring other operational definitions for it. We start by reviewing the commonly used two-alternative-forced-choice (2-AFC) task as a proxy for SL, highlighting both its merits and shortcomings in terms of the theoretical coverage it offers. We then consider alternative operational measures of learning discussing their possible contribution to SL theory. Subsequently, we employ novel measures to investigate the processing of regularities in the visual modality. We show that critical insight for understanding visual SL can be gained once novel “learning” perspectives are integrated into our theory of assimilating statistical regularities. Specifically, our investigation focuses on one important aspect in SL behavior – the trajectory of learning – which was mostly overlooked due to the commonly used SL tasks.

Insights from observing offline test performance

Most SL studies have been using the same experimental procedure that was originally employed by Saffran and her colleagues¹. The typical SL task comprises two parts: First, a familiarization phase, in which participants are exposed to a stream of stimuli in the auditory or visual modality. Unbeknownst to participants the stream consists of several repeated patterns (typically, pairs or triplets of syllables or shapes), which co-occur frequently, so that the first elements in the patterns reliably predict the other elements. The patterns appear for a pre-defined number of repetitions (a parameter that varies widely between studies, from 12 repetitions of each pattern, e.g., Sell & Kaschak, 2009, to as many as 300 repetitions, Saffran, Newport, Aslin, Tunick, & Barrueco, 1997). Importantly, during familiarization, participants are typically asked to just passively attend to the sensory stream (e.g., Saffran, Johnson, Aslin, & Newport, 1999), or they perform an unrelated cover task (e.g., Arciuli & Simpson, 2012), so that no information regarding the actual learning of the statistical properties is collected during the familiarization phase itself.

At a second step, a test phase begins. Participants’ sensitivity to the statistical properties of the stream is assessed, typically via a 2-AFC recognition test. In each trial, a configuration of stimuli that appeared together in the familiarization phase (i.e., a pattern with high TPs between elements) is paired with a ‘foil’ – a configuration of stimuli that either did not appear together at all during familiarization (i.e., TPs=0), or that co-occurred less frequently than the target (i.e., a foil of relatively low TPs). Participants are required to decide which pattern of stimuli they are more familiar with, and a score based on the number of correct identifications of targets upon foils, is taken to reflect their SL ability.

In the following we label this common measure of SL an offline measure. We define offline measures as proxies of learning performance which do not tap participants’ accumulated knowledge throughout the presumed learning process itself (i.e., the familiarization phase, in which participants actually pick up the statistical properties of the stream), but monitor it in a later stage, once the learning process itself is already over (see also, e.g., Batterink & Paller, 2017; Franco, Gaillard, Cleeremans, & Destrebecqz, 2015). Note that the 2-AFC procedure described above constitutes but one example of possible offline measures. Other offline measures focus on familiarity ratings (e.g., Jonaitis & Saffran, 2009), or on speed of identification of targets vs. foils (e.g., Barakat, Seitz, & Shams, 2013; Bertels, Franco, & Destrebecqz, 2012), but they all assess performance once learning is over.

The reliance on offline measures, and specifically on the common 2-AFC tasks, reflects a common goal of most SL research: to demonstrate that humans can detect and extract statistical regularities embedded in a range of sensory inputs, whether in the auditory (Endress & Mehler, 2009), or visual (Kirkham, Slemmer, & Johnson, 2002) modality, over verbal (Pelucchi, Hay, & Saffran, 2009) or nonverbal (Gebhart, Newport, & Aslin, 2009) material, across time or space (Fiser & Aslin, 2002), and when contingencies are either adjacent or non-adjacent (Gómez, 2002; Newport & Aslin, 2004). For that purpose, offline measures such as the number of 2-AFC correct responses are in fact apt. If a sampled group of participants scores significantly above the 50% chance-level on a series of 2-AFC trials, then the population from which the group has been sampled is taken to possess the ability to extract, at least to some extent, the relevant statistical properties embedded in the input. In other words, such offline measures are useful for assessing whether learning has occurred or not in a given sample under certain experimental conditions, and if learning has indeed occurred, offline measures can also quantify the overall extent of learning for the sample (i.e. how much better than chance performance was). Previous research has indeed successfully used offline measures to compare the extent of SL between different populations (e.g., dyslexics vs. controls, Gabay, Thiessen, & Holt, 2015, children in different age groups, Arciuli & Simpson, 2011, etc.), and between different learning conditions (e.g., incidental vs. intentional learning conditions, Arciuli, von Koss Torkildsen, Stevens, & Simpson, 2014, under different presentation parameters, Emberson, Conway, & Christiansen, 2011, etc.).

From a theoretical perspective, however, this form of operationalization is not optimal. First and foremost, its coverage of the full scope of “learning” as a theoretical construct is relatively thin. It only assesses the extent of behavioral changes at a single, arbitrary pre-defined time point following exposure to the input. SL, in contrast, is taken to be a process of continuously assimilating the regularities in the environment, where behavior changes incrementally over time. Second, offline measures inevitably extend to cover cognitive processes unrelated to SL. Because in the testing phase participants are required to explicitly recall and decide which patterns have occurred during familiarization and which have not, offline measures cannot disentangle SL abilities per-se from encoding and memory capacities, and decision-making biases. To complicate things further, the 2-AFC testing procedure often involves methodological confounds related to the recurrent repetitions of targets and foils during the test phase (see Siegelman, Bogaerts, Christiansen, & Frost, 2017, for an extended discussion). Note that these problems are particularly relevant to the recent interest in individual-differences in SL as predictors of linguistic functions (e.g., Arciuli & Simpson, 2012; Conway, Bauernschmidt, Huang, & Pisoni, 2010; Frost, Siegelman, Narkiss, & Afek, 2013), and as a window on SL mechanisms (Frost et al., 2015; Siegelman & Frost, 2015). Since learning is a continuous process, a comprehensive characterization of it for individuals as well as for specific populations, involves the manner by which it dynamically unfolds. Offline measures are by definition blind to this.

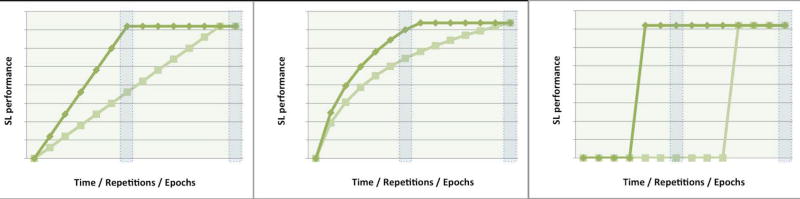
As a simple demonstration, Fig. 1 shows how a similar offline learning score can result from very different learning trajectories, which diverge in the shape of the function (linear, logarithmic, or a step-function), as well as in the speed of learning. From a theoretical perspective, knowing what statistical information is picked-up at a given point in time point and at what rate is an important step towards a mechanistic understanding of SL. In a nutshell, we view the learning dynamics as an integral part of the definition of SL as a theoretical construct. Thus, if similar offline performance following familiarization is consistently achieved through different learning trajectories, then this must tell us something important about the mechanisms of learning statistical regularities (see also Adini, Bonneh, Komm, Deutsch, & Israeli, 2015, for discussion in the context of procedural learning). In the same vein, if two populations with similar success rate in an offline task have different learning trajectories building up to this overall performance, then these two populations should not be considered as having identical SL abilities. Importantly, this holds not only for group-level research, but also for the study of individual differences. Individuals may differ from one another not only in their overall learning magnitude, but also in their speed of learning--- fast vs. slow learners, and these two operational measures may have distinct predictive power (Siegelman et al., 2017).

Figure 1.

A schematic depiction of different theoretically possible learning trajectories (from left to right: linear, logarithmic, step-function), all resulting in the same end performance. Light green lines represent a fast learning trajectory, dark green lines a slower one. Note that if one were to measure learning performance halfway, the offline learning score would be quite different depending of the shape of the function and the speed of learning.

Here we suggest to move from offline measuring of overall extent of learning to the online tracking of the learning process. The distinction between these measures reflects a different theoretical perspective: whereas current offline measures provide information regarding the representations of repeated patterns established after vast familiarization, online measures speak directly to how these representations are formed during learning, offering insight regarding the mechanisms of prediction which operate during the learning process. In general, SL research has provided little answer to questions such as how the continuous gradual learning of regularities results in the formation, updating and integration of representations in memory, and how such updating leads to predictions. Online measures have the promise to speak to these important questions directly.

Importantly, offering a novel operationalization to learning implicates not just theoretical considerations but also methodological ones. If the dynamic of learning is argued to be an essential part of our learning theory, one has to show first that its operational measures are reasonably reliable, and adequately valid. For if not, they cannot serve as proxy of SL. The present paper does exactly that. In Experiment 1, we consider an online measure that tracks the dynamics of learning regularities in the visual modality. We then explicitly test its reliability and validity. These findings serve as a springboard for putting to the test our main theoretical claim, that such online measures reveal invaluable information about the mechanisms of learning visual regularities which the typical offline measures are blind to. In Experiment 2 we focused on the extent of predictability in the stream and how different TPs impact learning. In Experiment 3 we targeted learning of more complex situations, where two streams of regularities are consecutively presented within a single experiment. Together, our findings reveal novel insights on how regularities in a visual input are perceived and learned.

Experiment 1

As noted above, we define online measures of performance as measures that assess performance throughout the learning process. They typically tap participants’ responses to a large number of stimuli throughout familiarization. The behavioral measure which is the focus of the present investigation considers the difference in RTs between stimuli given their predictability. According to SL theory, predictable elements should result in faster responses compared with unpredictable stimuli. This effect has been well documented in related paradigms in the field of implicit learning (such as the Serial Reaction Time task, SRT, e.g., Cleeremans & McClelland, 1991; Schvaneveldt & Gomez, 1998, or Contextual Cueing, e.g., Chun & Jiang, 1998).

Some recent studies have applied this simple experimental strategy to the domain of SL. For example, Misyak and colleagues employed an Artificial Grammar Learning (AGL) task in which participants heard sequences comprised of nonwords, and were simultaneously asked to click on corresponding written nonwords presented on the screen. RTs recorded for these mouse clicks showed that nonwords in predictable locations within sequences were recognized faster than nonwords in non-predictable locations (Misyak, Christiansen, & Tomblin, 2010b). In the same vein, Gomez and colleagues (2011) used a click-detection task, in which clicks were super-imposed on a speech stream comprising of tri-syllabic words. As learning proceeded, clicks in word boundaries were recognized faster than clicks within-words, and importantly, the RT difference between the two conditions increased throughout the familiarization phase (Gómez, Bion, & Mehler, 2011). Another recent example of an online measure is a self-paced Artificial Grammar Learning task (Karuza, Farmer, Fine, Smith, & Jaeger, 2014). Much like in the classic self-paced reading paradigm (Just, Carpenter, & Woolley, 1982), participants were asked to advance the elements in the sequences during familiarization at their own pace, by pressing the spacebar each time to advance to the next element in the stream. As predicted, presses for predictable stimuli were faster than those for unpredictable stimuli, with an increase in this RT difference over the course of familiarization (see also Amato & MacDonald, 2010 for a related self-paced reading paradigm in an Artificial Language Learning study). Another online measure of SL was offered by Dale and his colleagues in a paradigm similar to a SRT task, which continuously registered the mouse coordinates, measuring the extent to which participants anticipate the next stimulus in the sequence. Again, when stimuli in the stream were more predictable, participants tended to move the mouse in the direction of the stimulus already before it appeared, and this anticipatory behavior increased over the course of familiarization (Dale, Duran, & Morehead, 2012).

These findings raise a set of important methodological and theoretical questions. First, as we outlined above, an operational variable that is offered as proxy for a theoretical construct, should be proven to be 1) reliable – i.e., providing a stable and consistent measurement, and 2) valid – i.e., corresponds to the actual theoretical construct it presumably taps. Applying these criteria to the study of SL, a first critical question is whether the gain in RTs for predictable stimuli in the familiarization phase is a stable and reliable signature of each individual. The question of validity is somehow more complex. Theoretically, the online gain in RTs for predictable (vs. unpredictable stimuli) as learning proceeds seems evident. However, whether this speeding of response indeed reflects stable learning is an open question. Interestingly, there is little empirical evidence that the reported speeding to predictable stimuli indeed correlates with SL performance measured subsequent to familiarization. In fact, some recent studies have shown that the obtained RTs differences do not correlate with the standard offline measures (Franco, Gaillard, Cleeremans, & Destrebecqz, 2015; Misyak et al., 2010b; but see Dale et al., 2012; Karuza et al., 2014). These reports lead to a problematic state of affairs where the current online measures of SL remain invalidated, requiring additional scrutiny. Possibly, this lack of correlation is theoretically interesting showing that online and offline measures perhaps tap different sub-components of SL (see Misyak, Christiansen, & Tomblin, 2010a). Alternatively, it could be due to some peripheral methodological factors. First, gains in RTs are not independent of the overall speed of response. Fast responders would show then smaller gains regardless of their SL abilities. Second, it is possible that the mere presence of a secondary task employed during familiarization hinders learning due to its taxation on attentional resources (see Franco et al., 2014 for such direct evidence in the click detection SL task). This again poses a serious challenge for assessing the theoretical contribution of online measures. Impaired performance may hurt both the task’s reliability (Siegelman, Bogaerts, & Frost, 2016) and its validity (the online task perhaps measures SL, but may confound it with the ability to successfully divide attention between the primary and secondary tasks, Franco et al., 2014).

The goal of Experiment 1 was to address these challenges. First, we aimed to offer an online measure that tracks the dynamics of SL and provides information about the trajectory of learning in terms of time-course. Second, we endeavored to examine whether such measure withstands the psychometric requirement of test-retest reliability, so that it can be taken as a stable signature of the individual. Third, we sought to provide evidence for its validity in assessing SL ability.

We chose to focus on visual SL, where participants are expected to learn the transitional probabilities of visual shapes. Following a recent work by Karuza and her colleagues (Karuza et al., 2014), instead of asking participants to passively watch the stream of shapes, we asked them to actively advance the shapes in their own pace. In Experiment 1a we show that this simple procedure results in an online SL measure where RTs in advancing predictable shapes are faster than RTs in advancing non-predictable ones as learning proceeds. More importantly, in Experiment 1b, we show that this RT gain is a reliable signature of an individual. Experiments 1a and 1b also provide critical information regarding the validity of the measure (its correlation with the well-established offline learning score), and novel insight regarding the time course of learning in the group level.

Experiment 1a

Experiments 1a and 1b employed the typical design of visual SL experiments, where shapes are presented sequentially, and follow each other given a pre-determined set of transitional probabilities (e.g., Kirkham et al., 2002; Turk-Browne, Junge, & Scholl, 2005; Siegelman & Frost, 2015). This experimental paradigm has been used and validated extensively, and our main modification was to set the presentation of shapes to be participant determined, rather than at a fixed rate. On the group level this provided us with reliable information when learning occurs during the experimental session. On the individual level, it provided for each participant a new measure of learning that reflected his/her sensitivity to the statistical regularities embedded in the input stream.

Method

Participants

Seventy students of the Hebrew University (17 males) participated in the study for payment or for course credit. Participants had a mean age of 22.96 (range: 18–32), and had no reported history of reading disabilities, ADD or ADHD.

Design, Materials, and Procedure

Similar to a typical SL paradigm, our task consisted of a familiarization phase, followed by a test phase. The latent structure of the visual input stream presented during familiarization was also similar to that of multiple previously employed SL tasks (e.g., Frost, Siegelman, Narkiss, & Afek, 2013; Glicksohn & Cohen, 2013; Turk-Browne, Junge, & Scholl, 2005): the task included 24 complex visual shapes (see Appendix A), which were randomly organized for each participant to create eight triplets, with a TP of 1 between shapes within triplets. The familiarization stream consisted of 24 blocks, with all eight triplets appearing once (in a random order) in each block. Before familiarization, participants were told that they would be shown a sequence of shapes, appearing on the screen one after the other. Participants were instructed that some of the shapes tend to follow each other and that their task is to try to notice these co-occurrences². Importantly, in contrast to standard SL tasks, participants did not have to watch the stimuli appearing in a fixed presentation rate but were asked to advance the stream of shapes at the own pace, by pressing the space bar each time they wanted to advance to the next shape. There was no Inter Stimulus Interval (ISI) between shapes in familiarization. RTs for each press were recorded and served as the basis for the online measure of learning (see below).

Following familiarization, participants took a 2-AFC offline test, consisting of 32 trials. In each trial, participants were sequentially presented with two three-item sequences of shapes: (1) a target – three shapes that formed a triplet during the familiarization phase (TP=1), and (2) a "foil" – three shapes that never appeared together in the familiarization phase (TP=0). Foils were constructed without violating the position of the shapes within the original triplets (e.g., for the three triplets ABC, DEF and GHI, a possible foil could be AEI, but not BID). During test, shapes appeared in a fixed presentation rate of 800ms, with an ISI of 200ms between shapes within triplets, and a blank of 1000ms between triplets. Each of the eight familiarization triplets (i.e., targets) appeared four times throughout the test, with four different foils (each foil also appearing four times throughout the test, with different triplets). Before the test phase, participants were instructed that in each trial they would see two groups of shapes and that their task would be to choose the group that they are more familiar with as a whole. The offline test score ranged from 0 to 32, according to the number of correct identifications of targets over foils. Given the 2-AFC format, chance performance corresponds to a score of 16/32.

Results and Discussion

For each participant, RTs outside the range of 2 SD from the participant’s mean were trimmed to the cutoff value to minimize the effect of outliers (3.6% of all trials). Note also that, to account for variance in baseline RTs, all analyses were conducted on log-transformed RTs (rather than raw RTs). The use of a log-scale allows us to compare SL performance across individuals with different RT baselines. This is important because in the self-paced paradigm participants determine their own speed of advancing the stream of shapes. Consider, for example, two individuals (S1 and S2) with a mean difference of 100ms between predictable and unpredictable elements, but with a different baseline RT: S1 predictable = 900ms, unpredictable = 1000ms; S2 predictable = 300ms, unpredictable = 400ms. Without log-transformation, these two individuals will have a similar difference score (of 100ms), which is problematic as the relative speed-up of S2 to predictable stimuli is much larger than that of S1. In contrast, after log-transformation, the difference between predictable and unpredictable stimuli is indeed larger for S2 compared to S1: log difference of S1 = 0.11, S2 = 0.29.

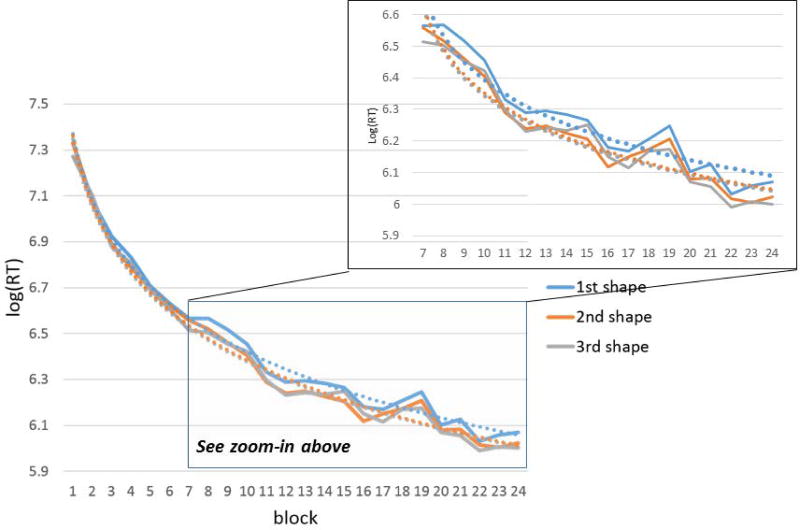
Table 1 presents the mean RTs and standard deviations of key presses for shapes in the first, second, and third positions within triplets. A one-way repeated measures ANOVA confirmed the effect of position on log-transformed RTs (F(2, 138) = 18.79, p < 0.001). Subsequent paired t-tests revealed a difference between shapes in the first versus second position within-triplets (t(69) = 4.32, p < 0.001) and between shapes in first versus third position (t(69) = 4.84, p < 0.001), but provided no evidence for a difference between shapes in second and third position (t(69) = 1.53, p = 0.13). Fig. 2 presents the response latencies for shapes in the first, second and third positions over familiarization blocks, and shows the divergence between shapes in first position, to those appearing in second and third positions.

Table 1.

Means and SDs for RTs and log-transformed RTs for shapes in first, second, and third positions.

	1st position	2nd position	3rd position
Raw RT (SD)	834.5 (377)	798.8 (340)	790.6 (339)
Log-transformed RT (SD)	6.43 (0.44)	6.39 (0.42)	6.38 (0.42)

Figure 2.

Response latencies to shapes in first, second, and third position over familiarization blocks. Dashed lines represent the best logarithmic fit. Zoom-in area presents blocks 7–24.

In light of these results, we next calculated the online measure of SL performance. This measure, formulated in (1) below, quantifies learning as the difference in log-transformed RTs between shapes in the unpredictable position (the first position within triplets) to the mean RTs for predictable shapes (in the second and third positions within triplets). A score of zero in this online measure reflects no learning of the statistical properties of the input (i.e., no difference between predictable and unpredictable stimuli), whereas positive values reflect learning (i.e., faster responses to predictable compared to unpredictable stimuli).

$$\mathit{\text{Online Measure of SL}}=\mathit{\text{log}}.\mathit{\text{RT}}(1\mathit{\text{st position}})-\mathit{\text{mean}}.\mathit{\text{log}}.\mathit{\text{RT}}(2\mathit{\text{nd}}\&3\mathit{\text{rd position}})$$ (1)

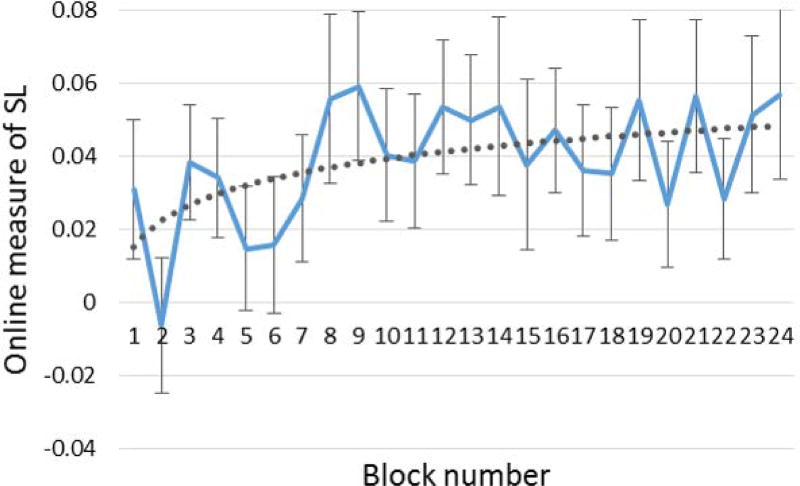
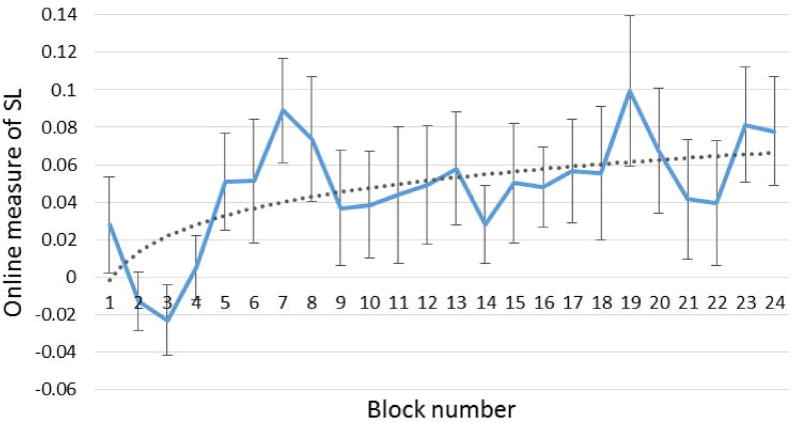
Fig. 3 shows the time-course of SL during familiarization, as reflected by the change in the online measure across the 24 blocks in the familiarization stream. Overall, the trajectory of the online measure seems to be well fitted by a logarithmic function – with relatively fast increase in SL until block 7 (i.e., after 7 repetitions), a point from which learning does not increase, with only random fluctuations around a fixed value. Indeed, a logarithmic curve better fitted the data compared to a linear function (R² = 0.29 vs. R² = 0.23)³. Relatedly, one-sample t-tests revealed that participants learned the underlying statistical structure of the input already relatively early in the familiarization – there was significantly larger than zero mean RT difference in all blocks from block 7 until the end of familiarization, showing robust and stable learning of patterns already after 7 repetitions. In addition, there were some earlier signs of learning, reflected by significant mean RT difference already in blocks 3 and 4 (all p_one-tailed’s < 0.05)⁴.

Figure 3.

Learning trajectory as reflected by the change in the online measure throughout familiarization blocks. Error bars represent standard errors. The dashed line represents the best logarithmic fit.

Validation

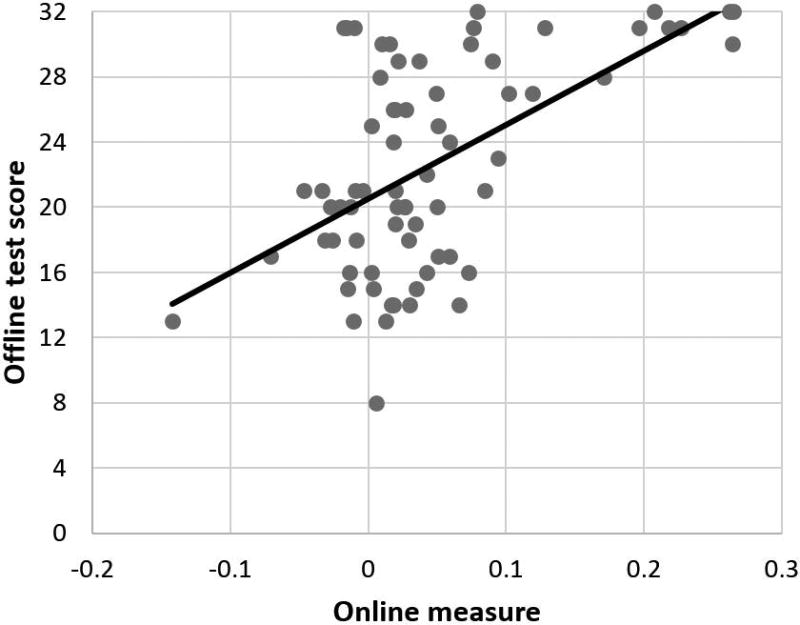
In order to validate the novel online measure of SL we examined its correlation with the standard 2-AFC offline test score (which presented above-chance mean performance of 22.57/32 (70.5%) trials, t(69) = 8.59, p_one-tailed < 0.001). For each individual, we calculated the overall extent of SL based on the online measure, by averaging the difference in log-transformed RTs between predictable and unpredictable shapes (formula (1) above) in blocks 7 to 24. We chose to focus on these blocks as these were the blocks in which stable significant learning was observed for the group as a whole, and since these included a large enough number of blocks to reduce measurement error. A strong correlation of r = 0.56 (p < 0.001, 95% CI: [0.37, 0.7]) was found between the individual gain in RTs for predictable shapes and his/her offline test performance (see Fig. 4)⁵. This result suggests that the online measure we proposed indeed taps into SL ability, validating it. Participants who score higher in the offline test are, on the average, faster with predictable vs. unpredictable stimuli.

Figure 4.

Scatter plot of the correlation between the online measure of SL and performance in the 2-AFC offline test. This correlation might seem to be over-estimated due to a few extreme observations (3 on top right corner, 2 on bottom left). However, it remains strong even when removing these data points: r = 0.46, p < 0.001.

Taken together, the results of Experiment 1a reveal the promise of an online measure in investigating visual SL. By merely asking participants to advance the shapes at their own pace rather than watching the visual input stream passively, we obtained novel information regarding the dynamics of learning. We found that learning was well fitted by a logarithmic fashion, and that significant learning of structure is present already after a small number of exposures to the repeated patterns. At least within our experimental parameters (eight triplets, TPs of 1.0) and dependent measure (log transformed RT gain), the data suggest that seven or eight repetitions of the triplets are sufficient to reach significant learning. Experiment 1a also showed that for a given individual, the gain in RT to predictable vs. unpredictable shapes is highly correlated with his/her standard (2-AFC) offline measure of performance. This demonstrates that the online measure is indeed a valid proxy of SL. What remains to be shown, however, is that the gain in RTs for predictable stimuli withstands the psychometric requirement of reliability, providing a signature of individual SL performance that is stable over time. Experiment 1b was set, therefore, to assess the test-retest reliability of this online measure.

Experiment 1b

In Experiment 1b we recalled our original sample, and retested participants with the same task, using different triplets. Again, we measured their individual gain in response time to predictable vs. unpredictable shapes, aiming to correlate their RT gain in the two experimental sessions.

Method

All subjects of Experiment 1a were contacted after their participation and were invited to return to the lab for a follow-up study in return for course credit or payment. Forty-seven participants (11 males; mean age 23.1, range: 18–32) replied positively, and were re-tested on the self-paced visual SL task. The task was identical to the one described in Experiment 1a. Note that while the stimuli used in Experiment 1b were the same as those in Experiment 1a, the triplets during familiarization were re-randomized for each participant so that the repeated patterns were not the same in the initial test and retest. The mean interval between the initial testing session (Experiment 1a) and retest (Experiment 1b) was 90.8 days (SD = 54 days).

Results

As in Experiment 1a, RTs outside the range of 2 SD from each participant’s mean were trimmed to the cutoff value to minimize the effect of outliers (3.7% of all trials). Table 2 presents the means and standard deviations of RTs and log-transformed RTs for shapes in first, second, and third positions. As in Experiment 1a, there was a significant effect of position (1^st, 2^nd, or 3^rd) on response latencies (F(2, 92) = 7.46, p = 0.001), stemming from a difference between first to second position (t(46) = 2.46, p = 0.009), and first to third position (t(46) = 2.95, p = 0.005). The online measure of SL was again calculated according to the formula in (1) above. Fig. 5 represents the learning dynamics across blocks, replicating the logarithmic function from Experiment 1a. In order to examine the correlation between the offline and online measures of performance in the retest data, the individual online measure score for each individual were again computed. As in Experiment 1a, this was done by averaging the difference in log-transformed RT in blocks 7 to 24.

Table 2.

Means and SDs for RTs and log-transformed RTs for shapes in first, second, and third positions, for the retest data.

	1st position	2nd position	3rd position
Raw RT (SD)	793.5 (368)	754.2 (346)	747.6 (339)
Log-transformed RT (SD)	6.40 (0.49)	6.36 (0.46)	6.35 (0.47)

Figure 5.

Learning trajectory as reflected by the change in the online measure throughout familiarization blocks, for the retest data. Error bars represent standard errors. The dashed line represents the best logarithmic fit.

In line with the results of Experiment 1a, a significant correlation between the online measure and success in the offline test was again observed (r = 0.4, p < 0.01, 95% CI: [0.13, 0.62]).

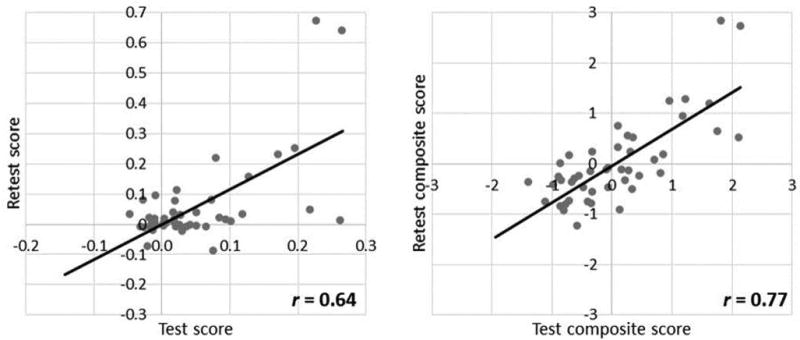
However, we were mainly concerned with the test-retest reliability of the gain in RTs for predictable stimuli. Fig. 6A shows the test-retest scatter plot, indicating a test-retest reliability of r = 0.64 (95% CI: [0.43, 0.78]). This result suggests that the extent of gain in RTs for predictable shapes is indeed a reliable signature of the individual. Offline test scores were also stable over time, with a test-retest reliability of r = 0.63 (95% CI: [0.42, 0.78]), roughly similar to a previous reliability estimation of the same task (Siegelman & Frost, 2015). Fig. 6B shows the test-retest reliability of a composite score taking together the online and offline measures of SL. For both test and retest, this composite measure was calculated by averaging the Z-score of the offline and online measures. The composite score had an even higher test-retest reliability of r = 0.77 (95% CI: [0.62, 0.86]). We return to this important point in the discussion below.

Figure 6.

Panel A shows the test-retest reliability of the online measure. Panel B presents the test-retest reliability of the offline-online composite score. Note that both coefficients might be over-estimated due to two observations (top right corner in both graphs). The test-retest coefficients, however, remained high even when removing these data points: r = 0.45, and r = 0.72, for online and composite scores, respectively.

Discussion

Taken together, the results of Experiment 1a and 1b point to a clear conclusion: The online measure of learning in the self-paced visual SL paradigm provides a promising way of assessing SL performance. In both experiments, a clear signature of learning was observed, as reflected by faster RTs for shapes in predictable relatively to unpredictable positions within triplets. Moreover, this gain in RTs was found to be a valid proxy of SL performance – as reflected by its correlation with the standard offline SL test. Importantly, our data also suggest that it is a stable characteristic of the individual. To our knowledge, this is the first study to directly examine the psychometric properties of such online measure, showing that it can indeed provide a reliable and valid assessment of SL performance.

Some readers may challenge our conclusion regarding the validity of the online measure on the grounds that the online-offline correlations we observed were only moderate (r = 0.56 in Experiment 1a, r = 0.4 in Experiment 1b), potentially reflecting mediocre validity. A point that needs emphasizing, however, is that these correlations most likely provide an underestimation of the true online-offline correlation due to the imperfect reliability of the two measures (estimated at around 0.6 for both). More formally, the correlation between two variables is upper-bound by the square root of the product of their reliability $({\rho }_{\mathit{\text{xy}}}\le \sqrt{{\rho }_{\mathit{\text{xx}}}\ast {\rho }_{\mathit{\text{yy}}}})$. When taking into account the measures’ reliability (using Spearman’s correction for attenuation formula, ${\rho }_{x\prime y\prime }=\frac{{\rho }_{\mathit{\text{xy}}}}{\sqrt{{\rho }_{\mathit{\text{xx}}}\ast {\rho }_{\mathit{\text{yy}}}}}$), even the lower offline-online observed correlation of 0.4 (from Experiment 1b) actually points to a higher expected correlation of 0.67. Hence, the observed offline-online correlation coefficients provide strong evidence for the validity of the online measure.

In terms of the stability of the measurement across time, it is important to note that the highest test-retest reliability coefficient was found for the composite measure, which averages both offline and online standardized scores. From a psychometric perspective, this result is not surprising – the composite score accumulates all available information regarding each individual’s SL performance throughout the whole testing session, thus minimizing measurement error. As such, the composite measure provides a simple and promising way of achieving maximal reliability for the assessment of SL individual abilities. It may prove particularly useful for future studies examining the predictive power of SL, where high reliability is a requisite for observing a correlation between SL and some outcome measure.

The validation of the online measure presents what might seem a challenge of circularity. On the one hand, we aim to show that it taps into SL performance, by examining its correlation with a standard offline test. On the other hand, we aim to offer it as an alternative operational proxy of SL ability, and to highlight the unique information it provides regarding SL processes. Note, however, that to validate the online measure of SL, we examined its individual-level correlation with the offline measure, averaging across many blocks in familiarization. This learning score was found to correlate with the offline test performance, presumably because both scores tap the overall extent of learning. Once this validation procedure has been successful, the online measure can be used as a unique method to track learning across the experimental session, providing new information regarding the dynamics of learning – that is, the changes in the extent of learning across time. This is done by averaging online performance across subjects, in each block of familiarization.

Indeed, tracking the dynamics of gain in RTs for predictable stimuli in Experiments 1a and 1b already provided us with some novel knowledge regarding how the learning of regularities in the visual modality proceeds. First, we found that the group-level learning trajectory in the task is well described by a logarithmic function, with a relatively steep curve at the onset of learning⁶. In addition, with the parameters employed in our design, significant learning was reached already after a relatively small number of repetitions. As most studies using identical parameters have employed familiarization phases with a much larger number of repetitions (typically 20–30, sometimes as many as 300 repetitions, e.g., Saffran et al., 1997), our findings suggest that these were perhaps redundant. Most importantly, this temporal information cannot be revealed by standard offline measures, exemplifying the improved sensitivity of online measures in comparison to offline tests. In Experiment 2, we further investigated the sensitivity of online measures to subtle manipulations of the extent of event predictability, and what they can reveal about learning dynamics.

Experiment 2

In Experiment 2, we harnessed our online measure to examine the trajectory of learning when patterns differ in extent of their predictability. Using the typical 2-AFC offline test, we have recently shown that extent of predictability, operationalized as within-pattern TPs, has a positive incremental impact on SL, with higher levels of predictability resulting in better SL performance (Bogaerts et al., 2016). The use of such offline measure, however, is inherently limited to reveal only the impact of predictability on the overall extent of SL, when exposure is completed. Our aims in Experiment 2 were, therefore, threefold. First, to test whether subtle manipulations of TPs impact the extent of gain in RTs to predictable vs. non-predictable stimuli. This speaks to the question of whether the online measure reveals sensitivity to quasi-regularities as the offline measure does. Second, previous data regarding the impact of TPs on SL performance (Bogaerts et al., 2016) did not tell us anything about the dynamics of learning when events in the stream implicate a range of quasi-regularities. Here we examined whether different levels of predictability result in similar or rather in different learning trajectories. Finally, by comparing the information regarding SL performance collected through online measures to that collected in a 2-AFC test, we could ascertain whether these two different measures of learning provide similar or non-overlapping information.

Method

Participants

Seventy-two students (26 males) participated in the study for payment or for course credit. Participants’ age ranged from 18 to 39 (M = 23.7) and all subjects had no reported history of reading disabilities, ADD or ADHD.

Design, Materials, and Procedure

The procedure was similar to that of Experiment 1, with a self-paced familiarization phase followed by an offline 2-AFC test. The task included the same 24 visual shapes from Experiment 1 (see Appendix A). These were, however, randomly organized into 12 pairs (rather than triplets) for each participant. The familiarization stream consisted of 30 blocks, with all 12 pairs appearing once (in a random order) in each block. Importantly, the 12 pairs were divided into three TP conditions: Four pairs with a TP=1, four with TP=0.8, and four with TP=0.6. The manipulation of TPs was done by including random noise in the TP=0.6 and TP=0.8 conditions: for example, for each pair AB during familiarization in the TPs=0.8 condition, shape B appeared after shape A 80% of the time, while in 20% of the time shape B was randomly replaced by another shape X, avoiding immediate repetitions of identical shapes (see also Bogaerts et al., 2016).

Following familiarization, participants took a 2-AFC test, consisting of 36 trials. In each trial, they were sequentially presented with two types of two-item sequences of shapes: (1) a target – two shapes that formed a pair during the familiarization phase (TP of 0.6, 0.8, or 1, according to TP condition), and (2) a "foil" – two shapes that never appeared together in the familiarization phase (TP=0; as in Experiment 1, without position violation of the shapes in the original pairs). During test, shapes appeared in a fixed presentation rate of 800ms, with an ISI of 200ms between shapes within pairs, and a blank of 1000ms between pairs. Each of the 12 familiarization pairs (i.e., targets) appeared 3 times throughout the test, with three different foils (each foil also appearing three times throughout the test, with three different triplets). Scores in the SL task ranged from 0 to 36, calculated as the number of correct identifications of target pairs during the test phase, and out of the overall 36 trials, there were 12 trials in each target TP condition – 12 trials with a target of TP=1, 12 with a target of TP=0.8, and 12 with a target of TP=0.6.

Results

As in the previous experiments, RTs outside the range of 2 SD from the participant’s mean were trimmed to the cutoff value to minimize the effect of outliers (3.7% of all trials). Note that for the TP=0.6 and TP=0.8 conditions, all analyses reported below include only the occurrences of pairs during familiarization in which there were no exceptions to the repeated pairs (i.e., trials in which the two shapes forming the target pair appeared together).

Table 3 presents the means and standard deviations of RTs and log-transformed RTs for shapes in the first and second positions within-pairs, in each of the three TP conditions. As before, all statistical analyses were performed on log-transformed RTs. A two-way repeated measures ANOVA with TP condition (0.6, 0.8 or 1) and position (1^st vs. 2^nd) as factors revealed a marginally significant effect for position (F(1,71) = 3.01, p = 0.08), with no effects for TP or TP by position interaction (p > 0.1). Subsequent paired t-tests revealed an overall significant position effect for pairs with TP=1 (t(71) = 2.03, p_one-tailed = 0.02), as well as TP=0.8 (t(71) = 1.77, p_one-tailed = 0.04), but not for pairs in the TP=0.6 condition (t(71) = −0.29, p > 0.1).

Table 3.

Means and SDs for RTs and log-transformed RTs for shapes in first and second positions, for each of the three TP conditions.

TP condition		1st position	2nd position
TP = 1	Raw RT (SD)	817.8 (435)	805.2 (413)
	Log-transformed RT (SD)	6.390 (0.48)	6.372 (0.47)
TP = 0.8	Raw RT (SD)	829.9 (453)	813.6 (419)
	Log-transformed RT (SD)	6.394 (0.49)	6.379 (0.47)
TP = 0.6	Raw RT (SD)	826.6 (449)	824.8 (416)
	Log-transformed RT (SD)	6.391 (0.49)	6.392 (0.47)

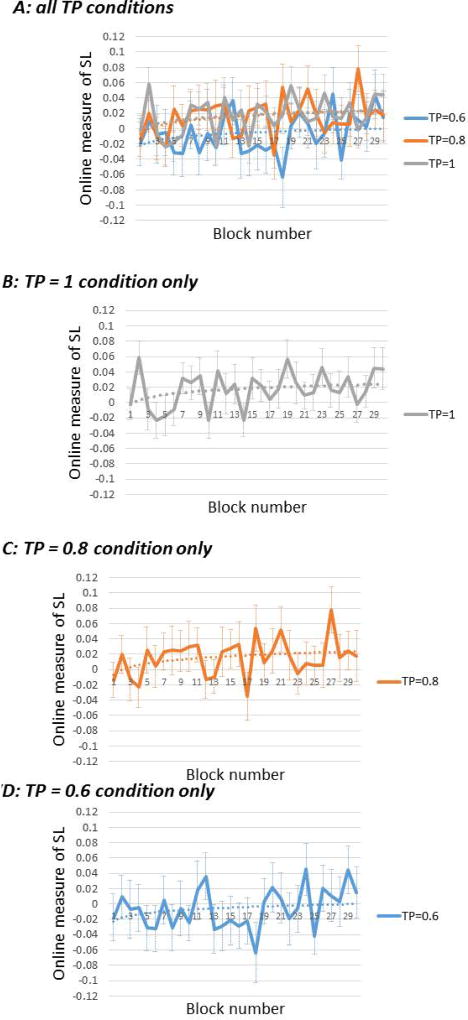
We next examined how the difference in log transformed RTs between shapes in the 1^st position (i.e., unpredictable stimuli) and those in 2^nd position (i.e., predictable stimuli) evolves over time. Fig. 7 presents the time course of learning for each of the TP conditions, as reflected by the change in the online measure across the 30 blocks of the familiarization phase. The upper panel of the figure (7A) presents all TP conditions super-imposed, and the three lower panels present the three TP conditions separately.

Figure 7.

Learning trajectory as reflected by the change in the online measure throughout familiarization blocks, for each of the three TP conditions. Error bars represent standard errors. Dashed lines represent best logarithmic fit.

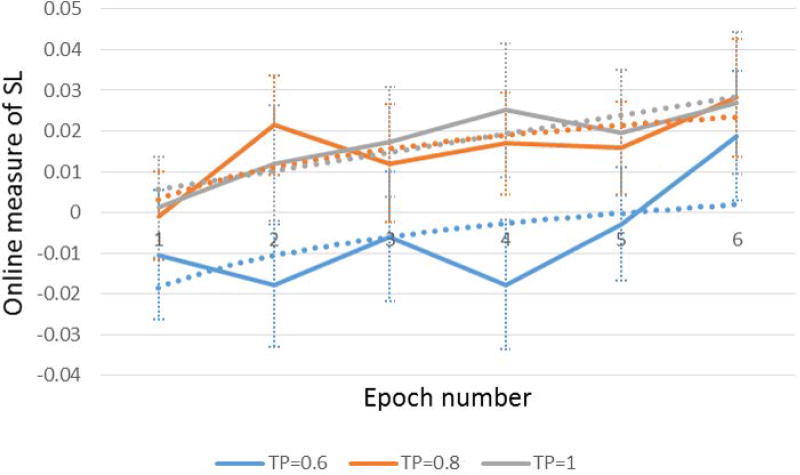
It is clear that Fig. 7 presents a much noisier picture of the learning dynamics than the graphs of Experiments 1a and 1b (Figures 3 and 5 above), as reflected by larger standard errors as well as larger fluctuations in the online measure throughout familiarization. This is not surprising considering that each data point in Fig. 7 includes a much smaller number of trials in comparison to the figures of Experiment 1a and 1b; patterns in the present experiment were pairs and not triplets (there was therefore only one predictable shape per pattern, instead of two), and there were only four pairs in each TPs condition per block (compared to eight patterns in Experiment 1a and 1b). In order to reduce measurement error, we averaged all observations from every five adjacent blocks into a single epoch, enabling a clearer picture of the learning dynamics in each TP condition. This smoothed learning trajectory for each of the three TP conditions is presented in Fig. 8.

Figure 8.

Smoothed learning trajectory: changes in the online measure of SL through epochs, for each of the three TP conditions. Each epoch corresponds to five blocks. Error bars represent standard errors.

Overall, the learning trajectories of the TP = 0.8 and TP = 1 conditions display a nearly identical time-course. Both present a logarithmic trajectory, as reflected by better fit for a logarithmic curve compared to a linear function (TP = 1: R²_logarthimic = 0.91 vs. R²_linear = 0.81; TP = 0.8: R²_logarthimic = 0.59 vs. R²_linear = 0.53), similar to the one found in Experiment 1a and 1b where TPs were 1 for all patterns. Moreover, in both conditions the online learning measure reached a value of around 0.02 in epochs 2–3, and stayed more or less constant until the end of familiarization. In contrast, the TP = 0.6 condition displays a very different learning trajectory. First, it does not show a logarithmic learning curve, as reflected by a worse fit for a logarithmic compared to a linear trajectory (R²_logarthimic = 0.31 vs. R²_linear = 0.5). Moreover, the TP=0.6 condition does not display any learning in epochs 1 to 5 (i.e., until the end of block 25), with a marginally significant learning only at epoch 6 (t(71) = 1.41, p_one-tailed = 0.08).

Offline test performance

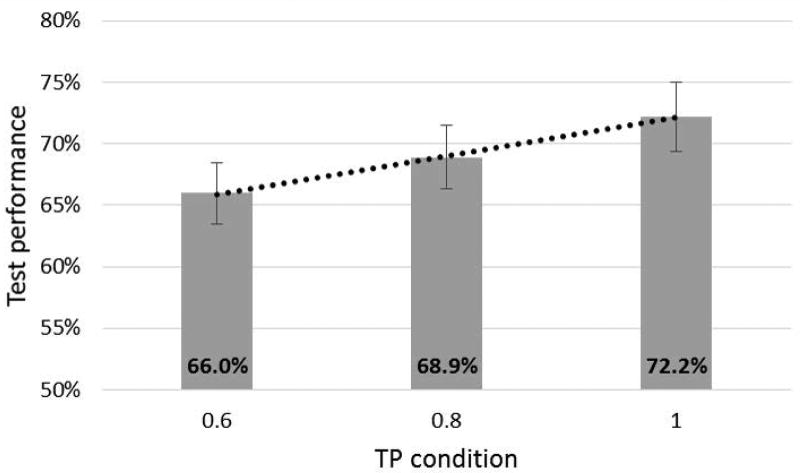
For each participant, we calculated his/her overall score in the 2-AFC test (scores ranging from 0–36), as well as the score on trials of each of the TP conditions (score: 0–12). Mean overall test performance was 24.85/36 (69%), with the sample showing significant learning of the overall latent statistical structure (t(71) = 8.05, p_one-tailed < .001). As in Experiments 1a and 1b, a strong correlation of r = 0.49 (95% CI: [0.29, 0.65]) was found between individuals’ offline test scores and their online measure of learning (averaged across epochs 2–6, i.e., blocks 6–30), again validating the online measure of SL. The correlations between online and offline performance within each of the TP conditions separately were also significant (TP = 0.6: r = 0.33, p = 0.004; TP = 0.8: r = 0.37, p = 0.001; TP = 1: r = 0.25, p = 0.03). Interestingly, the offline test performance displayed a very different pattern of results in terms of the effect of predictability level on SL. As shown in Fig. 9, the effect of TP condition on offline test performance was virtually linear – with an increase of 2.9% between TP=0.6 and TP=0.8, and an increase of 3.3% between TP=0.8 and TP=1. In addition, in each of the three TP levels, a significant learning effect was observed (all p_one-tailed’s < 0.001). We return to these apparent differences between the offline and online measures of SL in the discussion below.

Figure 9.

Offline test performance for each of the three TP conditions. Error bars represent standard errors.

Discussion

The results of Experiment 2 provide a replication of Experiment 1, showing that predictable stimuli are responded to faster compared to unpredictable stimuli, and that the gain in RTs correlates with the offline test scores. This again validates the self-paced VSL paradigm as a proxy for SL performance. However, more importantly, Experiment 2 also shows a clear dissociation between the information provided by offline and online measures of performance. Whereas the offline 2AFC test revealed a linear effect of TPs, the self-paced procedure revealed a qualitative difference in learning higher TPs (0.8, 1) vs. learning lower TPs (0.6). These divergent results suggest that, while both online and offline measures are indeed sensitive to extent of predictability, online measures provide additional information regarding the dynamics of the process, information that offline measures are blind to. Specifically, our online tracking suggests that when TPs in the visual stream are as low as 0.6, learning is exceedingly slow, occurring only after extensive repetitions.

Experiment 3

So far, we focused on the learning of a single set of regularities, where patterns were repeatedly presented from the beginning until the end of familiarization. Experiment 3 further extends our investigation to more complex settings where multiple statistical structures have to be learned. In this line of research, participants are typically exposed for some time to a first set of patterns; then the patterns change into a different set without an explicit cue regarding the change (e.g., Gebhart, Aslin, & Newport, 2009; Karuza et al., 2016). From a theoretical perspective, this procedure targets SL mechanisms in more ecologically valid real-life situations, when the environment offers multiple statistical structures that need to be perceived and assimilated (Karuza et al., 2016; see also Weiss, Gerfen, & Mitchel, 2009).

Although theoretically important, investigating the learning of more than one stream presents a real challenge to typical 2AFC offline tests, because the knowledge on both the first and second set of patterns has to be assessed at the end of all familiarization, after both sets of statistical regularities were presented. The typical finding in such experimental settings, at least in the auditory modality, is a primacy effect. That is, targets from the first stream seem to be recognized better than targets form the second stream, for which performance is often around chance level (Gebhart, Aslin, et al., 2009). This primacy effect was recently interpreted to reflect a non-unified sampling procedure, according to which humans decrease their sampling of regularities from the environment over time due to neural efficiency considerations (see Karuza et al., 2016, for details). This conclusion, however, requires further scrutiny because, by definition, the 2-AFC test is always administered at the end of the full familiarization phase, after the presentation of the second set of regularities. Performance at this late phase could reflect memory constraints rather than SL mechanisms (see Siegelman et al., 2017 for discussion). Moreover, as exemplified above in Experiment 1 and 2, it is possible that while offline test performance on the second stream of regularities is lower in the pre-defined arbitrary time-point in which it is administered, the trajectory of learning building up to this point holds additional information to which the offline tests are blind.

In Experiment 3 we thus examined consecutive learning of multiple structures using the online measure of performance. Participants were presented, within a single session, with two consecutive streams of shapes. In one condition the two streams employed different set of shapes, whereas in another more complex condition, the two streams employed the same set of shapes but with different rules of co-occurrence. We tracked performance of participants in these two conditions with both online and offline measures. This allowed us to examine what these two measures can tell us about the learning of complex statistical structures in the visual modality.

Methods

Participants

Ninety-nine students (24 males; mean age: 23.8, range: 19–31) took part in the experiment for payment or course credit. They had no reported history of reading disabilities, ADD or ADHD. Participants were randomly assigned to one out of two conditions: 50 students in the non-overlapping condition (henceforth Condition 1), and 49 students in the overlapping-condition (Condition 2).

Design, Materials, and Procedure

The procedure was similar to that of Experiment 1. It included a self-paced familiarization phase, followed by an offline 2-AFC test. However, in contrast to Experiment 1 and 2, the familiarization phase was comprised of two sub-streams, presented one after the other. Importantly, the instructions given to the participants were the same as in the previous experiments. Participants were not informed about the existence of two different streams nor that there was a break or any other cue indicating the switch between the streams. The materials consisted of 36 unique shapes. To get to this number we used an additional 12 visual shapes of a similar complexity as those in the set used in Experiments 1 and 2 (see Appendix B).

In Condition 1, for each individual subject, the 36 shapes were randomly assigned to create 12 triplets, six constituted the first stream and the remaining six the second stream. Triplets had a TP=1. Condition 2 differed from 1 in the way the second stream was constructed. Specifically, the second stream consisted of the same 18 shapes that comprised the first stream. The shapes were however rearranged in different triplet patterns. Triplets were created with the constraint that no two or more shapes forming a triplet in the first stream would be grouped in a second stream triplet. Both conditions comprised 12 blocks in each stream, with two breaks, splitting the total familiarization phase into three segments of eight blocks.

The offline 2-AFC test included 36 trials. In each trial a target and a foil were presented. Trials including a target from the first stream were alternated with trials including a target from the second stream (the participants were not informed of this structure). Note that since the shapes in the first and second sub-streams of Condition 2 overlapped, we made sure that the foils never involved two or more shapes that appeared together in a triplet in one of the two streams (see Appendix C for full details).

Results

Two participants (both from Condition 2) were excluded for having abnormally slow response latencies across the experimental session (average RTs more than 3SD from the condition mean). As in the previous experiments, RTs outside the range of 2 SD from the participant’s mean were trimmed to the cutoff value to minimize the effect of outliers (3.7% of all trials).

Table 4 presents the means and standard deviations of RTs and log-transformed RTs for shapes in the first, second and third positions within-triplets, for the two sub-streams in the two conditions. Interestingly, compared to the previous experiments our sample of participants presented a slower mean RT, with larger variance in their rate of response. This is the essence of self-paced performance, participants determine their own comfortable rate of advancing the shapes. Thus, whereas some participants were comfortable at a pace of 3 Hz, quite a few slow participants opted for a pace of 0.5 Hz. Log transforming RTs deals with these different baselines between samples and individuals. Importantly, despite this difference in participants’ baseline RTs, the results of Experiment 3 again show a clear effect of predictability: A one-way repeated measures ANOVAs revealed an effect of position (1^st, 2^nd, and 3^rd) on log-transformed RTs in each of the four sub-streams across the two conditions (F(2, 98) = 19.58, p < 0.001 for Condition 1, first stream; F(2, 98) = 17.89, p < 0.001 for Condition 1, second stream; F(2,92) = 36.1, p < 0.001 for Condition 2, first stream; and F(2,92) = 10.32, p < 0.001 for Condition 2, second stream). In line with Experiment 1, subsequent paired t-tests in all four sub-streams revealed a significant difference in response latencies between 1^st and 2^nd position, and between 1^st and 3^rd position (all p’s < 0.01) but provided no evidence for a RT difference between shapes in 2^nd and 3^rd position (all p’s > 0.05).

Table 4.

Means and SDs for RTs and log-transformed RTs for shapes in first, second, and third positions, for the two sub-streams in the two conditions.

a: Condition 1 (no-overlap), 1st sub-stream
	1st position	2nd position	3rd position
Raw RT (SD)	1404.7 (733)	1125.5 (501)	1143.3 (513)
Log-transformed RT (SD)	6.92 (0.53)	6.69 (0.44)	6.72 (0.45)

b: Condition 1 (no-overlap), 2nd sub-stream
	1st position	2nd position	3rd position
Raw RT (SD)	1050.7 (577)	824.8 (324)	837.3 (342)
Log-transformed RT (SD)	6.63 (0.54)	6.43 (0.41)	6.46 (0.42)

c: Condition 2 (overlap), 1st sub-stream
	1st position	2nd position	3rd position
Raw RT (SD)	1364.9 (740)	1088.1 (505)	1077.7 (455)
Log-transformed RT (SD)	6.86 (0.59)	6.63 (0.48)	6.63 (0.46)

d: Condition 2 (overlap), 2nd sub-stream
	1st position	2nd position	3rd position
Raw RT (SD)	1003.7 (636)	870.4 (473)	888.0 (510)
Log-transformed RT (SD)	6.55 (0.64)	6.44 (0.53)	6.45 (0.55)

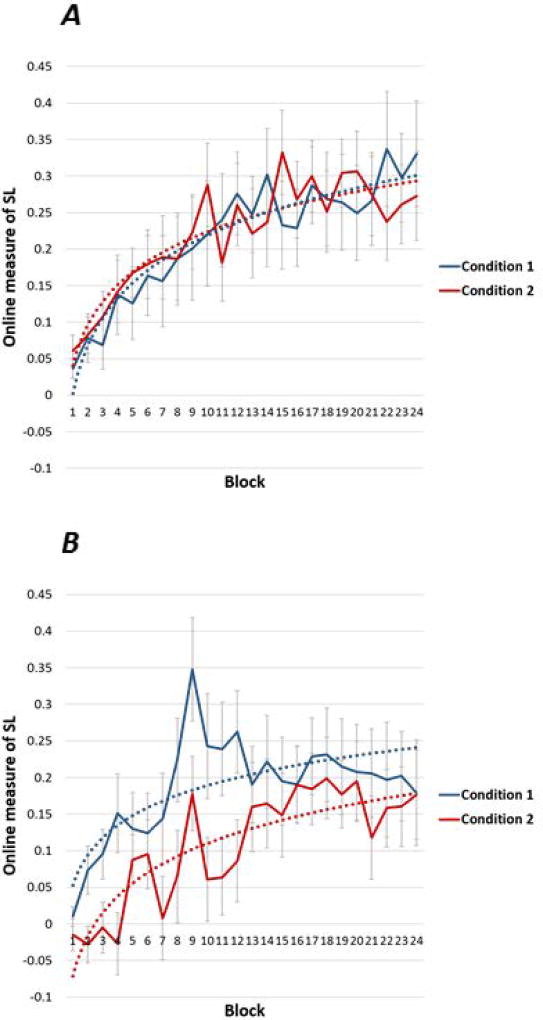
We next turned to examine the dynamics of learning (i.e., the difference in log-transposed RTs between shapes in 1^st position to the average of shapes in 2^nd and 3^rd positions) across the two conditions and in both sub-streams. The learning dynamics are presented in Fig. 10. Overall, the learning trajectories of the 1^st sub-streams in the two Conditions present a nearly identical time-course, as can be seen in Fig. 10a: Thus, similar to Experiment 1a, 1b, and 2, a logarithmic trajectory was observed in both conditions (Condition 1: R²_logarthimic = 0.9 vs. R²_linear = 0.83; Condition 2: R²_logarthimic = 0.82 vs. R²_linear = 0.67). In addition, in the first sub-stream in both conditions, the online measure reached a value significantly bigger than zero at a similar time point (in block 4, p_one-tailed = 0.008 for Condition 1, p_one-tailed = 0.002 for Condition 2), which remained significantly bigger than zero in all subsequent blocks, suggesting a very similar learning trajectory. In contrast, for the second sub-stream, the online measure revealed qualitative different learning dynamics in the two conditions (see Fig. 10b). While both trajectories were again well fitted by a logarithmic function (Condition 1: R²_logarthimic = 0.52 vs. R²_linear = 0.26; Condition 2: R²_logarthimic = 0.72 vs. R²_linear = 0.67), learning the second sub-stream of Condition 2 (the overlapping condition) was much slower. More specifically, while in the second sub-stream of Condition 1 significant learning was observed already in Block 2 (and remained significantly bigger than zero throughout the session), in Condition 2 a stable learning effect was reached much later, only in Block 12.

Figure 10.

Learning trajectory as reflected by the change in the online measure throughout familiarization blocks in the two conditions, for the first (Panel A) and second (Panel B) sub-streams.

Offline measure performance

As in the previous experiments, we measured offline performance for each participant according to his/her number of correct identifications of triplets over foils in the 2-AFC test (score range: 0–36), as well as the average offline scores for the two sub-streams in the two conditions. As in Experiments 1 and 2, a strong correlation (r = 0.53, 95% CI: [0.37, 0.66]) was found between the offline score and the online measure of performance (averaged throughout the familiarization phase, and calculated across participants in both conditions), replicating the validation of the online measure of SL. Importantly, however, the offline test performance displayed again a different pattern of results compared to the online measure with regards to the experimental manipulation. For Condition 1, the two measures of learning converged, showing similar recognition of triplets from the first and the second sub-streams (84.33% vs. 85.33%, paired samples’ t(49) = −0.51, p = 0.62). In contrast, for Condition 2, the online tracking and offline test-scores diverged. Whereas the online measure revealed a significant difficulty in learning the second sub-stream, the offline measure was practically insensitive to this, and performance on patterns from the first sub-stream did not differ from performance on patterns from the second sub-stream (72.7% vs. 74.35%, paired samples’ t(46) = −0.49, p = 0.64). Note that in all four sub-streams (across the two conditions) performance was significantly above chance-level (all p_one-tailed < 0.001). Also note that there was an overall difference in performance between Condition 1 and Condition 2 across the two sub-streams (Condition 1: 84.8% vs. Condition 2: 73.52%, independent samples’ t(95) = 3.12, p = 0.002). We return to the dissociation between the online and offline measures in the Discussion below.

Discussion

The results of Experiment 3 demonstrate again the validity of the online measure as a proxy of SL performance in the self-paced VSL paradigm: predictable stimuli incurred faster responses than unpredictable stimuli, and average RT gain correlated strongly with 2AFC test performance. More importantly, and in line with Experiment 2, online and offline measures provided non-overlapping information regarding learning. Specifically, the online measure revealed a clear effect of the between-condition experimental manipulation (i.e., whether elements in the two streams overlapped or not) on the learning trajectory of the second stream, an effect the offline measure did not reflect.

Taken together, the findings of Experiment 3 anew exemplify how online measures provide access to learning dynamics that cannot be observed when solely observing offline performance of SL. They provide important theoretical insights regarding how learning novel regularities (i.e., the second sub-stream) is affected by the statistics of previous input (i.e., the knowledge already assimilated from the first sub-stream). This resembles findings from related bodies of research on language learning, such as the effect of prior linguistic experience on the acquisition of novel syntactic structures (e.g., Fine, Jaeger, Farmer, & Qian, 2013), and the effect of previous word-level knowledge on the acquisition of grammatical gender (Arnon & Ramscar, 2012).

General Discussion

What exactly is “learning” in the context of “statistical learning”? How should we define it, and how should we measure it? If SL is taken to be the ability to extract the distributional properties of sensory input in time and space (e.g., Frost et al., 2015; Romberg & Saffran, 2010; Schapiro & Turk-Browne, 2015), what should be then a good operational measure of this ability? This question is not merely methodological, rather it is deeply theoretical. Consider a familiarization phase in which elements co-occur in some repeating patterns. SL in such paradigm can result for example in: (1) A perfect post-hoc recognition of a limited number of patterns, (2) some above chance recognition of all patterns, (3) fast formation of online predictions of upcoming stimuli, based on the statistical properties of some patterns, (4) slow formation of online predictions based on the statistics of the entire input, etc. These possible behavioral signatures represent not only different measures of learning, but also different mechanistic accounts of the possible representational changes incurred by exposure to a given sensory input. The operational proxies used to assess learning should maximally cover these potential accounts, to reflect the full scope of SL as a theoretical construct. Nevertheless, most SL research to date is based on this one specific paradigm, with a main operational proxy: 2-AFC performance following a familiarization stream (but see Batterink, Reber, Neville, & Paller, 2015; Bays, Turk-Browne, & Seitz, 2015; Bertels et al., 2012). This measure of SL does a good job in covering some of the possible theoretical definitions of SL, but fails to do so in others.

Our aim in the present study was to consider an alternative to the traditional 2-AFC measure, and expand the investigation of SL to track learning as it unfolds. We targeted in our set of experiments the ability to use the statistics in a visual input to make online predictions. Our study revealed important insights. First, all experiments produced an alternative measure of learning: participants formed online predictions during familiarization, as revealed by a significant RT gain to predictable compared to unpredictable stimuli. Interestingly, they did so already after a relatively small number of exposures. Learning, at least under the parameters in the current experiments, was well described by a logarithmic function. Most importantly, this RT gain was found to be a stable characteristic of an individual, as reflected by high test-retest reliability (Experiment 1b). The extent of gain in RTs for predicted stimuli seems then to be a consistent “signature” of a given participant. Third, all three experiments demonstrate that this online measure is a valid proxy of SL, as it is correlated with the standard offline performance: participants who gained much from predictions in term of fast RTs for predicted stimuli, also scored better in the post-familiarization test. Critically, Experiments 2 and 3 revealed that the online and offline measures are correlated but not interchangeable. Thus, the RT gain for predictable stimuli does not simply mirror offline test performance, rather, it provides additional information regarding SL processes.

Tracking the dynamics of learning in Experiment 2 and 3 revealed important insights regarding the processing of regularities in the visual modality. In Experiment 2 we examined how different levels of quasi-regularity in the visual stream affect learning, and in Experiments 3 we monitored the impact of changing the structural properties of the input while it unfolds. These manipulations are theoretically important because they extend the ecological validity of typical visual SL experiments. Co-occurrences of events in the environment are not necessarily characterized by fixed probabilities, and input streams often vary in their content and statistical structure. In Experiment 2, online performance revealed a qualitative difference between patterns with high predictability levels (TP = 1, 0.8) and those with lower levels of regularity (TP = 0.6). This suggests that the function relating the extent of quasi-regularity in the input to learning is complex, where low TPs require exceedingly high exposures. This pattern was not reflected in the offline test, which shows a simple linear impact of degree of predictability.

In Experiment 3, the online tracking of SL revealed that participants can learn complex sequences composed of two streams differing either in their constituent shapes or in their patterns of co-occurrence. Our findings show that once the structure of the sequence changes, a period of relearning is required, but participants do eventually assimilate the novel structural properties of the input. More importantly, we found that relearning is significantly slower if the constituent shapes remain unchanged, and only their rules of co-occurrence are altered. This finding is perhaps not surprising, since in this condition participants have to update their acquired knowledge regarding the statistical structure of the stream. What is striking, however, is that this information is absent when looking only at offline test performance.

Taken together, the results of Experiment 2 and 3 exemplify the non-overlapping information provided by the different types of SL measures. Both online and offline measures are clearly sensitive to the statistical properties of the input, but this sensitivity has different characteristics, reflecting perhaps different mechanisms. Consequently, when estimating the difference in SL abilities between different populations, experimental conditions, or individuals, the reliance on 2-AFC test scores alone may provide a partial view of the true difference in the underlying processes.

An important question is how are the online and offline measures mechanistically related. How come they reveal different information, so that the tracked performance as revealed by the online measure, ends up in a different end-state relatively to the offline measure? Our initial assumption is that during familiarization participants gradually form predictions regarding upcoming events in the stream. These predictions are continuously updated with repeated presentations of the stream’s constituents, and become increasingly precise with additional repetitions. The behavioral result of this gradual updating process is a continuous increase in speed of response time to the now well-predicted stimuli. In this sense, the online tracking offers a continuous measure of learning. This view is compatible with findings regarding the neurobiological underpinning of learning, where specific patterns of neural oscillations reflect predictions or surprise, while the power of this oscillatory activity is a continuous measure of the strength of the upcoming predictions (e.g., Batterink & Paller, 2017; Farthouat et al., 2016; Roux & Uhlhaas, 2014).

At the end of familiarization, (at least some) participants form stable representations of the extracted patterns. The offline test targets these representations, but in contrast to the online tracking it is blind to their dynamic formation. Our findings in Experiment 2 are then similar to the theoretical curves we have drawn in Figure 1. While online tracking shows that TPs of 0.6 are very difficult to learn, with enough repetitions they may end with relatively stable representations, not as stable as representations formed by TPs of 1 or 0.8, yet stable enough. However, the offline test which targets these representations, is based on a set of categorical yes/no decisions, which are coarse-grained by definition. Moreover, the test repeats, again and again, sets of targets and foils, thereby potentially changing the stability of the originally learned representations during the test phase. Probabilistically, at a given time point performance with TP of 1 will end up to be higher on the average than that of TPs of 0.8, and performance with TP of 0.8 will end up to be higher on the average than that of TP of 0.6. However, the measure is too coarse-grained, so that the nonlinearity observed with the online measure is lost.

Another advantage of online measures is that they can provide insights regarding the nature of the information extracted through the exposure to co-occurrence statistics. For example, previous research has dealt with the question of whether participants extract patterns by learning the TPs between elements (as implemented in Serial Recurrent Network model, SRN, Elman, 1990), or by parsing the stream into smaller chunks (see, e.g., PARSER model, Perruchet & Vinter, 1998; for discussion see Frank, Goldwater, Griffiths, & Tenenbaum, 2010). Previous works mostly used offline measures to try to differentiate between these models based on their predictions regarding formed representations (e.g., Giroux & Rey, 2009; Orbán, Fiser, Aslin, & Lengyel, 2008; but see Franco & Destrebecqz, 2012). Interestingly, these two accounts of learning also make contrasting predictions regarding the online formation of predictions and their temporal dynamics. In this context, it is interesting to note that in all experiments involving embedded triplets of stimuli in the current work (Experiments 1a, 1b, & 3) there was no difference in RTs between shapes in 2^nd position to those in 3^rd position, a result that is in line with predictions from chunk-based, but not TP-based, learning accounts (for discussion see Batterink, 2017; Minier, Fagot, & Rey, 2016). As this is a post-hoc null finding, it requires careful interpretation. Nevertheless, it shows how future research can benefit from combining online and offline measures, explicitly distinguishing between processes relating to the online formation of predictions, to those that have to do with the recognition of the already-established representations.

Our current results seem then to offer new and promising avenues for defining and assessing SL ability on both the group and individual level. This would shift the focus of research from the question of what can be learned, to the question of how exactly are representations updated online given exposure to a continuous sensory input characterized by statistical regularities, and to the question of how individuals differ in such update process (see also Hunt & Aslin, 2001 for discussion of individual differences in a SRT task). Clearly, such research would require additional parallel online measures. An important limitation of our current measure is that it provides reliable information regarding speed of learning at the group-level (i.e., after averaging online performance across all subjects), but not at the individual level. Since RTs measures are inherently noisy, pinpointing exactly when learning was first observed for a given participant is not possible, at least not with the present experimental design. This is an interesting challenge, because assessing individual-level learning dynamics has the promise of revealing critical information regarding SL abilities. Individuals may differ not only in their overall extent of learning, but also in their speed of learning, with potentially non-overlapping predictive power for the two measures, specifically when predicting linguistic outcomes (Siegelman et al., 2017). For example, it is reasonable to assume that the overall extent of pattern recognition (measured by offline tests) will not predict abilities related to online language processing, whereas measures tracking the ability to efficiently form predictions regarding upcoming events might serve as better predictors. Given the shortcoming of RTs measures, future research is left with the task of combining behavioral paradigms with parallel neurobiological online measures of SL performance such as Event Related Potentials (e.g., Jost, Conway, Purdy, Walk, & Hendricks, 2015) or change in rhythmic activity (Cashdollar, Ruhnau, Weisz, & Hasson, 2016; Farthouat et al., 2016) as well as eye-tracking procedures (e.g., Kidd, Piantadosi, & Aslin, 2012), in order to tap into the speed of learning at the individual-level and estimate its distinct predictive power. Note also that in our present investigation tracking SL online revealed important constraints regarding the detection of regularities in the visual modality. This opens a new set of questions regarding auditory SL where simple online tracking through self-paced methods may not necessarily work, and neurobiological tracking would then be a possible solution. This requires extensive investigation, but such lines of research have the promise of expanding the definition of SL as a theoretical construct, leading to a better understanding of its underlying mechanisms.

Appendix A

the 24 shapes used in Experiments 1 and 2.

Appendix B

the 36 shapes used in Experiment 3

Appendix C

structure of triplets and foils in Experiment 3. Each number (1–36) in the tables below represents a shape (assignment of shapes to numbers was randomized for each participant).

Condition 1 (no-overlap)

1st sub-stream		2nd sub-stream
Triplets	Foils	Triplets	Foils
1 2 3	1 5 9	19 20 21	19 26 33
4 5 6	4 8 12	22 23 24	22 29 36
7 8 9	7 11 15	25 26 27	25 32 21
10 11 12	10 14 18	28 29 30	28 35 24
13 14 15	13 17 3	31 32 33	31 20 27
16 17 18	16 2 6	34 35 36	34 23 30

Condition 2 (overlap)

1st sub-stream		2nd sub-stream
Triplets	Foils	Triplets	Foils
1 2 3	1 5 9	2 9 13	2 15 17
4 5 6	4 8 12	3 7 14	3 12 4
7 8 9	7 11 15	8 15 1	8 10 13
10 11 12	10 14 18	5 12 16	5 18 14
13 14 15	13 17 3	6 10 17	6 9 1
16 17 18	16 2 6	11 18 4	11 7 16