Abstract
Purpose
To compare estimates for the diffusional kurtosis in brain as obtained from a cumulant expansion (CE) of the diffusion MRI (dMRI) signal and from q-space (QS) imaging.
Theory and Methods
For the CE estimates of the kurtosis, the CE was truncated to quadratic order in the b-value and fit to the dMRI signal for b-values from 0 up to 2000 s/mm2. For the QS estimates, b-values ranging from 0 up to 10,000 s/mm2 were used to determine the diffusion displacement probability density function (dPDF) via Stejskal's formula. The kurtosis was then calculated directly from the second and fourth order moments of the dPDF. These two approximations were studied for in vivo human data obtained on a 3 T MRI scanner using three orthogonal diffusion encoding directions.
Results
The whole brain mean values for the CE and QS kurtosis estimates differed by 16% or less in each of the considered diffusion encoding directions, and the Pearson correlation coefficients all exceeded 0.85. Nonetheless, there were large discrepancies in many voxels, particularly those with either very high or very low kurtoses relative to the mean values.
Conclusion
Estimates of the diffusional kurtosis in brain obtained using CE and QS approximations are strongly correlated, suggesting that they encode similar information. However, for the choice of b-values employed here, there may be substantial differences, depending on the properties of the diffusion microenvironment in each voxel.
Keywords: kurtosis, q-space imaging, cumulant expansion, accuracy, diffusion MRI, brain
1. Introduction
The diffusional kurtosis is a quantitative measure for the non-Gaussianity of the water diffusion displacement probability density function (dPDF) [1]. Since diffusional non- Gaussianity in brain is strongly linked to microstructural tissue complexity, the kurtosis is of interest for investigating various neuropathologies [2,3], as well as for studying both aging [4,5] and development [6,7] in normal brain. The kurtosis is the basis of several rotationally invariant metrics, such as the mean kurtosis (MK) and the kurtosis fractional anisotropy, which augment the more traditional diffusion parameters of mean diffusivity (MD) and fractional anisotropy [1,8]. In addition, the directional dependence of the kurtosis in white matter can be exploited for fiber tractography [9-11].
The most common approach for estimating the kurtosis from diffusion MRI (dMRI) data is fitting with a signal model derived from an expansion in terms of cumulants for the dPDF [1,12,13]. This has the advantages of simplicity and practicality, and it corresponds to a natural extension of the widely used diffusion tensor imaging method [14]. With the cumulant expansion (CE), it is possible to obtain reproducible kurtosis estimates in brain within reasonable scan times [1,15,16]. The accuracy of these estimates is, nevertheless, limited by several factors, such as the signal-to-noise ratio (SNR), scanner hardware constraints, and the diversity of diffusion microenvironments within the brain [1]. As a consequence, apparent kurtosis values obtained for brain with the CE potentially have significant errors, depending on the region of interest and the specific imaging parameters employed [17-19]. In particular, the choice of maximum b-value corresponds to a trade-off between accuracy and precision, with a smaller maximum b-value typically resulting in a higher accuracy at the price of a lower precision.
An alternative method for estimating the kurtosis is to apply q-space (QS) imaging to determine the dPDF explicitly, from which the kurtosis may then be directly calculated [20-25]. This avoids the need for choosing to a specific signal model and is more conceptually straightforward than the CE. In spite of this, QS imaging has only been rarely used for in vivo kurtosis measurements of brain tissue due to its relatively demanding data acquisition requirements that include obtaining dMRI data for large b-values [20,22,23,26,27]. However, the growing availability of clinical MRI systems with maximum gradient strengths of up to 80 mT/m is likely to increase the utilization of QS imaging [28].
The specific purpose of this study is to compare CE and QS kurtosis estimates for in vivo human brain data and to determine the extent to which these two methods yield consistent results. Our broad motivation is to better understand the systematic errors associated with practical dMRI kurtosis measurements, which may eventually support developing methodologies, based on CE, QS, or other approaches, with improved accuracy. Better accuracy may be especially important when the kurtosis is used in the context of microstructural modeling [29,30].
To our knowledge, there is only one prior published work, by Latt and coworkers [26], in which both CE and QS kurtosis measurements are obtained for brain tissue. Although the two approaches are found to yield similar kurtosis values in several regions of interest, considerable differences are clearly apparent on the parametric kurtosis maps. Here we seek to further characterize such differences by more comprehensively quantifying their extent. There are two important technical distinctions between this prior investigation and our current study. First, we employed a substantially broader range of b-values for the QS analysis, which should improve its accuracy. Second, we acquired 16 spin excitations for each b-value and diffusion encoding direction in order to enhance the effective SNR, while Latt and coworkers [26] used one or two excitations for each set of imaging parameters.
2. Materials and methods
2.1. Stejskal's formula
Both the CE and QS approaches are based on Stejskal's formula that relates the dPDF to the dMRI signal [13,14,31,32]. Specifically,
| (1) |
where S(q) is the dMRI signal as a function of the q-value, P(s) is the dPDF as a function of the diffusion displacement, and S0 ≡ S(0). Here we are using the one-dimensional version of Stejskal's formula, as we shall be considering each diffusion encoding direction separately. It is only exact in the narrow gradient pulse limit, and so there is always some degree of approximation inherent in any application to measurements with finite pulse durations. However, it may be argued that errors due to this are small for CE kurtosis estimates in brain, even for long pulse durations [33], and similar considerations apply to QS imaging as well [23]. Therefore, we neglect this source of error in the CE and QS kurtosis estimates. In statistical equilibrium, the dPDF has the symmetry P(s) = P(−s), which implies that S(q) = S(−q) and that S(q) is a real function. These properties are assumed to hold throughout our analysis.
2.2. Cumulant expansion
The CE for the dMRI signal is obtained from Eq. (1) through the Taylor series approximation
| (2) |
where we have used the fact that the dPDF is an even function of the displacement and defined
| (3) |
and
| (4) |
Here κ2 and κ4 represent the two lowest order nonvanishing cumulants of the dPDF. These are related to the diffusivity, D, and diffusional kurtosis, K, by
| (5) |
and
| (6) |
with t indicating the diffusion time. For any Gaussian dPDF, one may verify that K = 0. For this reason, the kurtosis is a natural metric of non-Gaussianity. In terms of D and K, the CE of Eq. (2) may be rewritten as
| (7) |
where b ≡ (2πq)2t is the b-value. Thus the CE corresponds to a series expansion of the logarithm of the dMRI signal in powers of b.
Standard methods, such as diffusional kurtosis imaging (DKI) [1,12], estimate both the diffusivity and the kurtosis by fitting the signal model
| (8) |
to dMRI data, where Ŝ(b) is the dMRI signal as a function of the b-value. The signal model of Eq. (8) is equivalent to Eq. (7) when the third and higher order terms in the b-value are neglected. Because only the lowest order terms of the CE are utilized, there will generally be systematic errors associated with the fitted (apparent) values for both D and K. These can be reduced by decreasing the maximum b-value used for the fit, as this suppresses the effects of neglecting the third and higher order terms. However, lowering the maximum b-value also decreases the range of diffusion weightings and tends to increase random errors. Therefore, choosing a maximum b-value is a compromise between accuracy and precision. An alternative to decreasing the maximum b-value is to add a third order term to the signal model [34], which will tend to improve accuracy but also at the price of a lower precision.
For the special case in which dMRI data are acquired for b-values of 0, bce, and 2bce, the diffusivity and kurtosis obtained by fitting with Eq. (8) have the analytic formulae [1]
| (9) |
and
| (10) |
2.3. Q-space imaging
For QS imaging, one employs the discrete version of Stejskal's formula, which in one- dimension is given by
| (11) |
where 2N +1 is the total number of QS points,
| (12) |
and
| (13) |
In addition,
| (14) |
| (15) |
and Δq is the QS resolution.
The field of view in displacement space (dFOV) is
| (16) |
while the resolution in displacement space is
| (17) |
where qmax ≡ NΔq is the maximum q-value magnitude used in Eq. (12). Thus the dFOV is inversely related to the QS resolution, and the displacement resolution is inversely related to qmax. This is completely analogous to the familiar relationship for the k-space matrix with the resolution and field of view of an MRI image.
By exploiting the fact that the dPDF is an even function of displacement, Eq. (11) can be recast as
| (18) |
where
| (19) |
and
| (20) |
The inverse of Eq. (18) is
| (21) |
which can be used to calculate the dPDF. Note that Eq. (21) only requires the dMRI signal for the N +1 QS points with q ≥ 0.
Within the QS approximation, the kth moment of the dPDF is given by
| (22) |
Note that all odd order moments vanish by symmetry and that Eq. (11) implies μ0= 1. The lowest order nonvanishing cumulants are related to the moments by
| (23) |
and
| (24) |
which can be used together with Eqs. (5) and (6) to determine the QS estimates for D and K.
The N +1 b-values needed for the QS approximation are
| (25) |
where
| (26) |
The accuracy of the QS diffusivity and kurtosis estimates would usually improve as bqs is reduced and bN is increased, since this results in a larger dFOV and a higher displacement space resolution. However, expanding the range of b-values also raises the data acquisition and SNR requirements.
2.4. Accuracy
Although both the CE and QS approaches yield the true diffusivity and kurtosis in the ideal limits of bce → 0, bqs → 0, and N → ∞, in practice the CE and QS estimates may differ significantly due to systematic errors associated with the finite values of bce, bqs, and N used in any experimental measurement. In order to illustrate these differences, we write the dMRI signal as
| (27) |
where S0f (D′) corresponds to the inverse Laplace transform of Ŝ(b). For a system comprised of multiple non-exchanging Gaussian compartments, f (D′) simply represents the fraction of water with a compartmental diffusivity D′ and is therefore nonnegative, but it may take on negative values for more complex diffusion dynamics.
By applying Eqs. (9) and (10) to Eq. (27), one finds the systematic error in the CE diffusivity to be
| (28) |
and the systematic error in the CE kurtosis to be
| (29) |
which give the leading behaviors of ΔDce and ΔKce for small bce. A direct consequence of Eqs. (28) and (29) is
| (30) |
Thus the relative CE error in the diffusivity is typically small in comparison to the CE error for the kurtosis when Dbce < 1. For multiple Gaussian compartment models, Eqs. (28) and (29) also imply that ΔDce and ΔKce are, for small bce, proportional to the skewness of the water fraction density function, f (D′).
In order to find comparable analytic expressions for the QS errors, it is convenient to work in the limit N→∞, but with finite bqs. From Eqs. (5), (6), and (21)-(27), one finds a systematic error in the QS diffusivity of
| (31) |
and a systematic error in the QS kurtosis of
| (32) |
where
| (33) |
and
| (34) |
The function G(s) is related to the Jacobi theta function ϑ4 [35] by
| (35) |
It is straightforward to verify that both ΔDqs and ΔKqs vanish when bqs tends to zero, as expected on general grounds.
An interesting property of G(s) is that not only does it vanish in the limit s → 0, as follows directly from its definition, but so do all of its derivatives. Consequently, the QS errors of Eqs. (31) and (32) cannot be formulated as a power series expansion in the b-value, in contrast with the CE errors of Eqs. (28) and (29). A plot of G(s) is shown in Fig. 1. The fact that this function is monotonically increasing implies that ΔDqs is always negative for multiple Gaussian compartment models with N →∞, since in this case f (D′) ≥ 0.
Figure 1.
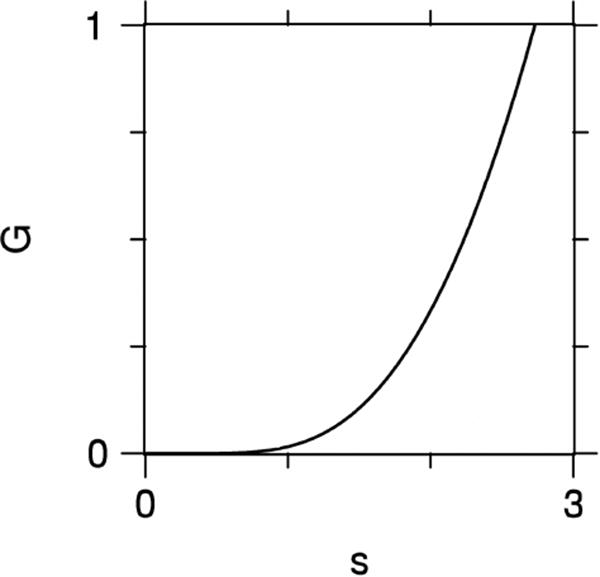
Plot of the function G(s) as defined by Eq. (33). The flatness of G(s) for small s is a consequence of all its derivatives vanishing for s = 0.
As a specific example, let us specialize to a two-compartment model with diffusivities μm2/ms for the first compartment and μm2/ms in the second. Also let the corresponding water fractions be f1 and f2 = 1 – f1. The total diffusivity is then
| (36) |
while the total kurtosis is [1]
| (37) |
The CE and QS errors for this case are plotted in Fig. 2 as a function of f1 for bce = 1000 s/mm2 and bqs = 400 s/mm2 (which are the b-values of our experimental setup, see below). The approximations of Eqs. (28), (29), (31), and (32) are shown together with exact results for the CE estimates obtained using Eqs. (9) and (10) and for the QS estimates found using Eqs. (21)-(24) with N = 5 (to match the experiment). The approximations are seen to be in reasonable agreement with the more exact calculations, although differences are apparent. More relevant to the present work is the observation that CE and QS systematic errors have no particular correspondence, reflecting the fact that the CE and QS are mathematically distinct methods of estimating the diffusivity and kurtosis. In particular, note that the CE errors vanish for either f1= 0 or f1 = 1, but this does not hold true for the QS errors which may be nonzero for a single Gaussian compartment.
Figure 2.
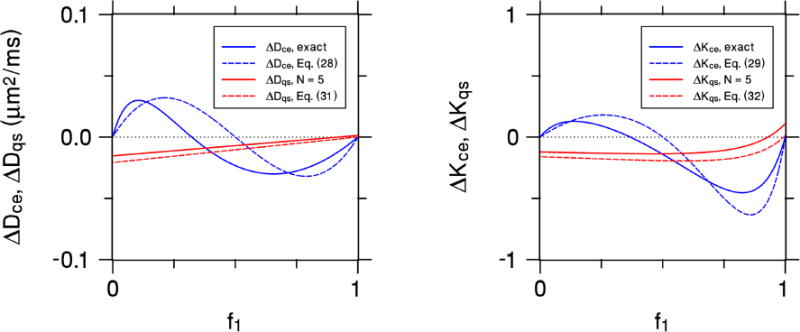
The systematic errors of the CE and QS diffusivities (leftmost panel) and kurtoses (rightmost panel) for a simple two-compartment model as a function of the water fraction f1 of the first compartment. The first compartment has a diffusivity of 0.5 μm2/ms, while the second compartment's diffusivity is 1.5 μm2/ms. The b-values are chosen with bce = 1000 s/mm2 and bqs = 400 s/mm2, in order to match our experimental setup. The solid blue curves represent the exact CE values, while the dashed blue curves are for the small bce approximations of Eqs. (28) and (29). The solid red curves are the QS values for N = 5, which matches the experiment, and the dashed red curves are for the N→∞ approximations of Eqs. (31) and (32). Both the CE and QS approximations capture the qualitative behavior of the more exact calculations. The CE and QS errors have markedly different dependencies on the water fraction, illustrating the distinction between the two approaches.
2.5. Precision
While the accuracy of the diffusivity and kurtosis estimates can, as we have seen, be improved by reducing both bce and bqs, doing this also tends to increase the estimates’ random errors due to signal noise [17-19]. We now demonstrate how to approximate these random errors in the limit of small bce and bqs. Our results are derived by applying the conventional error propagation formula for the variance, δ2F, of an arbitrary function F (x) of a random variable x [36]:
| (38) |
where NM is the number of measurements, xi is a component of x, an overbar indicates the mean value, and the angle brackets signify an ensemble average. To model the noise, we use the signal correlation function
| (39) |
with σ2 being the noise variance and δmn representing the Kronecker delta. The limit of N → ∞ is again assumed for the sake of simplicity and clarity.
For the CE estimates, one finds, by applying Eqs. (38) and (39) to Eqs. (9) and (10), a diffusivity variance of
| (40) |
and a kurtosis variance of
| (41) |
Hence the variance for the kurtosis grows more rapidly with decreasing bce than does the diffusivity variance, reflecting a greater sensitivity to noise.
A similar calculation for the QS estimates yields a diffusivity variance of
| (42) |
and a kurtosis variance of
| (43) |
From Eqs. (40)-(43), one sees that, for small bce and bqs,
| (44) |
and
| (45) |
For our experiment, we use bce/bqs = 2.5. In this case, Eqs. (44) and (45) give δ2Dqs/δ2Dce ≈ 6.8 and δ2Kqs/δ2Kce ≈ 78. Therefore, we expect the random errors for the QS estimates will mostly be larger than for the CE estimates, depending on the extent to which the higher order corrections to Eqs. (44) and (45) may be neglected.
2.6. Imaging
Diffusion weighted imaging data were acquired for a healthy volunteer (male, 57 yr) on a 3 T Prisma MRI scanner (Siemens Healthcare, Erlangen, Germany) under a protocol approved by the Medical University of South Carolina institutional review board. A twice-refocused echo planar imaging pulse sequence was utilized to minimize eddy current distortion [37], with fat suppression added to reduce artifacts. The “adaptive combine” coil data combination mode [38] was used with a bandwidth of 1648 Hz/pixel. Phase encoding was in the anterior-posterior direction, and the slice and phase encoding acceleration factors were both set to 2. A total of 42 axial brain slices with 3 mm slice thickness and 0 interslice gap were obtained. The echo time was 110 ms, the repetition time was 3800 ms, the field of view was 222×222 mm2, and the acquisition matrix was 74×74, resulting in isotropic voxels with dimensions of 3×3×3 mm3.
For each of three orthogonal diffusion encoding directions (slice, read, phase), diffusion weighted images were collected for b-values of 0, 400, 1000, 1600, 2000, 3600, 6400, and 10,000 s/mm2. For each direction and b-value, 16 separate images were obtained in order to increase the effective SNR. The total scan time was 27 min 12 s.
2.7. Data analysis
For each b-value and diffusion encoding direction, the 16 different signals obtained for every voxel were fit to a Rician distribution in order to estimate the ideal signal magnitude in the absence of noise. The choice of a Rician distribution was dictated by our use of the “adaptive combine” coil data combination mode, which is also known as the spatial matched filter method [39,40]. This fitting is similar in effect to signal averaging, but with less noise bias. As there were NM = 16 independent measurements for each set of imaging parameters, the SNR was increased by a factor of approximately 4, since the standard deviation for the signal estimate decreases as [36]. The raw SNR in the brain tissue voxels was about 50, with some variability due to regional differences in T2 and the g-factor. Therefore, after fitting the effective SNR was about 200. Sample fits for three different voxels are shown in Fig. 3. This meticulous noise reduction procedure was undertaken to minimize random errors and thereby better reveal the systematic differences between the CE and QS parameter estimates.
Figure 3.
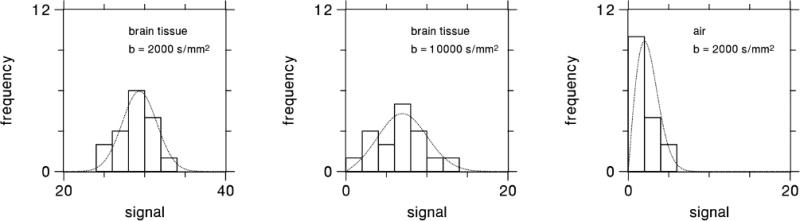
Histograms of the dMRI signal magnitude obtained from three representative voxels, together with fits to a Rician distribution. Fitting a Rician curve to the raw signal leads to a more precise estimate of the ideal signal, while also correcting for bias due to the use of magnitude data. Since NM = 16 measurements were obtained for each set of imaging parameters, we expect the effective SNR for the signal estimated from the fit to be about times higher than the SNR of the raw signal.
In order to reduce Gibbs ringing artifacts, the method of Kellner and coworkers [41] was applied to all of the denoised images. Subsequently, all images were smoothed with a Gaussian kernel of 1.25 times the voxel dimensions in order to further suppress the effects of signal noise and Gibbs ringing.
The CE estimates for the diffusivity and kurtosis in each direction were calculated from the post-processed diffusion weighted images with b-values of 0, 1000, and 2000 s/mm2 by using Eqs. (9) and (10) with bce = 1000 s/mm2 . This corresponds to a typical choice of b-values for DKI [1]. The QS estimates were determined from the images with b-values of 0, 400, 1600, 3600, 6400, and 10,000 s/mm2 by using Eqs. (5), (6), (17), (21)-(24), and (26) with N = 5 and bqs = 400 s/mm2. This value of bqs was chosen to be large enough to suppress the confounding effects of cerebral blood perfusion [42]. Note that the CE and QS calculations employ images with distinct sets of nonzero b-values in order to minimize their cross-correlations.
In addition to the parametric maps for the diffusivity and kurtosis in each individual direction, we also calculated averaged maps from the arithmetic mean of these. For the diffusivity, this yields the usual MD. However, for the kurtosis, the average over the three orthogonal directions does not give the MK as conventionally defined, since that requires data from at least 15 different diffusion encoding directions [1], but may nonetheless be regarded as approximating the MK.
In order to eliminate voxels containing substantial amounts of cerebrospinal fluid, voxels with MD > 1.5 μm2/ms were excluded from the analysis, where we used the CE maps for the MD to create the necessary mask. This resulted in a total of 32,351 voxels being included in our whole brain analysis. The consistency of the CE and QS diffusivity and kurtosis values were assessed both by computing their means and standard deviations over all voxels and by determining the voxelwise Pearson correlation coefficients. The percent difference between the mean CE and QS estimates for the diffusivity was obtained using
| (46) |
where Dce is the CE diffusivity and Dqs is the QS diffusivity. Similarly, the percent difference for the kurtosis was calculated as
| (47) |
where Kce is the CE kurtosis and Kqs is the QS kurtosis.
3. Results
Table 1 gives the mean estimates for the whole brain diffusivity in the three diffusion encoding directions, as well as for the direction-averaged diffusivity. The CE and QS values are all within 12%, and the Pearson correlation coefficients (r) exceed G.95, demonstrating the consistency of the two approximations. In addition, the standard deviations for the CE and QS diffusivities have comparable magnitudes.
Table 1.
Diffusivity for whole brain data.
| Slice | Direction Read | Phase | Average | |
|---|---|---|---|---|
| Dqs (μm2 /ms) | 1.134 (0.257) | 1.156 (0.265) | 1.168 (0.263) | 1.153 (0.221) |
| Dce (μm2 /ms) | 1.014 (0.219) | 1.036 (0.228) | 1.038 (0.222) | 1.030 (0.163) |
| εD | 11% | 11% | 12% | 11% |
| r | 0.954 | 0.961 | 0.955 | 0.976 |
Standard deviations are listed in parentheses.
The corresponding mean estimates for the whole brain kurtosis are shown in Table 2. The QS kurtosis values are 12% to 16% higher than the CE values, while the Pearson correlation coefficients range from 0.854 to 0.903. Although this suggests a fairly good agreement between the CE and QS approximations, the standard deviations for the QS kurtosis are approximately twice those for the CE kurtosis. Thus, the QS approximation yields substantially more voxels with extreme kurtosis values that are either very small or very large relative to the mean value. Linear regression for the direction-averaged kurtosis data yields the best fit line
Table 2.
Kurtosis for whole brain data.
| Slice | Direction Read | Phase | Average | |
|---|---|---|---|---|
| Kqs | 1.079 (0.657) | 1.038 (0.559) | 1.066 (0.663) | 1.061 (0.408) |
| Kce | 0.916 (0.282) | 0.917 (0.265) | 0.934 (0.312) | 0.922 (0.212) |
| εK | 16% | 12% | 13% | 14% |
| r | 0.854 | 0.886 | 0.903 | 0.856 |
Standard deviations are listed in parentheses.
| (48) |
For Kce = 0.707, we then have Kce ≈ Kqs, so that the two approximations give similar values. However, for Kce ≫ 0.707, Eq. (48) predicts Kqs to be substantially larger than Kce.
Parametric maps of the diffusivity for one axial slice (1322 voxels) are displayed in Fig. 4, illustrating the reasonably good agreement between the CE and QS results. The kurtosis maps for the same slice are shown in Fig. 5. Here pronounced differences are apparent in regions with kurtosis values large in comparison to one. For example, in the splenium of the corpus callosum for the slice direction, the QS kurtosis is about twice the CE kurtosis.
Figure 4.
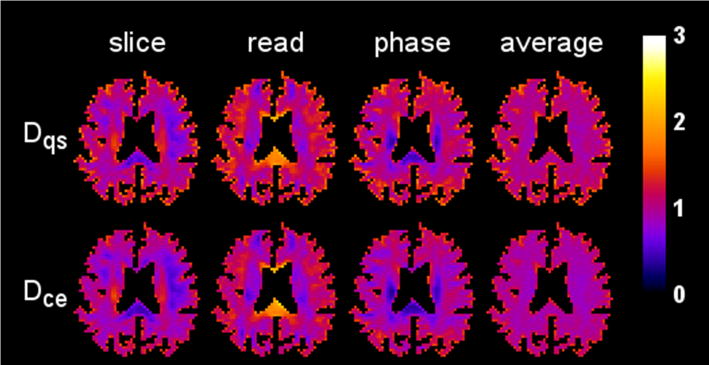
Diffusivity maps from a single axial brain slice for three different diffusion encoding directions (slice, read, phase) together with their arithmetic means (average). The first row shows the maps obtained with the QS approximation, while the second row shows those for the CE approximation. The scale bar is in units of μm2/ms.
Figure 5.
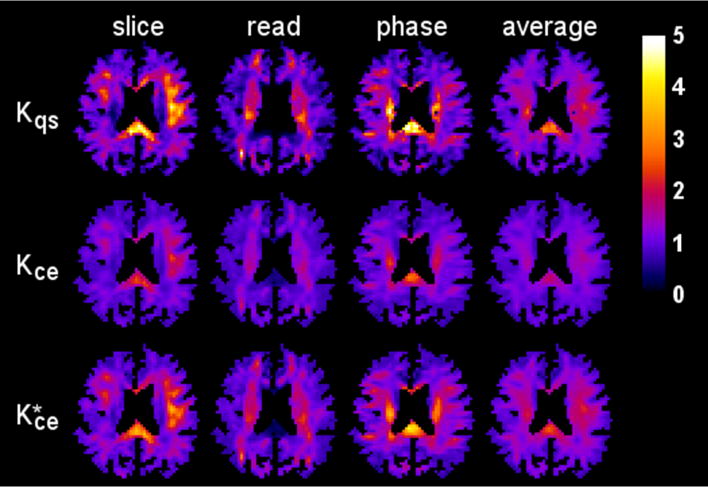
Kurtosis maps for the same anatomical slice and diffusion encoding directions as in Fig. 4. Notable differences are apparent between the QS approximation (first row) and the CE approximation (second row), especially in voxels with a high kurtosis. However, the rescaled CE kurtosis maps (third row), calculated using Eq. (49), more closely match the QS kurtosis maps, suggesting that the CE and QS kurtoses provide similar information. The scale bar is dimensionless.
Also shown in Fig. 5 is a rescaled CE kurtosis defined by
| (49) |
which is motivated by the best fit line of Eq. (48). Clearly, bears a close resemblance to Kqs, suggesting that CE and QS kurtoses contain similar information. We hasten to add that this rescaling is ad hoc and merely intended to highlight the correspondence between the two quantities rather than suggesting some type of general correction scheme.
Scatter plots corresponding to the maps of Figs. 4 and 5 are given by Fig. 6. Relatively strong linear correlations hold in every case, again implying that the CE and QS measures have similar information content. However, the slopes of the best fit lines for the kurtosis estimates deviate from unity considerably more than for the diffusivity.
Figure 6.
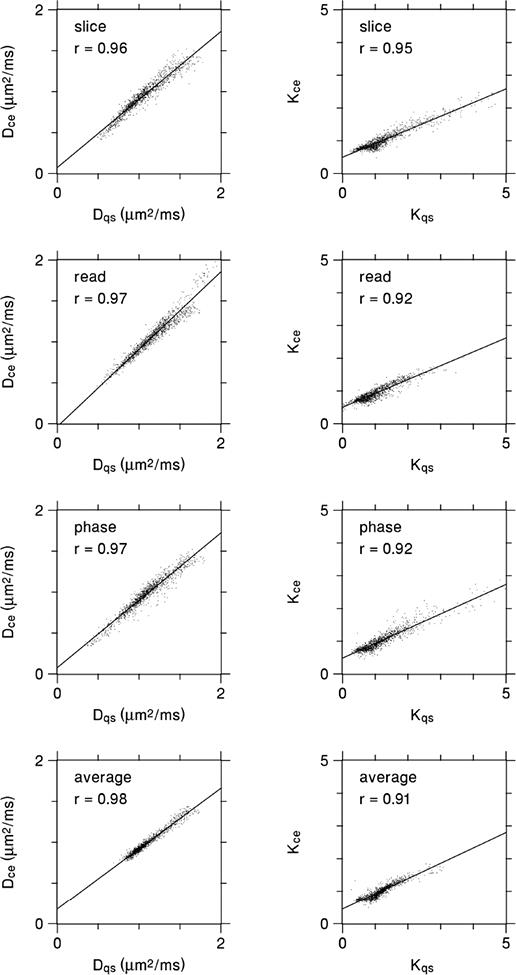
Scatter plots for the same diffusivity and kurtosis data as depicted in Figs. 4 and 5, with each data point representing an individual voxel. The CE and QS parameter estimates are strongly correlated in every case. The lines are best fits based on linear regression, and r indicates the Pearson correlation coefficient. For the diffusivity, the slopes of the best fit lines are all fairly close to one, reflecting the good agreement between Dce and Dqs. For the kurtosis, the slopes are somewhat lower, which is mainly due to Kce being substantially less than Kqs for the largest kurtosis values.
4. Discussion
The CE and QS approaches for estimating the diffusional kurtosis are complementary in being based on distinct mathematical approximations and in having markedly different data requirements. This is evident from Eqs. (29) and (32), which have markedly different analytic forms. The extent to which their estimates agree thus provides a useful test of their validity. In particular, for voxels with substantially different CE and QS values, at least one of these two approximations must be inaccurate.
Our data show that the CE and QS kurtosis values in brain are strongly correlated and have comparable mean values. These correlations are not noise artifacts, since distinct sets of diffusion weighted images were used for the CE and QS calculations. However, there are also notable differences in many voxels, as is especially evident when the kurtosis values are large in comparison to one. In such cases, the accuracies of these CE and QS kurtosis estimates are in question. Nonetheless, the information content of the two parameters is similar, as illustrated by the correspondence shown in Fig. 5 between the QS kurtosis and the rescaled CE kurtosis, and both parameters may be reasonably regarded as indices of diffusional non-Gaussianity even when they deviate from the true kurtosis. These results add to those of other recent studies on the accuracy and precision of kurtosis measurements [17-19].
It should be possible to refine the CE and QS approximations used here in order to improve the consistency of their kurtosis estimates. This would entail reducing bce and bqs, while increasing N . In doing this, care should be taken to correct for the intravoxel incoherent motion effects of cerebral blood perfusion, which can be important for b-values of about 200 s/mm2 or less [42]. In addition, the rapid increase in random errors associated with decreasing bce and bqs, as indicated by Eqs. (41) and (43), needs to be considered. Such refined CE and QS approximations could help to further elucidate their validity, particularly in regions such as the splenium of the corpus callosum where large discrepancies are observed in this study, and may support the development of improved methods of kurtosis estimation via dMRI.
In contrast to the kurtosis, our CE and QS estimates for the diffusivity are in reasonable accord for the vast majority of voxels, which suggests that they are fairly accurate. Of course, it is conceivable for there to be large systematic errors that just happen to be the same in both approximations, but this seems unlikely to occur consistently across the wide range of diffusion microenvironments sampled in our study. That the diffusivity estimates are more accurate than the kurtosis estimates is not surprising given the kurtosis depends on a higher order cumulant that reflects a more subtle feature of the dPDF. A higher relative accuracy for the diffusivity is also implied by Eq. (30) for Dbce ≈ 1 and K ≈ 1 in the limit of small bce.
A limitation of this study is that we have only analyzed a single whole brain dataset. Nevertheless, this comprised over 32,000 voxels that provided a sufficient dynamic range of diffusivities and kurtoses to meaningfully compare the CE and QS approximations. In extensions of this preliminary work, it would be valuable to include subjects with a variety of ages to investigate the generalizability of our results.
5. Conclusions
CE and QS estimates of the diffusional kurtosis in brain are found to be strongly correlated and have similar whole brain mean values for the relatively standard range of b-values employed here. Since the CE and QS approaches are quite distinct mathematically, there is no general reason for their systematic errors to correspond. Thus the observed agreement represents positive evidence supporting the accuracy of the estimates. Nonetheless, there are substantial differences in some brain regions for certain diffusion encoding directions. These warrant further investigation as may be achieved by refining the methods of this study.
Acknowledgments
This work was supported in part by National Institutes of Health research grants T32GM008716 (to P. Halushka) and T32DC0014435 (to J. Dubno) and by the Litwin Foundation (to J.A.H.).
Abbreviations
- CE
cumulant expansion
- dFOV
displacement field of view
- DKI
diffusional kurtosis imaging
- dMRI
diffusion MRI
- dPDF
displacement probability density function
- MD
mean diffusivity
- MK
mean kurtosis
- SNR
signal-to-noise ratio
- QS
q-space
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- 1.Jensen JH, Helpern JA. MRI quantification of non-Gaussian water diffusion by kurtosis analysis. NMR Biomed. 2010;23:698–710. doi: 10.1002/nbm.1518. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Steven AJ, Zhuo J, Melhem ER. Diffusion kurtosis imaging: an emerging technique for evaluating the microstructural environment of the brain. AJR Am J Roentgenol. 2014;202:W26–33. doi: 10.2214/AJR.13.11365. [DOI] [PubMed] [Google Scholar]
- 3.Marrale M, Collura G, Brai M, Toschi N, Midiri F, La Tona G, et al. Physics, techniques and review of neuroradiological applications of diffusion kurtosis imaging (DKI) Clin Neuroradiol. 2016;26:391–403. doi: 10.1007/s00062-015-0469-9. [DOI] [PubMed] [Google Scholar]
- 4.Coutu JP, Chen JJ, Rosas HD, Salat DH. Non-Gaussian water diffusion in aging white matter. Neurobiol Aging. 2014;35:1412–21. doi: 10.1016/j.neurobiolaging.2013.12.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Billiet T, Vandenbulcke M, Mädler B, Peeters R, Dhollander T, Zhang H, et al. Age- related microstructural differences quantified using myelin water imaging and advanced diffusion MRI. Neurobiol Aging. 2015;36:2107–21. doi: 10.1016/j.neurobiolaging.2015.02.029. [DOI] [PubMed] [Google Scholar]
- 6.Paydar A, Fieremans E, Nwankwo JI, Lazar M, Sheth HD, Adisetiyo V, et al. Diffusional kurtosis imaging of the developing brain. AJNR Am J Neuroradiol. 2014;35:808–14. doi: 10.3174/ajnr.A3764. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Grinberg F, Maximov II, Farrher E, Neuner I, Amort L, Thönneβen H, et al. Diffusion kurtosis metrics as biomarkers of microstructural development: a comparative study of a group of children and a group of adults. Neuroimage. 2017;144:12–22. doi: 10.1016/j.neuroimage.2016.08.033. [DOI] [PubMed] [Google Scholar]
- 8.Glenn GR, Helpern JA, Tabesh A, Jensen JH. Quantitative assessment of diffusional kurtosis anisotropy. NMR Biomed. 2015;28:448–59. doi: 10.1002/nbm.3271. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Lazar M. Mapping brain anatomical connectivity using white matter tractography. NMR Biomed. 2010;23:821–35. doi: 10.1002/nbm.1579. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Glenn GR, Helpern JA, Tabesh A, Jensen JH. Optimization of white matter fiber tractography with diffusional kurtosis imaging. NMR Biomed. 2015;28:1245–56. doi: 10.1002/nbm.3374. [DOI] [PubMed] [Google Scholar]
- 11.Glenn GR, Kuo LW, Chao YP, Lee CY, Helpern JA, Jensen JH. Mapping the orientation of white matter fiber bundles: a comparative study of diffusion tensor imaging, diffusional kurtosis imaging, and diffusion spectrum imaging. AJNR Am J Neuroradiol. 2016;37:1216–22. doi: 10.3174/ajnr.A4714. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Jensen JH, Helpern JA, Ramani A, Lu H, Kaczynski K. Diffusional kurtosis imaging: the quantification of non-Gaussian water diffusion by means of magnetic resonance imaging. Magn Reson Med. 2005;53:1432–40. doi: 10.1002/mrm.20508. [DOI] [PubMed] [Google Scholar]
- 13.Kiselev VG. The cumulant expansion: an overarching mathematical framework for understanding diffusion NMR. In: Jones DK, editor. Diffusion MRI: theory, methods and applications. Oxford; Oxford University Press; 2010. pp. 152–68. [Google Scholar]
- 14.Basser PJ. Relationships between diffusion tensor and q-space MRI. Magn Reson Med. 2002;47:392–7. doi: 10.1002/mrm.10052. [DOI] [PubMed] [Google Scholar]
- 15.Lätt J, Nilsson M, Wirestam R, Stâhlberg F, Karlsson N, Johansson M, et al. Regional values of diffusional kurtosis estimates in the healthy brain. J Magn Reson Imaging. 2013;37:610–8. doi: 10.1002/jmri.23857. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Shaw CB, Jensen JH, Deardorff RL, Spampinato MV, Helpern JA. Comparison of diffusion metrics obtained at 1.5T and 3T in human brain with diffusional kurtosis imaging. J Magn Reson Imaging. 2017;45:673–80. doi: 10.1002/jmri.25380. [DOI] [PubMed] [Google Scholar]
- 17.Gilani N, Malcolm PN, Johnson G. Parameter estimation error dependency on the acquisition protocol in diffusion kurtosis imaging. Appl Magn Reson. 2016;47:1229–38. doi: 10.1007/s00723-016-0829-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Chuhutin A, Hansen B, Jespersen SN. Precision and accuracy of diffusion kurtosis estimation and the influence of b-value selection. NMR Biomed. 2017 doi: 10.1002/nbm.3777. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Hutchinson EB, Avram AV, Irfanoglu MO, Koay CG, Barnett AS, Komlosh ME, et al. Analysis of the effects of noise, DWI sampling, and value of assumed parameters in diffusion MRI models. Magn Reson Med. 2017;78:1767–80. doi: 10.1002/mrm.26575. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Lätt J, Brockstedt S, Wirestam R, Larsson E, Stâhlberg F. Visualisation of displacement-distribution parameters in q-space imaging. In Proceedings of the 11th Annual Meeting of ISMRM; Toronto, Canada. 2003. p. 590. [Google Scholar]
- 21.Chin CL, Wehrli FW, Fan Y, Hwang SN, Schwartz ED, Nissanov J, et al. Assessment of axonal fiber tract architecture in excised rat spinal cord by localized NMR q-space imaging: simulations and experimental studies. Magn Reson Med. 2004;52:733–40. doi: 10.1002/mrm.20223. [DOI] [PubMed] [Google Scholar]
- 22.Chabert S, Meca CC, Le Bihan D. Relevance of the information about the diffusion distribution in vivo given by kurtosis in q-space imaging. In Proceedings of the 12th Annual Meeting of ISMRM; Kyoto, Japan. 2004. p. 1238. [Google Scholar]
- 23.Wedeen VJ, Hagmann P, Tseng WY, Reese TG, Weisskoff RM. Mapping complex tissue architecture with diffusion spectrum magnetic resonance imaging. Magn Reson Med. 2005;54:1377–86. doi: 10.1002/mrm.20642. [DOI] [PubMed] [Google Scholar]
- 24.Lätt J, Nilsson M, Malmborg C, Rosquist H, Wirestam R, Stâhlberg F, et al. Accuracy of q-space related parameters in MRI: simulations and phantom measurements. IEEE Trans Med Imaging. 2007;26:1437–47. doi: 10.1109/TMI.2007.907278. [DOI] [PubMed] [Google Scholar]
- 25.Farrell JA, Zhang J, Jones MV, Deboy CA, Hoffman PN, Landman BA, et al. Q-space and conventional diffusion imaging of axon and myelin damage in the rat spinal cord after axotomy. Magn Reson Med. 2010:1323–35. doi: 10.1002/mrm.22389. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Lätt J, Nilsson M, Wirestam R, Johansson E, Larsson EM, Stâhlberg F, et al. In vivo visualization of displacement-distribution-derived parameters in q-space imaging. Magn Reson Imaging. 2008;26:77–87. doi: 10.1016/j.mri.2007.04.001. [DOI] [PubMed] [Google Scholar]
- 27.Fujiyoshi K, Hikishima K, Nakahara J, Tsuji O, Hata J, Konomi T, et al. Application of q-space diffusion MRI for the visualization of white matter. J Neurosci. 2016;36:2796–808. doi: 10.1523/JNEUROSCI.1770-15.2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Setsompop K, Kimmlingen R, Eberlein E, Witzel T, Cohen-Adad J, McNab JA, et al. Pushing the limits of in vivo diffusion MRI for the Human Connectome Project. Neuroimage. 2013;80:220–33. doi: 10.1016/j.neuroimage.2013.05.078. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Fieremans E, Jensen JH, Helpern JA. White matter characterization with diffusional kurtosis imaging. Neuroimage. 2011;58:177–88. doi: 10.1016/j.neuroimage.2011.06.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Hui ES, Russell Glenn G, Helpern JA, Jensen JH. Kurtosis analysis of neural diffusion organization. Neuroimage. 2015;106:391–403. doi: 10.1016/j.neuroimage.2014.11.015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Stejskal EO. Use of spin echoes in a pulsed magnetic-field gradient to study anisotropic, restricted diffusion and flow. J Chem Phys. 1965;43:3597–603. [Google Scholar]
- 32.Jensen JH. Stejskal's formula for multiple-pulsed diffusion MRI. Magn Reson Imaging. 2015;33:1182–6. doi: 10.1016/j.mri.2015.07.001. [DOI] [PubMed] [Google Scholar]
- 33.Jensen JH, Helpern JA. Effect of gradient pulse duration on MRI estimation of the diffusional kurtosis for a two-compartment exchange model. J Magn Reson. 2011;210:233–7. doi: 10.1016/j.jmr.2011.03.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Kiselev VG. Fundamentals of diffusion MRI physics. NMR Biomed. 2017;30(3) doi: 10.1002/nbm.3602. [DOI] [PubMed] [Google Scholar]
- 35.Abramowitz M, Stegun I. Handbook of mathematical functions with formulas, graphs, and mathematical tables (9th printing) New York: Dover; 1972. p. 576. [Google Scholar]
- 36.Ku HH. Notes on the use of propagation of error formulas. J Res Natl Bur Stand. 1966;70C:263–73. [Google Scholar]
- 37.Reese TG, Heid O, Weisskoff RM, Wedeen VJ. Reduction of eddy-current-induced distortion in diffusion MRI using a twice-refocused spin echo. Magn Reson Med. 2003;49:177–82. doi: 10.1002/mrm.10308. [DOI] [PubMed] [Google Scholar]
- 38.Walsh DO, Gmitro AF, Marcellin MW. Adaptive reconstruction of phased array MR imagery. Magn Reson Med. 2000;43:682–90. doi: 10.1002/(sici)1522-2594(200005)43:5<682::aid-mrm10>3.0.co;2-g. [DOI] [PubMed] [Google Scholar]
- 39.Dietrich O, Raya JG, Reeder SB, Ingrisch M, Reiser MF, Schoenberg SO. Influence of multichannel combination, parallel imaging and other reconstruction techniques on MRI noise characteristics. Magn Reson Imaging. 2008;26:754–62. doi: 10.1016/j.mri.2008.02.001. [DOI] [PubMed] [Google Scholar]
- 40.Veraart J, Fieremans E, Novikov DS. Diffusion MRI noise mapping using random matrix theory. Magn Reson Med. 2016;76:1582–93. doi: 10.1002/mrm.26059. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Kellner E, Dhital B, Kiselev VG, Reisert M. Gibbs-ringing artifact removal based on local subvoxel-shifts. Magn Reson Med. 2016;76:1574–81. doi: 10.1002/mrm.26054. [DOI] [PubMed] [Google Scholar]
- 42.Federau C, Maeder P, O'Brien K, Browaeys P, Meuli R, Hagmann P. Quantitative measurement of brain perfusion with intravoxel incoherent motion MR imaging. Radiology. 2012;265:874–81. doi: 10.1148/radiol.12120584. [DOI] [PubMed] [Google Scholar]


