Skip to main content
PMC home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2018 Mar 2;140(13):4580–4587. doi: 10.1021/jacs.7b13624

A Linear Scaling Relation for CO Oxidation on CeO2-Supported Pd

Jin-Xun Liu 1, Yaqiong Su 1, Ivo A W Filot 1, Emiel J M Hensen 1,*
PMCID: PMC5890314  PMID: 29498273

Abstract

graphic file with name ja-2017-13624f_0006.jpg

Resolving the structure and composition of supported nanoparticles under reaction conditions remains a challenge in heterogeneous catalysis. Advanced configurational sampling methods at the density functional theory level are used to identify stable structures of a Pd8 cluster on ceria (CeO2) in the absence and presence of O2. A Monte Carlo method in the Gibbs ensemble predicts Pd-oxide particles to be stable on CeO2 during CO oxidation. Computed potential energy diagrams for CO oxidation reaction cycles are used as input for microkinetics simulations. Pd-oxide exhibits a much higher CO oxidation activity than metallic Pd on CeO2. This work presents for the first time a scaling relation for a CeO2-supported metal nanoparticle catalyst in CO oxidation: a higher oxidation degree of the Pd cluster weakens CO binding and facilitates the rate-determining CO oxidation step with a ceria O atom. Our approach provides a new strategy to model supported nanoparticle catalysts.

Introduction

Supported nanoparticle catalysts, which are pivotal to many chemical processes, can be optimized by tuning the interface of the nanoparticles with oxide supports.1,2 The interface depends on the shape and composition of the nanoparticles, which is influenced by adsorbates leading to promotion of the catalytic performance or deactivation. For instance, nanoparticles are prone to partial or complete transformation to corresponding oxides, carbides, nitrides, or sulfides.3−5 CO oxidation is a stock reaction in modern heterogeneous catalysis and also pivotal to the abatement of exhaust gases from many combustion processes. Operando characterization has already demonstrated that ultrathin oxide layers on Pt single crystals6 and unsupported Rh nanoparticles3 are more active surface structures for CO oxidation than the corresponding metallic surfaces. There is also growing evidence that the surface of supported precious group metals nanoparticle catalysts is oxidized during CO oxidation.7,8 Despite widespread research on controlling the morphology and composition of nanoparticles,9,10 we lack molecular understanding of the evolution of the active phase during the ongoing catalytic reaction. Experimentally, the relatively small amount of precious group metals used in environmental catalysts presents a considerable challenge in determining the active phase composition and structure during CO oxidation.11−13 Nanoparticle-support interactions further complicate the understanding of the relation between size, shape and composition of nanoparticles and catalytic performance.

A suitable model for supported nanoparticle catalysts in which metal–support interfaces play a role is ceria-supported palladium. Pd/CeO2 has attracted widespread attention due to its excellent catalytic performance in combustion processes.14 Pd is nowadays a common ingredient of three-way catalyst (TWC) convertor technology, mainly because of its relatively low cost and excellent low-temperature CO oxidation performance.15 The high catalytic performance is usually understood in terms of strong metal–support interactions (SMSI),16 which maintain a high Pd dispersion. An important property of ceria is its ability to release O atoms, allowing TWCs to retain a good oxidation performance under fuel-rich operating conditions.17 The oxidation state of the Pd nanoparticles is also affected by these strong particle-support interactions. Consequently, many investigations have attempted to relate low-temperature CO oxidation on Pd/CeO2 to the oxidation state of Pd, the role of ceria O vacancies, and the specific topological features of the Pd-CeO2 interface.18,19 For instance, there is an ongoing debate regarding whether the active phase in Pd/CeO2 is oxidic20,21 or metallic.22,23 The view that both metallic and oxidic Pd contribute to the activity suggests that a thin oxide overlayer on small Pd nanoparticles may be important.24

Density functional theory (DFT) has become a powerful tool to predict the rates of elementary reaction steps.25−28 By correlating surface topology and catalytic performance, computational chemistry contributes to the design of new and improved catalysts.29−32 Detailed knowledge of the structure of the catalytically active phase is essential for meaningful modeling of surface kinetics. The structure of CeO2-supported transition metals during CO oxidation has not been unequivocally determined, which explains the variety of surface models employed in computational modeling of these catalysts.33−43 The majority of such studies employ a small metallic cluster (e.g., Pt, Pd, Au) placed on an oxide support (e.g., CeO2, TiO2) as the model of the active phase. A more involved method for determining the exposed surfaces of catalytically active phases involves coupling DFT modeling with ab initio atomistic thermodynamics.44,45 This approach is especially suitable for extended surfaces encountered in single crystal studies44 or (large) Wulff-type nanoparticles.46 However, the selection of candidate structures for small supported clusters or nanoparticles placed on a support, which lack well-defined facets, is not straightforward. Then, manually generating a sufficient number of potential configurations becomes intractable. Accordingly, more systematic configurational sampling algorithms such as evolutionary algorithms, basin hopping and molecular dynamic simulations are required. A standard evolutionary algorithm for efficiently identifying the global minimum energy structure of particles was presented by Deaven and Ho.47 In practice, the particle is in contact with a gaseous atmosphere, which may change its chemical composition. The latter can be taken into account by grand-canonical Monte Carlo (GCMC) insertion and deletion of atoms in a basin-hopping approach.48 Janik and co-workers used this method to study the active phase of Pd/CeO2 for CH4 activation.49 These authors predicted an Pd-oxide structure for a ceria-support Pd7 cluster exposed to O2 by combining a GCMC approach with a reactive force field (ReaxFF). Drawbacks of using reactive force fields is that these are less accurate and cannot describe the transfer of electrons between the active phase and a reducible support like CeO2.49

In the present study, we employed a genetic algorithm (GA) according to the Deaven–Ho scheme to identify the minimum energy structure of a Pd8 cluster on CeO2(111), the most stable surface termination of ceria, at the DFT level (GA-DFT). We compared a stoichiometric and a defective CeO2 surface with an O vacancy. A basin hopping approach in the Gibbs ensemble (GCMC-DFT) was used to optimize the structure of the Pd8/CeO2(111) system in equilibrium with a gaseous O2 atmosphere. This simulation is connected to experiment by an equation of state that relates the chemical potential of O2 to temperature and pressure. In this way, we confirmed the oxidation of Pd during CO oxidation. For three DFT-GA-optimized Pd8/CeO2 as well as two GCMC-DFT optimized Pd8Ox/CeO2(111) structures, we then computed the kinetic barriers for all relevant steps involved in CO oxidation at the Pd-CeO2 interface. Microkinetics simulations demonstrate that the fully oxidized Pd8 catalyst has the highest activity in CO oxidation. The catalytic performance is strongly correlated to the binding strength of CO to the active Pd phase and first scaling law for a supported nanoparticle catalyst is presented. This work presents an advanced approach for determining the active phase structure and composition under practical reaction conditions, which we expect to become a standard given the rapid advances in computational power.

Methods

DFT Calculations

All spin-polarized DFT calculations were performed using the Vienna ab initio simulation package code.50,51 The projector augmented wave (PAW)52 potentials and Perdew–Burke–Ernzerhof (PBE) functionals were adopted.53 For all DFT calculations, Brillouin zone sampling was restricted to the Γ point. The energy cutoff of the plane-wave basis set was 300 eV for structural optimization by GA and GCMC calculations, employing the +U correction with Ueff = 5 for Ce. RPBE potentials were used to obtain accurate adsorption energies of the intermediates for determination of the CO oxidation cycle.54 The plane-wave basis with a cutoff energy of 400 eV was used for studying the CO oxidation mechanism. The climbing-image nudged elastic band (CI-NEB) method55 was used to locate the transition state for CO oxidation with a force tolerance of 0.05 eV/Å. Vibrational mode analysis was performed to verify the identified transition states.

Structure Optimization by GA-DFT

The employed GA approach consists of three main parts: the generation of an initial population of 12 random structures, optimization of each structure in the population at the DFT–PAW–PBE level, and the use of a selection operator to create the next generation of structures. Structures with a lower energy have a higher possibility of contributing one or more offspring in the next generation. After reproduction, new populations are generated by crossover, as discussed by Deaven and Ho,47 and mutations caused by randomly moving atoms and twist operators were also implemented. The calculated energies are used to determine the fitness. Energies and bond distances are used to judge whether two structures are the same to avoid multiple occurrences of one structure in the population. The cycle is terminated when no new structures are obtained for 80 cycles. Typically, several hundreds of structures have been optimized to obtain the global minimum structure of an initial population.

Structure Optimization by GCMC-DFT

Grand-canonical Monte Carlo (GCMC) simulations were performed to determine the global minimum structure of Pd8/CeO2 in an oxygen atmosphere. The method is an adaptation of the basin-hopping algorithm for optimizing particle structure. Besides allowing variation in structure, we varied the composition by adding and deleting O atoms. The compositional changes were simulated in the Gibbs ensemble, using an O2 reservoir at a given pressure and temperature. Typically, in each step, 25% of all the atoms in the supported cluster were allowed to translate. The translation movements and insertions/deletions were accepted according to a Metropolis scheme. More than five hundred structures were calculated for each specified condition.

More detailed information on GA-DFT, GCMC-DFT, DFT calculations, and microkinetics simulations are given in the SI.

Results and Discussion

Optimal Pd8/CeO2 Structure

To identify the minimum energy structure of a Pd8 particle on CeO2, we used a genetic algorithm at the DFT-GGA-PBE level. The fitness function is the minimization of the electronic energy. This implies that we neglect the contribution of the configurational entropy of the solid as a first approximation.56 The GA approach typically uses Lennard-Jones or other potentials to compute the energy.57,58 DFT has also been used, mostly for determining the optimal structure of unsupported metal clusters.59 The actual choice for Pd8 is a pragmatic one based on selecting a system with a large enough Pd cluster that resembles the structure of a Pd nanoparticle and small enough to be computationally tractable. Also, experiments have shown that Au8 and Pd8 clusters can be synthesized on MgO and Al2O3, respectively, displaying high activity in low-temperature CO oxidation and oxidative dehydrogenation of propane.60,61 The surface model consisted of a Pd8 cluster placed on the stoichiometric CeO2(111) surface (Pd8/CeO2) and a defective CeO2(111) surface, which contains one O vacancy (Pd/CeO2–x). We also optimized the structure of a free Pd8 cluster. The structures of the six lowest-energy isomers are presented in Figure S1. Figure 1a shows that the lowest energy structure of the free Pd8 cluster has a bicapped octahedral geometry with D2d symmetry. The surface Pd atoms of this cluster have coordination numbers of 4 and 5, which is consistent with the structure of gas-phase clusters.62

Figure 1.

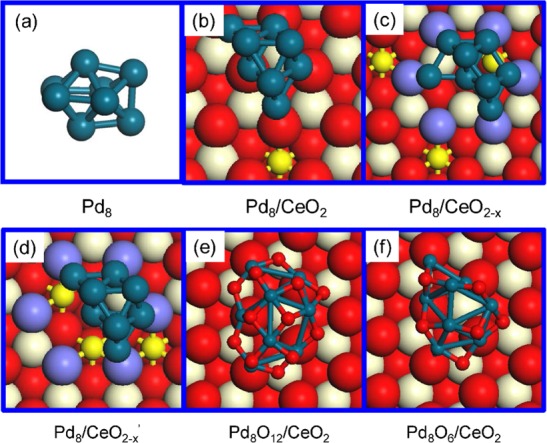
Figure 1

Open in a new tab

Structures of Pd8 and CeO2 supported Pd8 and Pd8Ox nanoparticles. (a–c) Optimized structure of Pd8 as a free particle, and on the stoichiometric and defective ceria surfaces (optimized by GA-DFT). (d) Metastable structure of Pd8 on the defective ceria. (e,f) Structures of Pd8Ox/CeO2 (x = 12 and 6) obtained by GCMC-DFT at 300 K with oxygen atmospheres of 1 atm and 10–20 atm, respectively. Color coding: cyan, red, white, and small yellow spheres represent Pd, O, Ce4+, and Ce3+ atoms, respectively; the purple spheres in defective ceria represent O atoms adjacent to O vacancy sites. This notation is used throughout this paper.

The same method was used to obtain the minimum-energy structures of Pd8/CeO2 (Figure 1b) and Pd8/CeO2–x (Figure 1c). A comparison to the optimized Pd8 cluster shows that the Pd-CeO2 interactions result in a completely different structure. On CeO2, the cluster adopts a bilayer structure and retains the bulk FCC-Pd structure in the first three coordination shells as follows from inspection of the radial distribution functions (Figure S2). Bilayer structures have been frequently observed for supported nanoparticles, e.g., Au/TiO2, Pd/MgO, and Cu/ZnO.60,63−65 For Pd8/CeO2, the topmost Pd layer comprises three Pd atoms, while the remaining five Pd atoms interact with five ceria oxygen atoms. In these calculations, we assumed that the support does not change its shape. We explored the impact of an O vacancy in the CeO2(111) surface. The Pd8 particle will then preferentially locate on this defect and adopt a slightly different geometry compared to Pd8/CeO2. For the sake of comparison, we also selected from the pool of optimized Pd8/CeO2–x configurations a less stable structure, Pd8/CeO2–x′ (ΔE = +0.21 eV, Figure 1d), in which Pd8 has the same structure as in the global minimum structure of Pd8/CeO2. Analysis of the electronic structure, which is possible because of the use of the DFT+U method ensuring proper localization of excess electrons in Ce-4f orbitals,66 shows that one Ce3+ ion is generated in Pd8/CeO2. A Bader charge analysis estimates the charge on Pd8 + 0.57e (Figure S3). For Pd8/CeO2–x, the CeO2 surface contains two additional Ce3+ ions and the charge on Pd8 is +0.40e. The slightly less stable Pd8/CeO2–x′ structure also contains three Ce3+ ions and the charge on Pd8 is +0.29e. These charge differences are qualitatively consistent with an earlier computational study of Au/CeO2.36 The three Ce3+ ions are located close to the cluster due to the choice of a 3 × 3 surface unit cell.67,68 These results demonstrate that the presence of an O vacancy has a strong impact on the structure of the supported metal cluster and the charge transfer from the particle to the ceria support.

We used a GCMC approach to also take into account possible compositional changes of Pd8/CeO2 due to contact with gaseous O2. In our GCMC-DFT approach, we accept trial moves (insertion, deletion, translation) on the basis of the Metropolis algorithm in which we use the Gibbs free energy μ(T, P) of existing and trial configurations. μ(T, P) is evaluated by considering the electronic energy of the solid and the Gibbs free energy of the gaseous O2 reservoir at (T, P) using data from thermodynamic tables. In 1 atm O2 and at 300 K, CeO2-supported Pd8 will be oxidized to Pd8O12 (Figure 1e). The radial distribution function of the Pd8O12/CeO2 structure in Figure S2 clearly shows that all Pd atoms are oxidized in line with a previous computational work demonstrating deep oxidation of a Pd7 cluster supported on CeO2 exposed to O2.49 Each Pd atom coordinates to four O atoms. At a low O2 pressure of 10–20 atm, the most stable state is Pd8O6 (Figure 1f), in which O atoms adsorb on the Pd8 surface in 3-fold and bridge sites. Some Pd–Pd bonds are retained and the Pd–O coordination number varies between 1 and 4. We also verified that GCMC-DFT will lead to rapid healing of O vacancies created in the CeO2 surface when it is exposed to O2. In this work, we did not investigate the disintegration of Pd clusters, which is known to occur at very high temperature in an O2 atmosphere.69,70

CO Oxidation

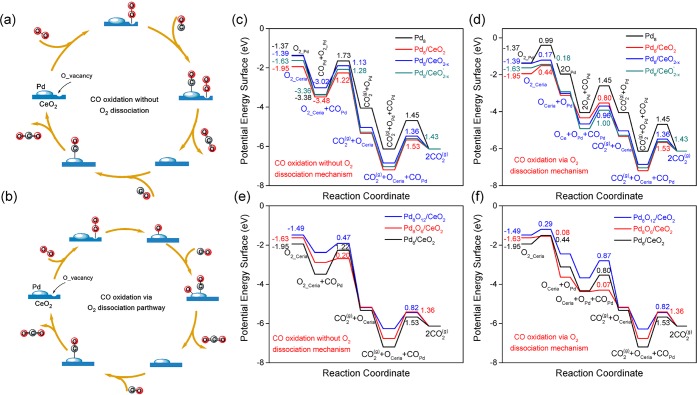
In order to determine the CO oxidation activity of the optimized structures, we explored the well-accepted Mars-van Krevelen mechanism for the oxidation of CO at the Pd-CeO2 interface (Figure 2). The O atoms of the ceria are involved in CO oxidation, which will result in ceria O vacancies close to the Pd cluster. Two different reaction pathways were explored. In the first one, adsorption of molecular O2 on a ceria O vacancy precedes reaction with CO adsorbed on the nanoparticle to generate CO2 (COPd + O2,ceria → CO2 + Oceria). This step heals the ceria O vacancy and the catalytic cycle is closed by reaction of adsorbed CO with a ceria O atom (Figure 2a). The alternative scenario is that molecular O2 adsorbed on the O vacancy first dissociates at the Pd-CeO2 interface, resulting in healing of the ceria O vacancy and migration of the other O atom to the Pd8 nanoparticle. Both O atoms are then removed by CO in two reaction steps (Figure 2b). The computed potential energy diagrams and corresponding transition state configurations are presented in Figure 2 and Figure 3, respectively. A complete overview of the configurations involved in CO oxidation on the six considered structures is given in the Figure S8–S19.

Figure 2.

Figure 2

Open in a new tab

Scheme of CO oxidation mechanism and computed potential energy surfaces for CO oxidation. (a) Scheme for CO oxidation without O2 dissociation and (b) scheme for CO oxidation via O2 dissociation at the interface of CeO2 supported Pd nanoparticles. (c,e) Potential energy diagrams for CO oxidation without O2 dissociation. (d,f) Potential energy diagrams for CO oxidation via O2 dissociation on Pd8, CeO2 supported Pd8, and Pd8Ox nanoparticles. The elementary reaction barriers are given in eV.

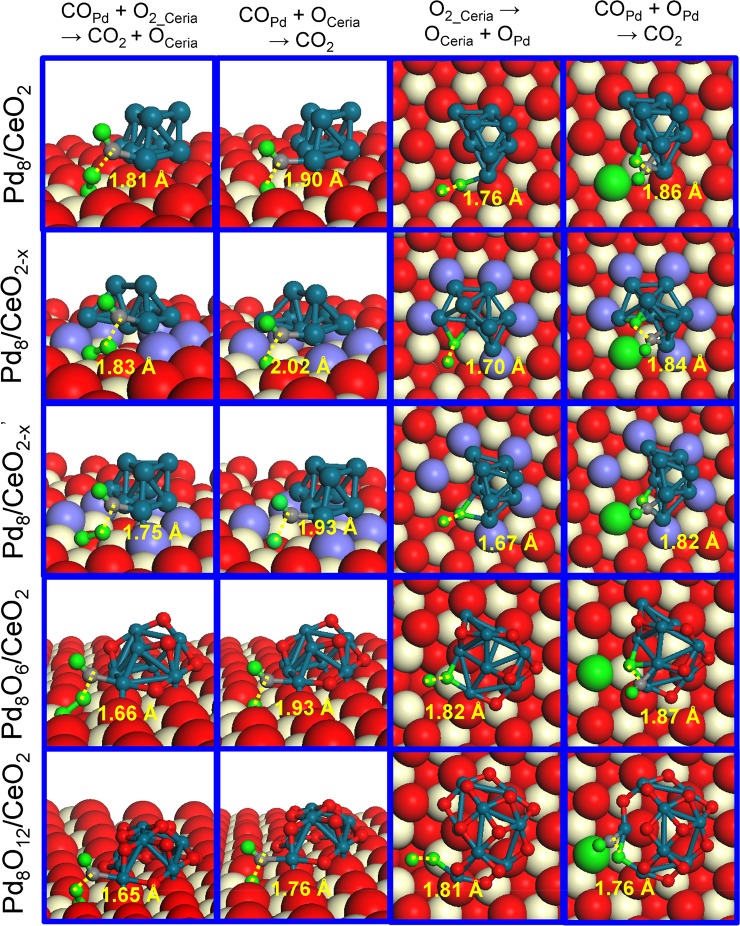
Figure 3.

Figure 3

Open in a new tab

Geometric structures of the transition states involved in CO oxidation on CeO2 supported Pd8 and Pd8Ox (x = 6 and 12) nanoparticles. The distances (dTS, in Å) between the two reacting fragments at the transition state are indicated. The green and gray spheres are O and C atoms involved in CO oxidation, respectively.

We start the discussion of the catalytic cycle from the state in which the ceria surface contains an O vacancy. Figure 2c shows that O2 adsorption is strongest at the O vacancy of Pd8/CeO2 (Eads = −1.95 eV). O2 adsorbs weaker on the defective Pd8/CeO2–x and Pd8/CeO2–x′ structures. The O2 adsorption energy is lowest for Pd8 (Eads = −1.37 eV). After O2 adsorption on the O vacancy site in ceria, the CO adsorption energy shows an opposite trend: Pd8 (−2.01 eV) > Pd8/CeO2–x′ (−1.73 eV) > Pd8/CeO2–x (−1.63 eV) > Pd8/CeO2 (−1.53 eV) > Pd8O6/CeO2 (−1.26 eV) > Pd8O12/CeO2 (−0.88 eV). The variation of the CO adsorption energy of the reduced Pd8 clusters correlates strongly with the positive charge on Pd8.

Oxidation of Pd8 results in weaker CO adsorption. The strong dependence of CO and O2 adsorption energies on the structure and composition of Pd8/CeO2 has a profound impact on the kinetics of CO oxidation. The overall activation barrier for CO oxidation without O2 dissociation on the free Pd8 nanoparticle is 1.73 eV. We considered two steps for this structure: COPd + O2,ads → CO2 + Oads (Eact = 1.73 eV) and COPd + Oads → CO2 (Eact = 1.45 eV). For the pathway involving only atomic O, O2 dissociation must also be considered (Eact = 0.99 eV). Accordingly, the reaction cycle will proceed according to the textbook Langmuir–Hinshelwood mechanism for CO oxidation on metal surfaces, involving O2 dissociation and CO+O reaction events. Under typical reaction conditions, the metallic surface will be poisoned by CO and high overall reaction barriers are predicted, which will result in low catalytic performance. In a similar manner, the Pd8 cluster placed on CeO2 will be covered mainly by CO as it binding strength is 1.19 eV higher than that of O2. Therefore, the contribution of CO oxidation pathways occurring exclusively on the Pd8 particles can be neglected.

For CO oxidation at the Pd cluster-CeO2 interface, the activation barrier for the COPd + O2,ceria → CO2 + Oceria step is within the 1.13–1.28 eV range. The COPd + Oceria → CO2 reactions have slightly higher barriers in the range 1.36–1.53 eV. O2 dissociation at the Pd–CeO2 interface is facile for all three supported Pd8 nanoparticles (Eact < 0.50 eV). The COPd + OPd → CO2 reaction has barriers of 0.80, 0.96, and 1.0 eV for Pd8/CeO2, Pd8/CeO2–x, and Pd8/CeO2–x′, respectively. These differences correspond well with the differences in CO adsorption strength. Figure 2c and Figure 2d show that the dissociative mechanism should be easier than the associative mechanism. The most difficult step is the removal of the ceria surface O atom and the overall barrier for this is lowest for the defective ceria surface.

CO oxidation on Pd8O12/CeO2 and Pd8O6/CeO2 is much easier. As illustrated in Figure 2e, the activation barrier for COPd + O2,ceria → CO2 + Oceria is reduced from 1.22 eV for Pd8/CeO2 to 0.20 eV for Pd8O6/CeO2. The barriers for O2 dissociation and COPd + OPd → CO2 are below 0.10 eV. The latter step is easier because of the weak binding of CO and O. Regenerating the O vacancy via COPd + Oceria → CO2 remains the most difficult step and involves a barrier of 1.36 eV on Pd8O6/CeO2. The dissociative mechanism is preferred for Pd8O6/CeO2. For Pd8O12/CeO2, the dissociative pathway is also slightly preferred over the associative mechanism. The most difficult steps are the removal of an O atom from the Pd8O12 surface and the formation of an O vacancy with activation barriers of 0.87 and 0.83 eV, respectively. The relatively low activation barrier for O removal from Pd8O12/CeO2 arises from weaker CO adsorption (Figure 2).

Microkinetics Simulations

CO oxidation reaction rates are predicted by microkinetics simulations based on the above potential energy diagrams. The migration of O atoms from the CeO2 surface to the PdOx cluster was taken into account based on calculated reaction barriers, which are shown in Table S2. The resulting kinetic data are plotted as Arrhenius curves in Figure 4. Clearly, the active sites at the Pd-CeO2 interface show a much higher CO oxidation rate than the surface of the free Pd8 cluster. The apparent activation energy for the free Pd8 cluster is 2.53 eV, while those for the supported reduced clusters are much lower, i.e., between 1.34 and 1.51 eV. Importantly, the presence of a defect in the CeO2 surface results in a nearly 2 orders of magnitude higher activity than obtained for the defect-free CeO2 surface. Pd8O6/CeO2 and Pd8O12/CeO2 exhibit the highest CO oxidation activities. The fully oxidized cluster has the highest activity with a lowest apparent activation energy of 0.90 eV. Figure 4 also illustrates that the CO oxidation rate of Pd8O12/CeO2 declines above 400 K, which is due to a decreased CO coverage as we will discuss below. A key finding from the combined GA/GCMC-DFT and microkinetics modeling is that CeO2-supported Pd clusters are oxidized in an O2 atmosphere and the resulting Pd-oxide structures exhibit a much higher CO oxidation activity than metallic Pd clusters on CeO2. These findings confirm earlier experimental suggestions that highly dispersed Pd-oxide on CeO2 is the active phase for CO oxidation.21,71,72 A comparison of computed TOFs (turnover frequencies) for various Pd8(Ox)/CeO2 structures with experimentally reported TOF values73−75 (Table S6) further confirms that oxidized Pd on CeO2 is the most likely active state in Pd/CeO2 catalysts.

Figure 4.

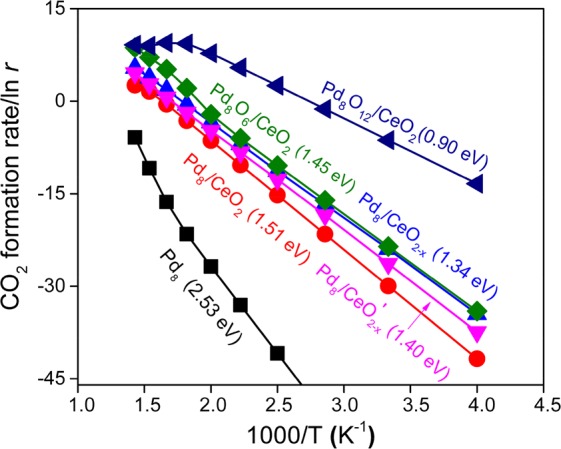
Figure 4

Open in a new tab

Microkinetics simulations for CO oxidation on Pd8 and CeO2 supported Pd8(Ox) nanoparticles. CO2 formation rates r (in mol·s–1) as a function of temperature on Pd8 and Pd8/CeO2, Pd8O6/CeO2, and Pd8O12/CeO2 catalysts are presented. The apparent activation barriers (in eV) indicated in parentheses are calculated using the Arrhenius equation. Dual-site microkinetics simulation models are considered for CeO2 supported Pd8(Ox) nanoparticles.

In order to gain a deeper insight into the underlying kinetics, we analyzed the surface coverages and degrees of rate control (DRC)76 as a function of temperature. Figure S4a shows that CO poisons the pure Pd8 cluster, which explains the high apparent activation energy. At low reaction temperature, the Pd-surface of the three reduced Pd8/CeO2 catalysts will also be mainly covered by CO. As CO adsorbs weakest on Pd8/CeO2, it is observed that CO coverage starts to decrease at a relatively low temperature. Under steady-state conditions, the concentration of ceria O vacancies is low, because the reaction between COPd and Oceria controls the reaction rate. The kinetics for Pd8O6/CeO2 and Pd8O12/CeO2 are very similar: the oxidized Pd clusters is mostly covered by CO and the removal of Oceria is the rate-controlling step. However, as CO adsorbs much weaker on the oxidized structures, CO coverage will decrease at relatively low temperature. Since, under relevant conditions, the reaction between CO and Oceria will still control the overall reaction rate, the decreased CO coverage is the primary cause of the lower activity. We find that the migration of an O atom from the ceria to the Pd8O6 cluster becomes rate-controlling at temperatures higher than 650 K only for Pd8O6/CeO2.

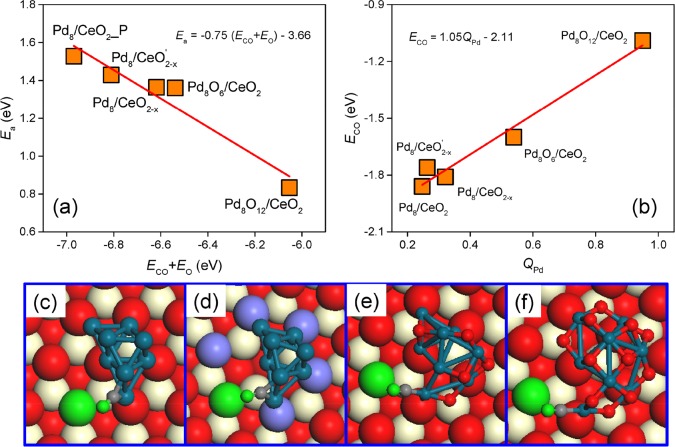
We then set out to determine how interactions of a Pd8 particle with CeO2 and O2 impact the active phase structure and composition and, consequently, CO oxidation activity. Under catalytic conditions, Pd will be oxidized, either to a Pd-oxide surface overlayer or, for small clusters, Pd-oxide. Figure 5 shows that the activation barrier for the rate-controlling oxidation step of adsorbed CO with a ceria O atom strongly correlates with the CO and O binding energies. The negative slope indicates that weaker CO and O adsorption facilitate the association step. The adsorption energies of CO and O on Pd8Ox (x = 0, 6, and 12) and CeO2 surfaces are shown in Table S1. The O vacancy formation energies vary only slightly among the optimized structures, implying that the O binding strength is less sensitive to structure and composition than the CO binding strength. Therefore, we can draw the important conclusion that the CO oxidation rate mainly depends on the binding strength of CO with Pd. The correlations in Figure 5 constitute a first example of a scaling relation for supported metal nanoparticles, similar to scaling laws that have already proven their use in predicting periodic trends in metal nanoparticle catalysis.29 Given that in this particular case the final state is CO2 in the gas phase, which has a relatively flat potential with respect to the reaction coordinate, we are able to provide a linear scaling relationship based purely on the adsorption energy rather than on the reaction energy as typically done within a Brønsted–Evans–Polanyi approximation. Under catalytic CO oxidation conditions, also out-of-equilibrium structures may exist and contribute to the catalytic performance. We computed the activation barrier for the rate-controlling step for three of such structures (Figure S6), representing Pd8Ox clusters with a different shape and composition than the most stable ones. The resulting activation barriers are shown in Figure S7 and follow the scaling law in Figure 5. This result strongly underpins the validity of our conclusions and the value of the scaling law presented. Since the CO oxidation activity is largely determined by the barrier of the CO oxidation step, we can in principle determine relative contributions of such less frequently encountered structures to the overall rate.

Figure 5.

Figure 5

Open in a new tab

CO adsorption on CeO2 supported Pd8 and Pd8Ox nanoparticles. (a) A linear scaling relationship between the reaction barriers of lattice oxygen vacancy formation and CO and O adsorption energies on Pd8(Ox) and CeO2, respectively. (b) A linear scaling relationship between CO adsorption energies and the charge state of the binding Pd atom. (e,f) Corresponding configurations for CO adsorption on Pd8/CeO2, Pd8/CeO2–x′, Pd8O12/CeO2, and Pd8O6/CeO2 structures, respectively.

Conclusion

In brief, our computational study predicts that oxidation of CeO2-supported Pd leads to enhanced CO oxidation activity. In an O2-containing atmosphere, Pd-oxide is more stable than reduced Pd particles. The lower binding energy of CO to Pd-oxide results in a lower barrier for CO2 formation by association with a ceria O atom, which is the rate-controlling step. The linear dependence between the activation barrier for this CO2 formation step and the CO binding energy is the first example of a linear scaling law for a supported metal catalyst in which the reactivity of the metal–support interface features prominently.

Acknowledgments

Access to supercomputing facilities were funded by The Netherlands Organization for Scientific Research. We acknowledge financial support by NWO-Vici and NWO-Top grants. This work has received funding from the European Union’s Horizon 2020 research and innovation programme under Grant No. 686086 (Partial-PGMs).

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/jacs.7b13624.

  • Detailed information on GA-DFT, GCMC-DFT, DFT calculations, and microkinetics simulations; Table S1–S7 and Figure S1–S19 (PDF)

The authors declare no competing financial interest.

Supplementary Material

ja7b13624_si_001.pdf (3MB, pdf)

References

  1. Fu Q.; Li W. X.; Yao Y.; Liu H.; Su H. Y.; Ma D.; Gu X. K.; Chen L.; Wang Z.; Zhang H.; Wang B.; Bao X. Science 2010, 328, 1141. 10.1126/science.1188267. [DOI] [PubMed] [Google Scholar]
  2. Graciani J.; Mudiyanselage K.; Xu F.; Baber A. E.; Evans J.; Senanayake S. D.; Stacchiola D. J.; Liu P.; Hrbek J.; Sanz J. F. Science 2014, 345, 546. 10.1126/science.1253057. [DOI] [PubMed] [Google Scholar]
  3. Grass M. E.; Zhang Y.; Butcher D. R.; Park J. Y.; Li Y.; Bluhm H.; Bratlie K. M.; Zhang T.; Somorjai G. A. Angew. Chem., Int. Ed. 2008, 47, 8893. 10.1002/anie.200803574. [DOI] [PubMed] [Google Scholar]
  4. Over H.; Kim Y. D.; Seitsonen A. P.; Wendt S.; Lundgren E.; Schmid M.; Varga P.; Morgante A.; Ertl G. Science 2000, 287, 1474. 10.1126/science.287.5457.1474. [DOI] [PubMed] [Google Scholar]
  5. de Smit E.; Cinquini F.; Beale A. M.; Safonova O. V.; van Beek W.; Sautet P.; Weckhuysen B. M. J. Am. Chem. Soc. 2010, 132, 14928. 10.1021/ja105853q. [DOI] [PubMed] [Google Scholar]
  6. Hendriksen B. L.; Ackermann M. D.; Van Rijn R.; Stoltz D.; Popa I.; Balmes O.; Resta A.; Wermeille D.; Felici R.; Ferrer S. Nat. Chem. 2010, 2, 730. 10.1038/nchem.728. [DOI] [PubMed] [Google Scholar]
  7. Ligthart D.; van Santen R. A.; Hensen E. J. Angew. Chem., Int. Ed. 2011, 50, 5306. 10.1002/anie.201100190. [DOI] [PubMed] [Google Scholar]
  8. Ackermann M. D.; Pedersen T. M.; Hendriksen B. L. M.; Robach O.; Bobaru S. C.; Popa I.; Quiros C.; Kim H.; Hammer B.; Ferrer S. Phys. Rev. Lett. 2005, 95, 255505. 10.1103/PhysRevLett.95.255505. [DOI] [PubMed] [Google Scholar]
  9. Hutchings G. J.; Kiely C. J. Acc. Chem. Res. 2013, 46, 1759. 10.1021/ar300356m. [DOI] [PubMed] [Google Scholar]
  10. Gilroy K. D.; Ruditskiy A.; Peng H.-C.; Qin D.; Xia Y. Chem. Rev. 2016, 116, 10414. 10.1021/acs.chemrev.6b00211. [DOI] [PubMed] [Google Scholar]
  11. Jacques S. D.; Di Michiel M.; Beale A. M.; Sochi T.; O’Brien M. G.; Espinosa-Alonso L.; Weckhuysen B. M.; Barnes P. Angew. Chem., Int. Ed. 2011, 50, 10148. 10.1002/anie.201104604. [DOI] [PubMed] [Google Scholar]
  12. Banger K.; Yamashita Y.; Mori K.; Peterson R.; Leedham T.; Rickard J.; Sirringhaus H. Nat. Mater. 2011, 10, 45. 10.1038/nmat2914. [DOI] [PubMed] [Google Scholar]
  13. Uchiyama T.; Yoshida H.; Kuwauchi Y.; Ichikawa S.; Shimada S.; Haruta M.; Takeda S. Angew. Chem., Int. Ed. 2011, 50, 10157. 10.1002/anie.201102487. [DOI] [PubMed] [Google Scholar]
  14. Bera P.; Hegde M. RSC Adv. 2015, 5, 94949. 10.1039/C5RA16474E. [DOI] [Google Scholar]
  15. Boronin A.; Slavinskaya E.; Danilova I.; Gulyaev R.; Amosov Y. I.; Kuznetsov P.; Polukhina I.; Koscheev S.; Zaikovskii V.; Noskov A. Catal. Today 2009, 144, 201. 10.1016/j.cattod.2009.01.035. [DOI] [Google Scholar]
  16. Tauster S.; Fung S.; Garten R. L. J. Am. Chem. Soc. 1978, 100, 170. 10.1021/ja00469a029. [DOI] [Google Scholar]
  17. Kehoe A. B.; Scanlon D. O.; Watson G. W. Chem. Mater. 2011, 23, 4464. 10.1021/cm201617d. [DOI] [Google Scholar]
  18. Wang B.; Weng D.; Wu X.; Ran R. Appl. Surf. Sci. 2011, 257, 3878. 10.1016/j.apsusc.2010.11.083. [DOI] [Google Scholar]
  19. Liu B.; Liu J.; Li T.; Zhao Z.; Gong X.-Q.; Chen Y.; Duan A.; Jiang G.; Wei Y. J. Phys. Chem. C 2015, 119, 12923. 10.1021/acs.jpcc.5b00267. [DOI] [Google Scholar]
  20. Faticanti M.; Cioffi N.; De Rossi S.; Ditaranto N.; Porta P.; Sabbatini L.; Bleve-Zacheo T. Appl. Catal., B 2005, 60, 73. 10.1016/j.apcatb.2005.02.022. [DOI] [Google Scholar]
  21. Luo M.-F.; Pu Z.-Y.; He M.; Jin J.; Jin L.-Y. J. Mol. Catal. A: Chem. 2006, 260, 152. 10.1016/j.molcata.2006.07.020. [DOI] [Google Scholar]
  22. Fernández-Garcıa M.; Martınez-Arias A.; Salamanca L.; Coronado J.; Anderson J.; Conesa J.; Soria J. J. Catal. 1999, 187, 474. 10.1006/jcat.1999.2624. [DOI] [Google Scholar]
  23. Hinokuma S.; Fujii H.; Okamoto M.; Ikeue K.; Machida M. Chem. Mater. 2010, 22, 6183. 10.1021/cm102355x. [DOI] [Google Scholar]
  24. Oh S.-H.; Hoflund G. B. J. Phys. Chem. A 2006, 110, 7609. 10.1021/jp060435u. [DOI] [PubMed] [Google Scholar]
  25. Liu Z.-P.; Gong X.-Q.; Kohanoff J.; Sanchez C.; Hu P. Phys. Rev. Lett. 2003, 91, 266102. 10.1103/PhysRevLett.91.266102. [DOI] [PubMed] [Google Scholar]
  26. Honkala K.; Hellman A.; Remediakis I. N.; Logadottir A.; Carlsson A.; Dahl S.; Christensen C. H.; Norskov J. K. Science 2005, 307, 555. 10.1126/science.1106435. [DOI] [PubMed] [Google Scholar]
  27. Qiao B.; Wang A.; Yang X.; Allard L. F.; Jiang Z.; Cui Y.; Liu J.; Li J.; Zhang T. Nat. Chem. 2011, 3, 634. 10.1038/nchem.1095. [DOI] [PubMed] [Google Scholar]
  28. Calle-Vallejo F.; Loffreda D.; KoperMarc T. M.; Sautet P. Nat. Chem. 2015, 7, 403. 10.1038/nchem.2226. [DOI] [PubMed] [Google Scholar]
  29. Norskov J. K.; Bligaard T.; Rossmeisl J.; Christensen C. H. Nat. Chem. 2009, 1, 37. 10.1038/nchem.121. [DOI] [PubMed] [Google Scholar]
  30. Yang X.-F.; Wang A.; Qiao B.; Li J.; Liu J.; Zhang T. Acc. Chem. Res. 2013, 46, 1740. 10.1021/ar300361m. [DOI] [PubMed] [Google Scholar]
  31. Wang Y.-G.; Mei D.; Glezakou V.-A.; Li J.; Rousseau R. Nat. Commun. 2015, 6, 6511. 10.1038/ncomms7511. [DOI] [PMC free article] [PubMed] [Google Scholar]
  32. Li W.-Z.; Liu J.-X.; Gu J.; Zhou W.; Yao S.-Y.; Si R.; Guo Y.; Su H.-Y.; Yan C.-H.; Li W.-X.; Zhang Y.-W.; Ma D. J. Am. Chem. Soc. 2017, 139, 2267. 10.1021/jacs.6b10375. [DOI] [PubMed] [Google Scholar]
  33. Camellone M. F.; Fabris S. J. Am. Chem. Soc. 2009, 131, 10473. 10.1021/ja902109k. [DOI] [PubMed] [Google Scholar]
  34. Hornés A.; Hungría A.; Bera P.; Cámara A. L.; Fernández-García M.; Martínez-Arias A.; Barrio L.; Estrella M.; Zhou G.; Fonseca J. J. Am. Chem. Soc. 2009, 132, 34. 10.1021/ja9089846. [DOI] [PubMed] [Google Scholar]
  35. Vayssilov G. N.; Lykhach Y.; Migani A.; Staudt T.; Petrova G. P.; Tsud N.; Skála T.; Bruix A.; Illas F.; Prince K. C.; Matolín V. r.; Neyman K. M.; Libuda J. Nat. Mater. 2011, 10, 310. 10.1038/nmat2976. [DOI] [PubMed] [Google Scholar]
  36. Kim H. Y.; Lee H. M.; Henkelman G. J. Am. Chem. Soc. 2012, 134, 1560. 10.1021/ja207510v. [DOI] [PubMed] [Google Scholar]
  37. Cargnello M.; Doan-Nguyen V. V.; Gordon T. R.; Diaz R. E.; Stach E. A.; Gorte R. J.; Fornasiero P.; Murray C. B. Science 2013, 341, 771. 10.1126/science.1240148. [DOI] [PubMed] [Google Scholar]
  38. Zhang L.; Kim H. Y.; Henkelman G. J. Phys. Chem. Lett. 2013, 4, 2943. 10.1021/jz401524d. [DOI] [PubMed] [Google Scholar]
  39. Satsuma A.; Osaki K.; Yanagihara M.; Ohyama J.; Shimizu K. Appl. Catal., B 2013, 132, 511. 10.1016/j.apcatb.2012.12.025. [DOI] [Google Scholar]
  40. Song W.; Su Y.; Hensen E. J. M. J. Phys. Chem. C 2015, 119, 27505. 10.1021/acs.jpcc.5b09293. [DOI] [Google Scholar]
  41. Liu B.; Zhao Z.; Henkelman G.; Song W. J. Phys. Chem. C 2016, 120, 5557. 10.1021/acs.jpcc.6b00253. [DOI] [Google Scholar]
  42. Ha H.; An H.; Yoo M.; Lee J.; Kim H. Y. J. Phys. Chem. C 2017, 121, 26895. 10.1021/acs.jpcc.7b09780. [DOI] [Google Scholar]
  43. Wang H.; Liu S.; Zhao Z.; Zou X.; Liu M.; Liu W.; Wu X.; Weng D. Catal. Sci. Technol. 2017, 7, 2129. 10.1039/C7CY00450H. [DOI] [Google Scholar]
  44. Reuter K.; Scheffler M. Phys. Rev. B: Condens. Matter Mater. Phys. 2001, 65, 035406. 10.1103/PhysRevB.65.035406. [DOI] [Google Scholar]
  45. Li W.-X.; Stampfl C.; Scheffler M. Phys. Rev. Lett. 2003, 90, 256102. 10.1103/PhysRevLett.90.256102. [DOI] [PubMed] [Google Scholar]
  46. Zhao S.; Liu X.-W.; Huo C.-F.; Li Y.-W.; Wang J.; Jiao H. Catal. Struct. React. 2015, 1, 44. 10.1179/2055075814Y.0000000007. [DOI] [Google Scholar]
  47. Deaven D.; Ho K. Phys. Rev. Lett. 1995, 75, 288. 10.1103/PhysRevLett.75.288. [DOI] [PubMed] [Google Scholar]
  48. Wales D. J.; Doye J. P. J. Phys. Chem. A 1997, 101, 5111. 10.1021/jp970984n. [DOI] [Google Scholar]
  49. Senftle T. P.; van Duin A. C.; Janik M. J. ACS Catal. 2017, 7, 327. 10.1021/acscatal.6b02447. [DOI] [Google Scholar]
  50. Kresse G.; Hafner J. Phys. Rev. B: Condens. Matter Mater. Phys. 1993, 47, 558. 10.1103/PhysRevB.47.558. [DOI] [PubMed] [Google Scholar]
  51. Kresse G.; Furthmüller J. Phys. Rev. B: Condens. Matter Mater. Phys. 1996, 54, 11169. 10.1103/PhysRevB.54.11169. [DOI] [PubMed] [Google Scholar]
  52. Blöchl P. E. Phys. Rev. B: Condens. Matter Mater. Phys. 1994, 50, 17953. 10.1103/PhysRevB.50.17953. [DOI] [PubMed] [Google Scholar]
  53. Perdew J. P.; Burke K.; Ernzerhof M. Phys. Rev. Lett. 1996, 77, 3865. 10.1103/PhysRevLett.77.3865. [DOI] [PubMed] [Google Scholar]
  54. Hammer B.; Hansen L. B.; Nørskov J. K. Phys. Rev. B: Condens. Matter Mater. Phys. 1999, 59, 7413. 10.1103/PhysRevB.59.7413. [DOI] [Google Scholar]
  55. Henkelman G.; Jónsson H. J. Chem. Phys. 2000, 113, 9978. 10.1063/1.1323224. [DOI] [Google Scholar]
  56. Laursen S.; Linic S. Phys. Chem. Chem. Phys. 2009, 11, 11006. 10.1039/b912641d. [DOI] [PubMed] [Google Scholar]
  57. Honeycutt J. D.; Andersen H. C. J. Phys. Chem. 1987, 91, 4950. 10.1021/j100303a014. [DOI] [Google Scholar]
  58. Shen L.; Dadras J.; Alexandrova A. N. Phys. Chem. Chem. Phys. 2014, 16, 26436. 10.1039/C4CP01877J. [DOI] [PubMed] [Google Scholar]
  59. Rogan J.; García G.; Valdivia J. A.; Orellana W.; Romero A.; Ramírez R.; Kiwi M. Phys. Rev. B: Condens. Matter Mater. Phys. 2005, 72, 115421. 10.1103/PhysRevB.72.115421. [DOI] [Google Scholar]
  60. Yoon B.; Häkkinen H.; Landman U.; Wörz A. S.; Antonietti J.-M.; Abbet S.; Judai K.; Heiz U. Science 2005, 307, 403. 10.1126/science.1104168. [DOI] [PubMed] [Google Scholar]
  61. Vajda S.; Pellin M. J.; Greeley J. P.; Marshall C. L.; Curtiss L. A.; Ballentine G. A.; Elam J. W.; Catillon-Mucherie S.; Redfern P. C.; Mehmood F. Nat. Mater. 2009, 8, 213. 10.1038/nmat2384. [DOI] [PubMed] [Google Scholar]
  62. Karabacak M.; Özçelik S.; Güvenç Z. Surf. Sci. 2002, 507, 636. 10.1016/S0039-6028(02)01328-6. [DOI] [Google Scholar]
  63. Chen M.; Goodman D. Science 2004, 306, 252. 10.1126/science.1102420. [DOI] [PubMed] [Google Scholar]
  64. Judai K.; Abbet S.; Wörz A. S.; Heiz U.; Henry C. R. J. Am. Chem. Soc. 2004, 126, 2732. 10.1021/ja039037k. [DOI] [PubMed] [Google Scholar]
  65. Martínez-Suárez L.; Frenzel J.; Marx D.; Meyer B. Phys. Rev. Lett. 2013, 110, 086108. 10.1103/PhysRevLett.110.086108. [DOI] [PubMed] [Google Scholar]
  66. Loschen C.; Carrasco J.; Neyman K. M.; Illas F. Phys. Rev. B: Condens. Matter Mater. Phys. 2007, 75, 035115. 10.1103/PhysRevB.75.035115. [DOI] [Google Scholar]
  67. Li H.-Y.; Wang H.-F.; Gong X.-Q.; Guo Y.-L.; Guo Y.; Lu G.; Hu P. Phys. Rev. B: Condens. Matter Mater. Phys. 2009, 79, 193401. 10.1103/PhysRevB.79.193401. [DOI] [Google Scholar]
  68. Ganduglia-Pirovano M. V.; Da Silva J. L.; Sauer J. Phys. Rev. Lett. 2009, 102, 026101. 10.1103/PhysRevLett.102.026101. [DOI] [PubMed] [Google Scholar]
  69. Peterson E. J.; DeLaRiva A. T.; Lin S.; Johnson R. S.; Guo H.; Miller J. T.; Kwak J. H.; Peden C. H.; Kiefer B.; Allard L. F. Nat. Commun. 2014, 5, 5885. 10.1038/ncomms5885. [DOI] [PubMed] [Google Scholar]
  70. Johns T. R.; Goeke R. S.; Ashbacher V.; Thüne P. C.; Niemantsverdriet J.; Kiefer B.; Kim C. H.; Balogh M. P.; Datye A. K. J. Catal. 2015, 328, 151. 10.1016/j.jcat.2015.03.016. [DOI] [Google Scholar]
  71. Meng L.; Jia A.-P.; Lu J.-Q.; Luo L.-F.; Huang W.-X.; Luo M.-F. J. Phys. Chem. C 2011, 115, 19789. 10.1021/jp2056688. [DOI] [Google Scholar]
  72. Zhou Y.; Lawrence N. J.; Wu T. S.; Liu J.; Kent P.; Soo Y. L.; Cheung C. L. ChemCatChem 2014, 6, 2937. 10.1002/cctc.201402243. [DOI] [Google Scholar]
  73. Li G.; Li L.; Yuan Y.; Shi J.; Yuan Y.; Li Y.; Zhao W.; Shi J. Appl. Catal., B 2014, 158, 341. 10.1016/j.apcatb.2014.04.030. [DOI] [Google Scholar]
  74. Wu J.; Zeng L.; Cheng D.; Chen F.; Zhan X.; Gong J. Chin. J. Catal. 2016, 37, 83. 10.1016/S1872-2067(15)60913-5. [DOI] [Google Scholar]
  75. Spezzati G.; Su Y.; Hofmann J. P.; Benavidez A. D.; DeLaRiva A. T.; McCabe J.; Datye A. K.; Hensen E. J. M. ACS Catal. 2017, 7, 6887. 10.1021/acscatal.7b02001. [DOI] [PMC free article] [PubMed] [Google Scholar]
  76. Stegelmann C.; Andreasen A.; Campbell C. T. J. Am. Chem. Soc. 2009, 131, 8077. 10.1021/ja9000097. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

ja7b13624_si_001.pdf (3MB, pdf)

Articles from Journal of the American Chemical Society are provided here courtesy of American Chemical Society

RESOURCES