Randomness in nonlocal games between mistrustful players

Abstract

If two quantum players at a nonlocal game G achieve a superclassical score, then their measurement outcomes must be at least partially random from the perspective of any third player. This is the basis for device-independent quantum cryptography. In this paper we address a related question: does a superclassical score at G guarantee that one player has created randomness from the perspective of the other player? We show that for complete-support games, the answer is yes: even if the second player is given the first player’s input at the conclusion of the game, he cannot perfectly recover her output. Thus some amount of local randomness (i.e., randomness possessed by only one player) is always obtained when randomness is certified from nonlocal games with quantum strategies. This is in contrast to non-signaling game strategies, which may produce global randomness without any local randomness. We discuss potential implications for cryptographic protocols between mistrustful parties.

INTRODUCTION

When two quantum parties Alice and Bob play a non-local game G and achieve a score that exceeds the best classical score ω_c(G), their outputs must be at least partially random. In other words, all Bell inequality violations certify the existence of randomness. This fact is at the center of protocols for device-independent quantum cryptography, where untrusted devices are used to per- form cryptographic procedures. In particular, this notion of certification is the basis for device-independent randomness expansion, where a small random seed is converted into a much larger uniformly random output by repeating Bell violations [1–12].

A natural question arises: is new randomness also generated by one player from the perspective of the other player? Specifically, if X denotes Alice’s outputs, Z denotes the post-measurement state that Bob has at the conclusion of the game, and F denotes all side information (including Alice’s input), is there a certified lower bound for the conditional entropy H(X | ZF)? Besides helping us understand the nature of certified randomness, this particular kind of randomness (local randomness) has applications in mutually mistrustful cryptographic settings, where Alice and Bob are cooperating but have different interests.

Quantifying local randomness (i.e., randomness that is only known to one player) is challenging because many of the known tools do not apply. Lower bounds for the total randomness (i.e, randomness from the perspective of an outside adversary) have been computed as a function of the degree of the Bell violation (see Figure 2 in [2]) but are not directly useful for certifying local randomness. One of the central challenges is that we are measuring randomness from the perspective of an active, rather than passive, adversary: Bob’s guess at Alice’s output occurs after Bob has carried out his part of the strategy for G. Current tools for device-independent randomness expansion are not designed to address the case where the adversary is a participant in the nonlocal game.

Does the generation of certified randomness always involve the generation of local certified randomness? The answer is not obvious: for example, in the non-signaling setting, Alice and Bob could share a PR-box¹ which generates 1 bit of certified randomness per use, but no new local randomness – Bob could perfectly guess Alice’s output from his own if he were given Alice’s input.

Motivated by the above, we prove the following result in this paper (see Theorem 14 for a formal statement).

Theorem 1 (Informal)

For any complete-support game² G, there is a constant C_G > 0 such that the following holds. Suppose Alice and Bob use a strategy for G which achieves a score that is δ above the best classical score (with δ > 0). Then, at the conclusion of the strategy and given Alice’s input, Bob can guess her output with probability at most (1 − δ²/C_G).

We note that similar problems have been studied in the literature in settings different from ours. There has been other work examining the scenario where a third party tries to guess Alice’s output after a game (e.g., [13], [14], [15]), and single-round games have appeared where Bob is sometimes given only Alice’s input, and asked to produce her output (e.g., [16], [17], [18]). (We believe the novelty of our scenario in comparison to these papers is that we consider the randomness of Alice’s output after Bob has performed his part of a quantum strategy, and thus has potentially lost information due to measurement.) Two recent papers also address randomness between multiple players, under assumptions about imperfect storage [19, 20].

In addition to the above, we prove a structural theorem for quantum strategies that allow perfect guessing by Bob. Not only do such strategies not achieve Bell inequalities, but they are also essentially classical in the following sense. Let D,E denote the quantum systems possessed by Alice and Bob, respectively

Theorem 2 (Informal)

Suppose that Alice’s and Bob’s strategy is such that if the game G is played and then Bob is given Alice’s input, he can perfectly guess her output. Then, there is an isometry mapping Bob’s system to E₁ ⊗ E₂ such that Bob’s strategy for G involves only E₁, and all of Alice’s observables commute with the reduced state on DE₁.

(See Theorem 5 and Corollary 7 for a formal statement.) Thus, in the case of perfect guessing, the strategy is equivalent to one in which Alice’s measurements have no effect on the shared state.

Structure of the paper

We begin with the case of perfect guessing. We formalize the concept of an essentially classical strategy, using a definition of equivalence between strategies which is similar to definitions used in results on quantum rigidity. We then give the proof of Theorem 2. It is known that two sets of mutually commuting measurements on a finite-dimensional space can be expressed as the pullback of bipartite measurements. This fact is used along with matrix algebra arguments to show the necessary splitting of Bob’s system into E₁ ⊗ E₂.

Then we proceed with the proof of Theorem 1. It has been observed by previous work (e.g., [16], [21]) that if a measurement {P_i} on a system D from bipartite state ρ_DE are highly predictable via measurements on E, then the measurement does not disturb the reduced state by much: Σ_i P_iρ_DP_i ~ ρ_D. In this paper we give a simplified proof of that fact (Proposition 11). The interesting consequence for our purpose is that if Alice’s measurements are highly predictable to Bob, then Alice can copy out her measurement outcomes in advance, thus making her strategy approximately classical. We take this a step further, and show that if Bob first performs his own measurement on E the resulting classical-quantum correlation is also approximately preserved by Alice’s measurements (which is not necessarily true of the original entangled state ρ_AB). This is sufficient to show that an approximately-guessable strategy yields an approximately classical strategy.

The subtleties in the proof are in establishing the error terms that arise when Alice copies out multiple measures from her side of the state. We note that the proof crucially requires that the game G has complete support. An interesting further avenue is to explore how local randomness may break down if the condition is not satisfied.

In section we discuss the implications of our result.

PRELIMINARIES

For any finite-dimensional Hilbert space V, let L(V) denote the vector space of linear automorphisms of V. For any M, N ∈ L(V), we let 〈M, N〉 denote Tr[M*N]. If S ⊆ V is a subspace of V, let P_S ∈ L(V) denote orthogonal projection onto V.

Throughout this paper we fix four disjoint finite sets 𝒜, ℬ, 𝒳, 𝒴, which denote, respectively, the first player’s input alphabet, the second player’s input alphabet, the first player’s output alphabet, and the second player’s output alphabet. A 2-player (input-output) correlation is a vector $(p_{\mathit{\text{ab}}}^{\mathit{\text{xy}}})$ of nonnegative reals, indexed by a, b, x, y ∈ 𝒜 × ℬ × 𝒳 × 𝒴 satisfying ${\sum }_{\mathit{\text{xy}}}{p}_{\mathit{\text{ab}}}^{\mathit{\text{xy}}}=1$ for all pairs (a, b), and satisfying the condition that the quantities

$$p_a^x≔{\sum }_y{p}_{\mathit{\text{ab}}}^{\mathit{\text{xy}}},p_b^y≔{\sum }_x{p}_{\mathit{\text{ab}}}^{\mathit{\text{xy}}}$$ (1)

are independent of b and a, respectively (no-signaling).

A 2-player game is a pair (q, H) where

$$q:𝒜\times ℬ\to [0,1]$$ (2)

is a probability distribution and

$$H:𝒜\times ℬ\times 𝒳\times 𝒴\to [0,1]$$ (3)

is a function. If q(a, b) ≠ 0 for all a ∈ 𝒜 and b ∈ ℬ, the game is said to have a complete support. The expected score associated to such a game for a 2-player correlation $(p_{\mathit{\text{ab}}}^{\mathit{\text{xy}}})$ is

$$\sum _{a,b,x,y}q(a,b)H(a,b,x,y)p_{\mathit{\text{ab}}}^{\mathit{\text{xy}}}.$$ (4)

We will extend notation by writing q(a) = Σ_b q(a, b), q(b) = Σ_a q(a, b), and q(a | b) = q(a, b)/q(b) (if q(b) ≠ 0).

A 2-player strategy is a 5-tuple

$$\mathrm{\Gamma }=(D,E,{\{{\{R_a^x\}}_x\}}_a,{\{{\{S_b^y\}}_y\}}_b,\gamma )$$ (5)

such that D, E are finite dimensional Hilbert spaces, ${\{{\{R_a^x\}}_x\}}_a$ is a family of 𝒳-valued positive operator valued measures (POVMs) on D (indexed by 𝒜), ${\{{\{S_b^y\}}_y\}}_b$ is a family of 𝒴-valued positive operator valued measures on E, and γ is a density operator on D ⊗ E. The second player states $p_{\mathit{\text{ab}}}^{\mathit{\text{xy}}}$ of Γ are defined by

$${\rho }_{\mathit{\text{ab}}}^{\mathit{\text{xy}}}≔{\text{Tr}}_D\left[\sqrt{R_a^x\otimes S_b^y}\gamma \sqrt{R_a^x\otimes S_b^y}\right]$$ (6)

(These states are, more explicitly, the subnormalized states of Bob’s system that arise after both Alice and Bob have performed their measurements.) Define ${\rho }_a^x$ by the same expression with $S_b^y$ replaced by the identity operator. (These represent the pre-measurement states of the second-player.) Define $\rho ≔{\text{Tr}}_D(\gamma )={\sum }_x{\rho }_a^x$ for any a.

We say that the strategy Γ achieves the 2-player correlation $(p_{\mathit{\text{ab}}}^{\mathit{\text{xy}}})$ if $p_{\mathit{\text{ab}}}^{\mathit{\text{xy}}}=\text{Tr}[\gamma (R_a^x\otimes S_b^y)]$ for all a, b, x, y. If a 2-player correlation $(p_{\mathit{\text{ab}}}^{\mathit{\text{xy}}})$ can be achieved by a 2-player strategy then we say that it is a quantum correlation.

If $(p_{\mathit{\text{ab}}}^{\mathit{\text{xy}}})$ is a convex combination of product distributions (i.e., distributions of the form $(q_a^x)\otimes (r_b^y)$ where ${\sum }_x{q}_a^x=1$ and ${\sum }_y{r}_b^y=1$ then we say that $(p_{\mathit{\text{ab}}}^{\mathit{\text{xy}}})$ is a classical correlation. Note that if the underlying state of a quantum strategy is separable (i.e., it is a convex combination of bipartite product states) then the correlation it achieves is classical. The maximum expected score that can be achieved for a game G by a classical correlation is denoted ω_c(G).

PERFECT GUESSING

We first address the case of perfect guessing — that is, the case when the second-player states ${\{{\rho }_{\mathit{\text{ab}}}^{\mathit{\text{xy}}}\}}_x$ that remain after the game is played are perfectly distinguishable by Bob. It turns out that this condition will imply some strong structural conditions on the strategy used by Alice and Bob, and it will imply in particular that Alice’s and Bob’s score at the game G cannot be better than that of any classical strategy.

Congruent strategies

It is necessary to identify pairs of strategies that are essentially the same from an operational standpoint. We use a definition that is similar to definitions from quantum self-testing (e.g., Definition 2.13 in [22]).

A unitary embedding from a 2-player strategy

$$\mathrm{\Gamma }=(D,E,{\{{\{R_a^x\}}_x\}}_a,{\{{\{S_b^y\}}_y\}}_b,\gamma )$$ (7)

to another 2-player strategy

$$\overline{\mathrm{\Gamma }}=(\overline{D},\overline{E},{\{{\{{\overline{R}}_a^x\}}_x\}}_a,{\{{\{{\overline{S}}_b^y\}}_y\}}_b,\overline{\gamma })$$ (8)

is a pair of unitary embeddings i : D ↪ D̅ and j : E ↪ Ē such that γ̅ = (i ⊗ j)γ(i ⊗ j)*, $R_a^x=i^{\ast }{\overline{R}}_a^{x}i$, and $S_b^y=j^{\ast }{\overline{S}}_b^{y}j$.

Additionally, if Γ is such that D = D₁ ⊗ D₂, and $R_a^x=G_a^x\otimes I$ for all a, x, then we will call the strategy given by

$$(D_1,E,{\{{\{G_a^x\}}_a\}}_x,{\{{\{S_b^y\}}_y\}}_b,{\text{Tr}}_{D_2}\gamma )$$ (9)

a partial trace of Γ. We can similarly define a partial trace on the second subspace E if it is a tensor product space.

We will say that two strategies Γ and Γ′ are congruent if there exists a sequence of strategies Γ = Γ₁, …, Γ_n = Γ′ such that for each i ∈ {1, …, n − 1}, either Γ_i+1 is a partial trace of Γ_i, or vice versa, or there is a unitary embedding of Γ_i into Γ_i+1, or vice versa. This is an equivalence relation. Intuitively, two strategies are congruent if one can be constructed from the other by adding or dropping irrelevant information. Note that if two strategies are congruent then they achieve the same correlation.

Essentially classical strategies

We are ready to define the key concept in this section and to state formally our main theorem.

Definition 3

A quantum strategy (5) is said to be essentially classical if it is congruent to one where γ commutes with $R_a^x$ for all x and a.

Note that if the above condition holds, then applying the measurement map

$$X\mapsto \sum _x\sqrt{G_a^x}X\sqrt{G_a^x}$$ (10)

to the system D leaves the state γ of DE unchanged.

We are interested in strategies after the application of which Bob can predict Alice’s output given her input. This is formalized as follows. If χ₁, …, χ_n are positive semidefinite operators on some finite dimensional Hilbert space V, then we say that {χ₁, …, χ_n} is perfectly distinguishable if χ_i and χ_j have orthogonal support for any i ≠ j. This is equivalent to the condition that there exists a projective measurement on V which perfectly identifies the state from the set {χ₁, …, χ_n}.

Definition 4

A quantum strategy (5) allows perfect guessing (by Bob) if for any a, b, y, ${\{{\rho }_{\mathit{\text{ab}}}^{\mathit{\text{xy}}}\}}_x$ is perfectly distinguishable.

Theorem 5 (Main Theorem)

If a strategy for a complete-support game allows perfect guessing, then it is essentially classical.

(We note that the converse of the statement is not true. This is because even in a classical strategy, Alice’s output may depend on some local randomness, which Bob cannot perfectly predict.)

Before giving the proof of this result, we note the following proposition, which taken together with Theorem 5 implies that any strategy that permits perfect guessing yields a classical correlation.

Proposition 6

The correlation achieved by an essentially classical strategy must be classical.

Proof

We need only to consider the case that γ commutes with $R_a^x$ for all a, x. For each a ∈ 𝒜, let V_a = ℂ^𝒳, and let Φ_a : L(D) → L(V_a ⊗ D) be the nondestructive measurement defined by

$${\mathrm{\Phi }}_a(T)=\sum _{x\in 𝒳}|x\rangle \langle x|\otimes \sqrt{R_a^x}T\sqrt{R_a^x}.$$ (11)

Note that by the commutativity assumption, such operation leaves the state of DE unchanged.

Since the measurements ${\{R_a^x\}}^x$ do not disturb the state of DE, Alice can copy out all of her measurement outcomes in advance. Without loss of generality, assume 𝒜 = {1, 2, …, n}. Let Λ ∈ L(V₁ ⊗ … ⊗ V_n ⊗ D ⊗ E) be the state that arises from applying the superoperators Φ₁, …, Φ_n, in order, to γ. For any a ∈ {1, …, n}, the reduced state Λ^V_aE is precisely the same as the result of taking the state γ, applying the measurement ${\{R_a^x\}}_x$ to D, and recording the result in V_a. Alice and Bob can therefore generate the correlation $(p_{\mathit{\text{ab}}}^{\mathit{\text{xy}}})$ from the marginal state Λ^V₁…V_nE alone (if Alice possesses V₁, …, V_n and Bob possesses E). Since this state is classical on Alice’s side, and therefore separable, the result follows.

Corollary 7

If a strategy for a complete-support game allows perfect guessing, the correlation achieved must be classical.

Proving Theorem 5

The proof will proceed as follows. First, we show that Alice’s measurements $R_a≔{\{R_a^x\}}_x$ induce projective measurements $Q_a≔{\{Q_a^x\}}_x$ on Bob’s system. Next, we argue that Q_a commutes with Bob’s own measurement $S_b≔{\{S_b^y\}}_y$ for any b. This allows us to isometrically decompose Bob’s system into two subsystems E₁ ⊗ E₂, such that S_b acts trivially on E₂, while E₂ alone can be used to predict x given a. The latter property allows us to arrive at the conclusion that R_a commutes with γ_DE1.

We will need the following lemma, which is well-known and commonly attributed to Tsirelson. We will only sketch the proof, and more details can be found in Appendix A of [23]. The lemma asserts that for families of positive semidefinite operators {M_j}, {N_k} on a finite-dimensional space V, commutativity (i.e., the condition that M_j, N_k commute for and j, k) implies bipartiteness (i.e., the condition that {M_j} and {N_k} can be obtained as pullbacks via a map V → V₁ ⊗ V₂ of operators on V₁ and V₂, respectively).

Lemma 8

Let {M_j}, {N_k} be positive semidefinite operators on a finite-dimensional Hilbert space V such that M_jN_k = N_kM_j for all j, k. Then, there exists a unitary embedding i : V ↪ V₁ ⊗ V₂ and and positive semidefinite operators $\overline{M_j}$ on V₁ and N̅_k on V₂ such that M_j = i* (M̅_j ⊗ 𝕀)i and N_k = i*(𝕀 ⊗ N̅_k)i for all j, k, ℓ, m.

Proof sketch

Via the theory of von Neumann algebras, there exists an isomorphism

$$V\cong \underset{\ell }{\oplus }{V}_{\ell }\otimes W_{\ell }$$ (12)

under which

$$M_j\cong \underset{\ell }{\oplus }{M}_j^{\ell }\otimes I,$$ (13)

$$N_k\cong \underset{\ell }{\oplus }I\otimes N_k^{\ell }.$$ (14)

Let V₁ = ⊕_ℓV_ℓ, V₂ = ⊕_ℓW_ℓ, and let ${\overline{M}}_j={\oplus }_{\ell }{M}_j^{\ell },{\overline{N}}_k={\oplus }_{\ell }{N}_j^{\ell }$.

Proof of Theorem 5

Express Γ as in (5). Without loss of generality, we may assume that Supp ρ = E. By the assumption that Γ allows perfect guessing, for any a, the second-player states ${\{{\rho }_a^x\}}_x$ must be perfectly distinguishable (since otherwise the post-measurement states ${\{{\rho }_{\mathit{\text{ab}}}^{\mathit{\text{xy}}}\}}_x$ would not be). Therefore, we can find projective measurements ${\{{\{Q_a^x\}}_x\}}_a$ on E such that

$$Q_a^x\rho Q_a^x={\rho }_a^x.$$ (15)

Note that for any fixed a, if Alice and Bob were to prepare the state γ_DE and Alice were to measure with ${\{R_a^x\}}_x$ and Bob were to measure with ${\{Q_a^x\}}_x$, their outcomes would be the same.

We have that the states

$${\rho }_{\mathit{\text{ab}}}^{\mathit{\text{xy}}}=\sqrt{S_b^y}{Q}_a^x\rho Q_a^x\sqrt{S_b^y}$$ (16)

$${\rho }_{\mathit{\text{ab}}}^{x\prime y}=\sqrt{S_b^y}{Q}_a^{x\prime }\rho Q_a^{x\prime }\sqrt{S_b^y}$$ (17)

have orthogonal support for any x ≠ x′. Since Supp ρ = E, we have c𝕀 ≤ ρ for some c > 0. Therefore,

$$\langle \sqrt{S_b^y}c{Q}_a^x\sqrt{S_b^y},\sqrt{S_b^y}c{Q}_a^{x\prime }\sqrt{S_b^y}\rangle =0,$$ (18)

which implies, using the cyclicity of the trace function,

$${\Vert Q_a^x{S}_b^y{Q}_a^{x\prime }\Vert }_2=0.$$ (19)

Therefore, the measurements ${\{Q_a^x\}}_x$ and ${\{S_b^y\}}_y$ commute for any a, b. (This is clear from writing out the matrix $S_b^y$ in block form under the subspaces determined by the projections ${\{Q_a^x\}}_x$.)

By Lemma 8, we can find a unitary embedding i : E ↪ E₁ ⊗ E₂ and POVMs ${\{{\overline{S}}_b^y\}}_y,{\{{\overline{Q}}_a^x\}}_x$ on E₁, E₂ such that $S_b^y=i^{\ast }({\overline{S}}_b^y\otimes 𝕀)i$ and $Q_a^x=i^{\ast }(𝕀\otimes {\overline{Q}}_a^x)i$. With

$$\overline{\gamma }=({𝕀}_D\otimes i)\gamma ({𝕀}_D\otimes i^{\ast }),$$ (20)

the strategy Γ embeds into the strategy

$$\mathrm{\Gamma }\prime ≔(D,E_1\otimes E_2,{\{{\{R_a^x\}}_x\}}_a,{{\{{\overline{S}}_b^y\otimes {𝕀}_{E_2}\}}_y\}}_b,\overline{\gamma }).$$

For any fixed a, the state γ̅ is such that applying the measurement ${\{R_a^x\}}_x$ to the system D and the measurement ${\{{\overline{Q}}_a^x\}}_x$ to the system E₂ always yields the same outcome. In particular, if we let

$${\tau }_a^x={\text{Tr}}_{E_2}\left({\overline{Q}}_a^x\overline{\gamma }\right),$$ (21)

then $\text{Tr}[R_a^{x\prime }{\tau }_a^x]$ will always be equal to 1 if x = x′ and equal to 0 otherwise. Therefore ${\{R_a^x\}}_x$ commutes with the operators ${\{{\tau }_a^x\}}_x$, and thus also with their sum ${\sum }_x{\tau }_a^x={\text{Tr}}_{E_2}\overline{\gamma }$.

Thus if we trace out the strategy Γ′ over the system E₂, we obtain a strategy (congruent to the original strategy Γ) in which Alice’s measurement operators commute with the shared state.

APPROXIMATE GUESSING

Next we address the case where the second-player states ${\rho }_{\mathit{\text{ab}}}^{\mathit{\text{xy}}}$ are not necessarily perfectly distinguishable as x varies, but are approximately distinguishable. (Thus, if Bob were given Alice’s input after the game was played and asked to guess her output, he could do so with probability close to 1.) We begin by quantizing “approximate” distinguishability.

Definition 9

Let ${\{{\rho }_i\}}_{i=1}^n$ denote a finite set of positive semidefinite operators on a finite dimensional Hilbert space V. Then, let

$$\text{Dist}\{{\rho }_i\}=\text{max}\sum _i\text{Tr}(T_i{\rho }_i),$$ (22)

where the maximum is taken over all POVMs ${\{T_i\}}_{i=1}^n$ on V.

Note that if Σ_i Tr(ρ_i) = 1, and each ρ_i is nonzero, then this quantity has the following interpretation: if Alice gives Bob a state from the set {ρ_i/Tr(ρ_i)} at random according to the distribution (Tr(ρ_i))_i, then Dist{ρ_i} is the optimal probability that Bob can correctly guess the state. This quantity is well-studied (see, e.g., [24]).

When we discussed perfect distinguishability, we made use of measurements that commuted with a given state. In the current section we will need an approximate version of such commutativity, and thus we make the following definition.

Definition 10

Let Φ: L(V) → L(V) denote a completely positive trace-preserving map over a finite-dimensional Hilbert space V. Let β ∈ L(V) denote a density operator on V. Then we say that Φ is ε-commutative with β if

$${\Vert \mathrm{\Phi }(\beta )-\beta \Vert }_1\le \epsilon .$$ (23)

Note that this relation obeys a natural triangle inequality: if Φ₁ is ε₁-commutative with β, and Φ₂ is ε₂-commutative with β, then

$${\Vert {\mathrm{\Phi }}_2({\mathrm{\Phi }}_1(\beta ))-\beta \Vert }_1\le {\Vert {\mathrm{\Phi }}_2({\mathrm{\Phi }}_1(\beta ))-{\mathrm{\Phi }}_2(\beta )\Vert }_1+{\Vert {\mathrm{\Phi }}_2(\beta )-\beta \Vert }_1\le {\Vert {\mathrm{\Phi }}_1(\beta )-\beta \Vert }_1+{\epsilon }_2\le {\epsilon }_1+{\epsilon }_2.$$

The following known proposition will be an important building block. We give a proof that is a significant simplification of a method from Lemma 29 in [21]. (See also Lemma 2 in [16] for a related result.)

Proposition 11

Let Λ ∈ L (A⊗B) be a density operator and ${\{F_i\}}_{i=1}^n$ a projective measurement on A such that the induced states ${\mathrm{\Lambda }}_i^B≔{\text{Tr}}_A(F_i\mathrm{\Lambda })$ satisfy

$$\text{Dist}\{{\mathrm{\Lambda }}_i^B\}=1-\delta .$$ (24)

Then, the superoperator X ↦ Σ_i F_i X F_i is $(2\sqrt{\delta }+\delta )$-commutative with Λ^A ≔ Tr_BΛ.

Proof

Let α = Λ^A. By assumption, there exists a POVM {G_i} on B such that

$$\sum _i\text{Tr}[(F_i\otimes G_i)\mathrm{\Lambda }]=1-\delta .$$ (25)

By standard arguments, we can assume without loss of generality that {G_i} is a projective measurement and that Λ is pure.³

There is a linear map M : ℂ^s → ℂ^r such that Tr_AΛ = M* M and α = Tr_BΛ = M M*. Upon choosing an appropriate basis for A and B, we can write M with a block form determined by the spans of {F_i} and {G_j}:

(26)

Let

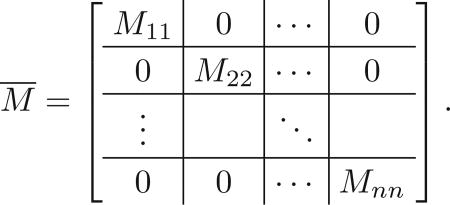(27)

Note that the probability of obtaining outcome F_i for the measurement on A and outcome G_j for the measurement on B is given by the quantity ${\Vert M_{\mathit{\text{ij}}}\Vert }_2^2$, and the probability that the outcomes of the measurements disagree is exactly ${\Vert M-\overline{M}\Vert }_2^2$. We have

$${\Vert M-\overline{M}\Vert }_2^2=\delta .$$ (28)

Additionally, we can compare ${\overline{\mathit{\text{MM}}}}^{\ast }$ to the post-measurement state Σ_i F_iαF_i. The latter quantity is given by

and therefore the difference $({\sum }_i{F}_i\alpha F_i-{\overline{\mathit{\text{MM}}}}^{\ast })$ is equal to

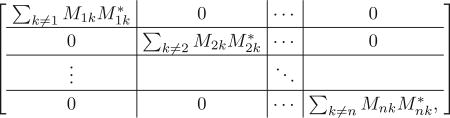which is a positive semidefinite operator whose trace is exactly ${\sum }_{i\ne j}{\Vert M_{\mathit{\text{ij}}}\Vert }_2^2=\delta$. Thus,

$${\Vert \sum _i{F}_i\alpha F_i-{\overline{\mathit{\text{MM}}}}^{\ast }\Vert }_1=\delta .$$ (29)

Therefore we have the following, using the Cauchy-Schwarz inequality:

$${\Vert \alpha -\sum _i{F}_i\alpha F_i\Vert }_1={\Vert {\mathit{\text{MM}}}^{\ast }-\sum _i{F}_i\alpha F_i\Vert }_1={\Vert M(M-{\overline{M}}^{\ast })+(M-\overline{M}){\overline{M}}^{\ast }+{\overline{\mathit{\text{MM}}}}^{\ast }-\sum _i{F}_i\alpha F_i\Vert }_1\le {\Vert M(M-{\overline{M}}^{\ast })\Vert }_1+{\Vert (M-\overline{M}){\overline{M}}^{\ast }\Vert }_1+{\Vert {\overline{\mathit{\text{MM}}}}^{\ast }-\sum _i{F}_i\alpha F_i\Vert }_1\le {\Vert M\Vert }_2{\Vert M-{\overline{M}}^{\ast }\Vert }_2+{\Vert M-\overline{M}\Vert }_2{\Vert {\overline{M}}^{\ast }\Vert }_2+\delta \le 1·\sqrt{\delta }+\sqrt{\delta }·1+\delta \le 2\sqrt{\delta }+\delta ,$$

as desired.

The previous proposition showed that if a measurement by Alice is highly predictable to Bob, then it does not disturb Alice’s marginal state by much. The next corollary asserts Alice’s measurement must also approximately preserve any existing classical correlation that Bob has with Alice’s state.

Corollary 12

Let Λ ∈ L(A ⊗ B ⊗ C) be a density operator which is classical on C. (That is, Λ = Σ_k Λ_k ⊗ |c_k〉 〈c_k| for some orthonormal basis {c₁, …, c_k} ⊆ C.) Suppose that ${\{F_i\}}_{i=1}^n$ is a projective measurement on A such that the induced states ${\mathrm{\Lambda }}_i^{\mathit{\text{BC}}}≔{\text{Tr}}_A(F_i\mathrm{\Lambda })$ satisfy

$$\text{Dist}\{{\mathrm{\Lambda }}_i^{\mathit{\text{BC}}}\}=1-\delta .$$ (30)

Then, the superoperator X ↦ Σ_i (F_i ⊗ I)X (F_i ⊗ I) is $(2\sqrt{\delta }+\delta )$-commutative with Λ^AC.

Proof

Let C̅ be a Hilbert space which is isomorphic to C, and let Λ̅ ∈ L (A ⊗ B ⊗ C ⊗ C̅) be the state that arises from Λ by copying out along the standard basis: $|c_i\rangle \mapsto |c_i\overline{c_i}\rangle$. This copying leaves the state ABC unaffected, so assumption (30) still applies. Thus by Proposition 11, the operator X ↦ Σ_i (F_i ⊗ I)X (F_i ⊗ I) is $(2\sqrt{\delta }+\delta )$-commutative with Λ^AC̅, and the same holds for the isomorphic state Λ^AC.

Now we prove a preliminary version of our main result. We assume that the states ${\{{\rho }_{\mathit{\text{ab}}}^{\mathit{\text{xy}}}\}}_x$ are highly distinguishable on average, and then deduce that Alice’s and Bob’s correlation must be approximately classical.

Proposition 13

Let

$$\mathrm{\Gamma }=(D,E,{\{{\{R_a^x\}}_x\}}_a,{\{{\{S_b^y\}}_y\}}_b,\gamma )$$ (31)

be a two-player strategy. Let

$$\delta =1-\frac{1}{|𝒜||ℬ|}\sum _{\mathit{\text{aby}}}\text{Dist}\{{\rho }_{\mathit{\text{ab}}}^{\mathit{\text{xy}}}|x\in 𝒳\}.$$ (32)

Then, there exists a classical correlation $({\overline{p}}_{\mathit{\text{ab}}}^{\mathit{\text{xy}}})$ such that

$$\frac{1}{|𝒜||ℬ|}\sum _{\mathit{\text{abxy}}}|p_{\mathit{\text{ab}}}^{\mathit{\text{xy}}}-{\overline{p}}_{\mathit{\text{ab}}}^{\mathit{\text{xy}}}|\le \sqrt{3\delta }|𝒜|.$$ (33)

Proof

We can assume without loss of generality that the measurements ${\{{\{R_a^x\}}_x\}}_a$ are all projective. We begin with the same strategy as in the proof of Proposition 6. For each a ∈ 𝒜, let V_a = ℂ^𝒳, and let Φ_a : L(D) → L(V_a ⊗ D) be the nondestructive measurement defined by

$${\mathrm{\Phi }}_a(T)=\sum _{x\in 𝒳}|x\rangle \langle x|\otimes R_a^x{\mathit{\text{TR}}}_a^x.$$ (34)

Let ${\mathrm{\Phi }}_a^{V_a}={\text{Tr}}_D◦{\mathrm{\Phi }}_a$ and let ${\mathrm{\Phi }}_a^D={\text{Tr}}_{V_a}◦{\mathrm{\Phi }}_a$. Likewise let W_b = ℂ^𝒴 for each b ∈ ℬ, let Ψ_b : L(E) → L(W_b ⊗ E) be the nondestructive measurement defined by

$${\mathrm{\Psi }}_b(T)=\sum _{y\in 𝒴}|y\rangle \langle y|\otimes \sqrt{S_b^y}T\sqrt{S_b^y}.$$ (35)

Let ${\mathrm{\Psi }}_b^{W_b}={\text{Tr}}_E◦{\mathrm{\Psi }}_b$ and ${\mathrm{\Psi }}_b^E={\text{Tr}}_{W_b}◦{\mathrm{\Psi }}_b$.

Assume without loss of generality that 𝒜 = {1, 2, …, n}. Let Λ ∈ L(V₁ ⊗ … ⊗ V_n ⊗ D ⊗ E) be the state that arises from applying the superoperators Φ₁ ⊗ I_E, …, Φ_n ⊗ I_E, in order, to γ. Let $({\overline{p}}_{\mathit{\text{ab}}}^{\mathit{\text{xy}}})$ be the correlation that arises from Alice and Bob sharing the reduced state Λ^V₁…V_nE, Alice obtaining her output on input a from the register V_a, and Bob obtaining his output from his prescribed measurements ${\{{\{S_b^y\}}_y\}}_b$ to E. Since the state Λ^V₁…V_nE is a separable state over the bipartition (V₁ … V_n | E), the correlation $({\overline{p}}_{\mathit{\text{ab}}}^{\mathit{\text{xy}}})$ is classical.

Let

$${\delta }_{\mathit{\text{ab}}}≔1-\sum _y\text{Dist}\{{\rho }_{\mathit{\text{ab}}}^{\mathit{\text{xy}}}|x\in 𝒳\}.$$ (36)

If Alice and Bob share the measured state (I_D ⊗ Ψ_b)(γ) partitioned as (D | EW_b), then the probability that Bob can guess Alice’s outcome when she measures with ${\{R_a^x\}}_x$ is given by (1 − δ_ab). By Corollary 12, the operator $({\mathrm{\Phi }}_a^D\otimes I_{W_b})$ is $(2\sqrt{{\delta }_{\mathit{\text{ab}}}}+{\delta }_{\mathit{\text{ab}}})$-commutative with $(I_D\otimes {\mathrm{\Psi }}_b^{W_b})\gamma$.

We wish to compare $(p_{\mathit{\text{ab}}}^{\mathit{\text{xy}}})$ and $({\overline{p}}_{\mathit{\text{ab}}}^{\mathit{\text{xy}}})$. For any a, b the probability vector ${({\overline{p}}_{\mathit{\text{ab}}}^{\mathit{\text{xy}}})}_{\mathit{\text{xy}}}$ describes the joint distribution of the registers V_aW_b under the density operator

$$(({\mathrm{\Phi }}_a^{V_a}◦{\mathrm{\Phi }}_{a-1}^D◦{\mathrm{\Phi }}_{a-2}^D◦\cdots ◦{\mathrm{\Phi }}_1^D)\otimes {\mathrm{\Psi }}_b^{W_b})\gamma ,$$ (37)

which by the previous paragraph is within trace-distance ${\sum }_{i=1}^{a-1}(2\sqrt{{\delta }_{\mathit{\text{ab}}}}+{\delta }_{\mathit{\text{ab}}})$ from the distribution described by ${(p_{\mathit{\text{ab}}}^{\mathit{\text{xy}}})}_{\mathit{\text{xy}}}$:

$$({\mathrm{\Phi }}_a^{V_a}\otimes {\mathrm{\Psi }}_b^{W_b})\gamma .$$ (38)

Thus we have the following, in which we use the Cauchy-Schwarz inequality:

$$\sum _{\mathit{\text{abxy}}}|p_{\mathit{\text{ab}}}^{\mathit{\text{xy}}}-{\overline{p}}_{\mathit{\text{ab}}}^{\mathit{\text{xy}}}|\le \sum _{\mathit{\text{ab}}}\sum _{i=1}^{a-1}(2\sqrt{{\delta }_{\mathit{\text{ib}}}}+{\delta }_{\mathit{\text{ib}}})$$ (39)

$$=\sum _{\mathit{\text{ab}}}(n-a)(2\sqrt{{\delta }_{\mathit{\text{ab}}}}+{\delta }_{\mathit{\text{ab}}}).$$ (40)

$$\le \sum _{\mathit{\text{ab}}}(n-a)3\sqrt{{\delta }_{\mathit{\text{ab}}}}$$ (41)

$$\le 3\sqrt{\sum _{\mathit{\text{ab}}}{(n-a)}^2}\sqrt{\sum _{\mathit{\text{ab}}}{\delta }_{\mathit{\text{ab}}}}$$ (42)

$$=3\sqrt{\sum _{\mathit{\text{ab}}}{(n-a)}^2}\sqrt{n|ℬ|\delta }$$ (43)

$$=3\sqrt{|ℬ|\sum _a{(n-a)}^2}\sqrt{n|ℬ|\delta }$$ (44)

$$=3|ℬ|\sqrt{\sum _a{(n-a)}^2}\sqrt{n\delta }$$ (45)

$$\le 3|ℬ|\sqrt{n^3/3}\sqrt{n\delta },$$ (46)

which simplifies to the desired bound.

Proposition 13 is useful for addressing any game (q, H) where the distribution q is uniform (i.e., q(a, b) = 1/(|𝒜||ℬ|).) We prove the following theorem which applies to more general games.

Theorem 14

Let G = (q, H) be a complete-support game and let

$$\mathrm{\Gamma }=(D,E,{\{{\{R_a^x\}}_x\}}_a,{\{{\{S_b^y\}}_y\}}_b,\gamma )$$ (47)

be a two-player strategy. Let

$$\epsilon =1-\sum _{\mathit{\text{ab}}}q(a,b)\sum _y\text{Dist}\{{\rho }_{\mathit{\text{ab}}}^{\mathit{\text{xy}}}|x\in 𝒳\}.$$ (48)

Then, the score achieved by Γ exceeds the best classical score ω_c(G) by at most $C_G\sqrt{\epsilon }$, where

$$C_G=(3/2)\sqrt{\sum _{\mathit{\text{ab}}}q(b){(q(a|b))}^{-1}}.$$ (49)

Proof

Define ${\overline{p}}_{\mathit{\text{ab}}}^{\mathit{\text{xy}}}$ and δ_ab as in Proposition 13. We have the following (again using the Cauchy-Schwartz inequality):

$$\sum _{\mathit{\text{abxy}}}q(a,b)|p_{\mathit{\text{ab}}}^{\mathit{\text{xy}}}-{\overline{p}}_{\mathit{\text{ab}}}^{\mathit{\text{xy}}}|$$ (50)

$$\le \sum _{\mathit{\text{ab}}}q(a,b)\sum _{i=1}^{a-1}(2\sqrt{{\delta }_{\mathit{\text{ib}}}}+{\delta }_{\mathit{\text{ib}}})$$ (51)

$$\le \sum _{\mathit{\text{ab}}}q(a,b)\sum _{i=1}^{a-1}3\sqrt{{\delta }_{\mathit{\text{ib}}}}$$ (52)

$$=\sum _{\mathit{\text{ab}}}(\sum _{k=a+1}^{n}q(k,b))3\sqrt{{\delta }_{\mathit{\text{ab}}}}$$ (53)

$$=\sum _{\mathit{\text{ab}}}\left(\frac{{\sum }_{k=a+1}^{n}q(k,b)}{\sqrt{q(a,b)}}\right)3\sqrt{q(a,b){\delta }_{\mathit{\text{ab}}}}$$ (54)

$$\le 3\sqrt{\sum _{\mathit{\text{ab}}}\frac{{({\sum }_{k=a+1}^{n}q(k,b))}^2}{q(a,b)}}\sqrt{\sum _{\mathit{\text{ab}}}q(a,b){\delta }_{\mathit{\text{ab}}}}$$ (55)

$$\le 3\sqrt{\sum _{\mathit{\text{ab}}}\frac{{({\sum }_{k=a+1}^{n}q(k,b))}^2}{q(a,b)}}\sqrt{\epsilon }$$ (56)

$$\le 3\sqrt{\sum _{\mathit{\text{ab}}}\frac{q{(b)}^2}{q(a,b)}}\sqrt{\epsilon }$$ (57)

$$\le 2C_G\sqrt{\epsilon }$$ (58)

Note that for any probability vectors t = (t₁, …, t_m) and s = (s₁, …, s_m) and any arbitrary vector (u₁, …, u_m) ∈ [0, 1]^m, we have

$$\sum _i{u}_i(t_i-s_i)\le \frac{1}{2}\sum |t_i-s_i|.$$ (59)

Applying this fact to the probability vectors ${(q(a,b)p_{\mathit{\text{ab}}}^{\mathit{\text{xy}}})}_{\mathit{\text{abxy}}}$ and ${(q(a,b){\overline{p}}_{\mathit{\text{ab}}}^{\mathit{\text{xy}}})}_{\mathit{\text{abxy}}}$ and the vector (H(a, b, x, y))_abxy implies that the difference between the score achieved by $(p_{\mathit{\text{ab}}}^{\mathit{\text{xy}}})$ and the score achieved by $({\overline{p}}_{\mathit{\text{ab}}}^{\mathit{\text{xy}}})$ is no more than half the quantity (58), which yields the desired result.

DISCUSSION

When two players achieve a superclassical score at a nonlocal game, their outputs must be at least partially unpredictable to an outside party, even if that party knows the inputs that were given. This fact is one of the bases for randomness expansion from untrusted devices [1], where a user referees a nonlocal game repeatedly with 2 or more untrusted players (or, equivalently, 2 or more untrusted quantum devices) to expand a small uniformly random seed S into a large output string T that is uniform conditioned on S. The players can exhibit arbitrary quantum behavior, but it is assumed that they are prevented from communicating with the adversary. At the center of some of the discussions of randomness expansion (e.g., [2]) is the fact that the min-entropy of the outputs of the players can be lower bounded by an increasing function of the score achieved at the game.

In this paper we have proven an analogous result for the case where one player in a game wishes to generate randomness that is unknown to the other player — in other words, we have achieved (one-shot) blind randomness expansion. (The second party, Bob, is “blind” to the randomness generated by Alice.) We have also proven a general rate curve for any game G, which relates the score achieve at G to the predictability of Alice’s output from the perspective of Bob – specifically, if G is a complete support game and Alice and Bob achieve score w, then Bob’s probability of guessing her output given her input is at most

$$f_G(w)=\{\begin{array}{cc}\hfill 1-{(w-{\omega }_c(G))}^2/C_G\hfill & \text{if }w\ge {\omega }_c(G)\hfill \\ \hfill 1\hfill & \text{otherwise},\hfill \end{array}$$

where C_G denotes the constant defined in equation (49).

A possible next step would be to prove a multi-shot version of Theorem 14, e.g., a proof that Alice’s outputs across multiple rounds have high smooth min-entropy from Bob’s perspective. With the use of a quantum-proof randomness extractor (e.g., [25]) this would imply that Alice has the ability to generate uniformly random bits, known only to her, through interactions with Bob. In the device-independent setting, this would mean that one device could be be reused in multiple iterations of randomness expansion without affecting the security guarantee, and in particular would decrease the minimum number of quantum devices needed to perform unbounded randomness expansion from four (as in [9, 26]) down to three.

The recent entropy accumulation theorem [11] proves lower bounds on smooth min-entropy in various scenarios where a Bell inequality is violated. It will be interesting to see if it can be generalized to cover blind randomness expansion as well. (The current results apply under a Markov assumption which is not satisfied in our case.)

A corollary of our result is that, for any complete-support game G, the range of scores that certify randomness against a third party are exactly the same as the range of scores that certify randomness for one player against the second — in both cases, any superclassical score is adequate. We point out, however, that the certified min-entropy can be different. A simple example of this is the Magic Square game, where Alice and Bob are given inputs a, b ∈ {1, 2, 3} respectively, and must produce outputs (x₁, x₂, x₃), (y₁, y₂, y₃) ∈ {0, 1}³ respectively which satisfy

$$x_1\oplus x_2\oplus x_3=0,$$ (60)

$$y_1\oplus y_2\oplus y_3=1,$$ (61)

$$x_b=y_a.$$ (62)

Self-testing [27] for the Magic Square game implies that if Alice and Bob achieve a perfect score, Alice’s output contains two bits of perfect randomness from the perspective of a third party, but only one perfect bit of randomness from the perspective of Bob. Optimizing the relationship between the game score and min-entropy in the blind scenario is an open problem.

A potentially useful aspect of Corollary 7 is that it contains a notion of certified erasure of information. For the example of the Magic Square game mentioned above, if Bob were asked before his turn to guess Alice’s output given her input, he could do this perfectly. (The optimal strategy for the Magic Square game uses a maximally entangled state and projective measurements, so each party’s measurement outcomes can be perfectly guessed by the other player.) Contrary to this, when Bob is compelled to carry out his part of the strategy before Alice’s input is revealed, he loses the ability to perfectly guess Alice’s output. Requiring a superclassical score from Alice and Bob amounts to forcing Bob to erase information. Different variants of certified erasure are a topic of current study [19, 20, 28]. An interesting research avenue is to determine the minimal assumptions under which certified erasure is possible.

Finally, we note that the scenario in which the second player tries to guess the first player’s output after computing his own output fits the general framework of sequential nonlocal correlations [29]. In [30] such correlations are used for ordinary (non-blind) randomness expansion. A next step is to explore how our techniques could be applied to more general sequential nonlocal games.