Highlights
-
•
Field, laboratory and theoretical work highlights the role of hydrologic controls on biota.
-
•
River networks act as ecological corridors for species, populations and pathogens.
-
•
A solid conceptual thread is identified via the directional dispersal induced by rivers.
-
•
Spatially explicit ecohydrological modeling of waterborne diseases is now thriving.
-
•
Notable perspectives are open to much development in ecohydrologic research.
Keywords: Metapopulation models, Metacommunity models, Spatially explicit ecology, Directional dispersal, Substrate topology
Abstract
This paper draws together several lines of argument to suggest that an ecohydrological framework, i.e. laboratory, field and theoretical approaches focused on hydrologic controls on biota, has contributed substantially to our understanding of the function of river networks as ecological corridors. Such function proves relevant to: the spatial ecology of species; population dynamics and biological invasions; the spread of waterborne disease. As examples, we describe metacommunity predictions of fish diversity patterns in the Mississippi–Missouri basin, geomorphic controls imposed by the fluvial landscape on elevational gradients of species’ richness, the zebra mussel invasion of the same Mississippi–Missouri river system, and the spread of proliferative kidney disease in salmonid fish. We conclude that spatial descriptions of ecological processes in the fluvial landscape, constrained by their specific hydrologic and ecological dynamics and by the ecosystem matrix for interactions, i.e. the directional dispersal embedded in fluvial and host/pathogen mobility networks, have already produced a remarkably broad range of significant results. Notable scientific and practical perspectives are thus open, in the authors’ view, to future developments in ecohydrologic research.
1. Introduction
1.1. The context
Although natural ecosystems are characterized by striking diversity of form and functions, they often exhibit symmetries, at times emerging across scales of space, time and organizational complexity (Levin, 1992). One angle through which such features could be looked at is via the necessary linkages among macroecological ‘laws’ (Banavar, Damuth, Maritan, Rinaldo, 2007, Southwood, May, Sugihara, 2006) where scaling theory offers a powerful tool to make way for coherent, unified descriptions of patterns in species’ numbers and their abundance and size. Patterns also emerge in relation to broad ecosystem features like the topology of the substrate for ecological interactions (Bertuzzo, Maritan, Gatto, Rodriguez-Iturbe, Rinaldo, 2007, Bertuzzo, Suweis, Mari, Maritan, Rodriguez-Iturbe, Rinaldo, 2011, Fagan, 2002, Muneepeerakul, Bertuzzo, Lynch, Fagan, Rinaldo, Rodriguez-Iturbe, 2008). It is remarkable that we observe some emerging features, like the distribution of species’ persistence times at observation sites (Bertuzzo et al., 2011b), that are controlled more by the nature of the landscape where interactions occur than by many features specific to the underlying ecosystem. A large body of empirical (Bertuzzo, Suweis, Mari, Maritan, Rodriguez-Iturbe, Rinaldo, 2011, Ricklefs, 1987) and laboratory (Altermatt, Bieger, Carrara, Rinaldo, Holyoak, 2011, Carrara, Altermatt, Rodriguez-Iturbe, Rinaldo, 2012, Giometto, Rinaldo, Carrara, Altermatt, 2013, Holyoak, Lawler, 2005) evidence was collected to support such a view. This result, a rather far-reaching one, is well captured by spatially explicit ecological approaches which we introduce below.
Within the above ecohydrological framework, river network structures and their embedded hydrologic dynamics play an important role (Rodriguez-Iturbe et al., 2009). In fact, they provide supporting landscapes for ecological processes, many of which are essential to human life and societies. To name a few, on which we shall return: Historically, human settlements followed the river networks for the necessary water resources (Ammermann and Cavalli-Sforza, 1984); River networks are home to (and provide hierarchical habitat features for) freshwater fish (Bertuzzo, Maritan, Gatto, Rodriguez-Iturbe, Rinaldo, 2007, Fagan, 2002, Muneepeerakul, Bertuzzo, Lynch, Fagan, Rinaldo, Rodriguez-Iturbe, 2008) and in general stream ecology (Battin, Kaplan, Findlay, 2008, Battin, Kaplan, Newbold, Hansen, 2003) as well as pathways to life-threatening waterborne human diseases (Rinaldo et al., 2017) and zoonoses, i.e. infections that can be passed between animals and humans. River networks may be also seen as meta-ecosystems that affect the metabolism of terrestrial organic carbon in freshwater ecosystems, an important part of the global carbon cycle (Battin, Kaplan, Newbold, Hansen, 2003, Raymond, Bauer, 2001) and the amount of nutrients removed from streams and reservoirs, affected by network structure and stream ecology therein (Alexander, Jones, Boyer, Smith, 2000, Battin, Kaplan, Findlay, 2008).
Thus, a broad and scientifically worth field of research exists where signatures coexist of the hydrologic, ecologic, and geomorphologic dynamics of river basins. This field has proved its importance e.g. by furthering our understanding of spatially explicit epidemiology and ecology (Sections 2–4). Our ultimate goal is a comprehensive theory of how dendritic structures, their associated features and interactions with external forcings (chiefly, hydrological stochasticity) shape emergent properties of various ecosystems. Such a theory would help us address a wide variety of important questions: from conservation plans for freshwater ecosystems to optimal control for containing water-borne disease epidemics to proper inclusion of riparian systems into large-scale resources management (D’Odorico, Laio, Porporato, Ridolfi, Rinaldo, Rodriguez-Iturbe, 2010, Rodriguez-Iturbe, Muneepeerakul, Bertuzzo, Levin, Rinaldo, 2009). Understanding and control of biological invasions is also part of this scheme. While providing what we believe is a useful review, the novelty of this paper lies in its global vision of a research area where hydrology, ecology, and geomorphology intersect and where we feel that important advances and their applications will be made in the near future. This is by no means a definitive statement of the roles of river networks as ecological corridors but rather a blueprint for future developments. Throughout the paper, in fact, we suggest research areas that look to us as particularly promising.
Including ecological dynamics into riverine systems is not an easy task, given the variety of the taxa involved, their trophic positions, the interactions between the different organisms ranging from competition to predation to parasitism. Very frequently, if the aim is to investigate population dynamics, the analysis is restricted to one or few species or functional groups. This is what has been done e.g. when exploring zebra mussel invasions (Mari et al., 2011) or cholera dynamics (Bertuzzo et al., 2011a). If instead the aim is to investigate general patterns of biodiversity, one usually considers specific taxa or groups, usually sharing the same trophic level, e.g. fish or phytoplankton or riparian vegetation. In this case, the main operating ecological interaction is interspecific competition, either indirect (e.g. exploitation of common food resources or nutrients) or direct (e.g. via interference). Available data are usually lists of presence/absence of species, possibly complemented by their relative abundances, the latter’s being averaged over time or simply measured in a given year. If the identity of the species is neglected, it is possible to derive species-abundance distributions, namely the number of species that have a certain abundance or a certain abundance rank. Static models of species-abundance relations have long been proposed to that goal (see e.g. Pielou, 1977 for an excellent review). Dynamic models, in which the observed relation is obtained as the long-term equilibrium of a model containing the basic time-dependent processes that shape community biodiversity, are more recent. The processes shaping the maintenance of biodiversity are four (Vellend, 2010): selection, namely the difference in the species fitnesses and therefore in their competitive ability - it operates in both ecological and evolutionary time; drift, namely the inherent stochasticity which brings species to extinction and operates in ecological time scale only when the size of the community is rather small; speciation, which counters drift and selection over evolutionary timescales; dispersal, which counters local species extinction via the movement of organisms across space and acts in ecological timescales. The seminal paper for the related dynamic models (Caswell, 1976) borrowed concepts of neutral molecular evolution and applied them to the ecological context. The organic development of a neutral theory of biodiversity have been presented in a unified way only much later (Hubbell, 2001). The main tenet therein assumes that all species are competitively equivalent at a per capita level, and that selection (i.e. differences in competitive ability, stated otherwise) is not operating, while drift is countered by speciation or dispersal (Chave et al., 2002). Concerning this last point, it is important to remark that most neutral theories are spatially implicit. Usually, they consider either an isolated community, whose composition is not location-specific and is driven by drift, while community survival is guaranteed by speciation, or a local non-isolated community, whose survival is guaranteed by immigration from a ‘background’ metacommunity. A coherent theory that considers all the four processes in a space-explicit framework distinguishing between ecological and evolutionary time scales is still lacking (but see Chave, Muller-Landau, Levin, 2002, Economo, Keitt, 2008 for notable attempts). The present paper aims at partially filling such a gap by presenting a series of models that are always space-explicit and suited to specifically describing the peculiar structure (and thus connectivity) of river basins. We proceed step by step, first including the dendritic substrate of river basins into the neutral paradigm of biodiversity, then breaking perfect neutrality by adding either space-dependent carrying capacities of local communities or elevational niche apportionment. Species invasion and disease spread is subsequently investigated by paying greater attention to realistic details, though with a species-specific focus and within fluvial ecological substrates.
To set the context, we start with an example of the simplest dynamic model of biodiversity, the neutral one (Hubbell, 2001). In fact, inclusion of all factors, no matter how detailed and realistic, seemed hardly a good starting point for the quest of how biodiversity patterns are influenced by river network configuration (Rodriguez-Iturbe et al., 2009). It should be noted that some unrealistic assumptions of the neutral theory have attracted much criticism (McGill, Maurer, Weiser, 2006, Nee, 2005, Purves, Turnbull, 2010) e.g. in terms of timescales, testability and robustness; also, the neutral theory overlooks much species-specific ecological information, which is required when studying the dynamics of the system or of a set of particular species and the interactions among them (Chave et al., 2002). However, the neutral model has the advantage of letting us introduce the biodiversity-shaping processes one by one; in fact, the neutral theory switches off all the differences between species and all the interactions with the exception of strong competition for space (both intra- and inter-species), as we shall recall below. Being focused on competition for space, it is thus particularly suited to test the fundamental differences between the spatial structure of river basins and 2D isotropic landscapes. Our first approach thus focuses on the quantitative assessment of the role of directionality and network structure on ecological organization, in particular on patterns of diversity distribution. Here, we show how the implementation of the neutral theory behaves in 2D lattices or 2D space-filling trees imposing directional dispersal (Muneepeerakul, Weitz, Levin, Rinaldo, Rodriguez-Iturbe, 2007, Rodriguez-Iturbe, Muneepeerakul, Bertuzzo, Levin, Rinaldo, 2009). Two different frameworks, namely an individual-based contact model and a metacommunity model, will be introduced to that end. The investigation on the differences between the two substrates (the common name for the ecosystem landscape where interactions occur) proved important to later developments, chiefly laboratory ones (Section 2).
1.2. Neutral individual-based models and beyond
In our neutral individual-based model, a 2D lattice is termed ‘savanna’ to echo its ecohydrological background, that is, the ecological substrate is represented simply by a square lattice in which each site, or pixel, is occupied only by one individual, say, a tree. By contrast, as river landscapes, we use a space-filling tree (an Optimal Channel Network (OCN, see Appendix) built in a lattice of the same size of the savanna. In a space-filling network, all sites are channelized (Fig. 1b). The dynamics at each time step is defined as follows. A randomly selected individual (i.e., at a randomly picked pixel) dies. With probability ν, termed diversification rate, this site is occupied by a new species; with probability the site is colonized by an offspring of one of the neighbours with equal probability. The two landscapes differ only in the definition of neighbours. For the savanna, in fact, the offspring that colonizes the empty site is chosen among the individuals that occupy the four nearest neighbours (boundary effects at the edges of the lattice are removed by implementing a genetic algorithm (Bertuzzo, Suweis, Mari, Maritan, Rodriguez-Iturbe, Rinaldo, 2011, Muneepeerakul, Weitz, Levin, Rinaldo, Rodriguez-Iturbe, 2007)). For the networked landscape, the neighbourhood of a pixel is constituted by the nearest pixels connected to it by the network edges. Thus dispersion is directional in that physical proximity may not imply connectivity. The number of drainage directions in or out of the node define the viable connectivity at any site (pixels physically neighboring the site where the individual dies do not count for its replacement if unconnected to the site). Notice that all pixels, except for the outlet, have only one downstream neighbour; source pixels have no upstream neighbours, whereas all the others have one or more upstream neighbours.
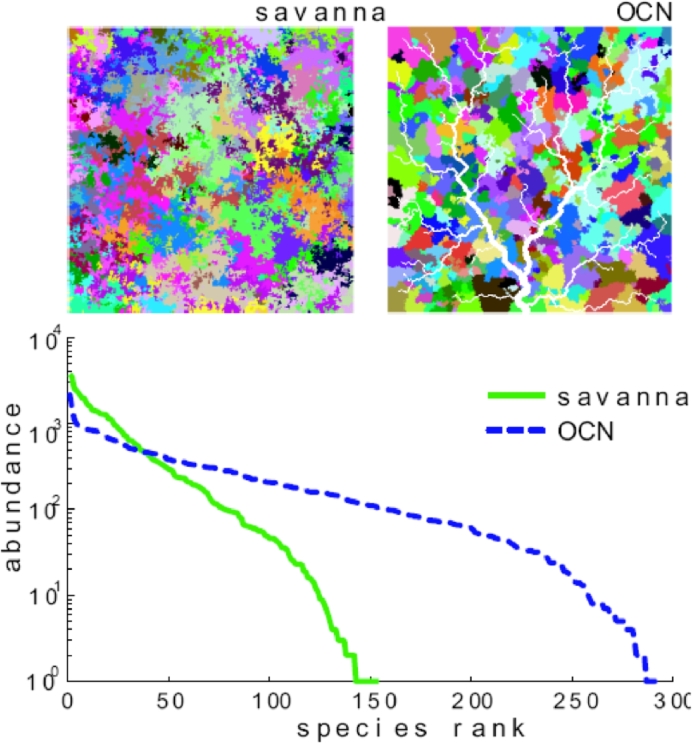
Fig. 1.
Comparison between neutral biodiversity patterns obtained by the neutral model described in the text within space-filling networks in a square domain: a ‘savanna’ (a two-dimensional lattice) and a fluvial network where directional dispersal to nearest-neighbours is regulated by an OCN connectivity matrix (Rodriguez-Iturbe and Rinaldo, 2001). We refer here to 2D landscapes as ‘savannas’ only for easier mental reference to the real world, as the neutral model used to produce the above plot does not include all ecological features of real savannas. These results form the basis of our theoretical motivation upon which additional realistic complications will be built. Species spatial patterns (upper insets) and their species rank-abundance curves are shown. The simulations are run on a 250-by-250 lattice with . (after Muneepeerakul, Weitz, Levin, Rinaldo, Rodriguez-Iturbe, 2007, Rodriguez-Iturbe, Muneepeerakul, Bertuzzo, Levin, Rinaldo, 2009).
Patterns are obtained by iterating the process until it reaches a stationary state. The two upper insets of Fig. 1 illustrate the resulting spatial biodiversity configuration in the two landscapes: pixels labeled by the same colour represent individuals belonging to the same species. The lower panel shows the typical associated rank-abundance curves. The results are remarkably different. It can be noticed, in particular, that the configuration of the space and the directionality of the dispersal imposed by the network landscape determine a higher species richness. Moreover, the spatial configuration of the patches of the same species in the network landscape have sharp boundaries that resemble the boundaries of subbasins. Differences only arise because of the different connectivity imposed by the two landscapes. Adding another factor typical of the dispersal in network landscape such as biased transport (e.g. offsprings colonizing preferably downstream) would only enhance the observed differences. This proved an important result.
Although the results from this simple neutral individual-based model are not to be taken as fully representative of reality, they rather forcefully demonstrate that differences may arise in key biodiversity features simply because of the presence of the drainage network acting as ecological substrate. Thus, the potentially fundamental roles played by the river network warranted more refined modelling schemes to investigate other important issues. In that light, another set of results from a more structured neutral model (Muneepeerakul, Bertuzzo, Lynch, Fagan, Rinaldo, Rodriguez-Iturbe, 2008, Muneepeerakul, Weitz, Levin, Rinaldo, Rodriguez-Iturbe, 2007) proves revealing. In this model, the landscape is organized in local communities (LC) each of which contains a certain number of sites; every site contains only one individual. In this way, a genuine metacommunity model is defined. The dynamic rule is similar to the one used for the previous unstructured model, and is repeated here for clarity. At each time step, an individual, randomly selected from all individuals in the system, dies. With probability ν, the diversification rate, this will be occupied by a new species; with probability the empty site will be colonized by an offspring of a species already existing in the metacommunity. In the latter case, the probability Pij that the empty site in LC i will be colonized by a species from LC j is determined as follows (Muneepeerakul et al., 2007):
| (1) |
where Kij is the dispersal kernel, the fraction of offspring produced at LC j that arrives at LC i after dispersal; Hj is the habitat size of LC j, that is the number of sites in LC j, and N is the total number of LCs. All individuals in LC j have the same probability of colonizing the empty unit in LC i where the death took place. Note that the standard neutral theory is in a way improved by assuming that different LCs have different habitat size. Neutrality still holds for dispersal, that is, the dispersal kernel of every species is assumed to be the same as in the previous example. In the context of metacommunity models, the dispersal kernel Kij contains the information on the landscape spatial structure and how individuals move about. Therefore, the key difference between savanna and river network metacommunities lies in their respective dispersal kernels. The dispersal kernels are typically assumed to take the form of exponential decay. Note that unlike in contact processes (REF.), an offspring can travel farther than its immediate neighbors in each time step.
In metacommunities, biodiversity patterns are measured by and γ-diversities (Anderson, Crist, Chase, 2011, Whittaker, 1972).α-diversity is a local description of biodiversity and γ- a global one, both being inventory measures because they refer to the number of species. β-diversity is a differentiation diversity measuring the rate of change in, or the turnover of, the species, measuring how species compositions in local communities differ from one another. In the following, γ-diversity is defined as the total number of species in the entire metacommunity. α diversity is a number of species in a randomly chosen LC; it is also useful to consider its mean value averaged across all LCs, denoted by ⟨α⟩. The between-community diversity, or β-diversity, is a conceptual quantity that can be defined in many ways, all of which share the same general idea: the higher the β-diversity, the more different the local communities. Here, it is defined as γ/⟨α⟩ and one is referred to the original references for related results (Muneepeerakul et al., 2007).
The main result of the structured metacommunity model is that network structure and dispersal anisotropy affect decisively any biodiversity measures. In this case, the dispersal rate is defined as the fraction of propagules that is dispersed away from their birth local community and the directionality is defined as the natural logarithm of the ratio between the fractions of propagules at the nearest neighbors in the preferred and opposite directions of dispersal (Muneepeerakul et al., 2007). All three diversity measures — in both types of landscapes shown in Fig. 1 — appear to be quite sensitive to dispersal anisotropy. In particular, river networks result in metacommunities with higher β diversity, i.e. more localized and heterogeneous ecosystems. This is due to a containment effect: in river basins, cross-subbasin dispersal is hindered by topographical divides, resulting in subbasins being more dissimilar from one another, echoing important field evidence (Fagan, 2002).
1.3. Distribution of persistence times
Another macroecological pattern is relevant to our general tenet. Specifically, we study the distributions of local species persistence time, τ, defined as the timespans between its emergence and local extinction in a given geographic region. Empirical distributions pertaining to different taxa have been analyzed in the above space-explicit framework (Bertuzzo et al., 2011b), notably breeding birds and herbaceous plants. The approach critically accounts for the finiteness of the observational period of any field data, a problem that is often overlooked and that may remarkably distort the true features of persistence times. Their distributions exhibit power-law scaling limited by a cut-off determined by the rate of emergence of new species (Bertuzzo et al., 2011b). Note that, although generalizations are possible, the study of persistence times was conducted on trophically equivalent co-occurring species.
Theoretical investigations on how the scaling features depend on the topological structure of the spatial interaction networks proved worthwhile (Bertuzzo et al., 2011b). At a local scale, τ is largely controlled by ecological processes operating at short timescales (e.g. population dynamics, immigration, contractions/expansions of species geographic ranges) as local extinctions are dynamically balanced by colonizations (Levins, 1969, MacArthur, Wilson, 1967, Ricklefs, 1987). At a global scale, originations and extinctions are controlled by mechanisms acting on macroevolutionary timescales (Diamond, 1989, Jablonski, 2008). From a theoretical viewpoint, the simplest baseline demographic model is a random walk without drift, according to which the abundance of a species in a geographic region has the same probability of increasing or decreasing by one individual at every time step. According to this scheme, local extinction is equivalent to a random walker’s first passage to zero, and thus the resulting persistence time distribution has a power-law decay with exponent 3/2 (Chandrasekhar, 1943, Newman, 2005). A more realistic description can be achieved by accounting for basic ecological processes like birth, death, migration and speciation, possibly in neutral mean field schemes (Hubbell, 2001, Muneepeerakul, Bertuzzo, Lynch, Fagan, Rinaldo, Rodriguez-Iturbe, 2008, Volkov, Banavar, Hubbell, Maritan, 2003), as described above. Here, when a randomly selected individual dies and the space or resources are freed up for colonization, with probability ν the site is taken by an individual of a species not currently present in the system. Thus ν is equivalent to a diversification rate and accounts for both speciation and immigration from surrounding communities. With residual probability the died individual is replaced by one offspring of an individual randomly sampled within the community (Chave, Muller-Landau, Levin, 2002, Durrett, Levin, 1996) (global, scale-independent dispersal). As such, the probability of colonization by a species depends solely on its relative abundance in the community. The asymptotic behavior (t ≫ 1) of the resulting persistence time distributions (i.e. pτ(t)) exhibits a power-law scaling limited by an exponential cut-off:
| (2) |
with exponent (Pigolotti et al., 2005). In Eq. (4), time is expressed in generation time units Hubbell (2001), i.e. it has been rescaled in such a way that the death rate is equal to one. Notably, in the mean field scheme the probability distribution depends solely on the diversification rate which accounts for speciation and migration processes and imposes a characteristic timescale 1/ν for local extinctions. While speciation rates are not expected to vary too much with the spatial scale of analysis, immigration rates decrease as the spatial scale increases. In fact, the possible sources of migration (chiefly dependent on the geometrical properties of the boundary and the nature of dispersal processes) are argued to scale sub-linearly with the community size (Bertuzzo et al., 2011b), which in turn is linearly proportional to geographic area (Brown, 1995, MacArthur, Wilson, 1967). As continental scales are approached, migration processes (almost) vanish and the diversification rate ultimately reflects only the speciation rate.
We now provide evidence of different, non-trivial exponents observable as a function of the topology of the substrate. Instead of a mean-field model, we use a space-explicit scheme in which dispersal limitation and the actual network of spatial connections are taken into account. The neutral game described above has been implemented in regular one-, two- and three-dimensional lattices (Fig. 2) in which every site represents an individual, whose species is labeled via a specific color (Bertuzzo et al., 2011b). Key to our reasoning, we explore the patterns emerging from the application of the model to dendritic structures mimicking riverine ecosystems where dispersal processes and ecological organization are constrained by the network structure. To this end, we use again Optimal Channel Networks (OCNs) (Rinaldo, Rigon, Banavar, Maritan, Rodriguez-Iturbe, 2014, Rinaldo, Rodriguez-Iturbe, Rigon, Bras, Vasquez, Marani, 1992, Rodriguez-Iturbe, Rinaldo, 2001, Rodriguez-Iturbe, Rinaldo, Rigon, Bras, Ijjasz-Vasquez, Marani, 1992) (Appendix) as space-filling (within arbitrary domains) mathematical constructs that yield aggregation patterns and landscape forms statistically indistinguishable from real-life river networks (Rinaldo et al., 1999). To account for limited dispersal effects, only the offsprings of the nearest neighbors of the dying individual are allowed to possibly colonize the empty site. In the networked landscape the neighbourhood of a site is defined by the closest upstream and downstream sites. Limited dispersal, in fact, promotes the clumping in space of species, which enhances their coexistence and survival probability (Chave, Muller-Landau, Levin, 2002, Kerr, Riley, Feldman, Bohannan, 2002).
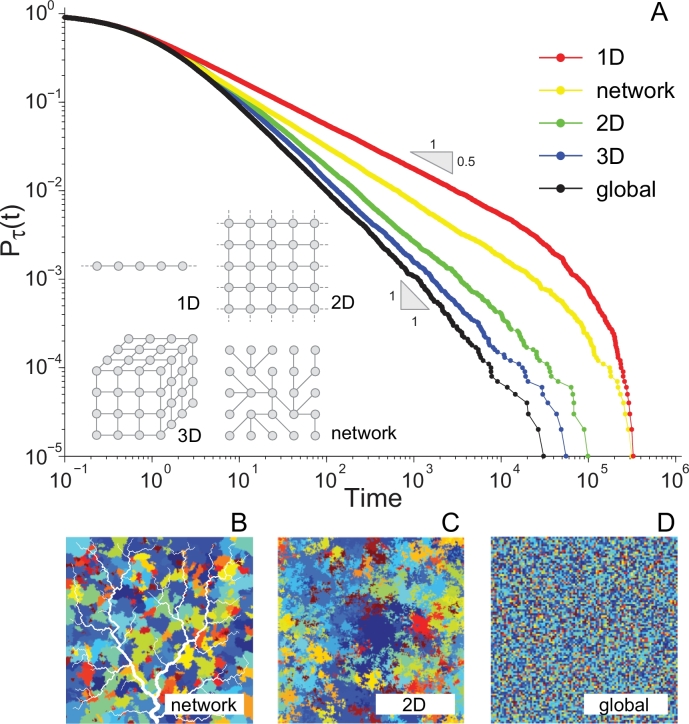
Fig. 2.
(A) Persistence time exceedance probabilities Pτ(t) (probability that species’ persistence τ be ≥ t) for the neutral individual-based model (Chave, Muller-Landau, Levin, 2002, Durrett, Levin, 1996, Hubbell, 2001) with nearest-neighbor dispersal implemented on the different topologies shown in the inset (Bertuzzo et al., 2011b). Note that in the power-law regime if pτ(t) scales as . It is clear that the topology of the substrate affects macroecological patterns. In fact, the scaling exponent α is equal to 1.5 ± 0.01 for the one-dimensional lattice (red), for the networked landscape (yellow), 1.82 ± 0.01 and 1.92 ± 0.01 respectively for the 2D (green) and 3D (blue) lattices. Errors are estimated through the standard bootstrap method. The distribution Pτ(t) for the mean field model (global dispersal) reproduces the exact value (black curve) (Bertuzzo et al., 2011b). For all simulations and time is expressed in generation time units (Hubbell, 2001). The panels in the lower part sketch a color-coded spatial arrangements of species in a networked landscape (B), in a two-dimensional lattice with nearest-neighbor dispersal (C), and with global dispersal (D). (after Bertuzzo et al., 2011b).
Fig. 2 shows the results of the neutral exercise described above – containing a truly remarkable message. In fact, in all the considered landscapes, persistence time distributions follow a finite-size power-law behaviour characterized by smaller, highly non-trivial scaling exponents, with respect to the mean-field model. These power laws too are inevitably limited by an upper exponential cutoff. Persistence time distributions deducted from the theoretical models change when dispersal kernels more general than dispersal from nearest neighbors are considered. As expected, as long as the mean dispersal distance remains small with respect to the system size, the distribution exhibits a longer transient regime but eventually ends up scaling as the one predicted by the nearest neighbors dispersal (Bertuzzo et al., 2011b).
Relaxing the neutral assumption (Hubbell, 2001) by implementing an individual-based competition/survival tradeoff model (Chave et al., 2002) has also been tested (Bertuzzo et al., 2011b). Specifically, species with higher mortality rates are assumed to hold more competitive ability in colonizing empty sites (Brown, 1995, Tilman, May, Lehman, Nowak, 1994). It is important to note that the trade-off model also exhibits power-law distributions of τ, showing exponents indeed close to those of the neutral model. By contrast, the mean time to extinction is larger in the trade-off model and consequently species richness is higher. We thus conclude that the theoretical results concerning the shape of persistence time distributions are robust with respect to both change in the dispersal range and relaxations of the neutrality assumptions. However, our results should not be seen as a test for the neutrality hypothesis (Hubbell, 2001) for empirical distributions, but rather as tools to reveal emerging universal and macroscopic patterns regardless of the detailed features of the particular model. Incidentally, a meaningful assessment of species’ local extinction rates is deemed valuable from a conservation perspective. Species persistence time distributions are in fact a robust tool to quantify the timespan of the species assembly currently observed within a given geographic area and, to some extent, predict the expected amount of future local extinctions. Mathematically, in fact, τ is defined as the time to local extinction of a species randomly sampled from the system regardless of its current abundance. Although these patterns cannot provide information about the behavior of a specific species or of a particular patch inside the ecosystem considered (e.g. a biodiversity hotspot) they can effectively describe the overall dynamical evolution of the ecosystem diversity.
1.4. Testing directional connectivity in the laboratory
The abstract examples discussed above strongly suggest that directional dispersal has a major impact on the resulting biodiversity distributions. In other words, the above examples imply that the topology of the substrate for ecological interactions has a defining role for the distribution of species richness in space and time regardless of the ecosystem’s specific features and environmental drivers. Clearly, this suggestion has had a fundamental importance in the way we now look at river networks as ecological corridors. For instance, β-diversities computed separately for headwaters and confluences test the differences in species composition within the river network structure. Headwaters exhibit not only a higher variability in α-diversity, but also a higher β-diversity compared with confluences (see Benda, Poff, Miller, 2004, Carrara, Altermatt, Rodriguez-Iturbe, Rinaldo, 2012, Fagan, 2002). These results reveal the crucial importance of headwaters as a source of biodiversity for the whole landscape. In natural systems, other local environmental factors may play a role in structuring ecosystems (Brown and Swan, 2010). Nevertheless, the neutral metacommunity approach sheds light on the single effect of directional dispersal on biodiversity. Note that the patterns found in river network geometries are predicted to be even stronger in the presence of a downstream dispersal, which is typical for many passively transported riparian and aquatic species in river basins (Bertuzzo, Maritan, Gatto, Rodriguez-Iturbe, Rinaldo, 2007, Morrissey, de Kerckhove, 2009). We thus suggest that species constrained to disperse within dendritic corridors are characterized by increased spatial persistence and lower extinction risks. On the other hand, heterogeneous habitats sustain higher levels of biodiversity among local communities that can be altered by modifying the connectivity of the system, with broad implications for community ecology and conservation biology. For simplified landscapes, often described geometrically by linear or lattice structures, a variety of local environmental factors exist that create and maintain diversity among habitats (de Aguiar, Baranger, Baptestini, Kaufman, Bar-Yam, 2009, Hubbell, 2001, Volkov, Banavar, Hubbell, Maritan, 2003). Many highly diverse landscapes, however, exhibit hierarchical spatial structures that are shaped by geomorphological processes. They are neither linear nor lattice-like, and therefore environmental substrates for ecological interactions shaped as trees may be appropriate to describe biodiversity of species living within fluvial dendritic ecosystems (Benda, Poff, Miller, 2004, Carrara, Altermatt, Rodriguez-Iturbe, Rinaldo, 2012).
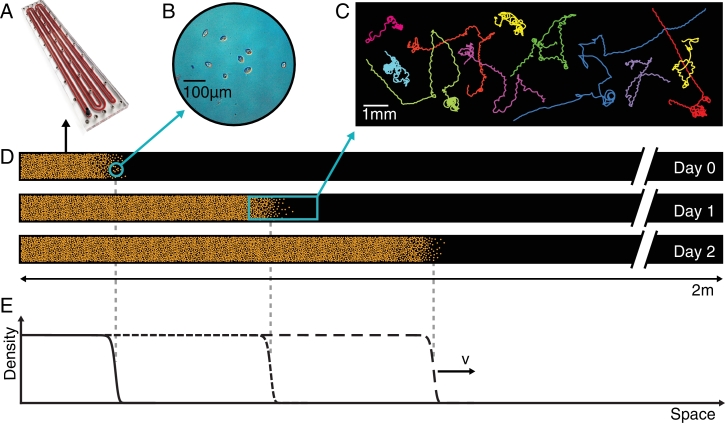
The above suggestions are far-reaching. In fact, species or populations whose ecological dynamics is constrained by directional dispersal would be inherently more predictable as the effects of other, uncontrollable heterogeneities would be less dominant. However, field validations cannot prove or disprove such ansatz, for a number of objective reasons (chiefly, the practical impossibility of replicating all ecological conditions in diverse topological substrates for the ecological interactions). We thus resorted to laboratory experimentation (Altermatt, Bieger, Carrara, Rinaldo, Holyoak, 2011, Altermatt, Schreiber, Holyoak, 2011, Holyoak, Lawler, 2005) to explore the extent of the validity of the theoretical prediction. As the theoretical work suggests that dispersal constrained by the connectivity of specific habitat structures, such as river networks, can explain observed features of biodiversity, we designed experiments to that end. Notice that no direct evidence existed at the time. Carrara et al. (2012); 2014) experimentally tested whether connectivity per se is capable of shaping diversity patterns in dendritic microcosm metacommunities at different levels. Fig. 3 illustrates the general setting of the lab experiments.
Fig. 3.
Design of the connectivity experiment carried out in the ECHO Lab at EPFL: (a) the river network (RN) landscape (Lower: red points label the position of LCs, and the black point is the outlet) derives from a coarse-grained optimal channel network (OCN) that reflects the 3D structure of a river basin (Upper); (b) to (e): the microcosm experiment involves 21 protozoan and rotifer species (Carrara, Altermatt, Rodriguez-Iturbe, Rinaldo, 2012, Carrara, Rinaldo, Giometto, Altermatt, 2014); (e) a subset of the species employed is shown to scale (for details see SI Materials and Methods in Carrara et al. (2012); 2014)) (scale bar = 100 µm); (c) communities were grown in 36-well plates, where the dispersal protocol has been carried out rather accurately and with an appropriate number of replicas (Altermatt, Bieger, Carrara, Rinaldo, Holyoak, 2011, Altermatt, Schreiber, Holyoak, 2011, Holyoak, Lawler, 2005); (d) and (e): dispersal to neighboring communities followed the respective network structure: blue lines are for RN (d), same network as in A, and black lines are for 2D lattice with four nearest neighbors (e) (after Carrara et al., 2012).
The main results produced along the above line of thought are summarized here. Local dispersal in isotropic lattice landscapes homogenizes local species richness and leads to pronounced spatial persistence (Fig. 4). On the contrary, dispersal along dendritic landscapes leads to higher variability in local diversity and among-community composition, thereby confirming by replicated laboratory experimentation the theoretical prediction based on abstract models (Carrara et al., 2012). Although headwaters exhibit relatively lower species richness, they are crucial for the maintenance of regional biodiversity. This result echoes prior theoretical evidence (Benda, Poff, Miller, 2004, Fagan, 2002). Such results establish that spatially constrained dendritic connectivity is a key factor for community composition and population persistence (Carrara et al., 2012).
Fig. 4.
Experimental and theoretical local species richness in river network (RN) and lattice (2D) landscapes. (A and B) Mean local species richness (α-diversity, color coded; every dot represents a LC) for the microcosm experiment averaged over the six replicates. (C and D) Species richness for each of these replicates individually. (E and F) The stochastic model predicts similar mean α-diversity patterns (note different scales).The effect of the hierarchical dendritic architecture proves statistically significant – in fact, decisive Carrara et al. (2014).
Moreover, further laboratory work experimentally disentangled the effect of local habitat capacity (i.e., the patch size) and dendritic connectivity on biodiversity in aquatic microcosm metacommunities by suitably arranging patch sizes within river-like networks (Carrara et al., 2014). Results are summarized in Fig. 5. Specifically, the individual effects of connectivity and habitat capacity on microbial diversity was singled out by using three different configurations of patch sizes (Riverine, Random, and Homogeneous), connected following a river network topological and aggregation template (Fig. 5) suitably derived from OCNs (Appendix). In Riverine landscapes, local habitat capacity correlates with position along the network and distance to the outlet (Fig. 5 A). Larger downstream communities thus consistently receive more immigrants from upstream communities. In the Homogeneous and Random landscapes (Fig. 5 B and C respectively), local habitat capacity (i.e., the patch size) does not preserve any geomorphological hierarchy embedded in the scaling of total contributing area at any point in the network scaling as observed in natural river systems (Leopold, Wolman, Miller, 1964, Rodriguez-Iturbe, Rinaldo, 2001).
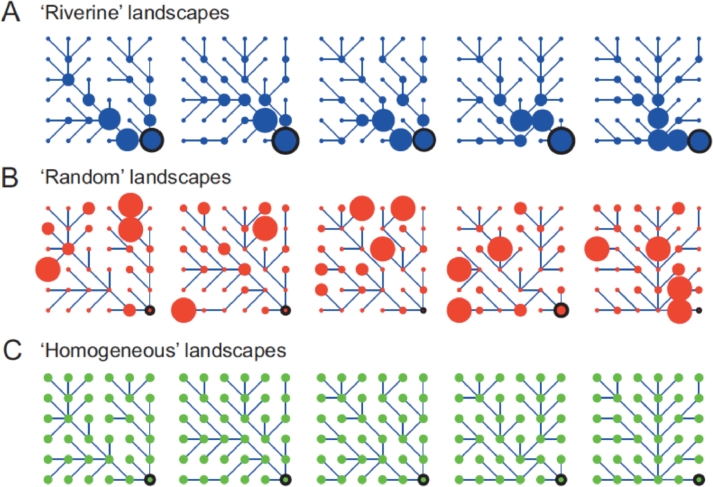
Fig. 5.
Spatial configuration of dendritic networks and corresponding patch sizes in the microcosm experiment. A, Riverine landscapes (blue) preserved the observed scaling properties of real river basins; B, Random landscapes (red) had the exact values of volumes as in the Riverine landscapes, randomly distributed across the networks; C, in Homogeneous landscapes (green) the total volume of the whole metacommunity was equally distributed to each of the 36 local communities. Patch size (size of the circle) is scaled to the actual medium volume. Five unique river-like (dendritic) networks were set up (columns); dispersal to neighboring communities followed the respective network structure, with a downstream bias in directionality toward the outlet community (black circled dot). (after Carrara et al. (2014)).
Overall, more connected communities that occupy a central position in the network exhibited higher species richness, irrespective of patch size arrangement. High regional evenness in community composition was found only in landscapes preserving geomorphological scaling properties of patch sizes (i.e. a patch volume proportional to the number of contributing nodes, see Carrara et al., 2014). In these landscapes, some of the rarer species sustained regionally more abundant populations compared to landscapes with homogeneous patch size or landscapes with spatially uncorrelated patch size (Carrara et al., 2014).
The bulk of the experimental replicas (Figs. 4 and 5) suggests that altering the natural link between dendritic connectivity and patch size strongly affects community composition and population persistence at multiple scales, precisely as predicted by the neutral model and by every (neutral and non-neutral) metacommunity framework applied to the same topologically diverse matrices. We note that the same applies to broader classes of networked environments (Benda et al., 2004), including those artificially created by human or host mobility networks (Erlander and Stewart, 1990) that are so relevant to the spread of disease epidemics – on which we shall return later.
2. Species’ dynamics and fluvial landscapes
In what follows we shall not pursue a review of the subject, broad as it is, but rather a specific choice of topics relevant to the general concepts outlined in Section 1, which will therefore find support and concrete applications.
2.1. Fish diversity in the Mississippi-Missouri river system
The first example deals with the prediction of fish diversity patterns in the large Mississippi-Missouri (MMRS) river system. In the specific case of riverine fish biodiversity, patterns of local and basin-scale differences must relate to energy availability, habitat heterogeneity, scale-dependent environmental conditions and river discharge (Fagan, 2002). Therefore, the neutral metacommunity models of the type introduced in Section 1 was made more realistic by better describing the structure of the local community (Muneepeerakul et al., 2008). In fact, each local community is endowed with a carrying capacity that depends on its location (specifically, total contributing catchment area as a proxy for fluvial habitat size (Rodriguez-Iturbe and Rinaldo, 2001)), and the relevant habitat, and each site within the LC does not host a single individual, rather a small subpopulation of a certain species. The physical context is described in Fig. 6.
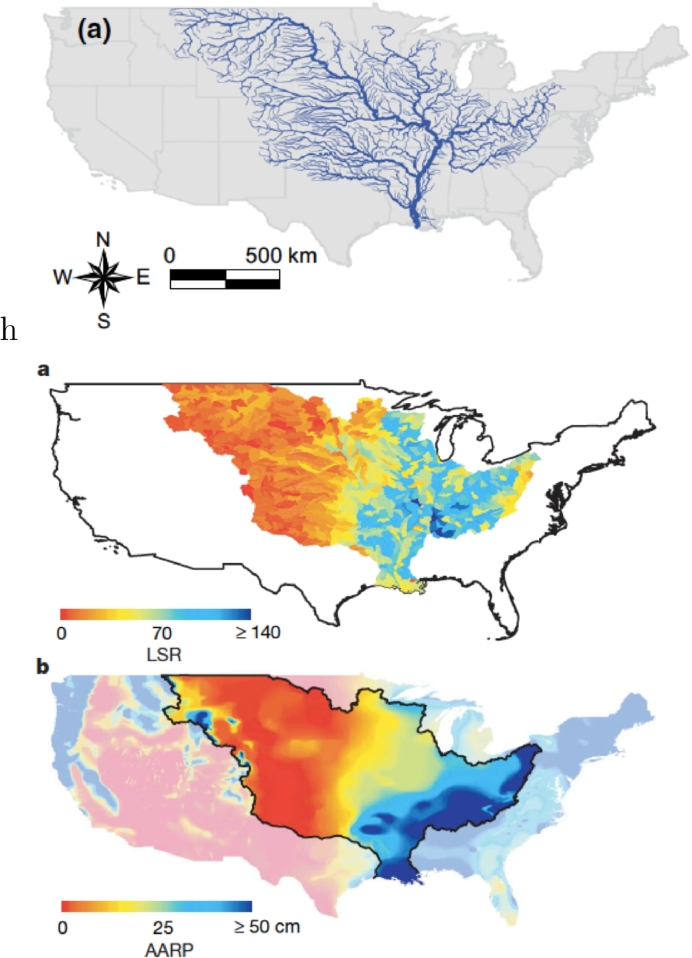
Fig. 6.
(a) River network geometry and localisation in the conterminous USA (Mari et al., 2011); (b) Local species richness (LSR), or α-diversity, of freshwater fish in each reference elementary area (or DTA) at the USGS HUC8 scale (Muneepeerakul et al., 2008) of the Mississippi-Missouri large river system. The biogeographical data on fish used in the analysis were obtained from the NatureServe (NatureServe, 2004) database of US freshwater fish distributions, which summarizes museum records, published literature and expert opinion about fish species distribution in the United States, and is tabulated at the USGS HUC8 scale (Seaber et al., 2004); (c) Annual average runoff production (AARP) (mm) in the same hydrologic system. AARP is the portion of precipitation drained by the river network at each site, computed from the water balance of precipitation, evapotranspiration and infiltration. The map in (c) is estimated from the streamflow data of small tributaries collected from about 12,000 gauging stations averaged over the period (Muneepeerakul et al., 2008).
Model simulations proceed largely through a spatially explicit approach akin to that described in Section 1, with slight modifications discussed below. Every direct tributary area (DTA, Fig. 6) is assumed to be always saturated at its capacity i.e. no available resources are left unexploited. Each DTA hosts a certain number of fish units, that depends on the location. At each time step, a fish unit, randomly selected from all fish ‘units’ (sensu (Muneepeerakul et al., 2008)) present in the system, dies and the resources that previously sustained the unit are freed and available for sustaining a new fish unit. With probability ν, the analog of the diversification rate in Section 1, the new unit will be occupied by a new species. Thus here the diversification is to be interpreted as a rate per death due to speciation, to external introduction of non-native species, or to immigration (and reimmigration) of a new species from outside the MMRS. With probability the new unit will belong to a species already existing in the system. In the latter case, with probability Pij (Eq. (1)) an empty unit in DTA i will be colonized by a species from DTA j (Muneepeerakul et al., 2008). In this context, with reference to Eq. (1), Hk is the habitat capacity of the DTA k (defined below), and N is the total number of DTAs (here, while the total number of fish units is 436,731). All the fish units in DTA j have the same probability of colonizing the empty unit in DTA i where the ‘death’ took place. Death must be interpreted as the extinction of the species subpopulation hosted by the fish unit. The model results that we outline in the following are the average patterns after the system reaches a statistically steady state. Specific dispersal kernels are assumed to determine how the fish species move within the river network (Muneepeerakul et al., 2008) (Kij in this context is the probability that a randomly selected fish species present in DTA j arrives at DTA i after dispersal. Here, normalization constants are determined numerically so that no fish can travel out of the network).
A necessary note pertains to the neutral assumption in this context, indeed strong because fish species obviously differ in their dispersal abilities. However, the ‘functional equivalence’ between species is a key way in which the neutral theory of biodiversity departs from classical ecological models. We assume the species equivalence to study just how good a fit the neutral metacommunity model can produce to our data in the absence of detailed, species-specific information. As such, the model is engineered to single out the individual role of the dendritic structure of the topological substrate for ecological interactions. An important innovation of the metacommunity model with respect to the zero-order model outlined in Section 1, concerns the imposition of hierarchical local habitat capacity at any site j, Hj. In fact, habitat capacity of DTA i, Hi, is determined by a properly normalized relation Hi∝AARPi WAi where WAi denotes total contributing (watershed) area at site i and AARPi is the average annual runoff production (Fig. 6c). Total contributing area at any point of a river network can be directly computed from suitably treated digital elevation maps (Rodriguez-Iturbe and Rinaldo, 2001).
The map of local species richness shown in Fig. 6b suggests that the DTA endowed with the maximum α-diversity (156 species) is observed somewhat mid-way through the MMRS. The sharp decrease empirically observed in species richness occurring around the 100°W meridian is known to correspond to sharp gradients of annual precipitation and runoff production (Muneepeerakul et al., 2008) (Fig. 6c). Although these gradients may partly explain the semi-arid climate and low fish diversity in the western half of the MMRS, Muneepeerakul et al. (2008) argued that the western DTAs are low in fish diversity both because their climate is dry and because they are upstream portions of the river network.
The results are displayed in Fig. 7. Fig. 7a illustrates the frequency distribution of local species richness (LSR), best fit to empirical data (Muneepeerakul et al., 2008), whose two peaks at low and high values reflect the difference between the western and eastern halves of the MMRS. Fig. 7 b,c shows computed and measured LSR as a function of the topological distance from the network outlet. It is totally remarkable the fact that the LSR profile shows a significant increase in the downstream direction, except at the very end where the freshwater fish-habitat capacities are significantly reduced by salinity, co-occurrence/intrusion by some freshwater-tolerant estuarine or coastal fish species, human disturbance and pollution. The overall downstream increase in richness results from the converging character of the river network and is steepened by the dry-wet climatic gradient (Muneepeerakul et al., 2008). The statistically significant, major impact of modulated habitat capacity is clearly suggested by the comparison of the results from the modified neutral metacommunity model and those from zero-order model where habitat capacity is assumed constant (Fig. 7c). Neutral metacommunity patterns result equally good for rank-abundance curves and suitable measures of β-diversity (not shown here, see Muneepeerakul, Bertuzzo, Lynch, Fagan, Rinaldo, Rodriguez-Iturbe, 2008, Fig. 4), where particularly significant is the resulting long-distance similarity in species composition maintained by species endowed with extremely large occupancies.
Fig. 7.
Patterns of local species richness (LSR) produced by the neutral metacommunity model in the MMRS system (Muneepeerakul et al., 2008). (a) Frequency distribution of LSR; (b) LSR profile as a function of the instream distance measured in DTA units from the outlet. The squares (average values) with error bars (ranging from the 25th to the 75th quantile) and bar plots represent empirical data, and the lines represent the average values of the model results; (c) as in (b) where for comparison a constant habitat capacity (dashed line) is employed (after Muneepeerakul et al., 2008).
The neutral metacommunity model reproduces surprisingly well the general spatial biodiversity patterns of the MMRS freshwater fish once hydrologic controls, like the effects of average annual runoff production on fish-habitat capacities, are enforced. A wide spectrum of observed biodiversity patterns are reproduced, as suggested by Figs. 6 and 7. As a specific example, in addition to the general trend and magnitude, the model also captures fine-structured fluctuations of the LSR profile (Fig. 6). Simultaneous fits of diverse patterns (and others, such as the species-area relationship) make for a very demanding test for any model, especially one using few parameters as in this case (Muneepeerakul et al., 2008). The model therefore provides ecological insight despite its simplicity.
One of the ecological meaningful insights obtained from the theoretical exercise is that the parameters corresponding to the best fit imply that the spread of the average fish species is quite symmetrical, i.e. it is not significantly biased either in the upstream or the downstream direction. The model results also suggest that, on average, most fish disperse locally (that is, to nearby DTAs) but a non-negligible fraction travel very long distances. Given the broad range of environmental conditions covered, the demonstration that a simple neutral metacommunity model coupled with an appropriate habitat capacity distribution and dispersal kernel can simultaneously reproduce several major observed biodiversity patterns has far-reaching implications. These results suggest that only parameters characterizing average fish behaviour – as opposed to those characterizing biological properties of all different fish species in the system – and habitat capacities and connected structure suffice for reasonably accurate predictions of large-scale biodiversity patterns, namely those patterns that do not include the identity of species. As we said in the previous section, neutral models cannot explain all those patterns that are species-specific. However, the neutral metacommunity model may represent a null model against which more biologically realistic models ought to be compared (sensu Akaike (Akaike, 1974, Corani, Gatto, 2007)). Moreover, furthering our understanding of fluvial ecological corridors (related to general metapopulation persistence criteria for spatially explicit models (Casagrandi, Gatto, 2002, Mari, Casagrandi, Bertuzzo, Rinaldo, Gatto, 2014)) will allow us to improve the alignment of ecological models and data.
2.2. Elevational gradients of biodiversity
The second example, which we deem paradigmatic as well, deals with geomorphic controls on elevational gradients of species’ richness (Bertuzzo et al., 2005). In this case, the lead role is taken by the structure of ecological interactions allowed by the available ecological substrate, the mountain landscape, which controls the gradients of biodiversity drivers. Key is the fluvial landscape again, this time suitably constructed in three dimensions. The fluvial landscapes we adopt are real topographies taken from digital elevation models (Rodriguez-Iturbe and Rinaldo, 2001), and replicated synthetic OCNs within a given domain through the transformation of a planar aggregation structure into a topographic landscape, which is made possible by the use of a slope-area relationship relating total contributing area at a point to the local topographic gradient (Rodriguez-Iturbe and Rinaldo, 2001). OCNs (Rinaldo, Rigon, Banavar, Maritan, Rodriguez-Iturbe, 2014, Rinaldo, Rodriguez-Iturbe, Rigon, Bras, Vasquez, Marani, 1992, Rodriguez-Iturbe, Rinaldo, 2001, Rodriguez-Iturbe, Rinaldo, Rigon, Bras, Ijjasz-Vasquez, Marani, 1992) (Appendix) prove once more extremely versatile.
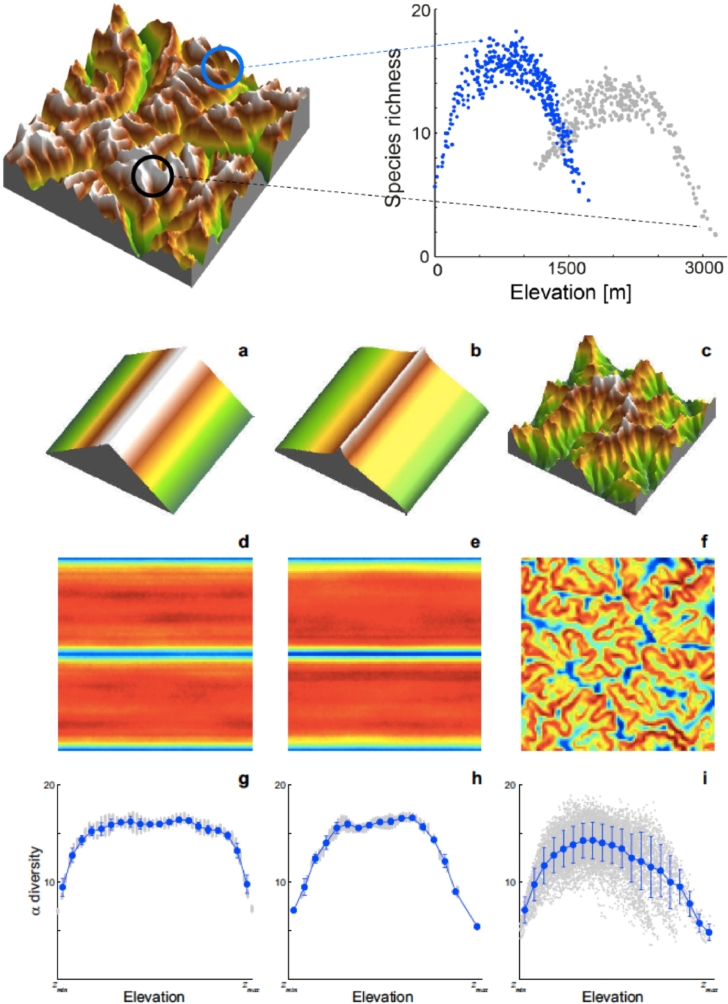
The rationale for our choice of examples is simple. How biodiversity changes with elevation has long attracted the interest of researchers because it provides key clues to how biota respond to geophysical drivers. Experimental evidence reveals that biodiversity in ecosystems significantly affected by the elevational gradients often peaks at intermediate elevations (Colwell, Rahbek, Gotelli, 2004, Gaston, 2000, Körner, 2000, Körner, 2007, Lomolino, 2001, McCain, Grytnes, 2010, Nogues-Bravo, Araujo, Romdal, Rahbek, 2008, Rahbek, 2005). A factor that had been overlooked for a long time was the fact that mountainous landscapes hold fractal properties (Mandelbrot, 1983, Rodriguez-Iturbe, Rinaldo, 2001) with elevational bands forming habitat patches that are characterized by different areal extent and connectivity, well-known drivers of biodiversity. Specifically, the frequency distribution of elevation in real-life landscapes is distinctly hump-shaped, with the majority of land situated at midelevations (Mandelbrot, 1983, Rodriguez-Iturbe, Rinaldo, 2001) (Fig. 8).
Fig. 8.
Comparison between (a) an oversimplified, 1D topographic gradient elevation field, and (b) a real-life elevation field (a fluvial landscape in the Swiss Alps, 50 × 50 km2); (c) hypsometric curve and (d) frequency distributions of elevation of the two landscapes. It is clear that 1D gradient experiments are unrealistic regardless of details on how the replicated real-life topographies are arranged (after Bertuzzo et al., 2005).
Elevational patterns showing a peak in elevational distributions at mid-elevation are ubiquitous in landscapes shaped by fluvial erosion when a sufficiently large region rather than a single slope or mountain is considered. It should be noted that this pattern is altered only if large areas outside runoff-producing zones (e.g., large plains) are included in the domain (Rodriguez-Iturbe and Rinaldo, 2001). Mountains are no cones (nor clouds are spheres or coastlines simple broken lines in the celebrated words of Mandelbrot, 1983) and therefore simple 1D slopes are highly misleading as representation of Nature’s topographies. Mountain landscapes are rather complex self-affine fractal structures (Rodriguez-Iturbe and Rinaldo, 2001). Within an ecological context, this fact has seriously misled researchers interested in elevational trends and in natural experiments conducted along gradients of elevation, because the mountain-cone analogy suggests a monotonically decreasing distribution of elevation. The area of available habitat within a given elevational band may have a direct effect on the diversity of the regional community it hosts (γ-diversity (Kraft, Comita, Chase, 2011, Rahbek, 1995, Rahbek, 2005, Sanders, 2002), as predicted by the species-area relationship (Rosenzweig, 1995)). The area of available habitat may also have an indirect effect on the local species richness because local communities can be assembled from a more diverse regional pool of species that are fit to live at similar elevation (Romdal and Grytnes, 2007).
Because there exist two classes of environmental drivers, those altitude-specific (such as atmospheric pressure and temperature) and those that are not (such as moisture, clear-sky turbidity and cloudiness, sunshine exposure and aspect, wind strength, season length, geology and human land use) (Körner, 2000, Körner, 2007), empirical results may hardly sort out unambiguously general rules, if at all existing. The importance of theoretical predictions of expected patterns of species richness with elevation could therefore hardly be overestimated. Bertuzzo et al. (2005) moved from this premise by exploiting universal self-affine features of elevation fields of fluvial landscapes, possibly obtained by planar aggregation structures where sensible local slope-area laws, reminiscent of the fluvial landscape, are enforced (Rodriguez-Iturbe and Rinaldo, 2001). Incidentally, they may apply equally well by using real topographies where the slope-area laws breaks down at the drainage density threshold. The nature of fluvial landscapes and their physical evolution, in fact, provide universal invariance of patterns of connected areas at same elevation (Rodriguez-Iturbe and Rinaldo, 2001).
This second example of biodiversity affected by the fluvial landscape structure thus describes how altitude-driven area connectivity fosters elevational gradients of species richness, and in particular the origins of empirically observed mid-altitude peaks. The analysis, as we said in the introduction, moves one further step away from neutrality by adding niche tradeoffs (for a somewhat similar attempt see Tilman, 2004). In fact, the model employs an altitude-dependent adaptive fitness of otherwise equal vital rates of species. Also, as briefly discussed in what follows, connectivity is based on the altitude-area relations expected in general by fluvial patterns. In order to investigate the role of the mountainous landscapes in shaping altitude gradient of species richness, a zero-sum metacommunity model is anyway adopted (Hubbell, 2001, Rosindell, Hubbell, Etienne, 2011), namely the system is always saturated. In this framework, the system comprises N local communities which are characterized by their position in space and by their mean altitude. Only communities organized in an equally spaced two dimensional lattice will be considered; however the model could be readily adapted to account for other connectivity structures like those investigated in the previous Section. Each local community assembles n individuals. Because of the zero-sum assumption, at any time the system is populated by N · n individuals belonging to S different species. Each species is characterized by a specific altitude niche which expresses, in this context, how the competitive ability of a species varies with altitude i.e. ci(z) measures the competitive ability of the individuals of species i at altitude z. This relationship is modelled as a Gaussian function:
| (3) |
where: is the optimal altitude of species i, that is where ci(z) equals its maximum . The parameter σi controls the dispersion of the Gaussian function, namely the niche width. In this example, the analysis is limited for simplicity to a ‘neutral’ case where all the species have the same parameters and . Fig. 9 illustrates how the niches of different species are modelled. Edge effects are also prevented (Bertuzzo et al., 2005). While species differ for their altitudinal niches, all other ecological traits (namely birth, death and dispersal rates) are identical like in the classical ecological neutral dynamics (Hubbell, 2001).
Fig. 9.
Habitat maps as a function of elevation. (A) A real fluvial landscape. (B) Fitness of three different species as a function of elevation. (C–E) Fitness maps of the three species shown in B. Darker pixels indicate higher fitness. Care is exerted in using landscapes holding the same frequency distribution of site elevation (i.e. the same hypsographic curve) of the reference mountainous landscape (after Bertuzzo et al., 2005).
Ecological interactions among individuals are simulated as follows. At each time step, a randomly selected individual dies and the resources are freed up and available for colonization. The empty site is occupied by an offspring of one of the individuals occupying either the local community of the dead individual or one of the four nearest-neighbour communities. A key variant of the standard spatially explicit neutral model follows. The offspring, in fact, is selected randomly with a probability proportional to ci(z) of all the candidate colonizing individuals evaluated at the elevation z of the local community of the dead individual. At each time step, with probability ν an additional individual, belonging to a species not currently present in the system, engages in the competition for colonizing the free spot (Bertuzzo et al., 2005). The optimal altitude of this individual is drawn from a uniform distribution spanning twice the altitude range of the system as described before (see also Fig. 9). Needless to say, introduction of new species is aimed at modelling both speciation and immigration from external communities. The model has been run also in three other landscape configurations (Bertuzzo et al., 2005). The alternative landscapes studied insure that the planar slope (Fig. 8a), and any linear slopes of variable gradients, are such that their hypsographic curves match that of the mountainous landscapes. By analyzing comparatively them, shape effects can be highlighted. The structure in Fig. 9 has been obtained by using a real-life elevation map where each pixel subsumes the mean altitude of a 500 × 500 m region. The local community size n is set to 100. The system is initially populated by one single species and is simulated until a statistically steady state is reached (105 generations, where a generation is N · n time steps). Periodic boundaries conditions are prescribed for both landscapes. Notice that model results do not depend on the actual altitude range [zmin , zmax ], but only on the ratio (Bertuzzo et al., 2005). Other pertinent details are reported therein.
Typical results of the metacommunity model are shown in Fig. 10. All landscapes produce to a different extent hump-shaped α-diversity curves, yet only the one corresponding to a real landscape produces realistic variability akin to that produced by field evidence. The values computed therein depend on specific choices of the niche width σ and on other parameters. It can be shown, however, that the trends outlined therein are valid irrespective of parameter values (Fig. 11).
Fig. 10.
(upper part) Local species richness (LSR) in different subdomains of the same size of the general landscape. The hump-shaped curve is evident although the relative values of α-diversity are evidently site-dependent. (a–c) Comparative landscape forms, note that (b) is constructed so as to yield the same hypsometric curve of (c); (d–f) maps of local species richness color-coded by the absolute values of α-diversity; (g–i) general plots relating LSR to elevation in the three domains, inclusive of the whole range of computed values, means and variances. Note that all the landscapes are constructed by gridding different elevation maps in a regular 100 × 100 lattice (). (after Bertuzzo et al., 2005).
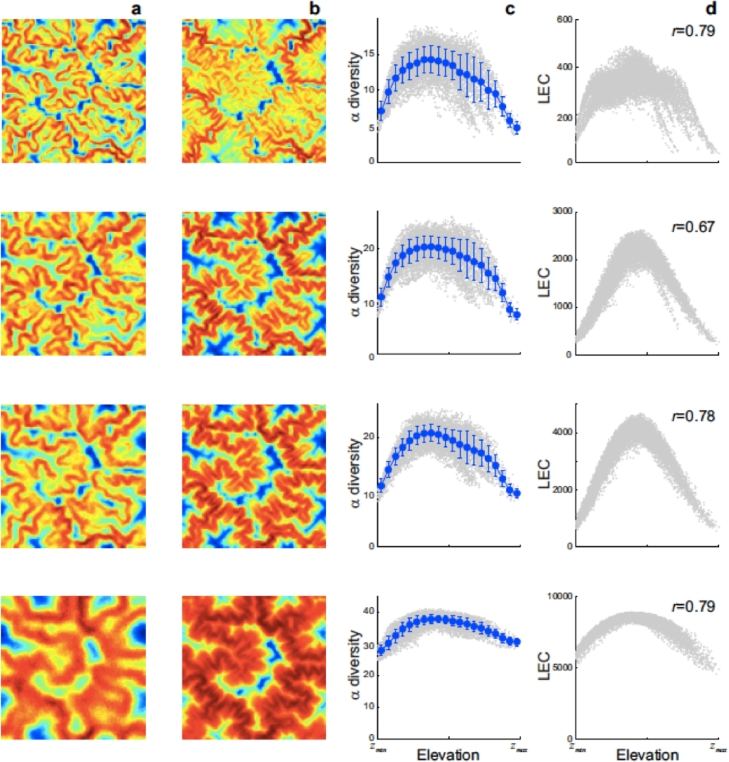
Fig. 11.
Elevational diversity patterns for different niche width σ. α-diversity (a,c) and a network connectivity measure based on elevations (LEC – an equivalent of the effective connectivity of any couple of sites i → j that accounts for the differences in elevation incurred in each intermediate planar step (Bertuzzo et al., 2005). In such a manner, LEC measures the likelihood for species to be able to settle in j crossing elevation-dependent unfavourable terrain. For a flat landscape LEC reduces to the distance between the two sites measured along the planar path) (b,d): spatial distribution (a,b) and elevational gradient (c,d). Symbols as in Fig. 9. Text in panels (d) reports the Pearson correlation coefficient between local values of α-diversity and the LEC. Different rows show different values of niche width. From top to bottom and 1. Simulations are performed over the same landscape used in Fig. 9. Averages over 500 realizations of the metacommunity model are shown. Other parameters are: (after Bertuzzo et al., 2005).
Fluvial landforms show deep similarities across many orders of magnitude despite great diversity of their drivers and controls (e.g., relief, exposed lithology, geology, vegetation, or climate) (Rodriguez-Iturbe and Rinaldo, 2001). Regardless of the self-affine nature of the elevation field as a whole, a marked heterogeneity of elevational distributions, and thus of ecological connectivity, characterizes the parts and the whole of real landscapes (Fig. 11). Nevertheless, the universality of the main attributes of the fluvial landscape naturally lends itself to the quest for general patterns of the ecological dynamics that such landscapes host (Bertuzzo, Suweis, Mari, Maritan, Rodriguez-Iturbe, Rinaldo, 2011, Brown, Swan, 2010, Rodriguez-Iturbe, Muneepeerakul, Bertuzzo, Levin, Rinaldo, 2009). Thus it is appealing that the α-diversity maps shown in Fig. 11 reveal such clear spatial patterns, with valleys and mountain tops characterized by lower species richness. All geomorphic factors resulting in self-affine landscapes where peaks or troughs my occur at any elevation within the range simultaneously concur to the formation of such a pattern, regardless of other elevation-independent factors. A factor is also the finiteness of the landscape elevational range: sites at mid-elevation can potentially be colonized by species that live at (and are fit for) higher and lower elevations, whereas sites at the lowest (highest) extreme are only subject to the colonizing pressure from higher (lower) elevations. In addition to this boundary effect, the geomorphic structure of fluvial landscapes results in a mid-elevation peak in both area and connectivity across the landscape, both of which promote diversity. Specifically designed simulations have disentangled the role of each of these factors (Bertuzzo et al., 2005). Results also show that without any of these effects, the model predicts no gradients of diversity. Each geomorphic factor produces, independently or in combination with others, a hump-shaped pattern of species richness. Moreover, the differential elevational connectivity characteristic of fluvial landscapes results in a marked variability of diversity for the same elevation. The results reveal that similar mid-peak elevational gradients of diversity can be observed at different scales of observation even if the domains span different elevational ranges. This pattern is thus a direct consequence of the nature of the substrate for ecological interactions, as in all the examples pursued here: in particular, of the self-affine fractal structure of fluvial landscapes that reproduces statistically similar fluvial landforms across scales (Rodriguez-Iturbe and Rinaldo, 2001). We thus show that deep similarities occur across many orders of magnitude despite great diversity of their drivers and controls (e.g., relief, exposed lithology, geology, vegetation, or climate). Results also show that, when the scale of observation is enlarged, different hump-shaped patterns are blended together, possibly producing a confounding effect (Bertuzzo et al., 2005), especially if the analysis is limited to the average diversity as a function of elevation. This feature might help in understanding why elevational diversity is often found to be dependent on the scale of observation (Nogues-Bravo, Araujo, Romdal, Rahbek, 2008, Rahbek, 1995, Rahbek, 2005).
The above results, as in most of the examples put forward in this paper, act as a proof of concept. In fact, we have presented results based on nearest-neighbour dispersal to highlight the role of elevational connectivity. Indeed the effect of elevational isolation is expected to be reduced as dispersal limitation decreases because species can overcome elevational constraints with long-distance dispersal (e.g., dispersing from one mountain top to another without going through unfavorable lower elevation habitats). Moreover, we have assumed that the landscape can be uniformly colonized, whereas real-life habitats are often composed by patches with different spatial connectivity and size (Hanski, 1998). Spatial and elevational connectivities can interact in complex ways to shape diversity patterns. While the modeling framework proposed can be easily generalized to accommodate both fragmented habitats and generic dispersal kernels, the coherent framework presented here has the potential to effectively describe how spatial and elevational connectivities shape diversity in complex 3D landscapes.
The above exploration of metacommunity patterns concludes our examples on how the ecological substrates affect in a decisive manner the ensuing biological diversity. It suggests that the specific spatial arrangement of sites at different elevation in fluvial landscapes suffices in inducing mid-peak elevational gradients of species richness without invoking specific assumptions, except that each species is fit for a specific elevation. In this framework, an elevation-dependent fitness applied to a real-life landscape translates into a fragmented habitat map. This conceptualization lends itself to the application of classic concepts of metacommunity dynamics (Hanski, 1998), according to which habitat size and connectivity are key drivers of biodiversity. We thus expect different metacommunity models to produce similar results. Needless to say, we do not dismiss as negligible other potential drivers of diversity, including those that often covary with elevation (e.g., habitat capacity, productivity, human disturbance). However, we argue that these drivers may act on top of the unavoidable effects provided by the geomorphic controls. A general consensus has thus been achieved on the fact that the analysis of elevational diversity should not seek one single overriding force but rather understand how different factors covariate to synergistically shape the observed patterns (Körner, 2007). Our results strongly suggest, however, that fluvial geomorphology has an important role, yet thus far overlooked, in driving emergent diversity elevational gradients of local species richness – inasmuch as the topology of the planar substrates dominates the structuring of general biodiversity patterns.
3. Population dynamics and riverine biological invasions
Biological dispersal is a key driver of many fundamental processes in nature (Clobert, Danchin, Dhondt, Nichols, 2001, Elton, 1958, Méndez, Fedotov, Horsthemke, 2010, Okubo, Levin, 2002, Shigesada, Kawasaki, 1997). Invasions controls the distribution of species within an ecosystem and critically affect their coexistence. In fact, the spread of organisms along ecological substrates (or corridors) governs not only the dynamics of invasive species, but also the spread of pathogens and the shifts in species ranges due to climate or environmental change. Obviously, the subject per se is a major chapter of ecology and we shall not deal with it here in a comprehensive manner. Our narrow perspective here deals rather with river networks as ecological corridors apt to population invasions. In fact, the role of the structure of river networks in modeling human-range expansions, i.e., predicting how populations migrate when settling into new territories, has been recognized through quantitative models of diffusion along fractal networks coupled with logistic reaction at their nodes (Campos et al., 2006). An essential ingredient therein is the fact that settlers did not occupy all the territory (isotropically, in the language of homogeneous continuous models), but rather followed rivers and lakes and settled near them to exploit water resources. It was thus interestingly argued in a quantitative manner that landscape heterogeneities must have played an essential role in the process of migration (Ammermann, Cavalli-Sforza, 1984, Campos, Fort, Mendez, 2006, Campos, Mendez, 2005, Méndez, Campos, Fedotov, 2004).
One interesting by-product of the analysis of migration fronts is the important role attributed to the structure of the network acting as the substrate for travelling wave propagations. This calls for specific structural models to be invoked, possibly including fractals that mimic natural forms (Rodriguez-Iturbe and Rinaldo, 2001). In the specific case, basic invariance properties may refer to the (relative) independence of the outcome of biological invasions from the seeding point chosen for spreading material and species along the network where reaction and diffusion occur. This is seen as a corollary of the type of scaling invariance shown by trees or networks where loops are observed (Banavar, Colaiori, Flammini, Maritan, Rinaldo, 2000, Banavar, Colaiori, Flammini, Maritan, Rinaldo, 2001, Maritan, Rinaldo, Rodriguez-Iturbe, Rigon, Giacometti, 1996, Rinaldo, Rigon, Banavar, Maritan, Rodriguez-Iturbe, 2014, Rodriguez-Iturbe, Rinaldo, 2001). The topological substrates that we shall consider here, namely OCNs (Rinaldo, Rigon, Banavar, Maritan, Rodriguez-Iturbe, 2014, Rinaldo, Rodriguez-Iturbe, Rigon, Bras, Vasquez, Marani, 1992, Rodriguez-Iturbe, Rinaldo, Rigon, Bras, Ijjasz-Vasquez, Marani, 1992), are tailored to the topology and geometry of real rivers (Rodriguez-Iturbe and Rinaldo, 2001). They allow us to produce replicas of network shapes and thus to seek for a proper statistic of the resulting biological dispersion processes.
To derive exact results one often resorts (Campos, Fort, Mendez, 2006, Mandelbrot, 1983, Marani, Rigon, Rinaldo, 1991) to the Peano network (Fig. 12), which is a deterministic fractal (Mandelbrot, 1983) whose main topological and metric features have been sorted out exactly (Marani et al., 1991). A good starting point is the analysis of Campos et al. (2006) concerning a reaction random-walk (RRW) process through a Peano construct and several replicas of OCNs. It is based on the following model. A particle, at an arbitrary node of the network, jumps, after a waiting time τ, to one of its z nearest neighboring nodes, with probability 1/z. During the waiting time τ, the particles ‘react’, i.e. evolve the scalar property (mass, density) labeling the particle by following the logistic equation. The determination of the wavefront speed that this process develops along a network path (Campos, Mendez, 2005, Méndez, Campos, Fedotov, 2004) is the starting point for the ensuing considerations. Fig. 12 illustrates the main result of the above premises. It shows that the isotropic diffusion-reaction front (Fisher’s model (Fisher, 1937)) propagates much faster than the wave forced to choose a treelike pathway. This proves that geometrical constraints imposed by a fractal network imply strong corrections on the speed of the fronts. It should be noted that it is not surprising that Peano networks and OCNs lead to similar results because the speed of the front depends on topological features that are indeed quite similar for all tree-like networks (rather different otherwise) (Rinaldo, Banavar, Maritan, 2006, Rodriguez-Iturbe, Rinaldo, 2001). In fact, it can be shown (Campos, Fort, Mendez, 2006, Méndez, Campos, Fedotov, 2004) that the wave speed is affected mostly by the gross structure encountered by the front while propagating along the network, chiefly the bifurcations. Hence topology, rather than the fine structure of the subpaths, dominates the process. It should be noted that the model proposed by Campos et al. (2006) assumes simple diffusive transport to describe migration fluxes. This seems indeed reasonable in the case of human population migrations: the need for water resources should drive settlers regardless of the direction of the flow. Variations on the theme, i.e. whether adding a bias to transport properties would basically alter this interesting picture, was investigated later (Bertuzzo et al., 2007). This was done on purpose: in fact, any other ecological agent (be it an aquatic organism or an infective agent of water-borne disease) would likely be affected by the flow direction to propagate within the network. Organisms can either move by their own energy (active dispersal) or be moved by water (passive dispersal). Most likely, movements along the flow direction would be favored, although movements against flow direction are completely admissible because of various ecological or physical mechanisms (Muneepeerakul, Bertuzzo, Lynch, Fagan, Rinaldo, Rodriguez-Iturbe, 2008, Muneepeerakul, Weitz, Levin, Rinaldo, Rodriguez-Iturbe, 2007). All this is of great interest for the problem of persistence of species along the ecological corridors that are shaped by the river network (Bertuzzo, Maritan, Gatto, Rodriguez-Iturbe, Rinaldo, 2007, Mari, Casagrandi, Bertuzzo, Rinaldo, Gatto, 2014).
Fig. 12.
(left) A river network thought of as a directed graph where nodes are sites of logistic population growth and edges are river reaches; (right) Invasion front speed as a function of the growth rate (T) of the logistic equation. Solid line is the exact solution of the continuous isotropic Kolmogorov–Fisher model. The dashed line and the dots represent exact and numerical values for propagation along the backbone of Peano networks (Mandelbrot, 1983, Marani, Rigon, Rinaldo, 1991, Rodriguez-Iturbe, Rinaldo, 2001) and OCNs, respectively (after Bertuzzo, Maritan, Gatto, Rodriguez-Iturbe, Rinaldo, 2007, Campos, Fort, Mendez, 2006).
A brief introduction of the theoretical context is perhaps useful. In a deterministic framework, the Fisher–Kolmogorov equation (Fisher, 1937, Kolmogorov, Petrovskii, Piskunov, 1937) reads:
| (4) |
where is the density of organisms, r the species’ growth rate, D the diffusion coefficient and K the carrying capacity. Eq. (4) is known to foster the development of undeformed traveling waves of the density profile (Murray, 2004). Mathematically, this implies that where v is the speed of the advancing wave. Fisher (1937) proved that traveling wave solutions can only exist with speed and Kolmogorov et al. (1937) demonstrated that, with suitable initial conditions, the speed of the wavefront is the lower bound (Fig. 12). The microscopic movement underlying the Fisher–Kolmogorov Eq. (4) is Brownian motion (Méndez et al., 2010).
Despite its relevance for important ecological processes, however, it was argued (Giometto et al., 2014) that the subject suffers an acknowledged lack of experimentation and current assessments point at inherent limitations to predictability even in the simplest ecological settings. Giometto et al. (2014) have instead shown, by combining replicated experimentation on the spread of the ciliate Tetrahymena sp. with a theoretical approach based on stochastic differential equations, that information on local unconstrained movement and reproduction of organisms (including demographic stochasticity) allows to predict reliably both the propagation speed and range of variability of invasion fronts over multiple generations. We shall briefly report their main findings as they are functional to the main tenet of this paper.
First, one wonders what are the sources of uncertainty and variance in the spread rates of biological invasions. The search for processes that affect biological dispersal and sources of variability observed in ecological range expansions, in fact, reveals fundamental insight into the study of invasive species dynamics, shifts in species ranges due to climate or environmental change and, in general, the spatial distribution of species (Andow, Kareiva, Levin, Okubo, 1990, Clobert, Danchin, Dhondt, Nichols, 2001, Elton, 1958, Grosholz, 1996, Hastings, Cuddington, Davies, 2005, Okubo, Levin, 2002, Shigesada, Kawasaki, 1997, Skellam, 1951). Dispersal is the key agent that brings favorable genotypes or highly competitive species into new ranges much faster than any other ecological or evolutionary process (Fisher, 1937). When organisms’ spread occurs on the timescale of multiple generations, it is the byproduct of active or passive movement and of the reproduction of individuals (Andow, Kareiva, Levin, Okubo, 1990, Hastings, Cuddington, Davies, 2005). The main difficulty in causally understanding dispersal is thus to upscale processes that happen at the short-term individual level to long-term and broad-scale population patterns (Andow, Kareiva, Levin, Okubo, 1990, Levin, 1992). Whether the variability observed in nature or in experimental ensembles might be accounted for by systematic differences between landscapes or by demographic stochasticity affecting basic vital rates of the organisms involved is key (Giometto, Rinaldo, Carrara, Altermatt, 2014, Hastings, Cuddington, Davies, 2005). Modeling of biological dispersal refers to the theoretical framework of reaction-diffusion processes (Fisher, 1937, Kolmogorov, Petrovskii, Piskunov, 1937, Méndez, Fedotov, Horsthemke, 2010, Murray, 2004, Skellam, 1951, Volpert, Petrovskii, 2009), which now finds common application in dispersal ecology (Andow, Kareiva, Levin, Okubo, 1990, Hastings, Cuddington, Davies, 2005, Lubina, Levin, 1988), control of the dynamics of invasive species (Elton, 1958, Grosholz, 1996, Skellam, 1951) and in related fields (Campos, Fort, Mendez, 2006, Murray, 2004). As noted in the introduction, reaction-diffusion models have also been applied to model human colonization processes, such as the Neolithic transition in Europe (Ammermann and Cavalli-Sforza, 1984) or the race to the West in the 19th century continental US (Campos et al., 2006). The extensive use of these models and the good fit to observational data favored their common endorsement as a paradigm for biological dispersal (Grosholz, 1996). However, certain assessments (Melbourne and Hastings, 2009) suggested inherent limitations to the predictability of the phenomenon, due to its intrinsic stochasticity. Therefore, single realizations of a dispersal event might deviate significantly from the mean of the process, making replicated experimentation necessary to allow hypothesis testing, identification of causal relationships and to potentially falsify the models’ assumptions. Giometto et al. (2014) provided instead replicated and controlled experimental support to the theory of reaction-diffusion processes for modeling biological dispersal in a generalized context that reproduces the observed fluctuations. Details on the experiment and on the theoretical analyses are reported therein.
Giometto et al. (2014) experimentally substantiated the Fisher–Kolmogorov mean speed of traveling wavefronts by measuring the individual components of the process. Stochasticity was included in the model to reproduce the observed variability in range expansions. Investigation of the movement behavior of Tetrahymena sp. shows that individuals’ trajectories are consistent with a persistent random walk with an autocorrelation time s. As the autocorrelation time for the study species is much smaller than the growth rate r (), an excellent approximation was provided (Giometto et al., 2014). The stochastic model equation reads:
| (5) |
where is a Gaussian, zero-mean white noise (i.e., with correlations where δ is the Dirac’s delta distribution) and σ > 0 is constant. The square-root multiplicative noise term in Eq. (5) is interpreted as describing stochasticity of demographic parameters and needs extra-care in simulations (Giometto et al., 2014). Data from the growth experiment in isolation were fitted to the equation
| (6) |
where is the local density, is a Gaussian, zero-mean white noise (i.e., with correlations ), σ > 0 is constant and l is the size of the region over which densities were measured (Giometto et al., 2014). Details are reported therein. In the experiments, the freshwater ciliate Tetrahymena sp. was employed because of its short generation time and its history as a model system in ecology (Carrara, Altermatt, Rodriguez-Iturbe, Rinaldo, 2012, Holyoak, Lawler, 2005). The experimental setup consisted of linear landscapes (Fig. 13), filled with a nutrient medium, kept in constant environmental conditions and of suitable size to meet the assumptions about the relevant dispersal timescales (see Materials and Methods in Giometto et al., 2014). Replicated dispersal events were conducted by introducing an ensemble of individuals at one end of the landscape and measuring density profiles throughout the system at different times. Density profiles are shown in Fig. 14 for six replicated dispersal events (panels A–F). Organisms introduced at one end of the landscape rapidly formed an advancing front that propagated at a remarkably constant speed (Fig. 14). The front position at each time was calculated as the first occurrence, starting from the end of the landscape, of a fixed value of the density (Fig. 14). As for traveling waves predicted by the Fisher–Kolmogorov equation, the mean front speed in the experiment is notably constant for different choices of the reference density value (Fig. 14). Note that the species’ traits r, K and D were measured in independent experiments. In the local growth experiment, a low-density population of Tetrahymena sp. was introduced evenly across the landscape and its density was measured locally at different times. Recorded density measurements were fitted to the logistic growth model, which gave the estimates for r and K (Giometto et al., 2014). In the local unimpeded movement experiment, the mean square displacement (SI) of individuals’ trajectories was computed to estimate the diffusion coefficient D in density-independent conditions (Giometto et al., 2014). The growth and movement measurements were performed in the same linear landscape settings as in the dispersal experiment and therefore are assumed to accurately describe the dynamics at the front of the traveling wave in the dispersal events. The comparison of the predicted front speed to the wavefront speed measured in the dispersal experiment, vo, yields a compelling agreement. The observed speed in the dispersal experiment was cm/day (mean ± SE) (Giometto et al., 2014), which we compare to the predicted one cm/day (mean ± SE). The two velocities are compatible within one standard error. A t-test between the replicated observed speeds and bootstrap estimates of gives a p-value of ( ). Thus, the null hypothesis that the mean difference is 0 was not rejected at the 5% level and there is no indication that the two means are different. As the measurements of r and D were performed independently at scales that were orders of magnitude smaller than in the dispersal events, the agreement between the two estimates of the front velocity was deemed remarkable.
Fig. 13.
Schematic representation of the invasion experiments. (A), Linear landscape. (B), Individuals of the ciliate Tetrahymena sp. move and reproduce within the landscape. (C), Examples of reconstructed trajectories of individuals. (D), Individuals are introduced at one end of a linear landscape and are observed to reproduce and disperse within the landscape (not to scale). (E), Illustrative representation of density profiles along the landscape at subsequent times. A wavefront is argued to propagate undeformed at a constant speed v according to the Fisher–Kolmogorov equation (after Giometto et al., 2014).
Fig. 14.
(left) Density profiles in the dispersal experiment and in the stochastic model. (A–F) Density profiles of six replicated experimentally measured dispersal events, at different times. Legends link each color to the corresponding measuring time. Black dots are the estimates of the front position at each time point. Organisms were introduced at the origin and subsequently colonized the whole landscape in 4 d ( ≈ 20 generations). (G and H) Two dispersal events simulated according to the generalized model equation, with initial conditions as at the second experimental time point. Data are binned in 5-cm intervals, typical length scale of the process. (right) Range expansion in the dispersal experiment and in the stochastic model. (A) Front position of the expanding population in six replicated dispersal events; colors identify replicas as in Fig. 2. The dark and light gray shadings are, respectively, the 95% and 99% confidence intervals computed by numerically integrating the generalized model equation, with initial conditions as at the second experimental time point, in 1020 iterations. The black curve is the mean front position in the stochastic integrations. (B) The increase in range variability between replicates in the dispersal experiment (blue diamonds) is well described by the stochastic model (red line). (C) Mean front speed for different choices of the reference density value at which we estimated the front position in the experiment; error bars are smaller than symbols. (after Giometto et al., 2014).
The conclusions of the study are remarkable in that the Fisher–Kolmogorov equation correctly predicts the mean speed of the experimentally observed invading wavefront, although its deterministic formulation prevents it to reproduce the variability that is inherent to biological dispersal. In particular, it cannot reproduce the fluctuations in range expansion between different replicates of dispersal experiments. The proposed generalization of the Fisher–Kolmogorov equation accounting for stochasticity showed that it is able to capture the observed variability in a linear landscape. As local, independent estimates were used in solving the generalized model equation, the result that the measured front positions agree with simulations show that one source of uncertainty in biological invasions can be quantified. Estimates for the front speed and its variability in the experiment prove in good agreement with simulations implying that stochasticity in population parameters can explain variability in range expansions not related to the topology of the substrate (Giometto et al., 2014). Generalizations to organisms endowed with different biology (e.g., growth rates and diffusion coefficients, possibly available in the literature) are in sight, supporting the view that our tenet may possibly provide a general predictive framework for biological invasions in natural environments.
A hydrologically notable example of biological invasion within the same Mississippi-Missouri river system (MMRS) investigated in Section 1 follows Mari et al. (2011). It deals with the zebra mussel, Dreissena polymorpha, a freshwater bivalve native to Eurasia. Owing to its adaptability to a wide range of environmental conditions, combined with dispersal abilities within fluvial systems that are unrivalled by other freshwater invertebrates, this invasive species managed to diffuse all over Europe and North America. After establishment, zebra mussel colonies can rapidly reach population densities in the order of tens (or even hundreds) of thousands of individuals per square meter and inflict huge ecological and economic damages. In fact, zebra mussel colonies may deeply alter invaded ecosystems by filtering large volumes of water, thus removing phytoplankton and boosting nutrients, and by severely impairing the functioning of water works (Mari et al., 2011). The zebra mussel has thus become a prototypical example of invasive species, rightly included in the 100 World’s Worst Invasive Alien Species list drawn up by the International Union for Conservation of Nature. One of the noteworthy features of zebra mussel invasions is the speed at which the species can spread over river networks. The example of the invasion of the Mississippi-Missouri river system (MMRS) is particularly revealing, see Fig. 15 (data available online at: http://fl.biology.usgs.gov/Nonindigenous-Species/ZM-Progression/zm-progression.html.
Fig. 15.
Synoptic view of the zebra mussel invasion pattern along the MMRS as recorded from field observations. (a) Spatiotemporal invasion pattern (first sightings) on the river network. (b) Progression of the invasion pattern (filled circles) and spatial extent of the spread (empty circles). Progression is evaluated as the distance traveled downstream by D. polymorpha along the backbone of the MMRS starting from the injection point (i.e., the distance traveled along the Illinois and Mississippi Rivers). Spatial extent is evaluated as the mean Euclidean distance between invaded sites on the river network and the injection point. The dotted line represents the length of the river network backbone. (c) Pervasiveness of the zebra mussel invasion, evaluated as the total fraction of invaded hydrologic unit codes (HUCs, defined in Mari et al. (2011) by a threshold that roughly corresponds to a colony of some hundreds of individuals in the reach represented by a node in the model (i.e. carrying a density larger than 0.01 mussels m2) of the MMRS as a function of time (after Mari et al., 2011).
The invasion, in fact, started from the Great Lakes region (Michigan), where some specimens were first sighted in the late 1980s after being probably introduced via ballast water sheddings by boats sailing from Europe. By 1990 D. polymorpha made its way into the Illinois River and by 1991 the zebra mussel started diffusing into the Mississippi, reaching Louisiana as soon as 1993. In the meanwhile, the species showed up also in some of its most important tributaries (Ohio, Tennessee, and Arkansas Rivers), as well as in other North American river systems (St. Lawrence, Hudson, and Susquehanna). The rate of spread of D. polymorpha has decreased remarkably after 1994, primarily because the species did not expand west of the 100th meridian. However, the zebra mussel has been steadily infilling and colonizing new reaches during the last decade. Quite surprisingly, a few connected river systems (most notably, the Missouri River) have not been invaded until recently (Stokstad, 2007). Nowadays, the zebra mussel steadily occupies much of central and eastern North America.
D. polymorpha invasion patterns result from the interplay between local demographic processes occurring over long time scales and basin-scale transport phenomena taking place over much shorter time spans (Mari et al., 2011). This is mainly due to the peculiarity of the species life cycle, which can be roughly subdivided into two main periods: a short larval phase, lasting from a few days to a few weeks (Stoeckel et al., 1997), and a relatively long adult stage, up to three years in North America (Casagrandi et al., 2007). Adults live anchored to a solid substratum, while larvae (also known as veligers) can be transported by the water flow, sometimes traveling for hundreds (or even thousands) of kilometers before settling (Stoeckel et al., 1997). Therefore, rivers represent the primary and natural pathway allowing species spread. However, anthropic activities can often result in extra-range dispersal, i.e., in the movement of propagules from the current species range to a new area of habitat, thus in turn remarkably favoring both the speed and the extent of the biological invasion (Mari et al., 2011).
In the zebra mussel case this has been known for a long time, as any human activity that involves the movement of a mass of water can be a potential vector for the spread of D. polymorpha (Carlton, 1993). Commercial navigation represents a major driver of mobility for the zebra mussel (Allen, Ramcharan, 2001, Mari, Bertuzzo, Casagrandi, Gatto, Levin, Rodriguez-Iturbe, Rinaldo, 2011). For instance, large quantities of veligers are often shipped within the ballast water of commercial vessels. As ports are located even hundreds of kilometers apart from each other, connections among them allow the species to disperse over very long distances and to colonize stretches of the river network that could not have been reached otherwise. Furthermore, empirical evidence suggests that recreational boating may be an important determinant of medium-range mussel redistribution (Chase, Bailey, 1999, Stoeckel, Padilla, Schneider, Rehmann, 2004, Stoeckel, Rehmann, Schneider, Padilla, 2004). A common mechanism associated with transient recreational boating is the transport of juveniles and adult mussels via macrophytes entangled on boat trailers (Carlton, 1993). This mechanism has been proposed as the most likely cause of D. polymorpha interbasin range expansion due to touristic boating. Therefore, commercial navigation represents an efficient vector of long-distance dispersal, while touristic boating can provide a capillary mechanism for medium-range mussel relocation.
Due to the importance of the zebra mussel as an ecosystem invader, significant modeling effort has already been devoted to understanding its demographic dynamics at a local scale (Casagrandi et al., 2007), as well as to the description of the species spread along rivers (Mari, Casagrandi, Pisani, Pucci, Gatto, 2009, Stoeckel, Schneider, Soeken, Blodgett, Sparks, 1997), and the analysis of long-distance dispersal (Wilson et al., 2009). To single out the role of drivers and controls of the MMRS invasion, spatially explicit, time-hybrid, multilayer network models were set up to address the intertwining of hydrologic controls, acting through the ecological corridors defined by the river network, with long- and medium-range dispersal controlled by anthropogenic factors, which define secondary movement networks. Integrating multiple dispersal pathways is crucial to understand zebra mussel invasion patterns and, in particular, the role played by human activities in promoting the spread. In particular, in this outstanding case commercial navigation has been the most important determinant of the early invasion of the Mississippi-Missouri, and recreational boating can explain the long-term, capillary penetration of the species into the water system. The spatially explicit ecohydrological model is described in detail elsewhere (Mari et al., 2011). Suffice here to mention the basic unity of the approaches with the ones described in greater detail in Section 2. Of great relevance here is the multiplex network of ecological interactions adopted (later re-discussed in the context of pathogen/host mobility in Section 4). In fact, while veligers diffuse and settle along one-dimensional substrates provided by the fluvial ecological corridors, hence determining a traditional travelling wave invasion front dynamics (sensu (Fisher, 1937, Kolmogorov, Petrovskii, Piskunov, 1937)), a much faster and heterogeneous spread can be envisioned and proved (Figs. 16 and 17): the ‘infection’, in fact, can be simply propagated by veligers trapped in the ballast water of commercial or recreational boats, possibly moved by land, surviving the trip and re-starting from scratch their colonization process.
Fig. 16.
Drivers of the secondary dispersal of D. polymorpha. (a) The main fluvial ports of the MMRS and the most important connections among them, which are respectively nodes and edges of the commercial network layer. Letters within green circles refer to the most important fluvial ports. (b) The main lakes, impoundments, and ponds of the MMRS. For exemplification, the inset shows the connections within the recreational network layer between one closed water body (marked in red) and its neighbors. (after Mari et al., 2011).
Fig. 17.
Zebra mussel invasion of the MMRS as simulated by the network model confined to the hydrologic layer. All plots are labeled as in Fig. 16. Red and blue lower insets refer to field data and simulation results, respectively (Mari et al., 2011). Parameter values as in Mari et al. (2011).
The scale of the modeling attempt and the ecohydrological interactions addressed by Mari et al. (2011) is noteworthy. As noted in Section 1, landscape heterogeneities, directional dispersal, and hydrologic controls shape ecological and epidemiological patterns. A novel factor, on which we shall elaborate further in the context of the spread of waterborne disease, concern human-mediated dispersal processes that prove of great importance as they allow species to disperse beyond their normal ranges, thus eventually shaping global biogeographical patterns (see e.g. Wilson et al., 2009). The model thus accounts for the interplay among a few selected mechanisms, such as density-dependent larval mortality, basin-scale hydrologic transport, and human-mediated dispersal due to either port-to-port commercial navigation or recreational boating, that are deemed of key importance in D. polymorpha invasions. The model, which succeeds in reproducing the zebra mussel invasion patterns observed in the MMRS at a regional spatial scale and over a 20 year time span, offers a hindcasting exercise for the MMRS, yet the proposed multilayer network approach could be applied to predict and control other potential invasions of the same or related alien species in the MMRS or other river systems, provided that a comprehensive analysis of extant ecological and hydrologic processes, as well as of relevant human-mediated transport mechanisms, is available. This seems of particular ecological relevance. In the context of biological invasions, in fact, taking early actions is difficult, yet extremely valuable. In the zebra mussel case, in particular, the containment and/or eradication of established colonies are very difficult and costly. Prevention should thus be favored over control, but this is possible only if quantitative tools to predict the development of the spread are available. To that end, we point out the importance of a fully dynamical and spatially explicit approach to modeling biological invasions, for it allows combined predictions of both temporal and spatial patterns of species spread. In addition, we deem our multilayer approach an effective and general framework to model the spread of species that are characterized by multiple dispersal pathways.
Biological invasions are inherently complex stochastic processes for which only a single realization is available for observation. As such, there exist obvious limits to our ability to actually predict them from models that necessarily need estimation of parameters from actual data (see Melbourne and Hastings, 2009 but also Giometto et al., 2014 mentioned above). However, forecasting the main (or mean, in some ensemble-averaging sense) patterns of spread of alien species is becoming increasingly important, though more and more difficult, with anthropic activities rapidly coming abreast of (or even overwhelming) natural invasion pathways. For all these reasons, including important details about the role of ecological corridors and of related anthropogenic drivers, is very valuable. A thorough, quantitative understanding of the different processes that boost the spread of alien species is in fact our only hope to prevent and, to some extent, control biological invasions.
4. Ecology of pathogens and the spread of waterborne disease
Here we shall introduce to the modelling rationale, that extends and specializes the reasoning presented in the previous Sections, with a view on a particularly important application, i.e. spatial epidemiology. As we shall see, river networks, and more in general waterways, play a fundamental role as epidemiological corridors. Waterborne diseases are infections caused by ingestion of (or, more in general, contact with) water contaminated by pathogenic organisms, ranging from micro- (typically viruses, bacteria and protozoans) to macro-parasites (mostly flat- and roundworms). They still represent a major threat to human health, especially in low-income countries. Most of the burden of waterborne infections is attributable to unsafe water supply, lack of sanitation and poor hygienic conditions, which either directly or indirectly affect exposure and transmission rates.
4.1. Of drivers and controls
Hydroclimatological forcings, the mobility of susceptible/infected individuals, and large-scale treatment are key drivers of waterborne disease transmission (Gurarie, Seto, 2009, Rinaldo, Bertuzzo, Mari, Righetto, Blokesch, Gatto, Casagrandi, Murray, Vesenbeckh, Rodriguez-Iturbe, 2012, Tien, Earn, 2010, Tien, Shuai, Eisenberg, van den Driessche, 2015). The direct inclusion of these factors into spatially explicit mathematical models of epidemic cholera, to quote an example of paramount importance, has improved the understanding of complex disease patterns (Bertuzzo, Azaele, Maritan, Gatto, Rodriguez-Iturbe, Rinaldo, 2008, Bertuzzo, Finger, Mari, Gatto, Rinaldo, 2016, Bertuzzo, Mari, Righetto, Gatto, Casagrandi, Rodriguez-Iturbe, Rinaldo, 2011, Chao, Halloran, Longini, 2011, Eisenberg, Kujbida, Tuite, Fisman, Tien, 2013, Mari, Bertuzzo, Finger, Casagrandi, Gatto, Rinaldo, 2015, Mari, Bertuzzo, Righetto, Casagrandi, Gatto, Rodriguez-Iturbe, Rinaldo, 2012, Rinaldo, Bertuzzo, Mari, Righetto, Blokesch, Gatto, Casagrandi, Murray, Vesenbeckh, Rodriguez-Iturbe, 2012, Tuite, Tien, Eisenberg, Earns, Ma, Fisman, 2011). Spatially explicit mathematical models encapsulate remotely acquired, relevant descriptions of human settlements, waterways where pathogens and/or intermediate hosts disperse, movement between human communities, hydrologic and climate variables, water resources development infrastructure (Finger, Knox, Bertuzzo, Mari, Bompangue, Gatto, Rodriguez-Iturbe, Rinaldo, 2014, Jutla, Akanda, Griffiths, Colwell, Islam, 2011, Jutla, Whitcombe, Hasan, Haley, Akanda, Huq, Alam, Sack, Colwell, 2013). Objective manipulation of such information yields characterizations of waterborne and water-based disease dynamics of unprecedented robustness that provides insight into the course of ongoing epidemics aiding short-term emergency management of health care resources and long-term assessments of alternative interventions (Chao, Halloran, Longini, 2011, Rinaldo, Bertuzzo, Mari, Righetto, Blokesch, Gatto, Casagrandi, Murray, Vesenbeckh, Rodriguez-Iturbe, 2012).
The general structure of spatially explicit models of waterborne disease is outlined in Fig. 18. The network nodes are animal communities with population Hi in which the disease can diffuse and grow. In human diseases the nodes can be identified with cities and villages. Locally, a generalization of classical SIR (Susceptible, Infected, Recovered) models (Heesterbeek and Roberts, 1995) is employed. To the traditional compartments one further compartment is added, that of pathogens in water (SIWR emphasizing the role of a water reservoir, W, determining disease transmission dynamics. For bacterial infections such models are typically called SIRB). For example, when the pathogen is a bacterium like in cholera, this amounts to including the concentration of bacteria in water. Therefore, the dynamics of the metacommunity model is represented by the evolution in time t of the following variables at each node i: Si(t) the susceptible hosts, Ii(t) the infected (and infectious), Ri(t) the recovered individuals, Bi(t) the bacterial concentration in the ith water reservoir, controlling the force of infection (Fig. 18). More complicate models may include an intermediate host living in water. For instance, in schistosomiasis humans host the adult stage of trematode parasites of the genus Schistosoma which reproduce inside humans releasing eggs via urine or faeces. The eggs released out of the human body that reach freshwater can hatch into larvae called miracidia, the parasite larval form that is infectious for the second host, freshwater snails, belonging to different genera. In the snail, miracidia undergo asexual replication, then the snail becomes infective and starts releasing tens of thousands of swimming larval stages, called cercariae, into the water. Cercariae infect humans penetrating their skin when they come into contact with contaminated freshwater. Inside the human body, cercariae develop into the adult parasite. Spatially explicit schemes assume that local human settlements undergo SIRB dynamics, whereas networks of connectivity redistribute pathogens and/or hosts among communities (Appendix).
Fig. 18.
(Upper left inset) A scheme of a metacommunity epidemiological model of the SIWR kind: the substrate for disease propagation is made up by nodes – human settlements or animal communities where disease can develop – and edges, in this case describing directional dispersal and hydrologic transport of waterborne or water-based pathogens. (Upper right inset) Schematic representation of the general spatially explicit modeling framework (the local model is supposed to be SIRB). Note the co-presence of a hydrologic connectivity matrix Pij to which a multiplex host mobility matrix Qij is superposed. For a detailed conceptual explanation and a full mathematical description, see Appendix. (Lower inset) Schematic representation of a local SIRB model at node i with the three additional compartments for vaccinated individuals: susceptible vaccinated, VS, infected vaccinated VI, and recovered vaccinated VR. For the mathematical transcription of the scheme see Appendix (after Bertuzzo, Finger, Mari, Gatto, Rinaldo, 2016, Bertuzzo, Mari, Gatto, Rodriguez-Iturbe, Rinaldo, 2010, Pasetto, Finger, Rinaldo, Bertuzzo, 2017).
The dynamics of disease spread reflects the spatial heterogeneity of its drivers, among which the most important are (reference is made to two paradigmatic cases of waterborne disease, one micro-parasitic, epidemic cholera, and the other macro-parasitic, endemic schistosomiasis, taken as examples of very diverse infections sharing the same hydrological matrix):
-
•
Climate, that affects transmission rates by displaying correlation with environmental variables like rainfall and air/ water temperature (Colwell, 1996, Constantin de Magny, Thiaw, Kumar, Manga, Diop, Gueye, Kamara, Roche, Murtgudde, Colwell, 2012, Emch, Feldacker, Islam, Ali, 2008, Hashizume, Armstrong, Hajat, Wagatsuma, Faruque, Hayashi, Sack, 2008, Jutla, Akanda, Islam, 2013, Koelle, Rodó, Pascual, Yunus, Mostafa, 2005, Lipp, Huq, Colwell, 2002, Pascual, Bouma, Dobson, 2002, Pascual, Rodó, Ellner, Colwell, Bouma, 2000, Ramírez, Grady, 2016, Reiner Jr., King, Emch, Yunus, Faruque, Pascual, 2012, Ruiz-Moreno, Pascual, Bouma, Dobson, Cash, 2007, Vezzulli, Grande, Reid, Hélaouët, Edwards, Höfle, Brettar, Colwell, Pruzzo, 2016, Rodó, Pascual, Doblas-Reyes, 2013). The role of large-scale climatic drivers on cholera dynamics is the subject of a lively debate especially about potential threats posed by warming temperatures and increasingly heterogeneous patterns (Baker-Austin, Trinanes, Taylor, Hartnell, Siitonen, Martinez-Urtaza, 2013, Cash, Rodó, Emch, Yunus, Faruque, Pascual, 2014, Cash, Rodo, Kinter, 2010, Escobar, Ryan, Stewart-Ibarra, Finkelstein, King, Qiao, Polhemus, 2015, Vezzulli, Colwell, Pruzzo, 2013, Vezzulli, Pezzati, Brettar, Höfle, Pruzzo, 2015). The links between climate and schistosomiasis are also being actively investigated (McCreesh, Booth, 2013, Pedersen, Midzi, Mduluza, Soko, Stensgaard, Vennervald, Mukaratirwa, Kristensen, 2014, Stensgaard, Utzinger, Vounatsou, 2013), in particular because climate change might hinder progress towards control in endemic countries (Stensgaard, Booth, Nikulin, McCreesh, 2016, Wang, Dai, Liang, 2014). Climate may also influence pathogen ecology and host exposure. Prospective climate change is speculated to bear fundamental impacts on the geography of waterborne diseases (Zhou et al., 2008);
-
•
Rainfall, that influences both cholera and schistosomiasis as well as other macroparasitic waterborne diseases (Bergquist et al., 2015). A variety of potential mechanisms exist whereby rainfall may alter infection risk, specifically: through flooding, leading to raw sewage contamination of water sources (Hashizume, Armstrong, Hajat, Wagatsuma, Faruque, Hayashi, Sack, 2008, Ruiz-Moreno, Pascual, Bouma, Dobson, Cash, 2007) and enhanced exposure to human-to-human transmission due to crowding (Boelee et al., 2013); increased rainfall-driven iron availability in environmental waters that enhances pathogen survival and expression of toxins (Faruque, Islam, Ahmad, Faruque, Sack, Nair, Mekalanos, 2005, Lipp, Huq, Colwell, 2002); dry spells and decreased water levels leading to increased usage of unsafe water sources (Rebaudet et al., 2013b).
A clear correlation between rainfall and enhanced transmission is found in regions hit by cholera epidemics (Constantin de Magny, Murtugudde, Sapiano, Nizam, Brown, Busalacchi, Yunus, Nair, Gil, Lanata, Calkins, Manna, Rajendran, Bhattacharya, Huq, Sack, Colwell, 2008, Jutla, Whitcombe, Hasan, Haley, Akanda, Huq, Alam, Sack, Colwell, 2013, Rebaudet, Sudre, Faucher, Piarroux, 2013, Rebaudet, Sudre, Faucher, Piarroux, 2013). Notably, for the Haiti outbreak, this link has been found empirically (Gaudart et al., 2013) and justified theoretically (Eisenberg, Kujbida, Tuite, Fisman, Tien, 2013, Rinaldo, Bertuzzo, Mari, Righetto, Blokesch, Gatto, Casagrandi, Murray, Vesenbeckh, Rodriguez-Iturbe, 2012) at all spatial scales and locations examined. Intense rainfall events were significantly correlated with increased cholera incidence with lags of the order of a few days, and forcing dynamic models with rainfall data invariably resulted in improved fits of reported infection cases. One approach (Rinaldo et al., 2012) suggested that bursts of infections could be best explained by accounting for increased contamination rates (flux I → W, see Fig. 18). An alternative approach Eisenberg et al. (2013) employed a rainfall-dependent exposure rate (S → I);
The relationship between precipitation and schistosomiasis is far from obvious. It has been argued (McCreesh and Booth, 2013), in fact, that rainfall could not only boost disease transmission (especially in dry climates where it is a key driver of habitat formation for the intermediate snail host) but also reduce it, e.g. by increasing water flow (which in turn decreases habitat suitability for both the snails and the larval stages of the parasites). Rainfall can also affect human activities related to water contact, thus potentially altering exposure and transmission risk (Lai et al., 2015). Also, the temporal fluctuations of rainfall patterns may be particularly important in determining the seasonality of transmission (McCreesh et al., 2015). Several studies in which the ecology of the intermediate snail hosts has been analyzed through field campaigns and geospatial models highlight the strength of the link between rainfall and schistosomiasis transmission (Hu, Zhang, Chen, Wang, Gao, Tao, Jiang, 2013, Lai, Biedermann, Ekpo, 2015, Perez-Saez, Mari, Bertuzzo, Casagrandi, Sokolow, De Leo, Mande, Ceperley, Frohelich, Sou, Karambiri, Yacouba, Maiga, Gatto, Rinaldo, 2015, Stensgaard, Booth, Nikulin, McCreesh, 2016, Stensgaard, Utzinger, Vounatsou, 2013). A hydrology-driven assessment of intermediate host habitat suitability thus seems necessary (Wu et al., 2008). Snail abundance, in fact, may depend upon density feedbacks that, in turn, can be driven by hydrologic controls, especially in ephemeral hydrologic regimes like those typical of sub-Saharan Africa (Perez-Saez et al., 2016). Therefore, a quantitative link exists between hydrological drivers and snail population dynamics, suggesting that statistical methods may provide reliable snail abundance projections (Perez-Saez et al., 2016), and that state-of-the-art mechanistic models of transmission (Gurarie et al., 2016) could be made dependent on habitat type (e.g. natural vs. man-made) and hydrological characteristics (e.g. ephemeral vs. permanent).
-
•
Water resources development (e.g. damming and irrigation), playing a significant role in the increase of disease burden owing to habitat expansion of pathogens and/or hosts, especially for schistosomiasis (Bergquist, Yang, Knopp, Utzinger, Tanner, 2015, Steinmann, Keiser, Bos, Tanner, Utzinger, 2006). Habitats are shaped naturally by the hydrology-geomorphology connections (Rodriguez-Iturbe and Rinaldo, 2001), defining the suitability of certain intermediate host species key to the closure of the pathogens’ life cycle, and the survival of pathogens in natural environments (Gurarie, King, Yoon, Li, 2016, Perez-Saez, Mande, Ceperley, Bertuzzo, Mari, Gatto, Rinaldo, 2016). However, the natural habitats are increasingly altered by humans, thus making it necessary to include land-use change as one of the most important drivers not only of biodiversity loss, but also of increased disease susceptibility. The development of agricultural practices is certainly one of the main causes of land-use change. Also, the larger and larger use of herbicides and fertilizers has also been shown to alter the ecological food-web and favor the proliferation of specific intermediate hosts (e.g. those of schistosomiasis (Rohr et al., 2008));
-
•
hydrologic transport (Bertuzzo, Azaele, Maritan, Gatto, Rodriguez-Iturbe, Rinaldo, 2008, Bertuzzo, Mari, Gatto, Rodriguez-Iturbe, Rinaldo, 2010) and human mobility (Bertuzzo, Mari, Gatto, Rodriguez-Iturbe, Rinaldo, 2010, Finger, Genolet, Mari, Constantin De Magny, Manga, Rinaldo, Bertuzzo, 2016, Mari, Bertuzzo, Finger, Casagrandi, Gatto, Rinaldo, 2015, Mari, Bertuzzo, Righetto, Casagrandi, Gatto, Rodriguez-Iturbe, Rinaldo, 2012, Perez-Saez, Mari, Bertuzzo, Casagrandi, Sokolow, De Leo, Mande, Ceperley, Frohelich, Sou, Karambiri, Yacouba, Maiga, Gatto, Rinaldo, 2015), which regulate, respectively, short- and long-range circulation of pathogens and hosts (Gurarie, Seto, 2009, Perez-Saez, Mari, Bertuzzo, Casagrandi, Sokolow, De Leo, Mande, Ceperley, Frohelich, Sou, Karambiri, Yacouba, Maiga, Gatto, Rinaldo, 2015). They also determine the spatial and temporal scales relevant to the analysis of epidemiological processes. Technological innovation provides information for their description at unprecedented rates (Bengtsson, Gaudart, Lu, Moore, Wetter, Sallah, Rebaudet, Piarroux, 2015, Ciddio, Mari, Sokolow, De Leo, Casagrandi, Gatto, 2017, Mari, Gatto, Ciddio, Dia, Sokolow, De Leo, Casagrandi, 2017). A significant role, relevant in particular to this review, emerges for the ecological corridors defined by waterways and river networks. Such hydrologic control derives from the transportation and redistribution of the free-living infective propagules. In particular, because vibrios of cholera can spread along stream both upstream and downstream with a slightly biased propagation downstream, the infection patterns prove markedly anisotropic (Bertuzzo et al., 2008), like all too evident in the early phases of the 2011 Haiti epidemics where the Artibonite river functioned as the corridor for the initial phase of the epidemic (Bertuzzo, Suweis, Mari, Maritan, Rodriguez-Iturbe, Rinaldo, 2011, Gaudart, Rebaudet, Barrais, Boncy, Faucher, Piarroux, Magloire, Thimothe, Piarroux, 2013);
-
•
‘social’ drivers, i.e. processes relevant to disease transmission mediated by human practice, broadly including inapparent infections (King et al., 2008), water, sanitation, hygiene (WASH) conditions (Azman, Ivers, Legros, Luquero, Mintz, 2016, Bi, Azman, Satter, Khan, Ahmed, Riaj, Gurley, Lessler, 2016, Freeman, Strunz, Utzinger, 2016, Grimes, Croll, Harrison, Utzinger, Freeman, Templeton, 2015, Mari, Bertuzzo, Righetto, Casagrandi, Gatto, Rodriguez-Iturbe, Rinaldo, 2012, Sokolow, Wood, Jones, 2016) and the differential outcomes of large-scale control strategies (Abubakar, Azman, Ivers, 2015, Azman, Lessler, 2014, Lo, Lai, Karagiannis-Voules, 2016). Considerable research exists on the impact of water treatment practices, hand washing and diet in urban (Dunkle et al., 2011) and rural (O’ Connor et al., 2011) settings on cholera risks in water and food sources (Hill et al., 2011). Others have evaluated the effectiveness of intervention efforts like treatment centers, educational campaigns and latrine building (Beau De Rochars, Tipret, Patrick, 2011, Ernst, Weinrobe, Bien-Aime, 2011). Two main types of large-scale medical treatments have been studied so far for cholera: vaccinations and the extended use of antibiotics (Abubakar, Azman, Ivers, 2015, Azman, Lessler, 2014, Ivers, Farmer, Almazor, 2010).
Spatially explicit process descriptions and data acquisition proved increasingly effective to understand the impact of various drivers on local disease transmission rates, and to realistically simulate large-scale infection patterns (Bertuzzo, Azaele, Maritan, Gatto, Rodriguez-Iturbe, Rinaldo, 2008, Tien, Earn, 2010). The robustness of simulations and predictions drawn from network models is granted by their spatial structure rooted in remotely acquired and objectively manipulated information, as shown e.g. by applications to epidemic cholera (Bertuzzo, Azaele, Maritan, Gatto, Rodriguez-Iturbe, Rinaldo, 2008, Bertuzzo, Finger, Mari, Gatto, Rinaldo, 2016, Bertuzzo, Mari, Righetto, Gatto, Casagrandi, Rodriguez-Iturbe, Rinaldo, 2011, Chao, Halloran, Longini, 2011, Finger, Genolet, Mari, Constantin De Magny, Manga, Rinaldo, Bertuzzo, 2016, Gatto, Mari, Bertuzzo, Casagrandi, Righetto, Rodriguez-Iturbe, Rinaldo, 2012, Mari, Bertuzzo, Righetto, Casagrandi, Gatto, Rodriguez-Iturbe, Rinaldo, 2012, Rinaldo, Bertuzzo, Mari, Righetto, Blokesch, Gatto, Casagrandi, Murray, Vesenbeckh, Rodriguez-Iturbe, 2012, Tuite, Tien, Eisenberg, Earns, Ma, Fisman, 2011) and proved formally via model selection techniques (Mari et al., 2015). Uncertainty analysis, data assimilation and filtering techniques for these spatially explicit schemes are now also available (Pasetto et al., 2017). They can reproduce complex stratifications of disease burden when transmission is heterogeneous, in part owing to river networks and connected waterways where the pathogen thrives, and in part due to host mobility, a key factor in the spreading of the pathogen. Although our lines of argument are meant to apply in general, specific cases (and references thereof) will first focus on cholera and schistosomiasis as significant examples of vastly different transmission mechanisms.
4.2. Spatially-explicit modelling of cholera and schistosomiasis
Spatially explicit disease infection models have radically changed the very concept of basic reproduction number R0. Indeed, challenging problems arise when observed infection patterns show spatial structure and/or temporal asynchrony. These features are ironed out by spatially implicit schemes that ignore spatial effects by assuming a uniform distribution of susceptible and infected individuals across the domain of interest. With these simplified assumptions the traditional definition of R0 applies: the average number of secondary infections produced by one infected individual introduced in a healthy population, which can be rather easily calculated from epidemiological parameters and the size of host population. Because of the current ease of mapping hydrology, sanitation and transportation infrastructures, in addition to the actual population distributions and proxies of their WASH conditions (a byproduct of remotely acquired and objectively manipulated information), the conditions leading to waterborne disease outbreaks can be studied in a spatially explicit framework. However, the adoption of spatially explicit schemes is only recent and mainly with reference to cholera (Gatto, Mari, Bertuzzo, Casagrandi, Righetto, Rodriguez-Iturbe, Rinaldo, 2012, Gatto, Mari, Bertuzzo, Casagrandi, Righetto, Rodriguez-Iturbe, Rinaldo, 2013, Mari, Casagrandi, Bertuzzo, Rinaldo, Gatto, 2014) and schistosomiasis (Gurarie, Seto, 2009, Perez-Saez, Mari, Bertuzzo, Casagrandi, Sokolow, De Leo, Mande, Ceperley, Frohelich, Sou, Karambiri, Yacouba, Maiga, Gatto, Rinaldo, 2015). We expect, however, that similar approaches will follow up soon for other diseases as well, because the underlying mathematical framework is general (Diekmann, Heesterbeek, 2000, Tien, Shuai, Eisenberg, van den Driessche, 2015). One important result that emerges from all the cases studied so far is that the requirement that all the local reproduction numbers be greater than one, i.e. the traditional epidemiological tenet mediated from spatially-implicit approaches, is neither necessary nor sufficient a condition for outbreaks to occur when spatial heterogeneity and pathogen redistributions are a factor (Fig. 19). This statement is not limited to waterborne diseases; rather, it holds in general whenever local epidemiological dynamics are coupled together by spatial connectivity. The basic reproduction number must be replaced by the dominant eigenvalue of the 4n × 4n Jacobian matrix (n is the number of nodes), linearized about the disease-free equilibrium. Moreover, the eigenvector associated with the dominant eigenvalue carries important information about the geography of waterborne or water-based disease (Gatto, Mari, Bertuzzo, Casagrandi, Righetto, Rodriguez-Iturbe, Rinaldo, 2012, Gatto, Mari, Bertuzzo, Casagrandi, Righetto, Rodriguez-Iturbe, Rinaldo, 2013, Mari, Casagrandi, Bertuzzo, Rinaldo, Gatto, 2014, Perez-Saez, Mari, Bertuzzo, Casagrandi, Sokolow, De Leo, Mande, Ceperley, Frohelich, Sou, Karambiri, Yacouba, Maiga, Gatto, Rinaldo, 2015).
Fig. 19.
Data and model predictions of cholera epidemic along the Thukela river, South Africa, network (A, Inset). (A) Total incidence data (weekly cases) from October 2000 to July 2001. Dotted lines mark the model calibration window. (B) Normalized spatial distribution of recorded cases cumulated during the epidemic onset phase (gray in A). (C) Spatial distribution of cases as predicted by the dominant eigenvector. (D) Spatial distribution of local basic reproduction numbers. Locations i in red (blue) are characterized by (). (E) Cholera cases (as in B). Red (blue) dots indicate communities with more (less) than 10 reported cases during disease onset (Gatto et al., 2012).
Human infections occurring through contacts with water contaminated with free-living macro-parasite stages pose other challenges largely mediated by the abundance of intermediate hosts possibly subject to a complex ecology (Colley et al., 2014). In the case of schistosomiasis, the disease transmission is controlled by contact with environmental freshwater infested with parasite larvae endowed with a complex life cycle and ecology (Perez-Saez, Mande, Ceperley, Bertuzzo, Mari, Gatto, Rinaldo, 2016, Sokolow, Lafferty, Kuris, 2014, Swartz, De Leo, Wood, Sokolow, 2015). Reinfection after treatment is a problem that plagues efforts to control parasites with complex transmission pathways, such as schistosomiasis. Low-cost, sustainable forms of intermediate host control coupled with drug distribution campaigns could reduce or locally eliminate the parasite (Grimes, Croll, Harrison, Utzinger, Freeman, Templeton, 2015, Sokolow, Huttinger, Jouanard, Hsieh, Lafferty, Kuris, Riveau, Senghor, Thiam, N’Diaye, Faye, De Leo, 2015). At regional scales, where the need for spatially explicit descriptions is particularly compelling, different communities are characterized by differential infection risks linked to their geographical and socio-economic context. A recent global assessment of schistosomiasis control over the past century has suggested that targeting the snail intermediate host works best (Sokolow et al., 2016). However, neither safe water supplies could completely prevent human contact with environmental freshwater, nor adequate sanitation could guarantee its generalized usage (Grimes et al., 2015). Moreover, agricultural, domestic, occupational and recreational tasks may foster contact with potentially infested water leading to non-negligible risk factors even in contexts where water provisioning and sanitation are adequate (Spear, 2012). This, coupled with differences in lifestyles, leads to complex determinants of transmission heterogeneity (Mari et al., 2017a). Social groups and ages are also a matter of concern for macro-parasitic infections, as e.g. people whose routinary activities bring them in contact with water (say, fishermen and farmers; or consider cultural settings in which women are more prone to water contact than men). Water-contact patterns may also vary over time as a response to seasonal changes in human activities, e.g. related to agriculture and farming, resulting in temporal heterogeneity in schistosomiasis transmission. Attempts to incorporate socioeconomic classes and risk groups into waterborne disease models are quite few in both applied (Remais et al., 2009) and theoretical studies (Barbour, 1978). Strong seasonal patterns in the transmission intensity and infection prevalence in both human and snail hosts still need a settlement within large-scale spatially explicit modeling frameworks.
4.3. Spatially-explicit modelling of PKD
One last example, which seems particularly fit to the focus on fluvial ecological corridors, concerns the spread, possibly rapid and deadly, of a particular fish disease. Proliferative kidney disease (PKD) is a high-mortality pathology that critically affects freshwater salmonid populations. Infection is caused by the endoparasitic myxozoan Tetracapsuloides bryosalmonae, that cycles between freshwater bryozoans and salmonids exploiting the former as primary hosts. Proliferative kidney disease (PKD) is recognized as a major threat to both wild and farmed salmonid populations in Europe and North America. Mortality due to PKD in farmed fish ranges from 20 to 100% (Clifton-Hadley, Richards, Bucke, 1986, Feist, Longshaw, 2006, Ferguson, Ball, 1979, Okamura, Hartikainen, Schmidt-Posthaus, Wahli, 2011). The impacts of PKD on wild fish populations are generally poorly known, although PKD has been linked to long-term decline of Swiss brown trout populations (Borsuk et al., 2006). PKD incidence and relevant fish mortality are strongly correlated with water temperature, therefore climate change is feared to extend the disease range to higher altitude and latitude regions with major consequences (Hari et al., 2006).
The first dynamical model of PKD epidemiology in local communities has recently been developed (Carraro et al., 2016). The local model accounts for local demographic and epidemiological dynamics of bryozoans and salmonids, explicitly incorporates the role of water temperature, and couples intra- and inter-seasonal dynamics. Fig. 20 shows that during the warm season (left column), susceptible bryozoans (BS) become covertly infected (BC) after contact with spores (ZF) released by infected fish. Infection in bryozoans cycles between covert and overt (BO) states. BS yield uninfected statoblasts SS (i.e. asexually produced propagules), while BC release both uninfected and infected (SI) statoblasts. Infected bryozoans may clear the infection. Susceptible fish (FS) are exposed to PKD after contact with spores (ZB) released by BO; after an incubation phase (FE), fish can either become acutely infected (FI) or directly enter an asymptomatic carrier state (FC). FI can die owing to PKD or become long-term disease carriers. FC may become susceptible again. Both FI and FC shed spores infective to bryozoans. At the beginning of a new warm season (central column), BS are comprised of susceptible colonies that survived during winter and by hatched SS; similarly, BC consist of survived colonies that were infected at the beginning of winter and of hatched SI. FS are composed by survived susceptible individuals and newborn fish from all classes. The abundance of FC is determined by the number of individuals belonging to classes FE, FI, and FC that survived through winter. Other classes are absent. The spatially explicit model (Fig. 20c) shows the connectivity of local models operating at the scale of a river reach of relatively homogeneous geomorphic features (i.e. a ‘node’) effectively carried out by the river network, the substrate for host and pathogen interactions (for mathematical details see Carraro et al., 2016).
Fig. 20.
Schematic representation of the proliferative kidney disease model. State variables and parameters are briefly mentioned in the text, and fully detailed in Tables S1 and S2 in Carraro et al. (2016). (a) Local intra-annual dynamics. Natural fish mortality is independent of epidemiological status, therefore it is not displayed for the sake of readability. (b) Local inter-annual dynamics. (c) Spatially explicit framework, showing the river network as the substrate for ecological iterations and for the spread of the infection. Note that the main symbols are: B, for the bryozoan submodel; F, for the fish submodel (adapted from Carraro, Mari, Gatto, Rinaldo, Bertuzzo, 2017, Carraro, Mari, Hartikainen, Strepparava, Wahli, Jokela, Gatto, Rinaldo, Bertuzzo, 2016).
A stability analysis of this time-hybrid system, performed via Floquet theory (Bacaër, Ouifki, 2007, Mari, Casagrandi, Bertuzzo, Rinaldo, Gatto, 2014) suggests that, whenever the epidemiological parameters are set to realistic values, the introduction of T. bryosalmonae in a previously disease-free community will most likely trigger a PKD outbreak. A sensitivity analysis of the system shows that, when the disease becomes endemic, the impact of PKD on fish population size is mostly controlled by the (temperature-dependent) rates of disease development in the fish host. On the other hand, this first model was still a local one with no regard to the fundamental role played by spatial dynamics. Indeed, understanding how different local communities distributed in space interact with each other is crucial to possibly predict the spreading of a PKD epidemic and the effect of intervention strategies. From a theoretical viewpoint, as we said above, the condition that disease-free equilibria in all local communities be unstable is neither necessary nor sufficient for the occurrence of outbreaks when such communities are connected by different layers of connectivity affecting transmission (Gatto et al., 2012). While the effects of landscape and river network connectivity have extensively been evaluated for waterborne diseases affecting humans, the literature focusing on modelling processes of waterborne animal diseases was scarce if not null in a spatial metacommunity framework. Yet the issue of pinpointing effective mitigation strategies for wildlife diseases such as PKD is becoming increasingly critical for environmental policy makers. A noteworthy example is given by the recent PKD outbreak occurred in the Yellowstone river (Montana, USA) (Robbins, 2016), where, due to an unprecedented fish kill, the local wildlife authorities imposed the closure of a 300 km-long river stretch and related tributaries to all recreational activities, to prevent farther spread of the parasite. A proper predictive tool for the spatial dynamics of PKD remains elusive to date, despite its clear importance for disease control and impact mitigation.
For this reason, Carraro et al. (2017) set out to study the key influence of network effects on PKD mortality and prevalence patterns, and on the celerity of disease propagation. Building on the recently proposed, first local model of PKD transmission (Carraro et al., 2016), a spatially-explicit metacommunity framework has been developed to study the spatial effects in the spread of the disease in idealized stream networks. At the local community scale, the model accounts for demographic and epidemiological dynamics of bryozoan and fish populations. At the network scale, the model couples the dynamics of each local community through hydrological transport of parasite spores and fish movement. The model also explicitly accounts for water temperature variations that influence epidemiological parameters, for heterogeneity in habitat characteristics, and for hydrological conditions along a river network.
The idealized stream network is obtained as an OCN, which defines a tree that spans the whole landscape. We consider landscapes formed by square lattices of pixels whose side has length Lp. In the real world, however, a drainage path becomes a stream only when certain hydrological conditions are met. The simplest, and most tested method assumes that pixels form a channel when their contributing area (a proxy of landscape-forming discharge) exceeds a certain threshold AC, T (Carraro et al., 2017). The network is then discretized into stretches, each of which defined as a sequence of channelized pixels starting from one pixel having either zero (river sources) or more than one channelized upstream pixels (confluences), and containing the downstream sequence of channelized pixels until another confluence or the outlet are reached. The obtained network of stretches is an oriented graph suitable for the application of the PKD metacommunity model. The second step in the generation of synthetic river networks consists in the definition of the geomorphological properties of each river stretch (NS is the number of stretches). Cross sections are approximated with rectangular shapes having width w, depth d and average water velocity v. To account for how these geometric variables change along the network, we exploit a classical result of river geomorphology (Rodriguez-Iturbe and Rinaldo, 2001), according to which w∝Q0.5, d∝Q0.4 and v∝Q0.1 where Q is river discharge. By invoking the proportionality between landscape-forming discharge and contributing area at-a-site, one has where the subscript k identifies a generic stretch k, and wo, do and vo are the maximum values (i.e. at the outlet) for width, depth and velocity, respectively; is the normalized contributing area to stretch k; subscript ik identifies the last downstream pixel of stretch k (the last element of ). The discharge at the outlet of the catchment reads then ; the water volume in a generic stretch k is where the length and if the flow direction along pixel i is parallel to a pixel side or if parallel to the pixel diagonal. The slope-area relationship allows one to evaluate the elevation of the network stretches. The elevation drop along a network pixel can indeed be expressed as where so is the outlet slope. This relationship can be iteratively applied starting from the outlet pixel (where an arbitrary elevation zo is imposed) towards all upstream paths, in order to reconstruct the elevation of each channelized pixel. The elevation of a stretch can be defined as the average elevation among all constituting pixels. Examples of OCNs obtained by changing only the location of the output pixel are shown in Fig. 21. Scale parameters that define the metric of the river network were chosen to be representative of a prealpine catchment of around 1000 km2.
Fig. 21.
(a) Example of an Optimal Channel Network. The elevation map has been obtained by extrapolating a deterministic slope-area law to unchanneled pixels as well; while this hypothesis is not generally valid in real landscapes, it has no implication for this work (Appendix). (b) Distribution of mean fish residence times for the OCN presented in panel (a). Mean residence times are computed by assuming reasonable parameters and spatially uniform fish density (Carraro et al., 2017). (c) A replica of OCN in the same domain with a different localization of the output pixel. (d) Tridimensional landscape generated by the OCN depicted in panel (c) Carraro et al. (2017).
The seasonal cycle of stream water temperature typically follows that of air temperature, albeit being damped and possibly delayed. However, notable deviations can be observed in streams with large impoundments or lakes upstream, or when the thermal regime is dominated by ice/snow melting. For this exercise, we assume that water temperature at the outlet reach To(τ) follows a sinusoidal function with period equal to one year. To derive time series of water temperature for all network stretches, we further assume that water temperature mirrors the environmental lapse rate of air temperature. Water temperature in a generic stretch k is then where Γw is the lapse rate and Δzk the difference in elevation with respect to the outlet. Lapse rates for air temperature can range from about 9.8 oC km for dry air (dry adiabatic lapse rate - DALR) to about 4.0 oC km for hot saturated air (saturated adiabatic lapse rate). We assume Γw equal to 6.5 oC km a typical value that is used as global mean environmental lapse rate for air temperature (Carraro et al., 2017).
The fish mobility rate li can be thought of as the inverse of the population-average residence time within stretch i. In general, stretches may have different geometric and physical characteristics (e.g. length, water volume and depth, velocity, fish carrying capacity) and thus li is expected to change across the river network. li is computed in such a way that the stationary state of the underlying diffusion process is a specific spatial distribution of fish abundances Fi. The underlying idea is that, in order to apply the model, first a distribution of fish abundance at carrying capacity is assigned according to the characteristics of each stretch, then a set of mobility rates li is derived so that fish movement leads, at steady state, to the desired abundance distribution. Once movements rules are determined (diffusion matrix P), the values of li such that a distribution of fish abundances Fi is an equilibrium state are obtained by solving the following linear system:
| (7) |
Note that only of the above equations are nontrivial identities: in fact, pij ≠ 0 only if stretches i and j are directly connected, and every stretch has one downstream connection, with the exception of the outlet stretch. The system has ∞1 solutions; indeed if a set of li is a solution, also the same set multiplied by a scalar is a solution. It is thus possible to focus on a single solution by specifying the average mobility rate across the network (lavg).
The model has been applied to several replicas of OCN landscapes (see Appendix) (Fig. 21). Results show how network connectivity and hydrological conditions critically control the spatial distribution of the prevalence of PKD and the celerity of invasion fronts in the upstream and downstream directions. Fig. 22 shows how connectivity and fish mobility affect the distribution of disease prevalence (i.e. the fraction of infected fish). Two main types of pattern arise: when mobility rates are considerably high, prevalence decreases as the distance from the outlet increases (Fig. 22a, d); when instead fish mobility is negligible, the sites with higher prevalence are those whose contributing area is higher (Fig. 22b,c). Contributing area is indeed a proxy of the abundance of parasite spores that enter a given stretch, which is the main driver of infection in the absence of fish movement. In this case, small headwater stretches in the proximity of the outlet are not invaded by the parasite (see magenta arrows in Fig. 22b). Conversely, high mobility rates enhance the mixing process among local communities, with the result that the variability in prevalence among neighbouring stretches is low and the average network prevalence increases. When mobility rates are tuned to more realistic values (i.e., by assuming the distribution of mean residence times of Fig. 21b), the distribution of prevalence shows an intermediate behaviour (blue lines in Fig. 22c, d). Patterns of fish loss exhibit an analogous trend.
Fig. 22.
Left and central columns: effect of the magnitude of fish mobility rates on PKD prevalence. Simulations are run for 50 years, the prevalence at the end of the 50th season is shown. A flat landscape is assumed. (a) Prevalence map for a given OCN and standard parameters (Carraro et al., 2017). (b) Prevalence map in absence of fish mobility. (c) Prevalence as a function of contributing area. For ten different OCNs, prevalence at each stretch is evaluated. Solid lines represent mean trends; shaded areas identify 25th–75th percentiles of the distribution. (d) Prevalence as a function of relative distance to the outlet. Right column: effect of elevation gradient on prevalence (e) and fish loss (f) when fish mobility is set to zero. Symbols are as in panel c. Epidemiological parameters are set to their reference value (Carraro et al., 2017).
The inclusion of an elevation gradient has a minor impact on the distribution of prevalence (Fig. 22e); of course, this depends on the lapse rate chosen. As a consequence of diminished temperature, a decrease of prevalence in upstream stretches is observed, which is not compensated for by a corresponding increment in lower altitude stretches. This causes a small reduction in the average network prevalence (about 1.5% regardless of fish mobility). As for the distribution of fish loss (Fig. 22f), the effects of non-uniform temperature are slightly accentuated. At the outlet, fish loss is generally higher (+4.3% when lavg is null) but the fish loss does not change substantially with respect to the flat landscape case. Also, a sensitivity analysis of disease propagation celerity with respect to the contamination rates (pathogen spores produced by both fish and bryozoans) and the fish mobility rate lavg has been conducted. Downstream propagation generally occurs after one to three seasons, much faster than upstream propagation (which reaches a steady state after around 100 seasons), as a consequence of the bias in the hydrological transport of spores and of its fast dynamics. Expectedly, both the fish mobility and the contamination rates are positively correlated with propagation celerity in both directions, although the role of lavg in downstream propagation is minor. When both contamination and mobility are small, rather obviously PKD might not establish in the network. Note that, while the absence of PKD at the outlet stretch implies that the whole network is disease-free, this is not necessarily true with regards to the headwaters. Similar effects are produced by variations of fish or variations of bryozoan contamination rates.
Fish movement and hydrological transport within a river network can thus produce a heterogeneous distribution of PKD prevalence and fish loss even in the absence of spatial gradients of fish and bryozoan densities, or of transmission rates (Carraro et al., 2017). The typical lifetime of PKD spores (around 1 day) allow them to travel along with the flow, and possibly infect fish, tens of kilometers downstream of the point where they are released. Stretches further downstream thus collect spores from the whole (or a large portion of the) upstream area and are therefore more likely to exhibit higher PKD prevalence and fish loss. Conversely, headwaters and low-order streams are subject only to the spore load that is locally released and thus tend to be relatively less affected by PKD. Therefore, hydrological transport of spores tends to produce spatial patterns of disease prevalence correlated to the upstream drainage area. This dominant pattern can partially be affected by fish mobility. Indeed, a headwater connected directly to a high-order stream is subject to immigration of likely-infected fish that foster local prevalence. Overall, fish mobility promotes the mixing between low- and high-order streams resulting in a net increase of overall prevalence at the network scale.
Elevation of river stretches is intimately related to the structure of the underlying river network. Indeed, the well-established and observed slope-drainage area relationship dictates that a network configuration is uniquely associated to a relative elevation distribution of river sites. Thus network structure controls, as a byproduct, also the distribution of elevations, a proxy of mean water temperature and in turn of PKD prevalence (Carraro et al., 2016). Indeed, water temperature generally decreases with elevation and thus with the distance to the outlet. Temperature gradients tend thus to produce distributions of PKD prevalence akin to those discussed above driven by hydrological transport and fish mobility. However, results report that, at least for the above example, the effect of temperature might be minor compared to that produced by spatial coupling mechanisms. The river network analyzed herein spans an elevation relief of about 1000 m, which translates in about 6.5 oC difference in mean water temperature. Larger network with more pronounced elevation relief can possibly lead to more important effect of temperature gradients.
The invasion celerity of PKD in the downstream direction is mostly controlled by hydrological transport of spores, whereas fish mobility has only a marginal effect. For transmission parameters leading to high PKD prevalence (above 90%, a value sometimes observed in affected river systems (Wahli, Bernet, Steiner, Schmidt-Posthaus, 2007, Wahli, Knuesel, Bernet, Segner, Pugovkin, Burkhardt-Holm, Escher, Schmidt-Posthaus, 2002)), the disease can invade from tens to hundreds of kilometers of river within a single proliferation season, provided that all sites are equally suitable for fish and bryozoans. Upstream invasion of PKD from a region of the network close to the outlet can occur only via fish swimming against the flow direction. The corresponding celerity is much slower than the downstream one. With realistic values of fish mobility (e.g. d), PKD can travel upstream only few kilometers per season.
Modelling fish mobility as a diffusion process implicitly assumes that fish engage in trips with a thin-tailed distribution of distance (Carraro et al., 2017). As discussed above, this is a useful working hypothesis. One might assume, on the contrary, different diffusion processes within the river network like e.g. a heavy-tailed distribution of reachable distances. This could lead to anomalous diffusion and enhanced celerity of propagation of disease fronts into disease-free regions. Other factors not included in this analysis, e.g. detailed descriptions of the transport of spores, or infection of bryozoans or statoblasts through ballast water or by waterfowl (Okamura et al., 2011), can boost the propagation in both directions via long-distance dispersal as well.
We conclude that spatial coupling mechanisms, i.e. hydrological transport of spores and fish mobility, matter only during the bryozoan proliferation season in which PKD can actually be transmitted (typically from April to November). While this hypothesis is reasonable for parasite spores, whose survival time-scale is much shorter than the duration of the winter season, it might be questionable as concerns fish. Indeed, fish movement in the cold season, even if it cannot spread the disease, can enhance the redistribution of PKD carriers. It is known that salmonids may move by several kilometers upstream in late summer or autumn for spawning, and an analogous distance is covered downstream in early spring. However, brown trout are usually subject to natal homing (Frank et al., 2012) and so they tend to return to the same place. Moreover, PKD is not vertically transmitted to newborn fish. Hence, we argue that neglecting winter fish mobility does not frustrate our model’s ability to capture the effect of this crucial process on the patterns of PKD prevalence.
The above results further our understanding of the drivers of fish distribution in riverine ecosystems and provide the basis for the development of intervention and management tools, which is one of the main tenets of this paper.
5. Concluding remarks
General lessons that can be drawn from our perspective pertain a twofold advance that we consider acquired. On the one hand, the role of directional dispersal embedded in the topology and metrics of river networks as the substrate for ecological interactions proves fundamental, theoretically and experimentally. Its remarkable effects are relevant to unfolding or declining biodiversity, population dynamics including biological invasions, the spread of waterborne disease. This is far from generally acknowledged to date, yet particularly clear in our view. On the other hand, spatially explicit metacommunity models (of biodiversity, of population dynamics as well as of waterborne and water-based disease transmissions) are fast learners from any source of distributed information. Dynamic models of this kind may be particularly effective in understanding patterns of biodiversity and of biological invasions, as well as in planning containment efforts of emerging infectious diseases – all of them being decisively affected by the topology and metrics of the river network, and the embedded directional dispersal allowed by their form and function. Despite differences in methods that will be tested through model-guided field validations, mathematical modeling of large-scale water controls on biota i.e. the core business of ecohydrology, offer a broad perspective on a range of biological processes, only briefly examined in this paper though following a coherent conceptual thread. We believe that neglecting opportunities to develop this path, or simply fostering a common cultural bias against modelling approaches especially in public health assessment, will contribute to keep the world’s social inequalities and injustice in the statu quo.
Several open issues remain in a number of areas relevant to this review. For example, the use of estimated hydrologic controls as a metric for model/study comparisons could parallel current practice as data on the biota, say related to waterborne disease, are often of limited quality such that it is often difficult to distinguish between models on the grounds of better or worse performance. Progress in data assimilation and model validation is also needed, in particular in view of the nature of available field data. The different datasets to be utilised, in fact, have rather different quality, because uncertainty on topographic, hydrologic or ecological data tends to be radically different. This constrains our ability to validate integrated models to some extent, and is keen to have an impact on the acceptance of spatial models in other communities, e.g. in the public health area. It is the authors’ belief, however, that these approach will become mainstream soon enough owing to their intrinsic advantages. Optimal control of intervention measures, possibly in emergency management, is a natural development of the current tools. It will naturally follow from the solid establishment of the field of spatially explicit ecohydrology of species, populations and pathogens of waterborne disease. Missing steps for advancing this area concern the availability of model-guided field validations and suitable data to be assimilated into the model. We expect significant steps forward in this area to come from remote sensing and digital image processing, and from other technological advances – like the widespread availability of human mobility fluxes tracked by cell phones, currently arbitrarily managed, at times in rather untransparent ways, by providers and monopolists. Environmental DNA fingerprinting is also a technique that will increasingly provide large amounts of field data of great ecological importance.
What limits the widespread uptake of models for decision making at the interface of hydrology and ecology is a serious matter of current debate. In the field of hydrology, it is widely accepted that modelling tools are needed to overcome the limitation of extrapolating from data in a nonstationary world. Therein, model-based decisions are the norm to investigate possible interventions under what-if scenarios. In biodiversity preservation, protection from unfolding biological invasions or public health control of waterborne disease transmission, such a transition has not yet happened. Perhaps what is missing to prompt a radical attitude change in these areas is a massive set of visible applications – the Haiti cholera epidemic (2011-) seems to have represented an important testbed to that end – or perhaps visible joint initiatives where direct comparisons between data-based strategies and modelling-aided scenarios are made. What we are about to pursue next is a generalized use of assimilated models of the spatially explicit type to assess optimal control of interventions strategies for the containment of waterborne disease spread (say, where to best allocate finite batch of vaccines in space and time). In epidemiology, this is way beyond current public health management of emergences. The road traced by hydrologists, and by oceanographers and meteorologists before them, will be eventually followed in the future by ecologists and public health officials in our (not so unbiased perhaps) view.
Acknowledgement
The authors gratefully acknowledge the support provided by the H2020 European Framework Programme through ECOPOTENTIAL Project 641762. The results presented here are also in part a spinoff of the ERC advanced grant RINEC-227612 (River networks as ecological corridors for species, populations and pathogens of waterborne disease), the Swiss National Science Foundation projects 200021_124930/1, 31003A_135622, PP00P3_150698 and 200021_172578, and the D4D (Data for Development) Senegal Challenge organized by Orange and Sonatel and funded by the Bill and Melinda Gates Foundation (grant OPP1114791). The authors wish to thank two anonymous reviewers for their insightful comments on an earlier version of the manuscript.
Appendix
Optimal Channel Networks (OCNs) and their landscapes
Moving from the exact result that drainage network configurations minimizing total energy dissipation are stationary solutions of the general equation describing landscape evolution (Banavar et al., 2000), it was argued (Rinaldo, Rigon, Banavar, Maritan, Rodriguez-Iturbe, 2014, Rinaldo, Rigon, Rodriguez-Iturbe, 1999, Rinaldo, Rodriguez-Iturbe, Rigon, Bras, Vasquez, Marani, 1992, Rodriguez-Iturbe, Rinaldo, 2001, Rodriguez-Iturbe, Rinaldo, Rigon, Bras, Ijjasz-Vasquez, Marani, 1992) that, at least in the fluvial landscape, nature works through imperfect searches for dynamically accessible optimal configurations and that purely random or deterministic constructs are unsuitable to properly describe natural network forms. Here, we review the model of river networks known as Optimal Channel Network (OCN) (Rodriguez-Iturbe et al., 1992). The OCN model was originally based on the ansatz that configurations occurring in Nature minimize a functional describing total energy dissipation and on the derivation of an explicit form for such a functional. The latter uses, locally, landscape-forming flowrates Qi and the drop in potential energy to define energy dissipation QiΔzi i.e. approximated by Qi ∼ Ai (where Ai is total contributing area at i) and by the drop in elevation with γ ∼ 1/2 (Rodriguez-Iturbe and Rinaldo, 2001). Spanning, loopless network configurations characterized by minimum energy dissipation are obtained by selecting the configuration, say s, that minimizes the functional:
| (A.1) |
where i spans the lattice, say of N sites. The configuration s determines uniquely, on a spanning tree, the values of Ai (see below) and it proves crucial (Banavar, Colaiori, Flammini, Maritan, Rinaldo, 2000, Rinaldo, Rigon, Banavar, Maritan, Rodriguez-Iturbe, 2014, Rinaldo, Rodriguez-Iturbe, Rigon, Bras, Vasquez, Marani, 1992, Rodriguez-Iturbe, Rinaldo, 2001, Rodriguez-Iturbe, Rinaldo, Rigon, Bras, Ijjasz-Vasquez, Marani, 1992) that one has a concave functional (i.e. γ < 1) directly from the physics of the problem subsumed by the slope-area relation.
The global minimum (i.e. the ground state) of the functional in Eq. (A.1) is exactly characterized by known mean field exponents (Rodriguez-Iturbe and Rinaldo, 2001), and one might expect to approach the mean field behavior by reaching a stable local minima upon careful annealing of the system. This is in fact the case. The proof of the above is not trivial: any stationary solution of the landscape evolution equation must locally satisfy the relationship between flux/area and the topographic gradient at any point i and gradients are approximated by Δzi, the largest drop in elevation at i. One can thus uniquely associate any landscapes with an oriented (spanning and loopless) graph on a lattice, and reconstruct the field of cumulative areas {Ai} corresponding to a given oriented spanning graph. Note also that we wish to emphasize the dependence on the configuration that the system assumes on the features of the oriented spanning graph associated with the landscape topography z through its gradients ∇z that uniquely defines total contributing areas in a N-site lattice. What is totally surprising is that empirically observed scaling features are only reproduced by myopic searches of dynamically accessible configurations, that cannot get rid of the inheritance of extant constraints. The scaling structure (topological and metric) of configurations characterized by suboptimal energy dissipation matches perfectly those observed in Nature, and differs significantly from ground states (Rinaldo, Banavar, Maritan, 2006, Rinaldo, Rigon, Banavar, Maritan, Rodriguez-Iturbe, 2014, Rinaldo, Rigon, Rodriguez-Iturbe, 1999).
Optimal arrangements of network structures and branching patterns thus result from the direct minimization of the functional in Eq. (A.1). The basic operational problem to obtain OCNs for a given domain is to find the connected path draining it that minimizes Hγ(s) without postulating predefined features, e.g. the number of sources or the link lengths. One key problem is the assessment of the robustness of OCN configurations selected by any minimum procedure. This has been studied (Rodriguez-Iturbe and Rinaldo, 2001) with respect to: the strategy for minimum search; the role of initial conditions; the robustness of the functional dependence on γ; the role of lattice anisotropies; the effects of ‘quenched’ randomness (Rinaldo et al., 1992). The basic optimization strategies are similar to algorithms developed in the context of non-numerable (NP-complete) problems where the exponential growth of possible configurations prevents complete enumeration. Iterated random searches work best in that context (Rodriguez-Iturbe and Rinaldo, 2001). The basic algorithm proceeds as follows. An initial network configuration, s, is chosen as a spanning tree on the grid to drain an overall area made up by N sites. This defines an orientation and a connection for each pixel stating to which of the eight neighboring pixels its area is draining, neighbors being assumed at unit distance from the centroid. This in turn needed both preliminary and a posteriori speculations on whether a triangular lattice - with six neighboring nodes - or an anisotropic scheme in which diagonal connections were weighted by a factor would be a better model of local interactions (Rodriguez-Iturbe and Rinaldo, 2001). A scalar state variable, Ai(t), denotes the total area at a point i at stage t of the optimization process, where Wij is the (now dynamic) functional operator that has the connectivity matrix as its static counterpart by:
(that is Wij(t) implies that j → i is a drainage direction). Note that j spans the 8 neighboring pixels of the arbitrary ith site. The unit mass added refers to the area representative of the actual site as a proxy of the distributed injection term. From the initial configuration (stage ), the basic strategy consists of drawing a site at random and perturbing the system by assigning a change δWij i.e. by modifying at random its connection to the former receiving pixel. Hence This corresponds to perturbing the configuration s (s → s′). Adjusting to such a local modification, all aggregated areas Ai are modified in the downstream region until the original and the modified path reconvene. The change is accepted if the modified value of Hγ(s′) is lowered by the random change (Hγ(s′) < Hγ(s)) and no loops are formed. Loops are excluded on a rigorous basis, as it was shown exactly that they lead to energetically unfavorable configurations (for the functional in Eq. with γ < 1 every tree is a local minimum of total energy expenditure (Rinaldo et al., 2006)). As the new configuration is adopted as a base configuration, the process is iterated. Otherwise, the change is discarded (if Hγ(s′) ≥ Hγ(s)), and the t-stage configuration s is perturbed again. The procedure leads to a configuration for which no improvement on total energy expenditure appears after a fixed (and large) number of iterations i.e. an OCN. The whole process may or may not be then reset and restarted from the same initial configuration. This is done several times at times to allow the random process a fair chance to capture nonlocal minima – should they be of interest. The configuration attaining the lowest energy dissipation amongst the trials described before is chosen as the OCN. Instructive visual schemes of the progress of the basic selection algorithm is illustrated elsewhere (Briggs, Krishnamoorthy, 2013, Rodriguez-Iturbe, Rinaldo, 2001).
This basic procedure, at times termed the Lin (or the greedy) approach because of the similarities with the N-city traveling salesman algorithm (Rodriguez-Iturbe and Rinaldo, 2001), respects the rules of a fair search for approximate solutions but is apt to yield trapping in local minimum energy. Variants of the basic algorithm, implemented to test the importance of choice of strategy for minimum search, include the Metropolis algorithm – multiple simultaneous perturbations and simulated annealing schemes are engineered to avoid trapping of the configuration into unsuitable local minima. This is done by accepting perturbations of the current configuration (s → s′) even if they yield Hγ(s′) ≥ Hγ(s) with a probability depending on a state parameter T. In practice, the probability of acceptance of the perturbation is given by the Metropolis rule, i.e. it is 1 if the resulting change corresponds to Hγ(s′) < Hγ(s)) or, if and and 0 otherwise, where R is a random number (R ∈ (0, 1)). To carry out proper annealing one makes changes in the parameter T from relatively high values at the start to low values towards the end of the analysis. Clearly for high values of T the likelihood of accepting unfavorable changes is high, whereas for T → 0 the rule is equal to that of the basic algorithm. A ‘cooling’ schedule for decreasing values of T as the procedure evolves is thus required (Rodriguez-Iturbe and Rinaldo, 2001).
Optimal arrangements of network structures and branching patterns thus result from the direct minimization of the functional in Eq. (A.1). The basic operational problem to obtain OCNs for a given domain is to find the connected path s draining it that minimizes Hγ(s) without postulating predefined features, e.g. the number of sources or the link lengths. Random perturbations of an initial structure imply disconnecting and reorienting a single link at a time (Rodriguez-Iturbe and Rinaldo, 2001). They lead to new configurations that are accepted, details aside, if they lower total energy expenditure – i.e. the functional in Eq. (A.1) – iterated until many perturbations are unable to prompt change by finding better configurations. Loops possibly generated by the random configuration search in the fitness landscape were excluded at first without a rigorous basis. Only later it was shown exactly that they lead to energetically unfavorable configurations (Banavar, Colaiori, Flammini, Maritan, Rinaldo, 2000, Banavar, Colaiori, Flammini, Maritan, Rinaldo, 2001, Rinaldo, Banavar, Maritan, 2006) for realistic values of γ derived from slope-area empirical evidence. Boundary conditions are required for the evolving optimal trees, as outlet(s) must be imposed (single or multiple outlets along drainage lines) as well as no-flux or periodic boundary conditions (Briggs, Krishnamoorthy, 2013, Rodriguez-Iturbe, Rinaldo, 2001).
Interesting issues emerge on the statics, dynamics and complexity of OCNs (Rinaldo et al., 2014). Exact results (reviewed in Rinaldo et al., 2014) exist on: the existence of many dynamically accessible stable states; the practical impossibility of pointing out a priori the most stable feasible state among all metastable states without an evolutionary account of the history of the current configuration of the system; the hierarchical structure and the universality class of dynamically accessible states. Although the above are features that river networks share with other natural complex systems, the extent of observations and comparative analyses, the exact relation to the general evolution equations and the broad range of scales involved suggest their interest as a general model system of how Nature works (Bak, 1996). Thus, one recurrent self-organized mechanism for the dynamic origin of fractal forms is the robust strive for imperfect optimality that we see embedded in many natural patterns, especially hydrologic ones.
Example of spatially explicit SIWR model.
A spatially explicit SIWR model of epidemic cholera is presented here as an Appendix to the main text. All spatially explicit epidemiological models follow from the same scheme, as they belong in a special class of metacommunity models (Section 2).
The basic epidemiological model derives from the spatially-distributed SIWR model (termed SIRB for bacterial diseases like cholera) (Bertuzzo, Carrara, Mari, Altermatt, Rodriguez-Iturbe, Rinaldo, 2005, Pasetto, Finger, Rinaldo, Bertuzzo, 2017). The population is subdivided into n communities. Each community is represented by a node of the model (Fig. 18). The individuals in each node i are subdivided into three separate categories, susceptible, symptomatic infected and recovered, whose number at time t are denoted with Si(t), Ii(t) and Ri(t), respectively. The concentration of V. cholerae in the local environment corresponding to node i is indicated with Bi(t). The following set of coupled ordinary differential equations describes the cholera transmission dynamics:
| (A.2) |
| (A.3) |
| (A.4) |
where the population Hi of each node is assumed to be at demographic equilibrium, if . Thus, the equation for susceptibles, in this case, reduces to . The term Fi(t) is called force of infection and represents the rate at which susceptible individuals are exposed to contaminated water, expressed as:
Parameter β denotes the maximum exposure rate, which, in this application, is assumed to differ among the nodes. The fraction is the probability of becoming infected due to the exposure to a concentration Bi of V. cholerae, K being the half-saturation constant (Codeço, 2001). The force of infection takes into account the possible disease propagation due to human mobility, with the idea that a fraction m of susceptible individuals daily commute between nodes and can thus be exposed to pathogens at the destination. Two options have been used to compute the probability Qij that an individual living at node i commutes to j: one is the gravity model (Erlander and Stewart, 1990) i.e. where the attractiveness of node j depends on its population size Hj, while the deterrence factor is assumed to be dependent on the distance dij between the two communities via an exponential kernel with shape factor D (alternatively, a radiation model may be implemented in uniformly dense contexts (Simini et al., 2012)). The second option has been to derive mobility fluxes Qij directly from the tracking of mobile phone records, a tool that proves essential in the case of non-routine gatherings (like religious pilgrimages in Senegal) that ignite infection spreads (Finger et al., 2016). A fraction σ of the infected individuals develops symptoms, thus entering class Ii. The remaining fraction is asymptomatic and therefore does not contribute to the disease transmission and enters the recovered compartment directly. Symptomatically infected individuals recover at a rate γ or die due to cholera or other causes at rates α or μ, respectively. Note that here α is set to zero to maintain the demographic equilibrium. In fact, a value of α different from zero under the assumption of constant population would imply that the birth rate increases to overcome the deaths due to cholera, which is inconsistent. Recovered individuals lose their immunity and return to the susceptible compartment at a rate ρ or die at a rate μ. Symptomatic individuals contribute to the environmental concentration of V. cholerae at a rate p/Wi, where p is the rate at which bacteria excreted by an infected individual reach and contaminate an imaginary environmental water reservoir of volume Wi (assumed to be proportional to population size, i.e., as in Rinaldo et al., 2012). Environmental V. cholerae are assumed to decay at a rate μB. The hydrologic dispersal of bacteria if embedded in the last term of Eq. (A.4) . Bacteria undergo hydrologic dispersal at a rate ℓ: pathogens can travel from node i to j with probability Pij. We assume the if j is the downstream nearest neighbor of node i and zero otherwise.
The mobility of infected individuals are not considered here (Bertuzzo, Finger, Mari, Gatto, Rinaldo, 2016, Pasetto, Finger, Rinaldo, Bertuzzo, 2017). While bacterial dispersal along the hydrological network is typically an important transmission process at the first stages of a cholera epidemics, subsequent current reported epidemiological data, as notably observed for the Haitian (2010-) epidemics are uncorrelated to the channel network. For what concern the mobility of infected individuals, most of them require urgent hydration treatment at healthcare points, thus the hypothesis that a relevant fraction of infect individuals commutes among the nodes is unconvincing. In order to express the deterioration of sanitary conditions caused by rainfall, the contamination rate p is increased by the rainfall intensity Ji(t) via a coefficient ϕ (Rinaldo et al., 2012). By introducing the dimensionless bacterial concentrations it is possible to group three model parameters into a single ratio (Bertuzzo et al., 2008). The weekly cholera cases are computed by integrating the number of new cases in every commune, i.e. σFiSi. The equations are usually been solved by Runge–Kutta methods (Bertuzzo, Finger, Mari, Gatto, Rinaldo, 2016, Pasetto, Finger, Rinaldo, Bertuzzo, 2017). To assess the impact of vaccination campaigns, the model needs be adapted to consider vaccinated individuals. We assume that vaccination targets individuals independently of their cholera infection history, i.e. both susceptible (S) and already immune individuals (R) are eligible with the same probability. Vaccinated individuals already immune are assumed to remain completely immune, while vaccinated susceptibles benefit from a leaky immunity with vaccine efficacy 0 < η < 1, thus reducing the susceptibility by η. Oral vaccination is assume to provide immunity with a delay of one week after administration of a single dose. Due to the short time horizon of the forecast, at this stage no assumption is made for the duration of the vaccine-induced immunity and individuals remain immune for the duration of this study. At each node i the number of vaccinated individuals at a time t is subdivided into three separate categories in addition to Si, Ii and Ri, denoted as vaccinated susceptible individuals, vaccinated individuals that become infected, and vaccinated recovered which have a complete immunity, . The equations are modified accordingly (Pasetto et al., 2017) as shown schematically in the scheme of Fig. 18d where the number of susceptible individuals is computed as . The model assumes a linear ramp-up of vaccine uptake, meaning that daily number of OCV doses distributed in each community, νi, is computed by equally deploying the available doses during the days of the campaign. Normally, vaccines are evenly distributed among susceptible and recovered individuals. The delay of one week in the vaccine-derived immunity is modelled by starting the OCV campaign with a delay of one week. To model the leaky immunity of vaccinated susceptible individuals, the force of infection Fi is decreased of a factor as depicted in Fig. 18.
References
- Abubakar A., Azman A.S., Ivers L.C. The first use of the global oral cholera vaccine emergency stockpile: lessons from South Sudan. PLoS Med. 2015;12(1):28–29. doi: 10.1371/journal.pmed.1001901. [DOI] [PMC free article] [PubMed] [Google Scholar]
- de Aguiar M., Baranger M., Baptestini E.M., Kaufman L., Bar-Yam Y. Global patterns of speciation and diversity. Nature. 2009;460(7253):384–388. doi: 10.1038/nature08168. [DOI] [PubMed] [Google Scholar]
- Akaike H. A new look at the statistical model identification. IEEE Trans. Autom. Control. 1974;19:716–723. [Google Scholar]
- Alexander R., Jones P., Boyer E., Smith R. Effect of stream channel size on the delivery of nitrogen to the Gulf of Mexico. Nature. 2000;403:758–761. doi: 10.1038/35001562. [DOI] [PubMed] [Google Scholar]
- Allen Y.C., Ramcharan C. Dreissena distribution in commercial waterways of the US: using failed invasions to identify limiting factors. Can. J. Fish. Aquat. Sci. 2001;58:898–907. [Google Scholar]
- Altermatt F., Bieger A., Carrara F., Rinaldo A., Holyoak M. Effects of connectivity and recurrent local disturbances on community structure and population density in experimental metacommunities. PLoS ONE. 2011;6 doi: 10.1371/journal.pone.0019525. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Altermatt F., Schreiber S., Holyoak M. Interactive effects of disturbance and dispersal directionality on species richness and composition in metacommunities. Ecology. 2011;92:859–870. doi: 10.1890/10-1095.1. [DOI] [PubMed] [Google Scholar]
- Ammermann A., Cavalli-Sforza L. Princeton Univ. Press; 1984. The neolithic transition and the genetics of population in Europe. [Google Scholar]
- Anderson M.J., Crist T.O., Chase J.M. Navigating the multiple meanings of β-diversity: a roadmap for the practicing ecologist. Ecol. Lett. 2011;14(1):19–28. doi: 10.1111/j.1461-0248.2010.01552.x. [DOI] [PubMed] [Google Scholar]
- Andow D., Kareiva P., Levin S., Okubo A. Spread of invading organisms. Landscape Ecol. 1990;4(2/3):177–188. [Google Scholar]
- Azman A.S., Ivers L.C., Legros D., Luquero F.J., Mintz E.D. Safe water, sanitation, hygiene, and a cholera vaccine. Lancet. 2016;387(1):28–29. doi: 10.1016/S0140-6736(15)01294-5. [DOI] [PubMed] [Google Scholar]
- Azman A., Lessler J. Reactive vaccination in the presence of disease hotspots. Proc. R. Soc. B. 2014;282(1):1–13. doi: 10.1098/rspb.2014.1341. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bacaër N., Ouifki R. Growth rate and basic reproduction number for population models with a simple periodic factor. Math. Biosci. 2007;210(2):647–658. doi: 10.1016/j.mbs.2007.07.005. [DOI] [PubMed] [Google Scholar]
- Bak P. Springer-Verlag, Berlin; 1996. How Nature Works. The Science of Self-Organized Criticality. [Google Scholar]
- Baker-Austin C., Trinanes J.A., Taylor N.G.H., Hartnell R., Siitonen A., Martinez-Urtaza J. Emerging vibrio risk at high latitudes in response to ocean warming. Nat. Clim. Chang. 2013;3:73–77. [Google Scholar]
- Banavar J., Colaiori F., Flammini A., Maritan A., Rinaldo A. Topology of the fittest transportation network. Phys. Rev. Lett. 2000;84:4745–4748. doi: 10.1103/PhysRevLett.84.4745. [DOI] [PubMed] [Google Scholar]
- Banavar J., Colaiori F., Flammini A., Maritan A., Rinaldo A. Scaling, optimality, and landscape evolution. J. Stat. Phys. 2001;104:1–48. [Google Scholar]
- Banavar J., Damuth J., Maritan A., Rinaldo A. Scaling in ecosystems and the linkage of macroecological laws. Phys. Rev. Lett. 2007;98(1):068104. doi: 10.1103/PhysRevLett.98.068104. [DOI] [PubMed] [Google Scholar]
- Barbour A. Macdonald’s model and the transmission of bilharzia. Trans. R. Soc. Trop. Med. Hygiene. 1978;72(1):1–6. doi: 10.1016/0035-9203(78)90290-0. [DOI] [PubMed] [Google Scholar]
- Battin T.J., Kaplan L.A., Findlay S. Biophysical controls on organic carbon fluxes in fluvial networks. Nature Geosci. 2008;1:95–100. [Google Scholar]
- Battin T., Kaplan L., Newbold J., Hansen C. Contributions of microbial biofilms to ecosystem processes in stream mesocosms. Nature. 2003;426:439–442. doi: 10.1038/nature02152. [DOI] [PubMed] [Google Scholar]
- Beau De Rochars V.E.M., Tipret J., Patrick M. Knowledge, attitudes, and practices related to treatment and prevention of cholera, Haiti. Emerg. Infect. Dis. 2011;17:2158–2161. doi: 10.3201/eid1711.110818. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Benda L., Poff N.L., Miller D. The network dynamics hypothesis: how channel networks structure riverine habitats. Bioscience. 2004;54:384–398. [Google Scholar]
- Bengtsson L., Gaudart J., Lu X., Moore S., Wetter E., Sallah K., Rebaudet S., Piarroux R. Using mobile phone data to predict the spatial spread of cholera. Sci. Rep. 2015;5:8923–8927. doi: 10.1038/srep08923. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bergquist R., Yang G.J., Knopp S., Utzinger J., Tanner M. Surveillance and response: tools and approaches for the elimination stage of neglected tropical diseases. Acta Trop. 2015;141:229–234. doi: 10.1016/j.actatropica.2014.09.017. [DOI] [PubMed] [Google Scholar]
- Bertuzzo E., Azaele S., Maritan A., Gatto M., Rodriguez-Iturbe I., Rinaldo A. On the space-time evolution of a cholera epidemic. Water Resour. Res. 2008;44:W01424. [Google Scholar]
- Bertuzzo E., Carrara F., Mari L., Altermatt F., Rodriguez-Iturbe I., Rinaldo A. Geomorphic controls on elevational gradients of species richness. Proc. Natl. Acad. Sci. USA. 2005;113:1737–1742. doi: 10.1073/pnas.1518922113. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bertuzzo E., Finger F., Mari L., Gatto M., Rinaldo A. On the probability of extinction of the Haiti cholera epidemic. Stoch. Environ. Res. Risk Assess. 2016;30:2043–2055. [Google Scholar]
- Bertuzzo E., Mari L., Gatto M., Rodriguez-Iturbe, Rinaldo A. On spatially explicit models of cholera epidemics. J. R. Soc. Interface. 2010;7:321–333. doi: 10.1098/rsif.2009.0204. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bertuzzo E., Mari L., Righetto L., Gatto M., Casagrandi R., Rodriguez-Iturbe I., Rinaldo A. Prediction of the spatial evolution and effects of control measures for the unfolding Haiti cholera outbreak. Geophys. Res. Lett. 2011;38:L06403. [Google Scholar]
- Bertuzzo E., Maritan A., Gatto M., Rodriguez-Iturbe I., Rinaldo A. River networks and ecological corridors: reactive transport on fractals, migration fronts, hydrochory. Water Resour. Res. 2007;43:W04419. [Google Scholar]
- Bertuzzo E., Suweis S., Mari L., Maritan A., Rodriguez-Iturbe I., Rinaldo A. Spatial effects for species persistence and implications for biodiversity. Proc. Natl. Acad. Sci. USA. 2011;108(11):4346–4351. doi: 10.1073/pnas.1017274108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bi Q., Azman A.S., Satter S.M., Khan A.I., Ahmed D., Riaj A.A., Gurley E.S., Lessler J. Micro-scale spatial clustering of cholera risk factors in urban Bangladesh. PLoS Negl. Trop. Dis. 2016;10:e0004400. doi: 10.1371/journal.pntd.0004400. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Boelee E., Mekonnen Y., Poda J.N., McCartney M., Checchi P., Kibret S., Hagos F., Laamrami H. Options for water storage and rainwater harvesting to improve health and resilience against climate change in Africa. Reg. Environ. Chang. 2013;13:509–519. [Google Scholar]
- Borsuk M.E., Reichert P., Peter A., Schager E., Burkhardt-Holm P. Assessing the decline of brown trout (Salmo trutta) in Swiss rivers using a Bayesian probability network. Ecol. Model. 2006;192(1–2):224–244. [Google Scholar]
- Briggs L., Krishnamoorthy M. Exploring network scaling through variations on optimal channel networks. Proc. Natl. Acad. Sci. USA. 2013;110:19295–19300. doi: 10.1073/pnas.1313866110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brown B., Swan C. Dendritic network structure constrains metacommunity properties in riverine ecosystems. J. Anim. Ecol. 2010;79:571–580. doi: 10.1111/j.1365-2656.2010.01668.x. [DOI] [PubMed] [Google Scholar]
- Brown J. The University of Chicago Press, Chicago; 1995. Macroecology. [Google Scholar]
- Campos D., Fort J., Mendez V. Transport on fractal river networks: application to migration fronts. Theor. Pop. Biol. 2006;69:88–93. doi: 10.1016/j.tpb.2005.09.001. [DOI] [PubMed] [Google Scholar]
- Campos D., Mendez V. Reaction-diffusion wavefronts on comblike structures. Phys. Rev. E. 2005;71:31–39. doi: 10.1103/PhysRevE.71.051104. [DOI] [PubMed] [Google Scholar]
- Carlton J. Lewis, Ann Arbor MH; 1993. Dispersal Mechanisms of the Zebra Mussel (Dreissena polymorpha) pp. 121–132. [Google Scholar]
- Carrara F., Altermatt F., Rodriguez-Iturbe I., Rinaldo A. Dendritic connectivity controls biodiversity patterns in experimental metacommunities. Proc. Natl. Acad. Sci. USA. 2012;109:5761–5766. doi: 10.1073/pnas.1119651109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Carrara F., Rinaldo A., Giometto A., Altermatt F. Complex interaction of dendritic connectivity and hierarchical patch size on biodiversity in river-like landscapes. Am. Nat. 2014;183(1):13–25. doi: 10.1086/674009. [DOI] [PubMed] [Google Scholar]
- Carraro L., Mari L., Gatto M., Rinaldo A., Bertuzzo E. Spread of proliferative kidney disease in fish along stream networks: a spatial metacommunity framework. Freshwater Biol. 2017:1–14. [Google Scholar]
- Carraro L., Mari L., Hartikainen H., Strepparava N., Wahli T., Jokela J., Gatto M., Rinaldo A., Bertuzzo E. An epidemiological model for proliferative kidney disease in salmonid populations. Parasite. Vect. 2016;9 doi: 10.1186/s13071-016-1759-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Casagrandi R., Gatto M. A persistence criterion for metapopulations. Theor. Pop. Biol. 2002;61:115–125. doi: 10.1006/tpbi.2001.1558. [DOI] [PubMed] [Google Scholar]
- Casagrandi R., Mari L., Gatto M. Modelling the local dynamics of the zebra mussel (Dreissena polymorpha) Freshwater Biol. 2007;52:1223–1238. [Google Scholar]
- Cash B., Rodó X., Emch M., Yunus M., Faruque A., Pascual M. Cholera and shigellosis: different epidemiology but similar responses to climate variability. PLoS ONE. 2014;9:e107223. doi: 10.1371/journal.pone.0107223. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cash D., Rodo X., Kinter J.L. Disentangling the impact of Enso and Indian ocean variability on the regional climate of Bangladesh: implications for cholera risk. J. Clim. 2010;23:2817–2831. [Google Scholar]
- Caswell H. Community structure: a neutral model analysis. Ecol. Monogr. 1976;46(3):327–354. [Google Scholar]
- Chandrasekhar S. Stochastic problems in physics and astronomy. Rev. Mod. Phys. 1943;15(1):1–89. [Google Scholar]
- Chao D.L., Halloran M.E., Longini I.M. Vaccination strategies for epidemic cholera in Haiti with implications for the developing world. Proc. Natl. Acad. Sci. USA. 2011;108:7081–7085. doi: 10.1073/pnas.1102149108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chase M.E., Bailey R. The ecology of the zebra mussel (Dreissena polymorpha) in the lower Great lakes of North America: I. Population dynamics and growth. J. Great Lakes Res. 1999;293:657–660. [Google Scholar]
- Chave J., Muller-Landau H., Levin S. Comparing classical community models: theoretical consequences for patterns of diversity. Am. Nat. 2002;159(1):1–23. doi: 10.1086/324112. [DOI] [PubMed] [Google Scholar]
- Ciddio M., Mari L., Sokolow S., De Leo G., Casagrandi R., Gatto M. The spatial spread of schistosomiasis: a multidimensional network model applied to Saint-Louis region, Senegal. Adv. Water Resour. in press. DOI. 2017 doi: 10.1016/j.advwatres.2016.10.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Clifton-Hadley R.S., Richards R.H., Bucke D. Proliferative kidney disease (PKD) in rainbow trout Salmo gairdneri: further observations on the effects of water temperature. Aquaculture. 1986;55(3):165–171. [Google Scholar]
- Clobert J., Danchin E., Dhondt A., Nichols J. Oxford Univ. Press, Oxford; 2001. Dispersal. [Google Scholar]
- Codeço C. Endemic and epidemic dynamics of cholera: the role of the aquatic reservoir. BMC Infect. Dis. 2001;1(1) doi: 10.1186/1471-2334-1-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Colley D., Bustinduy A., Secor W., King C. Human schistosomiasis. Lancet. 2014;383:2253–2264. doi: 10.1016/S0140-6736(13)61949-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Colwell R., Rahbek C., Gotelli N. The mid-domain effect and species richness patterns: what have we learned so far? Am. Nat. 2004;163:E1–E23. doi: 10.1086/382056. [DOI] [PubMed] [Google Scholar]
- Colwell R.R. Global climate and infectious disease: the cholera paradigm. Science. 1996;274:2025–2031. doi: 10.1126/science.274.5295.2025. [DOI] [PubMed] [Google Scholar]
- Constantin de Magny G., Murtugudde R., Sapiano M.R.P., Nizam A., Brown C.W., Busalacchi A.J., Yunus M., Nair G.B., Gil A.I., Lanata C.F., Calkins J., Manna B., Rajendran K., Bhattacharya M.K., Huq A., Sack R.B., Colwell R.R. Environmental signatures associated with cholera epidemics. Proc. Natl. Acad. Sci. USA. 2008;105:17676–17681. doi: 10.1073/pnas.0809654105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Constantin de Magny G., Thiaw W., Kumar V., Manga N., Diop B.M., Gueye L., Kamara M., Roche B., Murtgudde R., Colwell R.R. Cholera outbreak in Senegal in 2005: was climate a factor? PLoS ONE. 2012;7:e44577. doi: 10.1371/journal.pone.0044577. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Corani G., Gatto M. Structural risk minimization: a robust method for density-dependence detection and model selection. Ecography. 2007;30(2):400–416. [Google Scholar]
- Diamond J. The present, past and future of human-caused extinctions. Philos. Trans. R. Soc. London Ser. B. 1989;325(1228):469–477. doi: 10.1098/rstb.1989.0100. [DOI] [PubMed] [Google Scholar]
- Diekmann O., Heesterbeek J. Wiley; 2000. Mathematical Epidemiology of Infectious Diseases. [Google Scholar]
- D’Odorico P., Laio F., Porporato A., Ridolfi L., Rinaldo A., Rodriguez-Iturbe I. Ecohydrology of terrestrial ecosystems. Bioscience. 2010;11:898–907. [Google Scholar]
- Dunkle S.E., Mba-Jonas A., Loharikar A. Epidemic cholera in a crowded urban environment, Port-au-Prince, Haiti. Emerg. Infect. Dis. 2011;17:2143–2146. doi: 10.3201/eid1711.110772. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Durrett R., Levin S. Spatial models for species-area curves. J. Theor. Biol. 1996;179(2):119–127. [Google Scholar]
- Economo E., Keitt T. Species diversity in neutral metacommunities: a network approach. Ecol. Lett. 2008;11(1):52–62. doi: 10.1111/j.1461-0248.2007.01126.x. [DOI] [PubMed] [Google Scholar]
- Eisenberg M.C., Kujbida G., Tuite A.R., Fisman D.N., Tien J.H. Examining rainfall and cholera dynamics in Haiti using statistical and dynamic modeling approaches. Epidemics. 2013;5:197–207. doi: 10.1016/j.epidem.2013.09.004. [DOI] [PubMed] [Google Scholar]
- Elton C. Methuen, London; 1958. The Ecology of Invasions by Animals and Plants. [Google Scholar]
- Emch M., Feldacker C., Islam M.S., Ali M. Seasonality of cholera from 1974 to 2005: a review of global patterns. Int. J. Health Geogr. 2008;7:31. doi: 10.1186/1476-072X-7-31. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Erlander S., Stewart N.F. VSP Books; Zeist, The Netherlands: 1990. The Gravity Model in Transportation Analysis – Theory and Extensions. [Google Scholar]
- Ernst S., Weinrobe C., Bien-Aime C. Cholera management and prevention at hospital Albert Schweitzer, Haiti. Emerg. Infect. Dis. 2011;17:2155–2157. doi: 10.3201/eid1711.110815. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Escobar L.E., Ryan S.J., Stewart-Ibarra A.M., Finkelstein J.L., King C.A., Qiao H., Polhemus M.E. A global map of suitability for coastal Vibrio cholerae under current and future climate conditions. Acta Trop. 2015;149:202–211. doi: 10.1016/j.actatropica.2015.05.028. [DOI] [PubMed] [Google Scholar]
- Fagan W. Connectivity, fragmentation, and extinction risk in dendritic metapopulations. Ecology. 2002;83(12):3243–3249. [Google Scholar]
- Faruque S.M., Islam M.J., Ahmad Q.S., Faruque A.S.G., Sack D.A., Nair G.B., Mekalanos J.J. Self-limiting nature of seasonal cholera epidemics: role of host-mediated amplification of phage. Proc. Natl. Acad. Sci. USA. 2005;102:6119–6124. doi: 10.1073/pnas.0502069102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Feist S.W., Longshaw M. Fish Diseases and Disorders. P.T.K. Woo. Vol. 1. CABI Publishing; Wallingford, UK: 2006. Phylum myxozoa; pp. 230–296. [Google Scholar]
- Ferguson H., Ball H. Epidemiological aspects of proliferative kidney disease amongst rainbow trout Salmo gairdneri Richardson in Northern Ireland. J. Fish Dis. 1979;2(3):219–225. [Google Scholar]
- Finger F., Genolet T., Mari L., Constantin De Magny G., Manga N.M., Rinaldo A., Bertuzzo E. Mobile phone data highlights the role of mass gatherings in the spreading of cholera outbreaks. Proc. Natl. Acad. Sci. USA. 2016;113:6421–6426. doi: 10.1073/pnas.1522305113. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Finger F., Knox A.C., Bertuzzo E., Mari L., Bompangue D., Gatto M., Rodriguez-Iturbe I., Rinaldo A. Cholera in the Lake Kivu region (DRC): integrating remote sensing and spatially explicit epidemiological modeling. Water Resour. Res. 2014;50:5624–5637. [Google Scholar]
- Fisher R. The wave of advance of advantageous genes. Ann. Eugen. 1937;7:355–369. [Google Scholar]
- Frank B.M., Gimenez O., Baret P.V. Assessing brown trout (Salmo trutta) spawning movements with multistate capture-recapture models: a case study in a fully controlled Belgian brook. Can. J. Fish. Aquat. Sci. 2012;69(6):1091–1104. [Google Scholar]
- Freeman M.C., Strunz E., Utzinger J. Interventions to improve water, sanitation, and hygiene for preventing soil-transmitted helminth infection. Cochrane Database Syst. Rev. 2016;5:CD012199. doi: 10.1002/14651858.CD012199. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gaston K. Global patterns in biodiversity. Nature. 2000;405:220–227. doi: 10.1038/35012228. [DOI] [PubMed] [Google Scholar]
- Gatto M., Mari L., Bertuzzo E., Casagrandi R., Righetto L., Rodriguez-Iturbe I., Rinaldo A. Generalized reproduction numbers and the prediction of patterns in waterborne disease. Proc. Natl. Acad. Sci. USA. 2012;48:19703–19708. doi: 10.1073/pnas.1217567109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gatto M., Mari L., Bertuzzo E., Casagrandi R., Righetto L., Rodriguez-Iturbe I., Rinaldo A. Spatially explicit conditions for waterborne pathogen invasion. Am. Nat. 2013;182:328–346. doi: 10.1086/671258. [DOI] [PubMed] [Google Scholar]
- Gaudart J., Rebaudet S., Barrais R., Boncy J., Faucher B., Piarroux M., Magloire R., Thimothe G., Piarroux R. Spatio-temporal dynamics of cholera during the first year of the epidemic in Haiti. PLoS Negl. Trop. Dis. 2013;7:e2145. doi: 10.1371/journal.pntd.0002145. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Giometto A., Rinaldo A., Carrara F., Altermatt F. Emerging predictable features of replicated biological invasion fronts. Proc. Natl. Acad. Sci. USA. 2013;110:1–6. doi: 10.1073/pnas.1321167110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Giometto A., Rinaldo A., Carrara F., Altermatt F. Emerging predictable features of replicated biological invasion fronts. Proc. Natl. Acad. Sci. USA. 2014;111(1):297–301. doi: 10.1073/pnas.1321167110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Grimes J., Croll D., Harrison W., Utzinger J., Freeman M., Templeton M. The roles of water, sanitation and hygiene in reducing schistosomiasis: a review. Parasites Vect. 2015;8:156. doi: 10.1186/s13071-015-0766-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Grosholz E. Contrasting rates of spread for introduced species in terrestrial and marine systems. Ecology. 1996;77(6):1680–1686. [Google Scholar]
- Gurarie D., King C.H., Yoon N., Li E. Refined stratified-worm-burden models that incorporate specific biological features of human and snail hosts provide better estimates of Schistosoma diagnosis, transmission, and control. Parasites Vect. 2016;9:428–431. doi: 10.1186/s13071-016-1681-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gurarie D., Seto E.Y.W. Connectivity sustains disease transmission in environments with low potential for endemicity: modelling schistosomiasis with hydrologic and social connectivities. J. R. Soc. Interface. 2009;6:495–508. doi: 10.1098/rsif.2008.0265. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hanski I. Metapopulation dynamics. Nature. 1998;396:41–49. [Google Scholar]
- Hari R., Livingstone D.M., Siber R., Burkhardt-Holm P., Güttinger H. Consequences of climatic change for water temperature and brown trout populations in alpine rivers and streams. Glob. Chang. Biol. 2006;12(1):10–26. [Google Scholar]
- Hashizume M., Armstrong B., Hajat S., Wagatsuma Y., Faruque A.S., Hayashi T., Sack D.A. The effect of rainfall on the incidence of cholera in Bangladesh. Epidemiology. 2008;19:103–110. doi: 10.1097/EDE.0b013e31815c09ea. [DOI] [PubMed] [Google Scholar]
- Hastings A., Cuddington K., Davies K.F. The spatial spread of invasions: new developments in theory. Ecol. Lett. 2005;8(1):91–101. [Google Scholar]
- Heesterbeek J., Roberts M. Mathematical models for microparasites of wildlife. In: Grenfell B., Dobson A.P., editors. Ecology of Infectious Diseases in Natural Populations. Cambridge University Press; Cambridge, UK: 1995. pp. 90–122. [Google Scholar]
- Hill V., Cohen N., Kahler A.M. Toxigenic Vibrio cholerae O1 in water and seafood, Haiti. Emerg. Infect. Dis. 2011;17:2147–2150. doi: 10.3201/eid1711.110748. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Holyoak M., Lawler S. Advances in Ecological Research 37: Population Dynamics and Laboratory Ecology. Vol. 37. Academic Press, London, UK; 2005. The contribution of laboratory experiments on protists to understanding population and metapopulation dynamics; pp. 245–271. [Google Scholar]
- Hu Y., Zhang Z., Chen Y., Wang Z., Gao J., Tao B., Jiang Q. Spatial pattern of schistosomiasis in Xingzi, Jiangxi Province, China: the effects of environmental factors. Parasites Vect. 2013;6:214. doi: 10.1186/1756-3305-6-214. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hubbell S. Princeton Univ. Press, Princeton; 2001. The Unified Theory of Biodiversity and Biogeography. [Google Scholar]
- Ivers L.C., Farmer P., Almazor C.P. Five complementary interventions to slow cholera: Haiti. Lancet. 2010;376:2048–2051. doi: 10.1016/S0140-6736(10)62243-X. [DOI] [PubMed] [Google Scholar]
- Jablonski D. Extinction and the spatial dynamics of biodiversity. Proc. Natl. Acad. Sci. USA. 2008;105:11528–11535. doi: 10.1073/pnas.0801919105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jutla A., Akanda A., Griffiths J., Colwell R., Islam S. Warming oceans, phytoplankton and zooplankton blooms, and river discharge: implications for cholera outbreaks. Am. J. Trop. Med. Hygiene. 2011;85:303–308. doi: 10.4269/ajtmh.2011.11-0181. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jutla A.S., Akanda A.S., Islam S. A framework for predicting endemic cholera using satellite derived environmental determinants. Environ. Modell. Softw. 2013;47:148–158. [Google Scholar]
- Jutla A.S., Whitcombe E., Hasan N., Haley B., Akanda A.S., Huq A., Alam M., Sack R.B., Colwell R.R. Environmental factors influencing epidemic cholera. Am. J. Trop. Med. Hyg. 2013;89:597–607. doi: 10.4269/ajtmh.12-0721. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kerr B., Riley M., Feldman M., Bohannan B. Local dispersal promotes biodiversity in a real-life game of rock-paper-scissors. Nature. 2002;418(6894):171–174. doi: 10.1038/nature00823. [DOI] [PubMed] [Google Scholar]
- King A., Ionides E., Pascual M., Bouma M. Inapparent infections and cholera dynamics. Nature. 2008;454:877–880. doi: 10.1038/nature07084. [DOI] [PubMed] [Google Scholar]
- Koelle K., Rodó X., Pascual M., Yunus M., Mostafa G. Refractory periods and climate forcing in cholera dynamics. Nature. 2005;436:696–700. doi: 10.1038/nature03820. [DOI] [PubMed] [Google Scholar]
- Kolmogorov A., Petrovskii I., Piskunov N. A study of the diffusion equation with increase in the amount of substance, and its application to a biological problem. Bull. Mosc. Univ. Math. Mech. 1937;1(1):1–25. [Google Scholar]
- Körner C. Why are there global gradients in species richness? Mountains might hold the answer. Trends Ecol. Evol. 2000;15:513–514. [Google Scholar]
- Körner C. The use of altitude in ecological research. Trends Ecol. Evol. 2007;22(11):569–574. doi: 10.1016/j.tree.2007.09.006. [DOI] [PubMed] [Google Scholar]
- Kraft N.J.B., Comita L., Chase J.M. Disentangling the drivers of beta diversity along latitudinal and elevational gradients. Science. 2011;333:1755–1758. doi: 10.1126/science.1208584. [DOI] [PubMed] [Google Scholar]
- Lai Y.S., Biedermann P., Ekpo U.F. Spatial distribution of schistosomiasis and treatment needs in sub-Saharan Africa: a systematic review and geostatistical analysis. Lancet Infect. Dis. 2015;15:927–940. doi: 10.1016/S1473-3099(15)00066-3. [DOI] [PubMed] [Google Scholar]
- Leopold L., Wolman M., Miller J. Freeman, San Francisco; 1964. Fluvial Processes in Geomorphology. [Google Scholar]
- Levin S. The problem of pattern and scale in ecology. Ecology. 1992;76:1943–1963. [Google Scholar]
- Levins R. Some demographic and genetic consequences of environmental heterogeneity for biological control. Bull. Entomol. Soc. Am. 1969;15:237–240. [Google Scholar]
- Lipp E., Huq A., Colwell R. Effects of global climate on infectious disease: the cholera model. Clin. Microb. Rev. 2002;15:757–762. doi: 10.1128/CMR.15.4.757-770.2002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lo N.C., Lai Y.S., Karagiannis-Voules D.A. Assessment of global guidelines for preventive chemotherapy against schistosomiasis and soil-transmitted helminthiasis: a cost-effectiveness modelling study. Lancet Infect. Dis. 2016;16:1065–1075. doi: 10.1016/S1473-3099(16)30073-1. [DOI] [PubMed] [Google Scholar]
- Lomolino M. Elevation gradients of species-density: historical and prospective views. Global Ecol. Biogeogr. 2001;10(1):3–13. [Google Scholar]
- Lubina J., Levin S. The spread of a reinvading species: range expansion in the California sea otter. Am. Nat. 1988;131(4):526–543. [Google Scholar]
- MacArthur R., Wilson E. Princeton Univ. Press, Princeton; 1967. The Theory of Island Biogeography. [Google Scholar]
- Mandelbrot B. Henry Holt, New York; 1983. The Fractal Geometry of Nature. [Google Scholar]
- Marani A., Rigon R., Rinaldo A. A note on fractal channel networks. Water Resour. Res. 1991;27:3041–3049. [Google Scholar]
- Mari L., Bertuzzo E., Casagrandi R., Gatto M., Levin S.A., Rodriguez-Iturbe I., Rinaldo A. Hydrologic controls and anthropogenic drivers of the zebra mussel invasion of the Mississippi-Missouri river system. Water Resour. Res. 2011;47 [Google Scholar]
- Mari L., Bertuzzo E., Finger F., Casagrandi R., Gatto M., Rinaldo A. On the predictive ability of mechanistic models for the Haitian cholera epidemic. J. R. Soc. Interface. 2015;12:20140840. doi: 10.1098/rsif.2014.0840. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mari L., Bertuzzo E., Righetto L., Casagrandi R., Gatto M., Rodriguez-Iturbe I., Rinaldo A. Modelling cholera epidemics: the role of waterways, human mobility and sanitation. J. R. Soc. Interface. 2012;9:376–388. doi: 10.1098/rsif.2011.0304. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mari L., Casagrandi R., Bertuzzo E., Rinaldo A., Gatto M. Floquet theory for seasonal environmental forcing of spatially explicit waterborne epidemics. Theor. Ecol. 2014;7(4):351–365. [Google Scholar]
- Mari L., Casagrandi R., Bertuzzo E., Rinaldo A., Gatto M. Metapopulation persistence and species spread in river networks. Ecol. Lett. 2014;17(4):426–434. doi: 10.1111/ele.12242. [DOI] [PubMed] [Google Scholar]
- Mari L., Casagrandi R., Pisani M., Pucci E., Gatto M. When will the zebra mussel reach Florence? A model for the spread of Dreissena polymorpha in the Arno water system (Italy) Ecohydrology. 2009;2:428–439. [Google Scholar]
- Mari L., Ciddio M., Casagrandi R., Perez-Saez J., Bertuzzo E., Rinaldo A., Sokolow S., De Leo G., Gatto M. Heterogeneity in schistosomiasis transmission dynamics. J. Theor. Biol. 2017;118:inpress. doi: 10.1016/j.jtbi.2017.08.015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mari L., Gatto M., Ciddio M., Dia E., Sokolow S., De Leo G., Casagrandi R. Big-data-driven modeling unveils country-wide drivers of endemic schistosomiasis. Sci. Rep. 2017;7(1):489. doi: 10.1038/s41598-017-00493-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Maritan A., Rinaldo A., Rodriguez-Iturbe I., Rigon R., Giacometti A. Scaling in river networks. Phys. Rev. E. 1996;53:1501–1513. doi: 10.1103/physreve.53.1510. [DOI] [PubMed] [Google Scholar]
- McCain C., Grytnes J. Encyclopedia of Life Sciences. Wiley Online Library; 2010. Elevational gradients in species richness. [Google Scholar]
- McCreesh N., Booth M. Challenges in predicting the effects of climate change on Schistosoma mansoni and Schistosoma haematobium transmission potential. Trends Parasitol. 2013;29:548–555. doi: 10.1016/j.pt.2013.08.007. [DOI] [PubMed] [Google Scholar]
- McCreesh N., Nikulin G., Booth M. Predicting the effects of climate change on Schistosoma mansoni transmission in eastern Africa. Parasites Vect. 2015;8:4. doi: 10.1186/s13071-014-0617-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McGill B., Maurer B., Weiser M. Empirical evaluation of neutral theory. Ecology. 2006;87(6):1411–1423. doi: 10.1890/0012-9658(2006)87[1411:eeont]2.0.co;2. [DOI] [PubMed] [Google Scholar]
- Melbourne B., Hastings A. Highly variable spread rates in replicated biological invasions: fundamental limits to predictability. Science. 2009;325(5947):1536–1539. doi: 10.1126/science.1176138. [DOI] [PubMed] [Google Scholar]
- Méndez V., Campos D., Fedotov S. Analysis of front in reaction-dispersal processes. Phys. Rev. E. 2004;70:129–135. doi: 10.1103/PhysRevE.70.066129. [DOI] [PubMed] [Google Scholar]
- Méndez V., Fedotov S., Horsthemke W. Springer, Berlin; 2010. Reaction-Transport Systems. [Google Scholar]
- Morrissey M., de Kerckhove D. The maintenance of genetic variation due to asymmetric gene flow in dendritic metapopulations. Am. Nat. 2009;174:875–889. doi: 10.1086/648311. [DOI] [PubMed] [Google Scholar]
- Muneepeerakul R., Bertuzzo E., Lynch H., Fagan W., Rinaldo A., Rodriguez-Iturbe I. Neutral metacommunity models predict fish diversity patterns in Mississippi-Missouri basin. Nature. 2008;453(7192):220–224. doi: 10.1038/nature06813. [DOI] [PubMed] [Google Scholar]
- Muneepeerakul R., Weitz J., Levin S., Rinaldo A., Rodriguez-Iturbe I. A neutral metapopulation model of biodiversity in river networks. J. Theor. Biol. 2007;245:351–363. doi: 10.1016/j.jtbi.2006.10.005. [DOI] [PubMed] [Google Scholar]
- Murray J. Springer, Berlin; 2004. Mathematical Biology I: An Introduction. [Google Scholar]
- NatureServe . Technical Report. 2004. Distribution of Native US Fishes by Watershed. [Google Scholar]
- Nee S. The neutral theory of biodiversity: do the numbers add up? Funct. Ecol. 2005;19(1):173–176. [Google Scholar]
- Newman M. Power laws, Pareto distributions and Zipf’s law. Contemp. Phys. 2005;46(5):323–351. [Google Scholar]
- Nogues-Bravo D., Araujo M., Romdal T., Rahbek C. Scale effects and human impact on the elevational species richness gradients. Nature. 2008;453:216–219. doi: 10.1038/nature06812. [DOI] [PubMed] [Google Scholar]
- O’ Connor K.A., Cartwright E., Loharikar A. Risk factors early in the 2010 cholera epidemic, Haiti. Emerg. Infect. Dis. 2011;17:2136–2138. doi: 10.3201/eid1711.110810. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Okamura B., Hartikainen H., Schmidt-Posthaus H., Wahli T. Life cycle complexity, environmental change and the emerging status of salmonid proliferative kidney disease. Freshwat. Biol. 2011;56(4):735–753. [Google Scholar]
- Okubo A., Levin S. Springer, Berlin; 2002. Diffusion and Ecological Problems: Modern Perspectives. [Google Scholar]
- Pascual M., Bouma M., Dobson A.P. Cholera and climate: revisiting the quantitative evidence. Microbes Infect. 2002;4:237–245. doi: 10.1016/s1286-4579(01)01533-7. [DOI] [PubMed] [Google Scholar]
- Pascual M., Rodó X., Ellner S.P., Colwell R.R., Bouma M.J. Cholera dynamics and El Niño southern oscillation. Science. 2000;289:1766–1769. doi: 10.1126/science.289.5485.1766. [DOI] [PubMed] [Google Scholar]
- Pasetto D., Finger F., Rinaldo A., Bertuzzo E. Real-time projections of cholera outbreaks through data assimilation and rainfall forecasting. Adv. Water Resour. 2017;37 [Google Scholar]
- Pedersen U.B., Midzi N., Mduluza T., Soko W., Stensgaard A., Vennervald B.J., Mukaratirwa S., Kristensen T.K. Modelling spatial distribution of snails transmitting parasitic worms with importance to human and animal health and analysis of distributional changes in relation to climate. Geospat. Health. 2014;8:335–343. doi: 10.4081/gh.2014.23. [DOI] [PubMed] [Google Scholar]
- Perez-Saez J., Mande T., Ceperley N., Bertuzzo E., Mari L., Gatto M., Rinaldo A. Hydrology and density feedbacks control the ecology of the intermediate hosts of schistosomiasis across habitats in seasonal climates. Proc. Natl. Acad. Sci. USA. 2016;113:6427–6432. doi: 10.1073/pnas.1602251113. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Perez-Saez J., Mari L., Bertuzzo E., Casagrandi R., Sokolow S.H., De Leo G., Mande T., Ceperley N., Frohelich J.M., Sou M., Karambiri H., Yacouba H., Maiga A., Gatto M., Rinaldo A. A theoretical analysis of the geography of schistosomiasis in Burkina Faso highlights the roles of human mobility and water resources development in disease transmission. PLoS Neglect. Trop. D. 2015;9:e0004127. doi: 10.1371/journal.pntd.0004127. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pielou E. J. Wiley & Sons; New York, NY: 1977. Mathematical Ecology. [Google Scholar]
- Pigolotti S., Flammini A., Marsili M., Maritan A. Species lifetime distribution for simple models of ecologies. Proc. Natl. Acad. Sci. USA. 2005;102:147–151. doi: 10.1073/pnas.0502648102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Purves D., Turnbull L. Different but equal: the implausible assumption at the heart of neutral theory. J. Animal Ecol. 2010;79(6):1215–1225. doi: 10.1111/j.1365-2656.2010.01738.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rahbek C. The elevational gradient of species richness - a uniform pattern. Ecography. 1995;18:200–205. [Google Scholar]
- Rahbek C. The role of spatial scale and the perception of large-scale species-richness patterns. Ecol. Lett. 2005;8:224–239. [Google Scholar]
- Ramírez I.J., Grady S.C. El Niño, climate, and cholera associations in Piura, Peru, 1991–2001: a wavelet analysis. EcoHealth. 2016;13:83–99. doi: 10.1007/s10393-015-1095-3. [DOI] [PubMed] [Google Scholar]
- Raymond P., Bauer J. Riverine export of aged terrestrial organic matter to the north Atlantic ocean. Nature. 2001;409:497–501. doi: 10.1038/35054034. [DOI] [PubMed] [Google Scholar]
- Rebaudet S., Sudre B., Faucher B., Piarroux R. Cholera in coastal Africa: a systematic review of its heterogeneous environmental determinants. J. Infect. Dis. 2013;208:S98–S106. doi: 10.1093/infdis/jit202. [DOI] [PubMed] [Google Scholar]
- Rebaudet S., Sudre B., Faucher B., Piarroux R. Environmental determinants of cholera outbreaks in inland Africa: a systematic review of main transmission foci and propagation routes. J. Infect. Dis. 2013;208:S46–54. doi: 10.1093/infdis/jit195. [DOI] [PubMed] [Google Scholar]
- Reiner Jr. R.C., King A.A., Emch M., Yunus M., Faruque A.S., Pascual M. Highly localized sensitivity to climate forcing drives endemic cholera in a megacity. Proc. Natl. Acad. Sci. USA. 2012;109:2033–2036. doi: 10.1073/pnas.1108438109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Remais J.V., Zhong B., Carlton E., Spear R. Model approaches for estimating the influence of time varying socio-environmental factors on macroparasite transmission in two endemic regions. Epidemics. 2009;1:213–220. doi: 10.1016/j.epidem.2009.10.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ricklefs R. Community diversity - relative roles of local and regional processes. Science. 1987;235(4785):167–171. doi: 10.1126/science.235.4785.167. [DOI] [PubMed] [Google Scholar]
- Rinaldo A., Banavar J., Maritan A. Trees, networks and hydrology. Water Resour. Res. 2006;42:88–93. [Google Scholar]
- Rinaldo A., Bertuzzo E., Blokesch M., Mari L., Gatto M. Modeling key drivers of cholera transmission dynamics provides new perspectives on parasitology. Trends Parasitol. 2017;33:587–599. doi: 10.1016/j.pt.2017.04.002. [DOI] [PubMed] [Google Scholar]
- Rinaldo A., Bertuzzo E., Mari L., Righetto L., Blokesch M., Gatto M., Casagrandi R., Murray M., Vesenbeckh S., Rodriguez-Iturbe I. Reassessment of the 2010–2011 Haiti cholera outbreak and rainfall-driven multiseason projections. Proc. Natl. Acad. Sci. USA. 2012;109:6602–6607. doi: 10.1073/pnas.1203333109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rinaldo A., Rigon R., Banavar J., Maritan A., Rodriguez-Iturbe I. Evolution and selection of river networks: statics, dynamics, and complexity. Proc. Natl. Acad. Sci. USA. 2014;111(7):2417–2424. doi: 10.1073/pnas.1322700111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rinaldo A., Rigon R., Rodriguez-Iturbe I. Channel networks. Annu. Rev. Earth Plan. Sci. 1999;26:289–306. [Google Scholar]
- Rinaldo A., Rodriguez-Iturbe I., Rigon R., Bras R., Vasquez E., Marani A. Minimum energy and fractal structures of drainage networks. Water Resour. Res. 1992;28(9):2183–2195. [Google Scholar]
- Robbins, J., 2016. Tiny invader, deadly to fish, shuts down a river in Montana. In: The New York Times. URL: http://www.nytimes.com/2016/08/24/us/tiny-parasite-invader-deadly-to-fish-shuts-down-yellowstone-river-in-montana.html?_r=0. Accessed: 2016-10-10.
- Rodriguez-Iturbe I., Muneepeerakul R., Bertuzzo E., Levin S., Rinaldo A. River networks as ecological corridors: a complex systems perspective for integrating hydrologic, geomorphologic, and ecologic dynamics. Water Resour. Res. 2009;45 [Google Scholar]
- Rodriguez-Iturbe I., Rinaldo A. Cambridge University Press, New York; New York: 2001. Fractal River Basins. Chance and Self-Organization. [Google Scholar]
- Rodriguez-Iturbe I., Rinaldo A., Rigon R., Bras R., Ijjasz-Vasquez E., Marani A. Fractal structures as least energy patterns - the case of river networks. Geophys. Res. Lett. 1992;19(9):889–892. [Google Scholar]
- Rohr J.R., Schotthoefer A.M., Raffel T.R. Agrochemicals increase trematode infections in a declining amphibian species. Nature. 2008;455:1235–12539. doi: 10.1038/nature07281. [DOI] [PubMed] [Google Scholar]
- Romdal T., Grytnes J. An indirect area effect on elevational species richness patterns. Ecography. 2007;30:440–448. [Google Scholar]
- Rosenzweig M. Cambridge Univ. Press, Cambridge UK; 1995. Species Diversity in Space and Time. [Google Scholar]
- Rosindell J., Hubbell S., Etienne R. The unified neutral theory of biodiversity and biogeography at age ten. Trends Ecol. Evol. 2011;26:340–348. doi: 10.1016/j.tree.2011.03.024. [DOI] [PubMed] [Google Scholar]
- Ruiz-Moreno D., Pascual M., Bouma M., Dobson A.P., Cash B. Cholera seasonality in Madras (1901–1940): dual role for rainfall in endemic and epidemic regions. Ecohealth. 2007;4:52–62. [Google Scholar]
- Sanders N. Elevational gradients in ant species richness: area, geometry, and Rapoport’s rule. Ecography. 2002;25:25–32. [Google Scholar]
- Seaber P., Kapinos F., Knapp G. Technical Report. U. S. Geological Survey, Menlo Park CA, USA; 2004. Distribution of Native US Fishes by Watershed. [Google Scholar]
- Shigesada N., Kawasaki K. Oxford Univ. Press, Oxford; 1997. Biological Invasions: Theory and Practice. [Google Scholar]
- Simini F., González M.C., Maritan A., Barabási A.L. A universal model for mobility and migration patterns. Nature. 2012;484:96–100. doi: 10.1038/nature10856. [DOI] [PubMed] [Google Scholar]
- Skellam J. Random dispersal in theoretical populations. Biometrika. 1951;38:196–218. [PubMed] [Google Scholar]
- Sokolow S., Huttinger E., Jouanard N., Hsieh M., Lafferty K., Kuris A., Riveau G., Senghor S., Thiam C., N’Diaye A., Faye D., De Leo G. Reduced transmission of human schistosomiasis after restoration of a native river prawn that preys on the snail intermediate host. Proc. Natl. Acad. Sci. USA. 2015;112:9650–9655. doi: 10.1073/pnas.1502651112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sokolow S., Lafferty K., Kuris A. Regulation of laboratory populations of snails biomphalaria and bulinus spp.) by river prawns, macrobrachium spp. (Decapoda, Palaemonidae): implications for control of schistosomiasis. Acta Trop. 2014;132:64–74. doi: 10.1016/j.actatropica.2013.12.013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sokolow S.H., Wood C.L., Jones I.J. Global assessment of schistosomiasis control over the past century shows targeting the snail intermediate host works best. PLoS Neglect. Trop. D. 2016;10:e0004794. doi: 10.1371/journal.pntd.0004794. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Southwood T., May R., Sugihara G. Observations on related ecological exponents. Proc. Natl Acad. Sci. USA. 2006;103(1):6931–6933. doi: 10.1073/pnas.0600988103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Spear R. Internal versus external determinants of Schistosoma japonicum transmission in irrigated agricultural villages. J. R. Soc. Interface. 2012;9:272–282. doi: 10.1098/rsif.2011.0285. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Steinmann P., Keiser J., Bos R., Tanner M., Utzinger J. Schistosomiasis and water resources development: systematic review, meta-analysis, and estimates of people at risk. Lancet Infect. Dis. 2006;6(7):411–425. doi: 10.1016/S1473-3099(06)70521-7. [DOI] [PubMed] [Google Scholar]
- Stensgaard A., Booth M., Nikulin G., McCreesh N. Combining process-based and correlative models improves predictions of climate change effects on Schistosoma mansoni transmission in eastern Africa. Geospat. Health. 2016;11 doi: 10.4081/gh.2016.406. [DOI] [PubMed] [Google Scholar]
- Stensgaard A.S., Utzinger J., Vounatsou P. Large-scale determinants of intestinal schistosomiasis and intermediate host snail distribution across Africa: does climate matter? Acta Trop. 2013;128:378–390. doi: 10.1016/j.actatropica.2011.11.010. [DOI] [PubMed] [Google Scholar]
- Stoeckel J., Padilla D., Schneider D., Rehmann C. Laboratory culture of Dreissena polymorpha larvae: spawning success, adult fecundity, and larval mortality patterns. Can. J. Zool. 2004;82:1436–1443. [Google Scholar]
- Stoeckel J., Rehmann C., Schneider D., Padilla D. Retention and supply of zebra mussel larvae in a large river system: importance of an upstream lake. Freshwater Biol. 2004;49:919–930. [Google Scholar]
- Stoeckel J., Schneider D., Soeken L., Blodgett K., Sparks R. Larval dynamics of a riverine metapopulation: implications for zebra mussel recruitment, dispersal, and control in a large-river system. J. North Am. Benthol. Soc. 1997;16:586–601. [Google Scholar]
- Stokstad E. Feared quagga mussel turns up in western United States. Science. 2007;315:453–454. doi: 10.1126/science.315.5811.453. [DOI] [PubMed] [Google Scholar]
- Swartz S., De Leo G., Wood C., Sokolow S. Infection with schistosome parasites in snails leads to increased predation by prawns: implications for human schistosomiasis control. J. Exp. Biol. 2015;218:3962–3967. doi: 10.1242/jeb.129221. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tien J.H., Earn D.J.D. Multiple transmission pathways and disease dynamics in a waterborne pathogen model. Bull. Math. Biol. 2010;72:1506–1533. doi: 10.1007/s11538-010-9507-6. [DOI] [PubMed] [Google Scholar]
- Tien J., Shuai Z.S., Eisenberg M.C., van den Driessche P. Disease invasion on community networks with environmental pathogen movement. J. Math. Biol. 2015;70:1065–1092. doi: 10.1007/s00285-014-0791-x. [DOI] [PubMed] [Google Scholar]
- Tilman D. Niche tradeoffs, neutrality, and community structure: a stochastic theory of resource competition, invasion, and community assembly. Proc. Natl. Acad. Sci. USA. 2004;101(30):10854–10861. doi: 10.1073/pnas.0403458101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tilman D., May R., Lehman C., Nowak M. Habitat destruction and the extinction debt. Nature. 1994;371(6492):65–66. [Google Scholar]
- Tuite A., Tien J., Eisenberg M., Earns D.J.D., Ma J., Fisman D.N. Cholera epidemic in Haiti, 2010: using a transmission model to explain spatial spread of disease and identify optimal control interventions. Ann. Intern. Med. 2011;154:593–601. doi: 10.7326/0003-4819-154-9-201105030-00334. [DOI] [PubMed] [Google Scholar]
- Vellend M. Conceptual synthesis in community ecology. Q. Rev. Biol. 2010;85(2):183–206. doi: 10.1086/652373. [DOI] [PubMed] [Google Scholar]
- Vezzulli L., Colwell R.R., Pruzzo C. Ocean warming and spread of pathogenic vibrios in the aquatic environment. Microb. Ecol. 2013;65:817–825. doi: 10.1007/s00248-012-0163-2. [DOI] [PubMed] [Google Scholar]
- Vezzulli L., Grande C., Reid P.C., Hélaouët P., Edwards M., Höfle M.G., Brettar I., Colwell R.R., Pruzzo C. Climate influence on Vibrio and associated human diseases during the past half-century in the coastal North Atlantic. Proc. Natl. Acad. Sci. USA. 2016;113:5062–5071. doi: 10.1073/pnas.1609157113. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vezzulli L., Pezzati E., Brettar I., Höfle M., Pruzzo C. Effects of global warming on Vibrioecology. Microb. Spect. 2015;3:0004–2014. doi: 10.1128/microbiolspec.VE-0004-2014. [DOI] [PubMed] [Google Scholar]
- Volkov I., Banavar J., Hubbell S., Maritan A. Neutral theory and relative species abundance in ecology. Nature. 2003;424(6952):1035–1037. doi: 10.1038/nature01883. [DOI] [PubMed] [Google Scholar]
- Volpert V., Petrovskii S. Reaction-diffusion waves in biology. Phys. Life Rev. 2009;6(4):267–310. doi: 10.1016/j.plrev.2009.10.002. [DOI] [PubMed] [Google Scholar]
- Wahli T., Bernet D., Steiner P.A., Schmidt-Posthaus H. Geographic distribution of Tetracapsuloides bryosalmonae infected fish in Swiss rivers: an update. Aquat. Sci. 2007;69(1):3–10. [Google Scholar]
- Wahli T., Knuesel R., Bernet D., Segner H., Pugovkin D., Burkhardt-Holm P., Escher M., Schmidt-Posthaus H. Proliferative kidney disease in Switzerland: current state of knowledge. J. Fish Dis. 2002;25(8):491–500. [Google Scholar]
- Wang W., Dai J., Liang Y. Apropos: factors impacting on progress towards elimination of transmission of Schistosomiasis japonica in China. Parasites Vect. 2014;7:408. doi: 10.1186/1756-3305-7-408. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Whittaker R.H. Evolution and measurement of species diversity. Taxon. 1972;21(2):213–251. [Google Scholar]
- Wilson J., Dormontt E., Prentis P., Lowe A., Richardson D. Something in the way you move: dispersal pathways affect invasion success. Trends Ecol. Evol. 2009;24:136–144. doi: 10.1016/j.tree.2008.10.007. [DOI] [PubMed] [Google Scholar]
- Wu X.H., Zhang S.Q., Xu X.J., Huang Y.X. Effect of floods on the transmission of schistosomiasis in the Yangtze River valley, People’s Republic of China. Parasitology Intl. 2008;57:271–276. doi: 10.1016/j.parint.2008.04.004. [DOI] [PubMed] [Google Scholar]
- Rodó X., Pascual M., Doblas-Reyes F.J. Climate change and infectious diseases: can we meet the needs for better prediction? Clim. Chang. 2013;118:625–640. [Google Scholar]
- Zhou X.N., Yang G.-J., Yang K. Potential impact of climate change on schistosomiasis transmission in China. Am. J. Trop. Med. Hyg. 2008;78:188–194. [PubMed] [Google Scholar]