Abstract
Background
Identification of pharmacodynamic interactions is not reasonable to carry out in a clinical setting for many reasons. The aim of this work was to develop a model-informed preclinical approach for prediction of clinical pharmacodynamic drug interactions in order to inform early anti-TB drug development.
Methods
In vitro time–kill experiments were performed with Mycobacterium tuberculosis using rifampicin, isoniazid or ethambutol alone as well as in different combinations at clinically relevant concentrations. The multistate TB pharmacometric (MTP) model was used to characterize the natural growth and exposure–response relationships of each drug after mono exposure. Pharmacodynamic interactions during combination exposure were characterized by linking the MTP model to the general pharmacodynamic interaction (GPDI) model with successful separation of the potential effect on each drug’s potency (EC50) by the combining drug(s).
Results
All combinations showed pharmacodynamic interactions at cfu level, where all combinations, except isoniazid plus ethambutol, showed more effect (synergy) than any of the drugs alone. Using preclinical information, the MTP-GPDI modelling approach was shown to correctly predict clinically observed pharmacodynamic interactions, as deviations from expected additivity.
Conclusions
With the ability to predict clinical pharmacodynamic interactions, using preclinical information, the MTP-GPDI model approach outlined in this study constitutes groundwork for model-informed input to the development of new and enhancement of existing anti-TB combination regimens.
Introduction
TB remains a global health problem and is ranked as one of the leading causes of death due to an infectious disease worldwide.1 The four drugs making up the standard treatment regimen currently recommended by the WHO are rifampicin, isoniazid, ethambutol and pyrazinamide. Possible sub-optimal treatment, with regard to killing of non-multiplying bacteria, together with non-adherence and resistance development, is a major limitation in the treatment of the disease. An urgent need for new and improved drugs and drug regimens therefore exists. However, the currently used methodologies in drug development are not meeting this requirement. There is a lack of knowledge regarding the pharmacokinetic and pharmacodynamic (PD) properties and relationships of these drugs. A critical gap also exists when it comes to selection of optimal combination regimens.
Pharmacometric models have successfully been applied for the characterization of both preclinical experiments and clinical trials involving anti-TB drugs.2,3 However, for any treatment that involves the use of multiple drugs, the possibility of interactions between the drugs exists. A PD interaction is defined either as synergism or antagonism, which is a greater or lesser effect, respectively, of the drugs in combination than expected additivity based on the effects of each drug individually. The two most commonly used criteria used to describe PD interactions are Bliss independence (BI) and Loewe additivity (LA).4,5 There is, however, no definite answer to the question of which criterion is superior.6
The aim of this work was to develop a model-informed preclinical (in vitro) approach for the prediction of clinical PD interactions in order to inform early anti-TB drug development.
Materials and methods
In vitro assay
The Mycobacterium tuberculosis genotype strain Beijing VN 2002-1585 (BE-1585) was cultured in Middlebrook 7H9 broth (Difco Laboratories, Detroit, MI, USA) supplemented with 10% OADC (Baltimore Biological Laboratories, Baltimore, MD, USA), 0.5% glycerol (Scharlau Chemie SA, Sentmenat, Spain) and 0.02% Tween 20 (Sigma Chemical Co., St Louis, MO, USA), under shaking conditions at 96 rpm at 37 °C. Vials with M. tuberculosis suspensions were stored at −80 °C. Cultures on solid medium were grown on Middlebrook 7H10 agar (Difco Laboratories, Detroit, MI, USA), supplemented with 10% OADC and 0.5% glycerol for 28 days at 37 °C with 5% CO2. The concentration- and time-dependent killing capacities of isoniazid, rifampicin and ethambutol were determined as previously described; experiments were performed in duplicate.7 The limit of quantification (5 cfu) was calculated as the ratio of the volume in the growth medium to the plated volume.
Multistate TB pharmacometric (MTP) model
All cfu data used were transformed using natural logarithms for model building. The previously developed MTP model,8 describing three bacterial states representing fast-multiplying (F), slow-multiplying (S) and non-multiplying (N) bacteria, was used in order to identify the exposure–response relationships for rifampicin, isoniazid and ethambutol in monotherapy.
The MTP model was initially applied to the natural growth data, i.e. without drug treatment, with estimation of the growth rate (), the initial fast ()- and slow ()-multiplying bacterial number and the maximum system carrying capacity () as estimation of these parameters provided a better fit to the data compared with using fixed estimates from the original work using the H37Rv strain.8 Estimation of the bacterial transfer rate constants (, ) did not provide a better fit to the data and was therefore fixed to estimates from the original work.8 The use of an exponential function for description of the growth of the fast-multiplying bacteria was also evaluated.
Static drug concentrations were used as input to the PD modelling. The stability of the drugs allowed assessment of activity during the 6 days of the experiment without the need for replenishment.
Exposure–response relationships for mono exposure of rifampicin, isoniazid and ethambutol were evaluated using fixed natural growth parameters of the MTP model (Table 1), which were obtained using only the natural growth data. The antibacterial effects of rifampicin, isoniazid and ethambutol on the different bacterial states (F, S and N) were evaluated as inhibition of growth or as a kill rate using linear, Emax or sigmoidal Emax models as previously described.8
Table 1.
Final parameter estimates of the MTP model applied to cfu of M. tuberculosis with rifampicin, isoniazid or ethambutol in mono exposure
| Parameter | Description | Estimate [RSEa (%)] |
|---|---|---|
| Natural growth | ||
| kG (days−1) | growth rate of the fast-multiplying state bacteria | 0.796 (5) |
| (days−2) | second-order time-dependent transfer rate between fast- and slow-multiplying state | 0.166·10−2 fixedb |
| (days−1) | first-order transfer rate between fast- and non-multiplying state | 0.897·10−6 fixed |
| (days−1) | first-order transfer rate between slow- and non-multiplying state | 0.186 fixed |
| (days−1) | first-order transfer rate between slow- and fast-multiplying state | 0.0145 fixed |
| (days−1) | first-order transfer rate between non- and slow-multiplying state | 0.123·10−2 fixed |
| F0 (mL−1) | initial fast-multiplying state bacterial number | 209·103 (17) |
| S0 (mL−1) | initial slow-multiplying state bacterial number | 324·103 (12) |
| Exposure–response relationships | ||
| rifampicin | ||
| (days−1) | maximum achievable rifampicin-induced inhibition of fast-multiplying state growth | 1 fixed |
| (mg·L−1) | concentration at 50% of | 0.388 (19) |
| Hill factor drug effect | 2.8 (28) | |
| (days−1) | maximum achievable rifampicin-induced fast-multiplying state kill rate | 1.97 (3) |
| (mg·L−1) | concentration at 50% of | 0.00303 (10) |
| (days−1) | maximum achievable rifampicin-induced slow-multiplying state kill rate | 1.79 (4) |
| (mg·L−1) | concentration at 50% of | 0.0113 (32) |
| (days−1) | rifampicin linear non-multiplying state kill rate | 3.29 (17) |
| isoniazid | ||
| (days−1) | maximum achievable isoniazid-induced fast-multiplying state kill rate | 22.2 (35) |
| (mg·L−1) | concentration at 50% of | 0.168 (34) |
| Hill factor drug effect | 1.9 (11) | |
| (days−1) | maximum achievable isoniazid-induced slow-multiplying state kill rate | 8.55 (17) |
| (mg·L−1) | concentration at 50% of | 0.0329 (49) |
| Hill factor drug effect | 1.74 (25) | |
| rate of resistance development | 0.0206 (31) | |
| rate of resistance reversal | 0 fixed | |
| (days−1) | linear isoniazid adaptive resistance on fast-multiplying state kill | 522 (46) |
| (days−1) | linear isoniazid adaptive resistance on slow-multiplying state kill | 2350 (51) |
| ethambutol | ||
| (days−1) | maximum achievable ethambutol-induced fast-multiplying state kill rate | 2.21 (1) |
| (mg·L−1) | concentration at 50% of | 0.86 (16) |
| Hill factor drug effect | 2.46 (23) | |
| (days−1) | ethambutol linear slow-multiplying state kill rate | 4.39 (69) |
RSE, relative standard error reported on the approximate standard deviation scale obtained using sampling importance resampling (SIR).15
Fixed to previously published values.2
Different approaches, such as adaptive resistance, loss of active drug concentration by time or introduction of an additional bacterial sub-state representing a resistant drug sub-population, were evaluated to account for the observed decrease in isoniazid susceptibility during mono exposure. The adaptive resistance was evaluated using a function for development of resistance that was dependent on isoniazid concentration (CINH), previously used to describe resistance development by Pseudomonas aeruginosa to gentamicin.9 The adaptive resistance (ARon; Equation 1) was governed by the fraction of adaptive resistance relative to no resistance (ARoff; Equation 2), where all bacteria were assigned to the ARoff state at the start of the experiment. The ARon was evaluated as affecting either the maximum isoniazid effect (Emax; Equation 3) or the potency (EC50; Equation 4) of the inhibition of growth and/or kill rates that were identified describing the isoniazid antibacterial effect in mono exposure. The rate of development of resistance and the rate of resistance reversal were described using kon and koff, respectively. As no data were available on resistance reversal, koff was fixed to 0.
| (1) |
| (2) |
| (3) |
| (4) |
where ARmax is the maximum change in isoniazid Emax or EC50 and AR50 is the fraction of the resistant population that gives 50% of ARmax.
General PD interaction (GPDI) model
Assessment of PD interactions between the three drugs was done using the GPDI model,10 implemented in the BI additivity criterion.4 All PD interactions were evaluated as a change in EC50 (potency), identified in mono exposure. In accordance with the BI criterion and to account for differences in the three drugs’ maximum effects (Emax), scaling of each individual drug’s Emax from mono exposure by the largest predicted Emax from mono exposure was performed.11 If a linear function was identified in the evaluation of the effect from mono exposure the BI additivity was approximated by effect addition with scaling by Emax, i.e. due to the minor contribution of at concentrations well below the EC50. An example of the combined effect of EAB with potential PD interactions between two drugs (A and B) that display drug effects described by an Emax model is given in Equation (5), and an example of two drugs (C and D) described by an Emax and linear model, respectively, is given in Equation (6).
| (5) |
| (6) |
where CA, CB, CC and CD are the respective concentrations of drugs A, B, C and D. Emax and EC50 are the maximum achievable drug effect and the concentration that gives 50% of Emax, respectively. The maximum fractional changes in the respective PD parameters due to interaction between drugs A and B and between drugs C and D are reflected by the interaction parameters , and , . For an interaction term applied to EC50, an estimated INT parameter value of zero implies no change in EC50, a positive value an increased EC50 and a negative value a decreased EC50. The possibility of a non-linear interaction relationship across the concentration range (i.e. time- and concentration-dependent PD interactions) was evaluated using the parameters , , and , which reflected the concentrations of drug A, B, C and D at which 50% of the maximal fractional increase was predicted.
The assessment of PD interactions was performed in a stepwise manner, where the first step was evaluation of interactions in duo combinations, during which drug effects (exposure–response relationships) identified in mono exposure were fixed. The combination of three drugs was thereafter evaluated using fixed drug effect estimates related to the mono and duo combination data. As a starting point, the least complex GPDI model was used, in which , and , where and were the EC50 values of drugs A and B fixed to estimates obtained from only data of mono exposure. Estimates of separate INT and interaction EC50 parameters were then evaluated for statistical significance. Reduction of the interaction term to an on/off function was also evaluated. After the evaluation of the PD interaction of duo combinations, an assessment of the triple drug combination was done. The possibility of interactions between rifampicin + isoniazid and ethambutol, isoniazid + ethambutol and rifampicin, and rifampicin + ethambutol and isoniazid in the trio combination was evaluated by adding a modulator term ( to the interaction term identified for the duo combinations (Equation 7).
| (7) |
Lastly, a backwards deletion step was carried out in which all interaction terms were evaluated for statistical significance (P < 0.05). This step was performed including all mono, duo and trio exposure data. An attempt to estimate all parameters simultaneously, using the final model, was also made.
Clinically observed versus preclinically predicted PD interactions
The MTP-GPDI model-predicted PD interactions were compared with PD interactions observed in clinical early bactericidal activity (EBA) data reported earlier for days 0–14.12 To enable this, the corresponding EBA for the preclinical experiments using clinically relevant concentrations of rifampicin (2 mg/L), isoniazid (10 mg/L) and ethambutol (8 mg/L) combinations and using the last studied timepoint (6 days) was calculated. Further, the PD interactions from the clinical EBA were subjected to a classification in which the interactions were classified as more (synergy) or less (antagonism) effect than expected additivity.
Data analysis and software
All data analysis was performed in the software NONMEM (version 7.3; Icon Development Solutions, Ellicott City, USA; http://www.iconplc.com/innovation/nonmem).13 R (version 3.2; R Foundation for Statistical Computing; http://www.R-project.org), was used for data management, and Xpose (version 4.5.0; Department of Pharmaceutical Biosciences, Uppsala University, Sweden; http://xpose.sourceforge.net) was used for graphical assessment of results.14 PsN (version 4.4.5; Department of Pharmaceutical Biosciences, Uppsala University, Sweden; https://uupharmacometrics.github.io/PsN/) was used for running models and generating visual predictive checks.14 Numerical model comparison and a run record were utilized and maintained with the software Pirana (version 2.9.2; Pirana Software & Consulting, Denekamp, The Netherlands; http://www.pirana-software.com).14 Uncertainty in model parameters was calculated using sampling importance resampling (SIR) as implemented in PsN.15 Model evaluation was done by evaluation of goodness-of-fit plots, precision of parameters, objective function value (OFV), scientific plausibility and visual predictive checks. The OFV given by NONMEM, which approximates −2log(likelihood) of the data given the model, was utilized in likelihood ratio testing (LRT) to compare nested models. The difference in OFV (ΔOFV) is approximately χ2 distributed and dependent on the significance level and degrees of freedom. For this analysis, a significance level of 0.05 was used which hence corresponds to a critical ΔOFV of 3.84 for 1 degree of freedom. Data below the limit of quantification (LOQ) were handled using the M3 method,16 with LOQ set to 5 cfu.
Results
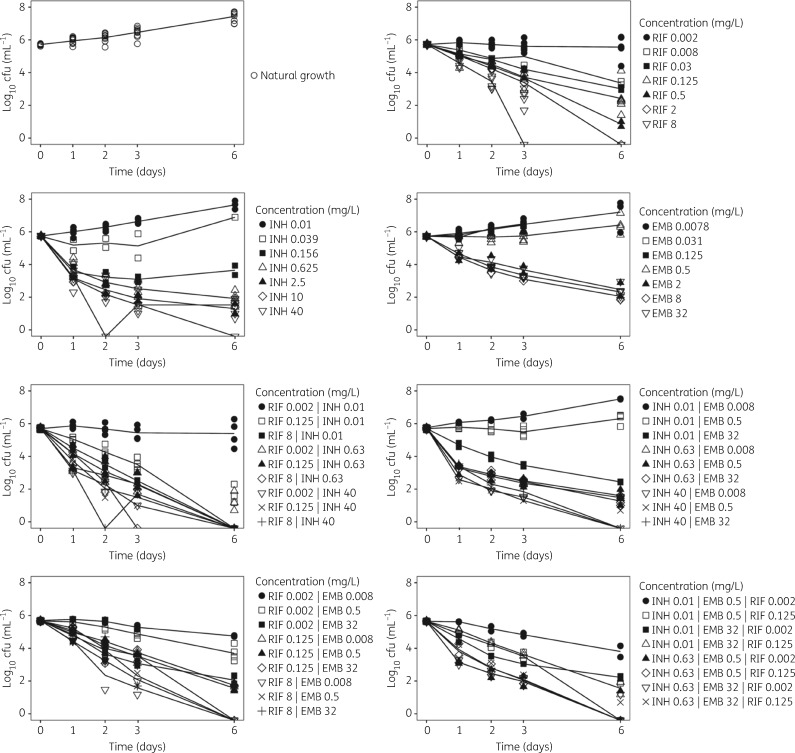
The MTP model was successfully applied to the natural growth data, i.e. absence of drug, and time–kill data of M. tuberculosis Beijing 1585 genotype in the presence of rifampicin, isoniazid and ethambutol in mono exposure. The MTP model was thereafter linked to the GPDI model in order to evaluate and describe PD interaction of the three drugs in duo and triple combinations as studied in the time–kill experiments (Figure 1). A schematic representation of the final model describing the natural growth, exposure–response relationships and the quantified PD interactions is shown in Figure 2. Visual predictive check plots for the mono, duo and trio combination data using the final MTP-GPDI model are shown in Figures S1 and S2 (available as Supplementary data at JAC Online). The growth function best describing the data was an exponential function where the growth rate was estimated as 0.796 days−1 (Table 1).
Figure 1.
Mean observed log10 cfu versus time for natural growth and time–kill curve studies with rifampicin (RIF), isoniazid (INH) and ethambutol (EMB) at different concentrations.
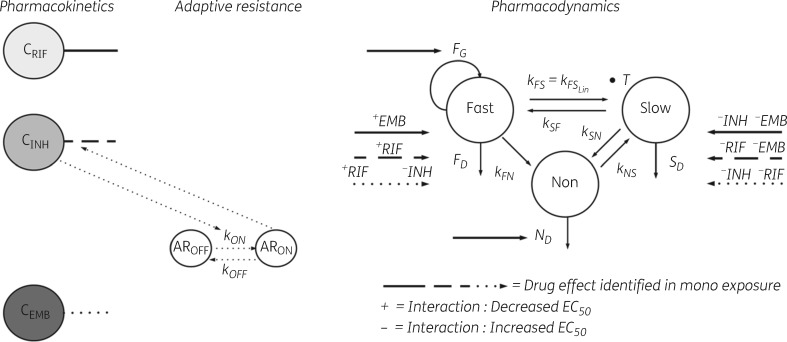
Figure 2.
Schematic illustration of the final MTP model linked to the GPDI model. CRIF, rifampicin concentration; CINH, isoniazid concentration; CEMB, ethambutol concentration; AROFF and ARON, states describing the development of adaptive resistance to isoniazid; kON, rate of resistance development; F, fast-multiplying bacterial state; S, slow-multiplying bacterial state; N, non-multiplying bacterial state; kG, growth rate of the fast-multiplying state bacteria; kFS, time-dependent linear rate parameter describing transfer from fast- to slow-multiplying bacterial state; kSF, first-order transfer rate between slow- and fast-multiplying bacterial state; kFN, first-order transfer rate between fast- and non-multiplying bacterial state; kSN, first-order transfer rate between slow- and non-multiplying bacterial state; kNS, first-order transfer rate between non-multiplying and slow-multiplying bacterial state; FG, drug effect as inhibition of fast-multiplying bacterial state bacterial growth; FD, drug effect as kill of fast-multiplying bacterial state bacteria; SD, drug effect as kill of slow-multiplying bacterial state bacteria; ND, drug effect as kill of non-multiplying bacterial state bacteria. The PD interactions are displayed as − and + symbols, indicating decrease or increase in the EC50s identified in mono exposure.
Rifampicin in monotherapy was found to exert an effect as inhibition of growth of F and as kill of the F, S and N bacterial sub-states (Figure 2). Isoniazid and ethambutol were found to exert a kill effect on both the F and S bacterial sub-states in monotherapy. Rifampicin displayed the smallest EC50 (0.003 mg·L−1) for kill of F sub-state bacteria whilst the smallest EC50 for isoniazid (0.03 mg·L−1) was found for S sub-state bacteria. For ethambutol, an Emax function could only be supported for the kill of F sub-state bacteria, with an estimated EC50 value of 0.86 mg·L−1. The ethambutol linear kill rate for the S sub-state was estimated to 4.39 days−1 in the final model. The observed decrease in isoniazid susceptibility (Figure 1) was best described as an adaptive resistance with a rate of resistance development (kon) estimated as 0.0206 mLmg−1day. The final parameter estimates of the MTP model describing natural growth data and exposure response relationships for the drugs in monotherapy are shown in Table 1.
After characterization of the exposure–response relationships of rifampicin, isoniazid and ethambutol using data from mono exposures, the potential PD interactions using drug combinations of the three drugs were assessed using the GPDI model.
The final equations describing the exposure–response relationships of rifampicin, isoniazid and ethambutol using data from mono exposures and the identified PD interactions using drug combinations of the three drugs are shown in Table 2.
Table 2.
Final equations describing the exposure–response for the three bacterial sub-states obtained for rifampicin, isoniazid or ethambutol and the identified PD interactions identified in different combinations
| Final exposure–response relationship and PD interactions for each drug and bacterial sub-state | PD interaction identified in combination exposure | ||
|---|---|---|---|
| F bacterial sub-state | |||
| rifampicin | none identified | ||
| isoniazid, ethambutol | |||
| isoniazid | rifampicin, ethambutol | ||
| ethambutol | isoniazid, rifampicin | ||
| S bacterial sub-state | |||
| rifampicin | isoniazid, ethambutol | ||
| isoniazid | rifampicin, ethambutol | ||
| ethambutol | isoniazid, rifampicin | ||
| N bacterial sub-state | |||
| rifampicin | none identified | ||
C is drug concentration, and are the maximal fractional change in EC50, related to the F and S bacterial sub-states respectively, due to an interaction between drug A and drug B. is the maximal fractional change in EC50 due to an interaction between the combination of drug A, B and drug C.
No PD interactions were identified for the rifampicin mediated exposure–response relationship on the inhibition of the growth of the F bacterial sub-state (). All three drugs were found to mediate killing of the F sub-state and interact at the level of killing. Ethambutol decreased the EC50 of rifampicin by 66% whereas rifampicin decreased the EC50 of isoniazid by 68%. The EC50 of ethambutol was decreased by 99% in the presence of rifampicin whereas the EC50 of isoniazid was increased in the absence of ethambutol by 72%. The final expressions for rifampicin-, isoniazid- and ethambutol-mediated killing of the F sub-state through , and , respectively, including PD interactions are displayed in Table 2. The final MTP-GPDI differential equation for the F bacterial sub-state was defined as:
| (8) |
where EFD represents the total effect according to the BI criterion, i.e. . In addition to the effect on the F state, all three drugs were found to mediate killing of, and interact on the level of, the S sub-state through , and , respectively, as displayed in Table 2. The EC50 of rifampicin increased by 109% when in combination with ethambutol whereas the EC50 of isoniazid increased by 42% in the presence of rifampicin. Ethambutol EC50 decreased when in combination with rifampicin (by 486%) and also when in combination with isoniazid (by 164%). The interaction between isoniazid and rifampicin was affected when in combination with ethambutol resulting in a decrease (75%) in the maximal fractional change in isoniazid’s interaction with rifampicin. The final MTP-GPDI differential equation for the S bacterial sub-state was defined as:
| (9) |
where ESD represents the total effect according to as and are both > at the highest ethambutol concentration. No PD interactions were identified for the rifampicin-mediated exposure–response relationship on the killing of the N bacterial sub-state (). Consequently, the final MTP-GPDI differential equation for the N bacterial sub-state was defined as:
| (10) |
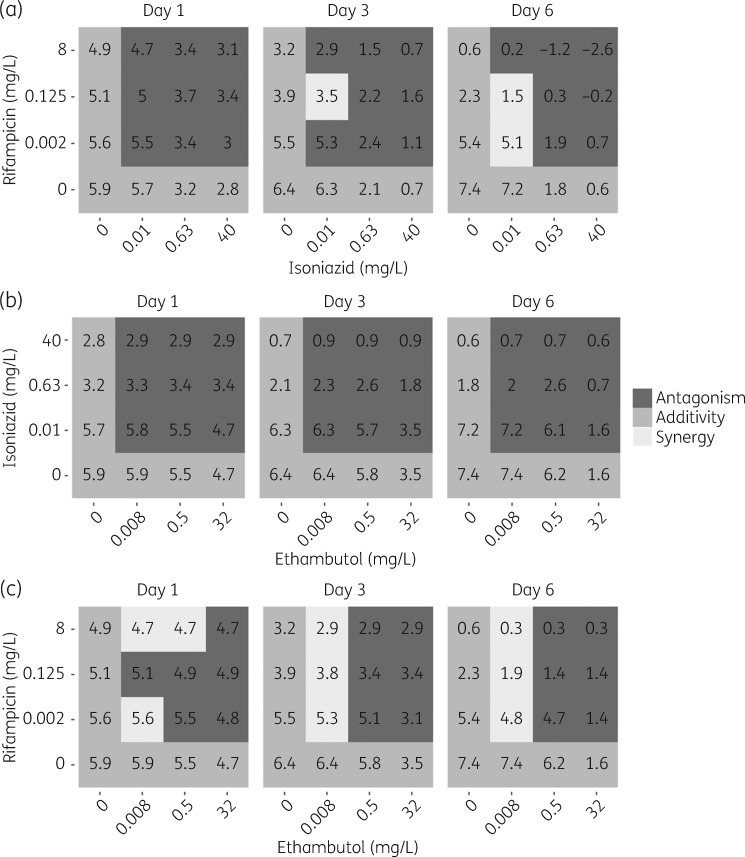
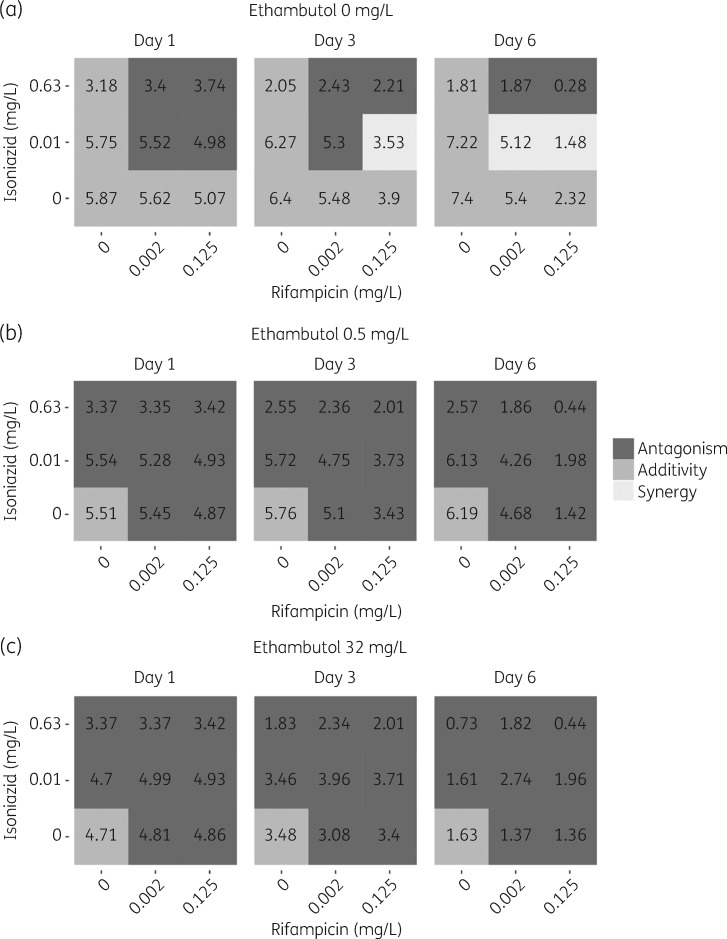
Final parameter estimates for the GPDI model are shown in Table 3. The final MTP-GPDI NONMEM model code is available as Supplementary data at JAC Online. In Figure S2 a comparison between the final MTP-GPDI model and a model assuming BI, i.e. ignoring the identified PD interactions, was made in order to predict the significance of the PD interactions based on the cfu biomarker. Quantification of the PD interaction, as more (synergy) or less (antagonism) effect than that of expected additivity, on the level of the biomarker (cfu) revealed that duo combinations showed time- and concentration-dependent interactions, i.e. a specific combination showed antagonism and synergism that varied with time and exposure (Figure 3). However, all duo combinations showed a higher effect at the highest exposure and last studied timepoint than any drug alone apart from isoniazid + ethambutol, where adding ethambutol did not provide higher efficacy than isoniazid alone (Figure 3). For the trio combination of isoniazid, rifampicin and ethambutol, all combinations were classified as antagonistic, i.e. less effect than expected from additivity, which was not dependent on time or concentration (Figure 4). However, all trio combinations showed a higher effect than the highest exposure and last studied timepoint than any drug alone (Figure 4).
Table 3.
Final parameter estimates of the GPDI model applied to cfu of M. tuberculosis with rifampicin, isoniazid and ethambutol in different combinations
| PD interaction | Parameter | Estimate [RSEa (%)] |
|---|---|---|
| Rifampicin/isoniazid | −0.679 (11) | |
| 0 fixedb | ||
| 1.42 (22) | ||
| 15.2 (49) | ||
| Isoniazid/ethambutol | 0 fixedb | |
| 1.72 (15) | ||
| 164 (259) | ||
| 0.0963 (81) | ||
| Rifampicin/ethambutol | −0.99 fixedc | |
| −0.668 (22) | ||
| 486 (12) | ||
| 2.09 (32) | ||
| Rifampicin/isoniazid/ethambutol | −0.749 (18) |
The PD interactions were estimated as a maximal fractional change in the exposure–response parameters EC50 (Table 1) obtained for rifampicin, isoniazid or ethambutol in mono exposure. Maximal fractional change of EC50 of different drugs in mono exposure as defined in Table 1. The interaction parameters INT were estimated as . The INT value reflects the deviation from expected additivity of drug effects identified, on either/both of the F or S sub-states, in mono exposure as fractional decrease (negative value, synergism), increase (positive value, antagonism) or no increase (0 fixed, no PD interaction) in EC50.
RSE, relative standard error reported on the approximate standard deviation scale obtained using sampling importance resampling (SIR).15
Fixed to 0, reflecting additivity of drug effects identified in mono exposure, i.e. no PD interaction.
Fixed to − 0.9999, reflecting a maximal decrease in EC50 identified in mono exposure.
Figure 3.
PD interaction classification on biomarker level, cfu, for duo combinations of (a) rifampicin and isoniazid, (b) isoniazid and ethambutol and (c) rifampicin and ethambutol. The classification was based on predictions from the final combined MTP-GPDI model and a model assuming only additive drug effect (i.e. only the MTP model). Dark grey indicates less effect than expected additivity (antagonism), grey indicates additivity and light grey indicates more effect than expected additivity (synergy). The numbers correspond to the log10 cfu at days 1, 3 and 6.
Figure 4.
PD interaction classification on biomarker level, cfu, for combinations of (a) rifampicin and isoniazid, (b) rifampicin, isoniazid and ethambutol (0.5 mg/L) and (c) rifampicin, isoniazid and ethambutol (32 mg/L). The classification was based on predictions from the final combined MTP and GPDI model and a model assuming only additive drug effect (i.e. only MTP model). Dark grey indicates less effect than expected additivity (antagonism), grey indicates additivity and light grey indicates more effect than expected additivity (synergy). The numbers correspond to the log10 cfu at days 1, 3 and 6.
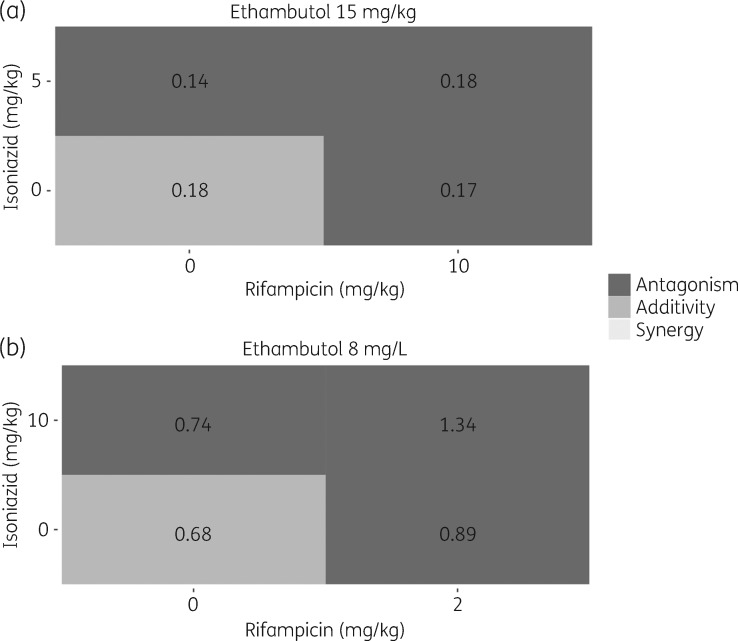
The predicted PD interactions from the MTP-GPDI modelling approach were found to be in agreement with observed PD interactions from a clinical setting (Figure 5).12 Based on deviation from expected additivity, antagonistic interactions were predicted for all duo and trio combinations of rifampicin, isoniazid and ethambutol in the clinical study.12 This is in agreement with the classification based on the in vitro data and the MTP-GPDI model approach in the present study, where antagonistic interactions were predicted for the drug combinations at clinically relevant concentrations (i.e. unbound maximal drug concentrations) and last studied timepoint (6 days) (Figure 5).
Figure 5.
Biomarker level (cfu) PD interactions, classified as deviation from expected additivity, between isoniazid, rifampicin and ethambutol in (a) observed clinical EBA 0–14 days data and (b) predicted from in vitro using the MTP-GPDI modelling approach using clinically relevant concentrations [i.e. unbound maximal drug concentrations and last studied timepoint (6 days)]. Dark grey indicates less effect than expected additivity (antagonism), grey indicates additivity and light grey indicates more effect than expected additivity (synergy). The numbers correspond to EBA (log10 cfu/mL/day) (a) 0–14 days and (b) 0–6 days.
Discussion
Proper characterization of PD interactions is crucial for the selection of drug combinations in early drug development. The PD interaction between drugs were quantified using the GPDI model,10 at one or several effect sites in the MTP model,8 such as inhibition of growth of the F bacterial sub-state and/or killing of the F, S or N bacterial sub-state. The decision to use the BI criterion was based on the different mechanisms of action of the three drugs and thus the possibility that each drug is able to act independently, which is in line with the BI criterion.4 Also, the three drugs displayed different maximal effects, which invalidates the assessment of pure LA. The GPDI model quantifies interactions on effect parameter level, in this case EC50, as either an increased or decreased EC50 depending on the deviation from a pure additive effect combination. However, in order to predict the impact of the interaction on the biomarker level and to judge whether a PD interaction is synergistic or antagonistic at a biomarker level, simulations need to be done. This is demonstrated in Figures 3 and 4 and in Figure S2, where predictions of change in cfu over time for different duo and trio combinations were compared with predictions of an MTP model assuming no interaction, i.e. no GPDI model and only assuming expected additivity of the rifampicin, isoniazid and ethambutol effects from mono exposure. In Figure S2, the predictions showed that for most duo and trio combinations a lower effect was achieved than predicted from a model assuming only additivity (grey shaded area), i.e. antagonism on a biomarker level. However, the drug effect of the combinations was higher than for any of the drugs alone, at highest exposure and last studied timepoint, apart from adding ethambutol to isoniazid in duo combination, which did not result in an increased effect compared with monotherapy with isoniazid alone. Similarly, the addition of ethambutol to the duo combination of isoniazid + rifampicin did not result in an increased effect, at highest exposure and last studied timepoint, compared with the duo combination of isoniazid and rifampicin. It is also important to keep in mind that the inclusion of ethambutol in the treatment regimen is not based on its high killing capacity but rather as a means of decreasing the risk of resistance development.
Synergy was, when identified, most profound on the effect site relating to the fast-multiplying bacterial state. The mechanism behind this synergy is, to our knowledge, not known, but a general hypothesis could be that there is a greater chance of drug-induced changes in cell physiology in actively multiplying bacteria. Such changes have previously been shown to lead to synergistic interactions against Escherichia coli.17,18 Previous results from a study of PD interactions, using the MTP-GPDI approach, between rifampicin, isoniazid, ethambutol and pyrazinamide in mice reported no PD interactions on the F bacterial sub-state.19 The PD interaction study in mice did identify PD interactions between rifampicin and ethambutol on the N bacterial sub-state,19 which our in vitro information does not support. Concurrence between the in vitro and the quantified antagonistic interaction in mice between rifampicin and isoniazid on the S bacterial sub-state can however be concluded. The less than expected additivity between rifampicin and ethambutol, as seen in this work as well as in clinical data,12 was also supported by the in vitro study by Dickinson et al.20 However, in our study, as well as in clinical data,12 the less than expected additivity observed for the combination of isoniazid with either rifampicin or ethambutol was not supported by either of two previous in vitro studies.20,21
The impact of PD interactions on the biomarker level would not have been possible to judge only by inspection of the change in EC50 (Table 1), where 3 out of 13 PD interactions led to decreased EC50 of the drugs. The quantification of the time and concentration dependency of the PD interactions was made possible by the inclusion of the whole time-course of the kill curve in the MTP-GPDI approach, as opposed to only using a summary endpoint. The time and concentration dependencies of the PD interactions are reflections of the differences in time–kill properties of the drugs and concentrations studied. The possibility of capturing this shows the strong value of a model-based evaluation approach for PD interactions. It is also important to note that without a proper characterization of the PD interaction the model would not have accurately described the combination data, whereas the MTP model alone very well described the change in cfu over time after mono drug exposure. The bacterial growth and antibacterial effect in mono exposure was characterized using the MTP model,8 which allows predictions of bacterial amounts of F, S and N bacterial sub-states with and without drug effect.3,8 The antibacterial effects of mono exposure to rifampicin, isoniazid and ethambutol quantified in this study indicated that rifampicin has an effect on all three bacterial states, whilst the data did not support an effect on the N sub-state by isoniazid and ethambutol. The origin of the observed decrease in susceptibility to isoniazid has been explored and discussed by others.22–27 In short, these studies have concluded that in vitro and in vivo observed isoniazid resistance has the potential to be of both a genotypic22 and a phenotypic7,23 nature. De Steenwinkel et al.7 have previously identified that, in the in vitro system used in this study, phenotypic efflux pump-mediated isoniazid resistance was predominant. In the final model the observed decrease in susceptibility to isoniazid was described using an empirical approach referred to as adaptive resistance.9 The adaptive resistance model is applicable for both genotypic and phenotypic resistance mechanisms. In this work, the data only supported resistance emerging from the F and S bacterial sub-populations. Resistance emerging from the N bacterial sub-population was not supported by the data in this study, most likely due to the relative low number of N sub-state bacteria in this system.
In summary, in this work we have characterized the in vitro natural growth and exposure–response relationships of M. tuberculosis Beijing 1585 genotype with respect to three first-line anti-TB drugs using the MTP model which was linked to the GPDI model in order to evaluate PD interactions for duo and trio drug combinations with successful separation of each drug’s effect on other drugs. Using in vitro time–kill data from exposure of rifampicin, isoniazid and ethambutol, alone or in combinations, the MTP-GPDI modelling approach was shown to correctly predict PD interactions as deviations from expected additivity when compared with clinical EBA data. The effect of immune response on EBA studies has previously been summarized by Sirgel et al.,28 who concluded that it would seem safe to test treated groups against zero indicating a stationary state with no or very little net change in bacterial load of untreated patients. Although the study by Sirgel et al.28 looked at a short time frame (0–2 days) the same type of behaviour is present in the study by Jindani et al.,12 which had an untreated group that was followed for 14 days.
The correct prediction of clinically observed PD interactions together with the proven possibility of separation of drug A’s interaction with B from drug B’s interaction with A, does suggest that the MTP-GPDI model could be suitable as input to selection of Phase 2b anti-TB combination regimens. However, more work is needed in terms of clinical studies of interactions between drugs, but this is limited by the unethical aspects of giving drugs in monotherapy and in combinations of fewer drugs than optimal.
Funding
The research leading to these results has received funding from the Swedish Research Council (grant number 521–2011-3442) and the Innovative Medicines Initiative Joint Undertaking (www.imi.europe.eu) under grant agreement n°115337, resources of which are composed of financial contribution from the European Union’s Seventh Framework Programme (FP7/2007–2013) and EFPIA companies’ in kind contribution.
Transparency declarations
None to declare.
Supplementary data
Supplementary data, including Figures S1 and S2, are available at JAC Online.
Supplementary Material
References
- 1. WHO. Global Tuberculosis Report 2016 http://apps.who.int/iris/bitstream/10665/250441/1/9789241565394-eng.pdf?ua=1.
- 2. Chen C, Ortega F, Rullas J. et al. The multistate tuberculosis pharmacometric model: a semi-mechanistic pharmacokinetic-pharmacodynamic model for studying drug effects in an acute tuberculosis mouse model. J Pharmacokinet Pharmacodyn 2017; 44: 133–41. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3. Svensson RJ, Simonsson USH.. Application of the multistate tuberculosis pharmacometric model in patients with rifampicin-treated pulmonary tuberculosis. CPT Pharmacometrics Syst Pharmacol 2016; 5: 264–73. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4. Bliss CI. The toxicity of poisons applied jointly. Ann Appl Biol 1939; 26: 585–615. [Google Scholar]
- 5. Loewe S. The problem of synergism and antagonism of combined drugs. Arzneimittelforschung 1953; 3: 285–90. [PubMed] [Google Scholar]
- 6. Goldoni M, Johansson C.. A mathematical approach to study combined effects of toxicants in vitro: evaluation of the Bliss independence criterion and the Loewe additivity model. Toxicol In Vitro 2007; 21: 759–69. [DOI] [PubMed] [Google Scholar]
- 7. de Steenwinkel JEM, de Knegt GJ, ten Kate MT. et al. Time-kill kinetics of anti-tuberculosis drugs, and emergence of resistance, in relation to metabolic activity of Mycobacterium tuberculosis. J Antimicrob Chemother 2010; 65: 2582–9. [DOI] [PubMed] [Google Scholar]
- 8. Clewe O, Aulin L, Hu Y. et al. A multistate tuberculosis pharmacometric model: a framework for studying anti-tubercular drug effects in vitro. J Antimicrob Chemother 2016; 71: 964–74. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9. Mohamed AF, Cars O, Friberg LE.. A pharmacokinetic/pharmacodynamic model developed for the effect of colistin on Pseudomonas aeruginosa in vitro with evaluation of population pharmacokinetic variability on simulated bacterial killing. J Antimicrob Chemother 2014; 69: 1350–61. [DOI] [PubMed] [Google Scholar]
- 10. Wicha SG, Chen C, Clewe O. et al. On perpetrators and victims: a general pharmacodynamic interaction model identifies the protagonists in drug interactions. Nat Comm 2017, in press. [DOI] [PMC free article] [PubMed]
- 11. Wicha SG, Kees MG, Kuss J. et al. Pharmacodynamic and response surface analysis of linezolid or vancomycin combined with meropenem against Staphylococcus aureus. Pharm Res 2015; 32: 2410–8. [DOI] [PubMed] [Google Scholar]
- 12. Jindani A, Aber VR, Edwards EA. et al. The early bactericidal activity of drugs in patients with pulmonary tuberculosis. Am Rev Respir Dis 1980; 121: 939–49. [DOI] [PubMed] [Google Scholar]
- 13. Beal S, Sheiner LB, Boeckmann A. et al. NONMEM User’s Guides (1989-2013). Ellicott City, MD: Icon Development Solutions, 2013. [Google Scholar]
- 14. Keizer RJ, Karlsson MO, Hooker A.. Modeling and simulation workbench for NONMEM: tutorial on Pirana, PsN, and Xpose. CPT Pharmacometrics Syst Pharmacol 2013; 2: e50.. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15. Dosne A-G, Bergstrand M, Harling K. et al. Improving the estimation of parameter uncertainty distributions in nonlinear mixed effects models using sampling importance resampling. J Pharmacokinet Pharmacodyn 2016; 43: 583–96. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16. Beal SL. Ways to fit a PK model with some data below the quantification limit. J Pharmacokinet Pharmacodyn 2001; 28: 481–504. [DOI] [PubMed] [Google Scholar]
- 17. Baba T, Ara T, Hasegawa M. et al. Construction of Escherichia coli K-12 in-frame, single-gene knockout mutants: the Keio collection. Mol Syst Biol 2006; 2: 2006.0008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18. Jawetz E, Gunnison JB.. Antibiotic synergism and antagonism; an assessment of the problem. Pharmacol Rev 1953; 5: 175–92. [PubMed] [Google Scholar]
- 19. Chen C, Wicha SG, de Knegt GJ. et al. Assessing pharmacodynamic interactions in mice using the multistate tuberculosis pharmacometric and general pharmacodynamic interaction models. CPT Pharmacomet Syst Pharmacol2017. doi:10.1002/psp4.12226. [DOI] [PMC free article] [PubMed]
- 20. Dickinson JM, Aber VR, Mitchison DA.. Bactericidal activity of streptomycin, isoniazid, rifampin, ethambutol, and pyrazinamide alone and in combination against Mycobacterium tuberculosis. Am Rev Respir Dis 1977; 116: 627–35. [DOI] [PubMed] [Google Scholar]
- 21. Bhusal Y, Shiohira CM, Yamane N.. Determination of in vitro synergy when three antimicrobial agents are combined against Mycobacterium tuberculosis. Int J Antimicrob Agents 2005; 26: 292–7. [DOI] [PubMed] [Google Scholar]
- 22. Gumbo T, Louie A, Liu W. et al. Isoniazid’s bactericidal activity ceases because of the emergence of resistance, not depletion of Mycobacterium tuberculosis in the log phase of growth. J Infect Dis 2007; 195: 194–201. [DOI] [PubMed] [Google Scholar]
- 23. Ahmad Z, Klinkenberg LG, Pinn ML. et al. Biphasic kill curve of isoniazid reveals the presence of drug-tolerant, not drug-resistant, Mycobacterium tuberculosis in the guinea pig. J Infect Dis 2009; 200: 1136–43. [DOI] [PubMed] [Google Scholar]
- 24. Bergval IL, Schuitema ARJ, Klatser PR. et al. Resistant mutants of Mycobacterium tuberculosis selected in vitro do not reflect the in vivo mechanism of isoniazid resistance. J Antimicrob Chemother 2009; 64: 515–23. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25. Lalande L, Bourguignon L, Maire P. et al. Mathematical modeling and systems pharmacology of tuberculosis: isoniazid as a case study. J Theor Biol 2016; 399: 43–52. [DOI] [PubMed] [Google Scholar]
- 26. Wallis RS, Palaci M, Eisenach K.. Persistence, not resistance, is the cause of loss of isoniazid effect. J Infect Dis 2007; 195: 1870–1.. [DOI] [PubMed] [Google Scholar]
- 27. Mitchison DA, Jindani A, Davies GR. et al. Isoniazid activity is terminated by bacterial persistence. J Infect Dis 2007; 195: 1871–2. [DOI] [PubMed] [Google Scholar]
- 28. Sirgel F, Venter A, Mitchison D.. Sources of variation in studies of the early bactericidal activity of antituberculosis drugs. J Antimicrob Chemother 2001; 47: 177–82. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.