A General CT Reconstruction Algorithm for Model-Based Material Decomposition

Abstract

Material decomposition in CT has the potential to reduce artifacts and improve quantitative accuracy by utilizing spectral models and multi-energy scans. In this work we present a novel Model-Based Material Decomposition (MBMD) method based on an existing iterative reconstruction algorithm derived from a general non-linear forward model. A digital water phantom with inserts containing different concentrations of calcium was scanned on a kV switching system. We used the presented method to simultaneously reconstruct water and calcium material density images, and compared the results to an image domain and a projection domain decomposition method. When switching voltage every other frame, MBMD resulted in more accurate water and calcium concentration values than the image domain decomposition method, and was just as accurate as the projection domain decomposition method. In a second, slower, kV switching scheme (changing voltage every ten frames) which precluded the use of traditional projection domain based methods, MBMD continued to produce quantitatively accurate reconstructions. Finally, we present a preliminary study applying MBMD to a water phantom containing vials of different concentrations of K₂HPO₄ which was scanned on a cone-beam CT test bench. Both the fast and slow (emulated) kV switching schemes resulted in similar reconstructions, indicating MBMD’s robustness to challenging acquisition schemes. Additionally, the K₂HPO₄ concentration ratios between the vials were accurately represented in the reconstructed K₂HPO₄ density image.

1. INTRODUCTION

While quantitative CT is an important tool in bone disease diagnosis and study,¹ traditional CT acquisitions are prone to beam hardening artifacts and reduced accuracy in quantitation.^2,3 By acquiring CT datasets at multiple energies, direct quantitative estimates of material density for particular targets of diagnostic interest can be obtained (e.g., calcium and water). This improved specificity, artifact reduction, and quantitative accuracy has the potential to improve diagnosis and study of diseases such as osteoporosis.

Material decomposition techniques can be grouped into three categories: image domain decomposition,² projection domain decomposition,⁴ and Model-Based Material Decomposition (MBMD).^5–9 Each technique requires datasets at multiple energies, traditionally acquired with either an energy discriminating detector or multiple X-ray sources/spectra. Image domain decomposition first reconstructs each dataset independently, and then decomposes the reconstructed images into different material density images. Projection domain decomposition first estimates the ideal line integrals corresponding to each material type, and then independently reconstructs each material density image from these line integrals. Finally, MBMD performs the reconstruction and decomposition simultaneously by minimizing an objective function based on a multi-energy forward model. MBMD is the most versatile option, as it does not require (as in projection domain decomposition) matched projection data with coincident measurements for each energy and since it is able to implicitly model and remove beam hardening artifacts (unlike image domain decomposition).

Previously, we have developed a general Model-Based Iterative Reconstruction (MBIR) algorithm capable of modeling a variety of system properties, and used it to model scintillator blur, focal-spot blur, and noise correlations.¹⁰ In this work we show that the same algorithm can be used for MBMD. This new method differs from previous MBMD methods^5–9 in that it does not require matched projection data (cf. Refs ^6,8) and is based on a Gaussian noise model (cf. Refs ^5–9). Because the projection data does not need to be matched, this method may be applied to novel acquisition protocols (e.g., kV switching or multiple X-ray sources with non-coincident rays) that can challenge traditional projection-domain and many MBMD methods. Because it is derived from a general forward model, this method may be improved with models of other system effects, such as blur and noise correlation. In this work we apply this novel MBMD method to simulation and test bench data in multiple kV switching scenarios.

2. METHODS

2.1 Forward model and objective

The authors have previously presented a parallel algorithm¹⁰ for MBIR with the following forward/noise model:

$$\overline{\mathit{y}}=\mathbf{B}\exp \left(-{\mathbf{M}}_{\mathbf{x}}\right)\mathbf{y}~\mathcal{N}\left(\overline{\mathit{y}},{\mathbf{K}}_Y\right),$$ (1)

and corresponding penalized-likelihood objective function:

$$\psi ={\left[\mathit{y}-\mathbf{B}\exp \left(\mathbf{M}\mathit{\mu }\right)\right]}^T{\mathbf{K}}_Y^{-1}\left[\mathbf{y}-\mathbf{B}\exp \left(\mathbf{M}\mathit{\mu }\right)\right]+\beta R\left(\mathit{\mu }\right).$$ (2)

This model is sufficiently general to accommodate a number of estimation problems including CT reconstruction with blurred projections.¹⁰ In this work we present a specific form of (1) suited to the material decomposition problem with multi-energy data. Specifically, we consider multiple materials (indexed by m) and K datasets (y_k) with different X-ray spectra (s_e,k), with energies indexed by e, such that measurements are given by

$${\overline{\mathit{y}}}_k={\displaystyle \sum _e{s}_{e,k}\exp }\left(-{\displaystyle \sum _m{p}_{e,m}\left[{\mathbf{A}}_k{\mathit{x}}_m\right]}\right).$$ (3)

For each material, the material density values (x_m) are forward projected (A_k). The forward projections may be different for each dataset (e.g., non-coincident as in kV switching acquisitions). The projections are scaled by the material mass attenuation coefficient at each energy (p_e,m). The energy-dependent line integrals are summed over all materials, exponentiated, and scaled by the X-ray spectrum associated with that dataset (s_e,k) before being summed over energy. Thus, in (1), the matrix M performs the projection, scaling by mass attenuation coefficients, and summing over materials; and B performs the scaling by X-ray spectra and the summation over energy. This formulation is consistent with (1), and therefore does not require changing the underlying optimization algorithm. (Note that the X-ray spectrum includes the detector response as well as the energy dependent X-ray fluence. Thus, the different datasets can result either from scans with different X-ray tube settings/filtration or a scan with an energy discriminating detector.)

2.2 Simulation study

A digital cylindrical water phantom with 0.125 mm × 0.125 mm voxels was created containing three calcium inserts, two with 600 mg mL⁻¹ Ca and the other with 100 mg mL⁻¹. Data were generated from this phantom using (3) with a source-detector distance of 1200 mm, a source-axis distance of 600 mm, and a detector with 0.097 mm pixels. Two X-ray spectra were used, 60 kVp and 120 kVp, with the latter containing additional filtration (4 mm of aluminum and 0.254 mm of silver).¹¹ Each energy response curve was normalized to sum to one, and then scaled by 2.5 × 10⁵ photons pixel⁻¹. Finally, we added Poisson noise to the data, binned it by a factor of four (resulting in a photon flux of 10⁶ photons pixel⁻¹), and added readout noise equivalent to 2.8 photons. Kilovolt switching was simulated by alternating the spectrum as a function of projection angle, resulting in 180 projections acquired with the 60 kVp spectrum and 180 with the 120 kVp spectrum, with consecutive projections separated by 1°. Two kV switching schemes were used: switching every other frame (KV1:1), and switching every 10 frames (KV10:10).

Data were reconstructed using three methods: projection domain decomposition, image domain decomposition, and MBMD. For the projection domain decomposition, (3) was used to generate a map from pairs of measurements to pairs of line integrals using interpolation.⁴ This relationship was used to estimate ideal line-inegrals for each material (i.e., Ax_m in (3)). (Note that this requires measurements to be matched, e.g., A₁ = A₂). In order to obtain matched projection data, the 60 kVp data and the 120 kVp data were upsampled to 360 projections each using linear interpolation. Because of the required interpolation, we only applied projection domain decomposition to the KV1:1 case. The decomposed line integrals were then used to generate ideal (i.e., monoenergetic) measurements, which were reconstructed using MBIR. The MBIR method minimized (2) with B = 10⁶ photons and M = A. For the image domain decomposition, the two energy scans were first reconstructed separately using the same MBIR method as the projection domain decomposition. Each of these reconstructions (μ₁, μ₂) was assumed to be a linear combination of the material density images:

$$\left[\begin{array}{c}{\mathit{\mu }}_1^T\\ {\mathit{\mu }}_2^T\end{array}\right]=\left[\begin{array}{cc}{f}_{11}& f_{12}\\ f_{21}& f_{22}\end{array}\right]\left[\begin{array}{c}{\mathit{x}}_1^T\\ {\mathit{x}}_2^T\end{array}\right]$$ (4)

where is the attenuation value of material i at the average energy of response curve j. This matrix was inverted and used to calculate the material density images.² To ensure nearly converged reconstructions, all MBIR algorithms ran for 20 000 iterations using 10 subsets. Additionally, Nesterov momentum acceleration^12,13 was used for the first 15 000 iterations. A Huber penalty¹⁴ was used with δ = 10³. All reconstructions used the same optimization algorithm.¹⁰

2.3 Bench study

To apply the new MBMD approach in physical data, we created a phantom with known concentrations of potassium phosphate dibasic (K₂HPO₄), with concentrations ranging from 50 mg mL⁻¹ to 300 mg mL⁻¹ to emulate a bone-water mixture. The phantom was scanned on a Cone-Beam CT (CBCT) test bench with a Varian Rad-94 (Varian, Salt Lake City UT) X-ray tube and a Varian 4030CB detector (Varian, Palo Alto CA). Data were acquired with two different X-ray spectra: 60kVp and 120kVp, with the later containing additional filtration (4 mm aluminum and 0.254 mm silver). The source-detector distance was 1214 mm and the source-axis distance was 604.1 mm. Each scan composed of 360 projections in 1° increments. Kilovolt switching was simulated by taking unique frames from the two data sets. In this preliminary study, MBMD was used to reconstruct KV1:1 and KV10:10 data. The X-ray spectra were calibrated from projections of Gammex calcium inserts with different concentrations. We obtained initial spectra from Spektr,¹¹ modified it with additional filters (aluminum, copper, tungsten, CsI, glass) and used CMA-ES¹⁵ to find optimal thicknesses of these materials to match the calibration data.

3. RESULTS

Figure 1 summarizes decomposition performance. Projection domain decomposition and MBMD produced the best reconstructions in terms of concentration accuracy and artifact reduction. Because image domain decomposition does not model the full spectrum through the phantom, it was unable to remove beam hardening artifacts in the center insert (visible in the zoomed image of insert 2 for the image domain decomposition in Figure 1A). The average concentration values in each insert ROI are compared in Figure 1B. Projection domain decomposition and MBMD produced the most accurate concentration values, while image domain decomposition underestimated calcium concentration and overestimated water concentration, particularly for the 600 mg mL⁻¹ inserts. MBMD also produced accurate concentration values in the challenging KV10:10 case.

Figure 1.

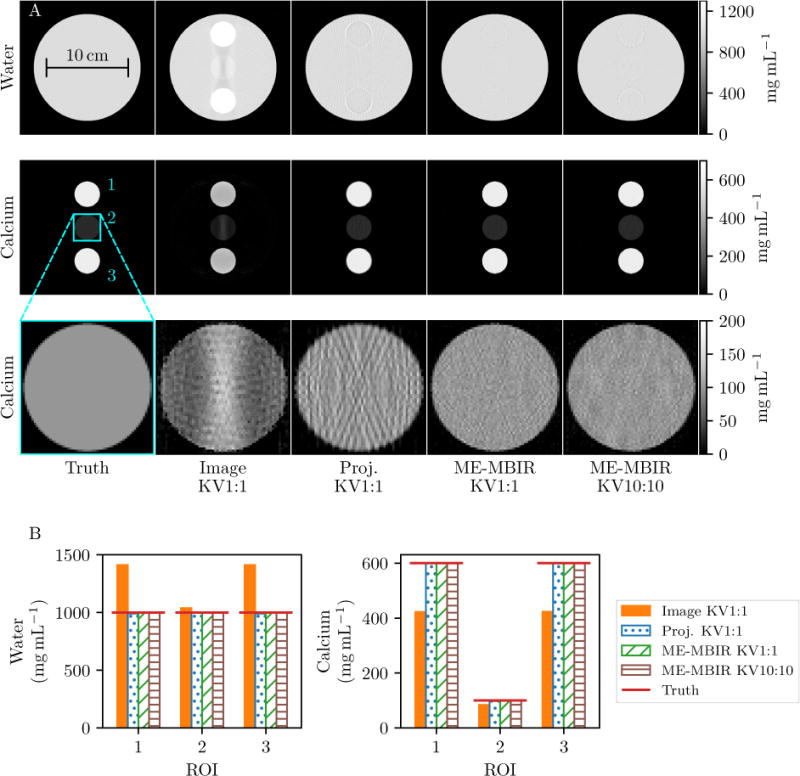
Simulation study results. A: Reconstructions. The insert ROIS are numbered from top to bottom. The standard deviations of the calcium concentrations in insert 1 are 10.60 mg mL⁻¹ for the image domain decomposition, 12.41 mg mL⁻¹ for the projection domain decomposition, 8.11 mg mL⁻¹ for MBMD KV1:1, and 8.71 mg mL⁻¹ for MBMD KV10:10. B: Average concentration in each insert for water (left) and calcium (right).

Figure 2C shows MBMD bench data reconstructions of both KV1:1 and KV10:10 data. The reconstructions are nearly identical, indicating that MBMD is well suited to challenging cases with unique sampling and measurement mismatch. The concentration values in the ROIs are also nearly identical (Figure 2D). However, the K₂HPO₄ concentrations are slightly greater than the ideal values, and the water concentrations are slightly lower. This is likely a result of inaccuracies in making the phantom or inaccuracies in our spectral estimation. Despite these inaccuracies, the relative K₂HPO₄ concentration values (as compared to the concentration in ROI 1) are fairly accurate (Figure 2D).

Figure 2.

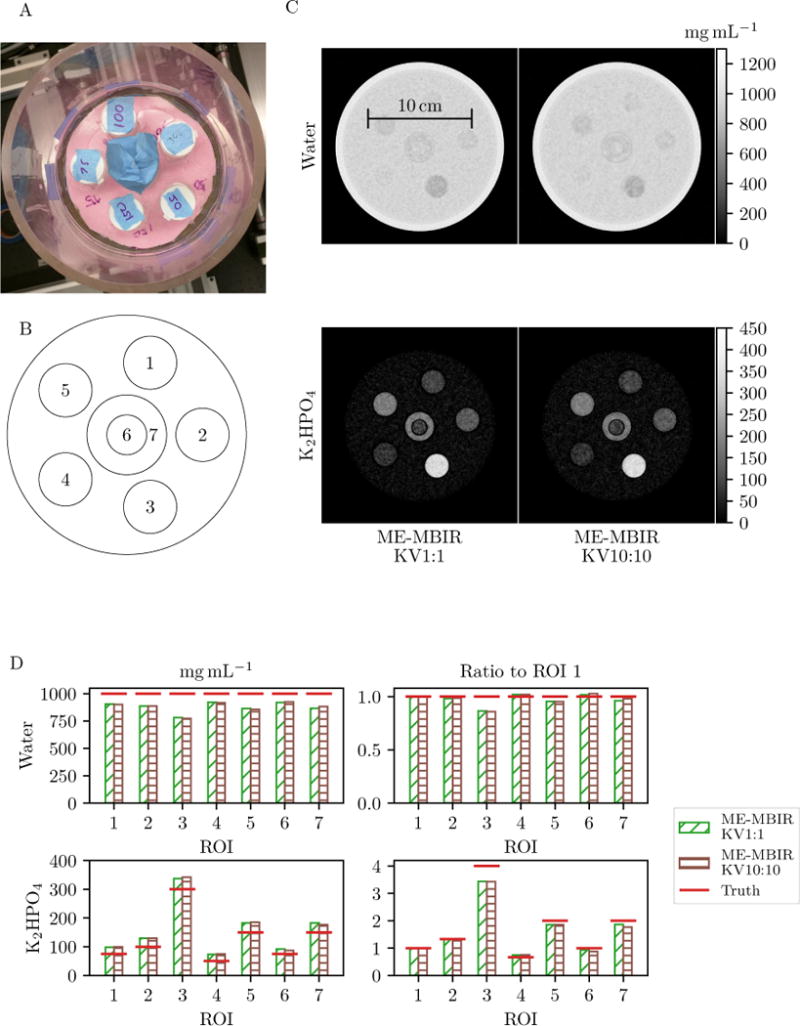
A: K₂HPO₄ phantom. B: Schematic of phantom indicating ROI locations. C: MBMD bench data reconstructions. D: Concentrations of different vials (left column) and concentration ratios relative to ROI 1 (right column).

4. DISCUSSION

We have shown that a previously derived optimization algorithm¹⁰ can be applied to multi-energy reconstruction, providing improved accuracy as compared to an image based decomposition method while being applicable to more scenarios than projection domain decomposition methods.

This method appears sensitive to an accurate spectral calibration, which is a potential cause for the mismatch in concentration values seen in the bench data results. However, once an accurate set of spectra are determined for a given scanner, the calibration will only need to be repeated occasionally. In future work we will evaluate more advanced calibration methods.^16,17

The MBMD method presented here is a general solution to multi-energy reconstruction, capable of being applied to many systems and acquisition protocols. For example, this method may be applied to complicated kV switching schemes with three or more spectra, or systems with multiple axially oriented X-ray sources.¹⁸ By using an already established reconstruction method based on a general forward model, this method can incorporate models of physical effects unique to specific CT systems, such as application specific flat-panel systems (e.g., scintillator blur and noise correlation). Accurately modeling these effects in an MBMD framework may improve resolution in addition to quantitative accuracy. Additionally, this method could incorporate spectral blurring and correlation between energy bins¹⁹ in energy-discriminating detectors. Ultimately, material separation and material density reconstruction enabled by accurate physical models has the potential to improve quantitative bone imaging for applications such as osteoarthritis/fracture healing diagnosis and study.