Scalable Bayesian Variable Selection Using Nonlocal Prior Densities in Ultrahigh-dimensional Settings

Abstract

Bayesian model selection procedures based on nonlocal alternative prior densities are extended to ultrahigh dimensional settings and compared to other variable selection procedures using precision-recall curves. Variable selection procedures included in these comparisons include methods based on g-priors, reciprocal lasso, adaptive lasso, scad, and minimax concave penalty criteria. The use of precision-recall curves eliminates the sensitivity of our conclusions to the choice of tuning parameters. We find that Bayesian variable selection procedures based on nonlocal priors are competitive to all other procedures in a range of simulation scenarios, and we subsequently explain this favorable performance through a theoretical examination of their consistency properties. When certain regularity conditions apply, we demonstrate that the nonlocal procedures are consistent for linear models even when the number of covariates p increases sub-exponentially with the sample size n. A model selection procedure based on Zellner’s g-prior is also found to be competitive with penalized likelihood methods in identifying the true model, but the posterior distribution on the model space induced by this method is much more dispersed than the posterior distribution induced on the model space by the nonlocal prior methods. We investigate the asymptotic form of the marginal likelihood based on the nonlocal priors and show that it attains a unique term that cannot be derived from the other Bayesian model selection procedures. We also propose a scalable and efficient algorithm called Simplified Shotgun Stochastic Search with Screening (S5) to explore the enormous model space, and we show that S5 dramatically reduces the computing time without losing the capacity to search the interesting region in the model space, at least in the simulation settings considered. The S5 algorithm is available in an R package BayesS5 on CRAN.

1 Introduction

In the context of hypothesis testing, Johnson and Rossell (2010) defined nonlocal (alternative) priors as densities that are exactly zero whenever a model parameter equals its null value. Nonlocal priors were extended to model selection problems in Johnson and Rossell (2012), where product moment (pMoM) prior and product inverse moment (piMoM) prior densities were introduced as priors on a vector of regression coefficients. In p ≤ n settings, model selection procedures based on these priors were demonstrated to have a strong model selection property: the posterior probability of the true model converges to 1 as the sample size n increases. More recently, Rossell et al. (2013) and Rossell and Telesca (2017) proposed product exponential moment (peMoM) prior densities that have similar behavior to piMoM densities near the origin. However, the behavior of nonlocal priors in p ≫ n settings remains understudied to date (particularly in comparison to other commonly used variables selection procedures), which serves as the motivation for this article.

We undertook a detailed simulation study to compare the performance of nonlocal priors in p ≫ n settings under sparsity with a host of penalization methods including the least absolute shrinkage and selection operator (lasso; Tibshirani (1996)), smoothly clipped absolute deviation (scad; Fan and Li (2001)), adaptive lasso (Zou, 2006), minimum convex penalty (mcp; Zhang (2010)), and the reciprocal lasso (rlasso), recently been proposed by Song and Liang (2015). The penalty function of the rlasso is equivalent to the negative log-kernel of nonlocal prior densities; further connections are described in Section 5. As a natural Bayesian competitor, we also considered the widely used g-prior (Zellner, 1986; Liang et al., 2008), which is a local prior in the sense of Johnson and Rossell (2010). We used precision-recall curves (Davis and Goadrich, 2006) as a basis for comparison between methods. These curves eliminate the effect of the choice of tuning parameters for each method so that the comparison across different methods can be transparent. It has been argued (Davis and Goadrich, 2006) that in cases where only a tiny proportion of variables are significant, precision-recall curves are more appropriate tools for comparison than are the more widely used receiver operating characteristic curves. While the ROC curves present a trade-off between the type I error and the power of a decision procedure, precision-recall curves examine the trade-off between the power and the false discovery rate.

Our studies indicate that Bayesian procedures based on nonlocal priors and the g-prior perform better than penalized likelihood approaches in a sense that they achieve a lower false discovery rate, while maintaining the same power of the decision procedure. Posterior distributions on the model space based on nonlocal priors were found to be more tightly concentrated around the maximum a posteriori model than the posterior based on g-priors, implying that they had a faster rate of posterior concentration. We also identified the oracle hyperparameter that maximizes the posterior probability of the true model for the Bayesian procedures. The growth-rate of these oracle hyperparameters with p also offers an interesting contrast between nonlocal and local priors. In the case of g-priors, the oracle value of g varied between 7.83 × 10⁸ and 4.29 × 10¹³ as p ranged between 1000 and 20000. For the same range of p, the oracle value of τ varied between 1.97 and 3.60, where τ is the tuning parameter for nonlocal priors described in Section 2. George and Foster (2000) argued from a minimax perspective that the g parameter should satisfy g ≍ p², which explains the large values of the optimal g. However, using asymptotic arguments to obtain default hyperparameters is difficult because the constant of proportionality is typically unknown. Moreover, when g is very large, the g-prior assigns negligible prior mass at the origin, essentially resulting in a nonlocal like prior. A similar point can be made about the recently proposed Bayesian shrinking and diffusing (BASAD) priors (Narisetty and He, 2014). On the other hand, the optimal hyperparameter value for the nonlocal priors is stable with increasing p, growing at a very slow rate.

Motivated by this empirical finding, we studied properties of two classes of nonlocal priors allowing the hyperparameter τ to scale with p. Using a fixed value of τ, it seems that strong model selection consistency is possible only when p ≤ n (Johnson and Rossell, 2012). In this article, we establish that nonlocal priors can achieve strong model selection consistency even when the number of variables p increases sub-exponentially in the sample size n, provided that the hyperparameter τ is asymptotically larger than log p. This theoretical result is consistent with our empirical finding.

2 Nonlocal prior densities for regression coefficients

We consider the standard setup of a Gaussian linear regression model with a univariate response and p candidate predictors. Let y = (y₁, …, y_n)^T denote a vector of responses for n individuals and X an n × p matrix of covariates. We denote a model by k = {k₁, …, k_|k|}, with 1 ≤ k₁ < …< k_|k| ≤ p. Given a model k, let X_k denote the design matrix formed from the columns of X_n corresponding to model k and β_k = (β_k,1, …, β_k,|k|)^T the regression coefficient for model k. Under each model k, the linear regression model for the data is

$$y=X_{\mathrm{k}}{\beta }_{\mathrm{k}}+\epsilon ,$$ (1)

where ε ∼ N_n(0, σ²I_n). Let t denote the true, or data-generating model and let ${\beta }_{\mathrm{t}}^0$ be the true regression coefficient under model t. We assume that the true model is fixed but unknown.

Given a model k, the product exponential moment (peMoM) prior density (Rossell et al., 2013; Rossell and Telesca, 2017) for the vector of regression coefficients β_k is defined as

$$\pi ({\beta }_{\mathrm{k}}|{\sigma }^2,\tau ,\mathrm{k})=C^{-\left|\mathrm{k}\right|}{\displaystyle \prod _{j=1}^{\left|\mathrm{k}\right|}\exp }\{-{\beta }_{\mathrm{k},j}^2/(2{\sigma }^2\tau )-\tau /{\beta }_{\mathrm{k},j}^2\}.$$ (2)

The normalizing constant C can be explicitly calculated as

$$C={\displaystyle {\int }_{-\infty }^{\infty }\exp }\{-t^2/(2{\sigma }^2\tau )-\tau /t^2\}dt={(2\pi {\sigma }^2\tau )}^{1/2}\exp \{-{(2/{\sigma }^2)}^{1/2}\},$$ (3)

since ∫ exp{−μ/t² – ζt²}dt = (π/ζ)^1/2 exp {−2(μζ)^1/2}.

Second, for a fixed positive integer r, the product inverse-moment (piMoM) prior density (Johnson and Rossell, 2012) for β_k is given by

$$\pi ({\beta }_{\mathrm{k}}|{\sigma }^2,\tau ,\mathrm{k})=C^{\ast -\left|\mathrm{k}\right|}{\displaystyle \prod _{j=1}^{\left|\mathrm{k}\right|}[{({\beta }_{\mathrm{k},j})}^{-2r}\exp \{-\tau /{\beta }_{\mathrm{k},j}^2\}],}$$ (4)

where C^∗ = τ^−r+1/2Γ(r − 1/2) for r > 1/2, where Γ(·) is the gamma function.

The piMoM and peMoM prior densities are nonlocal in the sense that the density value at the origin is exactly zero. This feature of the densities for a single regression coefficient is illustrated in Figure 1. Since the piMoM prior densities and the peMoM prior densities have the same term exp{−τ/β²} that controls the behavior of the density function around the origin, they attain almost the same shape of the density function at the origin, which yields the same theoretical results in an asymptotic sense. Further details regarding this point are discussed in Section 4.

Figure 1.

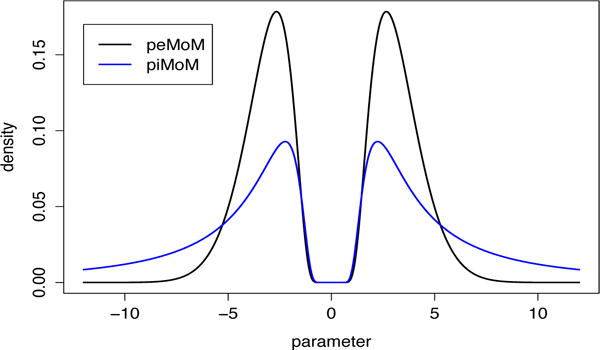
Nonlocal prior density functions for a single regression coefficient with τ = 5; for the piMoM prior, r = 1.

We focus on these two classes of nonlocal priors in the sequel. Note that in both (2) and (4), π(β_k) = 0 when β_k = 0; a defining feature of nonlocal priors. The distinction between the peMoM and the piMoM priors mainly involves their tail behavior. Whereas peMoM priors possess Gaussian tails, the piMoM prior densities have inverse polynomial tails. For example, piMoM densities with r = 1 have Cauchy-like tails, which has implications for their finite sample consistency and asymptotic bias in posterior mean estimates of regression coefficients. Since similar conditions are later imposed on the hyperparameter τ appearing in (2) and (4), at the risk of some ambiguity we use the same notation for the two hyperparameters in these equations.

In addition to imposing priors on the regression parameters given a model, we need to place a prior on the space of models to complete the prior specification. We consider a uniform prior on the model space restricted to models having size less than or equal to q_n, with q_n < n, i.e.,

$$\pi (\mathrm{k})\propto I(|\mathrm{k}|\le q_n),$$ (5)

where I(·) denotes the indicator function and with a slight abuse of notation, we denote the prior on the space of models by π as well. Similar priors have been considered in the literature by Jiang (2007) and Liang et al. (2013). Since the peMoM and piMoM priors already induce a strong penalty on the size of the model space (see Section 4), we do not need to additionally penalize larger models using, for example, model space priors of the type discussed in Scott and Berger (2010).

Under a peMoM prior (2) on the regression coefficients, the marginal likelihood m_k(y) under model k given σ² can be obtained by integrating out β_k, resulting in $m_{\mathrm{k}}(y)={(2\pi {\sigma }^2)}^{-\frac{n}{2}}{C}^{-\left|\mathrm{k}\right|}{Q}_{\mathrm{k}}\exp \{-{\stackrel{\sim }{R}}_{\mathrm{k}}/(2{\sigma }^2)\},$ where

$$\begin{array}{l}{\stackrel{\sim }{R}}_{\mathrm{k}}=y^T(I_n-{\stackrel{\sim }{\mathrm{P}}}_{\mathrm{k}})y,{\stackrel{\sim }{\mathrm{P}}}_{\mathrm{k}}=X_{\mathrm{k}}{(X_{\mathrm{k}}^{\mathrm{T}}{X}_{\mathrm{k}}+1/\tau {\mathrm{I}}_{\mathrm{k}})}^{-1}{X}_{\mathrm{k}}^{\mathrm{T}},\\ Q_{\mathrm{k}}={\displaystyle \int \exp \{-{({\beta }_{\mathrm{k}}-{\stackrel{\sim }{\beta }}_{\mathrm{k}})}^{\mathrm{T}}{\sum ^{\sim }}_{\mathrm{k}}^{-1}}({\beta }_{\mathrm{k}}-{\stackrel{\sim }{\beta }}_{\mathrm{k}})/(2{\sigma }^2)-{\displaystyle \sum _{j=1}^{\left|\mathrm{k}\right|}\tau }/{\beta }_{\mathrm{k},j}^2\}d{\beta }_{\mathrm{k}},\\ {\stackrel{\sim }{\beta }}_{\mathrm{k}}={(X_{\mathrm{k}}^{\mathrm{T}}{X}_{\mathrm{k}}+1/\tau {\mathrm{I}}_{\mathrm{k}})}^{-1}{X}_{\mathrm{k}}^{\mathrm{T}}y,{\sum ^{\sim }}_{\mathrm{k}}={(X_{\mathrm{k}}^{\mathrm{T}}{X}_{\mathrm{k}}+1/\tau {\mathrm{I}}_{\mathrm{k}})}^{-1}.\end{array}$$ (6)

Similarly, the marginal likelihood using the piMoM prior densities (4) can be expressed as $m_{\mathrm{k}}(y)={(2\pi {\sigma }^2)}^{-\frac{n}{2}}{C}^{\ast -\left|\mathrm{k}\right|}{Q}_{\mathrm{k}}^{\ast }\exp \{-R_{\mathrm{k}}^{\ast }/(2{\sigma }^2)\},$ where

$$\begin{array}{l}{R}_{\mathrm{k}}^{\ast }=y^{\mathrm{T}}(I_n-{\mathrm{P}}_{\mathrm{k}})y,{\mathrm{P}}_{\mathrm{k}}=X_{\mathrm{k}}{(X_{\mathrm{k}}^{\mathrm{T}}{X}_{\mathrm{k}})}^{-1}{X}_{\mathrm{k}}^{\mathrm{T}},\\ Q_{\mathrm{k}}^{\ast }={\displaystyle \int {\displaystyle \prod _{j=1}^{\left|\mathrm{k}\right|}{\beta }_{\mathrm{k},j}^{-2r}\exp }\{-{({\beta }_{\mathrm{k}}-{\widehat{\beta }}_{\mathrm{k}})}^{\mathrm{T}}{\sum }_{\mathrm{k}}^{\ast -1}}({\beta }_{\mathrm{k}}-{\widehat{\beta }}_{\mathrm{k}})/(2{\sigma }^2)-{\displaystyle \sum _{j=1}^{\left|\mathrm{k}\right|}\tau }/{\beta }_{\mathrm{k},j}^2\}d{\beta }_{\mathrm{k}},\\ {\widehat{\beta }}_{\mathrm{k}}={(X_{\mathrm{k}}^{\mathrm{T}}{X}_{\mathrm{k}})}^{-1}{X}_{\mathrm{k}}^{\mathrm{T}}y,{\sum }_{\mathrm{k}}^{\ast }={(X_{\mathrm{k}}^{\mathrm{T}}{X}_{\mathrm{k}})}^{-1}.\end{array}$$ (7)

The integrals for Q_k and $Q_{\mathrm{k}}^{\ast }$ cannot be obtained in closed forms, so for computational purposes we make Laplace approximations to m_k(y). The expressions for the marginal likelihood derived here is nevertheless important for our theoretical study in Section 4.

3 Numerical results

3.1 Simulation studies using precision-recall curves

To illustrate the performance of nonlocal priors in ultrahigh-dimensional settings and to compare their performance with other methods, we calculated precision-recall curves (Davis and Goadrich, 2006) for all selection procedures. A precision-recall curve plots the precision = TP/(TP + FP), versus recall (or sensitivity) = TP/(TP + FN), where TP, FP and FN respectively denote the number of true positives, false positives, and false negatives, as the tuning parameter is varied. The efficacy of a procedure can be measured by the area under the precision-recall curve; the greater the area, the more accurate the method. Since both precision and recall take values in [0, 1], the area under the curve for an ideal precision-recall curve is 1. We used two (n, p) combinations, namely (n, p) = (400, 10000) and (n, p) = (400, 20000), and plotted the average of the precision-recall curves obtained from 100 independent replicates of each procedure.

We compared the performance of peMoM and piMoM priors to a number of frequentist penalized likelihood methods: lasso (Tibshirani, 1996), adaptive lasso (Zou, 2006), scad (Fan and Li, 2001), and minimax concave penalty (Zhang, 2010). We used the R package ncvreg to fit these penalized likelihood methods. We also included reciprocal lasso in our simulation studies. However, due to computational constraints involved in implementing the full rlasso procedure, we followed the recommendation in Song and Liang (2015) and instead implemented the reduced rlasso. The reduced rlasso procedure is a simplified version of rlasso that uses the least square estimators of β when minimizing the rlasso objective function.

We considered Zellner’s g-prior (Zellner, 1986; Liang et al., 2008) as a competing Bayesian method, with ${\beta }_{\mathrm{k}}|\mathbf{k},{\sigma }^2~N(0,g{\sigma }^2{(X_{\mathrm{k}}^{\mathrm{T}}{X}_{\mathrm{k}})}^{-1})$ and g is the tuning parameter. With the prior π(σ²) ∝ 1/σ², the marginal likelihood $m_{\mathrm{k}}(y)\propto {(1+g)}^{-\left|\mathrm{k}\right|/2}{\{1+g(1-D_{\mathrm{k}}^2)\}}^{-(n-1)/2}$ can be obtained in a closed form; see for example, Liang et al. (2008, pp 412), where $D_{\mathrm{k}}^2$ is the ordinary coefficient of determination for the model k.

A uniform model prior (5) was considered for all Bayesian procedures. This prior was chosen for several reasons. First, construction of the PR curves requires maximization over model hyper-parameters, which is most easily achieved if there is only one unknown hyperparameter. We also wished to avoid providing an advantage to the Bayesian methods by introducing additional tuning parameters into these methods that were not present in the penalized likelihood methods. Furthermore, the use of non-uniform priors on the model space introduces (at least) one more degree of freedom into the comparisons between methods, and our intent was to compare the effects of the penalties imposed on regression coefficients by both penalized likelihood and Bayesian methods. At first blush, this might appear to put Bayesian methods like those based on the g-prior at a disadvantage, since such methods do not yield consistent variable selection even in p < n settings without prior sparsity penalties on the model space (when g is held fixed as n increases). However, in the construction of our PR curves, we allowed prior hyperparameters to increase with n, which effectively allowed the Bayesian methods to impose additional sparseness penalties through the introduction of large hyperparameter values.

We arbitrarily fixed r = 1 for the piMoM prior (4) and used an inverse-gamma prior on σ² with parameters (0.1, 0.1) for the peMoM, piMoM priors, and g-priors. Posterior computations for the peMoM, piMoM and g-priors were implemented using the Simplified Shotgun Stochastic Search with Screening (S5) algorithm described in Section 7. The maximum a posteriori model was used in each case to summarize the model selection performance. The precision-recall curves are drawn by varying the hyperparameters (τ for the nonlocal priors and g for the g-priors), so the comparison between the model selection based on the nonlocal priors and the g-prior is free of the choice of hyperparameters. Because of their high computational burden, we could not include BASAD (Narisetty and He, 2014) in the comparisons.

For each simulation setting, we simulated data according to a Gaussian linear model as in (1) with the fixed true model t = {1, 2, 3, 4, 5} with the true regression coefficient ${\beta }_{\mathbf{t}}^0={(0.50,0.75,1.00,1.25,1.50)}^{\mathrm{T}}$ and σ = 1.5. Also, the signs of the true regression coefficients were randomly determined with probability one-half. Each row of X was independently generated from a N(0, Σ) distribution with one of the following covariance structures:

• Case (1): compound symmetry design; ${\sum }_{jj\prime }=0.5$, if j ≠ j′ and Σ_jj = 1, 1 ≤ j, j′ ≤ p.

• Case (2): autoregressive correlated design; ${\sum }_{jj\prime }={0.5}^{|j-j\prime |}$, 1 ≤ j, j′ ≤ p.

• Case (3): isotropic design; Σ = I_p.

Figure 2 plots the precision-recall curves averaged over 100 simulation replicates for the different methods across the two (n,p) pairs and the three covariate designs. From Figure 2, it is evident that the precision-recall curves for the peMoM and piMoM priors have an overall better performance than the penalized likelihood methods lasso, adaptive lasso, scad, and mcp. For decision procedures having the same power, this implies that the nonlocal priors achieve lower false discovery rates. As discussed in Section 5, since the reduced rlasso shares the same nonlocal kernel as the nonlocal priors, it has a similar selection performance. The figure also shows that Zellner’s g-prior attains comparable performance with the nonlocal priors in terms of the precision-recall curves.

Figure 2.

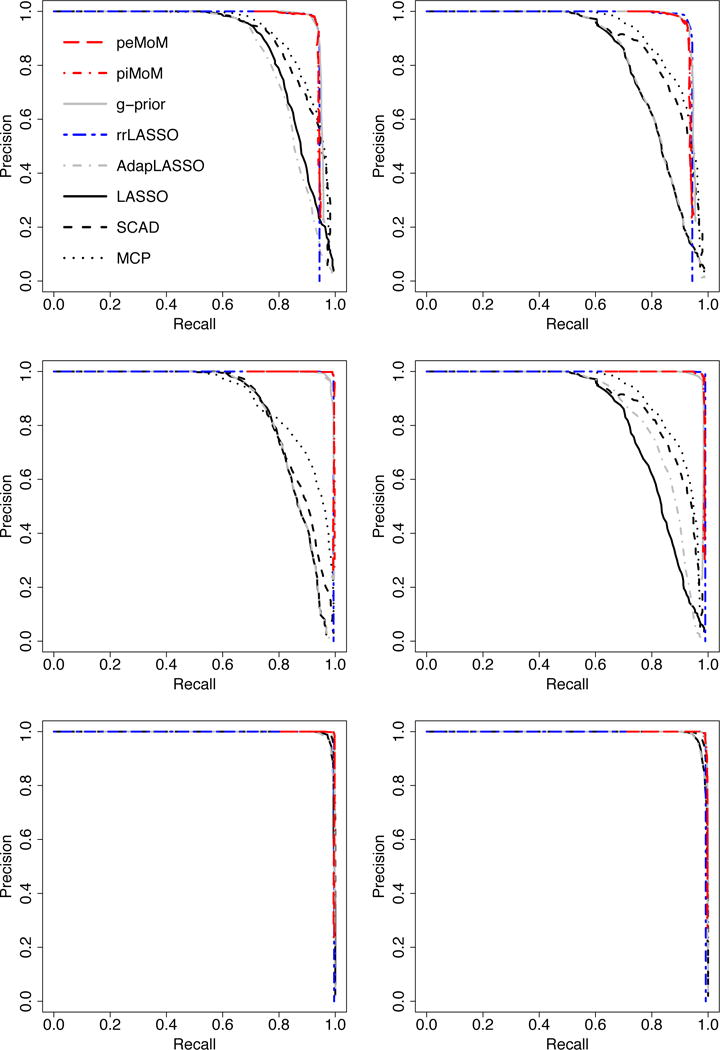
Plot of the mean precision-precision curves over 100 datasets with (n, p) = (400, 10000)(first column) and (n, p) = (400, 20000)(second column). Top: case (1); middle: case (2); bottom: case (3).

3.2 Further comparison with Zellner’s g-prior

The similarity of the performances of the g-prior and the nonlocal priors in terms of precision-recall curves begs for closer comparisons of these procedures. For this reason, we also investigated the concentration of the posterior densities around their maximum models. To this end, we fixed p = 20, 000 and varied n from 150 to 400; the data generating mechanism was exactly the same as in Section 3.1. The left column of Figure 3 displays the posterior probability of the true model under the peMoM, piMoM and g-prior models versus n for the three covariate designs in Section 3.1. The plot shows that the posterior probability of the true model increases with n for all three methods, with the peMoM and piMoM priors almost uniformly dominating the g-prior, implying a higher concentration of the posterior around the true model for the nonlocal priors.

Figure 3.

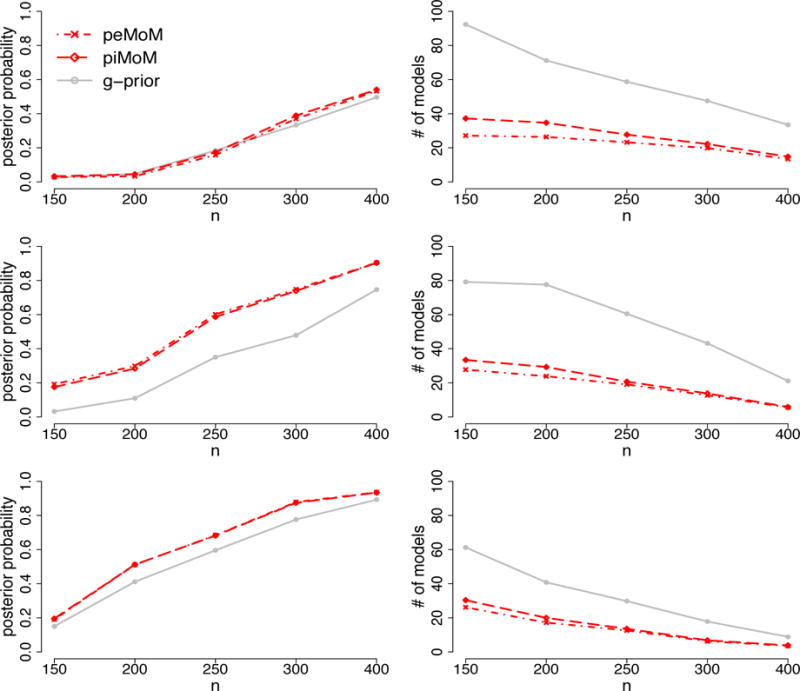
Averaged posterior true model probability and the number of models which attain the posterior odds ratio, with respect to the maximum a posteriori model, larger than 0.001 with the fixed p = 20000 and varying n. Top: case (1); middle: case (2); bottom: case (3).

This tendency is confirmed in the right panel of Figure 3, where we plot the number of models k which achieve a posterior odds ratio $\pi (\mathbf{k}|y)/\pi (\widehat{\mathbf{k}}|y)>0.001$, where $\widehat{\mathbf{k}}$ is the maximum a posteriori model. This plot clearly shows that the posterior distribution on the model space from the g-priors is more diffuse than those obtained using the nonlocal prior methods. These comparisons were based on fitting the hyperparameters g and τ at their oracle value, i.e., the value which maximized the posterior probability of the true model for a given value of n.

The magnitudes of the oracle hyperparameters under each model also present an interesting contrast between the local and nonlocal priors. We observed that the oracle value of g increased rapidly with p, whereas the oracle value of τ was much more stable. This phenomenon is illustrated in Table 1 that shows the oracle hyperparameter value averaged over 100 replicates for the three different covariate designs in Section 3.1. For this comparison, we fixed n = 400 and varied p between 1000 and 20, 000; five representative values are displayed. The oracle values for g are on a completely different scale from the oracle values τ, and they vary more with p. This table confirms the recommendations in George and Foster (2000) for setting g = p² based on minimax arguments. However, the finite sample behavior of the optimal choice of g is unclear, which means that the large variance of the optimal hyperparameter value is likely to hinder the selection of g in real applications. Finally, we note that such large values of g effectively convert the local g-priors into nonlocal priors by effectively collapsing the g-prior density to 0 at the origin.

Table 1.

Optimal hyperparameters for Bayesian model selection methods

		p = 1000	The number of predictors			p = 20000
			p = 2000	p = 5000	p = 10000
Case (1)	peMoM	2.24	2.72	2.88	3.32	3.60
	piMoM	2.16	2.59	2.70	3.04	3.26
	g-prior	7.83 × 108	2.87 × 109	3.05 × 109	9.66 × 109	1.70 × 1010
Case (2)	peMoM	1.97	2.29	2.34	2.75	3.00
	piMoM	1.97	2.20	2.32	2.66	2.86
	g-prior	8.56 × 109	2.55 × 1010	2.62 × 1010	6.58 × 1010	1.25 × 1011
Case (3)	peMoM	2.66	3.00	3.00	3.10	3.60
	piMoM	2.61	2.94	2.94	2.94	3.46
	g-prior	1.26 × 1012	8.84 × 1012	9.67 × 1012	6.81 × 1012	4.29 × 1013

4 Model selection consistency

The empirical performance of the peMoM and piMoM priors suggests that the hyperparameter τ should be increased slowly with p. While Johnson and Rossell (2012) were able to show strong selection consistency with a fixed value of τ, it is not clear whether their proof can be extended to p ≫ n cases. Motivated by the empirical findings of the last section, we next investigated the strong consistency properties of peMoM and piMoM priors when τ was allowed to grow at a logarithmic rate in p. We found that in such cases, both peMoM and piMoM priors achieve strong model selection consistency under standard regularity assumptions when p increases sub-exponentially with n, i.e., log p = O(n^α) for α ∈ (0, 1).

Henceforth, we use τ_n,p instead of τ to denote the hyperparameter in the peMoM and piMoM priors in (2) and (4) respectively. The normalizing constants for these priors is now denoted by C_n,p and $C_{n,p}^{\ast }$ respectively. Before providing our theoretical results, we first state a number of regularity conditions. Let ν_j(A) denote the j-th largest nonzero eigenvalue of an arbitrary matrix A, and let

$${\nu }_{\mathbf{k}\ast }=\underset{1\le j\le \mathit{min}(n,|\mathbf{k}|)}{\min }{\nu }_j(X_{\mathbf{k}}^{\mathrm{T}}{X}_{\mathbf{k}}/n),{\nu }_{\mathbf{k}}^{\ast }=\underset{1\le j\le \mathit{min}(n,|\mathbf{k}|)}{\max }{\nu }_j(X_{\mathbf{k}}^{\mathrm{T}}{X}_{\mathbf{k}}/n).$$ (8)

For sequences a_n and b_n, a_n ⪰ b_n indicates b_n = O(a_n), and a_n ≻ b_n indicates b_n = o(a_n). With this notation, we assume that the following regularity conditions apply.

Assumption 1

There exists α ∈ (0, 1) such that log p = O(n^α).

Assumption 2

log p ≺ τ_n,p ≺ n.

Assumption 3

|k| ≤ q_n, where $q_n\prec \frac{{\tau }_{n,p}}{\log p}$.

Assumption 4

$$\underset{\mathbf{k}:|\mathbf{k}|\le q_n}{\min }{\nu }_{\mathbf{k}\ast }\succ \frac{{\tau }_{n,p}}{n}.$$

Assumption 5

$C_1<{\nu }_{t\ast }\le {\nu }_{\mathbf{t}}^{\ast }<C_2$ for some positive constants C₁ and C₂.

Several comments regarding these conditions are worth making. Assumption 1 allows p to grow sub-exponentially with n. Our theoretical results continue to hold when p grows polynomially in n, i.e., at the rate O(n^γ) for some γ > 1. Assumption 2 reflects our empirical findings about the oracle τ ≡ τ_n,p in Section 3.1, which was observed to grow slowly with p. We need the bound on q_n in Assumption 3 to ensure that the least square estimator of a model is consistent when a model contains the true model. In the p ≤ n setting, Johnson and Rossell (2012) assumed that all eigenvalues of the Gram matrix $(X_{\mathrm{k}}^{\mathrm{T}}{X}_{\mathrm{k}})/n$ are bounded above and below by global constants for all k. However, this assumption is no longer viable when p ≫ n and we replace that by Assumption 4, where the minimum of the minimum eigenvalue of $(X_{\mathbf{k}}^{\mathrm{T}}{X}_{\mathbf{k}})/n$ over all submodels k with |k| ≤ q_n is allowed to decrease with increasing n and p. Assumption 4 is called the sparse Riesz condition and is also used in Chen and Chen (2008) and Kim et al. (2012). Narisetty and He (2014) showed that Assumption 4 holds with overwhelmingly large probability when the rows of the design matrix are independent with an isotropic sub-Gaussian distribution. Even though the assumption of sub-Gaussian tails on the covariates is difficult to verify, the results in Narisetty and He (2014) show that Assumption 4 can be satisfied for some sequence of design matrices.

We now state a Theorem that demonstrates that model selection procedures based on the pe-MoM and piMoM nonlocal prior densities achieve strong consistency under the proposed regularity conditions. A proof of the Theorem is provided in the Supplemental Materials.

Theorem 1

Suppose σ² is known and that Assumptions 1 – 5 hold. Let π(t | y) denote the posterior probability of the true model obtained under a peMoM prior (2). Also, assume a uniform prior on all models of size less than or equal to q_n, i.e., π(k) ∝ I(|k| ≤ q_n). Then, π(t | y) converges to one in probability as n goes to ∞.

Corollary 2

Assume the conditions of the preceding Theorem apply. Let π(t | y) denote the posterior probability of the true model obtained under a piMoM prior density (4). Then, π(t | y) converges to one in probability as n goes to ∞.

We note that these results apply also if a beta-Bernoulli prior is imposed on the model space as in Scott and Berger (2010), because the effect of that prior is asymptotically negligible when |k| ≤ q_n ≺ n.

In most applications, σ² is unknown, and it is thus necessary to specify a prior density on it. By imposing a proper inverse gamma prior density on σ², we can obtain the strong model consistency result stated in the Theorem below. The proof is again deferred to the Supplemental Materials.

Theorem 3

Suppose σ² is unknown and a proper inverse gamma density with parameters (a₀, b₀) is assumed for σ². Also, let π(t | y) denote the posterior probability of the true model evaluated using peMoM priors. Then if Assumptions 1 – 5 are satisfied, π(t | y) converges to one in probability as n goes to ∞.

Corollary 4

Suppose the conditions of the preceding Theorem apply, but that π(t | y) now denotes the posterior probability of the true model obtained under a piMoM prior density. Then π(t | y) converges to one in probability as n goes to ∞.

5 Connections between nonlocal priors and reciprocal lasso

In this section, we highlight the connection between the rlasso of Song and Liang (2015) and Bayesian variable selection procedures based on our nonlocal priors. We begin by noting that the objective function g(β_k; k) of rlasso on a model k can be expressed as follows:

$$g({\beta }_{\mathbf{k}};\mathbf{k})=\parallel y-X_{\mathbf{k}}{\beta }_{\mathbf{k}}{\parallel }_2^2+{\displaystyle \sum _{j=1}^{|\mathbf{k}|}{\tau }_{n,p}/|{\beta }_{\mathbf{k},j}|}.$$ (9)

The optimal model is selected by minimizing this objective function with respect to β_k and k. It is clear that the penalty function ${\displaystyle {\sum }_{j=1}^{\left|\mathbf{k}\right|}{\tau }_{n,p}/\left|{\beta }_{\mathbf{k},j}\right|}$ in (9) is similar to the negative log-density of piMoM nonlocal priors as proposed in Johnson and Rossell (2012, pp 659) and Johnson and Rossell (2010, pp 149). The main difference between the nonlocal prior version of rlasso and the piMoM-type prior densities proposed in the previous section is the power of β in the exponential kernels. For the rlasso penalty this power is 1, while for piMoM-type prior densities it is 2. The implications of this difference are apparent from the following proposition.

Proposition 5

For a given model k, suppose that ${\stackrel{\sim }{\beta }}_{\mathbf{k}}^{\ast }$ is the minimizer of the objective function (9), and again let ${\widehat{\beta }}_{\mathbf{k}}$ denote the least square estimator of β under model k. Assume that τ_n,p ≺ n, and there exist strictly positive contants C_L and C_U such that $C_L<{\nu }_{\mathbf{k}\ast }\le {\nu }_{\mathbf{k}}^{\ast }<C_U$. Then, for any ${\epsilon }_n^{\ast }\succ {({\tau }_{n,p}/n)}^{1/3}$,

$$P\left[{\stackrel{\sim }{\beta }}_{\mathbf{k}}^{\ast }\notin R\left({\widehat{\beta }}_{\mathbf{k}};{\epsilon }_n^{\ast }\right)\right]\to 0,$$

where R(u; ε) = {x ∈ ℝ^|k| : |x_j − u_j| ≤ ε, j = 1,…, |k|}.

The proposition shows that under standard conditions on the eigenvalues of the Gram matrix $X_{\mathbf{k}}^{\mathrm{T}}{X}_{\mathbf{k}}/n$, the estimator derived from (9) is asymptotically within (τ_n,p/n)^1/3 distance of the least squares estimator ${\widehat{\beta }}_{\mathbf{k}}$_. On the other hand, results cited in the previous section show that maximum a posteriori estimators obtained from the piMoM-type prior densities reside at an asymptotic distance of (τ_n,p/n)^1/4 from the least squares estimator. Variable selection procedures based on both forms of piMoM priors thus achieve adaptive penalties on the regression coefficients in the sense described in Song and Liang (2015).

Although rlasso is proposed as a penalized likelihood approach, the computational procedure to optimize its objective function is quite different from the other penalized likelihood methods. The resulting computational complexity of this optimization procedure, which contains a discontinuous penalty function, is NP-hard. This suggests that the formulation of this nonlocal penalty in a penalized likelihood framework is unlikely to provide significant computational advantages over related Bayesian model selection procedures, even though the inferential advantages of the Bayesian framework are lost.

6 Asymptotic behavior of marginal likelihoods based on non-local priors

From Lemma 1 in the Supplemental Materials, it follows that the asymptotic log-marginal likelihood of a model k based on a peMoM or piMoM prior density can be expressed as

$$\begin{array}{l}\log \pi (\mathbf{k}|y)=l({\widehat{\beta }}_{\mathbf{k}})+\log Q_{\mathbf{k}}-|\mathbf{k}|\log C_{n,p}\\ \approx l({\widehat{\beta }}_{\mathbf{k}})-{\displaystyle \sum _{j=1}^{|\mathbf{k}|}{p}_{{\tau }_{n,p}}({\widehat{\beta }}_{\mathbf{k},j})}+C,\end{array}$$

for some constant C, ${\widehat{\beta }}_{\mathbf{k}}$ is the maximum likelihood estimator under the model k, i.e. ${\widehat{\beta }}_{\mathbf{k}}={(X_{\mathbf{k}}^T{X}_{\mathbf{k}})}^{-1}{X}_{\mathbf{k}}^{T}y$, and

$$p_{{\tau }_{n,p}}({\widehat{\beta }}_{\mathbf{k},j})\approx \{\begin{array}{ll}{(n{\tau }_{n,p}{u}_{\mathbf{k}})}^{1/2},\hfill & \text{if}|{\widehat{\beta }}_{\mathbf{k},j}|<c{\left(\frac{n{u}_{\mathbf{k}}}{{\tau }_{n,p}}\right)}^{-1/4}\hfill \\ {\tau }_{n,p}/{\widehat{\beta }}_{\mathbf{k},j}^2,\hfill & \text{if}|{\widehat{\beta }}_{\mathbf{k},j}|\ge c{\left(\frac{n{u}_{\mathbf{k}}}{{\tau }_{n,p}}\right)}^{-1/4},\hfill \end{array}$$ (10)

for some constant c and some arbitrary sequence u_k with ν_k∗ ≤ u_k ≤ ν_k^∗. We note that the strength of the correlation between the variables in the model k affects the behavior of u_k, and (nu_k/τ_n,p)⁻¹/⁴ converges to zero as n tends to infinity due to Assumption 4 described in Section 4.

On the other hand, the penalty term in the other Bayesian model selection approaches is quite different from that of the nonlocal priors as in (10). The marginal likelihood based on the g-prior when σ² is known can be expressed as

$$l({\widehat{\beta }}_{\mathbf{k}})-\left|\mathbf{k}\right|\log (1+g)/2.$$

Narisetty and He(2014) demonstrated that BASAD achieves the strong model selection consistency. This consistency follows from that the fact that the BASAD “penalty” is asymptotically equivalent to

$$l({\widehat{\beta }}_{\mathbf{k}})-c\left|\mathbf{k}\right|\log (p),$$ (11)

where c is some constant. Yang et al. (2016) and Castillo et al. (2012) also considered a similar penalty term on the model space, which implies that the posterior probability for their procedures can be expressed in the same form as (11). When g = p^2c, the marginal likelihood based on a g-prior is asymptotically equivalent to (11).

The asymptotic term of the marginal likelihoods is quite different from that of the nonlocal priors, since the penalty terms in the other Bayesian approaches only focus on the model size without considering the different weights on variables in the model. The marginal likelihoods based on nonlocal priors, however, impose different penalties on each predictor in the given model. When the MLE of the regression coefficient in the model is asymptotically close to zero $(|{\widehat{\beta }}_{\mathbf{k},j}|<c{(n{u}_{\mathbf{k}}{/}_{n,p})}^{-1/4})$, the model that contains the corresponding variable would be strongly penalized by (nτ_n,pu_k)^1/2. In contrast, when the MLE is asymptotically significant $(|{\widehat{\beta }}_{\mathbf{k},j}|\ge c{(n{u}_{\mathbf{k}}{/}_{n,p})}^{-1/4})$, the penalty attains a different weight based on the MLE $(p_{{\tau }_{n,p}}({\widehat{\beta }}_{\mathbf{k},j})\approx {\tau }_{n,p}/{\widehat{\beta }}_{\mathbf{k},j}^2)$.

This analysis highlights the fact that the nonlocal priors are able to adapt their penalty for the inclusion of covariates based on the observed data, whereas the local priors must instead rely on a prior penalty on non-sparse models.

7 Computational strategy

In p ≫ n settings, full posterior sampling using existing Markov chain Monte Carlo (MCMC) algorithms is highly inefficient and often not feasible from a practical perspective. To overcome this problem, we propose a scalable stochastic search algorithm aimed at rapidly identifying regions of high posterior probability and finding the maximum a posteriori (MAP) model. Our main innovation is to develop a stochastic search algorithm combining isis-like screening techniques (Fan and Lv, 2008) and temperature control that is commonly used in global optimization algorithms such as simulated annealing (Kirkpatrick and Vecchi, 1983).

To describe our proposed algorithm, consider the MAP model $\widehat{\mathbf{k}}$ that can be expressed as

$$\widehat{\mathbf{k}}=\underset{\mathbf{k}\in \mathrm{\Gamma }\ast }{\arg \max }\{\pi (\mathbf{k}|y)\},$$ (12)

where Γ^* is the set of all models assigned non-zero prior probability.

7.1 Shotgun stochastic search algorithm

Hans et al. (2007) proposed the shotgun stochastic search (SSS) algorithm in an attempt to efficiently navigate through very large model spaces and identify global maxima. Letting nbd(k) = {Γ⁺, Γ⁻, Γ⁰}, where Γ⁺ = {k∪{j}: j ∈ k^c}, Γ⁻ = {k\{j} : j ∈ k}, and Γ⁰ = [k\{j}]∪{l} : l ∈ k^c, j ∈ k}, the SSS procedure is described in Algorithm 1.

Algorithm 1.

Shotgun Stochastic Search (SSS)

Choose an initial model k(1)

For i = 1 to i = N – 1

Compute π(k | y) for all k ∈ nbd(k(i))

Sample k+, k−, and k0, from Γ+, Γ−, and Γ0, with probabilities proportional to π(k | y)

Sample k(i+1) from {k+, k−, k0}, with probability proportional to {π(k+ | y), π(k− | y), π(k0 | y)}

The MAP model can be identified by the model that achieves the largest (unnormalized) posterior probability among those models searched by SSS.

7.2 Simplified shotgun stochastic search algorithm with screening (S5)

SSS is effective in exploring regions of high posterior model probability, but its computational cost is still expensive because it requires the evaluation of marginal probabilities for models in Γ⁺, Γ⁻, and Γ⁰ at each iteration. The largest computational burden occurs for the evaluation of marginal likelihood for models in Γ⁰, since |Γ⁰| = |k|(p − |k|). To improve the computational efficiency of SSS, we propose a modified version which only examines models in Γ⁺ and Γ⁻, which have cardinality p − |k| and |k|, respectively. However, by ignoring Γ⁰ in the sampling updates we make the algorithm less likely to explore “interesting” regions of high posterior model probability, and therefore more likely to get stuck in local maxima. To counter this problem, we introduce a “temperature parameter” analogous to simulated annealing which allows our algorithm to explore a broader spectrum of models.

Even though ignoring models in Γ⁰ reduces the computational burden of the SSS algorithm, the calculation of p posterior model probabilities in every iteration is still computationally prohibitive when p is very large. To further reduce the computational burden, we borrow ideas from the Iterative Sure Independence Screening (isis; Fan and Lv (2008)) and consider only those variables which have a large correlation with the residuals of the current model. More precisely, we examine the products $\left|r_{\mathbf{k}}^T{X}_j\right|$, where r_k is the residual of the model k, for j = 1, …, p, after every iteration of the modified shotgun stochastic search algorithm, and then restrict attention to variables for which $\left\{\right|r_{\mathbf{k}}^T{X}_j|:j=1,\dots ,p\}$ is large (we assume that the columns of X have been standardized). This yields a scalable algorithm even when the number of variables p is large.

With these ingredients, we propose a new stochastic model search algorithm called Simplified Shotgun Stochastic Search with Screening (S5), which is described in Algorithm 2.

In S5, S_k is the union of variables in k and the top M_n variables, obtained by screening using the residuals from the model k. The screened neighborhood of the model k can be defined as ${\text{nbd}}_{\mathit{scr}}(\mathbf{k})=\{{\mathrm{\Gamma }}_{\mathit{scr}}^{+},{\mathrm{\Gamma }}^{-}\}$, where ${\mathrm{\Gamma }}_{\mathit{scr}}^{+}=\{\mathbf{k}\cup \{j\}:j\in {\mathbf{k}}^c\cap {\mathbf{S}}_{\mathbf{k}}\}$.

Algorithm 2.

Simplified Shotgun Stochastic Search with Screening (S5)

Set a temperature schedule t1 > t2 > …> tL > 0

Choose an initial model k(1,1) and a set of variables after screening Sk(1,1) based on k(1,1)

For l = 1 in l = L

For i in 1, …, J − 1

Compute all π(k | y) for all k ∈ nbdscr(k(i,l))

Sample k+ and k−, from ${\mathrm{\Gamma }}_{\mathit{scr}}^{+}$ and Γ−, with probabilities proportional to $\pi {(\mathbf{k}|y)}^{1/t_l}$

Sample k(i+1,l) from {k+, k−}, with probability proportional to $\{\pi {({\mathbf{k}}^{+}|y)}^{1/t_l}$, $\pi {({\mathbf{k}}^{-}|y)}^{1/t_l}\}$

Update the set of considered variables ${\mathbf{S}}_{{\mathbf{k}}^{(i+1,l)}}$ to be the union of variables in k(i+1,l) and the top Mn variables according to $\{|r_{{\mathbf{k}}^{(i+1,l)}}^T{X}_j|:j=1,\dots ,p\}$

Even though this algorithm is designed to identify the MAP model, it also provides an approximation to the posterior model probability of each model. The uncertainty of the model space can be measured by approximating the normalizing constant from the (unnormalized) posterior probabilities of the models explored by the algorithm.

Denoting the computational complexity of the evaluation of the unnormalized posterior model probability of the largest model among searched models by E_n, the computational complexity of the SSS algorithm can be expressed as the product of the number of explored models by the algorithm and E_n, which is $[O\{N_p\}+O\{N_{q_n}\}+O\{N(p-q_n)q_n\}]\times E_n$, where q_n is the maximum size of model among searched models and q_n < n ≪ p.

On the other hand, the S5 only considers M_n variables after the screening step in each iteration, which dramatically reduces the number of models to be considered in constructing the neighborhood, O{JL(M_n − q_n)} + O(JLM_n). Therefore, the resulting computational complexity is

$$[O\{JL(M_n-q_n)\}+O(JL{M}_n)]\times E_n+O(\mathit{JLnp}),$$

where q_n < M_n. When the computational complexity for screening steps, O(JLnp), is dominated by the other terms, the computational complexity is almost independent of p. As a result, the proposed algorithm is scalable in the sense that the resulting computational complexity is typically robust to the size of p.

7.3 Performance comparisons between S5 and SSS

We examined the computational performance of S5 to SSS in identifying the MAP model under a piMOM prior with τ_n,p = log n log p and r = 1. We generated data according to Case (1) in Section 3, with a fixed sample size (n = 200), and a varying number of covariates p. We set M_n = 20, L = 20, and J = 20 for S5. To match the total number of iterations between S5 and SSS, we set N = 400 for SSS. All computations were implemented in R.

Figure 4 shows the average computation time and the number of models searched before hitting the MAP model for the first time for the S5 and SSS algorithms. All averages were based on 100 simulated datasets, and both algorithms obtained the same MAP model for all data sets. Panel (a) shows that the computation time of SSS increases roughly at a p² rate, but that the computation time for S5 was nearly independent of the number of covariates p (about 4 seconds). For example when p = 2, 000, SSS first found the MAP model in an average of 1,360 seconds (about 23 minutes), whereas S5 hit the MAP model after about only 4 seconds. Interestingly, panel (b) of Figure 4 also illustrates that the S5 algorithms explored only 181 models on average to hit the MAP model, whereas SSS typically visited slightly more than 38,000 models. Thus, not only is S5 much faster than SSS in identifying the MAP model, but it also visited far fewer models before visiting the MAP model.

Figure 4.

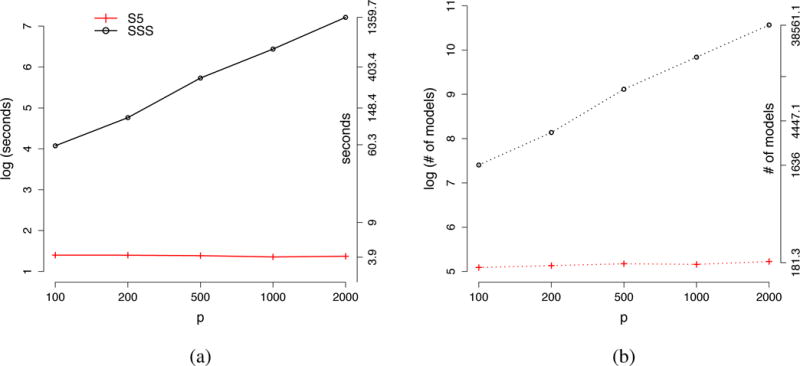
(a) the average computation time to first hit the MAP model; (b) the average number of models searched before hitting the MAP model. The left y-axis is in a logarithmic scale and the right y-axis is in the raw scale.

8 Real data analysis

8.1 Analysis of polymerase chain reaction (PCR) data

Lan et al. (2006) studied coordinated regulation of gene expression levels on 31 female and 29 male mice (n = 60). A number of psychological phenotypes, including numbers of stearoyl-CoA desaturase 1 (SCD1), glycerol-3-phosphate acyltransferase (GPAT) and phos- phoenopyruvate carboxykinase (PEPCK), were measured by quantitative real-time RT-PCR, along with 22,575 gene expression values. The resulting data set is publicly available at http://www.ncbi.nlm.nih.gov/geo (accession number GSE3330).

Zhang et al. (2009) used penalized orthogonal components regression to predict the three phenotypes mentioned above based on the high-dimensional gene expression data. Bondell and Reich (2012) also used the same data set to examine their model selection procedure based on penalizing regression coefficients within a (marginal or joint) credible interval obtained from a ridge-type prior. For brevity, we restrict attention here to SCD1 as the response variable.

Since the ground truth regarding the true significant variables is not known for this data, we compared our approach with a host of competitors on predictive accuracy and parsimony of the selected model.

Prior to analyses, we standardized the covariates and randomly split the data set into 5 test samples and 55 training samples to evaluate the out-of-sample mean square prediction error (MSPE)

$$\text{MSPE}={\displaystyle \sum _{i\in T_{\mathit{test}}}{(y_i-X_i^T{\widehat{\beta }}_{\widehat{\mathbf{k}}}^{tr})}^2/|T_{\mathit{test}}|},$$

where T_test is the index set of the test samples and ${\widehat{\beta }}_{\widehat{\mathbf{k}}}^{tr}$ is the least square estimator under the estimated model $\widehat{\mathbf{k}}$ based on the training samples. To avoid sensitivity to a particular split, we considered 100 replications of the training and test sample generation. To measure the stability of model selection, we considered the number of variables that were (i) selected at least 95 times, and (ii) at least once, out of the 100 replicates.

Due to the high-computational burden of the penalized credible interval (Bondell and Reich, 2012) approach, we followed the pre-processing step suggested in their article to marginally screen variables to reduce to 2000 variables (1999 genes and gender). For all the other approaches, all 22,575 genes were used. For the nonlocal priors, we considered both the MAP estimator and the least squares (LS) estimator from the MAP model. For the g-prior, we set g = p² as recommended in George and Foster (2000). For the penalized likelihood procedures, we used ten-fold cross validation to choose the tuning parameter.

To choose the hyperparameter τ_n,p for the nonlocal priors, we used a procedure proposed by Nikooienejad et al. (2016). That procedure sets the hyperparameter so that the L₁ distance between the posterior distribution on the regression parameters under the null distribution (i.e., β = 0) and the nonlocal prior distributions on these parameters is constrained to be less than a specified value (e.g., p^−1/2). The average value of the hyperparameter values chosen by this procedure were τ_n,p = 1.12 and τ_n,p = 1.16 for piMoM and peMoM priors, respectively.

To make the comparison between the nonlocal priors and the g-prior more transparent, we used the same beta-binomial prior on the model space in both models, rather than the uniform prior on the model space described previously. The form of the beta-binomial prior was given by

$$\pi (\mathbf{k})\propto {\rho }^{\left|\mathbf{k}\right|}{(1-\rho )}^{p-\left|\mathbf{k}\right|}I(|\mathbf{k}|\le q_n),$$ (13)

with a uniform prior on ρ and q_n = 40. We note that this prior does not strongly induce sparsity as does, for example, the prior obtained by imposing a Beta(1, p^u), u > 1 prior on ρ, as suggested in Castillo et al. (2015).

Table 2 summarizes the results from the analysis of the gene expression data set. On average, the nonlocal priors simultaneously produced the lowest MSPE and the most parsimonious model. The other model selection methods selected a wide array of different variables for different splits of the data set. In particular, lasso and the penalized credible region approach selected more than 180 different variables from 100 repeated splits, while the average size of the selected model was less than 20 and the number of frequently selected variables was only zero or one, indicating a potentially large number of false positives picked up by these methods.

Table 2.

Analysis of the PCR data. Marginal and Joint refer to the variable selection procedures (Bondell and Reich, 2012) based on Bayesian marginal credible set and Bayesian joint credible set, respectively. MS is the average size of the selected model. FS is the number of frequently selected variables, i.e., that were selected at least 95 times in 100 repetitions. TS refers to the total number of variables selected at least once from 100 repetitions. Standard errors are provided in parenthesis.

Method	MSPE	MS	FS	TS
piMoM(MAP)	0.283 (0.17)	1.00 (0.00)	1	1
piMoM(LS)	0.282 (0.17)	1.00 (0.00)	1	1
peMoM(MAP)	0.291 (0.18)	1.02 (0.14)	1	2
peMoM(LS)	0.287 (0.17)	1.02 (0.14)	1	2
g-prior	0.368 (0.20)	4.07 (0.56)	1	133
lasso	0.542 (0.39)	17.97 (8.62)	1	211
scad	0.308 (0.23)	12.66 (7.62)	2	163
mcp	0.308 (0.21)	2.20 (0.94)	0	29
Marginal(p = 2000)	0.456 (0.40)	17.47 (11.16)	0	273
Joint(p = 2000)	0.440 (0.40)	16.42 (11.06)	1	185

8.2 A simulation study based on the Boston housing data

We next examined the Boston housing data set that contains the median value of owner-occupied homes in the Boston area, together with several variables that might be associated with their median value. There were n = 506 median values in the data set, and we considered 10 continuous variables as the predictor variables: crim, indus, nox, rm, age, dis, tax, ptratio, b, and lstat. This data set has been used to validate a variety of approaches; some recent examples relevant to variable selection include Radchenko et al. (2011), Yuan and Lin (2005), and Rockova and George (2014).

To examine the model selection performance in high-dimensional settings, we added 1,000 noise variables that were generated independently from a standard Gaussian distribution (p = 1,010). The same competitors from the previous subsection were used with the aforementioned choice of hyperparameters. For nonlocal priors, the hyperparameter was chosen by the aforementioned procedure (Nikooienejad et al., 2016); the average of the chosen hyperparameter values were τ_n,p = 2.01 and τ_n,p = 0.47 for piMoM and peMoM priors, respectively. Prior to analyses, we standardized the covariates and considered a simulation test size of 100 samples.

The results of are analysis are summarized in Table 3. The conclusions are similar to those reported in Section 8.1; the nonlocal priors consistently choose more parsimonious models and had better predictive performance. The model selection procedure resulting from the nonlocal prior selects almost the same variables across the 100 repetitions. The average number of the original variables selected more than 95 times over 100 repetitions is 5, which is close to the average model size. It is also reliable in the sense that the average number of the original variables that are selected at least once across the repetitions is only 6. This means that model selection based on the nonlocal prior selects the same model in most data splits. On the other hand, penalized likelihood methods such as lasso and scad tend to select a large number of noise variables.

Table 3.

The Boston Housing data set: MS-O and MS-N refer to the average number of selected original variables and selected noise variables, respectively. FS-O is the number of original variables that are frequently selected at least 95 times out of 100 repetitions. TS-O refers to the number of original variables selected at least once from 100 repetitions.

Methods	MSPE	MS-O	MS-N	FS-O	TS-O
piMoM(MAP)	24.281 (9.01)	5.05 (0.22)	0.01 (0.10)	5	6
piMoM(LS)	24.265 (9.04)	5.05 (0.22)	0.01 (0.10)	5	6
peMoM(MAP)	24.156 (9.02)	5.02 (0.14)	0.00 (0.00)	5	6
peMoM(LS)	24.165 (9.00)	5.02 (0.14)	0.00 (0.00)	5	6
g-prior	26.314 (9.87)	3.10 (0.44)	0.00 (0.00)	3	5
lasso	30.243 (11.82)	5.07 (0.87)	7.77 (11.16)	4	8
scad	33.993 (10.66)	5.39 (0.57)	31.60 (28.28)	5	7
mcp	26.191 (9.87)	4.66 (0.74)	0.54 (1.04)	3	6
Marginal	26.612 (10.16)	3.74 (0.88)	0.41 (0.72)	3	7
Joint	26.385 (10.25)	3.77 (0.94)	0.02 (0.20)	3	6

9 Conclusion

This article describes theoretical properties of peMoM and piMoM priors for variable selection in ultrahigh-dimensional linear model settings. In terms of identifying a “true” model, selection procedures based on peMoM priors are asymptotically equivalent to piMoM priors in Johnson and Rossell (2012) because they share the same kernel, exp{−τ_n,p/β²}. We demonstrated that model selection procedures based on peMoM priors and piMoM priors achieve strong model selection consistency in p ≫ n settings.

In Section 3.1, precision-recall curves were used to show that the model selection procedure based on a g-prior can achieve nearly the same performance in identifying the MAP model as nonlocal priors when an optimal value for the hyperparameter g is chosen. However, as shown in Section 3.2, the value of the hyperparameter that maximizes the posterior probability of the true model is very large and has high variability, which may limit the practical application of this method. To overcome this problem, one can consider mixtures of g-prior as in Liang et al. (2008), but the asymptotic behavior of Bayes factor and model selection consistency in ultrahigh-dimensional settings have not been examined for hyper-g priors, and they are difficult to implement computationally.

In Section 7, we proposed an efficient and scalable model selection algorithm called S5. By incorporating the SSS with a screening idea and a temperature control, S5 was able to accelerate the computation speed without losing the capacity to explore the interesting region in the model space. Under some simulation settings, it outperformed the SSS in a sense that not only did S5 search the MAP model much faster than the SSS, but it also found exactly the same MAP model that was searched by the SSS.

Because the explicit form of the marginal likelihood of the nonlocal priors is not available, we used the Laplace approximation throughout the paper, and Barber et al. (2016) studied the accuracy of the approximation in Bayesian high-dimensional variable selection, especially when the dimension of the approximation (which is q_n) and n are both increasing. However, their results do not apply to the case of the nonlocal priors, since the nonlocal priors violate their regularity condition (nonzero density at the origin). While empirical results in this paper and Johnson and Rossell (2012) suggest that the use of the Laplace approximation is reasonable, in future work it is still worth paying attention to the approximation error of the Laplace approximation to the marginal likelihood of the nonlocal priors.

The close connection between our methods and the reduced rlasso procedures provides a useful contrast between Bayesian and penalized likelihood methods for variable selection procedures. According to the evaluation criteria proposed in Section 5, the two classes of methods appear to perform quite similarly. A potential advantage of the reduced rlasso procedure, and to the lesser extent the rlasso procedure, is reduced computation cost. This advantage accrues primarily because the reduced rlasso can be computed from the least squares estimate of each model’s regression parameter, whereas the Bayesian procedures require numerical optimization to obtain the maximum a posteriori estimate used in the evaluation of the Laplace approximation to the marginal density of each model visited. However, the procedures used to search the model space, given the value of a marginal density or objective function, are approximately equally complex for both classes of procedures. There are also potential advantages of the Bayesian methods. For example, it is possible to approximate the normalizing constant of the posterior model probability from the models visited by S5 algorithm, and to use this normalizing constant to obtain an approximation to the posterior probability assigned to each model. In so doing, the Bayesian procedures provide a natural estimate of uncertainty associated with model selection. These posterior model probabilities can also be used in Bayesian modeling averaging procedures, which have been demonstrated to improve prediction accuracy (e.g., Raftery et al. (1997)) over prediction procedures based on maximum a posteriori estimates. Finally, the availability of prior densities may prove useful in setting model hyperparameters (i.e., τ_n,p) in actual applications, where scientific knowledge is typically available to guide the definition of the magnitude of substantively important regression parameters.

We also developed an R package BayesS5 that provides all computational functions used in this paper, including a support of parallel computing environments. It is available on the author’s website and on CRAN.