Cardiac-driven Pulsatile Motion of Intracranial Cerebrospinal Fluid Visualized Based on a Correlation Mapping Technique

Abstract

Purpose:

A correlation mapping technique delineating delay time and maximum correlation for characterizing pulsatile cerebrospinal fluid (CSF) propagation was proposed. After proofing its technical concept, this technique was applied to healthy volunteers and idiopathic normal pressure hydrocephalus (iNPH) patients.

Methods:

A time-resolved three dimensional-phase contrast (3D-PC) sampled the cardiac-driven CSF velocity at 32 temporal points per cardiac period at each spatial location using retrospective cardiac gating. The proposed technique visualized distributions of propagation delay and correlation coefficient of the PC-based CSF velocity waveform with reference to a waveform at a particular point in the CSF space. The delay time was obtained as the amount of time-shift, giving the maximum correlation for the velocity waveform at an arbitrary location with that at the reference location. The validity and accuracy of the technique were confirmed in a flow phantom equipped with a cardiovascular pump. The technique was then applied to evaluate the intracranial CSF motions in young, healthy (N = 13), and elderly, healthy (N = 13) volunteers and iNPH patients (N = 13).

Results:

The phantom study demonstrated that root mean square error of the delay time was 2.27%, which was less than the temporal resolution of PC measurement used in this study (3.13% of a cardiac cycle). The human studies showed a significant difference (P < 0.01) in the mean correlation coefficient between the young, healthy group and the other two groups. A significant difference (P < 0.05) was also recognized in standard deviation of the correlation coefficients in intracranial CSF space among all groups. The result suggests that the CSF space compliance of iNPH patients was lower than that of healthy volunteers.

Conclusion:

The correlation mapping technique allowed us to visualize pulsatile CSF velocity wave propagations as still images. The technique may help to classify diseases related to CSF dynamics, such as iNPH.

Introduction

Understanding cerebrospinal fluid (CSF) dynamics is important in the fields of neurosurgery and physiology. Yamada et al. have reported that CSF movement can be visualized by a spin-labeling technique called Time-spatial Labeling Inversion Pulse (Time-SLIP).¹ On the other hand, in recent years, visualization of CSF dynamics in intracranial or spinal space by four-dimensional velocity mapping (4D-VM) based on a phase contrast (PC) MR technique, which provides the quantitative spatiotemporal velocity distribution of CSF motion during a cardiac cycle as vector cine images, has been conducted.^2–4 In addition to the quantitative property, 4D-VM is different from Time-SLIP in that the technique visualizes propagation of pulsatile CSF motion, for example, in spaces separated by a thin membrane-like structure, such as a Liliequist membrane, and an arachnoid cyst wall, through which no spin travels.⁵ Thus, 4D-VM may be useful to visualize the CSF dynamics in a manner different from Time-SLIP.

However, the cine images of velocity vectors or streamlines obtained by 4D-VM are sometimes too complex to be used for understanding CSF dynamics and diagnosing brain diseases, such as hydrocephalus. Therefore, a quantitative analysis technique, called correlation mapping, which presents propagation properties of CSF motion as a still image, was proposed.^6,7 This technique consists of two parts: delay time mapping and maximum correlation mapping. The former visualizes the correlation time or “delay” of the CSF velocity wave at each spatial point measured from a reference point within a cardiac cycle, while the latter tells us the similarity of the CSF velocity wave shape. CSF is an uncompressed liquid, so the presence of the propagation delay and the wave shape change indicate the presence of compliance in the CSF space. Although a similar technique for analyzing the blood flow of the middle cerebral artery in the brain has been reported in the past based on contrast-enhanced X-ray CT images,⁸ to the best of our knowledge, the present study is the first to observe the CSF velocity delay and correlation taken by non-contrast-enhanced MR images.

One of the most significant diseases caused by a disturbance of the CSF dynamics is idiopathic normal pressure hydrocephalus (iNPH). Because iNPH tends to be found in elderly individuals, investigation of CSF dynamics in the elderly is important to detect and classify the disease. Czosnyka et al. have suggested that the brain becomes more rigid with aging,⁹ meaning that tissue compliance decreases. Bech et al. speculate that brain compliance also decreases with a lesion, such as a small brain infarction accompanied by cerebral arteriosclerosis, in iNPH patients.¹⁰ A clear correlation exists between iNPH and low brain compliance. If the correlation mapping technique visualizes the CSF space compliance distribution indirectly, it is expected to discriminate between the brain tissue status in healthy, elderly individuals and iNPH patients. Thus, in the present study, we applied the correlation mapping technique to three different groups—young, healthy; elderly, healthy; and iNPH patients—to evaluate the feasibility of the technique for classifying the different environments of intracranial CSF.

Methods

Correlation mapping

The correlation mapping technique assumes that CSF motion is driven by pressure propagation from cardiac- or respiratory-driven pulsation of blood vessels and/or brain parenchyma and that CSF itself can be the media of such pressure propagation. Since the vascular bed and brain parenchyma are not rigid but elastic, there should be a delay and a spatiotemporal change in the CSF velocity. In this study, we focused on the cardiac-driven pulsation during a cardiac cycle.

The algorithm of the technique was based on calculating the delay time of the CSF motion propagating from the CSF or blood in a certain reference region. First, a PC velocity measurement was made to obtain the temporal change of CSF or blood flow along three spatial dimensions—x (Right-Left [RL]), y (Anterior-Posterior [AP]), and z (Inferior-Superior [IS])—in a right-handed coordinate system. Second, the time course of the velocity (hereafter “velocity waveform”) of CSF or blood motion at a particular spatial point or region was regarded as a reference. A velocity waveform at an arbitrary point was assumed to be similar to but delayed and modified from that at the reference point, as pressure gradient transmits and/or some amount of CSF travels with time. Third, the delay time was calculated as the amount of time-shift of the waveform to have the highest correlation coefficient with the reference waveform, as illustrated in Fig. 1. The correlation coefficient was calculated with the following equation, which is similar to but different from that used in the pulsatility-based segmentation (PUBS)¹¹.

$$\begin{array}{l}{P}_d=\frac{\sum _{k=1}^N(V_{R_k}-{\overline{V}}_R)(V_{A_{k-d}}-{\overline{V}}_A)}{\sqrt{\sum _{k=1}^N(V_{R_k}-{\overline{V}}_R{)}^2{(V_{A_{k-d}}-{\overline{V}}_A)}^2}}\\ d=(0,1,2,\cdots ,N-1)\end{array}$$ (1)

where P_d is the correlation coefficient with the number of delay time points d within a cardiac period, V_Rk is the velocity of the reference waveform, V̅_R is the average of V_Rk, V_Ak−d is the velocity at the arbitrary spatial location and shifted for d points with respect to the original, V̅_A is the average of V_Ak−d, k is the time index, and N is the total number of data points, and thus the number of images, within a cardiac period. The most important value derived from Eq. (1) is the delay time, d_max, which gives the maximum absolute value of P_d, because this states the delay in the propagation of CSF. The delay time was normalized by a cardiac period for comparison between the subjects. The maximum correlation yielded by d_max, denoted as P_dmax, is also important, since this represents the strength of the similarity between the reference and the target waveforms. Thus d_max and P_dmax were obtained at all voxels in the CSF space and then visualized as color-coded delay time and maximum correlation maps. Since the pulsatile motion induced by cardiac pulsation was periodic, the delay time maps were presented in a cyclic color-coded set. The possible delay time range was from −50% to 50%, because the motion at the reference region might be propagated from other regions.

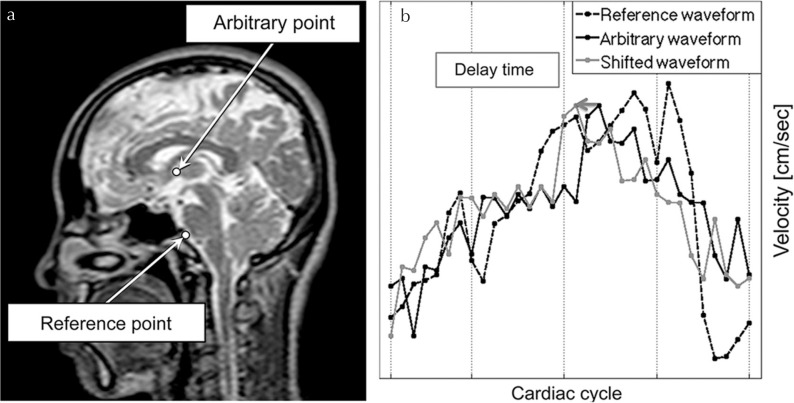
Fig. 1.

Schematic diagram of the delay time calculation. An example of the reference point and an arbitrary point are shown in (a). The velocity waveforms at those points are shown in (b). The waveform at an arbitrary point (black solid line) was shifted (gray solid line) to create the maximum value of correlation coefficient with that of the reference (black dashed line). The amount of the shift indicated by an arrow in (b) was defined as the “delay time,” whereas the maximum value of the correlation coefficient was defined as the “maximum correlation.”

As a general theory of Fourier transform, delay time in the time domain is exposed as a phase difference in the frequency domain. Therefore, the delay time of the velocity waveforms was calculated from the phase difference of the complex spectrum. Moreover, the correlation coefficient between the absolute spectra of the velocity waveforms was determined as the maximum correlation.

Phantom study

To validate the methodology and to confirm the accuracy of the correlation mapping technique, a phantom study was performed, the setup of which is shown in Fig. 2. The phantom consisted of three horizontal acrylic pipes with a 2 cm inner diameter. The pipe on the right in Fig. 2 was connected to the inflow from a roller pump (Mera HAD 101; Senko Medical Instrument Mfg. Co. Ltd., Tokyo, Japan), and that on the left returned the flow through the tube to a reservoir. The connections were made with expansion-free, tetrone-braided tubes. A sealed pipe with stationary fluid inside was placed at the center as a control. The phantom’s pipes were set to pass through a tub with internal dimensions of 18 × 25 × 11 cm³ filled with high water-absorption gel (FF350; Daiken Medical Co. Ltd., Osaka, Japan) to provide sufficient coil loading around the pipes. Rubber gaskets were installed to prevent a possible water leak from the tub walls.

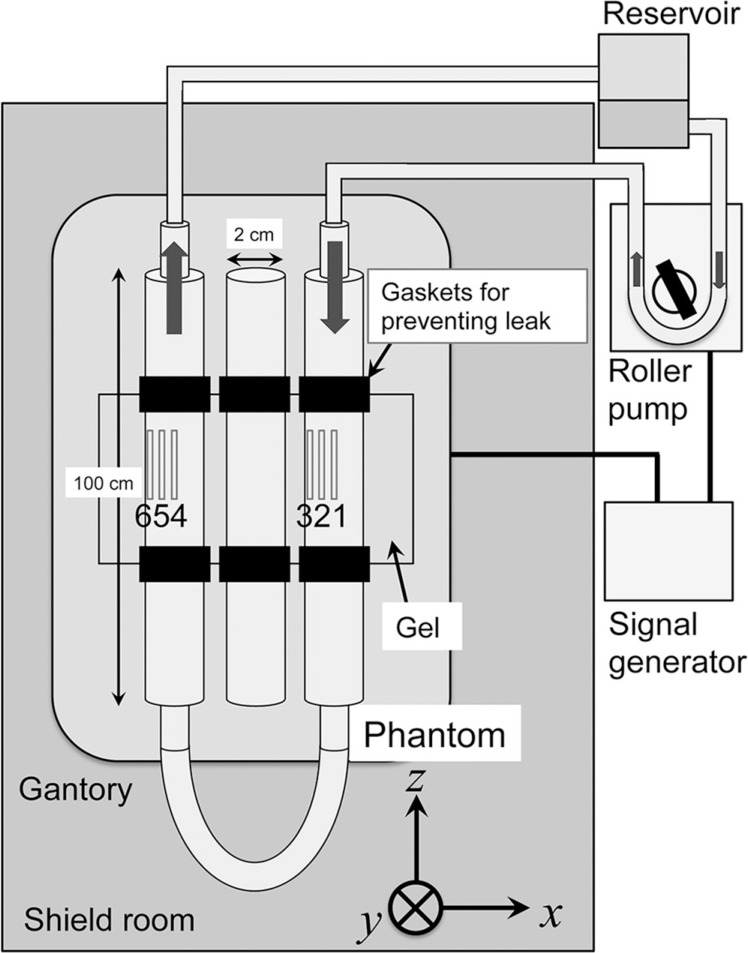
Fig. 2.

Setup for a phantom experiment. The phantom, consisting of three acrylic tubes 100 cm in length and with a 1 cm radius, was placed in a scanner along the magnetic flux of the static magnetic field. The phantom tubes were placed in a tub filled with a gel for coil loading and sealed with rubber gaskets. The middle tube was filled with saline to mimic cerebral spinal fluid (CSF) without motion. Saline in the other two tubes was pulsated and circulated by a cardiovascular roller pump. The direction of the motion is indicated by arrows. Six ROIs were placed in the fluid in the two tubes. The signal generator synchronized the pump and scanner operations. A reservoir was prepared for trapping air bubbles inside the phantom tubes.

Degassed physiological saline with 0.1% volume surfactant was used to mimic CSF. A signal generator (HP 33120a; Agilent Technologies Inc., Santa Clara, CA, USA) was connected to the roller pump and the MR scanner to synchronize the equipment with a simulated electrocardiography (ECG) signal. The pump was driven with a pulse mode triggered by the ascending edge of the simulated ECG signal of 1 Hz for simulating CSF pulsation. The threshold for triggering was set at 90% of the maximum voltage. The duty cycle of the pump was set at 50%, meaning the pump rolled for 0.5 s from the trigger and then rested for 0.5 s. The pump also had functionality for setting a delay time for starting its operation from the trigger signal. The same trigger signal was sent to the MR scanner via ECG cables to simulate cardiac-gated acquisition. After setting the flow rate of the pump at 0.5 L/min on the control panel, the actual flow rate of the pump was measured with a graduated cylinder before MR scanning.

A 1.5T MR scanner (Achieva, release 3.2.1.1, Philips Medical Systems Inc., Best, the Netherlands) equipped with a 32-channel cardiac-phased array coil was used. two dimensional (2D) PC MR in the coronal slice covering the central height of the phantom pipes was performed with the following conditions: flow-encoding direction, IS; TR, 17.4 ms; TE, 6.8 ms; flip angle, 20°; FOV, 28 × 28 cm²; acquisition matrix, 144 × 144; reconstruction matrix, 256 × 256; slice thickness, 5 mm; velocity encoding (VENC), 10 cm/s; number of cardiac phases, 32; slice selective direction, coronal. The image reconstruction was synchronized retrospectively by the simulated ECG signal.

PC images were acquired with various delay time settings for the pump, such as, 2, 10, 20, and 30, and 40% of a cardiac cycle. Six ROIs for evaluating delay time of the flow were set at the inflow and outflow tubes, indicated by gray rectangles in Fig. 2. ROI1 was placed at the center of the inflow tube, ROI3 was placed at the peripheral, and ROI2 was placed in between. ROIs 4–6 were similarly placed in the outflow tube. The measured delay time and the maximum correlation at each ROI at each pump delay were quantified and compared with the pump delay. Analyses were conducted on an independent workstation (Power Mac Pro, Quad-Core Intel Xeon; Apple Inc., Cupertino, CA, USA) by in-house software written with Matlab R2013a (Mathworks Inc., Natick; MA, USA).

Human study

Our institution’s internal review board approved this study. All volunteers were examined after we obtained appropriate informed consent, consistent with the terms of approval from the internal review board of Tokai University Hospital, Kanagawa, Japan.

We performed 4D-VM examinations in 13 young, healthy subjects (8 males and 5 females with mean ± SD age of 29 ± 5); 13 elderly, healthy subjects (4 males and 9 females with mean ± SD age of 72 ± 8); and 13 patient subjects with iNPH (2 males and 11 females with mean ± SD age of 75 ± 5). A 1.5T MR scanner equipped with an 8-channel phased array head/neck coil was used. 4D-VM image acquisition was performed with the following conditions: flow-encoding directions, IS, RL and AP; TR, 6.3–16.2 ms; TE, 3.7–7.1 ms; flip angle, 20°; FOV, 28 × 28 cm²; acquisition matrix, 144 × 144; reconstruction matrix, 320 × 320; slice thickness, 0.98 mm; slab thickness, 9.8 mm; VENC, 5–70 cm/s (VENC for all healthy volunteers was 5; VENC for the iNPH patients is summarized in Table 1); number of cardiac phases, 32; heart rate, 67 ± 13 beat/min; slice selective direction, sagittal. Acquisition time with the above parameters was 10 minutes for each encoding direction. Image reconstruction was synchronized retrospectively with signals from an ECG or a finger plethysmograph.

Table 1.

Velocity encoding (VENC) values and corresponding number of idiopathic normal pressure hydrocephalus (iNPH) patients

VENC (cm/sec)	Number of iNPH
10	1
15	2
20	3
30	4
50	1
60	1
70	1

To visualize CSF motion propagation by cardiac pulsation, the reference region was set at CSF near the basilar artery in the midline slice, because it has been reported that the pressure gradient of pulsatile CSF motion at the ventral surface of the brainstem is significantly higher than the other intracranial CSF spaces.¹² Although the mapping technique can be applied to a motion in arbitrary directions, the IS direction was analyzed in this study, because the to-and-fro CSF motion was expected to be dominant in this direction. The acquired PC images were analyzed with the same workstation and software as the phantom study.

The resultant delay time and maximum correlation maps were superimposed on the T₂-weighted image of the identical slice. The partial volume effect¹³ caused by the relatively large voxel size (approximately 1 mm³) used in this study made a simple threshold-based segmentation of the T₂-weighted image difficult. To segment CSF regions with a reasonably reduced partial volume effect, a previously proposed technique, called the spatial-based fuzzy clustering method (SFCM), was applied.¹⁴ This technique differentiated tissues with different signal intensities even in an identical voxel and determined the boundary between the tissues resulting in a reasonably segmented image.

Statistical analyses of the maximum correlation maps were performed in all the subjects to classify the subject groups from the viewpoint of compliance changed by iNPH and aging. The average and the standard deviation of the spatial distribution of the maximum correlation in the intracranial CSF space of each subject specified as the region of CSF above the atlas CI level in the midline slice were quantified and then depicted as a boxplot. Analysis of variance (ANOVA) was applied to the obtained data, followed by a multiple comparison test. All the statistical analyses were performed by using in-house Matlab software.

Results

Phantom study

A 2D PC velocity map at 2% delay is shown in Fig. 3a. The blue arrows indicate the flow direction, while the thin red rectangles indicate the locations of the six ROIs. The Reynolds number of the inflows and outflows at their maximum velocity was calculated as Re = 1075, which was sufficiently less than 2000. The flows were regarded to be laminar. Thus, the profiles were approximated by a quadratic function, delineated as yellow lines in Fig. 3a. The maximum absolute velocity at ROI1 was 7.16 ± 0.29 cm/s, which was close to the maximum velocity estimated from the flowmetry at a pump flow rate of 0.3 L/min. The velocity waveforms at ROI1 with different pump delays are shown in Fig. 3b. A waveform at ROI4 with 2% delay is also depicted in Fig. 3. Note that the waveform was reverted for comparison with those at ROI1. An example of delay time and maximum correlation maps obtained with a reference point set at ROI1 (black rectangle) is shown in Fig. 3c and d. Areas with a lower correlation (< 0.5) were masked. Almost no delay appeared in the inflow tube, while the delay appeared as a half-cycle period in the outflow tube. The correlation was approximately 1 in the entire regions of both tubes. Noisy maps appeared in the control tube, because there was no motion of the fluid. The shaded region observed at the superior part in the middle tube is thought to be an artifact from a rubber gasket containing a metal compound. Fortunately, the artifact was localized, so the results in the other tubes were unaffected.

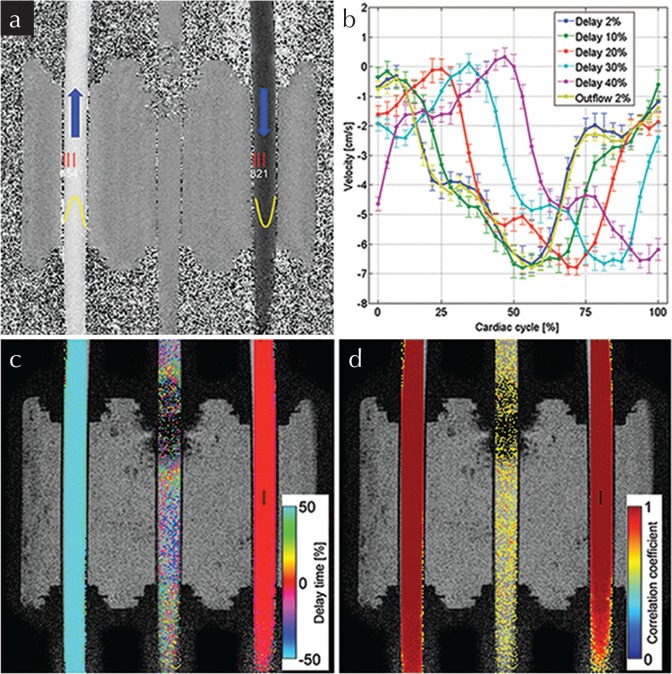
Fig. 3.

Phantom results. The acquired two dimensional-phase contrast (2D-PC) velocity map (a) at the first phase of the cardiac cycle is shown with six ROIs, indicated by red rectangles, while the flow profile approximated by quadratic function is shown in yellow. The velocity waveforms with different delays relative to the cardiac period at ROI1 and the inverted waveform at ROI4 are shown in (b). The error bars represent the range of standard deviation in the ROIs. The delay time map (c) and the maximum correlation map (d) obtained with the reference point set at ROI1 is indicated by a black rectangle. These maps were obtained for a 2% delay. Threshold-based segmentation by a correlation coefficient (<0.5) was applied to maps (c) and (d). The maps (a, c and d) were obtained from data of 2% delay. In (c), no delay appeared in the inflow tube, while a delay of exactly one half (50%) of the cardiac pulse period was in the outflow, proving the physical meaning of the delay time map. In (d), a high correlation coefficient (∼1.0) was distributed uniformly in the tubes with flow, while only noise appeared in the control tube.

Quantitative analyses of the delay time and maximum correlation at the ROIs are shown in Fig. 4. The horizontal axis in Fig. 4a is the delay time normalized by a “cardiac” cycle given by the pump, while the vertical axis is the delay measured by the proposed technique. The solid line indicates perfect agreement between the measured and the given “ideal” delay. The error bars indicate the range of standard deviations in each ROI. In Fig. 4b, the vertical axis is the correlation coefficient. As shown in Fig. 4a, the measured delay was slightly underestimated, with a root mean square (RMS) error from the given “ideal” delay of 2.27%. The error was larger in the smaller delay. This is also demonstrated in Fig. 4b, as the correlation is relatively lower at the smaller delay that at the larger.

Fig. 4.

The relationship between the measured and given delay time (a) and the maximum correlation coefficient (b) evaluated at the six ROIs. Although the measured delay was slightly lower than the given delay, the error was 2.27%, which was less than the temporal resolution of the phase contrast (PC) acquisition (3.13%).

Human study

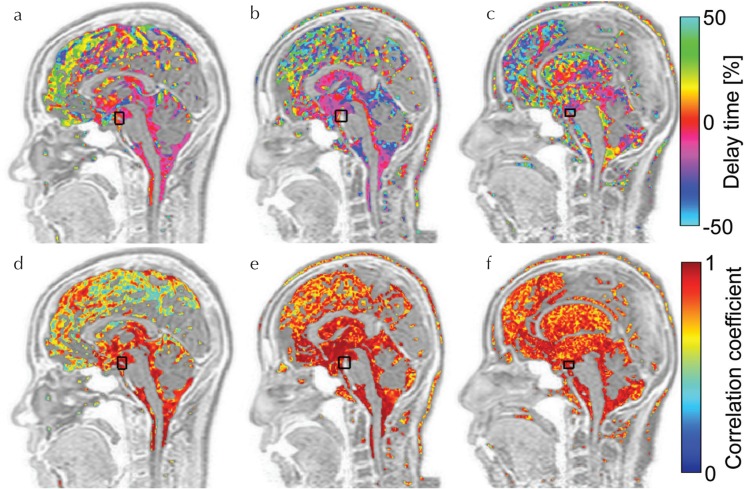
An example of the segmentation result with SFCM after manual intracranial region selection is shown in Fig. 5. The typical results of delay time and maximum correlation mapping for human subjects are shown in Fig. 6. Figure 6a, for a young, healthy subject demonstrates that the delay in the pulsatile CSF motion increased as the distance from the reference increased, particularly in the longitudinal cerebral fissure, although the delay was small around the brainstem. Figure 6b shows a similar result for an elderly, healthy subject, while the delay time distribution in the longitudinal cerebral fissure is slightly different. In contrast to these healthy subjects, the patient map in Fig. 6c exhibits a markedly larger or distributed delay in the entire CSF space. In the maximum correlation map of a young, healthy subject, shown in Fig. 6d, the correlation near the brainstem was high, which contrasts with the markedly lower correlation in the longitudinal cerebral fissure. Figure 6e shows a relatively higher and more homogenous correlation in the wider region in the longitudinal cerebral fissure of the elderly, healthy subject than that of the young, healthy subject, although a gradient seems to exist in the correlation according to the distance from the reference region. In the patient subject shown in Fig. 6f, the correlation did not present such a gradual distribution with the distance.

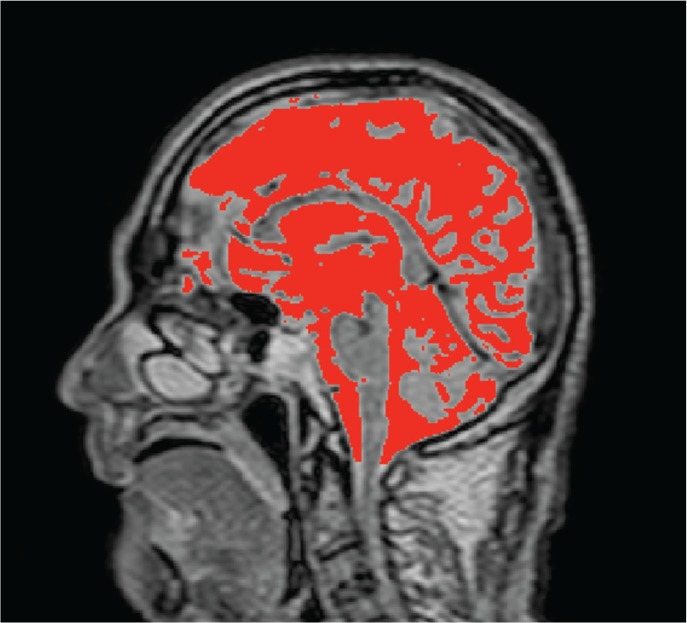
Fig. 5.

Typical result of segmentation of intracranial cerebral spinal fluid (CSF) space for quantitative analysis. After the space above C1 level was manually segmented, the CSF region, indicated in red, was extracted by using the spatial-based fuzzy clustering method.

Fig. 6.

Typical results of correlation mapping in the human study. The top row (a–c) shows delay time maps, and the bottom row (d–f) displays maximum correlation maps. Images (a) and (d) are of the young, healthy volunteer; (b) and (e) are of the elderly, healthy volunteer; and (c) and (f) are of the idiopathic normal pressure hydrocephalus (iNPH) patients. The black rectangles on the maps indicate the reference region set in the basilar artery for correlation calculation. Delay time maps (a) and (b) look similar, because the delay was homogeneous and close to zero in the ventricular system, whereas map (c) looks different. In the maximum correlation map of the young, healthy subject (d), relatively lower correlation distribution appeared in the longitudinal fissure. Such variation was not observed in (e) or (f).

CSF velocity waveforms quantified at the several regions and those power spectra are shown in Fig. 7. The power spectra indicate that the principal frequency components in the observed regions were common and agreed with the cardiac pulsation frequency (∼1.08 Hz). In addition, delay times at the ROIs, as shown in Fig. 7c, without foramen magnum and longitudinal fissure, were quantified, while the mean deviation of the delay times was calculated and is summarized in Table 2. The mean deviation demonstrates a difference of CSF motion propagation among the three subject groups. The quantitative values were obtained in a specific region, which had a spatially uniform distribution of delay time.

Fig. 7.

Results to evaluate the primary frequency components of the cerebral spinal fluid (CSF) motion propagation. (a) Velocity waveforms are shown at various tissue regions indicated by color squares on T₂ image (c). (b) Power spectra of those waveforms normalized by each peak are exhibited. Although the shape of the velocity waveforms appears to be different, the principal frequencies agree each other.

Table 2.

Fraction of delay time (%) of cerebral spinal fluid (CSF) motion propagation in a cardiac cycle at prepontine, 3rd ventricle, lateral ventricle, and 4th ventricle

	Prepontine	3rd V	LV	4th V	MD
Young healthy	0.90 ± 2.61	7.03 ± 6.47	12.01 ± 7.69	10.18 ± 9.41	14.25
Elderly healthy	−0.37 ± 2.82	5.02 ± 6.05	4.56 ± 6.99	5.22 ± 11.86	7.96
iNPH	−0.59 ± 3.88	2.24 ± 3.41	0.92 ± 5.36	2.75 ± 4.41	4.65

The rightmost column is the MD of the delay time fraction among the different regions, indicating the variety of the delay time in the intracranial space in each subject group. 3rd V, 3rd ventricle; LV, lateral ventricle; 4th V, 4th ventricle; iNPH, idiopathic normal pressure hydrocephalus; MD, mean deviation.

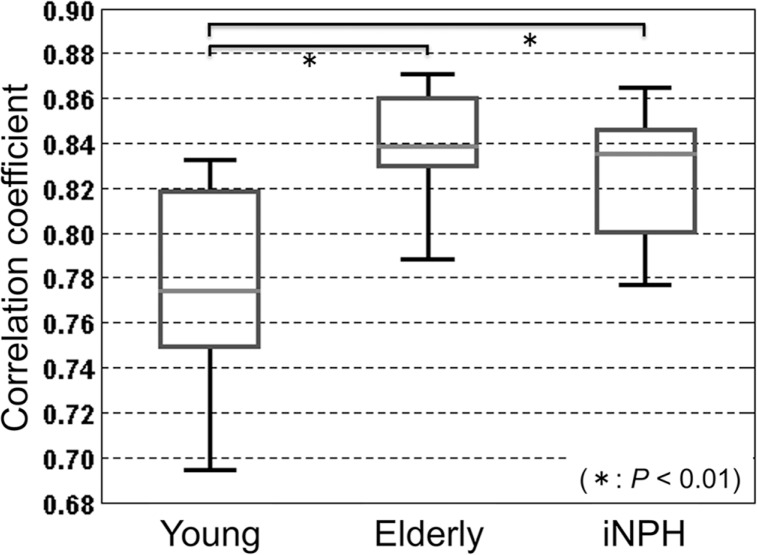
The results of the above-mentioned maximum correlation coefficient distribution in the segmented intracranial CSF space were quantitatively analyzed for all subjects, as shown in Fig. 8. There were significant differences between the young, healthy group and the others, although no significant difference was seen between the elderly, healthy group and iNPH patient groups. On the other hand, the standard deviations of the maximum correlation distribution in the same region exhibited significant differences between all groups, as shown in Fig. 9. Similar results were observed in the adjacent slices of the midline of each subject.

Fig. 8.

Boxplot of the mean correlation coefficient in the intracranial cerebral spinal fluid (CSF) space indicated in Fig. 5 for the three subject groups. Significant differences were observed between the young, healthy group and the others (P < 0.01).

Fig. 9.

Boxplot of the standard deviation of the correlation coefficient in the intracranial cerebral spinal fluid (CSF) space specified in an identical way with Fig. 7. Significant differences were recognized between all groups.

Discussion

The present study was conducted to see if the correlation mapping technique can visualize the propagation property of pulsatile CSF motion to help diagnose and understand CSF dynamics. The delay time and the maximum correlation maps were expected to provide information about compliance and pressure propagation in the intracranial CSF space.

In the phantom study, the correlation mapping technique was verified by an artificially generated flow in the tubes. As anticipated, the velocity waveforms with various delays of the pumping motion from the R-wave of the simulated ECG were almost unchanged and sufficiently reproducible, because the incompressible fluid moved in the rigid tubes. The outflow showed a half-cycle delay with regard to the inflow as the velocity direction. Thus, the waveform was inverted from the inflow. Reflecting the unchanged waveform regardless of the delay time, the maximum correlation map presented a complete homogeneous correlation (∼1).

In the quantitative analyses of delay time mapping, the proposed technique underestimated the delays, in particular in 8% and 18% delays. In addition, the slightly degraded correlation coefficient in this delay range was observed. These results may be attributed to various causes, such as incompleteness of the roller pump delay and output flow rate. In addition, the correlation coefficients at ROIs 3 and 6 seemed to be relatively lower than those in the others, probably because of a partial volume effect in ROIs set close to the tube walls. Tang et al. reported that the error of PC-based velocity measurement is within 10%.¹³ In addition, the temporal resolution of the PC acquisition was 3.13%, as a cardiac cycle was sampled with 32 temporal points. Considering the order of the velocity error and resolution of temporal sampling points, the above-mentioned underestimation (∼2.27%) in the delay time estimation should be acceptable. Thus, the homogeneous delay time distributions in the inflow and outflow tubes as well as the flat correlations demonstrate that the proposed technique successfully measured and mapped the features of the flow in terms of the velocity waveform delay and correlation.

For analysis of human data, SFCM segmentation with manual seeding was conducted to reduce the partial volume effect in the in-plane directions. In addition, the results of the quantitative analysis for the delay time and correlation coefficient in the neighboring slices were similar to those in the target slice, meaning the partial volume effect in the through-slice direction was minor. Thus, we think segmentation was achieved to a reasonable degree.

Reproducibility of CSF velocity measurement in iNPH patient should be considered. The peak CSF velocities in the cranial and caudal directions at the aqueduct obtained in the present study were 3.33 ± 1.74 and 3.60 ± 2.67 cm/s. These values are not significantly different from the previously reported values 1.99 ± 1.08 and 2.71 ± 1.73 cm/s,¹⁵ meaning that the CSF velocity measurement in the present study was reasonable._(R1-6)

Unlike the phantom with rigid tubes, the delay time and the maximum correlation maps for the healthy subjects exhibited gradual changes of the delay and correlation from the brainstem to the peripheral regions. Since the present results are based on the reference region set in the basilar artery, these maps imply that the pulsatile CSF motion was driven near the reference region and propagated to other regions in the CSF space. Our previous feasibility study in healthy subjects⁷ reported that the maximum correlation maps obtained by setting the reference regions near arteries—such as the vertebral, basilar, and anterior cerebral arteries—exhibited a similar trend in that the cardiac pulsatile CSF motion seemed to be induced by the arterial pulsations.

Quantification of the delay time indicated that the propagation delay of CSF motion varied across the groups. In addition, the mean deviation of the average delay time at various regions in intracranial CSF space was calculated for each group. The mean deviation indicates spatial diverseness of delay time in the space. When an uncompressed fluid moves in an uncompressible closed space, no delay time of fluid motion propagation occurs, denoting that the mean deviation is zero. Since CSF is assumed to be an uncompressed fluid, delay time in CSF motion is conceived to be a character reflecting compliance of the space. Because compliance of brain parenchyma and CSF space in the young, healthy group is thought to be relatively high, the delay time of CSF velocity propagation becomes long. Thus, the mean deviation of the young, healthy group is relatively high. The compliance of the elderly, healthy group is supposed to decrease with aging. Therefore, the mean deviation of the elderly, healthy group is lower than the young, healthy group. Compliance of the iNPH patient group is expected to decrease further according to iNPH status. In addition, the delay time of CSF velocity propagation shortens, and variation of the CSF velocity waveform is small. Hence, the mean deviation of the iNPH patient group is lower than the other groups. From these findings, the difference of the delay time map among the three subject groups may reflect the difference of compliance of the CSF space. Meanwhile, delay time distribution was disturbed in various places. The quantitative values at the third and lateral ventricles were obtained near the foramen of Monro, because CSF motion in the space was relatively simple.

When comparing the maximum correlation distributions in the young and elderly healthy subjects, there was a clear difference in that the young, healthy subjects had steeper gradients of correlation than the elderly, healthy subjects. This was also supported in the quantitative analyses. The difference in the delay time maps among the three subject groups also represents a possible difference of compliance in the CSF space caused by aging and/or hydrocephalus, because fluid motion is expected to propagate with less variation of the waveform if compliance of the space is lower. Thus, the study’s results imply that the CSF space is not rigid but elastic with spatially distributed compliance and that the present technique may reflect the presence of brain tissue compliance and its change with aging. The delay map of an iNPH subject was different from that of healthy subjects. The distribution in iNPH brain was heterogeneous and had no gradual spread from the reference point, unlike the healthy subjects. In addition, the maximum correlation map of an iNPH subject exhibited a clear difference from the young, healthy subjects and some faint difference from the elderly, healthy subjects. To make the difference between the elderly, healthy and patient groups, the average and the standard deviation of the correlation coefficient distribution in the entire intracranial CSF space were quantified. The results demonstrate that the standard deviation of the maximum correlation differed between the young, healthy; the elderly, healthy; and iNPH patient groups.

These observations imply that there was a possible compliance alternation with aging and/or iNPH status compared with the healthy subjects. A possible interpretation is that aging or hydrocephalic status may decrease compliance in the CSF space, making CSF motion propagate more directly. Moreover, in the iNPH status, the spatial variation of the correlation became smaller, which, in turn, indicates the compliance distribution was smaller than those in the healthy groups. Consequently, these results demonstrate that the proposed correlation mapping technique may characterize the subject groups via the difference in pressure propagation and compliance alternation.

A limitation of the present work is that we only aimed at pulsatile CSF motion induced by arterial pulsation by means of a cardiac-gated PC technique and ignored the other motions. In general, CSF motion is considered to be comprised of three components: cardiac-pulsatility-driven motion, respiratory-driven motion, and so-called bulk flow,¹⁶ which have not been distinguished completely to date. Since the energy of the pulsatile CSF motion derived from arterial pulsation is a hundredfold greater than that of the bulk flow,¹⁷ the bulk flow may be neglected. However, we included the respiratory-driven CSF motion in our velocity data. In a previous work using controlled respiration, the displacement of CSF by respiration-driven motion was significantly larger than that by arterial pulsation-driven motion.¹⁸ Other work also indicates that CSF motion is modulated by both respiration and cardiac motion.¹⁹ These reports suggest that our technique should be applied to both respiratory-driven and cardiac-driven components for understanding CSF dynamics in depth and that they may be useful to find the locations of the driving force origins of both motion components. To extract the two components separately, frequency domain analysis of the asynchronous, quasi-real-time 2D-PC technique rather than 4D-VM may be used.

The other limitation of using 4D-VM was the long acquisition time of 10 minutes for three velocity-encoding directions. To apply the present technique to clinical practice, 2D-PC should be used in place of 3D-PC after specifying the target slice location.

Conclusion

We applied delay time and maximum correlation mapping techniques to the intracranial CSF spaces in young, healthy; elderly, healthy; and iNPH patient groups and found that the spatial distributions of the delay time and maximum correlation were different in the three groups. In particular, the standard deviations of the maximum correlations exhibited a significant difference between the groups. Thus, the present technique may classify the alternation of the CSF dynamics induced by aging and/or hydrocephalic status.