A Formal Description of Middle Ear Pressure-Regulation

Abstract

Introduction

Middle ear (ME) pressure-regulation (MEPR) is a homeostatic mechanism that maintains the ME-environment pressure-gradient (MEEPG) within a range optimized for “normal” hearing.

Objective

Describe MEPR using equations applicable to passive, inter-compartmental gas-exchange and determine if the predictions of that description include the increasing ME pressure observed under certain conditions and interpreted by some as evidencing gas-production by the ME mucosa.

Methods

MEPR was modeled as the combined effect of passive gas-exchanges between the ME and: perilymph via the round window membrane, the ambient environment via the tympanic membrane, and the local blood via the ME mucosa and of gas flow between the ME and nasopharynx during Eustachian tube openings. The first 3 of these exchanges are described at the species level using the Fick’s diffusion equation and the last as a bulk gas transfer governed by Poiseuille’s equation. The model structure is a time-iteration of the equation: P^ME_{g(t=(i+1)Δt)} = Σ^s(P^ME_s(t=iΔt)+(1/(β^ME_sV^ME)Σ^P(Қ^P_s(P^C_s(t=(iΔt)-P^ME_s(t=(iΔt))). There, P^ME_g(t=iΔt) and P^ME_s(t=iΔt) are the ME total and species-pressures at the indexed times, P^C_s(t=iΔt) is the species-pressure for each exchange-compartment, β^ME_sV^ME is the product of the ME species-capacitance and volume, Қ^P is the pathway species-conductance, and Σ^S and Σ^P are operators for summing the expression over all species or exchange pathways.

Results

When calibrated to known values, the model predicts the empirically measured ME species-pressures and the observed time-trajectories for total ME pressure and the MEEPG under a wide variety of physiologic, pathologic and non-physiologic conditions.

Conclusions

Passive inter-compartmental gas exchange is sole and sufficient to describe MEPR.

1.0 INTRODUCTION

The middle ear (ME) is a relatively non-collapsible, biological gas pocket that is usually closed to direct communication with the ambient environment (Sade et al., 1997a). For hearing, the middle-ear (ME) functions to detect the near-continuous, low-magnitude, high-frequency, environmental pressure fluctuations associated with perceived “sound”, represent that flux as a pressure-time signal conditioned for effective gas-fluid coupling and present the conditioned pressure-time signals to the cochlear perilymph (Hawkins, 1964; Mason, 2016; Wilson, 1987). The sensory unit for this mechanism, the tympanic membrane (TM), functions like the diaphragm of a differential pressure-sensor. Consequently, optimal signal extraction requires that the ME medium be matched to that of the environment (i.e., gas-gas coupling) and that the ME “reference” pressure be maintained at near atmospheric levels. However, those requisite conditions are intrinsically unstable as environmental pressure independently fluctuates with changes in altitude and the movement of weather fronts and ME pressure is independently changed by diffusive gas transfers between the ME and adjacent anatomical compartments (Doyle, 2000). A ME-environment mismatch in pressure and/or media dampens TM responsiveness causing a conductive “hearing loss”.

In otherwise healthy MEs, hearing efficiency is inversely related to the absolute magnitude of the ME-environment gas-pressure gradient (MEEPG) measured at a standard ME volume (Austin, 1978; Lildholdt, 1983; Tonndorf, 1964; Wright, 1970; Zwislocki et al, 1970). Moreover, at an approximate MEEPG of −300 daPa, the accompanying mucosal-ME hydrostatic pressure gradient causes the ME gas pocket to “collapse” with fluids transferred from the local blood to the ME cavity (Alper et al., 1997; Flisberg, 1970; Swarts et al., 1995). That pathologic condition is associated causally with a moderate to severe conductive hearing loss (Dobie et al., 1979; Roland et al., 1989).

Biological homeostasis is the maintenance of a quasi-stable physiologic state by mechanisms that counter those processes that drive a system toward instability and, ultimately, functional failure (Recordati et al., 2004). For the ME, homeostasis refers to those mechanisms that maintain a negligible MEEPG (i.e. system regulators) by countering the effects of other processes that drive the development of non-zero MEEPGs (i.e. system stressors). This biofeedback mechanism is referred to as ME pressure-regulation (MEPR) (Doyle, 2000).

It is well accepted that the risks for certain types of conductive hearing loss and ME pathologies are inversely related to MEPR efficiency (Bluestone et al., 2007; Dobie et al., 1979; Kitahara et al., 1994; Roland et al., 1989; Truswell et al., 1979). Consequently, there is a continuing interest in developing medical and/or surgical interventions that improve MEPR efficiency in certain “at risk” populations (Kanemaru et al., 2005; Kanemaru et al., 2013; Kanemaru et al., 2004; Llewellyn et al., 2014; Yung, 1998). In application, this requires that the physiology of MEPR be well understood from a mechanistic perspective. Currently, a number of conceptually distinct mechanisms for MEPR have been described, with stable MEEPGs being volume-regulated, temperature-regulated, pressure-regulated, flow-regulated or regulated by some combinations of these mechanisms (Adams, 1954; Bluestone, 2005; Csakanyi et al., 2014; Doyle, 2000; Fooken Jensen et al., 2016; Gaihede et al., 2010; Hergils et al., 1988; Padurariu et al., 2015).

Traditional descriptions of MEPR are based on a flow-regulated model that for efficient function requires a balance in the volume of gas supplied to the ME during Eustachian tube (ET) openings with the volume removed from the ME by passive trans-barrier diffusive exchange with adjacent compartments. Here, a formal, mathematical model of flow-regulated MEPR that incorporates standard equations for passive inter-compartmental gas-exchange is developed (Ranade et al., 1980) and then used to test the hypothesis that a flow-regulated description of MEPR is sole and sufficient to explain the behaviors of ME pressure known from observation and experiment. To that end, the model was parameterized and evaluated for accuracy in predicting the empirically measured ME gas composition and the MEEPG trajectories observed under physiologic and non-physiologic conditions. Included in the latter are those that favor an increasing ME pressure over short time intervals, a phenomenon often attributed to gas-production by the ME mucosa (MEM) (Buckingham, 1990; Buckingham et al., 1980; Kanemaru et al., 2005; Kanemaru et al., 2004).

2.0 THEORY

2.1 Exchange System Structure

The functional ME is a temperature stable, relatively fixed-volume, gas-filled, bony cavity located within the petrosal portion of the temporal bone. That cavity is divided into two primary subcompartments, the anterior, ME proper and the posterior, mastoid air-cell system (MACS) (Bluestone, 2005). These subcompartments are continuous in the gas-phase via a fixed-diameter open channel, the mastoid antrum, and share a continuous mucosa consisting of a single layer of epithelial cells overlying a connective tissue matrix that embeds the arteries, veins and capillaries that support cellular metabolism. While the MACS volume is partitioned by mucosa covered bony septa into numerous gas-cells that communicate in the gas-phase, the ME proper is a single cell bridged by the 3 ossicles that condition and transmit externally applied forces (pressures) acting on the TM to the oval window of the cochlea. The TM, located along the lateral wall of that compartment, separates the ME from the ambient environment. The oval window, located along the medial wall of the compartment is fully fitted with the bony footplate of the stapes and is one boundary of a fluid-filled (perilymph) cochlear channel that terminates at the round window membrane (RWM) posterior and inferior to the oval window. Anteriorly, the ME is continuous with the lumen of the Eustachian tube (ET), a biological tube that extends between the ME and nasopharynx (NP) (Bluestone et al., 2007).

The ET consists of a “cane-shaped” superio-medial cartilage that is completed laterally and inferiorly by a membrane. This framework encloses a thick mucosa that surrounds the ET lumen which is continuous with that of the ME and NP. The ET lumen is open at the ME but, throughout its course, is usually closed by a mucosal tissue-pressure greater than atmospheric pressure. The tensor veli palatini, a thin inverted-triangular muscle, takes origin from the lateral membranous wall of the ET (Rood et al., 1978). Its fibers proceed laterally, inferiorly and anteriorly to converge as a tendon that rounds the hamulus to become continuous with the palatine aponeurosis. Contraction of that muscle during swallowing and other maneuvers by an as yet undefined action (e.g. yawning, jaw repositioning, etc.) actively opens the ET lumen (Cantekin et al., 1979a; Cantekin et al. 1979b). Also, the ET lumen is passively opened by the generation of NP (e.g. Valsalva maneuver) or ME pressures much greater than the periluminal pressures that hold the lumen closed (Doyle et al., 2013).

2.2. Definition of Gas Pressure

The gas species-pressure, P^C_s, for a compartment (C) containing gas in the gas-phase (G) or dissolved in a liquid (L) is equal to the product of the molar species-concentration, C^C_s, calculated as the ratio of species-moles, η^C_s, to compartment-volume, V^C, and the inverse of the species-capacitance coefficient for the medium, β^m_s,

$${{\mathbf{P}}^{\mathbf{C}}}_{\mathbf{s}}\mathbf{=}{{\mathbf{C}}^{\mathbf{C}}}_{\mathbf{s}}\mathbf{/}{{\mathbf{\beta }}^{\mathbf{C}}}_{\mathbf{s}}\mathbf{=}{{\mathbf{\eta }}^{\mathbf{C}}}_{\mathbf{s}}\mathbf{/}\mathbf{(}{\mathbf{V}}^{\mathbf{C}}{{\mathbf{\beta }}^{\mathbf{C}}}_{\mathbf{s}}\mathbf{)}(\text{Piper}1973).$$ EQ 1

Gas pressure can range from 0 to ∞ but cannot be negative since negative moles, volumes or capacitances are nonsensical. All references to “negative pressure” in the literature (e.g. tympanometric ME pressure) represent gauge-pressures defined as the extant pressure-gradient between a specified compartment and a reference compartment, usually the atmosphere (e.g. the MEEPG).

For gas-phase compartments such as the ME, NP and environment, the capacitance-coefficient for all “ideal” gases is equal to the inverse of the product of the universal gas constant, R, and the absolute (Kelvin) temperature, T^G. Substituting this relationship into Equation 1 yields the ideal gas law,

$${{\mathbf{P}}^{\mathbf{C}}}_{\mathbf{s}}\mathbf{=}\mathbf{(}{{\mathbf{\eta }}^{\mathbf{C}}}_{\mathbf{s}}\mathbf{/}{\mathbf{V}}^{\mathbf{C}}\mathbf{)}\mathbf{R}{\mathbf{T}}^{\mathbf{G}}.$$ EQ 2

For mixtures of gas species, the total gas-pressure, P^C_g, is calculated by Dalton’s law as the sum of the represented species-pressures,

$${{\mathbf{P}}^{\mathbf{C}}}_{\mathbf{g}}\mathbf{=}{\mathbf{\sum }}^{\mathbf{s}}{{\mathbf{P}}^{\mathbf{C}}}_{\mathbf{s}}\mathbf{=}\mathbf{(}\mathbf{R}{\mathbf{T}}^{\mathbf{G}}\mathbf{/}{\mathbf{V}}^{\mathbf{C}}\mathbf{)}{\mathbf{\sum }}^{\mathbf{s}}{{\mathbf{\eta }}^{\mathbf{C}}}_{\mathbf{s}},$$ EQ 3

where Σ^s is an operator that sums the results for the expression over all represented species.

The species capacitance-coefficient, β^L_s, for gases dissolved in a liquid such as blood and perilymph (or a solid), is equal to a species- and liquid-specific, temperature-dependent, solubility-coefficient, S^L_s ║T^L, expressed in units of concentration/pressure, where║indicates dependence on absolute temperature. Substituting this into Equation 1 yields Henry’s law,

$${{\mathbf{P}}^{\mathbf{C}}}_{\mathbf{s}}\mathbf{=}\mathbf{(}{{\mathbf{\eta }}^{\mathbf{C}}}_{\mathbf{s}}\mathbf{/}{\mathbf{V}}^{\mathbf{C}}\mathbf{)}{{\mathbf{S}}^{\mathbf{L}}}_{\mathbf{s}}\mathbf{/}\mathbf{/}{\mathbf{T}}^{\mathbf{L}}.$$ EQ 4

For the blood compartment, some gases (e.g. O₂, CO₂, CO) react with blood components and exist as free-gas, bound-gas and/or reaction products. The molar distribution of reactive gas among these states is in a kinetic equilibrium that responds to changes in local conditions (e.g. pH) and molar concentration. Because only free-gas contributes to species-concentration, it is useful in modelling to define an “effective” species solubility-coefficient, β^B’_s for blood that is a function of the species solubility-coefficient and the equilibrium-coefficients for all relevant reactions, β^B’_s = f(S^B_s, k^rxns_s). For reactive gases, this property buffers the magnitude change in blood species-pressure resulting from changes in species molar-concentration.

2.3 Processes that Affect ME Pressure

By Equations 2 and 3, the total ME gas-pressure is given by,

$${{\mathbf{P}}^{\mathbf{M}\mathbf{E}}}_{\mathbf{g}}\mathbf{=}{\mathbf{\sum }}^{\mathbf{s}}{{\mathbf{P}}^{\mathbf{M}\mathbf{E}}}_{\mathbf{s}}\mathbf{=}\mathbf{(}\mathbf{R}{\mathbf{T}}^{\mathbf{M}\mathbf{E}}\mathbf{/}{\mathbf{V}}^{\mathbf{M}\mathbf{E}}\mathbf{)}{\mathbf{\sum }}^{\mathbf{s}}{{\mathbf{\eta }}^{\mathbf{M}\mathbf{E}}}_{\mathbf{s}}$$ EQ 5

and ME pressure can be changed by changing ME temperature, volume, and/or species-moles. In homeotherms, ME temperature is relatively constant and the minor fluctuations that do occur are insufficient to effect a ME pressure change of sufficient magnitude to degrade hearing. With two exceptions, the TM and RWM, the bounding walls of the ME are bony which discounts the elasticity required for large volume and, consequently, large pressure change.

At fixed ME temperature and volume, the effect on ME pressure of changing species-moles is described by,

$$\mathbf{\partial }{{\mathbf{P}}^{\mathbf{M}\mathbf{E}}}_{\mathbf{g}}\mathbf{=}(\mathbf{R}{\mathbf{T}}^{\mathbf{M}\mathbf{E}}\mathbf{/}{\mathbf{V}}^{\mathbf{M}\mathbf{E}}\mathbf{)}{\mathbf{\sum }}^{\mathbf{s}}\mathbf{\partial }{{\mathbf{\eta }}^{\mathbf{M}\mathbf{E}}}_{\mathbf{s}},$$ EQ 6

which directly relates the change in ME gas-pressure, ∂P^ME_g, to the product of a constant, RT^ME/V^ME, and the algebraic sum of the molar changes for all represented species, Σ^s∂η^ME_s. Three processes can change compartment species-moles; participation in intra-compartmental chemical reactions (e.g. metabolism, binding, chemical conversion of free-gas), facilitated or active trans-barrier species-transport (uncommon requiring an external source of free-energy), and passive, gradient-driven, species-exchange with adjacent compartments. For the ME, only the last of these was shown by experiment and clinical observation to affect ME pressure. Moreover, non-zero species pressure-gradients within air-phase compartments or between compartments separated by a gas-permeable barrier represent spatial asymmetrical distributions in free-energy. Thus, for closed systems, passive dissipation of those gradients are energetically favorable, irreversible processes and a requisite consequence of the 2^nd law of thermodynamics. Thus, by application of Occam’s Razor, a first-level description of MEPR need include only inter-compartment species-exchanges, with other processes (such as: volume change by TM repositioning/mucosal swelling, mucosal gas production, facilitated counter-diffusion, etc.) added as refinements if, only if, empirically measured values for system parameters and/or observed system behaviors are not consistent with the predictions of the first-level description.

As described above, the ME is isolated from adjacent compartments by barriers of different compositions that do not contain defects or pores of sufficient size to allow inter-compartment gas-flow. Compartments separated by such barriers can exchange gas by passive diffusion if, and only if, at least one represented species is soluble in the barrier. Notably, the physiologic gases, H₂O, O₂, N₂, Ar and CO₂ (and other species such as N₂O and CO), are soluble in mucosal and membranous barriers, but not in bone at typically experienced pressures, making bone an impermeable barrier to gas-exchange. Consequently, the potential pathways for passive, gradient-driven, trans-barrier species-exchange are those between the ME and 1) the resident mucosal blood-volume via the MEM, 2) the fluid-volume of the perilymph via the RWM, and 3) the ambient environment via the TM. Additionally, a pathway for gradient-driven, bolus gas-flow between the gas-spaces of the ME and NP is introduced periodically when the ET is fully opened by either passive or active processes.

The equations that describe passive inter/intra-compartment gas-exchange all hold an analogy to Ohm’s law, I=ҚV, which relates current-flow through an electrical circuit, I, to the product of the circuit-conductance, Қ, a measure of the ease of current-flow and equal to the inverse of circuit-resistance, and the voltage difference across the circuit, V (Doyle, 2000). For passive gas-exchange, the inter-compartment molar flow-rate, M^C1–C2_s,g, is substituted for current-flow, the extant inter-compartmental species or total gas-pressure gradient, ΔP^C1–C2_s,g, is substituted for voltage, and an expression that defines the ease of gas/species-movement in the medium, Қ^m_s,g, is substituted for conductance. There, Δ is a shorthand operator indicating difference, the superscript, C1–C2, is read “between compartments 1 and 2” and the subscript, s,g, indicates “a consistent reference to either species or total gas”. Thus, a general equation describing the rate of gas-exchange between the ME and any adjacent compartment is:

$${{\mathbf{M}}^{\mathbf{C}\mathbf{-}\mathbf{M}\mathbf{E}}}_{\mathbf{s}\mathbf{,}\mathbf{g}}\mathbf{=}{{\mathbf{Қ}}^{\mathbf{m}}}_{\mathbf{s}\mathbf{,}\mathbf{g}}\mathbf{\Delta }{{\mathbf{P}}^{\mathbf{C}\mathbf{-}\mathbf{M}\mathbf{E}}}_{\mathbf{s}\mathbf{,}\mathbf{g}},$$ EQ 7a

where the exchange direction is specified by the sign of the gradient (Piper, 1973). By Equation 1, the effect of the exchange on compartment pressure is,

$$\mathbf{\partial }{{\mathbf{P}}^{\mathbf{C}}}_{\mathbf{s}\mathbf{,}\mathbf{g}}\mathbf{=}\mathbf{\partial }{{\mathbf{\eta }}^{\mathbf{C}}}_{\mathbf{s}}\mathbf{/}\mathbf{(}{\mathbf{V}}^{\mathbf{C}}{{\mathbf{\beta }}^{\mathbf{C}}}_{\mathbf{s}\mathbf{.}\mathbf{g}}\mathbf{)}\mathbf{=}{{\mathbf{M}}^{\mathbf{C}\mathbf{-}\mathbf{M}\mathbf{E}}}_{\mathbf{s}\mathbf{,}\mathbf{g}}\mathbf{/}\mathbf{(}{\mathbf{V}}^{\mathbf{C}}{{\mathbf{\beta }}^{\mathbf{C}}}_{\mathbf{s}\mathbf{.}\mathbf{g}}\mathbf{)}.$$ EQ 7b

Consequent to inter-compartmental species-exchange, the trans-barrier species-flux decreases as the species-pressure gradient decays to 0 at a rate given by,

$$\mathbf{\partial }\mathbf{\Delta }{{\mathbf{P}}^{\mathbf{C}\mathbf{-}\mathbf{M}\mathbf{E}}}_{\mathbf{s}}\mathbf{/}\mathbf{\partial }\mathbf{t}\mathbf{=}\mathbf{(}{{\mathbf{M}}^{\mathbf{C}\mathbf{\to }\mathbf{M}\mathbf{E}}}_{\mathbf{s}}\mathbf{/}\mathbf{(}{{\mathbf{\beta }}^{\mathbf{M}\mathbf{E}}}_{\mathbf{s}}{\mathbf{V}}^{\mathbf{M}\mathbf{E}}\mathbf{)}\mathbf{)}\mathbf{(}{{\mathbf{R}}^{\mathbf{\beta }\mathbf{V}\mathbf{(}\mathbf{M}\mathbf{E}\mathbf{/}\mathbf{C}\mathbf{)}}}_{\mathbf{s}}\mathbf{+}\mathbf{1}\mathbf{)},$$ EQ 8

where R^βV(ME/C)_s is the ratio of the products of species-capacitance and compartment-volume for the paired compartments, (β^ME_sV^ME)/(β^C_sV^C). Note that R^βV(ME/C)_s is 0 for the pairing of the ME with any compartment that has an “apparent” infinite volume (i.e. V^C>>>V^ME, e.g. the NP and atmosphere). There, the rate of decay of the species-pressure gradient is equal to the rate of change in ME species-pressure.

2.4 Trans-Barrier Species-Exchange with the ME

The variant of Equation 7a applicable to trans-barrier gas-exchange is given by Fick’s 1^st law of diffusion which relates species-flux across a barrier, ∅^b_s, in units of moles/distance/time, to the product of the barrier surface-area, A^b, the species diffusivity-coefficient for the barrier, D^b_s, and the spatially distributed, intra-barrier, species-concentration gradient, ∂C^b_s/∂L^b_d,

$${{\mathbf{\varphi }}^{\mathbf{b}}}_{\mathbf{s}}\mathbf{=}{\mathbf{A}}^{\mathbf{b}}{{\mathbf{D}}^{\mathbf{b}}}_{\mathbf{s}}\mathbf{\partial }{{\mathbf{C}}^{\mathbf{b}}}_{\mathbf{s}}\mathbf{/}\mathbf{\partial }{{\mathbf{L}}^{\mathbf{b}}}_{\mathbf{d}},$$ EQ 9a

where ∂C^b_s is the change in species concentration and ∂L^b_d is the change in linear distance (Ranade et al., 1980). This equation can be simplified by substituting a trans-barrier gradient for the distributed gradient, writing concentration in terms of pressure and recognizing that, by Henry’s law, the species-pressures at the opposing surfaces of the barrier are equal to the pressures of the facing compartments. For the ME, this simplification yields an equation for the rate of ME-compartmental trans-barrier molar-transfer, M^ME-C1_s, in units of species-moles/time,

$${{\mathbf{{\rm M}}}^{\mathbf{M}\mathbf{E}\mathbf{-}\mathbf{C}\mathbf{1}}}_{\mathbf{s}}\mathbf{=}\mathbf{(}{\mathbf{A}}^{\mathbf{b}}{{\mathbf{\beta }}^{\mathbf{b}}}_{\mathbf{s}}{{\mathbf{D}}^{\mathbf{b}}}_{\mathbf{s}}\mathbf{/}{{\mathbf{L}}^{\mathbf{b}}}_{\mathbf{d}}\mathbf{)}{{\mathbf{\Delta }}^{\mathbf{M}\mathbf{E}\mathbf{-}\mathbf{C}\mathbf{1}}}_{\mathbf{s}},$$ EQ 9b

where L^b_d is the trans-barrier diffusion-length measured as the average barrier thickness. Note that Equation 9b can be rewritten in a form identical to Equation 7a, such that: M^C→ME_s = we^b_sΔP^C-ME_s, where Қ^b_s is the species-conductance for the barrier calculated as A^bβ^b_sD^b_s/L^b_d. As discussed above, the redistribution of gas-moles between compartments secondary to inter-compartmental species-flow causes a progressive decrease in the inter-compartment species-pressure gradient and a consequent decrease in the rate of inter-compartment species-exchange.

2.5 Gas-Flow During ET Openings

Molar gas-flow between the ME and NP occurs in the gas-phase during ET openings and can be described by a variant of Poiseuille’s law,

$${{\mathbf{{\rm M}}}^{\mathbf{E}\mathbf{T}}}_{\mathbf{g}}\mathbf{=}{{\mathbf{Қ}}^{\mathbf{E}\mathbf{T}}}_{\mathbf{g}}\mathbf{\Delta }{{\mathbf{P}}^{\mathbf{M}\mathbf{E}\mathbf{-}\mathbf{N}\mathbf{P}}}_{\mathbf{g}},$$ EQ 10a

where ET gas-conductance (Қ^ET_g) is a function of the viscosity of air and the geometry of the ET lumen at each instant during an opening (Cantekin et al., 1979a). Practically, the effective Қ^ET_g for an active ET opening can be estimated using a parameter measured by standard function tests, the fractional gradient equilibrated by a swallow, K^FGE_g, which is defined as the change in ME pressure for a swallow divided by the pre-swallow ME-NP pressure-gradient (Doyle et al., 2014). The relational equation is,

$${{\mathbf{Қ}}^{\mathbf{E}\mathbf{T}}}_{\mathbf{g}}\mathbf{=}{{\mathbf{K}}^{\mathbf{FGE}}}_{\mathbf{g}}\mathbf{(}{\mathbf{V}}^{\mathbf{M}\mathbf{E}}\mathbf{/}\mathbf{R}{\mathbf{T}}^{\mathbf{M}\mathbf{E}}\mathbf{)},$$ EQ 11

where, V^ME/RT^ME, is a constant that converts ME gas-pressure to ME gas-moles. This result allows Equation 10a to be written as moles-exchanged per active tubal opening Δt^ET_o, which is equal to the integral of moles exchanged between ME and NP for the time of opening, M^ET_g/Δt^ET_o= ∫^Δto∂η^ME_g/∂t. Substituting these relationships into Equation 10a, yields,

$${{\mathbf{M}}^{\mathbf{E}\mathbf{T}}}_{\mathbf{g}}\mathbf{/}\mathbf{\Delta }{{\mathbf{t}}^{\mathbf{E}\mathbf{T}}}_{\mathbf{o}}\mathbf{=}{{\mathbf{K}}^{\mathbf{FGE}}}_{\mathbf{g}}\mathbf{(}{\mathbf{V}}^{\mathbf{M}\mathbf{E}}\mathbf{/}\mathbf{R}{\mathbf{T}}^{\mathbf{M}\mathbf{E}}\mathbf{)}\mathbf{\Delta }{{\mathbf{P}}^{\mathbf{M}\mathbf{E}\mathbf{-}\mathbf{N}\mathbf{P}}}_{\mathbf{g}}\mathbf{/}\mathbf{\Delta }{{\mathbf{t}}^{\mathbf{E}\mathbf{T}}}_{\mathbf{o}}.$$ EQ 10b

Because the NP has an apparent infinite gas-volume (V^NP/V^ME→∞), the resulting change in ME gas-pressure, ∂P^ME_g/opening, is given by,

$$\mathbf{\partial }{{\mathbf{P}}^{\mathbf{M}\mathbf{E}}}_{\mathbf{g}}\mathbf{/}\mathbf{\Delta }{{\mathbf{t}}^{\mathbf{E}\mathbf{T}}}_{\mathbf{o}}\mathbf{=}\mathbf{\Delta }{{\mathbf{P}}^{\mathbf{M}\mathbf{E}\mathbf{-}\mathbf{N}\mathbf{P}}}_{\mathbf{g}}\mathbf{/}\mathbf{\Delta }{{\mathbf{t}}^{\mathbf{E}\mathbf{T}}}_{\mathbf{o}}\mathbf{=}\mathbf{(}\mathbf{R}{\mathbf{T}}^{\mathbf{M}\mathbf{E}}\mathbf{/}{\mathbf{V}}^{\mathbf{M}\mathbf{E}}\mathbf{)}\mathbf{(}\mathbf{\partial }{{\mathbf{n}}^{\mathbf{M}\mathbf{E}}}_{\mathbf{g}}\mathbf{/}\mathbf{\Delta }{{\mathbf{t}}^{\mathbf{E}\mathbf{T}}}_{\mathbf{o}}\mathbf{)}.$$ EQ 12a

and the post-opening ME gas-pressure, P^ME_{g(t=iΔt+Δto)}, by:

$${{\mathbf{P}}^{\mathbf{M}\mathbf{E}}}_{\mathbf{g}\mathbf{(}\mathbf{t}\mathbf{=}\mathbf{i}\mathbf{\Delta }\mathbf{t}\mathbf{+}\mathbf{t}\mathbf{o}\mathbf{)}}\mathbf{=}{{\mathbf{P}}^{\mathbf{M}\mathbf{E}}}_{\mathbf{g}\mathbf{(}\mathbf{t}\mathbf{=}\mathbf{i}\mathbf{\Delta }\mathbf{t}\mathbf{)}}\mathbf{+}\mathbf{\partial }{{\mathbf{P}}^{\mathbf{M}\mathbf{E}}}_{\mathbf{g}}\mathbf{/}\mathbf{\Delta }{{\mathbf{t}}^{\mathbf{E}\mathbf{T}}}_{\mathbf{o}}.$$ EQ 13a

The change in ME species-pressure effected by an ET opening, ∂P^ME_s/Δt^ET_o, is calculated as the product of the change in ME total-pressure and the pre-opening, fractional species-pressure, P^sC_s/P^sC_g, for the source-compartment, sC, i.e. the compartment with the higher pre-opening total-gas pressure, or,

$$\mathbf{\partial }{{\mathbf{P}}^{\mathbf{M}\mathbf{E}}}_{\mathbf{s}}\mathbf{/}\mathbf{\Delta }{{\mathbf{t}}^{\mathbf{E}\mathbf{T}}}_{\mathbf{o}}\mathbf{=}\mathbf{(}\mathbf{\partial }{{\mathbf{P}}^{\mathbf{M}\mathbf{E}}}_{\mathbf{g}}\mathbf{/}\mathbf{\Delta }{{\mathbf{t}}^{\mathbf{E}\mathbf{T}}}_{\mathbf{o}}\mathbf{)}\mathbf{(}{{\mathbf{P}}^{\mathbf{s}\mathbf{C}}}_{\mathbf{s}}\mathbf{/}{{\mathbf{P}}^{\mathbf{s}\mathbf{C}}}_{\mathbf{g}}\mathbf{)},$$ EQ 12b

and the species-pressure after an opening is calculated using,

$${{\mathbf{P}}^{\mathbf{M}\mathbf{E}}}_{\mathbf{s}\mathbf{(}\mathbf{t}\mathbf{=}\mathbf{i}\mathbf{\Delta }\mathbf{t}\mathbf{+}\mathbf{t}\mathbf{o}\mathbf{)}}\mathbf{=}{{\mathbf{P}}^{\mathbf{M}\mathbf{E}}}_{\mathbf{s}\mathbf{(}\mathbf{t}\mathbf{=}\mathbf{i}\mathbf{\Delta }\mathbf{t}\mathbf{)}}\mathbf{+}\mathbf{(}\mathbf{\partial }{{\mathbf{P}}^{\mathbf{M}\mathbf{E}}}_{\mathbf{g}}\mathbf{/}\mathbf{\Delta }{{\mathbf{t}}^{\mathbf{E}\mathbf{T}}}_{\mathbf{o}}\mathbf{)}\mathbf{(}{{\mathbf{P}}^{\mathbf{s}\mathbf{C}}}_{\mathbf{s}}\mathbf{/}{{\mathbf{P}}^{\mathbf{s}\mathbf{C}}}_{\mathbf{g}}\mathbf{)}.$$ EQ 13b

Note that trans-ET gas-exchange does not affect the fractional species-pressures in the NP, or, in the source compartment, the ME, but will decrease the absolute value of the total-pressure gradient across the ET, │ΔP^ME-NP_g│, which is mathematically equivalent to the absolute value of the MEEPG. These equations also apply to ME-NP species-exchange for passive ET openings where the difference between the empirically measured passive ET opening, P^ETO_g, and closing, P^ETC_g, pressures is substituted for ∂P^ME_s/Δt^ET_o.

3.0 CALCULATIONS

Using these equations, a compartment-level, computational model describing MEPR was constructed for use in simulating MEEPG trajectories under defined conditions. That model treats ME gas-exchange as simultaneous, gradient-driven, trans-barrier diffusive molar species-exchanges between the ME and three fixed-volume, homogenous, mixed-gas compartments, the atmosphere, perilymph and MEM blood, and the intermittent bolus gas-flows between the ME and NP during active and passive ET openings. Ignored at this level of detail are the development and dissipation of distributed pressure-gradients within the exchange-barriers and compartments and the change in ME volume effected by TM displacements or MEM swelling.

For this compartment structure, the MEEPG (=ME gauge-pressure) trajectory can be calculated for any specified initial conditions as a time-series iteration of the pressure equation:

$${{\mathbf{P}}^{\mathbf{M}\mathbf{E}}}_{\mathbf{g}\mathbf{(}\mathbf{t}\mathbf{=}\mathbf{(}\mathbf{i}\mathbf{+}\mathbf{1}\mathbf{)}\mathbf{\Delta }\mathbf{t}}\mathbf{=}{\mathbf{\sum }}^{\mathbf{s}}\mathbf{(}{{\mathbf{P}}^{\mathbf{M}\mathbf{E}}}_{\mathbf{s}\mathbf{(}\mathbf{t}\mathbf{=}\mathbf{i}\mathbf{\Delta }\mathbf{t}\mathbf{)}}\mathbf{+}\mathbf{(}\mathbf{1}\mathbf{/}\mathbf{(}{{\mathbf{\beta }}^{\mathbf{M}\mathbf{E}}}_{\mathbf{s}}{\mathbf{V}}^{\mathbf{M}\mathbf{E}}\mathbf{)}{\mathbf{\sum }}^{\mathbf{B}}\mathbf{(}{{\mathbf{Қ}}^{\mathbf{B}}}_{\mathbf{s}}\mathbf{(}{{\mathbf{P}}^{\mathbf{C}}}_{\mathbf{s}\mathbf{(}\mathbf{t}\mathbf{=}\mathbf{(}\mathbf{i}\mathbf{\Delta }\mathbf{t}\mathbf{)}}\mathbf{-}{{\mathbf{P}}^{\mathbf{M}\mathbf{E}}}_{\mathbf{s}\mathbf{(}\mathbf{t}\mathbf{=}\mathbf{(}\mathbf{i}\mathbf{\Delta }\mathbf{t}\mathbf{)}}\mathbf{)}\mathbf{)}.$$ EQ 14

There, P^ME_g(t=iΔt) and P^ME_s(t=iΔt) are the ME total and species-pressures at the indexed times, P^C_s(t=iΔt) is the species-pressure for each exchange-compartment, β^ME_sV^ME is the product of the ME species-capacitance and volume, Қ^B_s is the species-conductance for each barrier, and Σ^S and Σ^B are operators for summing the expression over all species or exchange-barriers. Note that ME pressure is stable under this equation if, and only if, the molar transfers to and from the ME are equal within each time-interval and is semi-stable if the sum of those transfers is equal across longer time-periods, i.e. MEPR is a flow-regulated mechanism.

For any set of initial conditions, the expected semi-stable value of the MEEPG can be quantified for the model as the root-mean-square of the predicted/measured MEEPGs for the near-asymptotic time-period, or,

$$\mathbf{E}\mathbf{(}\mathbf{\Delta }{{\mathbf{P}}^{\mathbf{M}\mathbf{E}\mathbf{-}\mathbf{ATM}}}_{\mathbf{g}}\mathbf{)}\mathbf{=}\mathbf{(}\mathbf{(}{\mathbf{\sum }}^{\mathbf{i}}{\mathbf{(}\mathbf{\Delta }{{\mathbf{P}}^{\mathbf{M}\mathbf{E}\mathbf{-}\mathbf{ATM}}}_{\mathbf{g}\mathbf{(}\mathbf{t}\mathbf{=}\mathbf{i}\mathbf{)}}\mathbf{)}}^{\mathbf{2}}\mathbf{)}\mathbf{/}{\mathbf{i}\mathbf{)}\mathbf{)}}^{\mathbf{.}\mathbf{5}},$$ EQ 15

where i is the number of observations and E is a shorthand notation for “Expected Value” abbreviated “EV”. Because the ME gas pocket collapses at a critical MEEPG of approximately −300 daPa (Alper et al., 1997; Swarts et al., 1995), system configurations with an EV-MEEPG less than or equal to −300 daPa are assigned a MEPR efficiency of 0. The MEPR efficiency for EV-MEEPGs less than or equal to 0 daPa but greater than −300 daPa is calculated as one minus the EV-MEEPG divided by −300 as, for example, an efficiency of 1 is assigned to an EV-MEEPG of 0 daPa. While increasing positive MEEPGs over the range from 10 to +300 daPa are associated with increasing degrees of conductive hearing loss (Kitahara et al., 1994; Truswell et al., 1979), positive MEEPGs are typically of short-duration and are not an expected system steady-state. Consequently, MEPR efficiency is not defined for those transients.

The iterative procedure used to calculate the ME pressure-trajectory involves specifying a simulation time, T^S, partitioning that time into successive, equal-length, time-intervals, Δt, labeling those intervals with successive integers, i, from 0 to T^S/Δt, and then solving Equation 14 at each successive time-interval. The predictive accuracy of the model increases as the time-interval decreases and is maximized as Δt→0. To avoid circularities in the calculations for infinitely short intervals, each time-interval is considered to be bounded by an onset-time, iΔt, and an end-time, (i+1)Δt. By definition, molar gas-exchange occurs within the interval, is driven by the inter-compartment pressure-gradients at the onset-time, ΔP^C-ME_s,g(t=iΔt), and yields revised compartment species-pressures, P^C_{s,g(t=(i+1)Δt)}, at the end-time. In turn, the latter are used as the input values at the onset-time for the next iteration.

This model assumes that the exchange-system represented in the model is a self-contained, complete description of all possible exchange pathways. While that assumption holds for the ME, the pressure of the two infinite volume compartments, the environment and NP, is affected by changes in elevation and the movement of weather fronts, and of the two finite volume compartments, the perilymph and MEM blood, by gas-exchange with compartments external to the represented exchange-system. These effects are incorporated into the model as described below.

An atmospheric pressure-time function, P^ATM_s,g=f(t), is specified and its evaluation at each time, iΔt, is directly entered into the model for the atmosphere and NP pressures and is proportionally entered at those times for the blood and perilymph pressures such that, at any time, P^ATM_g = PNP_g = K^V/ATMP^V_g = K^IE/ATMP^IE_g, where K and K^V/ATM and K^IE/ATM are constants equal to the ratio of the venous or perilymph total gas-pressure to atmospheric total gas-pressure at sea-level. Typically, for the relatively short time-periods simulated using the model, the pressure-time function is a constant equal to the atmospheric pressure at t=0. While used here for 10 hour simulations, this simplification does not hold when describing long-term MEEPG behavior or behaviors for short periods characterized by rapid ambient pressure-change as occurs during diving and air-flight (Kanick et al., 2005).

The perilymph exchanges species-moles by diffusion with the ME, cerebrospinal fluid and the blood lining the perilymphatic space. Expectedly, the overall effect of these simultaneous, multi-pathway, species-exchanges is the development of steady-state species-pressures that is equal to the weighted average of the species-pressures for the three compartments exchanging gas with the perilymph and with weights proportionately assigned based on the species exchange-rate for each pathway. Given the low species-conductances for the RWM when compared to the other pathways (see Table II), it is assumed that the steady-state perilymph species-pressures are equal to venous blood and unaffected by species exchange with the ME.

TABLE II.

Volumes, Beta Coefficients and Species-Pressures at Sea-Level for Exchange Compartments

		β (μmols/ml/daPa)1			Pressure (daPa)2
	Volume	O2	CO2	N2	O2	CO2	N2	H2O
ATM*	∞	1.20	1.20	1.20	2120	4	7946	67
NP	∞	1.13	1.13	1.13	1547	387	7573	627
ME	FP1*	1.13	1.13	1.13	400	667	8442	627
Blood	CP1**	1.28×10−3	3.36×10−2	6.02×10−4	400	667	7639	627
Perilymph	0.16 ml	1.28×10−3	3.36×10−2	6.02×10−4	400	667	7639	627

¹Beta coefficients for Atmosphere given for room temperature, coefficients for other compartments given for body temperature. (http://faculty.etsu.edu/currie/gasexchange.htm)

²Literature Consensus Human ME at Sea Level Pressure, MEEPG=0, and fully saturated with H2O at body temperature(Felding et al., 1987; Hergils et al., 1988; Hergils et al., 1990; Hergils et al., 1997; Sade et al., 1993)

^*FP1 – imputed free parameter

^**CP1 – Calculated from imputed free parameters: V^rB= F^B/MEMV^MEM

The resident MEM blood exchanges gas with the ME by diffusion and exchanges volume with the blood in circulation by perfusion. The operation of these two processes results in resident-blood species-pressures that range between those for the ME at low perfusion-rates and the venous blood at high perfusion-rates. To incorporate these effects into the model, MEM blood is represented as a fixed-volume compartment embedded within the MEM. During residence, that volume exchanges gas with the ME in accordance with the standard two-compartment, trans-barrier exchange-equation but, at time-intervals specified by the blood perfusion-rate, the species-pressures of the resident blood-volume are reset to those of venous blood. Entered as model parameters are a fractional Blood/MEM multiplier, F^B/MEM, that calculates the resident MEM blood-volume, V^rB, as a fraction of the mucosal-volume, V^MEM, the perfusion-rate, Q^rB, in units of resident blood-volumes/time, and CO₂ and O₂ capacitance multipliers that convert species solubility-coefficients for blood, β^B_s, to “effective” free-species solubility-coefficients, β^B’_s, by accounting for reaction kinetics.

While trans-barrier, gas-exchange is a continuous process operating at the species level, that between the ME and NP occurs as a bolus transfer of mixed-gas from the high to low gas-pressure compartment during times of active or passive ET opening. Gas transfer during an active ET opening is represented in the model by imputing two parameters that define active ET opening efficiency, the basal ET opening frequency, F^ETO, and an estimator proportional to trans-ET conductance, K^FGE_g. At times specified by the opening frequency, the equations for trans-ET molar gas-flow are solved for the extant NP-ME gas-pressure gradient and assigned K^FGE_g. Absent maneuvers that actively increase NP pressures (e.g. Valsalva), the ET passively opens when the MEEPG exceeds the ET opening pressure, P^ET_o, and closes at the ET closing pressure, P^ET_C. Estimates for the opening and closing pressures available in the literature for clinical tests are inputted into the model and, at times when the MEEPG exceeds the ET opening pressure, the equations for trans-ET molar gas-flow are solved for a ME gas-pressure change equal to the difference between the ET opening and closing pressures.

Practically, these equations are programmed as a repeated sequence of T^S/Δt feedback loops, with each loop containing the same stepped series of mathematical operations that together input species-pressures for the four exchange compartments at time, iΔt, and output those parameters at time, (i+1)Δt. Briefly, this involves parameterizing the model using best-estimate values of compartment volumes, species-capacitances and baseline species-pressures and estimates of pathway species-conductances (Tables I, II). The initial conditions for the simulation (t=0) are specified by entering free-parameters that include ME volume, MEM blood perfusion-rate, and the ET opening frequency, conductance, opening pressure and closing pressure (Table III). A simulation time, T^S, and a fixed time-interval, Δt, are assigned, and time, iΔt, is set to 0, where i=0, as are time-counters for the ET opening frequency and MEM blood perfusion. The program then performs the following sequence of T^S/Δt looping operations.

Table I.

Abbreviations Used in Text and Symbols Used in Equations

Abbreviations: ET-Eustachian Tube; EV-Expected Value; FGE-Fractional Gradient Equilibrated in 1 swallow; ME-Middle Ear; MEEPG-Middle Ear to Environment Pressure Gradient; MEM-Middle Ear Mucosa; MEPR-Middle Ear Pressure Regulation; NP-Nasopharynx; TM-Tympanic Membrane.

Compartment Symbols: βCs.g –Capacitance Coefficient, CCs–Molar Concentration, ηCs.g–moles, SCs–Solubility, TC–Temperature (°K), PCs.g –Pressure, VC–Volume.

Barrier Symbols: Ab–Surface Area, βbs.g–Capacitance Coefficient, Dbs–Diffusivity-Coefficient, FB/MEM–Blood/Mucosa Volume Ratio, Кms.g–Conductance, Lbd–Diffusion Length, Vb–Volume, Vrb–Mucosal Blood Volume, Qrb–Volume Blood Perfusion Rate.

Eustachian Tube Symbols: FETO–Frequency Eustachian Tube Openings, ΔtETo–Active Eustachian tube opening time, КFGEg–Eustachian Tube Conductance Coefficient, PETOg–Eustachian Tube Opening Pressure, PETCg–Eustachian Tube Closing Pressure.

Exchange Symbols: t – Time, Øbs–species flux (moles/distance;time), MC1–C2s.g–Inter-Compartmental Molar Exchange Rate (moles/time).

Operator Symbols: ║–Given, Δ–Difference, ∂–Change, Σc Sum Over Categories C, ⊠ab–Area Under the Curve from A to B.

Superscript specifies compartment (C), barrier (b), subscript references total gas (g) or species (s).

Table III.

Properties of the three Barriers to Middle Ear Gas Exchange

		TM	RWM	MEM
Physical Properties	Diffusion Length (cm)	0.005	0.005	0.005
	Surface Area (cm2)	0.99	0.022	CP2*
	Volume (ml)**	0.005	0.0001	CP3**
Gas Conductances1	O2	7.25E-09	1.60E-10	7.24E-05
(uM/daPa.sec)	CO2	5.88E-08	1.29E-09	7.24E-04
	N2	3.63E-09	7.98E-11	3.62E-05

^*CP2 - Calculated from imputed free parameter: V^rB = F^B/MEMV^MEM

^**CP3 - Calculated from imputed free parameters: A^MEM = (A^ME/V^ME)V^MEM-A^RWM-A^TM1.

TM species-conductances were taken from the in vivo measurements made by Yuksel and colleagues on adult humans (Yuksel et al., 2011; Yuksel et al., 2009). RWM species-conductances were calculated under the assumption of identical species-diffusivities and solubilities for the RWM and TM (identical chemical compositions) and then adjusting for dimensional differences by applying the equation

K^RWM_S=K™_S(A^RWM/A™)(L™_d/L^RWM_d), a form of Equation 9a. MEM O2 conductance was calculated using a form of equation 9a, Қ^MEM_O2=A^MEMβ^MEM_O2D^MEM_O2/L^MEM_O2, under the assumption that the MEM behaves primarily as a water barrier and then calculating the N2 and CO2 conductances as the product of that value and the respective species/O2 conductance ratios reported for the human ME by Doyle and colleagues (Doyle et al., 2011). The validity of the assumption was tested by comparing the N2 pressure trajectories measured in humans by Kitsko and colleagues with that predicted by the model (data not shown) (Alper et al., 2011). Good agreement was achieved at an imputed mucosal blood perfusion-rate of 0.025 MEM blood-volumes/sec, a ME volume of 10 ml and MEM SA/V ratio of 16, values consistent with measurement on humans (Csakanyi et al., 2014; Swarts et al., 2010).

1. Calculate the species moles exchanged between the ME and perilymph via the RWM, ME and environment via the TM and ME and resident MEM blood via the MEM for the referenced interval, Δt, in that order using Equation 9c.

2. Calculate the species and gas-pressures at the interval end-time, t=1+iΔt, for the ME and MEM blood using Equation 14.

3. Adjust the total atmospheric, NP, perilymph and venous blood total-pressures using the specified atmospheric pressure-time function.

4. If the MEM perfusion time-counter for the interval is greater than or equal to 1/Q^rB, reset the counter to 0 and set the local blood species-pressures to those for venous blood; else, increase the counter by Δt.

5. If the ET opening-frequency time-counter is greater than or equal to the inverse of the specified opening-frequency, reset that counter to 0 and adjust ME species and gas-pressures for the effects of an active ET opening using equations 10 through 13; else, increase that counter by Δt.

6. If total ME gas-pressure is greater than or equal to the ET opening-pressure, adjust ME species and gas-pressures for the effects of a passive ET opening using equations 10 through 13.

7. Output and store the time and the species and gas-pressures for all exchange-compartments.

8. If i+1<T^S/Δt, go to Step 1, else continue.

9. Calculate the MEEPG at each time, plot the MEEPG trajectory as a time function and calculate the corresponding MEPR efficiency using Equation 15.

4.0 RESULTS

4.1 Contribution of Trans-TM/RWM species-exchange to MEPR

The model was calibrated using the standard values for the parameters listed in Tables II–IV and a 10-hour simulation was run under the conditions of no active ET openings (F^ETO=0) and: 1) no trans-TM or trans-RWM gas-exchange (Қ™_s and Қ^RWM_s=0) but trans-MEM gas-exchange set to its standard value, 2) gas-exchange across those membranes are set to their standard values but trans-MEM gas-exchange is ignored (Қ^MEM_s=0), and 3) gas-exchange across all 3 trans-barrier pathways. The predicted MEEPG trajectories are shown in Figure 1. Alone, gas-exchange across the 2 membranous barriers has little effect on the MEEPG with that gradient showing a shallow decrease followed by a low-magnitude increase at later times. Alone, trans-MEM gas-exchange causes progressively more negative MEEPGs which is attributable to gradient-driven transfer of N₂ moles from the ME to MEM blood (See Table I for species-pressure gradients). That trajectory is little affected by including the two trans-membrane exchange pathways. When isolated, the contribution of trans-RWM gas-exchange to any of the predicted MEEPG trajectories is negligible and this is not changed by varying the perilymph species-pressures over the range of reasonable values (data not shown). These results demonstrate that, under physiologic conditions, gas-exchange across the trans-TM and trans-RWM pathways does not contribute to MEPR but that trans-MEM gas-exchange acts as a stressor on MEPR by causing the MEEPG to deviate significantly from a value of 0 daPa. Below, all simulations were run with species-exchanges across the three trans-barrier pathways calibrated to their standard values.

Table IV.

Free-Parameters: Expected Range and Input Values for the Standard Model

PARAMETER	UNITS	RANGE	INPUT VALUE
ME Volume*	ml	1–20	10
ME Surface-Area/Volume*	/cm	8–30	16
Blood/Mucosa Volume Fraction	None	0.01–0.5	0.25
Perfusion Rate	MEM Vol/sec	0–10	0.05
CO2 Capacitance Multiplier	βB’CO2/βBCO2	1–10	1
O2 Capacitance Multiplier	βB’O2/βBO2	1–10	1
KFGEg**	None	0–1	0.5
ET Opening Frequency	/hour	0–60	4
ET Opening Pressure***	daPa	100–1000	500
ET Closing Pressure***	daPa	0–500	100
Ambient Pressure-Time Function	daPa/min	PATM=f(t)	PATM=C

^*From empirical measurement on the human ME done by Swarts and colleagues (Swarts et al., 2010)

^**From empirical measurements on the human ME done by Doyle and colleagues (Doyle et al., 2014)

^***From empirical measures on the human ET done by Doyle and colleagues (Doyle et al., 2013)

Figure 1.

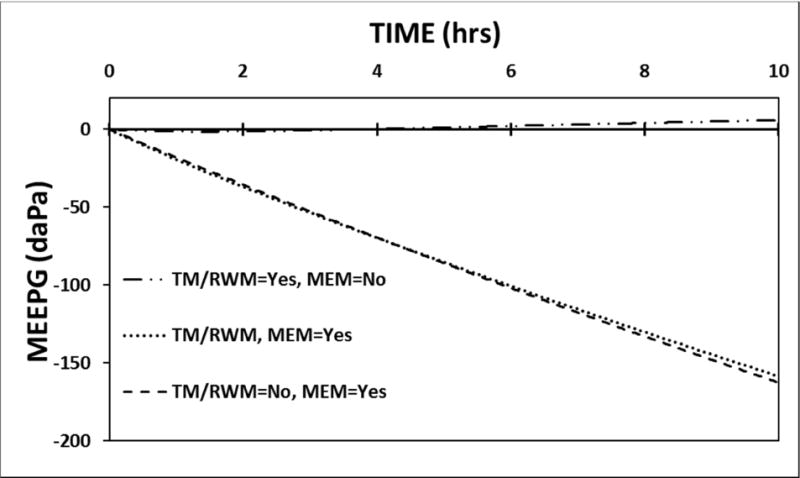
A 10-hour model simulation of the MEEPG trajectory predicted using the standard model parameters with no ET opening and with and without gas exchange across the different trans-barrier pathways.

4.2 Contribution of resident MEM blood volume to MEPR

The model parameters were calibrated to standard values and a 10-hour simulation was run with no ET openings (F^ETO=0) while varying the fractional MEM blood-volume (F^B/MEM); 0.10, 0.25 (standard) and 0.50. The predicted MEEPG trajectories are shown in Figure 2. There is a direct relationship between MEM blood-volume and the predicted rate of change in the MEEPG. This indicates that MEM blood-volume is one determinant of the rate of ME gas-loss caused by trans-barrier exchange, i.e. a variable-magnitude MEPR stressor.

Figure 2.

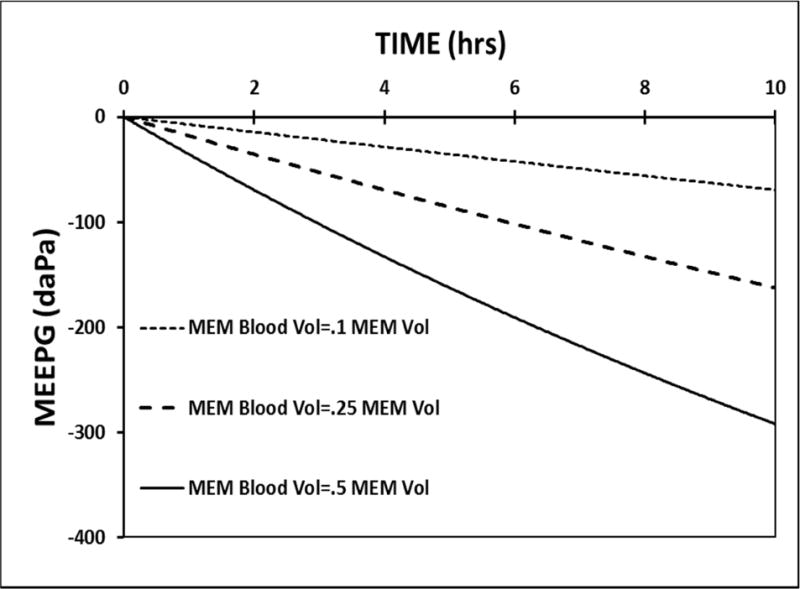
A 10-hour model simulation of the MEEPG trajectory predicted using the standard model parameters with no ET openings while varying the MEM blood-volume measured as a fraction of the total MEM volume.

4.3 Effect of mucosal blood perfusion-rate on MEPR

The model was calibrated to the standard parameters and a 10-hour simulation was run with no ET openings while varying the MEM blood perfusion-rate, Q^rB. Figure 3 shows the predicted MEEPG trajectories at a Q^rB of 0.02, 0.05, 0.2, 0.5 and 1.0 MEM blood-volumes/second. At the highest perfusion-rate, the MEEPG exhibits a curvilinear decrease to approach an asymptote, the EV-MEEPG, at ≈ −800 daPa. Thus, for the ME, the algebraic sum of molar species-exchanges across the three trans-barrier pathways is negative at all MEEPGs greater than its asymptote. At the asymptote, the ME species-moles exchange with all compartments is in a dynamic equilibrium such that the ME species-pressures approach those for venous blood and this result holds for both a gas and liquid medium. The family of displayed curves is characterized by the same EV-MEEPG, −800 daPa, and an identical curvilinear form, but the overall rate of change in the MEEPG is directly related to the MEM blood perfusion-rate. Thus, like the MEM blood-volume (see Simulation 2), the MEM blood perfusion-rate represents a variable-magnitude stressor.

Figure 3.

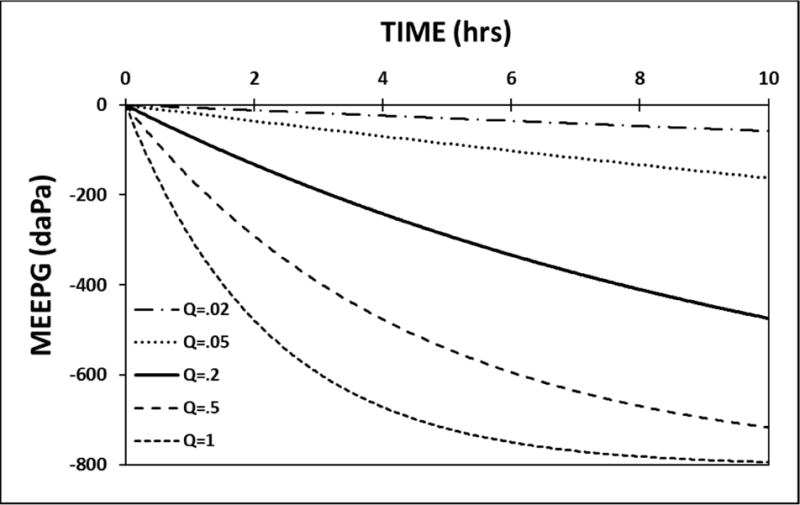
A 10-hour model simulation of the MEEPG trajectory calculated using standard model parameters with no ET openings while varying the MEM perfusion rate (Q, measured in resident blood volumes/second).

4.4 Effect of ET opening frequency on MEPR

To simulate the effect on MEPR of changing the ET opening frequency, F^ETO, the model parameters were set to standard values, the perfusion-rate was set to 1.0 MEM blood-volumes/second, trans-ET conductance was fixed at 0.5, and the ET opening frequency was varied over a range of values. Figure 4 shows the predicted MEEPG trajectories at an F^ETO of 0.0, 0.3, 1.0, 2.0 and 6.0 openings/hour. For this family of curves, the rate of MEEPG change between ET openings is identical, but the absolute value of the EV-MEEPG and the variance about that value are indirectly related to the ET opening frequency. The lesser EV-MEEPGs at progressively higher opening frequencies is reflected in the calculated MEPR efficiencies for those simulations of: 0.0, 0.0, 0.0, 0.22 and 0.68, respectively. Because MEPR efficiency is progressively increased by increasing ET opening frequencies, that parameter is a variable-magnitude MEPR regulator.

Figure 4.

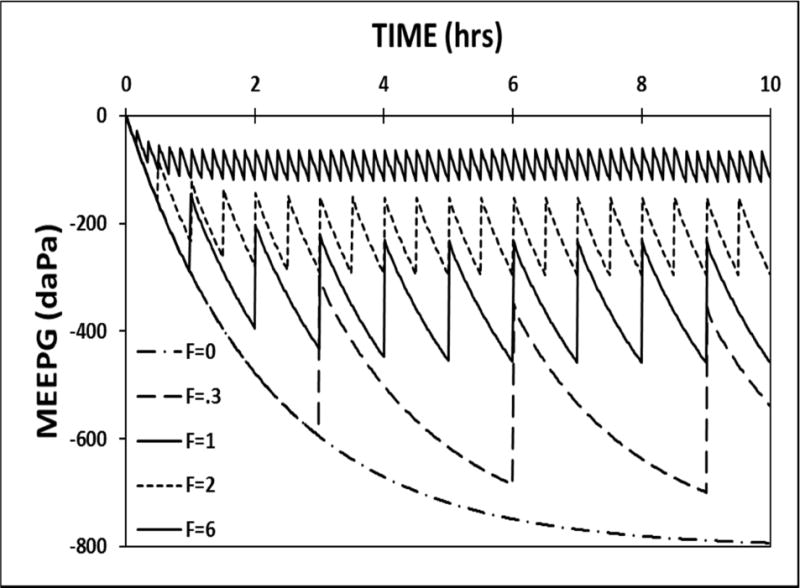
A 10-hour model simulation of the MEEPG trajectory calculated using standard model parameters while varying the active ET opening frequency (F, measured in functional openings/hour).

4.5 Effect of trans-ET gas conductance on MEPR

To simulate the effect of changing ET conductance, K^FGE_g, on MEPR, the perfusion-rate for the standard model was set to 1.0 MEM blood-volumes/second, the ET opening frequency was fixed at 6.0 openings/hour and the K^FGE_g was varied over a range of values. Figure 5 shows the MEEPG trajectories for a K^FGE_g of 0.0, 0.2, 0.3 and 1.0. At a fixed ET opening frequency, the absolute value of the EV-MEEPG is decreased with increasing ET conductance. The MEPR efficiencies for these four simulations is: 0.0, 0.0, 0.27 and 0.81, respectively which shows that, like the frequency of ET openings, ET conductance is a variable-magnitude MEPR regulator.

Figure 5.

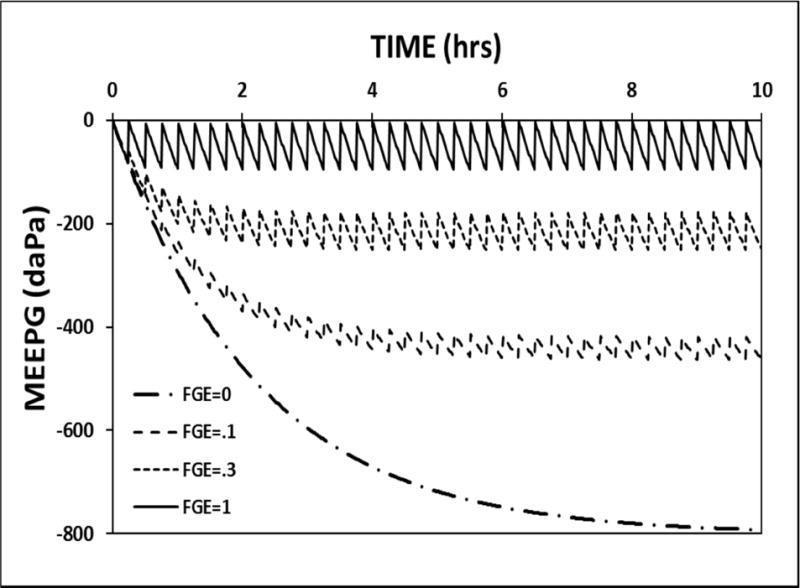
10-hour model simulation of the MEEPG trajectories calculated using the standard model parameters while varying the trans-ET conductance estimated as the FGE.

4.6 Interaction between homeostatic regulators and stressors

As demonstrated in the above simulations, the MEM blood-volume and perfusion-rate control the rate at which trans-barrier species-exchange drives the MEEPG to its expected value of ≈−800 daPa, while the two parameters of ET opening efficiency, opening frequency and trans-ET conductance, adjust the EV-MEEPG to values corresponding to higher MEPR efficiencies. Most simply, the former parameters control the rate of ME gas-loss secondary to trans-barrier exchange while the latter control the rate at which the depleted gas is replenished during ET openings, i.e ME gas-gain. These opposing ME gas-flows are characteristic of a flow-regulated mechanism such that MEEPG stability measured as MEPR efficiency is maximized if, for every near-zero, time-interval, the gas-flows to and from the ME are equal. Consequently, MEPR efficiency is affected by conditions that change either the rate of ME gas-loss, or gas-gain or both. This interaction is exemplified by the ME pressure-trajectories predicted by the standard model with a fixed ET opening efficiency of (ET opening frequency=2/hour; FGE=0.3) while varying the MEM blood perfusion-rate between 0.05 and 1.0 MEM blood-volumes/second. That family of curves is presented in Figure 6. At a fixed non-zero ET opening efficiency, the absolute value of the EV-MEEPG increases with progressively higher MEM blood perfusion-rates, an effect reflected in the calculated MEPR efficiencies of 0.83, 0.67, 0.40, 0.10 and 0.00 for MEM blood perfusion-rates of 0.05, 0.1, 0.2, 0.5 and 1 MEM blood-volumes/second, respectively.

Figure 6.

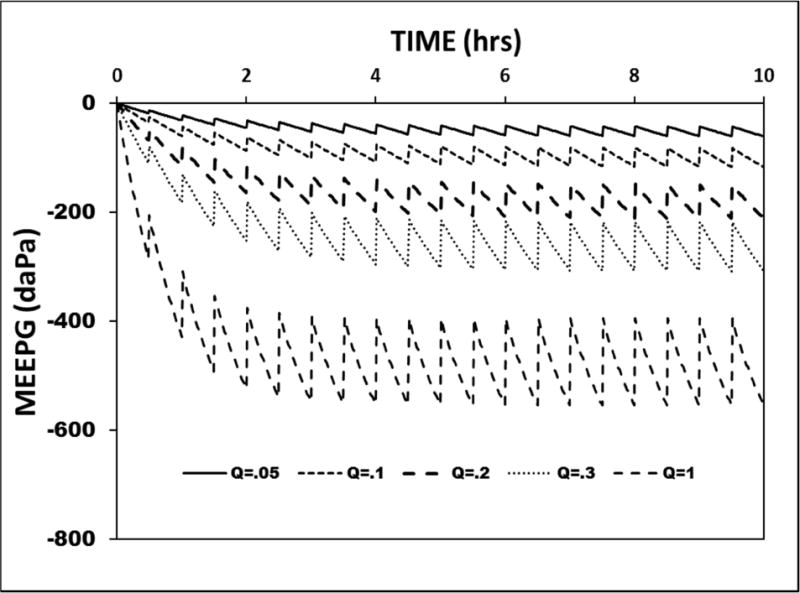
A 10-hour model simulation of the MEEPG trajectory calculated using the standard model parameters and a fixed ET opening frequency and conductance while varying the MEM blood perfusion rate (Q, measured in resident volumes/second).

4.7 The flow-regulated model predicts physiologic ME gas composition

Direct measurements consistently show that, while the ME O₂, H₂O and CO₂ pressures approximate those for venous blood, N₂ pressure is greater than that for the blood, atmosphere or any exchange compartment (Felding et al., 1987; Hergils et al., 1990; Hergils et al., 1997; Sade et al., 1993). Importantly, these measured ME species-pressures are predicted by any parameterization of the flow-regulated model that includes a non-zero ET opening efficiency and a near 0 EV-MEEPG. Moreover, simulated species-pressure vs. time functions show that, irrespective of the initial ME gas composition, that composition will evolve over time to converge on the measured physiologic values. This targeted evolution is illustrated in Figure 7 which shows the ME fractional species-pressure trajectories for O₂, CO₂ and N₂ and their expected values under the initial condition of a ME dry-gas composition of 100% O₂. There, the standard model was calibrated to the default values and the species-pressure trajectories were calculated over a 100-hour period. By 3 hours, the fractional ME CO₂ pressure increased from 0 to its venous/ME value of about 0.07; by 60 hours, the fractional O₂ pressure decreased from approximately 0.94 (remaining 0.06 is H₂O) to its venous/ME value of about 0.04 and, by 90 hours, fractional N₂ pressure had increased from 0 to its typically measured ME value of about 0.83. Simulations with other initial compositions, including those containing non-physiologic gases, have different trajectories and species-pressure equilibration times but all trajectories converge on their respective values for the “normal” ME. The 0.83 N₂ fraction for the ME is larger than that of air and blood because of the periodic introduction of NP gas to the ME coupled with the preferential loss of ME O₂ and CO₂ vis a vis N₂, a consequence of the relative trans-MEM conductances for those gases.

Figure 7.

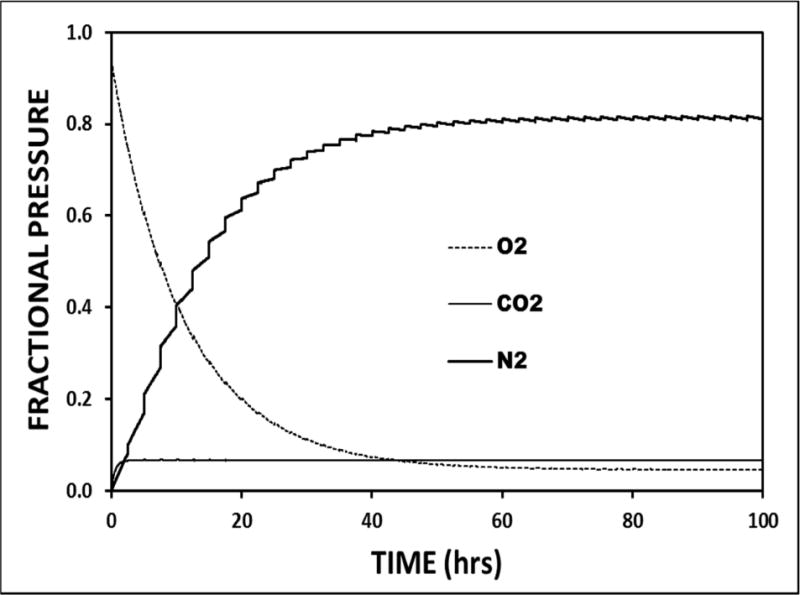
A 100-hour model simulation of the ME fractional species-pressures for O₂, N₂ and CO₂ as a function of time calculated using standard parameters, no ET openings and an initial ME gas composition of 100% O₂ saturated with H₂O at body temperature and standard atmospheric pressure.

4.8 The flow-regulated model predicts the MEEPG trajectory interpreted by some as evidence for “mucosal gas-production”

A pattern of progressively more positive MEEPGs is observed within the first hour after closing an existing trans-TM gas-phase communication between the ME and atmosphere as exists for ears with a patent ventilation tube or TM perforation (Buckingham, 1990; Buckingham et al., 1980). This ME pressure-behavior has been interpreted as evidencing MEM gas-production. To reproduce the conditions under which the phenomenon is observed, the initial ME gas composition for the standard model was set to that measured by Felding for MEs with a patent ventilation tube (Felding et al., 1987) and the MEEPG trajectory was simulated for a 10-hour period begun after closing that exchange-route. The simulation was repeated for the standard exchange parameters modified for conditions of 1) no ET openings, 2) functional ET openings, 3) no ET openings and a decreased MEM perfusion-rate and 4) no ET openings and an initial ME gas composition intermediate between that reported by Felding for MEs with and without a TM defect (Felding et al., 1987). All four simulations predict a MEEPG trajectory characterized by an initial phase of increasing MEEPGs which is followed for the 3 simulations without ET opening by a prolonged period of decreasing values to the EV-MEEPG of ≈−800 daPa (Figure 8). Changing the initial ME species-pressures or introducing ET openings affects the magnitude of the positive gradient phase, while changing the perfusion-rate affects the timing of the peak MEEPG. These results show that under initial conditions that replicate those associated with increasing MEEPGs in experiments, the pressure behavior is predicted by a passive exchange model, is driven by the abnormal ME species pressures established during an open communication with the atmosphere and is not evidence of MEM gas-production, counter-gradient trans-MEM gas-diffusion or facilitated gas-transport to the ME.

Figure 8.

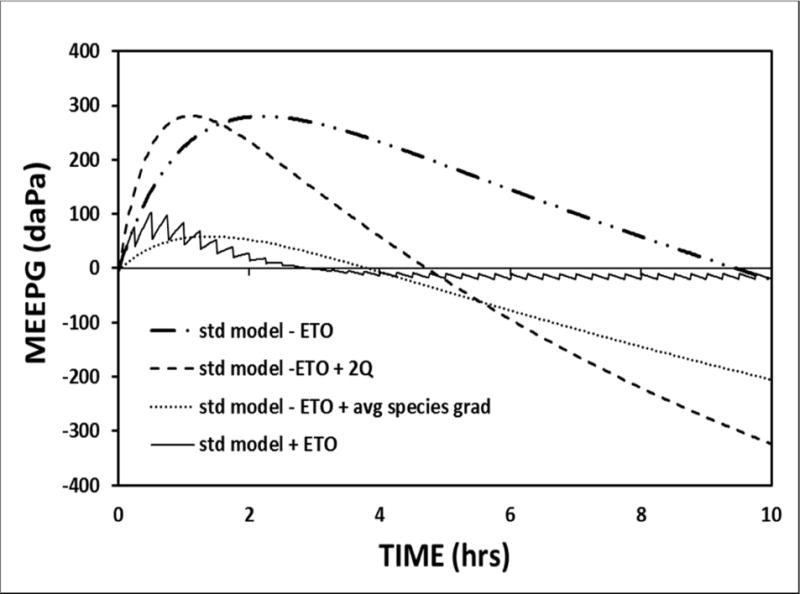
A 10-hour model simulation of the MEEPG trajectory for a closed ME calibrated to standard model parameters 1) with no ET openings, an initial ME gas composition equal to that measured for ears with functioning ventilation tube (Standard-ETO), 2) with no ET openings and an initial ME gas composition intermediate between those pressures and ME physiologic pressures (Standard-ETO+avg species gradient), 3) with no ET openings and a doubled mucosal blood perfusion rate (Standard-ETO+2Q), and with functional ET openings (Standard+ETO).

4.9 For the flow-regulated model, the ME surface-area/volume ratio influences the rate of change in the MEEPG caused by trans-barrier species-exchange

Some surgical procedures like mastoidectomy change the surface-area/volume ratio for the ME. For example, while ME volume is little affected by mastoidectomy, its surface-area is significantly reduced by the elimination of a majority of the high-surface area, small-volume mastoid air-cells (Csakanyi et al., 2014). The predicted effect of changing the ME surface-area/volume ratio on MEPR is shown in Figure 9 for simulations run using the standard model without ET openings. Like the consequences of changing MEM blood-volume or blood perfusion-rate, the rate of change in the MEEPG, but not the EV-MEEPG, is directly related to the ME surface-area/volume ratio. From the graphs shown in Figure 6, decreasing the rate of MEEPG change consequent to trans-barrier gas-exchange by any means including reducing the SA/volume ratio will increase MEPR efficiency for ears with a non-zero ET opening efficiency. This result has clinical implications with respect to the choice of procedures for mastoid reconstruction (Csakanyi et al., 2014; Yung, 1996) in that tissue engineering procedures intended to recreate a “normal” MACS geometry characterized by a high surface area/volume ratio (Kanemaru et al., 2005; Kanemaru et al., 2013; Kanemaru et al., 2004) are predicted, under this model, to impair rather than improve MEPR efficiency.

Figure 9.

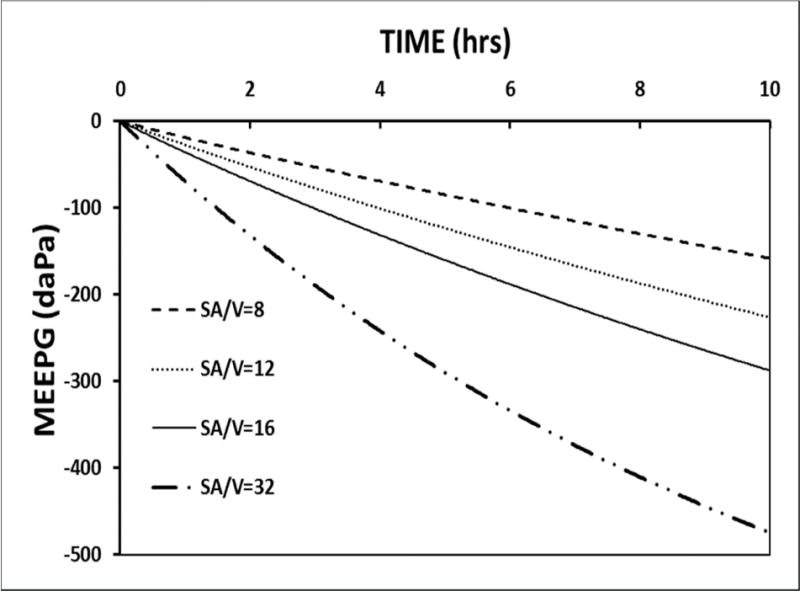
A 10-hour model simulation of the MEEPG trajectory calculated with no ET openings using the standard parameters while varying the ME surface-area/volume (SA/V) ratio.

5.0 DISCUSSION

Efficient ME function requires that the TM be maintained at maximum compliance with approximately equal ME and ambient total gas pressures. Because the ME is not in direct communication with the environment, ME and environmental pressures vary independently over time which causes significant MEEPGs. Dissipation of those gradients is accomplished by a homeostatic mechanism, MEPR, that has a very narrow tolerance for hearing efficiency, MEEPG range from approximately −100 to 100 daPa, and a wider, but still limited, tolerance for preservation of a healthy MEM and a fluid-free-gas space, MEEPGs greater than approximately −300 daPa (Doyle, 2000). Operationally, the mechanism of MEPR must be capable of detecting ME-ambient pressure deviations and then adjusting the ME gas-pressure to match environmental pressure. From an engineering perspective, there are a number of simple mechanical configurations with these capabilities, e.g. volume-regulation, pressure-regulation and flow-regulation.

Standard textbook descriptions of ET function assume that MEPR is a flow-regulated mechanism. Flow-regulation implies that ME gas-pressure is controlled only by the relative rates of the molar species-exchanges between the ME and atmosphere, perilymph and MEM blood by trans-barrier diffusion and the bolus gas-exchange between the ME and NP during ET openings (Doyle, 2000). Stable ME pressures and maximum TM compliance are predicted when the algebraic sum of the ME moles exchanged across all four pathways is 0 and stable MEEPGs are predicted when that condition is met and atmospheric pressure is constant. Because the equations that govern those types of exchanges are well known (Ranade et al., 1980), it is possible to formalize a flow-regulated description of MEPR as a mathematical model that can be calibrated to known values or narrow-range estimates of the controlling parameters (Doyle, 2000; Kanick et al., 2005). In turn, through simulations, that model can be interrogated to identify the parameters that modulate MEPR efficiency and also used as a platform for hypothesis development and testing. In this paper, a formal mathematical model of flow-regulated MEPR is developed and tested for predictive accuracy. Specifically, after calibrating the model parameters to known or expected values, simulations of MEEPG trajectories were run to identify the homeostatic stressors and regulators of MEPR, test the completeness of a flow-regulated description of system behavior and demonstrate the potential clinical utility of model predictions.

Simulations 1 through 6 identified the stressors and regulators of flow-regulated MEPR. Simulation 1 shows that, under physiologic conditions, the contributions to MEPR of the trans-RWM and trans-TM gas-exchanges are very limited. Simulations 2 and 3 show that trans-MEM gas-exchange is the primary intrinsic cause and atmospheric pressure change is the primary extrinsic cause of MEEPG instability and, thus, represent MEPR stressors. The rate of MEEPG change secondary to trans-barrier exchange, the intrinsic stressor magnitude, is directly related to the MEM blood perfusion-rate and, consequently, is increased by increasing the resident MEM blood-volume and/or the MEM blood perfusion-rate. Also, in all simulations with an ET opening efficiency of 0, the EV-MEEPG for trans-barrier exchange is approximately equal to the difference in N₂ pressure between the ME and venous blood, ≈−800 daPa, which is more than sufficient to cause significant conductive hearing losses (Austin, 1978; Dobie et al., 1979; Kitahara et al., 1994; Lildholdt, 1983; Tonndorf, 1964; Truswell et al., 1979) and precipitate the collapse of the ME gas-pocket (Alper et al., 1997; Flisberg, 1970; Swarts et al., 1995). Simulations 4 and 5 show that ET opening efficiency is the sole regulator of the EV-MEEPG magnitude, such that MEPR efficiency is directly related to both the trans-ET gas-conductance and the ET opening frequency. There, gradient-driven trans-ET gas-flow between the ME and NP during active ET openings at a positive or negative MEEPG and passive openings at a positive MEEPG decrease the absolute value of the pre-opening MEEPG. Finally, Simulation 6 shows that MEPR efficiency reflects a balance between stressor magnitude and regulator efficiency, such that, efficient MEPR can occur at a low stressor magnitude and low, but not zero, regulator efficiency or a high stressor magnitude coupled with a high regulator efficiency.

The predictive accuracy of this model is demonstrated by the close similarity between the simulated MEEPG trajectory at an ET opening efficiency of 0 and the observed trajectory for monkeys with experimentally abolished ET openings (Cantekin et al., 1980; Casselbrant et al., 1988). Also, it is known that ET opening efficiency has both a constitutive and a situational component and that constitutive efficiency is downgraded temporarily during conditional situations such as an extant viral upper respiratory infection (Doyle et al., 2014). Simulations 5 and 6 predict that a downgraded ET opening efficiency will be expressed as a less efficient MEPR for those periods which is accompanied by a consequent negative shift in the EV-MEEPG, effects validated by the change in MEEPG (tympanometric pressure) observed for children and adults during natural and experimental upper respiratory viral infections (Antonio et al., 2002; Buchman et al., 1995; Moody et al., 1998). In addition, emergent features of the model such as physiologic ME species-pressures (Simulation 6), the negative EV-MEEPG for all ET opening efficiencies not equal to 1 (Simulation 3), and the perfusion-limitation on the rate of MEEPG change (Simulations 2, 3) are consistent with clinical measurement (Antonio et al., 2002; Felding et al., 1987; Hergils et al., 1990; Hergils et al., 1997; Moody et al., 1998; Sade et al., 1993) and experimental results (Buchman et al., 1995; Teixeira et al., 2015; Teixeira et al., 2016).

Simulation 8 illustrates the model’s usefulness for hypothesis testing. There, the hypothesis that the increased MEEPG observed under certain atypical physiologic conditions is not consistent with a flow-regulated MEPR and the corollary that the observed phenomenon evidences MEM gas-production were tested. The results fail to support either the hypothesis or its corollary. Rather, they show that, under applicable conditions, the phenomenon is a predictable consequence of a flow-regulated MEPR and, by application of Occam’s Razor, does not require or evidence MEM gas-production.

Finally, Simulation 9 demonstrates the potential clinical utility of these types of models with respect to identifying the better choice of intervention options to maximize MEPR efficiency. Past work has called attention to preservation or re-establishment of efficient MEPR during or after surgical procedures that disrupt the compartment structure of the ME such as mastoidectomy (Csakanyi et al., 2014; Doyle, 2007; Kanemaru et al., 2005; Kanemaru et al., 2013; Kanemaru et al., 2004; Yung, 1996). Some investigators recommend reconstructing the typical MACS geometry after the mastoidectomy had created a large gas-cell by obliterating the honeycomb gas-cell structure of the MACS (Kanemaru et al., 2005; Kanemaru et al., 2013; Kanemaru et al., 2004; Yaguchi et al., 2007). Measurements show that simple mastoidectomy decreases the ME surface-area/volume ratio (Csakanyi et al., 2014) which implies that reconstructing the original MACS would increase that ratio (Doyle, 2007). Simulation 9 shows that MEPR efficiency is inversely related to the magnitude of the ME surface-area/volume ratio, an effect driven by the direct relationship between that ratio and the rate of ME gas-loss. This result predicts that, for flow-regulated MEPR, the recommended reconstruction would increase, not decrease, the risk for hearing loss and ME pathology.

Not included in this first generation model is the change in ME volume caused by TM displacement in response to non-zero MEEPG, MEM swelling and fluid transudation in response to hydrostatic pressure differences between the ME gas space and mucosal tissue or MEM swelling in response to noxious stimuli (Gaihede et al., 2010; Padurariu et al., 2015; Sade et al., 1996; Sade et al., 1997b). This omission was intentional so as to preserve the relative simplicity of the model structure but also to allow for direct comparisons between the MEEPGs predicted by the model and those reported in the literature. For the latter, most experimental and clinical reports on ME pressure behavior recorded tympanometric pressures which estimate the MEEPG at a neutral position, i.e. a restored/normalized ME volume. Also, the model was developed to describe MEPR in the normally functioning ME and all mechanisms of volume collapse including TM retraction, MEM swelling and fluid accumulation in the ME cavity are in and of themselves pathological expressions that downgrade ME hearing function.

Nonetheless, it has been suggested that ME volume change can buffer the MEEPG to the effects of trans-barrier molar exchanges (Ars et al., 1994; Cinamon et al., 2003; Hellstrom et al., 1983; Sade, 2000). Under the rules for model development stated in the Methods section, the introduction of these effects into the model is reserved for a later generation model. However, a simplified analysis that ignores the compliance of the ME collapsible structures shows that, within the context of a flow-regulated system, ME volume change will not affect the EV-MEEPR or prevent the pathological consequences of low EV-MEEPRs, i.e. contribute to MEPR. This can be appreciated by examining the effect of volume change on the pressure of a gas cavity experiencing molar gas loss at a rate proportional to the difference between the cavity pressure (e.g. the ME) and a reference compartment (e.g. the mucosal blood). Briefly, ME pressure will be stable (P₀^ME_g) under volume change if:

$$\mathbf{\partial }{\mathbf{V}}^{\mathbf{M}\mathbf{E}}\mathbf{/}\mathbf{\partial }\mathbf{t}\mathbf{=}\mathbf{\partial }{{\mathbf{n}}^{\mathbf{M}\mathbf{E}}}_{\mathbf{g}}\mathbf{/}\mathbf{\partial }\mathbf{t}\mathbf{(}\mathbf{R}{\mathbf{T}}^{\mathbf{M}\mathbf{E}}\mathbf{/}{\mathbf{P}}_{\mathbf{(}\mathbf{t}\mathbf{=}\mathbf{0}\mathbf{)}}{{\mathbf{ }}^{\mathbf{M}\mathbf{E}}}_{\mathbf{g}}\mathbf{)},\text{under the requirement that},\mathbf{\partial }{{\mathbf{n}}^{\mathbf{M}\mathbf{E}}}_{\mathbf{g}}\mathbf{/}\mathbf{\partial }\mathbf{t}\mathbf{=}\mathbf{\partial }{{\mathbf{n}}^{\mathbf{M}\mathbf{E}}}_{\mathbf{N}\mathbf{2}}\mathbf{/}\mathbf{\partial }\mathbf{t}\mathbf{=}{{\mathbf{K}}^{\mathbf{MEM}}}_{\mathbf{N}\mathbf{2}}\mathbf{\Delta }\mathbf{(}{\mathbf{P}}_{\mathbf{(}\mathbf{t}\mathbf{=}\mathbf{0}\mathbf{)}}{{\mathbf{ }}^{\mathbf{M}\mathbf{E}}}_{\mathbf{N}\mathbf{2}}\mathbf{-}{{\mathbf{P}}^{\mathbf{V}\mathbf{B}}}_{\mathbf{N}\mathbf{2}}\mathbf{)}\mathbf{\approx }\mathbf{600}{{\mathbf{K}}^{\mathbf{MEM}}}_{\mathbf{N}\mathbf{2}}$$ EQ16a

when pressures are measured in daPa. This relationship can be expressed more simply as,

$$\mathbf{\partial }{\mathbf{V}}^{\mathbf{M}\mathbf{E}}\mathbf{/}\mathbf{\partial }\mathbf{t}\mathbf{\approx }\mathbf{600}{{\mathbf{K}}^{\mathbf{MEM}}}_{\mathbf{N}\mathbf{2}}\mathbf{(}{{\mathbf{V}}^{\mathbf{M}\mathbf{E}}}_{\mathbf{(}\mathbf{t}\mathbf{=}\mathbf{0}\mathbf{)}}\mathbf{/}{{\mathbf{n}}^{\mathbf{M}\mathbf{E}}}_{\mathbf{g}\mathbf{(}\mathbf{t}\mathbf{=}\mathbf{0}\mathbf{)}}\mathbf{)}$$ EQ16b

which shows that rate of ME volume change required to stabilize ME pressure is a direct function of the trans-MEM N₂ exchange-constant and the initial ME volume and an inverse function of the total initial gas moles. More importantly, molar exchange driven volume change will continue unabated until either the volume is totally dissipated (i.e. total collapse of the gas pocket, e.g. a helium balloon in atmosphere, introduced fully collapsible biological gas pockets) or, as in the case of the ME, the maximum volume change is realized. At maximum volume change, ME volume is constant and ME pressure will decrease in accordance with the equations presented for the model to the predicted EV-MEEPG of ≈800 daPa. While this effect is conceptually simple, the true ME behavior is somewhat more complicated given the real-valued compliances of the ME structures. This introduces a phased transition in ME behavior from pure volume change to mixed volume/pressure change to pure pressure change, but there, the final MEEPG and all implications of the more simple analysis remain valid.

A large number of hypothetical mechanisms for MEPR has been published in the literature but operational details are lacking (Doyle, 2000). This functional ambiguity hinders advances in understanding of MEPR by ruling out formal comparisons among mechanisms with respect to predictive accuracy. To address this, a formal mathematical description of a flow-regulated mechanism that completely specifies the logical construct relating the underlying physiology to mechanistic function was developed and evaluated for predictive accuracy. This presentation format has the advantages of allowing all interested individuals to explore the inner working of the mechanism, design experiments to test mechanism validity, compare model accuracy with that for alternative mechanisms when formalized and explore the predicted efficacy of new interventions within a flow-regulated system.

7.0 CONCLUSIONS

A mathematical model of flow-regulated MEPR was developed and formalized. All processes included in the model have a well-established physiology that can be represented using simple mathematical equations. Thermodynamic considerations show that the included processes are energetically favorable as they obey the 2^nd law and reduce the free energy of the system to a local minimum. When linked within a formal model and calibrated to extant conditions, operation of those processes predicts observed system behaviors. By Occam’s razor, “Pluralitas non est ponenda sine necessitate”, or “Plurality is not to be posited without necessity (unless it is obvious unto itself)”, this energetically favored, minimalist should be considered the standard construct against which other models are compared for predictive accuracy. As such, the null hypothesis for testing in future studies is that this model is a complete description of MEPR with hypothesis rejection if and only if system behaviors not compatible with the model are observed.

• A mathematical description of middle-ear pressure-regulation as a flow-regulated process is developed from standard diffusion and air-flow equations.

• When parameterized to known values for the system and extant conditions, the model accurately predicts the middle-ear pressure-trajectories previously reported for clinical observations and interventional experiments.

• Operation of the model explains the generation of the measured higher than expected middle-ear N₂ pressures.

• The model predicts the time-limited increase in middle-ear pressure under certain initial conditions that was interpreted by some as evidencing gas production by the middle-ear mucosa.