Biological noise and positional effects influence cell stemness

Abstract

Biological (or cellular) noise is the random quantitative variability of proteins and other molecules in individual, genetically identical cells. As the result of biological noise in the levels of some transcription factors that determine a cell's differentiation status, differentiated cells may dedifferentiate to a stem cell state given a sufficiently long time period. Here, to provide direct evidence supporting this hypothesis, we used a live-cell monitoring system based on enhanced green fluorescent protein (eGFP) expression to continuously assess the “stemness” of individual human and murine malignant mesothelioma cells over a period of up to 3 months. Re-expression of the transcription factors, the top hierarchical stemness markers Sox2 (SRY-box 2) and Oct4 (octamer-binding transcription factor), monitored as cell eGFP expression was observed in a subpopulation of differentiated eGFP(−) malignant mesothelioma cells. However, we found that this transition was extremely rare. Of note, when it did occur, neighboring cells that were not direct descendants of a newly emerged eGFP(+) stem cell were more likely than non-neighboring cells to also become an eGFP(+) stem cell. This observation suggested a positional effect and led to a clustered “mosaic” reappearance of eGFP(+) stem cells. Moreover, stem cells reappeared even in cell cultures derived from one single differentiated eGFP(−) cell. On the basis of our experimental in vitro and in vivo findings, we developed a tumor growth model to predict the clustered localization of cancer stem cells within a tumor mass.

Introduction

Regarding the heterogeneity with respect to differentiation, cancer cell populations consist of cancer stem cells (CSCs)³ and a majority of non-CSC or “bulk” cancer cells. It is hypothesized that essentially the CSC subpopulation possesses the capability of tumor initiation and has the capacity for self-renewal (1, 2). Two main theories were initially developed to explain the distribution of CSC within a tumor: the hierarchical and the stochastic model (1). The hierarchical model suggests that the pool of CSC can only be maintained by cells that have CSC characteristics and, by definition, the ability to give rise to progeny with unlimited proliferative capacity. Thus, tumors contain: (i) proliferating CSCs that allow for tumor growth, (ii) transit amplifying cells that divide a certain number of times and then differentiate (or “mature”), and (iii) specialized tumor cells (bulk cells) that do not show mitogenic activity and thus do not contribute to tumor growth. According to this model, cells in a tumor are organized in a strictly hierarchical, assumingly one-directional system with CSCs at the top of the hierarchy, giving rise to all other cancer cell types. The stochastic model of cancer growth relies on a different concept for tumor growth. This model predicts that all cancer cells eventually have the same potential to grow and divide, but cells stochastically fluctuate between different states, i.e. between self-renewal and differentiation states. The cells in such a tumor do not operate in a deterministic, “well organized” system—any cell has the same intrinsic potential to contribute to tumor growth. Unlike in the hierarchical model, the stochastic model predicts that CSCs are not necessarily and exclusively derived from the CSC population. Currently, there is no definitive proof in favor of either model of tumor growth. The development of different cancer types may be explained in different ways; leukemia is thought to mostly follow the hierarchical model (3), whereas breast cancers likely develop according to the stochastic approach (4).

Malignant mesotheliomas (MMs) are tumors originating from the serosal cells covering the pleural, peritoneal, or pericardial cavities. MMs are highly aggressive neoplasms most often associated with asbestos exposure (5). One of the main major clinical issues with MM is that although initial tumor growth can be rather efficiently inhibited by first line chemotherapy (cis-platinum and pemetrexed), the few surviving cells lead to a rapid recurrence of the tumor. This subpopulation of tumor cells bearing increased chemotherapeutic resistance and augmented expression of stemness factors, including Sox2, Oct4, Nanog, Klf4, and c-Myc, are termed CSCs (6). In a recent study we identified and characterized MM cell subpopulations (CSC and non-CSC) in vitro based on their endogenous expression of Sox2 and Oct4 transcription factors (7) previously identified as stem cell markers (8). Sox2, Oct4, and Nanog are considered as transcriptional regulators of the core circuitry in the control of the stem cell state (9). In comparison to non-CSCs, we have shown before that MM CSCs possess different properties with respect to several clinically relevant parameters including chemoresistance in vitro and tumor initiating capacities in vivo (7). The Sox2/Oct4 reporter system, initially developed for the convenient identification of induced pluripotent cells (10), has been successfully applied to visualize early stages of cellular reprogramming (11) and in our case in MM cell lines to identify, isolate, and visualize CSCs by the expression of enhanced green fluorescent protein (eGFP) (7). Similar approaches were used in breast cancer cells with reporter systems for Sox2 and Oct4 (12), as well as for Nanog (13). These eGFP-based reporter systems allow isolating, visualizing, and observing in real-time the dynamics of CSC in vitro and in vivo.

Because a cell's differentiation status is also determined by the activity and levels of a number of transcription factors (both in normal primary and in cancer cells) (14), theoretically, as the result of biological noise (15), all differentiated cells might dedifferentiate to a stem cell state, if allowing sufficient time for this event to occur. In our study, we addressed the following questions: Can we observe dedifferentiation processes likely based on biological noise? Which type of stem cell model describes most accurately the experimental data obtained in vitro and in vivo? To provide answers to these questions, we continuously monitored and recorded selected (by FACS sorting based on eGFP expression levels) bulk and stem cell subpopulations for periods of several months.

Results

Steady-state equilibrium between eGFP(+) and eGFP(−) cells

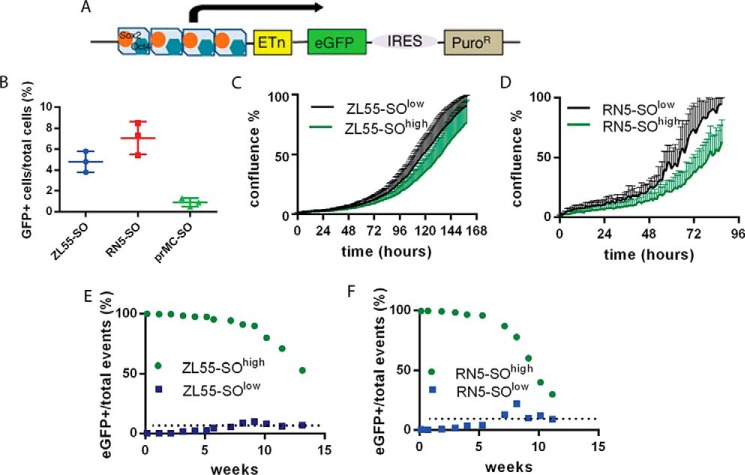
For the initial identification of cells with stem cell-like properties in MM and in primary mesothelial cells (prMCs), we made use of a tool initially developed for stem cell biology. In this lentivirus-based approach, mesothelioma cell lines of human (ZL55) and mouse origin (RN5), as well as normal mouse prMCs, were infected with a construct as described by Hotta et al. (10, 16) that contains Sox2- and Oct4-binding sites in the promoter region followed by an expression cassette coding for the eGFP and an internal ribosome entry site (IRES) connecting to a puromycin resistance cassette that allows for the puromycin selection of Sox2- and Oct4-expressing (SO) cells (Fig. 1A). However, we did not make use of the puromycin selection possibility in this study. The general infection efficacy in the used cells was determined by using another reporter construct: SORE6-mCMVp-dsCopGFP-PURO (12). In this plasmid the puromycin resistance is not under the regulation of the Sox2/Oct4 promoter as is the expression of eGFP. After infection, cells were selected with puromycin for 24 h. In the puro-resistant cell population, we observed ∼4% of eGFP(+) cells for ZL55 and ∼8% eGFP(+) cells for RN5 cells. These values are almost identical to the ones previously observed after transduction with the Hotta construct (10, 16), i.e. 4.8 and 7.1%, respectively (7). Sufficiently high expression levels of endogenous Sox2 and Oct4 drive eGFP expression, which allowed to identifying CSC. ZL55 and RN5 MM cells, as well as prMC cells infected with the stemness reporter lentivirus at a multiplicity of infection of 10 were called ZL55-SO, RN5-SO, and prMC-SO cells. After repetitive passaging and maintenance of ZL55 cells in culture for more than 1.5 months, the fraction of eGFP(+) cells within the entire cell population remained remarkably stable, i.e. ∼5%. Quantitative analyses by FACS revealed 4.8 ± 0.6% of eGFP(+) ZL55-SO cells (Fig. 1B); a similar consistent fraction of eGFP(+) cells (7.1 ± 1.5%) was observed over a period of 2 months in the population of murine MM RN5-SO cells. In long-term MM cell cultures (>2 months) the proportion of eGFP(+) cells varied to some extent, which we attributed to “biological noise”; however, no time-dependent trends toward either higher or lower proportion of eGFP(+) cells was observed (data not shown). After 2 weeks in culture, part of ZL55-SO and RN5-SO were sorted as described above and resulted in ZL55-SO^low, ZL55-SO^high, RN5-SO^low, and RN5-SO^high cell populations, characterized by either complete absence of eGFP (those with the superior label “low”: eGFP(−)) or essentially 100% of eGFP(+) (those with the superior label “high”) cells, respectively, as reported before (7). In the population of ZL55-SO^high and RN5-SO^high cells, mRNA expression levels of the stem cell markers Sox2 and Oct4, as well as other markers (Aldh1, Klf4, Nanog, and c-Myc) were elevated as reported before (7). Real-time cell growth curves obtained by live cell imaging of SO^low and SO^high cells revealed that SO^high generally grew slower than SO^low cells (Fig. 1, C and D); the effect was more evident in RN5 cells. CSCs are characterized by lower proliferation rates than non-CSCs (17).

Figure 1.

Properties of stem cell-enriched cell populations of mesothelial origin. A, schematic representation of the pL-SIN-EOS-S(4+)-EiP lentiviral construct with Oct4 (blue) and Sox2 (orange) binding sites. Upon Oct4 and Sox2 binding, expression of eGFP and Puro^R (driving puromycin-N-acetyl transferase) is induced. IRES, internal ribosome entry site. B, percentage of eGFP(+) cells typically observed after lentiviral transduction with the pL-SIN-EOS-S(4+)-EiP construct in human ZL55 MM cells, mouse RN5 MM cells, and mouse prMC. The lines represent means ± S.D.; n = 3 independent measurements. C and D, representative growth curves of sorted eGFP(−) and eGFP(+) cells derived from ZL55 (C) and RN5 (D) cells. Each point represents mean ± S.D.; n = 10. E, kinetics of disappearance of eGFP(+) ZL55 cells initially consisting of 100% (freshly sorted) eGFP(+) ZL55-SO^high cells (green dots) and appearance of eGFP(+) ZL55 cells from initially 100% (freshly sorted) eGFP(−) ZL55-SO^low cells (blue dots). After 13 weeks in vitro, the two curves are approaching the percentage of eGFP(+) cells observed in non-sorted ZL55-SO cells, i.e. ∼4.8% (dotted line), as shown in B. F, identical experiment with sorted RN5 cells; both populations approached the equilibrium of 7.8% observed in unsorted RN5-SO cells (dotted line).

In the next series of experiments, we explored the fate of eGFP(+) and eGFP(−) cells over time. For this, the sorted cell populations were continuously maintained in culture, and changes in the proportions of eGFP(+)/total cells were quantitatively analyzed weekly by FACS. In line with both, the hierarchical and stochastic model of stem cells, a fraction of eGFP(+) ZL55-SO^high and RN5-SO^high cells gradually lost eGFP expression, indicative of a loss of stemness and a differentiation toward bulk cancer cells. Within the population of SO^high cells, an eGFP(−) cell population slowly emerged; the rate of appearance with time is shown in Fig. 1 (E and F). Because the decrease of eGFP(+) cells could be the result of several processes including (i) loss of stemness caused by a decrease in Sox2/Oct4 levels resulting in a shift toward differentiation according to the stem cell models, (ii) faster growth of the already differentiated eGFP(−) population cells present in the original population of sorted cells, or (iii) inactivation of the promoter region of the transgene by DNA modification (e.g. methylation), we aimed to determine which mechanisms were likely implicated in the accumulation of eGFP(−) cells with time. Previously we have demonstrated the unlikeliness of promoter inactivation by an additional infection of RN5-SO^high cells with a lentivirus constitutively expressing NLS-mCherry (red fluorescent nuclei). These cells formed tumors in vivo as demonstrated after 8 weeks. Tumor-derived cells were cultivated in vitro and revealed that a fraction of NLS-mCherry(+) cells had lost eGFP expression. RN5-SO^{high/NLS-mCherry} cells were maintained in culture in vitro for 57 days and analyzed by FACS for green (eGFP) and red (NLS-mCherry) fluorescence. Although the fraction of NLS-mCherry(+) cells only marginally decreased from 99.8 to 99.0%, the fraction of eGFP(+) cells decreased from 99.6 to 77.8% (for details, see Ref. 7). Here we carried out a similar experiment with ZL55-SO^high and additionally RN5-SO^high cells that had been maintained in culture for 2 months, resulting in the appearance of eGFP(−) cells in both cell lines. These cells were reinfected with a lentivirus encoding all four Yamanaka factors (SOX2, OCT4, KLF4, and NANOG) (18). This resulted in an increase in eGFP expression in the previously eGFP(−) cells; the results are shown for ZL55-SO^high cells (Fig. S2).

A final series of experiments was carried out with the population of SO^low cells. After prolonged cultivation (>10 passages) and moreover with a very low probability, we were able to observe the appearance of eGFP(+) cells from the subpopulation of sorted initially 100% eGFP(−) cells. The population of selected ZL55-SO^low and RN5-SO^low cells was monitored continuously for 15 weeks, and the results are shown in Fig. 1 (E and F). After a lag phase of 1–1.5 months, in both cultured ZL55-SO^low and RN5-SO^low cells, eGFP(+) cells started to appear. Moreover, in close proximity of the eGFP(+) cells, new eGFP(+) non-daughter cells appeared; more details are described below. The proportion of eGFP(+) cells then reached a value closely approaching the initial proportional rate of the unsorted SO cells. The same held true for the proportion of the initially 100% eGFP(+) SO^high cells (Fig. 1, E and F). We presume that the fraction of eGFP(+)/total cells is an intrinsic property for a given MM cell line and that this property (information) is inherent for both, SO^high as well as SO^low cells.

Emerging of an eGFP(+) stem cell population from one single bulk cell

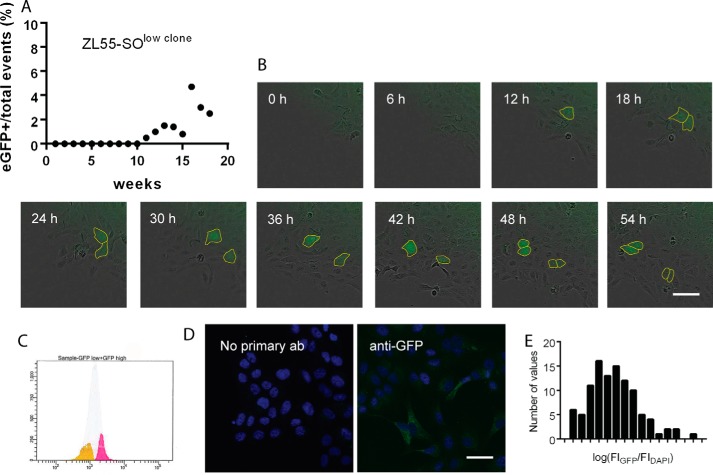
To determine, whether a stem cell population may emerge from one single ZL55-SO^low cell, clones originating from one single ZL55-SO^low cell were grown in culture. By single-cell cloning, several subpopulations of eGFP(−) cells were maintained for several passages (10–15 requiring ∼2.5 months); all cells within one well (clone) were initially 100% eGFP(−) (data not shown). The fate of the cell cultures was followed in vitro. At regular intervals (once per week), the cells were passaged, and the percentage of eGFP(+) cells was determined by FACS analyses. After 10 weeks in culture, we observed the appearance of the first eGFP(+) cells. In one case, the newly formed eGFP(+) cell divided; one daughter cell showed eGFP expression, whereas the other one was again eGFP(−) (Movie S1). After this initial event and further growing and passaging of the cell clone, the fraction of eGFP(+) cells reached a value of ∼5%, closely resembling the ratio observed in the parental (non-sorted) ZL55-SO cell population (4.86%; Fig. 2A). Thus, it appears that the spontaneous change from an eGFP(−) to a CSC-like eGFP(+) cell is determined by “rules” that will eventually lead to the initial (apparently intrinsic) steady-state ratio as is observed in the non-selected SO cells. ZL55-SO cells derived from a single cell (low eGFP clone) were sorted again after 20 weeks in culture based on their eGFP expression, resulting in ZL55-SO^clone-low (yellow) and ZL55-SO^clone-high (pink) cell populations (Fig. 2C). Note that eGFP expression histograms of low and high eGFP clones showed a Gaussian curve in these populations, characteristics of biological noise (19). Also when ZL55-SO^clone cells were immunostained for eGFP and the fluorescent intensities were normalized to DAPI staining (Fig. 2D), the histogram showed a log normal distribution. In comparison to ZL55-SO^clone-low cells, ZL55-SO^clone-high cells revealed higher mRNA expression levels of typical pluripotency stem cell markers including POU5F1, SOX2, and ALDH1A1 indicative of increased stemness potential acquired by the initially eGFP(−) cells (Table S1).

Figure 2.

Appearance of eGFP(+) (stem) cells in a ZL55-SO^low clone derived from a single, sorted eGFP(−) cell. A, a representative clone was monitored for over 18 weeks and at weekly intervals. FACS measurement revealed a constant increase in the percentage of eGFP(+) cells. From week 16 on, the percentage of eGFP(+) cells remained ∼4%, close to the value (4.8%) observed in unsorted ZL55-SO cells. B, time-lapse series of a cultured clone (ZL55-SO^clone) derived from ZL55-SO^low cells. At t = 12 h, an eGFP(+) cell (marked with yellow) appears among the eGFP(−) cells that divides during the next 6 h. The two daughter cells divide once more (between 42 and 48 h), yielding four eGFP(+) cells. C, ZL55-SO^clone cells were sorted again based on their eGFP expression resulting in a ZL55-SO^clone-low (yellow) and a ZL55-SO^clone-high (pink) population. It is of note that eGFP expression forms a Gaussian curve in this population. D, ZL55-SO^clone cells were immunostained against GFP, and the fluorescent intensity was normalized to DAPI staining. E, the histogram of the fluorescence ratio eGFP/DAPI in sorted ZL55-SO^clone-high cells showed a log normal distribution.

Clustered reappearance of eGFP(+) cells

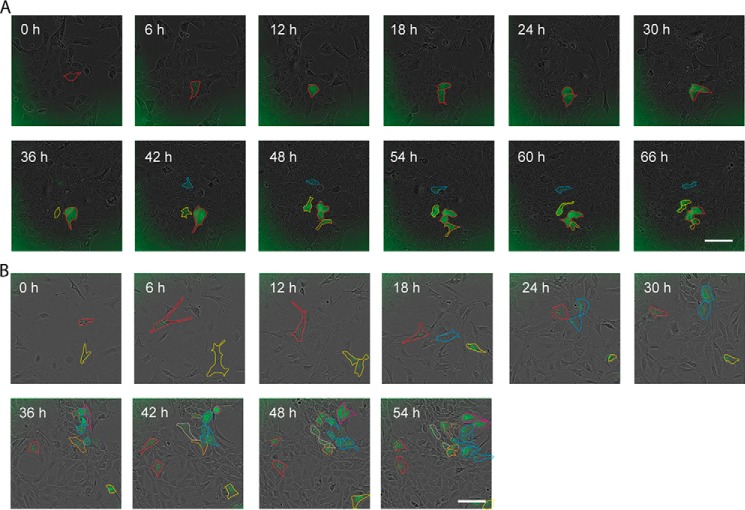
A closer inspection with respect to the reappearance of eGFP(+) cells revealed this process not to be of a stochastic nature. Not only daughter cells of newly formed eGFP(+) cells but also initially eGFP(−) cells in close vicinity of eGFP(+) cells showed a clearly higher propensity to become eGFP(+) cells (Fig. 3A). In ZL55-SO^low cultures we managed to record eight cases of newly generated eGFP(+) cells. A clustering behavior was observed in four of eight cases, where the spontaneous appearance of an eGFP(+) from SO^low cells was detected (Movies S2 and S3). In the other four cases, only one cell became green and not the neighbors. The appearance of an eGFP(+) cell from a SO^low cell occurred on average once every 7.2 weeks of observation. Considering that ∼1.5 × 10⁶ cells were generated during 1 week (one passage), the probability of a single cell to spontaneously convert to an eGFP(+) cell is estimated to be extremely low, in the order of 1:1.1 × 10⁸. Thus, spontaneous cell dedifferentiation is almost as likely as winning the lottery. The chance that two or three independent spontaneous cell transitions occur at the same time in the same area is equivalent to the probability of the event that two or three neighbors in the same week win the lottery. Because it is very unlikely, we assume an interaction during the stochastic processes to explain the experimentally observed phenomena.

Figure 3.

Clustered appearance of eGFP(+) stem cells. A, after the spontaneous appearance of a eGFP(+) cell, likely a cancer stem cell derived from a ZL55-SO^low population (marked with red), the cell divided within the next 12 h to give rise to two green eGFP(+) cells. Shortly afterward, in close vicinity of the cells marked with red, additional eGFP(+) cells (marked in yellow and blue) appeared, which are not daughter cells of the initial red-marked cells. Scale bar, 400 μm. B, appearance of eGFP(+), likely mesothelial stem cells in cultures of mouse prMC cells (marked in red and yellow). Also in cultures of prMC, in the vicinity of the eGFP(+) cells, additional eGFP(+) cells appeared (blue) that are not derived from the colonies marked with red and yellow. Scale bar, 400 μm. The time interval between all images was 6 h.

In the case of RN5 cells, we managed to record only once the reappearance of an eGFP(+) cell from an eGFP(−) cell culture. To test whether such clustering was an intrinsic property of transformed cells, i.e. MM CSCs, we also transduced prMCs with the eGFP reporter construct. The first observation was the lower percentage (0.9 ± 0.4%) of eGFP(+) cells in prMC cultures maintained in vitro for 1 month (Fig. 1B), but more importantly, we also observed the appearance of eGFP(+) cells from eGFP(−) prMC. In these cells we also found a clustered appearance of eGFP(+) cells in two of four cases (Fig. 3B and Movies S4 and S5). From these results, we conclude that the transition from a non-green to a green cell with stem cell properties is not linked to the transformation from normal to cancer cells but is also a property of normal untransformed primary cells.

Diffusing factors implicated in stem cell state determination

ZL55-SO cells were maintained either in fresh medium or conditioned medium from ZL55-SO^high cells, and the population of green cells was estimated by FACS analysis in these two conditions. In contrast to our initial expectation, the number of eGFP(+) cells was significantly lower in cells maintained in ZL55-SO^high medium (two-tailed paired t test, means ± S.D. of differences in green-cell percentage of total: 1.24 ± 0.56%, t(4) = 4.8, p < 0.01). Nonetheless, it indicated the presence of soluble factors produced by ZL55-SO^high cells affecting the stem cell state determination of the ZL55-SO cell population; possible mechanisms are discussed below. In addition to elevated levels of stemness factors in ZL55-SO^clone-high cells, we also found evidence for elevated levels of GLI1, a gene encoding a transcription factor that is directly modulated by the transcription factor Sonic Hedgehog implicated in morphogenesis (Table S1).

Numerical model for the locally interacting Markov-chain process

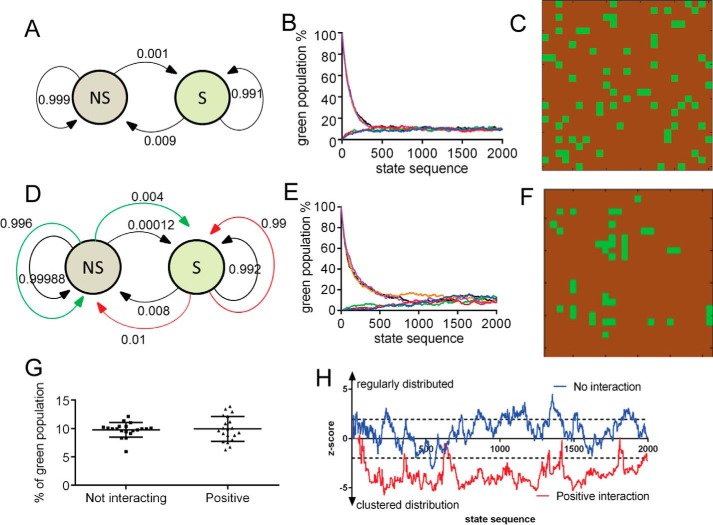
The features of the locally interacting Markov chain are described in the first model (Fig. 4, A–C). In this initial model, it is not necessary for cells to either divide or undergo apoptosis. As a feature of finite-state stochastic processes, the Markov chain will converge to equilibrium at a certain point of time independently of the initial condition. In our case, it did not matter whether the proportion of stem cells in the entire cell population was initially 0 or 100% (or any value in between). After a certain number of passages, the distribution always reached a certain steady-state proportion defined by the transition probabilities. Of note, the spatial distribution of cells in the S state (green) and NS state (brown) is entirely random (Fig. 4C and Movie S5).

Figure 4.

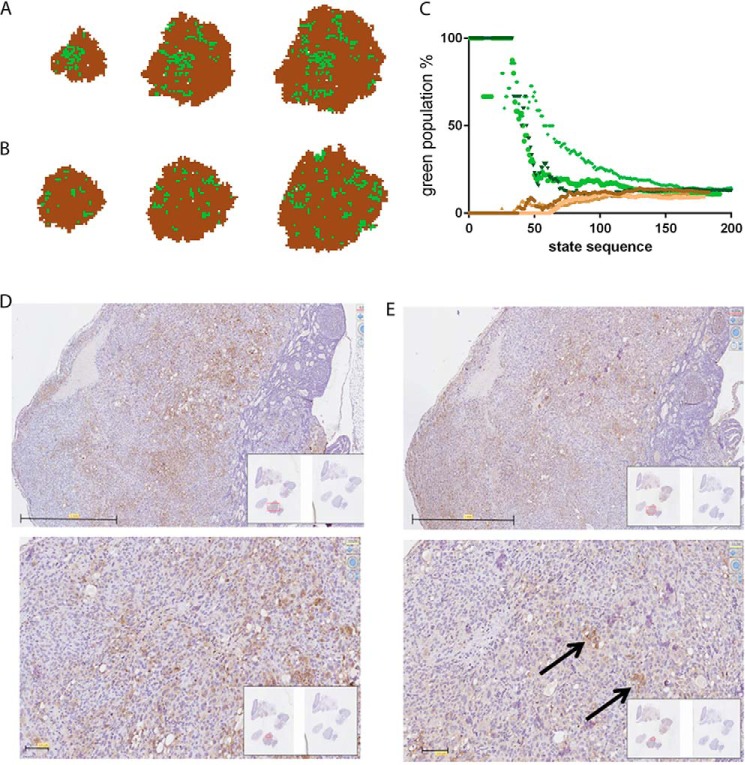
Features of spatially interacting Markov chain processes. A–C, model without interactions between cells. A, Markov graph of transition probabilities between bulk (NS, in brown) and stem cell (S, in green) states. B, state-sequence plot of 625 cells composed of either 100% N or 100% NS state cells. Each color represents one run. After ∼1000 steps the two populations reach a steady-state equilibrium. C, spatial pattern at steady-state equilibrium. Approximately 25% S state cells have a direct contact with another S state cell. D–F, models with positive cell–cell interactions. D, Markov graph of transition probabilities between bulk (NS) and stem cell (S) states. The outer colored lines represent the probabilities of changing states, if a cell in the opposite state is present in one of the nearest neighbor positions. E, state-sequence plot of 625 cells, if cells are either 100% in the N or 100% in the NS state. Each color represents one run. Of note, both curves (most notably for the ones in the NS state) have lag phases. F, spatial pattern at steady-state equilibrium. Most S cells are organized in clusters. G, in both models (not-interacting versus interacting), at equilibrium, the fraction of S state cells is essentially the same. Note the higher variability in the positive interaction model. H, the statistics on NNI index (z score) shows significant cluster formation in the interacting model.

The essential feature of the Markov chain processes to reach equilibrium remains, even if we assume local interactions between cells (Fig. 4, D–F). If an interaction is defined as a positive interaction, i.e. the state of a cell (S or NS) increases the probability of a neighboring cell to take up the same state, then the spatial distribution of cells with a given state will not be completely random. This in turn will lead to cell clusters in a given (S or NS) state (Fig. 4F and Movies S6 and S7). The other feature derived from the model, assuming a restricted (low) number of cells and moreover a very low probability of transition from one state to the other, predicts that the curve on the state proportion/state sequence plot would show an initial lag phase, best seen for the cells in the S state (Fig. 4E). This is in line with our in vitro results with ZL55-SO^low cells (Fig. 2). The appearance of eGFP(+) cells was observed only after a lag time of several weeks. However, after the appearance of such a low-probability event, the population of eGFP(+) and eGFP(−) cells reached the initial equilibria rather quickly. Of note, the proportion of S state cells is rather similar, whether using the simple Markov chain model (Fig. 4A) or the one with positive interactions (Fig. 4D). On the other hand, in the model allowing for interactions, the nearest neighbor index was clearly decreased, and the spatial patterns showed significant cluster formation (p < 0.05) (Fig. 4H). Also worth mentioning is the higher variability of the proportions of S state (green) cells in the numerous simulations, when applying the model with the positive interactions (Fig. 4, G and H).

Numerical model for tumor growth and in vivo testing

In the more realistic tumor growth model, we also took into account that cells divide and may undergo apoptosis. The experimentally determined spontaneous apoptosis rate, in both SO^low and SO^high populations, was found to be very low (less than 1% evidenced by annexin V–Cy3 staining), but they divided with different rates (Fig. 1D). Taking into account this information obtained in the in vitro model in the tumor growth model, we found that a tumor may be formed in silico from one single stem cell (S) or from one single bulk cell (NS) (Fig. 5, A and B, respectively). In both cases, the S state cells/total cells ratio tended toward steady-state equilibria (Fig. 5C). Another prediction derived from the model was the uneven distribution of S cells within the tumor mass. When starting from a single green S state cell (Fig. 5A and Movie S8) or from a single non-green (NS state) cell (Fig. 5B and Movie S9), the model predicted that S state cells will be preferentially localized in the center of the tumors and moreover organized in clusters.

Figure 5.

Tumor growth model and localization of MM cancer cells in a xenograft tumor in vivo. A and B, modeling of tumor growth starting from a single stem S cell (S, in green; A) or a single bulk cell (NS, in brown; B) and applying the “positional” concept. C, state-sequence plot when starting from an S cell (green dots, three runs) or when starting from an NS cell (brown dots, three runs). At each time point the percentage of S cells within the growing tumors are shown. D, injection of ZL55-SO^high cells (intraperitoneally) in NSG mice resulted in the formation of several tumors most often localized to the parietal pleura; staining of a representative tumor for the MM marker calretinin. The lower image was taken at a higher magnification. Scale bars, 1 mm (upper image) and 100 μm (lower image). E, staining of a parallel section for eGFP showed clustering of eGFP(+) cells often in the center of the tumor mass, in line with the predictions from the model (B). Scale bars, 1 mm (upper image) and 100 μm (lower image).

To test these model predictions, ZL55-SO^high cells were injected intraperitoneally into NSG mice. The identity of ZL55 tumor cells was assessed by staining for the MM marker calretinin (Fig. 5D). The staining showed the typical mosaic-like pattern as reported before in human breast cancer samples (12). Staining for eGFP revealed those cells to accumulate mainly in the center of the tumor mass and furthermore to form eGFP(+) cell clusters (Fig. 5E). Namely, the average maximum diameter of clusters was estimated as 62 ± 32 μm, the distance between the neighboring clusters was calculated as 271 ± 163 μm, and the closest distance between one cluster and the edge of the tumor was estimated as 168 ± 52 μm. Of note, because there is no straight border between eGFP-stained and unstained populations, the abovementioned values are only subjective estimations.

Discussion

The original hierarchical, unidirectional CSC model predicts that tumor cells lacking stem cell properties would not be able to initiate self-propagating tumors, and thus curative therapy should be targeted to fully eliminate the CSC population. This is expected to lead to complete tumor regression, even if all bulk non-CSC would initially remain (2). However, the stochastic appearance of CSC in populations of apparently “pure” bulk tumor cells (for technical considerations on the difficulties for identification and isolation of “pure” CSC and non-CSC populations; see also Ref. 20) strongly indicates that targeting of non-CSC bulk cells is equally important for tumor regression and cancer treatment. Most recently, the concept of bidirectional interconversion between CSCs and non-CSCs has gained wider acceptance (20), e.g. in the field of breast cancer (21).

We have reported previously on the successful approach to identify, characterize, and visualize a subpopulation of CSC-enriched MM cells by the Sox2/Oct4 reporter approach (7). eGFP(+) MM cells derived from ZL55 and RN5 cells were shown to display augmented stemness features including higher SOX2, POU5F1, KLF4, c-MYC, and ALDH1 mRNA expression levels. The eGFP(+) MM cells have also a higher tumor-initiating capacity in vivo, as well as an increased resistance to cisplatin treatment in vitro. They show a higher tumor sphere- and colony-forming capacity and moreover the ability to convert (differentiate) into bulk cancer cells (7).

In this study we found that the proportion of eGFP(+) cells—in the case of MM previously characterized stem cell-enriched cells (7)—within the entire cell population was clearly higher in tumor-derived (ZL55 and RN5) MM cells than in normal prMC (5–7% versus 0.9%, respectively). However, the precise identity of eGFP(+) prMC cells is currently unknown. Based on the elevated Sox2/Oct4 levels necessary to drive eGFP expression, the eGFP(+) prMC might be cautiously assumed to also represent a cell population with stem cell properties. Previously it was shown that mouse prMC may be cultured for more than 25–30 passages, until the symptoms of senescence become visible (22). Importantly, during this time period, a subset of cells were shown to express stem cell markers such as Sox9, Sox2, CD34, and Bmi1, and these cells showed adipogenic and osteogenic differentiation potential in vitro (22). This strongly indicates the presence of a prMC subpopulation with stem cell properties. To what extent the previously identified stem cell population and the eGFP(+) prMC reported here overlap needs to be addressed in further studies.

However, in both transformed and non-transformed cells, we observed the emergence of stem cell-like eGFP(+) cells from an isolated “pure” bulk eGFP(−) cell population, a finding that could be well explained by the stochastic model. In line with the hypothesis of increased “stemness” of the eGFP(+) population derived from a eGFP(−) ZL-55-SO^low clone, the stemness markers SOX2, POU5F1, and ALDH1 were all increased, excluding that the appearance of green cells was unrelated to increased stemness. The stochastic nature of the system might be the consequence of biological noise. Cell-to-cell variability or “noise” arises from the stochastic nature of biochemical processes within cells, in particular at the level of gene transcription (23) and translation (24).

In addition to our observation and modeling of bidirectional conversion between S (stem) and NS (bulk) states, the description of the “positional effect” is a principally novel concept in cancer stem cell biology. Although cell–cell adhesion and communication between CSCs, bulk (non-CSCs), and stromal cells has been investigated in some detail (reviewed in Ref. 25), our finding that CSCs usually appear in clusters indicates that the cell-fate transition also depends on the localization of a cell, more precisely on the prevailing status of its neighboring cancer cells. Either diffusing factors or direct cell–cell interactions may serve as information transfer mechanism(s); for simplicity, our model is based on a direct cell–cell contact factor. Although more complex models might incorporate diffusing factor(s) that then might act on somewhat longer distances, the basic consequences of such interactions on the tumor cell state would remain essentially the same. Activating and long-range inhibitory diffusing factors can even generate Turing patterns (26) with regularly spaced stem cell clusters. Our experiments with conditioned medium from eGFP(+) ZL55-SO^high cells, which resulted in a lower number of eGFP(+) cells in the non-sorted ZL55-SO cells, are indicative of such a long-range inhibitory diffusing factor secreted by the CSC population. Apparently when applied in a bulk fashion, such an inhibitory diffusing factor predominated against a short-range activating diffusing factor, likely to exist based on the observation of the positive positional effect observed in the newly appearing eGFP(+) cells. Currently nothing is known about the molecular identity of factors influencing the cell state fate, neither in normal mesothelial cells nor in MM cells. However, we have found that expression levels of GLI1 in ZL55-SO^clone-high cells were elevated compared with ZL55-SO^clone-low cells. Gli1 is a protein of the Sonic Hedgehog signaling pathway known to be involved in morphogenic processes but also related to carcinogenesis (27). In glioblastoma cells, bone morphogenic proteins (BMPs) are highly expressed and promote CSC differentiation, whereas the BMP antagonist Gremlin1 is secreted by CSC and prevents BMP-induced differentiation (28). Our model is taking into account that the differentiation state (S or NS) of a cell at the next time point is determined by its present state and the prevailing state of its neighbors and not on the past state of a given cell. This then leads to S state clusters (spatial regulation), whereas in simple stochastic models (4), the spatial regulation is not considered. A spatially organized localization of stem cells and differentiated cells has been previously observed in the case of human induced pluripotent stem cells (29). The authors concluded that stem cells might interact with and moreover “sense” the cellular composition (state) of their immediate neighbors and adjust their differentiation state accordingly. The same phenomenon was observed experimentally in our study, both in normal mesothelial cells and in MM cells, indicating that the “positional effect” is very likely a general mechanism influencing the cell state fate. Factors influencing the stem cell proportion were shown to be also extrinsic, e.g. originating from another cell type. Germline stem cells from Caenorhabditis elegans are maintained by signaling from a niche formed by the distal tip cell: repositioning of the niche induces germline stem cells at a new position (30). Moreover, many tissues and organs contain a small number of adult stem cells that help maintain them. Adult stem cells are thought to live in a specific niche of each tissue, where they are dividing and creating new cells only when the body needs more cells. For instance, intestinal stem cells reside at the crypt base and give rise to all cell types found within the crypt (31). These findings raise the possibility that the niche itself determines the cell stemness state and not an initially coded cell fate: the ability of cells to go through numerous cycles of cell division while maintaining the undifferentiated state (self-renewal) is only the consequence of their localization in the “stem cell niche,”, i.e. here within a cluster (Fig. 6).

Figure 6.

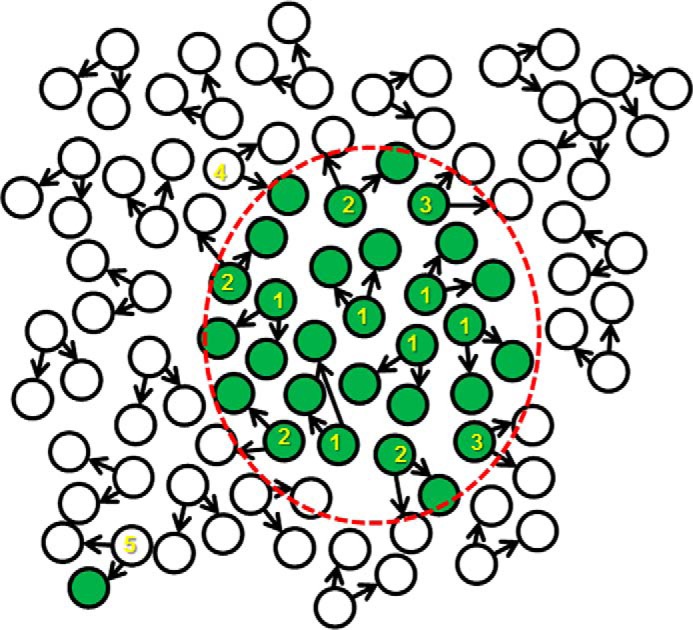
The new general positional stem cell model. In contrast to the existing stochastic or hierarchical model, the positional model produces spatial heterogeneities. In this model the localization and differentiation state of daughter cells has a huge impact on the differentiation state of a given cell. The stem cell niches, where the daughter cells have higher probabilities to remain in an undifferentiated state, are determined by cell–cell interactions, most probably by diffusing factors. Numbers in the scheme indicate the following processes: 1, symmetrical division of a stem cell producing two stem cells; 2, asymmetric division of a stem cell producing one bulk and one stem cell; 3, symmetric division of a stem cell producing two differentiated bulk cells; 4, a differentiated bulk cell entering the stem cell niche has a higher probability to dedifferentiate to a stem cell; and 5, a bulk cell outside of the stem cell niche has an extremely low probability to become a stem cell. The red dashed line represents the border of the stem cell niche. Of note, here the niche consists only of one cell type, unlike in a physiological situation, where niches are generally made up of various cell types.

We hypothesize that positional effect might represent a universal model for various cell types and might be of relevance also during physiological development. First, cells with stem cell properties have higher probabilities but not exclusivity to become a progenitor of an organ or tumor. Second, there are no strict stem cell or bulk cell lineages; these phenomena are the consequence of the low probability of the cell-fate transition (20). Finally, asymmetric cell division, i.e. a stem cell giving rise to one stem cell and one bulk cell, is only a spatial and/or stochastic effect, mostly based on where the daughter cells will be positioned. Thus, a stem cell might divide into two stem cells: one stem cell and one bulk cell or two bulk cells, as was experimentally proven (32, 33). This is fully consistent with our results obtained with ZL55-SO^high eGFP(+) cells that gave rise to zero, one, or two eGFP(+) daughter cells in vitro.

Another important consequence of the positional effect is the initial lag phase in the increase of S state cells, when starting from a bulk (NS) cell as shown in Fig. 4E simulation. In line with our model, experimentally we found that within the population of SO^low cells, it took several weeks before an eGFP(+) cell appeared. Yet as soon as one eGFP(+) state cell appeared, the proportion of eGFP(+) cells increased quite rapidly (Fig. 2A).

Whether cell-fate transitions are connected with the cell cycle remains an open question. The hierarchical model states that cells may change their differentiation state only during mitosis. The simple stochastic models postulate that the differentiation state may be changed independently of the cell cycle, even during the resting state (G₀ phase). Theoretically, a cell might change the differentiation state several times during one cell cycle; however, because cell-fate transitions are very rare events, the probability of multiple transitions tends toward zero. In our models we allowed for changes in the differentiation state during the cell cycle, but not if cells were in the resting G₀ phase. We reckon that recently developed methods for single-molecule imaging of transcription factors binding to DNA (34) might provide data, by which one may address the abovementioned questions and select or modify the appropriate model(s). Our tumor growth model considering the “positional effect” predicted that S state cells are located preferentially in the center of the tumor mass and moreover organized in clusters. This is in line with our in vivo data with tumors derived from ZL55-SO^high eGFP(+) cells. In general, tumor growth/proliferation is highest in the tumor periphery (35), whereas in the tumor center cell proliferation is restricted by the lack of space.

In conclusion, effective therapies should equally target S and NS state tumor cells to completely eradicate the transformed cells. Our important observation is that cell state is spatially determined. The factors influencing the spatial organization will need to be identified by further studies.

Materials and methods

Lentiviral constructs, vector production, and lentivirus isolation

The plasmid pL-SIN-EOS-S(4+)-EiP was obtained from Addgene (plasmid 21314) and was described before (10, 16). The SORE reporter construct pSORE6-mCMVp-dsCopGFP-PURO was a kind gift from Dr. Wakefield (12). The lentiviral plasmid pFUW-OSKM expressing mouse Oct4, Sox2, Klf4, and cMyc used for iPS cell generation (Addgene plasmid 20328) was a kind gift from Rudolf Jaenisch (18). To generate a lentivirus encoding a nuclear-targeted red fluorescent protein, the GFP cassette in pLVTHM (Addgene plasmid 12247) was replaced with a mCherry-NLS fragment. Briefly, the plasmid mCherry-NLS (gift from Martin Offterdinger; Addgene plasmid 39319) was digested with AgeI, filled with Klenow enzyme, and then digested with XbaI. The insert was ligated into pLVTHM using the compatible PmeI and SpeI sites. Lentiviruses were produced as described previously (36).

Cell culture and monitoring

The human mesothelioma cell line ZL55 and the murine mesothelioma cell line RN5 were maintained in RPMI1640 (Gibco) supplemented with 10% fetal bovine serum (Gibco), 100 units/ml penicillin, and 100 μg/ml streptomycin (1% PS). ZL55 was established from previously untreated patients as described before (37), whereas RN5 was established in our lab (38). prMCs were isolated from 4–6-month-old C57Bl/6J mice using a previously described protocol (39). PrMCs were grown in modified Connell's medium composed of Dulbecco's modified Eagle's medium/F-12 + GlutaMAX (Gibco), 15% fetal calf serum, 0.4 μg/ml hydrocortisone, 10 ng/ml epidermal growth factor, 1% insulin/transferrin/selenium, 1 mm sodium pyruvate, 0.1 mm β-mercaptoethanol, 1% non-essential amino acids, 1% penicillin-streptomycin, and 2% Mycokill (GE Healthcare) (40). The cells were transduced with lentivirus containing the stemness indicator construct pL-SIN-EOS-S(4+)-EiP. Transduced ZL55 and RN5 cell lines containing the stemness reporter are named as the cell line name followed by “SO.” They consist of two populations: an eGFP(+) population and an eGFP(−) population. The eGFP(+) population consists of cells in which expression levels of the stemness indicators Sox2 and Oct4 are sufficiently high to drive the expression of the reporter eGFP, whereas non-fluorescent cells comprise cells with low/absent levels of Sox2 and Oct4, as well as a small fraction of non-transduced cells. By the lentiviral transduction method, an almost 100% transduction efficacy was achieved as evidenced with the nuclear-targeted RFP construct.

Cultured cells were trypsinized, and cell pellets were washed three times with PBS and resuspended in PBS. FACS analysis was performed on a BD Accuri C6 (BD Biosciences) to quantify eGFP-expressing cells, and the data were analyzed with the FlowJo software (Tree star). The sorting of eGFP(+) cells (called SO^high) was performed on a BD FACS ARIA (BD Biosciences) cell sorter (100-μm nozzle, 20 p.s.i.) for cell culture in vitro. The cells showing no eGFP fluorescence were isolated, cultured, and termed (“SO^low”).

The cells were continuously monitored using the Incucyte live-cell imaging system (EssenBioscience, Ann Arbor, MI) as described previously (41). The cells were plated in 6-well plates (9 cm²), and images were collected from 49 consecutive zones every 2 h. The size of each zone is ∼0.5 mm². Merged images (fluorescence + phase contrast) were visually analyzed. Recordings showing relevant changes in the proportion of eGFP(+) and eGFP(−) cells were further evaluated by ImageJ software.

Selection of eGFP(−) clones

Clonal selection of ZL55-SO^low cells was performed as described before (38). Clones derived from a single cell were grown and monitored in the Incucyte live-cell imaging system. Clones were quantified regularly by flow cytometry for the presence of eGFP(+) cells until 120 days postselection.

In vivo localization of eGFP(+) cancer stem cells

ZL55-SO^low and ZL55-SO^high cells were sorted as described above, and 100,000 cells were injected subcutaneously into NOD/SCIDγ mice, and tumor formation was analyzed 36 days postinjection (4–5 mice/group). Tumor samples were excised and fixed with 4% paraformaldehyde and embedded in paraffin. Paraffin sections (3 μm) were used for immunohistochemistry as described before (38). Briefly, the sections were deparaffinized and permeabilized with 1% Triton X-100 and blocked with PBS-containing 10% of donkey serum. The sections were incubated with primary antibodies overnight at 4 °C (rabbit anti-eGFP (Sigma–Aldrich) or rabbit anti-calretinin (Swant, Marly, Switzerland); both 1:500), and biotinylated anti-rabbit secondary antibody (Sigma–Aldrich) 1:10,000. The sections were incubated with ABC reagent (Vectastain; Vector Laboratories, Burlingame, CA) and stained with diaminobenzidine, a sensitive colorimetric substrate, to reveal the eGFP(+) cells. All experiments were performed with permission of the local animal care committee (Canton of Fribourg, Fribourg, Switzerland) and according to the present Swiss law and the European Communities Council Directive of November 24, 1986 (86/609/EEC).

Determination of mRNA expression levels of stemness genes by quantitative RT-PCR

Total RNA extracted from 80% confluent cell cultures (peqGOLD, TriFast^TM) of sorted ZL55-SO cells (ZL55-SO^high and ZL55-SO^low) was used for quantitative RT-PCR following the manufacturer's instructions (Qiagen). The primer sequences are listed in the supplemental information. Changes were determined by the −ΔΔC_t method. GraphPad Prism version 6 software was used to perform rank Spearman tests for correlation analysis.

Mathematical modeling

We used stochastic cellular automata also known as locally interacting Markov-chain model (42) to assess the stem cell localization in a two-dimensional model. Cellular automata are often used to simulate solid tumor growth and cancer stem cell dynamics (43–45). The basic features of the positive interactions in the stochastic cellular automata were examined in a two-dimensional grid of size 25 × 25 cells. The non-interacting Markov chain is characterized by the probability distribution of the next state depending only on the current state and not on the sequence of events that preceded it. If we suppose spatial interaction, then the next state not only depends on the current state, but also on the current spatial position, i.e. the state of the neighbors. We used the following rules to determine the next state of the pattern in the grid. The letter S stands for the stem cell state, and NS stands for the non-stem cell state: (i) no interaction: P(NS → S) = 0.001 and P(S → NS) = 0.009 and (ii) positive interaction (i.e. when the state of one cell increases the chance of their neighbors to take up the same state at the next time point): P(NS → S) = 0.00012, if there is no S nearest neighbor; P(NS → S) = 0.004, when at least one nearest neighbor is present in the S state; P(S → NS) = 0.008, if there is no NS nearest neighbor; and P(S → NS) = 0.01, if at least one nearest neighbor is present in the NS state.

To measure the spatial distribution of the developed patterns and to see, whether it is regularly dispersed, randomly dispersed, or clustered, we used the nearest neighbor index calculation,

$$R_{\text{n}}=\frac{{\overline{D}}_{\text{O}}}{{\overline{D}}_{\text{E}}}=\frac{{\displaystyle {\sum }_{i=1}^{n-b}{d}_{\text{i}}}}{0.5\times \sqrt{\frac{A}{n}}}$$ (1)

where R_n is the nearest neighbor index, D̄_O is the observed mean distance between each stem cell, D̄_E is the expected mean distance according to a random pattern, d_i equals the distance between stem cell i and its nearest neighboring stem cell, n is the total number of stem cells, b is the number of stem cells located on the border (their distance to its neighbors were not taken into account − border correction), and A is the surface of the domain (25 × 25). The nearest neighbor formula produces a result with values between 0 and 2.15. If the index is less than 1, the pattern exhibits clustering. If the index is greater than 1, the trend is toward regular dispersion. If the index is close to 1, a random pattern is considered. The average nearest neighbor z score for the statistic is calculated as follows,

$$z=\frac{{\overline{D}}_{\text{O}}-{\overline{D}}_{\text{E}}}{SE}=\frac{{\overline{D}}_{\text{O}}-{\overline{D}}_{\text{E}}}{\frac{0.26136}{\sqrt{\frac{n^2}{A}}}}$$ (2)

where SE is the standard error. We rejected the null hypothesis (pattern is a random pattern), if the absolute z score was greater than or equal to 1.96 (46). The simulations were performed in a MATLAB environment.

Next, we simulated the tumor growth initiated from one single cell. In the tumor growth model we assigned a given cell three options during the next time period; it can (i) divide (undergo mitosis), (ii) remain silent, or (iii) undergo apoptosis with the probabilities (P_d, P_r, and P_a, respectively), such as P_d + P_r + P_a = 1. S and NS cells have different probabilities to undergo mitosis or apoptosis. In the model we used the following values for NS cells: P_d = 0.15, P_r = 0.848, and P_a = 0.002, and for the S cells: P_d = 0.07, P_r = 0.929, and P_a = 0.001. If a cell divides, then the first daughter cell occupies the original space of the parental cell, whereas the second one will randomly occupy one of the available places around the parent cell. If there is no “empty” space around a cell, then this cell cannot divide. If a cell is completely surrounded by their neighbors for a certain period of time, then we consider that this cell is now in a non-dividing (resting) G₀ state. In a non-dividing (resting) G₀ state, a cell cannot change its stem cell status. However, this cell can still undergo apoptosis. If as the result of cell death free space becomes available, a cell in the G₀ state can re-enter the cell cycle and undergo mitosis. In our model the cell-fate transition is not linked to cell division, but when a cell is out of the cell cycle (defined as G₀ phase), then this cell is unable to change its differentiation status. Different probabilities are assigned to the different processes to simulate the differentiation and dedifferentiation processes considering the status of the neighboring cells (“positional effect”). The following probabilities were used in the model: P(NS → S) = 0.0018, if there is no S nearest neighbor; P(NS → S) = 0.06, if at least one nearest neighbor is present in the S state; P(S → NS) = 0.03, if there is no NS nearest neighbor; and P(S → NS) = 0.06, if at least one nearest neighbor is present in the NS state. A flow chart of the simulation process and the decisions at the cell level are shown in Fig. S1. The simulations were performed in the MATLAB environment (MathWorks Inc., MA). The MATLAB codes are provided in the supplemental information.

Author contributions

W. B. and L. P. conceptualization; W. B., B. S., and L. P. data curation; W. B. and B. S. funding acquisition; W. B. validation; W. B., T. H., and L. P. investigation; W. B. and T. H. methodology; W. B., B. S., and L. P. writing-original draft; B. S. resources; B. S. project administration; B. S. and L. P. writing-review and editing; L. P. software.