Abstract
Objectives
The interaction between HIV and the immune system gives rise to a complex dynamical system. We therefore investigate whether delayed viral rebound after antiretroviral therapy (ART) interruption (ATI) may be due to an individual's viral-immune state being in a region of relative stability, and if so, how this can be extended.
Methods
Using a mathematical model duplicating plasma viral levels, HIV DNA and immune homeostatic dynamics for individuals on ART commenced at either primary (PHI) or chronic (CHI) HIV infection, we investigate whether latent reservoir reductions and perturbations in other infected and uninfected memory CD4+ T cell subsets can delay viral rebound.
Results
Solely decreasing the latent reservoir did not delay rebound unless ART was commenced at PHI. If ART was commenced at CHI, latent reservoir reductions paired with depletions of each of uninfected resting and activated cells could delay rebound indefinitely. Starting ART at PHI resulted in easier suppression if the reservoir was reduced in combination with each of six infected and uninfected subsets. Although these paired reductions maintained viral suppression, an opportunistic infection that increased activation to suitably high levels can lead to viral rebound.
Conclusions
If viral rebound is purely a stochastic process, suppression after an ATI requires reduction of the latent reservoir to extremely low levels. On the other hand, if suppression of the viral-immune system is due to stability properties of this complex system, then achievable latent reservoir reductions can lead to long-term suppression if combined with other cell subset modifications.
Keywords: latent reservoir; antiretroviral therapy; viral rebound; mathematical model; stable suppression
Introduction
The periods over which individuals maintain HIV viral suppression in the absence of antiretroviral therapy (ART) are usually short, with viral rebound (HIV RNA >50 copies/mL) occurring in about 2 to 3 weeks [1]. However, for some individuals viral rebound can be considerably delayed. The ‘Mississippi Baby’ treated early after birth maintained plasma HIV viral levels (pVL) below detection for 22 months after ART cessation before viral outgrowth [2]. A French teenager maintained HIV RNA at less than 4 copies/mL for 12 years without ART while showing little in the way of HLA type or an immune response that might explain this continued suppression [3]. Treating early is particularly helpful. Fourteen individuals within the VISCONTI study maintained low viraemia for between 4 and 9 years after cessation of ART initiated in primary HIV infection (PHI) [4]. HLA type and strength of CD8+ T cell responses did not seem to play a significant role. Lower proportions of CD4+ T cells, containing HIV DNA, have also indicated viral rebound might be delayed when ART is initiated at PHI [5,6].
Given the very slow decay of the latent reservoir [7], it is unlikely that HIV will be cured by ART, no matter the duration. On the other hand, these examples of extended HIV suppression without ART suggest a functional cure may be possible. Under what scenarios this can be achieved is uncertain, although limiting the size of the latent reservoir through early treatment seems to be a factor. Further reductions of the reservoir through the use of latency-reversing agents (LRA) may also assist delayed viral rebound. Although low latent reservoir levels seem necessary, they are not sufficient. Even an individual who achieved virtually undetectable viral levels through having commenced PrEP within days of infection, still failed to completely maintain viral suppression, although rebound was delayed by 225 days [8].
HIV infection establishes a complex dynamical interaction between the virus and the body's immune system, reflecting many aspects of a predator–prey problem. For these general nonlinear dynamical systems, extended periods of low predator levels (in our case pVL), can occur until prey levels reach a tipping point. These systems can often inhabit regions in their ‘state space’ where predator levels remain low over relatively long time scales. These systems are deterministic, so their stability is an inherent aspect of nonlinear systems. Can the nonlinearity of the HIV immune dynamical system also explain cases of individuals maintaining low pVL after ART cessation? This hypothesis that pVL suppression without ART may be due to properties of nonlinear dynamical systems differs from the usual explanation that viral resurgence is a stochastic event dependent on the size of the latent reservoir. In the stochastic scenario, low pVL prior to outgrowth is assumed to represent non-infectious virus; outgrowth waits for the chance event of activation of a resting cell containing replication-competent integrated HIV DNA. On the other hand, in this nonlinear dynamical scenario, infectious pVL can be generated continuously; it is just that the interaction between infectious virus and target cells is below the ‘herd-immunity level’.
The different hypotheses for delayed viral rebound have implications for how to achieve longer delays or perhaps even a functional cure. If delay in viral rebound is predominantly determined by latent reservoir size, then longer delays require greater reduction in the latent reservoir with estimates of a 10,000-fold reduction needed for a functional cure [9]. However, for predator–prey problems it is both size and the interaction between components that determine the dynamics – a smaller reduction in predator numbers might be sufficient if prey size is also targeted appropriately. It may be that the nonlinear dynamics of the interaction between HIV and its prey, largely memory CD4+ T cells, allows more efficient ways of achieving a functional cure. Conway and Perelson [10] have investigated this aspect of post-treatment control based on regions of system stability dependent on the level of the latent reservoir and the strength of the immune response.
Here we investigate whether the nonlinear dynamical system described by the interactions between the latent reservoir and memory CD4+ T cells, the phenotype in which this reservoir is embedded, can produce delays in viral rebound after treatment interruption and how best to achieve extended delays. We base our investigations on a mathematical description of the interaction between HIV and memory CD4+ T cell homeostasis that replicates dynamics of pVL and HIV DNA levels prior to, and over the course of, ART [11]. We find that this model of the HIV dynamical system can be driven into a variety of states after interruption of ART: where pVL rebound occurs quickly, where viral suppression is maintained for lengthy periods, and where plasma and cellular infection levels continue to decline. These different outcomes are not the result of stochastic events, although these can play a role in perturbing the system into different stability regions, but they arise from the nonlinearity of this deterministic dynamical system. Our main finding is that solely targeting the latent reservoir within resting non-dividing memory CD4+ T cells is generally insufficient to dramatically alter time to viral rebound or the desired longer-term outcome of eradication. Any substantial delay in viral rebound only occurs when other mainly uninfected memory CD4+ T cell subsets are also reduced in size. In these simulations, ART commenced during PHI more readily resulted in continued pVL suppression after ART interruption, providing a dynamic verification of observations in patients [4,6,12]. Our investigations describe interventions that could increase the percentage of post-treatment controllers from its current low percentage [13].
Methods
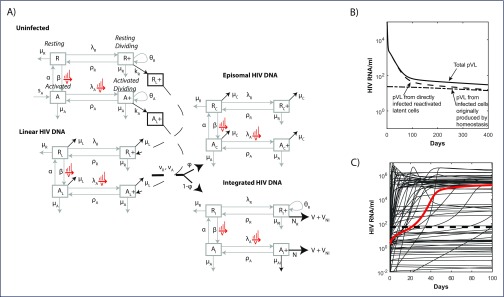
A full description of the mathematical model is contained in Murray et al. [11]. In brief, the model describes the homeostatic processes related to activation and division for memory CD4+ T cells related to CD38 and Ki-67 expression, respectively: resting and non-dividing (R), resting and dividing (R+, encompassing cells undergoing homeostatic proliferation), activated and non-dividing (A), and activated and dividing (A+, encompassing cells undergoing antigenic proliferation). The processes driving phenotypic changes between these compartments, their rates, and the impact of HIV infection as it establishes first unintegrated linear HIV DNA (subscript L), and then either a defective episomal form (subscript C) or integrated HIV DNA (subscript I), are shown in Figure 1. We also assumed that 50% of integration events gave rise to cells with defective infection (subscript ID), which did not produce virus.
Figure 1.
(A) A diagram of the mathematical model. HIV infection is assumed to be restricted to the dividing subsets, as are virion production from cells containing (replication-competent) integrated HIV DNA (
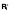 and
and
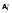 ). The majority (99.9%) of pVL production was assumed to be non-infectious VNI
[33], while 50% of integration events were replication incompetent. Activation of resting cells β, and rates of proliferation λ, are dependent on pVL in a Michaelis–Menten manner, e.g.
). The majority (99.9%) of pVL production was assumed to be non-infectious VNI
[33], while 50% of integration events were replication incompetent. Activation of resting cells β, and rates of proliferation λ, are dependent on pVL in a Michaelis–Menten manner, e.g.
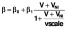 . Infection of target cells followed a similar pattern but was dependent only on the infectious virus component
. Infection of target cells followed a similar pattern but was dependent only on the infectious virus component
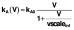 . (B) Contributions to total pVL (solid) from directly infected (dashed) and clonally expanded infected (dash-dot) memory CD4+T cells from the start of ART commenced at CHI. (C) pVL rebound after cessation of 6 years of ART commenced at CHI. The solution to the initial fitting procedure with bounds on rebound time in red and other fitted solutions from multiple nearby parameter sets in grey.
. (B) Contributions to total pVL (solid) from directly infected (dashed) and clonally expanded infected (dash-dot) memory CD4+T cells from the start of ART commenced at CHI. (C) pVL rebound after cessation of 6 years of ART commenced at CHI. The solution to the initial fitting procedure with bounds on rebound time in red and other fitted solutions from multiple nearby parameter sets in grey.
The model was calibrated to reproduce mean/median HIV RNA and HIV DNA data from the pilot integrase inhibitor trial (PINT) and PINT Extension studies of eight PHI and eight CHI enrolled on an ART regimen of raltegravir and Truvada and followed for 3 years [11]. For the cellular perturbation simulations, the model was run with the optimal parameter set with ART commencing at either PHI or CHI, depending on the scenario, and with ART interruption (ATI) after 6 years. At that point the levels of the chosen pair of cell subsets were reduced (1000-fold or 10-fold), while the remaining cell subsets were assumed not to change from their pre-ATI values. The model was then run for 4000 days from these starting values.
All model simulations and analyses were performed in Matlab R2016b (MathWorks Inc, Natick, MA, USA).
Results
The mathematical model reproduced levels and multiphasic dynamics of memory CD4+ T cells and their infected components plus pVL, from first infection and over 3 years of ART begun at PHI or CHI [11]. Under this model, low-level residual viraemia arose from previously infected cells that are induced to proliferate under antigenic or homeostatic processes and become virally productive, producing a mix of infectious V and non-infectious virus VNI. During ART, virion production was from a combination of clonally expanded infected cells and cells directly infected prior to ART (Figure 1B). After treatment interruption, pVL was soon dominated by productively infected cells resulting in viral rebound (HIV RNA ≥50 copies/mL) by 21 days (red line, Figure 1C).
The model had been constrained to ensure pVL rebounded between 5 and 50 days after stopping 6 years of ART [1,14]. To assess factors that might contribute to variability in pVL rebound, we determined model simulations that reproduced the data but also were not explicitly constrained in time to rebound. We first generated 100 parameter sets whose values were within ±log10 of the log (or logit) transformed optimal parameters using Latin Hypercube sampling. Each of these parameter sets were then used as initial guesses and the data were refitted, without constraining rebound time, to generate 95 new parameter solution sets (the optimisation procedure failed to converge for five parameter sets). In these first rebound simulations, we assume ART is commenced during chronic infection and is continued for 6 years before treatment interruption.
Although these parameter sets reproduced the data to a reasonable degree, they produced markedly different rebound dynamics (grey lines in Figure 1C) – the time until HIV RNA reached 50 copies/mL ranged from 0.1 days to never. In some instances, pVL continued to decline. Many of these outcomes can reflect the variability in responses exhibited by individuals upon ART cessation. Indeed, simulations where withdrawal of ART had no discernible impact on pVL reflect the normal situation for post-treatment controllers who maintain undetectable pVL after ART cessation [4]. We note that this lack of response in these simulations occurs despite ART being constrained to be at least 99% effective so that new infections become 100-fold more likely once ART is stopped. Although immune effectiveness has been shown to impact on viral rebound [15,16], all simulations in Figure 1C were produced with the same parameter values for virion and infected cell clearance rates.
Processes affecting time to rebound
What underlies a longer time to rebound was assessed in two ways: (1) the parameters in the model that represent the various infection and homeostatic processes were assessed for correlation with time to rebound (HIV RNA ≥50 copies/mL) for all parameter sets determining the solutions in Figure 1C – this indicates what processes may be impacted to curb rebound; and (2) the cell components themselves were perturbed to determine which of these may be reduced to extend periods of suppressed viraemia in the absence of ART. A partial rank correlation of all parameters from the 95+1 solutions depicted in Figure 1C determined seven of 21 parameters that significantly impacted time to pVL rebound. The parameters that significantly determined a faster rebound described infectivity processes: the rate of infection by virions (kA0, p=3×10−7, r=−0.55, where r is the partial rank correlation coefficient and a negative value means a larger parameter value results in faster rebound), and the rate of virion export by productively infected cells (N, p=0.00049, r=−0.39). Individuals who maintain low viral loads through an HLA type that more effectively presents viral antigens, and results in faster infected cell clearance by CD8+ T cells [15–17], have lower total virion production and consequently a reduced force of infection, consistent with these findings. Rebound was delayed if resting cells or unintegrated HIV DNA were cleared faster (μR, μC, μL, p≤0.016, r≥0.28). The faster turnover of resting cells or of linear HIV DNA within them would result in lower infection levels and delay rebound. A faster episomal HIV DNA clearance rate μC means that more initial infection will proceed to this episomal HIV DNA form rather than become integrated if it is to produce the levels of HIV DNA observed in the PINT patients. Although episomal circles are not directly relevant to viral rebound, being non-productive forms of infection, their levels and turnover rates are, as they reflect a lower likelihood of progression to the productive integrated form. A higher rate of virion production from resting dividing cells meant that a greater proportion of residual viraemia arose from resting infected cells undergoing homeostatic proliferation, resulting in slower rebound (NR, p=0.021, r=0.26); a higher rate of activated cells reverting from a dividing to a non-dividing state (ρA, p=0.023, r=0.026) also delayed rebound. Chronic CD4+ T cell activation would exacerbate the rate at which cells revert to a non-proliferating state, and is associated with higher pVL in untreated individual [18], while higher levels of cell-associated RNA result in faster rebound [19].
It is likely that for a given individual (reflected by a particular parameter set) slower rebound can be obtained by reducing some of the infected or target components. This is one of the aims of LRA that attempts to reduce replication-competent integrated HIV DNA levels within resting cells (represented in the model by RI). However, nonlinear system dynamics can be complex so that changes in individual components need not affect the system as much as combined perturbations. To assess this complex behaviour, we considered pairwise changes in cellular and infection levels at the end of 6 years of ART, commenced during CHI. Each of these simulations was performed with the same parameters the initial optimal parameter set, that results in rebound after 21 days with no subset perturbations (red line, Figure 1C).
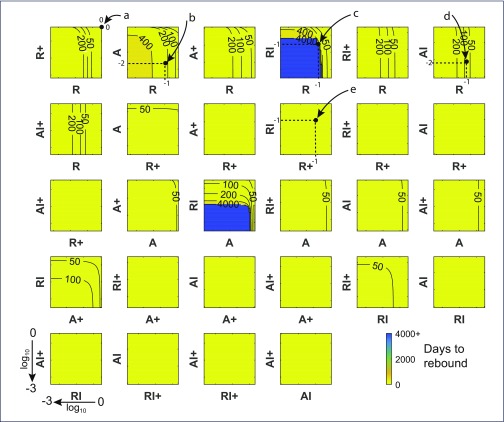
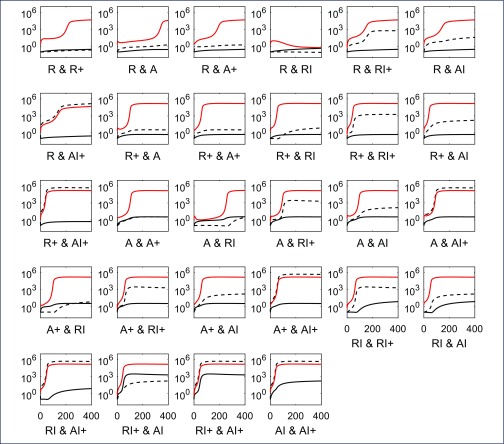
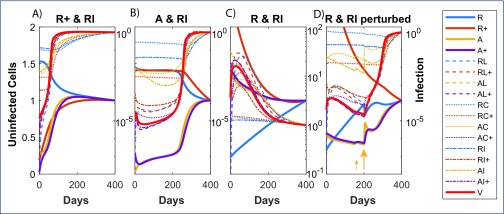
Despite reducing each component 1000-fold, some combinations showed virtually no impact on time to rebound (Figure 2). This is depicted in panels with a single yellow colour and where no contours occur (all changes in these panels result in viral rebound at the latest by day 50). For example, reducing either or both dividing resting cells (R+) and dividing activated cells (A+) led to viral rebound by day 50 (second row, third column, Figure 2). Reducing some single components, uninfected non-dividing activated cells (A) and uninfected resting cells (R), could impact on viral rebound. This is shown by panels where the contours are straight lines so time to rebound is independent of changes in the other cell component (see for example point ‘d’ where the level of AI has virtually no impact on rebound time but a 1 log10 reduction in R numbers has delayed viral rebound to between 50 and 100 days). Other single changes, even in the latent reservoir of infected, non-dividing resting cells containing integrated HIV DNA (RI), that are the specific targets of LRA, made no impact whatever despite being reduced 1000-fold (see the panel containing point ‘e’). However, reducing the latent reservoir (RI), could inhibit rebound completely (time to rebound ≥4000 days – the limit of the simulations), but only when combined with reductions in uninfected non-dividing cells (R or A). Hence LRA by themselves may not be effective but they could impact viral rebound if combined with reductions in uninfected memory subsets. Figure 3 illustrates how 10-fold reductions in each of the pairs in the panels in Figure 2 affect the dynamics of those components. Recall that these very different dynamics are produced with the same parameters. It indicates that rebound for an individual can be significantly altered when the correct cell components are targeted. Note that having the latent reservoir RI reduce over time is not sufficient to maintain suppression, as shown in the A & RI panel, where the virion-producing cells slowly increase over time and eventually push the system past its ‘tipping point’.
Figure 2.
Time to rebound for chronic infection. Contour plots displaying number of days to pVL rebound (HIV RNA = 50 copies/mL) when pairs of cell levels after 6 years of ART, commenced at CHI, are reduced between 0 and 3 log10 prior to ART interruption, using the optimal parameter set. The top right corner of each plot displays the days to rebound with 0 change in the pair of states and values (21 days); points to the lower-left show the effects of decreasing values of the two components on a log10 scale where the lower-left corner of each plot shows the number of days to rebound when both components are reduced by 3 log10 (1000-fold). After 6 years of ART, very few cells contained linear unintegrated HIV DNA so that decreases in their number had no impact on viral rebound, nor did cells containing defective integrated HIV DNA or the dead-end episomal forms, hence these cell components were not included. A panel that does not contain any contours, and is filled with the one colour, denotes rebound times <50 days for all values of the components. Resting cells are denoted by R, activated cells by A; dividing cell subsets contain a + in their name; subsets containing I denote cells with integrated HIV DNA; so for example RI+ describes resting dividing cells containing integrated HIV DNA. Simulations were limited to 4000 days after ART cessation so a failure to rebound by that time (blue regions) likely indicated continued suppression and infection loss. Examples: point ‘a’ has no change in either of the R and R+ subsets resulting in rebound after 21 days; point ‘b’ denotes a 1 log10 decrease in the number of R cells and a 2 log10 decrease in numbers of A cells immediately prior to ART cessation, resulting in pVL rebound occurring in the 200 to 400 day range; point ‘c’ denotes a 1 log10 decrease in each of the R and RI components yielding no rebound by 4000 days; point ‘d’ denotes a 1 log10 decrease in R cells and a 2 log10 decrease in AI cells, delaying rebound to the 50 to 100 day range. Since these contours are vertical, changes in the AI component have no impact on rebound, so that all change is due to the R component; point ‘e’ denotes a 1 log10 decrease in R+ cells and the ‘latent reservoir’ of RI cells and giving rise to rebound within 50 days – hence targeting the latent reservoir itself is not sufficient to markedly impact viral suppression
Figure 3.
HIV dynamics over the days following a 10-fold reduction in each of the cell components of the displayed pair, and treatment interruption after 6 years of ART commenced at CHI. Dynamics of the first component relative to starting value (prior to reduction) shown as black solid line with the second cell component as black dashed line while pVL is illustrated with a red line
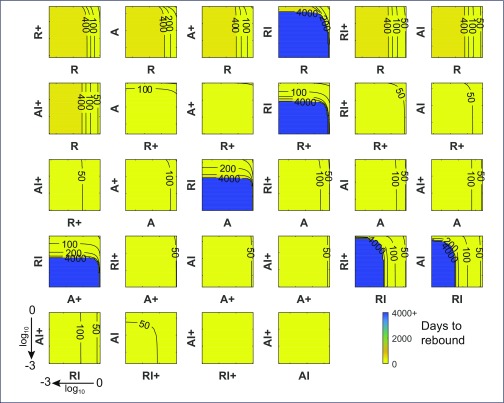
Commencing ART at the acute/early stage of HIV infection is more likely to result in delayed rebound after treatment interruption [19]. This was also true in our simulations using exactly the same parameter set as in Figure 2, but commencing ART at the mean estimated time after infection for the PINT PHI group of 4.5 months [20] (Figure 4). As above, these simulations also assume 6 years of ART before interruption. Whereas two of the pairwise reductions could delay rebound out to the 4000+ day mark in the CHI group, there were six pairs for the PHI group that could essentially suppress rebound, and all involved reductions in the latent reservoir component RI. It is striking that no amount of reduction in the latent reservoir by itself for the CHI group could lengthen rebound beyond the 20- to 50-day range (see point e) in Figure 2, but the same perturbations when commenced at PHI could maintain complete viraemia suppression. The better PHI response will be partly due to their lower infection levels since integrated HIV DNA levels were significantly lower at PHI [20]. Nevertheless, this will not be the sole reason as the reductions simulated here that achieved substantial delays when combined with R+ reductions for example, had no discernible impact for the CHI group. However, the higher infection levels for CHI also produced higher levels of CD4+ T cell activation [11], which provides more target cells for productive infection. Elevated activation from chronic HIV infection contributes to their poorer response in these simulations.
Figure 4.
Time to rebound for when ART is commenced in primary infection. Contour plots displaying number of days to pVL rebound (HIV RNA = 50 copies/mL) when pairs of cell levels after 6 years of ART, commenced at PHI, are reduced between 0 and 3 log10 prior to ART interruption, using the optimal parameter set
Three combinations of 10-fold reductions of the latent reservoir with another cell subset for the CHI group were compared to investigate factors underlying the different outcomes: early, late and no rebound (Figure 5). In each case, new infection events occur with the removal of ART, as shown by large increases in cells containing linear unintegrated HIV DNA (dashed lines). However, viral rebound did not necessarily occur then but was instead associated with how quickly activated cells (A) expanded. Figure 5B shows these cells, which provide the main target A+ cells in this model, slowly increasing despite ongoing infection, and not reaching the point where pVL accelerates until after 200 days. The scenario where pVL stays suppressed has decreasing levels of activated cells, once again in the presence of ongoing infection (Figure 5C). Although this last scenario is stable, it can be shocked out of this state by activation events. Ten-fold increased activation rates over 5 days starting at day 150 in Figure 5D were insufficient but 100-fold increases starting at day 200 resulted in perturbation of this complex system out of its stable region.
Figure 5.
Three combinations of 10-fold pairwise reductions in cell subsets prior to ART interruption with differing rebound dynamics for the CHI case: (A) immediate rebound; (B) rebound after 200 days; (C) no rebound. Panel (D) shows the scenario in panel (C) but where activation rates β0, β1 were increased 10-fold over a period of 5 days starting at day 150 for a period of 5 days, and 100-fold starting at day 200, reflecting spikes in immune activation from opportunistic infections. In each panel, pVL and all cell subsets are scaled relative to their day 400 levels to bring each component roughly to a similar range; uninfected cell subsets are shown on a linear scale relative to the left y-axes that all range between 0 and 2, while the infected cell subsets and pVL are shown on a log scale relative to the right y-axes
Discussion
Delays in viral rebound after ART cessation are mostly assumed to be due to the stochastic nature of activation events and the size of the latent reservoir. Consequently, any detectable viraemia prior to rebound is considered non-infectious. Our interpretation is very different – after ART cessation, new infections continually occur but their impact on activation and the homeostatic regulation of memory CD4+ T cells is insufficient to drive the system into explosive viral growth. In some instances, pVL can even increase but then wane over time, as observed in the R&RI panel of Figure 3. Our model, constructed to duplicate the dynamics of pVL and HIV DNA prior to and during ART, is deterministic, with quantifiable levels of viraemia and HIV DNA, yet the nature of nonlinear dynamical systems can give rise to slow progression, and even a continued reduction, if driven into the right region. This is likely to be similar to why some individuals are elite or viraemic controllers. Although immunovirological reasons such as a 32-base pair deletion in the CCR5 gene, or HLA type, are responsible for control in some of these individuals, that is not always the case. These individuals experience continued viral replication [21,22], but still suppress viraemia in the absence of ART. Approximately 25% of elite controllers stay suppressed for 12 years [23] while HIV infection controllers (pVL <500 copies/mL) can maintain suppression for 10 or more years [24], so the delay of 4000+ days in viral rebound for our simulations seems achievable if modulation of CD4+ T cell subsets is sufficient to effectively turn someone into one of these controller categories.
Longer time to rebound is correlated with lower levels of HIV DNA [5]. Elite controllers also have significantly lower levels of integrated HIV DNA [25]. Hence it is not surprising the only perturbations that could substantially impact time to rebound required lower levels of resting cells containing replication-competent HIV DNA (RI). On its own, reduction in this latent reservoir was generally insufficient in our simulations to substantially modify viral rebound. This is in agreement with stochastic modelling that estimated a 2000-fold reduction in the latent reservoir was required before rebound was delayed for a year in the majority of individuals [9]. It is also consistent with results from trials of LRA that induced elevated histone acetylation and pVL, but little change in HIV DNA levels [26–28]. There was some impact by panobinostat on HIV DNA levels and subsequently on delaying viral rebound to >1000 copies/mL (median 28 days versus 17 days [29]). Our analyses suggest that LRA that reduce the latent reservoir can have a substantial impact but generally only in combination with reductions in some other components. As with all modelling, these conclusions are dependent on the model assumptions and further investigation is required to determine if LRA by themselves or in combination with any cell subset perturbations can delay viral rebound. Others have also determined that a low latent reservoir in combination with a stronger immune response can exhibit these characteristics of driving the immunovirological dynamical system into a region of sustained viral suppression [10]. Combining both approaches may produce even greater viral rebound delays.
Simulations of scenarios exhibiting different rebound delays indicate activated CD4+ T cell levels are an important predictor (Figure 5). Circumstantially, this is also borne out by observations of increasing CD30+CD4+ T cells preceding viral rebound in two individuals who had delayed rebound for more than 200 days [8]. CD30 is expressed by a subset of activated memory CD4+ T cells [30] and may reflect a more refined subset of activated cells than modelled here that play a role in providing target cell availability for viral expansion (Figure 5B). It is difficult to see how expansion of this CD30+CD45RO+CD4+ T cell subset beginning more than 100 days prior to rebound would substantially influence frequency of stochastic activation events in the latent reservoir.
Although our simulations show reductions in the latent reservoir, and in uninfected memory CD4+ T cell subsets, can significantly delay rebound, it is under the assumption that HIV-specific immune functions are not deleteriously affected, since they are assumed to be at the same level throughout the simulations. Bone marrow transplants in two patients achieved significantly greater reduction in host immune cells but only delayed rebound until 12 and 32 weeks after ART interruption [31]. Unlike the ‘Berlin patient’ who went from having a CCR5 wild-type immune system to one that was homozygous for the 32-base pair deletion, and subsequently remained suppressed [32], these ‘Boston patients’ went from being heterozygous for delta-32 to wild type. Moreover, anti-HIV antibodies and their avidity decreased after transplant, possibly allowing for viral outgrowth that would have otherwise stayed suppressed. Strengthening the immune response may also impact viral rebound [10].
This theory of delayed viral rebound is analogous to the epidemiology of infectious diseases where outbreaks do not arise because of low numbers of susceptible individuals. In simulations here, viral rebound is delayed until activation pushes susceptible cell numbers above an in vivo herd-immunity level. Whereas immunisation in the epidemiology setting serves to protect a community from outbreaks, an in vivo intervention that suppresses the appropriate activated cell subset may play a similar role to lengthen delays in rebound while replacing the need to remove cells.
Acknowledgements
Declaration of interests
There are no conflicts of interest.
References
- 1. Davey RT Jr, Bhat N, Yoder C et al. HIV-1 and T cell dynamics after interruption of highly active antiretroviral therapy (HAART) in patients with a history of sustained viral suppression. Proc Natl Acad Sci U S A 1999; 96: 15109– 15114. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2. Luzuriaga K, Gay H, Ziemniak C et al. Viremic relapse after HIV-1 remission in a perinatally infected child. N Engl J Med 2015; 372: 786– 788. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3. Frange P, Faye A, Avettand-Fenoël V et al. HIV-1 virological remission lasting more than 12 years after interruption of early antiretroviral therapy in a perinatally infected teenager enrolled in the French ANRS EPF-CO10 paediatric cohort: a case report. Lancet HIV 2016; 3: e49– e54. [DOI] [PubMed] [Google Scholar]
- 4. Sáez-Cirión A, Bacchus C, Hocqueloux L et al. Post-treatment HIV-1 controllers with a long-term virological remission after the interruption of early initiated antiretroviral therapy ANRS VISCONTI Study. PLoS Pathog 2013; 9: e1003211. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5. Williams JP, Hurst J, Stöhr W et al. HIV-1 DNA predicts disease progression and post-treatment virological control. Elife 2014; 3: e03821. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6. Hocqueloux L, Avettand-Fènoël V, Jacquot S et al. Long-term antiretroviral therapy initiated during primary HIV-1 infection is key to achieving both low HIV reservoirs and normal T cell counts. J Antimicrob Chemother 2013; 68: 1169– 1178. [DOI] [PubMed] [Google Scholar]
- 7. Finzi D, Blankson J, Siliciano JD et al. Latent infection of CD4+ T cells provides a mechanism for lifelong persistence of HIV-1, even in patients on effective combination therapy. Nat Med 1999; 5: 512– 517. [DOI] [PubMed] [Google Scholar]
- 8. Henrich TJ, Hatano H, Bacon O et al. HIV-1 persistence following extremely early initiation of antiretroviral therapy (ART) during acute HIV-1 infection: an observational study. PLoS Med 2017; 14: e1002417. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9. Hill AL, Rosenbloom DIS, Fu F et al. Predicting the outcomes of treatment to eradicate the latent reservoir for HIV-1. Proc Natl Acad Sci U S A 2014; 111: 13475– 13480. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10. Conway JM, Perelson AS.. Post-treatment control of HIV infection. Proc Natl Acad Sci U S A 2015; 112: 5467– 5472. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11. Murray JM, Zaunders J, Emery S et al. HIV dynamics linked to memory CD4+ T cell homeostasis. PLoS One 2017; 12: e0186101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12. Lodi S, Meyer L, Kelleher AD et al. Immunovirologic control 24 months after interruption of antiretroviral therapy initiated close to HIV seroconversion. Arch Intern Med 2012; 172: 1252– 1255. [DOI] [PubMed] [Google Scholar]
- 13. Cockerham LR, Hatano H, Deeks SG.. Post-treatment controllers: Role in HIV ‘cure’ research. Curr HIV/AIDS Rep 2016; 13: 1– 9. [DOI] [PubMed] [Google Scholar]
- 14. Chun T-W, Davey RT, Engel D et al. Re-emergence of HIV after stopping therapy. Nature 1999; 401: 874– 875. [DOI] [PubMed] [Google Scholar]
- 15. Pereyra F, Jia X, McLaren PJ et al. The major genetic determinants of HIV-1 control affect HLA class I peptide presentation. Science 2010; 330: 1551– 1557. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16. Kelleher AD, Long C, Holmes EC et al. Clustered mutations in HIV-1 gag are consistently required for escape from HLA-B27–restricted cytotoxic T lymphocyte responses. J Exp Med 2001; 193: 375– 386. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17. Schneidewind A, Brockman MA, Yang R et al. Escape from the dominant HLA-B27-restricted cytotoxic T-lymphocyte response in gag Is associated with a dramatic reduction in human immunodeficiency virus type 1 replication. J Virol 2007; 81: 12382– 12393. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18. Catalfamo M, Di Mascio M, Hu Z et al. HIV infection-associated immune activation occurs by two distinct pathways that differentially affect CD4 and CD8 T cells. Proc Natl Acad Sci U S A 2008; 105: 19851– 19856. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19. Li JZ, Etemad B, Ahmed H et al. The size of the expressed HIV reservoir predicts timing of viral rebound after treatment interruption. AIDS 2016; 30: 343– 353. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20. Murray JM, McBride K, Boesecke C et al. Integrated HIV DNA accumulates prior to treatment while episomal HIV DNA records ongoing transmission afterwards. AIDS 2012; 26: 543– 550. [DOI] [PubMed] [Google Scholar]
- 21. Chun T-W, Shawn Justement J, Murray D et al. Effect of antiretroviral therapy on HIV reservoirs in elite controllers. J Infect Dis 2013; 208: 1443– 1447. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22. Noel N, Peña R, David A et al. Long-term spontaneous control of HIV-1 Is related to low frequency of infected cells and inefficient viral reactivation. J Virol 2016; 90: 6148– 6158. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23. Leon A, Perez I, Ruiz-Mateos E et al. Rate and predictors of progression in elite and viremic HIV-1 controllers. AIDS 2016; 30: 1209– 1220. [DOI] [PubMed] [Google Scholar]
- 24. Madec Y, Boufassa F, Porter K et al. Natural history of HIV-control since seroconversion. AIDS 2013; 27: 2451– 2460. [DOI] [PubMed] [Google Scholar]
- 25. Graf EH, Mexas AM, Yu JJ et al. Elite suppressors harbor low levels of integrated HIV DNA and high levels of 2-LTR circular HIV DNA compared to HIV+ patients on and off HAART. PLoS Pathog 2011; 7: e1001300. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26. Archin NM, Bateson R, Tripathy MK et al. HIV-1 expression within resting CD4+ T cells after multiple doses of vorinostat. J Infect Dis 2014; 210: 728– 735. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27. Elliott JH, Wightman F, Solomon A et al. Activation of HIV transcription with short-course vorinostat in HIV-infected patients on suppressive antiretroviral therapy. PLoS Pathog 2014; 10: e1004473. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28. Søgaard OS, Graversen ME, Leth S et al. The depsipeptide romidepsin reverses HIV-1 latency in vivo. PLoS Pathog 2015; 11: e1005142. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29. Rasmussen TA, Tolstrup M, Brinkmann CR et al. Panobinostat, a histone deacetylase inhibitor, for latent-virus reactivation in HIV-infected patients on suppressive antiretroviral therapy: a phase 1/2, single group, clinical trial. Lancet HIV 2014; 1: e13– e21. [DOI] [PubMed] [Google Scholar]
- 30. Ellis TM, Simms PE, Slivnick DJ et al. CD30 is a signal-transducing molecule that defines a subset of human activated CD45RO+ T cells. J Immunol 1993; 151: 2380– 2389. [PubMed] [Google Scholar]
- 31. Henrich TJ, Hanhauser E, Marty FM et al. Antiretroviral-free HIV-1 remission and viral rebound after allogeneic stem cell transplantation: report of two cases. Ann Intern Med 2014; 161: 319– 327. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32. Hutter G, Nowak D, Mossner M et al. Long-term control of HIV by CCR5 Delta32/Delta32 stem-cell transplantation. N Engl J Med 2009; 360: 692– 698. [DOI] [PubMed] [Google Scholar]
- 33. Rusert P, Fischer M, Joos B et al. Quantification of infectious HIV-1 plasma viral load using a boosted in vitro infection protocol. Virology 2004; 326: 113– 129. [DOI] [PubMed] [Google Scholar]