AMOEBA Polarizable Atomic Multipole Force Field for Nucleic Acids

Abstract

The AMOEBA polarizable atomic multipole force field for nucleic acids is presented. Valence and electrostatic parameters were determined from high-level quantum mechanical data, including structures, conformational energy and electrostatic potentials, of nucleotide model compounds. Previously derived parameters for the phosphate group and nucleobases were incorporated. A total of over 35 microseconds of condensed phase molecular dynamics simulations of DNA and RNA molecules in aqueous solution and crystal lattice were performed to validate and refine the force field. The solution and/or crystal structures of DNA B-form duplexes, RNA duplexes and hairpins were captured with an average RMSD from NMR structures below or around 2.0 Å. Structural details, such as base pairing and stacking, sugar puckering, backbone and χ torsion angles, groove geometries and crystal packing interfaces, agreed well with NMR and/or X-ray. The interconversion between A- and B-form DNAs was observed in ethanol-water mixtures at 328K. Crystal lattices of B- and Z-form DNA and A-form RNA were examined with simulations. For the RNA tetra loop, single strand tetramers, and HIV TAR with 29 residues, the simulated conformational states, ³J-coupling, NOE and RDC data were compared with NMR results. Starting from a totally unstacked/unfolding state, the rCAAU tetranucleotide was folded into A-form like structures during ~1μs MD simulations.

Graphical abstract

Introduction

Nucleic acids play significant roles in cells, including genetic information storage and translation, protein expression, catalysis, and regulation of gene activation.^1–5 There is a long history of studying nucleic acids by molecular mechanics (MM) and molecular dynamics (MD) simulations.^6–10 Over the years, significant effort has been devoted to developing and improving DNA and RNA force fields based on fixed-charge models, such as CHARMM,^{9, 11–12} AMBER,^{7, 13–19} and GROMOS.^20–22

DNA duplexes predominantly adopt a right-handed B-form structure in aqueous solution and functional organisms. However, some DNA sequences tend to crystallize in an A-form structure,^23–24 and reduced water activity due to the addition of solvents like ethanol, or the presence of protein or drug molecules, can induce an B→A transition.^25–36 A-form DNAs are also observed in bacterial cells in response to desiccation.³⁰ Moreover, in crystal structures or high salt solution, DNAs with alternating deoxyguanosine and deoxycytidine residues may form stable Z-form duplexes.^37–38 In previous studies,^{6, 39–40} stable B-DNA in aqueous solution and Z-DNA in a crystalline lattice have been reported from force field simulations. The interconversion between B-form and A-form DNA at different water activities has not been fully examined. Compared with the dominant duplex structure of DNA, the structure of RNA is highly diverse. Depending on the nucleotide sequence and the number of strands, RNA can form stable duplex A-form helices, internal/hairpin loops, pseudoknots and a wide variety of complex tertiary structures.^41–42 It is important for a general force field to describe nucleic acid structural diversity and the transitions between different types of structures.

The complex conformational states of DNA and RNA arise from the balance among the electrostatic interaction within nucleic acids and with surrounding ions, the intricate base pairing and stacking, the high degree of freedom inherent in backbone dihedrals and sugar puckering. Consequently, it has been challenging to develop accurate classical ^20–22 mechanics force fields for nucleic acids. Optimization of fixed-charge models has focused on modifying the torsional parameters,^{6–7, 13, 17, 19, 43–44} and some significant improvements have been achieved.^{7, 17–18} On the other hand, ab initio calculations have identified inadequacies of the fixed-charge models for representing the ion interactions,⁴⁵ hydrogen bonding⁴⁶ and base stacking,⁴⁷ which has been attributed to the intrinsic limitations of the physical models underlying fixed-charge force fields.

Polarizable force fields that explicitly account for electronic polarization offer more accurate description of electrostatic interactions and properties in complex physical and chemical environments.^{12, 48–64} Several polarizable force fields have been developed based on fluctuating charge,^61–62 Drude oscillator,^{39–40, 65–66} and induced dipole methods.^{50, 56, 67–72} CHARMM Drude force fields for DNA have been reported and exhibit notable advances over fixed-charge models.^{39–40, 65–66} The AMOEBA (Atomic Multipole Optimized Energetics for Biomolecular Applications) force field utilizes atomic charge, dipole and quadrupole moments to represent the permanent charge distributions around atoms and an interactive atomic dipole induction scheme to model the polarization effect, which has the potential to improve the accuracy and transferability of classical force fields. AMOEBA force fields have been developed for water, ions, organic molecules and proteins.^{50, 56, 67–69} Applications of AMOEBA include ion hydration and binding,^{53, 59, 73–77} protein-ligand binding,^{48–49, 52, 78}, organic molecules and crystals.^{8, 57–58, 79–81} AMOEBA DMP/TMP (dimethyl/trimethyl phosphate) model⁸⁰ was reported previously. Accurate condensed phase properties and balanced interactions with both water and metal ions were demonstrated. The nucleobase force field⁸¹ was also developed, with a focus on capturing and balancing the base-water interactions, base-base stacking, and base-base pairing interactions. These studies established the basis for the present AMOEBA nucleic acid force field.

Despite the urgent need, the development and application of advanced force fields in nucleic acid research has been limited in part by computational cost. The base pairing and stacking dynamics of DNA and RNA, such as bending, twisting, groove fluctuations and base pair opening, which are critical for function and important for recognition processes, typically occur on a time scale ranging from nanoseconds to microseconds.^82–84 Even for small RNA tetra loops, multi-microsecond simulations and enhanced sampling techniques are needed to achieve adequate sampling.^85–86 With the recent emergence of high-performance computing hardware and software,^{58, 87} polarizable MD simulations on the microsecond time scale are becoming accessible, making it possible to consider polarizable force fields for nucleic acids.

In this study, the development of the first-generation AMOEBA polarizable force field for DNA and RNA is presented. We first describe the parameterization procedures for DNA and RNA, including the electrostatics, van der Waals, valence and particularly torsional parameters. Comparing the AMOEBA conformational energy with QM data for various degrees of freedom in the backbone and sugar ring is an area of focus. Condensed phase simulations of a range of DNA and RNA molecules are discussed. For DNA, four double strand DNAs including the prototypical Dickerson-Drew DNA dodecamer,⁸⁸ starting from both A-form and B-form structures, were simulated in both aqueous solution and ethanol-water mixtures (90% volume ratio of ethanol) to investigate the stability and transition between the different helix forms. Two crystalline Z-form DNAs, one B-DND and one A-RNA were simulated to examine the force field in crystal lattice. For RNA, we simulated twelve molecules in aqueous solution, including single strand RNA tetramers, RNA duplexes, a tetraloop, and a larger HIV RNA. The force field validation consists of inspection of the stability of the native structure and comparison of simulated structures and properties (³J coupling, NOE, and RDC) with experimental results.

Methods

Potential energy functions in AMOEBA force field

Detailed equations defining the AMOEBA potential energy functions have been described previously.⁵⁰ Briefly, AMOEBA contains two types of energy terms, bonded (or valence) and non-bonded terms. In addition to the typical classical mechanical bonded energy terms (bond, angle, out of plane bending and torsion), AMOEBA also incorporates π-torsions terms, and bond-angle, bond-torsion, angle-torsion coupling terms,⁸⁰ which are essential for accurately describing valence structural changes and vibrational frequencies of nucleic acids backbones and sugar rings. The buffered 14–7 function is used in AMOEBA to describe the repulsion and dispersion interactions, commonly referred to as van der Waals (vdW) interactions.⁸⁹ Point charge, dipole, and quadrupole moments are placed on atoms to represent charge distributions and to evaluate permanent electrostatic interactions between atoms. In AMOEBA, the polarization effects are modeled by an interactive atomic induced dipole scheme. The induced dipole at each atom is the product of its atomic polarizability and the electrostatic field at this atom produced by permanent multipoles and induced dipoles of all other atoms. A group-based masking rule is applied so that the atomic permanent multipoles will only polarize atoms that are outside the same group (e.g. a benzene ring). The Thole’s damping scheme is employed in the iterative induced dipole moment calculation to avoid a “polarization catastrophe” at very short range and to provide anisotropic molecular dipole polarizability.⁹⁰ The same induction model applies to both intramolecular and intermolecular polarization. The intramolecular polarization occurs between the polarization groups as if they are separate molecules. The polarization energy between induced dipoles and permanent multipole moments is computed fully between atoms separated by three (1–4) or more bonds, and neglected between 1–2 and 1–3 pairs.

Model compounds used for developing DNA/RNA force field

Ab initio QM and AMOEBA force field studies on model compounds were performed using Gaussian 09⁹¹ and TINKER 7.0,⁹² respectively. In the conformational energy surface study, the energy minima of model compounds were first located with QM optimization. The polarizable continuum model (PCM)⁹³ was applied to introduce solvent effect into the QM calculations. Conformations were generated by systematically scanning relevant torsional angles away from the minima. Each conformation was then re-optimized using QM with the particular torsions fixed. Finally, single point energies were obtained with a larger basis set. For force field calculation, the MINIMIZE program in TINKER 7.0 was applied to relax the QM structures with relevant torsions restrained. The Generalized Kirkwood (GK) implicit solvent model⁹⁴ was used to compute the solvent effect in AMOEBA structure optimization and conformational energy calculations.

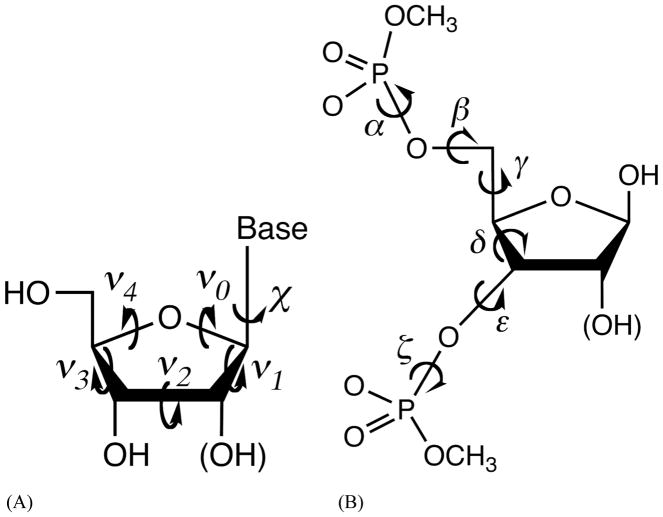
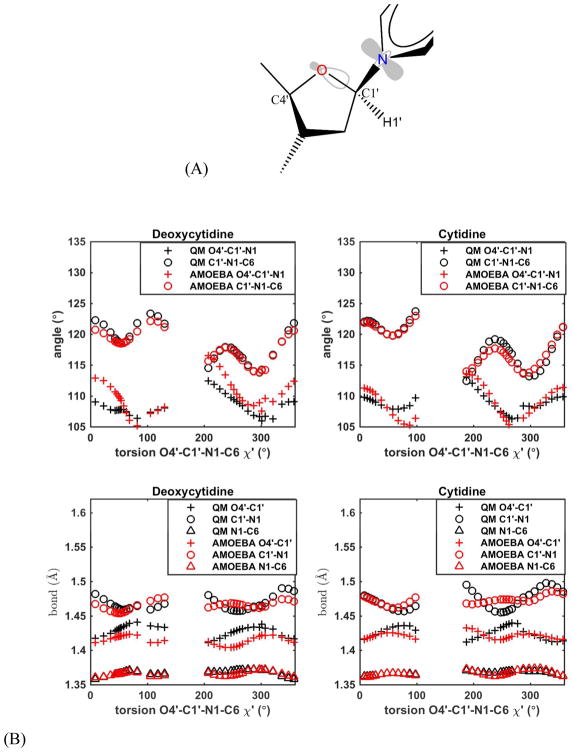
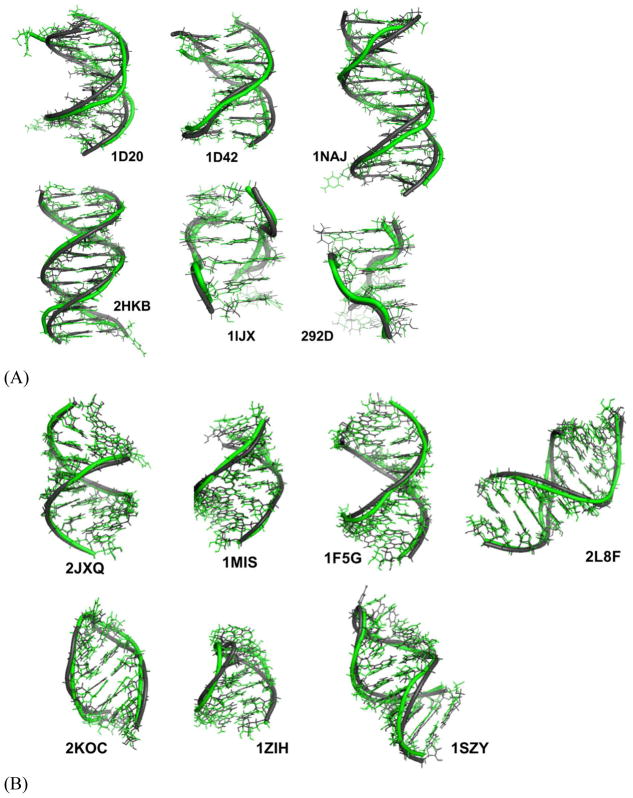
The force field parameters for sugars, bases and phosphate groups were derived using separate model compounds. Dimethyl phosphate (DMP) was the model for the backbone phosphate.⁸⁰ The four N-methylated nucleobases were also parameterized previously.⁸¹ The valence, vdW and electrostatic parameters of these model compounds were transferred to the phosphate and nucleobases groups of nucleic acids. The ribose and deoxyribose, plus the nucleosides (Figure 1A) were used to parameterize sugar valence terms, van der Waals (vdW) values and atomic multipole moments, and also used for modeling sugar puckering and χ torsions. (Deoxy)ribose 3,5-bis (methyl phosphate) (Figure 1B) was used to refine the nucleic acid atomic multipole (after emerging from the model compounds above) and parametrize the backbone torsions. Two other model compounds (Figure S8) were also selected for parameterization of RNA torsions. Torsion angle regions, syn (C, −30°–30°), gauche (G, 30°–90°), anticlinal (A, 90°–150°), and trans (T, 150°–210°), are named following IUPAC nomenclature conventions.

Figure 1.

Model compounds for nucleic acid force field development and definition of the torsion angles. (A) Nucleosides and the internal torsional angles. (B) (Deoxy)ribose 3,5-bis (methyl phosphate) and backbone torsional angles. χ is defined by O4′-C1′-N1-C2 for pyrimidines (C, T and U), and by O4′-C1′-N9-C4 for purines (A and G).

Atomic multipoles and polarization

The atomic multipole parameters for all model compounds were determined following the usual AMOEBA parameterization procedure as previously described for organic molecules and proteins.^68–69 High-level ab initio calculations were performed using Gaussian 09.⁹¹ QM-optimized sugar structures and the molecular vibration frequencies were used to fit the valence parameters (equilibrium bond and angle values and force constants). Permanent atomic multipole moments were initially derived by distributed multipole analysis (DMA) from an ab initio (MP2/6-311G**) wave function.⁹⁵ The atomic dipole and quadrupole moments of the model compounds were refined against high level QM electrostatic potentials calculated at the MP2/aug-cc-pVTZ level. The multipole and polarization parameters of sugar, nucleobases, and dimethyl phosphate were determined first, and then incorporated into nucleosides or (deoxy)ribose 3,5-bis (methyl phosphate) (Figure 1). The monopoles of the linking atoms (C1′, O5′, C5′, O3′ and C3′ of sugar and N1 or N9 of nucleobases) were slightly adjusted according to the net molecular charge and the dipole and quadruple moments of the linking atoms were optimized against QM electrostatic potentials of the nucleosides. Three polarization groups in each nucleotide were defined (Figure S1). Atomic polarizabilities were transferred from the existing AMOEBA polarizability database.

Parameterization of deoxyribose and ribose rings

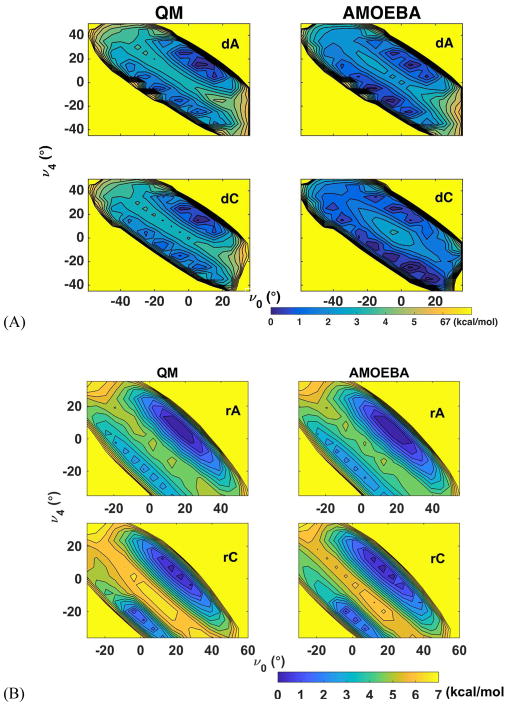
For the ribose and deoxyribose rings, we have carefully examined the distribution of puckering conformations, which is essential to the overall structure of nucleic acids. For instance, B-DNA mainly prefers a C2′-endo sugar conformation while RNA duplex and A-DNA prefers the C3′-endo structure. Typical AMOEBA vdW parameters and atomic polarizabilities of C, O and H were applied for sugar atoms.⁶⁸ The potential energy surfaces for isolated sugar rings were calculated as a function of internal sugar torsional degrees of freedom (Figure 1A). Since a 5-member ring has only two independent torsional angles, the ν₀ and ν₄ angles were selected as the degrees of freedom. The potential energy surfaces generated by scanning ν₀ and ν₄ of both deoxyribose and ribose are shown in Figure S2. MP2/6-311G** with PCM implicit solvent model was employed to compute the QM conformational energy. Due to the intrinsic restraint of the ring structure, both ν₀ and ν₄ were only allowed to vary between −60° and 60°. Both of the ribose and deoxyribose energy surfaces have two local minima: the bottom left minimum corresponds to the C2′-endo structure while the upper right portion of the conformational map corresponds to the C3′-endo structure. The root mean square error (RMSE) between the AMOEBA model and the QM results is 0.55 kcal/mol for ribose and 0.65 kcal/mol for deoxyribose.

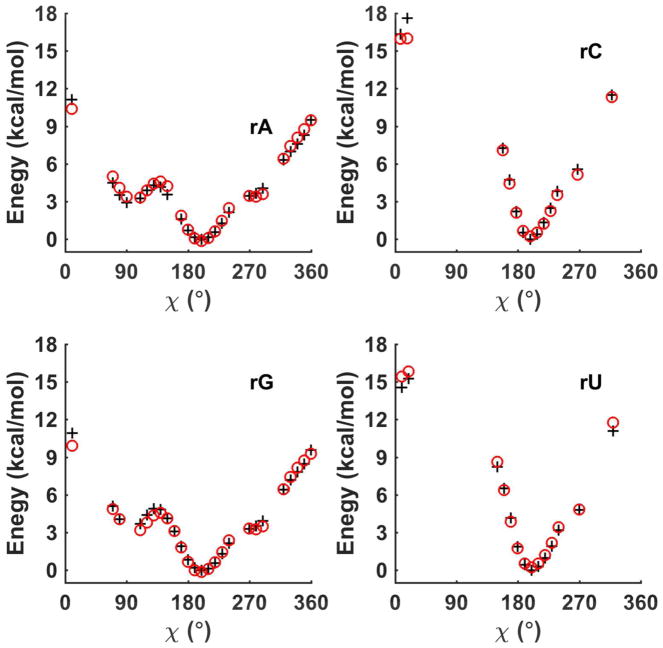
Parameterization of nucleosides

When merging the model compounds into nucleosides, the vdW parameters of the sugar and nucleobases were kept the same, with minor adjustment of monopole values on the linking carbon and nitrogen to match the formal molecular charge.

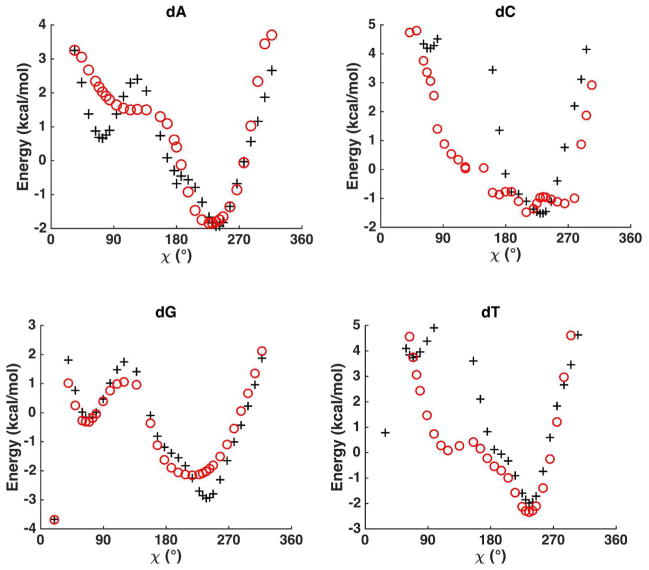
The torsional parameters related to sugar puckering, nucleobase rotation and hydroxyl group rotation were parametrized or refined to reproduce the QM potential energy surfaces. Sugar puckering of deoxyribonucleoside and ribonucleoside in a nucleoside was re-examined with the χ torsion angles fixed at 74° and 195°, respectively, which correspond to nucleoside low-energy conformations (see the χ torsional energy surfaces in Figure 3 and Figure 4). This step is important because sugar conformational energy surface is strongly affected by the presence of bases in the nucleosides. The QM (MP2/6-311**) potential energy surfaces for the nucleosides along ν₀ and ν₄ are shown in Figure 2 and Figures S3 and S4. All the energy surfaces of the nucleosides have two dominant minima corresponding to a C3′-endo structure and a C2′-endo structure, similar to the situation in isolated sugar molecules. From the QM results, the C3′-endo minimum is energetically lower than the C2′-endo minimum for both deoxyribonucleoside and ribonucleoside with χ torsions fixed at 74° and 195°, respectively. Under typical conditions, RNA ribose prefers A-form structure and the C3′ endo is more stable than C2′ endo. The ribose sugar torsions in RNA were parameterized via fitting against QM energy surface maps in Figure 2B and S4. The RMSE between QM and MM, is 0.53 kcal/mol for all data points, and the RMSE is 0.12 kcal/mol for the points with energy less than 6 kcal/mol above the global minimum. In B-DNA, the deoxyribose prefers C2′ endo conformation. Thus, the QM energy surface of the deoxyribose in nucleosides seems to miss certain environmental effects in B-DNA since the C3′-endo is actually lower in energy than C2′-end according to QM. The torsional parameters of deoxyribose in DNA were thus fit against a re-weighted QM surface (Figure 2A and S3), with the C2′-endo region lowered artificially by ~0.5 kcal/mol. As a result, the AMOEBA energy values of the C2′ and C3′ endo minima of the deoxyribonucleoside are more similar to each other than QM results. The final deoxyribose parameters proved to produce stable B-form DNA structures in the subsequence aqueous and crystal simulations.

Figure 3.

Potential energy surfaces along χ angle of deoxyribonucleoside. The abbreviations dA, dT, dG, dC denote deoxyadenosine, thymidine, deoxyguanosine and deoxycytidine, respectively. The deoxyribose sugar was kept at C2′-endo conformation in both QM (MP2/6-311G**, black plus) and AMOEBA calculations (red circle). Energy surfaces for C3′ endo conformation are included in Figure S5.

Figure 4.

Potential energy surfaces along the χ torsion angle of ribonucleosides. The abbreviations rA, rU, rG, rC denote adenosine, uridine, guanosine and cytidine, respectively. The ribose sugar was fixed at C3′ endo conformation for both QM (MP2/6-311G**, black plus) and AMOEBA calculation (red circle). The missing points are non-physical structures. Energy surfaces for C2′ endo conformation are included in Figure S5.

Figure 2.

Comparison of AMOEBA and QM sugar puckering energy maps for nucleosides. (A) deoxyadenosine (dA) and deoxycytidine (dC) maps with χ torsion fixed at 74°. (B) adenosine (rA) and cytidine (rC) maps with χ torsion fixed at 195°. The solvent effect was taken into account through use of PCM in QM calculations and Generalized-Kirkwood (GKSA) in AMOEBA calculations. The conformations with energy greater than 7 kcal/mol are shown in yellow color. The bottom left minimum corresponds to the C2′-endo structure and the upper right one corresponds to the C3′-endo structure.

The sugar pucker conformation and the χ angle together determine the stability of the A, B, or Z-forms of nucleotides. The χ angle which represents the nucleobase is shown in the schematic picture of Figure 1A. We further generated the optimized structures about the χ angle using restrained C2′-endo and C3′-endo sugar pucker conformations for both deoxyribonucleoside and ribonucleoside. QM (MP2/6-311**) energy for these structures were calculated to determine the χ torsion parameters. The C3′endo structures were assigned doubled weight over the C2′endo structures in fitting the ribonucleoside χ angle parameters. The QM and AMOEBA potential energies are shown in Figure 3, Figure 4, and S5. The AMOEBA results agree with QM data for most nucleoside conformations, especially around two important minima: χ near to 260°, which corresponds to the Bform conformation, and χ around 200°, which corresponds to the A-form conformation. Discrepancies exist in the high-energy regions but the structures in these regions are not relevant to either B-form or A-form conformation. The RMSE for the C2′ or C3′endo structures was about 0.4 kcal/mol. The hydroxyl rotational torsions around bonds C2′-O2′, C3′-O3′, and C5′-O5′ were also parameterized by fitting against the QM data (Figures S6 and S7).

Modeling stretch-torsion and angle-torsion coupling in nucleosides

There is notable anomeric effect in DMP and along the nucleic acid backbone, for which we have introduced new bond/angle-torsion coupling terms into AMOEBA to reproduce the bond/angle variations with respect to torsional rotation.⁸⁰ Like the C-O-P-O-C structure in DMP, in the ribose-nucleobase linking structure, C4′-O4′-C1′-N9/N1-C, both O4′ and N9 have lone electron pairs, and the N9 lone electron pair is delocalized into the nucleobase π system, which results in C1′ being an anomeric atom. In native RNA, the ribose is L-enantiomer and the rotational constraint of the sugar O4′-C1′ bond restricts the C4′-O4′-C1′-N9/N1 torsion to values between 200 and 270°. This torsion cannot adopt the gauche conformation (~±60°), where the anomeric effect is most significant. Thus, the anomeric effect mainly applies to the O4′-C1′-N9/N1-C angle (χ torsion), when the anti-bond orbital of O4′-C1′ is nearly parallel to the N9 electron lone pair (or called π electrons) and O4′-C1′-N9-C of a purine (A or G), or O4′-C1′-N1-C of a pyrimidine (T/U or C) is in the +Gauche or –Gauche conformation (Figure 5A).

Figure 5.

Angle- and bond-coupling with torsion O4′-C1′-N1-C6 (χ′) on Cytidine and Deoxycytidine. (A) Illustration of the frontier orbital interaction, which results in the anomeric effect. The O-C1′ antibonding orbital is shown near the oxygen, and the π orbital of N1 is shown on N1. (B) The QM-optimized structure data (MP2/cc-pVTZ level and with χ torsions fixed) are shown in black symbols, and AMOEBA energy-minimized structure data (with χ and C5′-C4′-C3′-O3′ torsions restrained) are shown in red symbols. Cytidine ribose is in C3′ endo conformation and Deoxycytidine deoxyribose is in C2′ endo.

QM calculations were carried out to study the bond and angle variation with χ′ (O4′-C1′-N9-C8 or O4′-C1′-N1-C6) torsion. The results show that the anomeric effect on χ′ torsion leads to significant variation of related angle and bond length with the torsional angle. The maximum angle change reaches ~10° and the maximum bond length change reaches ~0.05 Å (Figure 5B black symbols). Thus, stretch-torsion and angle-torsion coupling terms with χ′ torsion were added to nucleosides. Both of the angle and bond variation curves show a 3-fold symmetry with respect to the χ′ torsion. Thus, 3-fold parameters were added to all the coupling terms. In addition, a 1-fold parameter was added to coupling term for the angle C-N9/N1-C1′ with χ′. See the coupling term energy equations and the corresponding AMOEBA parameters in Table S1. The force constant of each term was adjusted to best match the QM optimized structures with AMOEBA minimized structures (see Figure 5B, red symbols).

Parameterization of nucleic acid backbone torsions

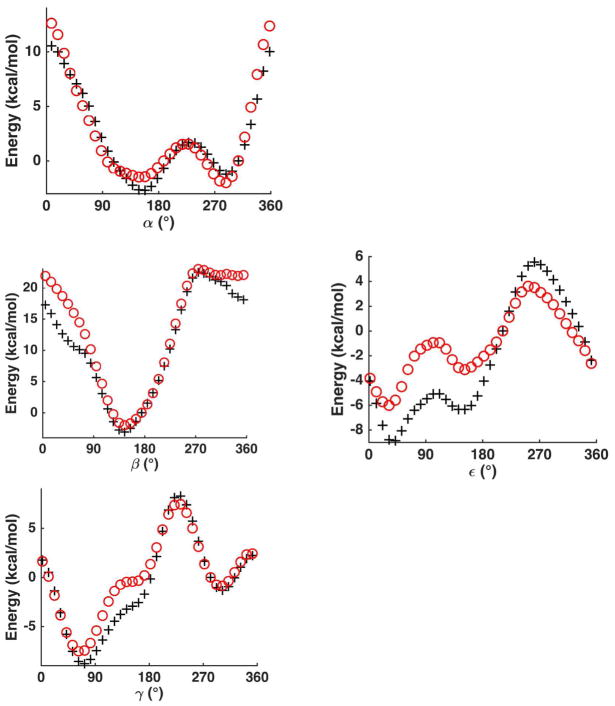
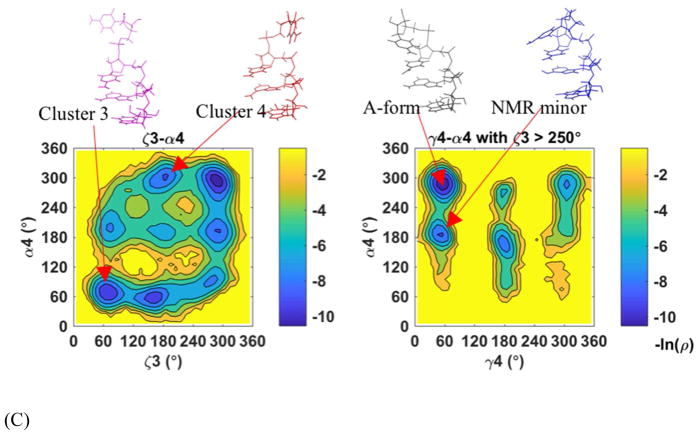
Each nucleotide has six backbone torsions, i.e., α, β, γ, δ, ε, and ζ, from 5′ terminus to 3′ terminus. DNA and RNA share the same α and ζ parameters, which were transferred from DMP. For the other 4 backbone torsions, different parameters were determined for DNA and RNA separately. Since the backbone angle δ is part of the 5-membered sugar ring, its effect is included in the 2-D energy surface of sugar with respect to ν₀ and ν₄.

For DNA β, γ and ε, as well as RNA ε backbone torsion parametrization, (deoxy)ribose 3,5-bis (methyl phosphate) (Figure 1B) was used as a model compound. The initial torsional angles for this model compound were α=308.21°, β=174.82°, γ=43.74°, ε =211.98°, ζ =285.00°, ν₀=13.74° and ν₄=14.22°, typical of an A-form backbone and sugar pucker conformation. While scanning was performed along a particular angle, all the other torsional angles were fixed. Backbone torsion parameters were initially determined by fitting against the QM energy surfaces and refined during the later DNA/RNA simulations. Figure 6 shows the comparison of the QM and the final AMOEBA conformational energy. For the β torsion, the QM and AMOEBA conformational energy was consistent except in the high energy regions. The potential energy surfaces around the γ angle showed two minima, one around 70° and the other at 300°. For ε, the QM and MM conformation energy profiles showed two low energy regions around 40° and 150°. The AMOEBA and QM relative energies in the regions of these minima were consistent but AMOEBA underestimated the barrier to the highest energy conformation. After transferring α and ζ torsional parameters from DMP, the torsional energy surfaces of the model compound around these two torsions were also reproduced by AMOEBA, especially in the low-energy regions. It should be noted the backbone torsions are correlated, and the interaction between nucleic acids and solvents can also alter the energy surface. Therefore, the most populated backbone conformations in condensed phase may not match exactly the minima in the individual conformational energy profiles in Figure 6.

Figure 6.

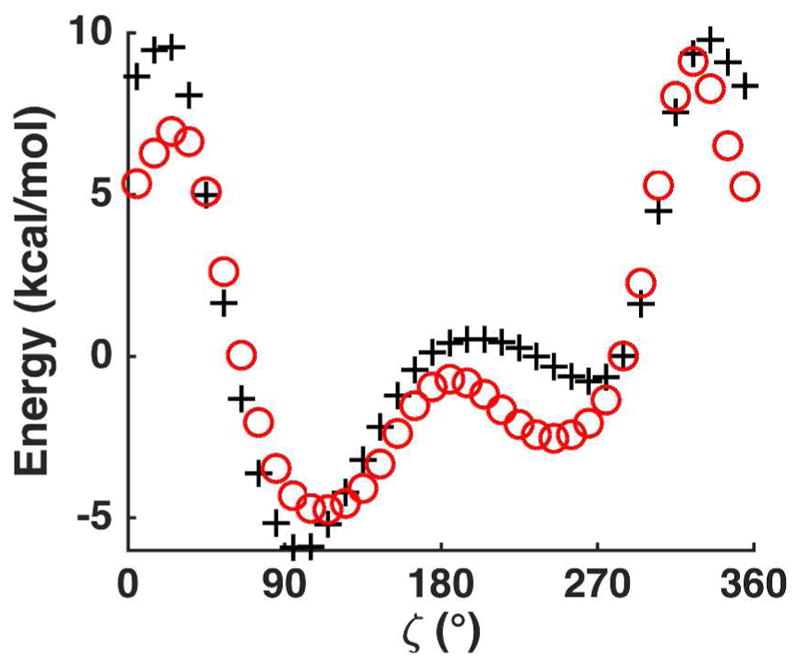
Potential energy surfaces along the backbone torsional angles of model compound deoxyribose 3,5-bis (methyl phosphate). In all plots, the QM results are shown in black plus symbols and the AMOEBA results are shown in red circles.

For RNA, two model compounds were used for the parameterization of the γ and β torsions. 2-Methyltetrahydrofuran phosphate (Figure S8C) was used as a model compound for γ torsion parameterization. Both C2′endo and C3′endo conformations were included with equal weight. The RMSE between the AMOEBA and QM conformational energy was within 0.50 kcal/mol (Figure S9). Methyl ethyl phosphate (Figure S8B) was used as the model compound for β torsional energy evaluation. However, the statistical potential energy profile of the β angle, derived using all RNA NMR structures from the PDB,⁹⁶ shows significantly higher barrier than the QM (Table S2). In the later test on tetramer simulations, the QM-fit β torsion parameters resulted in a backbone that was too soft and flexible. Thus, we used the statistical energy as the fitting target for β, which led to a larger force constant (Table S2).

Molecular dynamics simulations

Besides fitting to the QM results on model compounds, the AMOEBA nucleic acid force field parameters were also refined and validated through extensive molecular dynamics simulations of 20 DNA and RNA systems (see details in Table 1) in aqueous solution, ethanol-water mixture, and crystal lattice. Four NMR double strand DNAs (PDB ID: 1NAJ, 2HKB, 1D42 and 1D20) were selected for simulations in both aqueous solution and in 90%:10% (volume ratio) ethanol/water mixture to investigate the stability and transition between A and B-form structures.^97–100 Four RNA duplexes and three RNA hairpins were selected to investigate the stability of typical RNA molecules. The UUCG tetra loop (10 out 14 residues from 2KOC used) were further simulated with a total 5 μs simulations. Three single strand RNA tetramer AAAA, CAAU, and GACC and a 29-residue RNA, TAR form HIV virus were simulated and compared with experiments. Two Z-form double-strand DNA crystal structure (PDB ID: 1LJX¹⁰¹ and 292D¹⁰²) were selected to evaluate the stability of Z-form structures. Crystal simulations were also carried out on RNA (1RNA) and B-form DNA (1D23) using both unit cells and 2×2×2 super cells, which were compared to the parallel simulations of single 1RNA and 1D23 duplex in water solution. For 1RNA and 1D23, the solution simulations were for 400 and 600 ns respectively.

Table 1.

Details of the nucleic acid systems studied in this work. (A) DNA in solution. In the solvent column, EtOH/water means 90%:10% (volume ratio) ethanol-water mixture. (B) RNA in solution. In the sequence column, the non-WC pairs were underlined. (C) DNA/RNA in crystal. Simulation speed for these systems are provided in Table S4.

(A)
Type	PDB	Simulated Sequences (All WC pairs)	# of residues	# of traj.	Simul. time (ns)	solvent
DNA Double Helices	1D42	5′-GTATATACCATATATG-5′	16	1	850	Water
				1	450	EtOH/water
	1D20	5′-TCTATCACCGAGATAGTGGC-5′	20	1	500	Water
				1	420	EtOH/water
	1NAJ	5′-CGCGAATTCGCGGCGCTTAAGCGC-5′	24	1	1000	Water
				1	700	EtOH/water
	2HKB	5′-CTCGGCGCCATCGAGCCGCGGTAG-5′	24	1	660	Water
				1	500	EtOH/water

(B)
Type	PDB	Simulated Sequences	# of residues	Non-WC pairs and loops	# of traj.	Simul. time (ns)
Double chain (Duplex)	2JXQ	5′-GCAGAGAGCGCGUCUCUCGC-5′	20	All WC	2	800
	1MIS	5′-GCGGACGCCGCAGGCG-5′	16	G-A	2	800
	1F5G	5′-GCAGGCGUGCCGUGCGGACG-5′	20	G-G	2	800
	2L8F	5′-GUGAAGCCCGUUCACAGGAGGC-5′	22	A-A; A-G; G-G; A-C	2	800
Single chain (Hairpin)	2KOC		14	UUCG	2	1000
	1ZIH		12	G-U; GCAA	2	1000
	1SZY		21	CUCAUAA	2	800
Tetra loop	2KOC		10 of 14 used	UUCG	10	5000
tetramer	CAAU	CAAU	4	—	10	3000
	GACC	GACC	4	—	10	6000
	AAAA	AAAA	4	—	10	3000
HIV TAR	1ANR	GGCAGAUCUGAGCCUGGGAGCUCUCUGCC	29	UCU bulge and CUGGGA loop	8	1000

(C)
Type	PDB	Simulated Sequences (All WC pairs)	# of residues	# of traj.	Simul. time (ns)	Description
Z-DNA	1LJX	5′-TGCGCAACGCGT-5′	12	1	600	Na+, unit cell
DNA	292D	5′-CGCGCGGCGCGC-5′	12	1	1000	Na+, unit cell
B-form DNA	1D23	5′-CGATCGATCGGCTAGCTAGC-5′	20	3	1200	Mg2+, unit cell
				6	390	Mg2+, 2×2×2 cell
RNA	1RNA	5′-U-(UA)6-AA-(AU)6-U-5′	28	3	990	Na+, unit cell
				6	300	Na+, 2×2×2 cell

AMBER “tleap” program was used to build the solvated cubic box and add ions.¹⁰³ The shortest distance from the DNA or RNA molecule to the edge of the box is 13Å. The total systems were neutralized and the NaCl concentration is about 0.1 M. In ethanol-water mixtures and Z-DNA crystals, Na+ ions were added just enough to neutralize the negative charge. 1RNA and 1D23 crystals are in the P212121 space group, and in the unit cell, there were 4 copies of nucleic acid duplexes. In the 2×2×2 super cell, the number of copies was 32. The super cell crystal systems for 1RNA and 1D23 were constructed by following the work by Liu et al.¹⁰⁴ Na+ and Mg2+ ions were added to 1RNA and 1D23 crystals respectively to neutralize the negative charge. Details about the simulation setups are shown in Table S3.

All the system equilibration and the production simulations were performed with Tinker-OpenMM package^{58, 105} using the AMOEBA force field on GPUs (GTX 1070) with a mixed precision. The real-space electrostatic interactions and vdW interactions cutoffs were 7.0 Å and 12.0 Å, respectively. The Particle Mesh Ewald (PME) method was applied to treat the long-ranged polarizable multipole based electrostatic interactions,¹⁰⁶ with a grid space of ~0.9 Å in the reciprocal space. The polarization was solved by the Jacobi/Direct Inversion of the Iterative Subspace (JI/DIIS) method,⁸⁷ and the convergence criteria of polarization iteration was set to 10⁻⁴ Debye per atom. This setup was tested to be accurate enough in term of energy conservation for such moderate-size systems. Repartition of the mass of heavy atoms into the bonded hydrogen atoms (hydrogen atom mass increased from 1.0 to 4.0 Dalton) allows a time step of 3 fs to be used. All the systems were equilibrated before production runs. Each DNA/RNA system was relaxed with a series of NVT and NPT simulations. A 20 ns no-restraint NVT equilibration simulation was performed before all the production NVT MD simulations. The average box size in the equilibration NPT run were used for the production simulations. The RESPA integrator,¹⁰⁷ Bussi-Parrinello thermostat¹⁰⁸ and Monte Carlo barostat were used in all the MD simulations.

Analysis of MD trajectories

The conformations in simulation trajectories were superposed to the initial (experimental) structure using either all heavy atoms or heavy atoms without terminal residues. Usually the first NMR structure is the most stable structure in solution and was used as the initial structure for simulations and the target of RMSD calculations.

Curves+ package¹⁰⁹ was used to calculate the helical parameters of DNA or RNA helices using experimental or simulated structures, including a curvilinear axis and parameters relating the position of the bases to this axis, which characterize the subtle details of base paring and base stacking. It additionally provides a full analysis of backbone and χ torsions as well as groove widths and depths.

The distance and twist angle between nucleobase stacking steps in DNA/RNA duplex or the stem of RNA hairpin were also calculated using the C6-C8 long base-pair axis, which is useful especially for non-canonical duplex. The C6-C8 long base-pair axis is defined by the atom C8 of the purine (A or G) and the atom C6 of the pyrimidine (C or U).¹¹⁰ For example, the G-C pair long axis is the C8-C6 vector and the A-G pair long axis is the C8-C8 vector.

K-means clustering method was used for clustering all the conformations from production MD for the RNA tetra-loop and tetramers. An RMSD matrix, containing all RMSD between any two MD frames, was calculated first. The best cluster number for representing the conformations in the trajectories was found to be 4~5. The objective function for the clustering was to minimize the total distances (the square of RMSD) between any cluster point and its cluster center.

NMR distances between any two non-polar H atoms i and j were calculated by averaging the value in all the frames using the equation, $r_{\mathit{NOE}}={\left({\displaystyle \sum _{i=1}^N}\frac{r_i^{-6}}{N}\right)}^{-1/6}$. The same Karplus equations used by Turner and coworkers¹¹¹ were applied to calculate the ³J coupling using the corresponding torsion angles in RNA tetramer simulation (see SI method for equations). The same stacking scoring terms were used for evaluating base-base stacking: center distance, ω angle measuring the overlap between bases, and Ξ angle measuring the angle between the two base-ring planes.¹¹¹ RDC values for HIV TAR were calculated by applying the Prediction of ALignmEnt from Structure (PALES) program¹¹² onto all the MD snapshots and averaging the results.

Results and Discussion

Simulations of DNA duplexes in water

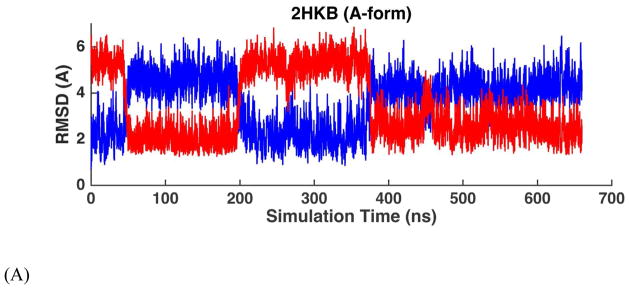
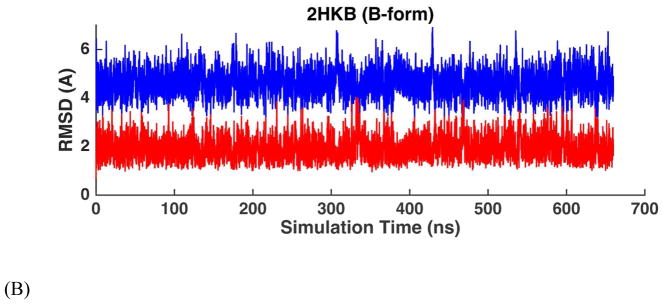
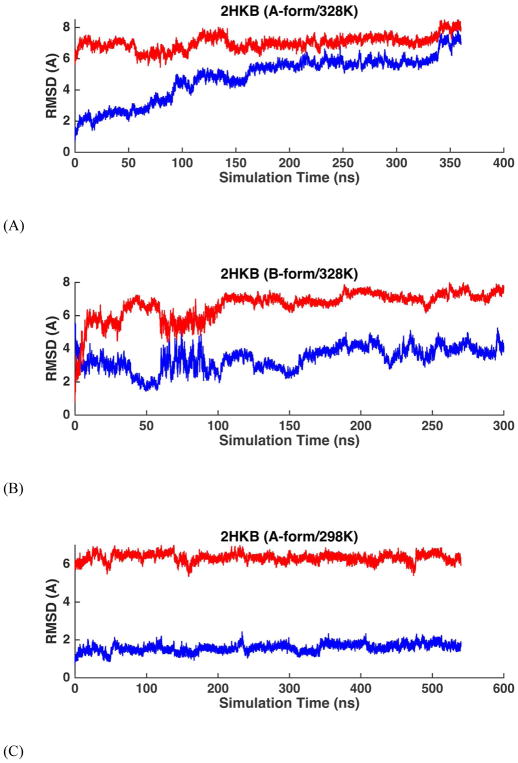
MD simulations were performed on four common double-stranded DNAs (Table 1A), starting from both A- and B-form structures. The solution NMR structures of these four duplexes in water all show typical right-handed B-form structures except that the structure of 1D20 is between A- and B-forms. The RMSDs of the non-terminal heavy atoms from the NMR structure were calculated from MD trajectories and shown in Table 2, as well as Figure 7 and Figure S11. When starting from B-form structures, AMOEBA force field maintained stable B-helices in aqueous solution. The averaged simulation structure for each of the 4 DNA sequences were superposed onto the first NMR structure and shown in Figure 14A. The RMSD values of all the duplexes were stable within hundreds of nanoseconds to microseconds with respect to either the A- or the B-form structures. The average RMSD values with respect to the B-form structures are 1.29 Å for 1NAJ, 1.63 Å for 1D42, 2.18 Å for 1D20 and 1.55 Å for 2HKB. It can be seen from Figure 7B and Figure S11B that the RMSD values with respect to B-form and A-form structures were clearly separated for 1NAJ, 1D42 and 2HKB, indicating the stability of the structures. For 1D20, the RMSD values with respect to A- and B-forms mixed after 300 ns, which agrees with the fact that the NMR structures of 1D20 are between A- and B-forms. In Figure 7A and Figure S11A, the MD trajectories starting from A-form structures are shown. 1D42 and 1NAJ transited from A-form structure to B-form structure in about 10 and 40 ns, respectively. 2HKB transited from A-from to B-form structure in 50ns but it converted back to A-form structure at about 200 ns; it transited back to and stay in B-form structure at about 375 ns (Figure 7A). The fluctuation between A and B-form structures of 2HKB was caused by the inappropriate contact between the phosphate groups and ions in the initial structure. A few sodium ions were put into the major groove in the initial structure of 2HKB and they form strong electrostatic interaction with the phosphate groups. The duplex was prone to bend and form A-form structure due to the inappropriate contact. After about 375 ns, the sodium ions diffused into the solvent and the stable B-form structure was maintained. In the simulations started from A-form, 1D20 fluctuated between A and B-forms and the RMSD values varied between 2~4 Å and the average of both curves were 2.38 Å, which is consistent with the results of simulations started from B-form.

Table 2.

Average RMSD of the simulations for RNA duplex, RNA hairpin, B-DNA duplex in water, and Z-DNA crystal lattice. For RNA molecules, the average RMSD values for each of the two trajectories were calculated. Loop RMSD for RNA hairpins was calculated by superposing the loop and the nearest two base-pair stems and calculating the RMSD of the loop only. The maximum RMSD between NMR structures of the same PDB entry was also calculated, except for 1MIS, 1SZY, and 1D20, each of which has only one NMR structure.

Type	PDB	Average heavy-atom RMSD without terminal base pair (Å)		Average heavy-atom RMSD with all residues (Å)		Loop RMSD (Å)		Maximum all-atom RMSD between NMR structures (Å)
RNA Duplex	2JXQ	1.25	1.41	1.98	2.38	—		0.44
	1MIS	1.51	1.54	1.77	1.74	—		—
	1F5G	1.97	1.98	2.53	2.53	—		1.20
	2L8F	1.50	1.47	2.42	2.14	—		1.09
RNA Hairpin	2KOC	1.72	1.90	1.78	1.95	1.71	2.14	0.97
	1ZIH	2.13	1.83	2.22	1.91	1.95	1.61	1.41
	1SZY	1.66	1.94	1.79	2.00	1.53	2.05	—
B-DNA Duplex	1NAJ	1.29		2.54		—		0.25
	1D42	1.63		1.87		—		1.78
	2HKB	1.55		2.01		—		0.47
	1D20	2.18		3.27		—		—
Z-DNA Crystal	1LJX	1.16		1.45		—		—
	292D	1.32		1.89		—		—
B-DNA Crystal	1D23 unit	0.90		0.93		—		—
	1D23 super	0.88		0.89		—		—
RNA Crystal	1RNA unit	1.22		1.34		—		—
	1RNA super	1.32		1.47		—		—

Figure 7.

RMSD trajectories of non-terminal heavy atoms of DNA dodecamer 2HKB with respect to A-form structure (blue) and B-form structure (red) in aqueous solution. (A) The simulation started with A-form structure. (B) The simulation started with B-form structure.

Figure 14.

The averaged simulation structures (green) superposed with NMR or X-ray crystal structures (black). (A) DNA structures. (B) RNA structures.

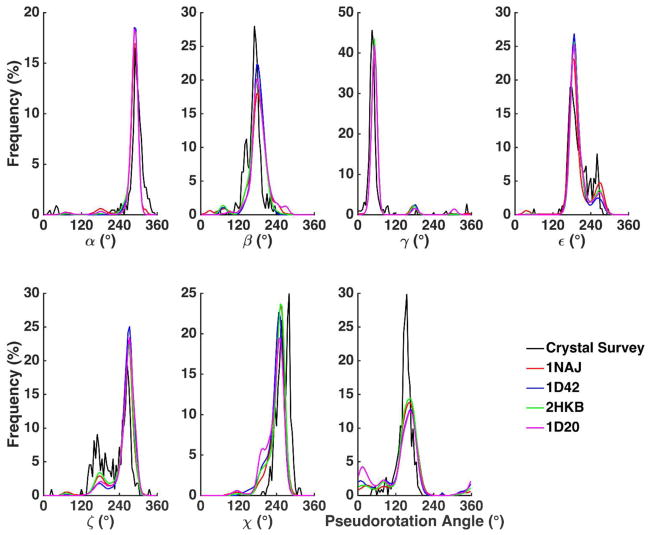
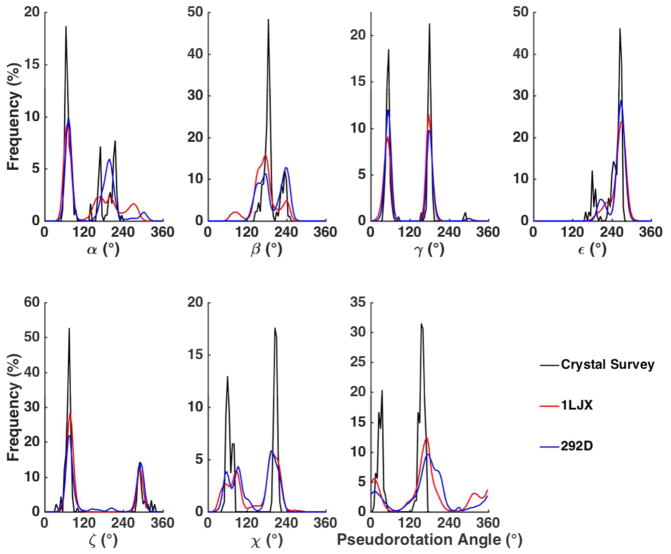
The dihedral angle distributions calculated from the B-form DNA simulations are shown in Figure 8. The dihedral distributions of B-DNA from a crystal survey by Lemkul et al. were used as the reference data³⁹ although it should be kept in mind that the simulations were in aqueous solution. The distributions of α and γ from all the B-form DNA simulations aligned almost perfectly with the data from the crystal survey. The highest peak around 180° and the lower peak around 150° in the β distributions were slightly underestimated compared to the crystal survey. This slight misalignment is not critical for the stability or flexibility of A or B-form structures since the β torsion angle degenerates in both A and B-form structures.²⁴ The ε and ζ distributions captured two major peaks and the higher peaks of ε around 180° and ζ around 260° represent the so-called BI substate of B-form structure and the lower peaks of ε around 260° and ζ around 180° represent the BII substate. The χ torsion angle and the pseudorotation angle of deoxyribose correlated with each other and jointly determined the sugar pucker conformation. The simulations underestimated the B-form like sugar pucker populations (χ around 270° and pseudorotation angle around 160°) but overestimated the A-form like sugar pucker conformations (χ around 200° and pseudorotation angle around 20°). Since all the reference data were from crystal survey and they may not reveal the correct structural fluctuation in aqueous solution, it is not necessary for the simulation results to completely agree with the reference data. Indeed, it was reported that the sugar pucker conformation is more flexible by NMR measurement in comparison with the crystal survey.³⁹

Figure 8.

The torsional angle probability distributions of the four B-DNA helices compared to a crystal survey of all B-DNA X-ray structures.³⁹

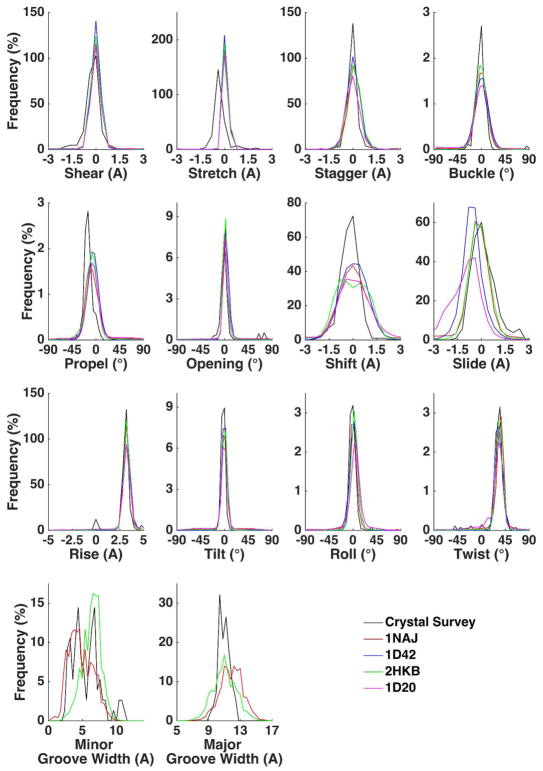
The distribution of the base pair and step parameters were calculated from simulated structures using Curves+ and compared with the survey of B-DNA X-ray structures.³⁹ As shown in Figure 9, the simulation results generally agreed with the crystal survey results. The stretch distribution from the simulation slightly shifted to the right by 0.4 Å compared with the crystal survey. In Figure S13(A–D), the helicoidal parameters were also compared with the corresponding NMR values and the discrepancy in the stretch parameter was noticeably reduced (below 0.3 Å) especially for 2HKB, 1D42, and 1D20 as well as 2JXQ (RNA). In Figure 9, the slide distributions of 1NAJ and 2HKB agree well with the crystal survey, as well as with NMR in Figure S13. The major and minor groove widths of 1NAJ and 2HKB were computed and compared with crystal survey in Figure 9 and NMR structures in Figure S14 A and B. Given the short sequences of 1D42 and 1D20, the groove widths for these two duplexes were not calculated. The major groove widths of both 1NAJ and 2HKB displayed larger fluctuations compared with crystal survey but the mean values are similar. For minor groove width, the crystal survey in Figure 9 shows two peaks and the distribution for 1NAJ mostly align with the peak at lower width and the distribution of 2HKB aligns with peak at higher value. This is expected because the sequence of 1NAJ contains A-tracts that typically have narrower minor groove widths compared with GC sequences. This is also confirmed by the comparison between simulations and NMR results (Figure S14 A and B). Contrasting the simulated structural distribution with NMR structures is perhaps more meaningful given both are in aqueous solution; however the NMR structures are rather limited compared to the comprehensive crystal survey.³⁹

Figure 9.

Comparison of helicodial parameters and groove width distributions between solution-phase simulation and a crystal survey of all B-DNA X-ray structures.³⁹

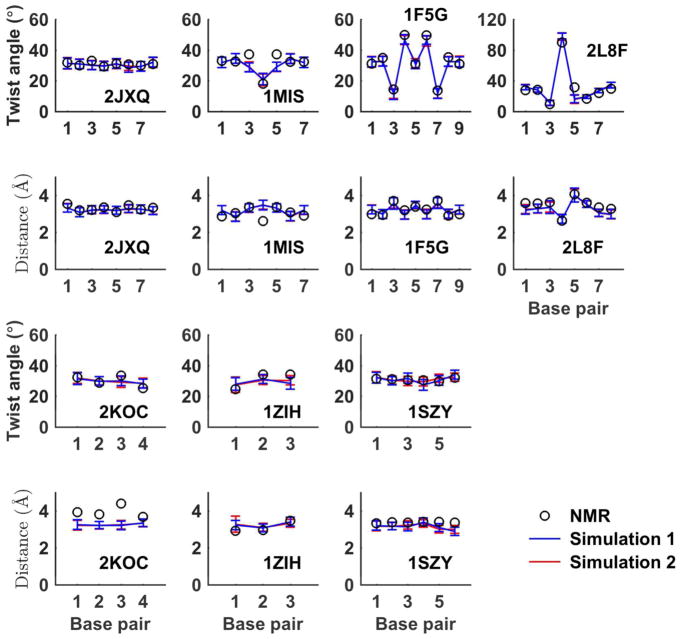
Using the C6-C8 base pair axis as described in the Method section, the distance and twist angle between every nucleobase stacking step were analyzed for the B-form DNA. The twist angles for all the DNA duplexes fluctuated between 30° and 40° with standard deviations <6°. The rise distances mostly fluctuated from 3.0 Å to 3.5 Å with standard deviations <0.3 Å. The RMSD between the simulation averages and the NMR measurements were only 2.96~5.01° for the twist angle and 0.20–0.28 Å for the rise distance, with the terminal residues not considered. The base stacking data also indicated that DNA duplex kept at stable B-form structures (1D20 occasionally transited to A-form structure).

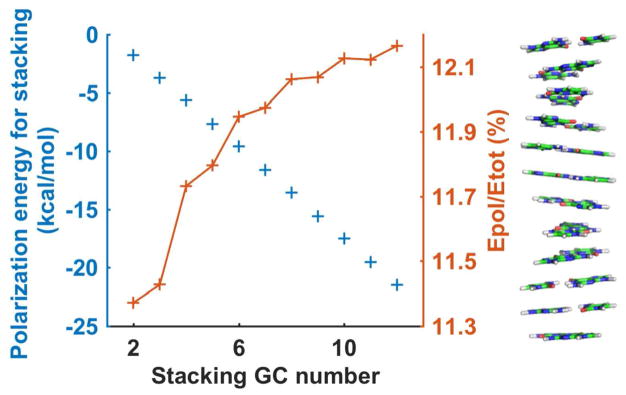
May-body polarization was investigated using a model system of base-pair stacking in standard B-DNA and A-RNA conformations (Figure 10 and S30). The polarization energy of nucleic bases contributed 11–12% to the total interaction energy in the B-DNA conformation, and contributed to 5–6% in the “single-stranded” A-RNA conformation. In both cases, the ratio of the polarization energy to the total energy increased with the number of bases, up to ~10 base/base pairs. The average induced dipole per GC based pair is 0.88 D, with 0.25 D along the helix axis (Figure 10). Aromatic systems such as the bases and benzene typically possess much larger polarizability in plane than out of plane. The strong polarization effect in the bases corroborates previous suggestions that many-body effects are important in the modeling of nucleic acid.^45–46

Figure 10.

Polarization energy of base pair stacking in standard [–(CG)_n–]₂ B-DNA. The stacking structure was constructed base on the standard B-DNA. The total energy (Etot) and polarization energy (Epol) are both interaction energy (system energy minus the sum of energy of individual base pair). The average induced dipole of each GC basepair was 0.88 Debye, and the component on the long axis (perpendicular to the base pairs) was 0.25 Debye.

In all the DNA simulations, the NaCl concentration is around 0.1 M and most of the sodium ions did not have contact with the phosphate group. In rare cases such as the 2HKB simulation in Figure 7A, when a few sodium ions were buried inside the major groove and had direct contact with the phosphate groups, they were able to perturb the structure in short time-scale. Previous experiment and simulation studies have shown that cations are important for stabilizing the DNA structures.^113–118 However, the mobile cations do not seem to have long time-scale effect for the stability of the DNA duplexes at this low salt concentration. Instead, the flexibility of DNA duplex depends on the nucleobase sequence.²³

Simulations of DNA duplexes in ethanol-water mixture

To examine the flexibility of DNA model in response to changes in water activity, we also simulated the four DNA duplexes in 90%:10% (volume ratio) ethanol-water mixtures starting from both A and B-forms. Typically, A-DNA is believed more stable than B-form in such mixtures. However, as suggested by previous studies, the stability of DNA A-form in ethanol/water mixture is highly sequence-dependent and the duplex with low GC content may not be able to maintain stable A-form.^{25–26, 32–34}

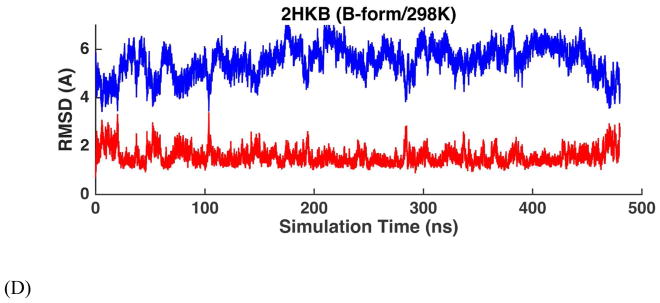
Simulations at 298K did not show any conversion between A and B-form (Figure 11C and D and Figure S12), and the structural RMSDs were quite stable over ~500 ns. We subsequently carried out simulations at higher temperature (328K) to speed up the dynamic conversion of double-stranded DNAs. In Figure 11A and S12, if the DNA duplex started from A-form structures at 328K, 2HKB, 1NAJ and 1D20 were able to maintain the A-form for the first 100–200 ns and then the RMSD values with respect to A-form increased slightly due to the high temperature we used, while the RMSD values relative to B-form remains large. The duplex structures denatured/melted after about 150 ns. However, 1D42 stayed between the A-form and B-form and then melted as other duplexes after 150 ns. 1D42, which has low GC content and is mostly composed of A-T pairs, never maintained a stable A-form in ethanol/water mixture. The high-temperature denaturation is expected based on the experimental temperature-ethanol concentration phase diagram of DNA,³³ which suggests DNA duplexes melt above 323K.

Figure 11.

RMSD trajectories of non-terminal heavy atoms of the DNA dodecamer 2HKB with respect to A-form structure (blue) and B-form structure (red) in ethanol-water mixture. (A) The simulation started with A-form structure at 328K. (B) The simulation started with B-form structure at 328K. (C) The simulation started with A-form structure at 298K. (D) The simulation started with B-form structure at 298K. At the higher temperature, the interconversion occurs rapidly.

On the other hand, as shown in Figure 11B and S12, when the initial structures of the simulations were in B-form, 2HKB, 1NAJ and 1D20 converted to A-forms during MD simulations at 328K. Depending on the sequences and stability of the double helices, the conversion occurred in 20 to 200ns. 1D42 slightly favored A-form during the first 200ns. The results suggest that the AMOEBA DNA force field can sensitively capture the A→B transition in both aqueous solution and water-ethanol mixtures (at least at high temperatures).

Simulations of Z-DNA duplexes in crystal lattice

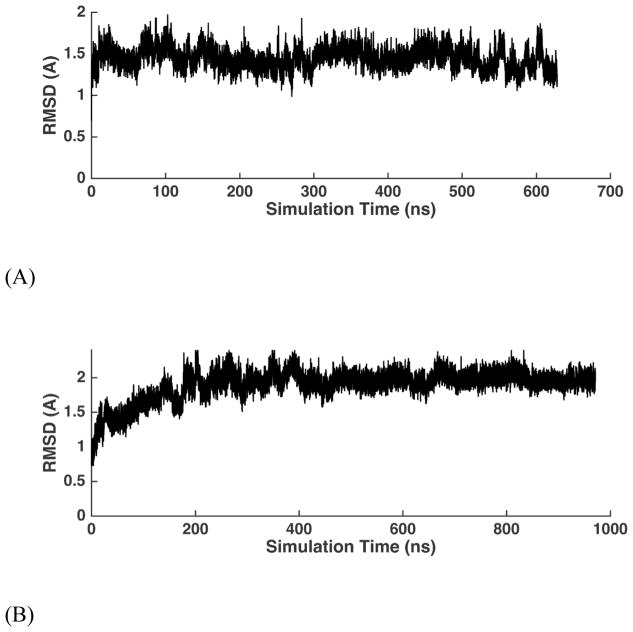
Two left-handed Z-DNA (1LJX and 292D) crystal structures were constructed and simulated for up to 1 μs using the AMOEBA force field. The heavy atom RMSDs of the entire sequences are shown in Figure 12. The average RMSDs of 1LJX and 292D are 1.45 Å and 1.89 Å (Table 2), respectively. If only non-terminal heavy atoms are considered, the average RMSDs of 1LJX and 292D are reduced to 1.16 Å and 1.32 Å. At the hundred-nanosecond to microsecond time scale, both simulations were able to maintain stable Z-form structures. The averaged simulation structures for the two Z-DNA are superposed onto the (first) NMR structures in Figure 14A. In the MD simulations, the 292D showed greater average RMSD than the 1LJX. An important factor in the stability of Z-DNAs is crystal packing. In the 1LJX crystal structure, the DNA terminal nucleobases form head to tail packing the terminal residues in the nearest unit cell but the in the 292D crystal structure, the DNA terminal nucleobases from two adjacent unit cells are slightly misaligned. In solution, it is known¹¹⁹ that the left-handed Z-form is stable at high salt concentrations.

Figure 12.

All heavy-atom RMSD trajectories of the two simulated Z-DNA duplexes in crystal lattices with respect to the experimental crystal structures. (A) 1LJX and (B) 292D.

The dihedral angle distributions of the Z-DNA was examined and compared with the PDB crystal survey³⁹ (Figure 13). Since in the Z-form structure, O4′ of each nucleotide alternatively faces to the opposite direction, the population distributions of all the dihedral angles show two peaks. As demonstrated in Figure 13, the peak positions from the simulation ensembles agree with the reference data for all dihedrals. However, the heights of the peaks are generally lower compared with the survey, suggesting the conformational fluctuations sampled in the simulations are larger than the distributions in the PDB crystal structures. Given the fact that the crystal structures in the survey were all coordinated with excess polyamines and multivalent ions, the high salt concentrations may help to reduce the local fluctuation of Z-DNA.

Figure 13.

The torsional angle probability distributions of the two Z-DNA helices compared to data from a PDB crystal survey.

Simulations of RNA double helix and hairpin

RMSDs between simulated structures and the first NMR structures from PDB are shown in Table 2 and Figure S10. The RMSDs for the hairpin loop regions were also calculated separately. The average RMSD values were all below or around 2.0 Å. The averaged simulation structure for each of the 7 sequences has been superposed onto the first NMR structure in Figure 14B.

The average base-pair rise distance and twist angle in the RNA simulations for each sequence were compared with the corresponding values of the first NMR structure (Figure 15). The average twist angles of one nucleobases stacking step in the all-WC duplex RNA 2JXQ were between 29.0° and 32.0°, with an average value 30.6°, same as that in NMR structure and standard A-form RNAs. The average rise distance between base pairs of 2JXQ simulation was 3.25 Å, compared to the average value of NMR structure, 3.31 Å. At 298 K, the base-pair steps showed a ±3.2° fluctuation in the twist angle and ± 0.22 Å fluctuation in the distance between the two neighboring base pairs. The root mean square twist angle deviations from NMR structures were 1.3°, 4.7°, 2.4°, and 6.6° for the four RNA duplexes 2JXQ, 1MIS, 1F5G, and 2L8F, respectively. The corresponding RMSDs of base-pair distance according to the NMR structures were 0.14, 0.39, 0.18, and 0.24 Å. Axis bend and groove parameters for the 4 RNA double helices in simulations were calculated using Curves+ program and compare with the values of NMR structures. Table S5 shows that axis bend angle of RNA in simulation has a ~2° per base pair average value and has a large fluctuation (was about 1° per base pair). Except for 1F5G, whose NMR structures have a very large total bend angle (~47°), the difference between average simulated and NMR bend values were less than 10°. The simulated groove parameters of RNA helices also generally agreed with the values computed from NMR structures. Figure S13E shows the helicoidal parameters of the canonical RNA duplex 2JXQ. Similar to the DNA simulations, the stretch parameters of 2JXQ simulated structures were a slightly more positive than the NMR values. Among the 12 parameters of 2JXQ, the stagger and buckle values deviated most from the NMR values.

Figure 15.

Twist angle and rise distance between every base-base stacking steps. The average values from each of the two simulations were compared with the corresponding values of the first NMR structure in PDB.

All the non-terminal WC base pairs of the 7 RNA molecules were well maintained in the simulations. Even most of the terminal base-pairs or the capping base pair of hairpin stem (12 out of 14) were stable in the simulations (Figure S16). The broken-up terminal base-pairs in 2JXQ and 2L8F reformed in about 200 ns (Figure S17). We analyzed the important hydrogen bonds for holding the non-WC pair and the hairpin loop (Table 3). For the 10 of the 14 hydrogen bonds of concern, over 95% of simulations frames kept these h-bonding contacts.

Table 3.

Important hydrogen bonds stabilizing the RNA local structure and the percentage of frames holding theses hydrogen bonds. The percentage of frames holding the concerned hydrogen bond in two trajectories is calculated and showed in the last column. A hydrogen bond is counted when the distance between H-donor and H-acceptor is less than 2.5 Å, and both the donor antecedent–donor–accepter angle and the accepter antecedent–accepter–donor angle are greater than 90°.

RNA	Description	Hydrogen bonds analyzed	Percentage of frames holding the hydrogen bonds (%)
1F5G	G4-G7 cis WC-Hoogsteen pair	G4H1-G7O6	99.0	99.1
		G4H2-G7N7	99.3	99.1
1MIS	G4-A5 cis WC-WC pair	G4H1-A5N1	99.8	99.2
		A5H6-G4O6	99.9	99.2
2L8F	A4-A7	A4N3-A7H2	98.0	99.0
	A5-G6	A5N7-G6H2	91.7	95.0
	G6-G5	G6N7-G5H2	96.2	95.8
	C7-A4	C7H4-A4N1	95.8	95.9
2KOC	U6-G9 sugar-WC pair	U6O2-G9H1	97.8	99.6
		U6HO2′-G9O6	80.4	75.4
1ZIH	G5-A8	G5H2-A8OP	95.0	91.3
		G5H2-A8N7	63.7	89.1
1SZY	U9-U12; C8-A14	U9H2-U12OP	97.9	90.0
		C8O1-A14H2	71.8	56.8

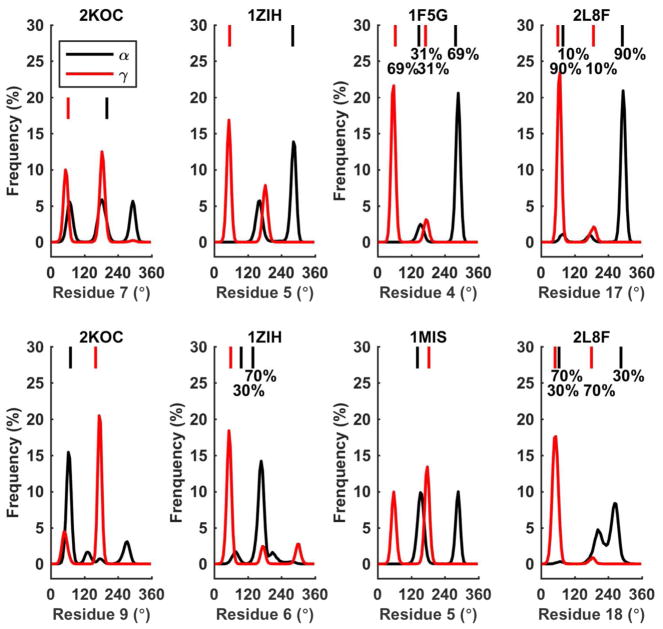
The backbone and χ torsion parameters are crucial for describing the conformations of various RNA structures, especially for the loop residues of hairpins and the non-WC pairing in duplexes, which are usually associated with important functions. We analyzed the torsions of all non-terminal residues and compared them with the values computed from the first NMR structures (Figure S18). Considering all non-terminal residues, 59% of the six types of torsion angles showed less than 10° deviation between the average simulation and NMR values and 83% showed deviations less than 20°. For most of the χ angles, the simulation values were about 5–15° smaller than the corresponding NMR structure values. Both α and γ torsions have two or more populated states in the non-WC pairs or the hairpin loop regions, where larger deviations were found between simulation and NMR. One of issue with the previous version of AMBER (parm99) forces field was the overpopulation of the α/γ = (G+, T).¹²⁰ Thus, the torsion populations on these sites have been analyzed (Figure 16). We found that most of the torsion populations observed in the simulations matched those in the NMR structures. For example, for residue 4 of 1F5G, these two conformations showed up in both simulation and NMR structures, with similar relative populations. In 1MIS simulation, α and γ torsions of residue A5 (named α5 and γ5) displayed another state, (G−, G+), which exist in all but one NMR structure. Interestingly, in 1MIS simulation, the configurations of α5 and γ5 varied cooperatively (Figure S19).

Figure 16.

Torsion α and γ conformation populations in simulations compared with NMR structures. If the difference between torsion angles of two NMR structures is less than 30°, they are considered as in one conformation. The average NMR torsion value and the population for each conformation are labeled on the top. No population label means that all NMR structure belong to one conformation, or there is only NMR structure (1MIS) in PDB.

All the frames of the 14 RNA simulation trajectories were used to analyze the population of sugar puckering conformations. A statistical population density map was plotted with respect to ν₀, and ν₄ (Figure S21). The C3′endo energy minimum had a ~34 times more population than C2′endo energy minimum, which translated into ~2 kcal/mol energy at 300K. The C3′endo minimum was located at (17°, 11°), which is rather consistent with the QM energy maps (Figure 2).

Simulations of DNA/RNA crystals

The temperatures for crystal simulations were set to the experimental crystallization temperatures, 308K for 1RNA and 277K for 1D23. For both systems, a unit cell and a 2x2x2 supercell have been simulated. Each of the duplex in the simulation cell was superposed onto the PDB crystal structure and the average RMSD value of the 4 (unit cell) or 32 (super cell) duplexes were calculated. The average RMSD values for 1RNA unit cell and 1D23 unit cell from NMR structure are only 1.22 and 0.90 Å, respectively (Table 2).

Curves+ helicoidal parameters calculated for unit cell or super cell simulated structures are almost identical (Figure S15). The Curves+ parameters of crystal simulations were also compared with those from solution simulations (Figure S15). Similar to solution simulations, the stretch parameters from 1RNA and 1D23 crystal simulations were also slightly more positive than those evaluated using the PDB X-ray structures. Except propel and opening, the 1RNA base pairing and stacking parameters of crystal simulations closely match those of solution simulations, and most of the parameters show less variations along the nucleotide position in comparison with the X-ray profiles. For 1D23, the difference of shear, stagger, tilt parameters between crystal, solution simulation and X-ray structure were insignificant. While the slide and twist parameters from crystal simulation agreed with X-ray values better than those from solution simulations, interestingly, the buckle, opening, shift, and rise parameters showed opposite trend. It is possible these differences in these parameters are insignificant given the X-ray values are well within the statistical ranges of both crystal and solution simulations, which reflects the dynamic nature of the nucleic acid molecules. The solution simulation of 1D23 did give a much larger axis bend angle than both the crystal simulation and X-ray structure did and the difference is statistically significant. The agreement between crystal simulation and X-ray axis bend is actually quite good. For 1RNA, no significant difference between solution and crystal simulations was observed for any of the structural parameters. Both crystal and solution simulations for the DNA/RNA showed reasonable grooves geometry with some individual discrepancies.

In addition to the individual duplex structure and conformation, the weak interactions between duplexes in the crystal lattice were analyzed. In the work of Liu et al,¹⁰⁴ 3 and 5 important interfaces/contacts were recognized in the 1RNA and 1D23 crystal, respectively, and the distance of special interaction pairs were measured to characterize the hydrogen bonding or van der Waals contacts. Following their methods, we have analyzed those interaction pairs in both super cell and unit cell simulations (Table 4). The results showed that super cell simulation results in a larger fluctuation of contact distance at these interfaces. For both 1RNA and 1D23, most of the distance of interacting atom pairs on interface were in better agreement with experimental (X-ray) values than the previous AMBER results by 0.5 – 1.5 Å, suggesting that the integrity of the crystal lattice and most of the duplex interfaces is significantly less degraded using AMOEBA force field. For both the DNA and RNA crystal, the average major groove-major groove interfaces seem less well maintained by both AMBER and AMOEBA but these distances tend to have large fluctuations in the MD simulations.

Table 4.

Interactions, including hydrogen bonds and van der Waals contacts, in RNA (PDB: 1RNA) or DNA (PDB: 1D23) crystal packing. The interaction definition followed the work of Liu et al. and the simulation results using AMBER were from the tables of their paper. The data in parentheses are standard deviations. The atom pairs with significant improvement using AMOEBA compared with AMBER were showed in bold. The distance values of atom pairs are in Å.

(A) 1RNA crystal
Interaction	Atom 1	Atom 2	X-ray	AMBER Super cell	AMOEBA Super cell	AMOEBA Unit cell
Minor groove-minor groove 1	O2/U1	O2′/A11	3.01	2.78(0.20)	2.86(0.22)	2.85(0.14)
	O2′/A28	O2/U18	3.02	2.80(0.19)	3.10(0.45)	3.02(0.37)
	O3′/A28	O2′/U18	3.00	3.10(0.23)	3.32(0.68)	3.30(0.66)
	O2′/U1	OP1/U12	3.30	4.28(0.55)	4.30(0.47)	4.27(0.39)
	O2′/U2	O2′/U10	2.46	4.02(0.80)	3.06(0.53)	3.10(0.60)
	O2′/A3	O2′/U20	3.20	3.86(0.86)	3.52(0.76)	3.44(0.62)
Minor groove-minor groove 2	O2/U15	O2′/A25	2.67	3.31(0.96)	2.84(0.18)	2.83(0.13)
	O2′/A14	O2/U4	2.77	2.99(0.39)	2.88(0.23)	2.86(0.15)
	O3′/A14	O2′/U4	3.01	3.69(1.36)	2.89(0.28)	2.87(0.25)
Major groove-major groove	C6/U15	O2′/U22	3.17	4.44(0.94)	4.87(0.99)	4.77(1.04)
	C5/U15	O3′/U22	2.80	3.75(0.69)	3.75(0.49)	3.71(0.44)
	O3′/A9	O5′/U1	3.53	4.10(1.11)	5.75(1.53)	5.13(1.33)
	O3′/A9	C5′/U1	3.30	4.26(1.10)	5.55(1.52)	4.91(1.24)
	OP1/U10	C5′/U1	3.32	4.19(1.21)	5.54(1.56)	5.00(1.24)

(B) 1D23 crystal
Interaction	Atom 1	Atom 2	X-ray	Amber Super cell	AMOEBA Super cell	AMOEBA Unit cell
Terminal-terminal	N3/C11	N3/G20	3.49	3.51(0.23)	3.46(0.23)	3.41(0.20)
	O3′/G10	O5′/C1	3.37	3.63(0.89)	3.73(1.07)	4.16(1.30)
Backbone-minor groove	OP1/A3	O4′/A17	3.65	4.77(1.08)	3.99(0.50)	3.89(0.39)
	P/A3	P/A17	6.49	7.59(1.53)	7.58(0.60)	7.63(0.56)
	P/T4	P/A17	4.65	5.79(1.93)	5.28(0.48)	5.39(0.41)
	OP1/T4	OP2/A17	3.88	5.83(1.33)	5.20(0.90)	5.46(0.80)
	OP2/T4	O5′/A17	3.79	4.62(0.96)	4.37(0.51)	4.39(0.49)
Backbone-backbone	OP1/A13	OP2/C9	3.90	5.24(1.39)	4.38(0.53)	4.33(0.50)
	O3′/G12	O5′/T8	3.93	5.23(1.45)	3.78(0.31)	3.74(0.28)
	P/A13	P/C9	5.15	6.65(1.29)	5.50(0.43)	5.42(0.41)
	P/G12	P/T8	8.25	7.12(1.08)	8.33(0.66)	8.35(0.62)
Minor groove-major groove	P/G6	O3′/G20	3.74	4.29(1.05)	4.21(0.64)	4.13(0.54)
	OP2/G6	O3′/G20	2.68	3.37(1.00)	3.18(0.69)	3.06(0.56)
	P/G6	P/G20	8.07	8.36(1.22)	8.38(0.82)	8.36(0.70)
	P/G12	P/G6	6.28	7.71(1.10)	6.41(0.69)	6.44(0.64)
Major groove-major groove	P/G16	O5′/C1	3.40	4.63(1.14)	4.49(0.71)	4.50(0.70)
	O3′/G10	P/G16	3.93	3.96(0.77)	4.43(0.64)	4.76(0.68)
	P/G16	P/G2	6.29	8.09(1.03)	7.60(1.08)	8.10(0.97)
	P/G10	P/G16	8.36	7.57(0.96)	7.08(1.23)	6.60(1.12)

Simulations of UUCG loop

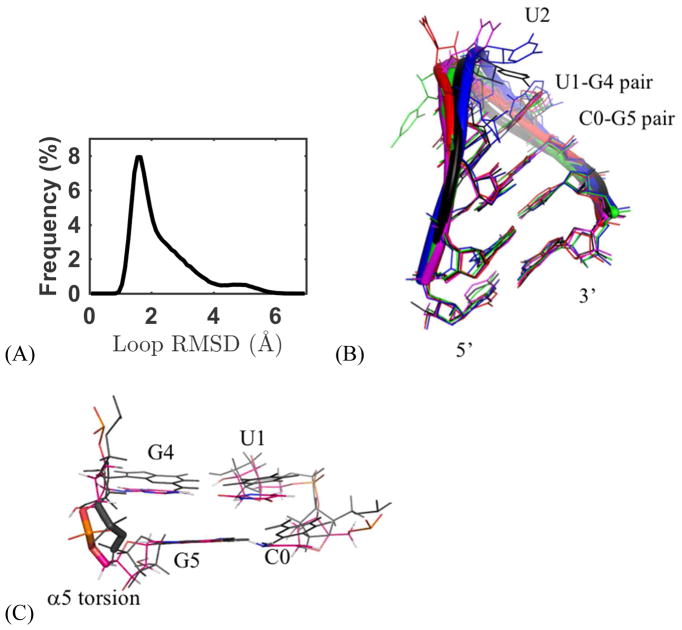
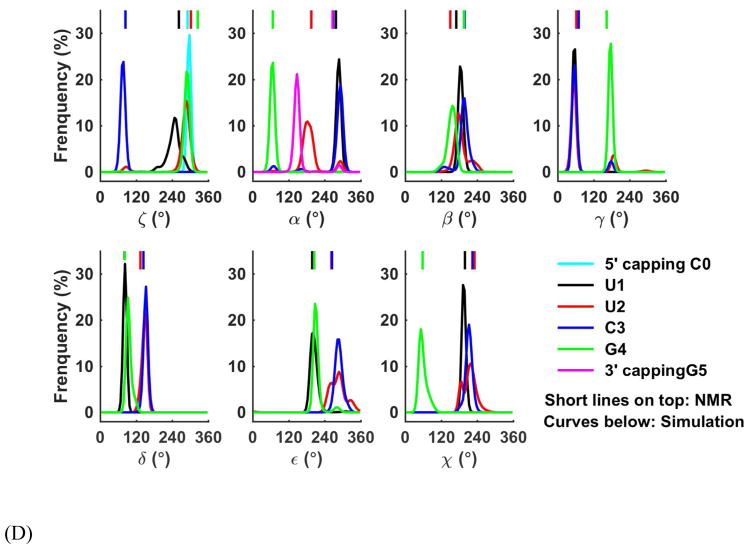
In addition to the MD simulation of the RNA hairpin 2KOC discussed above, the UUCG loop within 2KOC was further investigated. Previous work showed that the loop configurations sampled from MD simulation are inconsistent with those determined from NMR.¹²¹ The first five NMR structures of 2KOC (sequence rGGCAC-UUCG-GUGCC) were truncated and used as starting structures of MD simulations, following the previous work by Cheatham and co-workers.¹²¹ The RNA tetra loops were solvated with 5701 water molecules in a periodic cubic box. The nearest distance from the A-form RNA molecule to the edge of the box is about 13.5 Å. The total systems were neutralized with 21 sodium and 12 chloride ions (~0.1 M NaCl). During both the system preparation and production, the hydrogen bonds of the two terminal base pairs were restrained with a 20.0 kcal/mol Ų force constant. Thus, only the tetra loop and the capping C-G base pair were free to move. A box size of 55.811×55.811×55.811 ų was used in the production MD runs. For each of the 5 NMR structures two 500-ns simulations were performed at 277 K, the same temperature adopted in the previous work.¹²¹ Totally 10 trajectories (5μs) were obtained.

The 3 Watson-Crick pairs of the stem in each simulation frame were superposed to the corresponding residues of the NMR structure, and RMSD from NMR structure were calculated for all-heavy atoms of the four loop residues UUCG, as shown in Figure 17A. Then RMSD between every pair of simulation structures was also calculated, from which a RMSD matrix was built and used to cluster loop conformations. Five clusters were identified from all 10 trajectories (Figure 17B). The first three clusters, with a 0.8–3.5 Å RMSD from the NMR structure, accounted for 85% of the structures, and the major difference between these clusters was the swing of the base of the second loop residue U2. In cluster 4, the altered α and γ torsions of U2 caused the U2 base swing to the other side, which led a 3.0–4.5 Å RMSD from NMR structure. In cluster 5, the U2 moved further and C3 γ torsion also drifted, and U2-C3 formed base-base stacking. However, clusters 4 and 5 only accounted for 15% of all trajectory frames. The extension of trajectory 5 from 500 ns to 1 μs (Figure S26B) showed that the cluster 4 structure turned back to cluster 1 twice within another 350-ns simulation, although only stayed for about 10–15 ns. The first three cluster conformations (clusters 1–3) can easily transit from one to another (see the dynamics of the loop structure in Figure S20). The U1-G4 Sugar edge – Watson Crick edge hydrogen bonds were fairly strong. 99% of simulation frames showed the U1O1-G4H1 hydrogen bond and in 80 % frames the U1HO2′-G4O6 hydrogen bond was well maintained. Table S7 shows the other H-bond populations and the comparison with the performance of AMBER force fields.¹²² We also analyzed the backbone torsions of the loop (Figure 17D and Table S6). The major deviation from the NMR structure was the α torsion angle of the capping residue G5, which changed from negative gauche to near trans. The change of this torsion also led to large deviation (> 35°) in the ζ 4 and β4 from the NMR structure. We found that these changes of backbone torsions actually gave a stronger stacking between G4 and G5, and the stacking distance changed from ~3.9 Å to a regular value ~3.2 Å (Figure 17C).

Figure 17.

Analysis of UUCG loop simulations. (A) Loop RMSD distribution (see RMSD calculation method in main text). (B) Clusters detected in the simulation, the cluster 1–5 are shown in black, blue, magenta, red, and green. The four loop residues were labeled based on their position on the loop, and the capping residues were labeled as C0 and G5. (C) The change of α5 torsion (shown in sticks) result in a stronger G4–G5 stacking. NMR structure is shown in black, and the other structure is the average structure in simulations. (D) Loop torsion population from simulation.

Simulations of RNA single strand tetramer and the comparison with NMR data

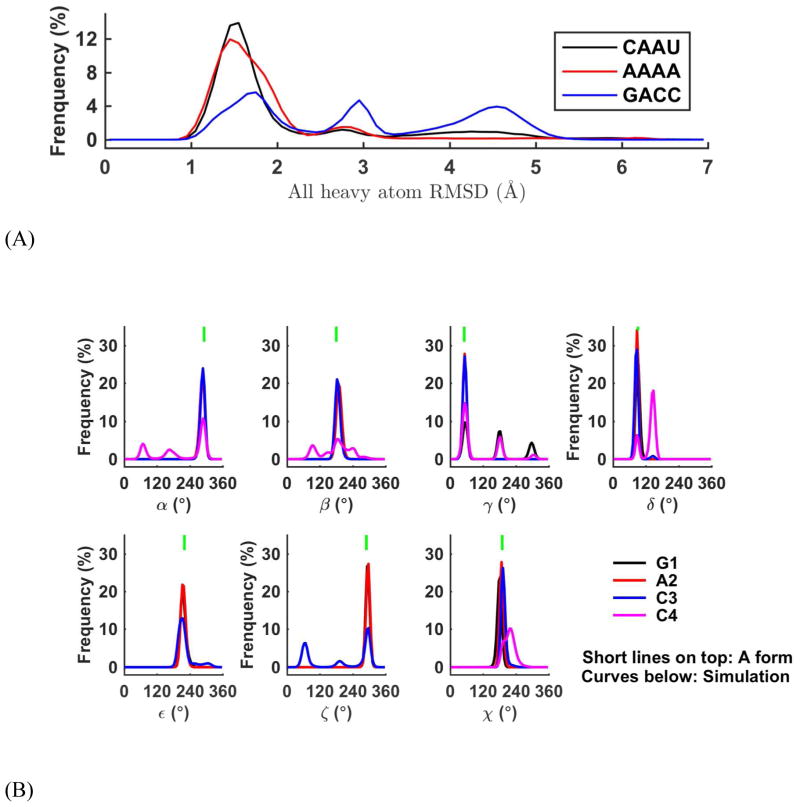
The initial conformations for RNA tetra nucleotides, CAAU, AAAA, and GACC, were taken from standard A-form portion of RNA NMR structures, 1BAU (structure 1, residues 3–6), 2K7E (structure 9, residues 8–11) and 1K5I (structure 2, residues 2–5) respectively. Each RNA tetramer was solvated with 3746 water molecules in a 48.42×48.42×48.42 ų periodic cubic box. The nearest distance from the A-form RNA molecule to the edge of the box was about 13.5 Å. The entire systems were neutralized with 10 sodium and 7 chloride ions (~0.1 M NaCl). 10 trajectories were obtained for each of the three tetramer sequences at 298 K. For each trajectory, the simulation time was 300 ns, 300 ns, and 600 ns, for CAAU, AAAA and GACC respectively.

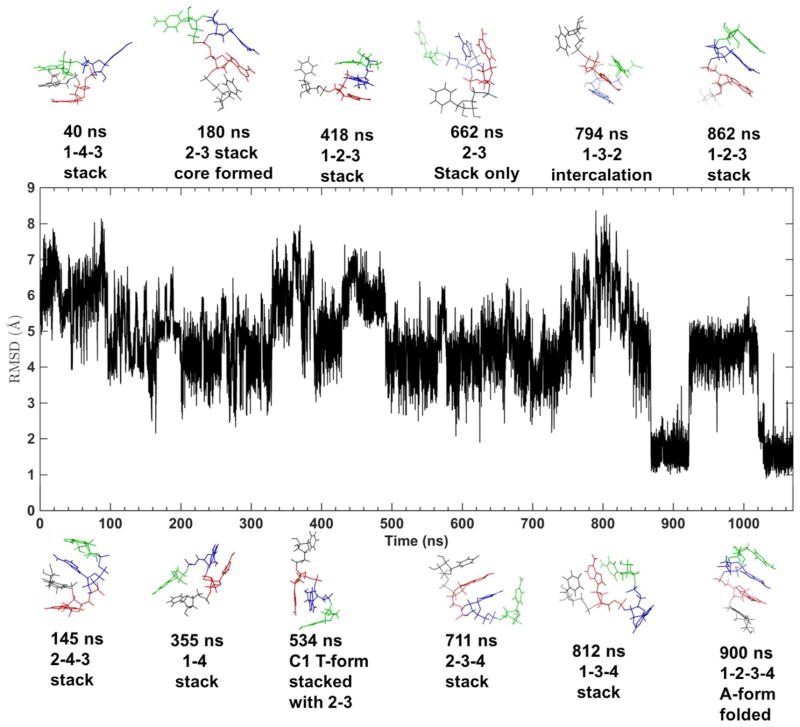
The middle two residues of the RNA in each simulation frame were superposed to the corresponding residues of standard A-form RNA. After supposition, all-heavy atom root mean square deviation from A-form (RMSD) were calculated. The RMSD plots of the three different tetramer sequences showed qualitatively similar distributions (Figure 18A). The most flexible residue was the 3′-terminal residue, on which each tetramer cluster had a major conformation (Figure 18C, S23B, and S24B). In the largest cluster with a < 2 Å RMSD to the standard A-form RNA, most conformations were in standard A form, and a small portion (5%–8%) of near-A form conformations had the same 3–4 stacking pattern but both of α4 and γ4 changed to trans-conformation (α3Tγ4T, see α3Tγ4T structure of rAAAA in Figure S24B). The second cluster was also near-A form conformation with a 2.2–3.2 Å RMSD and only the α torsion of the last residue changed to trans-conformation (α4T). The bases 3 and 4 were stacked in a different style, this structure was also observed in NMR (named NMR minor by Bergonzo et al.¹²¹). The RMSD distribution peak around 3.5–5.5 Å was related to the structures with bases 3 and 4 unstacked and could be clustered to two major conformations. A totally unfolded conformation cluster (with RMSD > 5.5 Å) was found in one of the CAAU 300 ns trajectory (trajectory 8 in Figure S25B). The first two clusters (Figure S22), whose structural properties were consistent with NMR data, contributed to 85.4%, 95.8%, and 60.0% of the simulated population for CAAU, AAAA, and GACC, respectively (see the populations of the tetramer clusters in Table S8). The conformation transitions from one to the other were observed in the initial (Figure S25) or extended simulations (Figure S26A and Figure 19). All the non-A-form conformations could transit back to a near A-form structure.

Figure 18.

Analysis of single strand RNA tetramer simulations. (A) RMSD distribution (see RMSD calculation method in main text). (B) Torsion population in rGACC compared with A-form values. (C) Statistical population maps of ζ3-α4 and α4 -γ4 torsions in rGACC. The contour colors show the value of the negative logarithm of the population density. The location of the central structure in each of the 4 clusters are indicated by arrows on the map.

Figure 19.

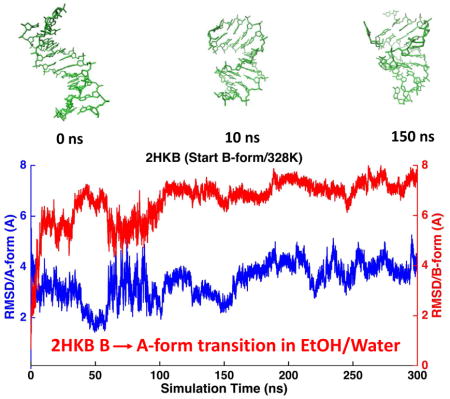
The rCAAU refolding simulation. Time 0 is the end of trajectory 8 at 300ns, at which the rCAAU tetramer was totally unfolded (no stacking in the structure, see the RMSD of trajectory 8 in Figure S25B). The rCAAU structures observed in the simulation are shown above and below the plot. Color scheme in the structure model: green, C1; blue, A2; red, A3; black, U4. At ~865 ns, the tetramer folded to A-form stacking structure.

Using the base-base stacking score adopted by Turner and coworkers for these tetramers,¹¹¹ we further confirmed that there was no 1–3, 1–4, 2–4 stacking, or intercalation in these initial simulation trajectories that started from A-form like structures. Only 1–2, 2–3, and 3–4 base-base stacking conformations were observed in the 3 – 6 μs total simulations in the current study, which was consistent with NMR data (Table 5). The Karplus equations¹²¹ were used for calculating the ³J coupling constants from the simulation trajectories (see the equations in supplementary method), which were related to the backbone torsion angles β, γ, and ε, as well as sugar puckering conformation (see the calculation results and the comparison with experiment in Table 6). 27 of the 30 backbone-torsion-related ³J coupling closely matched the NMR measurements (error < 1.5 Hz). This was consistent with the torsion analysis results, which showed that most of the torsion angles were kept in A-form-like (Figure 18B, S23A, and S24A). The [ζn, α(n+1)] conformation, which Gil-Ley et al. discussed,¹³ was only in NMR G−/G− or mainly in G−/G− conformation. The ³J coupling of γ4 of CAAU and GACC, and β4 of GACC were not correctly predicted, and they all belonged to the terminal torsions. The overestimated γ4 values of CAAU and GACC indicated that trans conformation was over-sampled in our simulation (Table S9). The large β4 of GACC means the 4th residue was perhaps too flexible, and the torsion angle deviated from the trans conformation (Table S9 and Figure 18B). For ³J coupling constants of the ribose sugar torsion, the incorrectly predicted ones were also located at the terminal.

Table 5.

Base stacking in the RNA tetramer simulations. In the tetramer (3μs or 6μs) simulations starting from A-form structures, the 2–3 stacking was very stable and only 1–2, 2–3 and 3–4 stacking were observed in the simulations.

sequence	CAAU		AAAA		GACC
Stacking definition	score > 1.0	score > 0.9	score > 1.0	score > 0.9	score > 1.0	score > 0.9
12stack	38.4%	48.6%	67.6%	75.6%	62.2%	71.4%
13stack	0	0	0	0	0	0
14stack	0	0	0	0	0	0
23stack	75.8%	82.1%	84.1%	89%	93.7%	95.4%
24stack	0	0	0	0	0	0
34stack	65.3%	67.6%	74.5%	78.7%	39.9%	42.2%

Table 6.

Comparison of the calculated ³J coupling values (in Hz) of the 3 single strand RNA tetramers with NMR values. The data with large deviation from NMR value (error > 1.5 Hz) were underlined.

Torsions		CAAU (cal)	CAAU (NMR)	AAAA (cal)	AAAA (NMR)	GACC (cal)	GACC (NMR)
β2		3.1, 3.0	3.7, 2,2	3.4, 2.1	3.8, 1.0	3.9, 1.8	3.7, 0.9
β3		3.1, 2.7	3.5, <1	2.7, 2.5	3.0, 1.0	3.1, 2.2	4.0, 2.0
β4		5.4, 3.6	3.8–4.3, 3.3	4.4, 2.9	3.2, 1.0	8.1, 6.2	4.4, 2.0
γ1		4.8, 3.5	~3.75, 1.6	4.4, 3.3	3.8, 2.0	5.9, 3.5	4.6, 2.3
γ2		2.2, 2.0	~2.8, ~2.1	2.1, 1.8	~2, ~1	2.2, 1.7	~2, ~2
γ3		2.1, 2.0	2.0, 1.3	2.0, 2.0	2.0, 2.0	2.1, 1.7	1.5, <1
γ4		2.4,2.2	1.0, <1	2.9, 2.0	2.0, 2.0	4.6, 1.9	1.8, 1.3
ε1		9.3	9.4–9.8	9.4	8.0–8.9	9.3	9.3
ε2		9.1	8.4	9.3	8.6–8.8	9.4	9.1
ε3		8.4	8.3	8.4	8.3–8.4	7.9	9
ν1	1	0.4	~1	0.0	2.0	0.0	1.8
	2	0.0	~1	0.0	1.0	0.0	<1
	3	0.1	1.4	0.2	1.0	0.4	<1
	4	6.7	3.7	4.7	2.75	8.1	2.5
ν2	1	3.1	4.5	3.2	3.4	3.2	4.4
	2	3.2	4.6	3.2	3.6	3.3	4.4
	3	3.3	4.3	3.3	4.0	3.2	4.0
	4	4.3	3.7	4.4	overlap	4.4	4.6
ν3	1	10.4	8.4	10.7	5.4–6.0	10.6	7.9
	2	10.8	8.3	10.8	7.3	10.8	8.9
	3	10.9	8.2–8.4	10.7	8.0	10.6	8.8
	4	4.6	overlap	5.8	6.0	2.9	7.2

NMR NOE measures the distance between neighboring hydrogen atoms. The NOE data were computed from simulation structures by averaging the distance with a negative sixth power weight (see the Method section). 42 of the 45 CAAU, 38 of the 39 GACC, and 23 of the 23 AAAA NOE peaks were predicted (calculated <6.0 and error <2.0) from the tetramer simulations (Tables 7 and S10). However, 54 predicted peaks were not observed in experiment. Overestimation of peaks seems to be a common problem with NOE prediction by simulation. The correlation coefficient (R²) between the NMR and calculated NOE is 0.57 (Figure 20).

Table 7.

Predicted NOE peak numbers for the three single strand tetramers.

Sequence	CAAU	GACC	AAAA
NMR peaks number	45	39	23
Predicted peaks	42	38	23
False positive peaks (<5.0)	10	15	29

Figure 20.

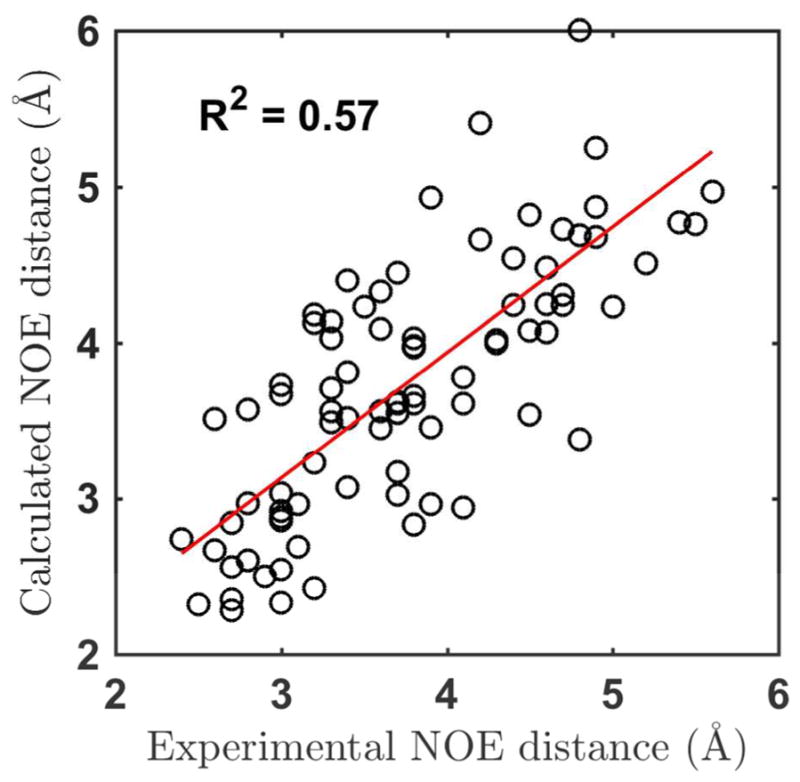
Calculated NOE distances compared with experimental values. Data of all the 3 tetramers (rAAAA, rCAAU, and rGACC) were used and only the experimental NOE data with exact values were included.

The extension of CAAU trajectory 8 started from a totally unfolded structure but converted back to an A-form 1-2-3-4 stacking structure after ~900 ns (fully folded, Figure 19). In ~77% of the extended simulation trajectory (172–764 ns and 819–1070 ns), the tetramer had the A2–A3 stacking core, and within these A2-A3 stacking but not fully folded frames, the near folded structures 2-3-4 stacking and 1-2-3 stacking accounted for about 60%. In Figure 19, the misfolded structures observed in the simulation, including C1-U4-A3, A2-U4-A3, C1-A3-A2, C1-A3-U4 stacking structure are shown. However, these misfolded structures were quite unstable, and only lasted less than 15 ns before breaking up. We also observed 1–4 stacking in the simulation momentarily. Between 500 and 560 ns, the C1 base formed a T-shape stacking with A2–A3 core.

Simulations of HIV TAR

The residual dipolar coupling (RDC) values measured in NMR experiment reflects the orientation of the hydrogen-related chemical bonds, which serves as a good benchmark for the accuracy of force fields. The RDC data for HIV TAR RNA has been reported and computed using AMBER force field.¹²³ TAR is a 59-nucleotide long RNA located at the 5′-end of HIV viral transcripts. The first four PDB structures of 1ANR¹²⁴ were chosen as the starting structures for MD simulations. 25 RDC values were calculated from structures (Table S11). Note that the PDB NMR structures were reported much earlier than the NMR RDC data. We found that the correlation between the PDB-structure calculated and the later reported RDC values was very poor, with R² between 0.20 and 0.45 (Figure S28). The poor correlation could be due to different sources of experiments that may have been performed under different conditions. It is also possible that RDC data cannot be reliably computed from limited NMR structures. On the other hand, using structures from 1 μs dynamics simulations with the AMOEBA force field, the calculated RDC values showed a good agreement with the reported RDC data (Figure S29), with a correlation coefficient (R2) of 0.76 (Figure 21B). The quality of our RDC values is similar to those computed in previous two studies^{123, 125} using AMBER force field. The order parameter (S²) on each residue was also calculated using all the trajectories (Figure 21A). The correlation coefficient R²) (between the calculated and experimental order parameters is 0.77 (Figure S27) and the flexibility of the loop domains was correctly predicted.

Figure 21.

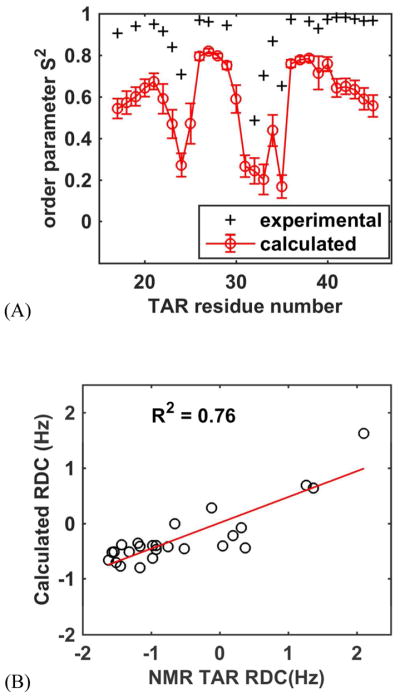
HIV TAR simulation analysis. (A) Comparison of the calculated order parameters S² with the experimental values. (B) The correlation of calculated average RDC using all of the 8 simulation trajectories with NMR data.

Conclusions

The AMOEBA force field for DNA and RNA has been developed based on high-level quantum mechanical calculations and comparison of over 30 microseconds MD simulations of 20 different DNA/RNA molecules with experimental measurements. Previously reported force fields for nucleobases and phosphate groups, which have been extensively validated for capturing base stacking/pairing and phosphate-water and phosphate-metal ion interactions, were incorporated. One focus of the current work is to derive the sugar-puckering, sugar-base and backbone torsion parameters that are crucial for the conformational flexibility of nucleic acids.

The polarization energy was found to contribute significantly the total interaction energy in base pairing and stacking, and varies with number of bases and conformation. In addition to the strong electrostatic polarization between phosphates and ions, the polarization energy observed in bases further substantiates previous suggestions that many-body effects are important in the modeling of nucleic acid.^45–46 However, further studies on specific systems will be necessary to fully illustrate the effect of polarization on nucleic acid structures and properties.

MD simulations of several DNA duplexes using the AMOEBA force field have been performed. The DNA double strands maintained the stable B-form structure in water and the conformational and structural distributions in general agreed with the experimental statistics. In addition to demonstrate that the force field prefers B-DNA in aqueous solution, the inter-conversion between A- and B-form DNAs in ethanol-water mixtures was also captured at 328K. Z-form crystal structures of DNAs were also well maintained in our crystal simulations.

The AMOEBA force field also well reproduced the conformations of several RNAs from crystal or NMR structures. The average RMSD for the 7 RNA duplexes and hairpins was below 2.0 Å, and the important hydrogen bonds in the simulations were maintained, even for most of the terminal pairs hydrogen bonds were preserved. The force field also produced a correct α and γ population for the flexible part of some RNAs. The UUCG tetra loop was simulated for a total of 5 μs, and 85% of the simulated structures matched the NMR conformational states. In at least 60% frames of the single strand tetramer (AAAA, CAAU, and GACC) trajectories, the structure kept in A-form or stacked near A-form structures. An ideal force field should reproduce both the most stable structure and the flexibility of the structures. The transitions between different conformation states were observed in the tetramer simulations, which indicate the force field’s ability to capture the flexibility of RNA tetramers. 27 of the 30-backbone related ³J-coupling and 29 of the 34 ribose-puckering related ³J-couplings were predicted. 104 of the 107 NMR NOE peaks were predicted although 44 predicted peaks were not observed in experiment. Over 85% of the ³J-coupling and NMR NOE results agree with the available experiment measurements. In HIV TAR simulation, there is a strong correlation between the calculated and experimental order parameters (R² = 0.77). Microsecond MD simulations of CAAU tetramer show that the force field can fold it into a well-stacked A-form structure as suggested by NMR. Several non-NMR stacked structures were observed in the folding process, but they were only present in a very short time.

Additional simulations of DNA and RNA in crystal lattice (in both unit cells and super cells) have been performed. The small RMSDs indicated the overall X-ray structures were well sustained by the force field simulations. The Curves+ program was applied to obtain detailed structural information on the simulated DNA and RNA duplexes both in crystal lattice and solution. In general, the base pair and stack as well as groove parameters from solution and crystal simulations are in reasonable agreement with values from the crystal survey and/or computed using the X-ray or NMR structures. For some structural parameters, simulations displayed larger (statistically significant) deviation from X-ray or NMR structures to varying degrees. These discrepancies are however not always systematic. In the unit and super cell crystal simulations, the duplex-duplex interfaces showed noticeable improvements over the previous AMBER simulation results, suggesting AMOEBA is capturing certain aspects of the long-range interactions between the duplexes.

Given the flexibility of the DNA/RNA structures and the sensitivity to their chemical and physical conditions, future studies over a wide range of sequences and environments, as well as extensive sampling over long MD simulations, are needed to fully examine and improve the force field. We believe the AMOEBA nucleic acid force field will bring fresh physical insights and new opportunities to understand nucleic acid systems in various biological processes using classical molecular mechanics modeling.

ABBREVIATIONS

DMP

dimethyl phosphate

QM

quantum mechanics

MD

molecular dynamics

AMOEBA

Atomic Multipole Optimized Energetics for Biomolecular Applications

RMSD

root mean squared deviation

RMSE

root mean squared error

PCM

polarizable continuum model

GK

Generalized Kirkwood

WC

Watson-Crick

PDB

protein databank

NMR

nuclear magnetic resonance

NOE

nuclear overhauser effect