Abstract
Numerous studies have suggested that medical image derived computational mechanics models could be developed to reduce mortality and morbidity due to cardiovascular diseases by allowing for patient-specific surgical planning and customized medical device design. In this work, we present a novel framework for designing prosthetic heart valves using a parametric design platform and immersogeometric fluid–structure interaction (FSI) analysis. We parameterize the leaflet geometry using several key design parameters. This allows for generating various perturbations of the leaflet design for the patient-specific aortic root reconstructed from the medical image data. Each design is analyzed using our hybrid arbitrary Lagrangian–Eulerian/immersogeometric FSI methodology, which allows us to efficiently simulate the coupling of the deforming aortic root, the parametrically designed prosthetic valves, and the surrounding blood flow under physiological conditions. A parametric study is carried out to investigate the influence of the geometry on heart valve performance, indicated by the effective orifice area (EOA) and the coaptation area (CA). Finally, the FSI simulation result of a design that balances EOA and CA reasonably well is compared with patient-specific phase contrast magnetic resonance imaging data to demonstrate the qualitative similarity of the flow patterns in the ascending aorta.
Keywords: Bioprosthetic heart valves, Patient-specific, Fluid, structure interaction, Immersogeometric analysis, Isogeometric analysis, Parametric design
1. Introduction
Computer simulations of fluid and solid mechanics greatly expand the scope of what can be inferred from non-invasive imaging of the cardiovascular system. This claim has been argued by academic researchers for at least 20 years, starting with the works of Makhijani et al. [1], Taylor et al. [2, 3], and Lemmon and Yoganathan [4]. But the recent entry of computational fluid dynamics (CFD) into mainstream clinical practice, as a method of estimating fractional flow reserve (FFR) from computed tomography angiography (CTA) [5, 6], has decisively proven that the paradigm of image-based predictive modeling of the cardiovascular system can simultaneously improve diagnoses and outcomes while reducing costs. However, the use of image-based CFD to circumvent costly invasive measurements of clinical quantities of interest realizes only a fraction of the potential benefits outlined in Taylor et al.’s proposed paradigm of predictive cardiovascular medicine [7]. Over the past decade or so, numerous studies have suggested that using medical images to construct computational mechanics models could reduce mortality and morbidity due to cardiovascular diseases by allowing for patient-specific surgical planning [8–14] or even customized design of medical devices [15–19].
The possibility of patient-specific prosthetic heart valve design is the topic of the present study. In particular, we focus on the potential role of computational fluid–structure interaction (FSI) analysis in the design of stentless aortic valve prostheses that conform to the aortic root geometries of individual patients, as obtained from non-invasive medical imaging modalities. Aortic valve replacement is commonly indicated for patients suffering from heart valve diseases; over 90,000 prosthetic valves are implanted in the United States each year [20]. While valves can sometimes be surgically repaired, prosthetic replacement is the only option for a vast majority of patients [21]. Replacement heart valves fabricated from biologically derived materials are referred to as bioprosthetic heart valves (BHVs). While these devices have blood flow characteristics similar to the native valves, device failure continues to result from leaflet structural deterioration, mediated by fatigue and/or tissue mineralization. Mechanical stress has long been known to play a role in this deterioration [22] and substantial work has been done by academic researchers to predict and optimize the distribution of this stress by using tools from engineering analysis to simulate (quasi-)static [23] and dynamic [24] structural mechanics, and, more recently, fluid–structure interaction [25].
Most BHVs consist of chemically-treated bovine pericardial leaflets sutured to a rigid stent [26]. Stents are available in multiple sizes, but this several-sizes-fit-all paradigm may not provide optimal results for many patients since valve performance is highly dependent on the geometry of the root and the leaflets. Alternatives to rigid stented valves include stentless valves [26], offering larger orifice areas and improved hemodynamics. However, as stated by Xiong et al. [27], the prosthetic leaflet geometry of a stentless valve plays a key role for its efficacy and durability. Auricchio et al. [17] found that geometrically symmetric stentless prosthetic valves implanted in patient-specific aortic roots, in general characterized by asymmetric sinuses, can cause heart valve misclosure, leading to valve insufficiency. Clinical aspects of stentless valves are reviewed in Ennker et al. [28]. The cited study concluded that stentless valves decrease the incidence of mismatch between patients and prostheses [28, pp. 81] and that all studies from the literature report a survival advantage for stentless prostheses relative to stented valves [28, pp. 77]. However, the authors also noted that many surgeons remain hesitant to use the total root technique or perform any kind of stentless valve implantation [28, pp. 79–80], due to the technical complexity of the operation. The implantation technique is non-trivial and therefore the clinical outcomes of these implants are strongly dependent on an appropriate choice of both prosthesis size and replacement technique, which is, at present, strictly related to the surgeon’s experience and skill [29]. In the present study, we propose a patient-specific computational approach to support pre-operative planning of stentless aortic valve implants by studying the sensitivity of prosthesis geometric features and determining the best-performing prosthesis shape. More precisely, we hypothesize that image-based patient-specific computational FSI analysis could provide a rational method for planning and optimizing the details of this complex surgery in advance, increasing the probability of realizing the full benefits of stentless valve replacement.
The construction of geometrical computer models of heart valves is already attracting interest from the medical device industry. For example, the Siemens eSie Valves system [30] is marketed as a means for physicians to extract geometrical quantities of interest (e.g., annulus diameter, orifice area, etc.) from medical images of patients’ heart valves. Desirable features of such a system are closely aligned with those of computer-aided design (CAD) programs used in engineering. For instance, a recent white paper [31] on the eSie Valves technology emphasizes the importance of “intuitive editing” of semi-automatically-generated segmentations of patients’ valve leaflets. Recent work by academic researchers also indicates that spline surfaces and curves used in CAD programs provide a convenient representation of heart valve geometries segmented from medical imaging data [32–34]. If we want to develop computational mechanics analysis technologies that align with this trend, we are naturally led to the field of isogeometric analysis (IGA).
Isogeometric analysis was originally proposed by Hughes et al. [35] as a way to unify engineering analysis and design, by directly employing designer-friendly representations of geometry as computational analysis models. This eliminates the difficult task of converting between design geometries and finite element/volume representations needed for numerical analysis. As mentioned above, clinicians would prefer design-like representations of geometry that can be intuitively manipulated. Obtaining these representations from medical images is itself nontrivial, but one can at least avoid doubling the segmentation workload by leveraging IGA to re-use these representations as analysis models. Image-based patient-specific IGA of heart valve structural mechanics has been previously studied by Morganti et al. [36], who found that IGA of heart valves does not just permit convenient re-use of intuitive geometry representations; it can also dramatically increase the accuracy of mechanical analyses relative to traditional finite element discretizations [36, Figures 13 and 14]. The current contribution extends this body of work on patient-specific heart valve IGA to include FSI analysis. Due to the difficulty of developing general-purpose methods for tracking fluid–solid interfaces through large and complex deformations, such as those undergone by aortic valve leaflets, we have combined ideas from IGA with the concept of immersed boundary FSI analysis [37–40]. We refer to this combination of ideas as immersogeometric FSI analysis [41].
Figure 13.
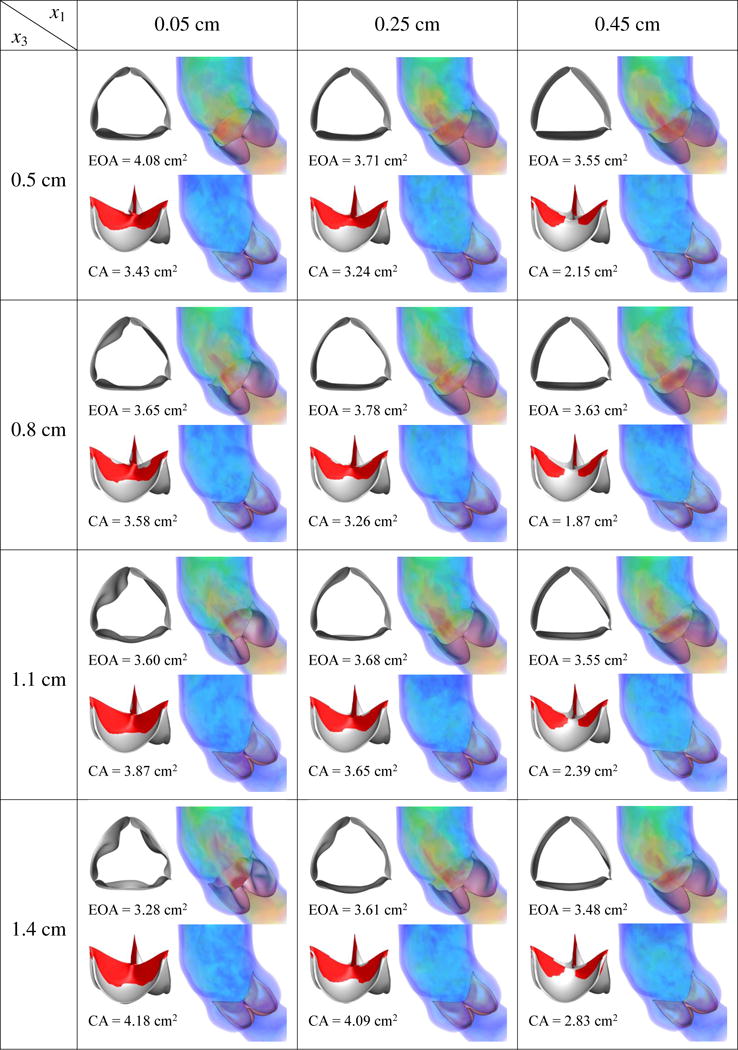
Results of different combination of design variables x1 and x3, with x2 being fixed as 0.5 cm. Velocity magnitude is plotted using a color scale ranging from 0 (blue) to ≥ 80 cm/s (red).
Figure 14.

Location of the cross section in the medical image data and in the simulation: (a) Long-axis view from MRI highlighting the cross section considered for phase-contrast blood velocity registration; (b) PC-MRI taken at peaksystole. The green circle highlights the ascending aorta cross section. Gray levels are associated to velocity values. (c) Cross section in the computational model taken consistent with that considered for in-vivo velocity registration.
Immersogeometric analysis is ideally-suited to automatic optimization of engineered systems and/or exploration of design spaces, as it directly immerses CAD boundary representations of engineering designs into unfitted discretizations of volumes [42, 43]. CAD geometries are often parameterized in terms of a few key dimensions; this is known as parametric design. Using traditional finite element or finite volume analysis methods, one would need to regenerate an analysis mesh every time a design parameter is modified, which often requires some manual intervention by the analyst. Using immersogeometric approaches, design parameters can be varied freely, and the modified design can be re-analyzed without human intervention. This is demonstrated by the parametric design optimization of a water brake in Wu et al. [44]. The idea of applying immersogeometric FSI analysis to a parametric BHV design is shown in Hsu et al. [45].
Parametric design of heart valve leaflet geometries dates back to Thubrikar [46, Chapter 1], which introduced a 3D geometry description of the aortic valve by considering the intersection surfaces of a cone with inclined planes and used this description to search for optimal prosthetic dimensions with appropriate coaptation, minimum volume, and efficient use of energy. Subsequent studies on parameterized heart valve geometries include Labrosse et al. [47], Auricchio et al. [17], Haj-Ali et al. [48], Kouhi and Morsi [49], Fan et al. [19], and Li and Sun [50]. These studies have focused on defining general guidelines for prosthetic valve design that might be expected to improve average outcomes for the population considered as a whole. However, with the advent of 3D bioprinting [51] (which has already been studied in the context of aortic valve replacement [52]), it may one day be possible to perform optimization of geometry on a per-patient basis, taking into account variations in patient aortic root geometry and other patient-specific factors. Computational methods enabling patient-specific simulations of native and prosthetic heart valves were reviewed by Votta et al. [53] and Soares et al. [54].
In this work, we develop a framework for designing patient-specific prosthetic heart valves using an IGA-based parametric design platform and immersogeometric FSI analysis. The patient-specific aortic root geometry is reconstructed from the medical image data and is represented using non-uniform rational B-splines (NURBS). The leaflet geometry is parameterized using several geometric design parameters which allows for generating various perturbations of the leaflet design for the patient’s aortic root. Each design is analyzed using our hybrid arbitrary Lagrangian-Eulerian/immersogeometric FSI solver, which allows us to efficiently perform a computation that combines a boundary-fitted, deforming-mesh treatment of the artery with a non-boundary-fitted treatment of the leaflets. We simulate the coupled dynamics of the patient-specific aortic root, parametrically designed heart valves, and surrounding blood flow, under physiological conditions. The leaflet and arterial wall motion are coupled using a penalty formulation imposed over the intersection of the artery wall with a fictitious smooth extension of the leaflets. The artery wall tissue prestress is included to improve the physical realism of the modeling. A parametric study is carried out to investigate the influence of the geometry on heart valve efficiency and performance, indicated by the effective orifice area (EOA) during the opening phase and the coaptation area (CA) during the closing phase, and to identify a design that balances EOA and CA reasonably well, Finally, the simulation result of this best-performing prosthetic valve is compared with the phase contrast magnetic resonance imaging (PC-MRI) data from the patient to demonstrate the qualitative similarity of the flow patterns in the ascending aorta.
The paper is organized as follows. In Section 2, we describe the tools that we use to perform patient-specific valve simulations: Section 2.1 introduces our techniques for obtaining spline-based geometrical representations of arteries and valves, using medical image processing and parametric design; Sections 2.2–2.5 cover the mathematical models of continuum mechanics that we assume for the fluid and structural components, and our isogeometric and immersogeometric discretizations of those models. In Section 3, we explore the parametric BHV design space and evaluates candidate valves in terms of clinical quantities of interest. In Section 4, we compare simulated hemodynamics with patient-specific magnetic resonance velocimetry data. Finally, the conclusions are presented in Section 5.
2. Modeling and simulation framework
This section describes our pipeline for processing medical image data into geometrical models of the ascending aorta, parameterizing patient-specific BHV design spaces, and discretizing FSI problems posed on these custom geometries.
2.1. Patient-specific geometry modeling
We demonstrate our geometrical modeling approach using ECG-gated CTA and PC-MRI of the aortic valve region of a 69 year-old patient. This data was obtained from the internal database of the IRCCS Policlinico San Donato hospital in Milan, Italy. The selected patient underwent radiological investigations for descending aorta disease, while being characterized as having a healthy aortic valve. This and the amount of available imaging data are the main reasons for choosing this specific patient.
2.1.1. Patient-specific medical image processing
Contrast enhanced multislice CTA was performed using a Siemens SOMATOM Definition AS scanner (Siemens Medical Solutions, Erlangen, Germany), with a collimation width of 0.6 mm, slice thickness of 0.75 mm, and pixel spacing of 0.685 mm × 0.685 mm. We process CTA images using the open-source Vascular Modeling ToolKit (vmtk) [55] to segment the aortic root from the left ventriculo-aortic junction to the sinotubular one. CTA images from end diastole have the highest quality and are therefore selected for segmentation. We use level sets following the approach proposed by Antiga et al. [56]. After completing the segmentation step, a triangulated surface representation of the aortic lumen is obtained using the marching cubes algorithm. A centerline of the aortic root segment is computed from its surface model using vmtk. A simple and fast least-squares approach is then adopted to map a primitive NURBS geometry (e.g., a cylinder) onto the obtained target lumen surface representation. We refer readers to Morganti et al. [36] for more details on this procedure.
As will become evident in the following sections, the end diastolic configuration presents a challenge for stentless valve design because the leaflets are highly deformed and subjected to nontrivial self-contact constraints, while supporting a substantial transvalvular pressure gradient. To avoid these complications, we scale the lumen surface radially by 1.1, which is the ratio between peak systolic and end diastolic radii observed from the patient’s PC-MRI images. The scaled geometry represents the peak systolic configuration and is used as the reference geometry. The final quadratic NURBS surface representation of the patient-specific aortic root is shown in Figure 1a.
Figure 1.
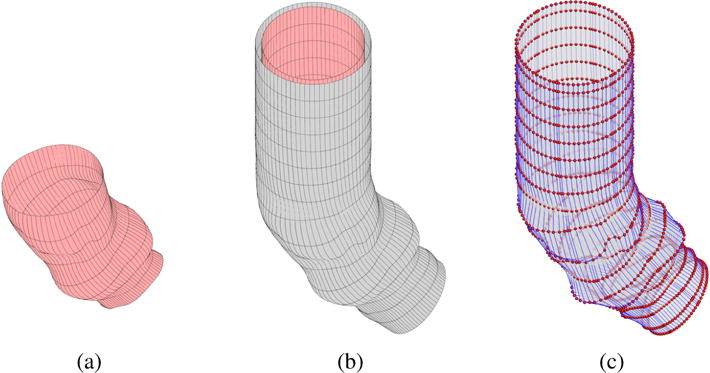
(a) The NURBS surface representation of the patient-specific aortic root. (b) The NURBS surfaces of the ascending aorta. The lumen surface (or the inner artery wall surface) is shown in red and the outer artery wall surface is shown in gray. (c) The control points and control mesh of the outer artery wall surface.
In this work, we plan to simulate the blood flow in a deforming ascending aorta interacting with different designs of the BHV. To do so, we first add a short tubular extension between the aortic root and the left ventricle, and a longer tubular extension between the aortic root and the arch. This gives us the lumen surface of our ascending aorta, extended from the patient-specific aortic root geometry. For the purpose of constructing a 3D discretization of the artery wall, we expand the lumen surface in the outward normal direction to obtain a model of the outer surface of the aortic wall. (As a result, the lumen surface also serves as the inner surface of the aortic wall.) For simplicity, we choose a constant wall thickness of 2.5 mm, which is in the range of physiological values [57]. The final NURBS surfaces of the ascending aorta are shown in Figure 1b. The control points and control mesh of the outer surface are shown in Figure 1c. The NURBS inner and outer surfaces are used to construct volumetric NURBS descriptions of the fluid (lumen) and solid (artery wall) domain geometries that are suitable for isogeometric analysis.
2.1.2. Trivariate NURBS parameterization of the ascending aorta
To obtain a volumetric parameterization of the artery and lumen, we first construct a trivariate multi-patch NURBS in a regular shape, e.g. a tubular domain, with lateral boundaries and an internal hypersurface that have the same control mesh topologies as the outer and inner surfaces of the artery wall shown in Figure 1b. We then solve a linear elastostatic, mesh moving problem [58–60] for the displacement from this regular domain to a deformed configuration that represents the artery and lumen. The control points shown in Figure 1c are used to prescribe Dirichlet boundary conditions on the displacement of the regular domain’s lateral boundaries and internal hypersurface. However, solving a linear elastostatic problem to obtain the deformed interior mesh is only effective for relatively mild or translational deformations. For scenarios that involve large rotational structural motions, such as the deformation of a straight tubular domain into the curved shape of patient-specific ascending aorta in Figure 1b, the interior elements can become severely distorted. To avoid this, we construct the initial regular domain in the following way.
We first obtain a centerline along the axial direction of the patient-specific artery wall surface. Along this centerline, we define a number of cross sections corresponding to the control points of the NURBS artery wall surface in the axial direction. (These cross sections are shown as blue curves in Figure 2a.) At each cross section, we calculate its unit normal vector nc and the effective radius rc, which is determined such that the area of a circle calculated using this radius matches the area of the cross section. (A circle corresponding to one of the cross sections is shown in the red curve in Figure 2a.) Finally, using this information, we construct a tubular NURBS surface that has the same control point and knot vector topology as the target patient-specific artery wall surface, as shown in Figures 2b and 2c. Another tubular surface corresponding to the lumen surface is also constructed, using the same cross sections but smaller effective radii coming from the lumen NURBS surface.
Figure 2.
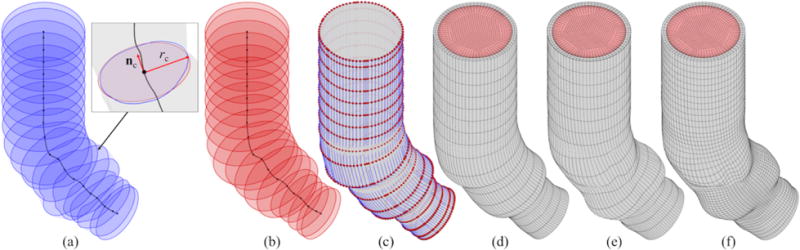
The construction of the volumetric NURBS discretization of the blood and the artery wall domains. (a) Cross sections of the artery wall surface. (b) Circular cross sections. (c) NURBS tubular surface and corresponding control points. (d) Primitive volume mesh. (e) Deformed volume mesh. (f) h-refined volume mesh.
These two tubular NURBS surfaces are used to construct a primitive trivariate multi-patch NURBS that includes (pre-images of) the solid and fluid subdomains, shown in gray and red, respectively, in Figure 2d. The multi-patch design avoids the parametric degeneracy that would occur in a cylindrical-polar single-patch parameterization. Due to this, a total of six C0-continuous locations are present in the circumferential direction of the NURBS domain.1 Basis functions are made C0-continuous at the fluid–solid interface, so that velocity functions defined using the resulting spline space conform to standard fluid–structure kinematic constraints while retaining the ability to represent non-smooth behavior across the material interface.
The resulting volumetric NURBS can then be morphed to match the patient-specific geometry with minimal rotation, so an elastostatic problem can provide an analysis-suitable parameterization. Mesh quality is further enhanced by including Jacobian-based stiffening techniques [62], to avoid excessive distortion of small elements in critical areas such as the vicinity of the fluid–solid interface. Displacements at the ends of the tube are constrained to remain within their respective cross sections. Finally, we refine the deformed trivariate NURBS for analysis purposes, by inserting knots at desired locations, such as around the sinuses and the flow boundary layers. The final volumetric NURBS discretization of the patient-specific ascending aorta is shown in Figure 2f. The mesh of the lumen and artery wall consist of 66,960 and 8,928 quadratic elements, respectively.
2.1.3. Parametric BHV design
In this paper, we aim to advance methods for designing effective prosthetic valves for specific patients. This requires the capability to control the design of aortic valve leaflets within the geometrical constraints imposed by an arbitrary patient-specific aortic root. We focus specifically on the leaflet geometry and assume that non-leaflet components of stentless valves move with the aortic root and do not affect aortic deformation or flow. Leaflets are therefore modeled as being directly attached to the aortic root. Starting from the NURBS surface of a patient-specific root, valve leaflets are parametrically designed as follows. We first pick nine “key points” located on the ends of commissure lines and the bottom of the sinuses. The positions of these points are indicated by blue spheres in Figure 3. These define how the leaflets attach to the sinuses. The key points solely depend on the geometry of the patient-specific aortic root and will remain unchanged for different valve designs. We then parameterize families of univariate B-splines defining the free edges and radial “belly curves” of the leaflets. These curves are shown in red and green in Figure 3. The attachment edges, free edges, and belly curves are then interpolated to obtain smooth bivariate B-spline representations of the leaflets.
Figure 3.
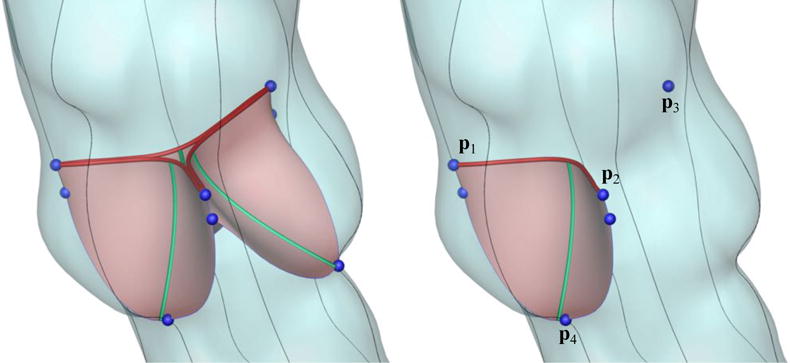
The key geometric features used to parametrically control the valve designs. The blue key points define the attachment of the valve to the root. The red and green curves are parametrically controlled for valve design.
Figure 4 shows the details of parameterizing the free-edge curve (red) and the belly-region curve (green). We take one of the three leaflets to address the parameters controlling the valve designs. In Figure 4, p1, p2 and p3 are the key points on the top of the commissure lines and p4 is the key point on the sinus bottom, as labeled in Figure 3. p1 to p3 define a triangle Δp1–3, with pc being its geometric center. The unit vector pointing from pc to pn (the geometric center of p1 and p2) is denoted as tp, and the unit normal vector of Δp1–3 pointing downwards is np. We first construct the free edge curve as a univariate quadratic B-spline curve determined by three control points, p1, pf, and p2. pf is defined by pf = pc + x1tp + x2np. By changing x1 and x2 to control the location of pf, the curvature (length) and the height of the free edge can be parametrically changed. We then take pm as the midpoint of the free edge, the point pb, and the key point p4 to construct a univariate quadratic B-spline curve (green). The point pb is defined by pb = po + x3np, where po is the projection of pm onto Δp1–3 along the direction of np. The physical meaning of x3 is the vertical distance between pb and Δp1–3. Thus, the free edge and the belly curve share the point pm in the physical space. Note that the aforementioned control points are used to construct the curves only and are not the control points of the final surface. Finally, the fixed attachment edges and the parametrically controlled free edge and belly curve are used to construct a cubic B-spline surface with desired parameterization.
Figure 4.
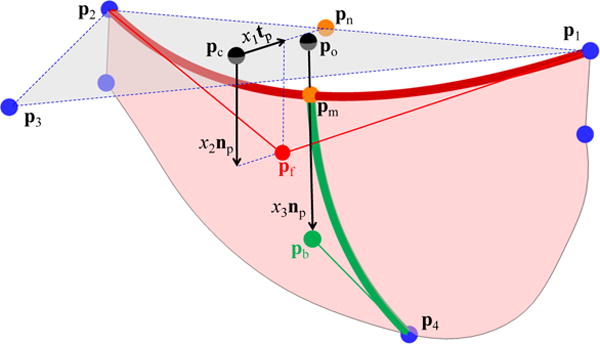
The parametric control of the valve designs. The key points (blue spheres) are identical to those in the right plot of Figure 3. x1, x2, and x3 control the location of Pf and Pb and thus control the curvature and height of the red free edge, and the curvature of the green belly curve.
By choosing x1, x2 and x3 as design variables, we can parametrically change the free edge and belly curve, and therefore change the valve design. This procedure is implemented in an interactive geometry modeling and parametric design platform [63] based on Rhinoceros 3D [64] and Grasshopper [65]. Some sample points in the design space are depicted in Figure 5, to illustrate the effect of each parameter on the geometry. Four examples of heart valve designs are shown in Figure 6.
Figure 5.
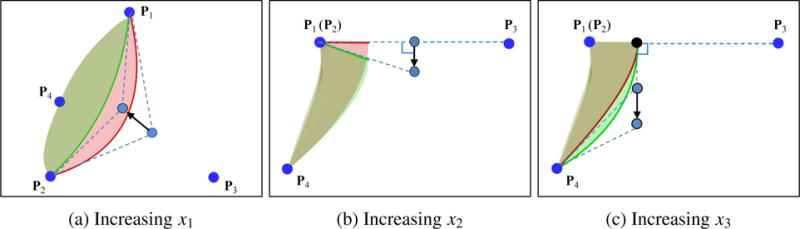
The effect of increasing design parameters x1, x2, and x3. Red surfaces denote designs before increasing the design parameters and green surfaces denote designs after increasing the design parameters.
Figure 6.
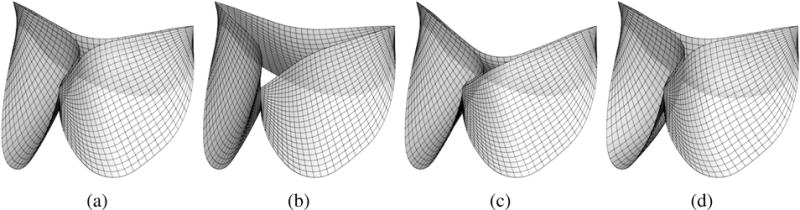
Selected examples of the heart valve designs used in this work. (a) x1 = 0.05 cm, x2 = 0.1 cm, and x3 = 0.8 cm. (b) x1 = 0.45 cm, x2 = 0.1 cm, and x3 = 0.8 cm. (c) x1 = 0.05 cm, x2 = 0.5 cm, and x3 = 0.8 cm. (d) x1 = 0.05 cm, x2 = 0.1 cm, and x3 = 1.4 cm.
2.2. Fluid–structure interaction problem
We model the ascending aorta and prosthetic valve leaflets at time t as elastic structures occupying a region (Ωs)t, coupled to blood flow through (Ωf)t by kinematic and traction compatibility conditions at the fluid–structure interface (ΓI)t. The blood flow within (Ωf)t is assumed to be incompressible and Newtonian. The subscript t may be omitted in some formulas below, when there is no risk of confusion. This coupled partial differential equation (PDE) system can be expressed in weak form as: Find a fluid velocity and pressure , a structural displacement field , and a fluid–solid interface traction such that for all , , , and ,
| (1) |
where and are trial solution and test function spaces, Bf, Ff, Bs, and Fs are variational forms defining the fluid and structure subproblems, us is the material time derivative of y, and β is a penalty parameter. The additional terms integrated over ΓI enforce the fluid–structure coupling conditions on the fluid–structure interface2. The presence of the last term facilitates the development of certain numerical schemes based on the “augmented Lagrangian” concept, as detailed in Bazilevs et al. [66, Section 2]. The forms defining the fluid and structure subproblems are specified in the sequel.
2.3. Structural formulations
The artery wall is substantially thicker than the valve leaflets. We model the artery wall as an elastic solid and we model the valve leaflets as a thin shell structure. This distinction can be formalized by introducing superscripts “so” and “sh” to denote the solid and shell, respectively, and expressing and , such that y ={yso, ysh} and . We can then write
| (2) |
and likewise for Fs.
Remark 1
In a slight abuse of notation, linear combinations of ws and y with functions defined on the fluid domain (as seen in the fluid–structure interface terms of (1)) are understood to involve only whichever component of the structure trial/test function tuple is defined at a given point on ΓI.
2.3.1. Artery wall modeling
The artery wall is modeled as a hyperelastic solid, subject to damping forces. We thus define
| (3) |
where is the portion of Ωs corresponding to the artery wall, ρs is the solid mass density, X are coordinates in the reference configuration, F is the deformation gradient associated with displacement y, S is the hyperelastic contribution to the second Piola–Kirchhoff stress tensor, S0 is a prescribed prestress in the reference configuration 3, fs is a prescribed body force, and hs is a prescribed traction on the Neumann boundary . The elastic contribution to the second Piola–Kirchhoff stress in (3) derives from a compressible neo-Hookean model with dilational penalty [67]:
| (4) |
| (5) |
where J = detF, C = FTF is the right Cauchy–Green deformation tensor, I1 = tr C, μ is the shear modulus, and κ is the bulk modulus. The stress–strain behavior of the model (5) was analytically studied on simple cases of uniaxial strain [60] and pure shear [68]. It was shown in Bazilevs et al. [69] that this model is appropriate for arterial wall modeling in FSI simulations; while the level of elastic strain in arterial FSI problems is large enough to preclude the use of linearized strain measures, it is small enough that any model with the correct tangent stiffness at small strains, relative to the reference configuration, is sufficient to capture the effects of arterial deformation on hemodynamics. We discretize this subproblem in space by using multi-patch trivariate quadratic NURBS to approximate each Cartesian component of the displacement.
The additional prestress S0 in (3) is needed because the aorta configuration at the peak systole is subject to blood pressure and viscous traction, and is therefore not stress-free. We determine S0 by setting the displacement from the imaged configuration to zero in (3) and assuming that external forces on the solid subproblem are due to interaction with the fluid. This leaves us with the problem: Find the symmetric tensor S0 such that for all ,
| (6) |
where 4 and is a prescribed fluid traction. may be obtained from a separate rigid-wall blood flow simulation on the reference domain with constant inflow pressure and resistance outflow boundary conditions. Because (6) is a vector-valued equation with a tensor-valued unknown S0, it, in principle, may have an infinite number of solutions. In this work, we obtain a particular solution for the state of prestress following the procedure proposed by Hsu and Bazilevs [70], Starting with step n = 1 and setting , we repeat the following steps:
Set and y = 0, which gives F = I and S = 0.
- From tn → tn+1, solve the following variational problem: Find y, such that for all ws,
(7) Update and increment n.
The above iteration is continued until y → 0. As a result, F → I, S → 0, and we arrive at a solution for (6).
2.3.2. Thin shell formulations for the leaflets
The portion of Ωs corresponding to the valve leaflets, denoted , is assumed to be extruded from a midsurface, . To facilitate the specification and discrete approximation of coupling conditions at the interface between the solid artery and the leaflets, we extend this parametric surface into the solid artery domain at time t = 0, such that , as illustrated in Figures 7 and 8. The shell structure problem for the valve leaflets (in the Lagrangian description) is then posed on . Since we assume the portion of the fluid–structure interface ΓI corresponding to the valve leaflets to coincide with in the reference configuration, we denote .
Figure 7.
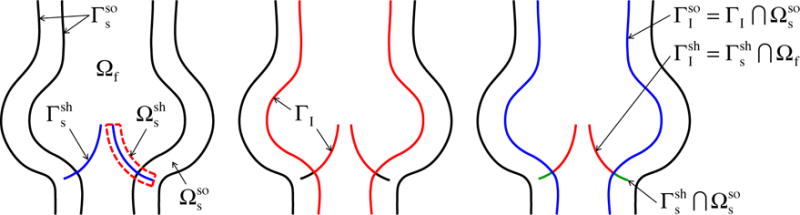
Illustration of the associated domains and boundaries on which the FSI problem is posed.
Figure 8.
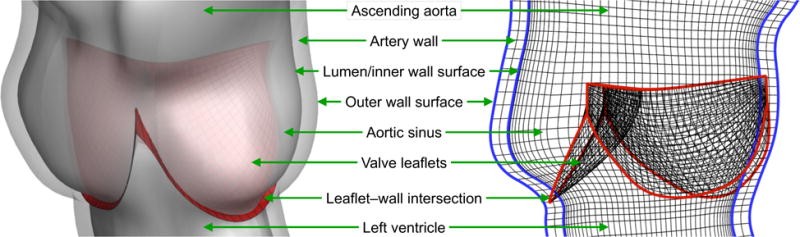
The aortic root magnified and shown in relation to the valve leaflets. A schematic of the wall, lumen and leaflet meshes is shown on the right. A fictitious smooth extension of the shell structure midsurface Γ extends into in the reference configuration to facilitate penalty coupling between the artery wall and leaflets.
The assumption that is extruded from is consistent with the kinematic assumptions used to derive the Kirchhoff–Love thin shell formulation. We model the valve leaflets using the isogeometric Kirchhoff–Love shell formulation studied by Kiendl et al. [71–73]. In summary, this amounts to defining
| (8) |
where ρs is the mass density of the structure, S is the second Piola–Kirchhoff stress, δE is the variation of the Green–Lagrange strain E, and are the shell midsurface in the reference and deformed configurations, respectively, ξ3 ∈ [−hth/2, hth/2] is the through-thickness coordinate, hth is the shell thickness, and sums traction contributions from the two sides of the shell. The Green–Lagrange strain used to compute S and δE is simplified, following the kinematic assumptions of Kirchhoff–Love thin shell theory, to depend entirely on the midsurface deformation, as detailed in Kiendl et al. [71]. In this paper, we assume that the material is incompressible and S is computed from (the simplified) E using an isotropic Fung-type material model, in which the matrix and fiber stiffening effect are modeled with neo-Hookean and exponential terms, respectively. Specifically,
| (9) |
where
| (10) |
and
| (11) |
In the above, C = 2E + I, p is a Lagrange multiplier enforcing incompressibility5, and c0, c1, and c2 are material parameters. A more detailed discussion of this model can be found in Hsu et al. [45].
By using at least C1 -continuous NURBS patches to represent the leaflets, the weak problem for the shell midsurface displacement can be discretized using a straightforward isogeometric Bubnov–Galerkin method, as in Kiendl et al. [71]. To represent approximate displacement solutions of the shell structure, we refine the spline space used to define the parametric leaflet geometry, by inserting knots. In the computations of this paper, the shell structure analysis mesh comprises 609 cubic B-spline elements for each leaflet, as shown in Figure 6. A schematic illustration of the artery wall, lumen and leaflet mesh relations is shown in Figure 8.
In principle, fluid–structure kinematics should prevent interpenetration of the valve leaflets if the fluid velocity field is continuous. (Under mild assumptions, it is not even possible for objects immersed in incompressible viscous flow to contact one another in finite time [74, 75].) However, in discrete solutions, the FSI kinematic constraint is only satisfied approximately and we find that penalizing leaflet interpenetration improves the quality of solutions. The penalty contact method used in this work is detailed in Kamensky et al. [41, Section 5.2].
2.3.3. Leaflet–artery coupling
The connection between the artery and the leaflets of the stentless prosthetic valve is modeled by constraining the shell structure midsurface displacement and its derivatives with respect to ξ1 and ξ2 to equal those of the solid artery displacement along the basal edge of each leaflet. The derivatives of the solid artery displacement with respect to the midsurface coordinates are well-defined due to the extension of the surface parameterization into the solid, as illustrated in Figures 7 and 8. This extension is not considered to be part of the leaflets; it is a fictitious extension for the purpose of formulating a coupling penalty. These coupling conditions are approximated in the discrete model by adding the following penalty term to Bs(ws, y):
| (12) |
This penalty term is integrated over the region labeled “leaflet–wall intersection” in Figure 8. The parameter βdisp > 0 is the penalty parameter. Numerical experiments indicate that βdisp = 1 × 108 dyn/cm3 is effective for the problem class considered in this paper. To effectively penalize displacement differences due to tensile forces, one would expect the penalty parameter to scale like tensile stiffness, i.e.
| (13) |
where E is some effective material stiffness with units of pressure (e.g. the Young’s modulus, in an isotropic material) and h is a length scale indicating the size of the shell elements. To penalize rotation about the boundary, βdisp would need to scale with bending stiffness, like
| (14) |
This suggests that a possible rule-of-thumb for estimating appropriate penalty values for this type of coupling might be
| (15) |
If one applies (15) to the computational models of the present study and estimates E ~ 107 dyn/cm2, the first branch of the max is taken for most elements and the resulting value of βdisp is of the same order of magnitude as the one selected through numerical testing. The h−4 dependency of the second branch prompts some concerns regarding discrete stability and conditioning in the limit of h → 0, but a systematic study of penalty parameter selection across different problem classes is beyond the scope of the present study.
2.4. Fluid formulation
The fluid subproblem in (1) is given in the arbitrary Lagrangian–Eulerian (ALE) description [76] as follows:
| (16) |
where ρf is the fluid mass density, ε is the symmetric gradient operator, σ = −pI + 2μfε (uf) is the fluid Cauchy stress, μf is the dynamic viscosity, γ ≥ 0 is a dimensionless parameter that improves the well-posedness of the problem when there is significant inflow through the Neumann boundary , nf is the outward-facing normal vector to the fluid domain, {·}− isolates the negative part of its argument, ff is a prescribed body force, and hf is a prescribed flux on . This flux is a traction on outflow portions of the boundary (where ) and some γ-dependent combination of traction and advective flux on the inflow portion of the boundary [77]. The introduction of the γ term serves to reduce the effects of artificial domain truncation on the fluid subproblem. This approach was proposed in Bazilevs et al. [78] and found to be the most effective out of several alternatives in Esmaily-Moghadam et al. [79]. The vector field is the (arbitrary) velocity with which the fluid subproblem domain (Ωf)t deforms and is a point in the reference fluid subproblem domain (Ωf)0.
This ALE Navier–Stokes subproblem is discretized using the variational multiscale (VMS) approach, with some modifications to the stabilization parameters to improve mass conservation, as described in Kamensky et al. [41] and the references cited therein. The ALE–VMS formulation may be interpreted both as a stabilized formulation and a large-eddy simulation (LES) turbulence model [80–83]. The stabilization due to the ALE–VMS formulation permits us to use arbitrary spaces to discretize the pressure and velocity fields; it does not require special inf–sup-stable combinations. We therefore take advantage of the possibility of using a single scalar trivariate NURBS space to represent the pressure and each Cartesian component of the fluid velocity (i.e. “equal-order interpolation”). The deformation velocity of the the fluid domain is determined solving a fictitious elastostatic problem for the displacement of the domain from each time step to the next, with local changes in stiffness to improve robustness, as detailed in Bazlievs et al. [60, Section 3.2].
2.5. Time integration and discretization of fluid–structure coupling
Partial derivatives with respect to time in the fluid and structure subproblem formulations are discretized using the generalized-α method [84]. The discrete spaces for the fluid and solid structure velocities are selected so as to conform to the FSI kinematic constraint; thus wf and are equal on and the Lagrange multiplier and penalty terms of (1) are zero. This is not true on ; we therefore need to approximate the Lagrange multiplier field on . The fluid–shell structure interface Lagrange multiplier is discretized in space and updated semi-implicitly in each time step following the procedures developed in Kamensky et al. [41]. In summary, the tangential component of the Lagrange multiplier is formally eliminated, leaving a penalty method to enforce the no-slip condition. The normal component λ = λ · nsh (where nsh is normal to ) is represented in the discrete setting by a set of scalars stored at the quadrature points used to compute integrals over Γsh. After solving implicitly for the n + 1 time level fluid and structure velocities, but holding λ fixed at λn, these scalar samples are updated using the formula
| (17) |
where is a perturbed normal constraint residual
| (18) |
In (18), n + αf is an intermediate time level, between steps n and n + 1, associated with the generalized-α approach (as detailed using such notation in Bazilevs et al. [60]). The constraint perturbation r ≥ 0 is a dimensionless parameter to ensure well-posedness in the steady limit (cf. the perturbed Lagrangian approach [85]). Following the conclusions of Kamensky et al. [86], we choose r ≪ 1 to ensure sufficient constraint enforcement. The details of this methodology, including choices of free parameters and analysis of stability and accuracy when applied to model problems, can be found in Kamensky et al. [87].
3. Application to BHV design
To determine an effective BHV design, we first need to identify quantitative measures of its performance. In this work, we focus on two quantities of clinical interest: to measure the systolic performance, we evaluate the effective orifice area (EOA), which indicates how well the valve permits flow in the forward direction. For a quantitative evaluation of the diastolic performance, we measure the coaptation area (CA), which indicates how well the valve seals and prevents flow in the reverse direction [54]. In this section, we study the impact of the design variables x1, x2, and x3 on our two quantities of interest. While a complete multi-objective optimization over our design space is outside the scope of the present study, we identify performance trends with respect to each design variable and highlight simulation results from a valve design that appears to function especially well.
3.1. Effective orifice area
The orifice area is defined as the aortic valve aperture during left ventricular ejection. Reduction in orifice area, due, for example, to the presence of aortic stenosis, makes the transvalvular blood flow more difficult, leading to a subsequent increase in left ventricular afterload [88]. Thus, all other things equal, a BHV with a larger orifice area is preferable.
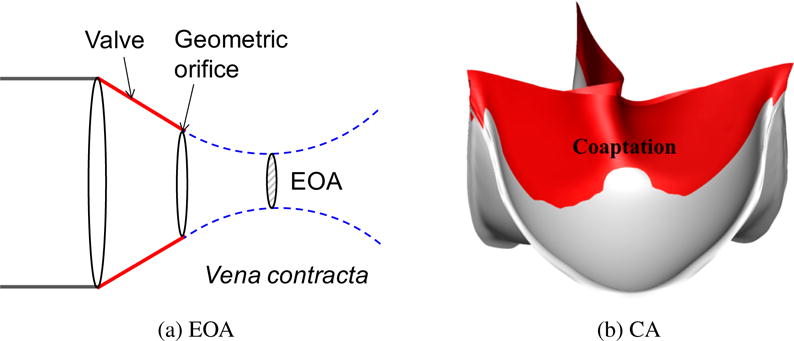
The EOA of a valve is defined as the minimal cross-sectional area of the flow jet downstream of the aortic valve, which corresponds to the location of vena contracta (See Figure 9a). We compute EOA using the Gorlin formula [88, 89],
| (19) |
where Q is the systolic flow rate in mL/s and the transvalvular pressure gradient, Δp, is the pressure difference at peak systole between the left ventricular outflow tract and the vena contracta, i.e., the point downstream of the valve with the largest fluid velocity. Δp in (19) uses the unit of mmHg. The resulting EOA is in cm2.
Figure 9.
The illustrations of effective orifice area (EOA) and coaptation area (CA).
3.2. Coaptation area
Coaptation area is a measure of how much the three aortic leaflets are in contact with each other during ventricular diastole. Normal coaptation can be directly associated with optimal long-term function of the valve [90]. If the leaflets do not seal properly during diastole, aortic regurgitation can occur, meaning that some of the blood that was already ejected from the left ventricle to the aorta leaks back into the heart, increasing the ventricular workload. This predicament generally requires surgical intervention. The success of the operation is typically evaluated by measuring post-operative coaptation [36]. Coaptation area has been an important index for identifying heart valve performance [91–95]. In this work, we consider a large coaptation area during the diastole to be preferable, since it reduces the possibility of aortic regurgitation. A typical coaptation is illustrated in Figure 9b. The coaptation area is calculated directly within our contact algorithm by summing over the quadrature points where contact occurs.
3.3. Simulation setup
Constitutive parameters in the governing equations are held constant over the design space. Fluid, solid, and shell structure mass densities are set to 1.0 g/cm3. The parameters of the Fung-type material model for the shell structure are c0 = 2.0 × 106 dyn/cm2, c1 = 2.0 × 105 dyn/cm2, and c2 = 100. The thickness of the leaflet is set to 0.0386 cm. The bulk and shear modluii for the arterial wall are selected to provide a Young’s modulus of 107 dyn/cm2 and Poisson’s ratio of 0.45 in the small strain limit. The inlet and outlet cross sections are free to slide in their tangential planes and deform radially, but constrained not to move in the orthogonal directions (see Bazilevs et al. [69] for details). Motion of the solid structure is damped by a body force of the form , with Cdamp = 104 Hz, to model the interaction of the artery with surrounding tissues and interstitial fluid. The damping also helps in removing the high-frequency modes of the structural deformation [96]. The dynamic viscosity of the fluid is set to μf = 3 × 10−2 g/(cm s) for human blood [97]. The non-dimensional parameter γ determining the interpretation of the prescribed Neumann boundary flux at inflow portions of the domain is chosen to be γ = 0.5. The choice of these values is based on the discussions in Hsu et al. [45] and references therein.
In the FSI simulation, we apply a physiologically-realistic left ventricular pressure time history shown in Figure 10 as a traction boundary condition at the inflow. The applied pressure signal is periodic, with a period of 0.86 s for one cardic cycle. The traction −(p0 + RQ)nf is applied at the outflow for the resistance boundary condition [98], where p0 is a constant physiological pressure level, R > 0 is a resistance coefficient, and Q is the volumetric flow rate through the outflow. In the present computation, we set p0 = 80 mmHg and R = 200 (dyn s)/cm5. These values ensure a realistic transvalvular pressure difference of 80 mmHg across a closed valve when Q = 0, while permitting a flow rate within the normal physiological range [99] and consistent with the flow rate estimated from the medical data (about 310 ml/s) during systole. A time step size of Δt = 10−4 s is used in all simulations. Each FSI simulation takes about 36 hours to compute a full cardiac cycle using 144 processor cores on Lonestar 56 [100] at the Texas Advanced Computing Center (TACC) [101]. A detailed technical explanation and scalability study of our parallelization strategy can be found in Hsu et al. [102].
Figure 10.
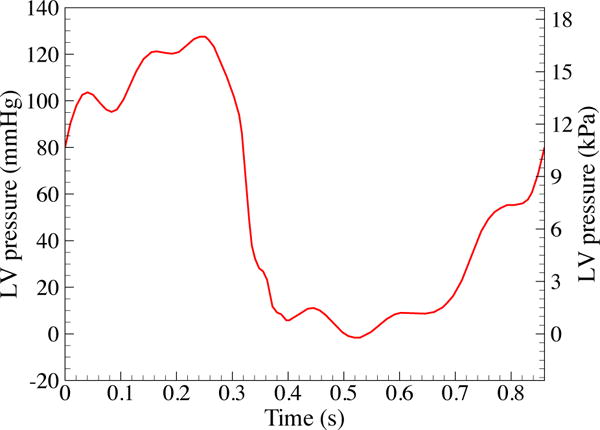
Left ventricular (LV) pressure profile applied at the inlet of the fluid domain. The data is obtained from Yap et al. [103]. The duration of a single cardiac cycle is 0.86 s.
To obtain the artery wall tissue prestress, we apply the highest left ventricular pressure during systole (127 mmHg at t = 0.25 s) on the inlet and a resistance boundary condition (p0 = 80 mmHg and R = 200 (dyn s)/cm5) on the outlet for the calculation of in the prestress problem (6) and solve for S0 following the procedure in Section 2.3.1.
3.4. Parametric study
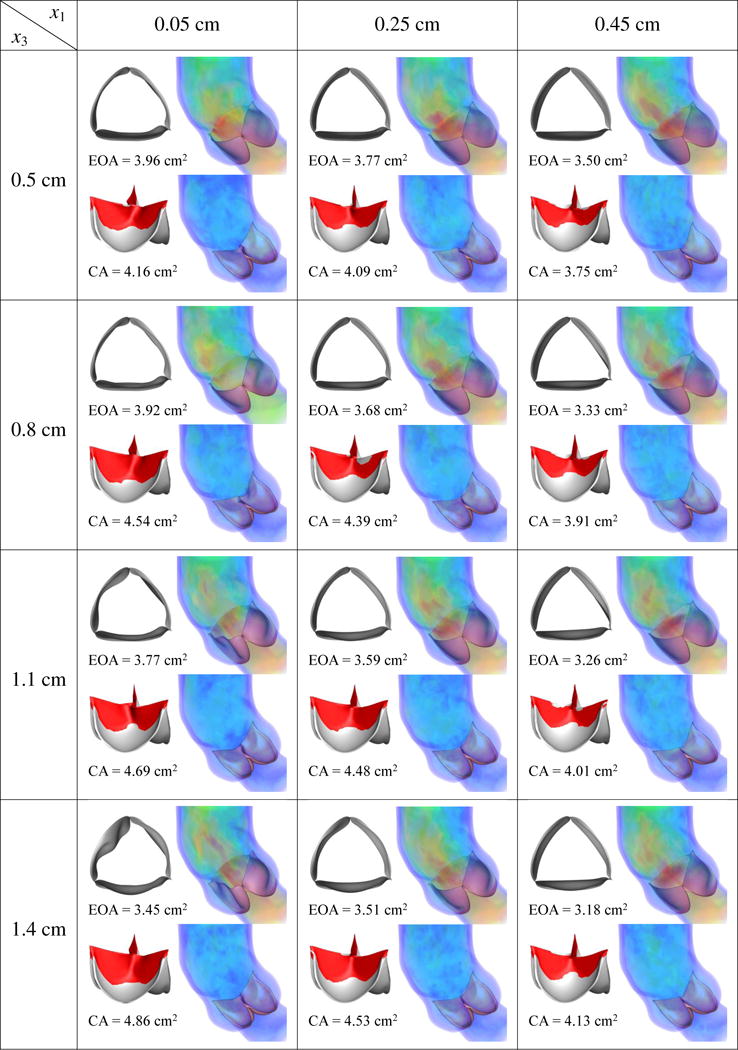
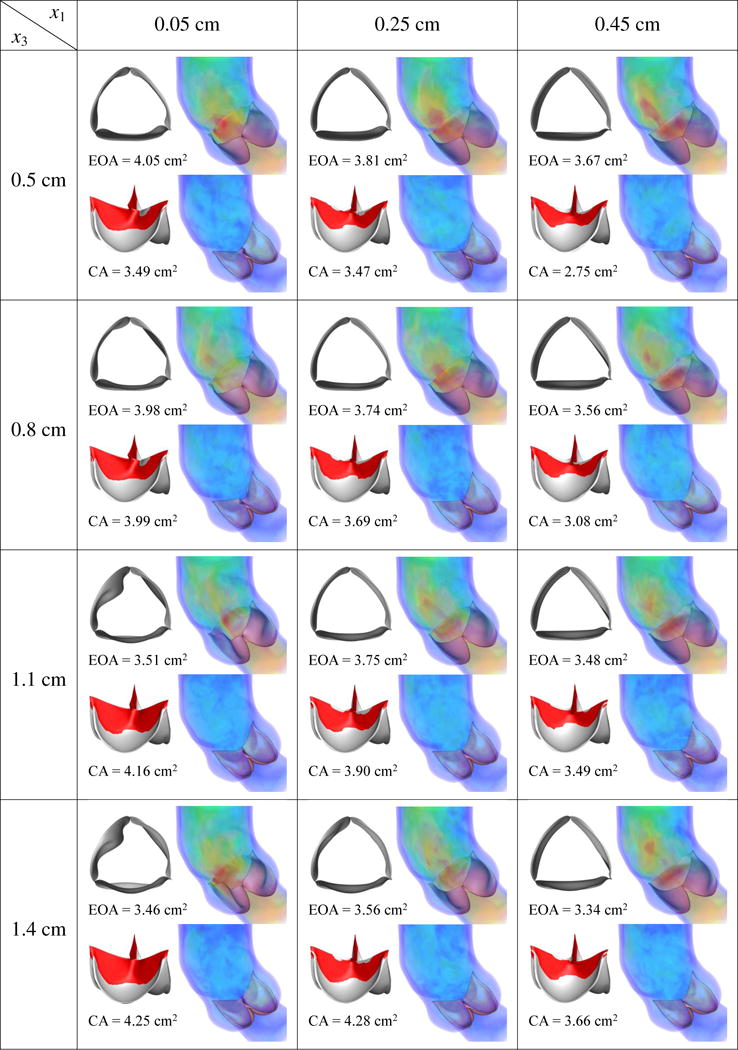
This section discusses the effects of the design parameters on our quantities of interest. We perform FSI simulations of each of (x1, x2, x3) ∈ ({0.05, 0.25, 0.45} cm, {0.1, 0.3, 0.5} cm, {0.5, 0.8, 1.1, 1.4} cm), then calculate the EOA at peak systole and the maximum CA occurring during ventricular diastole. The simulation results and quantities of interest for each case are reported in Figures 11–13. As discussed in Sections 3.1 and 3.2, an ideal valve would have both a large EOA and a large CA. However, these two quantities tend to compete with each other: valves that close easily can be more difficult to open and vice versa.
Figure 11.
Results of different combination of design variables x1 and x3, with x2 being fixed as 0.1 cm. Velocity magnitude is plotted using a color scale ranging from 0 (blue) to ≥ 80 cm/s (red).
From Figures 11–13, in general, the results show that increasing x1, which corresponds to decreasing the length of the free edge, decreases EOA and CA at the same time. Increasing x2, which decreases the height of the free edge, may increase EOA slightly but reduces CA significantly. The reduction of CA due to increasing x2 is particularly obvious from Figure 13, which shows that many cases cannot seal completely. Finally, increasing x3, which increases the surface curvature in the leaflet belly region, improves CA but decreases EOA.
Among the designs simulated in this paper, the combination of x1 = 0.05 cm, x2 = 0.1 or 0.3 cm, and x3 = 0.5 or 0.8 cm reliably yields a high EOA between 3.92 and 4.05 cm2, near the upper end of the physiological range of 3.0–4.0 cm2 in healthy adults [88], and a CA between 3.49 and 4.54 cm2. Among these four cases, x* = (x1, x2, x3) = (0.05 cm, 0.1 cm, 0.8 cm), which has a CA of 4.54 cm2 and EOA of 3.92 cm2, strikes the best compromise between EOA and CA.
Remark 2
The mesh independence study in Appendix A indicates that relative differences in CA and EOA on the order of a few percent are potentially influenced by discretization errors emanating from the choice of fluid and structure meshes. However, the conclusions drawn in this work are based on variations in the range of 10–20%, and it seems likely that the trends of these quantities of interest with respect to design parameters are less susceptible to discretization error than the precise numerical values. (Even in the complete absence of discretization error, the predicted numerical values for EOA and CA would most likely suffer from substantially-greater errors due to modeling assumptions, such as choices of boundary conditions and constitutive models.)
4. Comparison with patient-specific image data
We speculate that the valve geometry x* identified in the previous section might have comparable hemodynamics to the native valve of the considered patient, which, according to available records, was assessed to be functioning correctly. This leads us to compare the velocity field of the simulated blood flow with a velocity field reconstructed from PC-MRI data collected from the patient. The detailed FSI results of x* are shown in the present section and compared with patient-specific PC-MRI data. The comparisons are primarily qualitative in nature, and serve primarily to validate our design, as well as artificial domain extensions and boundary conditions of the fluid subproblem, by ensuring that these choices are not disrupting the overall aortic flow behavior.
4.1. Post-processing phase contrast magnetic resonance images
2D phase contrast magnetic resonance images were acquired using a Siemens Magnetom Aera 1.5T scanner. A virtual plane was positioned at the level of the sinotubular junction to record patient-specific flow data immediately downstream of the aortic valve with a temporal resolution of 30 samples per beat and pixel spacing of 2.08mm × 2.08mm. The cross section defined for blood velocity measurements shown in Figure 14 can be reconstructed from MRI output data7, such that the simulation results can be plotted and visualized exactly at the same level. We observed from dynamic MRI records that the identified cross section experiences negligible translation along the aortic centerline (i.e., towards or away from the heart), making the comparison with our fixed-plane measurements from the numerical simulations fair.
Figure 15 shows the comparison between the velocity field recorded using PC-MRI sequencies (right) and velocity results obtained from the immersogeometric simulation (left) for nine time points during the cardiac cycle. From a qualitative point of view, good agreement is observed: flow patterns of the measured and computed velocity fields are comparable. This tentatively suggests that, throughout the entire heart cycle, the developed simulation tool is able to provide hemodynamics predictions sufficiently accurate for medical applications. That is, it is capable of determining local flow profiles which can be associated to parameters of medical interest (e.g., blood flow alterations in case of cardiovascular disease, development of atherosclerosis [104], impairment of endothelial cells [105], and plaque or aneurysm formation [106, 107]). Differences between measured data and simulation results can be attributed to a combination of modeling assumptions (e.g., assumed pressure profile, simplified aortic wall material model, etc.) and measurement errors (e.g., limited PC-MRI spatial-temporal resolution, poor signal-to-noise ratio, and difficulty of accurately segmenting the moving vessel lumen to extract the blood flow velocities).
Figure 15.
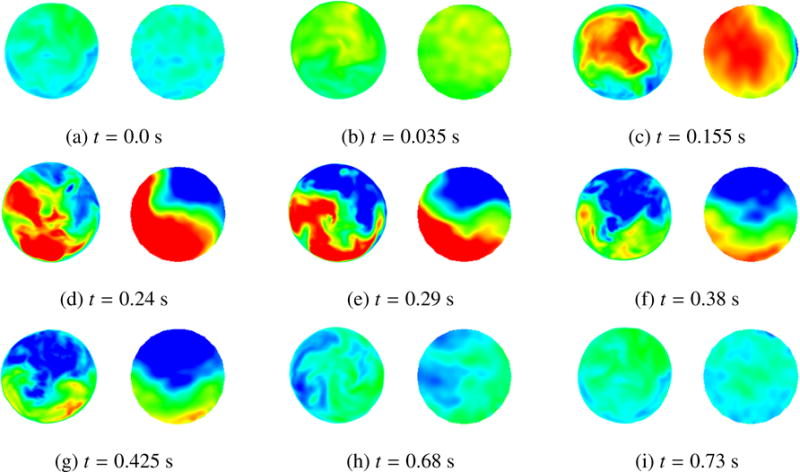
Comparison between FSI results (left) and patient-specific medical image data (right). The time t is synchronized with Figure 10 for the current cycle. Velocity magnitude is plotted using a color scale ranging from −20 cm/s (blue) to 60 cm/s (red). The time instant of the medical image is adjusted to match that of our FSI simulation.
Finally, Figure 16 shows several snapshots of the valve deformation and the details of the flow field at several points during the cardiac cycle. The color indicates the fluid velocity magnitude. The visualization of flows and structures clearly shows the instant response of the valve to the left ventricular pressure. The valve opens with the rising left ventricular pressure at the beginning stage of systole (0.0–0.20 s), and then stays fully open near the peak systole (0.25–0.27 s), allowing sufficient blood flow to enter the ascending aorta. A very quick valve closure is then observed at the beginning of diastole (0.32–0.38 s). This quick closure of the valve minimizes the reverse flow into the left ventricle as the left ventricular pressure drops rapidly in this period. After that, the valve properly seals and the flow reaches a near-hydrostatic state (0.65 s). These flow and structural features during the cardiac cycle characterize a well functioning valve within the objectives considered in this paper: a large EOA during systole and a proper CA during diastole. In Figure 17, the models are superposed in the configurations corresponding to the fully-open and fully-closed phases for better visualization of the leaflet–wall coupling results. The deformation of the attachment edges can be clearly seen. The expansion and contraction of the arterial wall as well as its sliding motion between systole and diastole can also be observed.
Figure 16.
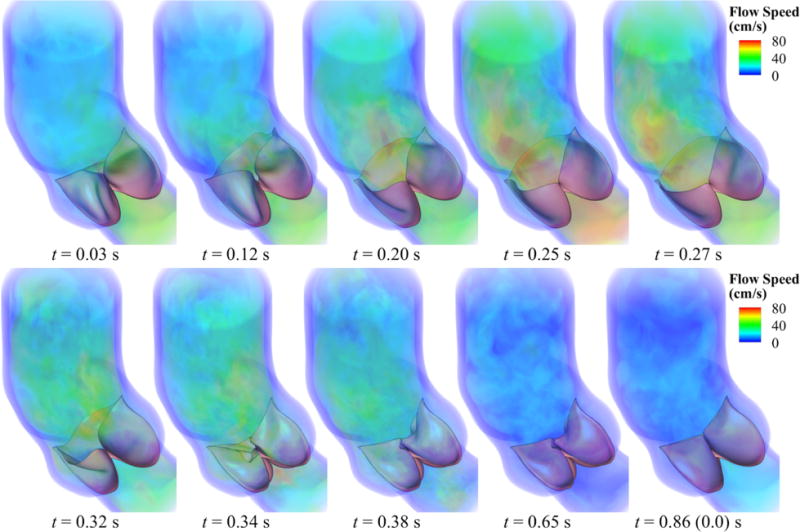
Volume rendering visualization of the velocity field from our FSI simulation at several points during a cardiac cycle. The time t is synchronized with Figure 10 for the current cycle.
Figure 17.
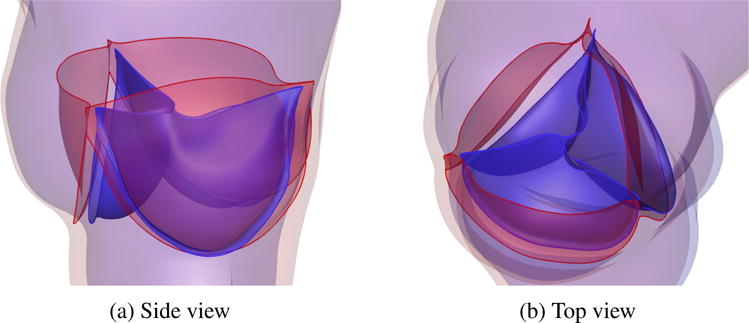
Relative displacement between fully-open (red) and fully-closed (blue) configurations, showing the effect of leaflet–wall coupling. The deformation of the attachment edges can be clearly seen. The expansion and contraction of the arterial wall as well as its sliding motion between systole (red) and diastole (blue) can also be observed.
5. Conclusions
This paper describes a framework for patient-specific design of aortic heart valve replacements. The framework is distinguished by its use of computational FSI models, derived from medical imaging data from patients, to predict the performance of different heart valve designs in conjunction with an individual patient’s aortic root geometry. The use of such predictive methods has the potential to create more effective designs and reduce patient–prosthesis mismatch.
In the present study, we have limited exploration of the prosthetic valve design space to a predetermined set of designs selected by the analyst. Such an approach is likely sufficient for use with present-day replacement valve technologies. Currently, clinicians have only a finite number of valves to choose from for each patient. However, in the direction of personalized medicine and looking forward to emerging technologies such as 3D bioprinting, we anticipate that future replacement valve geometries could be optimized and fabricated on a per-patient basis, and we believe that computational FSI models provide a rational basis for identifying optimal designs.
Extending the design space exploration to the full space of possible valve geometries will require some form of automated optimization. We have previously optimized FSI systems using the surrogate management framework (SMF) [44], which minimizes a single objective function. In the case of heart valve design, various objectives pose competing demands on the design, as we discussed in Section 3. This setting necessitates either the careful construction of a quantity of interest that balances the competing demands, or the use of techniques from multi-objective optimization to obtain a frontier of Pareto optimal designs. In future work, we plan to extend the framework presented in this paper to include automatic exploration of the design space, to locate optimal valve designs without manual selection of candidates and inspection of results by the analyst.
Some other limitations of this work are the lack of sophistication in the fluid subproblem boundary conditions, and the inclusion of potentially non-manufacturable leaflet geometries in the design space. We plan to address the first limitation in the near future, by incorporating Windkessel-type boundary conditions [108] and developing a systematic method of parameter selection for such models. The second limitation could be resolved by including constraints within an optimization framework such as SMF, e.g., that leaflet geometries have low intrinsic curvature and can therefore be fabricated from initially-flat sheets of bovine pericardium. We discuss imposition of constraints in SMF-based optimization of FSI systems in Wu et al. [44].
Figure 12.
Results of different combination of design variables x1 and x3, with x2 being fixed as 0.3 cm. Velocity magnitude is plotted using a color scale ranging from 0 (blue) to ≥ 80 cm/s (red).
Acknowledgments
This work was supported by the National Heart, Lung, and Blood Institute of the National Institutes of Health under award number R01HL129077. We thank the Texas Advanced Computing Center (TACC) at The University of Texas at Austin for providing HPC resources that have contributed to the research results reported in this paper. F. Auricchio, S. Morganti, and A. Reali were partially supported by Fondazione Cariplo - Regione Lombardia through the project “iCar- dioCloud” (no, 2013-1779) and the project “Verso nuovi strumenti di simulazione super veloci ed accurati basati sull’analisi isogeometrica” (within the program RST - rafforzamento). This support is gratefully acknowledged. The authors also acknowledge Dr. Francesco Secchi of IRCCS Policlinico San Donato for providing medical images, and Sean A. Wasion for his initial work on this research.
Appendix A. Mesh independence study
To show the convergence of the immersogeometric method, a refinement study based on three different meshes was carried out. The background meshes are denoted as M0, M1, and M2, where M1 is an h-refinement of M0 and M2 is an h-refinement of M1. The three BHV surface meshes are denoted as SM0, SM1 and SM2 in the same pattern. The BHV tested in this section corresponds to the point x* = (x1, x2, x3) = (0.05 cm, 0.1 cm, 0.8 cm) in the design space. The parametric study presented in Section 3 uses M1 and SM1. The mesh statics are given in Table A.1.
The penalty parameter in Eq (1) can be separated into the normal component βNOR and the tangential component βTAN. Following [44], we scale these penalty parameters in the following way:
| (A.1) |
| (A.2) |
where CNOR and CTAN are two constants, and h is the length scale of the fluid element intersected by the immersed boundary. In simulations using M1, the two penalty parameters are estimated to be βNOR = 2000 g/(cm2 s) and βTAN = 200 g/(cm2 s). Because error is assumed to be dominated by spatial discretization, we hold Δt = 1 × 104 s constant and select the penalty parameters as βNOR = 4000 g/(cm2 s) and βTAN = 100 g/(cm2 s) for M0 computations, and βNOR = 1000 g/(cm2 s) and βTAN = 400 g/(cm2 s) for M2 computations.
The mesh independence study is focused on the accuracy of the quantities of interest with which the present paper is concerned: CA and EOA. For simplicity, the artery wall is held rigid, so the effect of wall deformation is neglected. To study the convergence of CA, we first apply a pressure of p0 + RQ on the outlet, and a pressure of 0 mmHg on the inlet to close the valve. To investigate convergence of EOA, we apply a pressure of p0 + RQ on the outlet, and a pressure of 120 mmHg on the inlet. After the simulation converges to a quasi-steady state, we perform a time average of the flow field and the valve deformation to evaluate the CA and EOA. In both convergence studies, we set p0 = 80 mmHg and R = 200 (dyn s)/cm5. The results of CA and EOA with respect to the number of background elements are shown in Figure A.18. The relative error |CA1 – CA2|/CA2 is 3.69% and the relative error |EOA1 – EOA2|/EOA2 is 1.69%, where the subscript i denotes the results on Mi. While errors on the order of a few percent are not entirely negligible relative to the differences of 10–20% in EOA and CA found while exploring the BHV design space in Section 3, these discretization errors likely already pale in comparison to modeling errors, and little further insight would be gained by using higher resolutions.
Remark 3
The EOA and CA are smaller than the results in Section 3 since we neglect the wall deformation. This confirms the significance of wall–leaflets coupling in order to correctly predict the quantities of interest.
Figure A.18.
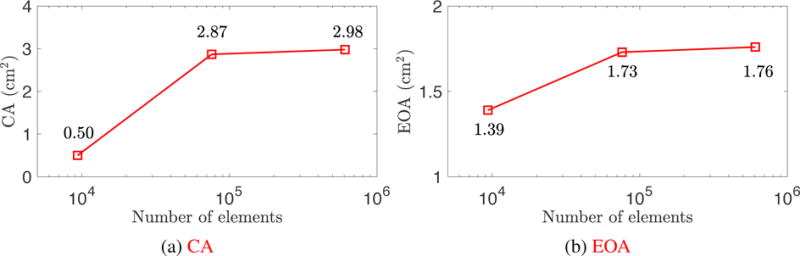
The CA and EOA of the rigid wall FSI simulation results. The results show convergence with mesh refinement.
Table A.1.
Mesh statistics.
| M0 | M1 | M2 | |
|---|---|---|---|
| Number of elements | 9,360 | 75,888 | 607,104 |
| SM0 | SM1 | SM2 | |
| Number of elements | 462 | 1,827 | 7,308 |
Footnotes
It is in fact possible to define an arbitrarily-smooth spline space over the entire tubular volume, by leveraging recent progress on polar splines [61], but we require only C0 continuity for the analysis methods used in the present work.
If the fluid and structural velocities and test functions are explicitly assumed to be continuous (i.e., uf = us and wf = ws) at the interface (e.g., matching lumen and inner artery wall surface meshes), these additional terms integrated over ΓI are zero.
(·)0 is a specific time instance of (·)t, for t = 0.
The notation indicates the topological closure of a set A.
For shell analysis, one can use the plane stress condition in order to analytically determine the Lagrangian multiplier p (see Kiendl et al. [73, Section 5.1] for details).
The system provides 1,252 compute nodes, each with two 2.6 GHz Intel E5-2690 v3 12-core (Haswell) processors and 64 GB of DDR4 memory.
Given the velocity encoding parameter, also known as venc (set to 150 cm/s for the considered MRI sequences), the gray-scale values of PC-MRI images can be translated in a velocity field description: phase images are in fact motion sensitive and can be adopted to measure local velocities of moving spins on a pixel-to-pixel basis.
References
- 1.Makhijani VB, Yang HQ, Dionne PJ, Thubrikar MJ. Three-dimensional coupled fluid–structure simulation of pericardial bioprosthetic aortic valve function. ASAIO Journal. 1997;43(5):M387–M392. [PubMed] [Google Scholar]
- 2.Taylor CA, Hughes TJR, Zarins CK. Finite element modeling of three-dimensional pulsatile flow in the abdominal aorta: relevance to atherosclerosis. Annals of Biomedical Mngineering. 1998;158:975–987. doi: 10.1114/1.140. [DOI] [PubMed] [Google Scholar]
- 3.Taylor CA, Hughes TJR, Zarins CK. Finite element modeling of blood flow in arteries. Computer Methods in Applied Mechanics and Engineering. 1998;158:155–196. [Google Scholar]
- 4.Lemmon JD, Yoganathan AP. Three-dimensional computational model of left heart diastolic function with fluid–structure interaction. Journal of Biomechanical Engineering. 2000;122(2):109–117. doi: 10.1115/1.429648. [DOI] [PubMed] [Google Scholar]
- 5.Taylor CA, Fonte TA, Min JK. Computational fluid dynamics applied to cardiac computed tomography for noninvasive quantification of fractional flow reserve. Journal of the American College of Cardiology. 2013;61(22):2233–2241. doi: 10.1016/j.jacc.2012.11.083. [DOI] [PubMed] [Google Scholar]
- 6.Zarins CK, Taylor CA, Min JK. Computed fractional flow reserve (FFTCT) derived from coronary CT angiography. Journal of Cardiovascular Translational Research. 2013;6(5):708–714. doi: 10.1007/s12265-013-9498-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Taylor CA, Draney MT, Ku JP, Parker D, Steele BN, Wang K, Zarins CK. Predictive medicine: Computational techniques in therapeutic decision-making. Computer Aided Surgery. 1999;4(5):231–247. doi: 10.1002/(SICI)1097-0150(1999)4:5<231::AID-IGS1>3.0.CO;2-Z. [DOI] [PubMed] [Google Scholar]
- 8.de Zélicourt DA, Pekkan K, Parks J, Kanter K, Fogel M, Yoganathan AP. Flow study of an extracardiac connection with persistent left superior vena cava. The Journal of Thoracic and Cardiovascular Surgery. 2006;131(4):785–791. doi: 10.1016/j.jtcvs.2005.11.031. [DOI] [PubMed] [Google Scholar]
- 9.Pekkan K, Whited B, Kanter K, Sharma S, de Zelicourt D, Sundareswaran K, Frakes D, Rossignac J, Yoganathan AP. Patient-specific surgical planning and hemodynamic computational fluid dynamics optimization through free-form haptic anatomy editing tool (SURGEM) Medical & Biological Engineering & Computing. 2008;46(11):1139–1152. doi: 10.1007/s11517-008-0377-0. [DOI] [PubMed] [Google Scholar]
- 10.Marsden AL, Bernstein AJ, Reddy VM, Shadden SC, Spilker RL, Chan FP, Taylor CA, Feinstein JA. Evaluation of a novel Y-shaped extracardiac Fontan baffle using computational fluid dynamics. The Journal of Thoracic and Cardiovascular Surgery. 2009;137(2):394–403. doi: 10.1016/j.jtcvs.2008.06.043. [DOI] [PubMed] [Google Scholar]
- 11.Neal ML, Kerckhoffs R. Current progress in patient-specific modeling. Briefings in Bioinformatics. 2010;11(1):111–126. doi: 10.1093/bib/bbp049. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Sankaran S, Moghadam ME, Kahn AM, Tseng EE, Guccione JM, Marsden AL. Patient-specific multiscale modeling of blood flow for coronary artery bypass graft surgery. Annals of Biomedical Engineering. 2012;40(10):2228–2242. doi: 10.1007/s10439-012-0579-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Morganti S, Conti M, Aiello M, Valentini A, Mazzola A, Reali A, Auricchio F. Simulation of transcatheter aortic valve implantation through patient-specific finite element analysis: Two clinical cases. Journal of Biomechanics. 2014;47(11):2547–2555. doi: 10.1016/j.jbiomech.2014.06.007. [DOI] [PubMed] [Google Scholar]
- 14.Morganti S, Brambilla N, Petronio AS, Reali A, Bedogni F, Auricchio F. Prediction of patient-specific post-operative outcomes of TAVI procedure: The impact of the positioning strategy on valve performance. Journal of Biomechanics. 2016;49(12):2513–2519. doi: 10.1016/j.jbiomech.2015.10.048. [DOI] [PubMed] [Google Scholar]
- 15.Zarins CK, Taylor CA. Endovascular device design in the future: Transformation from trial and error to computational design. Journal of Endovascular Therapy. 2009;16:I12–I21. doi: 10.1583/08-2640.1. [DOI] [PubMed] [Google Scholar]
- 16.Marsden AL, Reddy VM, Shadden SC, Chan FP, Taylor CA, Feinstein JA. A new multiparameter approach to computational simulation for Fontan assessment and redesign. Congenital Heart Disease. 2010;5(2):104–117. doi: 10.1111/j.1747-0803.2010.00383.x. [DOI] [PubMed] [Google Scholar]
- 17.Auricchio F, Conti M, Morganti S, Totaro P. A computational tool to support preoperative planning of stentless aortic valve implant. Medical Engineering & Physics. 2011;33(10):1183–1192. doi: 10.1016/j.medengphy.2011.05.006. [DOI] [PubMed] [Google Scholar]
- 18.Long CC, Marsden AL, Bazilevs Y. Shape optimization of pulsatile ventricular assist devices using FSI to minimize thrombotic risk. Computational Mechanics. 2014;54(4):921–932. [Google Scholar]
- 19.Fan R, Bayoumi AS, Chen P, Hobson CM, Wagner WR, Mayer JE, Jr, Sacks MS. Optimal elastomeric scaffold leaflet shape for pulmonary heart valve leaflet replacement. Journal of Biomechanics. 2013;46(4):662–669. doi: 10.1016/j.jbiomech.2012.11.046. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Pibarot P, Dumesnil JG. Prosthetic heart valves. Circulation. 2009;119(7):1034–1048. doi: 10.1161/CIRCULATIONAHA.108.778886. [DOI] [PubMed] [Google Scholar]
- 21.Otto CM. Timing of aortic valve surgery. Heart. 2000;84(2):211–218. doi: 10.1136/heart.84.2.211. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Thubrikar MJ, Deck JD, Aouad J, Nolan SP. Role of mechanical stress in calcification of aortic bioprosthetic valves. The Journal of Thoracic and Cardiovascular Surgery. 1983;86(1):115–125. [PubMed] [Google Scholar]
- 23.Sun W, Abad A, Sacks MS. Simulated bioprosthetic heart valve deformation under quasistatic loading. Journal of Biomechanical Engineering. 2005;127(6):905–914. doi: 10.1115/1.2049337. [DOI] [PubMed] [Google Scholar]
- 24.Kim H, Lu J, Sacks MS, Chandran KB. Dynamic simulation pericardial bioprosthetic heart valve function. Journal of Biomechanical Engineering. 2006;128(5):717–724. doi: 10.1115/1.2244578. [DOI] [PubMed] [Google Scholar]
- 25.Marom G. Numerical methods for fluid–structure interaction models of aortic valves. Archives of Computational Methods in Engineering. 2014;22(4):595–620. [Google Scholar]
- 26.Vesely I. The evolution of bioprosthetic heart valve design and its impact on durability. Cardiovascular Pathology. 2003;12(5):277–286. doi: 10.1016/s1054-8807(03)00075-9. [DOI] [PubMed] [Google Scholar]
- 27.Xiong FL, Goetz WA, Chong CK, Chua YL, Pfeifer S, Wintermantel E, Yeo JH. Finite element investigation of stentless pericardial aortic valves: relevance of leaflet geometry. Annals of Biomedical Engineering. 2010;38(5):1908–1918. doi: 10.1007/s10439-010-9940-6. [DOI] [PubMed] [Google Scholar]
- 28.Ennker J, Albert A, Ennker IC. Stentless aortic valves. Current aspects. HSR Proc Intensive Care Cardiovasc Anesth. 2012;4(2):77–82. [PMC free article] [PubMed] [Google Scholar]
- 29.David TE. Aortic valve sparing operations: a review. The Korean Journal of Thoracic and Cardiovascular Surgery. 2012;45(4):205–212. doi: 10.5090/kjtcs.2012.45.4.205. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Grbić S, Ionasec R, Vitanovski D, Voigt I, Wang Y, Georgescu B, Navab N, Comaniciu D. Complete valvular heart apparatus model from 4D cardiac CT. Medical Image Analysis. 2012;16(5):1003–1014. doi: 10.1016/j.media.2012.02.003. [DOI] [PubMed] [Google Scholar]
- 31.Mansi T, Houle H, Voigt I, Szucs M, Hunter E, Datta S, Comaniciu D. Quantifying heart valves: From diagnostic to personalized valve repair 2016. Siemens White Paper [Google Scholar]
- 32.Drach A, Khalighi AH, ter Huurne FM, Lee CH, Bloodworth C, Pierce EL, Jensen MO, Yoganathan AP, Sacks MS. Population-averaged geometric model of mitral valve from patient-specific imaging data. Journal of Medical Devices. 2015;9(3):030 952-1–030 952-3. [Google Scholar]
- 33.Lee CH, Rabbah JP, Yoganathan AP, Gorman RC, Gorman JH, Sacks MS. On the effects of leaflet microstructure and constitutive model on the closing behavior of the mitral valve. Biomechanics and Modeling in Mechanobiology. 2015;14(6):1281–1302. doi: 10.1007/s10237-015-0674-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Khalighi AH, Drach A, Bloodworth CH, Pierce EL, Yoganathan AP, Gorman RC, Gorman JH, Sacks MS. Mitral valve chordae tendineae: Topological and geometrical characterization. Annals of Biomedical Engineering. 2017;45(2):378–393. doi: 10.1007/s10439-016-1775-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Hughes TJR, Cottrell JA, Bazilevs Y. Isogeometric analysis: CAD, finite elements, NURBS, exact geometry, and mesh refinement. Computer Methods in Applied Mechanics and Engineering. 2005;194:4135–4195. [Google Scholar]
- 36.Morganti S, Auricchio F, Benson DJ, Gambarin FI, Hartmann S, Hughes TJR, Reali A. Patient-specific isogeometric structural analysis of aortic valve closure. Computer Methods in Applied Mechanics and Engineering. 2015;284:508–520. [Google Scholar]
- 37.Sotiropoulos F, Yang X. Immersed boundary methods for simulating fluid–structure interaction. Progress in Aerospace Sciences. 2014;65:1–21. [Google Scholar]
- 38.Peskin CS. The immersed boundary method. Acta Numerica. 2002;11:479–517. [Google Scholar]
- 39.Mittal R, Iaccarino G. Immersed boundary methods. Annu Rev Fluid Mech. 2005;37:239–261. [Google Scholar]
- 40.Mittal R, Seo JH, Vedula V, Choi YJ, Liu H, Huang HH, Jain S, Younes L, Abraham T, George RT. Computational modeling of cardiac hemodynamics: Current status and future outlook. Journal of Computational Physics. 2016;305:1065–1082. [Google Scholar]
- 41.Kamensky D, Hsu MC, Schillinger D, Evans JA, Aggarwal A, Bazilevs Y, Sacks MS, Hughes TJR. An immersogeometric variational framework for fluid–structure interaction: application to bioprosthetic heart valves. Computer Methods in Applied Mechanics and Engineering. 2015;284:1005–1053. doi: 10.1016/j.cma.2014.10.040. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Hsu MC, Wang C, Xu F, Herrema AJ, Krishnamurthy A. Direct immersogeometric fluid flow analysis using B-rep CAD models. Computer Aided Geometric Design. 2016;43:143–158. [Google Scholar]
- 43.Wang C, Xu F, Hsu MC, Krishnamurthy A. Rapid B-rep model preprocessing for immersogeometric analysis using analytic surfaces. Computer Aided Geometric Design. 2017;52–53:190–204. doi: 10.1016/j.cagd.2017.03.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Wu MCH, Kamensky D, Wang C, Herrema AJ, Xu F, Pigazzini MS, Verma A, Marsden AL, Bazilevs Y, Hsu MC. Optimizing fluid–structure interaction systems with immersogeometric analysis and surrogate modeling: Application to a hydraulic arresting gear. Computer Methods in Applied Mechanics and Engineering. 2017;316:668–693. [Google Scholar]
- 45.Hsu MC, Kamensky D, Xu F, Kiendl J, Wang C, Wu MCH, Mineroff J, Reali A, Bazilevs Y, Sacks MS. Dynamic and fluid–structure interaction simulations of bioprosthetic heart valves using parametric design with T-splines and Fung–type material models. Computational Mechanics. 2015;55:1211–1225. doi: 10.1007/s00466-015-1166-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Thubrikar M. The Aortic Valve. CRC Press, Inc; Boca Raton, Florida: 1990. [Google Scholar]
- 47.Labrosse MR, Beller CJ, Robicsek F, Thubrikar MJ. Geometric modeling of functional trileaflet aortic valves: Development and clinical applications. Journal of Biomechanics. 2006;39(14):2665–2672. doi: 10.1016/j.jbiomech.2005.08.012. [DOI] [PubMed] [Google Scholar]
- 48.Haj-Ali R, Marom G, Zekry SB, Rosenfeld M, Raanani E. A general three-dimensional parametric geometry of the native aortic valve and root for biomechanical modeling. Journal of Biomechanics. 2012;45(14):2392–2397. doi: 10.1016/j.jbiomech.2012.07.017. [DOI] [PubMed] [Google Scholar]
- 49.Kouhi E, Morsi YS. A parametric study on mathematical formulation and geometrical construction of a stentless aortic heart valve. Journal of Artificial Organs. 2013;16(4):425–442. doi: 10.1007/s10047-013-0719-z. [DOI] [PubMed] [Google Scholar]
- 50.Li K, Sun W. Simulated transcatheter aortic valve deformation: A parametric study on the impact of leaflet geometry on valve peak stress. International Journal for Numerical Methods in Biomedical Engineering. 2017;33(3):e02 814. doi: 10.1002/cnm.2814. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Murphy SV, Atala A. 3D bioprinting of tissues and organs. Nature Biotechnology. 2014;32(8):773–785. doi: 10.1038/nbt.2958. [DOI] [PubMed] [Google Scholar]
- 52.Duan B, Hockaday LA, Kang KH, Butcher JT. 3D bioprinting of heterogeneous aortic valve conduits with alginate/gelatin hydrogels. Journal of Biomedical Materials Research Part A. 2013;101(5):1255–1264. doi: 10.1002/jbm.a.34420. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Votta E, Le TB, Stevanella M, Fusini L, Caiani EG, Redaelli A, Sotiropoulos F. Toward patient-specific simulations of cardiac valves: state-of-the-art and future directions. Journal of Biomechanics. 2013;46(2):217–228. doi: 10.1016/j.jbiomech.2012.10.026. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Soares JS, Feaver KR, Zhang W, Kamensky D, Aggarwal A, Sacks MS. Biomechanical behavior of bioprosthetic heart valve heterograft tissues: Characterization, simulation, and performance. Cardiovascular Engineering and Technology. 2016;7(4):309–351. doi: 10.1007/s13239-016-0276-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.The Vascular Modeling Toolkit. http://www.vmtk.org/. Accessed 1 May 2017.
- 56.Antiga L, Piccinelli M, Botti L, Ene-Iordache B, Remuzzi A, Steinman DA. An image-based modeling framework for patient-specific computational hemodynamics. Medical & Biological Engineering & Computing. 2008;46(11):1097–1112. doi: 10.1007/s11517-008-0420-1. [DOI] [PubMed] [Google Scholar]
- 57.Turkbey EB, Jain A, Johnson C, Redheuil A, Arai AE, Gomes AS, Carr J, Hundley WG, Teixido-Tura G, Eng J, et al. Determinants and normal values of ascending aortic diameter by age, gender, and race/ethnicity in the Multi-Ethnic Study of Atherosclerosis (MESA) Journal of Magnetic Resonance Imaging. 2014;39(2):360–368. doi: 10.1002/jmri.24183. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Tezduyar T, Aliabadi S, Behr M, Johnson A, Mittal S. Parallel finite-element computation of 3D flows. Computer. 1993;26(10):27–36. [Google Scholar]
- 59.Johnson AA, Tezduyar TE. Mesh update strategies in parallel finite element computations of flow problems with moving boundaries and interfaces. Computer Methods in Applied Mechanics and Engineering. 1994;119:73–94. [Google Scholar]
- 60.Bazilevs Y, Calo VM, Hughes TJR, Zhang Y. Isogeometric fluid–structure interaction: theory, algorithms, and computations. Computational Mechanics. 2008;43:3–37. [Google Scholar]
- 61.Toshniwal D, Speleers H, Hiemstra RR, Hughes TJ. Multi-degree smooth polar splines: A framework for geometric modeling and isogeometric analysis. Computer Methods in Applied Mechanics and Engineering. 2017;316:1005–1061. [Google Scholar]
- 62.Stein K, Tezduyar T, Benney R. Mesh moving techniques for fluid–structure interactions with large displacements. Journal of Applied Mechanics. 2003;70:58–63. [Google Scholar]
- 63.Hsu MC, Wang C, Herrema AJ, Schillinger D, Ghoshal A, Bazilevs Y. An interactive geometry modeling and parametric design platform for isogeometric analysis. Computers and Mathematics with Applications. 2015;70:1481–1500. [Google Scholar]
- 64.Rhinoceros. http://www.rhino3d.com/. Accessed 1 May 2017.
- 65.Grasshopper. http://www.grasshopper3d.com/. Accessed 1 May 2017.
- 66.Bazilevs Y, Hsu MC, Scott MA. Isogeometric fluid–structure interaction analysis with emphasis on non-matching discretizations, and with application to wind turbines. Computer Methods in Applied Mechanics and Engineering. 2012;249–252:28–41. [Google Scholar]
- 67.Simo JC, Hughes TJR. Computational Inelasticity. Springer-Verlag; New York: 1998. [Google Scholar]
- 68.Lipton S, Evans JA, Bazilevs Y, Elguedj T, Hughes TJR. Robustness of isogeometric structural discretizations under severe mesh distortion. Computer Methods in Applied Mechanics and Engineering. 2010;199:357–373. [Google Scholar]
- 69.Bazilevs Y, Hsu MC, Zhang Y, Wang W, Kvamsdal T, Hentschel S, Isaksen J. Computational fluid–structure interaction: Methods and application to cerebral aneurysms. Biomechanics and Modeling in Mechanobiology. 2010;9:481–498. doi: 10.1007/s10237-010-0189-7. [DOI] [PubMed] [Google Scholar]
- 70.Hsu MC, Bazilevs Y. Blood vessel tissue prestress modeling for vascular fluid–structure interaction simulations. Finite Elements in Analysis and Design. 2011;47:593–599. [Google Scholar]
- 71.Kiendl J, Bletzinger KU, Linhard J, Wüchner R. Isogeometric shell analysis with Kirchhoff–Love elements. Computer Methods in Applied Mechanics and Engineering. 2009;198:3902–3914. [Google Scholar]
- 72.Kiendl J, Bazilevs Y, Hsu MC, Wüchner R, Bletzinger KU. The bending strip method for isogeometric analysis of Kirchhoff–Love shell structures comprised of multiple patches. Computer Methods in Applied Mechanics and Engineering. 2010;199:2403–2416. [Google Scholar]
- 73.Kiendl J, Hsu MC, Wu MCH, Reali A. Isogeometric Kirchhoff–Love shell formulations for general hyperelastic materials. Computer Methods in Applied Mechanics and Engineering. 2015;291:280–303. doi: 10.1016/j.cma.2015.05.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 74.Hillairet M. Lack of collision between solid bodies in a 2D incompressible viscous flow. Communications in Partial Differential Equations. 2007;32(9):1345–1371. [Google Scholar]
- 75.Rukmani R, Usha R. Arbitrary squeeze flow between two disks. International Journal of Mathematics and Mathematical Sciences. 1994;17:779–782. [Google Scholar]
- 76.Hughes TJR, Liu WK, Zimmermann TK. Lagrangian–Eulerian finite element formulation for incompressible viscous flows. Computer Methods in Applied Mechanics and Engineering. 1981;29:329–349. [Google Scholar]
- 77.Hughes TJR, Wells GN. Conservation properties for the Galerkin and stabilised forms of the advection–diffusion and incompressible Navier–Stokes equations. Computer Methods in Applied Mechanics and Engineering. 2005;194:1141–1159. [Google Scholar]
- 78.Bazilevs Y, Gohean JR, Hughes TJR, Moser RD, Zhang Y. Patient-specific isogeometric fluid–structure interaction analysis of thoracic aortic blood flow due to implantation of the Jarvik 2000 left ventricular assist device. Computer Methods in Applied Mechanics and Engineering. 2009;198:3534–3550. [Google Scholar]
- 79.Esmaily-Moghadam M, Bazilevs Y, Hsia TY, Vignon-Clementel IE, Marsden AL, of Congenital Hearts Alliance (MOCHA) M A comparison of outlet boundary treatments for prevention of baekflow divergence with relevance to blood flow simulations. Computational Mechanics. 2011;48:277–291. doi: 10.1007/s00466-011-0599-0. [DOI] [Google Scholar]
- 80.Hughes TJR, Mazzei L, Jansen KE. Large eddy simulation and the variational multiscale method. Computing and Visualization in Science. 2000;3:47–59. [Google Scholar]
- 81.Hughes TJR, Mazzei L, Oberai AA, Wray A. The multiscale formulation of large eddy simulation: Decay of homogeneous isotropic turbulence. Physics of Fluids. 2001;13:505–512. [Google Scholar]
- 82.Bazilevs Y, Calo VM, Cottrel JA, Hughes TJR, Reali A, Scovazzi G. Variational multiscale residual-based turbulence modeling for large eddy simulation of incompressible flows. Computer Methods in Applied Mechanics and Engineering. 2007;197:173–201. [Google Scholar]
- 83.Hsu MC, Bazilevs Y, Calo VM, Tezduyar TE, Hughes TJR. Improving stability of stabilized and multiscale formulations in flow simulations at small time steps. Computer Methods in Applied Mechanics and Engineering. 2010;199:828–840. [Google Scholar]
- 84.Chung J, Hulbert GM. A time integration algorithm for structural dynamics with improved numerical dissipation: The generalized-α method. Journal of Applied Mechanics. 1993;60:371–75. [Google Scholar]
- 85.Simo JC, Wriggers P, Taylor RL. A perturbed Lagrangian formulation for the finite element solution of contact problems. Computer Methods in Applied Mechanics and Engineering. 1985;50(2):163–180. [Google Scholar]
- 86.Kamensky D, Evans JA, Hsu MC. Stability and conservation properties of collocated constraints in immersogeometric fluid-thin structure interaction analysis. Communications in Computational Physics. 2015;18:1147–1180. [Google Scholar]
- 87.Kamensky D, Hsu MC, Yu Y, Evans JA, Sacks MS, Hughes TJ. Immersogeometric cardiovascular fluid–structure interaction analysis with divergence-conforming B-splines. Computer Methods in Applied Mechanics and Engineering. 2017;314:408–472. doi: 10.1016/j.cma.2016.07.028. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 88.Garcia D, Kadem L. What do you mean by aortic valve area: geometric orifice area, effective orifice area, or Gorlin area? Journal of Heart Valve Disease. 2006;15(5):601. [PubMed] [Google Scholar]
- 89.Gorlin R, Gorlin SG. Hydraulic formula for calculation of the area of the stenotic mitral valve, other cardiac valves, and central circulatory shunts. I. American Heart Journal. 1951;41(1):1–29. doi: 10.1016/0002-8703(51)90002-6. [DOI] [PubMed] [Google Scholar]
- 90.le Polain de Waroux JB, Pouleur AC, Robert A, Pasquet A, Gerber BL, Noirhomme P, El Khoury G, Vanoverschelde JLJ. Mechanisms of recurrent aortic regurgitation after aortic valve repair. JACC: Cardiovascular Imaging. 2009;2(8):931–939. doi: 10.1016/j.jcmg.2009.04.013. [DOI] [PubMed] [Google Scholar]
- 91.Chandran KB, Kim SH, Han G. Stress distribution on the cusps of a polyurethane trileaflet heart valve prosthesis in the closed position. Journal of Biomechanics. 1991;24(6):389–395. doi: 10.1016/0021-9290(91)90027-k. [DOI] [PubMed] [Google Scholar]
- 92.Grande KJ, Cochran RP, Reinhall PG, Kunzelman KS. Stress variations in the human aortic root and valve: the role of anatomic asymmetry. Annals of Biomedical Engineering. 1998;26(4):534–545. doi: 10.1114/1.122. [DOI] [PubMed] [Google Scholar]
- 93.Harringer W, Pethig K, Hagl C, Meyer GP, Haverich A. Ascending aortic replacement with aortic valve reimplantation. Circulation. 1999;100(suppl II):II24–II28. doi: 10.1161/01.cir.100.suppl_2.ii-24. [DOI] [PubMed] [Google Scholar]
- 94.Kim H, Lu J, Sacks MS, Chandran KB. Dynamic simulation of bioprosthetic heart valves using a stress resultant shell model. Annals of Biomedical Engineering. 2008;36(2):262–275. doi: 10.1007/s10439-007-9409-4. [DOI] [PubMed] [Google Scholar]
- 95.Marom G, Haj-Ali R, Raanani E, Schäfers HJ, Rosenfeld M. A fluid–structure interaction model of the aortic valve with coaptation and compliant aortic root. Medical & Biological Engineering & Computing. 2012;50:173–182. doi: 10.1007/s11517-011-0849-5. [DOI] [PubMed] [Google Scholar]
- 96.Takizawa K, Bazilevs Y, Tezduyar TE. Space–time and ALE-VMS techniques for patient-specific cardiovascular fluid–structure interaction modeling. Archives of Computational Methods in Engineering. 2012;19:171–225. [Google Scholar]
- 97.Rosencranz R, Bogen SA. Clinical laboratory measurement of serum, plasma, and blood viscosity. American Journal of Clinical Pathology. 2006;125(Suppl):78–86. doi: 10.1309/FFF7U8RRPK26VAPY. [DOI] [PubMed] [Google Scholar]
- 98.Vignon-Clementel IE, Figueroa CA, Jansen KE, Taylor CA. Outflow boundary conditions for three-dimensional finite element modeling of blood flow and pressure in arteries. Computer Methods in Applied Mechanics and Engineering. 2006;195:3776–3796. [Google Scholar]
- 99.Hammermeister KE, Brooks RC, Warbasse JR. The rate of change of left ventricular volume in man. Circulation. 1974;49(4):729–738. doi: 10.1161/01.cir.49.4.729. [DOI] [PubMed] [Google Scholar]
- 100.Lonestar 5 User Guide. https://portal.tacc.utexas.edu/user-guides/lonestar5. Accessed 1 September 2017.
- 101.Texas Advanced Computing Center (TACC) http://www.tacc.utexas.edu. Accessed 1 September 2017.
- 102.Hsu MC, Akkerman I, Bazilevs Y. High-performance computing of wind turbine aerodynamics using isogeometric analysis. Computers & Fluids. 2011;49:93–100. [Google Scholar]
- 103.Yap CH, Saikrishnan N, Tamilselvan G, Yoganathan AP. Experimental technique of measuring dynamic fluid shear stress on the aortic surface of the aortic valve leaflet. Journal of Biomechanical Engineering. 2011;133061(6):007. doi: 10.1115/1.4004232. [DOI] [PubMed] [Google Scholar]
- 104.Cheng C, Tempel D, van Haperen R, van der Baan A, Grosveld F, Daemen M, Krams R, de Crom R. Atherosclerotic lesion size and vulnerability are determined by patterns of fluid shear stress. Circulation. 2006;113:2744–2753. doi: 10.1161/CIRCULATIONAHA.105.590018. [DOI] [PubMed] [Google Scholar]
- 105.Chien S, Li S, Shyy Y. Effects of mechanical forces on signal transduction and gene expression in endothelial cells. Hypertension. 1998;313:162–169. doi: 10.1161/01.hyp.31.1.162. [DOI] [PubMed] [Google Scholar]
- 106.Wentzel JJ, Corti R, Fayad ZA, Wisdom P, Macaluso F, Winkelman MO, Fuster V, Badimon JJ. Does shear stress modulate both plaque progression and regression in the thoracic aorta? Human study using serial magnetic resonance imaging. Journal of the American College of Cardiology. 2005;45:846–854. doi: 10.1016/j.jacc.2004.12.026. [DOI] [PubMed] [Google Scholar]
- 107.Shojima M, Oshima M, Takagi K, Torii R, Hayakawa M, Katada K, Morita A, Kirino T. Magnitude and role of wall shear stress on cerebral aneurysm: computational fluid dynamic study of 20 middle cerebral artery aneurysms. Stroke. 2004;35:2500–2505. doi: 10.1161/01.STR.0000144648.89172.0f. [DOI] [PubMed] [Google Scholar]
- 108.Westerhof N, Lankhaar JW, Westerhof BE. The arterial Windkessel. Medical & Biological Engineering & Computing. 2009;47:131–141. doi: 10.1007/s11517-008-0359-2. [DOI] [PubMed] [Google Scholar]


