Abstract
Purpose/Objective(s)
In stereotactic radiosurgery (SRS), the multiple isocenters for multiple targets dynamic conformal arc (MIMT DCA) technique is traditionally used to treat multiple brain metastases, with one isocenter for each target. The single isocenter for multiple targets (SIMT) technique has recently been adopted to reduce the treatment time at the cost of plan quality. The objective of this study was to develop a restricted single isocenter for multiple targets DCA (RSIMT DCA) technique that can significantly reduce the treatment time but still maintain similar plan quality as the MIMT DCA technique.
Materials and Methods
Treating multiple brain metastases with a single isocenter poses a challenge to SRS planning using DCA beams that are intrinsically 3D and do not modulate the beam intensity to spare the normal tissue between targets. To address this obstacle, we have developed a RSIMT DCA technique and used it to treat SRS patients with multiple brain metastases since February 2015. This planning approach is similar to the SIMT technique except that the number of targets for each isocenter is restricted and the distance between the isocenter and target is limited. In this technique, the targets are first split into batches so that all targets in a batch are within a chosen distance (e.g., 7 cm) of each other. All targets in a batch are combined into one target and the geometric center of the combined target is the isocenter for the group of DCA beams associated with that batch. Each DCA group typically consists of 3-4 DCA beams to irradiate 1-3 targets. For each DCA beam, the collimator angle is adjusted to minimize the exposure of normal tissue between targets. The dose of each treatment group is normalized so that the maximal point dose to the combined target is 125% of the prescription dose, which is equivalent to normalize the prescription dose to 80% isodose line. If the maximal point dose of a target is <123%, an additional beam is used to boost the maximal point dose of that target to 125%. To evaluate the plan quality, we randomly selected 10 cases planned with the RSIMT DCA technique, and re-planned them using the MIMT DCA technique. There were in total 38 PTVs, and 22 isocenters were used to treat all of these targets. The prescription for each target was 20 Gy with a maximal point dose of 25 Gy. Plan quality indexes were calculated and compared. Paired sample t-test was performed to determine if the mean normalized difference, (RSIMT-MIMT)/MIMT of each plan index was statistically significantly (p-value < 5%) larger than 0.
Results
Satisfactory PTV coverage (V20Gy>95% and V19Gy=100%) was achieved for all plans using either technique. Most PTVs have a maximal point dose between 24.9 and 25.1 Gy, with 2 PTVs between 24.5 and 24.9 Gy. Overall, the plan quality was slightly better for the MIMT DCA technique and the normalized difference was statistically significantly larger than 0 for all investigated dose quality indexes. The normalized difference of body mean dose and conformity index (CI) between the RSIMT and MIMT techniques was respectively 4.2% (p=0.002) and 9.4% (p=0.001), indicating similar plan quality globally and in the high dose area. The difference was more pronounced for the mid-to-low dose spillage with the ratios of V12Gy and V10Gy/VPTV being 13.9% (p=3.8×10-6) and 14.9% (p=1.3×10-5), respectively. The treatment time was reduced by 30%-50% with the RSIMT DCA technique.
Conclusion
The RSIMT DCA technique can produce satisfactory SRS plans for treating multiple targets and can significantly reduce the treatment time.
Keywords: single isocenter for multiple targets, multiple isocenters for multiple targets, dynamic conformal arc, rotational error
Introduction
Brain stereotactic radiosurgery (SRS)(1) is a radiotherapy procedure that can deliver a very high single-fraction (on the order of 20 Gy) radiation dose to the treatment targets while sparing the surrounding normal tissues. In order to achieve the highest treatment accuracy, each SRS target is separately planned, set up and treated with its own isocenter (usually located at the geometric center of the treatment target). Traditionally, three-dimensional conformal radiotherapy (3D CRT) beams like static, conformal arc or dynamic conformal arc (DCA) fields are used for brain SRS treatment. For example, the multiple isocenters for multiple targets (MIMT) DCA(2, 3) technique is a standard SRS treatment approach in which one isocenter is used to treat one target with 3-5 DCA beams of various couch angles. The opening of a DCA beam is adjusted in real time so that it always conforms to the beams-eye-view projection of the planning target volume (PTV) during the arc delivery. In comparison to other 3D CRT SRS techniques, the DCA technique is simpler in planning and faster in delivery.
Even with DCA technique, brain SRS is a very time-consuming procedure, particularly when multiple targets are treated in a single SRS session. Therefore, in the past, the number of brain metastases treated with SRS was limited to a low number (e.g., less than four), while whole brain radiotherapy was used for more targets. However, recent studies have shown that brain SRS is superior to whole brain radiotherapy for managing multiple brain metastases(4-7). As a result, it is increasingly common that a high number (more than five) of lesions are treated within a single SRS session. This poses a serious challenge to the scheduling and quality assurance of SRS treatment, especially for linear accelerator (linac) based SRS that needs to share the machine time with other non-SRS procedures. To address this challenge, the single isocenter for multiple targets (SIMT) technique(8, 9) was developed to save the treatment time for SRS. In this technique, one isocenter is used for treating multiple lesions with several intensity-modulated radiotherapy (IMRT) beams using the step-and-shoot, sliding-window or volumetric arc therapy (VMAT) approach.
Since the isocenter is usually chosen as the geometrical center of the combined clinical target volumes (CTVs), one major complication of the SIMT technique is that the rotational error might become significant for targets that are far from the isocenter. For example, Roper et al.(10) introduced artificial rotational errors to fifty selected SRS cases using the SIMT technique and reported that D95 values and V95 coverage rates were > 95% in all cases at the 0.5° rotation error, but only 63% of the targets could achieve similar requirements at 2.0° rotation error. In addition, the risk of compromised coverage is more noticeable for smaller targets and increases with the amount of rotational error and the distance between targets(10). Stanhope et al.(11) performed a retrospective study of SRS patients treated with traditional MIMT technique to quantify initial (difference between the skull position at simulation and at treatment) and intra-operational (i.e. occurred during the treatment) rotational uncertainties. The authors reported a 0.35-mm margin is required per centimeter of target-to-isocenter separation to account for 95% of rotational uncertainties at initial setup. For intraoperative rotational uncertainties, the margin reduced to 0.1 mm per centimeter if the initial setup uncertainty was eliminated via image guidance. Ezzell(12) studied the spatial positioning uncertainties for SIMT SRS using a phantom made of three sections of wood beam of cross-section 8.7×8.7cm2, with 12 imbedded target BBs distributed up to 13.8 cm from the isocenter. The phantom was positioned at five different starting locations, then imaged and aligned using either the Brianlab ExacTrac system (Brainlab, Feldkirchen, Germany), or the cone-beam computed tomography of a Varian Truebeam (Varian Medical Systems, Palo Alto, CA, USA). The accuracy of the alignment of each imaging device was checked with the treatment beam at seven different gantry and couch angles. The results show that an additional 1-mm PTV margin is needed for targets up to about 7-8 cm from the isocenter.
We also developed a generalized statistical model to investigate the risk of compromised coverage due to different amounts of rotational error(13-15). This model incorporates the treatment uncertainty from both translational and rotational errors of SIMT technique. With this model, the author was able to calculate the loss of CTV coverage probability and demonstrate that the rotational error cannot be ignored for high-accuracy and high-precision treatments like SRS/SBRT, particularly when the distance between the isocenter and target is large. In addition, the data presented in these papers can be used to determine whether the additional rotational error can be ignored, and if the additional rotational error is significant, how much extra PTV margin is needed to maintain the desired CTV coverage probability.
In addition to IMRT and VMAT beams, SIMT technique can also be combined with 3D CRT beams to speed up the radiation delivery. Unlike the IMRT and VMAT beams, the 3D CRT beams do not modulate the radiation intensity so it is difficult to treat all CTVs and at the same time block the normal tissues between targets. Furthermore, in most cases, only one involved target can achieve the preferred maximal dose (e.g., 125% of the prescription dose) after dose normalization while the maximal dose to other targets can be significantly (up to 10%) lower.
As a result, a higher number of beams and more complex dose normalization are generally needed for brain SRS using SIMT 3D beams. Huang et al.(16) have used SIMT DCA beams for treating multiple brain metastases and reported similar plan quality as MIMT DCA but more efficient to delivery. In their approach, each target is treated with a set of dedicated DCA beams associated with a single isocenter instead of the center of the target so there is no significant difference in the total monitor units for treating each target. The more efficient delivery is therefore mainly due to less time spent on the patient setup since only one instead of multiple isocenters needs to be set up and validated.
In addition to the standard DCA planning tools available in modern treatment planning systems, vendors are also developing special planning software for optimizing SIMT DCA. One such planning tool currently commercially available is the Elements package developed by Brainlab (Brainlab, Feldkirchen, Germany). The details of this software were described in a publication by Gevaert et al.(17), who investigated the feasibility of this software and compared it with MIMT DCA and SIMT VMAT. In brief, starting with 10 DCA beams for 5 couch positions, the Elements software automatically optimizes the beam parameters including aperture opening, arc angle, beam weighting… to obtain the optimal plan for SIMT DCA. This automated planning tool can produce SIMT DCA plan with quality comparable to MIMT DCA, and with better dose gradients and normal tissue sparing over SIMT VMAT(17).
To reduce the treatment time while maintaining similar setup accuracy and plan quality, we have developed a “restricted single isocenter for multiple-targets DCA” (RSIMT DCA) technique for SRS planning and used it clinically since February 2015. In this technique, a group of DCA beams associated with a single isocenter are used to treat up to three targets so that the normal tissue between targets can be spared. In addition, to minimize the negative effect of rotational error, the targets treated by a group of RSIMT DCA beams are required to be within a sphere of a selected (e.g., 7 cm) diameter. Finally, the RSIMT DCA technique uses additional boost beams so that the maximal dose of each target can be boosted to the desired percent (e.g., 125%) of the prescription dose. To evaluate this new planning approach, we have performed plan comparison for ten SRS cases using both (RSIMT DCA and MIMT DCA) techniques. Plan quality indexes were calculated and compared, and the results are presented in this paper.
Materials and Methods
RSIMT DCA technique
Figure 1 illustrates the difference between the (A) SIMT and (B) RSIMT techniques. For the SIMT technique in Figure 1A, one isocenter is used to treat all five PTVs. While for the RSIMT technique in Figure 1B, the five PTVs are split into two batches. PTVs 1-3 are treated with one isocenter (“Iso1”) and PTVs 4-5 are treated with a second isocenter (“Iso2”). In comparison to the SIMT technique, two parameters are restricted for the RSIMT DCA technique. They are the number of targets treated with each isocenter and the distance between the isocenter and the targets. These two restrictions are imposed to minimize the additional exposure due to imperfect blocking of the normal tissues between the targets, and to reduce the negative effect of the unaccounted rotational error associated with the SIMT technique(10-15).
Figure 1.
Illustration of the (A) SIMT (single isocenter for multiple targets) and (B) RSIMT (restricted single isocenter for multiple targets) techniques. For the SIMT technique in (A), one isocenter is used to treat all five PTVs. While for the RSIMT technique in (B), the five PTVs are split into two batches. PTVs 1-3 are treated with one isocenter (“Iso1”) and PTVs 4-5 are treated with a second isocenter (“Iso2”).
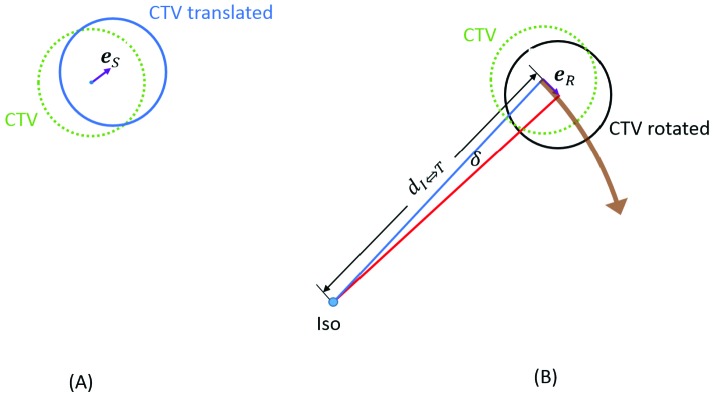
Figure 2 demonstrates the (A) translational and (B) rotational errors that introduce uncertainty to the CTV location. The translational error es illustrated in Figure 2A is a random vector the amplitude and direction of which remain the same regardless of the location of the CTV. The rotational error eR in Figure 2B is also a random vector. However, its amplitude increases with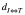 
, the distance between the isocenter and the CTV, and its direction is not fixed but along the rotational direction, which in turn depends on the relative location between the isocenter and the CTV. To minimize the negative effect of rotational error, the targets are first split into batches so that the largest 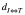is less than a predetermined threshold 
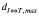. The isocenter is usually the center of gravity of the combined target in a batch, and “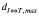” is chosen so that the additional PTV margin required to compensate for the rotational error can be ignored.
Figure 2.
Illustration of the (A) translational and (B) rotational errors. The translational error in (A) is a random vector the amplitude and direction of which remain the same regardless of the location of the CTV. The rotational error in (B) is also a random vector but its amplitude increases with dI⇔T, the distance between the isocenter and the CTV. In addition, the direction of the rotational error (purple arrow) is not fixed but along the rotational direction (brown arrow), which depends on the relative location between the isocenter and CTV.
To help determine the appropriate 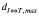we have developed a statistical model for analyzing the additional rotational errors for the SIMT technique(13-15). In this model, the term “intrinsic setup error” was used to indicate the random translational motion of CTV for the traditional setup when the isocenter is located at or close to the geometric center of the CTV. When the isocenter is outside the GTV, it is assumed that the rotation around the isocenter happens randomly and follows a three-dimensional (3D) independent normal distribution with a zero mean and a uniform standard deviation of σδ (in degree). This rotation leads to a setup error (i.e., eR in Figure 2) following a 3D independent normal distribution with a zero mean and a uniform standard deviation of σR =0.816 
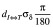(in mm). The rotational and translational uncertainties are added in quadrature to obtain the combined setup error from which the random motion of the CTV can be modeled. Based on this model the random motion in the radial direction follows a chi-distribution so the additional PTV margin for compensating for the extra rotational error can be calculated using the chi-square table as a function of σδ, 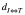, the intrinsic PTV margin for translational error, and the desired CTV coverage probability (e.g., 95% of the time the CTV is covered by the prescription dose). For example, if σδ = 0.45° (i.e., 0.0079rad) and the initial PTV margin is 2 mm for a CTV coverage parobability of 95%, a 0.2-mm or 0.1-mm additional PTV margin is needed for 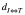of 5 cm or 3.5 cm, respectively. On the other hand, if a 0.2-mm or 0.1-mm additional PTV margin can be ignored, the 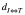can not exceed 5 cm or 3.5 cm, respectively.
For each isocenter, a group of 3-5 DCA beams are used to irradiate all targets in the batch. Because a DCA beam is intrinsically 3D, it cannot completely block the region between targets by modulating the beam intensity. Instead, the collimator angle of each DCA beam needs to be individually adjusted to minimize the exposure of normal tissues that cannot be blocked by the multi-leaf collimators (MLCs) at the default (0°) collimator angle. This can be achieved by visual inspection of the aperture of a DCA beam and adjusting the collimator angle accordingly. Alternatively, the collimator optimization function of the treatment planning system can be used. From our experience, an optimal collimator angle can usually be found without difficulties if there are three or less targets.
Dose Prescription
The dose of each treatment group is normalized so that the prescription dose corresponds to a preferred percent isodose line. For SRS, the 100% isodose line can be assigned to either (A) the isocenter (or the maximal point dose) or (B) the prescription dose. For example, in linac-based SRS using the MIMT technique, the isocenter dose (or the maximal point dose) is typically 25% higher than the prescription dose. If the first prescription system is used, the plan is normalized so that prescription dose corresponds to the 80% isodose line while the 100% isodose line is assigned to the isocenter (or the maximal dose point). This is equivalent to assigning the 100% isodose line to the prescription dose by renormalizing the maximal dose to 125% of the prescription dose using the second system. In this study, we used the latter for dose prescription (i.e., the prescription dose corresponds to 100% isodose line).
Maximal Dose Adjustment
Since there are multiple targets in a batch, after the dose normalization, only one target can achieve a maximal point dose of 125% of the prescription dose while the maximal point dose of other targets will be lower. If this is a concern, dose to the targets with a lower maximal point dose needs to be increased. This can be achieved in a variety of ways. First, the relative weightings of the DAC beams can be adjusted until the maximal point dose of each target reach a similar level. This usually works when the targets located more or less around the central region of an axial cut so that the average depth is similar for all targets. When the targets are at different axial level (i.e., one is more superior or inferior) or grouped on one (e.g., to the right) side of the brain, the maximal point dose level cannot be adjusted satisfactorily with this approach due to the large difference in depth. The coverage and maximal point dose of a target can also be adjusted using the paint brush to manually modify the margin between the beam edge and the target. Although this approach is very effective in improving the coverage, it has a limited capability in changing the maximal point dose (at most 1%-2%). A common problem with the above two methods are that they can be time consuming as both are kind of a trial-and-error approach. Consequently, we developed a third approach to adjusting the maximal point dose level more efficiently. That is, additional DCA beams (one DCA beam for each target) were added to boost the dose of the targets with a lower maximal point dose. Since each DCA boost beam only irradiates one target, it is easy to boost the maximal point dose of that target to the preferred level, e.g., 125% of the prescription dose.
Experiment
We randomly selected 10 cases planned with the RSIMT DCA technique, and re-planned them using the MIMT DCA technique, one isocenter with a group of dedicated DCA beams for each target. All plans were done using the traditional dynamic conformal arc technique in the Brainlab iPlan treatment planning system (TPS). IMRT QA was performed and passed for all RSIMT DCA beams using the MapCheck2 device before the first clinical use to validate the accuracy of dose delivery with a 3-mm, 3% criterion. In this study 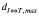, was chosen to be 3.5 cm assuming that σδ = 0.45° and a 0.1-mm extra PTV margin can be safely ignored. Since the isocenter could not be determined until all targets in a batch were selected, this criterion was fulfilled by selecting targets that were within 7 cm of each other. Table 1 lists of the number of targets and isocenters for each plan, as well as the ratio of the number of isocenters to the number of targets.
Table 1.
List of the number of targets and isocenters for the ten plans included in this study. Also listed is the iso-to-target ratio (i.e., number of isocenters divided by number of targets), which is an indicator for the time required to treat each target.
| Plan# | No. Target | No. Iso | Iso/Target ratio |
| 1 | 6 | 3 | 50.0% |
| 2 | 3 | 2 | 66.7% |
| 3 | 5 | 3 | 60.0% |
| 4 | 3 | 2 | 66.7% |
| 5 | 4 | 3 | 75.0% |
| 6 | 4 | 2 | 50.0% |
| 7 | 5 | 2 | 40.0% |
| 8 | 2 | 1 | 50.0% |
| 9 | 4 | 3 | 75.0% |
| 10 | 2 | 1 | 50.0% |
| Mean | 3.8 | 2.2 | 58.3% |
| Stdev | 1.3 | 0.8 | 12.1% |
The prescription dose (or the 100% isodose line) for each plan was 20 Gy with a maximal point dose of 25 Gy (or 125% isodose line). A typical beam arrangement consisted of three DCA beams at three (0-degree, 60-degree and 300-degree) couch angles although the exact couch angles might vary depending on the location and geometrical distribution of the targets in each batch. The collimator angle of each DCA beam was adjusted manually or using the collimator angle optimization function of the iPlan TPS. Most DCA beams span a 120-degree gantry rotation. Dose calculation was performed using the iPlan pencil beam algorithm with a dose grid size of 2 mm×2 mm×2 mm. The dose was normalized so that the maximal point dose of the combined PTV of each batch was 125% of the prescription dose. If the maximal point dose of a target was less than 123% of the prescription dose, an additional DCA (or sometimes static) beam was used to boost the maximal point dose of that target to 125% of the prescription dose.
Plan quality indexes were calculated using the dose volume histogram (DVH) of each plan to compare the plan quality of these two techniques. For PTV coverage, PTV V20Gy (percent volume of PTV covered by 100% of the prescription dose), PTV V19Gy (percent volume of PTV covered by 95% of the prescription dose) and PTVmean (mean dose of PTV) were calculated. For normal tissue dose, we calculated Bodymean (mean dose of the whole body), V12Gy (volume receiving 12 Gy dose), conformity index (CI, ratio of the volume receiving 100% of the prescription dose to the PTV volume), and V10Gy/VPTV (ratio of the volume receiving 10 Gy or 50% of the prescription dose to the PTV volume).
Treatment time was not measured but estimated based on the number of isocenters assuming that the treatment time for each isocenter is more or less the same. In this study, the treatment time was defined as the sum of beam-on time and time spent on validation of patient positioning under image guidance for all isocenters. Note that the initial setup time, i.e., the time spent on bringing the patient into the room and positioning the patient comfortably in the immobilization device, was not included. The beam-on time for an isocenter is proportional to the total monitor units of all associated DCA beams. Since similar beam parameters were used and the isocenter for the SIMT DAC is the averaged location of all targets, the total MU should be similar for each isocenter. In addition, because the number of couch kicks associated with an isocenter were kept the same for both (MIMT DCA and SIMT DCA) techniques considered in this study, the time spent on validation of patient positioning under image guidance for each isocenter should be approximately the same. The hypothesis that the treatment time is proportional to the number of isocenters is therefore justified.
Results
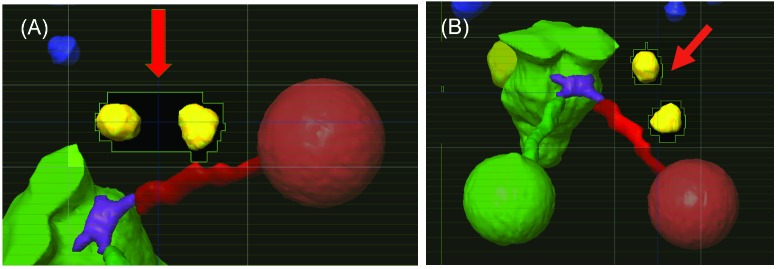
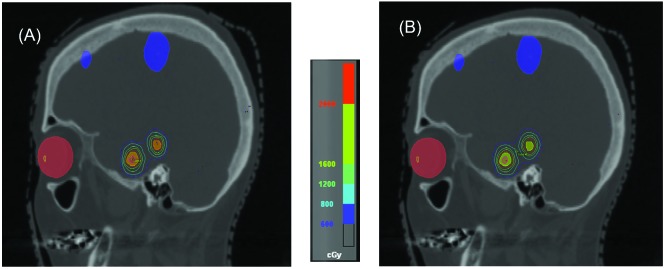
The replanning was successful for all 10 cases using the MIMT DCA technique. For plans using the RSIMT DCA technique, most PTVs had a maximal dose between 24.9 and 25.1 Gy, with 2 PTVs between 24.5 and 24.9 Gy. Figure 3 shows the beam eye view of a RSIMT DCA beam with (A) 0° and (B) 20° collimator angles to irradiate two targets. The red arrow points to the normal tissues between these two targets. By properly choosing the collimator angle (20°) in (B), exposure of the normal tissues between targets were significantly reduced in comparison to the default (0°) collimator angle in (A). Figure 4A demonstrates the iso-dose plot for a CT slice planned using the MIMT DCA technique, and Figure 4B is the iso-dose plot for the same CT slice planned using the RSIMT DCA technique. Similar dose distribution was achieved with both techniques. Figure 5 is plot of the mean and standard deviation of plan indexes for the 10 cases using the RSIMT and MIMT techniques. Table 2 lists the normalized difference, (RSIMT-MIMT)/MIMT of planning indexes for the 10 plans, and the results of the paired sample t-test to determine if the mean difference is statistically significantly larger than 0 for a 5% significance level. PTV coverage is similar, as the mean normalized difference of PTV V20Gy and PTV V19Gy between these two techniques is (0.0% and 0.1%) and not statistically significant (p=0.864 and 0.550). The body mean dose (“Bodymean”) and C.I. of the RSIMT technique are slightly higher (4.2%, p=0.004 and 9.4%, p=0.001, respectively) than that of MIMT technique, indicating slightly worse plan quality globally and in the high dose area for the RSIMT technique. The difference was most pronounced for the mid-to-low dose spillage, with the V10Gy/VPTV and V12Gy of the RSIMT technique being higher (14.9%, p=1.3×10-5 and 13.9%, p=3.8×10-6, respectively). Using the iso-to-target ratio in Table 1 as an indicator for the time required to treat each target, the treatment time for the RSIMT technique is on average ~41% less than that for the MIMT technique.
Figure 3.
The beam eye view of a RSIMT DCA beam with (A) 0° and (B) 20° collimator angles. The beam irradiates two targets. Red arrow: the normal tissues between two targets that was exposed in (A) but completely blocked in (B).
Figure 4.
Iso-dose plot for a CT slice planned using iPlanNet (A) MIMT DCA and (B) RSIMT DCA techniques.
Figure 5.
Plot of the mean and standard deviation of plan indexes for the ten cases planned using the RSIMT DCA and MIMT-DCA techniques. “PTVmean” is normalized to the prescription dose, i.e., 20 cGy. “V12Gy” is normalized to 10 cc.
Table 2.
List of the normalized difference of planning indexes (RSIMT-MIMT)/MIMT for the ten plans included in this study. The last row shows the result of paired sample t-test to determine if the mean difference is statistaically significantly different from 0 for a 5% significance level. “C.I.”: comformality index. “T” or “R” indicates that the p value was calculated for respectively a 2-tailed or a right-tailed t-test.
| Plan# | PTV V20Gy | PTV V19Gy | PTVmean | C.I. | Bodymean | V10Gy/ VPTV | V12Gy |
| 1 | -1.4% | -0.1% | -0.1% | 2.2% | 10.3% | 20.2% | 19.2% |
| 2 | 0.7% | 0.0% | 0.7% | 8.7% | 5.8% | 15.3% | 16.7% |
| 3 | -0.1% | 0.0% | 0.8% | 5.6% | 2.7% | 12.6% | 8.8% |
| 4 | 0.0% | 0.0% | 0.5% | 3.7% | 3.9% | 13.5% | 7.9% |
| 5 | -1.6% | -0.7% | 1.0% | 12.0% | 1.4% | 4.4% | 7.7% |
| 6 | 0.0% | 0.3% | -0.3% | 5.0% | 1.8% | 11.4% | 12.4% |
| 7 | 0.0% | 0.4% | 1.4% | 23.4% | 6.0% | 16.2% | 13.0% |
| 8 | 1.4% | 0.9% | 5.1% | 19.0% | 8.8% | 18.4% | 16.0% |
| 9 | 0.5% | 0.0% | 2.3% | 10.1% | 1.8% | 21.1% | 21.8% |
| 10 | 0.0% | 0.0% | -0.3% | 4.9% | 0.0% | 15.4% | 15.5% |
| Mean | 0.0% | 0.1% | 1.1% | 9.4% | 4.2% | 14.9% | 13.9% |
| Stdev | 0.9% | 0.4% | 1.6% | 6.9% | 3.4% | 4.9% | 4.8% |
| p | 0.864T | 0.550 T | 0.028 T | 0.001 R | 0.004 R | 1.3×10-05 R | 3.8×10-06 R |
Discussion
Both IMRT (step-and-shoot, sliding window, and VMAT) and 3D (static or DCA) beams have been used for single-fraction SRS. When treating multiple targets with a single isocenter, the IMRT technique is generally needed to modulate the intensity so that the surrounding normal tissues can be spared. The objective of this study was to develop an SRS planning strategy using the standard DCA beams (i.e., the RSIMT DCA technique) that can reduce the treatment time as the SIMT technique but still maintain plan quality similar to the multiple-isocenter (e.g., the MIMT DCA) technique that uses one isocenter for each target. The hypothesis of this study is that by limiting the number of targets treated by each isocenter and restricting the distance between the isocenter and targets, the RSIMT DCA technique can produce SRS plans with quality similar to the MIMT DCA technique. In addition, since up to three targets can be treated with one isocenter, the RSIMT DCA technique can significantly reduce the treatment time in comparison to the MIMT DCA technique.
Plan comparison study was performed by calculating and comparing plan quality indexes of these two planning techniques and the results basically agreed with these hypotheses. Overall, the plan quality is comparable between these two approaches but is slightly better for the MIMT DCA technique. Particularly, the indexes measuring the intermediate dose spillage, i.e., V12Gy and V10Gy /VPTV were > 10% higher for the RSIMT DCA technique. Difference in indexes for high dose spillage (i.e., C.I.), on the other hand, was smaller (~9% higher) between these two techniques. There was essentially no difference in PTV coverage. The difference in intermediate dose spillage was mainly due to the fact that the RSIMT DCA technique uses MLCs instead of jaws to block the radiation between targets and thus has a higher leakage dose to the normal tissues. The difference in high dose spillage, on the other hand, was due to the imperfect blocking of the surrounding normal tissues when multiple targets were treated with the RSIMT DCA technique. The MIMT DCA technique could instead achieve a better conformality and better sparing of surrounding normal since each target was individually treated.
Because the 3D DCA beam doesn’t modulate the beam intensity, it is critical to find the optimal collimator angle that best blocks the normal tissues between targets. This exercise is straightforward for two targets, becomes increasingly difficult for three targets and is almost impossible when there are four or more targets. As a result, each RSIMT DCA group can cover at most three PTVs although it is obvious that the time saving of the RSIMT DCA technique is proportional to the number of targets included in a batch. If more than three PTVs are within 7 cm of each other, these targets need to be split into more than one batch so that the normal tissues can be properly blocked and spared. Nevertheless, the setup time can still be reduced for cases like this if the same isocenter and couch angles are used for all batches since the patient position needs to be validated for each isocenter and couch angle.
The time saving can be further improved using a larger 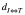,max to reduce the number of isocenters. However, a larger distance between the isocenter and treatment target leads to a higher uncertainty from the rotational error. Therefore, this tactic might worsen the negative effect of rotational error to an unacceptable level unless a larger PTV margin is used.
One drawback of the SIMT technique using IMRT beams is that the maximal dose to each target cannot be easily controlled to a preferred percent (e.g. 125%) of the prescription dose. This is not the case for the RSIMT DCA technique. As demonstrated in this paper, the maximal dose of an SRS plan can be easily normalized to 125% of the prescription dose for each individual PTV using boost fields. Although DCA beams were used as boost fields in this study, other (e.g., 3D static beam, IMRT…) beam modalities can serve the purpose equally well. In our clinic the IMRT beams are rarely used for single-fraction SRS to avoid IMRT QA. One might speculate that the boost fields need to be delivered with a different couch angle, which will significantly increase the treatment time. This is not necessary since the dose delivered by the boost fields is relatively low (on the order of one to two Gy). As a result, the boost fields can share the same couch angle with one of the primary DCA beams without significantly affecting the normal tissue dose.
In comparison to other similar SIMT approaches like those published by Huang et al.(16) and Gevaert et al.(17), the total treatment time for the RSIMT DCA technique presented in this paper is longer since more time is required for setting up multiple instead of a single isocenter. However, the RSIMT DCA technique restricts 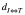to minimize the negative effect of rotational error, which was not considered by either group(16, 17). In addition, unlike the method developed by Huang et al.(16), the RSIMT DCA technique is more efficient in radiation delivery since each DCA beam is used to treat 1-3 targets instead of 1 target only. Moreover, the approach investigated by Gevaert et al.(17) requires the purchase of a commercial package, while the RSIMT DCA technique is done with the traditional dynamic conformal arc technique that is available in most (e.g., iPlan, Eclipse, Pinnacle…) treatment planning systems.
Morrison et al.(18) also investigated the quality of SIMT VMAT plans that use 2-3 isocenters to restrict the distance between isocenter and target to ~5cm, which is similar to the beam arrangement adopted in this study. This choice of similar 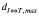by both studies is simply a coincidence. For the study by Morrison et al.(18), this distance was chosen so that all targets can be covered by leaves of the smallest (i.e., 2.5 mm) width for better conformality. The difference in conformality for various leaf widths was not considered in this study because the 5-mm, 3-mm and 2.5mm leaf widths are all currently used clinically for brain SRS. In addition, an earlier study performed by the first author of this paper and colleagues(19) demonstrated that the improvement of plan quality of 3-mm over 5-mm MLC is about 5%-10% for various indexes, which is on the same ballpark as that reported by Morrison et al(18). Therefore, the use of smaller leaf width is desirable but not mandatory as concluded by both studies(18, 19).
The restriction of 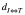,max to be less than 5 cm for RSIMT DCA in this study, on the other hand, was chosen so that, based on our statistical model(15), the extra PTV margin due to the additional rotational error can be safely ignored. As demonstrated in our previous study(19), a larger PTV margin will significantly increase the dose to surrounding normal tissue and hence the complication probability. Consequently, when the isocenter is located outside the CTV, the benefits of RSIMT DCA beam arrangement, combined with the added advantages of leaf-width MLC, might turn out to be the best compromise when considering all clinical factors including CTV coverage probability, normal tissue doses and treatment efficiency.
Conclusions
In conclusion, the RSIMT DCA technique can potentially replace the popular single-isocenter volumetric arc therapy technique for single-fraction SRS. The RSIMT DCA technique can provide similar plan quality as the multiple-isocenter technique but still save a significant amount of treatment time. In addition, with the RSIMT DCA technique, the maximal point dose to each target can be easily boosted to the preferred (e.g., 125%) percent of the prescription dose.
Acknowledgments
Authors’ disclosure of potential conflicts of interest
The authors have nothing to disclose.
Author contributions
Conception and design: Jenghwa Chang
Data collection: Jenghwa Chang, A Gabriella Wernicke, Susan Pannullo
Data analysis and interpretation: Jenghwa Chang, A Gabriella Wernicke, Susan Pannullo
Manuscript writing: Jenghwa Chang
Final approval of manuscript: Jenghwa Chang, A Gabriella Wernicke, Susan Pannullo
References
- 1. Schell MC, Bova FJ, Larson DA, Leavitt DD, Lutz WR, Podgorsak EB, et al. Stereotactic Radiosurgery: Report of Task Group 42, AAPM Radiation Therapy Committee Woodbury, NY: American Institude of Physics; 1995. [Google Scholar]
- 2. Grebe G, Pfaender M, Roll M, Luedemann L. Dynamic arc radiosurgery and radiotherapy: Commissioning and verification of dose distributions. International Journal of Radiation Oncology Biology Physics. 2001;49(5):1451-60. [DOI] [PubMed] [Google Scholar]
- 3. Solberg TD, Boedeker KL, Fogg R, Selch MT, DeSalles AAF. Dynamic arc radiosurgery field shaping: a comparison with static field conformal and noncoplanar circular arcs. International Journal of Radiation Oncology Biology Physics. 2001;49(5):1481-91. doi: http://dx.doi.org/10.1016/S0360-3016(00)01537-6. [DOI] [PubMed] [Google Scholar]
- 4. Andrews DW, Scott CB, Sperduto PW, Flanders AE, Gaspar LE, Schell MC, et al. Whole brain radiation therapy with or without stereotactic radiosurgery boost for patients with one to three brain metastases: phase III results of the RTOG 9508 randomised trial. The Lancet. 2004;363(9422):1665-72. doi: 10.1016/S0140-6736(04)16250-8. [DOI] [PubMed] [Google Scholar]
- 5. Aoyama H, Tago M, Shirato H. for the Japanese Radiation Oncology Study Group I. Stereotactic radiosurgery with or without whole-brain radiotherapy for brain metastases: Secondary analysis of the jrosg 99-1 randomized clinical trial. JAMA Oncology. 2015;1(4):457-64. doi: 10.1001/jamaoncol.2015.1145. [DOI] [PubMed] [Google Scholar]
- 6. Brown PD, Jaeckle K, Ballman KV, et al. Effect of radiosurgery alone vs radiosurgery with whole brain radiation therapy on cognitive function in patients with 1 to 3 brain metastases: A randomized clinical trial. JAMA. 2016;316(4):401-9. doi: 10.1001/jama.2016.9839. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7. Chang EL, Wefel JS, Hess KR, Allen PK, Lang FF, Kornguth DG, et al. Neurocognition in patients with brain metastases treated with radiosurgery or radiosurgery plus whole-brain irradiation: a randomised controlled trial. The Lancet Oncology. 2009;10(11):1037-44. doi: 10.1016/S1470-2045(09)70263-3. [DOI] [PubMed] [Google Scholar]
- 8. Clark GM, Popple RA, Prendergast BM, Spencer SA, Thomas EM, Stewart JG, et al. Plan quality and treatment planning technique for single isocenter cranial radiosurgery with volumetric modulated arc therapy. Pract Radiat Oncol. 2012;2(4):306-13. Epub 2012/10/01. doi: 10.1016/j.prro.2011.12.003. PubMed PMID: 24674169. [DOI] [PubMed] [Google Scholar]
- 9. Clark GM, Popple RA, Young PE, Fiveash JB. Feasibility of Single-Isocenter Volumetric Modulated Arc Radiosurgery for Treatment of Multiple Brain Metastases. International Journal of Radiation Oncology Biology Physics. 2010;76(1):296-302. doi: http://dx.doi.org/10.1016/j.ijrobp.2009.05.029. [DOI] [PubMed] [Google Scholar]
- 10. Roper J, Chanyavanich V, Betzel G, Switchenko J, Dhabaan A. Single-Isocenter Multiple-Target Stereotactic Radiosurgery: Risk of Compromised Coverage. International Journal of Radiation Oncology Biology Physics. 2015;93(3):540-6. doi: http://dx.doi.org/10.1016/j.ijrobp.2015.07.2262. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11. Stanhope C, Chang Z, Wang Z, Yin F-F, Kim G, Salama JK, et al. Physics considerations for single-isocenter, volumetric modulated arc radiosurgery for treatment of multiple intracranial targets. Practical Radiation Oncology. 2016;6(3):207-13. doi: http://dx.doi.org/10.1016/j.prro.2015.10.010. [DOI] [PubMed] [Google Scholar]
- 12. Ezzell GA. The spatial accuracy of two frameless, linear accelerator-based systems for single-isocenter, multitarget cranial radiosurgery. Journal of Applied Clinical Medical Physics. 2017;18(2):37-43. doi: 10.1002/acm2.12044. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13. Chang J. Statistical Analysis of the Rotation Error for Single-Isocenter Technique. International Journal of Radiation Oncology Biology Physics. 2016;96(2):E655. doi: 10.1016/j.ijrobp.2016.06.2269. [Google Scholar]
- 14. Chang J. MO-FG-CAMPUS-JeP3-01: A Statistical Model for Analyzing the Rotational Error of Single Iso-Center Technique. Medical Physics. 2016;43(6):3726-. doi: http://dx.doi.org/10.1118/1.4957376. [DOI] [PubMed] [Google Scholar]
- 15. Chang J. A statistical model for analyzing the rotational error of single isocenter for multiple targets technique. Med Phys. 2017;44(6):2115-23. Epub 2017/04/07. doi: 10.1002/mp.12262. PubMed PMID: 28382761. [DOI] [PubMed] [Google Scholar]
- 16. Huang Y, Chin K, Robbins JR, Kim J, Li H, Amro H, et al. Radiosurgery of Multiple Brain Metastases with Single-Isocenter Dynamic Conformal Arcs (SIDCA). Radiotherapy and Oncology. 2014;112(1):128-32. doi: http://dx.doi.org/10.1016/j.radonc.2014.05.009. [DOI] [PubMed] [Google Scholar]
- 17. Gevaert T, Steenbeke F, Pellegri L, Engels B, Christian N, Hoornaert M-T, et al. Evaluation of a dedicated brain metastases treatment planning optimization for radiosurgery: a new treatment paradigm? Radiation Oncology (London, England). 2016;11:13. doi: 10.1186/s13014-016-0593-y. PubMed PMID: PMC4736109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18. Morrison J, Hood R, Yin F-F, Salama JK, Kirkpatrick J, Adamson J. Is a single isocenter sufficient for volumetric modulated arc therapy radiosurgery when multiple intracranial metastases are spatially dispersed? Medical Dosimetry. 2016;41(4):285-9. doi: https://doi.org/10.1016/j.meddos.2016.06.007. [DOI] [PubMed] [Google Scholar]
- 19. Chang J, Kamil MY, Jiang K, Margie H, Ashwatha N. Effect of MLC Leaf Width and PTV Margin on the Treatment Planning of Intensity-Modulated Stereotactic Radiosurgery (IMSRS) or Radiotherapy (IMSRT). Medical Dosimetry. 2009;34(2):110-6. PubMed PMID: S0958-3947(08)00084-8. [DOI] [PubMed] [Google Scholar]