Impact of number of co-existing rotors and inter-electrode distance on accuracy of rotor localization

Abstract

Background

Conflicting evidence exists on the efficacy of focal impulse and rotor modulation on atrial fibrillation ablation. A potential explanation is inaccurate rotor localization from multiple rotors coexistence and a relatively large (9–11 mm) inter-electrode distance (IED) of the multi-electrode basket catheter.

Methods and results

We studied a numerical model of cardiac action potential to reproduce one through seven rotors in a two-dimensional lattice. We estimated rotor location using phase singularity, Shannon entropy and dominant frequency. We then spatially downsampled the time series to create IEDs of 2–30 mm. The error of rotor localization was measured with reference to the dynamics of phase singularity at the original spatial resolution (IED = 1 mm). IED has a significant impact on the error using all the methods. When only one rotor is present, the error increases exponentially as a function of IED. At the clinical IED of 10 mm, the error is 3.8 mm (phase singularity), 3.7 mm (dominant frequency), and 11.8 mm (Shannon entropy). When there are more than one rotors, the error of rotor localization increases 10-fold. The error based on the phase singularity method at the clinical IED of 10 mm ranges from 30.0 mm (two rotors) to 96.1 mm (five rotors).

Conclusions

The magnitude of error of rotor localization using a clinically available basket catheter, in the presence of multiple rotors might be high enough to impact the accuracy of targeting during AF ablation. Improvement of catheter design and development of high-density mapping catheters may improve clinical outcomes of FIRM-guided AF ablation.

Introduction

Spiral waves have been proposed to be drivers of atrial fibrillation (AF) [1,2], polymorphic ventricular tachycardia (VT) [3], and ventricular fibrillation (VF) [2,4]. Spiral waves result from an intrinsic property of the myocardium as a continuous, excitable system, to sustain high-frequency vortices in two dimensions (2-D), or vortex filaments in three dimensions (3-D) that are triggered by electrical stimuli during the vulnerable period [5]. The ‘rotor’ of a spiral wave is a rotation center from which a 2-D spiral wave of excitation rotates outward. The dynamics of rotors are determined by complex interactions between multiple factors, including ionic currents [6], action potential duration restitution properties, conduction velocity restitution properties, wavefront curvature of spiral waves, heterogeneity and anisotropy of the media, and coexisting rotors [7,8].

Rotor mapping and targeting using focal impulse and rotor modulation (FIRM) is one of the most well-studied approaches to catheter ablation of persistent AF [9] and VF [10]. Several mechanisms have been proposed as to how focal ablation of the rotor region results in AF termination [11]. However, clinical evidence is conflicting. Early clinical trials of rotor mapping in AF ablation showed promising results [9,12,13]. The results of early clinical trials, have not been replicated in recent studies [14–17]. In addition, there is no spatial correlation between rotors identified clinically and the underlying myocardial scar tissue [18,19]. One potential explanation to account for the apparent contradiction is an error associated with spatial localization of rotors using currently available mapping technologies. Another potential explanation is that human AF is sustained by electrical activation of different cycle lengths emanating from foci and breakthrough sites [20–22].

The standard methods to identify rotors include phase mapping [2], dominant frequency [23], and Shannon entropy [24,25]. In phase mapping, the electrograms in each region are mapped to a phase from −π to +π, and a rotor can be defined as a phase singularity [26] around which the phase progresses through a complete cycle from −π to +π [27]. A stationary rotor trajectory called a ‘core’ of spiral waves can also be localized as the region with the highest frequency of the electrogram called dominant frequency (DF), caused by the small path length of the rotor trajectory [1,23]. The Shannon entropy [28] of the electrogram localizes the core of spiral waves by quantifying the probability distribution of electrographic amplitudes [24]. These methods allow accurate detection of rotors in experimental (e.g. optical mapping) and simulation settings (e.g. finite element modeling) but require high spatial resolution. In contrast, the multi-electrode catheters used clinically to detect rotors have limited spatial resolution with an inter-electrode distance (IED) of 9–11 mm, which is considerably larger than the wavefront width (1–3 mm) [29,30]. Therefore, the representation of equiphase lines in phase mapping requires extensive interpolation to cover the large unexplored areas. This could erroneously join spatial points that are excited at the same time by phase mapping but actually belong to different wavefronts. In addition, interpolated equiphase lines may connect spatial points that have the same instantaneous phase value, but could belong to completely different equiphase lines.

In this study, we evaluated the impact of IED on the accuracy of rotor localization using standard methods, including phase singularity, dominant frequency and Shannon entropy in a numerical model of cardiac tissue. We tested the hypothesis that an error associated with spatial localization of the rotor or the rotor trajectory (core) increases with increasing IED, and this increase is larger when more than one rotors are present.

Materials and methods

Please refer to the Supplemental Methods section in the Supplemental Material for detailed methods. We performed data analysis using MATLAB R2017a (MathWorks Inc., Natick, MA).

Simulation of spiral waves

We simulated a system of a 2-D 12 × 12 cm² isotropic lattice of cardiac tissue using the Rogers-McCulloch model to represent cardiac action potential. The Rogers-McCulloch model accurately reproduces several important properties of cardiac tissue such as slowed conduction velocity, unidirectional block due to wavefront curvature, and spiral waves [31]. We converted the transmembrane potential to unipolar and bipolar voltage signal (see Supplemental Methods for details). The original spatial resolution is 1 × 1 mm². We simulated one through seven coexisting spiral waves with a time step of 0.063 msec, which was subsequently down-sampled at a sampling frequency of 500 Hz to reflect realistic measurements in human clinical electrophysiology studies [32]. This resulted in seven separate time series of one through seven coexisting spiral waves for a total duration of 10 s. We chose the observation time window of 10 s according to how focal FIRM localizes the rotor. FIRM uses ~50 cycles of spiral wave to localize the rotor, and with the cycle length of 120–240 msec (250–500 bpm), the observation window required to localize the rotor is 6–12 s [33].

Phase singularity

We estimated phase singularity using the instantaneous phase of the unipolar voltage signal time series (see Supplemental Methods for details). The dynamics of phase singularity at the original spatial resolution (IED = 1 mm) with each number of spiral waves served as the reference standard against which the error was calculated.

Dominant frequency

We estimated the dominant frequency on bipolar voltage signals. We rectified bipolar signal and then normalized it by subtracting its mean value. We subsequently filtered frequencies <3 Hz and >15 Hz using a bandpass finite impulse response (FIR) filter. We then applied a Hanning window to attenuate the effect of abrupt changes in time domain at the beginning and end of the time series [34,35]. Subsequently we performed a discrete Fourier transform to obtain the frequency spectrum of the time series. Dominant frequency is defined as the maximal frequency of the spectrum in each cell [1,35,36] (see Supplemental Methods for details).

Shannon entropy

For each mesh node, the bipolar voltage signal was binned according to its amplitude with bins of fixed amplitude 0.01 AU. For each bin, the relative probability density was defined as the number of counts in an amplitude bin divided by the sum of bin counts in all bins. Using this framework, one can compute the Shannon entropy (in bits) of each time-series process (see Supplemental Methods for details).

Error of rotor localization as a function of inter-electrode distance

To evaluate the impact of IED on spatial localization of rotors, we spatially downsampled the lattice (IED = 1 mm) in 6 different ways such that IED = 2, 4, 8, 10, 15, and 30 mm. We then linearly interpolated the lattice to maintain the same number of cells as the original lattice (120 × 120). We applied phase singularity, dominant frequency and Shannon entropy to localize the rotor or the rotor trajectory (core) in the interpolated lattice, just as in the clinical settings. For each IED, we defined the error of rotor localization (in mm) as the 2-D Euclidian distance between the center of mass of the estimated core and that of the reference standard. The reference standard is the center of mass of each rotor core, estimated by the phase singularity method, at the original spatial resolution (inter-electrode distance, IED = 1 mm). When more than one rotors are present, we defined the error of rotor localization by phase singularity, as the maximum 2-D Euclidian distance between the center of mass of each estimated core and that of the nearest reference standard. Since dominant frequency and Shannon entropy are designed to identify the “mother rotor” with the peak values of respective indices, when more than one rotors are present, we define the error of rotor localization as the 2-D Euclidian distance between the center of mass of the estimated core and that of the reference standard of the nearest core.

Sensitivity analysis

To address a potential impact of sampling frequency on rotor localization, we reproduced the same time series at a sampling frequency of 1 kHz with 1–7 spiral waves and the same duration (in seconds) as the original time series recorded at 500 Hz. We conducted an additional error analysis of rotor localization with all the three methods described above using the time series recorded at a sampling frequency of 1 kHz.

Results

Spiral waves

A snapshot of spiral waves is shown in Fig. 1 (unipolar voltage signal) and in Supplemental Fig. 1 (bipolar voltage signal). Video clips of the spiral waves are available on the Supplemental material (Supplemental Videos 1–7). For IEDs up to 4 mm there is essentially no distortion of the spiral wave contours. At IED at 8 mm, spiral wave contours become blurry but the overall spiral wave shape is preserved. However, at IED of 10 mm (Fig. 1, 5th column), which is similar to the IED of the clinically used basket catheter (9–11 mm), identification of the correct number of rotors becomes challenging. For example, the number of rotors is underestimated when five or more rotors are present. At IED of 15 and 30 mm, the number of rotors is further underestimated. Geometrical smoothing makes visual identification of spiral waves challenging.

Fig. 1.

Snapshots of spiral waves. Reconstruction of one (top row) through seven spiral waves (bottom row) identified by each inter-electrode distance (1, 2, 4, 8, 10, 15, and 30 mm) in a model of cardiac tissue. The color represents unipolar voltage signal, derived from normalized transmembrane potentials, in an arbitrary unit.

Phase singularity

The rotor trajectories identified by phase singularity are shown in Fig. 2, where each white spatial point represents the rotor at each time point. Video clips of the phase maps are available on the Supplemental material (Supplemental Videos 8–14). Overall, the rotor trajectory is practically undistorted for IED up to 4 mm. For IED of 8 and 10 there is distortion of rotor trajectories but the overall trajectory morphology is preserved. For IED of 15 and 30 mm the trajectory is entirely distorted. Increasing IED higher than 10 mm resulted in detection of synthesized phase singularities that may be inappropriately identified as rotors (red closed arrow). These phase singularities do not represent a true rotor but are artifacts introduced by interpolation and geometrical smoothing.

Fig. 2.

Rotor localization by phase singularity. The rows represent the number of rotors (one through seven), and the columns represent the inter-electrode distance (1, 2, 4, 8, 10, 15, and 30 mm). When one rotor is present (1st row, Fig. 2), the rotor follows a circular and relatively stationary core (closed arrow). When two rotors are present (2st row, Fig. 2), they drift by repelling each other; one rotor drifting from 9 o’clock to 12 o’clock (open arrow), and the other rotor drifting from 3 o’clock to 6 o’clock within the lattice (closed arrow). This occurs since when more than one rotors in the medium and the rotors are not too close to each other, they divide the medium to domains of influence. The boundaries of the domains behave similar to no-flux boundaries. Since these internal quasi-boundary is close enough to the rotor, it affect its drift in a similar way that a real boundary does. Of note, the reverse L-shaped trajectory of the latter rotor represents an artificial impact determined by the no-flux boundary condition of the model. When three rotors are present (3rd row, Fig. 2), they also repel with each other, with mechanism similar to what described above, but exhibit more complex behaviors. One rotor is pushed away in the left upper quadrant of the lattice following a dense stationary trajectory (open arrow), while the other two rotors draw a similar flower-like co-orbit but π out of phase (closed arrows). When four or more rotors are present (4th–7th row, Fig. 2), the rotors follow complex trajectories that can be either dense stationary or drifting helically in a circular fashion. For IED higher than 10 mm synthesized phase singularities are detected that may be inappropriately identified as rotors (red closed arrow). See text for details.

Dominant frequency

Dominant frequency maps are shown in Fig. 3. When one rotor is present (1st row, Fig. 3), for IED of 1–30 mm dominant frequency is distributed evenly on the lattice and is highest at the site of the core (shown in green and red, closed arrow). When two rotors are present (2nd row, Fig. 3), dominant frequency is higher at the area of the rotor trajectory for IEDs up to 15 mm (shown in light blue, closed arrow). For an IED of 30 mm there is only one area of highest dominant frequency in the proximity of the rotor that is located on the lower half of the lattice (shown in orange, open arrow). For more than three rotors (3rd–7th row, Fig. 3), the regions of high dominant frequency are detected in the proximity of rotor trajectory. However, the region of global dominant frequency maxima does not necessarily coincide with the core location.

Fig. 3.

Rotor localization by dominant frequency. The rows represent the number of rotors (one through seven), and the columns represent the inter-electrode distance (1, 2, 4, 8, 10, 15, and 30 mm). See text for details.

Shannon entropy

Shannon entropy maps are shown in Fig. 4. Overall, the areas of maximal Shannon entropy are practically undistorted for IED up to 4 mm. For IED of 8, 10 and 15 mm there is distortion of the areas of maximal Shannon entropy but their overall morphology is preserved. For IED of 30 mm the areas of maximal Shannon entropy are entirely distorted.

Fig. 4.

Rotor localization by Shannon entropy. The rows represent the number of rotors (one through seven), and the columns represent the inter-electrode distance (1, 2, 4, 8, 10, 15, and 30 mm). When one rotor is present (1st row, Fig. 4), Shannon entropy shows a characteristic spatial profile with low values inside the spiral wave core (shown in black, closed arrow) and highest Shannon entropy at the pivot of the core (shown in orange, open arrow). Low Shannon entropy within the core reflects no electrographic activity beyond the maximum curvature of wave propagation. High Shannon entropy at the rotor pivot represents high directional information content encoded in the electrocardiographic signals. When two rotors are present (2nd row, Fig. 4), low Shannon entropy occurs at the sites of core trajectories (shown in black, closed arrows) and high Shannon entropy at the pivot (shown in orange, open arrows). Similar patterns occur when more than two rotors are present. For example, when three rotors are present (3rd row, Fig. 4), the rotor in the left upper quadrant of the lattice demonstrates low Shannon entropy at the center of the core (shown in orange, closed white arrow) and high Shannon entropy at the core trajectory pivot (shown in bright yellow, open white arrow). However, for the other two rotors that follow a similar flower-like co-orbit, there is low Shannon entropy in the center of the combined rotor trajectory (shown in black, closed teal arrow) and high Shannon entropy in the pivot zone (sown in orange, open teal arrows). See text for details.

Error of rotor localization as a function of inter-electrode distance

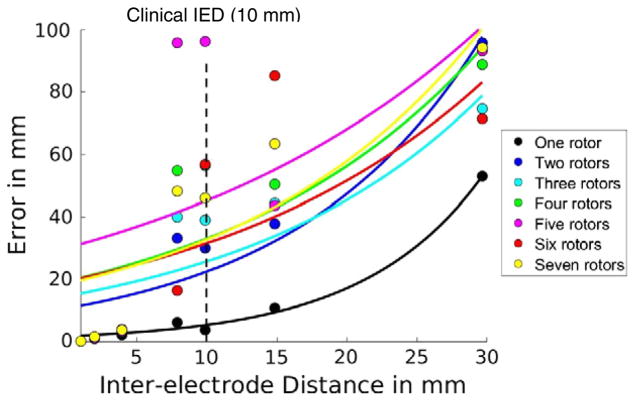
The error of rotor localization is summarized in Table 1. The error of rotor localization using phase singularity increases exponentially with increasing IED, with reference to the dynamics of phase singularity at the original spatial resolution (IED = 1 mm) (Fig. 5). When one rotor is present, for an IED of 10 mm, which is similar to the IED of the clinically used basket catheter, the error is 3.8 mm. As IED increases further, the error goes up to 52.8 mm at IED of 30 mm. When more than one rotors are present, the error increases at least ten-fold. At clinical IED of 10 mm, the error ranges between 30.0 mm (two rotors) and 96.1 mm (five rotors). As IED increases to 15 mm and 30 mm, the error goes up to 52.8–95.8 mm.

Table 1.

Error of rotor localization as a function of inter-electrode distance.

Method	Inter-electrode distance (mm)
	1	2	4	8	10	15	30
Phase singularity	Reference	1.2 ± 0.3	3.2 ± 0.6	42.0 ± 27.0	46.8 ± 26.2	47.8 ± 21.2	81.4 ± 14.8
Dominant frequency	10.6 ± 5.7	13.6 ± 7.0	11.9 ± 6.0	15.0 ± 8.4	13.5 ± 6.9	13.3 ± 9.0	28.3 ± 17.9
Shannon entropy	8.6 ± 4.5	11.2 ± 4.1	11.2 ± 3.0	14.0 ± 2.7	11.3 ± 3.3	20.7 ± 6.7	25.1 ± 11.6

Values are mean ± standard deviation. The error of rotor localization (in mm) is defined as the maximum 2-D Euclidian distance between the center of mass of the estimated core and that of the reference standard, which is the dynamics of phase singularity at the original spatial resolution (inter-electrode distance, IED = 1 mm) with each number of spiral waves. Clinical IED corresponds to IED = 10 mm.

Significance of bold emphasis highlighted the error in rotor localization for the clinically relevant inter-electrode distance.

Fig. 5.

Error of rotor localization by phase singularity. The x-axis is the inter-electrode distance and the y-axis is the error in mm. Each color corresponds to the same number of rotors.

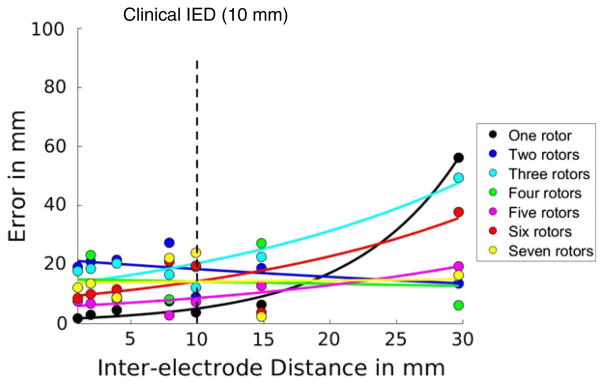
The error of rotor localization using dominant frequency at the original spatial resolution (IED = 1 mm) is 1.6 mm when one rotor is present. It increases exponentially with increasing IED and behaves overall similarly to the errors using phase singularity. At clinical IED of 10 mm, the error is 3.7 mm. For the highest IED (=30 mm), the error is 56.2 mm. When more than two rotors are present, error at the original spatial resolution (IED = 1) ranges between 7.5 and 19.1 mm. However, when two or more rotors are present, the error does not consistently increase. This is because dominant frequency fails to identify individual rotors but simply the one with the global maximal value within the lattice. At clinical IED of 10 mm, the error is 7.3–24.0 mm when two to seven rotors are present (Fig. 6).

Fig. 6.

Error of rotor localization by dominant frequency. The x-axis is the inter-electrode distance and the y-axis is the error in mm. Each color corresponds to the same number of rotors.

The error of rotor localization using Shannon entropy at the original spatial resolution (IED = 1 mm) is 9.7 mm when one rotor is present. The error remains relatively unchanged with increasing IED. At clinical IED of 10 mm, the error is 11.8 mm. With increasing IED up to 15 mm the region of the highest Shannon entropy is split into smaller regions of high Shannon entropy, but these smaller regions remain approximately near the rotor trajectory. At IED of 30 mm, the error is 5.5 mm, but the association between the high Shannon entropy region and the rotor trajectory is lost because of low spatial resolution. When more than one rotors are present the error at the original spatial resolution (IED = 1) ranges between 0.6 and 14.7 mm. The error increases exponentially with increasing IED but with varying rates. This is because Shannon entropy fails to identify individual rotors but simply the one with the global maximal value within the lattice. At clinical IED of 10 mm, the error is 6.2–15.4 mm when two to seven rotors are present (Fig. 7).

Fig. 7.

Error of rotor localization by Shannon entropy. The x-axis is the inter-electrode distance and the y-axis is the error in mm. Each color corresponds to the same number of rotors.

Sensitivity analysis

Rotor identification with all three methods was essentially identical in analysis of both 500 Hz and 1 kHz signals. The error of rotor localization for increasing IED, of 1 kHz signals, was similar to that of the 500 Hz signal (Supplemental Fig. 4, Supplemental Table 1). For the clinically relevant IED of 10 mm the mean error for rotor localization is 40.3 ± 16.8 mm with the phase singularity method, 19.2 ± 7.3 mm with the dominant frequency and 12.0 ± 4.2 with the Shannon entropy method.

Discussion

Main findings

We find that IED and number of coexisting rotors have a significant impact on the error of rotor localization using all the methods studied, including phase singularity, dominant frequency and Shannon entropy. When there are more than one rotors, the error of rotor localization by the phase singularity method is at least ten-fold higher. To our knowledge, this is the first study to systematically evaluate the effect of number of coexisting rotors on accuracy of rotor localization, by phase singularity, dominant frequency and Shannon entropy as a function of IED in two dimensions.

Our results are consistent with, and expand previous ex vivo and in silico studies. In ex vivo Langendorff perfused rabbit hearts, increasing IED from 2 to 8 mm resulted in distortion of rotor trajectory, when compared to high resolution optical mapping (pixel resolution of 0.16 mm). Increase of IED resulted in detection of fewer rotors, as well as inappropriate detection of pseudo rotors [37]. In three-dimensional AF simulation studies, accurate detection and tracking of rotors was feasible with high-density mapping catheters but not with low-resolution basket catheter. The minimum resolution required to accurately identify rotors was a linear function of spiral wave wavelength. For spiral wave wavelengths of 25–60 mm, the minimum IED ranged from 10 to 25 mm [38]. Nagashima et al., evaluated the impact of IED on the accuracy of dominant frequency localization using a linear octapolar catheter [39]. They found that, consistent with our findings, the absolute value of dominant frequency did not change with increasing IEDs (2, 5, 8, 11 and 14 mm), but the error of dominant frequency localization was smaller with narrower IEDs. Hwang et al., used a finite element model of AF to evaluate the accuracy of the dominant frequency and the Shannon entropy methods with reference to the phase singularity method. They showed that both methods accurately identified rotor locations, however, consistent with our findings, Shannon entropy was less accurate in localizing rotors [40]. None of these studies assesses the impact of number of coexisting rotors on error of rotor localization.

Inter-electrode distance and accuracy of ablation targeting

Our findings suggest that the magnitude of error of rotor localization using a clinically available multi-electrode basket catheter, when more than one rotors is present, is high enough to impact the accuracy of targeting during catheter ablation of AF. IED of the multi-electrode mapping catheter for FIRM-guided ablation of AF is 9–11 mm. Since the tissue contact of the basket catheter electrodes is relatively poor [14] with dynamic cardiac motion, actual sampling distance between two adjacent electrodes is likely to be even larger. When only one rotor is present, the error of rotor localization at the clinical IED of 10 mm, using either the phase singularity method (3.8 mm, Fig. 5), or the dominant frequency method (3.7 mm, Fig. 6) is just under the size of the ablation lesion. For example, the diameter of an open-irrigated radiofrequency ablation lesion ranges from 6.1–8.0 mm (35 W × 30 s) to 6.9–8.7 mm (35 W × 60 s) [41,42]. However, the error using the Shannon entropy method (11.8 mm, Fig. 7) is larger than the ablation lesion size, suggesting that accurate targeting might not possible. However, when more than one rotors are present, as in most cases of AF [9,43], the error of rotor localization at the clinical IED of 10 mm with the phase singularity method increases up to 30–96 mm. This is 5–16 times the size of an ablation lesion. The error at the clinical IED of 10 mm by dominant frequency and Shannon entropy is also significantly larger than an ablation lesion size.

Clinical implications

Our findings may account for the discrepancy among different studies evaluating the efficacy of FIRM-guided ablation of AF. The participants of the studies that report efficacy of FIRM-guided AF ablation, had fewer rotors (2.3 ± 0.9 rotors per patient) [9,43,44] than those in the studies that report lack of efficacy (2.3 ± 0.9, 2.6 ± 1.2, 3.0 ± 1.1 and 4.0 ± 1.2 rotors per patient) [14–17]. This indicates that in positive studies more patients had only one rotor, where the error of rotor localization is comparable to the ablation lesion size. In contrast, in negative studies there were more patients with more than one rotors, where the error of rotor localization could go up to 5–16 times the size of the ablation lesion. One potential solution to improve the clinical outcomes of rotor mapping and targeting while minimizing unnecessary tissue damage is a better mapping catheter design. Based on our results, IED of 4 mm would limit the error of rotor localization within an ablation lesion size, even when multiple rotors are present (3.2 ± 0.6 mm with the phase singularity method, Table 1). Practical deployment and recording system issues associated with the multi-electrode catheter design should be investigated in future studies.

Limitations

Several limitations need to be addressed before our findings are extrapolated to clinical settings. First, we used a simplified model of cardiac action potential (the Rogers-McCulloch model) with a homogeneous and isotropic lattice. Since the rotor dynamics in the myocardial tissue that is characterized by heterogeneity and anisotropy would be more complex, our analysis could have underestimated the error of rotor localization. Ex vivo studies [45] and numerical models of the heart show that anchoring of the rotors may occur in areas of tissue heterogeneity [46] and fibrosis [47], suggesting that stability of rotors may indicate the underlying substrate to perpetuate AF. However, clinical studies show that rotors drift in a large area of the atria, mostly in non-fibrotic regions [48]. In addition, there is no spatial correlation between rotors and the underlying fibrosis [18,19]. Second, we simulated spiral waves and rotors on a 2-D square lattice. This setup could have missed important 3-D features of cardiac dynamics arising from scroll waves and filaments. However, since clinical measurements of cardiac dynamics using the multi-electrode basket catheter are essentially 2-D, we believe that the current 2-D setup is adequate to answer questions pertinent to our hypothesis. Third, the Rogers-McCulloch model that we used in this study is a simplified model of ventricular myocardium and, as a result, some parameters, such as the specific values of DF, might be different from those of typical human atrial fibrillation. However, the specific values of DF do not impact the aim, the results, or the conclusion of our study to evaluate the error of rotor localization as a function of inter-electrode distance (IED). Last, we used 10-s time series recordings to evaluate the error of rotor localization. This relatively narrow window could have underestimated the error because rotors tend to drift and further complicate the trajectory when observed for longer periods of time [49].

Conclusions

IED and number of coexisting rotors have a significant impact on the error of rotor localization using phase singularity, dominant frequency and Shannon entropy. When more than one rotors are present, the magnitude of error of rotor localization using a clinically available multi-electrode basket catheter might be high enough to impact the accuracy of targeting during catheter ablation of AF. These findings may account for the discrepancy among different studies evaluating the efficacy of FIRM-guided ablation of AF. Improvement of catheter design and development of high-density mapping catheters could improve clinical outcomes of FIRM-guided AF ablation.

Supplementary data to this article can be found online at https://doi.org/10.1016/j.jelectrocard.2017.08.032.