On the contributing role of the transmembrane domain for subunit-specific sensitivity of integrin activation

Abstract

Integrins are α/β heterodimeric transmembrane adhesion receptors. Evidence exists that their transmembrane domain (TMD) separates upon activation. Subunit-specific differences in activation sensitivity of integrins were reported. However, whether sequence variations in the TMD lead to differential TMD association has remained elusive. Here, we show by molecular dynamics simulations and association free energy calculations on TMDs of integrin α_IIbβ₃, α_vβ₃, and α₅β₁ that α_IIbβ₃ TMD is most stably associated; this difference is related to interaction differences across the TMDs. The order of TMD association stability is paralleled by the basal activity of these integrins, which suggests that TMD differences can have a decisive effect on integrin conformational free energies. We also identified a specific order of clasp disintegration upon TMD dissociation, which suggests that the closed state of integrins may comprise several microstates. Our results provide unprecedented insights into a possibly contributing role of TMD towards subunit-specific sensitivity of integrin activation.

Introduction

Integrins are a major class of heterodimeric adhesion receptors consisting of α and β subunits¹ and are involved in the regulation of many biological events². Each subunit is formed by a large extracellular domain (ectodomain) connected to a short cytoplasmic tail through a single transmembrane domain (TMD)³. In providing a physical link between the exterior and the interior of the cell, the TMD serves as a translator of mechanical and biochemical signals in both directions across the plasma membrane, leading to inside-out and outside-in signaling^4–6. TMDs are directly involved in the mechanism of integrin activation⁷ in that the two transmembrane (TM) segments associate in the resting state^8–10 and dissociate upon activation^11–14. Structural features of the integrin TMD were revealed by nuclear magnetic resonance (NMR) structures^15–17, biochemical data^18,19, and electron microscopy^20–22. Two structural elements, the inner and outer membrane clasps (IMC and OMC)²³, were recognized as principal mediators of TMD assembly²⁴, together with electrostatic interactions in the membrane-proximal region. However, despite these unifying principles, there is also evidence for specific ways of helix-helix association among different isoforms²⁵, and it has remained unclear if and how these differences are linked to the subunit-specific sensitivity of integrin activation^26,27: Integrin α_IIbβ₃ has been described as basally inactive, in contrast to α_vβ₃, which was found to be in the active state by default in certain cell types^28,29, and β₁ integrins, which are considered to be basally active²⁶, with integrin α₅β₁ being among the most conformationally flexible integrins containing β₁²⁷. In addition, contradicting findings of NMR^24,30 and in vitro³¹ versus in vivo³² studies with respect to a salt bridge interaction between α_IIb-R995 and β₃-D723 might also be related to specific TMD associations (see below for details).

The TMD of a subunit is formed by a short α-helix³³, and two such TMDs are arranged in a right-handed coiled-coil conformation¹⁶ in the resting state of the integrin^9,10,34. The structure of the TMD of α_IIbβ₃ integrin¹⁵ revealed that the TM and membrane-proximal regions of the β₃ subunit form a continuous helical structure that is tilted by ~25° with respect to the membrane normal^16,17. In contrast, the α_IIb subunit is oriented in parallel to the membrane normal, breaks at G991, and bents towards the β₃ TMD. This allows the dimer to be stabilized by the OMC and IMC²³. The former is a GXXXG-like motif ³⁵, while the latter is a highly conserved GFFKR motif ³⁶, with the two Phe residues found in all α subunits³⁶. Mutational studies¹³, disulphide scanning¹¹ and Leu scanning¹¹ experiments confirmed the importance of the OMC, whose alteration prevents correct helix packing and abolishes helix association³⁶. However, different compositions of the GXXXG motif are found in α subunits, which makes it reasonable to hypothesize that the different OMC interfaces contribute to differential integrin activation. Likewise, the importance of the IMC, and, in particular, the two conserved Phe residues, in maintaining correct TMD packing and restraining integrin in the resting state has been shown^31,37. In contrast, it has remained controversial whether α_IIb-F992 engages β₃-K716 in hydrogen bond formation to support IMC formation¹⁷, or whether K716 “snorkels” towards the lipid head groups³⁸. Moreover, NMR spectroscopy²⁴ revealed the presence of a salt bridge between α_IIb-R995 and β₃-D723 at the membrane-proximal region, in immediate vicinity of the IMC, whose functional role in restraining integrin in the inactive state has been demonstrated^{24,30,39–41}. However, NMR structures in which both α_IIb-F992 and α_IIb-R995 point away from the β₃ subunit, thus, not making any interactions with the β₃ subunit, have also been determined³⁰. Likewise, mutational studies in which the breaking of the R995-D723 salt bridge did not cause immediate integrin activation were reported^14,39.

In order to provide insights at the atomistic level as to a potential influence of the TMD on the subunit-specific sensitivity of integrin activation, including the role of interactions across the IMC and OMC, here, we performed equilibrium molecular dynamics (MD) simulations in an explicit membrane environment of in total 9 μs length on the associated TMDs of integrins α_IIbβ₃, α_vβ₃, and α₅β₁, respectively, and potential of mean force (PMF) computations of TMD association of in total 3.5 μs sampling time, from which we derived association free energies. Our results show that the TMD of integrin α_IIbβ₃ is most stably associated compared to α_vβ₃ and α₅β₁. We relate these differences to particular interactions across the TMDs, with a focus on the different OMC compositions and an “OMC before IMC” order of clasp disintegration found for TMD dissociation. Our results provide unprecedentedly detailed and comparative insights into a possibly contributing role of the TMD towards subunit-specific sensitivity of integrin activation.

Results

Structural dynamics of the α_IIbβ₃, α_vβ₃, and α₅β₁ TMDs

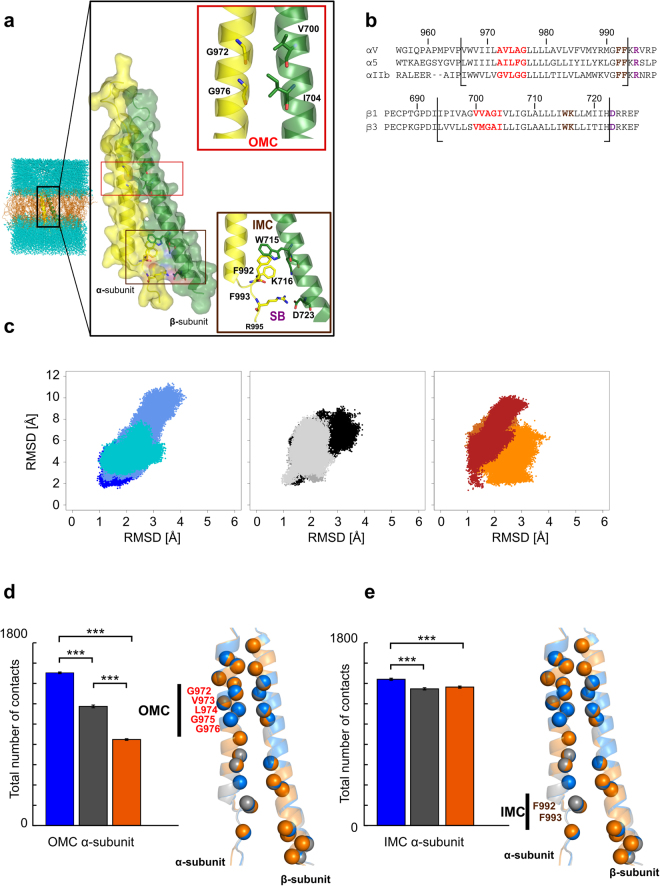
In order to investigate at an atomistic level possible subunit-specific differences in the association of TMDs of integrins α_IIbβ₃, α_vβ₃, and α₅β₁, the three TMDs were subjected to all-atom MD simulations in an explicit membrane and solvent environment (Fig. 1a). Prior to that, we generated homology models of α_vβ₃ and α₅β₁ TMDs using the NMR structure of α_IIbβ₃ TMD (PDB ID 2K9J)¹⁵ as a template. To estimate the quality of the models, we used the QMEANBrane version⁴² of the QMEAN scoring function implemented in the QMEAN server⁴³. QMEANBrane employs specifically trained potentials for three different segments (membrane, interface and soluble) in a transmembrane protein model to determine local (i.e., per residue) absolute quality estimates on the basis of a single model. With 1.0 as the optimal score, we found local scores of ~0.8 for the residues embedded in the membrane and ~0.6–0.8 when considering the overall structures (Fig. S1). The NMR structure showed very similar QMEANBrane scores, suggesting a sufficient local structural quality of the models. Sequence identities of 40% to 65% between respective template and target sequences furthermore suggest that the global folds are conserved. Note that we generally refer to the simulated systems as “TMD” here, although the actual TM region is prepended by 9–11 (8) residues of the linker to the calf-2 (β-tail) domain at the N-terminal end of the α (β) subunit, and appended by 5 (6) residues of the respective cytosolic domains at the C-terminal ends (Fig. 1b). For clarity, we furthermore only refer to the sequence numbering of integrin α_IIbβ₃ below (Fig. 1b).

Figure 1.

Structural integrity of the membrane-embedded helices throughout the MD simulations and contacts across the interface. (a) Exemplary simulation box generated to perform MD simulations including the NMR structure of α_IIbβ₃ TMD (PDB ID 2K9J; cartoon and surface representation) with the position of the OMC (red box) and IMC (brown box) indicated; phospholipids are shown as orange sticks, and water layers as blue spheres. Close-up views of the box contents show essential residues mediating the clasps: α_IIb-G972/G976 and β₃-V700/I704 for the OMC, α_IIb-F992/F993/R995 and β₃-W715/K716/D723 for the IMC plus the putative salt bridge. (b) Sequence alignment of the α_IIbβ₃, α_vβ₃, α₅β₁ TMD sequences used to generate the homology models. GXXXG and GFFKR motifs are highlighted in red and brown, respectively, and R995/D723 residues in purple. Black bars indicate the TMD borders as reported in ref.⁴⁵. (c) Two dimensional histograms of the RMSD values of all C_α atoms (ordinate values) and only those that are embedded in the membrane (abscissa values) (range of residues considered: P996-V1015 and D718-I747) calculated over three MD simulations. Blue, cornflowerblue, turquoiseblue colored dots represent α_IIbβ₃ (MD simulations 1, 2 and 3); darkgrey, black, lightgrey α_vβ₃; chocolate, orange, firebrick α₅β₁. (d,e) Histograms of the total number of overall contacts per residue at the OMC and IMC averaged over three MD simulations, with error bars showing the standard error of the mean (SEM; eq. 6) and stars indicating the statistical significance (see Methods section for definition). Here, only residues of the α subunit are shown (numbering refers to the α_IIb subunit). On the right of the plots, a superimposition of the α_IIbβ₃, α_vβ₃, and α₅β₁ TMDs in blue, grey, and orange, respectively, is shown. The C_α atoms of residues considered in the contact analysis are indicated as spheres, and the residues of the α subunit considered in the analyses are labeled.

Using the three TMD structures as starting structures, we performed three independent MD simulations of 1 μs length for each system, yielding in total 9 μs of simulation time. The structural variability was assessed in terms of root mean square deviations (RMSD) after a mass-weighted superimpositioning onto the respective starting structure. The RMSD of all C_α atoms, including those not embedded in the membrane, raises to values of ~7–10 Å. However, if only the TM region is considered, the RMSD amounts to ~2–4 Å (Fig. 1c). This data indicates that the structural integrity of the two TM helices remains intact throughout the MD simulations, whereas the TMD ends fray at about nine residues at either terminus of either helix. The finding that the overall configuration of the TMD remains intact during our simulations is congruent with a slow dissociation rate found for α_IIbβ₃ TMD⁴⁴. In agreement with our findings, NMR spectroscopy revealed a dynamically unstructured α_IIb linker⁴⁵. The convergence of the internal motions between independent MD simulations was assessed following ref.⁴⁶. In short, the overlap of histograms of principal component (PC) projections obtained in a pair-wise manner from each simulation for a given TMD system are looked at as a function of time (Fig. S2). The results reveal that the first three PCs are relatively well-converged after ~400 ns for α_IIbβ₃ TMD, whereas for α_vβ₃ and α₅β₁ TMDs it takes ~800 ns to reach a comparable level of convergence.

To conclude, RMSD values of membrane-embedded TMD parts generally below 4 Å reveal that both the secondary structure and overall configuration of the two TM helices remain intact throughout the MD simulations of all three TMDs. The convergence behavior of PC projections suggests larger and/or slower internal motions in α_vβ₃ and α₅β₁ TMDs than α_IIbβ₃ TMD.

Residue-wise analysis of contacts and mobility in the TMD interfaces

Next, we examined differences in the TMD topology of each system in terms of changes in the number of contacts present in the starting structure (“native contacts”) and those formed over the MD simulation time (“non-native contacts”). A contact is considered formed between the α and β subunits if any two atoms of two residues come closer than 7 Å⁴⁷. First, for globally comparing the three systems, we computed the average number of overall contacts. The total number of native contacts already present in the NMR structure of α_IIbβ₃ TMD (PDB ID 2K9J) is almost equal to that of the initial structure of α_vβ₃ TMD (6217 versus 6244), and only ~2% smaller than that of the initial structure of α₅β₁ TMD (6344). In contrast, compared to α_IIbβ₃, both α_vβ₃ and α₅β₁ reveal a highly significant reduction of overall contacts by ~10% (p < 0.0001) (Fig. S3) during the MD simulations. Second, from a list of residues conserved across the three α subunits and the contact map information, we extracted those residues accounting for the native and non-native contacts at the OMC and IMC interface between α and β subunit (Table S1). As to the former, compared to α_IIbβ₃ TMD, the overall average number of contacts is ~20% smaller in the α_vβ₃ TMD and ~40% smaller in the α₅β₁ TMD (Fig. 1d). Both differences are highly significant (p < 0.0001). As to the latter, compared to α_IIbβ₃ TMD, both α_vβ₃ and α₅β₁ TMDs reveal a significant reduction of overall contacts by ~10% (Fig. 1e) (p ≈ 0.003 and 0.006, respectively).

Furthermore, we computed residue-wise root mean square fluctuations (RMSF) as a measure of atomic mobility to identify local differences in the structural dynamics of the three TMD complexes, averaged over the respective three simulations. For both the α and β subunit, the α_IIbβ₃ TMD shows less pronounced residue motions, with the RMSF values of 60 out of 89 residues (~67%) being lower than those of α_vβ₃ and α₅β₁ (Table S2). To conclude, these results demonstrate on a per-residue level that the α_IIbβ₃ TMD forms generally more contacts across the TMD interface and shows less mobile residues in the TMD.

Subunit-specific differences in OMC and IMC distances

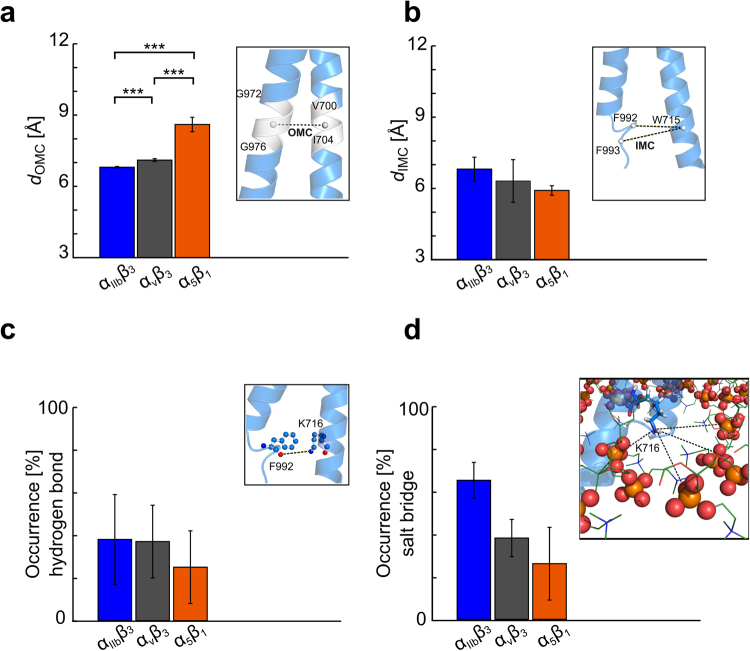
Both the OMC and IMC are considered necessary to maintain integrin in the low affinity state² (Fig. 1a). However, particularly in the OMC, each TMD has subunit-specific amino acids (Fig. 1b) that may be responsible for the above observed differences. The d_OMC (distance computed between the centers of mass (COM) of the C_α atoms of the GXXXG motif (G972-G976) on the α_IIb subunit and V700-I704 on the β₃ subunit) is 9.3 Å in the NMR structure of α_IIbβ₃ TMD (PDB ID 2K9J) and 7.3 Å in a structure based on Cys cross-linking results⁴⁸. The distance d_IMC computed as the minimal distance between the COMs of the aromatic rings of F992 or F993 on the α_IIb subunit and the aromatic ring of W715 on the β₃ subunit is 4.0 Å in the NMR structure and 5.4 Å in the structure based on Cys cross-linking results.

As to the MD simulations, first, the d_OMC averaged over three simulations is smaller by ~0.3 Å in the α_IIbβ₃ TMD (~6.8 Å, SEM ≈ 0.03 Å) than in the α_vβ₃ TMD (~7.1 Å, SEM ≈ 0.06 Å), and smaller by ~1.5 Å than in the α₅β₁ TMD (~8.4 Å, SEM ≈ 0.3 Å). All values are well in the range of inter-helical distances found for TM heterodimers containing an OMC-like structural motif⁴⁹. The differences are highly significant in all cases (p < 0.0001) (Fig. 2a, Table S3). Hence, the OMC interface is most compact in α_IIbβ₃ TMD, followed by α_vβ₃ and α₅β₁ TMDs. Second, the d_IMC averaged over three simulations remains below 7 Å in all cases: α_IIbβ₃ (~6.8 Å, SEM ≈ 0.5 Å), α_vβ₃ (~6.3 Å, SEM ≈ 0.9 Å) and α₅β₁ TMDs (~5.9 Å, SEM ≈ 0.2 Å) (Fig. 2b, Table S3). The differences are not significant (p ≈ 0.6 for α_IIbβ₃/α_vβ₃, ≈ 0.05 for α_IIbβ₃/α₅β₁, ≈ 0.5 for α_vβ₃/α₅β₁), however. Hence, we conclude that the IMC interface is equally maintained over the course of the MD simulations.

Figure 2.

Differences between interdomain interactions in α_IIbβ_3, α_vβ_3, and α₅β₁ TMDs. (a,b) Histograms of the distances d_OMC and d_IMC (see main text for definition) averaged over three MD simulations. From left to right, the α_IIbβ₃, α_vβ₃, and α₅β₁ TMDs are displayed in blue, grey, and orange, respectively. Within each plot, a close-up view of the NMR structure of α_IIbβ₃ TMD (PDB ID 2K9J) is colored in blue and indicates the analyzed distances (black dashed lines). White spheres indicate C_α atoms of the labeled amino acids. (c) Histogram of the mean relative occurrence of the hydrogen bond between K716_Nε and F992_O using a distance cutoff of 3.5 Å and an angle cutoff of 120°. Within the plot, a close-up view of the respective distance measured is shown (color code as in panel a). (d) Histogram of the mean relative occurrence of the salt bridge between K716_Nε and the oxygens of phospholipids head groups of the lower lipid leaflet applying a distance cutoff of 4 Å. Within the plot, a close-up view of the respective distance measured is shown, with the phospholipid head groups depicted as spheres. (a–d) Error bars show the SEM (eq. 5) and stars indicate the statistical difference (see Methods section for definition).

Subunit-specific interactions formed across the TMD interfaces

The IMC interface is adjacent to the membrane-proximal region, which is believed to be mainly stabilized by a salt bridge formed between α_IIb-R995 and β₃-D723². First, we computed the minimal distance between the atoms R995_Nη1/Nη2 and D723_Oδ1/Oδ2 for each system (Table 1). As next to R995 and D723, respectively, R997 is present on the α subunit and E726 on the β subunit, we also analyzed the minimal distances between atoms R995_Nη1/Nη2 and E726_Oε1/Oε2, R997_Nη1/Nη2 and D723_Oδ1/Oδ2, and R997_Nη1/Nη2 and E726_Oε1/Oε2 (Table 1; α₅β₁ integrin contains a Leu at position 997 such that the last two distances were not evaluated there). Then, to assess the frequency of occurrence of formed salt bridges, we applied a cutoff of 4 Å to the computed minimal distances, according to a previous study⁵⁰ (Table 1): 1) the R995-D723 salt bridge has the highest occupancy in the α_IIbβ₃ TMD (~58%), followed by the α_vβ₃ (~37%) and α₅β₁ TMDs (~39%). The differences between α_IIbβ₃ TMD and either α_vβ₃ or α₅β₁ TMDs are not statistically significant (p ≈ 0.3 for α_IIbβ₃/α_vβ₃, α_IIbβ₃/α₅β₁, and ≈ 0.9 for α_vβ₃/α₅β₁); 2) the R995-E726 salt bridge (the only alternative interaction that can be formed in α₅β₁) has the highest occupancy in the α₅β₁ TMD (~42%), followed by the α_IIbβ₃ (~33%) and α_vβ₃ TMDs (~39%). The differences are not significant (p ≈ 0.8 for α_IIbβ₃/α_vβ₃, α_IIbβ₃/α₅β₁, and ≈ 0.9 for α_vβ₃/α₅β₁); 3) the R997-D723 salt bridge is formed in both the α_IIbβ₃ (~47%) and α_vβ₃ TMDs (~48%) to a very similar extent (the difference is not significant (p ≈ 0.9)); 4) the R997-E726 salt bridge is formed to a lower extent in the α_IIbβ₃ (~17%) and α_vβ₃ TMDs (~31%), and the difference is not significant (p ≈ 0.4). To conclude, our results, in agreement with ref.²⁴, indicate that R995-D723 is not the only salt bridge that is formed across the TMD interface. In agreement with ref.⁵¹, the R995-D723 salt bridge dissociates intermittently, as indicated by occupancies ≪100%. However, the MD simulations reveal that, among all four possible salt bridges that can form in the membrane-proximal region, R995-D723 is the most prevalent interaction, followed by R995-E726, and R997-E726 is the least prevalent one.

Table 1.

Frequency of occurrence of the up to four salt bridges in the membrane-proximal region for each TMD system^[a].

Salt bridge	αIIbβ3 TMD			αvβ3 TMD			α5β1 TMD
	SimI	SimII	SimIII	SimI	SimII	SimIII	SimI	SimII	SimIII
R995-D723	47	92	35	57	8	46	14	66	38
	58 ± 6.7[b]			37 ± 14.8[b]			39 ± 15.0[b]
R995-E726	47	50	2	70	29	18	24	78	24
	33 ± 15.5[b]			39 ± 18.8[b]			42 ± 18.0[b]
R997-D723	23	95	23	84	52	7	—[c]	—[c]	—[c]
	47 ± 24.0[b]			48 ± 22.3[b]			—[c]
R997-E726	10	39	2	10	31	51	—[c]	—[c]	—[c]
	17 ± 11.2[b]			31 ± 11.8[b]			—[c]

^[a]In %.

^[b]Mean values and SEM (eq. 6), calculated over three MD simulations.

^[c]Interactions that cannot be formed in the TMD of integrin α₅β₁.

Subunit-specific contribution of K716 to the TMD stability

Finally, we investigated the behavior of K716, monitoring where the residue preferentially places its side chain, i.e., either as part of a hydrogen bond with F992 or by orienting the positive charge of N_ε towards the negatively charged head groups of the lipid bilayer³⁸. In the NMR structure of α_IIbβ₃ TMD (PDB ID 2K9J), the distance between N_ε of K716 and the carbonyl oxygen of F992 is 6.2 Å; in the structure based on Cys cross-linking results, it is 2.9 Å. During the three simulations of each system, the occupancy of the K716-F992 hydrogen bond was investigated applying a distance cutoff of 3.5 Å and an angle cutoff of 120°. On average, the hydrogen bond is formed in a similar manner in the α_IIbβ₃ (~38%) and α_vβ₃ TMDs (~37%), and to a lower extent in the α₅β₁ TMD (~25%) (Fig. 2c, Table S4). The differences between α_IIbβ₃ or α_vβ₃ TMDs with respect to α₅β₁ TMD result in p ≈ 0.6, respectively.

To evaluate the presence of electrostatic interactions between the K716 side chain and the head groups of lipids, first, we computed the minimal distance between N_ε of K716 and the nearest O atom of the phospholipid head groups from the lower lipid leaflet (d_snorkeling). Then, we applied a 4 Å cutoff to d_snorkeling and calculated the frequency of occurrence of a salt bridge. On average, the salt bridge is mainly formed in the α_IIbβ₃ TMD (~65%), followed by α_vβ₃ TMD (~38%), and to a lower extent in the α₅β₁ TMD (~26%) (Fig. 2d, Table S5). The differences between α_IIbβ₃ TMD with respect to α_vβ₃ or α₅β₁ TMDs result in p ≈ 0.08 and ≈ 0.1, while the difference between α_vβ₃ and α₅β₁ TMDs results in p ≈ 0.5. To conclude, the K716 sidechain is engaged in either a hydrogen bond across the TMD or a salt bridge with phospholipid head groups in the α_IIbβ₃ TMD (~100%), followed by α_vβ₃ (~75%) and α₅β₁ (~50%) TMDs, with the salt bridge being the more prevalent interaction in the case of α_IIbβ₃ TMD.

Configurational free energies of TM helix association

The above analyses strongly suggest that the TMDs of the integrin isoforms differ in their potential to associate. To corroborate these findings in an independent manner, we computed the configurational free energy (potential of mean force, PMF) of TM helix association using the distance between COMs of the sections of the α and β subunits embedded in the membrane as a reaction coordinate (referred to as d_COM-COM). The PMFs were computed using umbrella sampling⁵² along a pathway from the bound subunits to subunits where any pair of atoms between the two subunits is at least 10 Å apart, and WHAM⁵³ post-processing. The PMF profiles were obtained employing 16 biased MD simulations of 200 ns length for reaction coordinate values of d_COM-COM = 8 Å to 20 Å, and four biased MD simulations of 70 ns length for reaction coordinate values of d_COM-COM = 21 Å to 24 Å. Together, this sums up to a total of ~ 3.5 μs simulation time. Approximately Gaussian-shaped frequency distributions were obtained for each reference point along the reaction coordinates, with all such distributions well overlapping (Fig. S4). These are prerequisites for the successful application of WHAM to extract a PMF from these distributions⁵³. Repeating the computations of the PMFs for the range of d_COM-COM = 8 Å to 20 Å for parts of the simulation time demonstrates that, for all three systems, the PMFs are converged after at most 160 ns of simulation time per window (maximal difference between two PMFs: 0.2 kcal mol⁻¹) (Fig. S5). The same procedure was repeated for the PMFs from d_COM-COM = 20 Å to 24 Å (fully dissociated state), demonstrating that these PMFs are converged after at most 50 ns of simulation time per window (Fig. S5). For comparison, the PMF values at d_COM-COM = 20 Å were set to zero in all three cases (Fig. 3a).

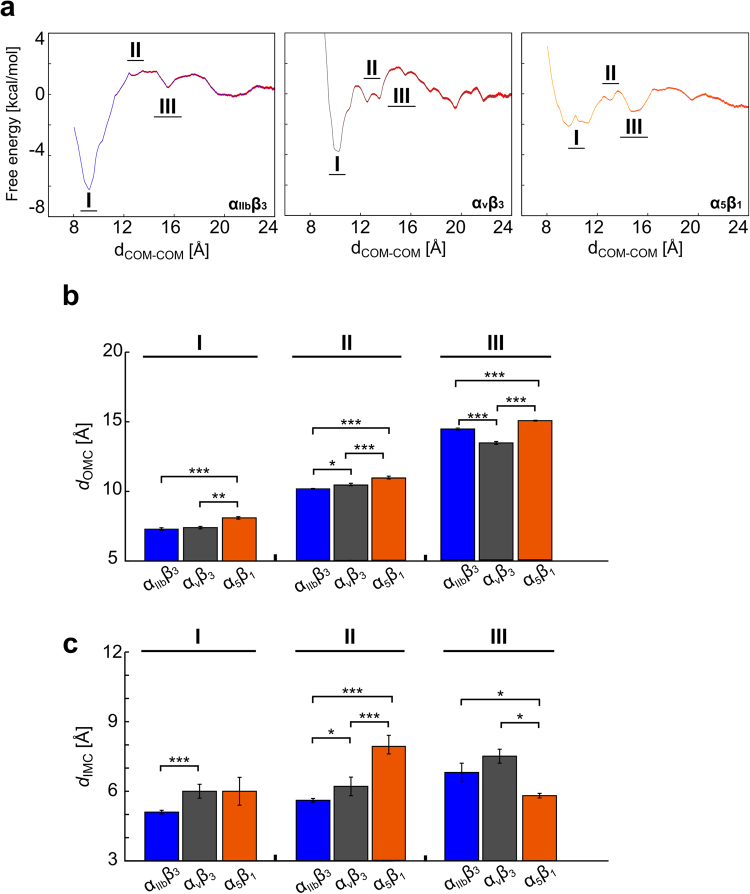
Figure 3.

Potential of mean force of TM helix association of α_IIbβ₃, α_vβ₃, and α₅β₁ TMDs and differences at the OMC/IMC interface with increasing d_COM-COM. (a) Configurational free energies as a function of the d_COM-COM used as a reaction coordinate for α_IIbβ₃ (left panel), α_vβ₃ (middle panel), and α₅β₁ (right panel) TMDs. Roman numbers indicate free energy minima. Statistical errors, calculated using bootstrap analysis, are displayed as red shaded curves added to the PMF profiles. The PMF values at d_COM-COM = 20 Å were set to zero. (b,c) Histograms of the averaged d_OMC (B) and d_IMC (C) across umbrella sampling windows linked to free energy minima I–III observed in panel (A) (see also Table S7), using reweighted (“unbiased”) TMD configurations. Error bars denote the SEM (eq. 5) and stars indicate the statistical difference (see Methods section for definition).

The global minima (d_COM-COM ≈ 9 Å) are in all three cases close to the initial distance (10 Å resp. 12.6 Å) calculated from the NMR structure of the α_IIbβ₃ TMD (PDB ID 2K9J) or the structure based on Cys cross-linking results, and the general shapes of the PMFs are comparable, with a rising free energy with increasing reaction coordinate values and rather flat PMFs beyond d_COM-COM ≈ 20 Å. Furthermore, in going from the global minima to d_COM-COM ≈ 20 Å, two local minima are passed (marked by roman numbers II and III in Fig. 3a). These minima are located at d_COM-COM ≈ 12 to 13 Å and d_COM-COM ≈ 15 Å in all three systems.

However, the PMFs also show pronounced differences. First, the global minima show values of −6.5, −3.8, and −2.1 kcal mol⁻¹ for the α_IIbβ₃, α_vβ₃, and α₅β₁ TMDs, respectively, demonstrating the largest tendency for the TM helices to associate in the case of α_IIbβ₃, and the lowest in the case of α₅β₁. For computing association free energies ΔG from the PMFs (eqs 1–3), we, first, assessed to what extent the dissociated TMD helices of α_IIb and β₃ sample the accessible configuration space on the simulated time scales. This yielded values for ||Ω||, a factor describing the restriction of the configurational space of the monomers upon dimer formation (eq. 4), of 0.05 to 0.10 (Table 2). Compared to the value of the overall accessible space of (2π)², these values indicate that the dissociated TMD helices sample only a fraction of the overall accessible space. Hence, we followed a procedure by Johnston et al.⁵⁴ to compute dimerization and mole fraction dimerization constants K_a and K_X, respectively, (eqs 1,2) and from there ΔG (eq. 3) (Table 2). The results indicate that α_IIbβ₃ TMD is the most stable system (ΔG = −3.8 kcal mol⁻¹), followed by α_vβ₃ and α₅β₁ TMDs (ΔG = −0.8 kcal mol⁻¹ and 0.5 kcal mol⁻¹, respectively). Note that the exact value of the dimerization distance D (eq. 1; here evaluated between 8 and 12 Å) has a low impact on the results (see Table S6 for ΔG values evaluated between 8 and 14 Å), because the integrals reach plateaus after ~10 Å⁵⁵. Second, the TM association requires to pass configurational free energy barriers that are similar for α_IIbβ₃ and α₅β₁ TMDs (~1.5 kcal mol⁻¹, respectively), whereas a larger barrier occurs in the case of α_vβ₃ TMD (~3 kcal mol⁻¹).

Table 2.

Thermodynamic quantities for each TMD system^[a].

System	αIIbβ3 TMD	αvβ3 TMD	α5β1 TMD
||Ω||[b]	0.07	0.05	0.1
K a [c]	38009.8	280.9	27.7
K X	543.0	4.0	0.4
ΔG[d]	−3.8	−0.8	0.5

^[a]The integral in eq. 1 was evaluated at D = 12 Å.

^[b]In radians.

^[c]In Ų.

^[d]In kcal mol⁻¹.

To conclude, the PMFs of TM helix association and computed association free energies show overall similar shapes but reveal that the α_IIbβ₃ TMD has the strongest tendency to associate, and the PMF of the α₅β₁ TMD shows the smallest configurational free energy changes.

Distinct order of TMD clasp formation and differences in the persistence of IMC and OMC with increasing helix-helix distance

To further investigate differences between the integrin isoforms in more detail, averaged d_OMC and d_IMC were computed on the reweighted (“unbiased”) configurations from umbrella sampling (reweighting done according to ref.⁵⁶) (Fig. S6) for free energy minima I – II, respectively (Fig. 3b,c; Table S7).

At the global minimum I, the d_OMC, averaged over windows 3–5, is very similar in the α_IIbβ₃ and α_vβ₃ TMDs (~7.3 Å, ~7.4 Å, SEM ≈ 0.09 Å), and smaller by ~0.8 Å than in the α₅β₁ TMD (~8.1 Å, SEM ≈ 0.09 Å). The differences between α_IIbβ₃ or α_vβ₃ TMDs versus α₅β₁ TMD are (highly) significant (p < 0.0001, and p ≈ 0.0003). The d_IMC is smaller by ~0.9 Å in the α_IIbβ₃ TMD (~5.1 Å, SEM ≈ 0.08 Å) than in the α_vβ₃ and α₅β₁ TMDs (~6.0 Å, SEM ≈0.3 Å and ≈ 0.6 Å, respectively). The difference between α_IIbβ₃ and α_vβ₃ TMDs is highly significant (p < 0.0001), while for that between α_IIbβ₃ and α₅β₁ TMDs, p ≈ 0.06 results. Hence, both the OMC and IMC are conserved, with the clasps being more compact in the α_IIbβ₃ TMD, followed by α_vβ₃ and α₅β₁ TMDs.

At minimum II, the d_OMC, averaged over windows 8–9, is slightly smaller in the α_IIbβ₃TMD (~10.1 Å, SEM ≈ 0.03 Å) than in the α_vβ₃ TMD (~10.4 Å, SEM ≈ 0.09 Å), and smaller by ~0.8 Å than in the α₅β₁ TMD (~10.9 Å, SEM ≈ 0.1 Å). The difference between α_IIbβ₃ and α_vβ₃ TMDs is significant (p ≈ 0.04) and highly significant in the other cases (p < 0.0001). The d_IMC is smaller by ~0.6 Å in the α_IIbβ₃ TMD (~5.6 Å, SEM ≈ 0.08 Å) than in the α_vβ₃ TMD (~6.2 Å, SEM ≈ 0.4 Å), and by ~2.4 Å than in the α₅β₁ TMD (~8.0 Å, SEM ≈ 0.4 Å). The difference between α_IIbβ₃ and α_vβ₃ TMDs is significant (p ≈ 0.03 Å), and highly significant in the other cases (p < 0.0001). Hence, the interface at the OMC is less compact than before and starts to disintegrate (d_OMC > 10 Å). In contrast, the IMC packing is conserved, similar to as before, but the interface is tighter in α_IIbβ₃ TMD than in α_vβ₃ and α₅β₁ TMDs.

Finally, at minimum III, d_OMC and d_IMC, averaged over windows 11–12, reveal that the OMC packing is largely lost (distances > 13 Å), while the IMC packing is still conserved. The d_IMC is ~0.8 Å smaller in the α_IIbβ₃ TMD (~6.8 Å, SEM ≈ 0.4 Å) than in the α_vβ₃ TMD (~7.5 Å, SEM ≈ 0.3 Å), and ~1 Å larger than in the α₅β₁ TMD (~5.8 Å, SEM ≈ 0.1 Å). The difference between α_IIbβ₃ and α_vβ₃ TMDs is not significant (p ≈ 0.2), but both differences versus α₅β₁ TMD are significant (p ≈ 0.005).

To conclude, our results suggest for all investigated integrin isoforms that helix association in the TMDs proceeds first via IMC formation, and that OMC formation then reinforces the coiled-coil conformation. The reverse order is suggested to occur upon helix dissociation. However, pronounced differences among the three TMDs as to the conservation of OMC/IMC packing with increasing d_COM-COM became obvious, with α_IIbβ₃ TMD showing the most persistent clasps.

Discussion

In this study, we have shown by molecular simulations at the atomistic level that the TMD of integrin α_IIbβ₃ is most stably associated compared to that of α_vβ₃ and α₅β₁, and that this difference is related to differences in particular interactions across the TMDs, notably in the OMC. We furthermore identified an “OMC before IMC” order of clasp disintegration upon TMD dissociation as a uniform property of all three investigated TMDs. Our study was motivated by the considerable evidence that the TMD separate upon integrin activation^{7,11,13,14,17,57–60} and so are expected to influence conformational properties of integrins, which, in turn, have been correlated to integrin adhesiveness and affinity^26,61–66. Furthermore, while the overall structural organization and activation mechanism of integrins appears largely conserved^{48,62,66–68}, subunit-specific differences in the activation sensitivity had been reported^26,27,29. Accordingly, here, we comparatively assessed the TMD of α₅β₁, a physiologically relevant^69,70 member of the β₁ integrin subfamily that is considered basally active²⁶ and TMDs of α_IIbβ₃ and α_vβ₃, physiologically relevant^71,72 members of the β₃ integrin subfamily that is considered basally inactive²⁶, although a cell-specific influence on the activation sensitivity has been reported for integrin α_vβ₃²⁹.

That α_IIbβ₃ TMD is most stably associated compared to that of α_vβ₃ and α₅β₁ has been demonstrated in two independent ways. First, we performed unbiased microsecond-long MD simulations at the atomistic level in explicit solvent and an explicit lipid bilayer on the three TMDs, likely the currently most accurate way to explore structure and dynamics of transmembrane proteins⁷³. The length of our MD simulations surpasses comparable previous ones on integrin TMDs by at least one order of magnitude^51,74,75. We performed triplicate MD simulations for each system, which allows probing for the influence of the starting conditions and determining the significance of the computed results by statistical testing and rigorous error estimation⁴⁶. As to the latter, we paid close attention to only consider uncorrelated instances for SEM calculations (eqs 5 and 6). The assessment of convergence of internal motions between independent MD simulations revealed for motions of the TMDs described by the first three PCs that they are relatively well-converged on the timescale of the simulations. For the MD simulations, we used established parameterizations for the solvent⁷⁶, lipids⁷⁷, and proteins⁷⁸; the latter, we had also applied successfully in other integrin simulations^79–82, although we note that more recent protein force fields have become available^83,84. Yet, the impact of force field deficiencies on our results is expected to be small due to cancellation of errors when comparatively assessing the TMDs. While for α_IIbβ₃ TMD an experimental structure was available for system setup¹⁵, structures generated by homology modeling were used for α_vβ₃ and α₅β₁ TMDs. Still, with sequence identities of 40 to 65%, C_α-RMSD values to the native structure below 1 Å and, hence, close to experimental uncertainty can be expected for transmembrane regions⁸⁵. The quality of the modeled starting structures is indirectly supported by the fact that for all three systems, very similar magnitudes of structural deviations along the MD trajectories were found (Fig. 1c). The simulated protein sequences contain a linker region at the N-terminal ends and up to six residues of the cytoplasmic domains at the C-terminal ends, in addition to the TM helices. For β₁ and β₃, the linker region is almost conserved (Fig. 1b), and the linker of α_IIb has been shown to be dynamically unstructured⁴⁵. Together with crystallographic studies of inactive ectodomains that were unable to obtain structural information on these linkers, indicating their high flexibility^48,86,87, we thus do not expect these linker regions to influence the TMD association differentially. In contrast, for the cytoplasmic membrane-proximal region, an influence on maintaining integrin inactivity has been suggested³⁶ (see also below). Of particular relevance is the choice of lipid type, as it has been shown that annular anionic lipids can stabilize α_IIbβ₃ TMD⁵¹. Therefore, our lipid bilayer consisted of zwitterionic 1,2-dioleoyl-sn-glycero-3-phosphocholine (DOPC) lipids, which were shown to interfere much less with inter-TM helix interactions⁵¹.

As a second, independent means to investigate the energetics of TMD association and because we cannot expect to observe a dissociation of the TMDs on the time scale of our MD simulations⁴⁴, we performed biased MD simulations at the atomistic level followed by PMF computations, using established protocols successfully applied previously by us^50,88,89 and d_COM-COM as an intuitive reaction coordinate previously applied on similar systems^6,90. To our knowledge, so far, the association energetics of integrin TMDs, by computational means, has only been investigated by coarse-grained MD simulations followed by PMF computations^6,90. By repeating the PMF computations for parts of the biased simulations, we demonstrated that the PMFs are converged with respect to the overall simulation time per sampling window (Fig. S5). Still, even with sampling times of up to 200 ns per sampling window, pronounced helix tilting or even helix rotation around an axis perpendicular to the helix axis, once the helices are separated by a large enough distance, cannot be expected. Likewise, such sampling times may not be sufficient to yield sampled helix-helix configurations that are completely unbiased from the respective starting structures. While these potential issues may be expected to disfavor separated helix-helix configurations with respect to associated TMD, their impact on our results is expected to be small due to cancellation of errors when comparatively assessing the respective TMD. Comparing quantitative results from the PMFs (Fig. 3a) and subsequent association free energy calculations⁵⁴ (Table 2) to experimental data lends remarkable support to the quality of the setup, parameterization, and execution of our simulations: (I) For α_IIbβ₃ TMD, association free energies of −4.33 and −4.84 kcal mol⁻¹ have been determined in 1-palmitoyl-2-oleoyl-sn-glycero-3-phosphocholine (POPC) lipids by NMR spectroscopy and calorimetry^44,51, and our computed ΔG of −3.8 kcal mol⁻¹ (Table 2) is within chemical accuracy of these results; (II) for α₅β₁, to our knowledge, the energetics of TMD association has not been explicitly probed experimentally. However, from comparing conformational equilibria between the extended-closed and extended-open states for full-length integrin α₅β₁ versus the α₅β₁ ectodomain, one may infer that the associated and dissociated states of the TMDs and cytoplasmic domains are almost isoenergetic²⁶, which is in very good agreement with a computed ΔG of 0.5 kcal mol⁻¹ (Table 2); (III) obtaining a barrier height pertinent to kinetics via a PMF has been debated⁹¹. Still, when inserting the configurational free energy barrier for α_IIbβ₃ TMD association of ~1.5 kcal mol⁻¹ (Fig. 3a) as ΔG^‡ in the transition state theory equation k = k^‡ exp(−ΔG^‡/RT)⁹² and approximating k^‡ with a collision frequency of a transmembrane protein of 10⁵ to 10⁶ s^{−1 93}, a rate k of ~8 * 10³ to ~8 * 10⁴ s⁻¹ is obtained as a coarse upper bound⁹⁴, in good to fair agreement with an association rate of α_IIbβ₃ TMD in phospholipid bicelles of 4.5 * 10³ s⁻¹ found by NMR spectroscopy⁴⁴. As to probing the internal consistency of our results, the shallow contact minimum found in the PMF for α₅β₁ TMD and the apparent lack of pronounced barriers towards the dissociated state suggest that in MD simulations that are long enough, the two helices should (start to) come apart. In fact, such a tendency is found as d_COM-COM in the unbiased MD simulations of α₅β₁ TMD is ~1 and 0.6 Å larger than for α_IIbβ₃ and α_Vβ₃ TMDs (Fig. S7, Table S8). Likewise, internal consistency can be probed by analyzing structural parameters of configurations from unbiased MD simulations and reweighted (“unbiased”) configurations from umbrella sampling simulations. This reveals qualitatively similar results for subtype-specific differences in the distances characterizing OMC formation (d_OMC; Fig. 2a versus Fig. 3b, part I), and likewise similar results for α_vβ₃ and α₅β₁ TMDs concerning the distance characterizing IMC formation (d_IMC; Fig. 2b versus Fig. 3c, part I), although the results for α_IIbβ₃ deviate in this case. The latter discrepancy may be explained in that distances in Fig. 2b where directly computed from the (tightly associated) α_IIbβ₃ TMD configurations in the unbiased MD simulations, while three umbrella sampling windows were evaluated for distances in Fig. 3c.

The PMF and association free energy calculations clearly revealed that α_IIbβ₃ TMD is most stably associated, followed by α_vβ₃ TMD and α₅β₁ TMD (Table 2). It had been previously suggested by experiment^13,39 and computations^49,95 that the two structural motifs OMC and IMC are responsible for the correct TMD packing but if, and how, sequence variations there (Fig. 1b), especially in the OMC, lead to differential TMD association has remained largely elusive. Our unbiased MD simulations reveal that the most stable association of α_IIbβ₃ TMD is paralleled by this TMD forming more contacts in general across the whole TMD interface (Fig. S3) as well as particularly in the OMC interface (Fig. 1d); also, this TMD shows the most compact OMC (Fig. 2a; Fig. 3b in part I). Although differences in the prevalence of single hydrogen bonds or salt bridges among the three TMDs were not significant, our unbiased MD simulations still suggest a trend, according to which the importance of the membrane-proximal region for TMD association is confirmed, particularly of the R995-D723 salt bridge^24,39,51, as this interaction is also most prevalent in α_IIbβ₃ TMD (>20%, Table 1). Our results may also provide an explanation as to why, in in vivo experiments on transgenic mice carrying a point mutation of the respective D723 of the β₁ subunit, a normal integrin function was found³²: In α₅β₁ TMD, the R995-E726 salt bridge is more prevalent than the R995-D723 one. Other questions relate to the role of β₃-K716 as a key determinant for the stability at the IMC interface⁹⁶ and whether the proposed stabilization arises from an engagement of K716 with the surroundings lipid molecules⁹⁶ or by forming a hydrogen bond with F992¹⁷. Our MD simulations revealed that K716 occurs most frequently in either a hydrogen bond across the TMD or a salt bridge with phospholipid head groups in α_IIbβ₃ TMD, followed by α_vβ₃ and α₅β₁ TMDs, consistent with the notion that K716 is important for integrin function in α_IIbβ₃, but not in α₅β₁²⁵.

Although more work would be required to establish unequivocally a link between differences in K716/phospholipid head group interactions and differences in TMD association free energies, we do not find it unlikely that this link exists. This link would then stress that (differences in) TMD association may be governed by additional factors besides sequence differences, including interactions to annular lipids, as previously demonstrated for the α_IIbβ₃ TMD⁵¹, or membrane tension⁹⁷. Along these lines, recent work on integrin α₅β₁ suggested the hypothesis that the non-ligand binding leg domains and N-glycans may have previously unappreciated roles in regulating integrin conformations²⁶. Hence, while considering a subsystem such as the TMD in this study has the benefit of yielding detailed answers under well-defined conditions, at the same time, it leads to the limitation that effects from other parts of the system are not accounted for.

To our knowledge, a novel aspect resulting from our study with respect to the question what governs integrin adhesiveness and affinity in relation to conformational changes is the finding that the two clasps disintegrate in the order “OMC before IMC” upon TMD dissociation. This finding leads to the relevant prediction that the closed state of integrins might not be single but rather comprising several microstates that vary in the extent of TMD association, e.g., with the TMD associated at both OMC and IMC, or with the TMD associated only at the IMC. A similar proposition was made for the extended state(s) of integrins based on the flexibility of integrin legs^26,67. Our finding may also be related to, not yet fully understood, results on conformational free energies for intact integrin α₅β₁ that revealed that the presence of the TMD and cytoplasmic domains favors considerably the bent-closed over the extended-closed conformation²⁶, when one considers that the bent-closed → extended-closed transition may already contain energetic contributions from a partial TMD dissociation in the OMC region. In that respect, computations as performed here may support valuable efforts of gaining affinity information for specific integrin conformational states²⁶ providing access to the energetic contributions of defined subsystems. Finally, we find it striking to note that the order of association free energies of the TMDs (α_IIbβ₃ ≪ α_vβ₃ < α₅β₁ (Table 2)) parallels reports on the basal activity of these integrins (α_IIbβ₃ ≪ α_vβ₃ < α₅β₁)^26,27. While it is not possible to establish a direct link between these two series from the comparative simulation studies on TMDs alone, our finding suggests, to our knowledge for the first time, that the sequence composition of the TM helices can have a decisive effect on free energies associated with distinct conformational states of different integrins. A likewise suggestion has been made regarding the strength of interactions between leg domains for integrins α_IIbβ₃ and α_vβ₃²⁹. Notably, the magnitude of differences in association free energies across the investigated TMDs (~2.7 kcal mol⁻¹; Table 2) is clearly in the range of observed changes in conformational free energies upon activation of full-length integrin α₅β₁ (~3.7 kcal mol⁻¹)²⁶, suggesting that TMD differences can indeed significantly impact overall conformational integrin energetics.

In summary, α_IIbβ₃ TMD is most stably associated compared to that of α_vβ₃ and α₅β₁, which is related to differences in particular interactions across the TMDs, notably in the OMC. The order of TMD association stability is paralleled by the basal activity of these integrins, which suggests that TMD differences can have a decisive effect on conformational free energies of integrin states. The “OMC before IMC” order of clasp disintegration upon TMD dissociation uniformly identified for all three investigated TMDs suggests that the closed state of integrins might not be single but rather comprising several microstates that vary in the extent of TMD association.

Methods

Generation of starting structures

The starting structure for MD simulations of the α_IIbβ₃ TMD was obtained from the coordinates of the NMR structure (PDB ID 2K9J) available in the RCSB Protein Data Bank⁹⁸. The starting structures for MD simulations of the α_vβ₃ and α₅β₁ TMDs were generated by homology modeling. The homology models were generated using MODELLER v9.9⁹⁹, and the NMR structure of the α_IIbβ₃ TMD was used as a template. In the case of α_vβ₃ integrin, only the α_v sequence was modeled based on an alignment with the α_IIb TMD with a sequence identity of 45%. In the case of the α₅β₁ TMD, the α₅ and β₁ sequences are 40% and 65% identical to those of α_IIbβ₃ TMD, respectively. The quality of the models was assessed by the QMEANBrane scoring function available in QMEAN server^42,43. A global QMEAN score of 0.60, 0.64, and 0.67 was computed for the α_IIbβ₃, α_vβ₃, and α₅β₁ TMDs, respectively.

Setup of simulation systems

The membrane builder tool available on the CHARMM-GUI website¹⁰⁰ was used for embedding the TMDs in a pre-equilibrated bilayer of DOPC lipids¹⁰¹ using the replacement method¹⁰². The PPM web server¹⁰³ was used to assess the correct orientation of the α_IIbβ₃ TMD relative to the hydrocarbon core of the lipid bilayer. The required rectangular simulation box was generated by defining the number of lipids (88 and 85 for the upper and lower leaflet, respectively) and setting a value of 17 Å for the water layer above and below the protein. The total system size is ~60,000 atoms, including TIP3P water molecules⁷⁶ and Cl^- counter ions.

Molecular dynamics simulations

All MD simulations were performed using the AMBER 14 suite of programs⁴⁷, the ff99SB force field for the proteins⁷⁸, the Lipid14 force field⁷⁷ for the lipids, and the TIP3P water model⁷⁶. The particle mesh Ewald method¹⁰⁴ was used to treat long-range electrostatic interactions, and bond lengths involving bonds to hydrogen atoms were constrained using the SHAKE algorithm¹⁰⁵. The time step for integrating Newton’s equations of motion was 2 fs with a direct space, nonbonded cutoff of 8 Å. Initially, harmonic restraints with a force constant of 500 kcal mol⁻¹ Å⁻² were applied to all solute atoms during the first 250 steps of steepest descent and then reduced to 25.0 kcal mol⁻¹ Å⁻² for the second 2500 steps of conjugate gradient minimization and 10 kcal mol⁻¹ Å⁻² for the last 2500 steps of conjugate gradient minimization. MD simulations in the NVT (constant number of particles, volume, and temperature) ensemble were carried out for 50 ps, during which the system was heated from 100 to 300 K. Subsequent MD simulations in the NPT (constant number of particles, pressure, and temperature) ensemble were used for 150 ps to adjust the solvent density. In both steps, a force constant of 10 kcal mol⁻¹ Å⁻² was applied to all solute and lipid atoms. The production MD simulations of 9 μs length were performed with the GPU version of the program pmemd¹⁰⁶ in the tensionless NPT ensemble using the anisotropic Berendsen barostat¹⁰⁷ to control the pressure (coupling constant = 1 ps) and the Langevin thermostat¹⁰⁷ to control the temperature (coupling constant = 1 ps), as suggested in ref.⁷⁷.

Potential of mean force computations

Profiles of the free energy of association of α_IIbβ₃, α_vβ₃, and α₅β₁ TMDs were constructed from umbrella sampling MD simulations^108,109 in combination with the WHAM method⁵³. As reaction coordination, the distance between the COMs of the TM segments embedded in the membrane was considered (C_α atoms of residues P996-V1015 and D718-I747, for the α_IIb and β₃ subunits, respectively (equivalent ranges of residues were used for α_vβ₃ and α₅β₁)). The initial distance computed from the NMR structure of the TMD of α_IIbβ₃ integrin is 10.0 Å. To generate starting structures for umbrella sampling, the initial distance was reduced to 8 Å and increased to 11 Å in 0.5 Å steps, and from 11 Å increased to 24 Å in 1 Å steps. Each TMD configuration was inserted in a pre-equilibrated bilayer of DOPC lipids as described above. This resulted in a total of 20 initial systems per TMD. Each of the 20 windows of the three integrin systems was subjected to umbrella sampling simulations, carried out in the NPT ensemble for 200 ns each for d_COM-COM = 8 Å to 20 Å and 70 ns each for d_COM-COM = 21 Å to 24 Å. This resulted in a total of ~3.5 μs of MD simulation time.

Within each umbrella sampling window, a harmonic potential with a force constant of 4 kcal mol⁻¹ Å⁻² was applied to restrain the conformations close to the reference point. Force constants of 20 kcal mol⁻¹ Å⁻² were also used to restrain conformations whose initial d_COM-COM ranged from 8.0 Å to 10 Å to generate approximately Gaussian-shaped frequency distributions. Otherwise, the parameters described above were used for thermalization and production runs. Finally, to compute the errors at the reference points of the PMF profiles, the Monte Carlo bootstrapping analysis implemented in WHAM using 200 resampling trials was applied.

Estimation of association free energy

An association free energy was estimated from the obtained PMF following the membrane two-body derivation from Johnston et al.⁵⁴. In brief, the PMF is integrated along the reaction coordinate to calculate an association constant (K_a), transformed to the mole fraction scale (K_x) taking into account the number of lipids N_L per surface area A, and this value is used to calculate the difference in free energy between dimer and monomers (ΔG), according to eqs 1–3

$$K_a=\frac{\left|\left|\Omega \right|\right|}{{(2\pi )}^2}{\int }_0^{D}r{e}^{\frac{-w\left(r\right)}{k_{B}T}}dr$$ 1

$$K_x=K_a\frac{N_L}{A}$$ 2

$$\mathrm{\Delta }G=-RTln(K_x)$$ 3

where r is the value of the reaction coordinate, w(r) is the PMF at value r, D is the maximum distance at which the protein is still considered a dimer, k_B is the Boltzmann constant, and T is the temperature at which the simulations were performed. Additionally, a factor that considers the restriction of the configurational space of the monomers upon dimer formation is included in terms of the sampled angle between the two chains in the dimeric state (eq. 4)

$$\left|\left|\Omega \right|\right|=\left[\max \left({\theta }_a\right)-\min \left({\theta }_a\right)\right]\ast \left[\max \left({\theta }_b\right)-\min \left({\theta }_b\right)\right]$$ 4

and the accessible space for the monomers, (2π)². In eq. 4, the angle θ_a is defined as the angle formed between the vectors connecting the COM of helix 1 with the COM of helix 2 and with the COM of residues V971 to V973 of the latter helix; θ_b is defined analogously starting from the COM of helix 2 and using the COM of residues L698 to V700 in helix 1.

Analysis of trajectories

For the analysis of the trajectories, ptraj/cpptraj¹¹⁰ of the AmberTools 14 suite of programs was applied. For the unbiased MD simulations, the first 200 ns were not considered for analysis. To evaluate the helix-helix interface (indicated as d_COM-COM-), a maximal distance of 3.5 Å and a minimal angle of 120° were used as exclusion criteria to identify hydrogen bond formation, as was a maximal distance of 4 Å to identify salt bridge formation. To examine the OMC interface, the distance between the C_α atoms of G972/G976 (α_IIb subunit) and V700/I704 (β₃ subunit) was computed (indicated as d_OMC). To evaluate the IMC interface, the distance between the centers of mass of the phenyl rings of F992 or F993 (α_IIb subunit) and W715 (β₃ subunit) (indicated as d_IMC1 and d_IMC2, respectively) was computed, and the smaller distance of the two was considered further as d_IMC. To evaluate the TMD association, we calculated the total number of native and non-native contacts formed between the two helices. A native contact was defined as a contact satisfying the distance cutoff of 7 Å in the first frame (used as reference frame), a non-native contact as a contact satisfying the distance cutoff of 7 Å without being already found in the reference frame. This definition is according to ref.⁴⁷. The same set of analyses was also carried out to analyze the configurations sampled during umbrella sampling. For all the configurations t generated, we estimated a weight w^t according to eqs 7 and 8 from ref.⁵⁶. The reweighting is performed over the entire ensemble of each system and, then, normalized by dividing each w^t by the sum of all w^t for each integrin system.

Statistical analysis

Results from three independent MD simulations are expressed as arithmetic means ± SEM calculated over the time. The overall SEM for each simulated system was calculated according to the law of error propagation (eq. 5):

$${\mathrm{SEM}}_{total}=\sqrt{{\mathrm{SEM}}_1^2+{\mathrm{SEM}}_2^2+{\mathrm{SEM}}_3^2}$$ 5

where the subscripts i = {1, 2, 3} indicate the three trajectories. SEM_i was computed following ref.¹¹¹ (see particularly eqs 11–13 there) by, first, detecting the decorrelation time of an investigated variable along each MD simulation and, second, establishing the effective sample size from that time, which is then used to compute SEM_i. In the case of hydrogen bond, salt bridge, and contact analyses, SEM is calculated from the standard deviation (SD) of the three means of the three MD simulations according to eq. 6, assuming that the three MD simulations are statistically independent:

$$SEM=SD/\sqrt{3}$$ 6

p values related to eq. 5 are calculated according to the Student’s t-test for parametric testing, with $N_{eff}\equiv (T-$$t_o+1)/g$, where $N_{eff}$ is the total number of uncorrelated frames within the trajectories based on the statistical inefficiency g_t0 and the simulation time range [t₀, T] following ref.¹¹¹; the same test is applied for p values related to eq. 6, with N_eff = 3. Differences between mean values are considered to be statistically significant if p < 0.05 and p < 0.001 (indicated as “*” and “**” in figures, respectively) and highly statistically significant if p < 0.0001 (indicated as “***” in figures). The statistical analysis was performed using the R software¹¹² and the pymbar module for MBAR¹¹³.

Data availability

All data generated or analyzed during this study are included in this published article (and its Supplementary Information files).

Author Contributions

H.G. designed research, G.P. performed research, G.P. and H.G. analyzed data and wrote the manuscript.

Competing Interests

The authors declare no competing interests.