Monolayer Single-Crystal 1T′-MoTe₂ Grown by Chemical Vapor Deposition Exhibits Weak Antilocalization Effect

Abstract

Growth of transition metal dichalcogenide (TMD) monolayers is of interest due to their unique electrical and optical properties. Films in the 2H and 1T phases have been widely studied but monolayers of some 1T′-TMDs are predicted to be large-gap quantum spin Hall insulators, suitable for innovative transistor structures that can be switched via a topological phase transition rather than conventional carrier depletion [Qian et al. Science 2014, 346, 1344–1347]. Here we detail a reproducible method for chemical vapor deposition of monolayer, single-crystal flakes of 1T′-MoTe₂. Atomic force microscopy, Raman spectroscopy, X-ray photoelectron spectroscopy, and transmission electron microscopy confirm the composition and structure of MoTe₂ flakes. Variable temperature magnetotransport shows weak antilocalization at low temperatures, an effect seen in topological insulators and evidence of strong spin–orbit coupling. Our approach provides a pathway to systematic investigation of monolayer, single-crystal 1T′-MoTe₂ and implementation in next-generation nanoelectronic devices.

Graphical abstract

Two-dimensional transition-metal dichalcogenides (MX₂) have attracted great attention due to the broad set of material characteristics that can be accessed by varying the identity of the transition metal and chalcogenide atoms.^1–6 The promise of MX₂ monolayer films for energy⁷ and other applications have been made apparent through investigations of their optical,^8,9 electrical,⁹ and mechanical¹⁰/tribological¹¹ properties. Development of reproducible growth methods for high-quality monolayer MX₂ films is a key step in advancing basic and applied research into these materials. MX₂ materials can crystallize in different forms¹² with the 2H phase of MoS₂ being most widely studied to date. Other structural phases, such as 1T and 1T′, are of great interest and are being explored at a rapid pace. The monolayer 1T′-MX₂ compounds with molybdenum or tungsten as the transition metal are predicted to be large-gap quantum spin Hall (QSH) insulators,¹³ making them promising for applications in novel switching devices,¹³ spintronics, and quantum computation.^14–16 One method to obtain 1T and 1T′-MX₂ is by phase transformation.¹⁷ Examples include transformation of MoS₂ from 2H to 1T by treatment with n-butyl lithium,¹⁸ and conversion of MoTe₂ from 2H to 1T′ by laser patterning.¹⁹ Computational studies suggest that it is possible to induce a transition from 2H to 1T′ phase in MX₂ materials by application of stress,²⁰ but this approach is complicated by the need to control the homogeneity of the strain across the sample. The metastable nature of 1T′-MoTe₂ makes direct growth by chemical vapor deposition (CVD) a challenge,²¹ but CVD growth of few-layer MoTe₂ in the 2H and 1T′ phases was recently reported.^21,22 There are as yet no reports of a reliable CVD growth method for monolayer, single-crystal, MoTe₂ in the 1T′ phase, which would represent a critical step to enable systematic investigations of topological effects in this system.

Here we report direct CVD growth of single-crystal monolayer flakes of MoTe₂ in the 1T′ phase along with associated measurements of key chemical, electrical, and physical properties. X-ray photoelectron spectroscopy (XPS) was used to confirm that the chemical composition of the monolayer flakes corresponds to MoTe₂. Atomic force microscopy (AFM) revealed that the flakes are monolayer thickness with minimal (<5%) bilayer and multilayer content. Raman spectroscopy, transmission electron microscopy (TEM), and aberration-corrected scanning TEM (ACSTEM) confirmed that the monolayer MoTe₂ flakes were single crystal and grown directly in the 1T′ phase. TEM imaging and electron diffraction were used to identify a preferential crystal growth direction along the $\stackrel{\rightharpoonup }{\mathbf{b}}$ axis. Finally, temperature-dependent magneto-conductance measurements showed a weak antilocalization effect, which is observed in many topological insulators due to their strong spin–orbit coupling.²³ These investigations set the stage for further explorations of monolayer MoTe₂ and its eventual application in next-generation electronic, sensor, and optoelectronic devices.

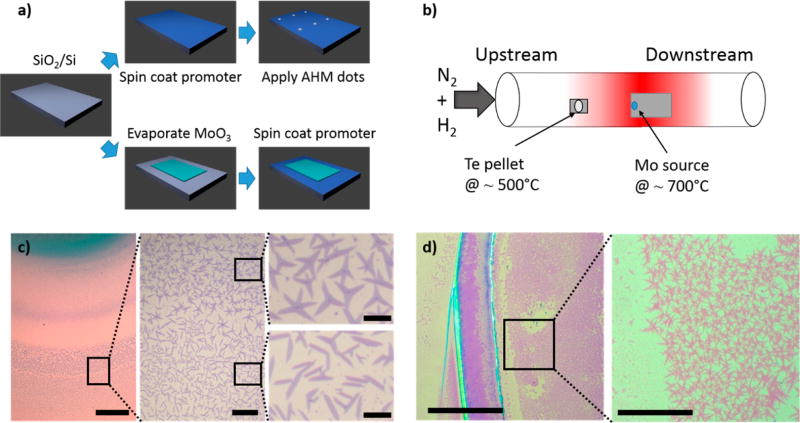
Monolayer MoTe₂ flakes were grown directly on a 300 nm SiO₂/Si substrate by CVD. First, a 1% sodium cholate solution, known to act as a growth promoter for MoS₂,²⁴ is spin coated at 4000 rpm for 60 s onto the SiO₂ substrate. A droplet of a saturated solution of ammonium heptamolybdate in deionized (DI) water is deposited onto the substrate, providing the molybdenum feedstock (Figure 1a). The substrate is placed in the center of a 1 in. CVD tube furnace, and 15 mg of solid tellurium is placed 5 cm upstream from the substrate (Figure 1b). Growth occurs at atmospheric pressure in a flow of 400 sccm of nitrogen gas and 25 sccm of hydrogen (both 99.999% purity). The furnace temperature is ramped to 700 °C at a rate of 70 °C min⁻¹. While the Mo source and SiO₂ growth substrate reach 700 °C, the maximum temperature of the tellurium pellet is ~500 °C. After a 5 min growth period, the furnace is opened, and the sample is rapidly cooled to room temperature in 1000 sccm flowing nitrogen.

Figure 1.

MoTe₂ growth. (a) Process steps for droplet (above) and evaporation (below) methods. (b) Schematic of the CVD growth setup. (c) Optical micrograph displaying MoTe₂ flakes grown by the droplet method revealing coffee ring growth region. The inner region has polycrystalline flakes while the outer region has single crystal flakes. Scale bars are 200, 40, and 10 µm, respectively. (d) Optical micrograph displaying MoTe₂ flakes grown by the evaporation method. Scale bars are 200 and 40 µm, respectively.

After growth, the substrate is typically sparsely covered with monolayer MoTe₂ flakes that grow in a millimeter-scale “coffee ring” pattern around the location of the AHM droplet. In contrast to very regular triangular domains observed for MoS₂ grown by CVD,²⁵ MoTe₂ flakes are frequently rectangular in shape, as expected for oriented, single crystalline material with typical dimensions of 3 × 10 µm (Figure 1c). Two distinct growth regions are observed in the coffee ring, each with different crystal growth shapes. In the inner part of the ring, the flakes are more dendritic in shape (polycrystalline), while in the outer part of the ring, the flakes are rectangular (single crystal). The crystal orientation can be determined from the shape of the flakes, as discussed below. These two different growth regions in the coffee ring suggest characteristics of the growth mechanism. The inner region of the coffee ring is closer to the Mo feedstock material (AHM). This region is expected to receive a larger Mo flux compared to the outer part of the ring. In the outer part of the coffee ring, the nucleation density and relative flux ratio of Mo to Te atoms are apparently better optimized for growth of single-crystal 1T′-MoTe₂ flakes with less perturbation from neighboring growth. In the inner region of the coffee ring, the flux of Mo atoms is higher, resulting in denser growth and polycrystalline 1T′-MoTe₂ flakes. This growth mechanism is in agreement with other reports of CVD growth of MX₂ materials.^24,26

A second growth method provided larger areal density of monolayer MoTe₂ flakes. A 20 nm thick rectangle of MoO₃ is deposited by thermal evaporation onto the growth substrate using a shadow mask. A 1% sodium cholate solution is spin coated onto the substrate at 4000 rpm for 60 s. The sample growth then proceeds as described above. Samples show a higher density of flakes (Figure 1d), mostly with a star shape, in contrast to the rectangular single crystal flakes described previously. The growth region in this case is the entire area covered by Mo source material, which is on the order of 1–5 cm² in this experiment. This large-area growth method thus offers a path for future optimization of flake shape and surface coverage. Flakes from both growth methods were characterized as described below, and no significant differences were found. We found that growth of single-crystal monolayer flakes requires both the presence of the growth promoter and careful control of the quantity of molybdenum source material. If either of these parameters is outside of the ideal window, there will either be no growth or multilayer crystallites will be formed.

XPS was used to determine the elemental and bond composition of the flakes. Peaks were observed at 572.1, 582.5, 227.7, and 231.0 eV, corresponding to the Te 3d_5/2, Te 3d_3/2, Mo 3d_5/2, and Mo 3d_3/2, respectively (Figure 2a,b).²¹ In group-6 TMDs, the 1T′ signal is typically downshifted by ~0.8 eV relative to the 2H phase,¹⁷ and the peaks we observe show the expected downshift compared to the XPS spectrum for 2H-MoTe₂ reported by others.²¹ XPS is not sensitive to the difference between the 1T and 1T′ structures.¹⁷ On the basis of these data, the Te/Mo atomic ratio is measured to be 2.1, very close to the ideal value for MoTe₂. The full XPS spectrum and details as to how the stoichiometry was determined can be found in the Supporting Information and Figure S1.

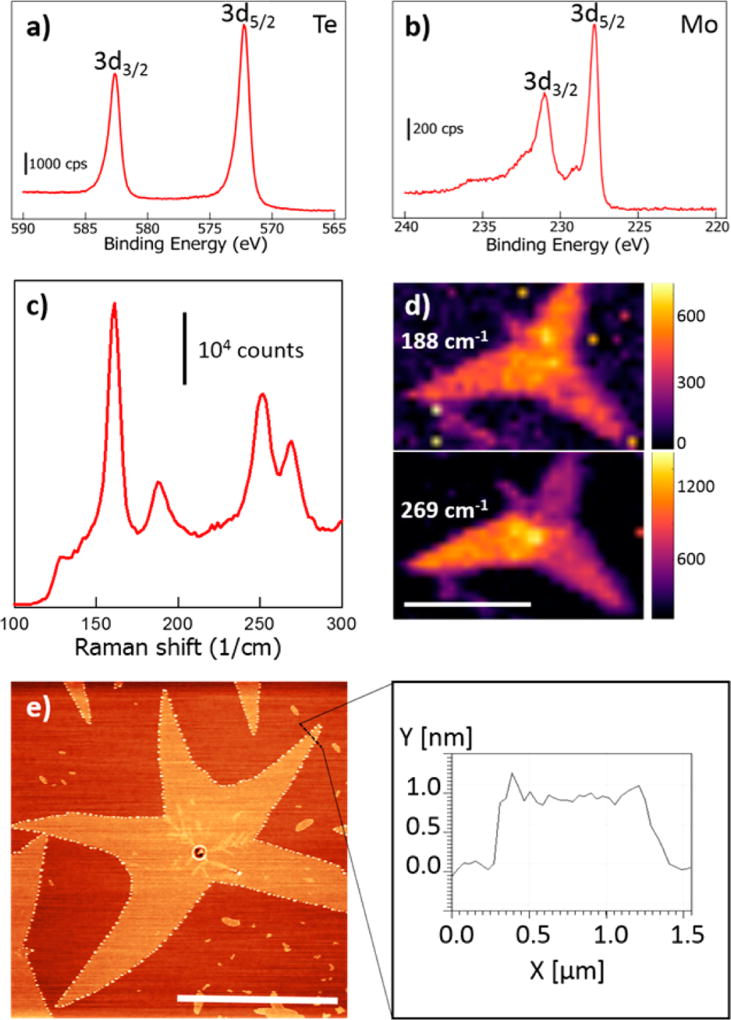
Figure 2.

Characterization of MoTe₂ flakes by XPS and Raman spectroscopy. (a) XPS spectrum showing 3d_3/2 and 3d_5/2 Te peaks. (b) XPS spectrum showing 3d_3/2 and 3d_5/2 Mo peaks. (c) Raman spectrum of MoTe₂ flake is consistent with monolayer 1T′-MoTe₂. (d) Raman mapping of the amplitude of the 188 and 269 cm⁻¹ peaks. The scale bar is 10 µm. (e) AFM topographic image reveals a clean surface with minimal bilayer content. The scale bar is 10 µm. The line scan indicates a thickness of 0.8 nm, as expected for monolayer material.

Raman spectroscopy with an excitation wavelength of 532 nm was performed to examine the vibrational modes of the MoTe₂ flakes. Raman peaks were observed at 112, 127, 161, 252, and 269 cm⁻¹ (Figure 2c), corresponding to five Raman-active Ag modes of monolayer MoTe₂ in the 1T′ phase predicted at 111.27, 125.69, 161.10, 254.58, and 269.22 cm⁻¹.²⁷ The spectrum agrees well with previous reports of few layer MoTe₂ in the 1T′ phase^21,22,28 and it differs significantly from the experimental spectrum for the 2H and theoretical 1T phase.^21,27,29 An additional predicted Raman-active mode²⁷ at 80.41 cm⁻¹ is removed by the edge filter of the apparatus and is not expected to be observed. To our knowledge, this is the first experimental report of the peak at 269 cm⁻¹, which is expected to blueshift from 258 to 269 cm⁻¹ as the material is reduced from bulk to monolayer.²⁸ Here, the peak is very distinct at 269 cm⁻¹, indicating the presence of monolayer 1T′-MoTe₂. Additionally, an unidentified peak at 188 cm⁻¹ was observed, which is in agreement with an earlier report.²¹ During Raman mapping measurements conducted in air, the flakes deteriorated over the course of a few hours, likely due to oxidation. To passivate the material, a sheet of monolayer CVD graphene was transferred over the sample immediately after growth and prior to taking Raman spectra, enabling the Raman mapping to be performed over many hours with no degradation of the material. The addition of the graphene layer did not affect the Raman modes (Figure S2). A Raman map of the amplitude of the 269 cm⁻¹ peak for a star-shaped MoTe₂ flake is shown in Figure 2d. The map shows a slight intensity variation among the three segments of the flake (we confirmed that the peak position was fixed at 269 cm⁻¹ over the entire flake). This suggests that the different arms of the star are each monolayer 1T′-MoTe₂ but with different crystal orientations. The 188 cm⁻¹ intensity map (Figure 2d) reveals that this peak is active across the entire flake, which argues against a contamination effect and raises the question of which yet unidentified vibrational mode is associated with the peak at 188 cm⁻¹. AFM reveals a sample height of ~0.8 nm, as expected for monolayer MoTe₂ (Figure 2e).^22,29 The AFM image also shows the growth of a partial second layer of MoTe₂ near the center of the flake.

To transfer CVD-grown monolayer MoTe₂ flakes onto a new substrate, a procedure was developed where the SiO₂ interface layer was etched using hydrofluoric acid (HF). In this process, the sample is first spin coated with C4 PMMA (Microchem) at 3000 rpm for 60 s, and then the sample is carefully floated on top of a dilute HF solution (1:50 in DI water). The sample is gently pressed down so the solution covers the edges of the SiO₂ without covering the PMMA. The HF solution etches the SiO₂ beneath the MoTe₂ flakes until the PMMA/MoTe₂ stack is released and floats on the solution. The sample is lifted using a polyethylene terephthalate (PET) sheet and transferred to multiple DI water baths to clean the sample. Finally the sample is picked up onto the desired substrate. The substrate is then put into an acetone bath for 3 min to dissolve the PMMA, rinsed in isopropanol for 1 min, and dried using a N₂ gun.

The crystal structure of as-grown MoTe₂ flakes was determined using selected area electron diffraction (SAED) after the sample was transferred onto a holey-carbon TEM grid (Figure 3a,b). A dark-field TEM (DF-TEM) image of rectangular MoTe₂ flake is shown in Figure 3a (200 kV accelerating voltage); the inset shows the associated diffraction pattern. Both bulk and monolayer 1T′-MoTe₂ belong to space group P2₁/m (No. 11). The rectangular reciprocal lattice is characteristic of the 1T′ phase, which is in contrast to the at least 3-fold symmetry expected for the 2H and 1T phases. The 21 screw axis is parallel to $\stackrel{\rightharpoonup }{\mathbf{b}}$ (Te zigzag chain direction) in 1T′-MoTe₂, so the odd (0k0) diffraction spots are forbidden, consistent with the observed SAED pattern. The SAED pattern shows excellent agreement with the simulated monolayer SAED pattern (Figure S3). A selected-area aperture of effective size ~1 µm was used, so the SAED pattern confirms that the MoTe₂ flakes are in the 1T′ phase and shows the long-range order of the 1T′ lattice. The (0k0) axis in the SAED pattern (purple line in inset) corresponds to the $\stackrel{\rightharpoonup }{\mathbf{b}}$ direction in the real-space DF-TEM image. Therefore, the lattice is oriented such that the $\stackrel{\rightharpoonup }{\mathbf{b}}$ direction points along the long-axis of the rectangular flake. This was confirmed by lattice resolution images at higher magnifications and was consistent for each observed flake. To our knowledge, this is the first demonstration of oriented crystallite growth in this system.

Figure 3.

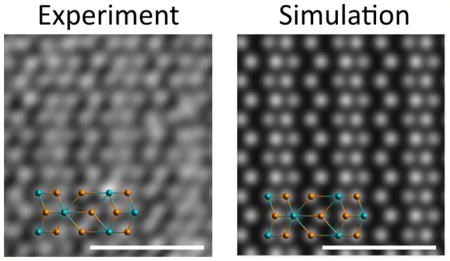
MoTe₂ TEM characterization. (a) DF-TEM image (200 keV) of a single-crystal, rectangular MoTe₂ flake on a holey-carbon TEM grid. The scale bar is 2 µm. Inset: SAED pattern of the MoTe₂ flake at 200 kV, revealing a single crystal in the 1T′ phase. The pink line indicates the direction of the (0k0) diffraction spots, corresponding to the $\stackrel{\rightharpoonup }{\mathbf{b}}$ direction (Te zigzag chain direction) in the real-space, dark-field image. (b) SAED pattern of a MoTe₂ flake at 80 kV, along the [001] zone axis (perpendicular to the monolayer flake), revealing a single crystal in the 1T′ phase. (c) HAADF image taken with ACSTEM revealing Mo and Te atoms in the monolayer 1T′ configuration. The schematic overlay shows the rectangular unit cell and the location of the Mo (blue) and Te (orange) atoms. The scale bar is 1 nm. (d) Multislice HAADF simulation of monolayer 1T′-MoTe₂, using lattice parameters a = 6.33 Å and b = 3.47 Å.³¹ (e) HAADF image of a bilayer region. The scale bar is 1 nm. (f) Multislice HAADF simulation of bilayer 1T′-MoTe₂.

In addition to single-crystal, rectangular monolayer MoTe₂ flakes, the growth procedure also produced polycrystalline flakes. The structure of one flake was analyzed by DF-TEM, where an aperture is used to select certain diffracted beams for image formation,^25,30 and a tilt boundary with a crystal lattice rotation of 121.7° ± 0.5° was identified, as shown in Figure S4. The measured boundary rotation, the SAED pattern at the boundary between the legs of the flake (Figure S4 center inset), and the DF-TEM image of the boundary indicate that the boundary lies along the (110) plane of one crystallite and the (11̄0) plane of the other, although grain boundaries were not imaged with atomic resolution. This particular rotation pattern was consistently observed in many polycrystalline flakes, implying that the legs of the polycrystalline flakes were grown at the same time and are not collisions of randomly oriented grains.

To image the atomic structure of 1T′-MoTe₂, aberration-corrected, high-angle annular dark field (HAADF) images were taken in a JEOL 200CF (Figure 3c,e) with a CEOS corrector for the STEM probe. The ACSTEM was operated at 80 kV to reduce beam-induced displacements (“knock-on” damage), although damage occurred, as expected given the weak bonding in MoTe₂. The images were postprocessed with a low-pass filter to remove high-frequency noise. The HAADF image in Figure 3c clearly reveals the atomic structure expected for monolayer 1T′-MoTe₂, where atoms in one of the unit cells are labeled for comparison. The HAADF image shows excellent agreement with the monolayer ball–stick model and a multislice HAADF simulation³² of monolayer 1T′-MoTe₂ (Figure 3d). The lattice constants are found to be a = 6.34 Å and b = 3.42 Å, which is in excellent agreement with previous reports.^13,31 In the images, the Te atoms are slightly brighter than the Mo atoms, as expected because the HAADF intensity is proportional to the square of the atomic number for monolayer samples. The majority of each flake was monolayer, but small (~10 × 10 nm) double-layer regions were also found, as shown in Figure 3e. The bilayer HAADF image is in excellent agreement with the simulated image (Figure 3f). The brightness in the double-layer regions is roughly twice that of the monolayer regions, which is in agreement with simulated images of mono- and bilayer regions (Figure S5). To our knowledge, this is the first report of atomic resolution images of monolayer 1T′-MoTe₂.

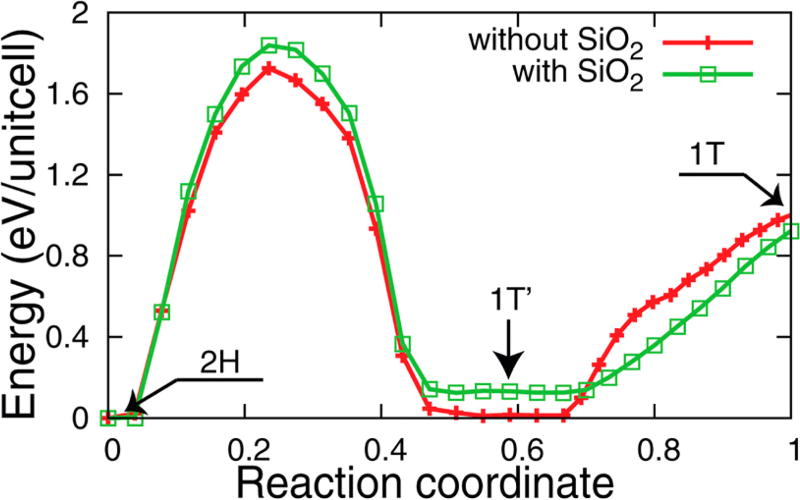
To further study the structural stability of monolayer 1T′-MoTe₂ on a SiO₂ substrate, we performed theoretical work using first-principles calculations. We first find that the 1T′-MoTe₂ layer adheres to the SiO₂ substrate with binding energy of 65 meV per unit cell of MoTe₂, which is a typical van der Waals-type interaction. We also find that the energy barrier between 1T′ and 2H increases from 1.73 to 1.85 eV/unit cell on the SiO₂ substrate (Figure 4). The 2H phase is slightly more stable on SiO₂, but the energy barrier between 1T′ and 2H is similar to and without a substrate. So while a phase transformation from 1T′ to 2H is possible if the right amount of energy is brought to the system, observing a phase transformation to 1T is unlikely as it would quickly revert back to the 1T′ phase. Thus, the SiO₂ substrate is a good platform to study the 1T′ phase of monolayer MoTe₂ and these computations support our hypothesis that monolayer MoTe₂ was grown directly in the 1T′ phase.

Figure 4.

Stability computation using first-principals. Structural stability of monolayer transition metal MoTe₂ with and without a SiO₂ substrate.

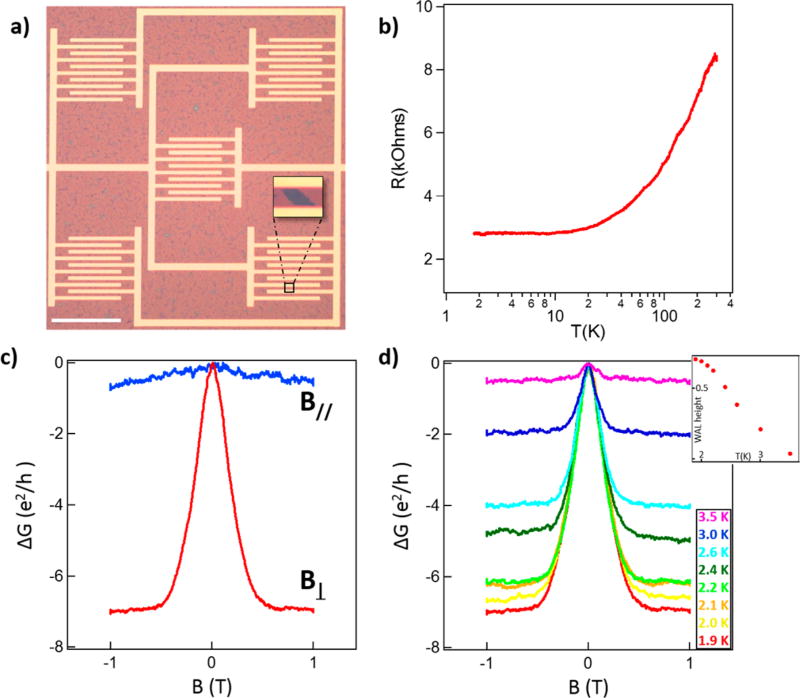
For electrical measurements of monolayer MoTe₂, samples were transferred onto a 275 nm SiO₂/Si substrate with prepatterned set of Au electrodes made by electron beam lithography. In order to preferentially probe the properties of the material rather than grain boundaries, care was taken to create the sample from a region dominated by rectangular single-crystal flakes rather than polycrystalline material. To minimize sample exposure to air, the transfer process was begun within minutes after growth and completed within 15–20 min. Each device contained five areas of interdigitated source and drain fingers (Figure 5a). To ensure that multiple MoTe₂ flakes bridge the electrode pairs, the electrode areas are separated laterally to sample a large growth area (~0.5 mm × 0.5 mm), and the source-drain separation is 5 µm, smaller than the typical size of MoTe₂ flakes (10–20 µm). Two devices were measured to determine the effect of temperature and applied magnetic fields on the electrical properties.

Figure 5.

Electrical measurements of monolayer MoTe₂-1T′. (a) Optical image of a device with MoTe₂ flakes contacted by electrodes. The scale bar is 100 µm. (Inset) Magnified view of a flake spanning the electrodes (image contrast has been enhanced). (b) Resistance versus temperature for monolayer 1T′-MoTe₂. (c) Magnetoconductance for applied fields parallel (blue) and perpendicular (red) to the sample at T = 1.9 K. (d) Magnetoconductance for temperatures from 1.9 to 3.5 K showing that the weak antilocalization feature disappears at higher temperatures. (Inset) WAL amplitude as a function of temperature.

The electrical resistance was monitored as the samples were cooled from 300 to 1.9 K. One sample had decreasing resistance with decreasing temperature, clearly demonstrating metallic behavior (Figure 5b). The resistance of the second sample generally increased with decreasing temperature, but nevertheless exhibited metallic behavior at low temperature as indicated by a positive slope of the reduced activation energy −d(ln R)/d(ln T) on a log–log plot versus temperature (Figure 6b). Measurements of the anisotropic magnetoconductance at various temperatures were quantitatively similar in both shape and absolute size for both samples (Figure 6d), strongly suggesting that the difference in temperature-dependent resistance arises from a series contact resistance. At low temperature, both samples exhibited a weak antilocalization (WAL) cusp-like feature at zero magnetic field (Figure 5c), which diminished with increasing temperature and could not be resolved for T > ~4 K (Figure 5d). The WAL effect is a signature of a metallic state in the presence of strong spin–orbit coupling^23,33,34 and can be associated with either bulk or topological surface states. A similar effect was recently reported for few-layer samples of WTe₂ produced by mechanical exfoliation.³⁶ We varied the applied field angle in order to examine the residual isotropic magnetoconductance. The WAL cusp disappears when the field is applied parallel to the plane of the material (Figure 5c), confirming the 2D nature of the WAL effect. Similar temperature and magnetic field dependence of the WAL cusp has been observed in topological insulator materials,^{23,33,35–38} and the data demonstrate that these materials possess strong electronic spin–orbit effects that are essential for the emergence of nontrivial topological electronic states.

In summary, we report the growth of monolayer, single-crystal 1T′-MoTe₂ over large areas by chemical vapor deposition. XPS measurements confirm the expected stoichiometry for MoTe₂. AFM, Raman, TEM, and ACSTEM measurements convincingly establish that the MoTe₂ material is of monolayer thickness in the 1T′ phase and single crystal. We were able to orient the crystalline axes based on the shape of rectangular crystallites, and we identified a clear preferential crystal growth direction for the MoTe₂ flakes along the $\stackrel{\rightharpoonup }{\mathbf{b}}$ axis. Low-temperature magnetoconductance measurements confirm the presence of a WAL cusp in monolayer MoTe₂. Thus, the structural and electronic ingredients necessary to realize topological surface states exist within this material. This advance in CVD growth and microscopic analysis paves the way for more detailed exploration of monolayer 1T′-MoTe₂, including its potential topological insulator properties and implementation in novel switching and sensor devices.

Methods

XPS

The chemistry of the near-surface region was investigated by XPS using a customized XPS spectrometer (VG Scienta AB, Uppsala, Sweden).³⁹ XPS analyses were performed using a monochromatic Al Kα source (photon energy 1486.6 eV). The residual pressure in the analysis chamber was less than 1 × 10⁻⁸ Torr. The spectrometer was calibrated according to ISO 15472:2001 with an accuracy of ±0.05 eV. Survey and high-resolution spectra were acquired in constant-analyzer-energy mode with the pass energies of 200 and 100 eV, respectively. The spectra were processed using CasaXPS software (v.2.3.16, Casa Software Ltd., Wilmslow, Cheshire, U.K.). Background subtraction was performed using the Shirley–Sherwood method. The quantitative evaluation of the XPS data was based on integrating the intensity of the Mo 3d_5/2 and Te 3d_5/2 peaks by taking the atomic sensitivity factors for those signals into account. The atomic sensitivity factors used were 1.66 for the Mo 3d_5/2 peak and 5.4 for the Te 3d_5/2 peak.⁴⁰ The reference energies for Mo 3d_5/2 and the Te 3d_5/2 peaks are 227.7 and 572.1 eV, respectively.

Raman

Raman was conducted on samples directly after growth. For single Raman spectra, spectroscopy was performed under ambient conditions with and excitation wavelength of 532 nm. An ND-MDT spectrometer was used. For Raman maps, graphene was transferred onto the MoTe₂ immediately following growth. This passivated the MoTe₂ from the environment and allowed Raman mapping to proceed for many hours without sample deterioration.

ACSTEM

For ACTEM imaging, MoTe₂ flakes were transferred onto a holey-carbon TEM grid using a PMMA-assisted transfer. ACSTEM of suspended MoTe₂ flakes was performed with a JEOL ARM 200CF equipped with a CEOS corrector. The TEM was operated at 80 kV to reduce knock-on damage. Images were acquired with a high-angle annular dark field detector. A low-pass filter was applied to the images to reduce noise. Selected-area electron diffraction patterns were acquired in TEM mode using a selected-area aperture with an effective size at the sample of ~1 µm.

HAADF Simulations

QSTEM³² was used to perform multislice HAADF-STEM simulations. Microscope parameters for the 80 kV JEOL ARM 200CF were used for the simulation. These include C_s = 635 nm and C₅ = −55 µm. Other parameters used were C_c = 1 mm, dE = 0.5 eV, convergence angle = 20 mrad, HAADF detector inner angle = 70 mrad, HAADF detector outer angle = 200 mrad, defocus = −2 nm, brightness = 5 × 10⁸ A/cm²sr, and a dwell time of 1 µs. For each simulation, the simulation window size used was one unit cell, 6.33 Å × 3.469 Å with sampling 20 pix × 20 pix.

Structural Stability Simulations

To access the influence of SiO₂ on the stability of MoTe₂ single layer in 1T′ phase, we performed first-principles calculations based on density functional theory (DFT). We use the Perdew–Burke–Ernzerhoftype generalized gradient approximation⁴¹ as implemented in the Quantum Espresso package.⁴² Norm-conserving, optimized, designed nonlocal pseudopotentials are generated using the Opium package.^43,44 The energy barriers of MoTe₂ were calculated employing the nudged elastic band (NEB) approach as found in the Quantum Espresso package. The SiO₂ substrate was modeled using a slab geometry with four unit cells along (100) and a 3 × 1 supercell along (010) and (001) directions, respectively. The outer oxide atoms were passivated with hydrogen atoms. A 2 × 2 unitcell of MoTe₂ of 1T′ phase was placed on a SiO₂ substrate, which induces a negligible strain on MoTe₂ and 15 and 7% artificial compressive strain on the SiO₂ substrate. The structure of substrate is fully optimized without MoTe₂ under strain then used throughout the energy barrier calculations of MoTe₂/SiO₂ system. The van der Waals interaction is described based on the semiempirical dispersion-correction DFT (DFT-D) method.⁴⁵

Electrical Measurements

Samples were loaded onto a rotating insert in a Quantum Design Physical Property Measurement System (PPMS). Temperature and magnetic field-dependent electrical measurements were taken using a 1.0 mV source-drain bias using a Keithley 237 Source-Measure Unit. Current–voltage curves were collected at temperatures from 1.9 to 300 K in order to determine the regime of linear operation, and the source-drain bias chosen accordingly. The angle of the magnetic field was calibrated first visually and then trimmed by nulling the WAL effect to determine the angle for B_‖.

ABBREVIATIONS

CVD

chemical vapor deposition

WAL

weak antilocalization

TEM

transmission electron microscopy

ACSTEM

aberration-corrected scanning TEM

TMD

transition metal dichalcogenide

AFM

atomic force microscopy

XPS

X-ray photoelectron spectroscopy