Periodic Arrays of Phosphorene Nanopores as Antidot Lattices with Tunable Properties

Abstract

A tunable band gap in phosphorene extends its applicability in nanoelectronic and optoelectronic applications. Here, we propose to tune the band gap in phosphorene by patterning antidot lattices, which are periodic arrays of holes or nanopores etched in the material, and by exploiting quantum confinement in the corresponding nanoconstrictions. We fabricated antidot lattices with radii down to 13 nm in few-layer black phosphorus flakes protected by an oxide layer and observed suppression of the in-plane phonon modes relative to the unmodified material via Raman spectroscopy. In contrast to graphene antidots, the Raman peak positions in few-layer BP antidots are unchanged, in agreement with predicted power spectra. We also use DFT calculations to predict the electronic properties of phosphorene antidot lattices and observe a band gap scaling consistent with quantum confinement effects. Deviations are attributed primarily to self-passivating edge morphologies, where each phosphorus atom has the same number of bonds per atom as the pristine material so that no dopants can saturate dangling bonds. Quantum confinement is stronger for the zigzag edge nanoconstrictions between the holes as compared to those with armchair edges, resulting in a roughly bimodal band gap distribution. Interestingly, in two of the antidot structures an unreported self-passivating reconstruction of the zigzag edge endows the systems with a metallic component. The experimental demonstration of antidots and the theoretical results provide motivation to further scale down nanofabrication of antidots in the few-nanometer size regime, where quantum confinement is particularly important.

Graphical abstract

Few-layer black phosphorus (BP) has prompted much interest recently due to the balance it brings between the semiconducting band gap and large on/off ratio of transition metal dichalcogenides (TMDs) and the high carrier mobility of graphene.¹ However, in order to make single-layer black phosphorus (“phosphorene”) more widely applicable in optoelectronic devices, it is necessary to devise methods to tune its ~2 eV electronic (transport) band gap as measured by scanning tunneling spectroscopy.² Nanostructures obtained by dimensionally reducing bulk BP to few-layers, nanoribbons (NRs), and quantum dots exhibit shifts in the intrinsic band gap due to quantum confinement.³ An increasing band gap with decreasing number of layers was predicted theoretically^2,4–13 and demonstrated experimentally from photoluminescence spectroscopy.^12,14–18 These theoretical and experimental studies collectively show that the band gap is direct irrespective of the number of layers. This is a further improvement over TMDs, which only have a direct band gap in the single-layer limit.¹⁹ Phosphorene nanoribbons (PNRs) also feature an increasing band gap with decreasing width for various edge configurations and dopants.^20–30 Additionally, the band gap of phosphorene quantum dots is predicted to be tunable by varying the shape, edge configuration, and edge dopant.^31–33

A dimensionally reduced form of phosphorene that has yet to be explored electronically is the antidot lattice,³⁴ which is a periodic array of holes embedded into a material. From the simplest perspective, shifts in the energy levels are expected due to quantum confinement in the nanoconstrictions between the holes. The entire structure can be also construed as a network of curved NRs in two dimensions. Effects due to edge configuration and dopant are also expected, as is the case for PNRs.^20–30 Theoretical studies have already predicted a tunable band gap in antidot lattices composed of graphene,^35–66 MoS₂,⁶⁷ and hexagonal BN.⁴⁷ In the original work on graphene, nearly circular holes were centered in hexagonal supercells. The band gap was found to scale with KN_R^0.5/N_T for values of the ratio up to around 0.02, where N_R is the number of atoms removed from a supercell with N_T total atoms, and K is 25 eV.³⁵ It was later shown that an integral parameter W could be used to characterize the hexagonal supercell, which revealed that the odd values had not been previously considered. In particular, the apparently off-centered placement of the circular hole in the supercell for odd W results in no band gap despite the presence of quantum confinement.⁴⁹ Similar behavior was shown to occur for rotated triangular, rectangular, and honeycomb supercells, where only one-third of the possible structures have a large band gap.⁴⁶ Furthermore, the band gap is tunable for triangular and rhombohedral holes with armchair or zigzag edges in square supercells and oscillates when plotted against particular geometric indices.⁴¹ Note that the band gap scaling follows the expected quantum confinement trends in general for the cases where there is no reduction by symmetry rules; that is, the band gap increases as the constrictions between the holes are narrowed.^41,46,49 To make a connection to experiments, one theoretical work considered holes deviating from regular shapes and showed that the symmetry rules resulting in a small band gap are less applicable as the disorder increases.⁵⁷ Experiments have also been used to formally confirm the opening of a transport gap in graphene antidot lattices,^68–74 where the gap increases as the constriction width is decreased.⁷¹ In addition, Raman spectroscopy has indicated the presence of systematic p-type doping,^73,75–77 which results from edge doping.⁷⁷

In this paper, we study BP antidot lattices experimentally and theoretically. Nanoscale antidots in few-layer BP capped by an oxide layer are fabricated using plasma thinning along with electron beam (EB) lithography. The structures are subsequently characterized by Raman spectroscopy. Using first-principles density functional theory (DFT) calculations, we also construct a number of realistic phosphorene antidot lattice (PAL) models, quantify structural stability, and describe the electronic properties by plotting the density of states. The density of states results in net and spatial distributions of the band gap, which elucidate the role of quantum confinement and its anisotropy, respectively. The impact of edge morphology on the electronic properties is determined by plotting the charge density corresponding to states at the edges of the band gap.

RESULTS AND DISCUSSION

Fabrication of Antidots

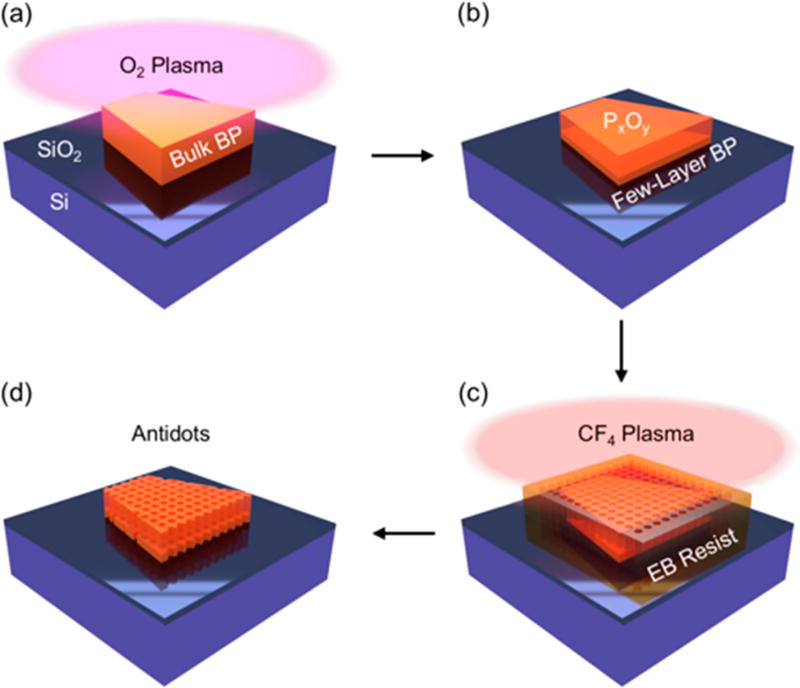
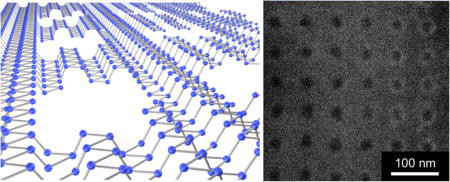
Figure 1 demonstrates the step-by-step fabrication procedure we developed to create antidot lattices in few-layer black phosphorus flakes using electron beam lithography, which has previously been used to fabricate similar structures in graphene.^68,78,79 Further experimental details can be found in the Methods section under Antidot Fabrication. Bulk BP flakes are first mechanically exfoliated onto SiO₂/Si substrates and thinned using a previously reported oxygen (O₂) plasma etching technique (Figure 1a).¹⁶ Thickness calibration curves obtained through simultaneous thinning, Raman, and atomic force microscopy (AFM) measurements can be found in Section S1 in the Supporting Information. The thinning process allows for precise control of the few-layer BP thickness and introduces a phosphorus oxide (P_xO_y) capping layer that greatly improves sample stability during lithography and in-air Raman measurements (Figure 1b). We find that a few-layer BP thickness of between 8 and 10 nm (13–16 layers) minimizes oxidation effects on the Raman map while maximizing signal-to-noise ratios. Since thinner BP samples experience an increased rate of oxidation and a drop in Raman signal intensity,⁸⁰ samples thinned to this range allow us to obtain measurable Raman signals with minimal oxidation over time scales of 10–12 h (see Figure S2.1). After thinning, samples are coated with a thin layer of resist and square antidot arrays are patterned using EB lithography (Figure 1c). Tetrafluoromethane (CF₄) plasma is then used to etch away the exposed material, resulting in an antidot-patterned few-layer BP flake passivated with P_xO_y (Figure 1d). After resist removal, the flakes are exposed to an additional plasma-cleaning step.

Figure 1.

Schematic of antidot fabrication steps in few-layer black phosphorus. (a) Exfoliation and O₂ plasma thinning of bulk BP on a SiO₂/Si substrate yields (b) a P_xO_y-capped few-layer BP flake. (c) After the sample is coated in resist, antidot arrays are patterned using electron beam lithography and etched in CF₄ to remove the exposed P_xO_y/BP. (d) Finally, the process yields a P_xO_y-passivated few-layer BP antidot lattice. Typical superlattice constants and antidot radii are 60–65 nm and 13–23 nm, respectively.

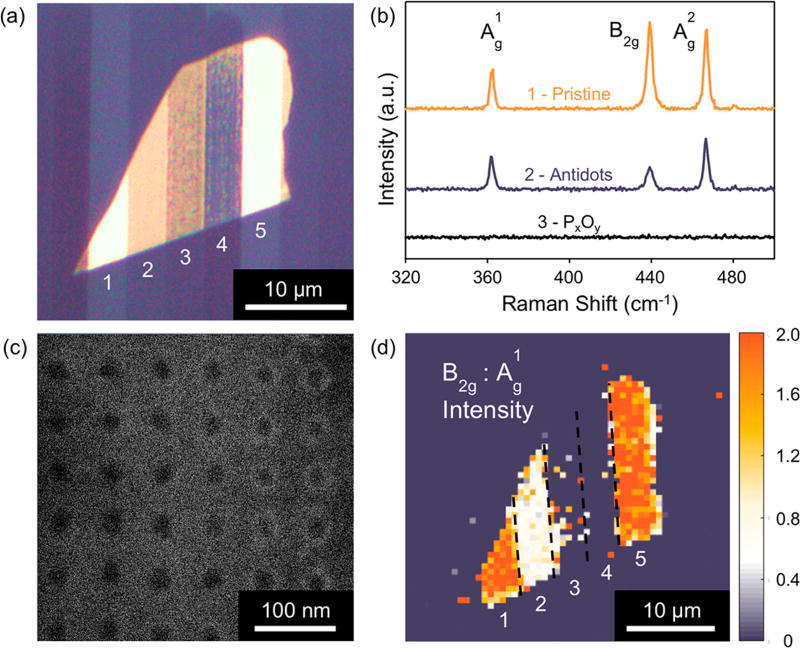
An optical image of a few-layer BP flake containing an antidot lattice is given in Figure 2a. Due to the thickness, oxidation, and orientation-dependent properties of black phosphorus,^1,6,12 regions (1) and (5) of the flake were not subjected to antidot patterning and are referred to as pristine. Regions (2), (3), and (4) correspond to a few-layer BP antidot lattice, P_xO_y, and a strip of the bare SiO₂/Si substrate, respectively. SEM images of multiple samples reveal highly uniform antidot lattices with superlattice constants (SC) of 60–65 nm and radii (R) of 13–23 nm (Figure 2c), in line with the smallest reported graphene antidots fabricated via EB lithography.⁷⁹

Figure 2.

Characterization of fabricated antidot arrays in few-layer BP. (a) Optical image of columnar regions with (1) pristine few-layer BP, (2) patterned antidots (SC = 60 nm and R = 23 nm), (3) P_xO_y, (4) bare SiO₂/Si substrate, and (5) pristine few-layer BP. (b) Raman spectra of (1) pristine few-layer, (2) antidot, and (3) P_xO_y regions normalized to the ${\mathrm{A}}_{\mathrm{g}}^1$ peak of (1), showing suppression of the in-plane modes (B_2g and ${\mathrm{A}}_{\mathrm{g}}^1$) in the antidot region. (c) SEM image of a square antidot array with SC = 65 nm and R = 13 nm. (d) ${\mathrm{B}}_{2\mathrm{g}}:{\mathrm{A}}_{\mathrm{g}}^1$ intensity Raman map from the sample in (a). Note: SC is the average in-plane superlattice constant and R is the average antidot radius.

Characterization of Antidots by Raman Spectroscopy

It has been shown that graphene antidot lattices exhibit p-type doping, as evidenced by strong Raman shifts in both the G and 2D peaks.^75,76 Here, we use Raman spectroscopy in order to analyze the effects of forming antidots in few-layer BP. The Raman spectrum from a 532 nm excitation line for black phosphorus reveals one out-of-plane mode ( ${\mathrm{A}}_{\mathrm{g}}^1$) and two in-plane modes that are associated with phonons in the zigzag (B_2g) and armchair ( ${\mathrm{A}}_{\mathrm{g}}^2$) directions. In particular, the frequency of the ${\mathrm{A}}_{\mathrm{g}}^2$ mode exhibits a strong thickness dependence with shifts from 466 cm⁻¹ for bulk black phosphorus up to 470–471 cm⁻¹ for monolayer phosphorene.^81,82 Thinned BP flakes, such as those found in region (1) from Figure 2a, exhibit ${\mathrm{A}}_{\mathrm{g}}^1$ (362 cm⁻¹), B_2g (439 cm⁻¹), and ${\mathrm{A}}_{\mathrm{g}}^2$ (467 cm⁻¹) peaks that are consistent with a few-layer (8–10 nm) structure (Figure 2b). Upon patterning, the antidot region (2) exhibits negligible changes (±0.5 cm⁻¹) in the frequency of all three major Raman modes. This result is also predicted theoretically by calculating the normal-mode frequencies for pristine phosphorene and a phosphorene antidot system using direct diagonalization of the dynamical matrix and the power spectrum method within DFT (see Theoretical Methods section and Figure S10). As suggested by a recent work, the absence of a shift in frequencies as well as full-widths at half-maximum (see Figure S2.1) rules out any n-type doping in the antidot lattice but is inconclusive toward the presence of p-type doping.⁸³ Furthermore, this result indicates the structure is likely free of any strain since stretching- and compression-induced Raman frequency shifts up to 11 cm⁻¹/(% strain) are expected in both phosphorene and few-layer BP.^84,85 We also note that across samples the ${\mathrm{A}}_{\mathrm{g}}^1:{\mathrm{A}}_{\mathrm{g}}^2$ intensity ratio (i.e., the ratio of peak heights) remains between 0.5 and 0.6 from pristine to antidot regions, excluding the likelihood of thinning or oxidation due to atmospheric exposure or patterning.⁸² In fact, overetching results in only amorphous P_xO_y (region (3)), which displays no discernible Raman signature as expected (Figure 2b).¹⁶

As shown in Figure 2b, we observe suppression of both in-plane modes in the antidot lattices in comparison to pristine few-layer BP. Figure 2d graphically shows that from the pristine few-layer BP to the patterned antidot region, the normalized ${\mathrm{B}}_{2\mathrm{g}}:{\mathrm{A}}_{\mathrm{g}}^1$ intensity ratio exhibits a significant drop from roughly 2.0 to 0.9, suggesting relatively strong suppression of the in-plane zigzag phonon mode. A similar, but comparatively weaker, effect is also observed for the in-plane armchair mode, as evidenced by the ${\mathrm{A}}_{\mathrm{g}}^2:{\mathrm{A}}_{\mathrm{g}}^1$ intensity Raman map in Figure S2.2. Further evidence of this effect can be found in Section S2 with additional Raman maps for fabricated antidot lattices. While strengthening of the in-plane Raman D mode in graphene antidot lattices has been shown to be due to fabrication-induced defects, suppression of the in-plane G mode has been attributed to a change in the phonon density of states (DOS) resulting from antidot-induced quantum confinement and follows a similar trend to what is demonstrated here.^53,75,86

Construction of Phosphorene Antidot Lattice Atomic Models

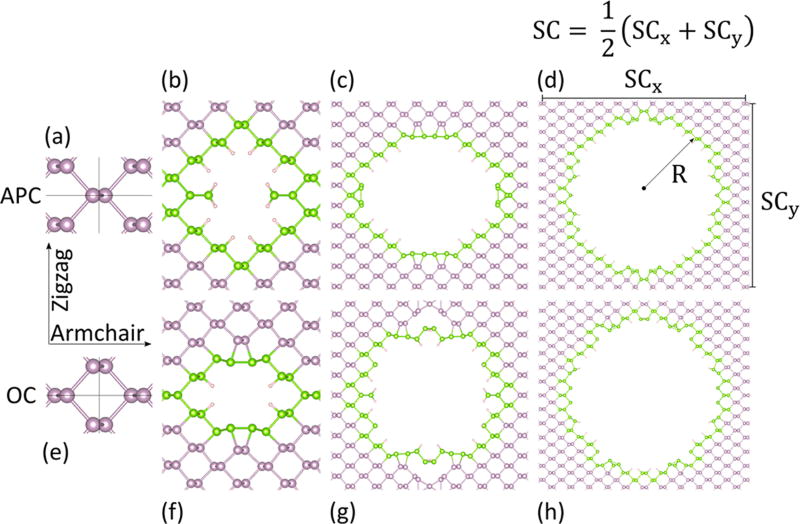
With the fabrication of few-layer black phosphorus antidot lattices with dimensions of tens of nanometers in radii and supercell size established, the rest of this paper explores the electronic properties of freestanding phosphorene antidot lattices at the few-nanometer scale, where the impact of quantum confinement and edge morphology becomes important. In order to be consistent with the experimental fabrication, roughly circular perforations placed on a rectangular superlattice are considered. The starting point is a phosphorene unit cell with armchair, zigzag, and out-of-plane directions extending along x, y, and z, respectively. Two different unit cell symmetries are used, atom pair center (APC) and open center (OC), as shown in Figure 3a and e, respectively. For each of these symmetries four different supercells are formed, with the center of the supercell defined as the origin. To describe the supercells with one parameter, the average in-plane superlattice constant SC is calculated (see Figure 3 for schematic representations of all relevant geometric parameters): the obtained values are 1.49, 3.02, 4.56, and 5.99 nm. The antidot geometries are formed by only considering the projection in the xy plane. Consequently, we will label the nth atom of the supercell as (x_n, y_n). The nth atom is removed from the supercell if (ΔR)_n > 0 and |(ΔR)_n| > R_c where (ΔR)_n = R − R_n, R is the targeted antidot radius, R_n² = x_n² + y_n², and R = 0.25 Å is a cutoff value that is chosen such that the resulting structure features as few dangling bonds as possible. In other words, an atom is removed if it is inside the targeted antidot circle by more than a cutoff value. The targeted radii are set to the same values for the APC and OC symmetries. After these structures are allowed to relax (which can lead to a number of self-passivation processes governed by edge reconstruction), we passivate phosphorus atoms with hydrogen to preserve a coordination number of 3 for each P and relax again. This procedure implicitly assumes that the lattice relaxation is faster than the adsorption of hydrogen to the edges, which is reasonable for a fabrication vessel under good vacuum. Figure 3 (b–d for APC and f–h for OC) provides a number of examples of optimized geometries, where the edge atoms are shown in green. Representations of all structures studied are archived in Section S3. There is clearly a difference between corresponding (same supercell size and nearly the same radius) APC and OC structures. A number of previously studied edge configurations (via PNRs) are found as a result of our optimization procedure, including the armchair (AC), zigzag single termination (ZZ-1), 2×1 inner-shifted reconstruction of the ZZ-2 edge (ZZRC-i), and the 2×1 outer-shifted reconstruction of the ZZ-2 edge (ZZRC-o). ZZ-2 is the zigzag double termination edge. Schematics for all of these edges are displayed in Figure 2a from our previous work.⁸⁷ During our minimization procedure, we also discovered a number of unreported stable edge reconstructions present in the edges that have yet to be studied independently. Our recent review article on black phosphorus nanostructures discusses other known self-passivating edge configurations that are not present in the antidot geometries.³ Specific edge configurations impact the stability and electronic properties, which will be discussed later. Numerical values for geometric parameters including the supercell size, radius (calculated as the average of all edge atom radii after relaxation), and the standard deviation in the radius are tabulated in Section S4. Details of the calculations and the edge-passivation process are deferred to the Theoretical Methods section. In this work the antidots were fabricated by exposure to CF₄ plasma, which would likely result in passivation of the dangling bonds at the hole edges by F due to its large electronegativity. The band gap scaling (which is the primary interest) for H or F passivation in AC and ZZ-1 PNRs follows the quantum confinement increase in band gap with decreasing width. The curves nearly overlap, except below widths of 1 nm, where the difference becomes up to ~0.5 eV.^21,24 A similar trend applies in comparing H to Cl or OH passivation.²¹ Therefore, the band gap scaling for the antidots passivated by H is expected to be similar to what it would be if the passivation was by F instead, except perhaps shifted for small constriction widths. The similarity between the edge dopants can be explained by noting that each requires interaction with one phosphorus dangling bond to complete the outer electronic shell.

Figure 3.

Optimized hydrogen-passivated phosphorene antidot lattices with defined edge atoms represented in green and interior atoms colored in purple.¹⁰¹ The geometric parameters are schematically defined for one of the structures. SC_x and SC_y refer to the in-plane superlattice constants along the armchair and zigzag directions, respectively. SC is then defined as the average of these two values, and R is the antidot radius, which is the average of the radii for the green edge atoms. Rows of atoms across from each other on the edges of the antidot unit cell are equivalent. (a) Illustration of the atom pair center (APC) symmetry; (b) APC with SC = 1.49 nm and R = 0.56 nm; (c) APC with SC = 3.02 nm and R = 1.14 nm; (d) APC with SC = 4.56 nm and R = 1.86 nm; (e) Illustration of the open center (OC) symmetry; (f) OC with SC = 1.49 nm and R = 0.43 nm; (g) OC with SC = 3.02 nm and R = 1.15 nm; (h) OC with SC = 4.56 nm and R = 1.86 nm.

Thermodynamic Stability (Edge Energy)

To quantify the stability of an antidot structure, the edge energy is defined

$$F_{\text{edge}}=\frac{1}{N}\{F_{\text{PAL}}-[N_{\mathrm{P}}{F}_{\mathrm{P}}+N_{\mathrm{H}}\left(\frac{F_{{\mathrm{H}}_2}}{2}\right)\left]\right\}$$ (1)

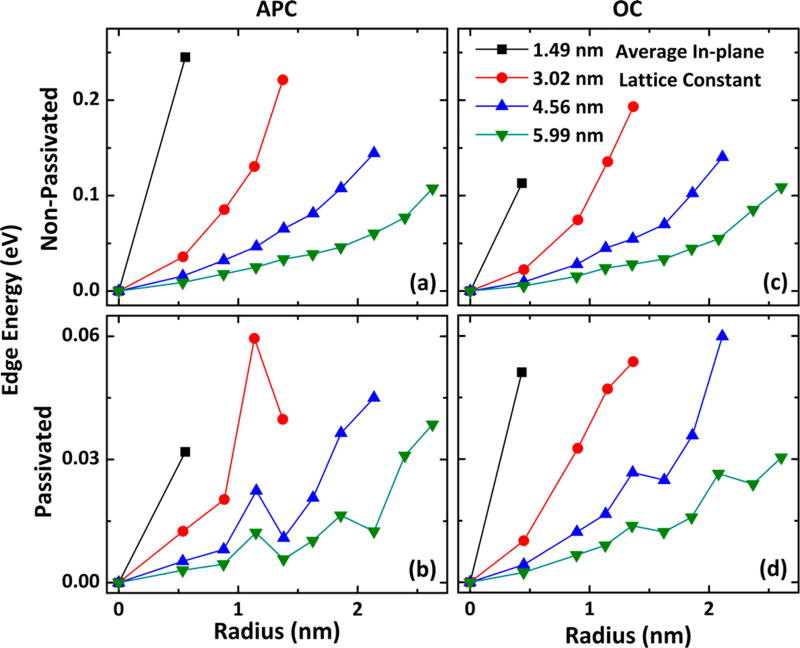
where F_P is the free energy per phosphorus atom in an infinite phosphorene layer, F_H2 is the free energy of an isolated hydrogen molecule, F_PAL is the total free energy of the antidot structure (PAL = phosphorene antidot lattice), N_P is the total number of phosphorus atoms, N_H is the total number of hydrogen atoms, and N is the total number of atoms. In other words, the total energy of the antidot structure is compared to the energy the system would have if the phosphorus atoms remained in the pristine phosphorene sheet and if the hydrogen atoms remained in the noninteracting gas phase. This value is then normalized to the total number of atoms to allow for comparison between structures. The edge energy was computed for every structurally relaxed non H-passivated and H-passivated structure for APC (Figure 4a,b) and OC (Figure 4c,d), respectively. For all cases, passivation stabilizes the structures (lowers the edge energy). The explicit difference in edge energy between the non-passivated and passivated cases is plotted in Figure S5.1. In considering decreasing the supercell size for a given radius or increasing the radius for a given supercell size, in general, both operations decrease the stability and increase the amount of energy by which passivation stabilizes a given structure. The presence of an edge, which is the destabilizing factor, represents a larger fraction of the system when the spacing between the holes is decreased or the radius of the holes is increased. For seven of the passivated cases incrementing the radius to the next largest value can stabilize the system. In each circumstance the number of self-passivation segments in the edge is larger in the less stable structure. This informally implies that hydrogen passivation is energetically preferable to self-passivation. However, this does not mean that self-passivated edges will transition to other edge configurations with dangling bonds and be subsequently hydrogen passivated and/or that the radius will increment to the next largest value spontaneously. Such conclusions would require studying the kinetics via transition state tools such as the nudged elastic band method, which has been applied to the edges of phosphorene in other works.^87,88 The energy barrier can then be compared to the thermal energy to determine the probability of a structural transformation. Furthermore, in incrementing to the next largest radius the removed phosphorus atoms do not automatically rearrange into a pristine phosphorene sheet, which is the free energy value that goes into the edge energy calculation. Another important feature to inspect is the difference in edge energy between corresponding APC and OC structures. For both the nonpassivated (Figure S5.2a) and passivated (Figure S5.2b) cases the energy difference is less than the order of the thermal energy at room temperature (25 meV). This implies that there is no expectation for a preferred symmetry to emerge in fabricated antidots. The only exception is the non-passivated SC = 1.49 nm case; however, the radii and shape of the hole between these two systems are sufficiently different to exclude this observation.

Figure 4.

Calculated stability as quantified by the defined edge energy (eq 1). (a) APC non-passivated. (b) APC passivated. (c) OC non-passivated. (d) OC passivated. For all cases, passivation stabilizes the structures (lowers the edge energy). The presence of an edge, which is the destabilizing factor, represents a larger fraction of the system when the spacing between the holes is decreased or the radius of the holes is increased (therefore edge energy increases). For seven of the passivated cases incrementing the radius to the next largest value can stabilize the system. In each circumstance the number of self-passivation segments in the edge is larger in the less stable structure.

Electronic Density of States

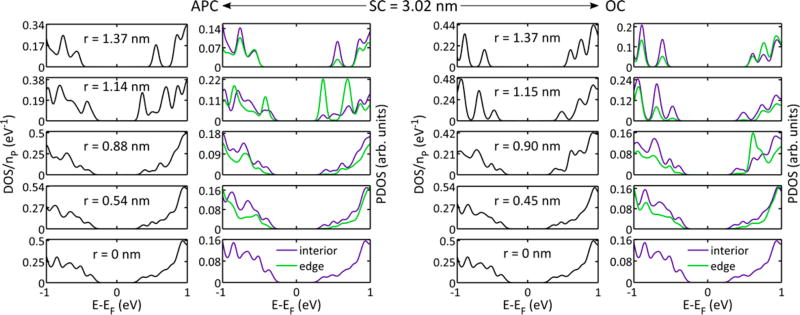
The electronic properties of the phosphorene antidot lattices were studied within DFT by inspecting the density of states and site-projected density of states (PDOS) for each structure (details of calculations in the Theoretical Methods section). The PDOS is decomposed into contributions from the edge (green) and interior (purple) atoms (see Figure 3 and Section S3 for edge/interior designation). The DOS and PDOS of the edge/interior are visualized in Figure 5 for SC = 3.02 nm for both APC (a) and OC (b) symmetries with all radii considered. All DOS and PDOS of the edge/interior plots for the different supercell sizes are given in Section S6. The DOS plots show that a non-negligible evolution of the band gap occurs as the radius is varied for a given supercell symmetry. In general, the PDOS from the edge is smaller than and/or similar in shape to the PDOS from the interior near the end points of the band gap. This suggests that the configuration of the edge will not significantly impact the band gap scaling with size. This is expected since the saturation of the edge dangling bonds by hydrogen pushes any in-gap states present in an unsaturated structure out of the gap. For example for H-passivated PNRs with AC,^20,22,25,30 ZZ-1,^20–22,25 ZZRC-o,²⁰ and diagonal²⁰ edges, the conduction band minimum (CBM) and valence band maximum (VBM) have charge densities that are global states (i.e., not edge-localized). There are still a few systems that contain a relatively large contribution from the edge. The notable feature of these systems is that they contain self-passivated edges. However, the band gap may not be affected by some of these edge morphologies because each PDOS curve is normalized to the respective number of atoms and therefore does not reflect the behavior of the DOS. Two structures have metallic signatures (APC SC = 4.56 nm and SC = 5.99 nm both with R = 1.15 nm; see Section S6), and this quite unexpected result will be discussed later in a separate section.

Figure 5.

Electronic density of states for SC = 3.02 nm calculated with DFT. The two left columns are for APC, and the two right columns are for OC (see Figure 3). The left column in each set is the total density of states with normalization to the number of phosphorus atoms (radii given), and the right column in each set is the site-projected density of states decomposed by edge and interior atoms with normalization to the respective number of atoms. In some cases, the size of the band gap is limited by contributions due to the edge atoms (for instance APC with R = 1.14 nm).

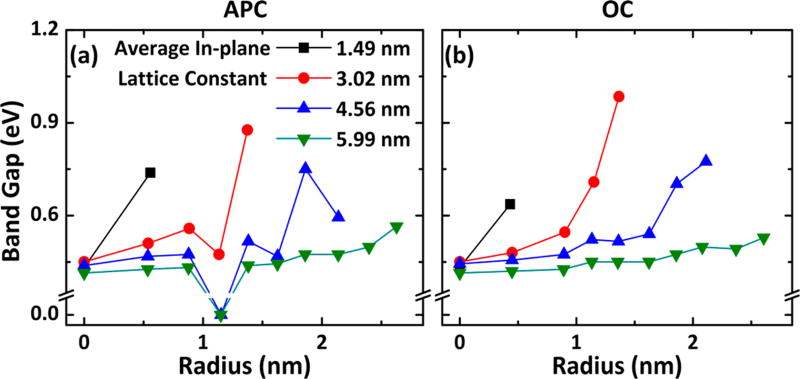
Electronic Band Gap Scaling

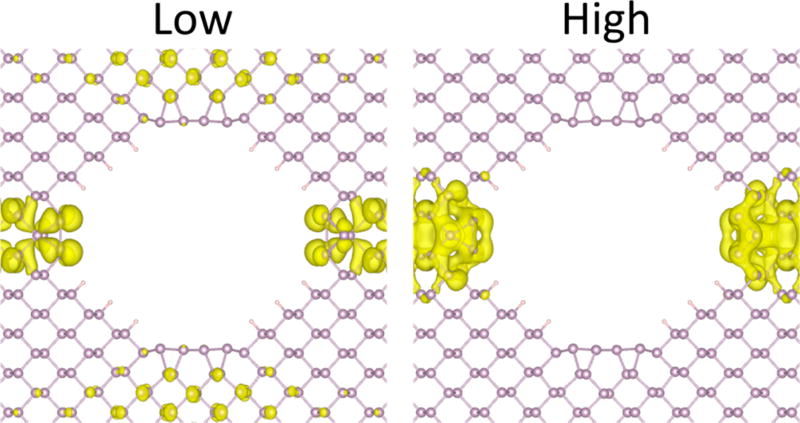
In order to compare the different antidot structures more systematically, the band gaps were calculated from the DOS and plotted against the radius. The band gap scaling relations for APC and OC are given in Figure 6a and 6b, respectively. As the nanoconstrictions (NCs) between the holes decrease in size, the increase in quantum confinement is expected to increase the band gap.³ This implies that for a constant radius decreasing the supercell size (decreasing the spacing between holes) should increase the band gap. Also, for a constant supercell size increasing the radius should increase the band gap. This trend is followed by 32/42 of the antidot structures considered here. To obtain some insight into the 10 deviations, the difference in the band gap between corresponding APC and OC structures was computed (Figure S7.1) and is non-negligible in several cases. Since the geometric parameters that determine quantum confinement effects are nearly the same, this suggests that the deviations could result from in-gap states from self-passivated regions in the edge. For instance, the band structure for PNRs with the ZZRC-i edge (which is found in a number of the PAL structures) contains a band below the Fermi energy with charge density corresponding to the edge.² A simple approach to evaluate this claim is to calculate the band gap using the phosphorus PDOS from all atoms (Figure S7.2) and the phosphorus PDOS excluding the edge atoms (Figure S7.3) and then compare the results. The band gap scaling trends differ negligibly, which suggests edge configuration cannot account for the deviations. However, when the wave function is projected onto the interior atoms, it contains the influence of the edge atoms. This means that the edge contribution cannot be completely removed using this method. A better approach is to evaluate the charge density corresponding to two different energy ranges: the first range is the lower edge of the band gap minus 0.2 eV (“low”), and the second range is the upper edge of the band gap plus 0.2 eV (“high”). This is visualized in Figure 7 for APC SC = 3.02 nm and R = 1.14 nm. The band gap limiting contribution originates from the self-passivating ZZRC-i edge on both the lower and upper edge of the band gap. The charge densities for all deviation cases (except for two metallic systems) are shown in Section S8. In 5/8 of the systems at least one of the lower and upper contributions results in part from self-passivation in the edge. In particular, in 4/5 cases the ZZRC-i edge is involved. For the other 3/8 cases it could be that the band gap is not underestimated, but rather the previous structure has an overestimated band gap. Such deviations can be rationalized by noting that the band gap scaling is slightly different between ZZ-1 and ZZRC-o hydrogen-saturated PNRs even though the VBM and CBM charge densities are globally distributed.²⁰ In other words, the edge atoms can couple to the interior atoms to produce global changes in the electronic properties. Although 0.2 eV is a significant fraction of the band gap, a sufficient energy range is required to generate non-zero values for the charge density. Even after correcting for edge effects, the band gap scaling laws would still not form smooth curves in general, as might be expected from an elementary quantum mechanics calculation. However, notice that the OC SC = 3.02 nm band gap scaling is smooth (see Figure 6b). In addition to not hosting any self-passivation in the edges, these systems have relaxed hole geometries that are nearly square, not circular. This suggests that the shape of the quantum well affects the band gap scaling in addition to the confinement length and edge morphology.

Figure 6.

Scaling of calculated band gap with radius for multiple supercell sizes. (a) APC symmetry. (b) OC symmetry. In increasing the radius or spacing the holes closer together, the nanoconstrictions narrow, which increases the band gap due to quantum confinement. Deviations can be primarily explained by edge morphology (see next figure). Note that DFT underestimates the band gap due to the structure of the approximate form of the exchange correlation energy functional.^102–104 Only the qualitative scaling is of interest.

Figure 7.

Band gap limiting charge density for APC with SC = 3.02 nm and R = 1.14 nm. The panel labeled “Low” corresponds to the energy range from the lower edge of the band gap to 0.2 eV lower, and the panel “High” corresponds to the energy range from the upper edge of the band gap to 0.2 eV higher. The isosurface values are 6.4 × 10⁻⁴ (low) and 8.2 × 10⁻⁴ (high) in units of a₀⁻³, where a₀ is the Bohr radius. In both cases the self-passivating zigzag reconstruction ZZRC-i is a limiting factor in the size of the band gap and describes the deviation in the band gap scaling from what is expected from quantum confinement. Recently the ZZRC-i edge was experimentally observed under TEM conditions.¹⁰⁵

A notable feature with important experimental implications is the “size effect” in the band gap scaling. The maximum radius of an antidot that can be formed increases as the size of the supercell increases. This enables the minimum obtainable confinement length in the armchair and zigzag NCs to be roughly the same between different supercell sizes. However, the maximum increase in the band gap that can be obtained from the maximal radius decreases as the supercell increases. This is apparent from the maximal radii in OC SC = 3.02, 4.56, and 5.99 nm (see Figure 6b) since edge effects do not impact these data points. To account for this observation, it can be shown that the limiting confinement length occurs along the diagonal direction and is dependent on the size of the supercell. For circular holes (radius R) in square supercells (superlattice constant L), simple geometric manipulations result in a diagonal length between the edges of d = √2L − 2R. The minimum confinement length along armchair and zigzag NCs occurs when R ≲ L/2. In this case the minimum confinement length along the diagonal direction is d_min ≳ (√2 − 1)L. This implies that the minimum confinement length that can be obtained is proportional to the size of the supercell. More importantly, the largest possible increase in the band gap decreases with increasing supercell size. This means that, in order to experimentally observe appreciable shifts in the band gap due to quantum confinement, the supercell dimensions need to be on the order of a few nanometers, not tens of nanometers as was previously considered for graphene.^68–74 Moreover, supercell and perforation geometries can be chosen to optimize the quantum confinement shift in the band gap using commensurate geometries. For instance, consider square supercells again, but now with square perforations of side length l. In this case the diagonal confinement length is d = √2(L − l). From the relation l ≲ L one obtains d ≳ 0. That is, there is no expected size effect for square perforations with square supercells, i.e., when the hole and supercell shapes are commensurate. However, achieving small square perforations may be more experimentally challenging since the fabrication probe is circular.

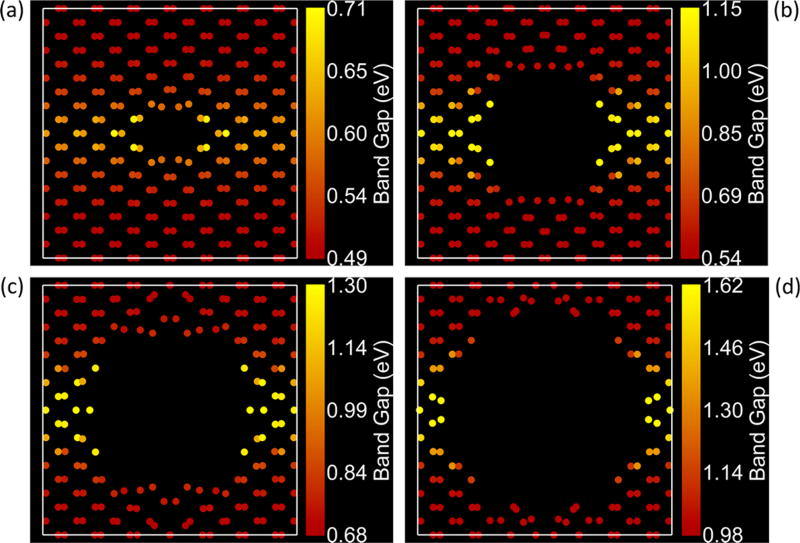
Spatial Distribution of the Band Gap: Anisotropy of Quantum Confinement

Since the PDOS was calculated, it is possible to obtain the effective local band gap and then plot the spatial distribution. This is shown in Figure 8 for all radii with the OC symmetry and SC = 3.02 nm and in Section S9 for all structures. The resulting distribution is approximately bimodal in all structures. In general, the higher band gap regions are located in the zigzag NCs and the lower band gap regions are present in the armchair NCs, both having a similar confinement width, thus demonstrating the anisotropy of quantum confinement effects in phosphorene. This is also consistent with the presence of stronger quantum confinement effects in hydrogenpassivated PNRs of ZZ-1 edge as compared to AC edge.^{20–23,25–29} By “stronger” it is meant that for a given NR width the PAGE quantum-confinement-induced increase in the band gap is larger, at least in the range of widths considered. Also, the band gap values decay away from the edge when the supercell size and radius dimensions result in a sizable “bulk” region. A possible explanation is that the large gradient in the potential from the edge of the phosphorene into the empty hole and/or the curvature of the quantum well at the edge have a strong effect on the local electronic properties.

Figure 8.

Spatial distribution of the band gap for OC with SC = 3.02 nm. The radii (in nm) are (a) 0.45, (b) 0.90, (c) 1.15, and (d) 1.37. The local band gap is defined as the band gap observed in the PDOS plot on each atom of the structure. The largest band gap atoms are present in the zigzag nanoconstrictions, which is consistent with the strength of quantum confinement effects in phosphorene nanoribbons.^{20–23,25–29}

Deviations from the general trend can be attributed to differences in edge configurations. In APC with SC = 3.02 nm and R = 1.14 nm the spatial distribution of the band gap becomes inverted, which places the lower band gap atoms along the zigzag direction and the higher band gap atoms along the armchair direction. The distinguishing attribute is the ZZRC-i edge, which is a large fraction of the total edge and the entire system. This agrees with the previous charge density calculations shown in Figure 7. In APC with SC = 5.99 nm and R = 2.63 nm the central part of the zigzag edge has the lowest band gap regions, but the highest band gap atoms still remain on the ends of the zigzag NCs. The characteristic feature is that the central region of the zigzag NC is a complete reconstruction of the phosphorene lattice due to the very narrow width. By comparison, the corresponding OC structure does not contain any significant structural changes, and the spatial distribution of the band gap is as expected. The metallic cases will be discussed separately.

So far in this analysis the impact of the diagonal phosphorene direction has been neglected. Note that the “diagonal” edge does not bisect the armchair and zigzag axes but is 36 degrees from the armchair direction. Hydrogen-passivated diagonal PNRs have a quantum confinement strength that falls in between AC and ZZ-1 PNRs.^20,28 This observation predicts a roughly trimodal spatial distribution of the band gap. However, in looking at the spatial distributions of the band gap, it is apparent that the lowest band gap atoms are contained within both the armchair and diagonal NCs. One explanation is that the larger strength of the quantum confinement effects in the diagonal NCs is offset by the fact that the armchair NCs have a smaller width. This assessment results in a contradiction since earlier the “size effect” in the band gap scaling was attributed to the fact that the limiting confinement length is along the diagonal and is proportional to the size of the supercell. This means the limitation in the band gap range should be unconnected to the armchair NCs. A simple way to reconcile the two observations is to consider the fact that the armchair, diagonal, and zigzag NCs are not independent, but are interacting with each other. In particular, the strong coupling between the armchair and diagonal NCs results in the quantum confinement limitations of the diagonal NCs being transferred to the armchair NCs. The strong coupling could originate from two sources. First, the phosphorene diagonal direction is closer to the armchair direction than the zigzag direction. Second, there are two diagonal NCs for every armchair NC per supercell. The full explanation is likely a combination of the two factors since there are also two diagonal NCs for every zigzag NC. Although the armchair and diagonal NCs contain the lowest band gap atoms, they are not necessarily the only limiting factors in the size of the net band gap. Put simply, the PDOS for each atom is not necessarily centered at the Fermi energy. This means that the largest band gap atoms could limit the size of the total band gap if they contribute states only at either the lower or higher energy end point of the net band gap. Lastly, it is interesting to note that rotating the antidot pattern on the phosphorene lattice would result in different edge morphologies in general. More importantly, the band gap scaling and spatial distribution of the band gap could be much different due to the anisotropy of quantum confinement effects. By forcing the zigzag edges to be along the diagonal of the antidot, it may be possible to increase the band gap shifts due to quantum confinement. This discussion highlights that using the band gap as a single number to characterize complex nanostructures can be misleading since spatial variations in the electronic properties can emerge.

The band gap scaling laws with width in hydrogen-passivated PNRs (AC ~1/w² and ZZ-1 ~1/w) imply that charge carriers along the armchair and zigzag directions are relativistic-like and non-relativistic, respectively.²⁶ This has been observed experimentally in black phosphorus via the ambipolar carrier mobility, which is an order of magnitude larger along the armchair as compared to the zigzag direction.⁸⁹ It is then expected that the NCs in the antidots will have similar transport properties, with the high mobility direction along the armchair direction. Conclusions can also be made about the concentration of charge carriers available for transport. From elementary solid-state theory, the electron or hole carrier concentration of an intrinsic semiconductor has a proportionality to exp(−E_g/2k_BT). Since the atoms along the armchair direction have a lower band gap, a greater concentration of carriers is thermalized along the armchair as compared to the zigzag direction.

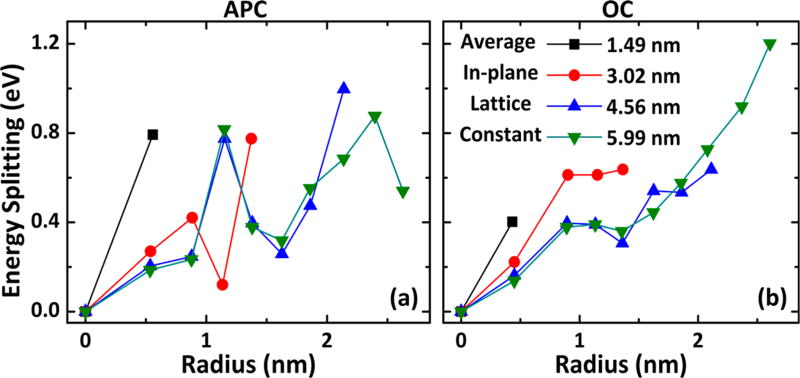
Furthermore, sophisticated calculations of the optoelectronic properties of PNRs using the GW-BSE method can be performed to predict the optical properties of the PALs. For hydrogen-passivated AC and ZZ-1 PNRs it was found that with decreasing width the electronic band gap, optical band gap, and exciton binding energies all increase (i.e., the quantities all follow the quantum confinement trends).²⁹ Since an antidot lattice is closely related to a network of curved NRs, it is reasonable to assume that the scaling of the optoelectronic properties with the geometric features in the PNRs and the PALs will be similar. Furthermore, it is expected that the spatial distribution of the optical band gap in the PALs will also be bimodal. The resulting experimental spectrum would display energetic splitting or false-broadening, depending on the line shape. The value of this splitting would be about equal to the difference between the largest and smallest band gaps, which is displayed in Figure 9 for APC (a) and OC (b). The values range from ~0.12 eV (APC SC = 3.02 nm, R = 1.14 nm) up to ~1.20 eV (OC SC = 5.99 nm, R = 1.14 nm). In general, the splitting increases with increasing radius and is independent of the supercell size. To explain this result, consider circular perforations in square supercells again. First, recognize that the minimum band gap is mainly determined by the diagonal NC width (l_d = √2L − 2r) and that the maximum band gap primarily comes from the zigzag NC width (l_z = L − 2r). Consider the following derivatives:

$${\frac{\partial l_{\mathrm{d}}}{\partial r}|}_L={\frac{\partial l_z}{\partial r}|}_L=-2$$

$${\frac{\partial l_{\mathrm{d}}}{\partial L}|}_r=\sqrt{2},{\frac{\partial l_z}{\partial L}|}_r=1$$

Figure 9.

Energy splitting (defined as the largest band gap minus the smallest band gap from the spatial distribution) as a function of the radius for multiple supercell sizes. (a) APC symmetry. (b) OC symmetry for a range of radii.

From the first set of derivatives, both length parameters change by the same amount in response to a change in radius with the supercell size held constant. However, since quantum confinement effects are stronger in the zigzag NCs, the quantum confinement induced change in the maximum band gap will be larger than in the minimum band gap when the radius is increased. This implies that the splitting will increase for an increasing radius with the supercell size held fixed. From the second set of derivatives, the diagonal NC width will change more than the zigzag NC width for a change in the supercell size with the radius held fixed. However, the stronger quantum confinement effects in the zigzag NCs can offset the larger change in the diagonal NC width. It follows that the minimum and maximum band gaps change by the same amount. This results in a net zero change in the value of the splitting energy when the supercell size is varied at constant radius. Both conclusions from the simple arguments are consistent with the first-principles calculations. Rather than trying to measure the splitting, more sophisticated techniques could be used to spatially map the optical signal and compare it to the calculated spatial distribution.

Metallic Systems

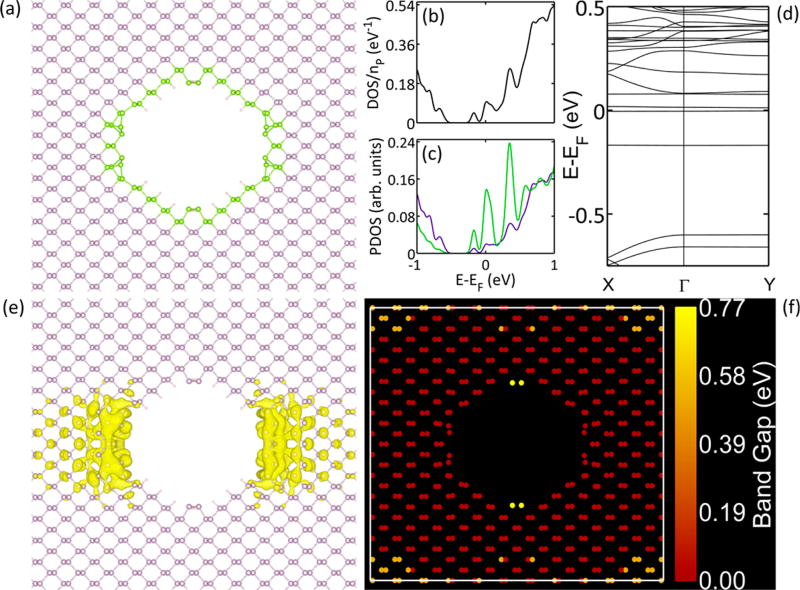
We now return to the two PAL systems with DOS signatures for metals: APC with SC = 4.56 nm and SC = 5.99 nm both with R = 1.15 nm. Only the smaller system is studied (SC = 4.56 nm) since the two hole edge configurations are identical. The atomic structure is visualized in Figure 10a. The metallic behavior is apparent from the electronic DOS (Figure 10b) and PDOS edge/interior (Figure 10c). The edge (green) and interior (purple) decomposition of the PDOS in Figure 10c indicates that the dominant contribution of states at the Fermi energy originates from the edge atoms since the edge peak is significantly larger than the interior peak. The band structure was also computed along the high-symmetry lines X − Γ − Y (Figure 10d). To gain insight into the origin of the two metallic bands, the charge density corresponding to each was calculated. Since the two results are similar, they were simply added together, and the total result is visualized in Figure 10e. The charge density emanates from the self-passivating 4×1 reconstruction of the zigzag edge, which suggests that this particular edge configuration is the origin of the unexpected metallicity. To our knowledge, this edge state has not been considered previously. Furthermore, from a plot of the spatial distribution of the band gap (Figure 10f) the majority of the structure is metallic. However, in the regions in the unit cell furthest away from the hole edges (i.e., the unit cell corners) the material remains semiconducting with a band gap slightly larger than unmodified phosphorene. Despite the interesting prediction of metallic states in a phosphorene nanostructure, the bands that produce this behavior are nearly flat (high effective mass), which suggests that electronic transport will not be supported.

Figure 10.

Analysis of the electronic properties of metallic PAL system (APC with SC = 4.56 nm and R = 1.15 nm). (a) Atomic model with edge atoms shown in green. (b) Total DOS. (c) PDOS decomposed by edge (green) and interior (purple) atoms shown in panel (a). (d) Band structure along the high-symmetry directions: armchair (Γ − X) and zigzag (Γ − Y). (e) Band decomposed charge density for the two bands in (d) near the Fermi energy. The isosurface value is 9.5 × 10⁻³ in units of a₀⁻³, where a₀ is the Bohr radius. (f) Spatial distribution of the band gap, which shows that most of the structure is metallic.

The metallic cases also illustrate that edge effects have a stronger impact on the total system properties when the edge represents a larger fraction of the entire system. The edge configuration that results in the metallic property only causes the atoms to have a zero band gap for about six rows along the diagonal direction in both cases. Since the hole is exactly the same for both metallic systems, the semiconducting islands are larger in the system with the larger supercell. That is, the effect of the edge configuration on the electronic properties decays away from the edge so that edge-mediated global states in large systems are not possible. However, next-generation technologies will scale down to the few-nanometer scale, so understanding the interplay between edge configuration and electronic properties is instrumental in designing effective devices.

CONCLUSION

Using electron beam lithography and plasma-based etching, we demonstrated the fabrication of antidots down to radii of 13 nm in P_xO_y-passivated few-layer BP flakes and observed in-plane phonon suppression via Raman spectroscopy. Further studies are needed to clarify the size- and polarization-dependence of these properties in phosphorene and few-layer BP antidot lattices. With first-principles DFT calculations, initial geometries using two different unit cell symmetries were defined, and a “rastering” approach was used to remove atoms. A quantum-confinement-induced increase in the band gap occurs as the nanoconstrictions between holes decrease in width. Most deviations from this trend can at least be partially attributed to self-passivating edge configurations. It is also possible that the edge atoms couple to the interior atoms to produce global changes in the electronic properties. For one set of antidots with square-shaped holes, the band gap smoothly follows the quantum confinement trend. This suggests that the shape of the quantum well determines the electronic properties in addition to quantum confinement and edge configuration. The band gap scaling displays a size effect, where the maximum obtainable shift in the band gap from the intrinsic value decreases as the size of the supercell increases. This results from the fact that when circular perforations are put into nearly square supercells, the minimum obtainable confinement length along the diagonal is proportional to the size of the supercell. The spatial distribution of the band gap gives insight into local electronic properties. In general, the lower band gap atoms occur in the armchair NCs and the higher band gap atoms occur in the zigzag NCs. This is indicative of anisotropic quantum confinement effects in phosphorene. Electrical transport is expected to be favored along the armchair direction. If the electronic and optical band gaps follow similar scaling behavior, then spectra should exhibit a splitting or false broadening due to the bimodality of the spatial distribution of the band gap. The spatial variations in the electronic properties highlight that using the band gap as a single number to characterize complex nanostructures is oversimplified. Two of the systems are partially metallic, which results from a new 4×1 self-passivating reconstruction of the zigzag edge. However, the associated bands are nearly flat, which suggests transport is not favorable. The interesting results from the DFT calculations provide motivation to develop fabrication techniques that can reach down to the few-nanometer scale. The tunable and spatially dependent electronic properties in phosphorene antidot lattices resulting from anisotropic quantum confinement, edge configuration, and quantum well shape have potential applications in next-generation devices. One could imagine fabricating LEDs with tunable emission in addition to photocells and photodetectors with tunable resonant absorption simply by varying only the geometric parameters of antidot lattices in phosphorene.

METHODS

Antidot Fabrication. Bulk BP flakes were exfoliated onto 150 nm SiO₂/Si substrates with blue Nitto tape and cleaned with acetone and 2-propanol followed by annealing at 180 °C to remove residual solvents. The flakes were thinned down to a few layers (8–10 nm) with an Oxford Plasmalab 80 Plus reactive ion etcher under an O₂ gas flow of 30 sccm and an RF power of 150 W. An initial pressure of 10 mTorr was used to induce the formation of the P_xO_y capping layer followed by layer-by-layer etching at 45 mTorr (see Section S1). Before thinning, total air exposure time was limited to less than 5 min to minimize oxidation and water condensation.⁵ Passivated flakes were coated at 4000 rpm with a layer of ZEP520A EB resist, and antidot arrays were patterned using an Elionix ELS-7500EX operating at 50 kV, which was also utilized for SEM imaging. This was followed by an additional etch under a CF₄ gas flow of 25 sccm and an RF power of 150 W to remove the exposed few-layer BP. Following liftoff in N-methylpyrrolidone, samples were gently cleaned under a short exposure to O₂ plasma.

Antidot Characterization

AFM and Raman measurements were taken before, during, and after the thinning process in order to monitor the BP and P_xO_y thicknesses. AFM measurements were taken in air using a Bruker Dimension Icon AFM. Unpolarized Raman measurements were obtained using an NTEGRA Spectra with 1800 lines/mm grating (0.5 cm⁻¹ resolution) attached to a Si CCD detector. The 532 nm (green) Nd:YAG laser excitation had a spot size of roughly 400 nm and was kept at a power below 150 µW to avoid laser-induced heating.⁸¹ Spectral maps were taken using a dwell time of 10 s per pixel and analyzed with custom-scripted MATLAB software.

Theoretical Methods

Plane-wave DFT calculations were performed using the Vienna Ab Initio Simulation Package (VASP).⁹⁰ To include local and nonlocal effects (including the van der Waals interaction), the optB86b functional was used.^91–93 Projector-augmented wave pseudopotentials⁹⁴ were used with an energy cutoff of 350 eV. Gaussian smearing of 0.05 eV was employed. The cutoff for electronic convergence was set to 10⁻⁵ eV. For bulk BP a Monkhorst–Pack k-point sampling⁹⁵ of 6 × 8 × 2 was used. The atoms and cell relaxed to a force cutoff of 0.01 eV/Å, which gave a = 4.36 Å (armchair), b = 3.33 Å (zigzag), and c = 10.48 Å for the lattice constants. This force cutoff was used for all relaxations. By removing four atoms from the bulk unit cell, extending c to 12 Å, and relaxing again the optimized phosphorene layer was obtained.

The supercells used for the PALs were constructed using the phosphorene lattice vectors and atomic coordinates. After removing atoms (as described in the text) each system was relaxed using an in-plane k-point sampling of 2 × 2 for SC = 1.49 nm and 1 × 1 for the larger supercells. Next the coordination number (CN) was computed for each atom, which is defined as the number of atoms within a cutoff distance of 2.5 Å from the given atom. If CN = 1, then passivation was by two H atoms, and if CN = 2, then the passivation was by one H atom. The H atoms were placed on a line joining the origin (center of the hole) and the P atom, at a distance of about 1 Å from the P atom and at the same z coordinate. When passivating with two H atoms, the H atoms were initially separated by 60 degrees. After relaxing the systems, the coordination numbers were checked again to make sure that the systems were passivated. In some cases the H atoms were rejected from the edge and formed H₂ molecules. To force passivation of the edges, the H atoms were reattached and rotated apart from each other and/or out-of-plane before relaxing again to create a more stable starting configuration. The only P atoms requiring double passivation were directly along the x axis. The P atoms were bent away from the edge, the two H atoms were bent out-of-plane toward the center of the phosphorene layer, and then the systems were re-relaxed. If passivation corrections were needed, the coordination numbers were checked again before declaring geometries finalized. Passivation not only stabilizes the edges but also removes any potential in-gap states, which would interfere with calculation of the band gap for a realistic system.

The frequencies for the Raman-active modes of interest were calculated for one antidot system (OC with SC = 1.49 nm and R = 0.43 nm) and the corresponding pristine supercell (OC with SC = 1.49 nm and R = 0 nm) using Phonopy.⁹⁶ The frequencies corresponding to ${\mathrm{A}}_{\mathrm{g}}^1$, B_2g, and ${\mathrm{A}}_{\mathrm{g}}^2$ are 356.4, 416.1, and 441.2 cm⁻¹ for the pristine phosphorene and 352.6, 414.6, and 440.9 cm⁻¹ for the antidot, respectively. The differences are more significant than was observed experimentally, which could be due to application of the harmonic approximation at zero temperature.

The power spectrum method can be used to determine the normalmode frequencies of a system with anharmonic phonon potentials at non-zero temperature. The power spectrum P(ω) is obtained by first performing a molecular dynamics run and then calculating the Fourier transform of the total velocity autocorrelation A_v(τ):⁹⁷

$$A_{\mathrm{v}}(\tau )=\sum _{n=1}^{N_{\text{atoms}}}{\int }_{-\infty }^{\infty }\mathrm{d}t{\overrightarrow{v}}_n(t)·{\overrightarrow{v}}_n(t+\tau )$$ (2)

$$P(\omega )=|m{\int }_{-\infty }^{\infty }\mathrm{d}\tau A_{\mathrm{v}}(\tau ){\mathrm{e}}^{-\mathrm{i}\omega \tau }|$$ (3)

The summation is over the number of atoms in eq 2, − v⃗_n(t) is the nuclear velocity of the nth atom at time t, and m is the reduced mass of the system. This method was carried out for the same systems that were studied with Phonopy. The time-dependent positions were calculated using ab initio molecular dynamics in VASP with a time step of 0.5 fs (with the other parameters described previously). The temperature was maintained at 300 K using the Nosé–Hoover chain thermostat.^98–100 The system was equilibrated for the first 5 ps, and the subsequent 50 ps of data were used for the power spectra. The velocities were calculated from the positions using a centered-difference formula with seven points. The frequencies corresponding to ${\mathrm{A}}_{\mathrm{g}}^1$, B_2g, and ${\mathrm{A}}_{\mathrm{g}}^2$ shift by ≲ 2, 0.3, and 0.1 cm⁻¹, respectively, which is in better agreement with the experimental results. Note that the power spectrum method does not provide information about the Raman selection rules and the peak intensities are not physically related to the Raman intensity. The calculated power spectra are shown in Figure S10.

The density of states calculations were performed using in-plane k-point grids of 11 × 11 for SC = 1.49 nm, 5 × 5 for SC = 3.02 nm, 3 × 3 for SC = 4.56 nm, and 1 × 1 for SC = 5.99 nm with 1000 energy grid points in the range E_F ± 3 eV. The DOS is normalized to the total number of phosphorus atoms. The PDOS plots are normalized to the respective number of atoms; that is, the edge PDOS is normalized to the number of edge phosphorus atoms, and the interior PDOS is normalized to the number of phosphorus interior atoms. The band gap is calculated by starting as close to the Fermi energy as possible and finding the energy range where the normalized DOS is less than a cutoff value of 0.001 eV⁻¹. The DOS can be normalized to only the number of phosphorus atoms for the band gap calculation since decomposing the PDOS into contributions from phosphorus and hydrogen atoms indicates that the hydrogen atoms contribute negligibly near the band gap edges. The band gaps from Section S7 were calculated using the normalized PDOS with the same cutoff criterion. Note that the PDOS is given in arbitrary units since the site projection includes only s, p, and d orbitals.

Band structures were computed using at least five bands per phosphorus atom, at least two bands per hydrogen atom, and 51 k-points along each high-symmetry direction. For band-decomposed charge density calculations all k-points were used. Since the band structure calculations were performed 3 k-points at a time, band-decomposed charge density calculations were partitioned likewise. For a given band or set of bands of interest all partial charge densities from the separate calculations were added together successively to get the final result.

A justification for neglecting spin-polarization is given in Section S11.