Monolayer WS₂ Nanopores for DNA Translocation with Light-Adjustable Sizes

Abstract

Two-dimensional materials are promising for a range of applications, as well as testbeds for probing the physics of low-dimensional systems. Tungsten disulfide (WS₂) monolayers exhibit a direct band gap and strong photoluminescence (PL) in the visible range, opening possibilities for advanced optoelectronic applications. Here, we report the realization of two-dimensional nanometersize pores in suspended monolayer WS₂ membranes, allowing for electrical and optical response in ionic current measurements. A focused electron beam was used to fabricate nanopores in WS₂ membranes suspended on silicon-based chips and characterized using PL spectroscopy and aberration-corrected high-resolution scanning transmission electron microscopy. It was observed that the PL intensity of suspended WS₂ monolayers is ~10–15 times stronger when compared to that of substrate-supported monolayers, and low-dose scanning transmission electron microscope viewing and drilling preserves the PL signal of WS₂ around the pore. We establish that such nanopores allow ionic conductance and DNA translocations. We also demonstrate that under low-power laser illumination in solution, WS₂ nanopores grow slowly in size at an effective rate of ~0.2–0.4 nm/s, thus allowing for atomically controlled nanopore size using short light pulses.

Graphical abstract

Nanopore sensors based on two-dimensional (2D) materials such as graphene, molybdenum disulfide (MoS₂), and boron nitride (BN) have been used to demonstrate biomolecule detection and analysis.^1–5 In these experiments, the molecules, suspended in an ionic solution, are driven by an electric field through a nanopore within a thin membrane, while the ionic current is monitored to detect the translocation of molecules across the nanopore, which typically appears as reductions in current. Atomically thin 2D membranes are ideal for nanopore devices as they exhibit larger ionic currents compared to those of thicker silicon-based membranes^1–3 and potential spatial sensitivity at the sub-nanometer scale for translocating molecules as only a small section of the molecule resides in the nanopore at a given time.² Furthermore, monolayers of semiconducting transition metal dichalcogenides (TMDs) possess enhanced optical properties,^6–8 a feature which could be further exploited for electrical and optical control of nanopores.

Among TMDs, monolayer tungsten disulfide (WS₂) has a direct band gap of 2.1 eV,⁹ and its photoluminescence (PL) emission is stronger than that in the well-studied MoS₂,^7,10 which enables application of WS₂ monolayers in optoelectronic devices.¹¹ It is also noteworthy that defects have been shown to modulate the PL signal of WS₂ monolayer flakes^12,13 and can hence be used as a means to fine-tune their optical response. One related property is the photo-oxidation of TMD monolayers in an oxidizing environment, such as air and water.^14,15 Introducing defects in the material can provide sites for light-facilitated oxidation and can be used to dynamically control defect size using optical excitation.

In this article, we demonstrate a class of optically active 2D nanopores in monolayer WS₂ membranes. We report WS₂ nanopore drilling using a focused electron beam and subsequent effects on PL spectra. We also demonstrate high ionic conductance and DNA translocations through these nanopores. Furthermore, during laser excitation of these nanopores at low power densities (λ = 532 nm, power density = 3 W/cm²), we note nanopore expansion at a rate of ~0.2–0.4 nm/s, potentially providing means to dynamically control nanopore dimensions with short light pulses.

RESULTS AND DISCUSSION

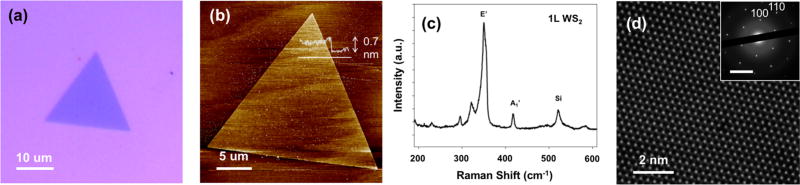
Figure 1 shows the material characterization of vapor-grown WS₂ triangular monolayers. Atomic force microscopy (AFM) of the flake (Figure 1b) shown in Figure 1a reveals a thickness of ~0.7 nm, which agrees with the reported thickness of monolayer WS₂.¹⁶ Using Raman spectroscopy, we observe the E′ (353 cm⁻¹) and A₁′ (418 cm⁻¹) modes of monolayer WS₂ as well as the Si peak from the substrate, centered at 521 cm⁻¹ (Figure 1c).¹⁶ The peak at 311 cm⁻¹ that is typically associated with multilayer flakes is notably absent,¹⁷ thus confirming the presence of monolayers. Figure 1d is an aberration-corrected high-resolution scanning transmission electron microscope (AC-HRSTEM) image of a freestanding WS₂ monolayer suspended on a perforated carbon grid. The tungsten (bright white) and sulfur (gray) atoms are clearly visible. Selected area electron diffraction (SAED) patterns (inset) also confirmed the expected hexagonal lattice of the 1H phase of WS₂ monolayers.

Figure 1.

Characterization of WS₂ flakes. (a) Optical micrograph and (b) AFM scan of a monolayer WS₂ flake. The line profile in white indicates a thickness of 0.7 nm, which corresponds to a monolayer. (c) Raman spectrum of monolayer WS₂ flake with corresponding E′ (356 cm⁻¹), A₁′ (418 cm⁻¹), and Si (521 cm⁻¹) peaks. (d) Gaussian blur-filtered AC-HRSTEM lattice image taken at 80 kV. The inset is a SAED pattern with expected (100) and (110) diffraction spots.

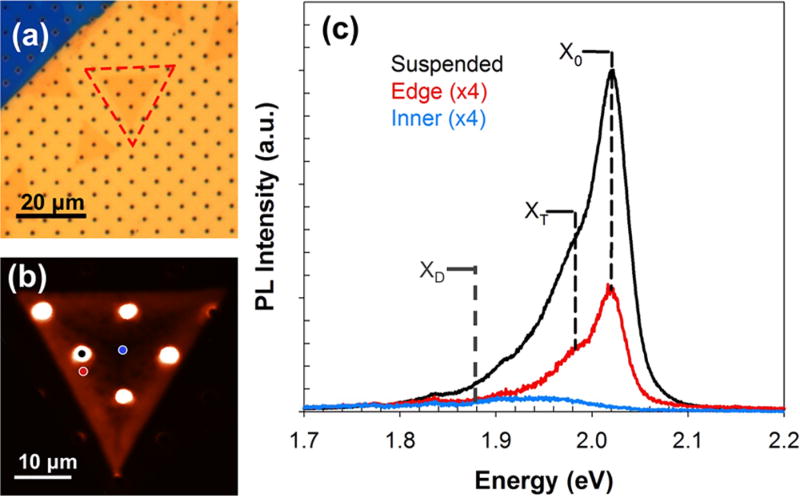
We further characterize the WS₂ monolayers using PL spectroscopy. WS₂ flakes were suspended onto a perforated silicon nitride grid (DuraSiN DTM-25231) using a standard poly(methyl methacrylate) (PMMA)-based wet transfer procedure (Figure 2a), and PL spectral maps were obtained using a 532 nm laser excitation (Figure 2b). The PL spectra from various regions of the flake—suspended, supported edge, and supported center—are plotted in Figure 2c. The PL signal exhibited three peaks: (i) the neutral exciton peak (X₀), which arises due to the radiative recombination of excitons across the band gap;^12,18,19 (ii) the charged trion peak (X_T), which comes from the recombination process requiring three charge carriers and as a result can arise due to charge doping^8,20,21 or strain;²² and (iii) defect peaks (X_D), which arise due to defect-induced midgap states that allow excitons to recombine at an energy lower than the band gap.^12,13 Lorentzian functions were used to fit the spectra for X₀, X_T, and X_D peaks. It was observed that the X₀ peak centered at ~2.02 eV red shifts (i.e., PL wavelength increases) and decreases in intensity (or peak area) from the flake edge inward until it becomes completely nonexistent at the center of the flake. On the other hand, the X_T peak shifts from 1.98 to 1.94 eV (i.e., red shifts), and the peak intensity decreases by 3 times from the edge of the flake to the inner region.⁸ The presence of the X_T peak lends the low-energy tail in the spectra and likely appears due to the substrate-induced strain in the transferred flake.²³ The enhancement of the PL spectral intensity was observed between the suspended and the nearby supported region, which was measured as the ratio of the X₀ peak intensity (I_sus/I_sup), to be ~10–15 times, irrespective of the position of the suspended region on the monolayer (i.e., edge or center). This effect has previously been observed and quantified in suspended MoS₂ monolayers where the enhancement was ~2–4-fold²⁴ and was attributed to PL quenching caused by charge doping of the substrate in the supported regions. Similar effects have been observed in suspended WS₂⁸ but were not quantified, to the best of our knowledge.

Figure 2.

Photoluminescence study of monolayer WS₂ flakes. (a) Optical image of monolayer WS₂ flake on a perforated silicon nitride grid, outlined in red, and (b) corresponding PL map with a 532 nm laser. PL spectra for suspended (black dot), supported edge (red dot), and supported center (blue dot) are plotted in (c). The neutral exciton peak, X₀, at ~2.02 eV, trion peak, X_T, at ~1.98 eV, and defect peak, X_D, at ~1.88 eV are shown with dotted lines. The edge (red) and center (blue) spectra are multiplied by a factor of 4 for better illustration.

Before a nanopore is drilled in a suspended region of a WS₂ flake, the position of the suspended region must first be located in the TEM, and as a result, the entire suspended region is exposed to electron beam (e-beam) doses on the order of ~10⁴–10⁵ e⁻/nm². It has been established that high-energy ebeams can introduce lattice defects in TMDs (such as sulfur vacancies in MoS₂²⁵) and in other 2D materials.²⁶ These defects can, in turn, cause changes in PL peak intensities due to trapped charge carriers or introduce additional peaks as a result of the creation of midgap states.^7,8,12,13 Thus, it is advantageous to study the effects of e-beam exposure on the PL of suspended WS₂ monolayers during nanopore drilling.

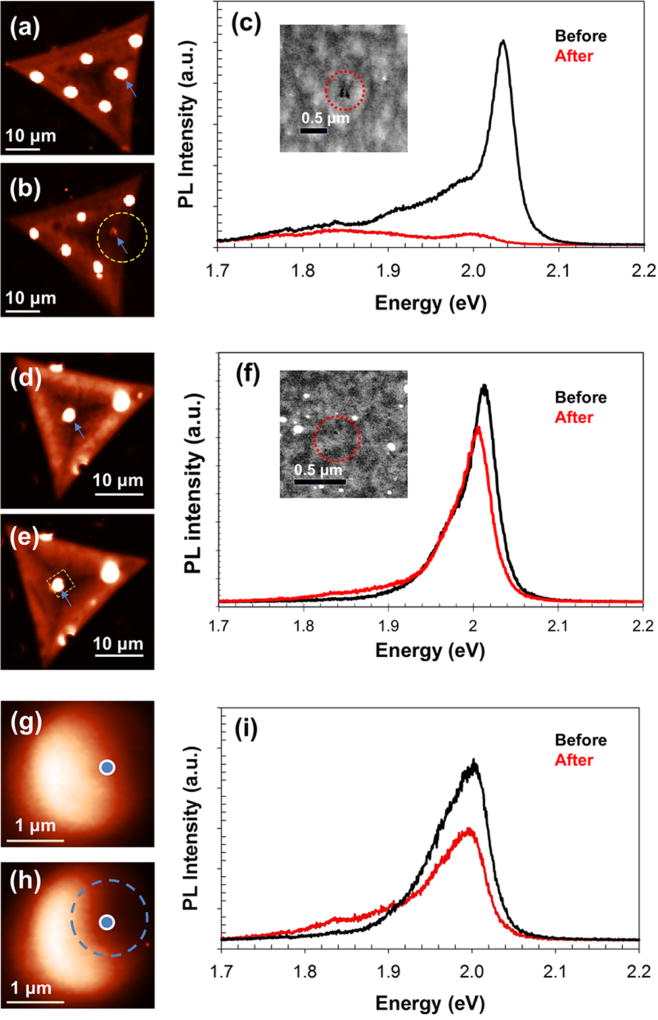
We observe a change in the intensity of PL signals and formation of additional defect peaks due to imaging and nanopore drilling in STEM mode with different e-beam doses. Prior to imaging, the samples were subjected to rapid thermal annealing at 300 °C for 90 min in H₂/Ar in order to reduce any carbon contamination during drilling.²⁶ PL maps of two different WS₂ flakes were obtained before (Figure 3a,d) and after e-beam drilling (Figure 3b shows dose A = 2.6 × 10⁵ e⁻/nm²; Figure 3e shows dose B = 5.5 × 10⁴ e⁻/nm²) in the suspended region marked with a blue arrow. After undergoing 3–4 min of e-beam exposure (STEM imaging), 2–3 nanopores with diameters of ~10 nm each were drilled in focused-spot mode in both membranes in close vicinity, as shown in the insets of Figure 3c,f. The nanopores were drilled close to each other (<0.5 µm apart) to roughly differentiate between effects arising from beam exposure versus nanopore drilling, as we were limited by lateral PL resolution of 0.5 µm. As can be seen from Figure 3b,e, the beam exposure is clearly visible in the PL map as a darker region around the suspended region (outlined in yellow), with more widespread damage from dose A rather than from dose B.

Figure 3.

Change in PL due to beam exposure and nanopore drilling. PL intensity maps of a flake (a) before and (b) after STEM drilling with dose A (2.6 × 10⁵ e⁻/nm²). Yellow dotted line in (b) shows the region damaged during STEM imaging. The region was viewed in STEM for ~3–4 min with two nanopores (diameters ~10 nm each) drilled in spot mode for 5 s. (c) PL of the suspended region, marked with blue arrows in (a,b), before and after STEM drilling. (Inset) STEM image of the drilled nanopores. PL intensity maps of a flake (d) before and (e) after STEM drilling with dose B (5.5 × 10⁴ e⁻/nm²); yellow dotted lines show the e-beam damage. The region was viewed for ~3–4 min with three nanopores (diameter ≤10 nm each) drilled in spot mode for 3 s. (f) Corresponding PL of the same spot before and after STEM drilling on the suspended region marked with blue arrows in (d,e). (Inset) STEM image of the nanopores. PL intensity maps of the zoomed-in suspended region of the flake shown in (d,e) before (g) and after (h) drilling, showing nanopore-induced PL change in the area outlined in blue (R_NP). (i) PL of the R_NP, marked with a blue dot in (g,h) before and after drilling.

The PL spectrum of the suspended membrane shown in Figure 3c reveals that imaging with dose A resulted in the quenching of the X₀ (neutral exciton) peak, a ~26-fold decrease of the X_T (charged trion) peak, and a ~2-fold increase of the X_D (defect) peak at ~1.85 eV. On the other hand, dose B (Figure 3f) led to almost no change of the X₀ and X_T peak intensities in addition to the formation of an additional X_D peak located at ~1.87 eV, which was initially absent for this flake. It should be noted that these spectra are obtained from the suspended region exposed only to the e-beam (R_BE) and not subjected to drilling (R_NP), which is studied next. These changes take place due to the e-beam bombardment damage that occurs during STEM imaging, which leads to sulfur vacancies and other defects with densities proportional to the e-beam dose.^25,26

To differentiate the effects due to beam exposure from those of nanopore drilling, we recorded PL maps of the suspended membrane near the nanopores, before (Figure 3g) and after (Figure 3h) drilling, and found variations in the PL intensity across the monolayer membrane. Although the entire suspended region was exposed to the scanning beam during imaging in STEM mode, a darker region to the right of the membrane (R_NP; outlined in blue; diameter ~0.6 µm) was observed where the nanopores were drilled while the left side of the membrane was relatively unaffected (R_BE). R_NP showed a 2-fold decrease in both the X₀ and X_T peak intensities and the formation of the X_D peak at ~1.88 eV (Figure 3i). The spectral weight percentage (i.e., intensity percentage) of X_D differed in the two regions, with 10% for R_BE and 47% for R_NP, thus showing higher density of defects occurring near the nanopore. It was also observed that while the enhancement factor (I_sus/I_sup) remained ~12 for R_BE, R_NP had a reduced enhancement factor of ~6. The defects introduced due to the nanopore drilling in the vicinity of R_NP can provide sites for oxidation, which we investigate later in our report. It should be noted that the laser exposure from PL and Raman measurements was not seen to introduce additional defects. This was verified by letting the focused laser beam (power density = 4.4 × 10⁴ W/cm²) illuminate suspended WS₂ regions (both with and without a nanopore) for at least 5 min. Raman measurements, from before and after exposure, also indicated no measurable change or shift in the WS₂ spectrum.

A schematic of a typical WS₂ nanopore device is shown in Figure 4a. Fifty nanometer thick suspended silicon nitride (SiN_x) membranes with dimension 50 µm × 50 µm were fabricated on 5 µm/500 µm SiO₂/Si wafers using optical lithography.^1,27 A 200–500 nm diameter hole (area = 0.03–0.2 µm²) was drilled in the SiN_x membrane using a focused ion beam (FIB) with a 10 pA, 30 kV Ga⁺ source, as illustrated in Figure 4b (inset). Monolayers of WS₂ were transferred onto the SiN_x membrane using either a Kapton-tape-based micromanipulation positioning technique or a PMMA-based wet transfer procedure (see Methods). A successful transfer is shown in Figure 4b. Using the focused STEM probe with dose B, nanopores of diameters ranging from 2 to 8 nm were then drilled in the WS₂ membranes suspended over the FIB holes. AC-HRSTEM images of similarly drilled nanopores are illustrated in Figure 4c.

Figure 4.

Fabrication and characterization of WS₂ nanopore devices. (a) Schematic of the nanopore device setup. The WS₂ flake (green) is suspended on a 200–500 nm FIB hole in a 50 nm thick and 50 µm × 50 µm dimensions SiN_x (deep blue) window, fabricated on a SiO₂/Si (orange/yellow) wafer. A 1 or 3 M KCl solution (light blue) is separated by the nanopore in the WS₂ flake. A bias voltage (V_B) is applied across the nanopore using Ag/AgCl electrodes (black), and the ionic current through the nanopore (I_B) is measured. (b) Optical image of a triangular WS₂ flake on a SiN_x window with a FIB hole. (Inset) Scanning electron microscopy image of a 300 nm FIB hole. (c) AC-HRSTEM image of (i) an undamaged suspended WS₂ membrane, (ii) a 0.3 nm nanopore, and (iii) a 1.3 nm nanopore drilled with accelerating voltage of 80 kV. (d) Plot of open pore conductance of WS₂ nanopores with the corresponding nanopore diameter. Inset shows the plot over a larger d_TEM range. The solution conductivity was calculated by fitting the equation for 2D nanopores (G₀ = σd_TEM) and found to be 13.5 ± 0.3 S/m. The nanopore diameter was calculated from the corresponding STEM image by defining a threshold for pixel intensities and selecting the pixels within that range in the vicinity of the pore in ImageJ software. This was repeated multiple times for a single pore, and the standard deviation was taken as the measurement error. Standard deviations in the slope of I_B vs V_B plots for each nanopore were used as the error in open pore conductance, which are very small and lie within each data point area.

After a PDMS measurement cell was loaded, the nanopore device was wet using an ethanol/water (v/v 1:1) solution,³ after which the electrolyte solution was introduced on both sides of the device. A bias voltage sweep (V_B) was applied across the membrane, and the ionic current (I_B) through the nanopore was monitored using a current amplifier in order to obtain the open pore conductance (G₀ = I_B/V_B). A 1 M KCl solution was used as the electrolyte for most of our experiments, unless otherwise noted (see Methods). G₀ was plotted with the measured nanopore diameter (d_TEM) for several nanopore devices (see Figure 4d). By fitting the graph to a linear function, solution conductivity was calculated to be 13.5 ± 0.3 S/m, in good agreement with the measured conductivity of 11.8 S/m, using the conductance formula for 2D nanopores:

$$G_0=\sigma d_{\text{TEM}}$$

where G₀ is the open pore conductance, σ is the calculated solution conductivity, and d_TEM is the diameter of the nanopore measured from the corresponding STEM image (see Methods).²⁸

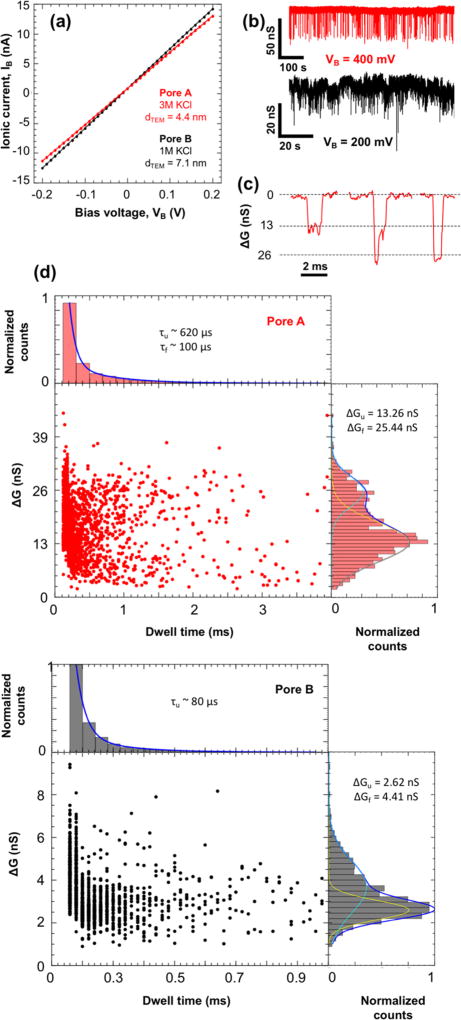
Open pore conductances for WS₂ nanopores with (i) d_TEM = 4.4 ± 0.9 nm (pore A, red) and (ii) d_TEM = 7.1 ± 0.5 nm (pore B, black) were obtained by cycling V_B between ±200 mV (Figure 5a). It should be noted that 3 and 1 M KCl solutions were used for pore A and pore B, respectively. The G₀ values thus obtained were 61.01 nS for pore A and 69.86 nS for pore B.

Figure 5.

Double-stranded DNA translocation through WS₂ nanopores. (a) Current–voltage measurement of WS₂ nanopores with diameters (d_TEM) of (i) 4.4 ± 0.9 nm (pore A in red) and (ii) 7.1 ± 0.5 nm (pore B in black), yielding open pore conductances of 61.01 nS and 69.86 nS, respectively. (b) Ionic conductance time trace of DNA translocation events through the nanopore devices shown in (a) with 10 ng/µL of 15 kbp dsDNA at V_B = 400 mV for pore A and V_B = 200 mV for pore B filtered at 10 kHz. (c) Zoomed-in events illustrating unfolded, partially folded, and folded (left to right) DNA translocation events with the open pore conductance subtracted for pore A. (d) Scatter plots of change in conductance vs event duration for (i) 1890 events (pore A) and (ii) 2030 events (pore B). The histogram on the right shows the change in conductance fitted with two Gaussian curves for unfolded (ΔG_u, yellow) and folded events (ΔG_f, cyan). The histogram on the top shows the event duration or dwell time fitted with two exponential decay curves for unfolded (τ_u) and folded (τ_f) events. The τ_f was not obtained for pore B as we were limited by the sampling rate of the current amplifier.

The 15 kbp double-stranded DNA (10 ng/µL, random sequence) in buffered KCl solution was then introduced into the cis chamber, and a constant V_B (400 mV for pore A and 200 mV for pore B) was applied to electrophoretically drive the DNA through the nanopore. The current traces hence obtained show DNA translocation events (see Figure 5b). We use the change in conductance (ΔG = ΔI_B/V_B) instead of change in ionic current to normalize our results. Scatter plots of (i) 1890 events and (ii) 2030 events were obtained from pores A and B, respectively, and the corresponding histograms of the event depths (change in conductance or ΔG) and dwell time (duration of events) are plotted in Figure 5d. As pore diameters here are ~2–3 times larger than the diameter of dsDNA (~2.1 nm), we observe events that can be interpreted as DNA translocating in three possible orientations—unfolded, partially folded, and folded—each resulting in different current blockage levels (Figure 5c).²⁹ We note that folded DNA translocation events in 3 M KCl have been reported in graphene and silicon nitride nanopores down to ~4.0 nm.^2,29

As partially folded events may have various degrees of folding depending on the percentage of overlap, one distinct Gaussian distribution might not be representative of all the possible partially folded translocations. As a result, the event depth histograms were fitted to only two Gaussian curves which correspond to unfolded events (ΔG_u represented by the yellow curve) and folded events (ΔG_f represented by the cyan curve). Average change in conductances of (i) ΔG_u = 13.26 nS and ΔG_f = 25.44 nS for pore A and (ii) ΔG_u = 2.62 nS and ΔG_f = 4.41 nS for pore B were obtained, yielding unfolded translocation blockage percentages (ΔG_u/G₀) of ~22 and ~4% for pores A and B, respectively. These compare well with previously reported 2D nanopores.^1,3,5 It is also common to fit the dwell time histogram to two exponential decay functions, one for unfolded events (τ_u) and one for folded events (τ_f).¹ In this case, we obtain time constants of (i) τ_u ~ 620 µs and τ_f ~ 100 µs for pore A and (ii) τ_u ~ 80 µs for pore B. τ_f was not obtained for pore B due to limitations in the sampling rate (50 kHz) of our current amplifier. High KCl concentration has been shown to reduce DNA–graphene interactions³⁰ and lead to shorter dwell times for folded dsDNA translocation events.² It is likely that a similar mechanism is happening in pore A.

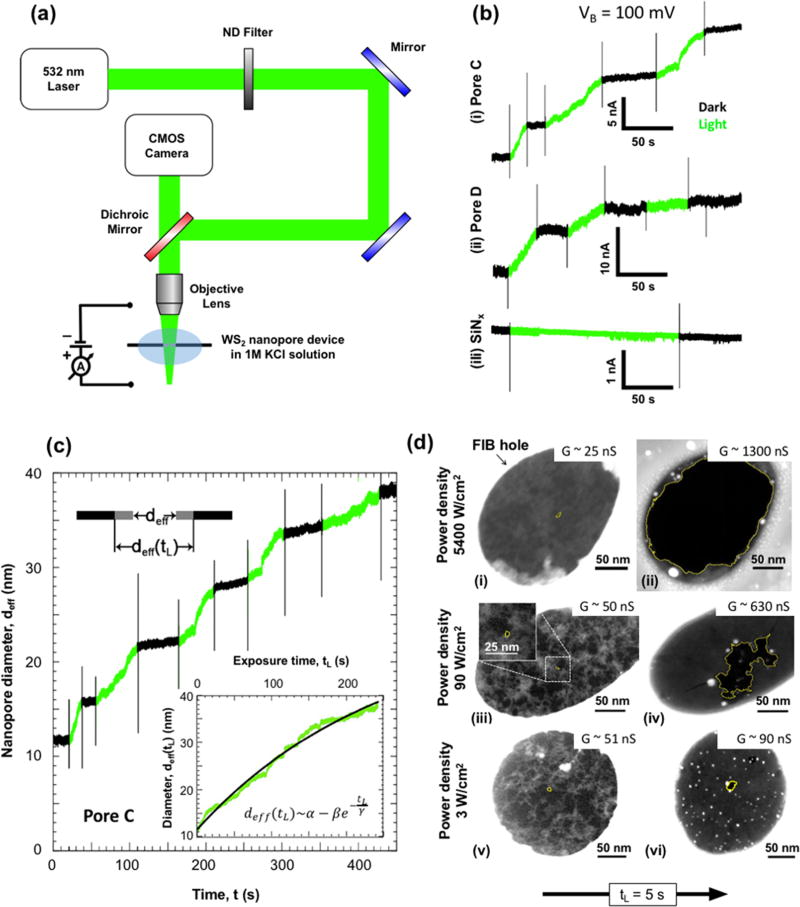
In addition to ionic current measurements in the dark, we also applied light to the nanopores to quantify the ionic current under illumination and explore the optical response of monolayer WS₂ nanopores in a biased ionic environment. The measurement setup is illustrated in Figure 6a. By means of a CMOS camera and a 4× objective lens (NA = 0.1), a 532 nm wavelength laser was monitored and focused on WS₂ nanopore devices mounted on a 3-axis micromanipulator stage. The power density of the laser was changed via a variable neutral density filter and by varying the laser driving current, both of which were calibrated using a power meter (see Methods).

Figure 6.

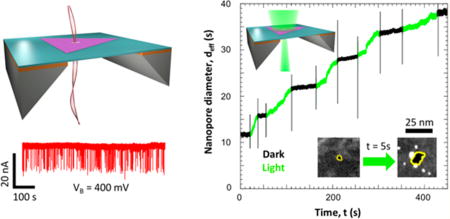
Optical activity of WS₂ nanopores in 1 M KCl solution. (a) Schematic of the optical measurement setup. A 532 nm (green) laser is focused onto a nanopore device using an objective lens (4×) and 3-axis micromanipulator stage. The positions of the laser and SiN_x window are monitored with a CMOS camera, while its power is controlled through a variable neutral density filter and the laser driving voltage. All measurements were performed in 1 M KCl solution. (b) Change in ionic current through WS₂ and SiN_x nanopores with laser exposure. Ionic current (I_B) measurements at V_B = 100 mV were obtained for two WS₂ nanopores of effective diameters (d_eff) of (i) 11.1 nm (pore C) and (ii) 43.2 nm (pore D) and a SiN_x nanopore with (iii) d_eff = 4.8 nm. Periods when the laser (power density = 3 W/cm²) is turned on (light) and off (dark) are represented in green and black, respectively. The spikes in I_B correspond to the capacitive noise from switching the laser on or off. (c) Change in effective diameter of pore C with time. The effective diameter (d_eff) was plotted against the experiment time, t. The regions with the laser on (green) were extracted and concatenated into a single plot (inset) as a function of exposure time, t_L. The resulting exponential fit for the relation between effective nanopore diameter and laser exposure time is given by α = 55.1 nm, β = 43.5 nm, and γ = 249.5 s. An illustration of the expansion of the pore is shown on the top left. (d) STEM observation of the laser-induced expansion of nanopores. STEM images were obtained of WS₂ nanopores (outlined in yellow) with initial diameters (d_TEM) of (i) 4.6, (iii) 4.0, and (v) 4.0 nm. Images after laser exposure (t_L ~ 5s) to power densities of (ii) 5400, (iv) 90, and (vi) 3 W/cm² at V_B = 0 V show expansion of pores. Corresponding conductance values before and after exposure are also provided.

In order to understand the effect of light on a WS₂ nanopore in an ionic solution, the pore conductance of multiple devices was measured as a function of laser exposure time. Here, we show results for a WS₂ nanopore (pore C) with an effective diameter (d_eff = G/σ) of 11.5 nm. As illustrated in Figure 6b(i), I_B was monitored at a constant V_B = 100 mV while the laser was turned on and off alternately with a constant power density of 3 W/cm². Before exposure, the pore conductance in the dark was stable over a period of 1 h. However, during laser exposure, the I_B was seen to increase (green) and remained constant when the laser was turned off (black). This seemed to be an irreversible effect, resulting in ionic current time traces consisting of a series of constant current periods (in the dark) connected by periods of increasing current (under laser illumination). Membrane charging cannot explain these observations, which would otherwise exhibit a return to the original conductance upon dissipation.³¹ We instead attribute it to a permanent physical expansion of the nanopore, confirmed by STEM imaging of nanopores, as discussed later. A similar result was obtained for (ii) another WS₂ nanopore (pore D, d_eff = 43.2 nm) under the same voltage and power density conditions. However, this was not the case for (iii) a SiN_x nanopore (d_eff = 4.8 nm), which showed no change in ionic current as a function of laser exposure at the same power density. This important control measurement demonstrates that solution evaporation and/or solution heating is also not the responsible mechanism for our observation, as either or both could cause a variation in ionic current regardless of the nanopore membrane material. It should be noted that enhancement of ionic current through a SiN_x nanopore has been reported previously but at power densities ~6 orders of magnitude higher than what is used here.³¹

The observed nanopore expansion was further characterized by calculating the change in the effective nanopore diameter throughout the experiment for pore C (Figure 6c). The regions when the pore was exposed to light (green) were extracted and concatenated (Figure 6c, inset) to help understand how d_eff changes with the laser exposure time (t_L). The d_eff versus t_L plot was best fit empirically to an exponential trend:

$$d_{\text{eff}}(t_{\mathrm{L}})~\alpha -\beta {\mathrm{e}}^{-t_{\mathrm{L}}/\gamma }$$

where α = 55.1 nm, β = 43.6 nm, and γ = 249.5 s. The rate of expansion of the nanopore can then be calculated as

$$\frac{\mathrm{d}[d_{\text{eff}}(t_{\mathrm{L}})]}{\mathrm{d}{t}_{\mathrm{L}}}~\frac{\beta }{\gamma }{\mathrm{e}}^{-t_{\mathrm{L}}/\gamma }$$

where β/γ is the initial rate of expansion of pore. For pore C, this value was calculated to be 0.2 nm/s, and for pore D, it was 0.4 nm/s (see Supporting Information). The approximate initial expansion rate was also calculated for other power densities by measuring the conductance change due to exposure of t_L = 5 s. It was seen that the expansion rate increased as the laser power density increased (see Supporting Information). It should be noted here that to ensure that the low V_B = 100 mV did not affect the nanopore, conductance was measured and seen to be constant for an hour in the dark. Nanopore illumination was also repeated with V_B = 0 V, and conductance was measured in the dark after illumination, resulting in outcomes similar to those presented here.

To gain a better understanding of how nanopore expansion varies with power density, three nanopores were subjected to different power densities for t_L = 5 s and observed under STEM. In all cases, we measured the conductance before and after exposure. After the ionic measurement, the membrane was rinsed from the salt solution with water and annealed to allow for subsequent STEM imaging. Figure 6d shows STEM images of WS₂ nanopores with d_TEM = 4.6 nm (i) before and (ii) after being exposed to a power density 5400 W/cm², d_TEM = 4.0 nm (iii) before and (iv) after being exposed to a power density of 90 W/cm², and d_TEM = 4.0 nm (v) before and (vi) after being exposed to power density of 3 W/cm². While the highest power density physically breaks the suspended membrane completely, the lower power densities gradually increase the pore size. This is also evident from the measured change in pore conductances, which increased by ~1275 nS for a power density of 5400 W/cm², by ~592 nS for 90 W/cm², and by ~39 nS for 3 W/cm². It is possible in some cases to find other pre-existing pores in the membranes that can further grow due to e-beam exposure during STEM imaging.

Even though we see irregular pore shape growth for large light intensities (90 W/cm²), we see steadier and more controlled expansion at lower light intensities (3 W/cm²), as shown in Figure 6d. By further optimization of this process, the use of controlled light pulses with controlled intensity and duration, it may be possible to make this process highly controllable and usable for applications. This is somewhat analogous to recently developed membrane electroporation protocols using voltage pulses.^32–34 While these voltage pulses can break the membrane at high voltage and long durations, the procedure has been optimized for nanopore formation by fine control of the magnitude and duration of the pulses.

We also explored the impact of laser exposure on intact suspended WS₂ membranes containing no e-beam-drilled nanopores. A rectifying curve is obtained initially with G₀ = 2 nS (corresponding to d_eff = 0.2 nm), possibly indicating the presence of intrinsic sub-nanometer pinholes in the membrane (see Supporting Information). Upon laser exposure (power density of 90 W/cm², t_L = 15 s), the conductance increased to 9 nS (d_eff = 0.8 nm). A further increase in power density (power density of 5400 W/cm², t_L = 6 s) did not increase the conductance or break the membrane. This seems to indicate that laser exposure might help form additional pathways for ionic flow if there are existing defects in the membranes. However, intentional e-beam damage used to create nanopores with exposed edges plays the dominant role in the further expansion of the nanopores upon illumination, and the ionic current through it is the major contribution to the measured ionic current in nanopore devices.

Experiments were also conducted wherein suspended WS₂ membranes were exposed to STEM damage (dose = 1.1 × 10⁴ e⁻/nm²) without nanopore drilling, and laser illumination (power density of 90 W/cm², t_L ~ 3 min) was applied to see if nanopores can be formed. No appreciable change in conductance was observed, suggesting no perceptible expansion of e-beam-induced defects from the applied dose. Further experiments are required to investigate the relation between e-beam dose, defect density and size, and the rate of defect formation and expansion in an ionic solution.

Based on our observations, we propose that e-beam-induced defects of optimal size provide sites for photo-oxidation to take place in WS₂ membranes in an ionic solution, which generally occur at grain boundaries,^14,15 leading to expansion of nanopores under laser illumination in KCl solution. Further studies are needed to explore the pore formation and expansion process in more detail and at the atomic scale using AC-HRSTEM characterization.

CONCLUSION

In summary, we present the demonstration of optically responsive WS₂ nanopore sensors for biomolecule analysis. We characterized our vapor-grown WS₂ monolayers using Raman spectroscopy, AFM, TEM imaging, and PL spectroscopy. We showed that imaging and drilling of nanopores using a focused e-beam can introduce defects in suspended WS₂ membranes, which appear as changes in the PL spectra. We determined a dose of 5.5 × 10⁴ e⁻/nm² in STEM mode to be sufficient to drill a nanopore while adequately preserving the optical properties of WS₂ monolayers. Fabricated nanopore devices were then used to detect double-stranded DNA translocations. In contrast to SiN_x pores, the diameter of the WS₂ nanopore was optically expanded using a focused 532 nm laser, varying the rate of expansion as a function of incident optical power density. A rate of ~0.2–0.4 nm/s was obtained for a power density of 3 W/cm². We attribute this phenomenon to the photo-oxidation of nanopore edges in the ionic solution. We believe this initial study of WS₂ demonstrating electron-beam-induced effects on PL, DNA translocations through nanopores, and light-enabled pore expansion will aid future optoelectronic experiments on other optically active TMD materials. Further studies may focus on understanding the detailed atomic mechanisms behind nanopore expansion in solution and using short laser pulses to potentially control nanopore edges at atomic scales.

METHODS

WS₂ Growth

WS₂ monolayers were synthesized by chemical vapor deposition through a method reported by Kim et al.⁸ First, a silicon oxide (SiO₂) substrate was spin-coated with solutions of 2% sodium cholate and ammonia metatungstate (3.1 mM) at 4000 rpm for 15 s. The substrate was then positioned in the middle of a 1 in. diameter tube furnace in addition to sulfur powder, which was placed upstream at a temperature of 150 °C. After the furnace was heated up to 800 °C, H₂ was introduced at a flow rate of 15 sccm. After 10 min, the H₂ was turned off and the furnace was rapidly cooled to room temperature.

Characterization

Monolayers of WS₂ were first selected through optical microscopy. AFM scans were obtained in a Bruker Dimension Icon operating in tapping mode. Raman spectroscopy and PL were performed in a NT-MDT NTEGRA Spectra system with an excitation laser wavelength of 532 nm with spectral resolutions of 0.5 cm⁻¹ and 10⁻³ eV, respectively. TEM images and SAED patterns were taken in a JEOL JEM-2010F TEM operating at 200 kV. High-angle annular dark field AC-HRSTEM images were obtained in FEI Titan G2 S/TEM operating at 80 kV. A Gaussian blur filter was applied to the AC-HRSTEM images using ImageJ software in order to reduce contrast from carbon contamination.

Nanopore Device Fabrication

WS₂ monolayers were separated from their SiO₂ growth substrate using a standard PMMA-based KOH wet etch at 75 °C. After being washed in H₂O for at least 1 h, the flakes were then transferred using one of two methods. The first method is a Kapton-tape-based method which utilizes a micromanipulator to position flakes onto previously described silicon nitride membranes.^1,27 The other is a standard wet transfer in which flakes were scooped out onto SiN_x membranes (Figure 4a), dried, and left in acetone for 24 h. The transfer yields obtained via micromanipulation and wet transfer were 60 and 80%, respectively. The slight variation of yield is mainly due to density of WS₂ monolayers used in each technique—micromanipulation for flakes grown at low density and wet transfer for flakes grown at high density. The devices were then washed with isopropyl alcohol and annealed at 300 °C for 90 min in 5% H₂/95% Ar. Nanopores were drilled in the suspended WS₂ membranes using a 200 kV JEOL JEM-2010F TEM operating in STEM mode with a spot size of 1 nm and drilling time of 3–5 s.

Ionic Measurements

The nanopore device was mounted on a PDMS platform using Kwikcast sealant over an underlying channel for ionic fluid. The setup was then placed in a beaker containing ethanol/water (v/v 1:1) solution for at least 30 min. Bubbles were removed using a pipet at 10 min intervals. The platform was removed, and the solution was carefully replaced with water, followed by the desired ionic solution in the channel underneath (trans reservoir) and a drop on the top (cis reservoir). Ag/AgCl electrodes were used to perform ionic measurements with EPC-10 HEKA (sample rate = 50 kHz) amplifier. The 1 M KCl (with 10 mM EDTA and 1 mM Tris; measured solution conductivity = 11.8 S/m, pH 8.7) and 3 M KCl (with 30 mM EDTA and 3 mM Tris; measured solution conductivity = 30.2 S/m, pH 7.8) solutions were prepared using DI water, and the conductivity and pH were measured with Accumet XL-20 pH conductivity meter. Translocation data were analyzed using Pypore (https://github.com/parkin/pypore) and custom Python scripts.

Optical Experiments

Samples were illuminated using a 532 nm (green) excitation laser (Laserglow Technologies) with a 5 mW power output. Power density was controlled by changing the laser driving current and via a variable neutral density filter (Thorlabs) and calibrated with a PHIR power meter located at the sample stage. All cables were kept electrically isolated or grounded to reduce any cross-talk. Alignment was performed by first focusing the laser on a white piece of paper and observing it using the CMOS camera. The laser spot was then centered and digitally marked in the image capture software window by changing the mirror orientations. This spot was then aligned to the nanopore device windows mounted on the micromanipulator stage with the laser beam turned off.