Predicting Thermal Behavior of Secondary Organic Aerosols

Abstract

Volume concentrations of steady-state secondary organic aerosol (SOA) were measured in 139 steady- state single precursor hydrocarbon oxidation experiments after passing through a temperature controlled inlet tube. Higher temperatures resulted in greater loss of particle volume, with all experiments following linear relationships between natural log of concentration vs. temperature⁻¹. Negatives of observed slopes are converted to effective enthalpies of vaporization (ΔH_eff) which range from 6 to 67 kJ mol⁻¹. These values depend upon the properties of the parent hydrocarbon (e.g. number of carbon atoms, number of internal or external double bonds, presence of aromatic or non-aromatic ring structures), as well as conditions of the experiment (relative humidity, oxidant system, oxidant concentrations) and the products of the complex reactions (e.g. aerosol loading). The observed response to change in temperature can be well predicted through a feedforward Artificial Neural Network. The most parsimonious model, as indicated by consensus of several Information Criteria, is comprised of 13 input variables, a single hidden layer of 3 tanh activation function nodes, and a single linear output function. This model predicts the thermal behavior of single precursor aerosols to less than +/− 5%, which is within the laboratory measurement uncertainty, while limiting the problem of overfitting. The selected model reveals that prediction of the thermal behavior of SOA can be performed by a concise number of molecular descriptors of the reactant hydrocarbon, and a general description of the conditions of laboratory oxidation, namely the oxidant in the experiment and the mass of SOA formed. The inclusion of detailed experimental conditions, such as reacted hydrocarbon concentration (Δ HC), chamber relative humidity, chamber volumetric residence time, and/or initial oxidant concentration lead to over-fitted models. Additional input variables are not necessary for an efficient, accurate predictive model of the thermal behavior of the SOA produced. This work indicates that similar predictive modelling methods may be advantageous over current descriptive techniques for assignment of input parameters into air quality models.

Graphical abstract

INTRODUCTION

In order to predict the temporal and spatial distribution of aerosols, particularly Secondary Organic Aerosols (SOA), it is important to understand the distribution of organic compounds between the gas and particle phases.¹ Key thermodynamic properties describing the gas to particle partitioning of organic compounds include saturation vapor pressures and the enthalpies of vaporization.^2–8 During the past several decades, several techniques have been developed to probe thermodynamic properties of low volatility organic molecules often found in atmospheric aerosols.^9–13 Evaluating the thermodynamic behavior of these compounds can be challenging, in part due to the low concentrations that need to be measured. Given that the number of organic molecules in the atmosphere may be in the range of tens of thousands or more, experimentally determined thermodynamic properties of compounds of atmospheric relevance is alarmingly limited.

Bilde et al.¹⁴ recently reviewed the current state-of-science on saturation vapor pressure measurement and estimation techniques. The extensive review focused on what they termed “top down” evaluation of individual compounds, and concentrated on dicarboxylic acids. Confounding experimental evaluation of atmospheric aerosol through the lens of individual compounds is the potential for complex chemical interactions with resultant nonideal behaviors. The number of potential combinations of such interactions leads to a large experimental domain to be evaluated. Thus, explorations of the thermal behavior of atmospheric aerosol gas/particle partitioning should reasonably rely, at least in part, on evaluations of bulk aerosols comprised of many combinations of compounds encompassing a broad range of potential interactions.

The work presented here describes what Bilde et al.¹⁴ term a “bottom up” laboratory effort focused on constraining bulk aerosol thermal behavior. Taken in light of their “top down” approach of exploring the behavior of individual aerosol constituents, the goal of this work is to begin to bridge the gap between expected behavior of single-components, through simple mixtures, toward complex, multiorigin atmospheric organic aerosols. To that end, effective enthalpies of vaporization of laboratory generated SOA are presented here from steady-state, individual precursor hydrocarbon oxidation experiments. Thermal behavior was evaluated by passing laboratory generated aerosols through a heated inlet tube held at different temperatures. The natural logs of the resulting particle volumes are linearly related to inverse temperature. The slopes of these relationships can be succinctly predicted by an artificial neural network utilizing only 11 descriptors, including the volume of aerosol formed, and partial descriptions of the oxidation conditions and the parent hydrocarbon. Model selection and predicted thermal behavior of these aerosols, including insights from predictions thereof, are explored and discussed.

MATERIALS AND METHODS

Experimental Section

Steady-state SOA was generated through a set of controlled photochemical reactions in a 14.5 m³ solid walled irradiation chamber.¹⁵ The TFE Teflon coated reaction chamber was operated as a continuous stirred tank reactor, producing a steady-state aerosol distribution that was repeatedly sampled. The residence time of gases in the chamber was typically 4 to 6 h. The SOA precursor hydrocarbons used in this study, along with the conditions of the experiments, are listed in the Supporting Information (SI). Briefly, 18 experiments were performed with isoprene, 23 with a monoterpene, 17 with a sesquiterpene, 37 with an aromatic hydrocarbon (BETX compounds), 12 with an n-alkane, 16 with an oxygenated VOC (e.g., MBO, linalool) and 11 with naphthalene or a monomethyl substituted naphthalene. In all, 139 experiments are included in the results presented here. Individual hydrocarbons, as well as nitric oxide (NO), were injected through mass flow controllers from high pressure cylinders containing neat compound in air, by passing air through an impinger containing the neat liquid at a set temperature, or from a syringe pump containing the neat liquid. Ozone was generated photolytically and injected directly into the chamber; N₂O₅ was synthesized and cryogenically trapped prior to injection via a stream of air being passed through the cryo-trapped solid. A solution of 50% hydrogen peroxide was injected into a heated bulb prior to injection into the chamber. Two oxidant precursors, NO and H₂O₂, were used in conjunction with lights, while the other two, ozone and N₂O₅, were used in the dark.

Inlet and chamber concentrations of reactant hydrocarbons were measured by gas chromatography with flame ionization detection. Ammonium sulfate seed aerosol was generated by nebulizing a 10 mg L⁻¹ aqueous solution (model 9032; TSI, Inc., Shoreville, MN). The seed aerosol stream then equilibrated to the dynamically controlled relative humidity (RH) in the chamber. In experiments conducted with NO or O₃, RH was typically 30% though select experiments ranged from < 2%).

Aerosol size distributions were measured after passing the aerosol through a heated inlet tube similar to the method of Rader and McMurry¹⁶ without the addition of dilution air. The heating apparatus is a 0.9 m, 0.64 cm i.d. stainless steel tube wrapped with heating tape. The temperature was controlled using an Omega 3000 Temperature Control Unit with a J-type thermocouple located in the center of the tube immediately upstream of the inertial impactor located at the inlet of the SMPS (model 3071A; TSI, Inc., Shoreville, MN). Measurements were performed at six temperatures over the range of 25 to 250 °C (25, 50, 100, 150, 200, and 250 °C). Average residence time in the heated tube was 25 s. Typically seven scans were recorded for each temperature. The SMPS was operated as follows: 0.2 lpm sample flow; 2 lpm sheath flow; scan from 16 to 982 nm. Number size distributions were measured by the SMPS, and have been transformed to volume distributions assuming spherical particle geometry.

Effective enthalpies of vaporization were estimated for the laboratory generated SOA produced. Details of the methods have been described earlier and are summarized here briefly.¹⁷ The natural log of the integrated aerosol volume is linearly correlated with inverse temperature (K⁻¹). From these linear relationships, effective enthalpies of vaporization are calculated. Performance of these systems has been previously evaluated.¹⁷ Results from single component aerosols showed agreement with previously published values. Further tests evaluating the reduction of the volumetric residence time of aerosols in the heated zone by 1/2 also showed no significant changes in the results, indicating that steady-state conditions had been achieved. Furthermore, analyses of single components that are known to be nonvolatile, such as sucrose, exhibited minimal changes with temperature. This demonstrates that transmission inefficiencies through the inlet tube are negligible and do not adversely impact the results shown.

Effective Enthalpies vs Volume Fraction Remaining

Calculation of the volume fraction remaining (VFR) has become common as a means to express the volume of SOA lost as temperature increase.^18,19 The VFR is calculated by normalizing the aerosol volume at a given temperature by the greatest volume measured, such that resulting VFR values range from unity toward zero. Unfortunately, VFR suffers from several limitations. The fitting of experimental data to sigmoid fits restricts the subsequent application of such experimental values, as extrapolation to temperatures lower than the laboratory conditions is problematic. The upper limit of the sigmoid fit, (e.g., refs ^{18 and 19}) are typically unity at the lowest experimental temperature. Projection of sigmoid fit parameters (midpoint slopes and midpoint temperatures) for predicting thermal behavior of aerosols at atmospheric conditions that have temperatures lower than the lowest experimentally determined (typically where VFR = 1), will occur regularly in air quality models. The result would be a prediction of no increase in the particle volume (i.e., VFR still equal to 1), despite the physical likelihood of particle growth (e.g., condensation).

One solution might be to expand conditions of experimental data to span all potential conditions in the atmosphere. To date, no laboratory exists to conduct such experiments which span all atmospherically relevant conditions. Considering the costs and time required to expand current laboratory capabilities in order to allow for much greater coverage of physical conditions (e.g., chamber temperature range from −40 to +50 °C), with corresponding minimum temperature of thermal analysis of aerosols, the linearization in calculating the effective enthalpy of vaporization is preferable. This may allow, with some limitations, the potential to extend to temperatures below the lowest used in generating the data set (25 °C in the data presented here).

Finally, for the experimental values presented here, there was not convergence on unique solutions for a small number of sigmoid fits (7 of 139). Conversely, linear slopes were determined for every experiment, even for experiments with less than a complete number of temperatures steps. As such, for the purposes of this study, calculation of effective enthalpies of vaporization is preferable to expressing response to temperature changes as volume fraction remaining (VFR) when attempting to predict thermal behavior of aerosols.

Predictive Statistical Modeling

Evaluations of thermal behavior of secondary organic aerosols has typically focused on explanatory and descriptive data analysis, with the goal of testing causal theory and developing a better understanding of the chemistry and physics driving the observed behaviors (e.g., refs ^15,18–25). However, Breiman²⁶ and Shmueli²⁷ both contend that there is often conflation of the results of explanation and prediction, with additional, often complementary understanding being developed through predictive techniques. One such predictive approach frequently used across a broad range of disciplines is the use of Artificial Neural Networks (ANNs;^28–32).

ANNs are a family of statistical models which can be used to estimate functions that depend on a number of inputs.^33–36 While conventional statistical techniques can have limiting assumptions (e.g., variable independence, linearity), ANNs are able to capture multidimensional complexity which otherwise may be very difficult or impossible to explain. Indeed, an important theoretical underpinning of ANNs is that a single hidden layer composed of sigmoid functions can approximate any continuous function of real variables.^37–39

ANNs are an interconnected pattern of neurons. Each connection has an activation function that converts a neuron’s weighted input to its output activation. The weights of the interconnections are optimized during the training process. For the commonly used feedforward network, these fitting parameters are often optimized using a gradient descent method to produce the smallest difference between measured and predicted output. This process can involve a large number of iterations and adjustments. In some cases, the solution space can be irregular where numerous contours cause the network to stagnate in local minima. One common approach to this problem is to “seed” the initial weights many times with random values to help ensure finding the global minimum. More detailed descriptions of ANNs are available elsewhere.^28–32

For the work described here, single hidden layer, feedforward neural networks were fit to the experimental data, utilizing SAS/Enterprise Miner v14.1 (PROC HPNEURAL) and associated techniques described by Sarle⁴⁰ and by Bishop.²⁸ Eighteen input variables listed in SI Table S1 were chosen based upon availability of laboratory data, as well as chemical understanding of precursors, oxidants, and experimental conditions of the reactions performed. Many potential input variables were integer valued, such as number of carbon atoms in the precursor and number of oxygen atoms in the precursor. Several potential input variables were real numbers, such as relative humidity of the reaction, the volumetric residence time of the chamber, reacted hydrocarbon concentration (ΔHC), molecular weight of the precursor hydrocarbon, and initial NO_x concentration. Four potential input variables were binary, indicating the introduction of that oxidant, or oxidant precursor, to the reaction chamber for the experiment (NO, H₂O₂, O₃, or N₂O₅). The first two of these also indirectly indicate the presence of UV light during the experiment, while the latter two indicate that the experiment was conducted in the dark. Collectively, the efficacy of these four binary input variables were explored together (all present or all absent), effectively reducing the number of input variables to 15. Furthermore, the number of methyl and ethyl functional groups were evaluated in unison (both inputs present, or both absent) thereby resulting in a smaller effective number of input variables¹⁴ to be explored. The single output variable was the effective enthalpy of vaporization, having units of kJ mol⁻¹ .

Networks were trained using the limited memory Broyden-Fletcher-Goldfarb-Shanno-LBFGS-algorithm (to determine the descent direction along the error surface⁴¹) and the More-´Thuente line search algorithm (to find a new minimum of the error function along that line.^28,42 While these algorithms are often quite good at not getting stuck in local optima, the nature of the input data, with multiple binary and integer values, was such that multiple random seeds were needed for each set of predictor variables and the models were trained for up to 10 000 iterations. Calculations were terminated when the average error gradient was ≤1 ×10⁻⁸.

Across the effective number of total combinations of input variables (214), there were clear indications of poor model performance (e.g., degradation of predictive accuracy, lack of convergence during fitting, etc.) as seen in Figure 1. The number of hidden nodes is practically limited by the degrees of freedom due to the relatively small number of laboratory measurements available for training (n = 139). As such, candidate networks were numerically evaluated by exhaustive search (100 random seeds × up to 44 hidden nodes × 16384 combinations of input variables ~7.2 × 107). The 50 best candidate models, as described below, were evaluated by initializing with 10,000 random seeds. Model selection was performed as follows.

Figure 1.

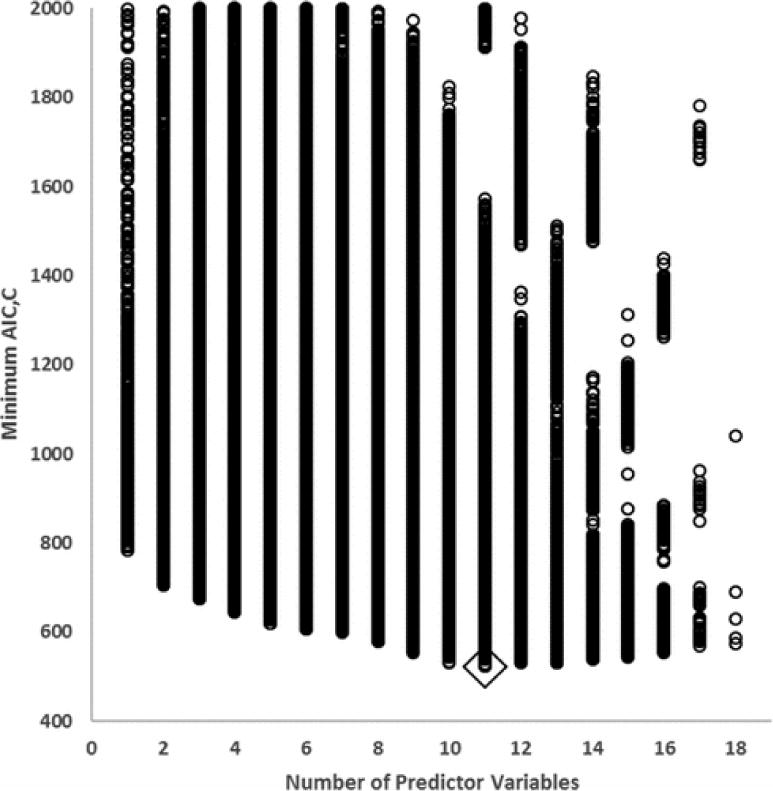
Plot of minimum value of Akaike’s Information Criteria, Corrected (AIC,C) for each architecture versus number of input variables (100 random seeds). Overall Minimum shown inside diamond. Minimum AIC,C values truncated at 2000. Lowest 50 values were re-evaluated with 10 000 random seeds for final model selection.

Model Selection

Calculation of a large number of potential predictive models leaves the difficult issue of choosing the “best” model, weighing the accuracy of the prediction relative to the potential for overfitting the model to the exiting data. Information criterion⁴³ have been developed and refined to help address this problem. There are advantages and disadvantages for each information criterion and debate exists over which is most appropriate and should be used to select the “best” model.^44,45 There exist several model assessment, selection, and comparison tools such as Akaike’s Information Criterion,^46,47 Akaike’s information Criterion, corrected for small sample sizes (AIC,C;⁴⁸), Schwarzs’ Bayesian Criterion (SBC;⁴⁹), Mallow’s Cp statistic (Cp;^50,51), and the Deviance Information Criterion.⁵² Simply, these provide a quantitative means for selection of a model that predicts well, but does not overfit the existing data. Burnham and Anderson^53–55 describe this information-theoretic approach of using Kullback–Leibler information⁵⁶ for model selection, to include testing, for the available data, a series of plausible models, and indicating a measure of the strength of evidence for which model is the best among those considered. As Symonds and Moussalli,⁵⁷ and Burnham et al.⁵⁸ explain, the relative likelihood of each model, given the data, provides a means for evaluating which model is best supported by the data. Using AIC,C as the InformationTheoretic criterion upon which this judgment is based results in a difference between models with the lowest and next lowest values of the selection criterion,⁵⁹ commonly referred to as ΔAIC,C, of 5.19. The model with the lowest value of AIC,C has an Akaike weight of 0.822, or an 82.2% chance that it is the best approximating model out of all 50 models using 10 000 initial seeds. The corresponding ratio of likelihoods, or model probabilities (also known as the evidence ratio⁵⁸), between the “best fit” (i.e., model with the lowest AIC,C) and the “next best” is 0.822/0.061 = 13.4 and indicates 13.4 times greater empirical support for the “best fit” model relative to the ‘next best fit.’

MODEL EVALUATION

Exhaustive cross validation is a technique to assess how a fitted model will generalize to an independent data set.^60–63 It can be used to estimate the accuracy of a predictive model. Generally, the data set is divided, removing p samples for use as a test set upon completion of training using only the remaining n–p samples. This is repeated for all possible combinations, making Leave-p-Out Cross Validation (LpO CV) computationally expensive, and most often infeasible even for small data sets. However, the particular case where p = 1 is known as LeaveOne-Out Cross Validation (LOOCV), and requires refitting of the model to the available data only n times. The process is similar to the Jackknife,^64,65 where measures of fit are computed on the remaining samples, however with LOOCV, the measure of fit is computed only on the sample left out of training the model. For the data presented here, LOOCV was performed after model selection using absolute error as the test metric, as the units remain kJ mol⁻¹ and are most directly comparable to measurements and corresponding measurement uncertainties. LOOCV absolute errors range from 9.66 ×10⁻⁸ up to 1.63, with errors of less than 1 × 10⁻⁵ in 120 cases of the LOOCV, while in only one instance the absolute error that was greater than 10% of the respective measurement error. That one case, (Cedrene/NO ; Exp’t 649) the LOOCV absolute error 1.63 kJ mol⁻¹ was smaller than the corresponding measurement error of 3.4 kJ mol⁻¹ and is reasonably small relative to the measured value (41.2 kJ mol⁻¹). Furthermore, this largest LOOCV absolute error was still reasonable when compared with all measurement uncertainties, which ranged from 0.28 to 10.9 kJ mol⁻¹ and averaged 3.6 (±2.9) kJ mol⁻¹ . The LOOCV indicates only one case of modest predictive accuracy under the broad range of experimental conditions, including relative humidities, volumetric residence times, oxidants, and precursor hydrocarbons. Thus, LOOCV shows that the selected model provides a robust, accurate prediction of the effective enthalpy of vaporization of the SOA.

RESULTS & DISCUSSION

Measured Size Distributions

Chamber generated SOA in this work typically had a volume mode diameter of between 100 and 400 nm. In all measurements, particle volume decreased at higher temperature. The natural log of the integrated volume is linearly related to one over temperature. The slope of this relationship, when multiplied by R, the gas constant, equals the effective Enthalpy of phase change for the aerosol.¹⁷ Volume size distributions at each temperature and the resulting relationship between total volume and inverse temperature for SOA generated from one representative isoprene/NO_x photo-oxidation are shown in SI Figure SI 1.

Values of Effective Enthalpy of Vaporization

Details of the initial conditions and the resulting thermal behavior of SOA for 139 hydrocarbon oxidations measured are listed in SI Table SI 1. For the range of experimental conditions considered here, negatives of measured values of effective enthalpies of vaporization, ΔH_eff range from 6 to 67 kJ mol⁻¹ (34 ± 14 kJ mol⁻¹ ; avg ± std dev) and depend largely on reactant hydrocarbon family. Broadly speaking, aromatic hydrocarbon precursors produce aerosols with effective enthalpies closest to zero, whereas n-alkanes produce aerosols that exhibit the greatest change in aerosol volume with a change in temperature. For aromatic hydrocarbons, photo-oxidation in the presence of NO_x produces values closer to zero (more muted response to change in temperature) than do the other oxidants. Falling between aromatic hydrocarbons and n-alkanes are aerosols produced from the oxidation of biogenic precursors, such as isoprene, α-pinene, and many others. For example, particles formed in the photochemical reaction of toluene/NO exhibit an average ΔH_eff of ~15 kJ mol⁻¹, while those formed from isoprene/NO average ~40 kJ mol⁻¹ and those formed from the oxidation of n-alkanes range from 55 to 67 kJ mol⁻¹, depending largely upon carbon backbone chain length, and/or molecular weight. For similar photochemical systems, these values are consistent with values reported earlier using this technique.¹⁷ In general, the addition of functional groups, such as methyl- functionalities, moves the effective enthalpy away from zero by about 8 kJ mol⁻¹ per methyl group. Similar responses are observed for ethyl moieties or oxygen atoms. Measurement errors are estimated as the standard error of the slope of the linear fits and range from 0.28 to 10.9 kJ mol⁻¹ and average 3.6 (±2.9) kJ mol⁻¹ (std dev). This translates to average measurement errors of 10.2% (±3.2% std dev).

Additional relationships can also be seen, such as a greater change in particle volume per unit change in temperature for SOA formed in the presence of H₂O₂ as the oxidant precursor, relative to that formed in the presence of NO, across the series of homologous aromatic hydrocarbons. Due to the large number of experiments and range of conditions across the experiments, the complexities and subtleties of multiple, possibly compound or nonlinear relationships can be difficult to reveal, isolate and understand. For example, Figure 2 shows linear relationships between ΔH_eff and four variables often considered to be important in understanding the thermal behavior of SOA: the molecular weight of the precursor hydrocarbon, the reacted hydrocarbon concentration, initial NO_x concentration, and the volume of aerosol formed during the reaction. Linear relationships are poor, at best, with R2 values being below 0.25, and multiple linear relationships do not greatly improving the descriptive relationships. So, for work aimed at building a predictive model of effective enthalpies from measured values, the use of standard feed forward neural networks is advantageous over explanatory data analysis, as ANNs are capable of arbitrarily accurate approximation to a function and its derivatives.^66,67

Figure 2.

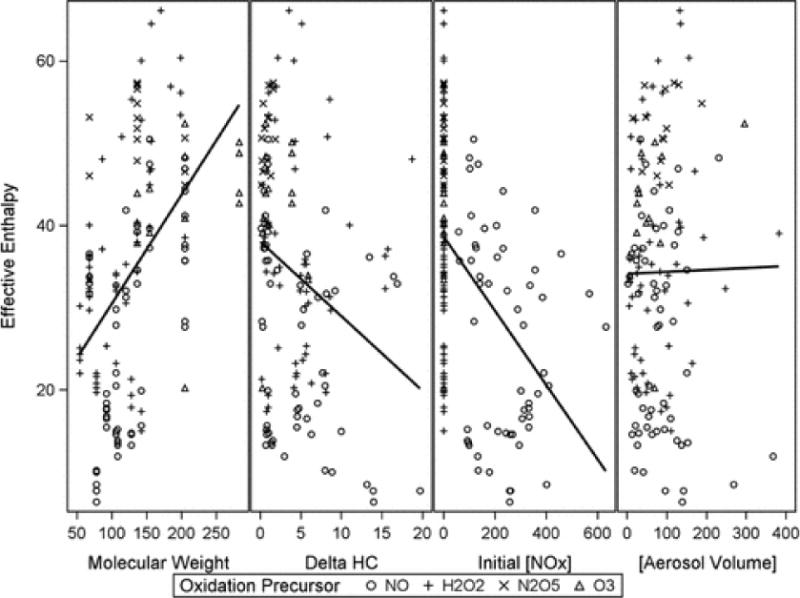
Measured effective enthalpies (kJ mol⁻¹) plotted against four experimental variables: precursor hydrocarbon molecular weight (g mol⁻¹), reacted concentration of precursor hydrocarbon (ppmC), initial NO_x concentration (ppb), and aerosol volume produced (nL m⁻³, or μg m⁻³ assuming unit density). Data labels indicate the oxidant precursor used in the reaction. Linear regression through all data is shown by the solid black line.

Model Description and Parameters

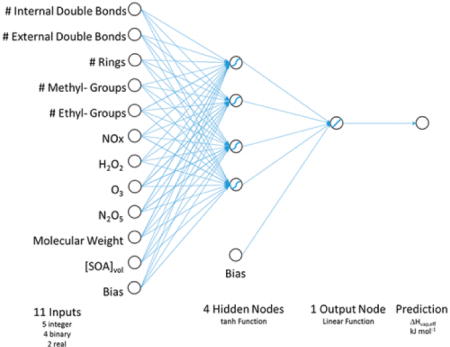
This selected model has 11 input parameters, one hidden layer consisting of 4 tanh activation functions, and a single linear output function (Figure 3).

Figure 3.

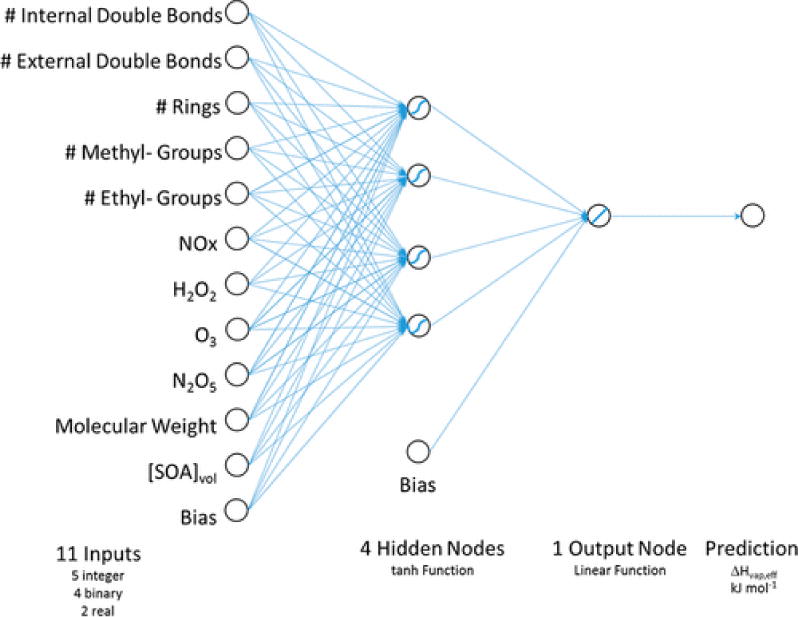
Architecture of Selected Neural Network.

There are 54 degrees of freedom in the model and 85 degrees of freedom for error. The resulting network architecture is

$${\widehat{H}}_{\text{eff}}={\displaystyle \sum (H_{\mathrm{i}}\times z_{\mathrm{i}})+C}$$

for i = 1 to 4, where

$$H_{\mathrm{i}}=\tanh ({\displaystyle \sum {\text{input}}_j\times {\mathrm{w}}_{1,j}+{\text{input}}_2\times {\mathrm{w}}_{2,j}+{\text{input}}_3\times {\mathrm{w}}_{3,j}+\dots +{\mathrm{b}}_j})$$

for j = 1 to 11, includes C and bj, which are intercepts, whereas zi and wi are weights. The mean squared error was 6.2 (Figure 4). The combinations of input variables utilized in the selected model are listed in SI Table S2, and model weights and biases are listed in SI Attachment S1.

Figure 4.

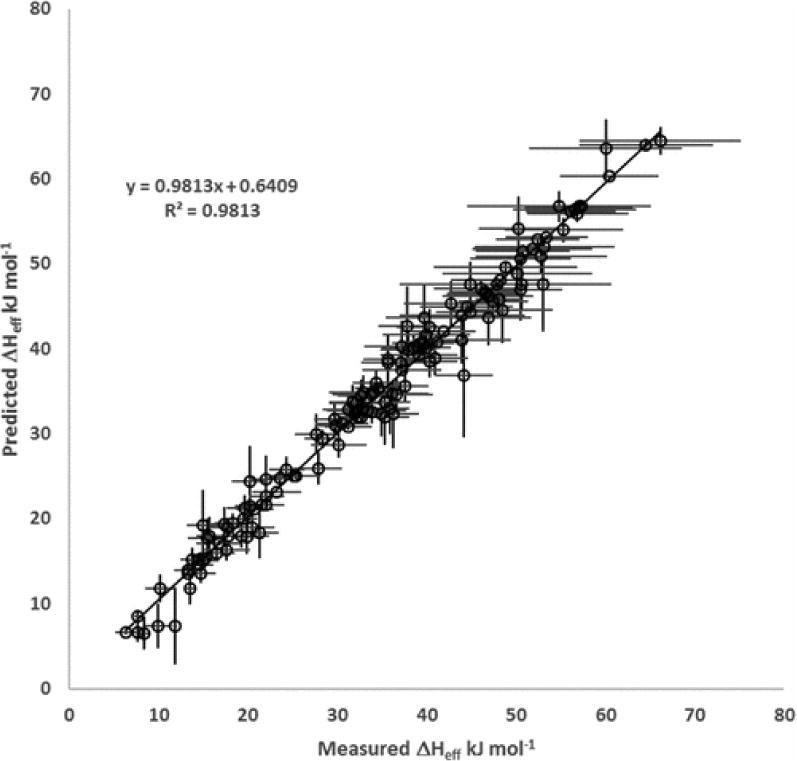
Predicted effective enthalpies (ΔĤ_eff) versus measured values (ΔH_eff), both in units of kJ mol⁻¹ . Horizontal error bars are measurement errors and vertical error bars are LOOCV absolute errors. See SI Figure SI-3 for a plot of residuals

This equation can be used to predict the effective enthalpy of any precursor/oxidant system under conditions spanned by these 139 experiments. That is, the predictive equation is applicable in any case where values for all input variables fall within the ranges of the variables in this series of 139 experiments, such as a precursor hydrocarbon with a molecular weight between 54.09 and 282.46, number of internal double bonds between 0 and 5, number of external double bonds between 0 and 2, number of ring structures between 0 and 3, number of methyl substituent groups between 0 and 4, number of ethyl substituent groups between 0 and 1, and a steady-state volume concentration of aerosol (or mass concentration in units of μg m⁻³ assuming unit density) produced between 2.21 and 382 nL m⁻³ . Use of this equation with even a single predictor variable outside those used to train the ANN should be expected to produce poor or erratic performance, and the results should not be considered reliable.

Application of the Neural Network

These results indicate that some potential input parameters, such as changes in the predicted mass dependence of effective enthalpies can readily be seen. This impact of predicting thermal behavior at a different aerosol loading is shown in Figure 5. Note that values close to zero indicate no change in descriptors of the experimental conditions, relative humidity, volumetric residence time, precursor carbon number, and number of oxygen atoms, are unnecessary for adequate prediction of the effective enthalpies of vaporization presented here. Implicit in this are some trade-offs that arise from parameter selection. For example, these results indicate that, all else being equal, the real number valued molecular weight of a precursor hydrocarbon is a better predictor variable than the integer valued number of carbon atoms in that same precursor. Additionally, while a binary indicator of which oxidant was used in the reaction is a good predictor variable, neither the concentration of nitrogen oxides, nor the amount of the precursor hydrocarbon that is consumed are not. However, efficient and parsimonious predication of the ΔH_eff uses the amount of aerosol formed, which is already known to depend upon several of the potential input parameters that are not in the final, selected “best” model. Thus, all of the previously known complexities of aerosol formation, such as dependence of yield on amount of aerosol formed (e.g., ref ⁶⁸), and dependence of effective enthalpy on the [NO_x] for α-pinene and toluene,¹⁷ are indirectly contained in several elements of the parametrization.

Figure 5.

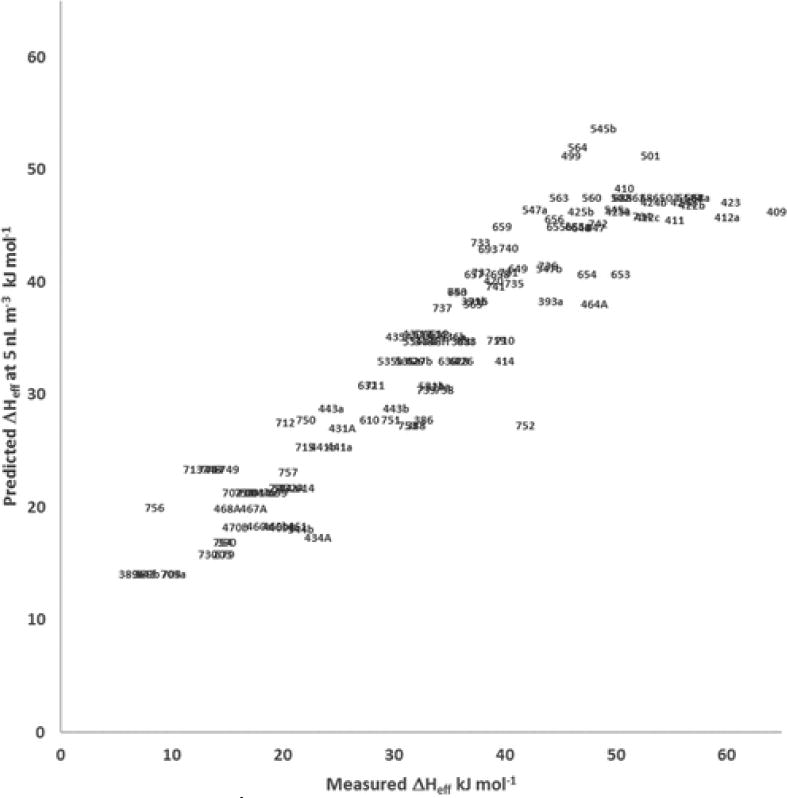
Predicted effective enthalpy (ΔĤ_eff) at minimum aerosol loadings (5 nL m³) plotted versus values measured at experimental conditions (ΔH_eff). Data labels indicate experiment number. Details of experimental conditions (precursor hydrocarbon and precursor oxidant) are listed in Supporting Information.

Exclusion from the statistical model does not imply that these are mechanistically (i.e., chemically) unimportant, but rather that over the range of conditions in the experiments presented here, such inclusion of potential input variables does not improve the prediction over what is already captured, directly or indirectly, through other variables. While this may be seen as a limitation from some perspectives, it presents new opportunities for exploring the physical and chemical relationships. For example, we can examine the impact of lowering the amount of aerosol formed during a hypothetical reaction on the effective enthalpies of vaporization across precursor hydrocarbon and oxidant systems described herein. By predicting the effective enthalpies at a more atmospherically relevant level, such as 5 nL m⁻³, (or 5 μg m⁻³, assuming unit density), aerosol volume per unit change in temperature. Overall, ΔH_eff values do not change greatly when projecting to this lower aerosol loading, with both modest increases and decreases from the values measured at the experimental conditions. Greatest increases occur for m- and p-cresol/NO photo-oxidations which indicate up to 16 kJ mol⁻¹ increase in ΔH_eff upon decreasing the aerosol loading to 5 nL m⁻³ . Greatest decreases occur for decane, undecane and dodecane in the absence of NO_x, with up to 18 kJ mol⁻¹ decrease in ΔH_eff. Overall, predicted values of ΔH_eff shift slightly to a tighter range, from 14.1 to 53.6 kJ mol⁻¹ at this more atmospherically relevant aerosol loading, while the overall average value remains unchanged (33.8 ± 10.9 kJ mol⁻¹) relative to the measured values at the conditions of the experiments.

Similarly, the influence of reaction pathways on the predicted values of ΔH_eff can be explored. Earlier work revealed moderate, apparently linear relationships between initial NO_x concentration and effective enthalpy values of SOA from α- pinene and toluene, respectively.¹⁷ In both cases increasing NO_x resulted in decreases in the observed effective enthalpy for both of the systems evaluated experimentally. Those relationships, in conjunction with several other reports of precursor and oxidant influences on the thermal behavior of secondary organic aerosols, have indicated that variations in the chemical mechanisms could result in changes in bulk thermal properties of the SOA formed.¹⁶ By changing only the input variables related to the oxidant pathway, that is, which oxidant precursor was used to initiate the reactions, the influence of reaction pathways can be explored. One complication in such exploration is that, for a given precursor, reactions utilizing differing oxidants or initial NO_x concentrations are not likely to produce the same aerosol loadings. This impact can be minimized by predicting to a common aerosol concentration, such as the value used in the earlier example (5 nL m⁻³).

In utilizing such a predictive model, care must be taken in order to select conditions which are realistic. For example, values of ΔH_eff can only be measured in experiments where the hydrocarbon reacted, and SOA was formed. An example of this hazard would be predicting an effective enthalpy for the reaction of n-alkanes with ozone. The selected ANN will readily predict effective enthalpies. However, the actual chemical system is highly unlikely to react and form SOA, either in the laboratory or in the atmosphere due to the slow kinetics of such reactions.^69,70

In addition, experimental bias is inherent in the nature of laboratory work with apparatus such as photochemical reaction chambers. One such example is the limit posed by the volumetric residence times over which such reactions can be performed. Additional issues include the operational constraints of the laboratory systems used, such as minimum and maximum relative humidities that are reasonably obtainable. Those constraints are not unique to these experiments or results, but rather are inherent in exploring atmospheric chemistry in a laboratory setting. Briefly, experimental feasibility imposes these and other unspecified constrains onto the exploration of the systems being studied. Such limitations are encapsulated in the bounded range over which this model can be used to efficiently and accurately predict ΔH_eff. As the goal of this work is efficient prediction, while balancing parsimony and accuracy, there are chemically important factors that do not rise to the level of predictive variables in the selected model. Experimental uncertainties (e.g., noise) makes such potential input variables comparatively less optimal than other model inputs which subsume the subtler, often more complex, “chemically relevant” parameters in the selected statistical model. Whether this predictive modeling approach can hold for more complex systems, such as mixtures of precursor hydrocarbons, or time-varying oxidation pathways, is not yet known and will be explored in subsequent work.