On nearest-neighbor Gaussian process models for massive spatial data

Abstract

Gaussian Process (GP) models provide a very flexible nonparametric approach to modeling location-and-time indexed datasets. However, the storage and computational requirements for GP models are infeasible for large spatial datasets. Nearest Neighbor Gaussian Processes (Datta A, Banerjee S, Finley AO, Gelfand AE. Hierarchical nearest-neighbor gaussian process models for large geostatistical datasets. J Am Stat Assoc 2016., JASA) provide a scalable alternative by using local information from few nearest neighbors. Scalability is achieved by using the neighbor sets in a conditional specification of the model. We show how this is equivalent to sparse modeling of Cholesky factors of large covariance matrices. We also discuss a general approach to construct scalable Gaussian Processes using sparse local kriging. We present a multivariate data analysis which demonstrates how the nearest neighbor approach yields inference indistinguishable from the full rank GP despite being several times faster. Finally, we also propose a variant of the NNGP model for automating the selection of the neighbor set size.

INTRODUCTION: GAUSSIAN PROCESSES

The growing capabilities of Geographical Information Systems (GIS) have resulted in a deluge of geo-indexed datasets observed over a very large number of locations. Gaussian Process-based models provide a very flexible non-parametric approach to capture the spatial patterns in such datasets. A Gaussian Process (e.g., Refs ^1,2) over a spatial domain 𝒟 ⊂ ℝ^d is a random surface w(s) over D with a well-defined probability law. It is customarily specified as w(s) ~ GP(m_θ(·), C_θ(·, ·)), where m_θ(s) is a mean function and C_θ(s, t) is a covariance function. This can be extended to a multivariate setup, where w(s) = (w₁(s), w₂(s), …, w_q(s))′ is a q × 1 vector and C_θ(·, ·) is a valid cross-covariance function (e.g., Ref 3), that is, for any two locations s and t, C_θ(s, t) is a q × q cross-covariance matrix whose (i, j)th entry is cov {w_i(s), w_j(t)}. The advantage of a Gaussian Process is that its finite dimensional realizations follow a multivariate Gaussian distribution. Specifically, if w = (w(s₁)′, w(s₂)′, …, w(s_n)′)′ is the nq × 1 vector of realizations of w(s) over a set of locations in S = {s₁, s₂, …, s_n}, then

$$p(w\mid \theta )\propto \frac{1}{det(C_{\theta })}\text{exp}\left(-\frac{1}{2}{(w-m_{\theta })}^{\prime }{C}_{\theta }^{-1}(w-m_{\theta })\right)$$ (1)

where m_θ = E[w | θ] is the nq × 1 mean vector and C_θ = cov (w| θ) is the nq × nq covariance matrix with (i, j)th block C_θ(s_i, s_j).

The popularity of Gaussian Processes among non-parametric models is largely indebted to their unparalleled out-of-sample predictive performance and ability to produce a stochastically interpolated surface with uncertainty quantified predictions at new locations. The latter (known as kriging) can be simply achieved using properties of multivariate Gaussian distributions. For example, if m_θ(·) is fixed and known over the entire domain, then, given the values of w(s_i) for locations in S, we can interpolate the value of the process at any arbitrary point s using

$$w(s)=m_{\theta }(s)+\sum _{j=1}^n{A}_{\theta j}(s)(w(s_j)-m_{\theta }(s_j))+\eta (s)$$ (2)

where $\eta (s)\stackrel{\mathit{ind}}{\sim }N(0,C_{\theta }(s,s)-C_{\theta }(s,S)C_{\theta }^{-1}{C}_{\theta }(S,s))$, C_θ(s, S) is the 1 × n block-matrix with C_θ(s, s_i) as the ith block, C_θ(S, s)) = C_θ(s, S)′ and the A_θj(s)s are q × q ‘kriging weights’ obtained by solving the linear system C_θA_θ(s) = C_θ(S, s) for A_θ(s) = [A_θ1(s): A_θ2(s): …: A_θn(s)]′. This results in $m_{\theta }(s_i)+{\sum }_{j=1}^n{A}_{\theta j}(s_i)(w(s_j)-m_{\theta }(s_j))=w(s_i)$ for each s_i in S. In fact, the right hand side of Eq. (2) is a deterministic interpolator since var (η(s_i)) = 0 for each s_i in S.

In practice, we often observe a q × 1 variate response y(s) along with a set of explanatory variables X(s) and the GP w(s) is used to capture the spatial patterns beyond the observed covariates. In a Bayesian setting, inference proceeds from the posterior distribution of all unknown parameters and spatial random effects, which is proportional to

$$p(\theta ,\tau ,\beta )\times N(w\mid 0,C_{\theta })\times \prod _{i=1}^{n}N(y(s_i)\mid X(s_i)\beta +w(s_i),D(\tau ))$$ (3)

The noise covariance D(τ) represents measurement error or microscale variation and depends upon a set of variance parameters τ. The regression component X(s_i)β conveniently retains the nice interpretive properties, whereas w(s) represents effects from unknown or unobserved factors. Without loss of generality the mean function of the GP is now taken to be zero as it corresponds to the residual process after adjusting for the regression. Additionally, in a Bayesian setup, priors for β, θ, and τ are included to complete the joint model specification.

If the number of locations n is large, traditional GP models run into multiple computational issues. Evaluation of the Gaussian density for w in Eqs (1) or (3) involves storing C_θ and computing its inverse and determinant. Memory requirements for storing the nq × nq matrix C_θ is O(n²q²) and may exhaust storage resources for large n. Even if C_θ can be stored, computing the inverse and determinant are both very expensive operations. This is typically best achieved using the Cholesky decomposition C_θ = LΛL′, where L is lower triangular and Λ is diagonal. However, the Cholesky decomposition takes O(n³q³) floating point operations (flops), so even for an univariate response (q = 1) and modestly large n (≈ 50,000) the computational demands cannot be met by a modern computer. This is often termed the ‘big-N’ problem in spatial statistics. This has necessitated computationally efficient alternatives to the traditional GP models.

In the next section, we provide a brief overview of the existing, and still growing, literature on modeling spatial and spatiotemporal datasets. Subsequently, we focus upon a class of highly scalable sparsity-inducing Gaussian process models for massive space-time data. This approach has recently been explored in Refs ^4,5, called Nearest-Neighbor Gaussian Processes (NNGP) using sparse Gaussian distributions on directed acyclic graphs. In this article, we offer an alternate development of how to construct a welldefined NNGP using essentially the kriging equation. This construction ensures a legitimate spatial process and one does not need to prove Kolmogorov’s existence or consistency conditions as described in Ref 4.

The remainder of this article evolves as follows. In Section Modeling Large Spatial Data we present a brief survey of approaches for modeling large spatial data, Section Nearest-Neighbor Gaussian Processes presents the construction of the NNGP, Section Multivariate Data Analysis presents a synthetic application of the NNGP to bivariate spatial outcomes and Section Choosing m extends the NNGP to learn about the number of neighbors (as opposed to fixing them). Finally, Section Conclusion concludes the article with some remarks.

MODELING LARGE SPATIAL DATA

There is a burgeoning literature on statistical modeling of large spatial and spatiotemporal datasets. Some approaches try to approximate the likelihood in Eq. (1) to obtain a computationally tractable pseudo-likelihood. Subsequently the covariance parameters θ are estimated using maximum composite likelihood approaches. The likelihood simplifications include pairwise differences composite likelihoods,^6,7 block composite likelihood,⁸ small conditioning sets^9,10 among others. Subsequently, kriging at a new location s₀ proceeds by imputing these estimates in Eq. (2). If n is large this can present a computational roadblock as one now needs to store the estimated covariance matrix C_θ̂ to calculate the kriging weights $C_{\widehat{\theta }}(s_0,S)C_{\widehat{\theta }}^{-1}$. For kriging at N new locations, the total flop count post estimation is still O(n³ + Nn²). So for large n and N these requirements remain prohibitive.

Compactly supported covariances (CSC)^11–15 are also popularly used to reduce the computational burden. CSC yields sparse correlation and precision structures to expedite calculations. Despite the sparsity, computing det(C_θ) may still remain problematic. Also, empirical studies revealed that tapered covariance-based approaches may sometimes perform worse than simple alternatives like block diagonal covariance matrices¹⁶ or nearest-neighbor type local approximations.¹⁷ Yet another approach embeds the irregular locations in a larger regular lattice to construct computationally tractable covariance matrices utilizing spectral properties¹⁸ or Gaussian Markov Random Fields.¹⁹ Inferences from these methods are limited to the resolution of the embedding lattice and cannot interpolate at finer resolutions.

In machine learning, Gaussian Process regression is used to facilitate uncertainty-quantified interpolation and smoothing of an outcome observed at a large number of inputs (locations). When the input-dimension d is large, Ref 20 exploits dimension-wise additive or multiplicative structure in the covariance functions to reduce computation using a multitude of fast algorithms and optimizations. The computational complexity of their algorithms decrease with increasing dimensionality and becomes asymptotically scalable (O(n)) at d = ∞. However, for large spatial data (d = 2), there is little computational gain accrued. Very recently, the study of Ref 21 demonstrated that exact kriging can be performed in a scalable fashion using a suitable sparse grid design for the locations. While it is feasible to control the input locations for computer experiments, most spatial datasets commonly found in forestry or ecology are observed at a very large number of irregular locations and any computationally scalable exact kriging method remains elusive.

For irregularly located large datasets, there is a considerable amount of literature on low-rank approaches for large spatial data.^2,22–33 Low-rank models approximate the covariance matrix C_θ as the sum of low rank and sparse (diagonal) matrices, that is, C_θ≈BKB′ +Δ where B is n × r, K is r × r and Δ is diagonal. Likelihood computations now only involve inversion of the r × r matrix K and, as r ≪ n, the flop count is limited to O(nr² + r³). Some low rank approaches^23,26 can be formulated as well-defined Gaussian Processes over the domain. This is very convenient as it provides an unified platform for parameter estimation and kriging at arbitrary resolutions. Furthermore, a full rank GP prior for the spatial random effects can be simply replaced with a low-rank GP prior in any hierarchical setup like Eq. (3). However, as demonstrated in,^4,34 low rank processes struggle to emulate the inference from the expensive full-rank GPs. The gain in computational efficiency is often offset by oversmoothed estimates of the spatial surface.

Localized GP regression based on few nearest neighbors has also been used to obtain fast kriging estimates. Ref 35 provides fast updates of kriging equations after adding a new location to the input set. Iterative application of their algorithm yields a localized kriging estimate based on a small set of locations (including few nearest neighbors). The local estimate often provides an excellent approximation to the global kriging estimate which uses data observed at all the locations to predict at a new location. However, this assumes that the parameters associated with the mean and covariance of the GP are known or already estimated. Local Approximation GPs (LAGP)¹⁷ extend this further to estimate the parameters at each new location. LAGP thus essentially provides a non-stationary local approximation to a Gaussian Process at every predictive location and can be used to interpolate or smooth the observed data.

Recently, Ref 4 proposed a NNGP for modeling large spatial data. NNGP is a well-defined Gaussian Process over a domain D ⊂ ℝ^d and yields finite dimensional Gaussian densities with sparse precision matrices. This has been also extended to a dynamic NNGP for massive spatiotemporal data.⁵ Like the Gaussian Predictive Process, NNGP enjoys all the benefits of being a proper GP. It delivers massive scalability both in terms of parameter estimation and kriging. Most importantly it does not oversmooth like low-rank processes and accurately emulates the inference from the full-rank GPs. In the next section, we provide a general method to construct scalable Gaussian processes and demonstrate how particular choices lead to the NNGP and dynamic NNGP models.

NEAREST-NEIGHBOR GAUSSIAN PROCESSES

The computational bottleneck in evaluating Eq. (1) lies in computing the Cholesky decomposition of C_θ. We show here how the NNGP models proposed by Refs ^4,5 can be constructed within an alternative framework by appropriately choosing the kriging weights in Eq. (2). Assume, without loss of generality, that m_θ = 0. We will construct the process in two steps. First, we specify a multivariate Gaussian distribution for the realizations of the process over a fixed finite set S = {s₁, s₂, …, s_n}. Subsequently we extend it to a process over the domain through kriging equations based on the locations in S. These two steps are described below:

$$\begin{gathered} w_S={(w{(s_1)}^{\prime },w{(s_2)}^{\prime },\dots w{(s_n)}^{\prime })}^{\prime }~N(0,K_{\theta }) \\ w(s)=\sum _{j=1}^n{A}_j(s)w(s_j)+\eta (s) \\ \eta (s)\stackrel{\text{ind}}{\sim }N(0,{\mathit{\Gamma }}_{\theta }(s))\text{for}\text{any}s\notin S \end{gathered}$$ (4)

where K_θ is a nq × nq positive definite matrix, each A_θj(s) is a q × q matrix and each Γ_θ(s) is a q × q positive definite matrix.

It is straightforward to see that the process defined by Eq. (4) is a well-defined Gaussian Process on the domain D. In fact, as demonstrated in,⁵ Eq. (4) subsumes a large class of Gaussian Processes. For example, if we choose K_θ = C_θ (the covariance of w_S assuming they are the realizations of the full GP), A_θ(s) to be the kriging weights $C_{\theta }(s,S)C_{\theta }^{-1}$ (as defined in Eq. (2)) and Γ_θ(s) to be the corresponding kriging variance $C_{\theta }(s,s)-C_{\theta }(s,S)C_{\theta }^{-1}{C}_{\theta }(S,s)$, then w(s) has the same distribution as the full GP with covariance function C_θ(·, ·). If S is chosen to be a small set of ‘knots,’ w(s) becomes a low-rank Gaussian Process. Instead of opting for low-rank specifications, we will use Eq. (4) to construct a class of sparsity-inducing NNGP. This construction of the NNGP is different from and perhaps more intuitive than Ref 4 and clearly reveals the NNGP as a fully model-based extension of alternative nearest neighbor approaches such as Refs ^9,10.

The construction in Eq. (4) yields a legitimate process for any finite collection of spatial locations S. One convenient choice is to let S be the set of observed locations. Then the choice of K_θ determines the scalability of parameter estimation whereas choices for the matrices A_θ(s) and Γ(s) determine the scalability for kriging. Let U = {u₁, u₂, …, u_N} be any finite set of locations outside S. Then, from Eq. (4) we have

$$P(w_{S\cup U})=N(w_S\mid 0,K_{\theta })\times N(w_U\mid A_U{w}_S,{\mathit{\Gamma }}_U)$$ (5)

where A_U = (A_θ(u₁)′, A_θ(u₂)′, …, A_θ(u_N)′)′ and Γ_U = diag(Γ_θ(u₁), Γ_θ(u₂), …, Γ_θ(u_N)) In a full GP, the conditional variance is $C(w_U\mid w_S)=C_{\theta }(u,u)-C_{\theta }(u,S)C_{\theta }^{-1}{C}_{\theta }(S,u)$. So, if two predictive locations u_i and u_j are nearby, their correlation is preserved in the conditional distribution. However, in practice, if the number of predictive locations is large, such joint kriging is rarely used as C(w_U |w_S) is large and generating predictive samples becomes computationally prohibitive. Instead, for large datasets it is customary to carry out predictions independently at each new location. Then the predictive variance becomes $C_{\theta }(u,u)-C_{\theta }(u,S)C_{\theta }^{-1}{C}_{\theta }(S,u)$. Independent kriging circumvents large matrix calculations and can also leverage embarrassingly parallel computing if available. Since, our scalable Gaussian Process is designed for large datasets, we build the predictive distribution by incorporating this conditional independence in the second equation of Eq. (4). If two predictive locations are sufficiently close, their neighbor sets will be same and, hence, although conditionally independent, marginally they will exhibit strong correlation. Also, a simulation study comparing the performance of full GP independent kriging, full GP joint kriging and NNGP kriging provided in (Appendix G)⁴ reveals that joint kriging hardly yields any noticeable benefits.

The Gaussian Process defined in Eq. (4) will be scalable if, for any finite U the storage and computation requirements for evaluating the joint likelihood P(w_{S ∪ U}) are both O(n + N), that is, linear in the total number of locations. A prerequisite for this is to construct $K_{\theta }^{-1}$ with O(n) non-zero entries. How can we achieve this?

One approach would be to avoid computing the Cholesky factorization and directly model K_θ = LΛL′, where L is unit lower-triangular (i.e., has I_q’s or q × q identity matrices along the diagonal) and Λ is block-diagonal with q × q positive-definite submatrices along the diagonal. In other words, we model the elements of L and Λ to construct K_θ. Note that det(K_θ) is the product of the diagonal entries of Λ. Since w_S ~ N(0, LΛL′), we have L⁻¹w_S ~ N(0, Λ). Letting L⁻¹ = I − A we have w_S = Aw_S + N(0, Λ). Since, L is lower triangular, so is A with q × q blocks A_i,j. If Λ_i denotes the ith diagonal block of Λ, we have

$$w(s_i)~N\left(\sum _{j=1}^{i-1}{A}_{i,j}w(s_j),{\mathit{\Lambda }}_i\right)$$ (6)

Let S_i = {s₁, s₂, …, s_{i − 1}}. If {A_i,j | j = 1, 2, …, i − 1} are chosen to be the kriging weights of w(s_i) based on w_Si (analogous to Eq. (2)), and Λ_i the corresponding kriging variance, we obtain K_θ = C_θ. However, this involves inverting (i − 1)q × (i − 1)q matrices C_θ(S_i, S_i) which will be computationally cumbersome for larger i.

Computational efficiency can be achieved by limiting the number of non-zero A_i,j blocks in each row of A to at most m where m ≪ n. Let N(s_i) denote {s_j |A_i,j ≠ O}. The non-zero A_i,js can then be obtained as the kriging weights of w(s_i) based on w_N(si). The kriging variance Λ_i becomes Λ_i = C_θ(s_i, s_i) − C_θ(s_i, N(S_i)) C_θ(N(s_i), N(S_i))⁻¹ C_θ(N(S_i), s_i). So, calculating A_i,js, Λ_is now only require inverting mq × mq matrices. The determinant of K_θ can now be easily calculated as $det(K_{\theta })={\prod }_{i=1}^{n}det({\mathit{\Lambda }}_i)$. Hence, the total flop count for evaluating the density N(w_S | 0, K_θ) can be shown to be O(nm³q³).

The size of the neighbor sets control the sparsity of $K_{\theta }^{-1}$ whereas the choice of the neighbor sets plays a vital role in determining how accurately K_θ can approximate C_θ. Refs ^4,10 used m nearest neighbors of s_i among S_i to construct N(s_i). As nearest neighbors corresponds to points with highest spatial correlation, this choice produced excellent approximations. In a spatiotemporal domain without any definition of distance, Ref 5 selected adaptive neighbor sets N_θ(s_i) based on the strength of the correlation function C_θ(·, ·).

NNGP uses nearest neighbors to create the small conditioning sets. Nearest neighbors have been shown to be sub-optimal for predicting at a new location—theoretically, for some special designs, in Ref 9 and empirically in Refs ^17,35 However, the alternatives proposed do not guarantee better performance. For example, Ref 9 proposes using few nearest neighbors and few distant ones. This often performs worse than nearest neighbors (Ref ⁴ Appendix I). The study of Ref 17 chooses the neighbor set sequentially by maximizing the reduction in predictive variance at each step of expanding the neighbor set. Ref 35 demonstrated that the optimal neighbor sets are not necessarily nested as their size increases. Hence, a greedy forward selection procedure like the one proposed in Ref 17 is not guaranteed to yield the optimal subset of size m. The construction of scalable Gaussian Processes does not require the neighbor sets to be nearest neighbors. Any subset of size m—including the choices used by Ref 9 can be used to construct valid sparse Gaussian Processes. However, through extensive simulations over a very wide range of scenarios documented in Ref 4, the simple choice of nearest neighbors is vindicated by the consistently accurate approximations of the full GP by NNGP.

Finally, we turn to define A_θ(s) = [A_θ1(s) : A_θ2(s) : … : A_θn(s)] and Λ_θ(s) for every s ∉ S. Once again sparsity is achieved by defining a small neighbor set N(s) ⊂ S and choosing the q × q blocks A_θj(s) = O if s_j ∉ N(s). The non-zero A_θj(s)s are simply obtained as the kriging weights for w(s) on w_N(s). Choosing Λ_θ(s) as the kriging variance var (w(s) |w_N(s)) completes the process specification. Evaluating the likelihood N(w(s) |A_θ(s)w_S, Λ_S) only requires inverting an mq × mq matrix. So for inference over S and N locations outside S, the total storage and computational requirements are O((N + n)m²q²) and O((n + N)m³q³), respectively. As these requirements are linear in N + n and m is typically very small (≈ 20) this ensures that the resulting GP is scalable to massive datasets.

As NNGP is a proper Gaussian process, we can use it as a prior for the spatial random effects in any hierarchical model formulation. For example, the Bayesian model in Eq. (3) now becomes:

$$p(\theta ,\tau ,\beta )\times N(w\mid 0,K_{\theta })\times \prod _{i=1}^{n}N(y(s_i)\mid X(s_i)\beta +w(s_i),D(\tau ))$$

An efficient Markov chain Monte Carlo (MCMC) sampler using Gibbs steps and random-walk Metropolis steps described in Ref 4 can now be used for updating w(s), β and the covariance parameters θ. Predictions at arbitrary locations in U = {u₁, u₂, …, u_N} are performed by sampling from the posterior predictive distribution

$$\int N(y_U\mid X_U\beta +w_U,D_U(\tau ))\times N(w_U\mid A_{\theta }(U)w_S,{\mathit{\Gamma }}_{\theta }(U))\times p(w_S,\beta ,\tau ,\theta \mid y_S)$$

where y_U = (y(u₁)′, y(u₂)′, …, y(u_N)′)′, X_U is the corresponding covariance matrix, D_U(τ) = diag(D(τ), D(τ), …, D(τ)), A_θ(U) = (A_θ(u₁)′, A_θ(u₂)′, …, A_θ(u_N)′)′ is the sparse kriging weights matrix and Γ_θ(U) = diag(Γ_θ(u₁), Γ_θ(u₂), …, Γ_θ(u_N))′. We refer the reader to Refs ^4,5 for details on these sampling methods.

MULTIVARIATE DATA ANALYSIS

We present the results of a multivariate simulation study to demonstrate the accuracy of scalable Gaussian Processes. The synthetic data comprises of q = 2 responses at each of n = 1000 locations within a unit square domain. The bivariate responses were generated as:

$$y(s)=\left(\begin{array}{l}{y}_1(s)\hfill \\ y_2(s)\hfill \end{array}\right)=N\left(\begin{array}{l}{\beta }_{10}+x_1(s){\beta }_{11}+w_1(s)\hfill \\ {\beta }_{20}+x_1(s){\beta }_{21}+w_2(s)\hfill \end{array},\left(\begin{array}{cc}{\tau }_1^2& 0\\ 0& {\tau }_2^2\end{array}\right)\right)$$ (7)

The spatial random effects w(s) = (w₁(s), w₂(s))′ are generated from a bivariate Gaussian process with a isotropic cross-covariance specification C(s_i, s_j | θ) = AΔA′, where A is 2 × 2 lower-triangular with positive diagonal elements, Δ is 2 × 2 diagonal with ρ(s_i, s_j; ϕ_b, ν_b) as the bth diagonal entry, b = 1, 2 (e.g., Ref 36). Here ρ(s_i, s_j; ϕ_b, ν_b) denote the Matérn correlation function, that is,

$$\rho (s_i,s_j;\varphi ,\nu )=\frac{1}{2^{\nu -1}\mathit{\Gamma }(\nu )}{(\Vert s_i-s_j\Vert \varphi )}^{\nu }{K}_{\nu }(\Vert s_i-s_j\Vert \varphi );\varphi >0,\nu >0$$ (8)

where ||s_i − s_j|| is the Euclidean distance between locations s_i and s_j with ϕ controlling the decay in spatial correlation and ν controlling the process smoothness.

The true parameter values used to generate the data are shown in the first column of Table 1. The non-intercept predictor columns x₁ and x₂ were drawn from N(0, 1). In Table 1, the first subscript on the regression coefficients index the response variable, for example, β_1,0 and β_1,1 are the intercept and slope associated with the first response variable. Here too, response-specific subscripts index the elements of the cross-covariance matrix AA′, nuggets ${\tau }_1^2$ and ${\tau }_2^2$, and correlation parameters {(ϕ_b, ν_b) | b = 1, 2}. Candidate models included the full Gaussian Process (Full GP) and NNGP with m = 5 and m = 10. The models were assessed using model fit and out-of-sample prediction. Metrics used were Deviance Information Criterion (DIC),³⁷ GPD score³⁸ or Root Mean Square Predictive Error (RMSPE).³⁹

TABLE 1.

Multivariate Synthetic Data Analysis Parameter Estimates and Computing Time in Minutes for Candidate Models. Parameter Posterior Summary 50 (2.5, 97.5) Percentiles

	True	NNGP		Full Gaussian Process
		m = 5	m = 10
β1,0	1	0.81 (0.22, 1.43)	0.64 (−0.05, 1.45)	0.82 (−0.11, 1.71)
β1,1	−5	−4.94 (−5.02, −4.85)	−4.95 (−5.04, −4.86)	−4.95 (−5.04, −4.86)
β2,0	1	1.03 (0.15, 2.02)	1.31 (0.26, 2.37)	0.95 (−0.27, 2.18)
β2,1	5	5.03 (4.91, 5.15)	5.02 (4.89, 5.14)	5.01 (4.89, 5.13)
$A{A}_{1,1}^{\prime }$	4	3.88 (3.14, 5.13)	4.06 (3.20, 5.80)	4.20 (3.21, 5.47)
$A{A}_{2,1}^{\prime }$	−4	−3.58 (−4.80, −2.87)	−3.66 (−5.50, −2.86)	−3.79 (−4.96, −2.87)
$A{A}_{2,2}^{\prime }$	8	7.31 (6.02, 9.15)	7.43 (6.07, 9.70)	7.18 (5.74, 9.15)
${\tau }_1^2$	0.1	0.07 (0.02, 0.25)	0.06 (0.02, 0.25)	0.07 (0.02, 0.24)
${\tau }_2^2$	0.1	0.10 (0.02, 0.87)	0.08 (0.02, 0.70)	0.09 (0.03, 1.33)
ϕ1	6	6.98 (4.05, 15.33)	7.09 (3.21, 14.61)	6.95 (3.79, 12.19)
ϕ2	6	4.14 (3.20, 8.07)	4.80 (3.14, 9.87)	5.47 (3.41, 12.07)
ν1	0.25	0.25 (0.19, 0.38)	0.27 (0.20, 0.37)	0.27 (0.21, 0.37)
ν2	0.25	0.22 (0.16, 0.42)	0.22 (0.15, 0.37)	0.23 (0.16, 0.68)
DIC	–	845.47	747.82	934.73
GPD	–	30,666.13	30,782.05	36,182.24
RMSPE	–	1.68	1.67	1.67
% CI coverage	–	94.7	94.7	94.1
Mean 95% CI width	–	6.31	6.24	6.14
Time (in minutes)	–	18.82	75.62	369.10

For all models, the intercept and slope regression parameters were given flat prior distributions. The variance components ${\tau }_1^2$ and ${\tau }_2^2$ were assigned inverse-Gamma IG(2, 1) priors, AA′ followed an inverse-Wishart IW(3, 0.1), and the Matérn spatial decay and smoothness parameters received uniform prior supports U(3, 30) and U(0.1, 1), respectively. These prior distributions on ϕ and ν correspond to support between approximately 0.05 and 1.3 domain distance units.

Candidate model parameter estimates and performance metrics based on 25,000 iterations are provided in Table 1. We discarded the first 5000 iterations as burn-in samples.

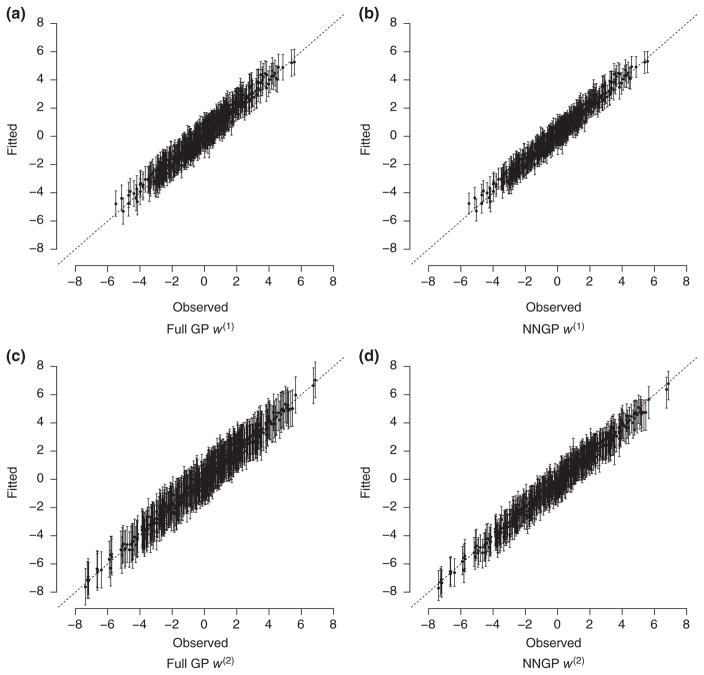
All model specifications produce similar posterior median estimates and 95% credible intervals that contain the true parameter values. DIC and GPD scores suggest the NNGP models have improved fit over the Full GP model. Figure 1 provides scatter plots of the response specific true random effects versus posterior estimates from the Full GP and NNGP models. These plots show that both models closely approximate the true multivariate process. Further, both models produce ~99% coverage rates for the random effects associated with the first and second response variables. However, the NNGP model provides marginally narrower credible interval widths, that is, NNGP mean widths of 1.66 and 1.77 for the first and second response, respectively, versus 1.8 and 2.6 from the Full GP model. The narrowing of the credible intervals is particularly apparent when comparing Figures 1a and 1b.

FIGURE 1.

Multivariate synthetic data analysis true versus fitted spatial random effects w for the full Gaussian Process (Full GP) and nearest neighbor Gaussian process (NNGP) for m = 5. Superscripts on w⁽¹⁾ and w⁽²⁾ correspond to the random effects associated with the first and second response variables. (a) Full GP w⁽¹⁾, NNGP w⁽¹⁾, (c) Full GP w⁽²⁾ and (d) NNGP w⁽²⁾

Turning to the out-of-sample prediction results, the NNGP and Full GP models produced comparable RMSPE and mean 95% credible interval widths as shown in Table 1. All models showed appropriate 95% credible interval coverage rates.

The last row in Table 1 provides model computing times for one chain of 25,000 iterations. Clearly the reduced dimensionality and computational complexity of the NNGP models provide enormous reductions in computing time over the conventional GP sampler.

CHOOSING m

The size of the neighbor sets m has direct impact on the storage and computation of a NNGP model. Simulation experiments detailed in Ref 4 demonstrates how one can run NNGP models for different choices of m (possibly in parallel) and choose m which minimizes some model evaluation metrics like RMSPE. Nevertheless, for large datasets or in absence of parallel resources, running the MCMC for multiple values of m may remain a computational challenge. We propose an alternative method that bypasses the need for multiple runs. We consider m as a parameter and update it dynamically in the Gibbs’ sampler. The neighbor sets and consequently the NNGP covariance K_θ now change with m. We denote them by N_m(s) and K_θ(m) respectively. If π(m) denotes a prior for the discrete parameter m, we can generate samples using the full conditional

$$p(m\mid ·)\propto \pi (m)N(w\mid 0,K_{\theta }(m))$$ (9)

The support of π(m) is chosen to be [1, m₀] where m₀ can be determined from the available computational resources, that is, choose m₀ for which $O(n{m}_0^2)$ storage is available and $O(n{m}_0^3)$ time is reasonable. Since, Eq. (9) does not correspond to any standard distribution, m can be updated using a Metropolis random walk step within the Gibbs’ sampler.

We illustrate the performance of this variable-m NNGP in a small simulation experiment. We generated data at 2000 locations within the unit square from the univariate model y(s) = β₁x₁(s) + β₂x₂(s) + w(s) + ε(s), where x₁ and x₂ were generated from N (0, 1), $\epsilon (s)\stackrel{\mathit{iid}}{\sim }N(0,{\tau }^2)$ and w(s) ~ a GP with exponential covariance structure (Matern covariance with ν = 0.5) with decay ϕ. For model fitting, we used a NNGP prior for w(s), improper prior (∝ 1) for β₁ and β₂, uniform prior for ϕ and inversegamma prior for σ² and τ².

We used 10,000 MCMC iterations and discarded the first 5000 as burnins. For the variable-m NNGP we used a discrete uniform prior for m with support {1, 2, …, 20}. We also fit regular NNGP models with m = 10 and m = 20 as benchmarks. The true and fitted values of the parameters are shown in Table 2. We observe that the coefficient estimates for β₁, β₂, and τ² were similar for all three models, whereas the estimate of σ² was much better for the variable-m NNGP. Also the posterior 95% credible intervals for σ² and ϕ were significantly narrower than those for the regular NNGPs. This observation is slightly surprising as the possible range of values of m includes both 10 and 20—the size of the neighbor sets for the regular NNGPs. Nevertheless, we observed that varying the size of the neighbor sets can yield improved confidence intervals in addition to saving additional computations for running multiple NNGPs.

TABLE 2.

Parameter Estimates (50% [2.5%, 97.5%] percentiles) for Fixed and Variable m NNGP Models

	True	NNGP m = 10	NNGP m = 20	NNGP Variable-m
β1	1	0.98 (0.95 1.02)	0.99 (0.95 1.02)	0.99 (0.95 1.02)
β2	5	4.98 (4.95 5.02)	4.98 (4.95 5.02)	4.98 (4.95 5.02)
σ2	1	1.64 (0.78 6.39)	1.36 (0.65 5.72)	1.17 (0.71 2.17)
τ2	0.5	0.47 (0.43 0.5)	0.47 (0.44 0.51)	0.47 (0.44 0.51)
ϕ	1	1.01 (0.26 2.55)	1.13 (0.26 2.87)	1.36 (0.66 2.21)

Computationally, the variable-m NNGP adds little to the storage and memory requirements of the standard NNGP. If m₀ denotes the upper bound for the support of m, then the storage requirements are $O(n{m}_0^2)$ and the computational complexity for evaluating the NNGP likelihood at the lth MCMC iteration will be O(nm(l)³) where m(l) denotes the updated value of m at the l^th iteration.

Figure 2 shows the posterior frequency distribution of m in the variable m NNGP. While the distribution of m is not interesting for any inferential purposes, the figure shows that although the prior is discrete uniform {1, 2, …, 20}, the posterior shows heavy left skewness with higher mass for larger values of m. This is expected as the data are generated from a full-rank GP which essentially corresponds to m = n. However, if computational resources demand that more mass towards smaller values of m is desirable, one can add a suitable prior penalizing large m.

FIGURE 2.

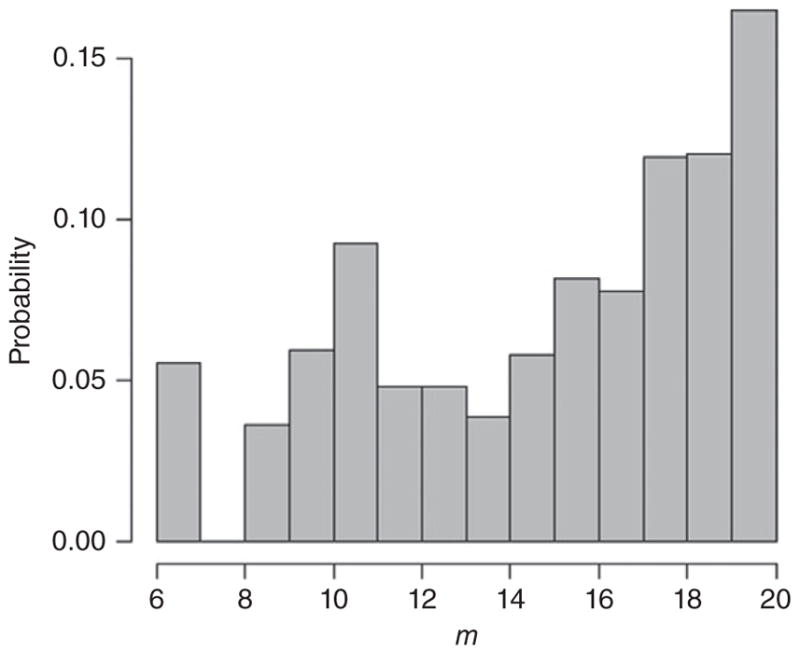
Posterior distribution of m for variable-m NNGP.

CONCLUSIONS

Fully model-based Bayesian inference for large spatial and spatiotemporal datasets is challenging because of expensive computations involving matrices without apparent exploitable structure. Recently Ref 4 proposed a NNGP which is a GP whose realizations over any finite collection of locations will have a sparse precision matrix. In this expository article, we have provided some further insight into the NNGP models and how they can be easily constructed as linear transformations of the process realizations over a fixed set of locations. We not only illustrate their use in Bayesian hierarchical modeling but also add some additional insight by modeling (rather than fixing) the number of neighbors.

The construction of NNGP requires a preo-rdering of the spatial locations. While the choice of ordering has been empirically shown to have little impact on the performance of the NNGP⁴ or other nearest neighbor based approaches,^9,10 it remains an annoyance from a purely theoretical perspective as spatial locations do not have any natural ordering.

Also, NNGP, in its current form is only constructed using stationary (or isotropic) covariance functions. Extending NNGP to create sparse Gaussian Processes for modeling non-stationary spatial surfaces also remains challenging. Kriging based on few Euclidean nearest neighbors may no longer remain accurate if the stationarity assumption is not valid. LAGP¹⁷ possess advantage in this aspect as the covariance parameters are estimated at each predictive location thereby incorporating non-stationarity. The implementation of LAGP in the R-package laGP is also extremely efficient.

The storage and computational requirements of NNGP are linear in size of the dataset and the dimension of the locations. Hence, it can easily scale to datasets with hundreds of thousands or possibly millions of high-dimensional locations. One potential area of concern is that, the spatial random effects are updated sequentially in the MCMC algorithm for NNGP described in.⁴ While empirical observations reveal that convergence is achieved very fast, a block update of the spatial random effects may speed up the MCMC significantly. Two possible algorithms were described in Ref 4 but their performances were not evaluated. More research is being undertaken to fully explore these possibilities. We also plan to migrate our lower level C++ code into an R package for wider accessibility.