Development of the Mechanisms Governing Midbrain Multisensory Integration

Abstract

The ability to integrate information across multiple senses enhances the brain's ability to detect, localize, and identify external events. This process has been well documented in single neurons in the superior colliculus (SC), which synthesize concordant combinations of visual, auditory, and/or somatosensory signals to enhance the vigor of their responses. This increases the physiological salience of crossmodal events and, in turn, the speed and accuracy of SC-mediated behavioral responses to them. However, this capability is not an innate feature of the circuit and only develops postnatally after the animal acquires sufficient experience with covariant crossmodal events to form links between their modality-specific components. Of critical importance in this process are tectopetal influences from association cortex. Recent findings suggest that, despite its intuitive appeal, a simple generic associative rule cannot explain how this circuit develops its ability to integrate those crossmodal inputs to produce enhanced multisensory responses. The present neurocomputational model explains how this development can be understood as a transition from a default state in which crossmodal SC inputs interact competitively to one in which they interact cooperatively. Crucial to this transition is the operation of a learning rule requiring coactivation among tectopetal afferents for engagement. The model successfully replicates findings of multisensory development in normal cats and cats of either sex reared with special experience. In doing so, it explains how the cortico–SC projections can use crossmodal experience to craft the multisensory integration capabilities of the SC and adapt them to the environment in which they will be used.

SIGNIFICANCE STATEMENT The brain's remarkable ability to integrate information across the senses is not present at birth, but typically develops in early life as experience with crossmodal cues is acquired. Recent empirical findings suggest that the mechanisms supporting this development must be more complex than previously believed. The present work integrates these data with what is already known about the underlying circuit in the midbrain to create and test a mechanistic model of multisensory development. This model represents a novel and comprehensive framework that explains how midbrain circuits acquire multisensory experience and reveals how disruptions in this neurotypic developmental trajectory yield divergent outcomes that will affect the multisensory processing capabilities of the mature brain.

Introduction

The brain has evolved the ability to integrate signals from different senses, thereby enhancing perception and behavior in ways that would not otherwise be possible (Stein, 2012). The neural machinery and computational principles underlying multisensory integration have been subjects of considerable speculation, much of which is based on studies of neurons in cat superior colliculus (SC) (Anastasio et al., 2000; Patton and Anastasio, 2003; Knill and Pouget, 2004; Rowland et al., 2007; Alvarado et al., 2008; Cuppini et al., 2010, 2011, 2012; Fetsch et al., 2011; Ursino et al., 2014; Miller et al., 2017). These studies focused on multisensory responses to spatiotemporally concordant crossmodal stimulus pairs, which are significantly more robust than those evoked by individual component stimuli (multisensory enhancement; Meredith and Stein, 1983). This increases the physiological salience of the initiating events and their likelihood of eliciting SC-mediated behaviors (Stein et al., 1989; Burnett et al., 2004; Gingras et al., 2009).

However, the capacity for SC multisensory enhancement is not present at birth (Wallace and Stein, 1997, 2001). Its development requires considerable postnatal experience with crossmodal cues (Wallace et al., 2004; Yu et al., 2010; Xu et al., 2014) and the formation of a functional synergy between convergent unisensory inputs from subregions of association cortex (Jiang et al., 2001, 2006; Alvarado et al., 2009; Rowland et al., 2014). In the cat, these cortical inputs primarily come from the anterior ectosylvian sulcus (AES) and serve as the substrate upon which crossmodal experience operates (Jiang et al., 2006; Rowland et al., 2014; Yu et al., 2016). In the absence of AES or multisensory experience, responses to concordant crossmodal cues are no more robust than those to the most effective modality-specific component cue.

A simple, intuitive hypothesis regarding this development is that the emergence of multisensory enhancement capabilities results from the strengthening of convergent, covariant crossmodal (e.g., visual and auditory) AES projections by a generic associative learning rule such as the Hebbian learning rule (Hebb, 1949) or Oja's rule (Oja, 1982). However, recent empirical evidence casts doubt on this hypothesis. First, convergent crossmodal AES–SC inputs become functional even in the absence of crossmodal experience and become stronger than normal even when multisensory enhancement capabilities do not develop (Yu et al., 2013). Second, development is specific: a neuron will only integrate and enhance responses to crossmodal cues belonging to modalities that have been paired in experience (Yu et al., 2010; Xu et al., 2012, 2015, 2017). This is not surprising given that adaptations are based on experience. However, implementation of this specificity requires more complexity than afforded by the generic associative rules, which predict that multisensory enhancement capabilities would emerge whenever convergent crossmodal neural connections are strengthened regardless of the specific experiences that produce this outcome.

The present effort reconciles these findings via a neurocomputational model that shows how multisensory SC enhancement capabilities can emerge during postnatal maturation with properties that reflect its particular history of crossmodal experience. The model was simulated under different rearing conditions with documented physiological effects.

Materials and Methods

Model summary.

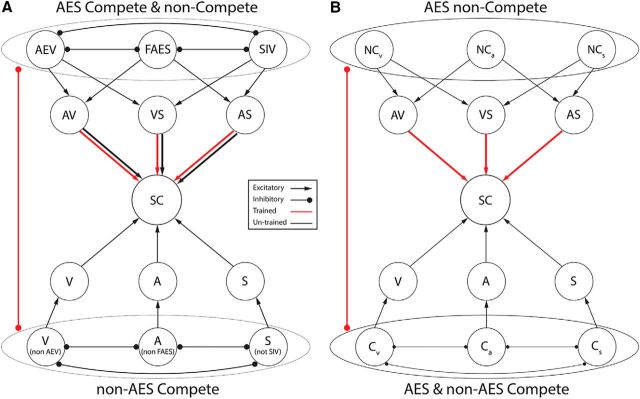
Neurons in the biological circuit communicate with each other and with other circuits in multiple ways. Several architectural simplifications and abstractions were imposed here to focus the model on the key dynamics believed to underlie the development of SC multisensory enhancement (Fig. 1A).

Figure 1.

Structure of the model. A, Reduced model is shown here to isolate the circuit components of interest. These include: (1) a region representing the SC, (2) a region representing projections to the SC from the modality-specific visual, auditory, and somatosensory zones of AES (AEV, FAES, and SIV, respectively), and (3) a region representing all non-AES inputs (subcortical and cortical) from these same modalities. For a better comprehension of the network, the two figures depict the connectivity among single units belonging to the different structures implemented in the model. Subregions in each input region extend net inhibitory connections with each other that implement a WTA competition for control over SC responses (see text for more details). In addition, the AES subregions project excitatory connections to the SC that do not participate in this competition (noncompetitive projection). The noncompetitive connections and the inhibitory connections between AES and non-AES are modifiable by crossmodal experience (indicated by red lines). B, This architecture is further simplified for efficient simulation by collapsing all sources (AES and non-AES) of competitive input for each modality (C_v, C_a, and C_s) into a single region because of their similar function, thereby separating them from the modifiable AES noncompetitive (NC_v, NC_a, and NC_s) projections.

The model contained artificial nodes (units) grouped into three topographically organized regions representing different circuit components: (1) the SC, (2) its unisensory AES afferents (“AES”), and (3) its unisensory afferents from all regions outside of AES (i.e., “non-AES”). Each of the two tectopetal regions was then functionally divided into three subregions: visual (V), auditory (A), and somatosensory (S). The tectopetal projections from these subregions were excitatory and topographic. The output of each unit in an input region represented the net influence of many neurons with similar sensitivities rather than an individual neuron. Similarly, units in the SC region represented the net activity of a pool of similar neurons.

Interactions between each of these modality-specific subregions implemented a default computation that approximated a winner-take-all (WTA) competition (Grossberg, 1973). Effectively, only the strongest input signal survived this competition with attrition to influence the target unit(s) in the SC. For simplicity, this competition to control the SC was implemented via direct inhibitory connections between units in different input regions; however, these were an abstraction and not intended to represent direct inhibitory synapses exchanged between biological neurons. The excitatory tectopetal connections extended by units influenced by this competition were collectively referred to as the “competitive projections.” For a more detailed discussion of this abstraction of competitive dynamics, see Cuppini et al. (2011, 2012).

In addition, subregions of AES extended a set of noncompetitive tectopetal projections that were excitatory, strictly topographic, modifiable by crossmodal experience (detailed below), and not influenced by the WTA competition. In these ways, they were functionally distinct from the competitive projections. Changes in these noncompetitive projections, along with changes in the inhibitory balance between AES and non-AES inputs, were hypothesized to account for the acquisition of multisensory enhancement capabilities during normal development.

This basic model schematic (Fig. 1A) was further simplified by regrouping units and connections into functional categories to improve simulation efficiency (Fig. 1B). In this simplified form, the sources of the competitive projections from non-AES and AES were collapsed into a single competitive region (C) and the sources of noncompetitive projections from AES were isolated as a separate noncompetitive region (NC). Connections from and among units in the competitive subregions (C_v = V, C_a = A, C_s = S) were fixed to implement the WTA. Excitatory connections from the noncompetitive subregions (NC_v, NC_a, and NC_s) targeted the SC region topographically and were pooled across their sensory-specific subregions in a pairwise fashion. The simplified model was used to simulate the effect of experience on the functional capabilities of the model and is described in detail below.

Simulated model.

Each of the tectopetal input subregions and the SC region were represented by arrays of 100 units. Each unit was referenced with superscripts to indicate its array and with subscripts to indicate its position within that array (indicating its spatial position/sensitivity). Therefore, the net input to a unit at location i within array h at time t was written u_i^h(t). The output of this unit, z_i^h(t), was determined by a first-order differential equation as follows:

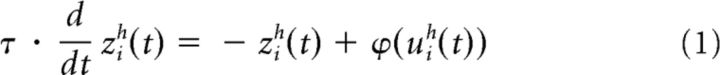Here, τ was a fixed time constant (identical for all neurons) and ϕ(… ) described a sigmoidal function with central point ϑ and central slope p:

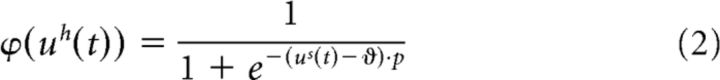The strength (i.e., weight) of an excitatory projection from a unit at position j in array k, to a unit at position i in array h, is written as W_i,j^h,k. Inhibitory connection strengths used the same convention, but were denoted by a capital L instead of W. Note that, for simplicity, we implemented 1-to-1 connections.

The net input to a unit in input region C or NC was determined by three components: an excitatory input representing an external stimulus (I_i^h, zero by default), a noise input randomly selected from a zero-mean Gaussian distribution with SD 2.5 (N(0,2.5)), and an inhibitory input derived from other input subregions (l_i^h(t)):

The inhibitory input for units in the noncompetitive subregions was determined by the following:

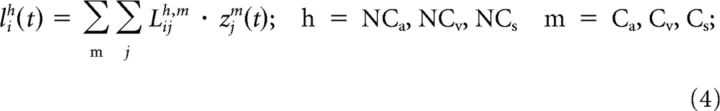The inhibitory input for units in the competitive subregions was as follows:

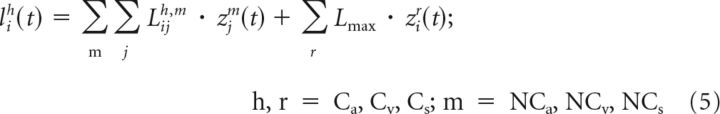Where L_max represents a fixed strength for the inhibitory connections between competitive subregions. These connections implemented the default WTA.

SC units pooled the output of units from all six input subregions. This was arranged by constructing multiple compartments within each SC unit that received input from specific subregions and not others (Fig. 1B). These compartments were computational abstractions to simplify the operation of the learning rule and were not intended to simulate any specific biological component of a neuron directly. Inputs from competitive subregions targeted compartments visual (V), auditory (A), and S, whereas noncompetitive inputs targeted compartments that pooled pairwise modality combinations: VA, VS, and AS. Therefore, the net input to a competitive input compartment s (either V, A, or S) dedicated to a competitive subregion r (either C_v, C_a, or C_s, respectively) was as follows:

The net input to a noncompetitive input compartment p (VA, VS, or AS) dedicated to a pair of noncompetitive subregions m and n (NC_a and NC_v, NC_v and NC_s, NC_a and NC_s) was as follows:

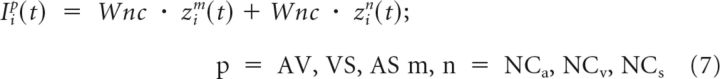Input compartment activity levels were calculated by applying Equations 5–6 to Equations 1–2 and then pooled, scaled by a weight, and combined with zero-mean Gaussian noise to yield the net input to a central compartment as follows:

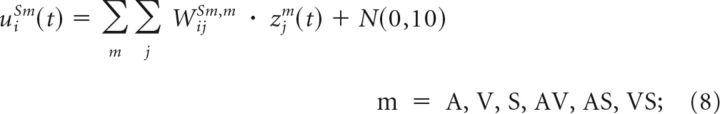This value was converted to SC output using Equations 1–2. Both bisensory (5 compartments: 4 input and 1 central) and trisensory (7 compartments: 6 input and 1 central) units were simulated. To reduce the number of free parameters, tectopetal weight matrices were selected so that the total amount of input to the SC from all of the competitive subregions was equal to the total amount of input from all of the noncompetitive subregions for a single point stimulus.

Learning rules.

To highlight the important features of the model in the present context, the only plastic (i.e., modifiable by sensory experience) connections in the network were the excitatory projections from the noncompetitive compartments (i.e., AV, VS, AS) to the SC unit and the mutual inhibitory projections between the competitive and noncompetitive regions (Fig. 1B). All other connections were assumed to be mature in the initial state of the model, which represented an early postnatal period just before multisensory enhancement capabilities emerge. Developmental events preceding this starting point (including unisensory development) were described previously (Cuppini et al., 2011, 2012).

In our model, plastic connections were modified by a Hebb-like learning rule augmented with two special constraints: (1) high activation thresholds for engagement and (2) a saturating upper bound. These constraints provided the rule with additional complexity beyond that of a simple generic associative learning rule. Mathematically, the rule for modifying the weight from a noncompetitive input compartment k (e.g., AV, VS, AS) indexed by j to the central compartment of the SC unit at location i was as follows:

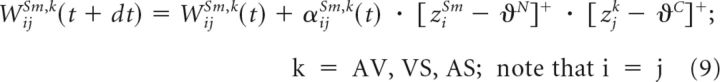In this equation, [… ]⁺ represents a rectification operation. Weights were only modified if activation thresholds were met by the SC neuron (ϑ^N) and the input compartment (ϑ^C), and this was obtained only in case of multisensory stimulation, when both input regions targeting the same input compartment were active. The learning factor α_ij^Sm,k(t) implemented a saturating upper bound:

In this equation, α₀ was a scalar and W_max was the maximum value for an individual weight.

Mutually inhibitory connections between the competitive and noncompetitive subregions were modified by a similar rule, replacing W with L, α with β, and ϑ^C with ϑ^N as follows:

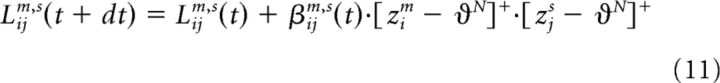These equations described the rule for the projections both from competitive regions (when m = NC_v, NC_a, or NC_s) to noncompetitive regions (when s = C_v, C_a, or C_s) and the projections in the reverse direction (when m = C_v, C_a, or C_s and s = NC_v, NC_a, or NC_s). The same activation threshold was required for both the projecting and receiving unit (ϑ^N); therefore, changes in L_ij^m,s and L_ij^s,m were identical.

To illustrate the crucial elements of the learning rule used here, we compared the results of the model obtained when using the learning rule above with those obtained when a generic Hebbian learning rule was substituted in its place (Eq. 12). In the generic rule, the connection (W) between the j^th neuron in the presynaptic region S and the i^th neuron in the postsynaptic area P was modified according to neurons' activities (z) at time t as follows:

In this equation, α is a learning factor kept constant throughout the training and ϑ represents a low activation threshold.

Simulations of multisensory development.

Exposure to a sensory cue was simulated by setting the external network input I to a value representing a point stimulus (I_training; Table 1), which was kept constant during a single training trial, updating the state of the network (Eqs. 1–7) until a steady state was reached, and applying the learning rules (Eqs. 9–12 or 13) to the plastic connections. Exposure to crossmodal cue combinations was simulated by setting input patterns for multiple subregions in the C and NC regions. External input patterns for each stimulus were identical for the relevant competitive and noncompetitive regions. As described above, a noise input randomly selected from a zero-mean Gaussian distribution with SD 2.5 (N(0,2.5)), was also added to the external input I.

Table 1.

Simulation parameters

Individual units	Input
N = 100	Itraining = 30
θ = 20	I = 19.5
s = 0.3	Training
τ = 3 ms	Wmax = 25
Connections	α0 = 0.1
Wnc = 21	Lmax = 15
Wc = 42	β0 = 0.001
WSm = 25	ϑN = 0.4
K = 15	ϑC = 0.7

Development was simulated by repeatedly exposing the network to different combinations of highly effective cues (500,000 trials). Different developmental circumstances were simulated by using different mixtures of cue combinations (i.e., different training sets) for different networks. In the normal-rearing training set, 40% of trials were VA, 30% VS, and 30% AS. In the dark-rearing training set (simulating rearing in a light-tight environment that precludes the visual-nonvisual experiences necessary for the development of SC visual-nonvisual multisensory integration (Yu et al., 2010, 2013), 50% of trials were AS, 25% were A, and 25% were S. There were no visual or visual–nonvisual cues. In the noise-rearing training set (simulating rearing in an omnidirectional sound environment that masks the transient auditory inputs necessary for the development of SC auditory-nonauditory multisensory integration; Xu et al., 2014, 2017), 50% of trials were VS, 25% were V, and 25% were S. There were no auditory or auditory–nonauditory cues.

Evaluations of developmental outcomes.

The end states of the model for the different developmental circumstances were evaluated by comparing the relationships between multisensory and unisensory responses predicted by the model with those that have been documented empirically from cats of either sex (Yu et al., 2010, 2013, Xu et al., 2012, 2014, 2015, 2017). These evaluations involved recording the responses of individual model units to simulated visual, auditory, and somatosensory cues presented alone or in different concordant crossmodal combinations (30 trials/test) and then calculating the proportionate difference (i.e., multisensory enhancement, ME) between the unit's mean response to each crossmodal cue combination and its most robust response to one of its modality-specific components. This value quantified how the unit integrated a particular crossmodal stimulus combination. To assess patterns of integration within the different simulated developmental circumstances, multiple units were tested with simulated cues having different levels of efficacy randomly selected from a Gaussian distribution with mean value I (Table 1).

Experimental design and statistical analysis.

Mean levels of ME and the relationship between ME and unisensory effectiveness were assessed for each cue combination and each developmental circumstance and compared with the same metrics obtained empirically. Individual model units were selected with unisensory response magnitudes similar to those of published biological exemplars for further illustration of similarities in developmental outcomes. Model performance was evaluated statistically by comparing the proportion of integrating neurons identified in different rearing environments and crossmodal configurations produced by the model to the distribution of empirically observed values described previously (Xu et al., 2015) using binomial tests.

Parameter selection and weight matrices.

Numerical parameter values for the model stimulations (Table 1) were selected so that units would respond rapidly to stimuli when present but otherwise maintain negligible levels of activity. The weights of all plastic connections were initialized to zero. Two other important design choices not described above are constraint 1 and constraint 2. For constraint 1, learning rate scalars for the excitatory weights between the noncompetitive input compartments and the central compartment of the SC unit were greater (faster) than learning rates for the plastic inhibitory connections between competitive and noncompetitive subregions. For constraint 2, the threshold value for the learning rule applied to the noncompetitive input compartments (ϑ^C) was set to require joint activation of afferents from both modalities for the rule to be engaged.

Results

The different simulated rearing paradigms (normal, dark-rearing, and noise-rearing) produced different developmental trajectories, yielding adult neurons that responded to different pairs of spatiotemporally concordant crossmodal cues in different ways. In each case, the model's end points were very similar to those observed empirically in SC neurons after the corresponding rearing condition (Yu et al., 2010, 2013, Xu et al., 2012, 2014, 2015, 2017). The model reproduced, with reasonable accuracy, both the overall population trends in the biological data as well as the behavior of individual exemplars. Essentially, whenever a particular crossmodal pair was present in the simulated training paradigm/rearing environment [e.g., an auditory–somatosensory (AS) stimulus pair during dark rearing], adult SC neurons would produce enhanced responses to that pair. However, when experience with a particular pair was excluded during training/development [e.g., visual–auditory (VA) pairs were precluded during dark rearing and disrupted in noise rearing by masking transient auditory cues] the response of the neuron to that pair was not enhanced; it was either equivalent to, or less than, the response to the most effective cue in the pair. These observations were found in both simulated bisensory and trisensory neurons. Therefore, both in the model and in the actual SC, neurons use crossmodal sensory experiences to develop the ability to integrate only those crossmodal combinations present in that environment to produce enhancement.

Initial state of the model

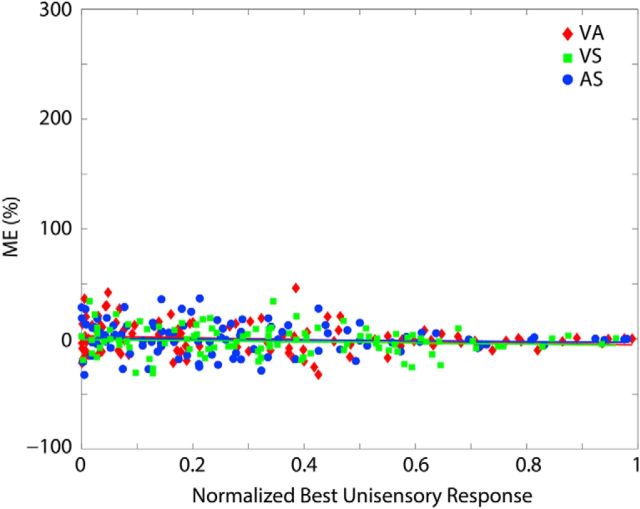
Tectopetal projections from the noncompetitive input region were initially ineffective: in its native state, the SC behavior was solely determined by the active and mature WTA competition implemented among the competitive input subregions. Therefore, when the network was tested with crossmodal cues at this time, the more efficacious cue suppressed the influence of the other and determined the SC response (after suffering some attrition). This occurred regardless of the relative positions of the cues within the array (i.e., simulated to be concordant or disparate in space). It is conceptually important to note that, according to the model, this experience-naive state is not one in which multisensory processing rules are absent; rather, it is one in which crossmodal cues interact competitively. The result, however, is that, in the native state, there is no multisensory enhancement evoked by crossmodal cues at any level of efficacy (Fig. 2).

Figure 2.

The native state. In the model's initial state, the responses of individual SC units are not enhanced by crossmodal cues at any level of stimulus efficacy. Plotted here is the amount of ME (y-axis) observed in response to crossmodal (VA, VS, and AS) cue pairs at multiple efficacy levels (x-axis) for a network before any simulated development. Each point represents the multisensory enhancement index of a single unit. All points, regardless of specific crossmodal convergence pattern, cluster around zero.

Changes during training:

Crossmodal cue pairs presented during simulated development evoked activity in SC units via the influence of the competitive input subregions (as noted above, this activity pattern was determined by the WTA). The noncompetitive input compartments also became activated by the simulated cues, although they did not yet influence the SC due to the ineffective state of their connections with the central SC compartment. However, the activity-dependent engagement criteria of the learning rule were met. This resulted in changes to the two sets of plastic connections (Fig. 3). In the first set, coactivation of the SC unit and the noncompetitive input compartment for a given crossmodal pair caused the learning rule to strengthen the connections between the input compartment and the central compartment (Fig. 1B, Eqs. 8–9). Because joint activation of both (crossmodal) inputs to the noncompetitive input compartment was required (constraint 2), these connections were not strengthened by modality-specific cues, only crossmodal cues. In the second set, coactivation of the competitive and noncompetitive input subregions also caused the mutual inhibitory connections between them to be strengthened (Eqs. 10–11). In this way, competitive input subregions and noncompetitive input subregions that were coactivated during training came to inhibit one another. However, like the excitatory projections described above, these changes were specific to the modalities presented together in the training set: a general inhibition did not form between all competitive and noncompetitive subregions (Fig. 3).

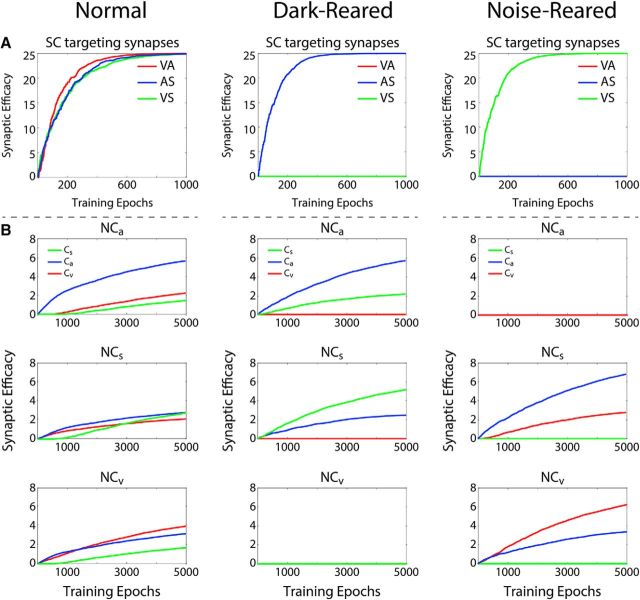
Figure 3.

Training changes connection strength (“weights”) during development. A, Plotted for the three different training paradigms/simulated rearing conditions (normal, dark-rearing, and noise-rearing) is the strength of the projection from each noncompetitive compartment (y-axis) as a function of training epoch (x-axis). Noncompetitive channels are identified by the modalities they pool (VA, AS, etc.). The normal training paradigm leads to a strengthening of all channels because all modality pairings are presented, whereas the dark-reared and noise-reared paradigms produce strengthening only in the crossmodal pair represented in the training set. B, Similar experience-specific effects are seen for the inhibitory projections from the noncompetitive subregions to the competitive subregions in each of the training paradigms (larger value = more inhibition). Reverse inhibitory projections from competitive subregions to noncompetitive subregions are symmetric and show equivalent development. Robust inhibition develops for each modality present in the training set and in proportion to its amount of representation. The consequence of this result is that inhibitory interactions are only formed between inputs that were coactivated during training, not all input subregions.

By design, the excitatory connections from the noncompetitive input compartments to the central compartment of the SC unit were more sensitive to the training paradigm (constraint 1) and, thus, were trained much faster than the inhibitory connections between the noncompetitive and competitive input subregions. This ensured that the noncompetitive subregions did not begin to suppress competitive inputs until their excitatory influences on the SC were mature, which was essential because their maturation required that SC activity be initially driven by the competitive input region. However, over the course of training, the noncompetitive input subregions eventually came to be the major determinants of the SC response. This was because a single stimulus saturated the net competitive input to the SC, but multiple (i.e., two) stimuli were needed to saturate the noncompetitive input. The effective impact was that the noncompetitive projection had reserved capacity to provide a more robust net input when multiple crossmodal cues were present.

Model end states and developmental outcomes

The most informative comparisons between the results of the simulations in the model and the empirical data were obtained by examining the response patterns of model trisensory units and biological trisensory neurons after different rearing conditions. Simulated development in bisensory neurons revealed equivalent results for their particular convergence pattern.

Exemplar comparisons

Figure 4 illustrates the unisensory and multisensory responses of three trisensory exemplar neurons recorded from the SC of normal (Fig. 4A), dark-reared (Fig. 4B), and noise-reared animals (Fig. 4C), and of three exemplar SC units of the model trained to simulate each of these conditions. Each real neuron and model unit was tested with visual, auditory, and somatosensory cues placed alone and together in different concordant pairwise combinations within overlapping regions of their respective receptive fields. The responses to different pairs and their unisensory components were collected in different experimental blocks (there was some small variation in the unisensory response magnitudes across blocks). In each case, there was a match between the patterns observed in the actual physiological responses (middle) and the model results (right). Whereas the normal-reared neuron evidenced robust response enhancement to each crossmodal combination, the responses of dark-reared neurons were enhanced only by the AS combination, and the noise-reared neurons were enhanced only by visual–somatosensory combination. The responses of the neurons to all other crossmodal combinations (i.e., those to which they were not exposed during rearing) were approximated by the more robust modality-specific component response or an average of the two comparator unisensory responses.

Figure 4.

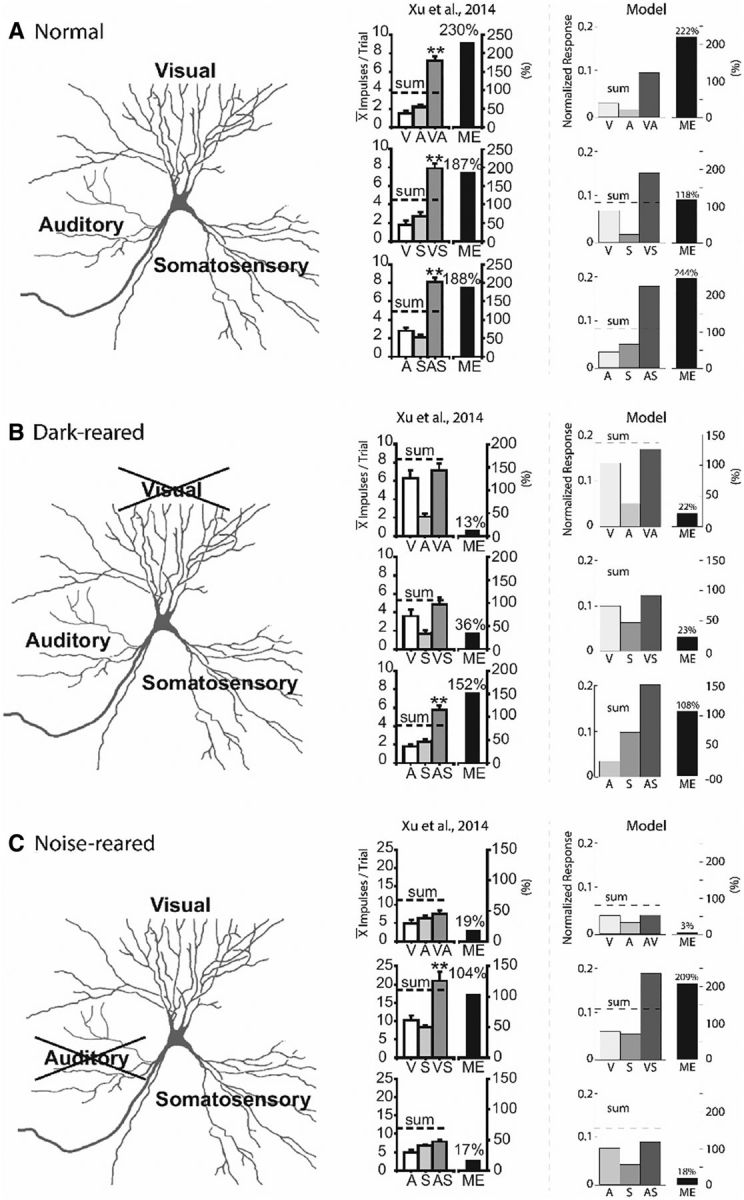
Empirical model parallels in multisensory and unisensory responses after different rearing conditions. A–C, Illustrations of the results obtained for three different rearing conditions/training paradigms: normal-rearing (A), dark-rearing (B), and noise-rearing (C). Illustrated for each condition is a schematic of the sensory convergence pattern (left), physiological recordings (Xu et al., 2015) of responses from an SC trisensory neuron tested with different cues (middle), and the model results for those responses (right). Bar graphs indicate the magnitude of the responses to V, A, and S stimuli presented alone or in different pairwise combinations (i.e., VA, VS, and AS), as well as the ME generated by each multisensory response. Note the striking parallels between the physiological response magnitudes (in units of mean impulses/trial) and the model responses (in normalized units). In both cases, the sum of the responses to the unisensory components are reported for comparison. (Adapted with permission from Xu et al., 2015). **p < 0.001.

The model explains how each of these patterns can result from differential development of the plastic noncompetitive projections. In the normal-reared paradigm, all noncompetitive projections are strengthened. But only the A-S noncompetitive projections are strengthened in the dark-reared paradigm and only the V-S noncompetitive projections are strengthened in the noise-reared paradigm. Whenever a noncompetitive projection representing a particular pairing was not strengthened, the response of the neuron to crossmodal cues belonging to that pairing was dictated by the competitive pathway. Therefore, these responses reflected the outcome of the WTA competition and were not enhanced.

Population comparisons

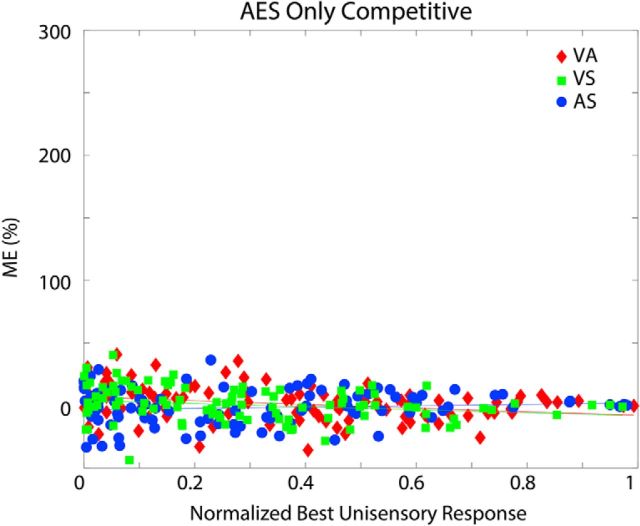
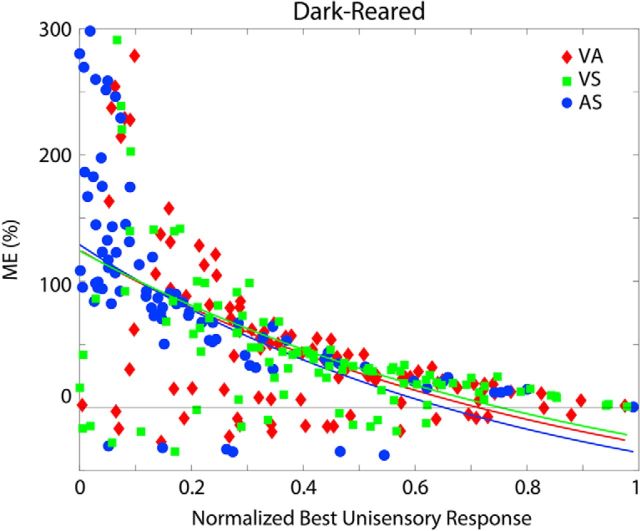
Figure 5 illustrates physiological results obtained from SC neural (left panels) and model populations (right column). In both model and biology, larger proportionate multisensory enhancements were more commonly associated with weaker modality-specific components, a common observation in normal-reared animals referred to as “inverse effectiveness” (Meredith and Stein, 1983). This feature varied in predictable ways across the different groups. For the normal-reared population (Fig. 5A), similar inverse trends were observed for each modality pairing in the model and the empirical dataset (Xu et al., 2015). For dark-reared and noise-reared populations (Fig. 5B,C, respectively), significant inverse trends only existed for modality pairings that were present in the rearing environment/training paradigm. The nonexperienced/untrained modality pairs showed no significant enhancement (and even multisensory depression) at all levels of unisensory effectiveness. In each case, the model provided a good match to the empirical trends.

Figure 5.

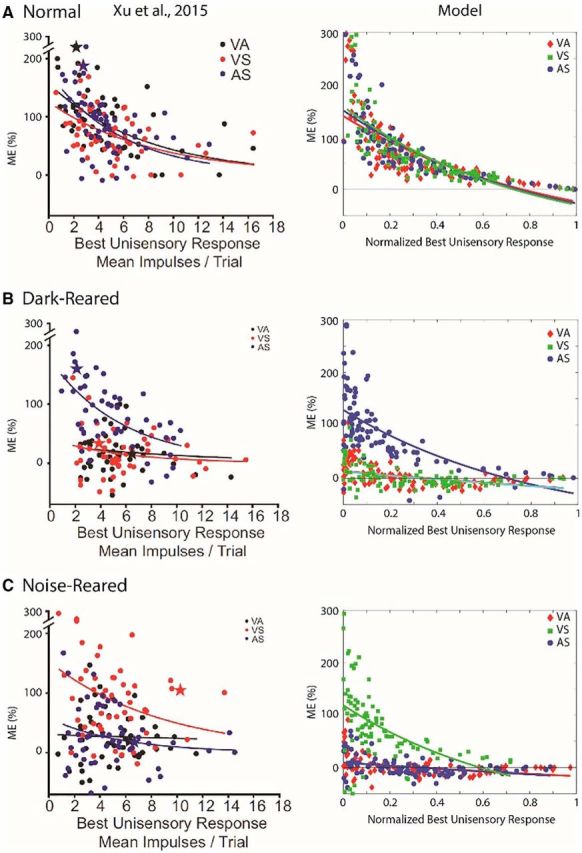
Empirical model parallels in ME and inverse effectiveness. Plotted are individual data points and trend lines relating proportionate ME (%) to the magnitude of the response to the most effective component stimulus (i.e., unisensory response) for the normal-reared (top), dark-reared (middle), and noise-reared (bottom) populations. The left panel for each population shows the empirical result from Figure 3 of Xu et al. (2015). The right plot shows the model results (each data point was derived from the mean responses of each model's unit computed over 30 trials/stimulus condition). In each case, modality pairings that were present in the rearing environment/training paradigm showed an inverse relationship between ME and the magnitude of the best unisensory response, a trend termed inverse effectiveness (Meredith and Stein, 1983). Pairings that were excluded from the rearing environment/training paradigm showed marginal, nonsignificant trends and no significant enhancement on average anywhere in the range. All fitted curves are exponential. (Insets adapted with permission from Xu et al., 2015).

Figure 6 summarizes the empirical and model results at a population level. One of the interesting features of the empirical data (Fig. 6A) was that, when a modality pairing was present in the environment, the average enhancement (ME) observed for that pair at the developmental end point (Fig. 6A, left) was approximately the same (∼90%) regardless of the specific modalities involved. When a pairing was excluded from the rearing environment, ME only averaged ∼20% in each case regardless of the specifics of the excluding environment. A similar result was seen in the probability that an adult trisensory neuron would exhibit significant multisensory enhancement in response to each crossmodal pairing. If the crossmodal pairing was included in the rearing environment, then the vast majority of these neurons (∼70%) generated enhanced responses to those cues when mature. Only a minority of neurons generated significantly enhanced responses to an excluded pairing. The model replicated all of these findings with a high level of accuracy (Fig. 6B). In each case, the model's proportion of integrating neurons are not statistically different from the empirically observed values with an evaluation criteria of (α = 0.01); in other words, the model's behavior is within the expected variation of the empirical results (Table 2).

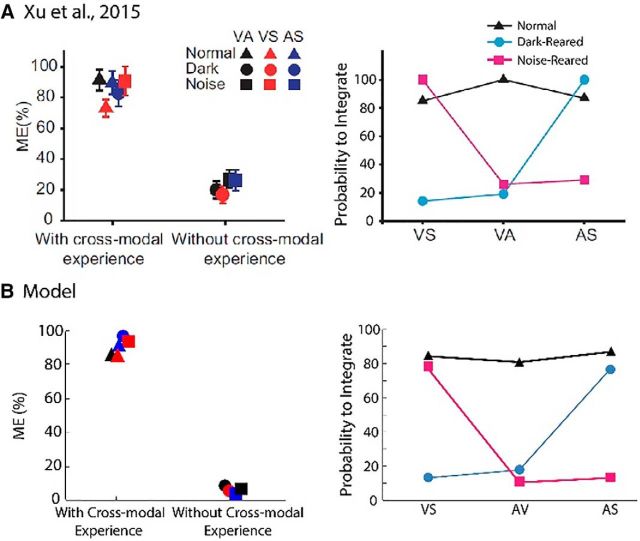
Figure 6.

Overall model and neuronal parallels. A, Empirical findings from Xu et al. (2015) indicate that multisensory enhancement is elicited by crossmodal pairings that were encountered in the rearing environment. Left, ME elicited by each crossmodal pairing (VA, black; VS, red; AS, blue) in populations of trisensory neurons recorded from animals reared under different conditions (normal, dark-rearing, or noise-rearing). Data are grouped on the x-axis according to whether each pairing would be encountered in the rearing environment (“with crossmodal experience”) or not. Right, Proportion of trisensory neurons in each population that generated significantly enhanced responses to each of the modality-pairings (see Fig. 3 in Xu et al., 2015). B, Model predictions for each of the data points in A obtained by the mean responses, as reported in Figure 5, of the simulated population of SC neurons in the model to different crossmodal pairs. There is a match between the trends in A and the model predictions in B. (Figures in A adapted with permission from Xu et al., 2015).

Table 2.

Comparisons of model and empirical results for the probability of a multisensory neuron (expressed as a percentage) producing an enhanced versus nonenhanced response in different stimulus conditions in different simulated rearing conditions

	Probability of integrating (%)
	Empirical	Model	p-value
Normal-reared
VA	84	82	0.56
AS	82	89	0.2
VS	77	86	0.07
Dark-reared
VA	17	18	0.81
AS	77	83	0.25
VS	11	13	0.51
Noise-reared
VA	22	10	0.04
AS	25	13	0.03
VS	75	83	0.16

p-values were obtained using the empirical data as the null hypothesis model in a binomial test. Empirical results were obtained from Xu et al. (2015).

Importance of model constraints revealed by a sensitivity analysis

The present model was reduced and simulated in a simple form to highlight the computational features of the circuit believed to be most crucial in accounting for the development of multisensory enhancement capabilities. One way to demonstrate the crucial nature of these particular features on the model's effectiveness is to remove them, “breaking” the model in specific ways, and then examining the impact on the model's developmental trajectories and endpoints.

One crucial feature of the model in the present context is that the SC receives input from both competitive and noncompetitive projections. The dominance of competitive projections in early life was a necessary constraint to explain how neonatal multisensory neurons can be responsive to multiple sensory modalities, yet not generate enhanced responses to their concordant stimulation. The importance of the noncompetitive projections in accurately explaining development was demonstrated by removing them from the model (Fig. 7). Because the model assumes that AES is the only source of the noncompetitive projections (and other sources exist for competitive projections), this manipulation can be thought of as equivalent to removing AES in early life (Jiang et al., 2006, 2007; Rowland et al., 2014). The consequence for the model was the same as that observed in those empirical studies: the SC never developed multisensory enhancement capabilities because it lacked the substrate that allows crossmodal signals to bypass the default competition (Fig. 7).

Figure 7.

Effect of removing the noncompetitive projections from the model. Shown are the model results trained with normal crossmodal experience without the noncompetitive projections. Because only the competitive projections remain intact, multisensory responses are not enhanced for any crossmodal combination at any level of efficacy. Conventions are the same as previous figures.

A second crucial feature of the model is that a joint activation between the presynaptic inputs is required to engage the learning rule operating on the noncompetitive projections. This augmentation elevates the complexity of the learning rule above that of a standard generic associative learning rule, requiring the whole triad of (multiple) presynaptic and (singular) postsynaptic elements to be activated in order for the connection to be strengthened. This requirement of a triad restricts the development of multisensory enhancement capabilities to those specific pairs that have been experienced. To illustrate the importance of this feature, a generic Hebbian learning rule (Eq. 12) was substituted in place of our modified learning rule and applied to the noncompetitive projection. Figure 8 illustrates the results obtained from the model for dark-reared simulations using the generic learning rule: the model SC units develop the ability to integrate all pairs of cues rather than only the AS pairs. This occurs because input from only a single modality is sufficient to strengthen the connection from any noncompetitive input compartment to which it connects because it meets the presynaptic requirement of the generic association rule. Therefore, if the training set/rearing environment includes even a single crossmodal pair (e.g., AS in dark rearing), then the connections from all noncompetitive input compartments become strengthened because each noncompetitive input compartment receives input from at least one of the modalities in the included pair. Therefore, by implementing a generic associative learning rule, multisensory enhancement capabilities develop for all modality pairings, patterns not actually seen in dark-reared or noise-reared animals (Yu et al., 2010, 2013; Xu et al., 2014). With a generic associative learning rule, the network would generalize any crossmodal experience and extend integrative abilities to crossmodal pairs never experienced during training.

Figure 8.

Effect of removing the constraint requiring the activation of two presynaptic elements. The adult expression of ME capabilities in a network trained in the dark-reared paradigm in which a generic associative learning rule was implemented (i.e., the training thresholds for the noncompetitive pathways have been lowered) so that activation of only one of the presynaptic elements was required. “Breaking” the network in this way produced results that no longer accurately reproduced the biological results. This network integrated all sensory combinations instead of only the AS combination. Conventions are the same as in previous figures.

Discussion

In the present model, the AES–SC projection is assumed to be active, efficacious, and composed of crossmodal convergent afferents in the absence of crossmodal experience; however, without such experience the crossmodal signals it relays interact competitively. With appropriate experience, a noncompetitive set of AES–SC inputs emerges and relays crossmodal signals that interact cooperatively. The present model replicates the specificity of the experience-dependent development of this multisensory integrative process as SC multisensory integration capabilities emerge and override the default state of crossmodal competition. The insights offered by the model in explaining why multisensory development proceeds in the way that it does and the predictions it makes for future evaluation are detailed below.

One of the theoretical insights of the model is that the initial default state of the circuit is one in which sensory inputs interact competitively regardless of their modality or the concordance of information they relay. This concept represents an evolution in our understanding of multisensory development, which previously viewed enhancement capabilities and integration capabilities more generally, as being built on a neutral or “unformed” substrate (Wallace and Stein, 1997, 2000; Wallace et al., 1997, 2004; Stein, 2005; Stein and Rowland, 2011), much as the emergence of other functional capabilities have been viewed (e.g., language, object recognition). However, this new perspective has intuitive appeal given the functional role of the SC in detecting and localizing external cues as a precondition for programming orientation responses. Because orientation can be directed at only one target at a time, a basic constraint imposed on multiple cues simultaneously seeking access to the sensorimotor circuitry of the SC is that they compete. In the adults, this is readily observable when within-modal or crossmodal cues are presented in different spatial locations: responses to either individual cue are often degraded (Alvarado et al., 2007; Gingras et al., 2009). The present model suggests that, in the absence of experiences that provide evidence for a common origin of a particular crossmodal configuration (i.e., spatially concordant; Kayser and Shams, 2015), the circuit extends its internal logic to process any two crossmodal cues as competitive.

The second model insight is that the internal structure of the multisensory circuit allows for the computational segregation of pairs of sensory modalities. This recognizes that neurons do not develop a generic integrative process that is then applied to all crossmodal pairs. Rather, specific processing capabilities develop so that a neuron can deal differently with different crossmodal pairs and perhaps different spatiotemporal configurations, depending on its experience with those particular stimulus conditions. This is accomplished via the noncompetitive input compartments (an architecture that extends previous proposals; cf. Rowland et al., 2007). There are many different biological mechanisms that could accomplish such functional compartmentalization; for example, by connections targeting adjacent dendritic locations (Poirazi et al., 2003); by interacting through NMDA-gated channels (Binns and Salt, 1996; Truszkowski et al., 2017); or by aligning inputs/EPSPs in temporal proximity or within a phase of an ongoing background oscillation (Lakatos et al., 2007; Senkowski et al., 2008; Engel et al., 2012). Equally likely is the possibility that the same endpoint is achieved through more indirect means; for example, by rebalancing contacts from or between interneuron populations which receive specific patterns of input [i.e., interneurons driven by AEV might reduce their inhibition of excitatory input from one region (e.g., FAES), but not from another (e.g., SIV)]. Until relevant physiological studies examine these possibilities, there is no compelling reason to favor one alternative over another.

A third insight of the model is that, although an associative learning rule can drive development in this circuit, it must be sensitive to the covariance among multiple presynaptic elements in addition to their common postsynaptic target. There is substantial evidence for the operation of Hebbian rules in multiple areas of the brain, including the SC (Bi and Poo, 2001), and there are several variants of the basic Hebbian learning rule that can implement such an idea. One of the most basic is a “sliding threshold” model (Bienenstock et al., 1982), in which the threshold required for the engagement of the learning rule is always just above the magnitude of the input from the most effective presynaptic element (e.g., unisensory input). In this way, both presynaptic elements must be active to engage the learning rule, which in turn causes strengthening of both, but in doing so, the threshold is also pushed higher so that it is always out of reach of a single element. In the present context, such a rule could apply to the development of both the competitive and noncompetitive projections, with only variation of a single parameter (the threshold) being sufficient to explain their developmental asymmetries. It should be noted that, although the simulated model applies changes to the strength of connections between compartments, this operation is equivalent to individually strengthening individual connections. Biophysical components such as the voltage-sensitive NMDA receptor may play a crucial role in implementing the proposed learning rule because “clusters” of AES contacts on target SC neurons that use NMDA receptors could conceivably implement the triadic covariance rule. NMDA receptors have previously been implicated as playing a crucial role in the expression of multisensory integration in the SC/tectum (Binns and Salt, 1996; Truszkowski et al., 2017) and it is possible that they are likewise important in its development.

The present model represents a focused attempt to describe this development at higher resolution in a well studied circuit. How these insights might extend to other multisensory circuits in the brain is unknown. One possibility is that the cooperative/competitive dynamics described here represent a general neural plan for signal filtering (i.e., figure/ground separation) that is engaged throughout the brain. A distinct alternative, however, is that the crucial multisensory computations engaged by each circuit depend on its unique computational goals. For example, a circuit computing an “optimal estimate” of a property of an external event might default to competitive dynamics, whereas one designed to enhance the simultaneous processing of multiple features would not. If the latter hypothesis is correct, then this diversity in the multisensory transform might reflect very different developmental dynamics.

The model makes several key predictions. First, in the absence of crossmodal experience, the default SC multisensory computation will be one of competition, not one of nonintegration (in which the less efficacious input would be discarded or ignored). Second, the SC multisensory products in SC neurons of animals lacking experience with a set of crossmodal cues will be equivalent regardless of whether those cues are spatiotemporally concordant or disparate. Third, as a consequence of averaging, multisensory responses will be depressed below the best component unisensory response when those crossmodal cues differ significantly in efficacy. Fourth, if NMDA receptors play a crucial role in this development, it should be possible to preclude this development by deactivating them during early life when multisensory experience is typically first acquired.

The model also suggests that the AES–SC projection has greater functionality than has been fully appreciated; in particular, that some of the competitive interactions observed in the SC reflect operations that take place within cortex itself and are then relayed to the SC. There is some tangential empirical evidence consistent with this idea. For example, AES deactivation has been noted to have a partial effect on the incidence and magnitude of multisensory depression in the SC evoked by spatially disparate crossmodal cues (Jiang and Stein, 2003). The present model provides the first explanation for this dependency and why it is only partial: it reflects the action of only a subset of the competitive crossmodal projections to the SC. However, to our knowledge, this prediction has not yet been examined systematically.

In addition, the model predicts that multisensory enhancement capabilities will not have a transitive inference property. Separately formed VA and AS associations will not automatically form a visual–somatosensory association; this requires visual–somatosensory experience. There are presently no empirical data that address this prediction. However, it could be tested in either dark-reared animals in which enhancement capabilities to AS inputs develop naturally and VA enhancement capabilities are later “trained” or in noise-reared animals in which two comparable pairs of effective crossmodal configurations are created (Yu et al., 2010, 2013; Xu et al., 2017). In both cases, the empirical test would be whether the untrained pair would now produce multisensory enhancement. The results of this empirical evaluation, and those described above, will further refine our conceptual frameworks for multisensory development and our understanding of its key mechanics.