Collective cell migration over long time scales reveals distinct phenotypes

Abstract

Introduction

Migratory phenotypes of metastasizing tumor cells include single and collective cell migration. While migration of tumor cells is generally less cooperative than that of normal epithelial cells, our understanding of precisely how they differ in long time behavior is incomplete.

Objectives

We measure in a model system how cancer progression affects collective migration on long time scales, and determine how perturbation of cell-cell adhesions, specifically reduced E-cadherin expression, affects the collective migration phenotype.

Methods

Time lapse imaging of cellular sheets and particle image velocimetry (PIV) are used to quantitatively study the dynamics of cell motion over ten hours. Long time dynamics are measured via finite time Lyapunov exponents (FTLE) and changes in FTLE with time.

Results

We find that non-malignant MCF10A cells are distinguished from malignant MCF10CA1a cells by both their short time (minutes) and long time (hours) dynamics. In addition, short time dynamics distinguish non-malignant E-cadherin knockdown cells from the control, but long time dynamics and increasing spatial correlations remain unchanged.

Discussion

Epithelial sheet collective behavior includes long time dynamics that cannot be captured by metrics that assess cooperativity based on short time dynamics, such as instantaneous speed or directionality. The use of metrics incorporating migration data over hours instead of minutes allows us to more precisely describe how E-cadherin, a clinically relevant adhesion molecule, affects collective migration. We predict that the long time scale metrics described here will be more robust and predictive of malignant behavior than analysis of instantaneous velocity fields alone.

1. Introduction

Cell migration has many implications for cancer progression [1, 2, 3, 4] and tumor growth [5]. The collective behavior of many cells is known to play an important role in a wide variety of biological processes from embryonic development [6, 7] to wound healing [8, 9], but there is an incomplete understanding of how individual cell behaviors lead to emergent collective properties of cell groups.

A common method used to study collective migration in epithelial systems is the scratch assay [10], which allows for the imaging of large cell sheets over time. Recent studies have expanded this concept to include unconstrained migration assays that do not scratch the cells [11, 12] and unique microenvironments to induce collective migration [13, 14]. As these experimental techniques have matured, there has been an increasing need for a quantitative understanding of collective cell motion. Many groups have adopted cell tracking and particle image velocimetry (PIV) based techniques to study correlations and swirls within the cell sheet [11, 15], the traction forces exerted by cells [16, 17], and a variety of other techniques comparing cell motion to fluid flows [18]. When applying these techniques to malignancy and metastasis, a single feature of collective motion may not provide enough information to understand the changes cells undergo during cancer progression. As an example, although various cancer cell lines may show changes in speed, previous work has shown that additional metrics of migration, such as directionality, are needed to make distinctions between malignant and non-malignant cell lines [12]. Furthermore, even when considering multiple metrics, most prior work has been limited to analysis of short term behavior, such as instantaneous speeds calculated on the scale of minutes. Here we argue that studying collective cell migration over multiple length and time scales provides additional information that is useful for distinguishing migration phenotypes. Although cell motion can occur on the time scale of minutes, cell division and metastatic invasion occur on time scales of hours or days. Thus we expect that including long time behavior over the course of hours into the collective motion phenotype may make the migration phenotype a better predictor of cancer metastasis.

In this work we study the collective behavior of normal but immortal MCF10A cells (referred to as M1) and the invasive, lung colony forming MCF10CA1a cells (referred to as M4) in an unconstrained collective migration assay. Previously described short time features of collective cell motion, such as directionality, are able to distinguish these two cell types [12]. We further explore the behavior of these cells, and find additional distinctions in metrics that describe long time dynamics measured over hours. To assess the importance of long time dynamics in understanding the migration phenotype, we present data on the perturbation of E-cadherin in these cell types. E-cadherin has been frequently studied in the context of cancer progression: its downregulation is considered a marker of the epithelial to mesenchymal transition (EMT) [19] and is often associated with a poor patient prognosis [20, 21]. Yet, recent studies have highlighted that the role of E-cadherin in cell-cell adhesion and collective migration is not simple [22, 23]. The long time dynamics of E-cadherin knockdown cells presented here reinforce this complex role of adhesion and provide tools for future studies on the effect of cell-cell adhesion in cancer progression.

2. Methods

2.1. Cell Culture

Normal but immortal MCF10A (M1) cells and invasive, lung colony forming MCF10CA1a (M4) cells were used in this study (Barbara Ann Karmanos Cancer Institute, Detroit, MI). M4 cells were cultured in DMEM/F12 medium supplemented with 5% horse serum (both from Invitrogen, Carlsbad, CA). M1 cells were cultured in M4 medium additionally supplemented with 10 μg/ml insulin (Invitrogen), 10 ng/ml EGF (Peprotech, Rocky Hill, NJ), 0.5 μg/ml hydrocortisone, and 100 ng/ml cholera toxin (both Sigma, St. Louis, MO). Cells were kept in a humidified atmosphere at 37°C and 5% CO₂.

For downregulation of E-Cadherin, cells were stably infected with pGIPZ lentiviral particles coding for shRNA (V2LHS_14838, V3LHS 346823, Dharmacon, Lafayette, CO). Non-coding RNA (’nonsense’) was used as a negative control. Infected cells were selected with and maintained in puromycin containing medium (5ug/ml). E-Cadherin expression levels were analyzed by Western blotting as described in the supplementary methods.

2.2. Migration Assay and Microscopy

Glass bottom 12 well plates were coated with 10 μg/ml collagen IV in 50mM HCl in a humid chamber at room temperature overnight, air dried, and stored at 4°C until further use. Cells were plated in a 10 μl drop at a concentration of 3 × 10⁶ cells/ml. After approximately one hour, non-adherent cells were washed off and the well was filled with media [12]. Two hours before imaging, the media were replaced with fresh media modified to have a concentration of 1% horse serum. The cells were imaged overnight for a period of 10 hours on an incubator microscope at 37°C and 5% CO₂ (Zeiss Observer. Z1, Zeiss, Goettingen, Germany). An automated stage was used to collect images on both the left and right edge of the cell monolayer for each well every three minutes using a 10x phase contrast objective.

2.3. Image Analysis: Particle Image Velocimetry

Particle Image Velocimetry (PIV) analysis using the MatPIV toolbox (J. Kristian Sveen, GNU general public license) for MATLAB (MathWorks, Inc.) was used to extract velocity information from time-lapse images, as previously described [24]. Multiple iterations of interrogation window sizes were used (two iterations of 64 × 64 pixel windows followed by two iterations of 32 × 32 pixel windows). At each interrogation step a 50% overlap was used; outliers were detected using a signal-to-noise filter. The resulting flow fields capture all motion within the collective cell sheet and provide motion information on a scale smaller than an individual cell. The resulting PIV vectors capture displacements on a time scale of three minutes.

The leading edge of the cell sheet was found using custom segmentation code in MATLAB. Phase contrast images of the monolayer are passed through a Sobel filter to emphasize edges. A median filter and morphological opening are used to clean up the edge image before finding the perimeter of the resulting binary images. The edge coordinates are then found using a MATLAB implementation of Dijkstra’s algorithm (“dijsktra path finder” by Sebastien PARIS, available on the MATLAB File Exchange at mathworks.com). Both the left and right edge of the monolayer are found over time and their relative position is determined from the microscope stage data. Together, these two edges can be fit to a circle which determines an effective radius and center of the roughly circular monolayer over time. A schematic of these calculations is shown in Supplemental Figure 1. Radial displacement values were calculated by subtracting the effective radius at t = 0h from the effective radius at t = 10h.

2.4. Migration Analysis

Angle distributions refer to the direction of the PIV velocity vectors with respect to radial expansion; the angle of the ith velocity vector, θ_i, is given by the inverse tangent of the velocity vector components in polar coordinates, as show in (1). This metric thus captures short time behavior on a scale of three minutes.

$${\theta }_i=ta{n}^{-1}(\frac{u_{\mathit{rotational}}}{u_{\mathit{radial}}})$$ (1)

Angular deviation was calculated as $\sqrt{2(1-z)}$ where z is defined in (2) and N is the number of velocity vectors within the flow fields being analyzed. Angular deviation therefore ranges from zero (aligned velocity vectors) to $\sqrt{2}$ (highly uncoordinated velocity vectors).

$$z=\frac{1}{N}{[{({\displaystyle \sum _{i=1}^N}\mathrm{Cos}{\theta }_i)}^2+{({\displaystyle \sum _{i=1}^N}\mathrm{Sin}{\theta }_i)}^2]}^{1/2}$$ (2)

Finite-time Lyapunov exponents (FTLEs) were calculated as previously described [24]. Briefly, FTLE values are calculated by computationally moving virtual tracer particles through the experimentally determined PIV flow field. We follow the tracer motion through the evolving PIV flow field for a deformation time of two hours. If the deformation time is long enough, the FTLE values asymptotically approach Lyapunov exponents [25]; we experimentally find that FTLE values in this system approach an asymptotic value after 2 hours. The tracer particles are initiated on the PIV grid points but are allowed to move off the grid as the flow field evolves. At the end of this time period, we calculate the logarithm of the largest eigenvalue of the Cauchy-Green strain tensor for each cluster of four tracers that were initially neighbors; this is the local FTLE value. Effectively, this measures how tracer particles passively flowing in the collective cell sheet would move apart from each other over time. Those tracers that move apart exponentially are sensitive to initial conditions and indicate regions of possibly chaotic flows. As the FTLE measurements are on the length scale of the PIV flow field, they include both cell body motion and subcellular motion such as membrane ruffling. Thus, the FTLE values represent the chaotic nature of the cell monolayer as a whole. By repeating this analysis for multiple starting frames of the deformation, we measure the evolution of FTLE values over time.

Fluctuation time scales were calculated from a coarse graining of the flow field as described previously [26]. The PIV flow field was averaged over increasing time intervals and the variance of the rotational velocity calculated. The variance decreases with increasing time interval and can be fit to an exponential decay to calculate a characteristic time scale (t_c) describing flow fluctuations, as was shown by Marel, et al. [26]. In our work, we fit the experimental variance, σ, to the exponential defined in (3). The second term of (3) accounts for the variability due to inaccuracy in the microscope stage. The movable stage in our multi-position imaging has a finite accuracy in returning to a position; the variance this introduces can be expected to decrease with the central limit theorem. In this theorem variance decreases with the square root of the number of samples, in our case the frame number, which introduces a term with a characteristic time scale t_imaging (in this case three minutes).

$$\sigma =A{e}^{-t/t_c}+\frac{B}{\sqrt{t/t_{\mathit{imaging}}}}+C$$ (3)

Spatial correlations were calculated for each individual frame of the PIV flow field and then averaged over a time period of one hour to study the change in spatial correlation over time. Correlations were calculated as

$$C(\mathrm{\Delta }r)=\frac{{\displaystyle {\sum }_{r_i}{v}_r\left(r_i\right)\ast v_r\left(r_i+\mathrm{\Delta }r\right)}}{{\left[{\displaystyle {\sum }_{r_i}{v}_r^2\left(r_i\right)\ast {\displaystyle {\sum }_{r_i}{v}_r^2\left(r_i+\mathrm{\Delta }r\right)}}\right]}^{\frac{1}{2}}}$$ (4)

where v_r refers to radial velocity.

For all figures, paired experiments are those time lapse images that were captured on the same day from different wells of the same 12 well plate. Paired differences refer to the M1 cells subtracted from the M4 cells or the relevant nonsense (NS) shRNA cell line subtracted from the corresponding E-cadherin shRNA cell line. Error bars indicate 95% confidence intervals. Distributions are cumulative over all time frames and spatial location. Slopes, where mentioned, were calculated from a linear fit of the data.

3. Results

To study the collective behavior of both the non-malignant M1 cells and the malignant M4 cells we imaged circular confluent cell monolayers over a period of ten hours. Our imaging field of view, shown in Figure 1(a – d) and Supplemental Movie S1, records the leading edge of a larger monolayer (see Figure S1). This assay, as well as similar techniques such as the scratch assay, are often used for assessing the collective migration of cells under a wide range of conditions. A common metric used to analyze these assays is displacement over a long time period [10], or in the case of our circular monolayers, the radial displacement over ten hours as shown in Figure 1(e). For both cell types, the monolayer expands a few hundred microns over ten hours and paired experiments show no difference in the displacement between the M1 and M4 cells (Figure 1(f)). By taking more frequent images of the monolayer and using particle image velocimetry (PIV), we extract speed distributions within the monolayer, shown in Figure 1(g). These speed distributions reflect the motion of the monolayer on a short time scale of three minutes. As expected from the radial displacement, the two cell types show a similar mean speed, but the long tail seen in the M4 distribution suggests that there are interesting differences in other migration dynamics features.

Figure 1.

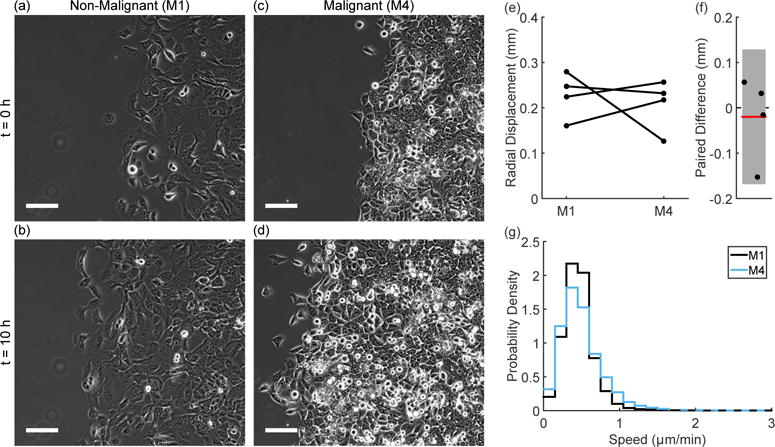
Phase contrast images of the non-malignant M1 cells (a; b) and the malignant M4 cells (c; d) show the radial migration assay at t = 0h (a; c) and t = 10h (b; d). These images are taken from Supplemental Movie 1. In all images, the scale bar indicates 100 μm. The absolute value of radial displacement varies (e), but paired experiments show no trend in the difference between M1 and M4 cells (f, error bar indicates 95% confidence interval). The speed distributions (cumulative over time and space) within the monolayer (cumulative from N = 4 experiments) show similar mean speeds, but the M4 distribution shows a longer high speed tail (g). Dashed lines indicate the region where the two curves overlap.

Our previous work has demonstrated that although M1 and M4 cells do not show a difference in mean speed, the M4 cells are less directional than the M1 cells [12]. The current data confirm this, as shown by the directional distributions in Figure 2(a). The M1 cells flow preferentially in the direction of radial expansion, while the M4 cells show a much broader distribution of directions.

Figure 2.

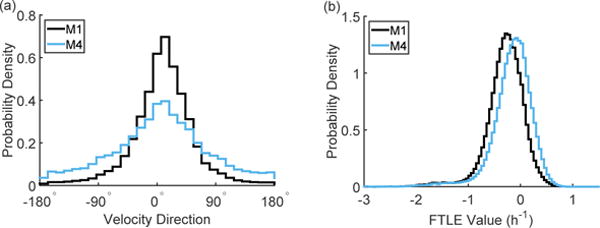
As shown by the angle distributions in (a), the M4 cells are less directional than the M1 cells. The M4 cells show more positive FTLE values than the M1 cells, as shown by the distributions in (b). Each distribution represents the cumulative data from N = 4 experiments and is cumulative over time and spatial location.

We have also previously demonstrated the use of finite time Lyapunov exponent (FTLE) values for distinguishing collective behavior in cell monolayers [24]. Unlike the distributions of speed and velocity direction, which reflect short time cell behavior on the time scale of imaging, FTLE values capture long time behavior. Here we have shown distributions of speed and velocity direction that are cumulative over 10 hours of motion, but each individual value in the distribution was calculated by looking at cell motion from frame to frame (3 minutes). The FTLE values are calculated through the evolution of cell motion over many frames (2 hours) and thus inherently capture longer time behavior. Positive FTLE values are a signature of chaotic flows and, as shown by the distributions in Figure 2(b), the M4 cells show a shift towards higher FTLE values resulting in more regions of flow with positive FTLE values.

We further explore the long time dynamics of collective migration by looking at the evolution of these metrics over the duration of the experiment. Representative speed traces from a paired experiment show that the mean speed of the monolayer tends to slightly decrease over time (Figure 3(a)), with the M1 and M4 cells showing a similar trend over ten hours, which is consistent with the radial displacement profiles seen in Figure 1(e). Angular deviation (a measure of the spread in velocity direction), shown in Figure 3(b), consistently shows a broader distribution for the M4 cells as was shown in Figure 2(a). However, looking at this distribution over ten hours provides added understanding of collective behavior by showing different long time trends for angular deviation; in the paired experiment shown in Figure 3(b), the M4 cells maintain a broad distribution over time while the M1 cells become more directed over time. A similar trend is seen in the FTLE analysis; we use the fraction of the cell monolayer with positive FTLE values (Figure 3(c)) as one indication of the amount of chaotic motion in the sheet over time. It is clear that the M4 cells remain steadily chaotic over time while the M1 cells show decreasing positive FTLE values over ten hours.

Figure 3.

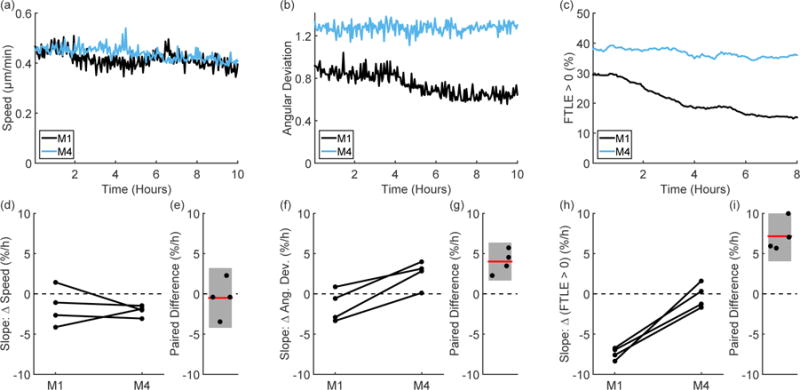
Representative time traces of speed (a), angular deviation (b), and FTLE values (c) from paired experiments show differences in the migration phenotype of the M1 and M4 cells. As shown by looking at the slope of speed over time (d), there is no trend in the difference between the M1 and M4 cells (e). However, the slope of angular deviation over time (f) tends to be higher in the M4 cells than in the M1 cells (the paired difference is shown in (g)). This is consistent with the trend seen in the FTLE values (h), where the M1 cells show a negative slope over time, while the M4 cells hold a fairly constant FTLE value over time and show a strong difference from the M1 cells (i). Lines in (d; f; h) pair experiments performed on the same day and error bars in (e; g; i) indicate 95% confidence intervals.

To compare these trends on the same scale, we report the fractional change over time for each metric by linearly fitting the percent change over time and reporting the slope in percent per hour (Figure 3(d – i)). As shown by the paired speed slopes in Figure 3(e), there is no difference in the long time speed behavior between the M1 and M4 cells. Yet, for each cell line, the slope of angular deviation over time is variable (Figure 3(f)), and paired experiments show that the M4 cells have a larger slope than the M1 cells. The M4 cells’ angular distribution therefore broadens more over time than the distribution for the M1 cells (Figure 3(g)). The difference in long time behavior is seen most clearly in the FTLE slopes. The M4 cells show stable fractions of chaos over time (approximately zero slope), while the M1 cells show decreasing amounts of positive FTLE values over time (Figure 3(h)) leading to a distinct paired difference on the order of 5-10% per hour (Figure 3(i)).

These results suggest that the M4 cells either remain disordered or become more disordered over time, while the M1 cells tend to remain ordered or become more ordered over time. Another way of looking at this behavior is to investigate the fluctuations within the cell sheet. As previously described [26], averaging the cell flow field over increasing time intervals decreases the variance in velocity. In Figure 4 we investigate the rotational velocity of the cells, i.e. the motion in a direction orthogonal to the expanding monolayer. For both cell types, the variance decreases as the flow field is averaged over increasing time intervals and can be fit to an exponential to determine a characteristic time scale; representative examples of this fit are shown in Figure 4(a) and Figure 4(b) for the M1 and M4 cells respectively. As shown in Figure 4(c), fluctuations in the M1 cells persist longer than in the M4 cells. That fluctuations in the M4 cells are more transient agrees with the trends seen in Figure 3; the M4 cells maintain a high angular deviation over time while also maintaining high FTLE values.

Figure 4.

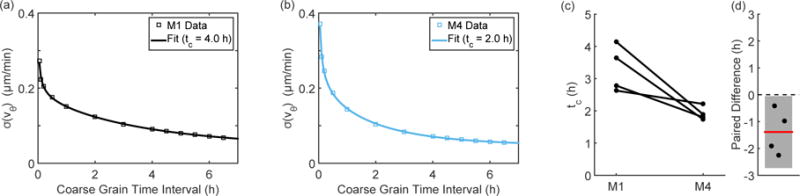
Representative examples of the velocity variance (σ) calculated during coarse graining (□) along with an exponential fit (solid line) for the M1 cells (a) and for the M4 cells (b). As shown by the paired values, the M4 cells show a shorter characteristic time scale than the M1 cells (c; d). Lines in (c) pair experiments performed on the same day and the error bar in (d) indicates the 95% confidence interval.

The trends in Figure 3 and Figure 4 show that looking at dynamics over a longer time scale (i.e. hours instead of minutes) provides additional information about the collective migration phenotype. This long time view can also be expanded to include spatial information by looking at velocity correlations. Representative correlations for the M1 (Figure 5(a)) and the M4 (Figure 5(b)) radial velocities show that spatial correlations vary over time in these cell types. Both the M1 and M4 cells initially migrate in a similarly correlated fashion. However, over the ten hour duration of the experiment, the M4 cells become less correlated, as shown by the sampling of the correlation function at a distance of approximately 100 μm (on the order of a few cells), which is shown in Figure 5(c). The M1 cells either become more correlated or remain correlated, eventually reaching the same correlation value over ten hours. The variability in initial correlation values for the M1 may reflect transient changes in behavior due to the initial plating of the cells, but the long time behavior confirms that the M1 cells move with correlations on the order of a few cells. The M1 cells thus organize their radial velocity over time, while the M4 cells loose coordination even on short length scales.

Figure 5.

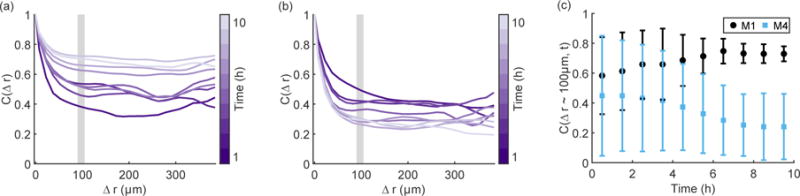
Representative spatial correlations for radial velocity of the M1 (a) and M4 (b) cell lines over time show two distinct migration phenotypes. Color in (a; b) indicates time, with earlier hours in dark purple and the end of the experiment in light purple. The trend in the region 90 μm < Δr < 105 μm (marked by the gray rectangles in (a; b)), shows that the M1 cells remain correlated over 10 hours, while the M4 cells become decreasingly correlated (c). Error bars in (c) indicate 95% confidence intervals.

E-cadherin and Collective Dynamics

E-cadherin plays an important role in cell-cell adhesion, and is expressed in both M1 and M4 cells (see the Western blot in Figure S2). To perturb the collective migration phenotype, we downregulated E-cadherin expression using shRNA in both the M1 and M4 cells. The knockdown cell lines show decreased expression of E-cadherin at cell-cell junctions as shown by immunofluorescence labeling (Figure S3 and S4) and we investigate how this change affects the long time dynamics of collective migration. In the following, we compare the E-cadherin knockdown cell lines to a nonsense shRNA (NS) control. The speeds, angular deviation, and FTLE values measured for the NS control may vary from the previously shown figures as the absolute speed and positive FTLE values are sensitive to day-to-day variations and thus must be compared in paired experiments. However, the long time dynamics we observe are robust to day-to-day variations and remain the same across our experiments. See Figures S5 and S6 for a paired comparison between the non-perturbed cells and NS control cells of the M1 and M4 cells respectively.

M1 E-cadherin shRNA Cell Lines

As with the comparison between parental cell lines, the M1 E-cadherin shRNA cell lines cannot be distinguished from their NS control by radial displacement or mean speed (Figure S7). Yet, the cells can still be distinguished by their short time behavior: E-cadherin knockdown reduces cohesivness enough to broaden the velocity direction distribution (Figure S8).

Migration behavior on the time scale of hours, however, remains similar to the control dynamics in all the shRNA cell lines. Speed decreases slightly over time (Figure 6(a)) without a strong difference between the NS control and the E-cadherin shRNA cell lines (Figure 6(d)). Although angular deviation is on the whole higher in the E-cadherin shRNA cell lines (Figure S8(a)), both cell lines show similar trends over time to the NS control (Figure 6(e)). The shRNA cell lines show variable increase in FTLE values (see Figure S8(b)), but still show a strong decrease in values over time (Figure 6(c)) without strong slope changes between the shRNA cell lines and the NS control (Figure 6(f)). Fluctuations within the knockdown cell lines continue to show a characteristic time scale on the order of three hours (Figure S10), as was found for the unperturbed cell lines (Figure 4).

Figure 6. M1 E-cadherin shRNA cells.

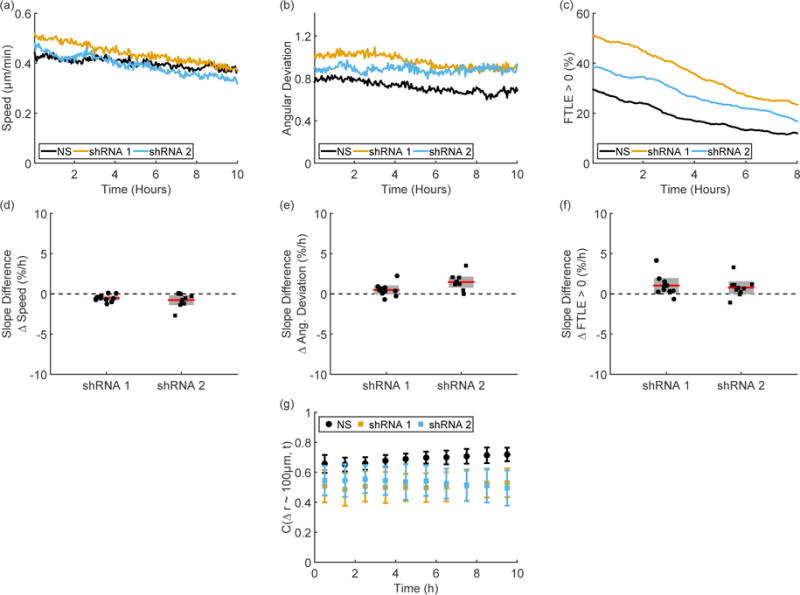
Representative time traces of speed (a), angular deviation (b), and FTLE values (c) from paired experiments show some changes between the nonsense (NS) and E-cadherin shRNA knockdown cell types but no changes in long time behavior. As shown by the experimentally paired differences between knockdown and NS in the slopes of speed (d), angular deviation (e), and FTLE values (f), there is no change in long time trends after E-cadherin knockdown. Although the E-cadherin shRNA cell lines show decreased correlations values compared to the NS cell line, the correlations are stable for each cell type, as shown by the correlations in the region 90 μm < Δr < 105 μm (g). Error bars in (d – g) indicate 95% confidence intervals.

A similar pattern is seen in spatial correlations over time. Although the knockdown cell lines show a slight decrease in overall correlation compared to the NS control, all M1 cell lines show a stable or slightly increasing correlation over ten hours (Figure 6(g)).

M4 E-cadherin shRNA Cell Lines

The M4 E-cadherin shRNA cell lines show similar speed distributions and radial displacement to their NS control (Figure S11). The NS cell lines already show a broad direction distribution and the shRNA cell lines show a similar short time behavior with wide velocity angle distributions (Figure S12).

Representative time traces of speed (Figure 7(a)) and angular deviation (Figure 7(b)) show similar ranges of values and confirm the similarity in short time behavior on the scale of minutes. Along with positive FTLE values (Figure 7(c)), these metrics show similar long time dynamics as well: the change over ten hours in all three metrics shows no difference between the E-cadherin shRNA and NS cell lines (Figure 7(d – f)). All M4 shRNA cell lines also show similar spatial fluctuations with a characteristic time scale of approximately two hours (Figure S14).

Figure 7. M4 E-cadherin shRNA cells.

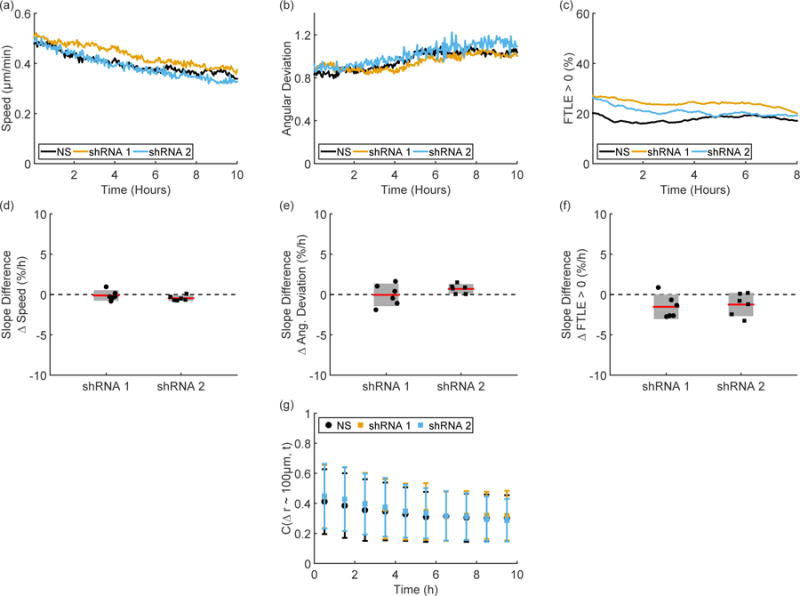
Representative time traces of speed (a), angular deviation (b), and FTLE values (c) from paired experiments show no distinct changes between the nonsense (NS) and E-cadherin shRNA knockdown cell types. As shown by the experimentally paired differences between knockdown and NS in the slopes of speed (d), angular deviation (e), and FTLE values (f), there is no change in long time trends after E-cadherin knockdown. The E-cadherin shRNA cell lines show similar correlation values compared to the NS cell line; (g) shows the correlation values in the region 90 μm < Δr < 105 μm over time. Error bars in (d – g) indicate 95% confidence intervals.

Spatial correlations in the M4 shRNA cell lines are also similar to those seen in the unperturbed M4 cells. On short distances, the M4 cells become decreasingly correlated over ten hours (Figure 7(g)), indicating a lack of coordinated motion even on the length scale of a few cells.

4. Discussion

Short term collective behavior is important for many systems: it is often studied in the context of flocking birds or schooling fish and has also been shown to be of interest in epithelial cell systems during development, wound healing, and tumor cell invasion. Here we argue that assessing long term collective behavior on the scale of hours is also necessary for understanding cell migration in the context of cancer progression. The importance of long time behavior in metastatic systems is intuitive; strands of malignant cells can spend days or weeks invading into the surrounding tissue from the primary tumor [3]. Despite the long time scales discussed in in vivo studies or the time lapse that might occur between patient visits in clinical data, in vitro studies of collective behavior often focus on short time dynamics such as instantaneous speed or directionality calculated over minutes or simply neglect dynamics to instead focus on the collective structure of the cells. As we have previously shown [12] and here confirm, short time metrics can be useful in distinguishing features of the non-malignant M1 and malignant M4 migration phenotypes. However, collective migration incorporates behaviors not captured by these short time scale measures – a strand of cells in vivo is inherently collective, but looking at the cells on short time scales does not inform us if the structure will remain the same over hours, if there will be small disturbances in the structure, or if the cells will undergo large scale rearrangements. We have recently developed new tools for the measurement of long time collective behavior [24] that reveal other interesting features of the collective migration phenotype. FTLE values reflect the evolution of a cell sheet over longer times and show less collective order in the M4 cells (Figure 2). In addition, the change in FTLE values over time provides insight into the migration phenotype by revealing that the M4 cells maintain a disordered flow over time, but that the M1 cells become more ordered over the course of ten hours (Figure 3). This same behavior can be seen in flow fluctuations (Figure 4) and the time evolution of spatial correlations (Figure 5). With multiple tools for quantifying collective behavior, we are able to provide additional understanding to the collective behavior changes observed in this cancer progression model.

These quantitative tools also allow us to investigate the role of E-cadherin, a clinically relevant cell-cell adhesion protein, in the collective migration phenotype. We find that in the non-malignant M1 cells, a reduction in E-cadherin expression results in decreased directionality. This decrease causes the M1 shRNA cell lines to resemble the M4 control cell lines when their dynamics are measured on the scale of minutes. As the M4 cells already show little coordinated behavior on short time scales, we found no change in directionality for the M4 shRNA cell lines. These metrics provide interesting insight into the role of E-cadherin in collective migration, but on their own may overstate the role that E-cadherin plays in M1 migration. The long time behavior, in fact, seems to suggest the opposite: despite the short time changes seen, the M1 E-cadherin shRNA cell lines continue to show increasing coordination over time scales of hours. As E-cadherin is one of the main players in epithelial cell-cell adhesion, at first glance it may seem surprising that it did not have a stronger influence on the collective phenotype. This could be due to the fact that the small remaining E-cadherin expression in the shRNA cells is enough to compensate for some of the effects of E-cadherin on long time dynamics. In addition, E-cadherin and adherens junctions are only one form of cell-cell adhesion; tight junctions, desmosomes, and gap juctions may all play a role in the collective behavior of the cell sheet. In the non-malignant M1 cells then, it is not surprising that knockdown of a single component of the intercellular adhesome does not abolish all types of collective behavior. In fact, a recent study has shown that while E-cadherin plays a role in migration, P-cadherin is a better predictor of intercellular tension, a mechanical feature also relevant to collective migration [22]. Looked at in the wider context of cell-cell adhesion, it is not surprising then that short time collective behavior and long time coherent migration are regulated differently. Our results indicate that the M1 cells use E-cadherin for coordination of collective motion on short times scales of minutes, yet even with decreased E-cadherin expression, the cells prefer to remain coordinated over longer time scales of hours. In contrast, the migration behavior of M4 cells, which already shows decreased collective dynamics on both time scales, is insensitive to the change in E-cadherin expression.

As decreasing E-cadherin does not perturb the changes in dynamics seen over hours, it is also possible that this feature of collective migration is regulated by a property other than cell-cell adhesion. In our experiments, although both cell lines were plated with the same initial cell number, by the time of imaging, the cells had reached different densities. This is likely due to a combination of the cells ability to initially adhere to the surface and the proliferation rates of each cell line. As can be seen in Supplemental Movie 1, the M4 cells proliferate more than the M1 cells, although both proliferation rates are of the same order of magnitude. This has been previously quantified for these cell lines, and was shown to not influence the overall displacement of the cell monolayer edge [12]; that result is consistent with other studies, such as Poujade, et al. [11], which found that migration proceeds even upon the inhibition of cell division. However, proliferation rates and density may influence collective behavior and lead to changes in metrics such as those presented in this work. Investigating the role of proliferation and density using fluorescent nuclei will be an interesting direction for future research on the dynamical changes that take place during collective migration.

In further research, the investigation of both short and long time dynamics will be useful in determining which aspects of collective behavior are most relevant to the metastatic process. There remain many unanswered questions about cell-cell adhesion components in the malignant migration phenotype; dynamical measurements may help to determine the role various junctions play in the changes seen during cancer progression. Determining which time scales are most predictive of malignant behavior could eventually lead to improved diagnosis and treatment options; here we present analysis of time scales of minutes and hours, but data on the clinical time scales of weeks and months will likely also show interesting migration dynamics. If, as we hypothesize, dynamical measurements on the scale of hours are able to predict tumor cell behavior over much longer time scales, information from simple in vitro studies on patient cells or perhaps future clinical imaging techniques may allow diagnosis without the need to monitor tumor growth over weeks or months.