Acoustic vaporization threshold of lipid-coated perfluoropentane droplets

Abstract

Phase shift droplets vaporizable by acoustic stimulation offer the advantages of producing microbubbles as contrast agents in situ as well as higher stability and the possibility of achieving smaller sizes. Here, the acoustic droplet vaporization (ADV) threshold of a suspension of droplets with a perfluoropentane (PFP) core (diameter 400–3000 nm) is acoustically measured as a function of the excitation frequency in a tubeless setup at room temperature. The changes in scattered responses—fundamental, sub-, and second harmonic—are investigated, a quantitative criterion is used to determine the ADV phenomenon, and findings are discussed. The average threshold obtained using three different scattered components increases with frequency—1.05 ± 0.28 MPa at 2.25 MHz, 1.89 ± 0.57 MPa at 5 MHz, and 2.34 ± 0.014 MPa at 10 MHz. The scattered response from vaporized droplets was also found to qualitatively match with that from an independently prepared lipid-coated microbubble suspension in magnitude as well as trends above the determined ADV threshold value.

I. INTRODUCTION

Gas-filled microbubbles encapsulated by lipids and other surfactants are highly responsive to ultrasound, which has led to their effective role as vascular agents for contrast enhanced ultrasound imaging (Klibanov, 2006; Ferrara et al., 2007; Paul et al., 2014). More recently, emulsions of phase shift droplets of volatile perfluorocarbon liquids, which can be vaporized in situ into highly echogenic microbubbles by external application of ultrasound pulses, are being investigated for imaging and drug delivery (Kripfgans et al., 2000b; Rapoport et al., 2007; Kaneda et al., 2009; Fabiilli et al., 2010; Wang et al., 2012; Kopechek et al., 2013; Sheeran et al., 2015). They are also being investigated for other biomedical applications such as embolotherapy (Kripfgans et al., 2000a; Kripfgans et al., 2002b; Samuel et al., 2012), phase aberration correction in ultrasound imaging (Kripfgans et al., 2002b; Haworth et al., 2008), and high-intensity focused ultrasound (HIFU) therapy (Zhang and Porter, 2010; Zhang et al., 2011; Aydin et al., 2016). Also note that while contrast microbubbles are restricted to vasculature and therefore cannot be used for extravascular imaging, nanometer sized phase shift droplets can extravasate through the leaky vasculature of cancerous tumors due to the enhanced permeability and retention (EPR) effect (Maeda et al., 2000; Mullin et al., 2011; Yuksel Durmaz et al., 2014). The phenomenon of acoustic droplet vaporization (ADV), specifically the threshold ultrasound excitation for vaporization, has been studied using both acoustic and optical means. Acoustic investigations determine ADV thresholds by the scattered signals. Optical investigations depend on direct observations of the vaporization using cameras. We review the past studies by both means and their findings in Table I. Note that even within one of the two classes of determination, acoustic and optical, the experimental setup varied significantly—e.g., droplets in interstitial space modeled by gel phantoms or droplets in vessels modeled by tubes—as did the signal processing method to determine the threshold. Therefore, the determined threshold values obtained by different studies differed. Here we have performed an acoustic investigation of the ADV threshold of perfluoropentane (PFP) droplets and its dependence on excitation frequency in a tubeless setup that minimizes the effects of the containment apparatus.

TABLE I.

ADV thresholds of PFP droplets reported in the literature using acoustical and optical means.

Reference	Technique	Excitation frequency (MHz)	Threshold (MPa)	Tube/medium inside the tube/outside the tube	Detection mode/transducer/scanner frequency	Diameter of droplets (μm)/coating
Kripfgans et al., 2000b	Acoustic/ADV	1.5	4.78	Dialysis tubing /saline solution/water at 37 °C	Active scanner 10 MHz	90% < 6/albumin
		3	1.5
		4	1
		5.5	0.8
		6	0.7
		7.6	0.7
		1.5	5.49	Zerdine tissue coating on tube at 37 °C
		1.5	5.42	Inside tube- blood solution at 37 °C
		1.5	6.21	Blood solution inside the tube/zerdine tissue coating on tube at 37 °C
Kripfgans et al., 2002b	Acoustic/ADV	2	3	Dialysis tubing /saline solution/water at 37 °C	Active scanner 10 MHz	90% < 6/albumin
		5	1.5
		7.5	1.5
		10	1
Kripfgans et al., 2004	Optical/ ADV	3	3.9–2.2	Polyethylene tube/saline sol/water at 37 °C		5-27 /albumin
		4	6.2–3.8
Lo et al., 2007	Acoustic/ADV	1.44	5.5	Dialysis tube/saline sol/water at 37 °C	Active scanner 10 MHz	< 6/albumin
Fabiilli et al., 2009	Acoustic/ADV	3.5	4.2–2.4	Dialysis tube/DI water/water at 37 °C	Active scanner 10 MHz	1–5/albumin
	Acoustic/IC		5.9–5.2		Hydrophone
Li et al., 2014a	Optical	7.5	3.6	Dialysis tube/ DI water/water at 37 °C		18/albumin
Giesecke and Hynynen, 2003	Acoustic/IC	0.74	0.7	Angioplasty balloon/polyethylene PBS sol/water at 37 °C	Passive 0.74 MHz	1.4–2/albumin
		1.1	1
		2.18	1.25
		3.3	1.75
Schad and Hynynen, 2010	Acoustic/ADV	1.736	3.8–0.5	Angioplasty balloon/polyethylene PBS sol/water at 37 °C	Active 5 MHz	2–8.5/lipid
		2.855	3.9–1
	Acoustic/IC	1.736	4.2–3.6		Passive 1.1 MHz
		2.855	5.2–4.8
Porter and Zhang, 2008	Acoustic/ADV	2	4	Dialysis tube/ PBS sol/water at 37 °C	Active 7.5 MHz	0.193/albumin
Zhang and Porter, 2009	Acoustic/ADV	2	8.5	Acrylic frame/albumin-acrylamide gel/water at 37 °C	Passive/Broadband transducer, 5 MHz high-pass filter	0.193/albumin
Sheeran et al., 2011b	Optical	5	3.91	Cellulose tube/DI water 37 °C		1–13/lipid
Reznik et al., 2011	Acoustic/ADV	7.5	1.5–2.2	Polyethylene tube/DI water/DI water at 28–42 °C	Active1.75 MHz	0.4/fluorinated surfactant
Williams et al., 2013	Acoustic/ADV	5	10	Polyacrylamide (PA) gel/water at 21 °C	Scanner 40 MHz	0.22/fluorinated surfactant
		10	8
		15	6
Reznik et al., 2014	Optical	5	3.5	Opticell/water/water at 37 °C		1–10/fluorinated surfactant
Kawabata et al., 2005	Acoustic/ADV	3.4	10 W/cm2 (pressure value not provided)	Tygon tube/ water/water at 30 °C	model EUP-L53S diagnostic probe	0.17/lipid
Mercado et al., 2016	Acoustic	2	3.7,3.3,3	Polyvinyl chloride tubing/PBS at 37 °C	Scanner (5 MHz)	2,3.5,9.75/albumin
Li et al., 2014b	Optical/ ADV	7.5	3.6	Degassed DI water/37 °C		18/albumin
Vlaisavljevich et al., 2015	Acoustic/optical/IC	0.345	10.8	Agarose tissue phantoms/DI water at 37 °C	Custom-built histrotripsy transducer	177.9/polymer
		0.5	10.3
		1.5	12.9
		3	14.7

Previous studies demonstrated that perfluorocarbon droplets vaporize into bubbles above a threshold value of the rarefaction pressure, namely, the ADV threshold (Kripfgans et al., 2000b). Although PFP and perflurohexane (PFH) have been the primary perfluorocarbon liquids used as the droplet core, perfluorobutane (PFB) and perfluoropropane, which are gaseous at room temperature, were also employed to make droplets via a microbubble condensation technique (Sheeran et al., 2011b; Sheeran et al., 2012; Dove et al., 2014). PFP droplets were made either by sonication (Zhang and Porter, 2010; Williams et al., 2013), mechanical agitation (Kripfgans et al., 2000b; Giesecke and Hynynen, 2003; Lo et al., 2007), or microfluidic fabrication (Martz et al., 2011; Duncanson et al., 2014; Moncion et al., 2017) of the perfluorocarbon liquid and surfactant solution.

Although a direct comparison between different threshold experiments listed in Table I is not possible due to the differences in the setups, one can look for trends of variation with important parameters. While optical investigations (Kripfgans et al., 2002a; Kripfgans et al., 2004) of a single droplet found the threshold to increase with increasing frequency, acoustic investigations (Kripfgans et al., 2000b; Schad and Hynynen, 2010; Williams et al., 2013) found it to decrease with frequency (Table I). Kripfgans et al. (2004), however, noted that the contradiction with their earlier acoustic investigation may be attributed to the complex acoustic field in presence of the flow tube and its location beneath the microscope objective. While investigating inertial cavitation (IC) threshold for an emulsion of albumin coated PFP droplets prepared using a similar protocol, Giesecke and Hynynen (2003) noted their acoustic finding to be opposite those of an earlier acoustic ADV threshold determination by Kripfgans et al. (2000b). The former used a passive detection of a strong nonlinear scattered signal for IC threshold, whereas the latter deemed a sudden change in the relative mean echo amplitude (MEA) of an active pulse-echo B-mode image as the criterion for ADV. Giesecke and Hynynen (2003) noted that the threshold values reported in the two articles are significantly different for certain frequencies. Later publications by Hynynen and co-workers, as well as others, made a distinction between IC (characterized by broadband emission) and ADV (characterized by a sudden rise in the MEA) thresholds, determined both for the same emulsion, and found the ADV threshold to be lower than that for IC (Fabiilli et al., 2009; Schad and Hynynen, 2010). A more recent optical observation for a different perfluorocarbon core—PFB—also has shown the ADV threshold increasing with increasing frequency (Sheeran et al., 2013). Note that the ADV threshold has been determined as a function of various other parameters. It decreases with increasing droplet size (Kripfgans et al., 2004; Fabiilli et al., 2009; Schad and Hynynen, 2010; Sheeran et al., 2011b), increasing droplet concentration (Reznik et al., 2011), increasing temperature (Fabiilli et al., 2009; Zhang and Porter, 2010; Reznik et al., 2011), and increasing number of exciting cycles (Lo et al., 2007; Schad and Hynynen, 2010; Reznik et al., 2011). Unlike for frequency, the trends of variation (increasing or decreasing) of ADV threshold with these parameters observed by different groups are consistent with each other.

Apart from the above observation, there remains considerable uncertainty regarding the exact mechanism of ADV—cavitation, homogeneous or heterogeneous nucleation, droplet deformation, nonlinear propagation, and focusing of superharmonics (Kripfgans et al., 2004; Li et al., 2014b; Shpak et al., 2014; Miles et al., 2016). It is evident that further investigation of ADV can make critical contributions toward understanding this complex phenomenon. Here, we have used the scattered signal—fundamental, sub-, and second harmonic—from an emulsion of PFP droplets, specifically their sudden increase with increasing excitation amplitude to determine the ADV threshold and its dependence on the excitation frequency. We employed a setup where the droplets were injected in the solution chamber from an immersed tube right above the focal volume. The droplets are free of tube wall effects while being ultrasonically excited, in contrast to flowing in a tube as in previous studies. The tube setup gives rise to a complex acoustic field in an optical investigation due to its location beneath the microscope objective (Kripfgans et al., 2004), nucleation sites at the tube wall, reflections from the tube wall or tube bending, all adding to some uncertainties in threshold determination. We discuss our criteria of the ADV threshold and the experimental methodology for determination in detail. We also measure the acoustic signals from a lipid-coated microbubble suspension to offer a qualitative comparison with that from vaporized PFP droplets.

II. EXPERIMENTAL METHODOLOGY

A. Synthesis of droplets

In this study, we have used PFP (FluoroMed, Round Rock, TX), which is liquid at room temperature (boiling point 29 °C), as the droplet core and lipids as the encapsulating shell. 1,2-dipalmitoyl-sn-glycero-3-phosphatidylcholine (DPPC) and 1,2-dipalmitoyl-sn-glycero-3-phosphatidylethanolamine-polyethyleneglycol-2000 (DPPE-PEG-2000) were purchased from Avanti Polar lipids (Alabaster, AL). DPPC and DPPE-PEG 2000 were mixed in a molar ratio of 60:40 to achieve a total lipid concentration of 1 mg/ml. We followed the thin film hydration technique used in the literature (Sheeran et al., 2011a; Zhang et al., 2013). The lipids were dissolved in chloroform in a glass round-bottom flask, and then it was rotated under a stream of nitrogen gas until the chloroform evaporated. After the evaporation of chloroform, a thin film of lipid formed at the bottom of the flask. The flask with the thin film of lipid was then connected to the vacuum to completely remove the solvent (chloroform) and it was left overnight in this condition. After the flask was disconnected from the vacuum, the film was hydrated with 20 ml of 55 °C -phosphate buffer saline (PBS) and then vortexed (VWR mixer, 120 V, model No. 945302, West Chester, PA) gently for 10 s at room temperature. The vortexed solution was further mixed for 30 min using a magnetic stirrer followed by a bath sonication (35 kHz, VWR, West Chester, PA) for 5 min. Once the lipid solution reached room temperature, 5 ml of lipid solution and 500 μl of PFP were added to a 50 ml centrifuge tube. An interface can be seen between the lipid solution and PFP, with PFP at the bottom of the tube. The lipid-PFP solution was then sonicated by placing the tip of a horn sonicator (Q500 sonicator, QSONICA, Newtown, CT) at the interface of the PFP- lipid solution. The sonicator was operated at 25% setting for 10 s, which is equivalent to delivering an acoustic power of 125 W for 10 s. To prevent temperature increase during sonication, the centrifuge tube was placed in an ice-water bath.

B. Synthesis of microbubbles

A microbubble suspension was prepared to compare the scattered response from droplets to that of microbubbles. To prepare lipid-coated microbubbles, 1.5 ml of the same lipid solution (prepared above) was added to a 3-ml glass vial. The remaining headspace was gas exchanged with PFB (Fluoromed, Round Rock, TX) passed through a needle inserted into the vial and connected by a pipe to a PFB cylinder at an exit pressure of 40–50 psi. Microbubbles were formed via mechanical agitation technique using a Vial Mixer (Bristol Myers Squibb, North Billerica, MA) for 45 s.

C. Size distributions of droplets and microbubbles

The size distribution and the concentration of droplets and microbubbles were determined using a qNano (Izon Science^™, Cambridge, MA). Droplets were diluted in PBS mixed with 0.03% Tween to ease passage of particles. For these measurements, we used three different elastomeric polyurethane nanopores (NPs) that covered a size range of 200–1000 nm (NP800), 1000–4000 nm (NP2000), and 4000–10000 nm (NP4000). Before and after each measurement, NPs were calibrated using appropriate plain polystyrene particles (provided by Izon Company) of known size and number. In our case, the applied stretching values were kept between 45.5 and 47 mm. The voltage was set between 0.2 and 0.5 V to keep the current ∼125 nA. For each sample, 1000 particles were counted and analyzed using the qNano software.

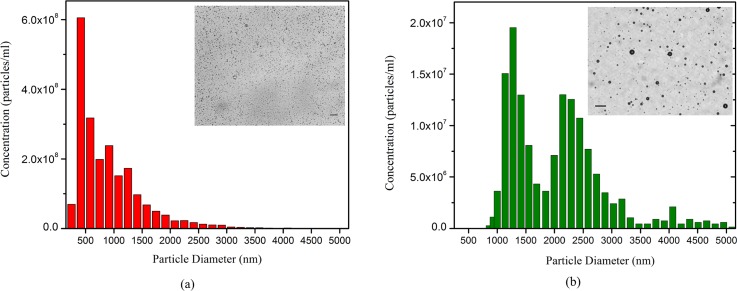
Figure 1 shows light microscope images and size distribution (determined by qNano) of the prepared PFP droplets, as well as PFB microbubbles, repeated two times. It can be seen in Fig. 1(a) that the droplet suspension contains both submicron and micron size (polydispersity index 0.3) with an average diameter of 890 nm and total concentration of 2.1 × 10⁹ droplets/ml. The ADV threshold determined here will be reflective of this polydisperse system. PFB microbubbles [Fig. 1(b)] had an average diameter of 1.6 μm and a total concentration of 2.05 × 10⁸ microbubbles/ml. The droplet suspension was 100 times diluted for the ADV threshold determination experiments. The droplet suspension was then checked optically (microscope) and acoustically for any bubble presence. To acoustically confirm that the freshly prepared droplet suspension was bubble free, 20 μl of suspension was dispersed in the solution chamber and then was excited by ultrasound at an excitation pressure of 500 kPa, which was below the minimum ADV threshold found in this study. The scattered response was found to be comparable with that of the background noise (a lower excitation amplitude of 200 kPa led to a similar result), confirming the suspension to be bubble free. Note that the current setup was found capable of detecting acoustical signals from even a very small amount (4 μl) of a microbubble suspension dispersed in the same chamber.

FIG. 1.

(Color online) Size distribution and concentration of (a) PFP droplets, (b) PFB microbubbles determined using a qNano system (Izon Science^™, Cambridge, MA). The insets show light microscope images of the same in diluted concentrations. Scale bar is 10 μm.

D. Experimental setup for ADV threshold determination

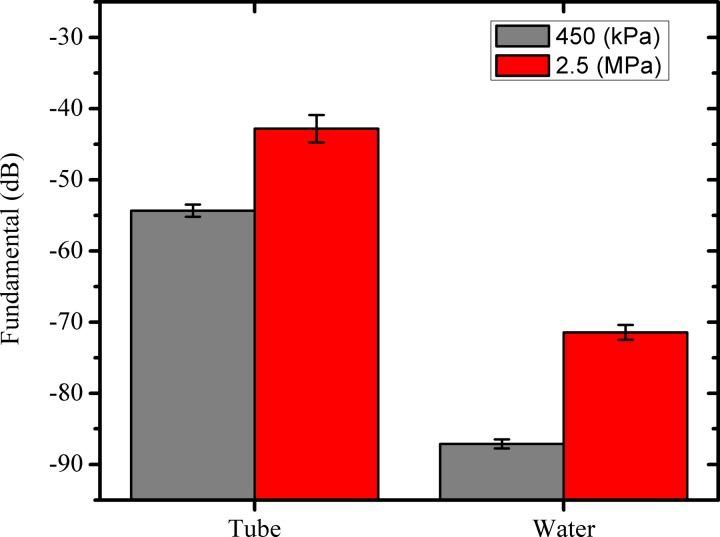
For ADV experiments, typically the droplet suspension is passed through the focal volume of a transducer in a flow setup. Here the focal volume is small (∼4.21 mm³ at 2.25 MHz) and this region decreases with increasing frequency (Table II). Previous investigators used dialysis tubes (Kripfgans et al., 2000b; Porter and Zhang, 2008; Sheeran et al., 2011b), tygon tubes (Lo et al., 2007), propylene tube (Burgess and Porter, 2015), polyethylene tubes (Reznik et al., 2011), or cellulose tubes (Sheeran et al., 2012) through which the droplet emulsion would flow. We believe that the current tubeless setup provides certain advantages. They are free of reflections from the wall of the tube that can reduce the amount of acoustic energy reaching the droplets, as well as the signals, from the vaporized droplets before reaching the receiving transducer. The loss in the signal may result in an overprediction of the ADV threshold. Although such tubeless setups have been used in the past for cavitation studies (Atchley et al., 1988), to our knowledge they have not been used to investigate ADV. Note that tube may help in restricting the radiation forces pushing droplets away from the focal volume. We measured significant reflections from propylene tubes compared to when there was no tube; the tube (outer diameter 7.3 mm, thickness 0.5 mm) gave rise to 33 dB and 29 dB enhancements at 450 kPa and 2.5 MPa, respectively, at an excitation frequency of 2.25 MHz (Fig. 2). Decibel values are computed with unity reference (1 V). We also found flexibility, e.g., of dialysis tubes, cause them to deform during the experiment and alter the boundary condition for each reading. Optical observations of ADV (Kripfgans et al., 2004; Li et al., 2014a; Li et al., 2014b; Shpak et al., 2014) have shown the nucleation to be homogeneous, i.e., it occurs inside the droplet volume. The tube surface offers potential nucleation sites, where heterogeneous nucleation (surface dependent) may occur. Note that the thresholds for homogeneous and heterogeneous nucleation are different (Jackson, 2006). Nucleation at the tube surface could lead to erroneous ADV threshold estimation. Here we avoid using a tube altogether in the ultrasound stimulation volume.

TABLE II.

Confocal region dimensions of different transducers.

Transmitter (MHz)	Receiver (MHz)	Focal region (μm × μm)
2.25	2.25	1615 × 1615
2.25	5	1615 × 727
5	2.25	727 × 1615
5	10	727 × 363
10	15	363 × 242

FIG. 2.

(Color online) Reflections from a propylene tube compared to control (water) at two different excitation amplitudes at 2.25 MHz (dB values are computed with unity reference).

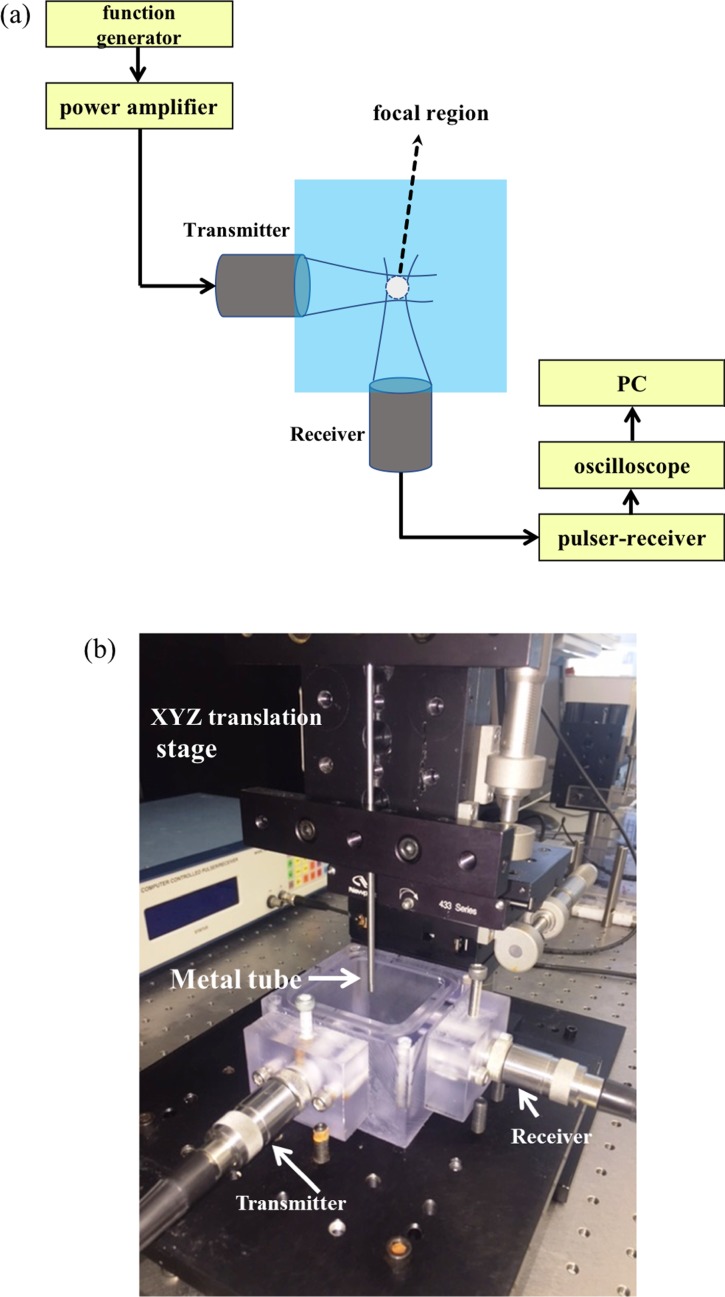
Figures 3(a) and 3(b) show a representation of our experimental setup for ADV threshold determination. A chamber (50 mm × 50 mm × 45 mm) made of polycarbonate was filled with deionized (DI) water. We employed two spherically focused immersion transducers (Panametrics Transducer, Olympus NDT Corporation, Waltham, MA), each having an element diameter of 1.27 cm and a focal length of 3.05 cm. The transmitting and receiving transducers were confocally positioned at right angles. Transducers with central frequencies of 2.25 MHz (Model V306; −6 dB: 1.48–2.90 MHz), 5 MHz (Model V309; −6 dB: 2.95–6.77 MHz), 10 MHz (Model V311; −6 dB: 6.96–13.16 MHz), and 15 MHz (Model V319; −6 dB: 10.10–18.97 MHz) were used in the experiments. All the transducers were calibrated using a needle hydrophone (HNC400, ONDA, Sunnyvale, CA; it has an uncertainty of ±1 dB). While transmitting transducers were excited at their central frequency, the receiving transducers for measuring fundamental, sub-, and second-harmonic scattering at that excitation frequency could have different central frequencies depending on the transducer bandwidth (indicated in Sec. III). Therefore, at the same excitation frequency, separate experiments were performed for measuring different harmonic components. An arbitrary/function generator (Agilent, 33250A, Santa Clara, CA) was utilized to generate an eight-cycle sinusoidal pulse of different frequencies at a pulse repetition frequency (PRF) of 100 Hz. This signal was then amplified using a 55 dB power amplifier (A-150, ENI, Rochester, NY) and used to excite the transmitting transducer. The scattered signal was passively received by the receiving transducer utilizing a pulser/receiver (5800, Panametrics-NDT, Waltham, MA) in receiving mode with a 20 dB gain (high-pass filter: 1 MHz, low-pass filter 35 MHz). The amplified signals were then fed into the oscilloscope (TDS 2012, Tektronix, Beaverton, OR) to view them in real time. Signals were acquired from the oscilloscope using LabView (National Instruments, Austin, TX) software. Thirty voltage-time RF traces were acquired in a sample mode and stored for further processing. Measurement for each setting was repeated five times.

FIG. 3.

(Color online) (a) Schematic representation (horizontal plane showing the transducers confocally aligned appears in top view). (b) Picture of the experimental setup used for determining ADV threshold. The droplet emulsion flows from an immersed metal tube [see (b)] 5 mm above the outer diameter of the transducers.

A syringe pump (KD Scientific Inc, Holliston, MA) was used to inject the droplet suspension into the solution chamber with a flow rate and particle velocity of 20 μl/s and 2 mm/s, respectively. The syringe exit was connected to a stainless steel tube (inner diameter 2.9 mm). The tube exit is immersed in the solution chamber and mounted ∼5 mm above the outer diameter of the transducers. The distance was sufficient so that the steel tube does not generate any signal. The steel tube was attached to the manual linear translation stage (Newport Corporation, Irvine, CA) having a sensitivity of 1 μm in all three directions. The dimensions of the focal region for a given frequency has been calculated by the formulae from the transducer manual (OLYMPUS-NDT, 2016) and listed in Table II. They were also verified with a needle hydrophone. For the confocally placed transmitting and receiving transducers, the effective volume is their intersection [Fig. 3(a)]. We ensure that the stream of droplets pass through the intersecting focal volume by first injecting a stream of propylene glycol (acoustic impedance is different from that of water) into the solution chamber via the steel tube to determine the proper position of the tube. When the steel tube is properly mounted so that the stream of propylene glycol passes through the focal volume, we obtain a strong signal. The positioning procedure is repeated before each experiment. Note that all the experiments here were performed at room temperature (20 °C) instead of the body temperature (37 °C), as was the usual practice in the past studies. Since the droplet temperature here is below the boiling temperature of the core liquid (29 °C), they are not in a superheated state. The ADV values determined here, therefore, are expected to be higher than what would be at 37 °C. To determine the ADV threshold, the excitation pressure was increased in steps of 500 kPa for each excitation frequency.

E. Criterion for deciding the ADV threshold

The scattered response from a droplet, which has not vaporized, contains the fundamental component and possibly small amounts of higher harmonics generated only due to the nonlinear sound propagation (Shpak et al., 2014). (We have investigated below the effects of nonlinear propagation and found them to not affect the ADV threshold values reported here.) In contrast, bubbles are far stronger scatterers—the scattering cross section of a bubble is several orders of magnitude higher than that of a droplet of the same size. Furthermore, upon vaporization, the droplet diameter increases by five- to sixfold resulting in a sudden jump in their scattered response. Here, we have found that for an ultrasound pulse strong enough for vaporization, the lipid-coated bubble response contains significant nonlinear components such as sub- or second harmonics (Chatterjee and Sarkar, 2003; Sarkar et al., 2005; Paul et al., 2010; Paul et al., 2013) apart from the fundamental response. We plot fundamental, subharmonic [when present; subharmonic response from a bubble occurs above a threshold excitation (Katiyar and Sarkar, 2011)], and second harmonic components of the scattered signal, as the ultrasound excitation amplitude was progressively increased. Specifically, the responses are seen to follow an approximately sigmoidal curve with a sharp change in slope in a range of excitation amplitude. To determine the ADV threshold based on this observation, we followed a curve fitting and slope based method pioneered by Fabiilli et al. (2009). Specifically, each dataset—fundamental, sub-, and second harmonic at each excitation frequency—was fitted to a sigmoidal curve

$$y=A_2+\frac{A_1-A_2}{1+e^{(x-x_0)/dx}},$$ (1)

using OriginLab (OriginPro8, OriginLab, Northampton, MA). Here, $A_1$ and $A_2$ are the minimum and the maximum y-values, respectively, $x_0$ is the $x$-value at the midpoint of the y range, and $dx=(x_{\max }-x_{\min })/20$. We defined the ADV threshold to be the pressure where the slope of the sigmoidal curve exceeded a predefined value. The predefined values (1.18 for fundamental, 4.2 for second harmonic, and 0.29 for subharmonic curves) were chosen by examining a smaller subset of the entire data near the threshold value and finding the derivative at the intersection of two approaching lines following an earlier investigation (Fabiilli et al., 2009). The ADV threshold values at each excitation frequency were determined using three different criteria—fundamental, sub-, and second harmonic (except when subharmonic was not found). The standard deviations for the threshold values were calculated by using the five replicates.

We also plotted the scattered signals from the microbubble suspension (preparation and sizes were described in Secs. II C and II D) for a qualitative comparison of trends and behaviors. Reznik et al. (2014) found that the scattered signal from a vaporized droplet was similar to that of a Sonovue (Bracco Diagnostics Inc., Geneva, Switzerland) microbubble. Note that we have used fundamental as well as sub- and second harmonic components for the vaporization threshold determination, specifically allowing for situations when the scattered signal did not contain subharmonic, but showed a distinct and sudden appearance of second harmonic. To further validate that the second harmonic appears primarily from vaporized droplets, and not from nonlinear propagation effects, we measure scattering from a stream of propylene glycol. Note that vaporization being a phase transition/nucleation phenomenon is stochastic in nature. Therefore, there is an uncertainty as to the first initiation of vaporization or sustained bubble activities. Unlike optical methods, which have their own limitation in field of view, the method here possibly is not sensitive enough to detect single bubble activities. In any event, we feel that the examination of different frequency components—they all show a sharp rise with increasing excitation amplitude—has certain merits. It is different from the previous acoustic investigations that primarily examined pulse echo B-mode images (Kripfgans et al., 2000b; Lo et al., 2007; Williams et al., 2013). The tubeless setup also adds to the significance of the study. In view of the stochastic nature, the ADV threshold values, although determined here as in the previous investigations through a quantitative method, are to be understood as a representative of the values of excitation where vaporization occurs, rather than a precise single value, with no vaporization below that range.

F. Statistical analysis

All the scattered responses are presented as the mean of the data sets acquired at each setting and their corresponding standard deviations. All experiments at each driving pressure and frequency were repeated five times. Data sets were further evaluated by one-tail Student's t-tests. Results were considered statistically significant for p < 0.05. At all the threshold values, the p-value was much lower than 0.01(confidence level > 99.9%) compared to the pre-threshold values. For the sigmoidal fitting of the scattered data, r² values were computed. The standard deviations of the ADV threshold values obtained by investigating a single frequency component were calculated based on the five replicates. Finally, the ADV threshold values from different components were averaged.

III. RESULTS AND DISCUSSION

A. ADV at 2.25 MHz

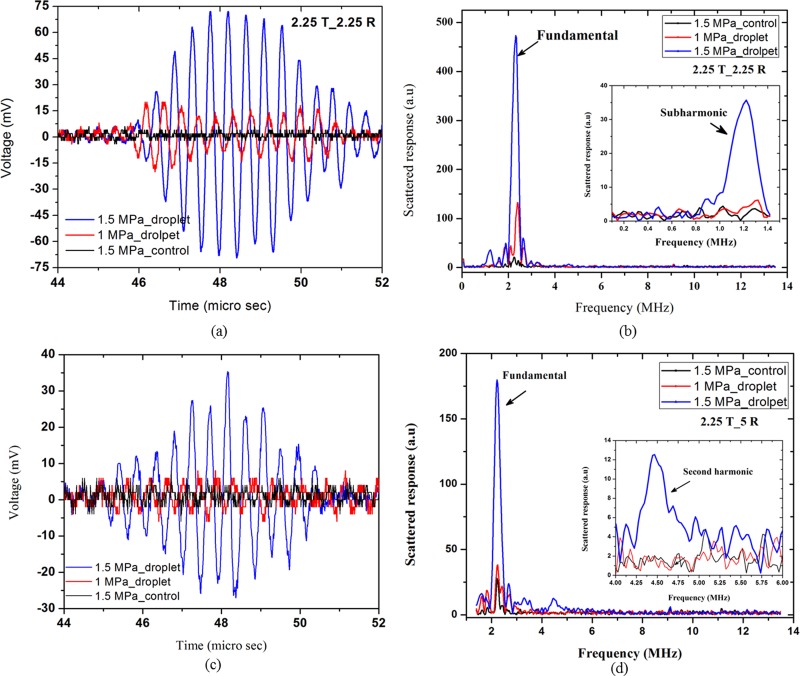
The typical raw RF data along with the corresponding frequency spectrum for the control and droplet suspension at the excitation frequency of 2.25 MHz and excitation amplitudes of 1 and 1.5 MPa are displayed in Fig. 4. Figures 4(a) and 4(b) represent data received by a transducer with a central frequency of 2.25 MHz. For recording the second harmonic signal at the same excitation frequency, as noted above, we perform a different set of experiments receiving with a 5 MHz transducer [Figs. 4(c) and 4(d)]. The droplet response at 1 MPa is small [not distinguishable from the control in Fig. 4(c) due to its reception with a 5 MHz transducer]. However, at 1.5 MPa, the droplet signal is significantly higher, indicating that vaporization has taken place at this excitation amplitude. Also note that Figs. 4(b) and 4(d) recorded a marked increase in sub- and second harmonic, respectively (as shown in the insets), underscoring the utility of separate experimental setups for sub- and second harmonics.

FIG. 4.

(Color online) (a) RF trace and (b) corresponding fast Fourier transform (FFT) from the control and droplet suspensions at 2.25 MHz (receiving transducer 2.25 MHz). (c) RF trace and (b) corresponding FFT from the control and droplet suspension at 2.25 MHz (receiving transducer 5 MHz). Insets of (b) and (d) show the same data but over limited frequency ranges displaying the sub- and second harmonics.

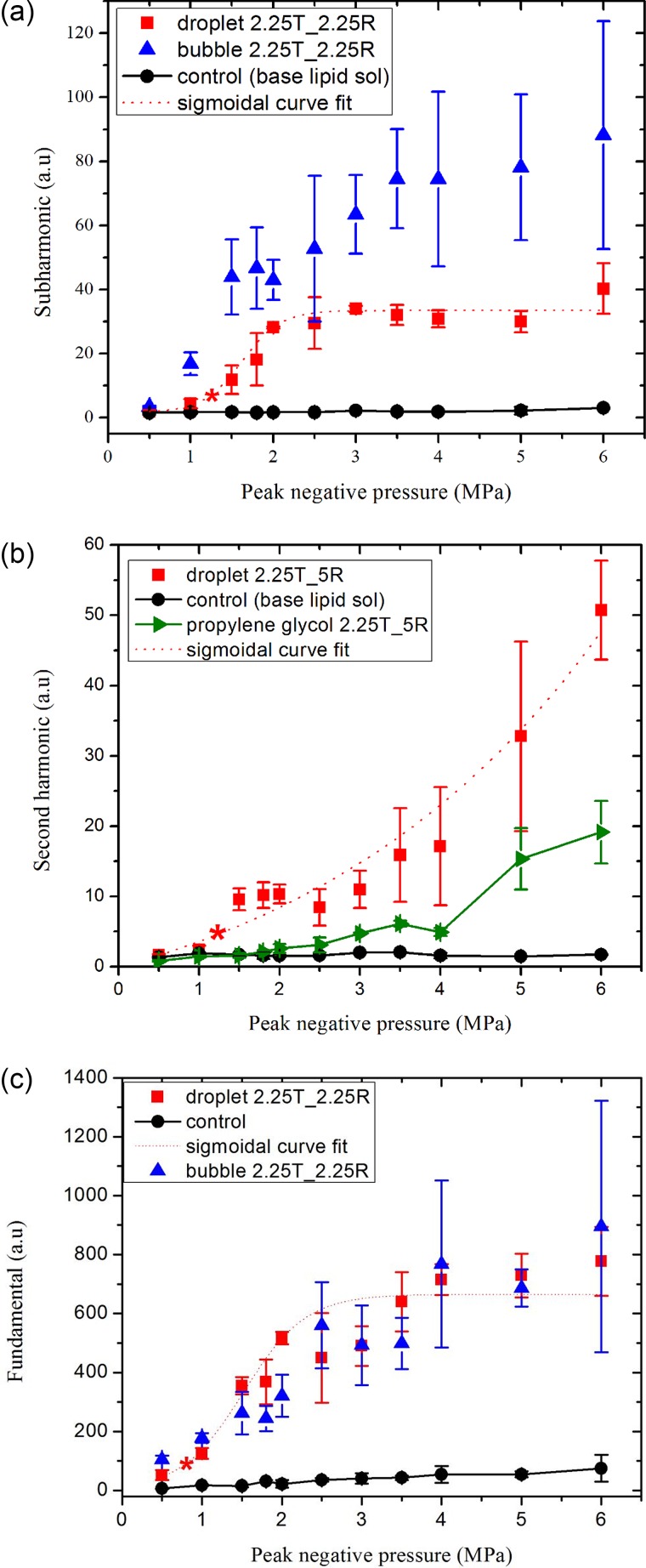
Figures 5(a), 5(b), and 5(c) plot the subharmonic (1.125 MHz), second harmonic (4.5 MHz), and the fundamental responses, respectively, from the droplet emulsion. In Fig. 5(a), we also plot the subharmonic response from microbubbles. At excitation amplitudes of 0.5 and 1 MPa, the signal from the droplet suspension is comparable to the control signal (base lipid solution), whereas the microbubbles have a subharmonic response above the control signal. Increasing the excitation steadily from 1 to 2 MPa, the subharmonic signals from microbubbles and droplets rise, becoming close to each other, and saturating beyond 2 MPa. We determine the threshold by the method described above as 1.22 ± 0.08 MPa, with the squared correlation coefficient (r²) equal to 0.99 for the sigmoidal fit. The second harmonic response from droplets in Fig. 5(b) also rises sharply above the control signal when the excitation amplitude is increased beyond 1 MPa. The fitted curve (r² = 0.84) gives rise to an ADV threshold of 1.22 ± 0.14 MPa. The fundamental response plotted in Fig. 5(c) records a much lower threshold of 0.72 ± 0.12 MPa (r² = 0.96), which could partially be attributed to the fact that while unvaporized droplets do not produce sub- and second harmonic, they can still produce fundamental response due to the acoustic impedance mismatch. The fundamental response from droplets and microbubbles also shows a qualitative match above 1 MPa. As one needs to use separate experiments with different transducers to measure sub- and second harmonic, the experiments with microbubbles were performed with only one set of receiving transducer to receive either the subharmonic or the second harmonic (except at 10 MHz). From all three criteria, the average ADV threshold at 2.25 MHz can be obtained as 1.05 MPa.

FIG. 5.

(Color online) (a) Subharmonic, (b) second harmonic, and (c) fundamental components of the scattered responses from droplets, microbubbles, propylene glycol stream, and control at an excitation frequency of 2.25 MHz. Central frequencies of transmitting (T) and receiving (R) transducers are indicated in the legends. The data sets were scaled by 10⁵ for easier display. The ADV threshold determined from each curve is denoted by ($*$).

In Fig. 5(b), the second harmonic response from the propylene glycol stream was found to be minimal indicating minimum contribution due to nonlinear propagation through the liquid. Note that with further increase in the excitation amplitude, the nonlinear propagation effect eventually builds up. Experiments in the literature (Table I) were mostly performed at 37 °C different from room temperature here—ADV threshold decreases with temperature (Fabiilli et al., 2009; Reznik et al., 2011). Also the difference in preparation protocols of droplet emulsions (and thereby droplet size distribution), as well as experimental setups (presence of tube), makes it difficult to compare with ADV threshold values from the past studies. Still a brief discussion is essential for the context. Porter and Zhang (2008) reported a threshold of 4 MPa in PBS solution at an excitation frequency of 2 MHz. The same authors found a value of 8.5 MPa in an albumin-acrylamide gel (Zhang and Porter, 2010) for the same frequency possibly due to the increased attenuation in the gel. Kripfgans et al. (2000b) reported an ADV threshold of 4.78 MPa at 1.5 MHz and 1.5 MPa at 3 MHz. They used the MEA obtained by a 10 MHz linear array of the ultrasound image of the droplet suspension passing through a tube before and after it was subjected to the vaporizing pulse. In later studies, the same group obtained threshold values of 3 MPa at 2 MHz (Kripfgans et al., 2002b) and 2.7 MPa at 3.5 MHz (Fabiilli et al., 2009). As mentioned above, the differences can be ascribed to the variations between different experiments and the different protocols of preparation of the droplet emulsion, as well as the intrinsic variability due to the stochastic nature of the vaporization phenomenon.

B. ADV at 5 MHz

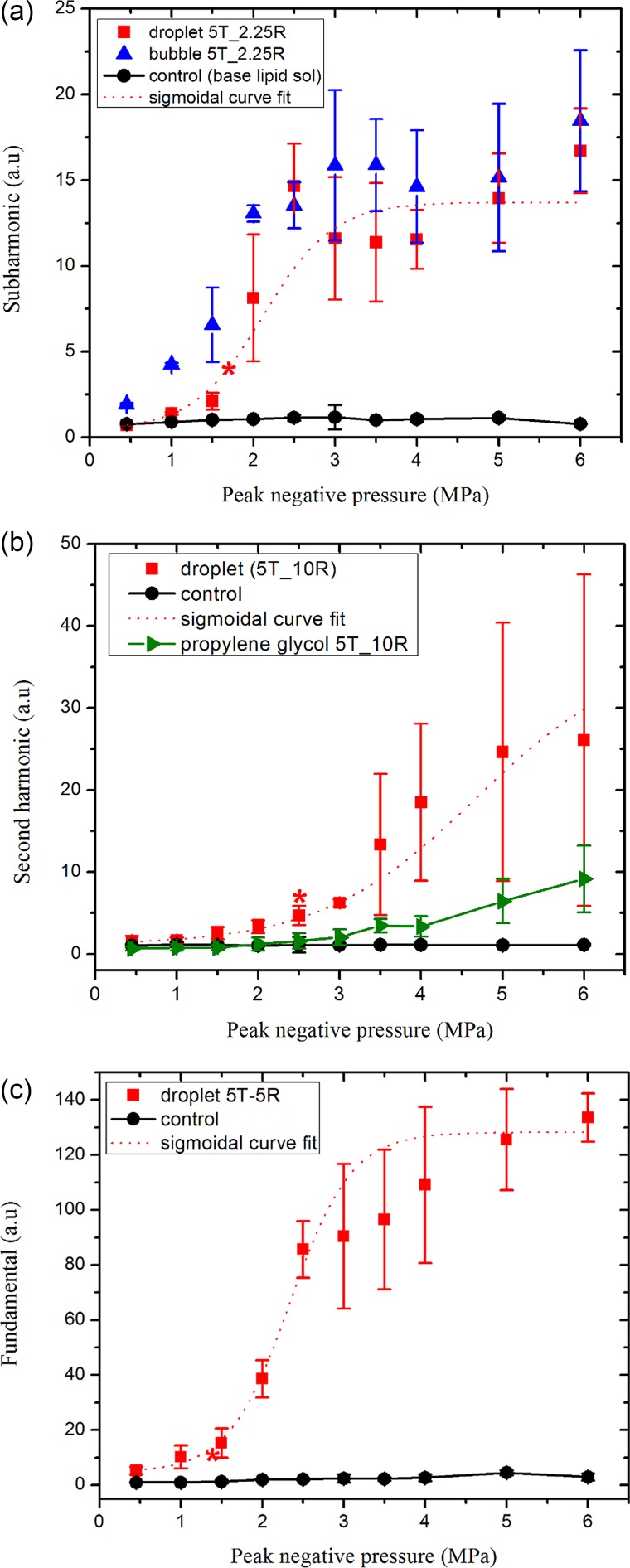
At 5 MHz excitation, the subharmonic response (at 2.5 MHz) from vaporized droplets is measured using a transducer with a central frequency of 2.25 MHz, and plotted in Fig. 6(a). Similar to at 2.25 MHz, it shows no subharmonic response from the droplet suspension at 0.5–1 MPa pressures. With increasing excitation amplitude, the subharmonic appears, rises, and saturates at 3.0 MPa, becoming eventually almost equal to that from the microbubbles. From the fitted curve, the ADV vaporization threshold is determined to be 1.72 ± 0.05 MPa (r² = 0.93). The fundamental component from the droplets received by a 5 MHz transducer, plotted in Fig. 6(c) results in the ADV threshold of 1.45 ± 0.09 MPa (r² = 0.98). The second harmonic component [Fig. 6(b)], received by a 10 MHz transducer, records a threshold of 2.55 ± 0.25 MPa (r² = 0.97). The different threshold values obtained by different spectral components—fundamental, sub-, and second harmonic—indicate limitations of the procedure adopted here. The average of the three values results in 1.89 MPa at 5 MHz excitation. The second harmonic response from the propylene glycol stream was found to be small, indicating that the signal from the droplets is from vaporized ones and not due to the nonlinear propagation. At this excitation frequency also, we briefly review the past studies, acknowledging the differences in size, setup, and temperature mentioned before. At 5.5 MHz, Kripfgans et al. (2000b) found the threshold to be 0.8 MPa by an acoustical means. In a later study, the same group reported a threshold value of 1.5 MPa at 5 MHz (Kripfgans et al., 2002b), closer to the one found here. Reznik et al. (2014) optically determined a value of 3.5 MPa at the same frequency. Williams et al. (2013) used a Vevo770 ultrasound biomicroscope with 40-MHz swept-scan probe (20–60 MHz imaging band) and found the threshold to be 10 MPa at 5 MHz in a polyacrylamide gel, where one would expect a higher value. Reznik et al. (2011) interrogated fundamental and second harmonic signals to obtain thresholds of 1.5–2.2 MPa at 7.5 MHz and 28 °C. They also observed that the bubbles continue to grow after the initial vaporization due to influx of dissolved gas, an effect that has been mathematically modeled (Katiyar et al., 2009; Sarkar et al., 2009; Katiyar and Sarkar, 2010).

FIG. 6.

(Color online) (a) Subharmonic, (b) second harmonic, and (c) fundamental components of the scattered responses from the droplets, microbubbles, propylene glycol stream, and control at an excitation frequency of 5 MHz. Central frequencies of transmitting (T) and receiving (R) transducers are indicated in the legends. The data sets were scaled by 10⁵ for easier display. The ADV threshold determined from each curve is denoted by ($*$).

C. ADV at 10 MHz

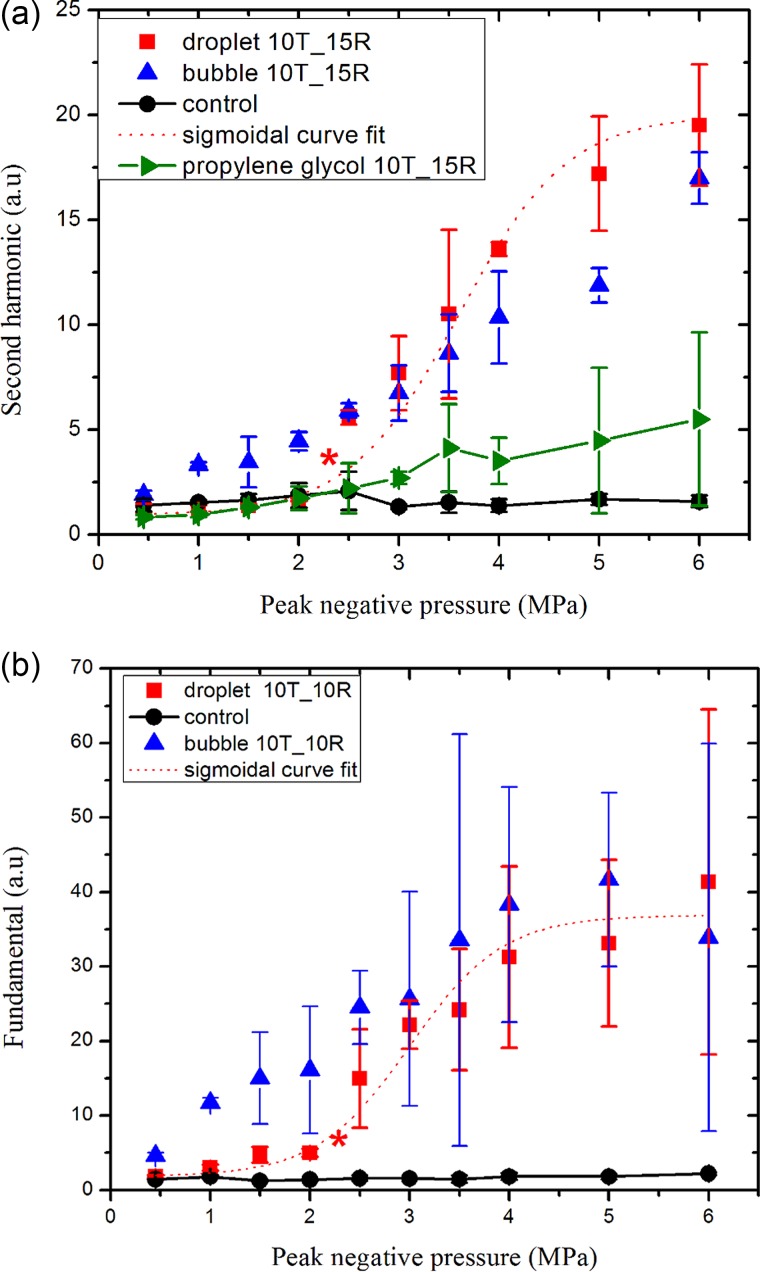
Here we measured second harmonic (20 MHz) as well as fundamental responses to determine the droplet vaporization threshold using two different receiving transducers with central frequencies of 15 MHz and 10 MHz, respectively, in two separate experiments. We did not find subharmonic signals from the droplets at this frequency (using a transducer with center frequency of 5 MHz). Figure 7(a) shows that the second harmonic response from PFP droplets are comparable to the control at excitations lower than 2 MPa, rising to become equal to the response from microbubbles at 2.5 MPa and above, and then grows slowly. The fitted curve results in the ADV threshold of 2.33 ± 0.2 MPa (r² = 0.94). Here also we found minimal second harmonic response from propylene glycol stream at the threshold value. Therefore, the enhancement in second harmonic response from the droplet emulsion above the ADV threshold is due to vaporized droplets and not due to the nonlinear propagation. Figure 7(b) shows that the fundamental response from the droplets also shows a rise in response starting at 1.5 MPa, and the fitted curve resulted in a threshold value of 2.35 ± 0.23 MPa (r² = 0.88). The average of the two values is 2.34 MPa. For 10 MHz, Williams et al. (2013), using a 40 MHz scanner, reported an ADV threshold of 8 MPa in a polyacrylamide gel, a higher value that again could be a result of the higher attenuation in that medium. Kripfgans et al. (2002b) recorded a threshold value of 1 MPa at this frequnecy.

FIG. 7.

(Color online) (a) Second harmonic and (b) fundamental components of the scattered response from the droplets, microbubbles, propylene glycol stream, and the control at an excitation frequency of 10 MHz. Central frequencies of transmitting (T) and receiving (R) transducers are indicated in the legends. The data sets were scaled by 10⁵ for easier display. The ADV threshold determined from each curve is denoted by ($*$).

D. Dependence of ADV threshold on frequency of excitation

A liquid droplet, when sonicated, is subjected to tension during the rarefaction phase of the ultrasound excitation. Above an excitation pressure threshold value, the peak negative pressure becomes high enough for the droplet to vaporize. One would expect that increasing the frequency, i.e., decreasing the time-period when the liquid is continuously under negative pressure, would increase the threshold of vaporization. The focal zone also becomes smaller at higher frequency decreasing the probability of nucleation inside the PFP droplet core. In Table III, we report the ADV threshold values obtained at three different excitation frequencies along with their averages and corresponding mechanical indices. We see an increasing trend with frequency, as was also seen in optical investigations by Kripfgans et al. (2004), Sheeran et al. (2013), and Martin et al. (2012). (In the Introduction section, we noted the differences between setups and the limitations described by the authors which may have affected some of the results.) However, the acoustical investigation by Kripfgans et al. (2000b) observed a decrease in ADV threshold with increasing frequency—5 MPa at 1.5 MHz, 1.5 MPa at 3 MHz, 1 MPa at 4 MHz, 0.8 MPa at 5.5 MHz, and 0.8 MPa at 7.6 MHz (Table I)—using a 10 MHz ultrasound scanner in a pulse-echo mode. Recently, Shpak et al. (2014) offered an elegant explanation of this counterintuitive observation, the decreasing trend of ADV threshold with increasing frequency. Based on their high-frame rate optical observation of ADV nucleation of PFP droplets—that it starts at an off-center position proximal to the transducer (also observed by Kripfgans et al., 2004)—Shpak et al. (2014) proposed an analytical model. The model suggests that ADV is initiated by a strong nonlinear distortion of the acoustic wave before it reaches the droplet, followed by a focusing of the distorted wave by the droplet at the nucleation initiation site. It could predict the optically observed off-center positions of the nucleation, thus, validating the mechanism of nonlinear distortion. The model suggests that a higher excitation frequency leads to a higher pressure amplification at the nucleation site, which may explain ADV threshold decreasing with increasing frequency. However, it should be noted that the off-center nucleation positions were optically observed only for larger droplets (radius > 4 μm) (Fig. 5B of Shpak et al., 2014) and the predicted pressure amplification with increasing frequency is less pronounced for smaller droplets (Figs. 3B and 4A of Shpak et al., 2014). The authors also noted that for smaller nanodroplets, a higher frequency of activation would be needed, where the attenuation at higher harmonics would also be correspondingly higher, effectively reducing the nonlinear distortion phenomenon. Note that Li et al. (2014b) also observed optically that acoustic lensing initiates nucleation in the proximal side of smaller (5 μm < diameter < 20 μm) and the distal side of larger PFP droplets. Subsequently, Miles et al. (2016) used classical nucleation theory to obtain the vaporization threshold, and modeled how superharmonic focusing can amplify the incident pressure inside the droplets. Using a 40 MHz scanner in a pulse-echo mode, Williams et al. (2013) found the ADV threshold decreasing with frequency. Schad and Hynynen (2010), using a 5 MHz transducer also in a pulse-echo mode, noted a similar trend. However, careful inspection of their Figs. 8(c) and 8(d) indicates ADV threshold in their recording also increased with frequency for smaller droplets, e.g., 3.9 MPa at 1.736 MHz and 4.8 MPa at 2 MHz for 2 μm sized droplets at 37 °C. The same investigators found the broadband emission threshold—deemed by the authors to be indicative of inertial cavitation—always higher than the ADV threshold, to decrease with decreasing frequency at 37 °C. However, note that for PFP droplets investigated here at a temperature below their bulk boiling point, the ultrasound excitation needed for vaporization may be strong enough to induce inertial cavitation of the vaporized droplets as well, which would also be characterized by the nonlinear signals recorded here above the threshold. In that case, the trend of the threshold increasing with frequency would be consistent with what has been observed in the literature for IC threshold in droplet systems. We conclude that through careful experiments at room temperature, we have observed a sharp rise in acoustic signals at the threshold values that are reported here, indicating definite presence of vaporized droplets. The threshold values are seen to increase with frequency investigated here. Future investigations with careful variation of all parameters would be needed to extend our understanding of the phenomenon.

TABLE III.

Frequency dependence of ADV threshold.

Excitation frequency (MHz)	Threshold (fundamental) (MPa)	Threshold (subharmonic) (MPa)	Threshold (second harmonic) (MPa)	Average threshold (MPa)	Mechanical index
2.25	0.72 ± 0.12	1.22 ± 0.08	1.22 ± 0.14	1.05 ± 0.28	0.7
5	1.45 ± 0.09	1.72 ± 0.05	2.55 ± 0.25	1.89 ± 0.57	0.84
10	2.35 ± 0.23	—	2.33 ± 0.2	2.34 ± 0.014	0.74

IV. CONCLUSION

Lipid-coated PFP droplets were excited with ultrasound pulses at various excitation frequencies at room temperature to find the threshold excitation for acoustic vaporization at those frequencies. Unlike previous investigations, we use a tubeless setup, where the vaporizing pulse and the received signals do not need to transmit across a tube wall. The fundamental, sub- and second harmonic components of the scattered responses were used to determine the threshold of vaporization. The scattered response from droplets was also compared with the scattered response from a PFB microbubble suspension at the corresponding excitation pressure and frequency. The scattered responses from droplets were comparable to the control (without any droplets) before vaporization; however, as the excitation pressure was increased, the responses experienced sharp increase—indicating vaporization—and subsequently showed a qualitative match in trend with responses from microbubbles. The ADV threshold, where the jump occurs, was found to increase with frequency. The ADV threshold values, as well as their trend with frequency, are discussed in the context of previous results from the literature. We find the frequency variation trend matches with previous optical observations, but differs from some acoustic ones.