Improved Spatial Localization in Magnetic Resonance Spectroscopic Imaging with Two-Dimensional PSF-Choice Encoding

Abstract

Purpose

Magnetic resonance spectroscopic imaging (MRSI), under low-spatial resolution settings, often suffers signal contamination from neighboring voxels due to ringing artifacts. Spatial localization can be improved by constraining the point-spread-function (PSF). Here the effectiveness of the two-dimensional PSF-Choice technique in providing improved spatial localization for MRSI is demonstrated.

Theory and Methods

The PSF-Choice technique constrains the PSF to a desired shape by manipulating the weighting of RF excitation pulse throughout phase-encode steps. Based on a Point REsolved SpectroScopy (PRESS)-type sequence, PSF-Choice encoding was implemented along two dimensions to excite a two-dimensional Gaussian profile, by replacing the usual RF excitation pulse with a train of pulses that is modified at each phase-encoding step. The method was proven mathematically, and demonstrated experimentally in phantoms containing prostate relevant metabolic compounds of choline, creatine and citrate.

Results

Using a dedicated prostate-mimicking spectroscopy phantom surrounded by oil, it was found that there is significantly less signal contamination from oil for PSF-Choice encoding compared with standard phase encoding. In particular, with standard phase encoding, there was a significant difference (p=0. 014) between ratios of Choline+Creatine to Citrate for voxels well within the phantom compared to voxels within the phantom but near the boundary with oil. The ratios in boundary voxels were also significantly different (p=0. 035) from reference values obtained using the prostate phantom with no oil present. In contrast, no significant differences were found in comparisons of these ratios when encoding with PSF-Choice.

Conclusion

The PSF-Choice scheme applied along two dimensions produces MR spectroscopic images with substantially reduced truncation artifacts and spectral contamination.

Graphical abstract

1. Introduction

Voxel bleeding, which is essentially a Gibbs ringing phenomenon, is an artifact frequently encountered in Magnetic Resonance Spectroscopic Imaging (MRSI)^1–4. A conventional approach to suppress this artifact, which is caused by truncation in k-space, is to apply a low-pass filter to the data prior to reconstruction. Although this is effective in removing the artifact, it does so at the expense of decreased spatial resolution^5,6. An example of a more advanced reconstruction method⁷ involves re-computing smooth regions with piecewise analytic functions in a Gegenbauer polynomial basis. Unfortunately, numerical instabilities occur for certain applications depending on the choice of parameters⁸. Another potential workaround has been based on finding optimal local subvoxel shifts to sample the ringing pattern at the zero-crossings of the oscillating sinc-function⁹. A natural extension to MRSI would be to apply sub-voxel shifts to all images acquired at all free induction delay (FID) time points; however, it is difficult in a practical setting to determine the exact shift needed to minimize artifact overall.

From the perspective of image acquisition, using a finer spatial resolution is one way to combat the ringing artifacts but this poses a difficulty in MRSI applications due to limited SNR and extended scan times. Somewhat similar to low-pass filtering in post-processing is the approach of variable density sampling during acquisition, which has been applied successfully in one, two, and three dimensions^10–12. The method involves spending more time sampling the k-space center and less time at the edge¹³. When k-space sampling density and data windowing are modified proportionally, no compromise has been shown in noise variance¹² and the effective reduction of spatial side lobes has been demonstrated in chemical shift imaging¹³. In addition, compared with Cartesian sampling using the same number of readouts, non-Cartesian trajectories such as radial sampling demonstrate much less ringing artifact. This approach has been applied in a non-MRSI context towards eliminating dark-rim artifacts in first-pass myocardial perfusion imaging¹⁴.

While most of the aforementioned strategies involve different reconstruction methods or employing alternative k-space sampling strategies, this paper aims to demonstrate an approach using a manipulation of the RF excitation to counteract the ringing effects. Conventional Fourier (phase) encoding involves scaling gradient amplitudes across multiple steps to encode the volume and results in a sinc-shaped point-spread-function (PSF). In contrast, the so-called non-Fourier encoding approach, also known as RF encoding, modifies RF selective excitations on each encoding step¹⁵ and produces PSFs that are dependent on the shape of the excitation profiles.

The technique, PSF-Choice, which is explored in this work, has been described previously¹⁶. It is a hybrid approach that combines elements of both Fourier and non-Fourier encoding. With a special scheme to adjust the RF excitation weights across phase-encoding steps, the PSF can be shaped along phase-encoding dimensions. There is some apparent similarity of PSF-Choice with the technique of tagging. In PSF-Choice, a regular, grid-like variation is imposed on the FOV via RF excitation as it is in tagging, although in PSF-Choice the image resolution is too coarse for the ‘tags’ to be seen (as the pixel dimensions coincide exactly with the grid dimensions). An important difference with PSF-Choice is that, unlike tagging, the RF amplitudes in PSF-Choice are varied on each individual shot and, as will be shown, this varying of RF amplitudes is critical to being able to manipulate the PSF.

Unlike the low-pass filtering approach, which eliminates ringing at the expense of the spatial resolution, the PSF-Choice method maintains the original spatial resolution without penalty in acquisition time. The method has previously been implemented and evaluated for prostate MRSI, with PSF-Choice encoding scheme applied along one single dimension¹⁷. Here, we describe the development of PSF-Choice scheme along multiple phase-encoding dimensions in MRSI to eliminate signal contamination from neighboring (out-of-voxel) areas.

2. Theory

In this section we present a mathematical justification for the PSF-Choice scheme, demonstrating that it leads to a modification of the imaging PSF as claimed. First, it will be shown that, in the small-tip angle regime, the spatial profile resulting from an RF excitation is related to a Fourier transform of some ‘excitation k-space’ description of the RF pulse. From there, it is shown that the segmented RF excitations in PSF-Choice, in their sum, result in the same RF excitation profile as the full non-segmented excitation. This profile is shown to have the form of a classic point-spread-function.

2.1. Signal from a hard-pulse RF excitation

We begin by considering a simple excitation hard pulse excitation, where a flip angle of θ will result in a weighting of sinθ on the transverse magnetization across the entire volume. This weighting is approximately equal to θ under the small-angle approximation. A subsequent gradient pulse along x will then introduce a spatially dependent phase e^2πir_xx, such that r_x is equal to γ̶ ∫ G_x(t) dt (meters⁻¹), where G_x(t) is a time-dependent gradient waveform and γ̶ is gyromagnetic ratio for the proton (42.58 MHz/Tesla). The integration is performed from the time right after the hard pulse to some time after the application all gradients. Similarly, for a gradient pulse along y, there is a y-dependent phase e^2πir_yy Overall, the signal generated by the magnetization at spatial coordinate (x, y) from the single RF excitation can be expressed by

$$\rho (x,y)\theta e^{2\pi i(r_{x}x+r_{y}y)}$$ [1]

where ρ(x, y) is the spin density in the excited volume integrated along z such that ∫ ρ(x, y, z) dz = ρ(x, y). To discretize the phase terms, we define increments (Δ^r_x, Δ^r_y) such that r_x = p_xΔ^r_x and r_y = p_yΔ^r_y where p_x and p_y are integers. The total signal coming from the volume due to the single hard pulse excitation is:

$$f(p_x,p_y)=\iint \rho (x,y)g(p_x,p_y)e^{2\pi i(p_x{\mathrm{\Delta }}^{r_x}x+p_y{\mathrm{\Delta }}^{r_y}y)}dxdy$$ [2]

Here we have replaced θ by the term g(p_x, p_y) to account for an RF pulse amplitude that may vary with the gradient induced (encoded) phase, as indexed by p_x and p_y.

2.2. Excitation profile from an RF pulse train

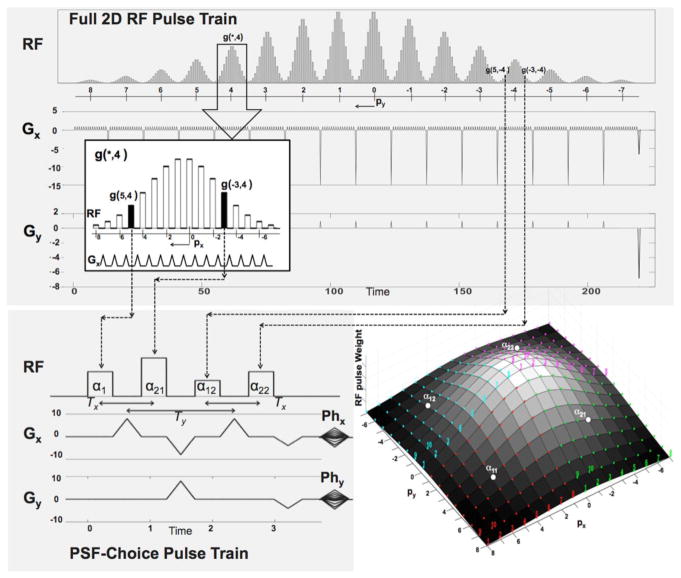
Figure 1 shows an example of a hard pulse train with its accompanying x and y gradient waveforms (top of Fig. 1). This particular RF pulse train is comprised of 16 segments with 16 hard pulses per segment. The hard-pulse amplitudes vary both within and between segments with an apparent Gaussian-shaped weighting. The x-gradient waveforms are repeated for each individual segment. Within the segments, the y-gradient is not applied, however, a y-gradient pulse is applied between segments. It is important to note that p_x and p_y are defined such that Eq.2 is applicable for any single hard pulse in the train, assuming the effective time is at the end of the application of both sets of gradient pulses.

Figure 1.

Top: RF and gradient waveforms for a 2D RF Pulse. The inset shows a zoomed-in portion of the pulse showing detail of a RF hard-pulse train interleaved with short gradient pulses. The hard-pulse amplitudes follow a Gaussian weighting. Note that each hard pulse samples a unique location in excitation k-space. Bottom Left: A 2×2 sub-pulse train used in a 2D PSF-Choice implementation. Amplitudes of the 4 RF pulses and the gradients, Ph_x and Ph_y, are set on each of the 8×8 encoding steps (shots). The PSF-Choice encoding scheme is designed so that each of the 256 excitation k-space locations (4×8×8) is sampled over the course of 64 shots (with 4 locations per shot). The time scales for the RF diagrams are in arbitrary units included only to show the relative duration of the RF trains for the PSF-Choice RF pulse train compared to the full 2D pulse train. Bottom Right: Excitation k-space representation for the 2D RF pulse. The RF pulse train for PSF-Choice consists of a subset of 4 hard pulses (α₁₁, α₁₂, α₂₁ and α₂₂) sampling 4 excitation k-space locations on each of 64 shots (with shot number as indicated for the first 10 shots). The locations in excitation k-space sampled by the 4 pulses are represented by the red, blue, green and purple colored dots respectively. Amplitude settings for the pulses are represented by height of the mesh plot, giving an overall Gaussian weighting across the excitation k-space.

Under the small-flip-angle assumption, the total signal from a full 2D excitation by an RF pulse train such as in Fig. 1 can be obtained by simply summing the result, f(p_x, p_y), from all individual sub-pulse (hard-pulse) excitations:

$$\begin{gathered} s=\sum _{p_x}\sum _{p_y}f(p_x,p_y)=\iint \rho (x,y)\left[\sum _{p_x}\sum _{p_y}g(p_x,p_y)e^{2\pi i(p_x{\mathrm{\Delta }}^{r_x}x+p_y{\mathrm{\Delta }}^{r_y}y)}\right]dxdy \\ =\iint \rho (x,y)G(x,y)dxdy \end{gathered}$$ [3]

In Eq. [3], we note that the summation within square brackets is in the form of a complex Fourier series expansion of a continuous spatial function G(x, y), which is periodic in two dimensions over a grid size of (1/Δ^r_x, 1/Δ^r_y). This grid is essentially the field of excitation (FOE) of the 2D RF pulse. As a multiplicative weighting on the spin density, G(x, y) can be viewed as the excitation profile. Therefore, by an appropriate choice of amplitude weights g(p_x, p_y) for the hard pulses, we can produce G(x, y) in any desired shape; e.g., a Gaussian shape as is obtained with the particular weighting shown in Fig. 1.

The bottom right of Fig. 1 shows a 2D mesh plot of the amplitude weights, g(p_x, p_y), for the RF pulse train at the top of Fig. 1. The weights form a Gaussian-shaped profile in both p_x and p_y directions. When the axes are viewed as increments of Δ^r_x and Δ^r_y, the representation is consistent with the ‘excitation k-space’ interpretation of the RF pulse. Note that each of the colored dots represents one hard pulse in the RF pulse train. In other words, each hard pulse represents a sample in the 2D excitation k-space.

2.3. PSF-Choice RF excitation

The main distinguishing feature of a PSF-Choice implementation, is that a full 2D excitation is split across multiple shots with only a subset of the RF hard pulses executed on each shot. In the example of Fig. 1, the full 2D excitation of 256 hard pulses is split across 64 shots with only 4 sub-pulses per shot, or 4 excitation k-space samples per shot. The bottom left of Fig. 1 shows a hard-pulse train used for PSF-Choice. The Ph_x and Ph_y gradients (bottom left of Fig. 1) are used to move the excitation k-space sampling locations in increments of Δ^r_x, Δ^r_y. The excitation k-space locations sampled for one specific shot are labeled with α₁₁, α₁₂, α₂₁, and α₂₂ in the 2D mesh plot (bottom right of Fig. 1). Locations of excitation k-space samples for different shots are represented by the colored-coded numbers in the figure. All 256 excitation points in the excitation k-space are covered in the course of 64 shots.

In general, we perform L_x × L_y hard-pulse excitations per shot (2 × 2 in our implementation). The incremental step in excitation k-space between samples on each of the M_x × M_y shots (8 × 8 in Fig. 1) is [M_xΔ^r_x, M_yΔ^r_y]. On each shot indexed with [m_x, m_y], excitation k-space is sampled in horizontal steps of Δ^r_x, and vertical steps of Δ^r_y. Let us assume that during the first shot (m_x = 0, m_y = 0), excitation k-space is sampled at [ $R_o^x-l_x{M}_x,R_o^y-l_y{M}_y$]. Here $R_o^x=(L_x{M}_x/2)$ and $R_o^y=(L_y{M}_y/2)$ are integers (assuming M_x and M_y are even) that define the positive limits of the 2D excitation k-space, where l_x and l_y range from 0 to L_x-1 and from 0 to L_y-1 respectively. Since L_x=L_y=2 in our implementation (Fig. 1) the indices l_x and l_y take only the values of 0 or 1. Subsequent excitations sample at [ $R_o^x-l_x{M}_x-m_x,R_o^y-l_y{M}_y-m_y$], where m_x = 0 ⋯ (M_x − 1) and m_y = 0 ⋯ (M_y − 1).

2.4. Reconstruction of PSF-Choice images

With a simple adaptation of Eq.3, the total signal from spins on each individual shot [m_x, m_y] in the PSF-Choice scheme can be written as s(m_x, m_y) given below:

$$s(m_x,m_y)=\iint \rho (x,y)\left[\sum _{l_x=0}^{L_x-1}\sum _{l_y=0}^{L_y-1}g(p_x[l_x,m_x],p_y[l_y,m_y])\dots \sum e^{2\pi i(p_x[l_x,m_x]{\mathrm{\Delta }}^{r_x}x+p_y[l_y,m_y]{\mathrm{\Delta }}^{r_y}y)}\right]dxdy$$ [4]

where $p_x[l_x,m_x]=(R_o^x-l_x{M}_x-m_x)$ and $p_y[l_y,m_y]=(R_o^y-l_y{M}_y-m_y)$.

Note that in PSF-Choice the M_x × M_y multiple shots are executed as M_x × M_y (phase) encoding steps. For reconstruction, we simply perform inverse discrete Fourier transformation of the data from all shots, producing the M_x × M_y image, S(u_x, u_y), as expressed in Eq.5:

$$\begin{gathered} S\left(u_x,u_y\right)=\frac{1}{M_x{M}_y}\sum _{m_x=0}^{M_x-1}\sum _{m_y=0}^{M_y-1}s\left(m_x,m_y\right)e^{2\pi i\left(u_x\frac{m_x}{M_x}+u_y\frac{m_y}{M_y}\right)} \\ =\frac{1}{M_x{M}_y}\iint \rho (x,y)\left\{\sum _{m_x=0}^{M_x-1}\sum _{m_y=0}^{M_y-1}\left[\sum _{l_x=0}^{L_x-1}\sum _{l_y=0}^{L_y-1}g(p_x[l_x,m_x],p_y[l_y,m_y])\dots \sum e^{2\pi i[p_x[l_x,m_x]{\mathrm{\Delta }}^{r_x}x+p_y[l_y,m_y]{\mathrm{\Delta }}^{r_y}y]}\right]e^{2\pi i\left(u_x\frac{m_x}{M_x}+u_y\frac{m_y}{M_y}\right)}\right\}dxdy \end{gathered}$$ [5]

Here the quadruple summations illustrate that in two dimensions there are M_x × M_y shots with L_x × L_y coordinates excited per shot. The quadruple summation can now be restructured into a double summation. By reversing the summation order in Eq.5 and then substituting ( $R_o^x-l_x{M}_x-p_x$) for m_x and ( $R_o^y-l_y{M}_y-p_y$) for m_y we obtain Eq.6 as follows:

$$S\left(u_x,u_y\right)=\frac{1}{M_x{M}_y}\iint \rho (x,y)\left\{\sum _{l_x=0}^{L_x-1}\sum _{l_y=0}^{L_y-1}\left[\sum _{p_x=R_o^x-l_x{M}_x-(M_x-1)}^{R_o^x-l_x{M}_x}\sum _{p_y=R_o^y-l_y{M}_y-(M_y-1)}^{R_o^y-l_y{M}_y}g\left(p_x,p_y\right)\dots e^{2\pi i[p_x{\mathrm{\Delta }}^{r_x}x+p_y{\mathrm{\Delta }}^{r_y}y]}{e}^{2\pi i\left(u_x\frac{R_o^x-l_x{M}_x-p_x}{M_x}+u_y\frac{R_o^y-l_y{M}_y-p_y}{M_y}\right)}\right]\right\}dxdy$$ [6]

Note that throughout l_x terms, the index p_x runs in a consecutively decreasing order and can be joined in a single sequence from ( $R_o^x-L_x{M}_x+1$) to $R_o^x$, similarly for p_y running from ( $R_o^y-L_y{M}_y+1$) to $R_o^y$. Additionally, the fact that $2R_o^x=M_x{L}_x,2R_o^y=M_y{L}_y$ and that e^2nπi = 1 (n ∈ ℤ) helps to simplify the second exponential term in which e^2πi(u_xl_x) and e^2πi(u_yl_y) are equal to 1, as are $e^{2\pi i(u_x\frac{L_x}{2})}$ and $e^{2\pi i(u_y\frac{L_y}{2})}$ when L_x and L_y are both even integers (=2 in our implementation). Note that, in case of odd L_x (or L_y), the sign will be flipped on odd rows (or columns) of S(u_x, u_y). This can be simply corrected in reconstruction by applying a sign reversal at the appropriate pixel locations. To continue with the assumption of even L_x and L_y, Eq. [6] can be expressed as below:

$$S\left(u_x,u_y\right)=\frac{1}{M_x{M}_y}\iint \rho (x,y)\left[\sum _{p_x=-R_o^x+1}^{R_o^x}\sum _{p_y=-R_o^y+1}^{R_o^y}g\left(p_x,p_y\right)e^{2\pi i(p_x{\mathrm{\Delta }}^{r_x}x+p_y{\mathrm{\Delta }}^{r_y}y)}{e}^{-2\pi i\left(u_x\frac{p_x}{M_x}+u_y\frac{p_y}{M_y}\right)}\right]dxdy$$ [7]

Finally, we note that summations in Eq. [7], compared to summations in Eq. [3], have the additional term $e^{-2\pi i·\left(u_x\frac{p_x}{M_x}+u_y\frac{p_y}{M_y}\right)}=e^{-2\pi i\left(p_x{\mathrm{\Delta }}^{r_x}\frac{u_x}{M_x{\mathrm{\Delta }}^{r_x}}+p_y{\mathrm{\Delta }}^{r_y}\frac{u_y}{M_y{\mathrm{\Delta }}^{r_y}}\right)}$. According to the Fourier shift theorem, this produces an expansion of G(x, y) that is shifted in space by $\left(\frac{u_x}{(M_x{\mathrm{\Delta }}^{r_x})},\frac{u_y}{(M_y{\mathrm{\Delta }}^{r_y})}\right)$ Hence each reconstructed value S(u_x, u_y) can be viewed as the integrated signal density ρ(x, y) sampled at discrete locations of grid size in $\left(\frac{u_x}{(M_x{\mathrm{\Delta }}^{r_x})},\frac{u_y}{(M_y{\mathrm{\Delta }}^{r_y})}\right)=\left(u_x{\mathrm{\Delta }}_x,u_y{\mathrm{\Delta }}_y\right)$, where (Δ_x, Δ_y) is the image spatial resolution.

$$S\left(u_x,u_y\right)=\frac{1}{M_x{M}_y}\iint \rho (x,y)G(x-u_x{\mathrm{\Delta }}_x,y-u_y{\mathrm{\Delta }}_y)dxdy$$ [8]

As the function G(x, y) is assumed symmetric, it can be rewritten as G(u_xΔ_x − x, u_yΔ_y − y) in Eq.8, taking the form of a classic PSF, which convolves with an input function ρ(x, y) to produce the output image S(u_x, u_y). Here a point source ρ(x₀, y₀) = δ(x₀ − x, y₀ − y) will produce G(u_xΔ_x − x₀, u_yΔ_y − y₀), which is a discrete sampling of G centered at (x₀, y₀). Therefore we can see that in the PSF-Choice scheme the imaging PSF is uniquely defined by the excitation profile G(x, y).

2.5. Theoretical spatial resolution with PSF-Choice

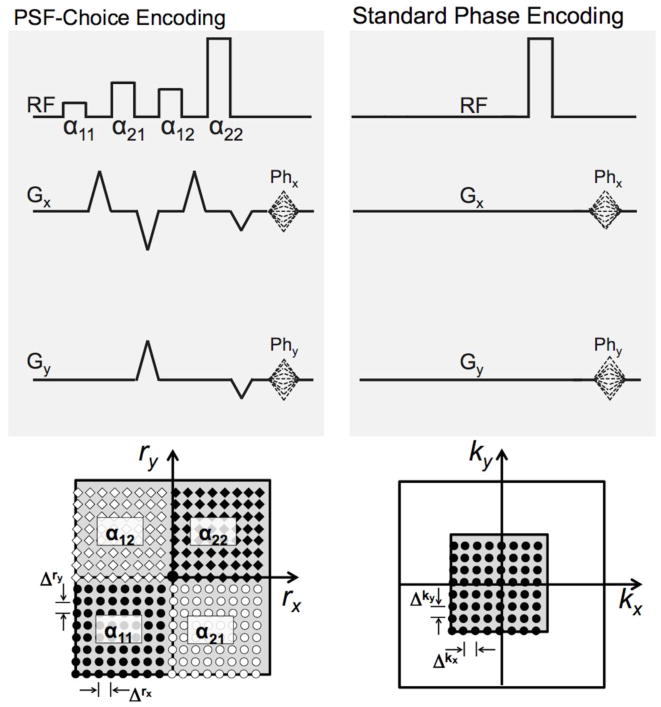
Figure 2 shows a comparison between the excitation k-space sampling with PSF-Choice (left) and k-space sampling with a standard phase encoding method (right). Note that both approaches involve the same number of encoding steps (8×8). Because the phase encoding gradients (Ph_x and Ph_y) are the same for both PSF-Choice and standard phase encoding, the increment of sampling in excitation k-space, Δ^r_x, Δ^r_y, is the same as the k-space sampling increment for phase encoding, Δ^k_x, Δ^k_y. In the previous section, we defined the image resolution for PSF-Choice as $\left({\mathrm{\Delta }}_x,{\mathrm{\Delta }}_y\right)=\left(\frac{1}{(M_x{\mathrm{\Delta }}^{r_x})},\frac{1}{(M_y{\mathrm{\Delta }}^{r_y})}\right)$. To ensure this, we need the width (spread) of the PSF (e.g. the full width at half maximum or FWHM) to be equal to (Δ_x, Δ_y). This implies that the spread of the weight function in excitation k-space must be (M_xΔ^r_x, M_yΔ^r_y). This is the same size as the k-space extent for standard phase encoding (see bottom right of Fig. 2) and thus results in the same theoretical spatial resolution (with M_x=M_y=8) for both methods.

Figure 2.

The schematic at the top left shows the RF pulse train and gradients used in the current implementation of PSF-Choice. The bottom left shows locations in excitation k-space sampled by the α₁₁, α₁₂, α₂₁ and α₂₂ hard pulses over the course of all shots (encodes) as represented by black circles, white diamonds, white circles, and black diamonds respectively. The exact location excited by each hard pulse is governed by the setting of the phase-encoding gradients, Ph_x and Ph_y. The schematic at the top right shows a simple 2D phase-encoding sequence with the same phase-encoding gradients as used for PSF-Choice. The sampled k-space locations are shown at the bottom-right. Note that the 2D phase-encoding k-space sampling increments, Δ^k_x and Δ^k_y, are equal to the sampling increments in excitation k-space, Δ^r_x and Δ^r_y, for the PSF-Choice implementation. The number of encoding steps is also the same for both sequences (= 8x8). However, the area of excitation k-space covered in the PSF-Choice encoding sequence is four times that of k-space covered with the standard phase-encoding sequence.

It is important to note here that, as demonstrated in Fig. 2, although there is a difference between the extent of excitation k-space sampled in the PSF-Choice method and the extent of k-space sampled in the standard phase-encoding method, the resolution, as defined by the width or spread of the PSF, is the same for both methods. While PSF-Choice clearly involves sampling a greater range of spatial frequencies, this does not go towards increasing spatial resolution, but instead allows for achieving a sharper (more localized) point-spread-function.

2.6. Choice of point-spread-function

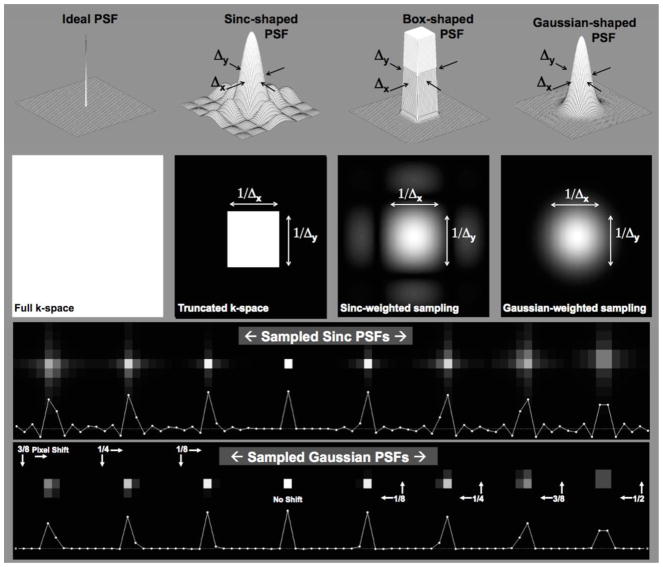
The PSF describes the degree of blurring or spreading of a point source object and, in this sense, directly measures the quality of the imaging device. Desirable properties of a PSF include a narrow main lobe with no or minimal side lobes. The ideal case for the PSF is a Dirac-delta function. However, because the Dirac-delta function (left side of Fig. 3) has a flat response in all frequencies, it would require sampling an infinite range of spatial frequencies and is, therefore, not a practical option.

Figure 3.

The top of the figure illustrates various 2D PSF shapes, which are, from left to right: the Delta function, the sinc-shaped function corresponding to the PSF for conventional Fourier imaging, a smoothed Box-shaped function and, on the far right, a Gaussian function corresponding to the PSF characterizing the PSF-Choice implementation. Note that the width (Δ_x,Δ_y) of all the PSF’s shown is the same, except for the Delta function. The second row shows the corresponding 2D k-space representation for each of the corresponding point-spread-functions. The bottom rows show simulations of point-source images where the point source is placed at various positions within the imaging pixel (voxel). For both the sinc-shaped and the Gaussian-shaped PSF’s, there is significant signal intensity in more than one pixel, except for the case where there is no shift in the position of the point source (e.g. the case labeled as ‘No Shift’).

Conventional Fourier-encoding uses constant weights across a truncated k-space. This results in the expected sinc-shaped PSF (center-left in Fig. 3). Note that the truncation artifacts become substantial when the edge transition in the object is on the order of or is smaller than the pixel size prior to any zero filling¹⁸. Another option for the PSF might be a compact boxcar shape (center-right in Fig. 3). In excitation k-space, this PSF is represented by the sinc-shaped function. The side lobes characteristic of this function make this option less practical for implementation due to the need to sample very high spatial frequencies. The Gaussian shape (right side of Fig. 3) provides good a compromise between the compactness of PSF and tapered expansion of frequency response and, therefore, this is the function that was chosen for the implementation of PSF-Choice.

Note that the three PSF’s in Fig. 3 other than the delta function have the same PSF width (Δ_x, Δ_y), which defines the spatial resolution. (Δ_x, Δ_y). However, the degree of compactness or localization of the functions is significantly different in the three cases. The range of spatial frequencies covered for the three cases is also very different with the narrowest spatial frequency range for the case of the sinc-shaped PSF. The Gaussian function represents an optimal compromise between compactness in both the spatial extent of the PSF and of the distribution of spatial frequencies.

As discussed previously, imaging a point source results in a discrete sampling of the theoretical point-spread-function. The resultant image depends intimately on the position of the point within the imaging voxel. This is demonstrated at the bottom of Fig. 3 for both the sinc-shaped and the Gaussian PSF’s. Note that, if the point source is positioned precisely at the center of the imaging voxel, the resultant image shows no sign of ringing as seen in the result labeled, ‘No Shift’. This is due to a sampling of the sinc-function at the zero crossings. For most other positions, however, there is significant signal contribution from the side-lobes of the sinc-shaped function. For the Gaussian PSF, when the point source is away from the center of the voxel, there is significant signal in more than one voxel, e.g., as seen on the far right for a point-source shift of half a voxel dimension. In general, however, signal remains significantly better localized than for the sinc-shaped PSF.

2.6. Signal-to-noise

It has been demonstrated in previous studies, both experimentally and through simulation that no significant difference in SNR is found whether using PSF-Choice encoding or standard phase encoding^16,17. Theoretically, this makes sense. The PSF-Choice method can be seen as performing Fourier (phase) encoding of the signal integrated under a set of sampling functions (PSF’s) shifted across the FOV. In fact, standard phase encoding has been implemented with our sequence by appropriate manipulation of the RF weights, giving a sinc-shaped PSF. Since Fourier encoding and decoding/reconstruction are employed regardless of the PSF, the treatment of noise does not vary. Only the total signal sampled by the PSF causes a variation in SNR between different implementations, e.g. whether the PSF is Gaussian or sinc-shaped. Thus, as long as the integral under the PSF is the same, the SNR will be identical.

In order to insure that the integral under different PSF’s are the same, we required that the RF weights were scaled to have the same maximum value for any chosen PSF. Since flip angles also must be the same regardless of PSF, we further required that the maximum heights of the PSF’s be the same, implying that the sums of the weights for all PSF’s are equal. Note that a further constraint is that the width (or spread) of the RF weight functions must also be the same to maintain equivalent spatial resolution. We confirmed via simulation that for the chosen weight distribution to obtain the desired Gaussian PSF, the resultant signal level obtained by summing all transverse magnetization vectors, was the same as that obtained for the Fourier case (sinc-shaped PSF).

3. Methods

3.1 Pulse sequence implementation for PSF-Choice encoding

PSF-Choice was implemented by modifying the 3D-PROSE [PROstate Spectroscopy and Imaging Examination] sequence on a 3T GE Signa MRI system. PROSE itself is a modification of a standard point-resolved spatially localized spectroscopy (PRESS) sequence. Our modification to PROSE includes replacing the 90° excitation pulse with a train of 2×2 (L_x = 2, L_y = 2) hard RF pulses separated by gradient pulses along two of the phase encoding directions (x and y, as illustrated at the bottom left of Fig. 1). One result of our scheme is the loss of capability in the original RF excitation pulse for selecting the PRESS box along one dimension. To provide this selectivity for the PSF-Choice sequence, an additional 180° spatially selective (but non-spectrally selective) refocusing pulse was inserted after the train of excitation sub-pulses. In our experiments, the optional outer-volume suppression pulses were also selected for all acquisitions.

The finite time gap between RF sub-pulses α₁₁, α₂₁, α₁₂ and α₂₂ (Fig. 1) result in a phase evolution between sub-pulses due to off-resonance. This introduces a difference in effective TE (dependent on T_x and T_y of the sub-pulses and can result in ghosting artifact if sharp phase transitions are introduced between encoding steps. To avoid these artifacts, an incremental echo shifting across encoding steps was implemented so that the phase transition is made linear across the steps (Δt_x = T_x/M_x along x and Δt_y = T_y/M_y along y).

During the RF excitation, a list of pre-calculated weights is applied on each sub-pulse across encoding steps in order to generate the desired 2D excitation in the x-y plane. For low flip-angle excitation, weights can be obtained by simply taking the Fourier Transform of the desired point-spread-function. However, for high flip-angle excitation, i.e. greater than about 45°, using weights from a direct Fourier Transform of the desired PSF produces some distortion in the form of an extra side lobe in the resultant PSF shape¹⁹. Therefore weights were adjusted to account for the non-linear response due to 90° flip-angle excitations. To determine these adjusted weights, we begin first with the weights obtained by direct Fourier Transform. We then calculate the response to the excitation by solving the Bloch equations for a simulated spatial distribution of spins. Modifications are made to the weights based on the desired response versus the computed solution in an iterative fashion²⁰.

As previously mentioned, a Fourier encoding scheme can be implemented while using the PSF-Choice sequence. In this case, the sub-pulse weights are obtained from an excitation k-space profile that is just a uniform square padded with outer zeros (see truncated k-space in Fig. 3). With this scheme, there is only one sub-pulse at a time (e.g. on any one shot) with a nonzero weight and the sequence effectively reverts to a standard phase encoding scheme. This option has been used to allow for a more direct comparison of results between Gaussian and Fourier PSF’s.

For acceleration in 3D MRSI, as an option, an echo planar imaging (EPI) train of gradient pulses with alternating polarity can be added to the sequence during acquisition of the FID in order to implement echo-planar spectroscopic imaging (EPSI) in which case a readout direction is encoded in a single shot^21–23. EPSI differs from typical echo-planar imaging in that no phase encode blips are applied during the gradient train. In all experiments, both with and without EPSI, a total of 512 time points were sampled along the FID. For the EPSI case, the sample dwell was set so that 512×32 data points were acquired under the train of 512 gradient pulses, giving 32 data points per echo. Echo data acquired under negative gradient lobes are flipped and then shifted to properly align with the positive-lobe data. Odd and even echoes may be reconstructed separately, however, at the expense of spectral bandwidth. Several data points are acquired under the gradient ramps and are generally not included in order to simplify reconstruction. Alternatively, if they are included, re-gridding becomes necessary to avoid distortions.

3.2 Experimental point-spread-function validation and SNR comparison

All phantom imaging acquisitions were conducted at 3T using either a GE MR750W or HDxt system. The 2D PSF obtained with this technique was experimentally verified using a GE spherically-shaped prostate phantom of 10 cm in diameter. The phantom solution contains 50 mM potassium phosphate monobasic, 33 mM sodium citrate tribasic dihydrate, 4 mM choline chloride, 10 mM creatine monohydrate, 12 mM lithium l-lactate and 0.1% sodium azide.

Ideally, the PSF is the image one would obtain when the target object is a point of infinitesimal size. To simulate this scenario, all acquisitions were prescribed with the PRESS-localized spectroscopy box set to select a volume significantly smaller than the imaging voxel - equal to one half the length of the imaging voxel along each of three dimensions (one-eighth of the imaging voxel in volume). The imaging parameters were: FOV = 40×40×40 cm³, matrix = 8 × 8 × 8 along PSF/PSF2/EPSI dimension, TE/TR = 85/1500ms, spectral width = 976Hz. To map the PSF, 16 acquisitions were collected with −frac34;, −¼, ¼ and ¾ voxel shifts in each of the two PSF-Choice encoding directions. Each dataset was then reconstructed in spatial and spectral dimensions. The final multi-dimensional image array of spatial-spectral data was obtained by interleaving the 16 separate data sets along the two PSF-Choice encoded dimensions to form high-density PSF maps.

These datasets were used in order to confirm the prediction that SNR was the same for Gaussian and sinc-shaped PSF’s. A measurement of the noise level was obtained by taking the standard deviation in a frequency range and region-of-interest that appeared to be free of any obvious structured signal components. The SNR was then computed for the signal in the range of frequencies covering the metabolites of interest and compared for the two different PSF’s.

3.3 Experimental verification of improvement in spectroscopic localization

To evaluate the quality of spatial localization using the PSF-Choice method, MRSI was performed using the GE prostate phantom sitting on a bath of olive oil. Voxels that were completely within the prostate phantom but close to the oil compartment were examined as to the degree of contamination from the oil spectra. Acquisition parameters were as follows: TE/TR = 85/1000ms, spectral width = 976Hz, slice thickness = 1 cm (voxel thickness in the EPSI direction), and FOV = 8 × 8 cm² with an acquisition matrix = 8 × 8 along the two PSF-Choice encoding directions, resulting in an imaging voxel volume of 1 ml. Dimensions of the prescribed PRESS box were 3×5×3 cm. Shimming over the region of the PRESS box was performed using the standard auto-shim procedure using linear gradient shims only.

Post-processing was performed using in-house software with MATLAB (Mathworks, Natick, MA). Phase correction was performed on spectra with sufficient water peak intensity (above 10% of the maximum water peak) to obtain the real component, i.e. absorption spectrum. A first-order phase factor was determined as the slope from linear fitting of unwrapped phase of the FID array. The zeroth-order phase factor was estimated from the remaining average phase. Baseline removal was performed to remove the tail of the water signal. While tools such as LCModel²⁴ might have been used for quantification, we instead employed simple integration over the spectral range of the relevant metabolites. Reconstruction in spatial dimensions involved Fourier transformation only with no additional corrections applied.

3.4. Statistical Tests

The ratio of (Choline+Creatine)/Citrate was computed for all voxels containing spectra. Distributions of ratios did not pass the Lilliefors test for normality, thus, we performed the Wilcoxon rank sum test, comparing ratios in voxels inside the prostate phantom against voxels on the boundary between the prostate phantom and the oil, as well as comparing against gold-standard reference (from prostate phantom alone without surrounding oil). This was done for ratios acquired both with the PSF-choice and the Fourier encoding schemes. The significance level was set at p < 0.05.

4. Results

4.1 Verification of 2D point-spread-functions

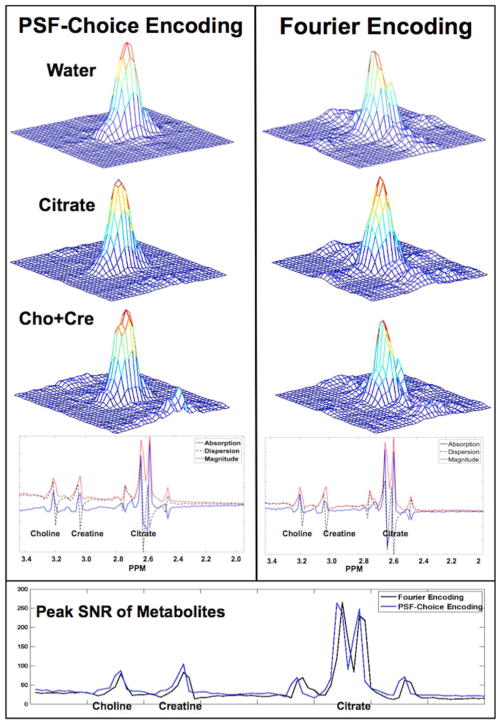
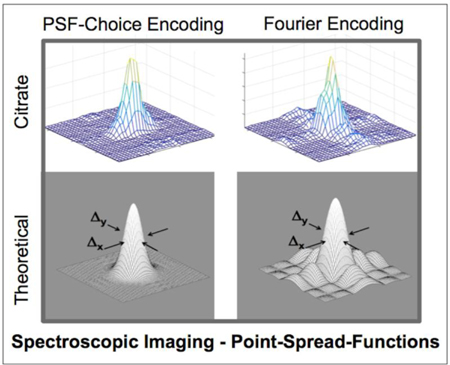
The experimental results of the point-spread-function mapping using PSF-Choice and conventional phase encoding schemes are shown in Fig. 4. The PSFs of metabolites were constructed by integrating the signal from the absorption spectra under the peaks of interest: choline-plus-creatine, and citrate. The PSF of the residual-water peak is also shown. We note that for the metabolic components, the 2D PSF mapped using the Gaussian PSF-Choice encoding scheme is essentially free of side lobes surrounding the main peak (second and third rows, left column of Fig. 4) although there does appear to be some artifact that rises above the background noise level for the choline-plus-creatine result. The results obtained using the Fourier-based encoding scheme show significant side lobes with magnitudes up to 10% of the maximum peak value. This ringing of the PSF is clearly seen along both axes (right column of Fig. 4). Clarity of the PSF is particularly notable for the high-SNR, residual-water peak. Representative spectra of the metabolites, obtained using both encoding schemes, are shown at the bottom of Fig. 4. Spectral quality is effectively identical in the two cases.

Figure 4.

The figure shows experimental results of point-spread-function mapping obtained using a spherical prostate spectroscopy phantom with a solution containing the prostate-relevant metabolites: Choline-plus-Creatine, and Citrate. The experimental point-spread-function mapping was performed for the MRSI sequences implemented using both Gaussian PSF-Choice and standard Fourier encoding where (magnitude) results are shown in left and right columns respectively. Representative spectra for individual voxels with examples for both methods are shown below the point-spread-function results. The plot at the bottom of the figure shows the SNR computed within the spectral range of interest for both Fourier and PSF-Choice encoding.

A comparison of the SNR over the range of the metabolites of interest is shown at the bottom of Fig. 4. The noise measure was obtained from the standard deviation in an ROI and in a frequency range free of signal components. The noise level for the Fourier-encoded result was slightly higher than for PSF-Choice encoding but differed by less than 1.5 percent. Peak SNR of the metabolites for the two encoding methods is comparable as it should be, although SNR for PSF-Choice encoding is slightly higher than for Fourier encoding across the frequency range of interest. Note that the two datasets were acquired separately as evidenced by the small frequency shift of the spectra. The observed differences in SNR may be due to sub-optimal calibration between the two scans resulting in slightly different signal levels.

4.2 Lipid contamination of spectra

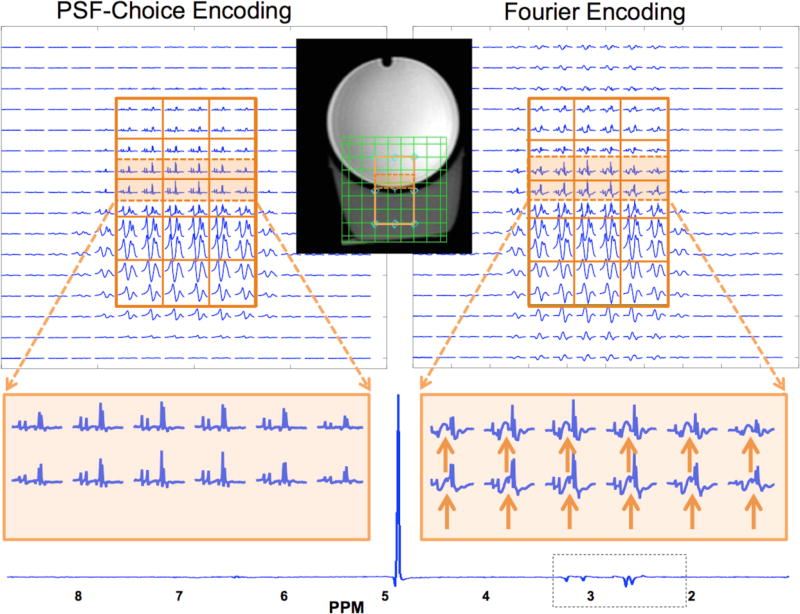
The PRESS box was prescribed in order to cover part of the GE prostate phantom along with part of the volume containing oil, as shown by the inset image in Fig. 5. The through-plane (or slice) direction is the EPSI-encoded direction. Grids of spectra obtained with the Gaussian PSF-Choice encoding scheme and the Fourier-encoding scheme are shown at the top of Fig. 5 with a zoomed portion below for two rows of voxels that are at the edge of the prostate phantom and close to the oil compartment. Note that Fig. 5 shows the result for only one section (slice) of the three sections within the PRESS box (which was prescribed to be 3 cm in the slice direction). In the analysis of results comparing PSF-Choice and Fourier encoding, voxels from the center section (slice) inside the PRESS box was chosen as it had the highest SNR.

Figure 5.

Results from phantom MRSI experiments with the prostate phantom and a surrounding compartment below containing vegetable oil. Results are for scanning with the PSF-Choice method (left side of the figure) and the standard Fourier-encoding method (right side). A PRESS box was prescribed with an upper portion within the spherical GE spectroscopy phantom and the lower portion inside the vegetable oil. The orange lines in the inlaid image demarcate the PRESS box selected for the experiment. The grid of green lines in the inlaid image shows the imaging FOV and the location of the individual voxels. The figure shows results for one section (slice) out of the three that were within the 3×5×3 cm PRESS box. Voxel size is 1×1×1 cm. The spectra acquired with PSF-Choice encoding demonstrate the relative lack of lipid contamination from neighboring voxels, versus the spectra in Fourier encoding scheme. A zoomed in portion is shown at the bottom of the figure. Solid orange-colored arrows point to portions of the spectra that are contaminated by lipids from the Fourier-encoded result. Note that for both methods 8x8 data arrays of spectra were obtained with half-pixel shifting in both directions, giving four 8x8 arrays. These data were then interleaved to give the 16×16 arrays of spectra shown in the displays. For reference, a spectral plot at the full spectral width is shown for one PSF-Choice encoded voxel within the phantom.

A visual inspection of voxel signals for the two methods shows a generally higher level of signal outside the selected PRESS box for the Fourier-encoding method. A close inspection of the zoomed spectra for the PSF-Choice result (bottom left of Fig. 5) demonstrates that the metabolic components in the prostate phantom-only region are qualitatively uncontaminated by contributions from out-of-voxel lipids. Results obtained from the Fourier encoding scheme, however, show significant contamination from lipid signal in voxels within the prostate phantom (see orange arrows at bottom right of Fig. 5).

The out-of-voxel lipid contamination observed with conventional Fourier encoding complicates interpretation of the spectra in the prostate-only region. Specifically, it can be seen that the clinically relevant ratio of Choline+Creatine to Citrate is affected in the voxels near the phantom boundary. The ratios computed from voxels well within the phantom (n=18) and voxels at the phantom boundary (n=11 are 0.47 ± 0.047 and 0.56 ± 0.097 respectively with Fourier encoding, representing a statistically significant difference (p = 0.014). In contrast, comparing ratios from inner voxels (0.50 ± 0.039, n=18) and boundary voxels (0.49 ± 0.069, n=11) with PSF-Choice encoding, there is no statistical significance (p=0.637). We also computed ratios of Choline+Creatine to Citrate from the prostate phantom alone (no surrounding oil) to obtain a gold-standard reference (0.48 ± 0.043). Comparing ratios in the boundary voxels against the gold-standard reference, there is a statistically significant difference when using Fourier encoding (p = 0.035) but no statistically significant difference when PSF-Choice was used (p=0.935). There is no statistical difference when comparing ratios for voxels well inside the phantoms with either Fourier encoding or PSF-Choice encoding against the gold-standard reference (i.e. in the prostate phantom with no surrounding oil).

It should be noted that the olive oil is mostly beneath the prostate phantom so that most lipid contamination due to ringing should to be expected in the vertical direction. To validate that both PSF-Choice encoding directions have less out-of-voxel contamination than for the Fourier case, we ran a second set of experiments, swapping encoding directions between horizontal and vertical. For example, referring to the two PSF-Choice encoding directions as PSF_A and PSF_B, in the first set of experiments, PSF_A was vertical and PSF_B was horizontal. In the second set of experiments PSF_B was horizontal and PSF_A was vertical. Results in terms of the degree of lipid contamination were similar in both sets of experiments.

5. Discussion

In this work, the PSF-Choice method was implemented to minimize the voxel bleeding artifacts in MR spectroscopic images that arise due to the inherently low spatial resolution characteristic of MRSI. The unique aspect of the current work is that the method is applied along two separate phase-encoding directions to achieve improved spatial localization. We have included a detailed mathematical exposé of the technique along with experimental validation in a series of MRSI experiments using a prostate spectroscopy phantom.

Validation of the method has been limited here to experiments using a phantom containing metabolic components relevant for prostate spectroscopic imaging²⁵. However, prior work has also validated the method using a phantom containing metabolic components relevant for neuroimaging. While a previous study with one-dimensional PSF-Choice reported results with a group of patients, it remains for future work to demonstrate the two-dimensional method in vivo. We do not anticipate effects limiting in vivo performance that are any different from those encountered in standard phase encoding. Sensitivity of PSF-Choice to problems such as susceptibility and motion are also expected to be the same as for standard phase encoding. Most sequence parameter adjustments can be made using phantoms prior to conducting in vivo work. Adjustments, such as shimming, that must be made at exam time will be identical to those required for MRSI with standard phase encoding. EPSI should be considered for in vivo acquisitions in order to reduce the exam times^21–23. While we have included EPSI as an option in this implementation, further work on the reconstruction algorithm remains to be done in order to improve the correction for misalignment between even and odd echoes as well as for re-gridding of the ramp-sampled data.

It could be argued that even better spatial localization could be accomplished by choice of a sharper and more spatially constrained PSF than the Gaussian scheme implemented here (e.g. the box-shaped PSF in Fig. 3). However, because this involves sampling higher spatial frequencies in excitation k-space, a greater number of sub-pulses beyond the 2 × 2 sub-pulse train used in the Gaussian scheme would be required. The longer pulse trains come at the inevitable cost of longer duration of the RF excitation, affecting the minimum TE of the sequence. Longer pulse trains are also more susceptible to off-resonance effects.

In analogy with multi-shot EPI, in our implementation we used a corresponding echo shifting to control the off-resonance effect and avoid serious artifacts. Essentially, the delay between the sub-pulse set and the acquisition window of the sequence was arranged to avoid sharp phase transitions in excitation k-space and instead created a smooth linear phase evolution. The result of this scheme is that, after reconstruction, the spectral images are shifted spatially in both PSF-Choice encoding directions with the amount of shifting depending on the duration of the echo-shift increment and the resonant frequency of individual metabolites. It should be noted here that, with appropriate manipulation of the phase of the RF pulses on each shot, we are able to achieve a controlled shifting of the spectral images, an approach that was used to produce the images of the point-spread-functions shown in Fig. 4.

In previous one-dimensional implementations of PSF-Choice, trains of slice-selective RF pulses were used^16,17. In this two-dimensional PSF-Choice implementation, trains of hard pulses were employed to minimize duration of the pulse trains at the expense of removing the slice-selective capability of the initial RF excitation. The use of slice-selective sub-pulses is not precluded in the two-dimensional implementation; however, this inevitably leads to longer overall RF pulse train duration and, as discussed, with all the disadvantages this entails. A scheme implemented on a system equipped with parallel transmitters might be envisioned, potentially allowing for the use of shorter sub-pulse trains.

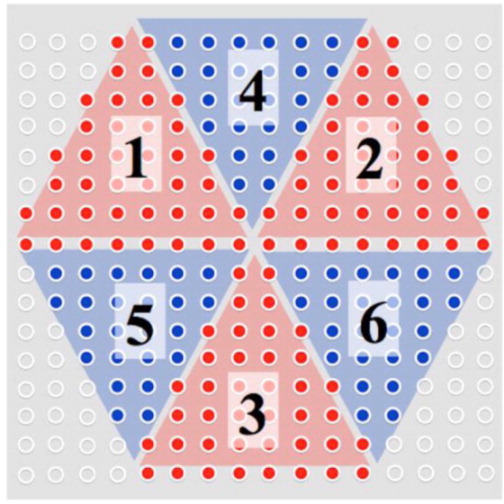
Alternate sampling schemes can be considered for traversing the excitation k-space when implementing PSF-Choice. We note that, in principle, to expand a n-dimensional space, a structural element must have a minimum number of vertices equal to n + 1. Therefore, one might conceive of using just three instead of four sub-pulses to cover a two-dimensional excitation k-space (or four sub-pulses in a three-dimensional implementation). By virtue of puzzle solving, a design using a train of three evenly spread sub-pulses to cover a hexagon-like area in an 8 × 8 matrix is illustrated in Fig. 6. Besides benefiting from a shorter sub-pulse train, this scheme samples the excitation k-space similarly as in elliptical sampling of k-space with a low-pass filtering effect to boost SNR. As the areas of excitation k-space that are not sampled are in the high-frequency corners, the impact on the PSF is expected to be minimal. For the three-dimensional implementation, it is possible to expand a truncated octahedron using a tetrahedron element formed by sampling with a four-sub-pulse train.

Figure 6.

Demonstration of the excitation k-space sampling for a hypothetical three-pulse PSF-Choice encoding scheme. The sub-pulse sampling is evenly distributed in three orange sections (sections 1,2 and 3) and three blue sections (sections 4,5 and 6). Those corner locations remaining unsampled with this scheme are marked with white dots. The resulting hexagon mask applied on 16×16 Gaussian shaped matrix should produce minimal changes to the PSF compared to the current four-pulse implementation since only the corners of excitation k-space are not covered in this scheme.

6. Conclusions

In conclusion, we have implemented a PSF-Choice method for encoding in two phase-encoding dimensions and demonstrated both theoretically and through phantom experiments that the resultant PSF is free of the ripple characteristic of standard Fourier encoding. The phantom experiments demonstrated the superior spatial localization of the technique at prostate cancer-relevant metabolic peaks. The reduction of contamination from surrounding lipid signals was further demonstrated for MRSI at 3T.

Highlights.

• A MR Spectroscopic Imaging method to improve spatial localization was implemented.

• A true 2D Gaussian imaging point-spread-function was obtained without filtering.

• Spectral contamination from surrounding fat was minimized in a prostate phantom.