Abstract
The human visual cortex extracts both spatial and temporal visual features to support perception and guide behavior. Deep convolutional neural networks (CNNs) provide a computational framework to model cortical representation and organization for spatial visual processing, but unable to explain how the brain processes temporal information. To overcome this limitation, we extended a CNN by adding recurrent connections to different layers of the CNN to allow spatial representations to be remembered and accumulated over time. The extended model, or the recurrent neural network (RNN), embodied a hierarchical and distributed model of process memory as an integral part of visual processing. Unlike the CNN, the RNN learned spatiotemporal features from videos to enable action recognition. The RNN better predicted cortical responses to natural movie stimuli than the CNN, at all visual areas, especially those along the dorsal stream. As a fully observable model of visual processing, the RNN also revealed a cortical hierarchy of temporal receptive window, dynamics of process memory, and spatiotemporal representations. These results support the hypothesis of process memory, and demonstrate the potential of using the RNN for in‐depth computational understanding of dynamic natural vision.
Keywords: deep learning, natural vision, neural encoding, process memory, recurrent neural network, temporal receptive window
1. INTRODUCTION
Human behavior depends heavily on vision. The brain's visual system works efficiently and flexibly to support a variety of tasks, such as visual recognition, tracking, and attention, to name a few. Although a computational model of natural vision remains incomplete, it has evolved from shallow to deep models to better explain brain activity (Khaligh‐Razavi, Henriksson, Kay, & Kriegeskorte, 2017; Kriegeskorte, 2015), predict human behaviors (Canziani & Culurciello, 2015; Fragkiadaki, Levine, Felsen, & Malik, 2015; Mnih, Heess, & Graves, 2015), and support artificial intelligence (AI) (LeCun, Bengio, & Hinton, 2015; Silver et al., 2016). In particular, convolutional neural networks (CNNs)—trained with millions of labeled natural images (Russakovsky et al., 2015)—have enabled computers to recognize images with human‐like performance (He, Zhang, Ren, & Sun, 2015). CNNs bear similar representational structures as the visual cortex (Cichy, Khosla, Pantazis, Torralba, & Oliva, 2016; Khaligh‐Razavi & Kriegeskorte, 2014) and predict brain responses to natural stimuli (Eickenberg, Gramfort, Varoquaux, & Thirion, 2017; Güçlü & van Gerven, 2015a; Wen et al., 2017a; Wen, Shi, Chen, & Liu, 2017b; Yamins et al., 2014). It thus provides new opportunities for understanding cortical representations of vision (Khaligh‐Razavi et al., 2017; Yamins & Di Carlo, 2016).
Nevertheless, CNNs driven for image recognition are incomplete models of the visual system. CNNs are intended and trained for analyses of images in isolation, rather than videos where temporal relationships among individual frames carry information about action. In natural viewing conditions, the brain integrates information not only in space (Hubel & Wiesel, 1968) but also in time (Hasson, Yang, Vallines, Heeger, & Rubin, 2008). Both spatial and temporal information is processed by cascaded areas with increasing spatial receptive fields (Wandell, Dumoulin, & Brewer, 2007) and temporal receptive windows (TRWs) (Hasson et al., 2008) along the visual hierarchy. That is, neurons at progressively higher levels of visual processing accumulate past information over increasingly longer temporal windows to account for their current activity. In such a hierarchical system for spatiotemporal processing, Hasson, Chen, and Honey (2015) proposed a notion of “process memory.” Unlike the traditional view of memory being restricted to a few localized reservoirs, process memory is hypothesized to be intrinsic to information processing that unfolds throughout the brain on multiple timescales (Hasson et al., 2015). However, CNNs only model spatial processing via feedforward‐only computation, lacking any mechanism for processing temporal information.
An effective way to model temporal processing is by using recurrent neural networks (RNNs), which learn representations from sequential data (Goodfellow, Bengio, & Courville, 2016). As its name indicates, an RNN processes the incoming input by also considering the RNN's internal states in the past. In AI, RNNs have made impressive progress in speech and action recognition (Donahue et al., 2015; Greff, Srivastava, Koutník, Steunebrink, & Schmidhuber, 2016; Jozefowicz, Zaremba, & Sutskever, 2015), demonstrating the potential to match human performance on such tasks. In addition, RNN can be designed with an architecture that resembles the notion of “process memory” to accumulate information in time as an integral part of ongoing sensory processing (Hasson et al., 2015). Therefore, RNN is a logical step forward from CNN toward modeling and understanding the inner working of the visual system in dynamic natural vision.
In this study, we designed, trained, and tested an RNN to model and explain cortical processes for spatial and temporal visual processing. This model began with a static CNN pre‐trained for image recognition (Simonyan & Zisserman, 2014). Recurrent connections were added to different layers in the CNN to embed process memory into spatial processing, so that layer‐wise spatial representations could be remembered and accumulated over time to form video representations. While keeping the CNN intact and fixed, the parameters for the recurrent connections were optimized by training the entire model for action recognition with a large set of labeled videos (Soomro, Zamir, & Shah, 2012). Then, we evaluated how well this RNN model matched the human visual cortex up to linear transform. Specifically, the RNN was trained to predict functional magnetic resonance imaging (fMRI) responses to natural movie stimuli. The prediction accuracy with the RNN was compared with that of the CNN, to address whether and where the recurrent connections allowed the RNN to better model cortical representations given dynamic natural stimuli. Through the RNN, we also characterized and mapped the cortical topography of temporal receptive windows and dynamics of process memory. By doing so, we attempted to use a fully observable model of process memory to explain the hierarchy of temporal processing, as a way to directly test the hypothesis of process memory (Hasson et al., 2015).
2. METHODS AND MATERIALS
2.1. Experimental data
The experimental data were from our previous studies (Wen et al., 2017a, 2017b; Wen, Shi, Chen, & Liu, 2017c), according to a research protocol approved by the Institutional Review Board at Purdue University. Briefly, we acquired fMRI scans from three healthy subjects while they were watching natural videos. The video‐fMRI data was split into two datasets to train and test the encoding models, respectively, for predicting fMRI responses given any natural visual stimuli. The training movie contained 12.8 h of videos for Subject 1, and 2.4 h for the other subjects (Subjects 2 and 3). The testing movie for every subject contained 40 min of videos presented 10 times during fMRI (for a total of 400 min). These movies included a total of ∼9,300 continuous videos without abrupt scene transitions, covering a wide range of realistic visual experiences. These videos were concatenated and then split into 8‐min movie sessions, each of which was used as the stimuli in a single fMRI experiment. Subjects watched each movie session through a binocular goggle (20.3°×20.3°) with their eyes fixating the center of the screen (red cross). Although the fixation was not ensured, our prior study has demonstrated the ability to use this video‐fMRI dataset to map the retinotopic organization in early visual areas (Wen et al., 2017a), lending indirect support to stable eye‐fixation. Whole‐brain fMRI scans were acquired in 3‐T with an isotropic resolution of 3.5mm and a repetition time of 2s. The fMRI data were preprocessed and co‐registered onto a standard cortical surface (Glasser et al., 2013). More details about the stimuli, data acquisition, and preprocessing are described in Wen et al. (2017a, 2017b).
2.2. Convolutional neural network (CNN)
Similar to our prior studies (Wen et al., 2017a, 2017b, 2017c), a pretrained CNN, also known as the VGG16 (Simonyan & Zisserman, 2014), was used to extract the hierarchical feature representations of every video frame as the outputs of artificial neurons (or units). This CNN contained 16 layers of units stacked in a feedforward network for processing the spatial information in the input. Among the 16 layers, the first 13 layers were divided into five blocks (or submodels). Each block started with multiple convolutional layers with Rectified Linear Units (ReLU) (Nair & Hinton, 2010), and ended with spatial max‐pooling (Boureau, Ponce, & LeCun, 2010). To simplify terminology, hereafter we refer to these blocks as layers. The outputs from every layer were organized as three‐dimensional arrays (known as feature maps). For the first through fifth layers, the sizes of feature maps were 64 × 112 × 112, 128 × 56 × 56, 256 × 28 × 28, 512 × 14 × 14, and 512 × 7 × 7, where the first dimension was the number of features, the second and third dimensions specified the width and the height (or the spatial dimension). From lower to higher layers, the number of features increased as the dimension per feature decreased. This CNN was implemented in PyTorch (http://pytorch.org/).
2.3. Recurrent neural network (RNN)
An RNN was constructed by adding recurrent connections to the four out of five layers in the CNN. The first layer was excluded to reduce the computational demand as in a prior study (Ballas, Yao, Pal, & Courville, 2015). The recurrent connections served to model distributed process memory (Hasson et al., 2015), which allowed the model to memorize and accumulate visual information over time for temporal processing.
Figure 1a illustrates the design of the RNN for extracting layer‐wise feature representations of an input video. Let the input video be a time series of color (RGB) frames with 224 × 224 pixels per frame. For the video frame at time t, . The internal states of the RNN at layer l, denoted as , was updated at each moment, according to the incoming information and the history states , as expressed in Equation (1).
| (1) |
where was the spatial features encoded at layer l in the pre‐trained CNN, so was the extracted feature representations of the current input . Importantly, was the so‐called “forget gate” essential to learning long‐term temporal dependency (Pascanu, Mikolov, & Bengio, 2013). As its name indicates, the forget gate determined the extent to which the history states should be “forgotten,” or reversely the extent to which the incoming information should be “remembered.” As such, the forget gate controlled, moment by moment, how information should be stored into vs. retrieved from process memory. Given a higher value of the forget gate, the RNN's current states were updated by retrieving less from its “memory” , but learning more from the representations of the current input . This notion was expressed as the weighted sum of the two terms in the right‐hand side of Equation (1), where stands for Hadamard product and the weights of the two terms sum to 1. In short, the RNN embedded an explicit model of “process memory” (Hasson et al., 2015).
Figure 1.
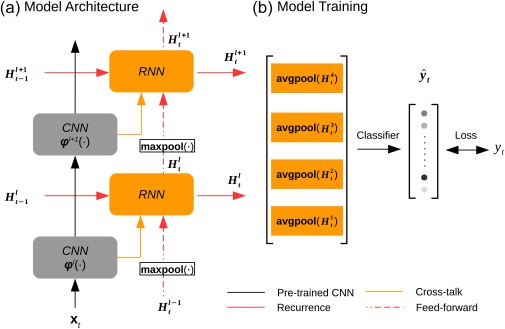
The recurrent model of vision. (a) The architectural design of the RNN. (b) The model training strategy. The gray blocks indicate the CNN layers; the orange blocks indicate the RNN layers. The CNN was pretrained and fixed, while the RNN was optimized on the task of action recognition [Color figure can be viewed at http://wileyonlinelibrary.com]
Note that the forget gate was time dependent but a function of the time‐invariant weights, denoted as , of the recurrent connections, expressed as below:
| (2) |
where is the sigmoid function whose output ranges from 0 to 1.
As expressed in Equation (2), the forget gate was the weighted sum of three terms: the RNN's previous output , the CNN's current output , and the RNN's current input from the lower layer . Here, maxpool(•) stands for the max‐pooling operation, which in this study used a kernel size of 2 × 2 and a stride of 2 to spatially subsample half of the RNN's output at layer l‐1 and fed the result as the input to layer l in the RNN. Note that the weighted summation was in practice implemented as convolving a 3 × 3 kernel (with a padding of 1) across all three input terms concatenated together, as expressed by cat(•) in Equation (2). This reduced the number of unknown parameters to be trained. In other words, , where M and N were the numbers of output and input feature maps, respectively.
2.4. Training the RNN for action recognition
The RNN was trained for video action recognition by using the first split of the UCF101 dataset (Soomro et al., 2012). The dataset included 9,537 training videos and 3,783 validation videos from 101 labeled action categories, which included five general types of human actions: human–object interaction, body motion, human–human interaction, playing musical instruments, and sports. See Appendix for the list of all action categories. All videos were resampled at 5 frames per second, and preprocessed as described elsewhere (Ballas et al., 2015), except that we did not artificially augment the dataset with random crops.
To train the RNN with labeled action videos, a linear softmax classifier was added to the RNN to classify every training video frame as one of the 101 action categories. As expressed by Equation (3), the inputs to the classifier were the feature representations from all layers in the RNN, and its outputs were the normalized probabilities, by which a given video frame was classified into predefined categories (Figure 1b).
| (3) |
where reduced from a 3‐D feature array to a 1‐D feature vector by averaging over the spatial dimension (or average pooling); further concatenated the feature vectors across all layers in the RNN; was a trainable linear function to transform the concatenated feature vector onto a score for each category; converted the scores into a probability distribution, , to report the result of action categorization given each input video frame.
The loss function for training the RNN was defined as below:
| (4) |
where stands for the true action category labeled for the input . Here, the learning objective was to maximize the average (over T samples) log probability of correct classification conditioned on the input and parameterized by linear projection and the recurrent parameters .
The RNN was trained by using mini‐batch gradient descent and back‐propagation through time (Werbos, 1990). The parameters were initialized as random values from a uniform distribution between −0.01 and 0.01. For the training configurations, the batch size was set to 10. The sequence length was 20 frames, so that the losses were accumulated over 20 consecutive frames before back‐propagation. A dropout of 0.7 was used to train . The gradient vector was normalized to 5. The gradient descent algorithm was based on the Adam optimizer (Kingma & Ba, 2014) with the learning rate initialized as 1e‐3. The learning rate was decayed by 0.1 every 10 epochs, while the learning iterated across all training videos in each epoch.
To evaluate the RNN on the task of action recognition, we evaluated the top‐1 accuracy given the validation videos, while being top‐1 accurate meant that the most probable classification matched the label. In addition, we also trained a linear softmax classifier based on the feature representations extracted from the CNN with the same training data and learning objective, and evaluated the top‐1 accuracy for model comparison.
2.5. Encoding models
For each subject, a voxel‐wise encoding model (Naselaris, Kay, Nishimoto, & Gallant, 2011) was established for predicting the fMRI response to natural movie stimuli based on the features of the movie extracted by the RNN (or the CNN for comparison). A linear regression model was trained separately for each voxel to project feature representations to voxel responses, similar to prior studies (Eickenberg et al., 2017; Güçlü & van Gerven, 2015a, 2015b; Wen et al., 2017a, 2017b, 2017c). As described below, the same training methods were used regardless of whether the RNN or the CNN was used as the feature model.
Using the RNN (or the CNN), the feature representations of the training movie were extracted and sampled every second. Note that the feature dimension was identical for the CNN and the RNN, both including feature representations from four layers with exactly matched numbers of units in each layer. For each of the four layers, the number of units was 401408, 200704, 100352, and 25088. Combining features across these layers ended up with a very high‐dimensional feature space. To reduce the dimension of the feature space, principal component analysis (PCA) was applied first to each layer and then to all layers, similar to our prior studies (Wen et al., 2017a, 2017b, 2017c). The principal components (PCs) were identified based on the feature representations of the training movie, and explained 90% variance. Such PCs defined a set of orthogonal basis vectors, spanning a subspace of the original feature space (or the reduced feature space). Applying this basis set as a linear operator, B, to any representation, X, in the original feature space, converted it to the reduced feature space, as expressed by Equation (5); applying the transpose of B to any representation, Z, in the reduced feature space, converted it to the original feature space.
| (5) |
where stands for the representation of the RNN (or the CNN) with T samples and q units; is a q‐by‐p matrix that consists of the PCs identified with the training movie; and stands for the p‐dimensional feature representations after dimension reduction (p < q).
The feature representations after dimension reduction (i.e. columns in Z) were individually convolved with a canonical hemodynamic response function (HRF) (Buxton, Uludağ, Dubowitz, & Liu, 2004) and downsampled to match the sampling rate for fMRI. Then, was used to fit each voxel's response during the training movie through a voxel‐specific linear regression model, expressed as Equation (6).
| (6) |
where is a columnar vector of regression coefficients specific to voxel , and is the error term. To estimate , L2‐regularized least‐squares estimation was used while the regularization parameter was determined based on fivefold cross‐validation.
| (7) |
To train this linear regression model, we used the fMRI data acquired during the training movie. The model training was performed separately for the two feature models (the RNN and the CNN) using the same training algorithm. Afterwards, we used the trained encoding models to predict cortical fMRI responses to the independent testing movie. The prediction accuracy was quantified as the temporal correlation (r) between the observed and predicted responses at each voxel. As in our previous studies (Wen et al., 2017a, 2017b, 2017c), the statistical significance of the prediction accuracy was evaluated voxel‐by‐voxel with a block‐permutation test (Adolf et al., 2014) corrected at the false discovery rate (FDR) .
Given the dimension reduction of the feature space, described the contributions to voxel v from individual basis vectors in the reduced feature space (i.e., columns of B in Equation (5)). As the dimension reduction was through linear transform, the voxel‐wise encoding models (Equation (6)) could be readily rewritten with the regressors specific to individual units (instead of basis vectors) in the RNN (or the CNN). In this equivalent encoding model, the regression coefficients, denoted as , reported the contribution from every unit to each voxel, and could be directly computed from as below.
| (8) |
For each voxel, we further identified a subset of units in the RNN that contributed to the voxel's response relatively more than other units. To do so, half of the maximum in the absolute values of was taken as the threshold. Those units, whose corresponding regression coefficients had absolute values greater than this threshold, were included in a subset (denoted as ) associated with voxel v.
2.6. Model evaluation and comparison
After training them using the same training data and the same training algorithms, we compared the encoding models based on the RNN and those based on the CNN. For this purpose, the encoding performance was evaluated as the accuracy of predicting the cortical responses to every session of the testing movie. The prediction accuracy was measured as the temporal correlation (r) and then was converted to a z score by Fisher's z‐transformation. For each voxel, the z score was averaged across different movie sessions and different subjects, and the difference in the average z score between the RNN and the CNN was computed voxel by voxel. Such voxel‐wise difference (Δz) was evaluated for statistical significance using the paired t test across different movie sessions and different subjects (p < 0.01). The differences were also assessed at different ROIs, which were defined based on the cortical parcellation (Glasser et al., 2016), and evaluated for statistical significance using the paired t test across voxels (p < .01). For the voxels where RNN significantly outperformed CNN, we further divided them into the voxels in early visual areas, dorsal‐stream areas, and ventral‐stream areas. We evaluated whether the improved encoding performance (Δz) was significantly higher for the dorsal stream than the ventral stream. For this purpose, we applied two‐sample t test to the voxel‐wise Δz value in the dorsal versus ventral visual areas with the significance level at 0.01.
We also compared the encoding performance against the “noise ceiling,” or the upper limit of the prediction accuracy (Nili et al., 2014). The noise ceiling was lower than 1, due to the fact that the measured fMRI data contained ongoing noise or activity unrelated to the external stimuli, and thus the measured data could not be entirely predictable from the stimuli even if the model were perfect. As described elsewhere (Kay, Winawer, Mezer, & Wandell, 2013), the response (evoked by the stimuli) and the noise (unrelated to the stimuli) were assumed to be additive and independent and follow normal distributions. Such response and noise distributions were estimated from the data. For each subject, the testing movie was presented ten times. For each voxel, the mean of the noise was assumed to be zero; the variance of the noise was estimated as the mean of the standard errors in the data across the 10 repetitions; the mean of the response was taken as the voxel signal averaged across the 10 repetitions, and the variance of the response was taken as the difference between the variance of the data and the variance of the noise. From the estimated signal and noise distributions, we conducted Monte Carlo simulations to draw samples of the response and the noise, and to simulate noisy data by adding the response and noise samples. The correlation between the simulated response and noisy data was calculated for each of the 1,000 repetitions of simulation, yielding the distribution of noise ceilings at each voxel or ROI.
2.7. Mapping the cortical hierarchy for spatiotemporal processing
We also used the RNN‐based encoding models to characterize the functional properties of each voxel, by summarizing the fully‐observable properties of the RNN units that were most predictive of that voxel. As mentioned, each voxel was associated with a subset of RNN units I v. In this subset, we calculated the percentage of the units belonging to each of the four layers (indexed by 1–4) in the RNN, multiplied the layer‐wise percentage by the corresponding layer index, and summed the result across all layers to yield a number (between 1 and 4). This number was assigned to the given voxel v, indicating this voxel's putative “level” in the visual hierarchy. Mapping the voxel‐wise level revealed the hierarchical cortical organization for spatiotemporal visual processing.
2.8. Estimating temporal receptive windows
We also quantified the temporal receptive window (TRW) at each voxel v by summarizing the “temporal dependency” of its contributing units I v in the RNN. For each unit , its forget gate, denoted as , controlled the memory storage vs. retrieval at each moment t. For simplicity, let us define a “remember” gate, , to act oppositely as the forget gate. From Equation (1), the current state (or unit activity) was expressed as a function of the past input .
| (9) |
where . In Equation (9), the first term was zero given the initial state . The second term was the result of applying a time‐variant filter to the time series of the spatial representation extracted by the CNN from every input frame . In this filter, each element reflected the effect of the past visual input (with an offset ) on the current state . As it varied in time, we averaged the filter across time, yielding to represent the average temporal dependency of each unit i.
From the observable temporal dependency of every unit, we derived the temporal dependency of each voxel by using the linear unit‐to‐voxel relationships established in the encoding model. For each voxel v, the average temporal dependency was expressed as a filter , which was derived as the weighted average of the filters associated with its contributing RNN units , as in Equation (10).
| (10) |
Of , the elements delineated the dependency of the current response at voxel v on the past visual input with an offset prior to the current time. The accumulation of temporal information was measured as the sum of across different offsets in a given time window. The window size that accounted for 95% of the accumulative effect integrated over an infinite past period was taken as the TRW for voxel v. In the level of ROIs, the TRW was averaged across voxels within each predefined ROI. The difference in TRW between different ROIs was evaluated using two‐sample t tests (p < .01).
2.9. Spectral analysis of forget gate dynamics
We also characterized the temporal fluctuation of the forget gate at each unit in the RNN. As the forget gate behaved as a switch for controlling, moment by moment, how information was stored into versus retrieved from process memory, its fluctuation reflected the dynamics of process memory in the RNN given natural video inputs.
To characterize the forget‐gate dynamics, its power spectral density (PSD) was evaluated. The PSD followed a power‐law distribution that was fitted with a descending line in the double‐logarithmic scale. The slope of this line, or the power‐law exponent (PLE) (Miller, Sorensen, Ojemann, & Den Nijs, 2009; Wen & Liu, 2016), characterized the balance between slow (low‐frequency) and fast (high‐frequency) dynamics. A higher PLE implied that slow dynamics dominated fast dynamics; a lower PLE implied the opposite. After the PLE was evaluated for each unit, we derived the PLE for each voxel v as a weighted average of the PLE of every unit i that contributed to this voxel ( ), in a similar way as expressed in Equation (10).
3. RESULTS
3.1. RNN learned video representations for action recognition
We used a recurrent neural network (RNN) to model and predict cortical fMRI responses to natural movie stimuli. This model extended a pretrained CNN (VGG16) (Simonyan & Zisserman, 2014) by adding recurrent connections to different layers in the CNN (Figure 1). While fixing the CNN, the weights of recurrent connections were optimized by supervised learning with >13,000 labeled videos from 101 action categories (Soomro et al., 2012). After training, the RNN was able to categorize independent test videos with 76.7% top‐1 accuracy. This accuracy was much higher than the 65.09% accuracy obtained with the CNN, and close to the 78.3% accuracy obtained with the benchmark RNN model (Ballas et al., 2015).
Unlike the CNN, the RNN explicitly embodied a network architecture to learn hierarchically organized video representations for action recognition. When taking isolated images as the input, the RNN behaved as a feedforward CNN for image categorization. In other words, the addition of recurrent connections enabled the RNN to recognize actions in videos, without losing the already learned ability for recognizing objects in images.
3.2. RNN better predicted cortical responses to natural movies
Accompanying its enriched AI, the RNN learned to utilize the temporal relationships between video frames, whereas the CNN treated individual frames independently. We asked whether the RNN constituted a better model of the visual cortex than the CNN, by evaluating and comparing how well these two models could predict cortical fMRI responses to natural movie stimuli. The prediction was based on voxel‐wise linear regression models, through which the representations of the movie stimuli, as extracted by either the RNN or the CNN, were projected onto each voxel's response to the stimuli. Such regression models were trained and tested with different sets of video stimuli (12.4 or 2.4 h for training, 40 min for testing) to ensure unbiased model evaluation and comparison. Both the RNN and the CNN explained significant variance of the movie‐evoked response for widespread cortical areas (Figure 2a,b). The RNN consistently performed better than the CNN, showing significantly (p < .01, paired t test) higher prediction accuracy for nearly all visual areas (Figure 2d), especially for cortical locations along the dorsal visual stream relative to the ventral stream (p < .01, two‐sample t test) (Figure 2c). The response predictability given the RNN was about half of the “noise ceiling”—the upper limit by which the measured response was predictable given the presence of any ongoing “noise” or activity unrelated to the stimuli (Figure 2d). This finding was consistently observed for each of the three subjects (Figure 3).
Figure 2.
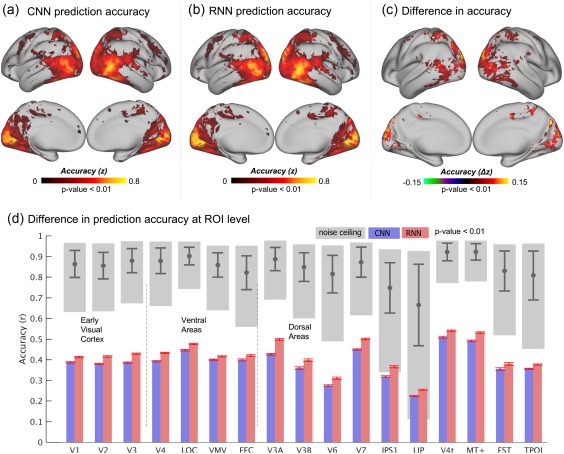
Prediction accuracies of the cortical responses to novel movie stimuli. (a) Performance of the CNN‐based encoding model, averaged across testing movie sessions and subjects. (b) Performance of the RNN‐based encoding model, averaged across testing movie sessions and subjects. (c) Significant difference in the performance between the RNN and CNN (p < .01). The values of the difference were computed by subtracting (a) from (b). (d) Comparison of performance at different ROIs with noise ceilings. The accuracy at each ROI is the voxel mean within the region, where the red bars indicate the standard error of accuracies across voxels. The gray blocks indicate the lower and upper bounds of the noise ceilings and the gray bars indicate the mean and standard deviation of the noise ceilings at each ROI [Color figure can be viewed at http://wileyonlinelibrary.com]
Figure 3.
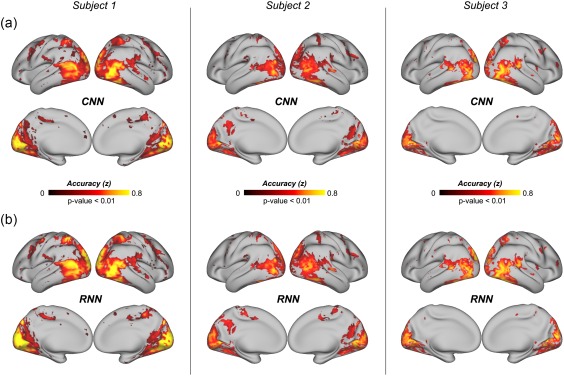
Prediction accuracies of the cortical responses to novel movie stimuli for individual subjects. (a) Performance of the CNN‐based encoding model, averaged across testing movie sessions. (b) Performance of the RNN‐based encoding model, averaged across testing movie sessions [Color figure can be viewed at http://wileyonlinelibrary.com]
3.3. RNN revealed a gradient in temporal receptive windows (TRWs)
Prior studies have shown empirical evidence that visual areas were hierarchically organized to integrate information not only in space (Kay et al., 2013) but also in time (Hasson et al., 2008). Units in the RNN learned to integrate information over time through the unit‐specific “forget gate,” which controlled how past information shaped processing at the present time. Through the linear model that related RNN units to each voxel, the RNN's temporal “gating” behaviors were passed from units to voxels in the brain. As such, this model allowed us to characterize the TRWs, in which past information was carried over and integrated over time to affect and explain the current response at each specific voxel or region.
Figure 4a shows the response at each given location as the accumulative effect integrated over a varying period (or window) prior to the current moment. On average, the response at V1 reflected the integrated effects over the shortest period, suggesting the shortest TRW at V1. Cortical areas running down the ventral or dorsal stream integrated information over progressively longer TRWs (Figure 4a). Mapping the voxel‐wise TRW showed a spatial gradient aligned along the visual streams, suggesting a hierarchy of temporal processing in the visual cortex (Figure 4b). In the ROI level, the TRWs were significantly shorter for early visual areas than those for higher‐order ventral or dorsal areas; and the dorsal areas tended to have longer TRWs than the ventral areas (Figure 4c). While Figure 4 shows the results for Subject 1, similar results were also observed in the other subjects (Supporting Information, Figures S1 and S2). We interpret the TRW as a measure of the average capacity of process memory at each cortical location involved in visual processing.
Figure 4.
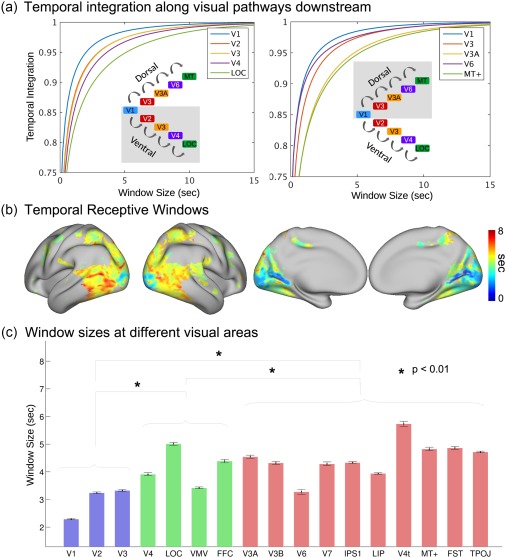
Model‐estimated TRWs in the visual cortex of Subject 1. (a) The accumulation of information at different ROIs along ventral and dorsal streams. Window size represents the period to the past, and temporal integration indicates the relative amount of accumulated information. (b) The cortical map of TRWs estimated by the RNN. The color bar indicates the window sizes at individual voxels. (c) Average TRWs at individual ROIs. The blue bars represent the early visual cortex, the green bars the ventral areas, and the red bars the dorsal areas. The black error bars indicate the standard errors across voxels [Color figure can be viewed at http://wileyonlinelibrary.com]
3.4. RNN revealed the slow versus fast dynamics of process memory
In the RNN, the forget gate varied from moment to moment, indicating how the past versus current information was mixed together to determine the representation at each moment. Given the testing movie stimuli, the dynamics of the forget gate was scale free, showing a power‐law relationship in the frequency domain. The power‐law exponent (PLE) reported on the balance between slow and fast dynamics: a higher exponent indicated a tendency for slow dynamics and a lower exponent indicated a tendency for fast dynamics.
After projecting the PLEs from units to voxels, we mapped the distribution of the voxel‐wise PLE to characterize the dynamics of process memory (Hasson et al., 2015) at each cortical location. As shown in Figure 5, the PLE was lower in early visual areas but became increasingly larger along the downstream pathways in higher order visual areas. Such trend was similar to the gradient in TRWs (Figure 4b), where the TRWs were shorter in early visual areas and longer in higher order visual areas. In general, lower PLEs were associated with areas with shorter TRWs; higher PLEs were associated with areas with longer TRWs.
Figure 5.
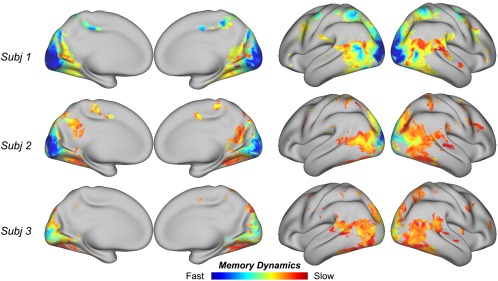
Model‐estimated memory dynamics in the visual cortex. Consistent across subjects, lower PLEs are associated early visual areas, and higher PLEs are associated with later stages of visual processing [Color figure can be viewed at http://wileyonlinelibrary.com]
We further evaluated the correlation (across voxels) between PLE and the improved encoding performance given RNN relative to CNN. The correlation was marginally significant (r = 0.16 ± 0.04, p = .04), suggesting a weak tendency that RNN better explained cortical responses at the voxels with relatively slower dynamics.
3.5. RNN revealed the cortical hierarchy of spatiotemporal processing
CNNs revealed the hierarchical organization of spatial processing in the visual cortex (Eickenberg et al., 2017; Güçlü & van Gerven, 2015a; Horikawa & Kamitani, 2017; Wen et al., 2017a). By using the RNN as a network model for spatiotemporal processing, we further mapped the hierarchical cortical organization of spatiotemporal processing. To do so, every voxel, where the response was predictable by the RNN, was assigned with an index, ranging continuously between 1 and 4. This index reported the “level” that a voxel was involved in the visual hierarchy: a lower index implied an earlier stage of processing; a higher index implied a later stage of processing. The topography of the voxel‐wise level index showed a cortical hierarchy (Figure 6). Locations from striate to extrastriate areas were progressively involved in early to late stages of processing the information in both space and time.
Figure 6.
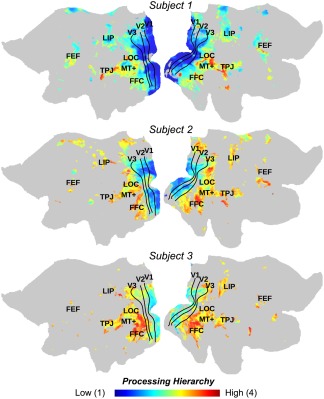
Model‐estimated hierarchical organization of spatiotemporal processing. Consistent across subjects, lower layer indices are assigned to early visual areas and higher layer indices are assigned to later stages of visual processing. The color bar indicates the range of layer assignment, from layer 1 to 4 [Color figure can be viewed at http://wileyonlinelibrary.com]
4. DISCUSSION
Here, we designed and trained a recurrent neural net (RNN) to learn video representations for action recognition, and to predict cortical responses to natural movies. This RNN extended from a pretrained CNN by adding layer‐wise recurrent connections to allow visual information to be remembered and accumulated over time. In line with the hypothesis of process memory (Hasson et al., 2015), such recurrent connections formed a hierarchical and distributed model of memory as an integral part of the network for processing dynamic and natural visual input. Compared to the CNN, the RNN supported both image and action recognition, and better predicted cortical responses to natural movie stimuli at all visual areas, especially those along the dorsal stream. More importantly, the RNN provided a fully observable computational model to characterize and map temporal receptive windows, dynamics of process memory, and a cortical representational hierarchy for dynamic natural vision.
4.1. A network model of process memory
Our work was in part inspired by the notion of “process memory” (Hasson et al., 2015). In this notion, memory is a continuous and distributed process as an integral part of information processing, as opposed to an encapsulated functional module separate from the neural circuits that process sensory information. Process memory provides a mechanism for the cortex to process the temporal information in natural stimuli, in a similarly hierarchical way as cortical processing of spatial information (Hasson et al., 2015). As explored in this study, the RNN uses an explicit model of process memory to account for dynamic interactions between incoming stimuli and the internal states of the neural network, or the state‐dependent computation (Buonomano & Maass, 2009). In the RNN, the “forget gate” controls, separately for each unit in the network, how much its next state depends on the incoming stimuli versus its current state. As such, the forget gate behaves as a switch of process memory to control how much new information should be stored into memory and how much history information should be retrieved from memory. This switch varies moment to moment, allowing memory storage and retrieval to occur simultaneously and continuously.
As demonstrated in this study, this model of process memory could be trained, with supervised learning, for the RNN to classify videos into action categories with a much higher accuracy than the CNN without any mechanism for temporal processing. It suggests that integrating process memory to a network of spatial processing indeed makes the network to be capable of spatiotemporal processing, as implied in previous theoretical work (Buonomano & Maass, 2009).
4.2. From theoretical modeling to empirical evidence of process memory
A unique contribution of this study is that computational modeling of process memory is able to explain previous empirical evidence for process memory. One of the strongest evidence for process memory is that the cortex organizes a topography of temporal receptive window (Hasson et al., 2008; Honey et al., 2012), which may be interpreted as the voxel‐wise capacity of process memory. To probe the TRW, an experimental approach is to scramble the temporal structure of natural stimuli in multiple timescales and measure their resulting effects on cortical responses (Hasson et al., 2008). The TRW measured in this way increases orderly from early sensory areas to higher order perceptual or cognitive areas (Hasson et al., 2015), suggesting a hierarchical organization of temporal processing. With this approach, the brain is viewed as a “black box” and is studied by examining its output given controlled perturbations to its input.
In this study, we have reproduced the hierarchically organized TRW by using a model‐driven approach. The RNN tries to model the inner working of the visual cortex as a computable system, such that the system's output can be computed from its input. If the model uses the same computational and organizational principles as does the brain itself, the model's output should match the brain's response given the same input (Naselaris et al., 2011; Wu, David, & Gallant, 2006). By “matching,” we do not mean that the unit activity in the model should match the voxel response in the brain with one‐to‐one correspondence, but up to linear transform (Yamins & Di Carlo, 2016) because it is unrealistic to exactly model the brain. This approach allows us to test computational models against experimental findings. The fact that the model of process memory explains the topography of TRW (i.e., the hallmark evidence for process memory) lends synergistic support to process memory as a fundamental principle for spatiotemporal processing of natural visual stimuli.
4.3. RNN extends CNN as both a brain model and an AI
Several recent studies explored deep‐learning models as predictive models of cortical responses during natural vision (Cichy et al., 2016; Eickenberg, et al., 2017; Güçlü & van Gerven, 2015a, 2015b; Horikawa & Kamitani, 2017; Khaligh‐Razavi & Kriegeskorte, 2014; Wen et al., 2017a, 2017b, 2017c; Yamins et al., 2014). Most of the prior studies used CNNs that extracted spatial features to support image recognition, and demonstrated the CNN as a good model for the feedforward process along the ventral visual stream (Eickenberg, et al., 2017; Güçlü & van Gerven, 2015a; Khaligh‐Razavi & Kriegeskorte, 2014; Yamins et al., 2014). In our recent study (Wen et al., 2017a), the CNN was further found to be able to partially explain the dorsal‐stream activity in humans watching natural movies; however, the predictive power of the CNN was lesser in the dorsal stream than in the ventral stream. Indeed, the dorsal stream is known for its functional roles in temporal processing and action recognition in vision (Goodale & Milner, 1992; Rizzolatti & Matelli, 2003; Shmuelof & Zohary, 2005). It is thus expected that the limited ability of the CNN for explaining the dorsal‐stream activity is due to its lack of any mechanism for temporal processing.
Extending from the CNN, the RNN established in this study offered a network mechanism for temporal processing, and improved the performance in action recognition. Along with this enhanced performance toward humans’ perceptual ability, the RNN also better explained human brain activity than did the CNN (Figure 2). The improvement was more apparent in areas along the dorsal stream than those along the ventral stream (Figure 2). It is worth noting that when the input is an image rather than a video, the RNN behaves as the CNN to support image classification. In other words, the RNN extends the CNN to learn a new ability (i.e., action recognition) without losing the already learned ability (i.e. image recognition). On the other hand, the RNN, as a model of the visual cortex, improves its ability in predicting brain activity not only at areas where the CNN falls short (i.e., dorsal stream), but also at areas where the CNN excels (i.e., ventral stream). As shown in this study, the RNN better explained the dorsal stream, without losing the already established ability to explain the ventral stream (Figure 2).
This brings us to a perspective about developing brain models or brain‐inspired AI systems. As humans continuously learn from experiences to support different intelligent behaviors, it is desirable for an AI model to continuously learn to expand capabilities while keeping existing capabilities. When it is also taken as a model of the brain, this AI model should be increasingly more predictive of brain responses at new areas, while remaining its predictive power at areas where the model already predicts well. This perspective is arguably valuable for designing a brain‐inspired system for continuous learning as does the brain itself.
Our finding that RNN outperformed CNN in explaining cortical responses most notably in the dorsal stream might also be due to the fact that the RNN was trained for action recognition. In fact, action recognition is commonly associated with dorsal visual areas, whereas object recognition is associated with ventral visual areas (Yoon, Humphreys, Kumar, & Rotshtein, 2012). As a side exploration in this study, we also used a meta‐analysis tool (http://neuronsynth.org) to map the cortical activations with visual action related tasks primarily in supramarginal gyrus, pre‐/post‐central sulcus, intraparietal sulcus, superior parietal gyrus, and inferior frontal gyrus. Such areas overlapped with where we found significantly greater encoding performance with RNN than with CNN. However, this overlap should not be simply taken as the evidence that the better model prediction is due to the goal of action recognition, instead of the model's memory mechanism. The memory mechanism supports the action recognition; the action recognition allows the mechanism to be parameterized through model training. As such, the goal and the mechanism are tightly interconnected aspects of the model. Further insights await future studies.
4.4. Comparison with related prior work
Other than RNN, a three‐dimensional (3‐D) CNN may also learn spatiotemporal features for action recognition of videos (Tran et al., 2015). A 3‐D CNN shares the same computational principle as an otherwise 2‐D CNN, except that the input to the former is a time series of video frames with a specific duration, whereas the input to the latter is a single video frame or image. Previously, the 3‐D CNN was shown to explain cortical fMRI responses to natural movie stimuli (Güçlü & van Gerven, 2015b). However, it is unlikely that the brain works in a similar way as a 3‐D CNN. The brain processes visual information continuously delivered from 2‐D retinal input, rather than processing time blocks of 3‐D visual input as required for 3‐D CNN. Although it is a valid AI model, 3‐D CNN is not appropriate for modeling or understanding the brain's mechanism of dynamic natural vision.
It is worth noting that the fundamental difference between the RNN model in this study and that in a recently published study (Güçlü & van Gerven, 2017). Here, we used the RNN as a feature model or the model of the visual cortex, whereas Güçlü and van Gerven used the RNN as the response model in an attempt to better describe the complex relationships between the CNN and the brain. Although a complex response model is potentially useful, it defeats our purpose of seeking a computational model that matches the visual cortex up to linear transform. It has been our intention to find a model that shares similar computing and organization principles as the brain. Toward this goal, the response model needs to be as simple as possible, independent of the visual input, and with canonical or independently defined HRF.
4.5. Future directions
The focus of this study is on vision. However, the RNN is expected to be useful, or even more useful, for modeling other perceptual or cognitive systems beyond vision. RNNs have been successful in computer vision (Donahue et al., 2015), natural language processing (Hinton et al., 2012; Mikolov, Karafiát, Burget, Cernocký, & Khudanpur, 2010), attention (Mnih et al., 2014; Sharma, Kiros, & Salakhutdinov, 2015; Xu et al., 2015), memory (Graves, Wayne, & Danihelka, 2014), and planning (Zaremba & Sutskever, 2015). It is conceivable that such RNNs would set a good starting point to model the corresponding neural systems, to facilitate the understanding of the network basis of complex perceptual or cognitive functions.
The RNN offers a computational account of temporal processing. If the brain performs similar computation, how is it implemented? The biological implementation of recurrent processing may be based on lateral or feedback connections (Kafaligonul, Breitmeyer, & Öğmen, 2015; Lamme, Super, & Spekreijse, 1998). The latter is of particular interest, since the brain has abundant feedback connections to exert top–down control of feedforward processes (de Fockert, Rees, Frith, & Lavie, 2001; Itti, Koch, & Niebur, 1998). However, the feedback connections are not taken into account in this study, but may be incorporated into the models in the future by using such brain principles as predictive coding (Rao & Ballard, 1999) or the free‐energy principle (Friston, 2010). Recent efforts along this line are promising (Canziani & Culurciello, 2017; Lotter, Kreiman, & Cox, 2016) to merit further investigation.
Supporting information
Additional Supporting Information may be found online in the supporting information tab for this article.
Supporting Information Figure S1
Supporting Information Figure S2
ACKNOWLEDGMENTS
This work was supported in part by NIH R01MH104402. The authors would like to recognize the inputs from Dr Eugenio Culurciello on the discussions of deep neural networks. The authors have no conflict of interest.
APPENDIX 1. THE FULL LIST OF ACTION CATEGORIES IN UCF101 DATASET
Apply eye makeup, apply lipstick, archery, baby crawling, balance beam, band marching, baseball pitch, basketball shooting, basketball dunk, bench press, biking, billiards shot, blow dry hair, blowing candles, body weight squats, bowling, boxing punching bag, boxing speed bag, breaststroke, brushing teeth, clean and jerk, cliff diving, cricket bowling, cricket shot, cutting in kitchen, diving, drumming, fencing, field hockey penalty, floor gymnastics, Frisbee catch, front crawl, golf swing, haircut, hammer throw, hammering, handstand pushups, handstand walking, head massage, high jump, horse race, horse riding, hula hoop, ice dancing, javelin throw, juggling balls, jump rope, jumping jack, kayaking, knitting, long jump, lunges, military parade, mixing batter, mopping floor, nun chucks, parallel bars, pizza tossing, playing guitar, playing piano, playing tabla, playing violin, playing cello, playing Daf, playing dhol, playing flute, playing sitar, pole vault, pommel horse, pull ups, punch, push‐ups, rafting, rock climbing indoor, rope climbing, rowing, salsa spins, shaving beard, shot put, skate boarding, skiing, skijet, sky diving, soccer juggling, soccer penalty, still rings, sumo wrestling, surfing, swing, table tennis shot, tai chi, tennis swing, throw discus, trampoline jumping, typing, uneven bars, volleyball spiking, walking with a dog, wall pushups, writing on board, and yo yo.
Shi J, Wen H, Zhang Y, Han K, Liu Z. Deep recurrent neural network reveals a hierarchy of process memory during dynamic natural vision. Hum Brain Mapp. 2018;39:2269–2282. 10.1002/hbm.24006
Funding information National Institute of Mental Health, Grant/Award Number: R01MH104402
REFERENCES
- Adolf, D. , Weston, S. , Baecke, S. , Luchtmann, M. , Bernarding, J. , & Kropf, S. (2014). Increasing the reliability of data analysis of functional magnetic resonance imaging by applying a new blockwise permutation method. Frontiers in Neuroinformatics, 8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ballas, N. , Yao, L. , Pal, C. , & Courville, A. (2015). Delving deeper into convolutional networks for learning video representations. arXiv, 1511.06432. [Google Scholar]
- Boureau, Y.‐L. , Ponce, J. , & LeCun, Y. (2010). A theoretical analysis of feature pooling in visual recognition. Paper presented at the Proceedings of the 27th international conference on machine learning (ICML‐10).
- Buonomano, D. V. , & Maass, W. (2009). State‐dependent computations: Spatiotemporal processing in cortical networks. Nature Reviews. Neuroscience, 10(2), 113. [DOI] [PubMed] [Google Scholar]
- Buxton, R. B. , Uludağ, K. , Dubowitz, D. J. , & Liu, T. T. (2004). Modeling the hemodynamic response to brain activation. NeuroImage, 23, S220–S233. [DOI] [PubMed] [Google Scholar]
- Canziani, A. , & Culurciello, E. (2015). Visual attention with deep neural networks. Paper presented at the Information Sciences and Systems (CISS), 2015 49th Annual Conference on.
- Canziani, A. , & Culurciello, E. (2017). CortexNet: A generic network family for robust visual temporal representations. arXiv, 1706.02735. [Google Scholar]
- Cichy, R. M. , Khosla, A. , Pantazis, D. , Torralba, A. , & Oliva, A. (2016). Comparison of deep neural networks to spatio‐temporal cortical dynamics of human visual object recognition reveals hierarchical correspondence. Scientific Reports, 6, 27755. [DOI] [PMC free article] [PubMed] [Google Scholar]
- de Fockert, J. W. , Rees, G. , Frith, C. D. , & Lavie, N. (2001). The role of working memory in visual selective attention. Science, 291(5509), 1803–1806. [DOI] [PubMed] [Google Scholar]
- Donahue, J. , Anne Hendricks, L. , Guadarrama, S. , Rohrbach, M. , Venugopalan, S. , Saenko, K. , & Darrell, T. (2015). Long‐term recurrent convolutional networks for visual recognition and description. Paper presented at the Proceedings of the IEEE conference on computer vision and pattern recognition. [DOI] [PubMed]
- Eickenberg, M. , Gramfort, A. , Varoquaux, G. , & Thirion, B. (2017). Seeing it all: Convolutional network layers map the function of the human visual system. NeuroImage, 152, 184–194. [DOI] [PubMed] [Google Scholar]
- Fragkiadaki, K. , Levine, S. , Felsen, P. , & Malik, J. (2015). Recurrent network models for human dynamics. Paper presented at the Proceedings of the IEEE International Conference on Computer Vision.
- Friston, K. (2010). The free‐energy principle: A unified brain theory? Nature Reviews. Neuroscience, 11(2), 127–138. [DOI] [PubMed] [Google Scholar]
- Glasser, M. F. , Coalson, T. S. , Robinson, E. C. , Hacker, C. D. , Harwell, J. , Yacoub, E. , … Jenkinson, M. (2016). A multi‐modal parcellation of human cerebral cortex. Nature, 536(7615), 171–178. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Glasser, M. F. , Sotiropoulos, S. N. , Wilson, J. A. , Coalson, T. S. , Fischl, B. , Andersson, J. L. , … Jenkinson, M. (2013). The minimal preprocessing pipelines for the Human Connectome Project. NeuroImage, 80, 105–124. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Goodale, M. A. , & Milner, A. D. (1992). Separate visual pathways for perception and action. Trends in Neurosciences, 15(1), 20–25. [DOI] [PubMed] [Google Scholar]
- Goodfellow, I. , Bengio, Y. , & Courville, A. (2016). Deep learning. MIT Press. [Google Scholar]
- Graves, A. , Wayne, G. , & Danihelka, I. (2014). Neural turing machines. arXiv, 1410.5401. [Google Scholar]
- Greff, K. , Srivastava, R. K. , Koutník, J. , Steunebrink, B. R. , & Schmidhuber, J. (2016). LSTM: A search space odyssey. IEEE Transactions on Neural Networks and Learning Systems. [DOI] [PubMed] [Google Scholar]
- Güçlü, U. , & van Gerven, M. A. (2015a). Deep neural networks reveal a gradient in the complexity of neural representations across the ventral stream. Journal of Neuroscience, 35(27), 10005–10014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Güçlü, U. , & van Gerven, M. A. (2015b). Increasingly complex representations of natural movies across the dorsal stream are shared between subjects. NeuroImage. [DOI] [PubMed] [Google Scholar]
- Güçlü, U. , & van Gerven, M. A. (2017). Modeling the dynamics of human brain activity with recurrent neural networks. Frontiers in Computational Neuroscience, 11. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hasson, U. , Chen, J. , & Honey, C. J. (2015). Hierarchical process memory: Memory as an integral component of information processing. Trends in Cognitive Sciences, 19(6), 304–313. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hasson, U. , Yang, E. , Vallines, I. , Heeger, D. J. , & Rubin, N. (2008). A hierarchy of temporal receptive windows in human cortex. Journal of Neuroscience, 28(10), 2539–2550. [DOI] [PMC free article] [PubMed] [Google Scholar]
- He, K. , Zhang, X. , Ren, S. , & Sun, J. (2015). Delving deep into rectifiers: Surpassing human‐level performance on imagenet classification. Paper presented at the Proceedings of the IEEE international conference on computer vision.
- Hinton, G. , Deng, L. , Yu, D. , Dahl, G. , Mohamed, A‐R. , Jaitly, N. , … Kingsbury, B. (2012). Deep neural networks for acoustic modeling in speech recognition: The shared views of four research groups. IEEE Signal Processing Magazine, 29(6), 82–97. [Google Scholar]
- Honey, C. J. , Thesen, T. HOMAS. , Donner, T. OBIAS H. , Silbert, L. AUREN J. , Carlson, C. HAD E. , Devinsky, O. RRIN. , … Hasson, U. RI. (2012). Slow cortical dynamics and the accumulation of information over long timescales. Neuron, 76(2), 423–434. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Horikawa, T. , & Kamitani, Y. (2017). Generic decoding of seen and imagined objects using hierarchical visual features. Nature Communications, 8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hubel, D. H. , & Wiesel, T. N. (1968). Receptive fields and functional architecture of monkey striate cortex. The Journal of Physiology, 195(1), 215–243. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Itti, L. , Koch, C. , & Niebur, E. (1998). A model of saliency‐based visual attention for rapid scene analysis. IEEE Transactions on Pattern Analysis and Machine Intelligence, 20(11), 1254–1259. [Google Scholar]
- Jozefowicz, R. , Zaremba, W. , & Sutskever, I. (2015). An empirical exploration of recurrent network architectures. Paper presented at the Proceedings of the 32nd International Conference on Machine Learning (ICML‐15).
- Kafaligonul, H. , Breitmeyer, B. G. , & Öğmen, H. (2015). Feedforward and feedback processes in vision. Frontiers in Psychology, 6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kay, K. N. , Winawer, J. , Mezer, A. , & Wandell, B. A. (2013). Compressive spatial summation in human visual cortex. Journal of Neurophysiology, 110(2), 481–494. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Khaligh‐Razavi, S.‐M. , Henriksson, L. , Kay, K. , & Kriegeskorte, N. (2017). Fixed versus mixed RSA: Explaining visual representations by fixed and mixed feature sets from shallow and deep computational models. Journal of Mathematical Psychology, 76, 184–197. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Khaligh‐Razavi, S.‐M. , & Kriegeskorte, N. (2014). Deep supervised, but not unsupervised, models may explain IT cortical representation. PLoS Computational Biology, 10(11), e1003915. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kingma, D. , & Ba, J. (2014). Adam: A method for stochastic optimization. arXiv, 1412.6980. [Google Scholar]
- Kriegeskorte, N. (2015). Deep neural networks: A new framework for modeling biological vision and brain information processing. Annual Review of Vision Science, 1(1), 417–446. [DOI] [PubMed] [Google Scholar]
- Lamme, V. A. , Super, H. , & Spekreijse, H. (1998). Feedforward, horizontal, and feedback processing in the visual cortex. Current Opinion in Neurobiology, 8(4), 529–535. [DOI] [PubMed] [Google Scholar]
- LeCun, Y. , Bengio, Y. , & Hinton, G. (2015). Deep learning. Nature, 521(7553), 436–444. [DOI] [PubMed] [Google Scholar]
- Lotter, W. , Kreiman, G. , & Cox, D. (2016). Deep predictive coding networks for video prediction and unsupervised learning. arXiv, 1605.08104. [Google Scholar]
- Mikolov, T. , Karafiát, M. , Burget, L. , Cernocký, J. , & Khudanpur, S. (2010). Recurrent neural network based language model. Paper presented at the Interspeech.
- Miller, K. J. , Sorensen, L. B. , Ojemann, J. G. , & Den Nijs, M. (2009). Power‐law scaling in the brain surface electric potential. PLoS Computational Biology, 5(12), e1000609. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mnih, V. , Heess, N. , & Graves, A. (2014). Recurrent models of visual attention. Paper presented at the Advances in neural information processing systems.
- MNIH, V. OLODYMYR., KAVUKCUOGLU, K. ORAY., SILVER, D. AVID., RUSU, ANDREIA., VENESS, J. OEL., BELLEMARE, MARCG., … HASSABIS, D. EMIS. (2015). Human‐level control through deep reinforcement learning. Nature, 518(7540), 529–533. [DOI] [PubMed] [Google Scholar]
- Nair, V. , & Hinton, G. E. (2010). Rectified linear units improve restricted boltzmann machines. Paper presented at the Proceedings of the 27th international conference on machine learning (ICML‐10).
- Naselaris, T. , Kay, K. N. , Nishimoto, S. , & Gallant, J. L. (2011). Encoding and decoding in fMRI. NeuroImage, 56(2), 400–410. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nili, H. , Wingfield, C. , Walther, A. , Su, L. , Marslen‐Wilson, W. , & Kriegeskorte, N. (2014). A toolbox for representational similarity analysis. PLoS Computational Biology, 10(4), e1003553. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pascanu, R. , Mikolov, T. , & Bengio, Y. (2013). On the difficulty of training recurrent neural networks. Paper presented at the International Conference on Machine Learning.
- Rao, R. P. , & Ballard, D. H. (1999). Predictive coding in the visual cortex: A functional interpretation of some extra‐classical receptive‐field effects. Nature Neuroscience, 2(1), 79. [DOI] [PubMed] [Google Scholar]
- Rizzolatti, G. , & Matelli, M. (2003). Two different streams form the dorsal visual system: Anatomy and functions. Experimental Brain Research, 153(2), 146–157. [DOI] [PubMed] [Google Scholar]
- Russakovsky, O. LGA. , Deng, J. IA. , Su, H. AO. , Krause, J. ONATHAN. , Satheesh, S. ANJEEV. , Ma, S. EAN. , … Fei‐Fei, L. I. (2015). Imagenet large scale visual recognition challenge. International Journal of Computer Vision, 115(3), 211–252. [Google Scholar]
- Sharma, S. , Kiros, R. , & Salakhutdinov, R. (2015). Action recognition using visual attention. arXiv, 1511.04119. [Google Scholar]
- Shmuelof, L. , & Zohary, E. (2005). Dissociation between ventral and dorsal fMRI activation during object and action recognition. Neuron, 47(3), 457–470. [DOI] [PubMed] [Google Scholar]
- Silver, D. AVID. , Huang, A. JA. , Maddison, ChrisJ. , Guez, A. RTHUR. , Sifre, L. AURENT. , van den Driessche, G. EORGE. , … Hassabis, D. EMIS. (2016). Mastering the game of Go with deep neural networks and tree search. Nature, 529(7587), 484–489. [DOI] [PubMed] [Google Scholar]
- Simonyan, K. , & Zisserman, A. (2014). Very deep convolutional networks for large‐scale image recognition. arXiv, 1409.1556. [Google Scholar]
- Soomro, K. , Zamir, A. R. , & Shah, M. (2012). UCF101: A dataset of 101 human actions classes from videos in the wild. arXiv, 1212.0402. [Google Scholar]
- Tran, D. , Bourdev, L. , Fergus, R. , Torresani, L. , & Paluri, M. (2015). Learning spatiotemporal features with 3d convolutional networks. In Proceedings of the IEEE international conference on computer vision (pp. 4489–4497).
- Wandell, B. A. , Dumoulin, S. O. , & Brewer, A. A. (2007). Visual field maps in human cortex. Neuron, 56(2), 366–383. [DOI] [PubMed] [Google Scholar]
- Wen, H. , & Liu, Z. (2016). Separating fractal and oscillatory components in the power spectrum of neurophysiological signal. Brain Topography, 29(1), 13–26. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wen, H. , Shi, J. , Zhang, Y. , Lu, K.‐H. , Cao, J. , & Liu, Z. (2017a). Neural encoding and decoding with deep learning for dynamic natural vision. Cerebral Cortex, doi: 10.1093/cercor/bhx268. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wen, H. , Shi, J. , Chen, W. , & Liu, Z. (2017b). Deep residual network reveals a nested hierarchy of distributed cortical representation for visual categorization. bioRxiv, 151142. [Google Scholar]
- Wen, H. , Shi, J. , Chen, W. , & Liu, Z. (2017c). Transferring and generalizing deep‐learning‐based neural encoding models across subjects. bioRxiv, 171017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Werbos, P. J. (1990). Backpropagation through time: What it does and how to do it. Proceedings of the IEEE, 78(10), 1550–1560. [Google Scholar]
- Wu, M. C. K. , David, S. V. , & Gallant, J. L. (2006). Complete functional characterization of sensory neurons by system identification. Annual Review of Neuroscience, 29, 477–505. [DOI] [PubMed] [Google Scholar]
- Xu, K. , Ba, J. , Kiros, R. , Cho, K. , Courville, A. , Salakhudinov, R. , … Bengio, Y. (2015). Show, attend and tell: Neural image caption generation with visual attention. Paper presented at the International Conference on Machine Learning.
- Yamins, D. L. , & Di Carlo, J. J. (2016). Using goal‐driven deep learning models to understand sensory cortex. Nature Neuroscience, 19(3), 356. [DOI] [PubMed] [Google Scholar]
- Yamins, D. L. , Hong, H. , Cadieu, C. F. , Solomon, E. A. , Seibert, D. , & Di Carlo, J. J. (2014). Performance‐optimized hierarchical models predict neural responses in higher visual cortex. Proceedings of the National Academy of Sciences, 111(23), 8619–8624. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yoon, E. Y. , Humphreys, G. W. , Kumar, S. , & Rotshtein, P. (2012). The neural selection and integration of actions and objects: An fMRI study. Journal of Cognitive Neuroscience, 24(11), 2268–2279. [DOI] [PubMed] [Google Scholar]
- Zaremba, W. , & Sutskever, I. (2015). Reinforcement learning neural turing machines. arXiv, 1505.00521, 419. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Additional Supporting Information may be found online in the supporting information tab for this article.
Supporting Information Figure S1
Supporting Information Figure S2


