Abstract
Cracks in articular cartilage are a common sign of joint damage, but failure properties of cartilage are poorly understood, especially for damage initiation. Cartilage failure may be further complicated by rate-dependent and depth-dependent properties, including the compliant surface layer. Existing blunt impact methods do not resolve local cartilage inhomogeneities and traditional fracture mechanics tests induce crack blunting and may violate underlying assumptions of linear elasticity. To address this knowledge gap, we developed and applied a method to indent cartilage explants with a sharp blade and initiate damage across a range of loading rates (strain rates 0.5%/s to 500%/s), while recording local sample deformation and strain energy fields using confocal elastography. To investigate the importance of cartilage’s compliant surface, we repeated the experiment for samples with the surface removed. Bulk data suggest a critical force at which the tissue cuts, but local strains reveals that the deformation the sample can sustain before reaching this force is significantly higher in the surface layer. Bulk and local results also showed significant rate dependence, such that samples were easier to cut at faster speeds. This result highlights the importance of rate for understanding cracks in cartilage and parallels recent studies of rate-dependent failure in hydrogels. Notably, local sample deformation fields were well fit by classical Hookean elasticity. Overall, this study illustrates how local and global measurements surrounding the initiation of damage in articular cartilage can be combined to reveal the importance of cartilage’s zonal structure in protecting against failure across physiologically relevant loading rates.
Keywords: Injury, Toughness, Biomaterials, Strain rate, Osteoarthritis
1. Introduction
Cracks in articular cartilage are a common sign of joint damage. In clinical settings, fissures are often observed during arthroscopic inspection of an injured joint (Bauer and Jackson, 1988; Curl et al., 1997). Such injuries predispose patients to chronic joint damage and disease, including osteoarthritis (Brown et al., 2006). In orthopedics, clinicians and researchers acknowledge the importance of cracks by including them in various arthroscopy and histopathology grading schemes (Outerbridge, 1961; Pritzker et al., 2006). Basic science and engineering studies have also associated cartilage cracks with increased cell death and matrix degradation (Anderson et al., 2011; Lewis et al., 2003), suggesting they can disrupt the homeostasis that is essential for joint health. As such, cracks in cartilage have the potential to be an important early marker of cartilage damage and disease. However, beyond these basic observations, cartilage cracks are poorly understood and many questions must be answered before cracks can guide clinical decision-making.
One complication for studying cracks in cartilage is that cartilage is highly anisotropic and heterogeneous, with mechanical properties and composition that vary with depth. The superficial 100–300 μm of tissue, known as the surface layer, has lower compressive and shear moduli than the bulk (Buckley et al., 2010; Schinagl et al., 1997), which may be explained by variations in composition (Silverberg et al., 2014). Additionally, the collagen alignment varies with depth, where fibers near the surface are predominantly parallel to that surface with an additional in-plane alignment known as the split-line pattern (Below et al., 2002; Benninghoff, 1925; Roth and Mow, 1980). Recent results have further demonstrated that the surface layer may serve a mechanically protective role (Bartell et al., 2015; Buckley et al., 2013). Beyond variations in composition and alignment, cartilage has a complex rate-dependence from both viscoelastic and poroelastic effects (Mow et al., 1980). All of these factors may influence cartilage fracture and failure, but are difficult to disentangle without studying cartilage at spatial resolutions of around ten microns.
Experimentally, cartilage cracks are generally studied in two contexts: blunt overload or traditional fracture mechanics geometries, such as the notch test. In overload experiments, such as a drop-tower test, a blunt object rapidly and forcefully impacts cartilage (Argatov and Mishuris, 2015; Henak et al., 2016; Jeffrey et al., 1995, 1995; Repo and Finlay, 1977; Scott and Athanasiou, 2006; Waters et al., 2014). When this loading is faster than the poroelastic time scale, fluid is trapped and pressurizes, thus stressing the surrounding solid matrix, which ultimately ruptures (Morel and Quinn, 2004). This loading is analogous to physiologic injuries, but the geometry of the sample and loading both influence fluid pressurization and so the material properties are difficult to disentangle. Moreover, the exact location of crack initiation is unknown prior to loading, making it experimentally difficult to study local material behavior. In contrast, traditional fracture mechanics experiments apply standardized sample and loading geometries to articular cartilage that are designed to concentrate stress at a particular point, leading to material failure (Ahsan and Sah, 1999; Chin-Purcell and Lewis, 1996; Oyen-Tiesma and Cook, 2001; Taylor et al., 2012). By linking a specific geometry to linear elasticity, such data can be used to calculate material properties, such as toughness, which describes the ability to absorb energy without cracking. In soft tissues, however, finite strains may violate the assumptions of linear elasticity and it is unclear to what degree this affects the understanding of cartilage failure. Studies applying the well-known notch test to cartilage show the tissue failing by crack-blunting and plastic yielding rather than traditional brittle crack propagation, indicating that tissue microstructure inhibits the stress concentration necessary to propagate brittle-like cracks (Hui et al., 2003; Stok and Oloyede, 2007). Additionally, such methods study steady-state crack growth, rather than damage initiation, though the latter may be equally important physiologically. Thus, neither blunt overload nor traditional fracture tests are adequate to fully understand cracks in articular cartilage, especially damage initiation.
To address this knowledge gap, this study aimed to develop an indentation-based method to study damage initiation in articular cartilage. By indenting samples with a sharp blade, we created a crack at a known location, in a well-defined geometry, and with more stress-concentration than notch tests (Johnson, 1987). Moreover, because the crack location was known, we could utilize recently developed confocal elastography techniques to study both global and local material behavior and investigate the importance of material inhomogeneity and finite strains when interpreting damage initiation in cartilage. We further investigated how rate modulates the observed damage initiation by indenting over a wide range of loading rates. Combined, this method simultaneously observed the local, global and time-dependent processes that are potentially important to understanding damage initiation in articular cartilage.
2. Methods
1.1. Sample preparation
Chondral explants were harvested from condyles of 13 neonatal calves (sex unknown; Gold Medal Packing, Oriskany, NY) (Figure 1A). Explants were immersed in PBS and stored at 4°C for up to 48 h. For testing, explants were trimmed to 3 mm deep and bisected perpendicular or parallel to the known split-line direction (Silverberg et al., 2013), creating 125 hemi-cylindrical samples. In some samples, a sledge microtome was used to remove 500 μm from the articular surface, creating a surface-removed group. Information about each sample was recorded, including source animal, condyle (medial or lateral), orientation (parallel or perpendicular to split-line), time between dissection and testing, and surface condition (intact or removed).
Figure 1.
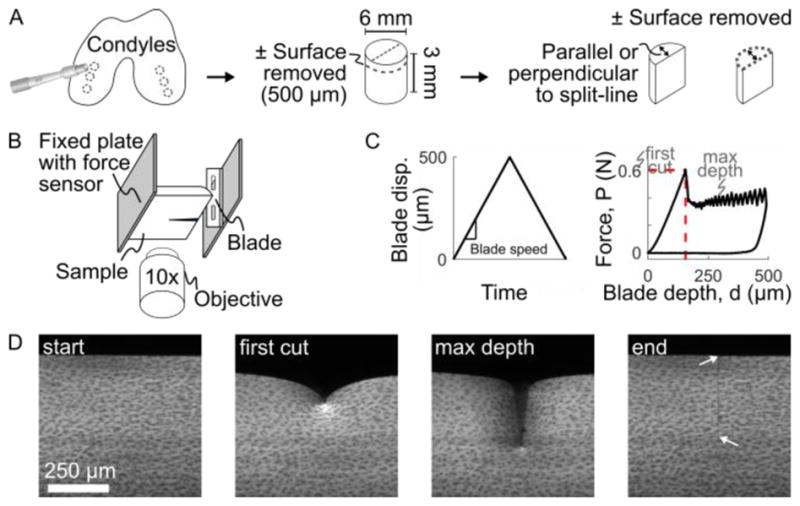
Outline of experimental methods. (A) Cylindrical plugs were harvested from medial and lateral condyles, trimmed to 3 mm deep, with the surface either intact or removed, and then bisected to create hemi-cylindrical samples. (B) Samples were mounted to the fixed plate of the test frame, with the cartilage surface facing the blade. The test frame was mounted on a confocal microscope to image local sample deformation. (C) The blade was driven into the sample at a fixed speed to a maximum displacement of 500 μm while the bulk force response was recorded at the fixed plate using a force sensor. A characteristic force-depth curve is shown with the point of first-cut marked by the dashed red lines. (D) Example confocal images taken throughout the experiment. At the end, after the blade has retracted, arrows mark the extent of the remaining crack. Note there is no residual deformation, indicating elastic deformation, other than the newly-created crack surface.
1.2. Indentation device
To test cartilage failure properties, a razor blade (#27-251, Razor Blade Company, Van Nuys, CA; ~150 nm tip diameter, Appendix A) was mounted to the piezoelectric-driven plate of a Tissue Deformation Imaging Stage (TDIS; Harrick Scientific, Ithaca, NY) and used to indent cartilage, thus creating cracks in a known location (Figure 1B,C). Samples were glued to the fixed plate of the TDIS, as described previously (Buckley et al., 2010). During indentation, force was measured using a 2 kg (19.6 N) load cell (S300, Strain Measurement Devices, Wallingford, CT) and blade displacement was recorded from the piezoelectric monitor. The blade was driven to 500 μm displacement and retracted at fixed speeds of 2.5 to 1000 μm/s. Each sample was immersed in PBS throughout testing and indented only once with a fresh blade.
The TDIS was mounted onto an inverted confocal microscope (LSM 5 LIVE, Carl Zeiss Inc., Oberkochen, Germany), to observe local sample deformation. For imaging contrast, samples were stained for 50 minutes in 14 μM 5-DTAF (Buckley et al., 2010). Videos of deformation during indentation were recorded at 15 to 60 frames per second, depending on blade speed, with a 512 pixel (666 μm) field of view (Figure 1D).
1.3. Data analysis
For each experiment, force (F) verses blade depth (d) plots were characterized. Force was smoothed using a moving-average filter with a window size of 1 μm blade displacement (scaled in time based on the blade speed). The blade depth was calculated as the blade displacement minus the slight displacement of back plate resulting from the strain-based load cell. The critical force, FC, and depth, dC, at first-cut were extracted, and the data were integrated up to this critical point to extract strain energy, WC. For these three responses (critical force, depth, and energy), mixed-effects linear regression models were implemented to test which parameters significantly affected each response (Appendix B).
Confocal videos were processed to extract local deformation and energy fields. Videos were analyzed from zero blade depth to just beyond the point of first cut using Ncorr (2D image correlation; widow size 19.7 μm, grid spacing 3.9 μm, smoothing radius 27.5 um; Blaber et al., 2015). Images were generally well tracked, except the area closest to the blade tip. When the first cut in the bulk response did not agree with that observed in the confocal video, likely due to misalignment, samples were excluded from local deformation analysis.
Deformation fields were used to compute local strain energy density. Strain energy was calculated by assuming a 2D neo-Hookean constitutive model with depth-dependent Lamé parameters taken from the literature (Schinagl et al., 1997; Silverberg et al., 2013). Local deformations were compared to the 2D functional form predicted by contact mechanics. According to Johnson (1987), line loading of a Hookean elastic half-space yields the radial displacement field:
| (1) |
where ur is the radial displacement, r is the radial distance from the applied load, θ is the circumferential direction (θ = 0 parallel to the applied load), ν and E are the Poisson’s ratio and Young’s modulus, P is the applied force per length, and r0 is a scaling constant. Thus, 2D displacement data for each sample were fit to:
| (2) |
using a nonlinear least-squares approach with fitting coefficients βi. Note that β2 incorporates both the scaling term r0 and any overall sample displacement resulting back plate displacement, α.
3. Results
Bulk indentation force-depth data showed similar behavior across all samples, including a smooth rise up to the point of first cut, followed by a dramatic drop and then a sawtooth-like pattern as the blade continued to cut (Figure 2A). The critical force, depth, and energy at first-cut were extracted and fit to linear mixed-effects models (Figure 2B–D). All three outcomes depended significantly on indentation rate (p = 2.6×10−5, 5.5×10−21, and 6.1×10−16 for critical force, depth, and energy, respectively). Moreover, the critical depth and energy were significantly lower for surface-removed samples (p = 1.2×10−29 and 1.7×10−4, respectively). Notably, no other terms were significant in the models.
Figure 2.
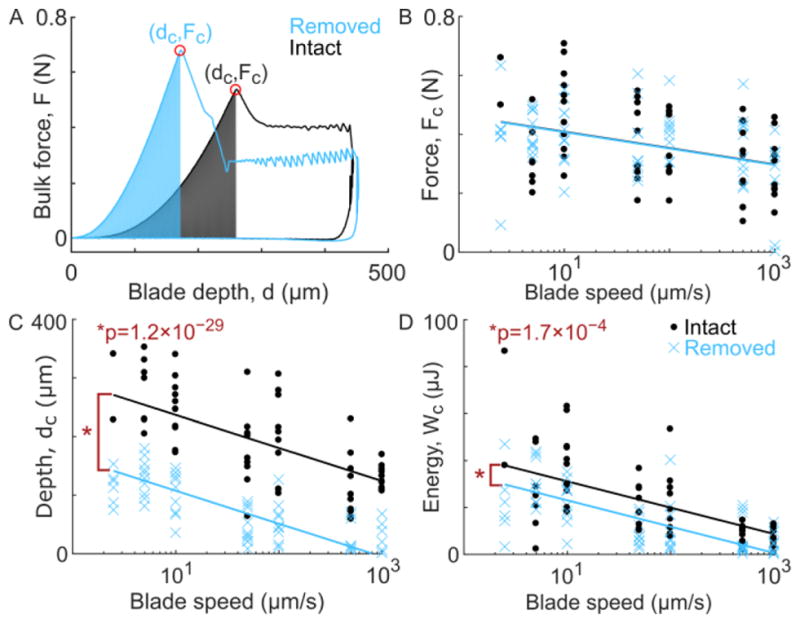
(A) Characteristic force vs. blade depth curves for one surface-intact and one surface-removed sample. Both samples were taken from the 10 μm/s blade speed group. For all samples, the force and depth at first cut (dC and FC, respectively) were extracted and the integration of force verses depth up to that point, a measure of strain energy (WC), was computed. (B–D) The force, depth, and energy at first cut for all experiments (circles or crosses), shown with the corresponding reduced linear model fits (solid lines), for surface-intact (black) and surface-removed (blue) samples. For all three measures, the response was significantly dependent on blade speed (p-values: 2.6×10−5, 5.5×10−21, and 6.1×10−16, respectively). Additionally, surface-removed samples had a lower critical cut depth and energy, as compared to surface-intact (p-values: 1.2×10−29 and 1.7×10−4, respectively). See Appendix B for full statistical models.
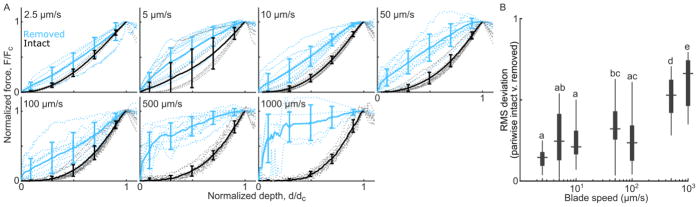
Normalizing each bulk force curve by the critical force and depth collapsed the data to reveal overall trends that varied with loading rate (Figure 3A). At slower blade speeds, surface-intact and -removed samples showed similar trends, including a slight “J”-shaped response. At higher blade speeds, the surface-removed samples showed a dramatic change in concavity, with a steep initial rise in the force response. For each blade speed, the difference between surface-intact and -removed trends was characterized by the root-mean-square (RMS) deviation between each pair of normalized force-depth curves (Figure 3B). This RMS deviation confirmed that intact and removed samples became increasingly distinct at faster indentation.
Figure 3.
(A) Force verses blade depth curves, up to the point of first-cut, normalized by the cut force and cut depth, and grouped by blade speed. Individual samples are shown in dotted lines and group averages +/− standard deviation are shown in solid lines. Surface-intact samples (gray curves) show characteristic “J”-shaped response. In the 2.5 μm/s group, surface-removed samples follow a similar trend. However, at higher speeds the surface-intact and -removed groups become increasingly distinct and, instead of a toe-region, surface-removed samples show a sharp initial rise. (B) A Tukey box plot of the RMS deviation between each pair of normalized force curves, as a function of blade speed. Groups that share a letter are not significantly different, confirming that the intact and removed samples become increasingly distinct (higher deviation) at faster speeds.
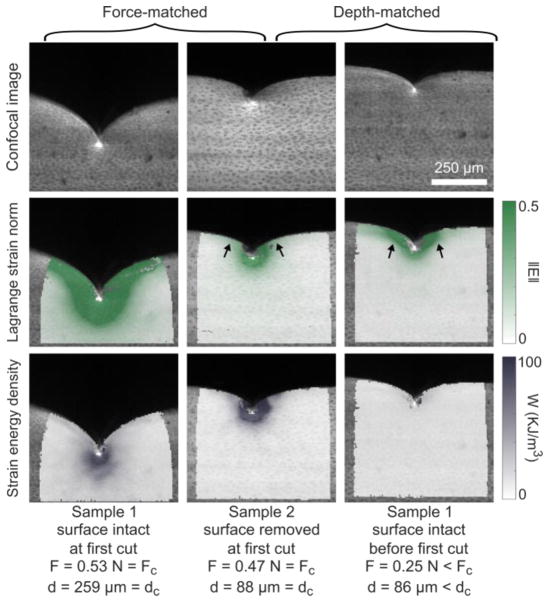
In addition to the bulk response, confocal videos were analyzed to extract local deformation fields and calculate strain energy density. Samples showed high strain and strain energy near the tip, though the shape and magnitude varied between groups. Figure 4 compares characteristic samples from the surface-intact and -removed groups at similar bulk force and again at similar blade depths. At first-cut, the strain was higher in magnitude and spread over a larger region of the surface-intact sample. The strain energy density fields looked more similar between the groups. Comparing the samples at matched-depth instead, the surface intact sample still showed more lateral spread of strain across the compliant articular surface (arrows), while the strain energy density field was much lower in magnitude.
Figure 4.
Local deformation analysis for strain and strain energy density. Columns 1–2 compare one surface-removed and one surface-intact sample at first cut, i.e. with similar bulk force. Alternatively, columns 2–3 compare the same two samples, but at similar blade depths (i.e. prior to the first cut for the surface-intact sample). Row 1 shows the raw confocal images, row 2 shows the resulting Lagarange strain norm, and row 3 shows the corresponding strain energy density. Note that both strain and strain energy are in deformed coordinates. In the force-controlled comparison, strain fields are distinct between surface-intact and -removed, but the strain energy fields are more similar. The opposite is true (similar strain but distinct strain energy) for the depth-controlled comparison. Arrows highlight differences in how the strain field spreads across the surface layer.
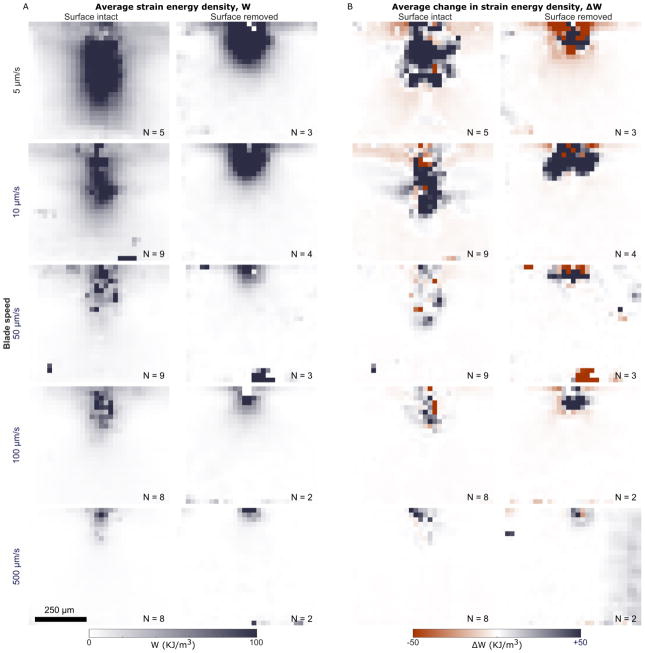
To characterize overall trends, strain energy density fields were grouped by surface condition and indentation rate, and averaged (Figure 5A). The 2.5 and 1000 μm/s groups only had one sample each and thus were excluded. Two trends were apparent from these plots. First, the magnitude of the strain energy decreased with increasing blade speed, in agreement with the bulk results (Figure 2D). Second, strain energy fields in surface-intact samples were more oblong, extending farther both along the surface and deeper into the tissue, while surface-removed fields were more radially symmetric (Appendix C). Figure 5B shows the average change in strain energy density before and after first cut, when the blade had moved 20 μm further. These ΔW fields highlight where strain energy was lost to create the resulting initial cut (ΔW<0), and where additional strain energy was gained as the blade advanced (ΔW>0). These ΔW fields decreased in spatial extent with increasing rate.
Figure 5.
(A) Average strain energy density fields at first cut, grouped by surface condition (columns) and blade speed (rows), in undeformed coordinates, where the top-center of each frame corresponds to the point of blade indentation. In general, the surface-intact strain energy field is more oblong, extending deeper into the sample and laterally along the surface, while the surface-intact strain energy field is more radially symmetric about the point of indentation. In both surface-intact and surface-removed groups, the strain energy density decreases as blade speed increases, in agreement with the bulk results. (B) Similar plots of the average change in strain energy density from just before the point of first cut to a few frames after, when the blade has moved 20 μm further. Note that some areas of the field have decreased strain energy (i.e. negative ΔW) while others have increased (i.e. positive ΔW). As in the strain energy fields shown in (A), the overall extent of ΔW fields also decreases with increased blade speed. Numbers (N) at the bottom of each frame indicate the number of samples averaged to produce the given field. The scale bar applies to all frames.
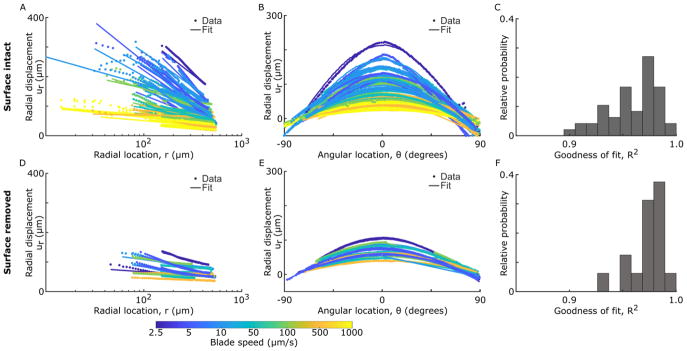
Displacement fields were fit to the form predicted by contact mechanics. Figure 6 shows cuts of the raw data and associated 2D fits to Equation 2 for constant θ and varying r (A,D) and for constant r and varying θ (B,E). For all samples, βi coefficients fell in the in the expected range, given values of ν and E taken from the literature and FC taken from this study (Appendix D). Despite assumptions of small-strain Hookean elasticity and infinite boundaries, these fits recapitulated the overall trends with coefficients of determination greater than 0.9 in all cases (R2, Figure 6C,F). In fact, the surface-intact samples tended to have lower R2, since the data deviated more from the fit at smaller values of r and was more sharply peaked in θ. This observation is not surprising, considering that the model assumes homogeneous material properties and the surface-intact samples have a mechanically-distinct surface layer.
Figure 6.
Cuts of the 2D displacement data and associated 2D fits to the functional form predicted by contact mechanics (Equation 2). Data and fits are shown for (A–C) surface-intact samples and (D–F) surface-removed samples, with cuts taken (A,D) at θ = 0° and (B,E) at r = 300 μm. Color reflects blade speed. (C,F) Associated histograms of the goodness of fit (coefficient of determination) for each fit. In general, this equation fits the data well (R2>0.9), though there are larger deviations at small values of r and, for surface-intact samples, the data’s trend with θ is more sharply peaked. See Appendix D for data and fits normalized by the fitting parameters.
4. Discussion
Our blade indentation experiments with confocal elastography revealed strong rate dependence in both bulk and local results, such that samples were easier to cut at faster speeds. As rate increased, the first-cut occurred at lower force, lower blade depth, lower energy, more localized strain field, and smaller radial displacement (Figure 2, Figure 5, Figure 6). Moreover, in surface-removed samples, normalized bulk force trends with depth switched from a strain-stiffening to a strain-weakening behavior with increasing indentation speed (Figure 3). This rate dependence may be explained by the depth-varying poroelastic and viscoelastic time scales inherent to articular cartilage. Here, the relevant characteristic length scale determining the rate of fluid flow in the tissue may vary from the radius of the blade tip (≈150 nm) to the decay length of the strain field (≈500 μm). These length scales result in characteristic poroelastic time scales of 0.1 ms to 40 s, spanning the range from faster to slower than the indentation rate. Thus, at slower rates, fluid pressurization and flow is unlikely to be a dominant factor, but it may come into play at faster rates. The viscoelasticity of cartilage may introduce another time scale. Using data from Hayes and Bodine (1978), the viscosity of the solid matrix at 20 Hz is about 23 kPa·s, which, dividing by the storage modulus, gives a time scale of about 15 ms. Thus, viscoelastic dissipation in the solid matrix is less likely to influence the results here, except at the faster indentation rates. Overall, the rate dependence studied here is physiologically relevant, ranging from nearly static (≈0.5%/s) to injurious (≈500%/s) rates (Morel and Quinn, 2004; Rolauffs et al., 2010)
In addition to this rate-dependence, both bulk and local responses varied between surface-intact and surface-removed sample groups. While the groups had similar critical bulk force, surface-removed samples had significantly lower critical depth and energy (Figure 2). Locally, the strain and strain energy fields spread across the compliant surface layer, but strain was more localized near the tip in surface-removed samples (Figure 4, Figure 5). Combined, these results suggest a critical force at which the tissue cuts, but the deformation the sample can sustain before reaching this force is significantly higher for the surface layer. In vivo, this behavior would allow the surface to better conform to local defects in the loading geometry before cracking. Combined with the fact that the surface is more dissipative than the bulk, these results reinforce the idea that the surface tissue may serve a mechanically protective role in the joint (Bartell et al., 2015; Buckley et al., 2013).
Separately, it is interesting to note that, other than indentation rate and surface condition, no variables significantly affected any of the responses measured in this study. The fact that neither orientation, nor its interaction with surface condition was significant implies that, while the compliant surface is mechanically important, the orientation of the thin zone of highly aligned fibers at the articular surface did not have a large effect on any of the responses studied here. While these results are surprising, they may change with tissue maturity as the collagen alignment develops further (Lewis and Johnson, 2001).
The primary focus of this study was connecting the local and global trends up to and at first-cut, i.e. for damage initiation. In the literature, the propagation of existing cracks is also an important topic that, like damage initiation, is understudied in the context of articular cartilage. The existing studies often computed toughness during crack propagation as characterized by the strain energy release rate (energy released per crack area), yielding values ranging from 140 J/m2 to over 1000 J/m2 (Chin-Purcell and Lewis, 1996; Simha et al., 2003; Stok and Oloyede, 2007; Taylor et al., 2012). To compare our results to these studies, we extracted a similar estimate of toughness from the bulk force-displacement data which averaged to 32.3 J/m2 for surface-intact samples and 68.0 J/m2 for surface-removed samples (Appendix E). While this measure excludes the superficial-most tissue (≈50 μm) and is lower than the other literature values, it suggests that toughness increases with depth into the tissue. It is especially interesting to note that our measure of toughness is closest to that measured by Chin-Purcell and Lewis for their cartilage samples that displayed the most brittle-like response (1996), similar to the cracking observed in the present study. This comparison highlights that, although the loading geometry used here does not mimic that experienced physiologically, it carries some advantages of traditional fracture mechanics approaches, including localized stress concentration in a standardized geometry that encourages brittle-like fracture modes over a wide-range of physiologically relevant loading rates.
In the broader field of material damage and failure, the effects of both inhomogeneous material properties and time-dependent processes are active areas of research, especially for soft materials, such as hydrogels. In layered systems, cracks have been observed to propagate toward and then along interfaces (Barthelat et al., 2016; Dunlop et al., 2011), which is not unlike the crack deflection often observed in articular cartilage (Jeffrey et al., 1995; Men et al., 2017; Thambyah et al., 2012), and may be related to the difference between surface-intact and -removed groups observed here. In hydrogels, both viscoelasticity and poroelasticity are known to modify the material failure and damage in complex ways (Bouklas et al., 2015; Fakhouri et al., 2015). Indentation and compression based experiments, similar to the method used here, have recently shown promise for studying this time-dependent behavior in hydrogels (Fakhouri et al., 2015). Another interesting parallel is with recently-developed double-network hydrogels which, with a combination of elastic and ductile (i.e. dissipative) networks, can have extremely high toughness (Gong, 2010; Long and Hui, 2016). Cartilage, one of the toughest, soft bio-materials, may also be considered a double-network (elastic collagen, dissipative proteoglycan networks) and so this interpretation may be relevant for cartilage failure. Beyond hydrogels, a similar “stick-slip” sawtooth region was observed when performing displacement-controlled blade indentation on rubbers (Lake and Yeoh, 1978). This comparison suggests that, after first cut, friction may also play a role in our study. In the future, it would be interesting to explore the above parallels in more detail, since each has important implications for both the likelihood of native cartilage failing during normal or super-physiological use, as well as designing engineered tissues that can withstand the complex, dynamic loading environment in a joint.
Though useful for resolving the importance of rate and local material behavior in initiating cartilage damage, this study is not without limitations. In particular, neonatal bovine articular cartilage explants were used. Neonatal tissue is known to have an under-developed collagen alignment (Roth and Mow, 1980), and so the response of mature tissue may be further modulated by its stronger collagen alignment (Lewis and Johnson, 2001). The tissue toughness may also increase as collagen density and cross-linking increase with maturity (Bank et al., 1998). Nonetheless, the shear properties of immature and mature tissues are similar (Buckley et al., 2010) and immature tissue provides a framework for studying injury (Li et al., 2013; Rolauffs et al., 2013). Another limitation is the use of a neo-Hookean constitutive model to calculate strain energy fields. This model does not perfectly capture cartilage’s response (Brown et al., 2009), and parameters were taken from the literature instead of sample-specific measurements. Nonetheless, the neo-Hookean model performs adequately when compared to others (Brown et al., 2009), and is designed for situations with large deformations, such as those observed in this study (Holzapfel, 2000).
The combination of bulk and local measurements surrounding cartilage damage and cracking demonstrated in this study provides a fruitful ground for bridging the gap between traditional fracture mechanics, local damage theories, and clinically-relevant articular cartilage failure. In future work, it would be interesting to develop this method further, building theoretical underpinnings to extracting relevant material damage and failure properties as a function of location in the tissue. Also, as confirmed in this study, loading rate is central to understanding articular cartilage both ex vivo and in vivo, including its failure. To that end, future work with this method can address this rate dependence in more detail, including its link to cutting-edge research regarding the effects of poroelasticity, viscoelasticity, and secondary-networks on the strength and failure of hydrogel-like materials. Overall, this study illustrates how combining local and global measurements surrounding the initiation of damage in articular cartilage can be used to reveal the importance of cartilage’s known layered structure in protecting against failure across physiologically relevant loading rates.
Supplementary Material
Supplemental Figure 1. A SEM image showing the tip of a fresh razor blade. The radius of the tip is approximately 75 nm.
Supplemental Figure 2. Analysis of the spatial extent of the strain energy density field in the lateral and depth dimensions. (A) Example strain energy density field showing the points above the threshold value of 20 KJ/m3. Points above this threshold were analyzed to calculate the variance in the (B) depth and (C) lateral directions for surface-intact samples (black circles) and surface-removed samples (blue circles). This data was fit to a fixed-effects model based on the log of the blade speed and the surface condition and these fits are shown as solid lines. The fits are further detailed in Supplementary Table 2.
Supplemental Figure 3. Cuts of the 2D displacement data and associated 2D fits to the functional form predicted by contact mechanics. Data and fits are shown for (A) surface-intact and (B) surface-removed samples, with cuts take at θ = 0°. The data and fits were scaled based on the fitting parameters and are shown on a linear-log plot to emphasize the collapse and logarithmic scaling of the data. Note, this is the same data as shown in Figure 6, but scaled.
Supplemental Figure 4. Histograms of the fit coefficients (A) β1 and (B) β3 obtained by fitting local displacement data to Equation 2. Note that, the values lie in the expected range of values and values for surface- intact samples are generally higher than surface-removed.
Supplemental Figure 5. Histograms of the (A) Young’s modulus and (B) Poisson’s ratio calculated from the ) β1 and β3 fitting coefficients. Note that, the values lie in the expected ranges for articular cartilage and surface-removed values are generally higher than surface-intact.
Supplemental Figure 6. (A) Characteristic force vs. blade displacement curves for one surface-intact and one surface-removed sample, up to the blade turn-around point. Both samples were taken from the 10 μm/s blade speed group and are the same samples shown in Figure 2A. For all samples, the energy expended during the full cutting time was integrated, as depicted by red areas. This energy was divided by the final cut area as a measure of toughness. (B) The toughness for all experiments (circles or crosses), shown with the corresponding reduced linear model fits (solid lines), for surface-intact (black) and surface-removed (blue) samples. This measure of toughness was significantly dependent on blade speed (p-value: 3.1×10−5) and surface condition, with surface-removed having a higher toughness (p-value: 6.4×10−25).
Supplementary Table 1. Coefficients, significance values, and goodness of fit values for the reduced mixed-effects linear models of critical bulk force, depth, and energy at first cut, and the toughness (throughout cutting) as shown in Figure 2B–D. In all cases, the full model was reduced by removing insignificant higher-order fixed effects (p > 0.01), resulting in the final two-parameter model shown here.
Supplementary Table 2. Coefficients, significance values, and goodness of fit values for the linear fixed-effects models of the lateral and depth extent of the strain energy fields, as shown in Supplemental Figure 2B–C.
Supplementary Table 3. Fit coefficients for surface-intact and surface-removed samples obtained by fitting local displacement data to Equation 2 in a 2D, least-squares sense. For each coefficient, the average value and the standard error of the mean are shown.
Supplementary Table 4. Coefficients, significance values, and goodness of fit values for the linear mixed-effects models of toughness as shown in Supplemental Figure 6. In all cases, the full model originally included random effects for source animal and fixed effects for log of the blade speed, surface condition, storage time before testing, orientation in the joint, and condyle, with all interaction terms. The model was then reduced by removing insignificant higher-order fixed effects (p > 0.01), resulting in the final two-parameter model shown here.
Acknowledgments
This study was supported by the National Science Foundation (NSF) under award number CMMI 1536463. L.R.B. was supported by the National Institutes of Health, under award number 1F31-AR069977. This work made use of the Cornell Center for Materials Research Shared Facilities, which are supported through the NSF MRSEC program (DMR-1719875). The authors would also like thank Lynn Johnson at the Cornell Statistical Consulting unit, Prof. C. Y. Hui, and members of the Cohen and Bonassar lab for useful discussions.
Footnotes
Conflict of interest statement
The authors have no conflicts of interest to declare for this research.
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- Ahsan T, Sah RL. Biomechanics of integrative cartilage repair. Osteoarthritis Cartilage. 1999;7:29–40. doi: 10.1053/joca.1998.0160. https://doi.org/10.1053/joca.1998.0160. [DOI] [PubMed] [Google Scholar]
- Anderson DD, Chubinskaya S, Guilak F, Martin JA, Oegema TR, Olson SA, Buckwalter JA. Post-traumatic osteoarthritis: Improved understanding and opportunities for early intervention. J Orthop Res. 2011;29:802–809. doi: 10.1002/jor.21359. https://doi.org/10.1002/jor.21359. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Argatov I, Mishuris G. A phenomenological model of damage in articular cartilage under impact loading. Mech Res Commun. 2015;69:87–90. https://doi.org/10.1016/j.mechrescom.2015.06.013. [Google Scholar]
- Bank RA, Bayliss MT, Lafeber FPJG, Maroudas A, Tekoppele JM. Ageing and zonal variation in post-translational modification of collagen in normal human articular cartilage: The age-related increase in non-enzymatic glycation affects biomechanical properties of cartilage. Biochem J. 1998;330:345–351. doi: 10.1042/bj3300345. https://doi.org/10.1042/bj3300345. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bartell LR, Fortier LA, Bonassar LJ, Cohen I. Measuring microscale strain fields in articular cartilage during rapid impact reveals thresholds for chondrocyte death and a protective role for the superficial layer. J Biomech. 2015;48:3440–3446. doi: 10.1016/j.jbiomech.2015.05.035. https://doi.org/10.1016/j.jbiomech.2015.05.035. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Barthelat F, Yin Z, Buehler MJ. Structure and mechanics of interfaces in biological materials. Nat Rev Mater. 2016;1:16007. https://doi.org/10.1038/natrevmats.2016.7. [Google Scholar]
- Bauer M, Jackson RW. Chondral lesions of the femoral condyles: A system of arthroscopic classification. Arthrosc J Arthrosc Relat Surg. 1988;4:97–102. doi: 10.1016/s0749-8063(88)80074-4. https://doi.org/10.1016/S0749-8063(88)80074-4. [DOI] [PubMed] [Google Scholar]
- Below S, Arnoczky SP, Dodds J, Kooima C, Walter N. The split-line pattern of the distal femur: A consideration in the orientation of autologous cartilage grafts. Arthrosc J Arthrosc Relat Surg. 2002;18:613–617. doi: 10.1053/jars.2002.29877. https://doi.org/10.1053/jars.2002.29877. [DOI] [PubMed] [Google Scholar]
- Benninghoff A. Form und Bau der Gelenkknorpel in ihren Beziehungen zur Funktion. Z Für Zellforsch Mikrosk Anat. 1925;2:783–862. https://doi.org/10.1007/BF00583443. [Google Scholar]
- Blaber J, Adair B, Antoniou A. Ncorr: Open-Source 2D Digital Image Correlation Matlab Software. Exp Mech. 2015;55:1105–1122. https://doi.org/10.1007/s11340-015-0009-1. [Google Scholar]
- Bouklas N, Landis CM, Huang R. Effect of Solvent Diffusion on Crack-Tip Fields and Driving Force for Fracture of Hydrogels. J Appl Mech. 2015;82:081007–081007-16. https://doi.org/10.1115/1.4030587. [Google Scholar]
- Brown CP, Nguyen TC, Moody HR, Crawford RW, Oloyede A. Assessment of common hyperelastic constitutive equations for describing normal and osteoarthritic articular cartilage. Proc Inst Mech Eng [H] 2009;223:643–652. doi: 10.1243/09544119JEIM546. https://doi.org/10.1243/09544119JEIM546. [DOI] [PubMed] [Google Scholar]
- Brown TD, Johnston RC, Saltzman CL, Marsh JL, Buckwalter JA. Posttraumatic Osteoarthritis: A First Estimate of Incidence, Prevalence, and Burden of Disease. J Orthop Trauma. 2006;20:739–744. doi: 10.1097/01.bot.0000246468.80635.ef. https://doi.org/10.1097/01.bot.0000246468.80635.ef. [DOI] [PubMed] [Google Scholar]
- Buckley MR, Bergou AJ, Fouchard J, Bonassar LJ, Cohen I. High-resolution spatial mapping of shear properties in cartilage. J Biomech. 2010;43:796–800. doi: 10.1016/j.jbiomech.2009.10.012. https://doi.org/10.1016/j.jbiomech.2009.10.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Buckley MR, Bonassar LJ, Cohen I. Localization of Viscous Behavior and Shear Energy Dissipation in Articular Cartilage Under Dynamic Shear Loading. J Biomech Eng. 2013;135:031002–031002. doi: 10.1115/1.4007454. https://doi.org/10.1115/1.4007454. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chin-Purcell MV, Lewis JL. Fracture of Articular Cartilage. J Biomech Eng. 1996;118:545–556. doi: 10.1115/1.2796042. https://doi.org/10.1115/1.2796042. [DOI] [PubMed] [Google Scholar]
- Curl WW, Krome J, Gordon ES, Rushing J, Smith BP, Poehling GG. Cartilage injuries: A review of 31,516 knee arthroscopies. Arthrosc J Arthrosc Relat Surg. 1997;13:456–460. doi: 10.1016/s0749-8063(97)90124-9. https://doi.org/10.1016/S0749-8063(97)90124-9. [DOI] [PubMed] [Google Scholar]
- Dunlop JWC, Weinkamer R, Fratzl P. Artful interfaces within biological materials. Mater Today. 2011;14:70–78. https://doi.org/10.1016/S1369-7021(11)70056-6. [Google Scholar]
- Fakhouri S, Hutchens BS, Crosby JA. Puncture mechanics of soft solids. Soft Matter. 2015;11:4723–4730. doi: 10.1039/c5sm00230c. https://doi.org/10.1039/C5SM00230C. [DOI] [PubMed] [Google Scholar]
- Gong JP. Why are double network hydrogels so tough? Soft Matter. 2010;6:2583–2590. https://doi.org/10.1039/B924290B. [Google Scholar]
- Hayes WC, Bodine AJ. Flow-independent viscoelastic properties of articular cartilage matrix. J Biomech. 1978;11:407–419. doi: 10.1016/0021-9290(78)90075-1. https://doi.org/10.1016/0021-9290(78)90075-1. [DOI] [PubMed] [Google Scholar]
- Henak CR, Bartell LR, Cohen I, Bonassar LJ. Multi-scale strain as a predictor of impact-induced fissuring in articular cartilage. J Biomech Eng. 2016 doi: 10.1115/1.4034994. https://doi.org/10.1115/1.4034994. [DOI] [PMC free article] [PubMed]
- Holzapfel GA. Nonlinear solid mechanics: a continuum approach for engineering. Wiley; Chichester: 2000. [Google Scholar]
- Hui CY, AJ, Bennison SJ, Londono JD. Crack blunting and the strength of soft elastic solids. Proc R Soc Lond Math Phys Eng Sci. 2003;459:1489–1516. https://doi.org/10.1098/rspa.2002.1057. [Google Scholar]
- Jeffrey JE, Gregory DW, Aspden RM. Matrix Damage and Chondrocyte Viability Following a Single Impact Load on Articular-Cartilage. Arch Biochem Biophys. 1995;322:87–96. doi: 10.1006/abbi.1995.1439. https://doi.org/10.1006/abbi.1995.1439. [DOI] [PubMed] [Google Scholar]
- Johnson KL. Contact Mechanics. Cambridge University Press; New York: 1987. [Google Scholar]
- Lake GJ, Yeoh OH. Measurement of rubber cutting resistance in the absence of friction. Int J Fract. 1978;14:509–526. https://doi.org/10.1007/BF01390472. [Google Scholar]
- Lewis JL, Deloria LB, Oyen-Tiesma M, Thompson RC, Ericson M, Oegema TR. Cell death after cartilage impact occurs around matrix cracks. J Orthop Res. 2003;21:881–887. doi: 10.1016/S0736-0266(03)00039-1. https://doi.org/10.1016/S0736-0266(03)00039-1. [DOI] [PubMed] [Google Scholar]
- Lewis JL, Johnson SL. Collagen architecture and failure processes in bovine patellar cartilage. J Anat. 2001;199:483–492. doi: 10.1046/j.1469-7580.2001.19940483.x. https://doi.org/10.1046/j.1469-7580.2001.19940483.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li Y, Frank EH, Wang Y, Chubinskaya S, Huang HH, Grodzinsky AJ. Moderate dynamic compression inhibits pro-catabolic response of cartilage to mechanical injury, tumor necrosis factor-α and interleukin-6, but accentuates degradation above a strain threshold. Osteoarthritis Cartilage. 2013;21:1933–1941. doi: 10.1016/j.joca.2013.08.021. https://doi.org/10.1016/j.joca.2013.08.021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Long R, Hui CY. Fracture toughness of hydrogels: measurement and interpretation. Soft Matter. 2016;12:8069–8086. doi: 10.1039/c6sm01694d. https://doi.org/10.1039/C6SM01694D. [DOI] [PubMed] [Google Scholar]
- Men Y, Jiang Y, Chen L, Zhang C, Ye J. On mechanical mechanism of damage evolution in articular cartilage. Mater Sci Eng C. 2017;78:79–87. doi: 10.1016/j.msec.2017.03.289. https://doi.org/10.1016/j.msec.2017.03.289. [DOI] [PubMed] [Google Scholar]
- Morel V, Quinn TM. Cartilage injury by ramp compression near the gel diffusion rate. J Orthop Res. 2004;22:145–151. doi: 10.1016/S0736-0266(03)00164-5. https://doi.org/10.1016/S0736-0266(03)00164-5. [DOI] [PubMed] [Google Scholar]
- Mow VC, Kuei SC, Lai WM, Armstrong CG. Biphasic Creep and Stress Relaxation of Articular Cartilage in Compression: Theory and Experiments. J Biomech Eng. 1980;102:73–84. doi: 10.1115/1.3138202. https://doi.org/10.1115/1.3138202. [DOI] [PubMed] [Google Scholar]
- Outerbridge RE. The Etiology of Chondromalacia Patellae. Bone Jt J. 1961;43B:752–757. doi: 10.1302/0301-620X.43B4.752. [DOI] [PubMed] [Google Scholar]
- Oyen-Tiesma M, Cook RF. Technique for estimating fracture resistance of cultured neocartilage. J Mater Sci Mater Med. 2001;12:327–332. doi: 10.1023/a:1011247104621. https://doi.org/10.1023/A:1011247104621. [DOI] [PubMed] [Google Scholar]
- Pritzker KPH, Gay S, Jimenez SA, Ostergaard K, Pelletier JP, Revell PA, Salter D, van den Berg WB. Osteoarthritis cartilage histopathology: grading and staging. Osteoarthritis Cartilage. 2006;14:13–29. doi: 10.1016/j.joca.2005.07.014. https://doi.org/10.1016/j.joca.2005.07.014. [DOI] [PubMed] [Google Scholar]
- Repo RU, Finlay JB. Survival of articular cartilage after controlled impact. J Bone Jt Surg. 1977;59:1068–1076. [PubMed] [Google Scholar]
- Rolauffs B, Kurz B, Felka T, Rothdiener M, Uynuk-Ool T, Aurich M, Frank E, Bahrs C, Badke A, Stöckle U, Aicher WK, Grodzinsky AJ. Stress-vs-time signals allow the prediction of structurally catastrophic events during fracturing of immature cartilage and predetermine the biomechanical, biochemical, and structural impairment. J Struct Biol. 2013;183:501–511. doi: 10.1016/j.jsb.2013.06.011. https://doi.org/10.1016/j.jsb.2013.06.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rolauffs B, Muehleman C, Li J, Kurz B, Kuettner KE, Frank E, Grodzinsky AJ. Vulnerability of the superficial zone of immature articular cartilage to compressive injury. Arthritis Rheum. 2010;62:3016–3027. doi: 10.1002/art.27610. https://doi.org/10.1002/art.27610. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Roth V, Mow VC. The intrinsic tensile behavior of the matrix of bovine articular cartilage and its variation with age. J Bone Jt Surg. 1980;62:1102–1117. [PubMed] [Google Scholar]
- Schinagl RM, Gurskis D, Chen AC, Sah RL. Depth-dependent confined compression modulus of full-thickness bovine articular cartilage. J Orthop Res. 1997;15:499–506. doi: 10.1002/jor.1100150404. https://doi.org/10.1002/jor.1100150404. [DOI] [PubMed] [Google Scholar]
- Scott CC, Athanasiou KA. Mechanical Impact and Articular Cartilage. Crit Rev Biomed Eng. 2006;34:347–378. doi: 10.1615/critrevbiomedeng.v34.i5.10. https://doi.org/10.1615/CritRevBiomedEng.v34.i5.10. [DOI] [PubMed] [Google Scholar]
- Silverberg JL, Barrett AR, Das M, Petersen PB, Bonassar LJ, Cohen I. Structure-Function Relations and Rigidity Percolation in the Shear Properties of Articular Cartilage. Biophys J. 2014;107:1721–1730. doi: 10.1016/j.bpj.2014.08.011. https://doi.org/10.1016/j.bpj.2014.08.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Silverberg JL, Dillavou S, Bonassar L, Cohen I. Anatomic variation of depth-dependent mechanical properties in neonatal bovine articular cartilage. J Orthop Res. 2013;31:686–691. doi: 10.1002/jor.22303. https://doi.org/10.1002/jor.22303. [DOI] [PubMed] [Google Scholar]
- Simha NK, Carlson CS, Lewis JL. Evaluation of fracture toughness of cartilage by micropenetration. J Mater Sci Mater Med. 2003;15:631–639. doi: 10.1023/b:jmsm.0000026104.30607.c7. https://doi.org/10.1023/B:JMSM.0000026104.30607.c7. [DOI] [PubMed] [Google Scholar]
- Stok K, Oloyede A. Conceptual fracture parameters for articular cartilage. Clin Biomech. 2007;22:725–735. doi: 10.1016/j.clinbiomech.2007.03.005. https://doi.org/10.1016/j.clinbiomech.2007.03.005. [DOI] [PubMed] [Google Scholar]
- Taylor D, O’Mara N, Ryan E, Takaza M, Simms C. The fracture toughness of soft tissues. J Mech Behav Biomed Mater. 2012;6:139–147. doi: 10.1016/j.jmbbm.2011.09.018. https://doi.org/10.1016/j.jmbbm.2011.09.018. [DOI] [PubMed] [Google Scholar]
- Thambyah A, Zhang G, Kim W, Broom ND. Impact induced failure of cartilage-on-bone following creep loading: A microstructural and fracture mechanics study. J Mech Behav Biomed Mater. 2012;14:239–247. doi: 10.1016/j.jmbbm.2012.06.007. https://doi.org/10.1016/j.jmbbm.2012.06.007. [DOI] [PubMed] [Google Scholar]
- Waters NP, Stoker AM, Carson WL, Pfeiffer FM, Cook JL. Biomarkers affected by impact velocity and maximum strain of cartilage during injury. J Biomech. 2014;47:3185–3195. doi: 10.1016/j.jbiomech.2014.06.015. https://doi.org/10.1016/j.jbiomech.2014.06.015. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Supplemental Figure 1. A SEM image showing the tip of a fresh razor blade. The radius of the tip is approximately 75 nm.
Supplemental Figure 2. Analysis of the spatial extent of the strain energy density field in the lateral and depth dimensions. (A) Example strain energy density field showing the points above the threshold value of 20 KJ/m3. Points above this threshold were analyzed to calculate the variance in the (B) depth and (C) lateral directions for surface-intact samples (black circles) and surface-removed samples (blue circles). This data was fit to a fixed-effects model based on the log of the blade speed and the surface condition and these fits are shown as solid lines. The fits are further detailed in Supplementary Table 2.
Supplemental Figure 3. Cuts of the 2D displacement data and associated 2D fits to the functional form predicted by contact mechanics. Data and fits are shown for (A) surface-intact and (B) surface-removed samples, with cuts take at θ = 0°. The data and fits were scaled based on the fitting parameters and are shown on a linear-log plot to emphasize the collapse and logarithmic scaling of the data. Note, this is the same data as shown in Figure 6, but scaled.
Supplemental Figure 4. Histograms of the fit coefficients (A) β1 and (B) β3 obtained by fitting local displacement data to Equation 2. Note that, the values lie in the expected range of values and values for surface- intact samples are generally higher than surface-removed.
Supplemental Figure 5. Histograms of the (A) Young’s modulus and (B) Poisson’s ratio calculated from the ) β1 and β3 fitting coefficients. Note that, the values lie in the expected ranges for articular cartilage and surface-removed values are generally higher than surface-intact.
Supplemental Figure 6. (A) Characteristic force vs. blade displacement curves for one surface-intact and one surface-removed sample, up to the blade turn-around point. Both samples were taken from the 10 μm/s blade speed group and are the same samples shown in Figure 2A. For all samples, the energy expended during the full cutting time was integrated, as depicted by red areas. This energy was divided by the final cut area as a measure of toughness. (B) The toughness for all experiments (circles or crosses), shown with the corresponding reduced linear model fits (solid lines), for surface-intact (black) and surface-removed (blue) samples. This measure of toughness was significantly dependent on blade speed (p-value: 3.1×10−5) and surface condition, with surface-removed having a higher toughness (p-value: 6.4×10−25).
Supplementary Table 1. Coefficients, significance values, and goodness of fit values for the reduced mixed-effects linear models of critical bulk force, depth, and energy at first cut, and the toughness (throughout cutting) as shown in Figure 2B–D. In all cases, the full model was reduced by removing insignificant higher-order fixed effects (p > 0.01), resulting in the final two-parameter model shown here.
Supplementary Table 2. Coefficients, significance values, and goodness of fit values for the linear fixed-effects models of the lateral and depth extent of the strain energy fields, as shown in Supplemental Figure 2B–C.
Supplementary Table 3. Fit coefficients for surface-intact and surface-removed samples obtained by fitting local displacement data to Equation 2 in a 2D, least-squares sense. For each coefficient, the average value and the standard error of the mean are shown.
Supplementary Table 4. Coefficients, significance values, and goodness of fit values for the linear mixed-effects models of toughness as shown in Supplemental Figure 6. In all cases, the full model originally included random effects for source animal and fixed effects for log of the blade speed, surface condition, storage time before testing, orientation in the joint, and condyle, with all interaction terms. The model was then reduced by removing insignificant higher-order fixed effects (p > 0.01), resulting in the final two-parameter model shown here.