A Threshold-free Summary Index of Prediction Accuracy for Censored Time to Event Data

Abstract

Prediction performance of a risk scoring system needs to be carefully assessed before its adoption in clinical practice. Clinical preventive care often uses risk scores to screen asymptomatic population. The primary clinical interest is to predict the risk of having an event by a pre-specified future time t₀. Accuracy measures such as positive predictive values have been recommended for evaluating the predictive performance. However, for commonly used continuous or ordinal risk score systems, these measures require a subjective cut-off threshold value that dichotomizes the risk scores. The need for a cut-off value created barriers for practitioners and researchers. In this paper, we propose a threshold-free summary index of positive predictive values that accommodates time-dependent event status and competing risks. We develop a nonparametric estimator and provide an inference procedure for comparing this summary measure between two risk scores for censored time to event data. We conduct a simulation study to examine the finite-sample performance of the proposed estimation and inference procedures. Lastly, we illustrate the use of this measure on a real data example, comparing two risk score systems for predicting heart failure in childhood cancer survivors.

1. Introduction

Clinical medicine is facing a paradigm shift from current diagnosis and treatment practices to prevention through earlier intervention based on risk prediction [1]. Diagnosis and treatment approaches help individual patients seek relief from their symptoms. However, evidence is mounting that health interventions may be more effective in improving long-term health outcomes when they target asymptomatic individuals who are predicted to be at high risk for the condition of interest [2, 3]. The condition of interest typically has the following characteristics: 1) its seriousness may result in a high risk of mortality or significantly affect the quality of life; 2) early detection/intervention can make a difference in disease prognosis; and importantly but subtly 3) its event rate is low. A prevention approach to medicine relies on the development of risk scores to stratify individuals into different risk groups. Early intervention strategies are typically recommended to subjects who are in the high-risk group.

In the prevention paradigm, the use of risk scores as population screening tools is increasingly advocated in clinical practices, e.g. 2013 American College of Cardiology/American Heart Association guideline on the assessment of cardiovascular risk [4]. In a systematic review on risk prediction for type 2 diabetes, forty-six algorithms were identified [5]. Another study established several risk score systems to predict congestive heart failure for childhood cancer survivors who are at an elevated risk due to treatment toxicity [6]. One of the defining characteristics of screening is a low event rate in the targeted asymptomatic population. Taking the aforementioned two diseases as an example, the crude prevalence of undiagnosed type 2 diabetes, a common disease, was low at 3.5% in 1987 and 5.7% in 1992 [7], while the cumulative event rate of congestive heart failure by 35 years post childhood cancer diagnosis was 4.4% [6]. The event rate is much lower for other serious conditions such as cancer, multiple sclerosis, AIDS, and dementia. A low event rate and a focus on prevention necessitate the development of screening tools such as risk scores.

Before a risk scoring system is adopted for clinical screening, evaluation of its predictive accuracy is critical. The most popular accuracy metric used in the clinical literature is the area under the receiver operating characteristic (ROC) curve (AUC). The AUC is a summary index of two accuracy metrics: true positive rate (TPR) and false positive rate (FPR). In the literature, TPR is also referred to as sensitivity, and 1–FPR is referred to as specificity. These two metrics are both outcome conditional. In other words, they evaluate the ability to predict the classification of risk score given the as-yet unknown outcome [8]. Thus the AUC does not reflect the ability of predicting the future outcome conditional on the risk score. Indeed, one influential article criticized the outcome conditional metrics such as TPR, FPR, and AUC as being of little use for clinicians because clinical interest almost always focuses on prediction [9]. In contrast, a risk score conditional measure, such as positive predictive value (PPV), does reflect the ability to predict the future outcome. A risk score with high sensitivity and specificity, and thus a high AUC, can have poor PPV when applied to low-prevalence populations. This limitation is often overlooked by clinicians and biomedical researchers. Despite its popularity, studies confirm that the AUC is insensitive in evaluating risk prediction models. For example, including a marker with a risk ratio of 3.0 showed little improvement on the AUC, while it could shift the predicted 10-year disease risk for an individual patient from 8% to 24% [10]. This magnitude of difference in risk would result in different recommendations on follow-up/intervention strategies.

Compared to the AUC, in some clinical applications such as screening, the PPV provides an attractive metric to assess the predictive performance of the risk score [11]. The PPV is calculated with data from a prospective cohort, where the risk scores are computed using baseline information and the outcome is followed prospectively. Originally, the PPV was defined for a dichotomous test. Moskowitz and Pepe (2004) extended the definition of PPV for a continuous risk score [11]. Assuming that the higher the risk score, the greater the individual risk, the PPV is defined as the probability of having the disease when the risk score value is larger than a given cut-off value z,

$$\text{PPV}(z)=\mathit{Pr}\{D=1|Z\ge z\}\text{and}\text{NPV}(z)=\mathit{Pr}\{D=0|Z<z\},$$ (1)

where D = 1 indicates the presence of the disease, and D = 0 indicates the absence of the disease. Zheng et al. (2008) further generalized the definition to accommodate the censored event time outcome [12]. Since the PPV is threshold dependent, as seen in (1), it is often evaluated at several fixed quantiles of the risk scores [12]. Such evaluations allow the comparison across different risk score systems [11, 13]. However, the selection of specificities or quantiles can be subjective, and it is possible that different systems could outperform others, depending on the cut-off points selected [14].

For the above reasons, a threshold-free summary metric for the PPV is attratcive to facilitate its clinical usage. Two curves of PPV have been investigated in the literature. Raghavan et al. (1989) and Zheng et al. (2010) considered a curve of PPV versus quantiles of the risk score [14, 15]. However, they did not provide a summary index of the proposed PPV curve. A second curve is called the precision-recall (PR) curve, which was proposed in the information retrieval community [15, 16], where precision is equivalent to the PPV and recall is equivalent to the TPR. The relationship of PR and ROC curves and the area under them has been discussed[17, 18]. It has been shown that the PR curve of a risk score system dominates that of another system if its ROC curve is also dominant [17]. However, such a relationship does not exist for the area under these two curves [18]. Two recent papers illustrated the advantage of using the area under the PR curve over the AUC for predicting low prevalence diseases [19, 20]. We refer to the summary metric for the area under the PR curve as the average positive predictive value (AP) [19]. These previous research on the area under the PR curve have only considered binary outcomes. However, for many clinical applications, the outcome is time to event.

In this paper, we make the following contributions in the assessment of risk scoring systems. First, we define a time-dependent AP, AP_t0 for censored event time outcomes. We propose a robust nonparametric estimator of AP_t0 without modeling assumptions on the relationship between the risk score and event time. Second, we extend the definition and estimation procedure of AP_t0 to the setting of competing risks, which broaden the use of AP_t0 in a variety of studies. Third, we provide a statistical inference procedure to compare two risks scores in terms of the AP_t0. Fourth, we provide an R package to implement our method. The paper is organized as follows. In Section 2, we introduce the definition and interpretation of AP_t0. In Section 3, we present estimators in absence and presence of competing risks, and the inference procedures for obtaining 95% confidence interval and comparing two competing risk scores. In Section 4, we conduct a simulation study to investigate the performance of the proposed estimation and inference procedures in finite samples. In Section 5, we illustrate the proposed metric AP_t0 by analyzing two risk score systems with data from the Childhood Cancer Survival Study [21]. We conclude with a discussion and suggestions for future work in Section 6.

2. Time-dependent Average Positive Predictive Values

Consider a continuous risk score Z. Let T be the time to the event of interest. Time-dependent PPV and TPR [12, 22] are defined as

$${\text{PPV}}_{t_0}(z)=\mathit{Pr}\{T<t_0|Z\ge z\}\text{and}{\text{TPR}}_{t_0}(z)=\mathit{Pr}\{Z\ge z|T<t_0\}.$$ (2)

In the above setting, the event status is time-dependent, i.e., D_t0 = I(T < t₀), where I(·) is an identity function. Consequently, the PPV and TPR are also functions of t₀.

Following Yuan et al. [19], we define AP_t0, as the area under the time-dependent PR curve {(TPR_t0 (z), PPV_t0 (z)), z ∈ ℛ},

$${\text{AP}}_{t_0}={\int }_{\mathcal{R}}{\text{PPV}}_{t_0}(z)d{\text{TPR}}_{t_0}(z).$$ (3)

Note that the TPR describes the distribution function of Z in subjects who experience the event of interest by time t₀, i.e. T < t₀. It can be shown that AP_t0 = E_Z1 {PPV_t0(Z₁)}, where Z₁ denotes the risk score for subjects with T < t₀. In the real data example of Section 5, we will show that AP is estimated to be 0.107 at t₀ = 35 years for a risk score system. That is, by 35 years post diagnosis, we expect that on average 10.7% of the subjects with a high risk score (compared to the risk score of a randomly selected subject who experiences the event before t₀) will experience the event of interest.

In addition, PPV_t0(z) can be written as PPV_t0(z) = P(Z ≥ z | T < t₀)P(T < t₀)/P(Z ≥ z) = π_t0 {1 − F₁(z)} / {1 − F(z)}, where F₁(z) = Pr(Z < z | T < t₀) = P(Z₁ < z) is the distribution function of the risk score Z₁ for subjects with T < t₀, F(z) = P(Z < z) is the distribution function of the risk score Z for the target population, and π_t0 = Pr(T < t₀) is the event rate by time t₀ in the target population. Thus, the AP can be written as

$${\text{AP}}_{t_0}={\pi }_{t_0}{\int }_{\mathcal{R}}\frac{1-F_1(z)}{1-F(z)}d{F}_1(z).$$ (4)

A perfect risk score system would always assign higher values to subjects with T < t₀, compared to subjects with T ≥ t₀, i.e. P(Z ≥ Z₁ | T ≥ t₀) = 0. This leads to AP_t0 = 1 from equation (4). A non-informative risk score system would randomly assign risk scores to both subjects with T < t₀ and T ≥ t₀. i.e., P(Z ≥ z | T ≥ t₀) = P(Z ≥ z | T < t₀) for each z, which leads to AP_t0 = π_t0. Thus, the theoretical range of AP_t0 is [π_t0, 1].

3. Estimating and Comparing AP_t0

3.1. Nonparametric Estimator of AP_t0 for a single risk score

Often, the event times of some subjects are censored due to the end of the study or loss to follow up. Due to censoring, one can only observe X = min{T, C} where C is the censoring time, and δ = I(T < C). Let {(X_i, δ_i, Z_i), i = 1, ⋯, n} be n independent realizations of (X, δ, Z).

In the presence of censoring, event status at t₀, I(T_i < t₀), may not be observed for some subjects. We suggest using the inverse probability weighting (IPW) to account for censoring [23, 24]. The proposed estimator is a nonparametric estimator, which does not imposes any assumptions on the relationship between the risk score Z and the event time T. The time-dependent PPV and TPR are estimated by

$${\widehat{\text{PPV}}}_{t_0}(z)=\frac{{\sum }_{i=1}^n{\widehat{w}}_{t_0,i}I(Z_i\ge z)I(X_i<t_0)}{{\sum }_{i=1}^{n}I(Z_i\ge z)}\text{and}{\widehat{\text{TPR}}}_{t_0}(z)=\frac{{\sum }_{i=1}^n{\widehat{w}}_{t_0,i}I(Z_i\ge z)I(X_i<t_0)}{{\sum }_{i=1}^n{\widehat{w}}_{t_0,i}I(X_i<t_0)},$$

where ŵ_t0,i is the inverse of the estimated probability that the time-dependent event status I(T_i < t₀) is observed, specifically

$${\widehat{w}}_{t_0,i}=\frac{I(X_i<t_0){\delta }_i}{\widehat{\mathcal{G}}(X_i)}+\frac{I(X_i\ge t_0)}{\widehat{\mathcal{G}}(t_0)},$$ (5)

where 𝒢̂(c) is a consistent estimator of the survival function of the censoring time, 𝒢(c) = Pr(C ≥ c). Under the assumption of independent censoring, i.e., the censoring time C is independent of both the event time T and the risk score Z, 𝒢(c) can be obtained by the nonparametric Nelson-Aalen or Kaplan-Meier estimator. If the censoring time C depends on the risk score Z, additional model assumptions might be required. For example, a proportional hazards (PH) model could be fit to estimate 𝒢_z(t) = Pr(C ≥ c | Z = z). Note that the weights have expectation 1 given (T_i, Z_i).

Based on the estimated PPV_t0 (z) and TPR_t0 (z), AP_t0 can be estimated by

$${\widehat{\text{AP}}}_{t_0}=\frac{{\sum }_{j=1}^{n}I(X_j\le t_0){\widehat{w}}_{t_0,j}{\widehat{\text{PPV}}}_{t_0}(Z_j)}{{\sum }_{i=1}^{n}I(X_j\le t_0){\widehat{w}}_{t_0,j}}.$$ (6)

Uno et al. [23] shows that ${\widehat{\text{PPV}}}_{t_0}(z)$ and ${\widehat{\text{TPR}}}_{t_0}(z)$ are both consistent estimators. Thus, ${\widehat{\text{AP}}}_{t_0}$ is also a consistent estimator of AP_t0 for any given value of t₀.

In practice, we often deal with discrete risk scores, where tied risk scores are common. Following Pepe's proposal [25], we modify the above estimator (6) to accommodate tied risk scores by replacing ${\widehat{\text{PPV}}}_{t_0}(Z_j)$ with

$${\stackrel{\sim }{\text{PPV}}}_{t_0}(Z_j)=\frac{{\sum }_{i=1}^n{\widehat{w}}_{t_0,i}\{I(Z_i>Z_j)+\frac{1}{2}I(Z_i=Z_j)\}I(X_i<t_0)}{{\sum }_{i=1}^n\{I(Z_i>Z_j)+\frac{1}{2}I(Z_i=Z_j)\}}.$$

To construct confidence intervals, we suggest the nonparametric bootstrap [26] method. Specifically, let ${\widehat{\text{AP}}}_{t_0}^{\mathbb{B}}=\{{\widehat{\text{AP}}}_{t_0}^b,b=1,2,\cdots ,B\}$ denote the estimated AP_t0 obtained from B bootstrape resamples. A 95% confidence interval (CI) for the AP_t0 is given as ( ${\widehat{\text{AP}}}_{t_0}^{\mathbb{B},0.025},{\widehat{\text{AP}}}_{t_0}^{\mathbb{B},0.975}$), where ${\widehat{\text{AP}}}_{t_0}^{\mathbb{B},0.025}$ and ${\widehat{\text{AP}}}_{t_0}^{\mathbb{B},0.975}$ are the 2.5% and 97.5% empirical percentiles of the ${\widehat{\text{AP}}}_{t_0}^{\mathbb{B}}$, respectively.

3.2. Estimator of AP_t0 under competing risks

In many studies, the event time of main interest might not be observed because of other events rather than censoring. These other events are referred to as the competing risk events. For example, in Section 5, we analyze a data set from the Childhood Cancer Survival Study [21]. The event of main interest is the occurrence of congestive heart failure (CHF). However, the CHF event might not be observed due to death from other causes such as cancer recurrence and progression [27]. In this section, we describe a straightforward extension of the IPW estimator of time-dependent AP to accommodate competing risks; see Li et al. [28] and Blanche et al. [29] for a similar extension for the estimation of time-dependent AUC under competing risk.

Let us take the Childhood Cancer Survival Study as an example. Let ε denote the event type. Specifically ε_i = 1 if the subject i experienced a CHF event; ε_i = 2 if the subject i experienced death from other causes. Let Δ_i = δ_iε_i, and Δ_i = 0 if censored, = 1 if an CHF event is observed, = 2 if a death due to other causes is observed. Accordingly, let T_i1 and T_i2 denote the time to type 1 event and type 2 event respectively. The observed data in this example is denoted as 𝒟 = {(X_i, Δ_i, Z_i}, where X_i = min{T_i1, T_i2, C_i}, and Z_i denote the risk scores. Here the censoring C_i is due to administrative reasons such as the end of follow up, and thus we assume C_i is independent of both T_i1 and T_i2.

In the presence of competing risks, subjects who experience the event of interest are those with X_i < t₀ and Δ_i = 1. Based on this definition, for a risk scoring system Z, the time-dependent PPV and TPR for CHF are defined as

$${\text{PPV}}_{t_0}^{\text{CHF}}(z)=\mathit{Pr}\{T<t_0,\mathrm{\Delta }=1|Z\ge z\}\text{and}{\text{TPR}}_{t_0}^{\text{CHF}}(z)=\mathit{Pr}\{Z\ge z|T<t_0,\mathrm{\Delta }=1\}.$$

Consequently, the time-dependent AP is defined as ${\text{AP}}_{t_0}^{\text{CHF}}=\int {\text{PPV}}_{t_0}^{\text{CHF}}(z)d{\text{TPR}}_{t_0}^{\text{CHF}}(z)$.

With the observed data 𝒟, the PPV and TPR can be estimated by

$${\widehat{\text{PPV}}}_{t_0}^{\text{CHF}}(z)=\frac{{\sum }_{i=1}^n{\widehat{w}}_{t_0,i}I(Z_i\ge z)I(X_i<t_0)I({\mathrm{\Delta }}_i=1)}{{\sum }_{i=1}^{n}I(Z_i\ge z)},{\widehat{\text{TPR}}}_{t_0}^{\text{CHF}}(z)=\frac{{\sum }_{i=1}^n{\widehat{w}}_{t_0,i}I(Z_i\ge z)I(X_i<t_0)I({\mathrm{\Delta }}_i=1)}{{\sum }_{i=1}^n{\widehat{w}}_{t_0,i}I(X_i<t_0)I({\mathrm{\Delta }}_i=1)},$$

where ${\widehat{w}}_{t_0,i}^C$ is the same as the one given in equation (5). Note that the weights have expectation 1 given (T_i1, T_i2, Z_i). Under competing risks, conditioning on (T_i1, T_i2, Z_i), whether or not an event (type 1 or 2) is observed before time t₀ depends on only the censoring distribution. Thus, the weights remain the same as equation (5).

3.3. Comparing two risk scores

We consider comparing two risk scores Z₁ and Z₂ in terms of AP_t0. In many studies, both risk scores Z₁ and Z₂ are calculated for each individual. With paired data, we can quantify the relative predictive performance of Z₁ vs. Z₂, using the difference or ratio of their respective time-dependent AP, specifically

$$\mathrm{\Delta }{\text{AP}}_{t_0}={\text{AP}}_{Z_1,t_0}-{\text{AP}}_{Z_2,t_0}\text{and}{\text{rAP}}_{t_0}={\text{AP}}_{Z_1,t_0}/{\text{AP}}_{Z_2,t_0},$$

where AP_Z1,t0 and AP_Z2,t0 denote the time-dependent AP for Z₁ and Z₂ at t₀ respectively.

The AP difference ΔAP_t0 and AP ratio rAP_t0 can be estimated by ${\widehat{\mathrm{\Delta }\text{AP}}}_{t_0}={\widehat{\text{AP}}}_{Z_1,t_0}-{\widehat{\text{AP}}}_{Z_2,t_0}$ and ${\widehat{\text{rAP}}}_{t_0}={\widehat{\text{AP}}}_{Z_1,t_0}/{\widehat{\text{AP}}}_{Z_2,t_0}$ respectively, where ${\widehat{\text{AP}}}_{Z_1,t_0}$ and ${\widehat{\text{AP}}}_{Z_2,t_0}$ are the the nonparametric estimator ${\widehat{\text{AP}}}_{t_0}$ in (6) of Z₁ and Z₂ respectively. The bootstrap method descried in Section 3.1 can be used to construct a CI for ΔAP_t0 or rAP_t0, and test H₀ : ΔAP_t0 = 0 or H₀ : rAP_t0 = 1 for any given time point t₀. Specifically, for ΔAP_t0 and rAP_t0, the CI could be obtained based on the empirical distribution of the B bootstrap counterparts of ${\widehat{\mathrm{\Delta }\text{AP}}}_{t_0}$, denoted by ${\widehat{\mathrm{\Delta }\text{AP}}}_{t_0}^b={\widehat{\text{AP}}}_{Z_1,t_0}^b-{\widehat{\text{AP}}}_{Z_2,t_0}^b$, and of ${\widehat{\text{rAP}}}_{t_0}$, denoted by ${\widehat{\text{rAP}}}_{t_0}^b={\widehat{\text{AP}}}_{Z_1,t_0}^b/{\widehat{\text{AP}}}_{Z_2,t_0}^b$, respectively, where ${\widehat{\text{AP}}}_{Z_1,t_0}^b$ and ${\widehat{\text{AP}}}_{Z_2,t_0}^b$ are the estimated AP_t0 for Z₁ and Z₂ based on the same bootstrap resample, b = 1, ⋯, B.

4. Simulation study

We conducted a simulation study to examine the performance of the time-dependent AP estimator in finite samples. In this simulation study, we considered two risk scores U₁ and U₂. They were generated from a standard normal distribution N(0, 1). The event time associated with both risk scores for the i-th subject was generated from the following model

$$log(T_i)=7.2-1.1U_{i1}-2.5U_{i2}-1.5\mathit{log}(U_{i1}^2)+{\epsilon }_T,$$

where ε_T ∼ N(0, 1.5). This setting provides an example where the ROC curves of the two risk scores cross at time t₀ = 8, shown in Figure 1, with AUC_U1,t0 and AUC_U2,t0 are similar in values. On the other hand, the PR curve of U₁ dominates that of U₂ over the most range of the TPR with AP_t0 of U₁ greater than that of U₂.

Figure 1.

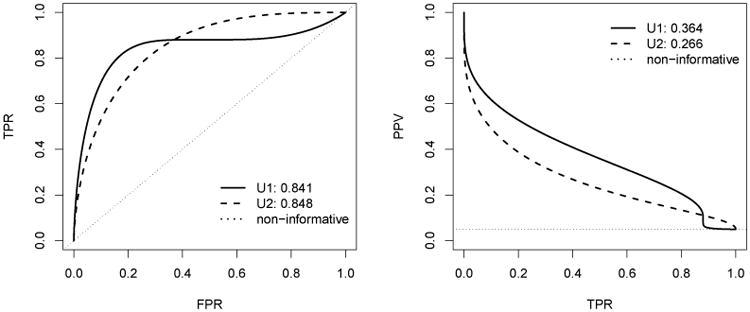
The ROC curves in the left panel and the precision-recall curves in the right panel for the two risk scores U₁ and U₂ at t₀ = 8 when the event rate is 5%. In the right panel, the dotted curve for the non-informative marker corresponds to cumulative incidence rate of the event in the target population. The numbers shown in graph correspond to the AUC and the AP values.

The censoring time C_i was generated following C_i = min(A_i, B_i + 1) where A_i ∼ Uniform(0, 50), and B_i ∼ Gamma(25, 0.75). This configuration results in about 50% of censoring overall. Let X_i = min(T_i, C_i), δ_i = I(T_i ≤ C_i). In this setting, the censoring time is independent of both the event time and risk scores.

We considered three prediction time points t₀ where the corresponding event rates, r = P(T_i < t₀), are 0.01, 0.05 and 0.1, respectively. To allow a reasonable number of events by t₀, we generated the data {(X_i, δ_i, U_1i, U_2i), i = 1,…, n} with sample size n being 2000 and 5000 (Tables 1 and 2). In each table, we report the summary statistics of the estimators of two time-dependent APs for two risk scores as well as the two forms of the comparison between these two risk scores, ΔAP_t0 = AP_U1,t0 − AP_U2,t0 and rAP_t0 = AP_U1,t0/AP_U2,t0. The summary statistics are calculated based on 1000 repetitions, and they are bias, empirical standard error (ESE) of the estimator, average standard errors from bootstrap (ASE^b), and the empirical coverage probability (ECOVP^b) of 95% confidence intervals obtained from 1000 bootstrap resamples as described in Section 3.

Table 1. Results of simulation with sample size 2000.

t0	Event rate	Risk score	AP					AUC
			TRUE	BIAS	ESE	ASEb	ECOVPb(%)	TRUE
0.5	0.0101	U1	0.182	0.0361	0.0806	0.0794	92.2	0.920
		U2	0.124	0.0339	0.0687	0.0679	94.1	0.904
		Δ	0.058	0.0251	0.102	0.116	96.1	0.016
		Ratio	1.47	0.4820	1.470	1.740	92.4	1.02
8	0.0495	U1	0.364	0.0085	0.0508	0.0499	94.4	0.841
		U2	0.266	0.0121	0.0435	0.0439	94.8	0.848
		Δ	0.098	-0.0028	0.0707	0.072	96.3	-0.007
		Ratio	1.37	0.0123	0.310	0.322	95.8	0.99
36	0.0991	U1	0.462	0.0060	0.0416	0.0431	94.2	0.786
		U2	0.375	0.0074	0.0387	0.0393	96.3	0.824
		Δ	0.087	-0.0045	0.0655	0.0633	95.7	-0.038
		Ratio	1.23	-0.0010	0.189	0.187	94.5	0.95

Table 2. Results of simulation with sample size 5000.

t0	Event rate	Risk score	AP					AUC
			TRUE	BIAS	ESE	ASEb	ECOVPb(%)	TRUE
0.5	0.0101	U1	0.182	0.0185	0.0498	0.0503	93.6	0.920
		U2	0.124	0.0154	0.0415	0.0415	93.6	0.904
		Δ	0.058	0.0056	0.0696	0.0712	94.2	0.016
		Ratio	1.47	0.1490	0.709	0.756	92.9	1.02
8	0.0495	U1	0.364	0.0041	0.0327	0.0324	94.0	0.841
		U2	0.266	0.0043	0.0285	0.0280	95.5	0.848
		Δ	0.098	-0.0005	0.0473	0.0460	96.3	-0.007
		Ratio	1.37	0.0099	0.209	0.204	94.5	0.99
36	0.0991	U1	0.462	0.0023	0.0273	0.0275	95.0	0.786
		U2	0.375	0.0015	0.0247	0.0251	95.5	0.824
		Δ	0.087	0.0003	0.0398	0.0402	95.1	-0.038
		Ratio	1.23	0.0058	0.117	0.120	95.0	0.95

These results show that the estimators of both time-dependent APs and the comparisons have small biases for all t₀ values and different sample sizes. The bias decreases with increasing event rate and increasing sample size. Also, the standard errors ASE^b obtained from bootstrap were close to the empirical standard errors. Thus, the confidence intervals attained the nominal coverage probabilities for both smaller sample size 2000 and larger sample size 5000.

We remark that this simulation provides an illustrative example of the relationship between ROC curve and PR curve as well as the relationship between the AUC and the AP [17, 18]. When the ROC curves of two competing risk scores cross, the PR curves cross too. In situations like this, the AUC and the AP may rank the risk scores differently. In our simulation setting, U₂ outperforms U₁ according to the AUC, which indicates that U₂ is better at discriminating between subjects who experiences the event before t₀ and those who are event-free. On the other hand, U₁ outperforms U₂ according to the AP, which suggests that U₁ is a better screening tool for stratifying subjects into different risk groups.

5. Data Analysis

In this section, we illustrate the use of AP_t0 metric with a data set from the Childhood Cancer Survivor Study [21]. This cohort follows children who were initially treated for cancer at 26 US and Canadian institutions between 1970 and 1986 and who survived at least 5 years after their cancer diagnosis. Among the survivors, cardiovascular disease has been recognized as a leading contributor to morbidity and mortality [30]. To inform future screening and intervention strategy for congestive heart failure (CHF) in this population, Chow et al. [6] developed several risk score systems using the CCSS data and validated them on external cohorts. For the purpose of illustration, we chose two of these risk scores and evaluated their predictive performance using the proposed AP_t0.

We included 11,457 subjects in our analysis from the CCSS study who met the original study inclusion criteria and had both risk scores. In this data, a total of 248 subjects experienced the CHF and 842 subjects died due to other causes by the end of last follow up. Between the two risk scoring systems we focused on in this data analysis, the simpler model used information on age at cancer diagnosis, sex, whether the patient was exposed to chest radiotherapy, and whether the patient was exposed to a particular chemotherapy agent. We refer to this model as the simple model. The more elaborate model, known as the heart dose model, included detailed clinical information on the average radiation dose to the heart and the cumulative dose of the specific chemotherapy agent, along with age at diagnosis and sex. This is an example where a simple risk score system utilizes minimum treatment information and can be used for any patient by virtually all clinicians, while the more complex risk score system demands specific dose information which may not be readily available to clinicians providing long-term follow-up care. We obtained the original risk scores of the simple model and the heart dose model from the reference study [6]. Briefly, these scores were constructed via linear combinations of the corresponding covariates, where the regression coefficients were obtained from Poisson regression models.

The outcome of interest in this data analysis is the time to the occurrence of CHF. However, the CHF event might not be observed due to death from other causes such as cancer recurrence and progression [27], which are competing risk events. Since the CHF is our main interest, we only show the results for CHF. Table 3 reports the estimated AP_t0 with 95% CIs for both the simple model (denoted by AP_s,t0) and heart dose model (denoted by AP_h,t0) at t₀ = 20 and 35 years post-diagnosis where the corresponding estimated event rates were 1.2% and 4.4% respectively. These two models were compared using the difference and ratio of AP, i.e. ΔAP_t0 = AP_h,t0 − AP_s,t0 and rAP_t0 = AP_h,t0/AP_s,t0. In addition, we also provided the estimated time-dependent AUC (AUC_t0) at these two time points as well as the difference and ratio of AUCs between these two models ΔAUC_t0 = AUC_h,t0 − AUC_s,t0 and rAUC_t0 = AUC_h,t0/AUC_s,t0. To illustrate the time-varying performance for each model as well as the comparison between these two models over time, the estimates of AP_t0, AUC_t0, ΔAP_t0, ΔAUC_t0, rAP_t0, and rAUC_t0 versus t₀ = 15, 16, ⋯, 34, 35 were plotted in Figure 2. Note that the time-dependent AUC for CHF is also estimated using the extension of the IPW estimator under competing risks [28, 29].

Table 3.

Estimated ${\text{AP}}_{t_0}^{\text{CHF}}$ and AUC^CHF_t0 with 95% CIs for two risk scoring systems at t₀ = 20 and 35 years, respectively. The first comparison is difference measured by ΔAUC and ΔAP, and the second comparison is ratio measured by rAP and rAUC.

t0	Event rate	Risk score system	APCHF	AUCCHF
20 years	0.0120	Simple	0.037 (0.028, 0.051)	0.786 (0.746, 0.824)
		Heart dose	0.072 (0.047, 0.120)	0.820 (0.780, 0.859)
		Δ	0.035 (0.015, 0.077)	0.035(0.013, 0.056)
		Ratio	1.95 (1.42, 2.90)	1.04 (1.02, 1.07)
35 years	0.0440	Simple	0.073 (0.062, 0.088)	0.812 (0.778, 0.846)
		Heart dose	0.107 (0.088, 0.135)	0.820 (0.784, 0.856)
		Δ	0.034(0.020, 0.055)	0.008 (-0.016, 0.029)
		Ratio	1.46 (1.26, 1.71)	1.01 (0.98, 1.04)

Figure 2.

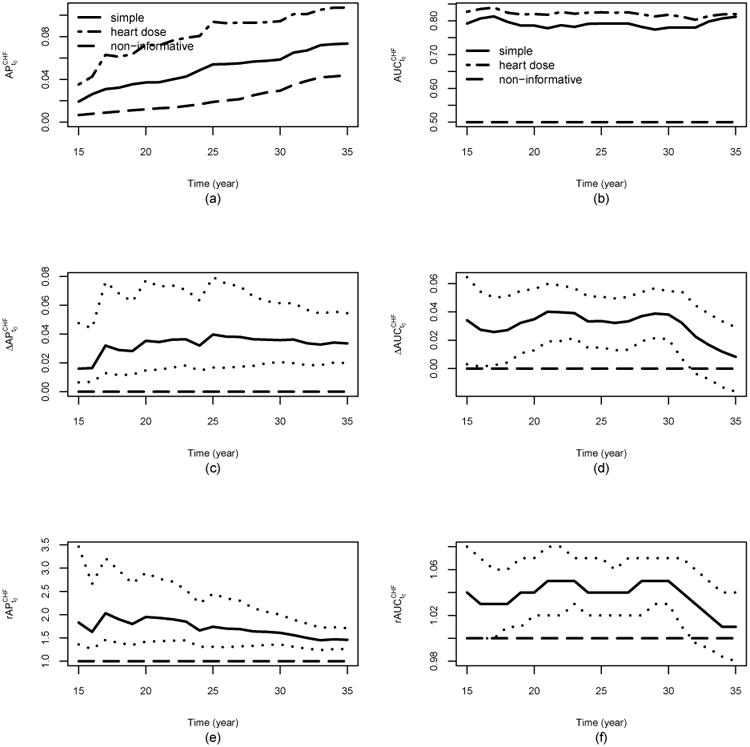
CCSS Data analysis: panel (a) shows the estimates of the time-dependent AP with interest as CHF for the simple model ${\text{AP}}_{s,t_0}^{\text{CHF}}$ and heart dose model ${\text{AP}}_{h,t_0}^{\text{CHF}}$; panel (b) shows the estimates of the time-dependent AUC with interest as CHF for the simple model ${\text{AUC}}_{s,t_0}^{\text{CHF}}$ and heart dose model ${\text{AUC}}_{h,t_0}^{\text{CHF}}$; panel (c) shows the estimates of $\mathrm{\Delta }{\text{AP}}_{t_0}^{\text{CHF}}={\text{AP}}_{h,t_0}^{\text{CHF}}-{\text{AP}}_{s,t_0}^{\text{CHF}}$, the difference of the time-dependent AP between the heart dose model and the simple model with interest as CHF; panel (d) shows the estimates of $\mathrm{\Delta }{\text{AUC}}_{t_0}^{\text{CHF}}={\text{AUC}}_{h,t_0}^{\text{CHF}}-{\text{AUC}}_{s,t_0}^{\text{CHF}}$, the difference of the time-dependent AUC between the heart dose model and the simple model with interest as CHF; panel (e) shows the estimates of ${\text{rAP}}_{t_0}^{\text{CHF}}={\text{AP}}_{h,t_0}^{\text{CHF}}/{\text{AP}}_{s,t_0}^{\text{CHF}}$, the ratio of the time-dependent AP of the heart dose model over that of the simple model with interest as CHF; panel (f) shows the estimates of ${\text{rAUC}}_{t_0}^{\text{CHF}}={\text{AUC}}_{h,t_0}^{\text{CHF}}/{\text{AUC}}_{s,t_0}^{\text{CHF}}$, the ratio of the time-dependent AUC of the heart dose model over that of the simple model with interest as CHF. The dotted lines in panels (c) to (f) represent the pointwise 95%CI for $\mathrm{\Delta }{\text{AP}}_{t_0}^{\text{CHF}}$, $\mathrm{\Delta }{\text{AUC}}_{t_0}^{\text{CHF}}$, ${\text{rAP}}_{t_0}^{\text{CHF}}$, and ${\text{rAUC}}_{t_0}^{\text{CHF}}$, respectively. In all the plots, the dash line for the non-informative marker corresponds to cumulative incidence rate of the event in the target population.

The results in Table 3 show that the heart dose model outperforms the simple model at both time points. For example, the estimated AP₂₀ of the heart dose model is 0.072, which indicates that by 20 years post-diagnosis, using the risk score from the heart dose model, we expect that on average 7.2% of subjects with a high risk score (compared to the risk score of a randomly selected subject who experiences the event before t₀) will experience heart failure. This AP is six times of the event rate 1.2%, which corresponds to the AP of a non-informative risk score system. In contrast, the estimated AP₂₀ of the simple model is 0.037, roughly half of that of the heart dose model ( ${\widehat{\text{rAP}}}_{20}=1.95$ with 95% CI: 1.42 - 2.90; ${\widehat{\mathrm{\Delta }\text{AP}}}_{20}=0.035$ with 95% CI: 0.015 - 0.077). At 35 years post diagnosis, the heart dose model is significantly better than the simple model with ${\widehat{\text{rAP}}}_{35}=1.46$ (95% CI: 1.26 - 1.71) and ${\widehat{\mathrm{\Delta }\text{AP}}}_{35}=0.034$ (95% CI: 0.020 - 0.055). Indeed, the plots (c) and (e) in Figure 2 show that in terms of the AP_t0, the heart dose model outperforms the simple model at identifying the high risk subjects from the targeted population at all time points considered. On the other hand, the plots (d) and (f) in Figure 2 show that the AUCs are similar between these two models towards the end of time period. Especially, ΔAUC is not significantly different from 0 after t₀ = 31. For example ${\widehat{\mathrm{\Delta }\text{AUC}}}_{35}=0.008$ (95% CI: -0.016 - 0.029, p-value=0.47) and ${\widehat{\text{rAUC}}}_{35}=1.01$ (95% CI: 0.98 - 1.04), shown in Table 3. It suggests that according to the AUC, the heart dose model performs similar when compared to the simple model towards the end of the time period under consideration. If, due to incorporating more information, the heart dose model is indeed superior to the simple model in terms of identifying the high risk individuals, the results in Table 3 and Figure 2 implies that the AP might be a better metric for discriminates the risk prediction performance than the AUC does.

6. Discussion

One main goal of clinical risk prediction is to screen the asymptomatic population and to stratify them for tailored intervention. Accuracy measures such as PPV_t0 is preferred for this purpose. However, the calculation of PPV_t0 demands a threshold for continuous risk scores, which can create practical difficulties for evaluating risk score systems, especially when more than two systems are compared. In this paper, we defined and interpreted AP_t0, which is the area under the time-dependent precision-recall curve, for event time data. We proposed a nonparametric estimator of AP_t0 as well as a difference estimator and a ratio estimator of AP_t0 for comparing two competing risk score systems. We also extend the estimation procedure to the setting of competing risks. We suggested the use of the bootstrap method for inference, which is broadly applicable in practical settings. We also developed an R package APtools for download available in CRAN which implements our method for binary and survival outcomes. Our proposed metric is of interest when the outcome being examined is infrequent, as often the case with disease screening.

AUC has been the most widely used performance metric in the clinical research community. A number of authors have pointed out that the AUC is informative on the classification performance and discrimination power [31, 12, 19]. However, for some clinical settings such as screening, AUC might not be the optimal metric for assessing the predictive accuracy performance [11, 12]. Consistent with the criticism on the insensitivity of the AUC in evaluating risk prediction models [10], our data analysis illustrated that using the AUC as the metric, the performance of the simple model and the heart dose model appears close towards the end of the time period under consideration. However, based on the AP, the heart dose model outperforms the simple model at all times.

McIntosh and Pepe [32] showed that the true risk probability P(T < t₀ | Z) is the optimal risk score function of a marker Z because the ROC curve is maximized at every point. Thus, the AUC is maximized under the true risk probability. The relationship between the ROC curve and the PR curve implies that the true model also optimizes the PR curve [17], which means that the AP is maximized under the true model. Therefore, both AUC and AP are proper scoring rules [33], but not strictly proper scoring rules. This is because they are both order-based metrics, so the optimal risk scores are not unique.

In practice, finding the true model is challenging because the disease mechanisms are often complicated. The available risk score systems are usually not optimal. When comparing different non-optimal risk score systems, the ranking of their AUCs and APs are not necessarily concordant; our simulation study in Section 4 gives such an example. Risk scores which perform well in separating individuals experienced event of interest from event-free individuals (as measured by the AUC) may perform poorly in identifying a higher risk subpopulation (as measured by the AP). We are not suggesting that AP can replace AUC. When the objective is screening through risk stratification, compared to the AUC, the AP as the summary metric of PPV is an alternative metric, which might be better suited, for evaluating the usefulness of the risk scores and comparing the predictive performance among competing risk scores.

In comparing AUCs of different risk scores, the comparison takes the form of the difference rather than the ratio almost exclusively in the literature. In comparing APs, we prefer to use the ratio of APs. First, the form of ratio has been used in [12] to compare PPV. In addition, AP depends on the event rate. Taking the ratio provides a measure of comparative effect size, and gives an “honest” comparison of different risk scores with the influence of the event rate minimized. Particularly, for a single risk score Z, the ratio AP_z,t0/π_t0 can be regarded as the relative predictive performance of Z compared to a non-informative risk score.

Zheng et al. [12, 14] proposed to use the curves of PPV_t0 versus risk score quantiles as an assessment tool for quantifying predictive accuracy. One curve corresponds to one particular value of t₀, which limits its ability to assess the accuracy across time points. In contrast, plotting AP_t0 against time could facilitate visualizing the performance of different risk score systems over time in one single plot.

Making the appropriate choice of prediction accuracy metrics is guided by primary research interests. Discrimination is a key component in evaluating the performance of the risk scores. Other aspects are also important such as calibration, which captures how well the predicted risks agree with the actual observed risks.

Another relatively new method for the evaluation of prediction models is the decision curve analysis (DCA) which uses the concept of net benefit [34, 35]. AP_t is similar to DCA in that they are both developed specifically for evaluating prediction performance with clinical utility in mind. Both are relatively easy to understand and to apply by clinical researchers, and can be directly applied to a validation dataset. In addition, neither requires information on the cost of treatment or patient values to compare competing models. There are also important differences between these two methods. AP is a threshold free summary index of the Precision-Recall curve, but the net benefit relies on threshold probability values. We can plot AP_t vs. time plot to inspect the prediction performance overtime, which is not feasible in DCA analysis without specifying a threshold probability for net benefit. AP_t is an overall metric of prediction accuracy while the DCA is decision-analytic in nature and facilitates an informed decision based on the clinical values of the prediction model. In addition, to carry out DCA for competing models, one assumption is that all models to be compared are well calibrated, which is not necessary for AP because it is a rank-based statistic.

Unlike the AUC, the AP is event rate dependent and should be estimated in a prospective cohort or population-based study. AP cannot be estimated from a case-control study; the estimate will be of very little use because the prevalence rate is artificially fixed by the study design. While the range of the AUC is always between 0.5 and 1, the range of AP is between the event rate and 1. While AP's wide range could be advantageous in differentiating risk score systems, caution is needed when re-evaluating risk score systems in other study populations for the same outcome. This is because the underlying event rate may differ among populations. Thus, it is possible that AP will select different risk score systems as superior for the same outcome in different study populations.

For future work, we will consider estimating the time-dependent AP with multiple risk factors, as well as the incremental value of AP by adding new risk factors such as biomarkers on top of an existing risk profile. In addition, similar to the partial AUC, partial AP could be defined as the area over a certain range of interest, such as those at the low values of TPR where PPV is typically high.