L-edge sum rule analysis on 3d transition metal sites: from d¹⁰ to d⁰ and towards application to extremely dilute metallo-enzymes

Abstract

According to L-edge sum rules, the number of 3d vacancies at a transition metal site is directly proportional to the integrated intensity of the L-edge X-ray absorption spectrum (XAS) for the corresponding metal complex. In this study, the numbers of 3d holes are characterized quantitatively or semi-quantitatively for a series of manganese (Mn) and nickel (Ni) complexes, including the electron configurations 3d¹⁰→3d⁰. In addition, extremely dilute (<0.1% wt./wt.) Ni enzymes were examined with two different approaches: 1) by using a high resolution superconducting tunnel junction (STJ) X-ray detector to obtain XAS spectra with very high signal-to-noise ratio, especially in the non-variant edge jump region; and 2) by adding an inert tracer to the sample that provides a prominent spectral feature to replace the weak edge jump for intensity normalization. In this publication, we present for the first time: 1) L-edge sum rule analysis for a series of Mn and Ni complexes that include electron configurations from an open shell 3d⁰ to a closed shell 3d¹⁰; 2) a systematic analysis on the uncertainties, especially on that from the edge jump, which was missing in all previous reports; 3) a clearly-resolved edge jump between the pre-L₃ and the post-L₂ regions from an extremely dilute sample; 4) an evaluation of an alternative normalization standard for L-edge sum rule analysis. XAS from two copper (Cu) proteins measured with a conventional semiconductor X-ray detector are also repeated as bridges between the Ni complexes and the dilute Ni enzymes. The differences between measuring 1% Cu enzymes and measuring < 0.1% Ni enzymes are compared and discussed. This study extends L-edge sum rule analysis to virtually any 3d metal complex and any dilute biological samples that contain 3d metals.

1. Introduction

The oxidation state is an indicator of the degree of oxidation for a particular atom and is one of the most-pursued quantities in chemistry, because the distribution of electron/charge density in inorganic complexes or enzymatic metal sites determines their chemical, physical and biological functions/properties. Unlike alkali or alkaline earth metals, transition metals can have different oxidation states, and thus different chemical properties. For example, manganese (Mn) complexes^{1, 2} can have possible Mn^II to Mn^VII including electron configurations from 3d⁵ to 3d⁰, nickel (Ni) complexes^{3, 4} can have Ni⁰ to Ni^IV (from 3d¹⁰ to 3d⁶), while copper complexes can have Cu^I and Cu^II sites. In inorganic and bioinorganic chemistry, resolved oxidation states, i.e. the measured number of electrons/holes localized in the bonding orbital, have helped understand the chemical and biochemical roles of many metal sites,^4–6 while unresolved oxidation states have contributed to longstanding controversies in many systems.^{3, 7–11} The oxidation state is typically characterized by an integer, which is the hypothetical charge in an atom assuming the bonding is 100% ionic. Since a real 100% ionicity does not exist, and there is ambiguity of the assignment of the oxidation state of the electronegative ligands, metal oxidation states may be represented more quantitatively by the number of vacancies (holes) localized at the metal sites (e.g. Mn or Ni).⁴

X-ray absorption spectroscopy (XAS), especially L-edge XAS (or L XAS), is one of the best methods to investigate the oxidation states of 3d transition metals via absorption edge positions as well as their spectral features.^{12,4, 13} In an L XAS, the L₃ edge’s centroid energies, the branching ratios of I_L3/(I_L2+I_L3), and the rich multiplet structures are all sensitive to electronic structures.^{4, 14–16} For example, L XAS exhibit about 2 eV per oxidation state change (eV/oxi) for the Mn complexes and 0.9 eV/oxi for Ni complexes. L-edge centroids will often be sufficient to assign oxidation states.^4,34–36 For Mn complexes, the branching ratio has also been used to determine the Mn oxidation states.^{1, 17} Nevertheless, the shifts in L₃ centroids are also affected by the changes in the final state in addition to the differences in the ground states. The spectral multiplets and branching ratios are also sensitive to metal’s electronic spin states and its coordination geometries, in addition to their oxidation states.

Sum rules link the integrated XAS absorption intensity to the number of holes localized in the X-ray absorbing metal.^{4, 18} For 3d metals, L-edge XAS probes electronic transitions at 2p→3d, 2p→4s, and 2p→continuum, as shown in Fig. 1 (middle panel). A typical L-edge XAS spectrum therefore has a pair of strong absorption peaks corresponding to 2p_3/2→3d and 2p_1/2→3d transitions (2p→4s is 20-fold weaker) and an invariant edge jump step between the pre-L₃ and post-L₂ regions corresponding to 2p→continuum transitions. Therefore the total number of 3d holes localized in the X-ray absorber is proportional to the integrated L_2,3-edge peaks (2p_{1/2, 3/2}→3d) intensity when normalized to this invariant edge jump, as reported previously.^{4–6, 19–21} Besides being able to obtain a number of 3d holes (H_3d), the integrated L intensity I_L is a pure ground state property and is well-suited for investigating d-shell vacancies.⁴ In the past, L-edge sum rule analysis has been applied to one set of Ni⁴ and one set of Cu^{5, 6} model complexes, and a few Cu proteins with Cu concentrations of order ~1% wt./wt.^{5, 6} However, the error bars for their XAS (especially for the weak edge jump) were not well-discussed or controlled. In addition, L-edge sum rule analysis on Mn or other 3d metal complexes and on samples with < 0.1% wt./wt. metal concentration are not available.

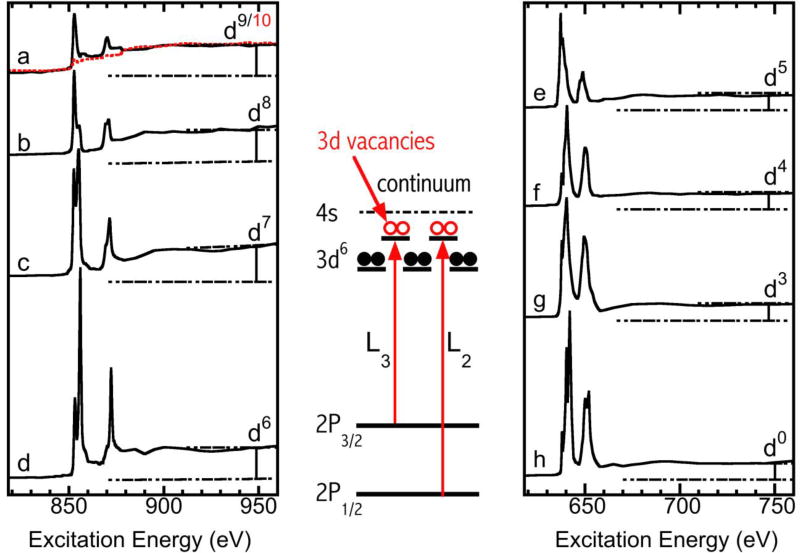
Figure 1.

Normalized L-edge XAS spectra. Left panel (from top to bottom): Na₂[Ni⁰(RS)₄] (a, dashed red line), Na[Ni^I(RS)₄] (a, black line), Ni^IIO (b), K₃Ni^IIIF₆ (c), KNi^IVIO₆ (d); right panel (from top to bottom): Mn^IIO (e), LiMn^IIIO₂ (f), Mn^IVO₂ (g), KMn^VIIO4 (h); the schematic energy diagram in the middle panel illustrates the 3d holes and the L₃ and L₂ (2p→3d) transitions.

In this publication, we first characterize a series of Mn and Ni complexes with L-edge sum rule analysis. We then extend this analysis to NiFe hydrogenase (H₂ase) and CO-dehydrogenase (CODH), which have an extremely dilute Ni concentration of < 0.1% wt./wt. Two approaches to make this extension available are discussed. The differences between measuring 1% Cu enzymes and measuring < 0.1% Ni enzymes are also addressed. For the first time, we present: 1) L-edge sum rule analysis on a series of 3d metal complexes, which include electron configurations from an open shell 3d⁰ to a closed shell 3d¹⁰; 2) a systematic analysis of the error bars for L-edge XAS, especially for their edge jump regions; 3) a clearly-resolved edge jump between the pre-L₃ and the post-L₂ regions for an extremely dilute sample (< 0.1% Ni); and 4) a detailed evaluation on using an alternative normalization standard for L-edge sum rule analysis.

2. Experimental section

Samples

Ni^IIF₂, Ni^IICl₂, Ni^IIBr₂, Ni^IIO, Ni^II(OH)₂, Mn^IIO, LiMn^IIIO₂, Mn₂^IVO₃, Mn^IVO₂, and KMn^VIIO₄ were purchased from Sigma-Aldrich, stored in desiccator and used without further treatment. Ionic K₃Ni^IIIF₆ complex²² and LiNiO₂, Ni₂O₃, KNi^IVIO₆^{23, 24} were provided by Dr. Neil Bartlett from UC Berkeley and Dr. Melendres from Argonne National Lab respectively. Covalent Ni-S complexes Na₂[Ni⁰(SR)₄], Na[Ni^I(SR)₄], [Ni^II(SR)₄], where (SR)₄ = bis(diphenylbis((methylthio)methyl)borate and [PhTt^tBu]Ni^ICO, [PhTt^tBu]Ni^II(Cl), where PhTt^tBu = phenyltris((tert-butylthio)methyl)borate,^{25, 26} were prepared in Dr. Charles Riordan’s group from the University of Delaware. All solid model complexes were finely ground and pressed onto a piece of UHV compatible carbon tape inside a nitrogen (N₂) atmosphere glovebox (although not all the samples are air sensitive). Such prepared samples were loaded into the UHV measurement chamber with a vacuum loadlock.

Blue Cu protein from the construct engineered azurin and from plastocyanin were prepared^{5, 27–29} by Professor E.I. Solomon’s laboratory at Stanford University. They were used as examples of metalloenzymes with moderate metal concentration (e.g ~1% Cu, wt./wt.). Clostridium thermoaceticum-CODH (or Ct-CODH) was purified and prepared^{30, 31} in Dr. P. W. Ludden’s laboratory. The 310 kDa tetramer has four Ni sites, corresponding to about 770 ppm (or 0.077%) Ni concentration. The as-isolated and H₂ reduced NiFe H₂ase solution samples (< 0.067% wt./wt.) were prepared from D. gigas H₂ase^{12, 32, 33} at Lawrence Berkeley National Laboratory. The two Ni enzymes were examples of extremely dilute samples with < 0.1% metal concentration. For most enzyme samples, partially dehydrated films were made by drying the solution samples on sapphire substrates under a H₂ atmosphere (for the H₂ reduced NiFe H₂ase sample) or a N₂ atmosphere (for other samples). For Ct-CODH enzyme, a frozen solution sample was prepared instead of partially dehydrated films.

The Ce M₅ edge at 881.7 eV is close to Ni L₃ edge at 852.6 eV and can be used as an intensity normalization standard in the Ni L-edge sum rule analysis instead of the more commonly used edge jump. To establish the method, a testing complex mixture was first prepared and evaluated. Inside the glovebox, 0.1M NiBr₂-TRIS-HCl solution was prepared, providing a sample with ~ 0.6% Ni concentration (wt./wt). The Ce(NO₃)₃•6H₂O (or Ce(NO₃)₃ for short) was then added to the 0.1M solution. Due to the extremely short penetration depth by soft X-rays (0.5 µm in H₂O and ~200Å in typical solids), the Ni, Ce and buffer mixture must be homogenized on a microscopic scale in solution. Experimentally, the best molar ratio for NiBr₂:Ce(NO₃)₃ was found to be ~ 1:5.5, when compatible signal intensities for Ni L₃ and for Ce M₅ edges were obtained in the XAS spectra. For NiFe H₂ase, Ce(NO₃)₃ was added to the as-isolated enzyme solution. The H₂-reduced solution was then prepared by incubating the as-isolated H₂ase with added Ce(NO₃)₃ under pure H₂ for >8 hours. This maintains a constant Ni:Ce ratio in the as-isolated and the reduced samples, although their absolute concentration may be different.

XAS Measurements

L-edge XAS was measured at Stanford Synchrotron Radiation Laboratory (SSRL) beamline 8–2³⁴ and at Advanced Light Source (ALS) beamline 9.3.2³⁵ and 4.0.2³⁶ inside a UHV chamber under windowless operation.^{13, 37} These beamlines have an energy resolution of 1.0 eV, 0.4 eV and 0.2 eV, respectively, at the Ni L-edge at 850 eV. For concentrated Mn and Ni complexes, the XAS spectra were measured by total electron yield (TEY)¹⁵ using a Galileo 4716 channeltron electron multiplier as photoelectron detector. The incident beam intensity (I₀) was monitored through a gold-plated grid. For biological samples or dilute NiBr₂ matrix samples, XAS were measured by partial X-ray fluorescence yield (PFY)^{12, 31} using a 30-element germanium (Ge) array detector with 180 eV energy resolution, or a 9- or 36-element superconducting tunnel junction (STJ) detector with 15 eV energy resolution.^39,40 For measuring < 0.1% Ni Ct-CODH, the use of an STJ detector was necessary to extract the weak Ni signal from the high spectral background. During these measurements, one region was defined around Ni L, Cu L or Ce M partial fluorescence signal (PF), which is proportional to the metal absorbance and incident X-ray beam intensity, while the second region was set at around the oxygen (O) K fluorescence signal used as a measure of I₀.

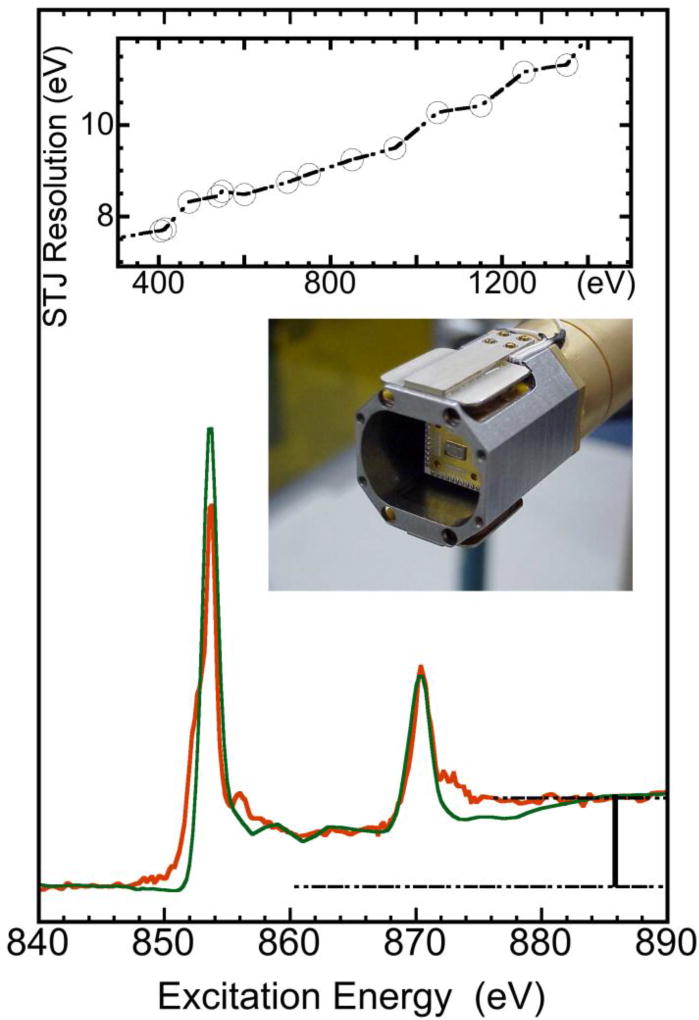
Superconducting tunnel junctions (STJs)^38–41 are high-resolution X-ray detectors that consist of two superconducting electrodes separated by an extremely thin layer of insulating material. Electric current can pass through the STJ junction via the quantum-mechanical tunneling effect. X-rays absorbed in one of the electrodes will generate free excess charges in proportion to the X-ray energy, and the subsequent increase in tunneling current can be directly read out with a room temperature amplifier. STJ X-ray detectors exploit the extremely small (~1 meV) energy gap in superconductors to achieve an order of magnitude higher energy resolution than conventional semiconductor detectors, which have an energy gap of ~1 eV. In general, our Nb-based STJ detector has a 10–20 eV energy resolution^{39, 42, 43} while a semiconductor detector has 100–300 eV^{38, 44, 45}. The higher energy resolution allows a more effective rejection of unwanted background counts and increases the signal-to-noise ratio (S/N) for the L- and M-edge PFY XAS spectra for dilute samples.^{39, 42, 43} This is especially true for resolving the weak features, such as the edge jump steps.

For the measurements at SSRL, each concentrated Ni complex spectrum was the sum of 5–6 raw scans, each blue Cu protein spectrum was the sum of 20 scans, while each NiFe H₂ase spectrum represented the sum of 40 raw scans. The Ni complexes were measured at room temperature, while the blue Cu enzymes and NiFe H₂ases were measured at 10K maintained with a liquid helium flow cryostat. At ALS, each Mn complex spectrum was the sum of 3–5 raw scans, each dilute NiBr₂ spectrum was the sum of 6 raw scans, while each Ct-CODH spectrum represented the sum of 10 raw scans. The energies were calibrated with MnO at 638.7 eV, NiF₂ at 852.7 eV, and CuO at 932.7 eV for the respective samples.⁴⁶ As the beam intensity is much stronger at ALS in comparison with that at SSRL, all the spectra were recorded at 10K (using a LHe cryostat). To further minimize the possible radiation damage and photoreduction, the position of the X-ray beam on the sample was moved for every scan. We also tested multiple short scans at one spot for all the samples at the ALS and at SSRL, but observed no spectral change under our experimental conditions.

The L-edge data processing for complex samples involves subtraction of the spectral background, using their sample holders XAS as reference (as will be addressed in detail in the Error Analysis section). These L XAS spectra were then normalized to the invariant edge jump between the pre-L₃ and the post-L₂ regions to produce the integrated L-edge spectra. The non-resonant edge jumps were then removed by subtracting a simulated two-step function. The L₃ and L₂ intensities (I_L3 and I_L2) were obtained from these spectra by integration over 929–936 and 950–955 eV for Cu proteins, over 851–858 and 868–875 eV for Ni samples, and over 634.2–657.6 eV for Mn complexes. For STJ measured Ct-CODH XAS, a process similar to the one for processing Ni complex data was used to calculate I_L3 and I_L2. For the NiFe H₂ase and the dilute NiBr₂ XAS, the integrated Ce M₅-edge intensity was used as an alternative intensity normalization standard, because these spectra do not exhibit an observable edge jump.

K-edge XAS for MnO, Mn₂O₃ and KMnO₄ were measured at BL08B2 of the SPring-8 synchrotron radiation facility in Hyogo Prefecture, Japan. The main X-ray optical elements consist of a first Rh-coated vertical collimation mirror, a double-crystal monochromator and a second Rh-coated vertical refocusing mirror. A water-cooled Si (111) double-crystal monochromator was used to produce a ~1 eV bandwidth X-ray beam with a beam size of 2.0 mm in the horizontal direction and 0.5 mm in the vertical direction. The K-edge XAS data were measured in transmission mode over an energy range from −330 to 1500 eV with respect to the Mn absorption edge by using ionization chambers to record the incoming and transmitted intensities. The transmission measurement is possible because Mn K-edge has a transmission depth of ~1 mm. The Mn K absorption edge was defined as the first peak in the first derivative spectrum of XAS data. A Mn foil with an XAS absorption edge at 6539 eV was used as the energy calibration standard for the monochromators.

3. Results and discussions

Five published Ni XAS spectra⁴ were either re-measured (on NiF₂, K₃NiF₆ and KNiIO₆) or cited (for [Ni^I/II(SR)₄]^−/0) and compared with the XAS for five new Ni and five additional Mn complexes. The errors for all fifteen L-edge XAS spectra were evaluated or re-evaluated with the new method.

XAS Spectra of Ni and Mn Complexes

Examples of the observed Ni and Mn L-edge spectra are shown in Fig. 1, with Ni complexes from d¹⁰ to d⁶ in the left panel and Mn complexes from d⁵ to d⁰ in the right panel. Since [Ni⁰(SR)₄]²⁻ has a closed 3d¹⁰ shell, its 2p→3d resonance intensity should be absent, and this is indeed the case (Fig 1a, dashed red line). The L-edge XAS spectrum is then dominated by the 2p→continuum transition, also called the edge jump. This edge jump does not change with the number of 3d holes and can therefore be used to normalize XAS spectra. All spectra in Fig. 1 were normalized to their corresponding edge jumps between the pre-L₃ and post-L₂ regions. Although [Ni⁰(SR)₄]²⁻ may not be an interesting compound in synthetic chemistry, it did provide us with the first L-edge XAS for a real d¹⁰ sample, which is rare. We emphasize that although Ni metal is also nominally Ni⁰, it has an electronic configuration of 3d⁸4s² rather than 3d¹⁰, and a typical Ni^II L-XAS feature as shown in Fig. S1 in the supplemental information (SI).

In contrast, [Ni^I(SR)₄]⁻ has a 3d⁹ configuration, opening up one d hole for obvious 2p_3/2→3d and 2p_1/2→3d resonant transitions (Fig. 1a, solid black line). As the oxidation state further increases to Ni^II, Ni^III, and Ni^IV, the number of d-holes increases gradually, and so does the L-edge resonance intensity (Fig. 1a→1d).⁴

In the right panel, although the d⁵ MnO₂ has the smallest intensity among the Mn complexes, it still has higher L₃ and L₂ intensities than the highest Ni intensity (for KNi^IVIO₆). As the Mn oxidation state continues to increase (d⁵→d⁴→d³→d⁰ in Fig. 1e→1h), the L-edge resonance intensity also increases significantly as expected. In addition to the integrated intensities, these Ni and Mn spectra contain additional information, such as L₃ centroid energies, branching ratios of I_L3/(I_L2+I_L3), and multiplet structures.^{4, 14–16} Nevertheless, as mentioned in the introduction, only integrated L intensity is a pure ground state property.

L-edge sum rule

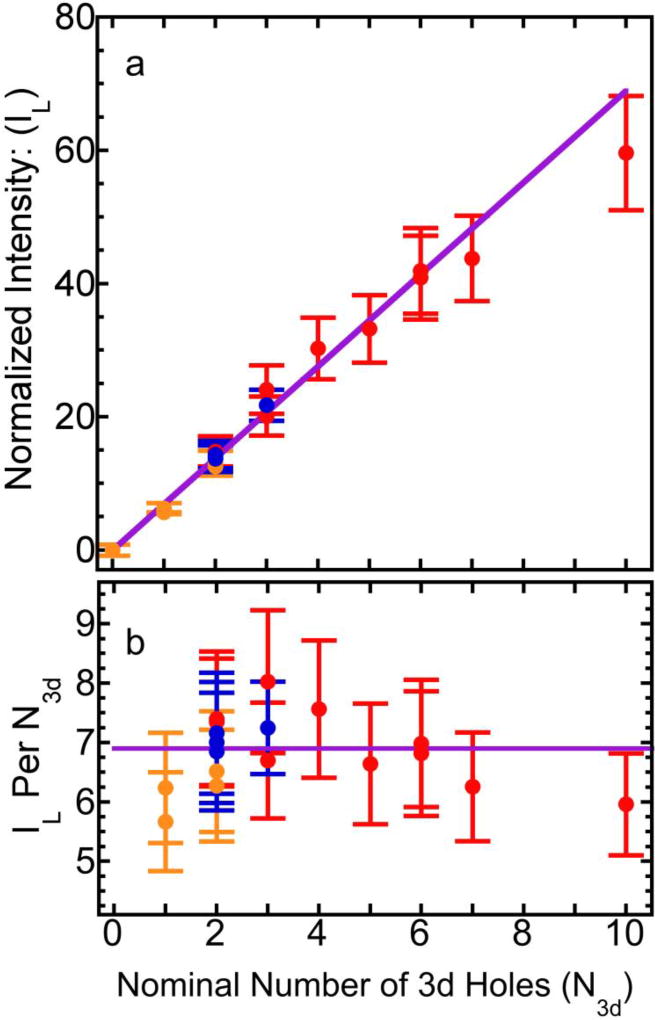
With the L-edge XAS spectra normalized to the invariant edge jump, the integrated L-edge absorption intensities I_L for our Ni and Mn complexes are listed as in Table-1 and shown as in Fig. 2a. For example, we observe 0 for [Ni⁰(SR)₄]²⁻ (d¹⁰), 14.7 for Ni^IIO (d⁸), 29.4 for KNi^IVIO₆ (d⁶), 36.8 for Mn^IIO (d⁵), 40.9 for Mn^III₂O₃ (d⁴), and 59.6 for KMn^VIIO₄ (d⁰). Here we did not attempt to evaluate the trace amount “resonant” intensity for [Ni⁰(SR)₄]²⁻ but simply set it to zero. There is a roughly linear dependence between the integrated L-edge intensity (I_L) and the nominal number of 3d holes (N_3d) as expected. The slope, which we call R, shows an averaged normalized intensity per nominal 3d hole of about R = 6.9 in Fig. 2a. Each individual data point has an errorbar, which will be discussed in the next section.

Table 1.

The integrated and normalized L intensities (I_L), edge jumps (J), L intensity derived number of 3d holes (H_3d) and their corresponding errors (δα and δ_H3d) for a series of Ni and Mn complexes with different ligand types.

Complex	dN	Coord. Atom	IL	J	α=IL/J	δα/α	δα	Obs. H3d	Obs. δH3d
Na2[Ni0(SR)4]	d10	S	0.00	1.01	0.00	--	--	0.00	--
Na[NiI(SR)4]	d9	S	5.39	0.95	5.67	0.107	0.61	0.66	0.071
[PhTttBu]NiI(CO)	d9	S	6.43	1.03	6.24	0.109	0.68	0.73	0.079
NiIIBr2	d8	Br	15.07	1.10	13.70	0.103	1.41	1.59	0.164
NiIICl2	d8	Cl	14.29	1.02	14.01	0.105	1.48	1.63	0.172
NiIIF2	d8	F	14.46	1.01	14.32	0.101	1.44	1.66	0.168
NiIIO	d8	O	16.02	1.09	14.70	0.105	1.54	1.71	0.179
[NiII(SR)4]	d8	S	11.55	0.92	12.55	0.112	1.41	1.46	0.164
K3NiIIIF6	d7	F	25.05	1.04	24.09	0.111	2.68	2.80	0.312
KNiIVIO6	d6	O	29.95	1.02	29.36	0.113	3.30	3.41	0.384
MnIIO	d5	O	34.60	0.94	36.81	0.115	4.24	4.28	0.493
LiMnIIIO2	d4	O	41.50	0.99	41.92	0.116	4.87	4.87	0.566
MnIII2O3	d4	O	42.53	1.04	40.89	0.117	4.78	4.76	0.555
MnIVO2	d3	O	45.23	1.01	44.78	0.107	4.77	5.21	0.555
KMnVIIO4	d0	O	65.56	1.10	59.60	0.097	5.78	6.93	0.672

Figure 2.

(a) The integrated L-edge intensity I_L (= I_L3+I_L2) as a function of the nominal number of 3d holes (N_3d); (b) the I_L per nominal 3d hole (per N_3d) vs. nominal number of 3d holes (N_3d). The solid purple lines are the linear correlation functions for the data presented here.

In Fig. 2a and 2b, some additional trends are worth noticing: 1) S and N based covalent Ni complexes have obviously lower R values in comparison with O and F based ionic complexes, because the S, N have lower ionicity than the more electronegative O and F; 2) For the complexes with the same ligand donor (e.g. O), the L intensity per nominal 3d hole (R value) decreases as the number of nominal 3d holes increases. This again is consistent with the lower expected ionicity for higher-valence complexes; 3) Comparison of F vs. Cl and Br complexes show R_F > R_Cl > R_Br as well (Table-1). This is caused by different negativities of the different ligands⁴⁷.

To convert the measured I_L to the numbers of actual 3d holes (H_3d, not nominal N_3d) on a calibrated absolute scale, we use standard samples for which the real numbers of 3d holes (H_3d) and their L XAS intensities (I_L) are accurately known⁴. In this study, we have: 1) Ni metal, which has an I_L = 13.1±0.7 with a band structure calculated H_3d = 1.5±0.1 per Ni atom^16,48,49; 2) NiO, for which we measure I_L = 14.7, with an estimated Ni H_3d = 1.72 from references.^{50, 51} With these two standards, the integrated L-edge intensity per 3d hole for the calibration samples is obtained as R_cal = 8.6. The average ionicity for our Ni and Mn complexes is therefore R/R_cal = 6.9/8.6 ≈ 80%.

Error Analysis

If I_L represents the L-edge peak integral and J represents the edge jump height, we can define the normalized integrated L intensity as α=I_L/J. Then the error for this normalized intensity is given by:

$$\mathrm{\delta }\mathrm{\alpha }/\mathrm{\alpha }={[{(\mathrm{\delta }{\mathrm{I}}_{\mathrm{L}}/{\mathrm{I}}_{\mathrm{L}})}^2+{(\mathrm{\delta }\mathrm{J}/\mathrm{J})}^2]}^{1/2}$$ (1)

or

$$\mathrm{\delta }\mathrm{\alpha }=({\mathrm{I}}_{\mathrm{L}}/\mathrm{J}){[{(\mathrm{\delta }{\mathrm{I}}_{\mathrm{L}}/{\mathrm{I}}_{\mathrm{L}})}^2+{(\mathrm{\delta }\mathrm{J}/\mathrm{J})}^2]}^{1/2}$$ (2)

Note that both δI_L/I_L and δJ/J contribute to δα. The δI_L is primarily from the integral’s statistical error and the uncertainty in the choice of the integration range, while δJ is due to the uncertainty in judging the height of the edge jump. As shown in the Table-1, δI_L/I_L varies between ±2.5% and ±5.0%. The relatively small uncertainty δI_L is consistent with the fact that I_L is an integrated value, which has an averaging effect. On the other hand, δJ/J is larger and varies between ±9.0 and ±11.8%. As illustrated in Fig. 3, the higher δJ/J is due to the shape of the spectral baseline (especially its tilt angle) in the edge jump region, which can be difficult to define and therefore increases the uncertainty in δJ. As it dominates the uncertainty of δα, δJ or δJ/J must be evaluated carefully. However, the errors for δα in most previous publications included only the statistical errors of δI_L plus 10% “instrumental error”,^{4,5, 6} without any consideration of δJ.

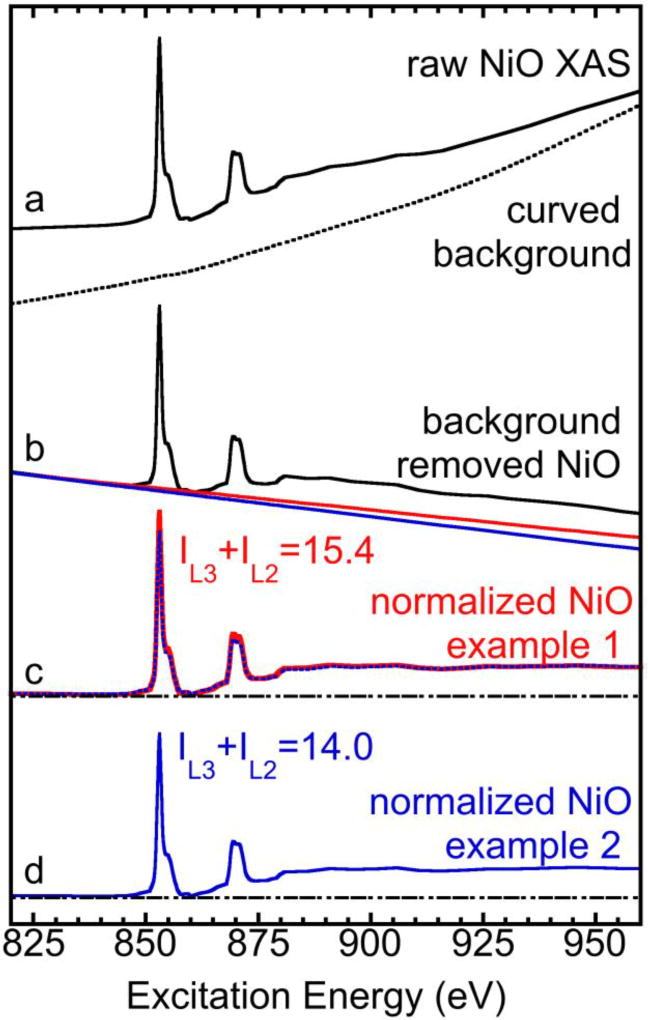
Figure 3.

(a) The measured raw NiO XAS (solid line) vs. the sample holder (as a background line reference) (dotted line); (b) NiO XAS with the background removed vs. the two possible new background slopes (blue and red); (c) NiO L XAS normalized with the example 1 processed baseline step (red) vs. the one normalized with example 2 processed baseline step (blue); (4) NiO L XAS normalized with example 2 processed baseline (blue).

To estimate the error δJ, we demonstrate the data processing for the L-edge sum rule analysis as in Fig. 3, which includes the removal of a spectral background to produce an intermediate XAS spectrum with a linear background (b, black) and the subsequent removal of this linear background to produce the final spectrum (c). Although the blank sample holder spectrum was measured every time, the real XAS background used in the data process is often its manipulation (tilt or bend) or simply a theoretical polynomial (a, dashed black line). In short, the initial background is just the fit of the XAS spectra in the non-resonance regions. The choice of the tilted background slope introduces a major error to δJ, with two extreme cases for NiO shown in Fig. 3 (b, red and blue spectra), although the judgement on edge jump step’s height may also bring in a minor error. The difference between the slopes for the two background lines is about 25%, while the difference in the peak heights for the two “final” NiO spectra (c) is about 20%. The final value for δJ/J is ± 9.9%, while its δI_L/I_L is ±3.4%. The δI_L/I_L and δJ/J for other complexes are listed in Table-1. According to equation (1), δα/α is about ±10.5% for NiO and ±9.7% – ±11.7% for other complexes. These errors are presented in Table-1 and Fig.2. Most of the “instrumental error” is actually calibratable while the rest random error should already be included in our statistical error of the data, therefore we do not need to add an arbitrary 10% instrumental error to the analysis.

When the number of 3d holes is small, the above approach (with δα/α ~ ±0.11) is still accurate enough to at least semi-quantitatively identify the metal’s oxidation state and its number of 3d holes (H_3d). For example, nominal-d⁸ [Ni^II(SR)₄] has an observed H_3d ~ 1.30–1.62 (1.46±0.16), which is clearly higher than d⁹ [Ni^I(SR)₄]⁻ (0.59–0.73); similarly, d⁷ K₃Ni^IIIF₆ has a H_3d ~ 2.49–3.11, which is also significantly higher than d⁸ Ni^IIF₂ (1.53–1.89). This is true even for some ultra-covalent complexes which have very small difference between different oxidation states. For example, derived from I_L=8.69, 11.33, 13.25,⁵² the 38–50% covalent (Ph₄As)₂Ni[S₂C2(CF₃)₂]₂, (Bu₄N)Ni[S₂C₂(CF₃)₂]₂, and Ni[S₂C₂(CF₃)₂]₂ complexes have distinguishable (meaning difference > δα defined by δα/α ~ ±0.11) H_3d=1.01, 1.32 and 1.54. Their reported L XAS⁵² are cited as in Fig. S2 in SI for a reference.

However, as α increases, the observed H_3d values for the two consecutive oxidation states can overlap if error-bars are included. Thus a clear assignment of the oxidation state is less obvious. For example, as shown in Table 1, the d⁴ Mn^III₂O₃ has a α value of 40.89±4.78, ranging from 36.11 to 45.67, while d³ Mn^IVO₂ has 44.78±4.77 (from 40.01 to 49.55) which is overlap with the α region for d⁴ Mn^III₂O₃. Under these circumstances, one has to either improve the XAS to reduce uncertainties in the edge jump δJ, or to search for alternative features in the XAS as a normalization standard for I_L. These approaches are the central topic of this publication, and we will discuss them with the L-edge sum rule analysis for dilute samples in the following sections.

Dilute Samples

For concentrated samples, the absorption features from the element of interest dominate the XAS, like those in Fig. 1. X-ray absorption of other elements such as C, N and O still contributes to the spectra as background, but their spectral features tend to be much smaller than those from the metal of interest. For dilute samples whose metal signal is weak, most spectral counts and features are due to the large background rather than due to the metal of interest. These background intensities (B) also contributes significant statistical noise δB ~ B^1/2 to both I_L and J, which increases the uncertainty of α to the point that accurate analysis eventually becomes impossible. This background problem for dilute samples can be resolved by using only the X-ray fluorescence from the element of interest as a measure of absorption in XAS, instead of using the total electron yield. If the fluorescence from the element of interest can be separated efficiently from the huge background fluorescence after X-ray excitation, the XAS detection limit can be improved significantly.

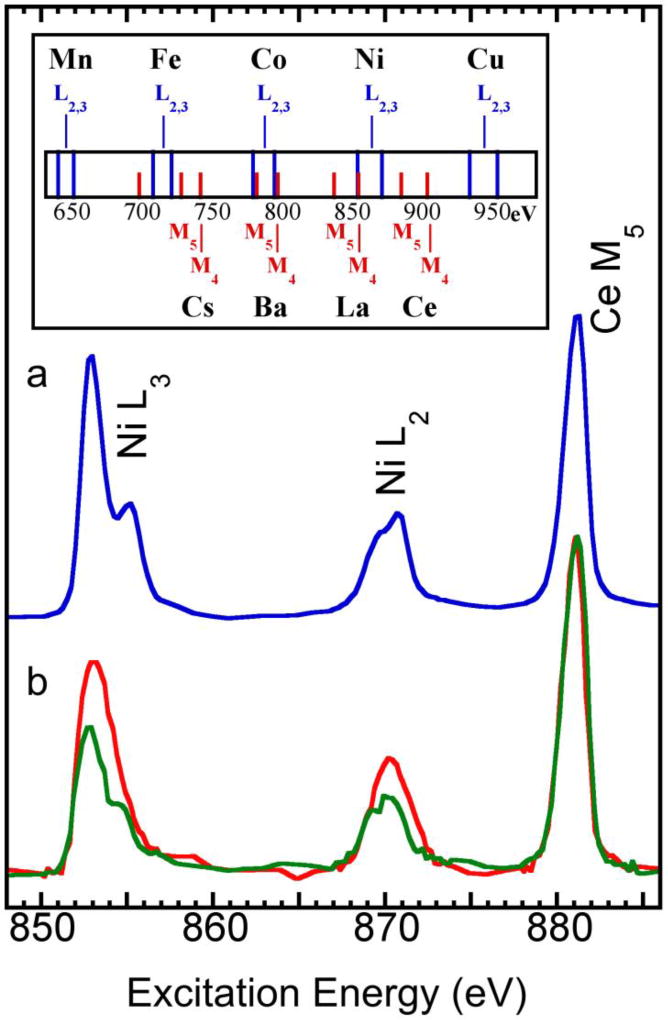
A metal concentration of ~ 1% is the highest concentration for L XAS with fluorescence detection before saturation effects start to distort the spectra.⁵³ Therefore blue copper proteins, which have a Cu concentration ~ 1% wt./wt.,^{5, 54} represent the most favorable candidates for L XAS and L-edge sum rule studies.^{5, 55,6} In this publication, we repeated Cu L-edge sum rule analysis on the blue Cu enzymes from plastocyanin (Fig. 4 insert i1)⁵ and from the construct engineered azurin (b or i2)⁶ with a Ge X-ray fluorescence detector and use them as bridges between the concentrated Ni complexes and the <0.1% Ni enzymes. Our spectra reveal a H_3d = 0.4 (i1) and 0.2 (i2) per Cu atom, respectively.

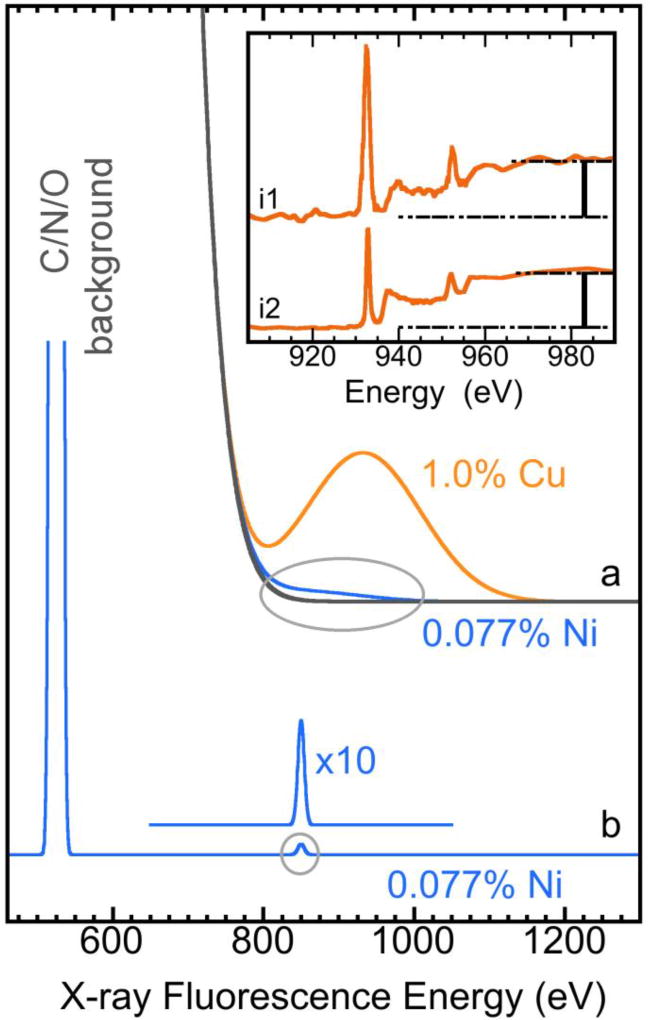
Figure 4.

An theoretical X-ray fluorescence spectrum for a hypothetical sample of 1% Cu and 0.077% Ni and O in balance: (a) measured with a 180 eV energy resolution X-ray fluorescence detector; or (b) measured with an STJ detector with 15 eV energy resolution; Inset: the normalized L XAS for Cu proteins from engineered azurin (i1)⁵ and from plastocyanin (i2)⁶ measured with a 180 eV Ge detector.

Measuring <0.1% Ni Enzymes Using A STJ detector

CODH catalyzes CO oxidation and acetyl-CoA synthesis. It is found in acetogenic, methanogenic, and sulfate-reducing bacteria, and fixes carbon on a global scale.⁵⁶ The Ct-CODH has a Ni concentration of 770 ppm, only 1/13 of the Cu concentration in blue Cu proteins, which complicates L XAS and L-edge sum rule analysis. In frozen solution samples, the Ni concentration is further reduced. Fig. 4(b) illustrates an idealized fluorescence signal for a hypothetical sample with 0.077% Ni, 1.0% Cu and O in balance, assuming negligible background from pile-up or second order excitation (the detector’s electronic background). While it is fine to resolve the 1% Cu signal with a 180 eV resolution Ge detector (Fig. 4a, orange), it is harder to resolve a signal from <0.1% Ni with the same detector and the same procedure (Fig. 4a, blue), even without any additional background. A lower metal concentration and a Ni X-ray energy of 850 eV (closer to the O background fluorescence) make the resolution of a <0.1% Ni signal difficult, let alone the resolution of its weak edge jump step J for L-edge sum rule analysis. With a 180 eV resolution Ge detector, the edge jump is often washed out or buried under the huge background and pile-up from light elements like C, N, O and Na.^{12, 31,57, 58}

STJ detectors have an energy resolution of ~15 eV instead of 180 eV. Measuring XAS with an STJ therefore produces a high resolution X-ray fluorescence spectrum, in which the hypothetical 0.077% Ni signal becomes clearly resolvable from the huge O background (Fig. 4b). In Fig. 5, the STJ measured L_2,3 XAS of Ct-CODH (<0.077% Ni, green) is compared to the channeltron measured XAS for the concentrated covalent [Ni^II(SR)₄] complex (red), both spectra show a clear low spin Ni^II feature and both have a clear edge jump J. The L-edge sum rule analysis leads to a α= I_L/J = 12.2 and a H_3d = 12.2/8.6 = 1.42, corresponding to a typical Ni^II site. With STJ detectors, L-edge sum rule analysis can readily be extended to samples with a Ni concentration <0.1%, such as Ct-CODH frozen solution (<0.077% Ni), because its edge jump can be clearly observed. The same procedure will also be useful in studying other Ni enzymes with a Ni concentration below 0.1%, such as Ni in NiFe H₂ases. The advantage of this measurement is that it keeps the same ratio of normalized L intensity α and hole density H_3d for different measurements or for different samples. On the other hand, the disadvantage is: this approach will become difficult when H_3d is large (e.g. for Mn) because a perfect edge jump is almost impossible to obtain even with STJ detectors and a less perfect edge jump will introduce too much noise to the Δα and ΔH_3d because Δα (ΔH_3d) is large.

Figure 5.

Normalized L XAS for Ni inside a dilute Ct-CODH enzyme (<0.077% Ni) measured by partial fluorescence yield with an STJ detector (red) and inside a concentrated [Ni^II(RS)₄] complex measured by total electron yield with a channeltron (green). The top inset shows the energy resolution in the region of 300–1500 eV for an advanced STJ detector. The middle inset is a photo of a STJ head snout.

Measuring < 0.1% Ni Enzymes with Alternative Standard

Alternatively, we can introduce an external feature S to the XAS with its integrated intensity I_S comparable to I_L and use it as the intensity normalization standard instead of using J. For example, as Ce has a M₅ edge at 881.7 eV (close to Ni L_2,3 at 852.6 eV), we add chemically inert Ce(NO₃)₃ to the samples to be measured and use the Ce M₅ edge (I_S) as the normalization standard for Ni L_2,3. In this case we define α’= I_L/I_S. This was first tested on a NiBr₂/Ce(NO₃)₃/buffer matrix with a 0.6% Ni concentration, as detailed in the experimental section. Compatible XAS intensities for Ni L₃ and for Ce M₅ edges were obtained for a molar ratio of NiBr₂:Ce(NO₃)₃ = 5.5:1 (Fig. 6a). The advantages of this procedure includes: one can still use a Ge detector with 180 eV resolution because it can resolve the Ni L and Ce M₅ peaks from the background; and one can have a minimum errorbar for δα’/α’. For the 0.6% NiBr₂ sample, the uncertainty δI_L/I_L is about 4%, while the uncertainty of the Ce M₅ δI_S/I_S is about 4.1%, leading to a total error of ~5.7% for α’, much smaller than when using J for normalization. This minimized δα’ increases the accuracy of the intensity ratio α’=I_L/I_S. Note that I_L/I_S depends on the accurate knowledge of the Ni:Ce concentration ratio in a sample, and can therefore be different in different samples because the Ce concentration can vary. That complicates extracting an absolute value for the hole density H_3d from α’=I_L/I_S directly and makes this approach less attractive in comparison with the STJ option.

Figure 6.

Ni L XAS spectra for the 0.6% wt. Ni in a NiBr₂ matrix (a, blue), along with the as-isolated (b, red) and H₂-reduced (b, green) D. gigas NiFe H₂ase. All samples are doped with chemically-inert Ce(NO₃)₃. The top inset shows the M-edge positions for various rare earth elements in the region of 600–1000 eV.

Nevertheless, it successfully opens another pathway to extend L-edge sum rule analysis to <0.1% Ni enzymes, such as H₂ases (0.067% Ni)¹². These enzymes catalyze the reversible reaction of hydrogen (H₂) production and consumption, and monitoring their Ni oxidation states in their catalytic circle^{8, 12, 59–61} is critical to understanding their catalytic mechanisms. As discussed in the experimental section, we added Ce(NO₃)₃ as intensity normalization standard S in the as-isolated sample before the H₂-reduction, both H₂ase samples therefore have the same Ce:Ni ratio, although their absolute metal concentration may be different. We obtained I_L/I_S values of 0.92 and 0.66 (Fig. 6b), leading to a ratio of 0.92/0.66=1.39 between them. This number of 1.39 is independent of the Ce concentration and is consistent with a Ni^III → Ni^II reduction for these two H₂ase samples studied^{12, 59, 60}. This approach should also be a good way to study dilute systems with higher H_3d, such as Mn sites.

Besides Ce, a series of potential intensity standards in the spectral region from 600 to 1000 eV are also shown in the top inset of Fig. 6. For example, the Cs M₅-edge at 726 eV is a good candidate as an intensity standard for Fe L_2,3-edges at 706 and 720 eV. In addition, to avoid the uncertain concentration ratio of Ce:Ni, some intrinsic elements in the enzymes can also be used as a standard. For example, the as-isolated D. gigas NiFe H₂ase contains 12 Fe (66 3d holes) and 1 Ni atoms (3 3d holes). In principle, both Fe and Ni could have a charge change when the H₂ase oxidation state varies by ±1. However, even if we assume all the ±1 change occur in Fe, its total number of 3d holes should only change 1/66=1.5%. Fe can therefore be treated as a constant and be used as a normalization standard for L-edge sum rule analysis for Ni. In this special case, the Fe and Ni concentrations will always be the same for any given protein samples (e.g. D. gigas NiFe H₂ase).

Comparison with K-edge XAS

L-edge XAS and K-edge XAS offer complementary advantages. For example, K-edge XAS is bulky sensitive, and the edge energies of different elements are widely spaced, which allows XAS be extended to the useful EXAFS region (Fig. S3).⁶² In addition, since K X-rays have higher energies than L X-rays, K-edge XAS does not require a vacuum chamber, and a higher fluorescence yield which enables the analysis of more dilute samples.

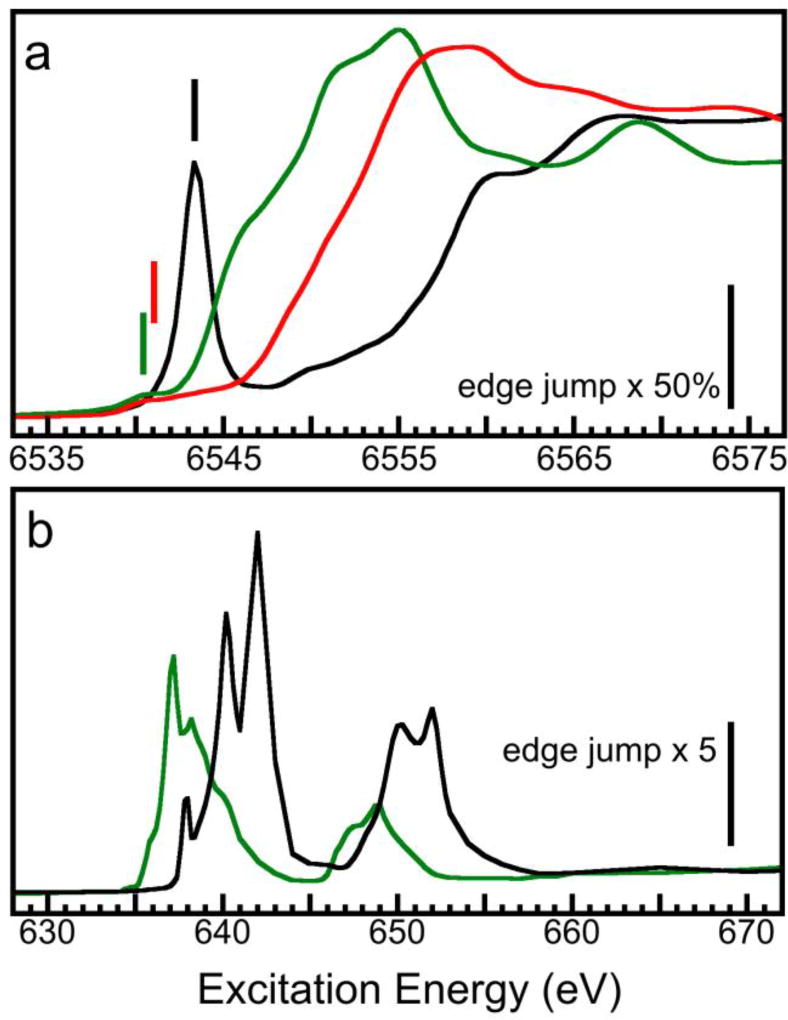
On the other hand, L XAS has richer spectral features that provide a finger print of the sample’s electronic structure. L-edges also have a much narrower line widths than K-edges (0.2 eV vs. 1 eV) that allow measuring these spectral features. For sum rule analysis, L XAS is favored over K XAS because L XAS measures 2p→3d transitions and therefore provides direct information about 3d bonding orbitals. These transitions are dipole allowed and therefore much stronger and more stable than the pre-K 1s→3d. As illustrated in Fig. 7, the maximum 1s→3d feature in K XAS (Fig. 7a, black) is still smaller than its edge jump, while most of the 1s→3d features are barely visible (Fig. 7a, green and red). Meanwhile, L XAS has a signal size several times stronger than its corresponding edge jump and 10–500 times stronger than the corresponding 1s→3d features in K XAS, because 2p→3d transitions are dipole allowed but 1s→3d is not. Moreover, as 1s→3d is not dipole allowed, the weak feature’s intensity heavily depends on the extent of its orbital mixture with other dipole allowed transitions and thus on the geometric structures of the complex. This also makes 1s→3d transitions dependent on changes in the electronic structure and difficult to interpret. For example, according to the L-edge sum rule analysis, H_3d for MnO should be about 60% of that for KMnO₄. However, this ratio is only a few percent in K-edge XAS (Figure 6a, green vs. black), and Mn^IIIO₃ actually has slightly lower intensity than Mn^IIO in K-edge XAS.

Figure 7.

(a) The K XAS for MnO (green), Mn₂O₃ (red) and KMnO₄ (black) in the pre-edge 1s→3d region; (b) the L XAS for MnO (green) and KMnO₄ (black).

4. Summary

According to sum rules, the integrated L XAS intensity I_L (when normalized by the invariant edge jump J) is proportional to the number of 3d holes localized in the X-ray absorber (H_3d). We have used L-edge sum rules to obtain the H_3d from their corresponding I_L/J for a series of Ni and Mn complexes (3d¹⁰→3d⁰). In complementary to the previous reports, errors in estimating the edge jump (δJ) are identified as dominant and must be carefully controlled. When the number of 3d holes is small, the I_L/J approach is accurate enough to at least semi-quantitatively define the metal’s oxidation state. However, as I_L/J increases, the H_3d observed values for the two consecutive oxidation states can overlap and a clear assignment of the oxidation state is less obvious. In this case, one has to either improve the accuracy of the setup and measure XAS with a clearer edge jump J (with a smaller error δJ), or to use alternative spectral features I_S to normalize I_L.

We have examined these two approaches to measure and extended the method to studies of extremely dilute biological samples (<0.1% Ni), such as Ct-CODH and NiFe H₂ase. For higher-accuracy XAS, we use a ~15 eV high resolution STJ detector to separate the extremely weak Ni fluorescence from the huge background to obtain the edge jump J with high signal-to-noise ratio, and continue to use the L-edge sum rule procedure developed for Ni complexes. The STJ measured L XAS for Ct-CODH (< 0.077% Ni) illustrates this option and conclude it has a Ni^II site. As an alternative spectral feature, we have added inert Ce to our samples and use the Ce M₅ as the new intensity normalization standard for I_L. This reduces the total error in α= I_L/I_S, as demonstrated with a dilute NiBr₂ (0.6% Ni) samples and with NiFe H₂ase samples (0.067% Ni). Although this analysis depends on the Ce concentration, changes in oxidation state for a given sample do not change the Ni:Ce ratio. This is shown in the comparison of as-isolated and H₂-reduced NiFe H₂ase samples, whose ratio of 1.39 is consistent with a Ni^III→Ni^II reduction. These experimental approaches will enable us to extend L-edge sum rule analysis to virtually any dilute biological metals in the future.