Skip to main content
PMC home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2018 Mar 16;51(7):2411–2417. doi: 10.1021/acs.macromol.7b02353

Size-Dependent Submerging of Nanoparticles in Polymer Melts: Effect of Line Tension

Shanqiu Liu †, Anupam Pandey ‡, Joost Duvigneau †,*, Julius Vancso †, Jacco H Snoeijer ‡,§
PMCID: PMC5895979  PMID: 29657338

Abstract

graphic file with name ma-2017-023532_0004.jpg

Adhesion of nanoparticles to polymer films plays a key role in various polymer technologies. Here we report experiments that reveal how silica nanoparticles adhere to a viscoelastic PMMA film above the glass transition temperature. The polymer was swollen with CO2, closely matching the conditions of nanoparticle-nucleated polymer foaming. It is found that the degree by which the particles sink into the viscoelastic substrate is strongly size dependent and can even lead to complete engulfment for particles of diameter below 12 nm. These findings are explained quantitatively by a thermodynamic analysis, combining elasticity, capillary adhesion, and line tension. We argue that line tension, here proposed for the first time in elastic media, is responsible for the nanoparticle engulfment.

1. Introduction

The diminishing size of nanoparticles results in a tremendous increase in their surface to volume ratio, leading to unexpected and highly exciting properties.1−3 In polymer technology, the interface between nanoparticles and a surrounding matrix can indeed dominate the properties of the hybrid (composite) material.4−10 With the growing interest in nanoparticles as fillers and/or active component in polymers, it is of key importance to develop a detailed understanding of the role of this interface on the resulting material properties.

Recent studies have focused on the adhesion of nanoparticles present at polymer/gas interfaces.11−18 Nanoparticles, for example, serve as highly efficient foam cell nucleation agents in CO2 blown polymer foams19 or are very useful to prepare templated surfaces with controlled porosities and antireflective properties.20 However, the process of adhesion or embedding of nanoparticles presents a great challenge. Rubner and co-workers20 reported the controlled thermally assisted particle embedding of surface deposited silica nanoparticles at the surface of poly(methyl methacrylate) (PMMA) polymer films. Particle embedding was controlled by varying the thermal treatment temperature and time, and similar results were obtained for surface modified silica nanoparticles in films of PMMA and poly(methyl methacrylate-co-methacrylic acid).17 As alternative to thermal annealing, Loos and co-workers18 reported the embedding of gold nanoparticles in polystyrene (PS) films via CO2 saturation of the polymer substrate at relatively low temperatures. The CO2 saturated polystyrene surface exhibits an increased polymer mobility causing the particles to sink in the surface. Surprisingly, we find that reducing the particle size to macromolecular length scale even leads to complete engulfment of the nanoparticle into a polymer film.

From a theoretical perspective, the adhesion of nanoparticles requires a revision of the classical JKR theory,21,22 as it does not account for capillary effects at small scale. Recent studies showed that particle adhesion is governed by the elastocapillary length γs/E,23−26 where γs is the “solid surface tension” and E is the Young’s modulus of the elastic polymer film. While particles much larger than γs/E follow the JKR law, smaller particles are dominated by capillary forces. In the latter case the film’s bulk elasticity is negligible, and the adhesion was proposed to be equivalent to particle adsorption at a liquid interface. However, these proposed descriptions do not predict any engulfment, nor have they been compared directly to experiments on nanoparticles.

Here we reveal a transition from adhesion, to wetting, to complete engulfment of silica nanoparticles on a PMMA film above the glass transition. By use of atomic force microscopy (AFM), it is found that the relative degree by which the particles sink into the substrate is strongly size dependent and leads to complete engulfment for particles below 12 nm. These findings are explained quantitatively by a thermodynamic analysis, combining elasticity, capillary adhesion, and line tension. We argue that line tension, here proposed for the first time in elastic media, is responsible for the nanoparticle engulfment.

2. Experimental Section

Materials

Tetraethyl orthosilicate (TEOS, ≥99.0%) and 2-propanol (99.5%) were purchased from Aldrich (Milwaukee, WI). (3-Aminopropyl)triethoxysilane (APTES, 99%), hydrocholoric acid (37%), and poly(dimethylsiloxane) monoglycidyl ether terminated (PDMS-G, Mw = 1000 g mol–1) were purchased from Sigma-Aldrich (St. Louis, MO). Calcium chloride (CaCl2) was purchased from Aldrich Chemical Co. Ltd. (Gillingham, England). PMMA was a gift from Arkema (VM100, i.e., a PMMA-co-EA polymer) (La Garenne-Colombes, France). Absolute tetrahydrofuran (THF) were purchased from Biosolve (Valkenswaard, The Netherlands). Ethanol absolute for analysis was purchased from Merck (Darmstadt, Germany). Milli-Q water was produced by a Millipore Synergy system (Billerica, MA). Nanoparticles with diameters of ∼12 nm (B220), ∼20 nm (B130), and ∼60 nm (Levasil 50/50) were purchased from AkzoNobel (Bohus, Sweden). These particles were dispersed in aqueous solution and have surface exposed hydroxyl groups on the surface as received. Unless otherwise mentioned, all other chemicals were used as received.

Stöber Nanoparticle Preparation

To prepare Stöber silica nanoparticles (SiO2) with a diameter ∼80 nm, 168 mL of ethanol was mixed with 28 mL of Milli-Q water and 30 mL of TEOS in the presence of 2 mL of ammonium hydroxide while stirring at 500 rpm at room temperature. After 1.5 h the obtained SiO2 dispersion was centrifuged at 10 000 rpm for 30 min. Subsequently, the collected SiO2 was redispersed in ethanol and centrifuged again. This washing step was repeated two more times followed by vacuum drying the collected SiO2 nanoparticles at room temperature for 12 h. To synthesize the 40 nm particles, 84 mL of ethanol was mixed with 14 mL of Milli-Q water and 15 mL of TEOS in the presence of 0.75 mL of ammonium hydroxide in a 250 mL round-bottom flask while stirring at 500 rpm. The reaction was conducted for 1.5 h at room temperature. To synthesize the 120 nm particles, 100 mL of ethanol was mixed with 8 mL of Milli-Q water and 5 mL of TEOS in a round-bottom flask stirring at 500 rpm, and subsequently 5 mL of ammonium hydroxide was added and reacted for 3 h at 50 °C. To synthesize 150 nm SiO2, 8 mL of Milli-Q water, 10 mL of TEOS, and 5 mL of ammonia hydroxide solution were added to 100 mL of ethanol, followed by stirring at 50 °C for 4.5 h. To synthesis nanoparticles of 310 nm, 100 mL of ethanol was mixed with 8 mL of H2O and 10 mL of TEOS, followed by the addition of 7 mL of ammonium hydroxide, and the reaction mixture was left at 50 °C for 4.5 h. The collection, washing, and drying steps for these nanoparticles were the same as described for the 80 nm nanoparticles.

Hydrolysis

To introduce silanol groups on the surface of the prepared SiO2 nanoparticles, the particles were redispersed in Milli-Q water by sonication (BRANSON 2510, Canada) for 1 h. Subsequently, hydrochloric acid was added to the dispersion while stirring at 500 rpm until the pH of the solution reached a value of approximately 1. After 4 h the dispersion was centrifuged at 10 000 rpm for 30 min. The collected nanoparticles were redispersed in Milli-Q water and centrifuged again. This washing step was repeated two more times followed by drying the silanol functional nanoparticles (SiO2–OH) in vacuum at room temperature for 12 h.

Amino Functionalization

1.5 g of SiO2–OH nanoparticles was redispersed in 50 mL of ethanol followed by the addition of 7.5 mL of APTES. The dispersion was left to stir at 500 rpm at room temperature for 17 h. The APTES functionalized nanoparticles (SiO2–NH2) were collected by centrifugation at 10 000 rpm for 30 min and redispersed in ethanol and centrifuged again. This washing step was repeated two more times followed by drying the collected SiO2–NH2 nanoparticles in a vacuum at room temperature for 12 h. Because of the small size of B220 (12 nm) and B130 (20 nm), the nanoparticles could not be collected by centrifugation. After amino functionalization 1 mL of CaCl2 (1 M) was added to 15 mL of the reaction mixture of B130 and B220 to change the surface zeta potential of the nanoparticles. This caused reversible agglomeration of the nanoparticles and made it possible to separate them from the ethanol during centrifugation.

Grafting to of PDMS-G to Silica Nanoparticles

1.0 g of SiO2–NH2 nanoparticles was redispersed in 20.5 mL of THF and 15 g of PDMS-G while stirring at 500 rpm for 1 h followed by sonication for 1 h. Subsequently, THF was removed by rotary evaporation, and the resulting silica nanoparticle dispersion in PDMS-G was immersed in an oil bath thermostated at 80 °C for 17 h. Following cooling to room temperature, the reaction mixture was washed with THF and centrifuged at 10 000 rpm for 30 min. This washing step was repeated two more times, followed by vacuum drying the PDMS-G grafted silica nanoparticles (SiO2–PDMS) at room temperature for 12 h.

Sample Preparation for Embedding Treatment

PMMA films of approximately 50 μm thick were prepared by drop casting a polymer–chloroform solution (0.1 g/mL) onto silica wafers (1 cm × 1 cm). Subsequently, the substrates were dried in air for 16 h followed by annealing at 135 °C for 12 h to relieve any potentially present residual stresses in the film before being slowly cooled to room temperature. Prior to particle deposition, the prepared nanoparticles (SiO2–OH and SiO2–PDMS) were redispersed in 2-propanol by sonication and diluted to a concentration of 0.005 wt %. Subsequently, a drop of the diluted nanoparticle solution was placed on the PMMA film, followed by drying the samples in a nitrogen box at room temperature for 12 h. The particles did not sink in into the glassy polymer surfaces as a result of this preparation method as was confirmed by AFM height measurements.

Once prepared, the samples were placed inside a pressure vessel (Julabo, Seelbach, Germany). The temperature of the setup was set to 40 °C, and the setup was flushed with CO2 for 20 s. Subsequently, the CO2 pressure was set to 58 bar. To ensure that the nanoparticles obtain an equilibrium state at the interface of the polymer matrix, the samples were saturated in CO2 for 7 h (we notice that longer time saturation did not lead to any further embedding of the nanoparticles into polymer matrix); subsequently, the pressure was slowly released, and the samples were quenched to room temperature for further analysis.

Atomic Force Microscopy (AFM) Characterization

The apparent height of the nanoparticles before and after embedding was determined by AFM (MFP-3D, Asylum Research, Santa Barbara, CA) analysis in tapping mode (amplitude set-point 250 mV) using a silicon cantilever (Nano Word) with a resonance frequency of 320 kHz and a spring constant of 42 N m–1. The substrates were scanned at a minimum of three different positions, and the obtained height images were analyzed. The heights of more than 100 individual isolated particles were analyzed for each data point.

3. Results and Discussion

Experimental Results

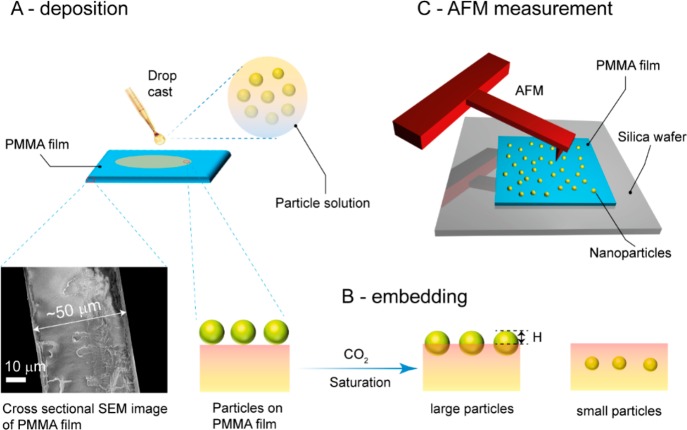
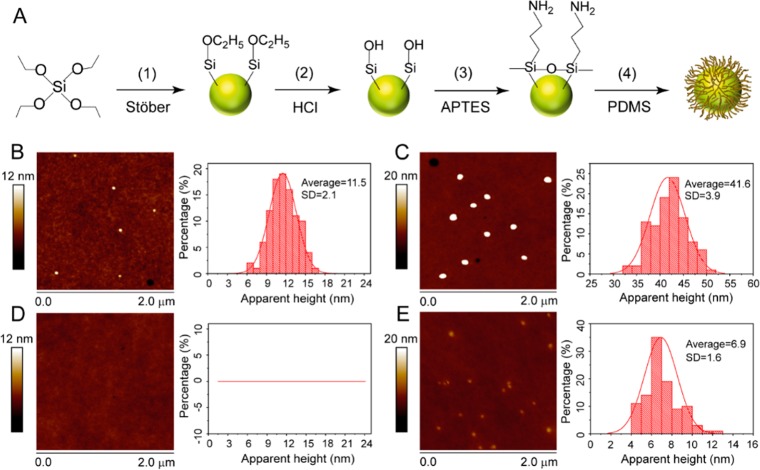
The present study reports the adhesion of two types of silica nanoparticles, i.e., bare (SiO2–OH) and PDMS-coated core–shell particles (SiO2–PDMS), with different silica (core) diameters on the surface of CO2 swollen PMMA films. The schematic drawings of sample preparation as well as AFM measurement for the prepared samples are shown in Figure 1A–C. Silica nanoparticles were deposited by drop casting the particle solution diluted with 2-propanol on PMMA films (see Figure 1A). Upon saturation of the PMMA samples with 58 bar of CO2 at 40 °C, the PMMA reaches a viscoelastic state,27−29 and the particles residing at its surface sink (partly/fully) into the bulk. The equilibrium position of the particles is determined from the residual particle height (H) by AFM tapping mode imaging (see Figure 2B,C). The key point to note here is that the polymer has a finite storage modulus (G′) at zero frequency, called the shear modulus G (G′(w = 0)), which governs the equilibrium particle height H. Experimental details can be found in the Experimental Section. Figure 2A shows the synthesis of nanoparticles via a Stöber reaction (step 1), followed by the hydrolysis of the surface exposed ethoxy groups to silanol moieties (step 2). The hydrolyzed particles (SiO2–OH) were modified with APTES, which results in the formation of amine-functionalized nanoparticles (SiO2–NH2) (step 3). Subsequently, PDMS-G was covalently attached to the surface of the nanoparticles via the grafting to method (step 4) to yield SiO2–PDMS core–shell nanoparticles. The successful modification of the nanoparticles was confirmed by FTIR as is shown in Figure S1 of the Supporting Information.

Figure 1.

Figure 1

Open in a new tab

Schematic showing deposition (A) and embedding (B) of nanoparticles on a PMMA film. CO2 treatment of the particle-laden PMMA layer leads to embedding and even engulfment of the nanoparticles by the polymer film. The degree by which the particles sink into the PMMA is quantified by measuring the height of nanoparticles above the polymer layer using an AFM (C).

Figure 2.

Figure 2

Open in a new tab

Stöber nanoparticle synthesis and subsequent derivation of PDMS grafted nanoparticles (A). AFM images of as deposited ∼12 nm (B) and ∼40 nm (C) bare particles (SiO2–OH) on glassy PMMA surfaces. In (D) and (E) the respective AFM images of the PMMA surfaces after embedding are shown. For a clear display of the embedded nanoparticles the maximum Z-scale for (C) and (E) was set to be 20 nm.

The key parameter of interest is the apparent height H of nanoparticles deposited on PMMA film surfaces, before and after CO2-assisted embedding. The height profiles of the nanoparticles were obtained via tapping mode AFM measurements. All the obtained height values presented in this paper are the Gauss-averaged values for experiments over more than 100 individual isolated particles. We first discuss results on the stiff, glassy PMMA substrate, where no particle engulfment is expected. Figures 2B and 2C show AFM height images for bare particles on the glassy PMMA respectively for particle diameters of 12 and 40 nm. The average apparent heights of the deposited silica particles prior to CO2 treatment of the PMMA surface agree well with the diameters of these nanoparticles determined by scanning electron microscopy (Figure S1). As expected, there is no embedding of nanoparticles in the polymer surface prior to CO2 treatment. In addition, decreasing the tapping mode set point values (which corresponds to lighter normal load on the particles imaged) did not alter the obtained height values. Thus, the agreement of the height values obtained with AFM and diameters obtained with scanning electron microscopy for the used nanoparticles confirms that the tapping mode AFM imaging conditions employed are suitable to accurately determine the apparent height of the nanoparticles on the polymer films.

The main interest of this study is to present the size-dependent particle embedding in the CO2 saturated and softened polymer films. Remarkably, Figure 2D shows that the 12 nm particles are completely engulfed into the substrate, as they are no longer visible in the AFM measurement. By contrast, the 40 nm particles bare particles are still partly visible (see Figure 2E). For these nanoparticles we determined that the average height H was 6.9 nm, which corresponds to a ratio H/D of 0.17. Hence, the particle attachment and embedding to the softened PMMA film are strongly size dependent.

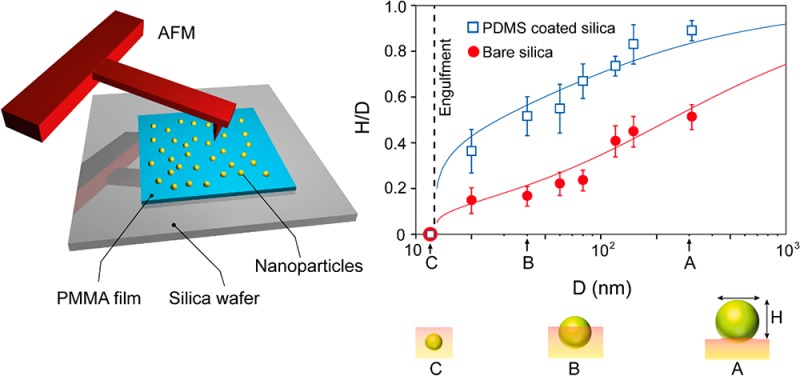
The relative degree of particle embedding can be quantified by the ratio H/D, which reflects the position of the particle at interface. This ratio is not universal but depends on the particle size. This is shown in Figure 3, where we report the ratio H/D for different particle diameters D. The PDMS-coated particles (blue squares) are systematically less embedded than the bare particles (red circles), as can be seen from the larger values of H/D. This can be attributed to the low surface energy and high CO2-philicity of the grafted PDMS as compared with the untreated particles. These differences in the interfacial interactions between the nanoparticles and the CO2 softened polymer explain this observation. Another clear trend from Figure 3 is that large particles do not sink very deeply into the polymer films as shown in the schematic of panel A. Smaller nanoparticles exhibit a wetting-like behavior (panel B) analogous to colloidal particles floating at a liquid interface. Finally, regardless of the surface chemistry of the particles, complete engulfment is observed for particles with a diameter of approximately 12 nm and less (schematic shown in panel C). These behaviors are explained below in detail.

Figure 3.

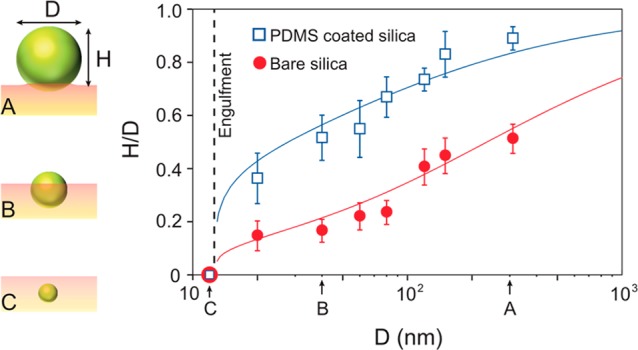
Figure 3

Open in a new tab

Engulfment of silica nanoparticles in a viscoelastic PMMA film. The nanoparticle embedding exhibits a double transition upon reducing the size, from adhesion (A), to wetting (B), and engulfment (C). The plot shows measurements of the relative degree of embedding of the nanoparticles: the apparent height H normalized by the particle diameter D is shown for different particles sizes (circles for bare silica particles, squares for PDMS-coated particles). H vanishes for both the bare and coated nanoparticles of diameter below 12 nm, indicated by the dashed line, signifying a complete engulfment. The observed critical size of engulfment is thus between 12 and 20 nm for both the bare and coated nanoparticles. Solid lines correspond to the combined minimization of bulk energy, surface energy, and line tension, given by eq 4. Particle sizes corresponding to the schematics of the left panel are marked along the x-axis of the plot.

Thermodynamic Model

While size-dependent adhesion of nanoparticles has been predicted in theory and simulations,30,31 these do not capture the present experiments—in particular, they do not predict the engulfment phenomenon. Given that the sample preparation ensures equilibrium, we propose a thermodynamic model. We split the free energy in bulk contributions, surface contributions, and a contribution due to the formation of a contact line. The latter term, referred to as line tension, is commonly used for wetting of nanodroplets. Here it is introduced for an elastic interface, motivated by recent studies on the equivalence between elastic and liquid contact lines and wetting.26

The free energy can thus be written as

graphic file with name ma-2017-023532_m001.jpg 1

The first term represents the elastic energy due to the indentation, for which we will use the Hertz scaling law Fel ∼ h5/2, where h = D – H is the indentation (see Figure 4). The second term represents the exchange of particle–vapor surface with PMMA–particle surface, which gives a change in surface energy (γsp – γp) times the relevant area Ac. Creating the contact also removes part of the solid–vapor energy. The associated solid surface energy is denoted as γs, while the area is approximated as πa2 where a is the radius of the contact. Up to this point, the free energy is identical to that posed in ref (24) which does not lead to engulfment. The key addition is the final term in eq 1 containing the line tension τ, representing the energy necessary to create a contact line of perimeter 2πa.

Figure 4.

Figure 4

Open in a new tab

Thermodynamic model: transition from adhesion to wetting to engulfment of nanoparticles, based on eq 4. The red dashed line represents the adhesion to wetting transition for θy = 45°, for the case without line tension (lτ = 0). The gray solid lines incorporate line tension effects for lτ/lec = 10–5, 10–4, and 10–3 from left to right. The corresponding circles represent the critical nanoparticle diameter for engulfment given by eq 6. The inset shows a nanoparticle in and out of contact with a polymer film and relevant geometric variables. The difference in energy between the two states leads to eq 1.

The ratios of bulk-to-surface energy and of surface-to-line energy naturally introduce two length scales in the problem, to which the particle diameter D needs to be compared. The first is the elastocapillary length, lec = γs/E, where E is the Young’s modulus of the polymer. We treat the polymer to be incompressible for which E = 3G. The Young’s modulus of the swollen PMMA film is approximated as E ∼ 106 Pa (see Supporting Information), while γs is approximately 21 mN/m.32 This gives lec ∼ 20 nm, which is indeed a relevant scale for the particles considered here. The second scale is the so-called tension length, lτ = τ/γs, which is known in the context of nanodroplets.33,34 It is commonly accepted that lτ should be of molecular scale,35 though much larger values are often claimed in the literature. The ratio lτ/lec is thus expected to be much smaller than unity and will appear as a parameter in the model. Another dimensionless parameter can be obtained from the work of adhesion

graphic file with name ma-2017-023532_m002.jpg 2

which quantifies the energy per unit area required to separate two surfaces. Here we wrote it directly in terms of Young’s angle θy, which will be used as a model parameter. For liquid media this parameter can be measured as the contact angle of macroscopic droplets. However, such a calibration is not feasible for materials with an elastic modulus, such as PMMA under the given experimental conditions. Namely, the contact of the PMMA sample with a flat silica surface will be dominated by elasticity, and the Young’s angle only appears below the elastocapillary length.26

To explicitly perform the minimization, we express the free energy in terms of the indentation depth h = D – H. For a spherical particle, one finds the geometric relations Ac = πDh and 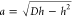Inline graphic. On the basis of this, we rewrite the free energy as

graphic file with name ma-2017-023532_m004.jpg 3

Here we closely followed ref (24) by approximating the elastic energy by the small deformation expression and using c = 8/5√3 to recover the JKR result for large particles. The equilibrium position is obtained from dF/dh = 0, which, upon writing h̅ = h/D and setting the Poisson ratio υ = 1/2 (due to incompressibility), can be rearranged to

graphic file with name ma-2017-023532_m005.jpg 4

As anticipated, the contact angle θy and the two length scales, lec and lτ, appear as the relevant parameters. By solving h̅ from eq 4, we can determine the sought-for equilibrium position H/D = 1 – h̅.

The typical predictions of eq 4 are illustrated in Figure 4, showing H/D as a function of the particle diameter normalized by the elastocapillary length, D/lec. One indeed finds a monotonic dependence on the particle size. At large D/lec, there is barely any indentation, and the result coincides with the classical JKR law. For D/lec ≤ 1, however, one observes that the particles tend toward a preferred position that is governed by the Young’s angle θy. This is because for smaller particles the surface energies start to dominate over the bulk elastic term. The red dashed line is the result without line tension, for which the particle position indeed approaches this wetting condition as previously found for elastocapillary adhesion.24 Formally, this corresponds to lτ = 0 in the limit lec ≫ 1 and gives H/D = (1 – cos θy)/2.

The addition of line tension dramatically changes the behavior for small particle sizes and leads to engulfment. This can be inferred from the solid lines of Figure 4, which were obtained for different strengths of the line tension, namely lτ/lec = 10–5, 10–4, and 10–3. The line tension introduces a critical particle diameter below which stable solutions cease to exist. Instead, one observes a bifurcation where the lowest free energy is achieved by completely engulfing the particle inside the elastic layer. The critical diameter for engulfment increases with lτ. For the largest tension length shown in Figure 4, the plateau due to the wetting regime is no longer visible. We note that we implicitly assumed that line tension takes a positive value, which need not be the case.33−39 For a negative line tension small particles are not engulfed. Instead, they would move to a position where H/D = 1/2 to maximize the length of the contact line.

Such a line-tension-induced bifurcation was previously observed for nanoparticles at liquid interfaces,36 and the same mechanism appears to be at play here. In the model, the critical diameter Dc for engulfment is due to the disappearance of the energy minimum. The disappearance of the minimum can be found by the combined condition dF/dh = 0, written as eq 4, and d2F/dh2 = 0. A closed form analytical expression for Dc is obtained in the physically relevant limit lτ ≪ lec, for which the elastic term can be treated upon expansion. This gives the critical diameter below which nanoparticles are unstable at the polymer interface:

graphic file with name ma-2017-023532_m006.jpg 5

where f(x) = (16/3√3π)x–1/3(x1/3 – 1)−4(x1/3 + 1)−5/2. The first term in the above expression has been previously obtained as the critical size for engulfment in the context of purely liquid interfaces.36 Here we find the correction in Dc due to finite elasticity. Indeed, the critical diameter is directly proportional to the tension length lτ. However, there is an intricate dependence on the contact angle. In particular, we find for θy ≪ 1 that (neglecting elasticity)

graphic file with name ma-2017-023532_m007.jpg 6

The dependence ∼1/θy3 shows that for small contact angles the critical diameter for engulfment can be orders of magnitude larger than the tension length. This pushes the engulfment diameter to the range of tens of nanometers. This effect is due to a geometric amplification of the influence of line tension, arising since contact lines with small θy only probe the “flat” part of the top of the particle.

Comparison to Experiment

Finally, we compare the theoretical prediction to our experiments. The results are shown as the solid lines in Figure 3, capturing the full range of data including the engulfment. Importantly, the model contains three parameters, one of which is eliminated by setting the critical diameter to 12 nm. Using the two remaining parameters to fit the experiment, we obtained for the coated particles (blue line) θy = 55°, lτ = 5 nm, and lec = 12 nm, while for the bare particles (red line) θy = 34°, lτ = 0.6 nm, and lec = 70 nm. This corresponds to a positive line tension which for the estimated γs = 21 mN/m implies 1.3 × 10–11 J/m (bare particle) and 10.5 × 10–11 J/m (PDMS-coated particle). These values are of the expected order of magnitude.33−39

A few observations can be made. Most importantly, the values obtained for the tension lengths are of the expected order. This makes a strong case that even relatively large particles, possibly tens of nanometers, can be engulfed by line tension when θy is sufficiently small. When comparing the fitted values of the bare particles and the PDMS-coated particles, we find that the PDMS induces a higher contact angle, as to be expected. However, the fitting requires an elastocapillary length lec that is substantially smaller for the coated particle. A possible explanation is the rather crude approximation of the elastic energy, which is based on the result of linear elasticity and only holds for H/D not too far from unity. Still, the thermodynamic model proposed here provides a very good description of the experimental data and in particular explains the engulfment.

4. Conclusions

In this paper we experimentally showed how nanoparticle adhere to viscoelastic (plasticized) PMMA films. Upon decreasing the size of the particles, we found a gradual transition from a classical adhesion regime to a complete engulfment of the particle into the PMMA. These observations were explained by thermodynamic considerations but work only when a line tension contribution is incorporated. Even though the PMMA has a nonzero elastic modulus, the contact line behaves very much like that of a liquid at the nanoscale. The modeling presented here is crude in the sense that all molecular interactions are described by effective free energies. An important direction for future work is to reveal further details near the contact line by molecular simulations and make the explicit link between molecular aspects and thermodynamics of nanoparticle adhesion.

Despite this, it is now anticipated that for instance in heterogeneous nanocellular polymer foaming the contribution of line tension to the free energy of cell nucleation must be considered.40−42 In particular, when nucleating particle dimensions are at the macromolecular length scale for which we have shown that line tension can severely influence the three phase contact line, its effect cannot be ignored. In addition, our results demonstrate that when interested in obtaining surface topology effects, the use of the smallest nanoparticles on viscoelastic surface/interfaces may provide unexpected results due to line tension effects. Thus, a deeper and better quantified understanding of the effect of line tension on nanoparticles is needed from both a physical as well as a practical point of view.

Acknowledgments

S.L. acknowledges financial support from the China Scholarship Council. A.P. and J.H.S. acknowledge financial support from ERC (the European Research Council) Consolidator Grant No. 616918. This research was supported by the MESA+ Institute for Nanotechnology, University of Twente.

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acs.macromol.7b02353.

  • FTIR results, SEM images of the nanoparticles, and results of rheological experiments (PDF)

Author Contributions

S.L. and A.P. contributed equally to this work.

The authors declare no competing financial interest.

Supplementary Material

ma7b02353_si_001.pdf (364.2KB, pdf)

References

  1. Basiuk V. A.; Basiuk E. V.. Green Processes for Nanotechnology: From Inorganic to Bioinspired Nanomaterials; Springer: 2015. [Google Scholar]
  2. Gan Y.; Sun L.; Banhart F. One- and Two-dimensional Diffusion of Metal Atoms in Graphene. Small 2008, 4, 587–591. 10.1002/smll.200700929. [DOI] [PubMed] [Google Scholar]
  3. Cheng S.; Xie S.; Carrillo J. Y.; Carroll B.; Martin H.; Cao P.; Dadmun M.; Sumpter B. G.; Novikov V. N.; Schweizer K. S.; Sokolov A. P. Big Effect of Small Nanoparticles: A Shift in Paradigm for Polymer Nanocomposites. ACS Nano 2017, 11, 752–759. 10.1021/acsnano.6b07172. [DOI] [PubMed] [Google Scholar]
  4. Schadler L. Nanocomposites: Model Interfaces. Nat. Mater. 2007, 6, 257–258. 10.1038/nmat1873. [DOI] [PubMed] [Google Scholar]
  5. Smith S. J.; Lau C. H.; Mardel J. I.; Kitchin M.; Konstas K.; Ladewig B. P.; Hill M. R. Physical Aging in Glassy Mixed Matrix Membranes; Tuning Particle Interaction for Mechanically Robust Nanocomposite Films. J. Mater. Chem. A 2016, 4, 10627–10634. 10.1039/C6TA02603F. [DOI] [Google Scholar]
  6. Fu S.; Feng X.; Lauke B.; Mai Y. Effects of Particle Size, Particle/Matrix Interface Adhesion and Particle Loading on Mechanical Properties of Particulate–polymer Composites. Composites, Part B 2008, 39, 933–961. 10.1016/j.compositesb.2008.01.002. [DOI] [Google Scholar]
  7. Balazs A. C.; Emrick T.; Russell T. P. Nanoparticle Polymer Composites: Where Two Small Worlds Meet. Science 2006, 314, 1107–1110. 10.1126/science.1130557. [DOI] [PubMed] [Google Scholar]
  8. Siqueira G.; Bras J.; Dufresne A. Cellulose Whiskers Versus Microfibrils: Influence of the Nature of the Nanoparticle and Its Surface Functionalization on the Thermal and Mechanical Properties of Nanocomposites. Biomacromolecules 2009, 10, 425–432. 10.1021/bm801193d. [DOI] [PubMed] [Google Scholar]
  9. Li Q.; Barrett D. G.; Messersmith P. B.; Holten-Andersen N. Controlling Hydrogel Mechanics via Bio-inspired Polymer–nanoparticle Bond Dynamics. ACS Nano 2016, 10, 1317–1324. 10.1021/acsnano.5b06692. [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Bansal A.; Yang H.; Li C.; Benicewicz B. C.; Kumar S. K.; Schadler L. S. Controlling the Thermomechanical Properties of Polymer Nanocomposites by Tailoring the Polymer–particle Interface. J. Polym. Sci., Part B: Polym. Phys. 2006, 44, 2944–2950. 10.1002/polb.20926. [DOI] [Google Scholar]
  11. Fakhraai Z.; Forrest J. Measuring the Surface Dynamics of Glassy Polymers. Science 2008, 319, 600–604. 10.1126/science.1151205. [DOI] [PubMed] [Google Scholar]
  12. Teichroeb J.; Forrest J. Direct Imaging of Nanoparticle Embedding to Probe Viscoelasticity of Polymer Surfaces. Phys. Rev. Lett. 2003, 91, 016104. 10.1103/PhysRevLett.91.016104. [DOI] [PubMed] [Google Scholar]
  13. Karim T. B.; McKenna G. B. Evidence of Surface Softening in Polymers and Their Nanocomposites as Determined by Spontaneous Particle Embedment. Polymer 2011, 52, 6134–6145. 10.1016/j.polymer.2011.10.045. [DOI] [Google Scholar]
  14. Sharp J.; Teichroeb J.; Forrest J. The Properties of Free Polymer Surfaces and Their Influence on the Glass Transition Temperature of Thin Polystyrene Films. Eur. Phys. J. E: Soft Matter Biol. Phys. 2004, 15, 473. 10.1140/epje/i2004-10078-0. [DOI] [PubMed] [Google Scholar]
  15. Rudoy V.; Dement’eva O.; Yaminskii I.; Sukhov V.; Kartseva M.; Ogarev V. Metal Nanoparticles on Polymer Surfaces: A New Method of Determining Glass Transition Temperature of the Surface Layer. Colloid J. 2002, 64, 746–754. 10.1023/A:1021558424276. [DOI] [Google Scholar]
  16. Deshmukh R. D.; Composto R. J. Direct Observation of Nanoparticle Embedding into the Surface of a Polymer Melt. Langmuir 2007, 23, 13169–13173. 10.1021/la7025544. [DOI] [PubMed] [Google Scholar]
  17. Qu M.; Meth J.; Blackman G.; Cohen G.; Sharp K.; Van Vliet K. Tailoring and Probing Particle–polymer Interactions in PMMA/Silica Nanocomposites. Soft Matter 2011, 7, 8401–8408. 10.1039/c1sm05668a. [DOI] [Google Scholar]
  18. Yang Q.; Xu Q.; Loos K. Enhanced Polystyrene Surface Mobility Under Carbon Dioxide at Low Temperature for Nanoparticle Embedding Control. Macromolecules 2015, 48, 1786–1794. 10.1021/ma5025686. [DOI] [Google Scholar]
  19. Liu S.; Zoetebier B.; Hulsman L.; Zhang Y.; Duvigneau J.; Vancso G. J. Nanocellular Polymer Foams Nucleated by Core-shell Nanoparticles. Polymer 2016, 104, 22–30. 10.1016/j.polymer.2016.09.016. [DOI] [Google Scholar]
  20. Tan W. S.; Du Y.; Luna L. E.; Khitass Y.; Cohen R. E.; Rubner M. F. Templated Nanopores for Robust Functional Surface Porosity in Poly (methyl methacrylate). Langmuir 2012, 28, 13496–13502. 10.1021/la3024887. [DOI] [PubMed] [Google Scholar]
  21. Johnson K.; Kendall K.; Roberts A. In Surface Energy and the Contact of Elastic Solids. Proc. R. Soc. London, Ser. A 1971, 324, 301–313. 10.1098/rspa.1971.0141. [DOI] [Google Scholar]
  22. Kendall K. The Adhesion and Surface Energy of Elastic Solids. J. Phys. D: Appl. Phys. 1971, 4, 1186. 10.1088/0022-3727/4/8/320. [DOI] [Google Scholar]
  23. Hui C.; Liu T.; Salez T.; Raphael E.; Jagota A. In Indentation of a Rigid Sphere into an Elastic Substrate with Surface Tension and Adhesion. Proc. R. Soc. London, Ser. A 2015, 471, 20140727. 10.1098/rspa.2014.0727. [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. Style R. W.; Hyland C.; Boltyanskiy R.; Wettlaufer J. S.; Dufresne E. R. Surface Tension and Contact with Soft Elastic Solids. Nat. Commun. 2013, 4, 2728. 10.1038/ncomms3728. [DOI] [PubMed] [Google Scholar]
  25. Ina M.; Cao Z.; Vatankhah-Varnoosfaderani M.; Everhart M. H.; Daniel W. F.; Dobrynin A. V.; Sheiko S. S. From Adhesion to Wetting: Contact Mechanics at the Surfaces of Super-Soft Brush-like Elastomers. ACS Macro Lett. 2017, 6, 854–858. 10.1021/acsmacrolett.7b00419. [DOI] [Google Scholar]
  26. Karpitschka S.; van Wijngaarden L.; Snoeijer J. H. Surface Tension Regularizes the Crack Singularity of Adhesion. Soft Matter 2016, 12, 4463–4471. 10.1039/C5SM03079J. [DOI] [PubMed] [Google Scholar]
  27. Handa Y. P.; Kruus P.; O’Neill M. High-pressure Calorimetric Study of Plasticization of Poly (methyl methacrylate) by Methane, Ethylene, and Carbon Dioxide. J. Polym. Sci., Part B: Polym. Phys. 1996, 34, 2635–2640. . [DOI] [Google Scholar]
  28. Kasturirangan A.; Koh C. A.; Teja A. S. Glass-transition Temperatures in CO2 Polymer Systems: Modeling and Experiment. Ind. Eng. Chem. Res. 2011, 50, 158–162. 10.1021/ie100479z. [DOI] [Google Scholar]
  29. Handa Y. P.; Zhang Z. A New Technique for Measuring Retrograde Vitrification in Polymer–gas Systems and for Making Ultramicrocellular Foams from the Retrograde Phase. J. Polym. Sci., Part B: Polym. Phys. 2000, 38, 716–725. . [DOI] [Google Scholar]
  30. Cao Z.; Stevens M. J.; Dobrynin A. V. Adhesion and Wetting of Nanoparticles on Soft Surfaces. Macromolecules 2014, 47, 3203–3209. 10.1021/ma500317q. [DOI] [Google Scholar]
  31. Carrillo J.-M. Y.; Raphael E.; Dobrynin A. V. Adhesion of Nanoparticles. Langmuir 2010, 26, 12973–12979. 10.1021/la101977c. [DOI] [PubMed] [Google Scholar]
  32. Goel S. K.; Beckman E. J. Generation of Microcellular Polymeric Foams Using Supercritical Carbon Dioxide. I: Effect of Pressure and Temperature on Nucleation. Polym. Eng. Sci. 1994, 34, 1137–1147. 10.1002/pen.760341407. [DOI] [Google Scholar]
  33. Schimmele L.; Dietrich S. Line Tension and the Shape of Nanodroplets. Eur. Phys. J. E: Soft Matter Biol. Phys. 2009, 30, 427–430. 10.1140/epje/i2009-10542-3. [DOI] [PubMed] [Google Scholar]
  34. Weijs J. H.; Marchand A.; Andreotti B.; Lohse D.; Snoeijer J. H. Origin of Line Tension for a Lennard-Jones Nanodroplet. Phys. Fluids 2011, 23, 022001. 10.1063/1.3546008. [DOI] [Google Scholar]
  35. De Gennes P. G.; Brochard-Wyart F.; Quéré D.. Capillarity and Wetting Phenomena: Drops, Bubbles, Pearls, Waves; Springer Science & Business Media: 2013. [Google Scholar]
  36. McBride S. P.; Law B. M. Influence of Line Tension on Spherical Colloidal Particles at Liquid-vapor Interfaces. Phys. Rev. Lett. 2012, 109, 196101. 10.1103/PhysRevLett.109.196101. [DOI] [PubMed] [Google Scholar]
  37. Law B. M.; McBride S. P.; Wang J. Y.; Wi H. S.; Paneru G.; Betelu S.; Ushijima B.; Takata Y.; Flanders B.; Bresme F.; Matsubara H.; Takiue T. Line Tension and Its Influence on Droplets and Particles at Surfaces. Prog. Surf. Sci. 2017, 92, 1–39. 10.1016/j.progsurf.2016.12.002. [DOI] [Google Scholar]
  38. Wang J. Y.; Betelu S.; Law B. M. Line Tension Approaching a First-Order Wetting Transition: Experimental Results from Contact Angle Measurements. Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top. 2001, 63, 031601. 10.1103/PhysRevE.63.031601. [DOI] [PubMed] [Google Scholar]
  39. Tadmor R. Line Energy, Line Tension and Drop Size. Surf. Sci. 2008, 602, L108–L111. 10.1016/j.susc.2008.05.018. [DOI] [Google Scholar]
  40. Hienola A.; Winkler P.; Wagner P.; Vehkamäki H.; Lauri A.; Napari I.; Kulmala M. Estimation of Line Tension and Contact Angle from Heterogeneous Nucleation Experimental Data. J. Chem. Phys. 2007, 126, 094705. 10.1063/1.2565769. [DOI] [PubMed] [Google Scholar]
  41. Lazaridis M. The Effects of Surface Diffusion and Line Tension on the Mechanism of Heterogeneous Nucleation. J. Colloid Interface Sci. 1993, 155, 386–391. 10.1006/jcis.1993.1051. [DOI] [Google Scholar]
  42. Iwamatsu M. Line-tension-induced Scenario of Heterogeneous Nucleation on a Spherical Substrate and in a Spherical Cavity. J. Chem. Phys. 2015, 143, 014701. 10.1063/1.4923237. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

ma7b02353_si_001.pdf (364.2KB, pdf)

Articles from Macromolecules are provided here courtesy of American Chemical Society

RESOURCES