Summary
Fast-spiking, parvalbumin-expressing GABAergic interneurons (PV+-BCs) express a complex machinery of rapid signaling mechanisms, including specialized voltage-gated ion channels to generate brief action potentials (APs). However, short APs are associated with overlapping Na+ and K+ fluxes and are therefore energetically expensive. How the potentially vicious combination of high AP frequency and inefficient spike generation can be reconciled with limited energy supply is presently unclear. To address this question, we performed direct recordings from the PV+-BC axon, the subcellular structure where active conductances for AP initiation and propagation are located. Surprisingly, the energy required for the AP was, on average, only ∼1.6 times the theoretical minimum. High energy efficiency emerged from the combination of fast inactivation of Na+ channels and delayed activation of Kv3-type K+ channels, which minimized ion flux overlap during APs. Thus, the complementary tuning of axonal Na+ and K+ channel gating optimizes both fast signaling properties and metabolic efficiency.
Keywords: parvalbumin-expressing GABAergic interneuron, axon, action potential, energy efficiency, inhibition, fast spiking, subcellular patch clamp, sodium channel, Kv3 channel, modeling
Highlights
-
•
Brief AP duration and high AP frequency in PV+-BCs may imply high metabolic cost
-
•
Energy for AP generation in PV+-BC axons is only 1.6 times the theoretical minimum
-
•
Fast Nav inactivation and delayed Kv3 activation maximize AP energy efficiency
-
•
Tuning of Nav–Kv3 gating optimizes fast signaling and energetics in interneurons
Hu et al. demonstrate that action potentials in parvalbumin-expressing GABAergic interneuron axons are energetically efficient, which is highly unexpected given their brief duration. High energy efficiency emerges from the combination of fast inactivation of voltage-gated Na+ channels and delayed activation of Kv3 channels in the axon.
Introduction
Fast-spiking, parvalbumin-expressing GABAergic interneurons (PV+-BCs) play a key role in several higher microcircuit functions, such as feedforward and feedback inhibition, high-frequency network oscillations, and pattern separation. For all of these functions, the fast signaling properties of these neurons play a critical role (Hu et al., 2014). A functional hallmark of PV+-BCs is the fast-spiking phenotype, i.e., the ability of the neurons to generate high-frequency trains of action potentials (APs) during sustained current injection in vitro (Rudy and McBain, 2001). A related property is the brief duration of the AP, referred to as “thin spike” in the classical literature (Mountcastle et al., 1969). Both functional properties are generated by the expression of specific types of voltage-gated ion channels, most importantly the selective expression of Kv3-type K+ channels in these neurons (Rudy and McBain, 2001). Short APs generate a short refractory period and therefore allow PV+-BCs to produce high-frequency activities under a variety of behavioral conditions in vivo, for example with a frequency of ∼20 Hz during theta periods and ∼120 Hz during sharp-wave ripples in the hippocampal CA1 region (Lapray et al., 2012, Gan et al., 2017). Short APs also generate a brief presynaptic Ca2+ current in presynaptic terminals (Bischofberger et al., 2002), and thereby trigger fast and temporally precise transmitter release at PV+-BC output synapses (Goldberg et al., 2005). Thus, brief APs are key components of the repertoire of fast signaling mechanisms of PV+-BCs.
AP generation in neurons is energetically expensive. Previous calculations suggested that up to 50% of the total energy budget of the brain is required for AP mechanisms (Attwell and Laughlin, 2001). In essence, Na+ and K+ ion fluxes during APs dissipate ion gradients, and the action of the Na+/K+ ATPase is required to re-establish these gradients. PV+-BCs may require an excessively large amount of energy. First, PV+-BCs generate spikes at a much higher frequency than principal neurons under in vivo conditions. Second, brief spikes are considered energetically expensive (Carter and Bean, 2009). Short APs are associated with large K+ conductances in the repolarization phase, leading to overlapping Na+ and K+ fluxes in this period. As these counterfluxes do not contribute to membrane potential changes, but need to be reversed by Na+/K+ ATPase activity, short APs are predicted to be energetically inefficient. Consistent with this prediction, the ratio of total Na+ flux to the theoretical minimum, is substantially larger than 1 in several models of fast-spiking neurons (Wang and Buzsáki, 1996, Sengupta et al., 2010) and in direct measurements from cell bodies of GABAergic interneurons (Carter and Bean, 2009). The combination of fast-spiking activity and high-energy cost per spike in PV+-BCs might be a major challenge for the brain’s energy budget. However, these conclusions were based on the analysis of voltage-gated Na+ channels in neuronal somata. Whether they hold in axons of PV+-BCs, where >95% of Na+ channels are located in this cell type (Hu and Jonas, 2014), remains an open question.
The energy efficiency of APs in axons of different cell types varies over a wide range (Table S1). In the squid giant axon and other invertebrate axons, the AP-related total Na+ influx is ∼4 times the theoretical minimum; thus, the AP is considered energetically inefficient in this type of axon (Hodgkin and Huxley, 1952, Hodgkin, 1975, Sengupta et al., 2010). In the axon of neocortical layer 5 pyramidal neurons, the Na+ entry ratio is ∼1.8–2.3 (Hallermann et al., 2012). In contrast, in hippocampal mossy fiber axons, the total Na+ influx is only ∼1.3 times the theoretical minimum; thus, the AP is considered energetically efficient (Alle et al., 2009). How the energy efficiency of APs in GABAergic interneuron axons compares to these values is, at present, unknown. To measure the energy efficiency of APs in PV+-BCs, we made direct recordings from the axon of these neurons. We found that the energy efficiency of APs was higher than expected, approaching the value previously reported in hippocampal mossy fiber axons. Combined analysis of channel gating and modeling identified the combination of fast Na+ channel inactivation and delayed activation of Kv3 channels as the key mechanism generating short, energy-efficient APs.
Results
Short APs in PV+-BC Axons at Physiological Temperature
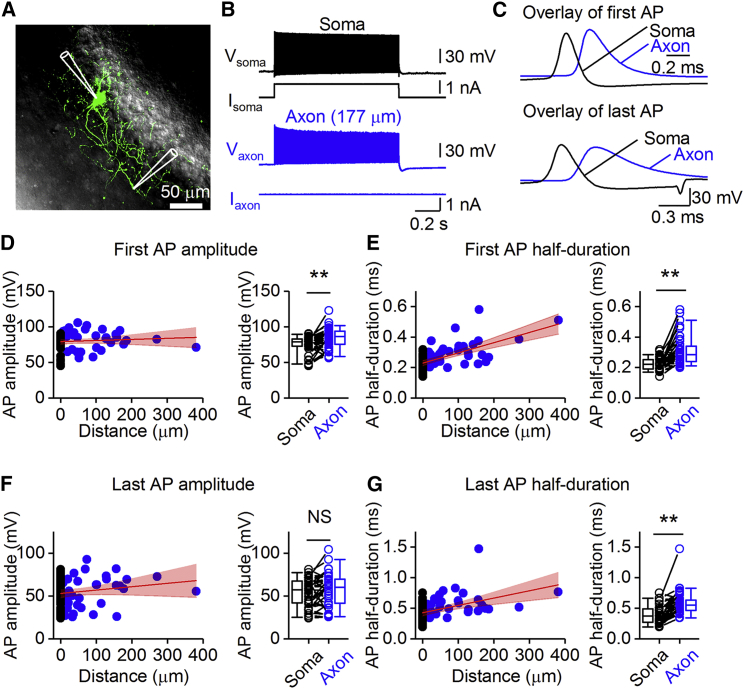
To determine the relation between AP duration and energy efficiency of the AP, we first measured AP amplitude and half-duration in PV+-BC axons (Figure 1). Recordings were performed at physiological temperature (34°C–37°C), because energy efficiency was previously reported to be temperature dependent (Yu et al., 2012). Axonal APs in PV+-BC axons at physiological temperature showed an overshooting amplitude and a short duration (Figures 1D and 1E). For the first axonal AP in a high-frequency train, the median peak amplitude was 86.4 ± 2.2 mV, and the half-duration was 0.29 ± 0.02 ms. For the last axonal AP in a high-frequency train, the amplitude was 59.1 ± 3.2 mV, and the half-duration was 0.55 ± 0.03 ms (Figures 1F and 1G; Table S2). Detailed analysis of axonal and somatic APs revealed that the AP amplitude was slightly larger (p < 0.01 for the first AP, Figures 1D and 1F), and the half-duration was slightly longer in the axon than in the soma (p < 0.01 for both first and last AP, Figures 1E and 1G). In comparison to principal neurons (Kole et al., 2007, Geiger and Jonas, 2000), the somatic AP was substantially faster in PV+-BCs (Kole et al., 2007), whereas the axonal AP waveforms were comparable in the two types of cells. These properties of the AP could contribute to the energy efficiency of the spike in PV+-BC axons.
Figure 1.
Brief APs in PV+-BC Axons at Physiological Temperature
(A) Maximal confocal stack projection of a fast-spiking, parvalbumin-expressing BC in the dentate gyrus filled with Alexa Fluor 488 during the experiment. Recording pipettes are illustrated schematically.
(B) A simultaneous soma-axon recording of a high-frequency AP train in response to a 1 s depolarizing current pulse applied at the soma. Black traces, somatic voltage and corresponding current. Blue traces, axonal voltage and corresponding current (177 μm from the soma).
(C) First (top) and last (bottom) APs in the high-frequency train plotted at an expanded timescale. Data in (B) and (C) are from the same cell.
(D) Left: plot of AP peak amplitude against distance of the axonal recording site from the soma for the first AP in the high-frequency train. Data were fit with a linear function (red line, Spearman ρ = 0.24, p = 0.04). Red area represents 95% confidence interval. Black circles, data from 36 somatic recordings; blue circles, data from 36 axonal recordings. Right: summary graph of somatic and axonal AP peak amplitudes in 41 soma-axon recordings. Data points from the same experiment are connected by lines. Open circles, data from individual recordings; box chart, median value and distribution of all data points. ∗∗p = 0.001.
(E) Left: plot of AP half-duration against distance of the axonal recording site from the soma for the first AP. Data were fit with a linear function (red line, Spearman ρ = 0.58, p < 0.0001). Red area represents 95% confidence interval. Black circles, data from 36 somatic recordings; blue circles, data from 36 axonal recordings. Right: summary graph of somatic and axonal AP half-durations in 41 soma-axon recordings. Data points from the same experiment are connected by lines. Open circles, data from individual recordings; box chart, median value and distribution of all data points. ∗∗p < 0.0001.
(F) Similar to (D) but for the last AP in the high-frequency train. Spearman ρ = 0.11, p = 0.36. Data from 32 (left) and 36 (right) soma-axon recordings. NS indicates p = 0.16.
(G) Similar to (E) but for the last AP in the high-frequency train. Spearman ρ = 0.53, p < 0.0001. Data from 32 (left) and 36 soma-axon recordings (right). ∗∗p < 0.0001.
Whiskers in box charts indicate the 5th and 95th percentile of data points, and the box itself indicates median, first quartile, and third quartile of the data points.
Energy-Efficient APs in PV+-BC Axons
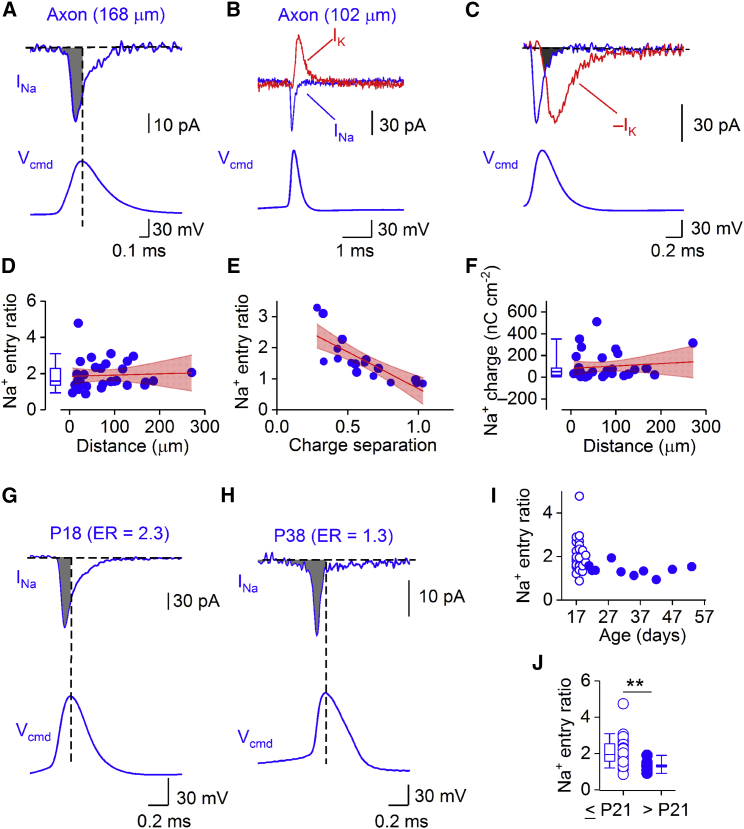
Next, we directly measured the energy efficiency of APs in PV+-BC axons (Figures 2A–2F). APs were recorded in the axon and applied as voltage-clamp commands to subsequently excised outside-out patches (Figures 2A–2C). To quantify AP energetics, we used three previously established measures: the Na+ entry ratio, the Na+-K+ charge separation, and the total charge transfer in comparison to the theoretical minimum (Figure S1) (Carter and Bean, 2009, Alle et al., 2009, Hallermann et al., 2012). In PV+-BC axons, the median entry ratio for the first AP in a high-frequency train was 1.60 ± 0.13 (34 axonal recordings; Figure 2D) and the charge separation was 0.59 ± 0.06 (18 axonal recordings; Figure 2E). Entry ratio and charge separation in single cells were negatively correlated, suggesting that both quantities provided related information about energy efficiency (Figure 2E). The entry ratio was independent of distance of the axonal recording site from the soma (Figure 2D), and slightly decreased during repetitive stimulation (Figure S2). As the excitability of PV+-BCs is known to mature during development (Doischer et al., 2008, Okaty et al., 2009, Goldberg et al., 2011), we further analyzed the dependence of the entry ratio on the age of the animals (Figures 2G–2J). Surprisingly, the entry ratio significantly declined as a function of age (p = 0.002), suggesting developmental maturation of energy efficiency.
Figure 2.
Energy-Efficient APs in PV+-BC Axons
(A) Na+ current (top) evoked by an AP waveform (bottom) in an outside-out patch excised from a PV+-BC axon (168 μm from the soma). Filled gray area represents Na+ entry before the AP peak.
(B) Na+ and K+ currents (top) evoked by an AP waveform (bottom) in an outside-out patch excised from a PV+-BC axon (102 μm from the soma).
(C) Na+ and K+ currents in (B) shown at expanded scales. The K+ current was inverted (−IK) to illustrate the overlap of Na+ and K+ currents (filled gray area). Bottom traces in (A)–(C) indicate previously recorded AP applied as voltage-clamp command (Vcmd). Data in (B) and (C) are from the same recording.
(D) Left: box chart of Na+ entry ratio (34 axonal recordings) in PV+-BC axons. Right: plot of Na+ entry ratio against distance from the soma in 31 axonal recordings. Red line represents a linear function fit to the data points (Spearman ρ = 0.28, p = 0.13).
(E) Plot of Na+ entry ratio against Na+-K+ charge separation in 18 axonal recordings. Data were fit with a linear function (red line, Spearman ρ = −0.92, p < 0.0001).
(F) Left: box chart of Na+ charge transfer (36 axonal recordings) in PV+-BC axons. Right: plot of Na+ charge transfer against distance from the soma (33 axonal recordings). Red line represents a linear function fit to the data points (Spearman ρ = 0.08, p = 0.67). In (D)–(F), blue circles represent data from individual recordings, and red area depicts 95% confidence interval.
(G) Na+ current (top) evoked by an AP waveform (bottom) in an outside-out patch excised from a P18 PV+-BC axon with a Na+ entry ratio (ER) of 2.3. Filled gray area represents Na+ entry before the AP peak.
(H) Similar to (G) but from a P38 PV+-BC axon with an ER of 1.3.
(I) Summary plot of Na+ entry ratio against postnatal age.
(J) Summary plot of Na+ entry ratios in young (≤P21) and mature (>P21) PV+-BC axons. Open circles in (I) and (J), data from 25 young (≤P21) PV+-BC axons; filled circles, data from 9 mature (>P21) PV+-BC axons; box chart, median value and distribution of all data points. ∗∗p = 0.002.
Whiskers in box charts indicate the 5th and 95th percentile of data points, and the box itself indicates median, first quartile, and third quartile of the data points.
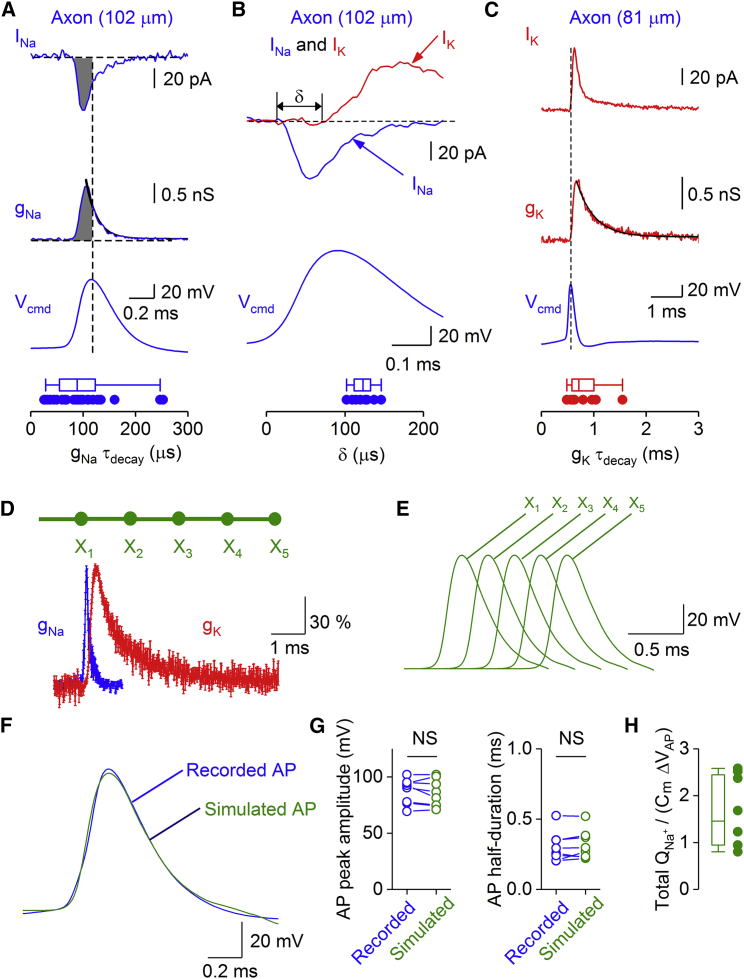
Next, we computed the Na+ charge transfer during single APs (Figure 2F). The median Na+ charge density was 51.7 ± 19.6 nC cm−2 for the first AP. The Na+ charge density was independent of distance (Figure 2F) and markedly decreased during repetitive firing (Figure S2). To compare the Na+ charge transfer during an AP to the theoretical minimum of a pure capacitor (Alle et al., 2009, Carter and Bean, 2009), we computed Na+ and K+ conductance (gNa and gK) waveforms during APs at physiological temperature, dividing current by driving force at each time point (Figures 3A–3C). We inserted experimentally measured conductance waveforms into a passive cable model of an axon and coupled them to a threshold trigger mechanism (Alle et al., 2009; Figure 3D–3H; Method Details). We then estimated peak conductance densities by minimizing the sum of squared errors between measured and simulated APs. This approach allowed us to compare the Na+ charge density with the product of specific capacitance (0.9 μF cm−2) × AP amplitude (Alle et al., 2009). The ratio of ionic charge density to capacitive charge density was 1.46 ± 0.27 (8 axonal recordings). Thus, by all measures of energetics, APs in PV+-BC axons were more energy efficient than expected from their brief duration. Energetic efficiency was higher than in squid axons (Hodgkin, 1975, Sengupta et al., 2010) and pyramidal neuron axons (Hallermann et al., 2012) and almost approached that in hippocampal mossy fiber axons (Alle et al., 2009).
Figure 3.
Complementary Tuning of Na+ and K+ Conductances Enhances AP Energy Efficiency in PV+-BC Axons
(A) Top: Na+ current (INa) and corresponding conductance (gNa) evoked by an AP waveform in an axonal membrane patch 102 μm from the soma. Black line indicates a monoexponential function fit to the decay phase of gNa. Bottom: summary graph of the gNa decay time constant. Filled circles, individual data points in 28 axonal recordings, box chart indicates the median and distribution of data points.
(B) Top: Na+ current (INa, blue) evoked by an AP waveform superimposed on the K+ current (IK, red) recorded from the same outside-out patch (102 μm from the soma) to illustrate the delay (δ) between the onset of Na+ current and K+ current. Bottom: summary graph of the delay. Filled circles, individual data points in 8 axonal recordings, box chart indicates the median and distribution of data points. Traces in (A) and (B) are from the same recording.
(C) Top: K+ current (IK) and corresponding conductance (gK) evoked by an AP waveform in an axonal membrane patch (81 μm from the soma). Black line indicates a monoexponential function fit to the decay phase of gK. Bottom: summary graph of the gK decay time constant. Filled circles, individual data points in 8 axonal recordings, box chart indicates the median and distribution of data points.
(D) Simulation of APs in a hybrid model, in which experimentally determined conductance traces were introduced into a computational model by a threshold trigger mechanism (Alle et al., 2009). Top: structure of the axon cable used for simulations. For further model parameters, see Method Details. Bottom: plot of normalized gNa and gK versus time (average from 8 axonal recordings; error bars indicate SEM). Individual conductance values were normalized to peak value for each cell, averaged, and normalized to the peak of the average trace to account for slight differences in peak time.
(E) Propagation of the AP along the axon. Traces represent membrane potential at 5 equally spaced axonal sites. Note that the model predicts fast AP propagation.
(F) Overlay of experimentally recorded AP (blue) and simulated AP (green) in the center of the cable. Peak conductance values (gNa and gK) and threshold in the model were varied to provide the best fit to experimental observations. Both traces were vertically aligned by subtracting the membrane potential before the AP and horizontally aligned by subtracting the AP peak time. Weight factors for tpeak − 250 μs ≤ t ≤ tpeak + 500 μs set to 1, and to 0.2 otherwise. Note that measured and simulated traces were in good agreement.
(G) Summary graph of AP peak amplitude (left) and half-duration (right). Note that the model accurately reproduced the experimental observations. Data points representing individual experimentally recorded APs and corresponding simulated APs were connected by lines. NS indicates p = 0.23 and 0.36, respectively.
(H) Summary graph of total Na+ charge, relative to the theoretical minimum.
Whiskers in box charts indicate the 5th and 95th percentile of data points, and the box itself indicates median, first quartile, and third quartile of the data points.
Fast Na+ Channel Inactivation and Delayed K+ Channel Activation during APs
To determine the mechanisms underlying the energy efficiency of the AP in PV+-BC axons, we examined the kinetic properties of gNa and gK during APs at physiological temperature (Figures 3A–3C). gNa reached its peak during the AP upstroke and subsequently decayed with a time constant of 89 ± 11 μs (Figure 3A). In contrast, gK rose with a significant delay. Consequently, the time difference between the onset of INa and IK was 123 ± 5 μs (Figure 3B). Finally, gK decayed with a time constant of 714 ± 124 μs (Figure 3C). Thus, the rapid decay of gNa combined with the delayed rise of gK minimized Na+-K+ charge overlap, enhancing the energy efficiency of the AP.
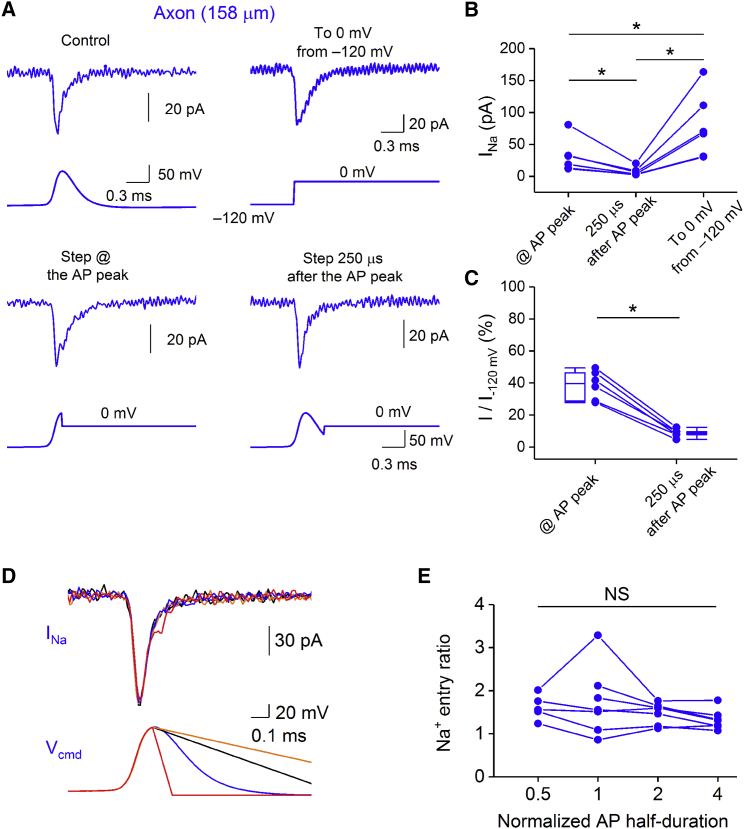
Which mechanisms contribute to the rapid gNa decay? Na+ channels may close by deactivation, inactivation, or a combination of these mechanisms (Raman and Bean, 1997, Carter and Bean, 2009). To distinguish between these possibilities, we applied test pulses to 0 mV at different time points after the AP peak (Figure 4A). Test pulses added 250 μs after the AP peak produced only minimal additional current, indicating that Na+ channels were fully inactivated (Figures 4A–4C). Furthermore, we scaled the repolarization phase of AP voltage-clamp waveforms (Figures 4D and 4E). Broadened APs produced current responses that were nearly identical to those of short APs. Furthermore, control and broadened APs gave the same Na+ entry ratio, indicating complete Na+ channel inactivation. Thus, Na+ inflow during axonal APs was terminated by Na+ channel inactivation rather than deactivation. Taken together, fast inactivation of Na+ channels and delayed activation of K+ channels underlies the generation of short, highly energy-efficient APs in PV+-BC axons. Additionally, fast deactivation of K+ channels will facilitate repetitive high-frequency firing (Rudy and McBain, 2001).
Figure 4.
Rapid and Complete Na+ Channel Inactivation during APs Promotes Energy Efficiency in PV+-BC Axons
(A) Top: Na+ currents evoked by an AP waveform (left) or a test pulse to 0 mV from a membrane potential of −120 mV (right) in an axonal outside-out patch (158 μm from the soma). Bottom: a test pulse to 0 mV was applied at the peak (left) or 250 μs after the peak (right) of the AP to determine the degree of Na+ channel inactivation. All traces are from the same experiment.
(B) Summary graph showing the amplitude of Na+ currents evoked by the test pulse applied at the peak or 250 μs after the peak of the AP waveform and that of the Na+ current elicited by applying the test pulse from −120 mV. ∗p = 0.04.
(C) Summary graph showing the degree of Na+ channel inactivation at the peak and 250 μs after the AP peak. Na+ channel inactivation was quantified as the ratio (I/I-120mV) of current amplitudes evoked by the test pulse applied at or after the AP peak to the maximal amplitude of the Na+ current elicited by the test pulse applied from a membrane potential of −120 mV. Data from the same experiment were connected by lines. Box charts indicate the median value and distribution of all data points. ∗p = 0.04.
(D) Na+ currents elicited by AP waveforms of different half-durations in an axonal outside-out patch. To systematically scale the half-duration of the AP waveform, we replaced the repolarization phase of the AP waveform with linear functions of different slope values. Each AP waveform and its corresponding Na+ current trace were plotted in the same color.
(E) Summary graph showing the effects of changing AP half-duration on Na+ entry ratio in 7 axonal recordings. Data from the same experiment were connected by lines. NS indicates p = 0.4.
Whiskers in box charts indicate the 5th and 95th percentile of data points, and the box itself indicates median, first quartile, and third quartile of the data points.
Gating and Subcellular Distribution of Na+ and K+ Channels in PV+-BC Axons
To reveal the biophysical mechanisms of energy-efficient APs in PV+-BC axons, we characterized gating kinetics and channel distribution. For voltage-gated Na+ channels, we analyzed steady-state activation and inactivation curves, activation and deactivation time constants, as well as inactivation onset and recovery time constants (see Hu and Jonas, 2014; Figure S3; Table S3). For voltage-gated K+ channels, we measured steady-state activation curves, as well as activation and deactivation time constants (Figure S4; Table S4). High activation threshold, fast deactivation at negative membrane potentials, and sensitivity to 1 mM tetraethylammonium (TEA) indicated that gK was primarily mediated by Kv3-type K+ channels (Rudy and McBain, 2001, Bean, 2007). Comparison of Na+ and K+ channel gating revealed that Na+ channel inactivation was substantially faster than K+ channel activation over a wide range of membrane potentials (p = 0.041 to 0.002 in the membrane potential range from −20 to 40 mV; Figure S3D versus Figure S4E), providing a biophysical explanation of the separation between gNa and gK during APs. Finally, we mapped the density of and in PV+-BC axons and compared them with those in the somata and dendrites (Figure S5). Whereas increased by more than 10 times along the dendritic-somatic-axonal axis (Hu and Jonas, 2014), was more uniformly distributed (Figure S5B). Median was 113.1 pS μm−2 in proximal axons, 145.1 pS μm−2 in distal axons, 115.9 pS μm−2 at the soma, and 80.0 pS μm−2 in dendrites. Thus, the to ratio increased >10-fold along the dendrite-soma-axon axis (Figure S5E). The channel distribution in PV+-BCs differed from that in pyramidal neurons, in which both Na+ and K+ channels were highly enriched in the axon initial segment (Kole et al., 2007) and density of A-type K+ channels markedly increased as a function of distance in dendrites (Hoffman et al., 1997).
Energy-Efficient and Inefficient Regimes of Fast AP Generation in Models
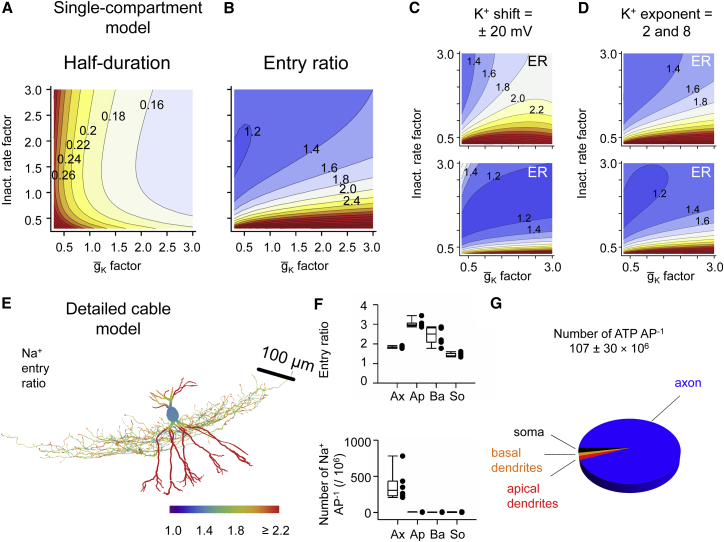
With these detailed descriptions of channel kinetics and distribution in our hands, we performed computational modeling to analyze how the complex interplay between Na+ and K+ channel gating determined AP energy efficiency in PV+-BC axons. First, we developed gating models of Na+ and K+ channels in PV+-BC axons, which precisely captured our experimental observations (Hille, 2001; Figure S6). Next, we introduced these models into a single-compartment neuron to simulate the energy efficiency of the AP (Figure 5). For the standard values, the Na+ entry ratio was 1.60, close to our experimental measurements. Finally, we varied Na+ channel inactivation rates and (the main determinants of AP duration) relative to standard values and generated contour plots of both AP half-duration and entry ratio against the two scaling factors (Figures 5A and 5B). When inactivation rates and were varied by a factor of 0.3–3, the AP half-duration changed between 0.14 and 0.44 ms (Figure 5A). In parallel, the entry ratio varied between 1.2 and 4.8 (Figure 5B). Unexpectedly, changes in entry ratio and half-duration in the parameter space were largely orthogonal. Thus, a short AP duration was reached by combination of either fast Na+ channel inactivation and low , or by combination of slow Na+ channel inactivation and high (Figures 5A and 5B). However, only the first regime was highly energy efficient, whereas the second regime was not. To explore the contribution of K+ channel gating to energy efficiency, we further modified the K+ channel properties (Figures 5C and 5D). Attenuating the characteristic gating properties of Kv3 channels, by either shifting the activation curve in the negative direction or abolishing the delay in activation, markedly increased the entry ratio, while accentuating these properties had opposite effects. Thus, the specific gating properties of Kv3 channels contribute to the energy efficiency of the AP in PV+-BC axons.
Figure 5.
Matched Na+ and K+ Channel Gating Maximizes Energy Efficiency in PV+-BC Axons
(A and B) Computational analysis of AP half-duration (A) and Na+ entry ratio (B) in a single-compartment model as a function of scaling factors for Na+ channel inactivation rates (ordinate) and maximal K+ conductance (abscissa). Scaling factors of 1 correspond to the experimentally determined default values. Short APs can be generated with a wide range of Na+ entry ratios. For model parameters, see Tables S5 and S6.
(C and D) Analysis of Na+ entry ratio (ER) with altered K+ channel gating. K+ channel activation curves were shifted by 20 mV in the hyperpolarizing (C, top) or depolarizing (C, bottom) direction, and delayed rectifier properties were altered by reducing (from 4 to 2; D, top) or increasing (from 4 to 8; D, bottom) the exponent of K+ channel activation. Note that both shift of the K+ channel activation curve in the hyperpolarizing direction and reduction of the exponent of K+ channel activation increased the Na+ entry ratio, i.e., decreased the energy efficiency. Numbers near contour lines indicate half-duration values in ms (A) or Na+ entry ratio values (B–D).
(E) Analysis of AP energetics in a detailed cable model of a dentate gyrus basket cell (BC2 from Nörenberg et al., 2010). Color code indicates Na+ entry ratio; scale bar shown as inset. For model parameters, see Table S7. Note that the entry ratio is lower in the axon than in the dendrites, whereas the subcellular distribution of the total Na+ charge is opposite, suggesting that subcellular structures with high Na+ load show better optimized entry ratio. Ax, axon; Ap, apical dendrite; Ba, basal dendrite; So, soma.
(F) Box chart of entry ratio (top) and total Na+ entry (bottom) in different subcellular compartments. Box charts indicate median and distribution of data points.
(G) Single-cell energy budget of PV+-BCs (number of ATP per AP).
Whiskers in box charts indicate the 5th and 95th percentile of data points, and the box itself indicates median, first quartile, and third quartile of the data points.
Subcellular Allocation of Energy Efficiency in Detailed Active Models
Finally, we examined the subcellular distribution of energy efficiency of the AP in detailed active cable models of PV+-BCs (Figures 5E–5G). In six fully reconstructed PV+-BCs (Nörenberg et al., 2010), quantitative analyses revealed a characteristic pattern of AP energy efficiency at the subcellular level, with the local Na+ entry ratio being substantially lower in the axon than in the dendrites (Figure 5F). However, the total Na+ inflow showed an opposite subcellular location dependence, with 94.1% axonal contribution and 3.4% dendritic contribution (Figure 5F). Based on the results from detailed active cable models of PV+-BCs, we were able to estimate the AP-related single-cell energy budget of these neurons. The total Na+ inflow was 322 ± 90 × 106 Na+ ions per single AP. With the known stoichiometry of the Na+/K+ ATPase (Rakowski et al., 1989), this corresponded to 107 ± 30 × 106 hydrolyzed ATP molecules per AP, with a major axonal and a minor dendritic signaling component (Figure 5G). Thus, the energy required per AP in a single PV+-BC is substantially lower than in a layer 5 pyramidal neuron (400–800 × 106 ATP AP−1; Hallermann et al., 2012).
Discussion
It is widely thought that short APs, like those in GABAergic interneurons, are energetically inefficient. Our results change this view (Table S1). In comparison to invertebrate axons, energy efficiency (as judged by the total Na+ charge divided by the theoretical minimum) was much higher than in squid axons (Hodgkin, 1975) or crab axons (Sengupta et al., 2010). In comparison to other mammalian axons, energy efficiency (as judged by Na+ entry ratio) was higher than in pyramidal neuron axons (Hallermann et al., 2012). Remarkably, energy efficiency (as judged by total Na+ charge over the theoretical minimum) came close to that in hippocampal mossy fiber axons (Alle et al., 2009). Finally, the total number of hydrolyzed ATP molecules per AP was substantially lower in PV+-BCs than in layer 5 pyramidal neurons (Hallermann et al., 2012). Thus, by all measures, APs in PV+-BCs were more energy efficient than previously thought.
AP Mechanisms in PV+-BCs: Speed versus Energy Efficiency?
Short APs in axons make important contributions to the function of PV+-BCs in microcircuits (Hu et al., 2014). Short APs are also important to minimize the refractory period following the AP (Rudy and McBain, 2001), a key requirement for the fast-spiking AP phenotype. Short APs also generate a brief presynaptic Ca2+ current in presynaptic terminals (Bischofberger et al., 2002), which, in turn, triggers fast and temporally precise transmitter release (Goldberg et al., 2005). Consequently, short APs contribute to both the ability of PV+-BCs to generate high-frequency activity (Lapray et al., 2012) and fast, temporally precise transmission at interneuron output synapses (Gan et al., 2017).
It is generally thought that short APs are energetically inefficient (Carter and Bean, 2009). The simple rationale is that the short repolarization of these APs is associated with a high delayed rectifier K+ conductance, which generates overlapping Na+ and K+ fluxes. However, our results demonstrate that the situation is mechanistically more complex. Our computational analysis based on realistic models of Na+ and K+ channel gating in PV+-BC axons revealed that Na+ entry ratio and half-duration can be dissociated. Short APs can be generated in regimes with fast Na+ channel inactivation combined with small K+ conductance or with slow Na+ channel inactivation together with large K+ conductance. PV+-BC axons operate in the first regime, which is highly energy efficient.
Our results demonstrate that the energy efficiency of the AP in PV+-BC axons is under developmental regulation. Previous work revealed that fast signaling properties of fast-spiking neurons mature during development, reflected by a shortening of the AP and an increase in the maximal AP frequency (Doischer et al., 2008, Okaty et al., 2009, Goldberg et al., 2011). Based on these findings, a developmental decrease of energy efficiency might have been expected. However, we found that energy efficiency slightly, but significantly, increased with age (Figures 2G–2J). These results corroborate the conclusion that short AP duration and high energy efficiency are not mutually exclusive, but can be correlated under specific conditions.
Reciprocal Tuning of Na+ and K+ Channel Gating Generates Fast, Energy-Efficient APs
Our results identify fast inactivation of voltage-gated Na+ channels as a key mechanism underlying energy-efficient APs in PV+-BC axons. Previous results demonstrated that inactivation of axonal Na+ channels is ∼2-fold faster than that of somatic channels in both hippocampal granule cells and PV+-BCs (Engel and Jonas, 2005, Hu and Jonas, 2014). While fast Na+ channel inactivation is expected to increase energy efficiency, it may interfere with the fast-spiking AP phenotype. However, our results demonstrate that Na+ channels in PV+-BC axons also show a fast time course of recovery from inactivation (Figure S3; see Martina and Jonas, 1997). The combination of fast onset of inactivation and rapid recovery from inactivation guarantees energy efficiency during a spike, and at the same time ensures short refractory periods required for the fast-spiking AP phenotype.
In addition to fast Na+ channel inactivation, the functional properties of voltage-gated K+ channels contribute to energy efficiency. Both gating and pharmacological properties suggest that the K+ channels expressed in PV+-BC axons are mainly of the Kv3 type (Martina et al., 1998). Previous work demonstrated that fast deactivation and high activation threshold critically contribute to the fast-spiking AP phenotype of these neurons (Rudy and McBain, 2001, Bean, 2007). Our results indicate that the high activation threshold and, relatedly, the delayed activation of Kv3 channels in the overshoot phase of the AP play an important role in energy efficiency, providing a molecular mechanism for charge separation. Thus, the specific gating properties of Kv3 channels not only facilitate fast spiking, but also optimize the energy efficiency of the AP.
Our simulations reveal that a −20 mV shift of the Kv3 channel activation curve markedly decreases the energy efficiency of the AP in PV+-BC axons (Figure 5C). Such a shift makes the channel activation curve almost Kv1-like (Table S4; Geiger and Jonas, 2000). Thus, our simulations suggest that the use of Kv3 channels for repolarization conveys higher energy efficiency than the use of Kv1 channels. Consistent with this simple idea, neocortical layer 5 pyramidal neuron axons exhibit a lower energy efficiency (Hallermann et al., 2012) and a larger Kv1-like conductance (Kole et al., 2007) than PV+-BC axons. However, in apparent contrast with this possibility, mossy fiber axons show both high energy efficiency and large Kv1 conductance (Geiger and Jonas, 2000). Both the uniquely fast inactivation of Na+ channels in mossy fiber axons (Engel and Jonas, 2005) and the preferential activation of Kv3 channels in Kv1/Kv3 channel mixtures by short APs (Alle et al., 2011) may explain this apparent discrepancy. Strategic subcellular distribution of Kv3, Kv1, and other K+ channel types may further contribute to parallel optimization of function and energetic efficiency (Rowan et al., 2014).
Neuronal Polarity Contributes to Energy Saving
Our computational analysis further reveals that the marked polarity of PV+-BCs, i.e., the steep gradient of Na+ channel density along the dendrite-soma-axon axis, works as an energy-saving mechanism. In PV+-BCs, the dendritic component of Na+ influx and energy cost of the AP is only 3.4%, because voltage-gated Na+ channels are largely absent from dendrites in these cells (Hu et al., 2010). In contrast, in thick-tufted layer 5 pyramidal neurons the dendritic contribution to the total Na+ entry is ∼30% (Hallermann et al., 2012). Limited excitability of dendrites of PV+-BCs will save energy but restrict synaptic plasticity at glutamatergic input synapses, which often requires backpropagated APs (Mishra et al., 2016). Additionally, the absence of a region of high density of voltage-gated Na+ channels in the axon initial segment in PV+-BCs (Figure S5) may contribute to energy saving (Fleidervish et al., 2010, Hallermann et al., 2012). Finally, our computational results demonstrate a correlation between absolute Na+ entry and energy efficiency, such that subcellular elements with the highest absolute Na+ entry show the highest energetic efficiency. This is consistent with the hypothesis that energy consumption was an important factor in the optimization of PV+-BC function during evolution.
Contribution of Fast-Spiking Cells to the AP Signaling-Related Energy Budget
The present results allow us to obtain improved estimates of the contribution of different cell types to the total energy budget required for AP signaling (Attwell and Laughlin, 2001, Buzsáki et al., 2007, Howarth et al., 2012). The proportion of PV+ GABAergic interneurons has been estimated as 2.6% in the hippocampus (Bezaire and Soltesz, 2013) and 4.6% in the neocortex (estimated from the proportion of GABAergic interneurons, Meyer et al., 2011, and the percentage of PV+ cells, Tremblay et al., 2016). However, the average firing frequency of PV+-BCs in vivo is several-fold higher (∼20 Hz; Lapray et al., 2012) than that of the principal neuron population (∼1 Hz; Kowalski et al., 2016, Gentet et al., 2010). Using estimated ATP consumption values for PV+-BCs (107 × 106 ATP per spike, this paper) and pyramidal neurons (400 × 106 ATP for tick-tufted layer 5 pyramidal cells; Hallermann et al., 2012), we calculate that the contribution of PV+-BCs to the total energy consumption is ∼14%–25%. If the energy efficiency of PV+-BCs would be as high as that of hippocampal mossy fiber axons (entry ratio 1.26; Alle et al., 2009), this contribution would become slightly reduced, to ∼11%–19%. However, if the energy efficiency was comparable to that of the squid giant axon (entry ratio 4; Hodgkin, 1975), this number would substantially rise to ∼35%–62%. Thus, the optimization of the energy efficiency of single APs prevents PV+-BCs from consuming a major fraction of the total AP-related energy budget.
Whether similar conclusions apply to fast-spiking neurons in other brain circuits remains to be determined. However, it is intriguing that other types of central axons in the mammalian CNS specialized on high-frequency coding also co-express fast-inactivating Na+ channels and Kv3 channels (Leão et al., 2005, Ritzau-Jost et al., 2014). Thus, matched Na+ and K+ channel gating may represent a widely used design principle to implement metabolically efficient high-frequency coding schemes in the mammalian brain. Previous estimations suggested that low AP energy efficiency enforces low spike frequency and sparse coding in pyramidal neurons in vivo (Lennie, 2003). Following the same logic, our results imply that high AP energy efficiency contributes to the ability of GABAergic interneurons to generate high-frequency trains of spikes.
Our results may also shed light on the complex disease phenotype of Kv3 channelopathies (Kaczmarek and Zhang, 2017). Intriguingly, mutations in the Kv3.3 gene, which shift the activation curve in the hyperpolarizing direction, cause a neurodevelopmental-neurodegenerative disease phenotype, characterized by mild mental retardation and ataxia with early onset and slow progression (Waters et al., 2006). It is tempting to speculate that reduced AP energy efficiency, expected from left-shifted K+ channel activation, contributes to the neurodegenerative component of the disease.
STAR★Methods
Key Resources Table
| REAGENT or RESOURCE | SOURCE | IDENTIFIER |
|---|---|---|
| Chemicals, Peptides, and Recombinant Proteins | ||
| NaCl | VWR | 27810.364 |
| NaHCO3 | VWR | 27778.293 |
| KCl | VWR | 26764.298 |
| NaH2PO4 | VWR | 28013.264 |
| D-glucose | VWR | 101175P |
| Sucrose | VWR | 27480.294 |
| MgCl2 | VWR | 25108.260 |
| CaCl2 | VWR | 22317.297 |
| K-gluconate | Sigma-Aldrich | G4500 |
| EGTA | Sigma-Aldrich | E4378 |
| HEPES | Sigma-Aldrich | H3375 |
| ATP | Sigma-Aldrich | A8937 |
| CdCl2 | Sigma-Aldrich | 208299 |
| 4-AP | Sigma-Aldrich | 275875 |
| TEA | Sigma-Aldrich | T2265 |
| Alexa Fluor 488 hydrazide | Thermo Fisher Scientific | A10436 |
| Experimental Models: Organisms/Strains | ||
| Wistar rats | Charles River and Preclinical Facility, IST Austria |
Strain code: 273 |
| Software and Algorithms | ||
| Igor Pro 6 | Wavemetrics | V6.20–6.37 |
| Fpulse | Ulrich Fröbe, University of Freiburg | 3.19, 3.33 |
| Stimfit | Guzman et al., 2014 (https://github.com/neurodroid/stimfit) | V0.9.2–0.13.2 |
| Mathematica | Wolfram Research (http://www.wolfram.com/mathematica) | V11.0 |
| NEURON | https://www.neuron.yale.edu/neuron/ | V7.4 |
| pClamp 9 | Molecular Devices | V9.2.1.9 |
| Origin | OriginLab | Origin 2015 |
| ImageJ | https://imagej.nih.gov/ij/ | V1.51j8 |
| CorelDRAW | Corel Corporation | X8 |
| Velocity | PerkinElmer | V5.5.1 |
| Minitab | Minitab | V17 |
Contact for Reagent and Resource Sharing
As Lead Contact, Peter Jonas is responsible for all reagent and resource requests. Please contact Peter Jonas (peter.jonas@ist.ac.at) with requests and inquiries.
Experimental Model and Subject Details
Experiments on Wistar rats were approved by the Bundesministerium für Wissenschaft, Forschung und Wirtschaft (A. Haslinger, Vienna) and the responsible veterinarian at the University of Oslo, and were performed in strict accordance with institutional, national, and European guidelines for animal experimentation.
Recordings from axons of fast-spiking PV+-BCs of the dentate gyrus in slices from 17- to 53-day-old Wistar rats of either sex were performed according to previously established experimental protocols (Hu and Jonas, 2014).
Method Details
Axonal patch-clamp recording
Recordings from axons of fast-spiking PV+-BCs of the dentate gyrus were performed according to previously established experimental protocols (Hu and Jonas, 2014). Transverse hippocampal slices (thickness 350 μm) were prepared from the brains of 17- to 53-day-old Wistar rats of either sex. Rats were maintained under light (7 am–7 pm) and dark cycle (7 pm–7 am) conditions and were kept in a litter of 8–10 animals together with the mother in a single cage. Slices were cut in ice-cold, sucrose-containing physiological extracellular solution using a vibratome (VT1200, Leica Microsystems), incubated in a maintenance chamber filled with standard physiological extracellular solution at ∼34°C for 30 min, and subsequently stored at room temperature. Slices were then individually transferred into a recording chamber and superfused with standard physiological extracellular solution. For analysis of Na+ and K+ currents during APs, recordings were performed at near-physiological temperature (∼35°C; range: 34–37°C), because the energy efficiency of the AP is known to be highly temperature-dependent (Yu et al., 2012). In these experiments, the bath solution was warmed by a resistive heating unit (Sigmann Elektronik, Hüffenhardt, Germany) prior to entering the recording chamber, and the recording temperature was continuously monitored with a micro thermistor positioned in the vicinity of the recorded neuron. For biophysical analysis of channel gating, recordings were made at room temperature (∼24°C; range: 22–25°C) to maximize the precision of kinetic measurements. In each experiment, temperature was held constant within ± 0.5°C.
For recordings from interneuron axons, the following experimental strategy was used. First, a somatic recording was obtained, using an internal solution containing Alexa Fluor 488 (50 or 100 μM, Invitrogen). Second, after ∼30 min of somatic whole-cell recording, the fluorescently labeled axon was tangentially traced from the PV+-BC soma through the granule cell layer with a Nipkow spinning disk confocal microscope (Ultraview live cell imager, Perkin Elmer, equipped with an Orca camera, Hamamatsu and a solid-state laser, excitation wavelength 488 nm). Exposure time was minimized to avoid phototoxic damage. Finally, fluorescent and infrared differential interference contrast (IR-DIC) images were compared and axons were patched under IR-DIC. Recordings were made from either axon shafts or small spherical axon expansions, presumably representing “blebs” formed during the slicing procedure (Shu et al., 2006), at distances up to 418 μm from the soma. Axonal whole-cell recordings were readily obtained, consistent with minimal myelination in the dentate gyrus at the developmental stage used (Hu and Jonas, 2014, Halasy and Somogyi, 1993, Micheva et al., 2016). This procedure resulted in a simultaneous axon–soma recording configuration. From this configuration, axonal outside-out patches were obtained by slowly withdrawing the axonal pipette. In all cases, axons could be unequivocally distinguished from dendrites on the basis of smaller diameter, location within or adjacent to the granule cell layer, and abundance of tangential collaterals. As shown previously, AP properties and conductance values were similar between bleb and shaft recordings (Hu and Jonas, 2014). For documentation purposes, 6 cells were rescanned with a Leica TCS SP5 II confocal microscope (Leica Microsystems; Figure 1A).
Patch pipettes were fabricated from thick-walled borosilicate glass tubing (outer diameter: 2 mm, inner diameter: 1 mm) with a horizontal pipette puller (P-97, Sutter Instruments). When filled with internal solution, they had a resistance of 2–10 MΩ for somatic recording and 6–40 MΩ for axonal recording. Current- and voltage-clamp recordings were performed using a Multiclamp 700B amplifier (Molecular Devices). Series resistance was 15–90 MΩ. Cells with somatic resting potentials more positive than −50 mV were discarded. Pipette capacitance and series resistance compensation (bridge balance) were applied throughout current-clamp experiments. Bridge balance was monitored and readjusted as required. BCs were held at a membrane potential of ∼−65 mV, injecting a holding current at the soma (range: −150 to +200 pA) or at the axon (range: −20 to −100 pA).
Signals were low-pass filtered at 10 kHz (or 4 kHz in a subset of experiments to measure gK density, Figure S5), and sampled at 100 kHz with a CED power interface (Cambridge Electronic Design) or a Digidata 1322 converter board (Molecular Devices). Pulse protocols were generated using custom-made data acquisition software (FPulse versions 3.19 and 3.33, Ulrich Fröbe, University of Freiburg) running under Igor 6.20–6.37 (WaveMetrics) or pCLAMP 9 (Molecular Devices). To elicit Na+ and K+ currents that flow during APs, we applied an AP waveform that was previously recorded from the same axon (Figures 2, 3, and Figure S2) or a pre-recorded AP waveform from the axon of a different neuron (in a subset of recordings in Figure 2E and Figure 4) as the voltage-clamp command to the outside-out patch. Na+ currents were pharmacologically isolated with 5–20 mM tetraethylammoniumchloride (TEA), 1–10 mM 4-aminopyrididine (4-AP), and 50–100 μM CdCl2 added to the bath solution. To separate Na+ and K+ currents in the same axonal recording (Figures 2B, 2C, 2E, and 3B), we first recorded the total current in the presence of CdCl2 and subsequently used TEA, 4-AP, and CdCl2 to isolate the Na+ current component. The K+ current component was obtained by digital subtraction. The holding potential before and after the pulse sequence was −70 mV (Figures 2, 3, and 4 and Figure S2) or −90 mV (Figures S3–S5). In a subset of experiments in Figures 2E and 4, a 50-ms prepulse to −120 mV was applied to outside-out patches to remove Na+ channel inactivation. Voltage protocols were applied to outside-out patches once every 3–15 s. Leak and capacitive currents were subtracted online using a ‘P over −4’ or ‘P over −8’ correction procedure.
PV+-BCs were identified based on the non-accommodating, fast-spiking AP phenotype (average AP frequency > 50 Hz at room temperature and >150 Hz at physiological temperature in response to 1 s, 0.3- to 1-nA somatic current pulses), and the morphological properties of the axonal arbor, which was largely restricted to the granule cell layer and established basket-like structures around granule cell somata in confocal images. At ∼35°C, the maximal AP frequency was 239 ± 8 Hz (range: 188–420 Hz, 46 cells, ≤2 nA current injection). In a subset of cells, identification was confirmed by post hoc biocytin labeling. In a previous sample of fast-spiking interneurons in the dentate gyrus analyzed in detail by light microscopy, the fast-spiking AP phenotype was tightly correlated with the expression of parvalbumin (Hu et al., 2010). Furthermore, 78 of 83 cells were classical basket cells with tangential axon collaterals and basket-like branches around granule cell somata, whereas 5 out of 83 were axo-axonic cells with radial axon collaterals (Hu et al., 2010). Based on these results, the recorded cells in the present study were termed PV+-BCs throughout.
Solutions and chemicals
The standard physiological extracellular solution contained 125 mM NaCl, 25 mM NaHCO3, 3.5 mM KCl, 1.25 mM NaH2PO4, 2 mM CaCl2, 1 mM MgCl2, and 25 mM D-glucose (equilibrated with 95% O2 and 5% CO2 gas mixture). In experiments to determine Na+ channel gating properties and K+ channel density (Figures S3 and S5), the extracellular KCl concentration was reduced to 2.5 mM. For tail current measurements (Figures S4A–S4E), we raised the extracellular KCl concentration to 25 mM and reduced the concentration of NaCl to 102.5 mM accordingly.
The intracellular solution contained 120 mM K-gluconate, 20 mM KCl, 10 mM EGTA, 2 mM MgCl2, 2 mM Na2ATP, 10 mM HEPES, and 0%–0.2% biocytin, pH adjusted to 7.3 with KOH. 50–100 μM Alexa Fluor 488 (Invitrogen) was added to the internal solution for all somatic recording electrodes.
Data analysis
Analysis was performed using Stimfit 0.9.2–0.13.2 (Guzman et al., 2014), Clampfit 9 (Molecular Devices), Origin 2015 (Microcal), Excel (Microsoft), and Minitab 17 (Minitab). AP amplitude was measured from threshold (50 V s−1), and half-duration was defined as the width of the AP at its half-maximal amplitude. To determine the AP metabolic efficiency, we used three different previously established quantities: Na+ entry ratio, Na+-K+ charge separation, and total Na+ charge in comparison to the theoretical minimum (Figure S1). The Na+ entry ratio was calculated by dividing the total Na+ charge during the AP by the Na+ charge before the AP peak (Figure S1A) (Carter and Bean, 2009, Hallermann et al., 2012). To account for the delay caused by the 10 kHz external filter and the lag introduced by uncompensated series resistance (Carter and Bean, 2009), current traces were shifted by 58 μs with respect to the voltage-clamp waveform. This time-lag value was determined from the latency between the onset of the test pulse and the time point of half-maximal rise of tail currents during the deactivation protocol (Bischofberger et al., 2002). The charge separation was calculated by dividing the non-overlapping Na+ charge by the total Na+ charge during APs (Alle et al., 2009; Figure S1B). This parameter quantifies the overlap of Na+ influx and K+ efflux, during which the effects of these opposing currents on membrane potential cancel out. Only Na+ currents with an amplitude exceeding five times the standard deviation of the background noise (0.5–2.0 pA) were included in the analysis of Na+ entry ratio and charge separation.
Finally, we determined the total Na+ influx relative to the theoretical capacitive minimum, using an approach similar to that developed by Alle et al. (2009) (Figures 3D–3H). APs were simulated in a hybrid model, in which experimentally measured conductance traces were inserted into a passive cable model by a threshold trigger mechanism (ModelDB accession number 135838). Conductance values during an AP were determined from the respective Na+ and K+ currents, normalized to the maximum, and temporally aligned so that the onset of the Na+ conductance corresponded to t = 0. The onset point was measured as the intersection of a line through the 20 and 80% amplitude points of the rising phase with the baseline. Experimentally determined gNa and gK traces were filtered with a sliding window (±three sample points) and incorporated into Neuron mod files. Simulations were performed using NEURON 7.4 (Carnevale and Hines, 2006). Conductances were inserted into a simplified cylindrical axon (diameter 0.9 μm, total length 910 μm), in which 5 boutons (diameter 2 μm) were added equidistantly in an en passant manner (Engel and Jonas, 2005, Alle et al., 2009, Hu and Jonas, 2014). Conductances were activated when membrane potential at a given location exceeded a threshold value. To initiate APs, a current pulse was applied to one end of the axon. The three parameters of the model, Na+ peak conductance, K+ peak conductance, and activation threshold (range: −60 to −45 mV), were then varied until the sum of squared differences between simulated AP at the center bouton and measured AP were minimal. Finally, energy efficiency was calculated as the ratio of the Na+ charge QNa = ∫ INa(t) dt over the product Cm x ΔV, where INa is the Na+ current, Cm is the specific membrane capacitance (0.9 μF cm−2, Table S6, Nörenberg et al., 2010) and ΔV is the peak amplitude of the AP (Alle et al., 2009). AP amplitude was measured from threshold (50 V s−1) rather than baseline, because our axonal recording sites were relatively proximal; consequently, the AP was preceded by an axonal depolarization reflecting somatic current injection.
The K+ channel activation curve was obtained by plotting the peak amplitude of tail currents elicited by stepping to −130 mV after a voltage pulse against the absolute value of the voltage pulse, and data points were normalized to the maximal value in each experiment. The activation curve was fit with a Boltzmann function f = 1 / (1+Exp[ (V1/2 − V)/k]), where V is the membrane potential, V1/2 is the midpoint potential, and k is the slope factor. K+ current activation time constant was obtained by fitting the rising phase of the K+ current with a function of the form I(t) = a × (1 − Exp[- (t − δ) / τ]) for t > δ and I(t) = 0 for t ≤ δ, where δ is a delay, τ is activation time constant, and a is the amplitude value. K+ current deactivation time constant was obtained by fitting the decay phase of K+ tail currents with a single exponential function. To plot conductance density against distance (Figure S5), was calculated based on the peak current at 0 mV and a maximal Na+ channel open probability of 0.66 at this membrane potential (Hu and Jonas, 2014), assuming an Na+ current reversal potential of 70 mV (Martina and Jonas, 1997). was calculated from the steady-state current amplitude at 70 mV, assuming a maximal K+ channel open probability of 1 at 70 mV, and a K+ current reversal potential −95 mV (Martina et al., 1998).
Modeling of axonal Na+ and K+ channel gating
To determine the effects of Na+ and K+ channel gating on energy efficiency, we fit the experimental voltage-clamp data with models of Na+ and K+ channel gating (Hodgkin and Huxley, 1952, Hille, 2001, Engel and Jonas, 2005). For Na+ channels, the total dataset consisted of activation curve, steady-state inactivation curve, activation time constant, activation delay, deactivation time constant, onset of inactivation, and recovery from inactivation. For K+ channels, the full dataset was comprised of activation curve, activation time constant, activation delay, and deactivation time constant. Steady-state values of gating parameters were calculated as x∞ = αx / (αx + βx), and time constants were computed as τx = 1 / (αx + βx), where x = m, h, n, or n’. For fitting of steady-state activation and inactivation curves, m∞3, n∞3 n’∞, and h were compared against the measured values. Similarly, for fitting the inactivation time constants, τh was compared against the experimental values. For fitting of activation and deactivation time constants, Na+ or K+ currents were simulated as m(t)3 or n(t)3 n’(t), with x(t) = x∞ − (x∞ − x0) Exp(−t / τx), with x = m or n. Simulated traces were then fit with an exponential function including (activation) or not including a delay (deactivation). The sum of squares of differences between experimental observations and model predictions was minimized using FindMinimum of Mathematica 11 (Wolfram Research) running under Windows 7. Weight factors were approximately set according to the inverse of squared standard errors of the data points.
The forward and backward rate constants were determined as:
| (Eq. 1a) |
| (Eq. 1b) |
| (Eq. 2a) |
| (Eq. 2b) |
where V is membrane potential. The Na+ conductance was calculated as x m3 x h (Table S5).
To accurately describe the K+ channel gating, simple Hodgkin-Huxley equations were inadequate. We therefore adopted a more complex model with two sets of rates:
| (Eq. 3a) |
| (Eq. 3b) |
| (Eq. 4a) |
| (Eq. 4b) |
where the K+ conductance was calculated as x n3 x n’ (Table S5).
Computational models of AP energy efficiency and requirement in PV+-BC axons
To model the energy efficiency of the AP, we first used a single-compartment model (Table S6) (Wang and Buzsáki, 1996). was set to 500 pS μm−2 and to 150 pS μm−2, consistent with the experimental observations. To account for the differences in the recording temperature in voltage-clamp and current-clamp recordings, rates αx and βx were scaled assuming a 11.5°C temperature difference and Q10 values of 2.2, 2.9, and 3.0 for x = m, h, and n or n’ (Schwarz and Eikhof, 1987, Frankenhaeuser and Moore, 1963). The equilibrium potentials for Na+ and K+ ions were assumed as +55 mV and −90 mV, respectively. The voltage dependence of Na+ channel gating was shifted by 20 mV toward positive potentials to account for differences in the Donnan potential between whole-cell and isolated patch configuration (Fenwick et al., 1982) and time- and temperature-dependent shifts of activation and inactivation curves. Na+ entry ratio was calculated as the total Na+ charge over its fraction before the peak of the AP (Alle et al., 2009, Carter and Bean, 2009). To minimize effects of stimulation on the entry ratio, APs were initiated by setting the initial condition V(t = 0) to a value above AP voltage threshold.
To determine the energy efficiency in different subcellular compartments, we further used detailed cable models of BCs (Table S7). Simulations were performed using NEURON 7.4 (Carnevale and Hines, 2006) in combination with Mathematica. Detailed passive cable models of BCs taken from the previously published sample of Nörenberg et al., 2010 (cell 2, and other cells from the sample as indicated; ModelDB accession number 140789). Neurons had been filled with biocytin during recording, stained with 3,3′-diaminobenzidine, and fully reconstructed (including soma, dendrites, and entire axon) using a Neurolucida reconstruction system, as described in the previous publication (Nörenberg et al., 2010). The specific cable parameters were chosen according to approximate average values (Nörenberg et al., 2010). The integration time step was set to 1 or 5 μs. To convey maximal accuracy, the number of segments per section (nseg) was determined according to the “d-lambda rule” as nseg = L / (0.03 λ1 kHz), where L is the length of the section and λ1 kHz is the alternating current length constant at 1 kHz. Na+ and K+ channels were inserted using the experimentally derived Na+ and K+ channel models. was set to 500 pS μm−2 in the axon, 200 pS μm−2 at the soma, and 50 pS μm−2 at the dendrite. was uniformly set to 300 pS μm−2 in all compartments. The reversal potential of the leak conductance was chosen as −70 mV. APs were evoked by brief current pulses at the soma (2–4 nA, 1 ms). Subcellular analysis of Na+ entry ratio revealed that the entry ratio was higher in the dendrites, but lower at the soma in comparison to the axon (Figure 5E). The higher dendritic entry ratio was expected for a passively propagated signal (Hallermann et al., 2012). In contrast, the lower somatic entry ratio was explained by the presence of the stimulus electrode at this site, as revealed by shifting the stimulation site from the soma into the proximal axon (unpublished observations).
Quantification and Statistical Analysis
Membrane potentials are specified without correction for liquid junction potentials. Values indicate median value ± standard error (SEM) unless stated otherwise. Whiskers in box charts indicate the 5th and 95th percentile of data points, and the box itself indicates median, first quartile, and third quartile of the data points. Significance of difference between two groups of data was assessed by a two-sided nonparametric Wilcoxon signed rank test or Wilcoxon rank sum test. For comparison among multiple groups, we used nonparametric Friedman or Kruskal-Wallis tests. Differences were considered significant if p < 0.05. Correlation between two variables was assessed with the nonparametric Spearman rank correlation test. Distances were measured from the point of origin of the axon to the axonal recording site along the axonal trajectory in the confocal maximal intensity stack projection, in which sections at different focal planes had been merged following each experiment. In five recordings, the axon could not be traced back from the recording site to the soma. These recordings were excluded from the analyses of distance-dependence. Conductance density values were calculated from conductance values using the previously established relation between patch area and pipette resistance (Hu and Jonas, 2014), requiring recalculation for previous dendritic measurements (Hu et al., 2010).
Data and code availability
Original data and programs were stored in the scientific repositories of the Institute of Science and Technology Austria and the University of Oslo and are available on request.
Acknowledgments
We thank Drs. Thomas Klausberger and Arnd Roth for critically reading a previous manuscript version. We also thank Florian Marr for technical assistance, Eva Kramberger for editorial support, and Drs. Michael Hines and Ted Carnevale for useful suggestions. This project has received funding from the European Research Council (ERC) under the European Union’s seventh framework programme, grant agreement number 268548 (to P.J.), under the European Union’s Horizon 2020 research and innovation programme, grant agreement number 692692 (to P.J.), the Fond zur Förderung der Wissenschaftlichen Forschung (P 24909-B24; Z 312-B27, Wittgenstein award to P.J.), the Norwegian Research Council, grant agreement number 250866 (to H.H.), and the European Union’s seventh framework programme (FP7-PEOPLE-2013-COFUND), grant agreement number 609020 -Scientia Fellows (to H.H. and F.C.R).
Author Contributions
H.H., F.C.R., and D.V. performed experiments and analyzed data. P.J. performed modeling. H.H. and P.J. wrote the paper. All authors jointly revised the paper.
Declaration of Interests
The authors declare no competing interests.
Published: March 15, 2018
Footnotes
Supplemental Information includes six figures and seven tables and can be found with this article online at https://doi.org/10.1016/j.neuron.2018.02.024.
Contributor Information
Hua Hu, Email: huah@medisin.uio.no.
Peter Jonas, Email: peter.jonas@ist.ac.at.
Supplemental Information
References
- Alle H., Roth A., Geiger J.R.P. Energy-efficient action potentials in hippocampal mossy fibers. Science. 2009;325:1405–1408. doi: 10.1126/science.1174331. [DOI] [PubMed] [Google Scholar]
- Alle H., Kubota H., Geiger J.R.P. Sparse but highly efficient Kv3 outpace BKCa channels in action potential repolarization at hippocampal mossy fiber boutons. J. Neurosci. 2011;31:8001–8012. doi: 10.1523/JNEUROSCI.0972-11.2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Attwell D., Laughlin S.B. An energy budget for signaling in the grey matter of the brain. J. Cereb. Blood Flow Metab. 2001;21:1133–1145. doi: 10.1097/00004647-200110000-00001. [DOI] [PubMed] [Google Scholar]
- Bean B.P. The action potential in mammalian central neurons. Nat. Rev. Neurosci. 2007;8:451–465. doi: 10.1038/nrn2148. [DOI] [PubMed] [Google Scholar]
- Bezaire M.J., Soltesz I. Quantitative assessment of CA1 local circuits: knowledge base for interneuron-pyramidal cell connectivity. Hippocampus. 2013;23:751–785. doi: 10.1002/hipo.22141. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bischofberger J., Geiger J.R.P., Jonas P. Timing and efficacy of Ca2+ channel activation in hippocampal mossy fiber boutons. J. Neurosci. 2002;22:10593–10602. doi: 10.1523/JNEUROSCI.22-24-10593.2002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Buzsáki G., Kaila K., Raichle M. Inhibition and brain work. Neuron. 2007;56:771–783. doi: 10.1016/j.neuron.2007.11.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Carnevale N.T., Hines M.L. Cambridge University Press; 2006. The Neuron Book. [Google Scholar]
- Carter B.C., Bean B.P. Sodium entry during action potentials of mammalian neurons: incomplete inactivation and reduced metabolic efficiency in fast-spiking neurons. Neuron. 2009;64:898–909. doi: 10.1016/j.neuron.2009.12.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Doischer D., Hosp J.A., Yanagawa Y., Obata K., Jonas P., Vida I., Bartos M. Postnatal differentiation of basket cells from slow to fast signaling devices. J. Neurosci. 2008;28:12956–12968. doi: 10.1523/JNEUROSCI.2890-08.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Engel D., Jonas P. Presynaptic action potential amplification by voltage-gated Na+ channels in hippocampal mossy fiber boutons. Neuron. 2005;45:405–417. doi: 10.1016/j.neuron.2004.12.048. [DOI] [PubMed] [Google Scholar]
- Fenwick E.M., Marty A., Neher E. Sodium and calcium channels in bovine chromaffin cells. J. Physiol. 1982;331:599–635. doi: 10.1113/jphysiol.1982.sp014394. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fleidervish I.A., Lasser-Ross N., Gutnick M.J., Ross W.N. Na+ imaging reveals little difference in action potential-evoked Na+ influx between axon and soma. Nat. Neurosci. 2010;13:852–860. doi: 10.1038/nn.2574. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Frankenhaeuser B., Moore L.E. The effect of temperature on the sodium and potassium permeability changes in myelinated nerve fibres of Xenopus laevis. J. Physiol. 1963;169:431–437. doi: 10.1113/jphysiol.1963.sp007269. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gan J., Weng S.M., Pernía-Andrade A.J., Csicsvari J., Jonas P. Phase-locked inhibition, but not excitation, underlies hippocampal ripple oscillations in awake mice in vivo. Neuron. 2017;93:308–314. doi: 10.1016/j.neuron.2016.12.018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Geiger J.R.P., Jonas P. Dynamic control of presynaptic Ca2+ inflow by fast-inactivating K+ channels in hippocampal mossy fiber boutons. Neuron. 2000;28:927–939. doi: 10.1016/s0896-6273(00)00164-1. [DOI] [PubMed] [Google Scholar]
- Gentet L.J., Avermann M., Matyas F., Staiger J.F., Petersen C.C. Membrane potential dynamics of GABAergic neurons in the barrel cortex of behaving mice. Neuron. 2010;65:422–435. doi: 10.1016/j.neuron.2010.01.006. [DOI] [PubMed] [Google Scholar]
- Goldberg E.M., Watanabe S., Chang S.Y., Joho R.H., Huang Z.J., Leonard C.S., Rudy B. Specific functions of synaptically localized potassium channels in synaptic transmission at the neocortical GABAergic fast-spiking cell synapse. J. Neurosci. 2005;25:5230–5235. doi: 10.1523/JNEUROSCI.0722-05.2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Goldberg E.M., Jeong H.Y., Kruglikov I., Tremblay R., Lazarenko R.M., Rudy B. Rapid developmental maturation of neocortical FS cell intrinsic excitability. Cereb. Cortex. 2011;21:666–682. doi: 10.1093/cercor/bhq138. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Guzman S.J., Schlögl A., Schmidt-Hieber C. Stimfit: quantifying electrophysiological data with Python. Front. Neuroinform. 2014;8:16. doi: 10.3389/fninf.2014.00016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Halasy K., Somogyi P. Subdivisions in the multiple GABAergic innervation of granule cells in the dentate gyrus of the rat hippocampus. Eur. J. Neurosci. 1993;5:411–429. doi: 10.1111/j.1460-9568.1993.tb00508.x. [DOI] [PubMed] [Google Scholar]
- Hallermann S., de Kock C.P., Stuart G.J., Kole M.H. State and location dependence of action potential metabolic cost in cortical pyramidal neurons. Nat. Neurosci. 2012;15:1007–1014. doi: 10.1038/nn.3132. [DOI] [PubMed] [Google Scholar]
- Hille B. Sinauer; 2001. Ion Channels of Excitable Membranes. [Google Scholar]
- Hodgkin A. The optimum density of sodium channels in an unmyelinated nerve. Philos. Trans. R. Soc. Lond. B Biol. Sci. 1975;270:297–300. doi: 10.1098/rstb.1975.0010. [DOI] [PubMed] [Google Scholar]
- Hodgkin A.L., Huxley A.F. Currents carried by sodium and potassium ions through the membrane of the giant axon of Loligo. J. Physiol. 1952;116:449–472. doi: 10.1113/jphysiol.1952.sp004717. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hoffman D.A., Magee J.C., Colbert C.M., Johnston D. K+ channel regulation of signal propagation in dendrites of hippocampal pyramidal neurons. Nature. 1997;387:869–875. doi: 10.1038/43119. [DOI] [PubMed] [Google Scholar]
- Howarth C., Gleeson P., Attwell D. Updated energy budgets for neural computation in the neocortex and cerebellum. J. Cereb. Blood Flow Metab. 2012;32:1222–1232. doi: 10.1038/jcbfm.2012.35. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hu H., Jonas P. A supercritical density of Na+ channels ensures fast signaling in GABAergic interneuron axons. Nat. Neurosci. 2014;17:686–693. doi: 10.1038/nn.3678. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hu H., Martina M., Jonas P. Dendritic mechanisms underlying rapid synaptic activation of fast-spiking hippocampal interneurons. Science. 2010;327:52–58. doi: 10.1126/science.1177876. [DOI] [PubMed] [Google Scholar]
- Hu H., Gan J., Jonas P. Interneurons. Fast-spiking, parvalbumin+ GABAergic interneurons: from cellular design to microcircuit function. Science. 2014;345:1255263. doi: 10.1126/science.1255263. [DOI] [PubMed] [Google Scholar]
- Kaczmarek L.K., Zhang Y. Kv3 Channels: Enablers of rapid firing, neurotransmitter release, and neuronal endurance. Physiol. Rev. 2017;97:1431–1468. doi: 10.1152/physrev.00002.2017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kole M.H., Letzkus J.J., Stuart G.J. Axon initial segment Kv1 channels control axonal action potential waveform and synaptic efficacy. Neuron. 2007;55:633–647. doi: 10.1016/j.neuron.2007.07.031. [DOI] [PubMed] [Google Scholar]
- Kowalski J., Gan J., Jonas P., Pernía-Andrade A.J. Intrinsic membrane properties determine hippocampal differential firing pattern in vivo in anesthetized rats. Hippocampus. 2016;26:668–682. doi: 10.1002/hipo.22550. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lapray D., Lasztoczi B., Lagler M., Viney T.J., Katona L., Valenti O., Hartwich K., Borhegyi Z., Somogyi P., Klausberger T. Behavior-dependent specialization of identified hippocampal interneurons. Nat. Neurosci. 2012;15:1265–1271. doi: 10.1038/nn.3176. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Leão R.M., Kushmerick C., Pinaud R., Renden R., Li G.L., Taschenberger H., Spirou G., Levinson S.R., von Gersdorff H. Presynaptic Na+ channels: locus, development, and recovery from inactivation at a high-fidelity synapse. J. Neurosci. 2005;25:3724–3738. doi: 10.1523/JNEUROSCI.3983-04.2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lennie P. The cost of cortical computation. Curr. Biol. 2003;13:493–497. doi: 10.1016/s0960-9822(03)00135-0. [DOI] [PubMed] [Google Scholar]
- Martina M., Jonas P. Functional differences in Na+ channel gating between fast-spiking interneurones and principal neurones of rat hippocampus. J. Physiol. 1997;505:593–603. doi: 10.1111/j.1469-7793.1997.593ba.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Martina M., Schultz J.H., Ehmke H., Monyer H., Jonas P. Functional and molecular differences between voltage-gated K+ channels of fast-spiking interneurons and pyramidal neurons of rat hippocampus. J. Neurosci. 1998;18:8111–8125. doi: 10.1523/JNEUROSCI.18-20-08111.1998. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Meyer H.S., Schwarz D., Wimmer V.C., Schmitt A.C., Kerr J.N.D., Sakmann B., Helmstaedter M. Inhibitory interneurons in a cortical column form hot zones of inhibition in layers 2 and 5A. Proc. Natl. Acad. Sci. USA. 2011;108:16807–16812. doi: 10.1073/pnas.1113648108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Micheva K.D., Wolman D., Mensh B.D., Pax E., Buchanan J., Smith S.J., Bock D.D. A large fraction of neocortical myelin ensheathes axons of local inhibitory neurons. eLife. 2016;5:e15784. doi: 10.7554/eLife.15784. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mishra R.K., Kim S., Guzman S.J., Jonas P. Symmetric spike timing-dependent plasticity at CA3-CA3 synapses optimizes storage and recall in autoassociative networks. Nat. Commun. 2016;7:11552. doi: 10.1038/ncomms11552. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mountcastle V.B., Talbot W.H., Sakata H., Hyvärinen J. Cortical neuronal mechanisms in flutter-vibration studied in unanesthetized monkeys. Neuronal periodicity and frequency discrimination. J. Neurophysiol. 1969;32:452–484. doi: 10.1152/jn.1969.32.3.452. [DOI] [PubMed] [Google Scholar]
- Nörenberg A., Hu H., Vida I., Bartos M., Jonas P. Distinct nonuniform cable properties optimize rapid and efficient activation of fast-spiking GABAergic interneurons. Proc. Natl. Acad. Sci. USA. 2010;107:894–899. doi: 10.1073/pnas.0910716107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Okaty B.W., Miller M.N., Sugino K., Hempel C.M., Nelson S.B. Transcriptional and electrophysiological maturation of neocortical fast-spiking GABAergic interneurons. J. Neurosci. 2009;29:7040–7052. doi: 10.1523/JNEUROSCI.0105-09.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rakowski R.F., Gadsby D.C., De Weer P. Stoichiometry and voltage dependence of the sodium pump in voltage-clamped, internally dialyzed squid giant axon. J. Gen. Physiol. 1989;93:903–941. doi: 10.1085/jgp.93.5.903. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Raman I.M., Bean B.P. Resurgent sodium current and action potential formation in dissociated cerebellar Purkinje neurons. J. Neurosci. 1997;17:4517–4526. doi: 10.1523/JNEUROSCI.17-12-04517.1997. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ritzau-Jost A., Delvendahl I., Rings A., Byczkowicz N., Harada H., Shigemoto R., Hirrlinger J., Eilers J., Hallermann S. Ultrafast action potentials mediate kilohertz signaling at a central synapse. Neuron. 2014;84:152–163. doi: 10.1016/j.neuron.2014.08.036. [DOI] [PubMed] [Google Scholar]
- Rowan M.J., Tranquil E., Christie J.M. Distinct Kv channel subtypes contribute to differences in spike signaling properties in the axon initial segment and presynaptic boutons of cerebellar interneurons. J. Neurosci. 2014;34:6611–6623. doi: 10.1523/JNEUROSCI.4208-13.2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rudy B., McBain C.J. Kv3 channels: voltage-gated K+ channels designed for high-frequency repetitive firing. Trends Neurosci. 2001;24:517–526. doi: 10.1016/s0166-2236(00)01892-0. [DOI] [PubMed] [Google Scholar]
- Schwarz J.R., Eikhof G. Na currents and action potentials in rat myelinated nerve fibres at 20 and 37°C. Pflugers Arch. 1987;409:569–577. doi: 10.1007/BF00584655. [DOI] [PubMed] [Google Scholar]
- Sengupta B., Stemmler M., Laughlin S.B., Niven J.E. Action potential energy efficiency varies among neuron types in vertebrates and invertebrates. PLoS Comput. Biol. 2010;6:e1000840. doi: 10.1371/journal.pcbi.1000840. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shu Y., Hasenstaub A., Duque A., Yu Y., McCormick D.A. Modulation of intracortical synaptic potentials by presynaptic somatic membrane potential. Nature. 2006;441:761–765. doi: 10.1038/nature04720. [DOI] [PubMed] [Google Scholar]
- Tremblay R., Lee S., Rudy B. GABAergic interneurons in the neocortex: From cellular properties to circuits. Neuron. 2016;91:260–292. doi: 10.1016/j.neuron.2016.06.033. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang X.J., Buzsáki G. Gamma oscillation by synaptic inhibition in a hippocampal interneuronal network model. J. Neurosci. 1996;16:6402–6413. doi: 10.1523/JNEUROSCI.16-20-06402.1996. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Waters M.F., Minassian N.A., Stevanin G., Figueroa K.P., Bannister J.P., Nolte D., Mock A.F., Evidente V.G., Fee D.B., Müller U. Mutations in voltage-gated potassium channel KCNC3 cause degenerative and developmental central nervous system phenotypes. Nat. Genet. 2006;38:447–451. doi: 10.1038/ng1758. [DOI] [PubMed] [Google Scholar]
- Yu Y., Hill A.P., McCormick D.A. Warm body temperature facilitates energy efficient cortical action potentials. PLoS Comput. Biol. 2012;8:e1002456. doi: 10.1371/journal.pcbi.1002456. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
Original data and programs were stored in the scientific repositories of the Institute of Science and Technology Austria and the University of Oslo and are available on request.