Abstract
In brain structural segmentation, multi-atlas strategies are increasingly being used over single-atlas strategies because of their ability to fit a wider anatomical variability. Patch-based label fusion (PBLF) is a type of such multi-atlas approaches that labels each target point as a weighted combination of neighboring atlas labels, where atlas points with higher local similarity to the target contribute more strongly to label fusion. PBLF can be potentially improved by increasing the discriminative capabilities of the local image similarity measurements. We propose a framework to compute patch embeddings using neural networks so as to increase discriminative abilities of similarity-based weighted voting in PBLF. As particular cases, our framework includes embeddings with different complexities, namely, a simple scaling, an affine transformation, and non-linear transformations. We compare our method with state-of-the-art alternatives in whole hippocampus and hippocampal subfields segmentation experiments using publicly available datasets. Results show that even the simplest versions of our method outperform standard PBLF, thus evidencing the benefits of discriminative learning. More complex transformation models tended to achieve better results than simpler ones, obtaining a considerable increase in average Dice score compared to standard PBLF.
Keywords: Patch-based label fusion, Multi-atlas segmentation, Neural networks, Embedding, Brain MRI, Hippocampus
1. Introduction
Segmentation of brain structures from magnetic resonance images (MRI) is an important step in many neuroscience applications, including discovery of morphological biomarkers, monitoring disease progression or diagnosis. For example, segmentation is widely used as basic image quantification step in studies of early brain development (Benkarim et al., 2017) and dementia (Chupin et al., 2009; Li et al., 2007).
Multi-atlas segmentation (MAS) is being increasingly used for segmenting brain MRI (Sanroma et al., 2016). In MAS, a set of atlas images are first registered to the image to be segmented (i.e., target) along with their anatomical labelmaps containing the spatial overlay of the anatomical structures. Then, the so-called label fusion process, labels each target point using the support of the corresponding atlas labels. Compared to using a single atlas, MAS can potentially fit a wider anatomical variability and has higher robustness to registration errors. Image intensities are often not sufficient for globally discriminating the different structures and therefore, spatial constraints are essential (Colliot et al., 2006). Such spatial constraints are usually implemented by restricting the set of feasible labels for each target point to the set of labels in neighboring atlas points.
Patch-based label fusion (PBLF) is a popular approach that computes each target label as a weighted combination of neighboring atlas labels, where atlas locations with higher local image similarity to the to-be-segmented target point have higher weight in the combination (Artaechevarria et al., 2009; Coupé et al., 2011; Wang et al., 2013). Here, the similarity between local image patches around each target and atlas point is taken as a proxy for the local registration accuracy and hence, for anatomical correspondence.
PBLF can potentially be improved by increasing the discriminative capabilities of patch similarity measurements. For example, we proposed to learn discriminative patch embeddings reflecting the latent anatomical similarity between patches (Sanroma et al., 2015a). A similar approach was recently proposed using convolutional neural networks (CNNs) (Yang et al., 2016). Such learned embeddings are then used in standard PBLF. Other supervised approaches for learning optimal fusion rules have been presented. For example, in Sanroma et al. (2015b) we proposed a transductive learning approach, and in Benkarim et al. (2016) we proposed to integrate discriminative learning into probabilistic label fusion. Semi-supervised learning approaches have also been proposed for propagating the anatomical labels from atlases to targets (Guo and Zhang, 2012; Koch et al., 2014). Machine learning techniques such as support vector machines (SVM) (Cortes and Vapnik, 1995) have also been used (Bai et al., 2015; Hao et al., 2013; Sdika, 2015).
In practice, most of these methods learn a different model (i.e., classifier) at each location (Bai et al., 2015; Benkarim et al., 2016; Guo and Zhang, 2012; Hao et al., 2013; Koch et al., 2014; Sanroma et al., 2015a; 2015b; Sdika, 2015). This serves two purposes: (1) it implicitly imposes spatial constraints by restricting the training samples on each model to only neighboring atlas locations; and (2) it divides the difficult problem of finding a single global model into the problem of finding multiple simpler local models. However, this increases the complexity of storage and use of the method due to the high number of local models generated, which can easily reach several hundred thousands, even after restricting the modeling to only the most challenging regions. Another difficulty when using local models is that training images must be in spatial correspondence in order to retrieve the training data for each local model. As a result, some methods opt for training the models in a common template space (Sanroma et al., 2015a). This implies that the target image must be segmented in the template space, incurring in interpolation errors when re-sampling the resulting segmentation to the original target space. Moreover, methods that consider pairwise relationships (Benkarim et al., 2016; Sanroma et al., 2015a; Yang et al., 2016) need pairwise registrations among the training images to evaluate the similarity between the embedded patches. This has memory complexity 𝒪(N2) during training, with N being the number of atlases, thus limiting the amount of atlases that can effectively be used for training. A related approach uses convolutional neural networks (CNN) for segmenting cardiac images (Yang et al., 2016). For an input image, they obtain a stack of output images by applying the learned convolutional filters. The number of images in the stack is related to the dimensionality of the output embeddings. Thus, memory requirements for label fusion are 𝒪 (N × d), where N is the number of atlases and d the dimensionality of the output embedding. This poses serious limitations on the number of atlases at test time (in fact they only use 5 atlases for each target image). In brain MRI segmentation, usually more than 10 atlases are used (Aljabar et al., 2009; Lotjonen et al., 2010; Sanroma et al., 2014).
To overcome these issues, we propose a method to learn discriminative patch embeddings using neural networks,2 with the following contributions:
By incorporating our method into the regular label fusion process, we focus on the problem of learning the model, thus leveraging the capability of the label fusion process of restricting the set of possible labels at each point.
The previous contribution facilitates that we compute a single model per bilateral structure (i.e., one model for both left and right parts of each structure). We take advantage of stochastic gradient descent (SGD) in order to process the vast amounts of data in small mini-batches. Therefore, our method allows for a practical storage and use.
We learn the model in the native space of each training atlas instead of using a template. Therefore, models are learned in the same space as they were annotated, thus avoiding interpolation artifacts during training. Another advantage is that models are orientation-invariant and hence target images can directly be segmented in their native space. As consequence of this, the target anatomy can directly be quantified from the resulting segmentation, without need to correct for geometric distortions caused by the transformation to the template space.
We learn the embeddings using patch relationships within the same image, leading to an attractive 𝒪 (N) storage complexity at training (with N the number of atlases), compared to more costly approaches (Benkarim et al., 2016; Sanroma et al., 2015a; Yang et al., 2016) that require pairwise atlas registrations in this phase.
Our method embeds the image patches independently rather than the whole images. Therefore, we can generate output embeddings of arbitrary dimensionality without compromising the number of atlases that can reasonably be handled (memory requirement at segmentation time is 𝒪 (N)).
We apply our method to segment the whole hippocampus and the hippocampal subfields (see Section 4), a structure targeted by many studies on psychiatric and neurological disorders (Chupin et al., 2009; Li et al., 2007). Accurate segmentation methods are required in order to quantify the subtle morphological changes undergone by these structures, especially in the early stages of the disease (Frisoni et al., 2010; West et al., 2004).
In the next section, we introduce multi-atlas segmentation and how it can be improved by using embedding techniques, before describing our method in Section 3.
2. Multi-atlas segmentation
Let us denote X̂ the target image to be segmented and Xi, i = 1, …, N a set of atlas images along with their corresponding labelmaps Yi containing the anatomical information. Multi-atlas segmentation (MAS) aims at estimating the segmentation on the target image using the atlas images and their labelmaps.
This is implemented by (1) registering the atlas images to the target and (2) computing each target label as a combination of locally corresponding atlas labels, the so-called label fusion.
Weighted voting is a popular label fusion approach that computes the target label as a weighted combination of atlas labels (Artaechevarria et al., 2009; Coupé et al., 2011; Wang et al., 2013). More formally, the label ŷp for a given target point p ∈ Ω in the image domain Ω, is computed as:
| (1) |
where yiq is the label in ith atlas at point q ∈ 𝒩p in the spatial neighborhood of p ∈ Ω, ωiq is the weight denoting the importance of yiq in determining the target label, and δ is Kronecker’s delta (i.e., δ[ a = b] is 1 if a = b, 0 otherwise).
One of the earliest label fusion approaches, known as majority voting (Heckemann et al., 2006; Rohlfing et al., 2004) assigns each target label the atlas label occurring most frequently, which is equivalent to using a constant weight, i.e., ωiq = c, ∀i, q. This simple strategy already achieves substantial improvement over single-atlas segmentation. Other techniques such as STAPLE estimate the weights using rater statistics (Warfield et al., 2004).
Global weighted voting strategies, assign the same weight globally to all atlas points, i.e., ωiq = αi, ∀q ∈ Ω (Artaechevarria et al., 2009). However, local weighted voting strategies (Artaechevarria et al., 2009; Coupé et al., 2011; Wang et al., 2013) have ended up dominating over global weighting, due to their greater flexibility to adapt to unevenly distributed registration errors.
2.1. Patch-based label fusion
A crucial step here is how to estimate the weights ωiq denoting the importance of the ith atlas label at location q. Patch-based label fusion (PBLF) is a popular approach that uses patch similarity. A widely adopted patch similarity measure is the exponential of the negative sum of squared differences (SSD) (Coupé et al., 2011; Giraud et al., 2015; Sanroma et al., 2015a):
| (2) |
where x̂p and xiq are the local target and atlas intensity patches, respectively, around voxels p ∈ Ω (in the target image X̂) and q ∈ 𝒩p (in the spatial neighborhood of p in the registered atlas image X̃i); and β ∈ ℝ+ is a scaling parameter controlling the smoothness of the similarity function. Other similarity measures can also be used such as the inverted SSD [||x̂p − xiq ||2]−β, with β ∈ ℝ+ a gain parameter (Artaechevarria et al., 2009; Wang et al., 2013). The motivation is that the higher the local similarity between atlas and target images, the lower the registration error and therefore the more reliable is the anatomical correspondence.
Sparse regression (Olshausen and Field, 1996) was also used to compute patch similarity with the idea of minimizing the amount of atlases contributing to the fusion of each target point (Tong et al., 2013; Wu et al., 2015; Zhang et al., 2012). Sparse regression, originally used in compressed sensing for representing a signal using a minimal number of base signals, turned out to be successful in PBLF. Further approaches have extended PBLF by having into account pair-wise correlations between atlas patches (Wang et al., 2013), using multi-resolution strategies (Wu et al., 2015), implementing local fusion in probabilistic approaches (Asman and Landman, 2013; Cardoso et al., 2013) and incorporating an efficient PatchMatch search strategy (Barnes et al., 2009) to search for the most similar patches (Giraud et al., 2015).
2.2. Embedding
PBLF can potentially benefit from increasing the discriminative capabilities of patch similarity measurements. Some methods learn an embedding function f (x) that transforms the original image patch to a space emphasizing the features related to anatomical variations (Sanroma et al., 2015a; Yang et al., 2016). Such space is defined so that the Euclidean distance between the transformed patches || f (x̂p) − f (xiq)||2 is a more reliable indicator of anatomical similarity.
Embedding approaches aim at finding a new representation of the data z = f (x) that preserves some desirable properties, with z ∈ IRd usually of lower dimensionality than the input data x ∈ IRD (d < D). For example, Laplacian Eigenmaps (LE) (Belkin and Niyogi, 2003) tries to find an embedding that preserves the local structure of the data
| (3) |
where Aij encodes the adjacency (or similarity) between two data points (e.g., using the exponential of the negative SSD). The idea is that points that are close in the original feature space must lie also close in the embedded space. In LE, the embedding is only defined for the training samples, but linearized versions have also been presented such as Locality Preserving Projections (LPP) (He and Niyogi, 2004), defining the embeddings as a linear transformation on the input space z = W⊤x. Similar approaches include Local Linear Embeddings (LLE) (Roweis and Saul, 2000) and its linearized version, Neighborhood Preserving Embeddings (NPE) (He et al., 2005).
However, these approaches are unsupervised, so they cannot guarantee that the computed embeddings represent better the anatomical similarity than the original data. To solve this problem, we must leverage the anatomical label yi at each patch xi to enforce the embeddings to be anatomically representative. Following the idea of the previous approaches, Marginal Fisher Analysis (MFA) (Yan et al., 2007) still preserves the local structure of the data but adds discriminative information via a properly defined adjacency. The optimized function is:
| (4) |
where
| (5) |
Here, the idea is to use the two adjacency matrices A and B denoting the same-class and different-class neighborhoods, respectively, to bring same-class neighbors close together and push different-class neighbors far apart. It is important to note that we refer to neighbors in the feature space, as opposed to the concept of spatial neighborhood used in the previous section. By definition, PBLF always deals with spatially neighboring patches. However, we want to enforce spatially close patches with the same label to be also close in the feature space (i.e., appearance similarity). Another embedding approach following a similar idea is Discriminative Neighborhood Embeddings (DNE) (Zhang et al., 2006).
We recently proposed a discriminative label fusion approach that extended the idea of MFA by using non-binary adjacency matrices in order to emphasize the contribution of the most similar patches without using a hard threshold (Sanroma et al., 2015a).
3. Method
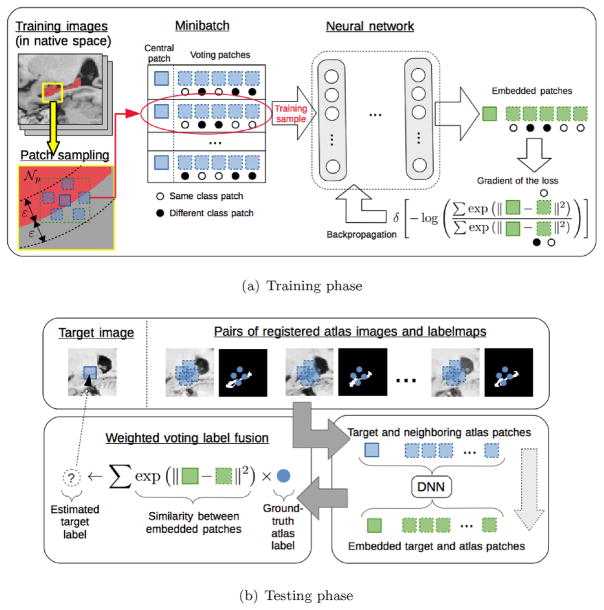
We present a new method to learn non-linear patch embeddings z = f (x) using neural networks. The pipeline of the method is shown in Fig. 1. In the training phase, patches are sampled from atlas images near the boundary of the structures (yellow square in Fig. 1(a)). Note that training images are in their native space (i.e., not registered to any template). A training sample is composed of a central patch and neighboring voting patches at both sides of the boundary. Neighboring patches are sampled within the same image, thus obviating the need for pairwise registration during training. This is based on the assumption that the relationships between neighboring patches within the same image are similar to those between different images during testing, which is reasonable given that images are registered during testing. To validate this assumption, we tried both sampling strategies (i.e., within the same image and between (training) target and registered (training) atlases), and did not find statistical performance improvements by the second strategy despite the considerable increase in training complexity. We process the vast amounts of data in smaller subsets, called mini-batches, via SGD. A mini-batch of samples is put through the neural network to obtain patch embeddings (green squares in Fig. 1(a)). The loss of a mini-batch reflects the accuracy of labeling the central patch using the neighboring patches. The gradient of the loss is used to update the embedding parameters so as to improve the label fusion accuracy. In the testing phase, image patches are obtained around the to-be-labeled target point and the neighboring points in the registered atlases (top panel in Fig. 1(b)). Embedded patches are obtained by applying the neural network to the original patches (bottom right panel in Fig. 1(b)). The target label is obtained via similarity-weighted voting using the embedded patches (bottom left panel in Fig. 1(b)). By integrating our method into standard PBLF, the important issue of enforcing spatial constraints is handled by the weighted voting procedure. Moreover, by computing the embeddings at patch level (rather than the image level) our method scales linearly with the number of atlases at test time.
Fig. 1.
Pipeline of the method for the training and testing phases. (For interpretation of the references to color in this figure, the reader is referred to the web version of this article.)
In the following, we describe all the steps in the training phase of our method, namely, the learning of the model (Section 3.1), the initialization of parameters (Section 3.2) and the sampling of patches (Section 3.3). The testing phase, consisting in standard PBLF with the embedded patches, will not be further discussed beyond what has been mentioned above.
3.1. Model
Each sample in our training set is composed of a pair of target patch and ground-truth label, denoted as (x̂i, ŷi), i = 1, …, m (with m the size of the mini-batch), along with their corresponding set of voting patches and labels, denoted as {(xij, yij)}, j = 1, …, n (with n the number of voting patches), casting the votes on the target label. In Section 3.3 we will describe the procedure used to retrieve such training samples.
We define the notion of similarity between two embedded patches using the softmax operator as follows:
| (6) |
In PBLF, this measure can be interpreted as the probability of patches x̂i and xij having the same label, given the embedding f, when using the similarity measure defined in Eq. (2). Note that the scaling parameter related to the smoothness of the weights (β in Eq. (2)) is here implicit in the embedding f. Non-local weighted voting label fusion (Coupé et al., 2011) proposes to heuristically set it to β = 1/min (|| x̂i − xij ||2). As we will see in next section, scaling is relevant for the initialization of the network since it affects the behavior of the softmax.
Our goal is to optimize the label fusion accuracy of PBLF, i.e., we want to maximize the sum of probabilities of the same-class patches. Let us define 𝒞i = {j| ŷi = yij} as the indices of the same-class patches in the set of voting patches. Further, we denote the activation between patches x̂i and xij as:
| (7) |
Using the expression of Eq. (6), the sum of probabilities for the same-class patches can be defined as:
| (8) |
This measure provides a likelihood of correct label fusion through similarity weighted voting (Eq. (1)). In the ideal case (Ji ≃ 1), the sum of similarities of different-class samples will be negligible compared to correct class ones (and in the worst case Ji ≃ 0).
We want to maximize the expected likelihood of correct labeling over a training set of patches. We adopt the common strategy of minimizing the average of the negative log-likelihood across the training samples. This corresponds to the following energy:
| (9) |
The gradient of this energy with respect to the activations of each patch has the following expression:
| (10) |
where Pij is the softmax defined in Eq. (6) and is a restricted softmax which only considers the samples within the same class. This is,
| (11) |
As we can see in Eq. (10), the gradient of our objective function leads to a very simple expression . Let us interpret this expression to have an idea of the behavior of the optimization. In the case of activations aij of same-class samples, the value of the gradient will be always negative (since , ∀ i, j) which means that the optimization will try to increase their value with a strength proportional to the magnitude of the gradient. This is, the worse the configuration of activations is (i.e., the higher the activations of the different-class patches), the higher the magnitude of the (negative) gradient for same-class activations (because ) and, as consequence, the optimization will try to correct the situation with a higher strength. Conversely, the gradient of different-class activations will always be positive, which means that the optimization will try to decrease their value. The larger the softmax Pij of a different-class activation, the stronger the optimization will try to decrease its value. Finally, in the ideal case that all same-class activations are significantly higher than the different-class ones, we have that . Then, it follows that the gradient for all same-class activations aij, thus corresponding to an optimum of the objective function. For different-class activations, the gradient will also be 0 because, by definition of the ideal situation, their softmax will be also close to zero. That is, the system will push to the correct solution (optimum) with a strength proportional to how far it is from it.
We indirectly optimize activations through the embeddings of the patches. Remember that aij = −|| f (x̂i) − f (xij)||2, so increasing an activation aij implies increasing the similarity of two embeddings f (x̂i) and f (xij). Now, these embeddings are defined as
| (12) |
| (13) |
| (14) |
The final embedding f (x; θ) in Eq. (12) in the output layer consists of a linear combination of the last hidden layer, hL−1, where θ are the parameters of the network and L is the number of layers. The hidden layers hL−l in Eq. (13) are defined as a linear combination of the previous hidden layer hL−l−1 followed by a non-linearity σ(·) such as the sigmoid, the hyperbolic tangent or the rectifier linear unit (ReLU). The first hidden layer h0 corresponds to the input patches (x), as denoted in Eq. (14). Note that for L = 1 this corresponds to a linear model. The parameters θ = {W1, …, WL, b1, …, bL}, consisting of the linear transformation matrices (W) and biases (b) of each layer, are the actual variables optimized through gradient descent (by means of the aforementioned activations).
Regularization
Some methods have shown that promoting the sparsity of the similarity-based weights leads to better label fusion results (Guo and Zhang, 2012; Tong et al., 2013; Wu et al., 2015; Zhang et al., 2012). This is, many atlas patches xij are encouraged to have weights ωij ≃ 0. One widely adopted strategy is to minimize the L1-norm of the resulting similarity-based weights ω. Since we are dealing with probability distributions, we adopt here the well-known strategy of penalizing the KL-divergence of the set of weights with respect to the binomial distribution with a small probability ρ = 0.05 (Ranzato et al., 2007), as follows:
| (15) |
where is the average jth activation value over a mini-batch. The first term in this expression enforces high label fusion accuracy and the second term enforces the sparsity of the similarity-based weights.
Optimization
We optimize the objective function via SGD by partitioning the full training set into small mini-batches. The optimization is carried out for a certain number of epochs, where one epoch corresponds to the processing of the whole dataset over mini-batches. SGD is a convenient strategy to account for the vast amount of data involved in training similar models (the number of samples involved in a moderately-sized structure can easily scale-up to several thousands). In Section 3.3, we will explain how to sample the mini-batches from the training images.
3.2. Initialization
For optimization, we use the common strategy of initializing the biases to zero, b = 0 and the transformation matrices W randomly. Random initialization is important to break the symmetry and avoid all the units behaving the same way (Bengio, 2012). Moreover, when initializing the hidden layers, we have to be careful that the output distribution of the linear transformation Wlhl−1 + bl does not fall into the saturated regime of the non-linearity σ(·), so that the gradients can flow through the network. In the case of the hyperbolic tangent, this is accomplished by initializing each element , where φ is the standard Gaussian distribution and din is the input dimensionality of the layer (Glorot and Bengio, 2010). For the sigmoid, this is (Glorot and Bengio, 2010) and for ReLUs (He et al., 2015).
The output of the network consists of a softmax fed by a linear transformation (Eqs. (6) and (12), respectively). The behavior of the softmax is heavily influenced by the implicit scale of the embeddings, i.e., a high scale will saturate the softmax producing sparse outputs and a low scale will produce uniform outputs. In order to begin the optimization with a reasonable scale, we randomly initialize the transformation matrix in the output layer WL as described above and then adjust the scale as follows: WL ← β̂ ⊙ WL, where ⊙ denotes the element-wise multiplication and β̂ is an optimal scale parameter. The importance of learning the proper scale parameter has also been studied in the context of belief propagation in weighted graphs (Zhu et al., 2003). Here, we learn the optimal scale β̂ for the output layer of the randomly initialized network by minimizing the negative log-likelihood over a large batch of training samples:
| (16) |
where aij are the activations obtained through Eq. (7) with the randomly initialized network and m′(> m) is the batch size used for scale estimation. This procedure is similar to the network training described before but only optimizing one scalar β̂ over a single batch.
3.3. Sampling
We need a procedure to sample the mini-batches that will be used for optimization with SGD. Following the idea of importance sampling (Rubinstein and Kroese, 2011), we sample patches from regions near the boundaries of the structures, since these are the most critical for PBLF. We denote the training images and ground-truth labelmaps as Xi and Yi, i = 1, …, N, respectively. We sample the target patch and label (x̂ip, ŷip) uniformly at random across images and with a probability negatively correlated with the distance to the boundary across locations. That is, i ~ 𝒰 (1, …, N), and position p ~ [ 1 − B (p)/ε]+, where B (p) denotes the distance from p to the boundary, ε denotes the maximum distance to the boundary and [·]+ is an operator that truncates the negatives to zero. For each target patch and label pair (x̂ip, ŷip), we sample a set of voting patches and labels {(xiq, yiq)} from neighboring locations q ∈ 𝒩p within the same image as (x̂ip, ŷip). This avoids the need of using pairwise registrations during training, which simplifies the training procedure and considerably improves the memory requirements. We randomly sample n neighboring patches by trying to create a balanced set when possible, i.e., samples with yiq = ŷip and samples with yiq ≠ ŷip. Each mini-batch is composed of m target patches and labels with their corresponding n voting patches and labels.
4. Experiments and results
We perform several experiments applying the proposed method for segmenting the whole hippocampus and the hippocampal subfields. We compare the proposed method with the following state-of-the-art PBLF techniques: majority voting (MV) (Heckemann et al., 2006; Rohlfing et al., 2004), local weighted voting (LWV) (Artaechevarria et al., 2009), non-local weighted voting (NLWV) (Coupé et al., 2011) and Joint label fusion (JOINT) (Wang et al., 2013). It is worth mentioning that NLWV is considered the baseline since it is equivalent to our method but using original image patches instead of embeddings.
We include the following versions of our method to evaluate the contribution of each part:
SCALE: this version does not use any embedding and is equivalent to baseline NLWV but using a global optimal scaling β estimated through Eq. (16). This provides the performance that can be obtained by optimizing only one global scale parameter.
AFFINE: this is a simplified version of the proposed method without any hidden layer (i.e., L = 1), illustrating the improvement of using the proposed embeddings consisting of an affine transformation (Eq. (12)).
NL1: this a full version of our method with one hidden layer (i.e., L = 2), demonstrating the benefits obtained by using a non-linear model with an extra layer, compared to the AFFINE version.
NL2: this another full version with two hidden layers (i.e., L = 3), representing the improvement of adding yet another hidden layer.
We used our own implementation of LWV and NLWV, where LWV consists of a restricted version of NLWV enforcing one-to-one correspondence when retrieving the atlas voting labels. We used the same base implementation for JOINT, which is similar to LWV and NLWV except for the label fusion part that considers pair-wise atlas patch correlations. Our proposed method also uses the same base implementation for testing, except that patches are transformed with the learnt embeddings before label fusion. In this way, we make sure that performance differences of the methods are due to the label fusion strategy and not due to implementation-specific details.
For JOINT, we set the exponent of the similarity (β in Wang et al., 2013) to the best value in the set β = [ 0.005, 0.05, 0.5, 1.0, 2.0, 3.0, 4.0, 5.0], which were β = 3.0 and β = 0.05 for whole hippocampus and hippocampal subfield datasets, respectively. As for the regularization in the JOINT similarity matrix (α in Wang et al., 2013), we set it to the recommended value α = 0.1 after making sure that the maximum similarities had similar scales as in the original paper (between 1 and 4). For segmentation, we set the patch radius to 3 voxels and the search radius for the voting atlas labels to 1 voxel, which achieved good results for all the methods. Patches were normalized to zero mean and unit standard deviation for all the methods, except for JOINT that uses zero mean and unit L2-norm. All images were non-rigidly registered to the MNI152 template (Fonov et al., 2009) with ANTs (Avants et al., 2008) using a symmetric diffeomorphism (SyN) and pairwise registrations were obtained by concatenating the deformations through the template. All methods used the same target images and registered atlases as inputs. The following pre-processing steps were applied: (1) de-noising (Manjon et al., 2010), (2) N4 bias correction (Tustison et al., 2010), (3) histogram matching (Nyul and Udupa, 1999). We do all the processing (including segmentation) in the native target space, thus avoiding as much as possible interpolation effects.
All images were divided into an atlas-set (i.e., training) and a target-set (i.e., test). To make sure both sets were well distributed, we computed the pair-wise similarity between all the images in a region-of-interest (ROI) around the to-be-segmented structure and selected the atlas-set so as to be well spread across the manifold. For all the methods, we segment the target-set using the atlas-set.
For training the proposed method, 10 instances of each model were independently trained for each structure with hyper-parameters selected uniformly at random among a range of values. We divided the training set into training and validation sets and the best model was used for segmenting the target-set according to the performance on the validation set. We used the following range of values for sparse regularization, λ = [0, 0.0002, 0.002, 0.02]. The same number of units were used in each layer, which was selected among the values 100, 200, 500. As non-linearities, we used hyperbolic tangent, sigmoid and ReLUs. The size of the mini-batch and number of voting patches were set to m = 50 and n = 50, respectively, (we did not find that this value affected the results for a fairly wide range of values). The size of the batch for the estimation of the optimal scale parameter in Eq. (16) was set to m′ = 1000. The radius of the neighborhood 𝒩p for sampling voting patches for training was set to 4 voxels. We used Adam (Kingma and Ba, 2014) variant of SGD with a learning rate of 0.0003. Batch normalization was used in all the model instances containing non-linearities (Ioffe and Szegedy, 2015). The training was stopped when no further improvement in the validation set was obtained, which usually occurred before 3 epochs. In the Section 4.3, we report the frequencies of the selected hyper-parameters.
4.1. Whole hippocampus
Data used in this experiment were obtained from the Alzheimer’s Disease Neuroimaging Initiative (ADNI) database (http://www.adni.loni.usc.edu).3 We used a subset of 135 T1 MR images with ground-truth hippocampal segmentations according to the harmonized protocol by the EADC-ADNI effort4 (Boccardi et al., 2015). The size of the images is 197 × 233 × 189 with a resolution of 1 mm isotropic. The distribution of subjects according to their clinical status is the following: N = 44 normal control, N = 46 mild cognitive impairment and N = 45 Alzheimer’s disease; and the distribution according to age is: N = 40 between 60 – 70 yrs., N = 55 between 70 – 80 yrs. and N = 40 with more than 80 yrs. We selected 35 images as atlases and 100 images as targets.
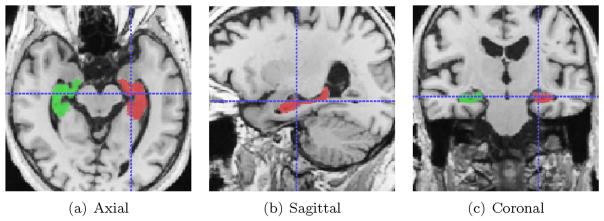
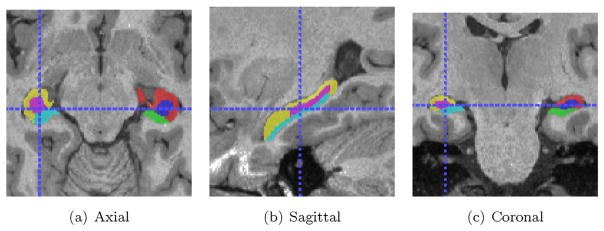
Fig. 2 shows an example image with overlaid ground-truth segmentations of left and right hippocampi.
Fig. 2.
A sample image from ADNI after pre-processing with ground-truth hippocampal labels overlaid.
The first set of experiments compares different choices in the label fusion pipeline including similarity metrics, patch normalization and Softmax scaling. The goal of these experiments is to motivate the choices by the proposed method and to provide insight on the crucial aspects affecting label fusion performance. The second set of experiments compares the proposed methods to the state-of- the-art.
4.1.1. The effects of similarity metric, patch normalization and softmax scaling
Here, we compare several factors influencing the label fusion performance. The first obvious candidate is the similarity metric used to compute the weights. As similarity metrics, we compare (1) the negative SSD (negSSD) between a target patch x̂i and the jth atlas patch in the library xij, (the proposed one), and (2) the locally normalized cross-correlation (LNCC), . We also tried the cosine similarity, , but got similar results to LNCC, so we do not include the results here.
The type of normalization applied to the patches also has important effects regarding the invariance properties of the similarity. This is especially important for the negSSD metric, which is not normalized (we did not find any effect in normalizing the patches for LNCC similarity, since LNCC is already normalized). We evaluate three strategies for normalizing the patches x before negSSD, namely, (1) no normalization (negSSD-none), where the original patches are used to compute the similarity, (2) zero mean and unit standard deviation (negSSD-zscore, the one used by our method) x̃ = (x − μx)/σx, where μx and σx are the mean and standard deviation of patch x, respectively, and (3) unit L2-norm (negSSD-L2) x̃ = x/||x||2.
Finally, we evaluate the effect of the scaling of the similarity on the behavior of the Softmax. Although scaling is the simplest way of modifying the Softmax operator, it will already provide an intuitive understanding of its influence. We compare three different scaling strategies, namely, (1) no scaling, , where the weights wij are obtained directly by applying the Softmax to the similarities aij, (2) inverse of the minimum distance (or maximum similarity) (Coupé et al., 2011), , where h = maxk aik is the maximum similarity (or minimum distance) (this version is equivalent to the baseline NLWV), and (3) proposed scale, , where β̂ is the optimal scale as in Eq. (16) (this version is equivalent to the proposed SCALE version of our method).
Table 1, shows the mean and standard deviation in Dice scores (DS) obtained by the different choices using the baseline NLWV method.
Table 1.
Mean (std) of DS by using different similarity metrics, patch normalization strategies and Softmax scalings. Star (★) denotes significantly better than the same metric with the scaling strategy at the left. Circle (∘) denotes significantly different than the LNCC metric with the same scaling strategy (Wilcoxon signed-rank test). One marker denotes p < .05; two markers, p < .005.
| Whole hippocampus (DS) | |||
|---|---|---|---|
| No scaling | NLWV (Coupé et al., 2011) | Proposed SCALE (Eq. (16)) | |
| LNCC | 81.49(± 2.80) | 84.43(± 2.41)★★ | 85.39(± 2.15)★★ |
| negSSD-none | 84.60(± 2.42)∘∘ | 84.25(± 2.60) | 84.49(± 2.41) |
| negSSD-zscore | 81.63(± 2.33) | 84.58(± 2.38)★★ | 85.36(± 2.15)★ |
| negSSD-L2 | 80.76(± 2.29) | 83.74(± 2.54)★★ | 85.16(± 2.29)★★ |
As we can see, for a given scaling strategy, there are no significant differences between using LNCC and negSSD metrics. The only exception is negSSD with no scaling (negSSD-none), which turns out to be scaled properly for the Softmax, as shown by the good results when no scaling factor is used (‘No scaling’ column). Note that the negSSD-none results are highly dependent on the particular configuration (intensity range, patch size, …) and would not generalize to a change in these parameters. Furthermore, we note that there are performance differences depending on the scaling strategy, with the proposed scaling strategy obtaining the best results.
4.1.2. Methods comparison
Before comparing the methods, we assess the effect of the number of atlases on the segmentation performance. To that end we segmented the 100 target subjects with baseline NLWV using an increasing number of atlases (ranked according to the normalized correlation in an ROI around the hippocampus). Average Dice scores (DS) using the best 5 and 15 atlases are 83.82 ±(2.59) and 84.58 ±(2.38), respectively, thus stressing the importance of the scalability of the method w.r.t. the number of atlases. We found a slight decrease in performance when using 35 atlases, therefore we used 15 atlases in the rest of the experiments in the ADNI dataset.
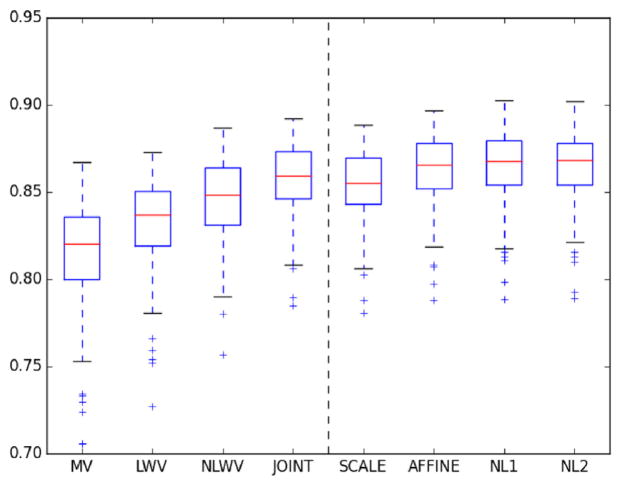
In Fig. 3, we show a boxplot with the distribution of DS across the target population for each method. As we can see, all versions of the proposed method performed better than the baseline NLWV. Such improvements are related to the learning of different discriminative transformations. In order to better appreciate performance differences, in Table 2 we show the mean and standard deviation in DS.
Fig. 3.
Boxplots of DS in hippocampus segmentation in the ADNI dataset. The dashed vertical line separates the competing methods and the proposed ones.
Table 2.
Mean and standard deviation of DS in hippocampus segmentation in ADNI dataset. Star (★) and dagger (†) denote significantly better than NLWV and JOINT, respectively, according to Wilcoxon signed-rank test (non-parametric). One marker denotes p < .05; two markers p < .005).
| Whole hippocampus (DS) | ||||||||
|---|---|---|---|---|---|---|---|---|
| MV | LWV | NLWV | JOINT | SCALE | AFFINE | NL1 | NL2 | |
| Mean | 81.35 | 83.05 | 84.58 | 85.72★★ | 85.36★ | 86.19★ | 86.45★★† | 86.38★★† |
| Std. | ± 3.34 | ± 2.82 | ± 2.38 | ± 2.12 | ± 2.15 | ± 2.15 | ±2.12 | ± 2.11 |
As we can see, the performance improves as model complexity increases up to NL1, where the performance stabilizes in a > 2% improvement with respect to the baseline NLWV. Supervised learning of a SCALE parameter leads to an improvement of ~0.75% w.r.t. NLWV. Further optimizing an AFFINE transformation leads to extra ~0.8% improvement w.r.t SCALE. Adding an extra layer with a non-linearity (i.e., NL1) improves an extra ~0.25%. Finally, adding an extra layer (i.e., NL2) does not involve any noticeable improvement w.r.t. NL1 in this dataset. JOINT achieves a slightly better performance than our SCALE version and is outperformed by our NL1 and NL2 versions.
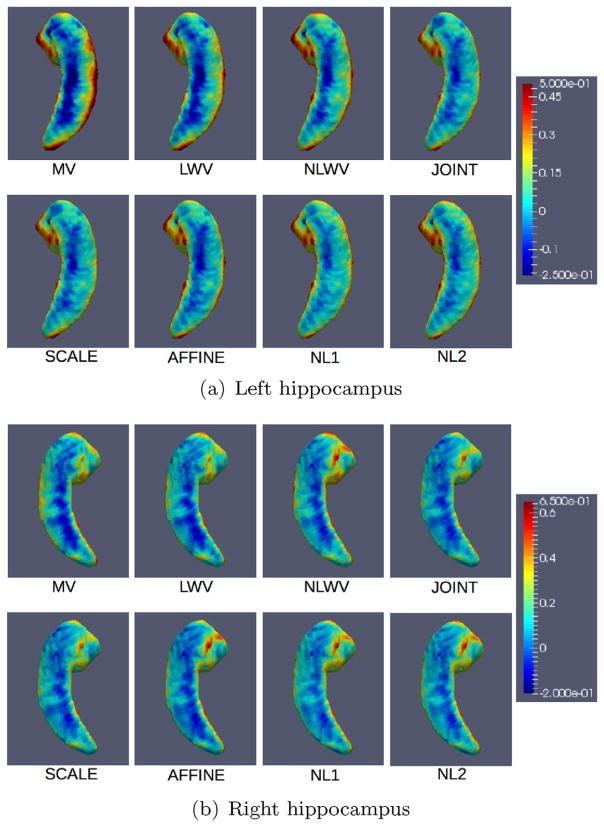
Besides measuring the accuracy of the methods via the Dice score, we are also interested in their bias. In order to measure the bias, Fig. 4 shows the average signed distances by each method across the population. Each point on the surface shows the average signed distance between the ground-truth and estimated surfaces, where blue denotes that the method tends to shrink the structure and red denotes that the method tends to expand it.
Fig. 4.
Spatial distribution of the average signed distance between estimated and ground-truth surfaces across the population. Average signed distances for each method are mapped onto a template hippocampal surface. (For interpretation of the references to color in this figure, the reader is referred to the web version of this article.)
As we can see, all the methods tend to under-segment the frontal part of the hippocampus and tend to over-segment along the sides from head to tail. This is especially evident in the worst performing methods. Also, the proposed method shows consistently lower bias towards shrinkage of the frontal part for both left and right hippocampi, especially the NL1 and NL2 versions.
4.2. Hippocampal subfields
We also assessed the performance of the proposed method in hippocampal subfield segmentation experiments using the Bernasconi’s dataset (Kulaga-Yoskovitz et al., 2015). This dataset consists of high-resolution T1- and T2-weighted MRI from 25 healthy subjects (31 ±7 yrs, 13 females) obtained with a 3 T MRI system. We use the T1-w images in the experiments (3D-MPRAGE), which are of size 336 × 384 × 240 and resolution 0.6 mm isotropic. The dataset contains ground-truth annotations of the hippocampal substructures, which divide the hippocampal formation into three subregions: subicular complex (Subiculum), merged Cornu Ammonis 1, 2 and 3 (CA1-3) subfields, and CA4-dentate gyrus (CA4-DG).
Fig. 5 shows an example T1-w MR image with overlaid ground-truth segmentations of the mentioned hippocampal substructures. We divided the 25 images into 13 atlases and 12 targets. As in the previous experiments, selection was carried out so as to ensure that atlases were well spread in the manifold.
Fig. 5.
A sample image from Bernasconi’s dataset after pre-processing with ground-truth hippocampal subfields overlaid.
First, we assessed the segmentation performance w.r.t. the number of atlases. Table 3 shows the results using 3 vs. 13 (i.e., all the available) atlases when segmenting the 3 (bilateral) substructures. Compared to ADNI experiments, here we used less atlases in the restricted case due to the significantly larger size of the images.
Table 3.
Mean (std) DS by baseline NLWV in different subfields using different numbers of atlases.
| Number of atlases | ||
|---|---|---|
| 3 atlases | 13 atlases | |
| CA1-3 | 84.02(± 1.63) | 86.99(± 1.30) |
| Subiculum | 80.47(± 2.51) | 83.39(± 2.18) |
| CA4-DG | 74.98(± 2.02) | 79.26(± 2.10) |
As we can see, a larger set of atlases lead to average DS increases of 3 – 4%, which supports the importance of methods that are scalable w.r.t. the number of atlases. Fig. 6 shows boxplots with the distribution of DS for all the methods in the 3 hippocampal substructures, namely, CA1-3, Subiculum, and CA4-DG. The different versions of the proposed method tend to have higher DS than the baseline NLWV. In general the more complex versions of the proposed method achieve higher average DS, with NL2 barely obtaining any noticeable increase over NL1. In order to better appreciate the differences, in Table 4 we show the mean and standard deviation of DS across the target subjects.
Fig. 6.
Boxplots of DS in hippocampal subfield segmentation in Bernasconi’s dataset. The dashed vertical lines separate the competing methods and the proposed ones.
Table 4.
Mean and standard deviation DS in segmentation of the hippocampal subfields in Bernasconi’s dataset. We did not find statistically significant differences between any methods.
| CA1-3 (DS) | ||||||||
|---|---|---|---|---|---|---|---|---|
| MV | LWV | NLWV | JOINT | SCALE | AFFINE | NL1 | NL2 | |
| Mean | 83.94 | 85.49 | 86.99 | 87.64 | 87.03 | 87.70 | 88.08 | 87.86 |
| Std | ± 1.14 | ± 1.17 | ± 1.30 | ± 1.36 | ± 1.26 | ± 1.29 | ±1.25 | ± 1.24 |
| Subiculum (DS) | ||||||||
| Mean | 81.37 | 82.26 | 83.39 | 84.08 | 83.73 | 84.52 | 84.65 | 84.67 |
| Std | ± 2.02 | ± 2.00 | ± 2.18 | ± 2.09 | ± 2.09 | ± 2.17 | ± 2.12 | ±2.12 |
| CA4-DG (DS) | ||||||||
| Mean | 78.19 | 78.70 | 79.26 | 80.62 | 79.46 | 80.34 | 80.42 | 80.43 |
| Std | ± 2.19 | ± 2.12 | ± 2.10 | ±1.83 | ± 1.92 | ± 1.77 | ± 1.18 | ± 1.52 |
In CA1-3, our proposed NL1 obtains the highest average DS, approximately ~1% higher than the baseline NLWV. In the Subiculum, NL1 and NL2 achieve the highest average DS, which is > 1% higher than the baseline NLWV. In CA4-DG, JOINT label fusion obtains the highest DS, followed by our NL1 and NL2 versions. As in ADNI, the average DS of NL2 is close to that of NL1. Although the proposed methods obtained the highest average Dice scores in most of the sub-structures, we did not find statistically significant differences between any methods.
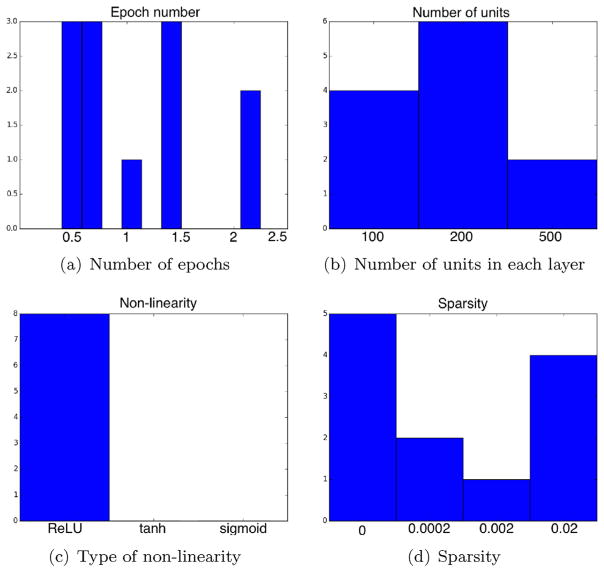
4.3. Hyper-parameter selection
Ten instances of each model were independently trained for each structure with the values of the hyper-parameters selected uniformly at random among a range of values. The best performing models in the validation set were used in the above segmentation experiments. Fig. 7 shows histograms of hyper-parameter values used by the best performing models as well as the number of epochs required for obtaining the best performance. The shown hyper-parameters are: number of units in each layer, type of non-linearity and strength of sparsity regularization (λ in Eq. (15)). The horizontal and vertical axes correspond to the hyper-parameter value and the number of models that ended up having such value, respectively. The total number of models for most of the parameters was (1 + 3) × 3 = 12, that is, 1 model for ADNI +3 models for Bernasconi, which equals 4 models ×3 variants, namely, AFFINE, NL1 and NL2. The type of non-linearity parameter only applies to NL1 and NL2 variants, hence 8 models.
Fig. 7.
(a) Histogram with the number of epochs needed by the best performing models to obtain the top performance. (b)–(d) Histograms with the hyper-parameter values used by the best performing models.
As we can see, the best performance is obtained in all cases before 3 epochs. Even though we continued training for longer, the performance on the validation set did not improve any further. In some cases, the best performance was obtained even before the 1st epoch, that is, even before the model had seen all the training data once. This is possibly because the inherent redundancy in the data sampled near the same region and the ability of the sampling procedure to retrieve all relevant data before all data was sampled. Regarding the number of units, we see a slight preference for using 200 units, which corresponds to the number of units used both in the hidden layers (when applicable) and in the output layer, which relates to the dimensionality of the output embedding. We did not use different numbers of units at each layer as we did not fore-see great performance differences at the cost of considerably enlarging the hyper-parameter space. The experiments show a stark evidence for the preference of ReLU non-linearities over the rest, since these were used by all the best performing models. Finally, the histograms show conflicting evidence for the benefits of explicit sparse regularization, since there are two peaks corresponding to no sparsity (i.e., λ = 0) and strongest sparsity (i.e., λ = 0.02).
5. Discussion
Results show that the scaling of the similarities used in the Softmax has higher impact on performance than the similarity metric. We argue that one of the reasons for the success of our method lies in the ability of the proposed affine and non-linear transformations to jointly influence the Softmax and the similarity metric in more nuanced ways than a simple scaling. Due to the similar performance of LNCC and negSSD, we conclude that a more important factor than their performance for integrating them in our method is the form of the resulting gradients when optimizing affine and non-linear patch embeddings through gradient descent.
Results also show that the number of atlases has an important effect on the multi-atlas segmentation performance. In particular, we found that using ~15 atlases led to reasonable results in both datasets. This is a limiting factor for methods computing the embedding on whole images before segmentation (Yang et al., 2016), since their memory requirements are of the order 𝒪 (N × d), where N is the number of atlases and d is the dimensionality of the output embedding.
Results show that methods incorporating appearance information perform better than methods only using label information (i.e., MV). This is in line with previous studies that showed that appearance information is a powerful proxy for driving anatomical correspondence (Aljabar et al., 2009; Artaechevarria et al., 2009; Coupé et al., 2011; Sanroma et al., 2014). Another interesting observation is that PBLF methods enforcing one-to-one correspondence in the search of candidate atlas patches (i.e., LWV) underperform compared to the others not enforcing such constraint, which is also in line with other experimental findings (Coupé et al., 2011; Rousseau et al., 2011). Regarding the proposed method, results show a clear improvement in the more complex versions of our method compared to the simpler ones, thus suggesting that hierarchical models containing non-linearities are suitable for computing embeddings for PBLF. The simplest version of our method estimating an optimal SCALE parameter for computing the patch similarity, obtained average DS increases of ~1% compared to using the (unsupervised) heuristic by NLWV (Coupé et al., 2011) in the presented experiments. The advantage of learning a discriminative AFFINE transformation is evidenced by an increase in average DS of > 0.5% w.r.t. to the SCALE version. Compared to SCALE, the AFFINE version features a full linear transformation and also implements the SGD strategy over mini-batches instead of using a single (larger) batch. NL1 is the simplest full-fledged version of our proposed method featuring a hierarchy of linear and non-linear transformations and SGD optimization. The increase in average DS achieved by NL1 compared to AFFINE range between ~0.1% and ~0.3%. Finally, we did not observe a consistent increase in NL2 by adding an extra layer on top of NL1. This suggests that, the capacity of NL1 is sufficient to capture the discriminative patterns characterizing the studied anatomical structures in the available databases. The reported improvements were statistically significant in the ADNI dataset. In the Bernasconi dataset, although the proposed method tended to achieve the highest Dice scores, no statistically significant differences were obtained by any method.
Strategies such as ensembling (Giraud et al., 2015) and/or corrective learning (Wang et al., 2011) may be applied to further improve the segmentation performance. We consider these strategies as post-processing steps complementary to the main aim of the paper centered in the merits of label fusion, involving, the patch representations, similarity metrics and the weights optimization.
Regarding the hyper-parameter values, we found clear evidence of the superiority of ReLUs over the rest of non-linearities. Moreover, we did not find strong evidence supporting the benefits of explicit sparse regularization in the similarity-based weights. Several works have shown the benefits of inducing sparsity in PBLF (Guo and Zhang, 2012; Tong et al., 2013; Wu et al., 2015; Zhang et al., 2012). We found that the similarity weights obtained with our embeddings without explicit sparse regularization were already sparser than the ones obtained using the original patches. Therefore, it is possible that the explicit sparsity did not add significantly to it. Moreover, recent works suggest that explicit regularization may not play a central role in the generalization abilities of neural networks (Zhang et al., 2016) (as opposed to other machine learning techniques). It is suggested that the neural network architectures already exert some form of regularization even though it is not explicit in the optimization. Also, contrarily to other machine learning techniques, increasing the capacity of neural nets (i.e., by increasing the number of units) does not usually lead to greater overfitting (i.e., poor generalization). In summary, the roles of regularization and model capacity in the generalization abilities of neural networks are a topic of open research (Zhang et al., 2016).
Regarding the computational complexity of the training procedure, we did not find significant advantages of using GPU compared to CPU. This might be due to the relatively equivalent training and sampling times in our method. This contrasts with more complex architectures with a higher number of parameters (such as some modern CNNs), where computational requirements for training are comparatively larger than the ones required for sampling. All our models were trained in less than a day in a machine with multiple cores, so that multiple model instances (i.e., 10) with randomly sampled hyper-parameters could be trained in parallel. Each instance is composed of 2 processes running in parallel: while one trains the model, the other segments the validation images with the latest available model (for obtaining the validation performance). We run each process in 2 of the cores of an AMD Opteron Abu Dhabi 6378 processor. Our code uses Theano and can be found at https://github.com/gsanroma/deeplf.
6. Conclusions
We have presented a method for learning discriminative image patch embeddings for optimal PBLF. We applied it to the segmentation of brain structures such as the hippocampus and hippocampal substructures. We used neural networks optimized via stochastic gradient descent (SGD) to learn a single model per bilateral structure. We analyzed the effectiveness of SGD in minimizing the desired objective function. We learned optimal patch embeddings using neighboring patches sampled within the same image. Segmentation results using a varying number of atlases highlighted the importance of the scalability of the methods w.r.t. the number of atlases. We showed the improvements by the proposed framework at different complexity levels. We did not find the choice of similarity metric to significantly affect the label fusion performance. On the other hand, a simple scaling of the similarities according to the proposed SCALE method already improves the segmentation performance compared to using an heuristic (unsupervised) strategy. Optimizing a full affine transformation via SGD further improved the segmentation performance and, adding an extra layer with a non-linearity increased the performance even further compared to the affine model. Finally, we did not find consistent improvements by adding extra layers to the model, which suggests that a depth-1 model has the right capacity for PBLF in these particular datasets. We showed that the performance of the method is stable across a range of values for most hyperparameters except for the type of non-linearity, where ReLUs were consistently picked over the rest. We did not obtain convincing evidence that regularization improved performance and connected this finding with recent discussions on the links between model capacity, regularization and generalization abilities in neural networks.
Acknowledgments
The first author is co-financed by the Marie Curie FP7-PEOPLE- 2012-COFUND Action, Grant agreement no: 600387.
This work is partly supported by the Spanish Ministry of Economy and Competitiveness under the Maria de Maeztu Units of Excellence Programme (MDM-2015-0502).
Part of the data used for this project was funded by the Alzheimer’s Disease Neuroimaging Initiative (ADNI) (National Institutes of Health Grant U01 AG024904) and DOD ADNI (Department of Defense award number W81XWH-12-2-0012).
Footnotes
The code of the method is available at https://github.com/gsanroma/deeplf.
The ADNI was launched in 2003 as a public–private partnership, led by Principal Investigator Michael W. Weiner, MD. The primary goal of ADNI has been to test whether serial magnetic resonance imaging (MRI), positron emission tomography (PET), other biological markers, and clinical and neuropsychological assessment can be combined to measure the progression of mild cognitive impairment (MCI) and early Alzheimer’s disease (AD). For up-to-date information, see http://www.adni-info.org.
References
- Aljabar P, Heckemann RA, Hammers A, Hajnal JV, Rueckert D. Multi-atlas based segmentation of brain images: atlas selection and its effect on accuracy. NeuroImage. 2009;46(3):726–738. doi: 10.1016/j.neuroimage.2009.02.018. [DOI] [PubMed] [Google Scholar]
- Artaechevarria X, Muñoz-Barrutia A, de Solorzano CO. Combination strategies in multi-atlas image segmentation: application to brain MR data. IEEE Trans Med Imaging. 2009;28(8):1266–1277. doi: 10.1109/TMI.2009.2014372. [DOI] [PubMed] [Google Scholar]
- Asman AJ, Landman BA. Non-local statistical label fusion for multi-atlas segmentation. Med Image Anal. 2013;17(2):194–208. doi: 10.1016/j.media.2012.10.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Avants BB, Epstein CL, Grossman M, Gee JC. Symmetric diffeomorphic image registration with cross-correlation: evaluating automated labeling of elderly and neurodegenerative brain. Med Image Anal. 2008;12(1):26–41. doi: 10.1016/j.media.2007.06.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bai W, Shi W, Ledig C, Rueckert D. Multi-atlas segmentation with augmented features for cardiac MR images. Med Image Anal. 2015;19(1):98–109. doi: 10.1016/j.media.2014.09.005. [DOI] [PubMed] [Google Scholar]
- Barnes C, Schechtman E, Finkelstein A, Goldman DB. PatchMatch: a randomized correspondence algorithm for structural image editing. ACM Trans Graph. 2009;28(3):24:1–24:11. [Google Scholar]
- Belkin M, Niyogi P. Laplacian eigenmaps for dimensionality reduction and data representation. Neural Comput. 2003;15(6):1373–1396. [Google Scholar]
- Bengio Y. Neural Networks: Tricks of the Trade. Springer; 2012. Practical recommendations for gradient-based training of deep architectures; pp. 437–478. Lecture Notes on Computer Science. [Google Scholar]
- Benkarim OM, Piella G, Ballester MAG, Sanroma G. Enhanced probabilistic label fusion by estimating label confidences through discriminative learning. In: Ourselin S, Joskowicz L, Sabuncu M, Unal G, Wells W, editors. Proceedings of the 2016 International Conference on Medical Image Computing and Computer- Assisted Intervention (MICCAI) 2016. [Google Scholar]
- Benkarim OM, Sanroma G, Zimmer VA, Muñoz-Moreno E, Hahner N, Eixarch E, Camara O, Ballester MAG, Piella G. Toward the automatic quantification of in utero brain development in 3D structural MRI: a review. Hum Brain Mapp. 2017;38(5):2772–2787. doi: 10.1002/hbm.23536. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Boccardi M, Bocchetta M, Morency FC, Collins DL, Nishikawa M, Ganzola R, Grothe MJ, Wolz D, Redolfi A, Pievani M, Antelmi L, Fellgiebel A, Matsuda H, Teipel S, Duchesne S, Jack CR, Frisoni GB. Training labels for hippocampal segmentation based on the EADC-ADNI harmonized hippocampal protocol. Alzeimer’s Dement. 2015;11(2):175–183. doi: 10.1016/j.jalz.2014.12.002. [DOI] [PubMed] [Google Scholar]
- Cardoso MJ, Leung K, Modat M, Keihaninejad S, Cash D, Barnes J, Fox NC, Ourselin S. STEPS: Similarity and truth estimation for propagated segmentations and its application to hippocampal segmentation and brain parcelation. Med Image Anal. 2013;17(6):671–684. doi: 10.1016/j.media.2013.02.006. [DOI] [PubMed] [Google Scholar]
- Chupin M, Gerardin E, Cuingnet R, Boutet C, Lemieux L, Lehericy S, Benali H, Garnero L, Colliot O. Fully automatic hippocampus segmentation and classification in Alzheimer’s disease and mild cognitive impairment applied on data from ADNI. Hippocampus. 2009;19(6):579–587. doi: 10.1002/hipo.20626. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Colliot O, Camara O, Bloch I. Integration of fuzzy spatial relations in deformable models – application to brain MRI segmentation. Pattern Recognit. 2006;39(8):1401–1414. [Google Scholar]
- Cortes C, Vapnik V. Support vector networks. Mach Learn. 1995;20(3):273–297. [Google Scholar]
- Coupé P, Manjón JV, Fonov V, Pruessner J, Robles M, Collins DL. Patch-based segmentation using expert priors: application to hippocampus and ventricle segmentation. NeuroImage. 2011;54(2):940–954. doi: 10.1016/j.neuroimage.2010.09.018. [DOI] [PubMed] [Google Scholar]
- Fonov V, Evans AC, McKinstry RC, Almli CR, Collins DL. Unbiased nonlinear average age-appropriate brain templates from birth to adulthood. NeuroImage. 2009;47(1):S102. [Google Scholar]
- Frisoni GB, Fox NC, Jack CR, Scheltens P, Thompson PM. The clinical use of structural MRI in alzheimer disease. Nat Rev Neurol. 2010;6(2):67–77. doi: 10.1038/nrneurol.2009.215. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Giraud R, Ta VT, Papadakis N, Manjon JV, Collins DL, Coupe P. An optimized PatchMatch for multi-scale and multi-feature label fusion. NeuroImage. 2015;124:770–782. doi: 10.1016/j.neuroimage.2015.07.076. [DOI] [PubMed] [Google Scholar]
- Glorot X, Bengio Y. Understanding the difficulty of training deep feedforward neural networks. Proceedings of the Thirteenth International Conference on Artificial Intelligence and Statistics (AISTATS).2010. [Google Scholar]
- Guo Q, Zhang D. Semi-supervised sparse label fusion for multi-atlas based segmentation. In: Liu CL, Zhang C, Wang L, editors. Proceedings of the 2012 Communications in Computer and Information Science (CCPR) 2012. [Google Scholar]
- Hao Y, Wang T, Zhang X, Duan Y, Yu C, Jiang T, Fan Y. Local label learning (LLL) for subcortical structure segmentation: application to hippocampus segmentation. Hum Brain Mapp. 2013;35(6):2674–2697. doi: 10.1002/hbm.22359. [DOI] [PMC free article] [PubMed] [Google Scholar]
- He K, Zhang X, Ren S, Sun J. Delving deep into rectifiers: surpassing human- level performance on ImageNet classification. Proceedings of the 2015 IEEE International Conference on Computer Vision (ICCV).2015. [Google Scholar]
- He X, Cai D, Yan S, Zhang H-J. Neighborhood preserving embedding. Proceedings of the Tenth IEEE International Conference on Computer Vision (ICCV).2005. [Google Scholar]
- He X, Niyogi P. Locality preserving projections. Proceedings of the 2004 Neural Information Processing Systems (NIPS).2004. [Google Scholar]
- Heckemann RA, Hajnal JV, Aljabar P, Rueckert D, Hammers A. Automatic anatomical brain MRI segmentation combining label propagation and decision fusion. NeuroImage. 2006;33(1):115–126. doi: 10.1016/j.neuroimage.2006.05.061. [DOI] [PubMed] [Google Scholar]
- Ioffe S, Szegedy C. Batch normalization: accelerating deep network training by reducing internal covariate shift. CoRR. 2015 arXiv: abs/1502.03167. [Google Scholar]
- Kingma DP, Ba J. Adam: a method for stochastic optimization. CoRR. 2014 arXiv: abs/1412.6980. [Google Scholar]
- Koch LM, Wright R, Vatansever D, Kyriakopoulou V, Malamateniou C, Patkee PA, Rutheford M, Hajnal JV, Aljabar P, Rueckert D. Graph-based label propagation in fetal brain MR images. In: Wu G, et al., editors. Proceedings of the 2014 Machine Learning in Medical Imaging (MLMI) 2014. [Google Scholar]
- Kulaga-Yoskovitz J, Bernhardt BC, Hong S-J, Mansi T, Liang KE, van der Kouwe AJW, Smallwood J, Bernasconi A, Bernasconi N. Multi-contrast submillimetric 3 Tesla hippocampal subfield segmentation protocol and dataset. Sci Data. 2015:2. doi: 10.1038/sdata.2015.59. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li S, Shi F, Pu F, Jiang T, Xie S, Wang Y. Hippocampal shape analysis of Alzheimer disease based on machine learning methods. Am J Neuroradiol. 2007;28(7):1339–1345. doi: 10.3174/ajnr.A0620. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lotjonen JM, Wolz R, Koikkalainen JR, Thurfjell L, Waldemar G, Soininen H, Rueckert D. Fast and robust multi-atlas segmentation of brain magnetic resonance images. NeuroImage. 2010;49(3):2352–2365. doi: 10.1016/j.neuroimage.2009.10.026. [DOI] [PubMed] [Google Scholar]
- Manjon JV, Coupe P, Marti-Bonmati L, Collins DL, Robles M. Adaptive non-local means denoising of MR images with spatially varying noise levels. J Magn Reson Imaging. 2010;31(1):192–203. doi: 10.1002/jmri.22003. [DOI] [PubMed] [Google Scholar]
- Nyul LG, Udupa JK. On standardizing the MR image instensity scale. Magn Reson Med. 1999;42(6):1072–1081. doi: 10.1002/(sici)1522-2594(199912)42:6<1072::aid-mrm11>3.0.co;2-m. [DOI] [PubMed] [Google Scholar]
- Olshausen BA, Field DJ. Emergence of simple-cell receptive field properties by learning a sparse code for natural images. Nature. 1996;381:607–609. doi: 10.1038/381607a0. [DOI] [PubMed] [Google Scholar]
- Ranzato M, Poultney C, Chopra S, LeCun Y. Efficient learning of sparse representations with an energy-based model. Proceedings of the 2007 Neural Information Processing Systems (NIPS).2007. [Google Scholar]
- Rohlfing T, Brandt R, Menzel R, Maurer CR. Evaluation of atlas selection strategies for atlas-based image segmentation with application to confocal microscopy images of bee brains. NeuroImage. 2004;21(4):1428–1442. doi: 10.1016/j.neuroimage.2003.11.010. [DOI] [PubMed] [Google Scholar]
- Rousseau F, Habas PA, Studholme C. A supervised patch-based approach for human brain labeling. IEEE Trans Med Imaging. 2011;30(10):1852–1862. doi: 10.1109/TMI.2011.2156806. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Roweis ST, Saul LK. Nonlinear dimensionality reduction by locally linear embedding. Science. 2000;290(5500):2323–2326. doi: 10.1126/science.290.5500.2323. [DOI] [PubMed] [Google Scholar]
- Rubinstein RY, Kroese DP. Simulation and the Monte Carlo Method. John Wiley & Sons; 2011. [Google Scholar]
- Sanroma G, Benkarim OM, Piella G, Wu G, Zhu X, Shen D, Ballester MAG. Discriminative dimensionality reduction for patch-based label fusion. In: Bhatia K, Lombaert K, editors. Proceedings of the 2015 Machine Learning Meets Medical Imaging (MLMI) 2015. [Google Scholar]
- Sanroma G, Wu G, Gao Y, Shen D. Learning to rank atlases for multiple-atlas segmentation. IEEE Trans Med Imaging. 2014;33(10):1939–1953. doi: 10.1109/TMI.2014.2327516. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sanroma G, Wu G, Gao Y, Thung KH, Guo Y, Shen D. A transversal approach for patch-based label fusion via matrix completion. Med Image Anal. 2015;24(1):135–148. doi: 10.1016/j.media.2015.06.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sanroma G, Wu G, Kim MJ, Ballester MAG, Shen D. Multiple-atlas segmentation in medical imaging. In: Zhou K, editor. Medical Image Recognition, Segmentation and Parsing. Academic Press; 2016. [Google Scholar]
- Sdika M. Enhancing atlas based segmentation with multiclass linear classifiers. Med Phys. 2015;42(12):7169–7181. doi: 10.1118/1.4935946. [DOI] [PubMed] [Google Scholar]
- Tong T, Wolz R, Coupe P, Hajnal JV, Rueckert D. Segmentation of MR images via discriminative dictionary learning and sparse coding: application to hippocampus labeling. NeuroImage. 2013;76:11–23. doi: 10.1016/j.neuroimage.2013.02.069. [DOI] [PubMed] [Google Scholar]
- Tustison NJ, Avants BB, Cook PA, Zheng Y, Egan A, Yushkevich PA, Gee JC. N4ITK: Improved N3 bias correction. IEEE Trans Med Imaging. 2010;29(6):1310–1320. doi: 10.1109/TMI.2010.2046908. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang H, Das SR, Suh JW, Altinay M, Pluta JB, Craige C, Avants B, Yushkevich PA. A learning-based wrapper method to correct systematic errors in automatic image segmentation: consistently improved performance in hippocampus, cortex and brain segmentation. NeuroImage. 2011;55(3):968–985. doi: 10.1016/j.neuroimage.2011.01.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang H, Suh JW, Das SR, Pluta JB, Craige C, Yushkevich PA. Multi-atlas segmentation with joint label fusion. IEEE Trans Pattern Anal Mach Intell. 2013;35(3):611–623. doi: 10.1109/TPAMI.2012.143. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Warfield SK, Zou KH, Wells WM. Simultaneous truth and performance level estimation (STAPLE): an algorithm for the validation of image segmentation. IEEE Trans Med Imaging. 2004;23(7):903–921. doi: 10.1109/TMI.2004.828354. [DOI] [PMC free article] [PubMed] [Google Scholar]
- West MJ, Kawas CH, Stewart WF, Rudow GL, Troncoso JC. Hippocampal neurons in pre-clinical Alzheimer’s disease. Neurobiol Aging. 2004;25(9):1205–1212. doi: 10.1016/j.neurobiolaging.2003.12.005. [DOI] [PubMed] [Google Scholar]
- Wu G, Kim MJ, Sanroma G, Wang Q, Munsell BC, Shen D. Hierarchical multi-atlas label fusion with multi-scale feature representation and label-specific patch partition. NeuroImage. 2015;106:34–46. doi: 10.1016/j.neuroimage.2014.11.025. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yan SC, Xu D, Zhang BY, Zhang HJ, Yang Q, Lin S. Graph embedding and extensions: a general framework for dimensionality reduction. Pattern Anal Mach Intell. 2007;29(1):40–51. doi: 10.1109/TPAMI.2007.12. [DOI] [PubMed] [Google Scholar]
- Yang H, Sun J, Li H, Wang L, Xu Z. Deep fusion net for multi-atlas segmentation: application to cardiac MR images. In: Ourselin S, Joskowicz L, Sabuncu M, Unal G, Wells W, editors. Proceedings of the 2016 Medical Image Computing and Computer-Assisted Intervention (MICCAI) 2016. [Google Scholar]
- Zhang C, Bengio S, Hardt M, Recht B, Vinyals O. Understanding deep learning requires rethinking generalization. CoRR. 2016 arXiv: abs/1611.03530. [Google Scholar]
- Zhang D, Guo Q, Wu G, Shen D, et al. Sparse patch-based label fusion for multi-atlas segmentation. In: Yap PT, et al., editors. Proceedings of the Second International Conference on Multimodal Brain Image Analysis. 2012. pp. 94–102. [Google Scholar]
- Zhang W, Xue X, Lu H, Guo YF. Discriminant neighborhood embedding for classification. Pattern Recognit. 2006;39(11):2240–2243. [Google Scholar]
- Zhu X, Ghahramani Z, Lafferty J. Semi-supervised learning using gaussian fields and harmonic functions. Proceedings of the 2003 International Conference on Machine Learning (ICML).2003. [Google Scholar]