The Role of Interfacial Water in Protein-Ligand Binding: Insights from the Indirect Solvent Mediated PMF

Abstract

Classical density functional theory (DFT) can be used to relate the thermodynamic properties of solutions to the indirect solvent mediated part of the solute-solvent potential of mean force (PMF). Standard, but powerful numerical methods can be used to estimate the solute-solvent PMF from which the indirect part can be extracted. In this work we show how knowledge of the direct and indirect parts of the solute-solvent PMF for water at the interface of a protein receptor can be used to gain insights about how to design tighter binding ligands. As we show, the indirect part of the solute-solvent PMF is equal to the sum of the 1-body (energy + entropy) terms in the inhomogeneous solvation theory (IST) expansion of the solvation free energy. To illustrate the effect of displacing interfacial water molecules with particular direct/indirect PMF signatures on the binding of ligands, we carry out simulations of protein binding with several pairs of congeneric ligands. We show that interfacial water locations that contribute favorably or unfavorably at the 1-body level (energy + entropy) to the solvation free energy of the solute can be targeted as part of the ligand design process. Water locations where the indirect PMF is larger in magnitude provide better targets for displacement when adding a functional group to a ligand core.

Graphical abstract

Introduction

It is widely believed that the displacement of water from binding sites at protein receptor surfaces plays a key role in determining protein-ligand binding affinity^1–15. The loosely expressed idea is that by displacing a water molecule whose thermodynamic signature is “unfavorable” relative to the bulk, a ligand may gain extra binding affinity as compared with displacing a water molecule with a “favorable” signature. While this suggestion appears frequently in the literature, the idea is not clearly formulated when expressed in this way, as it is well known that the free energy (chemical potential) of the solvent is constant throughout the solution^16–17. However, the excess chemical potential of the solvent in solution, which is closely related to the solute-solvent potential of mean force (PMF) varies throughout the solution, and knowledge of the direct and indirect parts of the solute-solvent PMF can be used to inform the ligand design process, as we illustrate in this work. Earlier efforts to take the thermodynamic signatures of interfacial waters into account as part of the protein ligand design process have been based on inhomogeneous solvation theory (IST)^18–32. In the IST formulation of the problem, the position dependent excess energies and entropies of the solution are the objects for analysis. There are 1-body and 2-body contributions to the excess energy. The excess entropy is expressed as an infinite series expansion in the thermodynamic limit; in the IST analysis of binding, only the 1-body entropy term is usually retained. Friesner, Berne and co-workers developed a practical method called WaterMap based on IST to analyze hydration sites around the protein surface where the water density is significantly denser than the bulk fluid^5,22. Lazaridis and co-workers applied the method of solvation thermodynamics of ordered water (STOW) to compute the thermodynamics of specific water molecules in protein cavities²⁸. Further, a grid based implementation of the IST equations was developed by Gilson, Kurtzman and co-workers called GIST^26–27. In the IST approach, the excess energy and excess entropy at each location are calculated separately, and the “local free energy” is estimated by integrating the energy and entropy densities over a small volume at the interface with the receptor. Besides the approaches based on IST, one is able to quantify the thermodynamic properties of water in protein-ligand binding from several other methods like 3D-RISM^33–35, SZMAP³⁶ and GRID³⁷.

Classical density functional theory (DFT)^38–49 can also be used as a framework to identify locations at the interface of a protein receptor which might be targets for ligand design; the goal being to displace a solvent molecule at these locations by a ligand functional group. Both IST and DFT have been formulated in a way that uses two “end point” simulations, one of the pure solvent and the other of the protein in solution. We have written recently about the relationship between end point formulations of IST and DFT⁵⁰. In contrast to the IST approach where the excess energy and entropy are the objects of analysis, the DFT formulation focuses on the solute-solvent PMF, a free energy difference, and its direct and indirect parts. As illustrated in the results described below, we show that in order to improve ligand binding affinity, interfacial water molecules located at positions where the indirect solute-solvent PMF is large in magnitude, regardless of the sign, are prime candidates for displacement by a ligand functional group, when considering congeneric ligand pairs or de novo design.

The first target protein we chose is coagulation factor Xa (FXa; see Figure 1), which has been the focus of previous studies using the WaterMap and GIST approaches based on IST^5,26. We compare the binding of pairs of congeneric ligands which share structural similarity. In the cases illustrated here, the difference in the binding affinity between congeneric ligands has a large component that can be related to the properties of the displaced water. Two other examples are also investigated: the binding of biotin to streptavidin to illustrate the effect of displacing water at a hydrophobic interface^22,51, and binding to a dry region (cavity) of the mouse major urinary protein (MUP)²⁹ binding site.

Figure 1.

Representative structure of protein FXa with ligand XLC bound. For the ligand molecule, H1 and H2 in the label are the two hydrogen atoms which are modified to fluorine atoms.

Methods

Density Functional Theory

In this section, we review a derivation of the classical DFT equations related to the potential distribution theorem⁵². In a solution containing one solute molecule, the solvation free energy Δμ, representing the free energy change for turning on the intermolecular interaction of the solute with the solvent, can be expressed using the Kirkwood charging formula as⁵³

$$\mathrm{\Delta }\mu ={\int }_0^{1}d\lambda \int d\mathbf{x}\frac{\partial u_{\lambda }(\mathbf{x})}{\partial \lambda }{\rho }_{\lambda }(\mathbf{x})$$ (1)

Here x represents the complete set of position and orientation variables of a solvent molecule relative to the solute molecule. u_λ (x) is the solute-solvent interaction energy that is gradually turned on with the coupling parameter λ (0 ≤ λ ≤1). ρ_λ denotes the solvent density distribution around the solute at the coupling parameter λ. A density functional is introduced through partial integration of Equation 1:

$$\mathrm{\Delta }\mu =\int d\mathbf{x}u(\mathbf{x})\rho (\mathbf{x})-{\int }_0^{1}d\lambda \int d\mathbf{x}\frac{\partial {\rho }_{\lambda }(\mathbf{x})}{\partial \lambda }{u}_{\lambda }(\mathbf{x})$$ (2)

where ρ(x) represents ρ_λ (x) at λ = 1 and u(x) represents u_λ (x) at λ = 1. The first term of Equation 2 is an integration of the density weighted direct part of the solute-solvent PMF. The second term of Equation 2 can be approximated by a free energy density functional as discussed in previous papers.^46,50.

The indirect part of the solute-solvent PMF ω_λ can be expressed^46,50

$${\omega }_{\lambda }(\mathbf{x})=-k_{B}Tln\frac{{\rho }_{\lambda }(\mathbf{x})}{{\rho }_0(\mathbf{x})}-u_{\lambda }(\mathbf{x})$$ (3)

where k_B is the Boltzmann constant and T is the temperature. ρ₀(x) denotes ρ_λ (x) at λ = 0, indicating the density in the pure solvent system. In this formula, the total PMF corresponds to the first term of the right-hand side of Equation 3 and can be decomposed into the direct solute-solvent interaction plus the remaining indirect solvent-mediated term. Rearranging terms in Equation 3 to separate u_λ (x), then replacing u_λ (x) and u(x) in Equation 2, the solute excess chemical potential can be written (see references^46,50 for a detailed derivation)

$$\mathrm{\Delta }\mu =-k_{B}T\int d\mathbf{x}[\rho (\mathbf{x})-{\rho }_0(\mathbf{x})]+\int d\mathbf{x}\rho (\mathbf{x})[-\omega (\mathbf{x})]+{\int }_0^{1}d\lambda \int d\mathbf{x}{\mathrm{\omega }}_{\lambda }(\mathbf{x})\frac{\partial {\rho }_{\lambda }(\mathbf{x})}{\partial \lambda }$$ (4)

where ω(x) represents ω_λ (x) at λ = 1, meaning the indirect part of PMF in the solution when the solute is fully coupled to the solvent. Equation 4 can be further rewritten as:

$$\mathrm{\Delta }\mu =-k_{B}T\int d\mathbf{x}[\rho (\mathbf{x})-\rho (\infty )]-\int d\mathbf{x}\rho (\mathbf{x})[\omega (\mathbf{x})-\omega (\infty )]+{\int }_0^{1}d\lambda \int d\mathbf{x}{\mathrm{\omega }}_{\lambda }(\mathbf{x})\frac{\partial {\rho }_{\lambda }(\mathbf{x})}{\partial \lambda }$$ (5)

where ρ(∞) and ω(∞) denote the value of the solvent density ρ(x) and the indirect PMF ω(x) in the bulk far from the solute calculated in the canonical ensemble. The second term in Equation 5 is an integration of −[ω(x)−ω(∞)] weighted by the density distribution ρ(x) in solution. Based on the definition of ω(x), −[ω(x)−ω(∞)] is the change of the indirect part of the PMF by displacing one water molecule from the configuration x to the bulk. When this displaced water located at x interacts more favorably with the other solvent molecules than those in the bulk ω(x) < ω(∞), the positive value of the second term of the integrand in Equation 5 contributes unfavorably to the solvation free energy of the solute, Δμ. When the displaced water is subject to an unfavorable interaction with the other solvent molecule compared with bulk ω(x) > ω(∞), water at this location makes a favorable contribution to Δμ through the second term in Equation 5. Furthermore, the total PMF WT(x) to transfer a water molecule from the pure solvent to location x at the interfacial region can be expressed as:

$$WT(\mathbf{x})=-k_{B}Tln\frac{\rho (\mathbf{x})}{{\rho }_0(\mathbf{x})}=T{s}^{(1)}(\mathbf{x})$$ (6)

where s⁽¹⁾(x) is the one-body term of the space-resolved entropy at location x in solution from the IST expression^50,54,55. We note that the difference between using the bulk solvent density ρ(∞) far from the solute and the pure solvent density ρ₀(x) as the reference for the PMF vanishes in the thermodynamic limit. When integrating the PMF over the entire volume V however, care must be taken in how the reference is treated⁵⁰. Since the direct part of the PMF u(x) is equivalent to the one-body term (solute-solvent term) of the space-resolved energy in the IST expression e⁽¹⁾(x)⁵⁰, the indirect PMF corresponds to the one-body term in the IST (energy + entropy) expansion for the solvent excess chemical potential:

$$\omega (\mathbf{x})=WT(\mathbf{x})-u(\mathbf{x})=-[e^{(1)}(\mathbf{x})-T{s}^{(1)}(\mathbf{x})]$$ (7)

When expressed in this way, it is now clear from Equations 4, 5 and 7 why water molecules at the interface with a repulsive indirect PMF make a favorable (stabilizing) contribution at the 1-body level to the excess chemical potential of the solute, while water molecules with an attractive indirect PMF make an unfavorable (destabilizing) contribution at the 1-body level to the excess chemical potential of the solute. When the indirect PMF ω(x) at x is positive, the 1-body contribution to the free energy to move a water to x from the bulk (or pure solvent) is attractive and vice versa. We show in the results section, that regardless of whether interfacial water molecules make a stabilizing or destabilizing contribution to the excess chemical potential of the solute at the 1-body level, when the indirect solute-solvent PMF term is large in magnitude (i.e. |ω(x)| is large), displacing these waters by an appropriately hydrophilic or hydrophobic ligand functional group, depending on the sign of ω(x), can significantly increase ligand binding affinity.

In approximate implementations of IST formulas for the solute chemical potential and for the analysis of interfacial solvent effects on protein-ligand binding, the 2-body energy replaces the third term of Equation 5, and the first term is dropped. Two-body and higher order terms in the IST entropy expansion however are usually not included in the IST analysis of the thermodynamic signatures of interfacial waters, although there have been a few reports which include two body entropies^{21,24,56–57}. A key distinction between IST and DFT is that IST includes two body energies in the analysis while DFT does not. Our ansatz is that the DFT formulas which are based as on the analysis of the indirect solute-solvent PMF, and therefore include the IST 1-body energy and 1-body entropy terms but not the 2-body energy, provides a well balanced approximation, especially for strongly associating liquids like water for which cancellation between the second order energy and the second and higher order entropy terms is more likely. For example, the strengthened hydrogen bonding around a hydrophobic solute decreases both the two body energy and the two body and higher entropies; so that including the two-body energy in the IST analysis while dropping the excess entropy terms beyond first order may well be unbalanced. In order to further motivate why the analysis of the indirect PMF ω holds information about the role of interfacial water in protein-ligand binding, we have designed a thermodynamic cycle to show how the relative binding free energy ΔΔG_bind between a pair of congeneric ligands can be expressed in a way that includes the contribution ω from displaced water explicitly. The thermodynamic cycle is described in the Appendix, and considered in the Discussion.

Simulation Method

All MD simulations were performed in GROMACS package version 5.1.2^58–60. In order to evaluate the difference of binding affinity between FXa with a pair of ligands, we calculated the standard binding free energy of FXa with each of the ligands using the double decoupling method in which a thermodynamic cycle was designed⁶¹. In the first step of the cycle, the ligand was decoupled from the protein-ligand complex in aqueous solution. The PDB code of the complex is 1MQ5, which is the crystal structure of the ligand with identification XLC bound to FXa⁶². Chain A of the protein, ligand XLC and the coordinated cation Ca²⁺ were extracted from the crystal structure and solvated in a cubic TIP3P^63–64 water box with dimensions 8.0 nm × 8.0 nm × 8.0 nm using the genbox tool in GROMACS. This ensures that each atom of the complex was at least 1.0 nm away from the edge of the box. In this way, a total of 15919 water molecules were contained in the box with 3 additional Cl⁻ to neutralize the system. The AMBER99SB-ILDN force field⁶⁵ was applied as the potential with ligand parameters assigned from Amber Tool⁶⁶. The external coordinates of the ligand relative to the protein denoted as (r, θ, ϕ, Θ, Φ, Ψ) were restrained to their equilibrium values in the bound state as described previously^67–68 so that the ligand remains in the binding pocket as the interactions between the protein and ligand were progressively removed. The other degrees of freedom of the protein and ligand were allowed to move freely. The effect of the restraints on the ligand when unbound in solution can be accounted for by an analytical term⁶⁷ in the final standard binding free energy calculation. This set of decoupling simulations involved a total of 41 simulation windows. Among these windows, different lambda states for applying the restraints, and removing the Coulombic interactions and Van der Waals interactions were assigned. The positional restraints were first turned on with the values of coupling parameter lambda as follows: 0.0, 0.01, 0.025, 0.05, 0.075, 0.1, 0.2, 0.35, 0.5, 0.75 and 1.0. Then the Coulombic interaction of the ligand with the protein and water was turned off with lambda values as follows: 0.0, 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9 and 1.0. Finally, the Van der Waals interaction of the ligand with the protein and water was turned off with lambda values as follows: 0.0, 0.05, 0.1, 0.15, 0.2, 0.25, 0.3, 0.35, 0.4, 0.45, 0.5, 0.55, 0.6, 0.65, 0.7, 0.75, 0.8, 0.85, 0.9, 0.95 and 1.0. For each window, energy minimization was performed first, followed by 100 ps NPT equilibration and 10 ns NVT production sampling. Temperature was maintained at 300 K using the Berendsen coupling scheme with time constant of τ_t = 1.0 ps⁶⁹. For the constant pressure simulation, the pressure was kept constant by the Berendsen pressure barostat with a pressure relaxation time of 0.5 ps. The LINCS algorithm⁷⁰ was used to constrain bond lengths involving hydrogen atoms. The Van der Waals interaction was truncated at 1.0 nm. The long-range electrostatic interaction was treated using the smooth particle-mesh Ewald approach^71–72 with a real-space cutoff of 1.0 nm, a spline order of 4, a reciprocal-space mesh size of 72 for each of the x, y and z directions. Dynamics was propagated using a leap-frog stochastic dynamics integrator with a 2.0 fs timestep. Trajectory files were saved every 0.5 ps and energy files were saved every 0.04 ps. The decoupling free energies of the ligand from the complex solution, ΔG_complex, were estimated using Bennett’s acceptance ratio method (BAR) for each adjacent window pair using the GROMACS tool⁷³.

In another step of the thermodynamic cycle, the ligand was decoupled from pure solvent. The ligand was solvated in a cubic box with dimensions 3.8 nm × 3.8 nm × 3.8 nm, resulting in a total of 1702 water molecules. The same force field parameters and simulation methods as ligand decoupling from the protein-ligand solution system were applied except that no restraints were required and the ligand was allowed to move freely during the simulation. Only Coulombic and Van der Waals interactions were turned off with a total of 31 simulation windows.

Finally, the standard binding free energy between the protein and ligand, ΔG_bind can be obtained via the double decoupling method (DDM) thermodynamic cycle from:

$$\mathrm{\Delta }{\mathrm{G}}_{\text{bind}}=\mathrm{\Delta }{\mathrm{G}}_{\text{solvation}}+\mathrm{\Delta }{\mathrm{G}}_{\text{restraint}-\text{on}}+\mathrm{\Delta }{\mathrm{G}}_{\text{complex}}+\mathrm{\Delta }{\mathrm{G}}_{\text{restraint}-\text{off}}$$ (8)

Here, ΔG_solvation is the free energy to decouple the ligand from pure solvent without restraint. ΔG_restraint-on is the free energy to turn on the restraint in the unbound state. ΔG_complex is the free energy for turning on the Coulombic and Van der Waals interactions between protein and ligand in the presence of the restraint. Finally, ΔG_{restraint-off} is the free energy to turn off the restraint in the protein-ligand bound state. ΔG_solvation, ΔG_complex and ΔG_{restraint-off} are obtained from the simulations mentioned above; ΔG_restraint-on is calculated analytically⁶⁷ as 6.90 kcal/mol.

To compute the total PMF to move a tagged water molecule from the bulk solvent far from the protein to the interfacial region, the tagged water molecule was labelled with a special name different from the other solvent molecules in the topology file so that this tagged water can be distinguishable. Previously, we have shown the same total PMF values can be obtained from two approaches⁵⁰. One involves the integration of the mean force exerted on the tagged water by the solute and other solvent molecules^74–75 while another is based on the particle insertion method. In this work, the later approach was adopted, the total PMF is equivalent to the difference between the solvation free energy to insert the tagged water in the location x at the solute interface and in the bulk. In these two sets of simulations of tagged water insertion, the protein structure was frozen, which is different from the decoupling simulation of the ligand from complex, when the protein and ligand were allowed to move freely except for the relative position and orientation restraints on the ligand. The tagged water was grown at a fix position and orientation in the interfacial region or in the bulk by turning on the Coulombic and Van der Waals interactions using a total of 31 simulation windows. The interfacial water locations selected for the protein-solvent potential of mean force analysis were chosen from the trajectories of the solvated protein using a combination of criteria: strength of the direct interaction with the protein; solvent density estimated by clustering the water oxygen locations in the trajectories; descriptions of the corresponding locations in the IST WaterMap literature^5,22,29 for the proteins chosen for study here.

Results

Ligands Binding to Factor Xa

We begin by describing our results for congeneric ligand pairs binding to FXa. Although the structures of congeneric pairs are alike overall, differences may still arise in more than one region. Taking ligands XLC and XLD as examples, ligand XLD has an extra methoxy group compared with XLC; in addition, a six-membered ring in XLC is replaced by a five-membered ring in XLD. The existence of dissimilarities in these regions makes multiple contributions to the effects of solvent displacement on the ligand binding, which complicates our analysis of the thermodynamic signatures of the displacement of water molecules located at specific positions at the interface. To simplify the problem initially, we substitute a functional group for one of the hydrogen atoms in the XLC ligand as a starting point. This minimal structural perturbation leads to only one extra water molecule being displaced during the binding between FXa and the modified ligand; this perturbation serves as a first example.

In order to make a comparative study, hydrogen atoms located in two distinct positions in XLC were modified which involve the displacement of water molecules with significantly different thermodynamic signatures as the added functional groups replaces the two hydrogen atoms at different positions on the ligand. As shown in Figure 1, two hydrogen atoms labeled as H1 and H2 in different local environments were chosen. H1 is attached to the methyl group on the piperazine ring of the ligand close to the protein surface in the bound complex (Figure 2A, 2C), while H2 is attached to the chloro-benzene ring of the ligand which is pointing away from the protein (Figure 2B, 2D). The perturbations are polar substitutions, changing the selected hydrogen into fluorine as shown in Figure 2C, 2D, with the modified ligand molecules labeled XLC-F1 and XLC-F2. The Van de Waals radius of fluorine is slightly larger than that of the hydrogen it displaces, ensuring the displacement of just one water molecule in region 1 or region 2 shown in Figure 2A, 2B. The standard binding free energy values between FXa and several pairs of ligands obtained using the double decoupling method are listed in Table 1. The statistical uncertainties were estimated using the block average method⁷⁶. ΔΔG was calculated from the difference of the absolute standard binding free energy between the initial (ΔG_ini) and final (ΔG_fin) ligand binding to FXa. A considerable gain in the relative binding affinity, ΔΔG = −4.03 kcal/mol, was observed for the modified XLC-F1 ligand relative to the binding of XLC; while there was significantly less gain in the relative binding affinity for XLC-F2 with ΔΔG = −1.50 kcal/mol. In an attempt to account for this difference, we identified the extra displaced single water molecules in these two cases and dissected the PMF contributions into direct and indirect parts, as the water is brought from the bulk to the locations at the interface occupied by F1 and F2. The extra displaced water can be identified by comparing the excluded volume of the initial and modified ligands, which was defined as the space within 0.2 nm of any heavy atoms of the ligand when it formed the complex with the protein²². The total PMF was computed by the particle insertion method for transferring the water from the bulk to the designated position at the protein interface where the water was displaced when the ligand XLC is converted to XLC-F1. The direct term is straightforwardly obtained from the pair interaction between the protein and displaced water; while the indirect contribution can be derived from the difference between the total PMF and the direct contribution. As shown in Table 2 row 1 and row 2, the densities at the locations of these displaced water molecules, one from XLC-F1 and the other from XLC-F2, are almost equal to the bulk density with the total PMF WT = 0.02 kcal/mol and WT = −0.04 kcal/mol respectively. However, the direct and indirect components are quite distinct. For the displaced water in region 1, ω is substantially larger than 0 with a value of +4.83 kcal/mol, indicating that the interaction between the displaced water and the other surrounding water molecules is unfavorable compared with bulk. We verified this by examining the average number of hydrogen bonds formed between the displaced water molecule with other waters. Two water molecules are considered as hydrogen bonding if the oxygen-oxygen distance is less than 0.35 nm and the O-O-H angle is less than 30° ⁷⁷. On average, the displaced water can form ~2.7 hydrogen bonds with other water molecules in region 1; in contrast, a water molecule can form ~3.3 hydrogen bonds with surrounding solvent in the bulk on average. The decrease of water-water hydrogen bonds for the water in region 1 is balanced by the water-solute hydrogen bond involving residue GLU 97 on the protein surface, leading to a favorable direct part of the PMF with a value of −4.81 kcal/mol. According to the thermodynamic signature of the water in region 1, we characterize it as “bulk density hydrophilic water” as shown in Table 3. Displacement of a “bulk density hydrophilic water” with this thermodynamic signature can make a favorable contribution to the binding free energy, which we find empirically corresponds to the reward of ΔΔG = −4.03 kcal/mol for the binding free energy change when the ligand XLC is transformed to XLC-F1. On the other hand, the indirect PMF ω is close to 0 with a value of 0.18 kcal/mol for the displaced water molecule in region 2. This water has only a small favorable direct interaction with the protein, but it can interact with the other solvent molecules as strongly as if it is located in the bulk. Displacement of a water with this signature makes a much smaller contribution to the enhancement of binding affinity compared with that of the “bulk density hydrophilic water” in region 1, even though the density at both positions is close to the bulk. As distinguished from the “bulk density hydrophilic water” in region 1, which has a relatively strong favorable interaction with the protein (which is approximately cancelled by the indirect term), we refer to the water in region 2 as “bulk density water”, which has total PMF, direct PMF and indirect PMF all close to 0 as summarized in the last row in Table 3. The results of these two initial examples which involve a minimal perturbation of the ligand structure, provide a first hint that the analysis of ω, the indirect part of the PMF, may be useful as part of the ligand design process.

Figure 2.

(A) Transforming the ligand XLC to XLC-F1 causes the displacement of one water molecule in region 1 (B) Transforming XLC to XLC-F2 causes the displacement of one water molecule in region 2 (C) Chemical structures from XLC to XLC-F1 (D) Chemical structures from XLC to XLC-F2

Table 1.

Standard binding free energy data between protein (FXa for the first 9 examples, streptavidin for the 10th, 11th example and MUP for the last example) and several pairs of ligands.

initial ligand	final ligand	ΔGini (kcal/mol)	ΔGfin (kcal/mol)	ΔΔG (kcal/mol)
XLC	XLC-F1	−5.57±0.28	−9.60±0.60	−4.03±0.66
XLC	XLC-F2	−5.57±0.28	−7.07±0.25	−1.50±0.38
XLC	XLD	−5.57±0.28	−11.35±0.34	−5.78±0.44
XLC	XLD-P1	−5.57±0.28	−11.23±0.48	−5.66±0.56
XLC	XLD-P2	−5.57±0.28	−6.17±0.79	−0.60±0.84
IIA	IIB	−7.69±0.47	−12.47±0.41	−4.78±0.62
IIA	IIB-P1	−7.69±0.47	−10.73±0.69	−3.04±0.83
IIA	IIB-P2	−7.69±0.47	−8.46±0.50	−0.77±0.69
RRP	RTR	−4.83±0.56	−6.75±0.06	−1.92±0.56
biotin-O	biotin	−7.40±0.58	−9.94±0.29	−2.54±0.65
biotin-deuri	biotin	−2.58±0.32	−9.94±0.29	−7.36±0.43
OC9	F09	−8.33±0.35	−9.08±0.22	−0.75±0.41

Table 2.

The total PMF (WT), direct PMF (u) and indirect PMF (ω) for the displaced water molecule by the modified ligand binding to protein compared with the reference ligand.

Perturbation	Occupation	Number	Type	WT(kcal/mol)	u(kcal/mol)	ω(kcal/mol)
XLC to XLC-F1	region 1	1	BD phil	0.02	−4.81	4.83
XLC to XLC-F2	region 2	1	BD wat	−0.04	−0.22	0.18
XLC to XLD-P1	region 3	1	HD phil	−5.50	−13.05	7.55
XLC to XLD-P2	region 4	1	BD wat	−0.27	−1.68	1.41
XLC to XLD-P2	region 4	2	BD wat	−0.61	−0.14	−0.47
XLC to XLD-P2	region 4	3	BD wat	−0.08	0.64	−0.72
IIA to IIB-P1	region 5	1	HD phil	−1.96	−6.95	4.99
IIA to IIB-P2	region 6	1	BD wat	−1.71	−3.60	1.89
RRP to RTR	region 7	1	HD phil	−6.51	−12.76	6.25
RTR to RRP	region 8	1	BD wat	−0.45	−1.13	0.68
biotin-O to biotin	region 9	1	HD phob	−5.10	−0.08	−5.02
biotin-deuri to biotin	region 10	1	HD phil	−5.12	−12.39	7.27
biotin-deuri to biotin	region 10	2	HD phil	−3.58	−10.02	6.44
OC9 to F09	region 11	1	LD dry	1.97	−0.28	2.25

Table 3.

Thermodynamic signatures of interfacial water

type	WT	ρ/ρ0	u	ω	1-body effect on μ	design target
bulk density hydrophilic (BD phil)	≈ 0	≈ 1	≤ −4	≈ −u	stabilize	yes
high density hydrophilic (HD phil)	< 0	> 1	≤ −4	≫ 0	stabilize	yes
high density hydrophobic (HD phob)	< 0	> 1	≈ 0	< 0	destabilize	yes
low density dry water (LD dry)	> 0	< 1	≈ 0	> 0	stabilize(small)	?
bulk density water (BD wat)	≈ 0	≈ 1	≈ 0	≈ 0	…	no

We now turn to an analysis of how the thermodynamic signatures of interfacial water affect the affinity of real congeneric ligand pairs with experimentally determined structures bound to FXa. Double decoupling calculations revealed that the relative standard binding free energy between congeneric ligands XLC and XLD was −5.78 kcal/mol shown in Table 1. A detailed comparison of the difference in the excluded volume between XLC and XLD in Figure 3 reveals that two regions can be depicted as extra excluded volume regions where water is displaced when XLC is transformed into XLD. The first one is located around the methyl group connected to the nitrogen atom near the five-membered ring in XLD, causing the displacement of one water molecule in region 3 as shown in Figure 3A. Dissection of the PMF to move this displaced water from the bulk indicates that it has a large repulsive value of the indirect PMF ω = +7.55 kcal/mol and a quite favorable direct interaction u(x) = −13.05 kcal/mol as shown in Table 2 row 3. The favorable direct contribution dominates the unfavorable indirect contribution, so the total PMF WT is much more favorable compared to the bulk with a value of −5.50 kcal/mol. We describe the thermodynamic signature of this water in region 3 as “high density hydrophilic water”, with thermodynamic characteristics summarized in the second row in Table 3. Based on our previous discussion, if this region is occupied by growing a functional group from the XLC ligand to liberate the water, which can also mimic some of the favorable direct interaction between the displaced water and the solute while eliminating the unfavorable indirect components, the added functional group can make a significant contribution to the binding affinity. In order to verify this, ligand XLD-P1 with structure shown in Figure 3D was designed with the same structure as XLC except that the terminal six-membered ring is replaced by the corresponding part of the five-membered ring connected with the NCH₃ group from XLD, ensuring that region 3 is the only extra excluded volume when comparing the interfacial water structure of XLD-P1 with XLC. Impressively, ΔΔG is −5.66 kcal/mol for this transformation, which is almost all the gain in the affinity by changing XLC to XLD (−5.78 kcal/mol). An additional excluded volume region of XLD compared with XLC arises from the presence of an additional methoxy group attached to the benzene ring, which enables exclusion of three water molecules in region 4 as shown in Figure 3B. However, the indirect PMF ω for all these three displaced water molecules are small with values of 1.41 kcal/mol, −0.47 kcal/mol and −0.72 kcal/mol respectively in Table 2 row 4, row 5 and row 6. From our analysis of the signatures of interfacial waters, displacement of these water molecules is expected to make small contributions in the gain of binding affinity. This is confirmed by the double decoupling result ΔΔG = −0.60 kcal/mol between ligand XLC and XLD-P2. Here, XLD-P2 with structure shown in Figure 3E is designed based on the addition of a methoxy group in the benzene ring of XLC to displace only the waters in region 4. This example clearly illustrates the utility of evaluating the indirect part of the PMF at locations where interfacial waters would be displaced by adding a functional group to a ligand core.

Figure 3.

(A) Transforming the ligand XLC to XLD causes the displacement of one water molecule in region 3 (B) Transforming XLC to XLD causes the displacement of three water molecules in region 4 (C) Chemical structures from XLC to XLD (D) Chemical structure of XLD-P1 (E) Chemical structure of XLD-P2

Another pair of congeneric ligands IIA/IIB, with chemical structures shown in Figure 4C, binding to FXa was also investigated. As shown in Figure 4, the perturbation of structure between IIA/IIB is smaller compared with XLC/XLD, with only one hydrogen atom in the benzene ring changed to a methyl group in region 5 and another hydrogen atom in the five-membered ring changed to a cyano group in region 6. In each of the two regions, one extra water molecule is displaced by the additional functional group of IIB, leading to a standard binding free energy difference for the ligand pairs with a value of −4.78 kcal/mol in Table 1. Further calculation of the indirect PMF contributions of the two displaced water molecules discloses that the water in region 5 has a much larger indirect PMF (ω = 4.99 kcal/mol) than the water in region 6 (ω = 1.89 kcal/mol) although their total PMFs and therefore densities were similar as shown in Table 2 row 7 and row 8. To characterize the effect of displacement of these two water molecules separately, we further designed two ligand molecules IIB-P1 and IIB-P2 with structures shown in Figure 4D, 4E. IIB-P1 is derived from the change of the hydrogen atom of IIA in region 5 to a methyl group with other parts of the structure unperturbed so that only the water with the larger value of ω was displaced. A significant gain in the binding affinity with ΔΔG = −3.04 kcal/mol was observed in the binding of IIB-P1 with FXa. On the other hand, IIB-P2 is obtained by the replacement of the hydrogen atom in IIA with a cyano group in region 6, resulting in the exclusion of a single water with the smaller value of ω. Correspondingly, only a slight gain in the binding affinity with ΔΔG = −0.77 kcal/mol is observed for this transformation.

Figure 4.

(A) Transforming the ligand IIA to IIB causes the displacement of one water molecule in region 5 (B) Transforming IIA to IIB causes the displacement of one water molecule in region 6 (C) Chemical structures from IIA to IIB (D) Chemical structure of IIB-P1 (E) Chemical structure of IIB-P2

In the above two pairs of congeneric ligands, the transformation consists of the perturbation of the smaller functional groups in the initial ligand to larger functional groups in the final ligand which can displace several extra water molecules due to the enlargement of the excluded volume. In this example, we consider a pair of ligands RRP and RTR (chemical structure shown in Figure 5C) with almost equal excluded volume, displacing the same number of water molecules but at different positions. As shown in Figure 5, the ligands RRP and RTR are isomers with the substituted group –CN₂H₃ located at different positions on the aromatic ring. As the ligand is transformed from RRP to RTR in panel A, the para-substituent causes the displacement of one water molecule in region 7 and at the same time another water molecule appears in region 8 due to the annihilation of the meta-substituted group; while as the ligand is changed from RTR to RRP in panel B, the meta-substituent causes the liberation of one water molecule in region 8 and the occupation of region 7 by another water molecule due to the disappearance of the para-substitutional group. In this example, one water molecule disappears while another water molecule appears at the same time, which is different from previous examples where water molecules are displaced as a smaller congeneric ligand is transformed to a larger one. In this case, a comparison of the thermodynamic signatures of both the appearing and disappearing water molecules is necessary in order to analyze the relative binding affinity change during the transformations. Region 7 is more buried inside the binding pocket within which the water has a stronger direct interaction with the protein compared with water in region 8 as listed in Table 2 row 9 and row 10. The favorable water-solute interaction is partially counterbalanced by the unfavorable water-water interaction, with a large value of ω = 6.25 kcal/mol for the displaced water in region 7. Similar to the water in region 3 shown in table 2, the displaced water in region 7 is also classified as a “high density hydrophilic water”. Exclusion of a water molecule with this thermodynamic signature will contribute more significantly to the enhancement of binding affinity compared with expulsion of water with small ω (0.68 kcal/mol) in region 8. Overall, ligand RTR with the para-substituent binds more tightly to FXa relative to RRP due to the displacement of a “high density hydrophilic water”, which is in line with ΔΔG = −1.92 kcal/mol from Table 1.

Figure 5.

(A) Transforming the ligand RRP to RTR causes the displacement of one water molecule in region 7 (B) The back transformation of RTR to RRP causes the displacement of one water molecule in region 8 (C) Chemical structures from RRP to RTR (D) Chemical structures from RTR to RRP

In the above discussion of FXa binding with pairs of congeneric ligands, the transformed ligand with significantly higher binding affinity compared with the initial reference ligand, usually involves the displacement of water molecules with “hydrophilic” thermodynamic signatures (Table 3) that have strong direct interactions with the protein. Due to the competition between direct and indirect parts of the PMF for waters with “hydrophilic” signatures, these waters also have large repulsive values of ω. If the indirect part approximately counterbalances the favorable direct part to keep the total PMF close to zero, we classify these water molecules as “bulk density hydrophilic water”; on the other hand, if the direct part is sufficiently favorable that the indirect part is unable to offset most of the direct contribution, these water molecules are classified as “high density hydrophilic water” with favorable WT compared to the bulk. We have shown that displacement of these two types of interfacial water at the protein receptor interface can make favorable contributions to the enhancement of the binding affinity; with the larger contribution associated with locations where the indirect PMF ω(x) is more repulsive.

Ligands Binding to Streptavidin

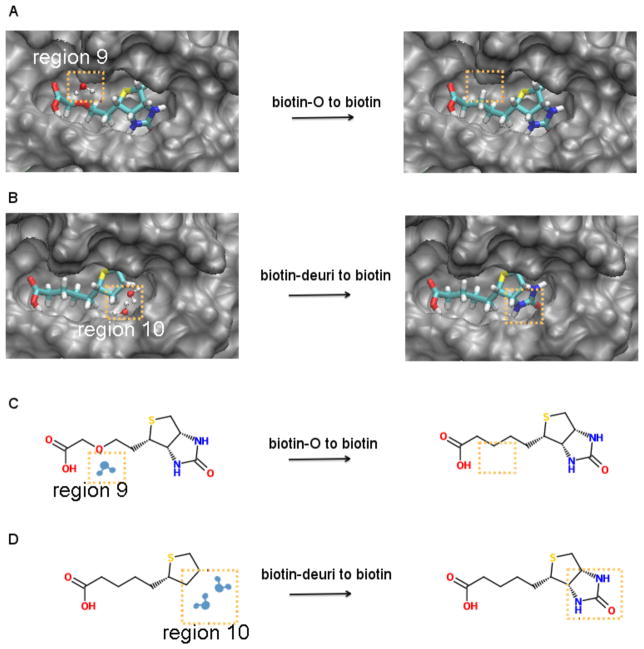
In the next example, we consider the displacement of another type of water molecule, one at a hydrophobic interface where the direct interaction between interfacial water and the protein is quite weak but the total PMF is very favorable due to the indirect PMF contribution. It has been reported that the hydrophobic enclosure effect²² is important for the binding between streptavidin and ligands in addition to the electrostatic polarization effect⁷⁸. Following reference 22, we chose streptavidin as the target protein and identified a water molecule that is located around a hydrophobic patch of streptavidin, which is close to Gly-48 in region 9 as shown in Figure 6A. Further analysis of the thermodynamic properties of the water in Table 2 row 11 indicates that the direct interaction between the water and protein is negligible with a value of −0.08 kcal/mol, but the indirect PMF is quite favorable ω = −5.02 kcal/mol. In Table 3, this type of water is defined as “high density hydrophobic water”. In order to demonstrate the effect of the displacement of a “high density hydrophobic water” on protein-ligand binding, we designed a modified ligand based on biotin. Biotin, with structure shown in Figure 6C, can bind to streptavidin with an extraordinarily strong binding affinity, ΔG = −18.3 kcal/mol, estimated from titration calorimetric measurements⁵¹. We replaced the beta carbon with oxygen in biotin so that the excluded volume of the modified ligand is smaller than that of biotin. The modified ligand is labelled as “biotin-O” with structure shown in Figure 6C. As a result, when biotin-O is changed to biotin as shown in Figure 6A, this requires the displacement of the “high density hydrophobic water” in region 9 that we identified. In Table 1, we compared the relative binding affinity of ligand pairs biotin-O/biotin with streptavidin. There is a gain in the binding affinity with a value of ΔΔG = −2.54 kcal/mol due to the displacement of the “high density hydrophobic water”. We note that the calculated absolute standard binding free energy between streptavidin and biotin is −9.94 kcal/mol, which deviates substantially from the experimental result −18.3 kcal/mol. The reason for this underestimate suggests a force field issue since the potential parameters we apply here are not polarizable and it has been pointed out that electrostatic polarization is critical for the strong binding between streptavidin and biotin⁷⁸. This underestimate is not a key issue in this study since we are interested in the relative binding affinity ΔΔG of the two closely related ligands biotin and biotin-O.

Figure 6.

(A) Transforming the ligand biotin-O to biotin causes the displacement of one water molecule in region 9 (B) Transforming biotin-deuri to biotin causes the displacement of two water molecules in region 10 (C) Chemical structures from biotin-O to biotin (D) Chemical structures from biotin-deuri to biotin

We further notice that there is the formation of a five-membered water ring in the binding pocket of streptavidin, in the absence of bound ligand. It has been reported that displacement of these entropy restricted water molecules also play a significant role in the binding between streptavidin and biotin from an analysis based on IST²². We analyzed the thermodynamic properties of two water molecules belonging to this five-membered water ring buried inside the binding pocket around residues Ser-27, Ser-45 and Asp 128 in region 10 as shown in Figure 6B. Due to favorable hydrogen bonding with the polar protein residues, these two water molecules display quite strong direct interactions as shown in Table 2 row 12 and row 13. Consequently, the total PMFs are favorable (WT = −5.12 kcal/mol and WT = −3.58 kcal/mol respectively) although the positive indirect PMFs counterbalance some of the stabilizing effect from the direct interactions. In the IST discussion²², these two water molecules bear large entropic penalties, which is consistent with the negative total PMFs in our discussion according to Equation 6. Based on our previous definition, these two water molecules belong to the “high density hydrophilic water” category and displacement of these waters is predicted to lead to a significant enhancement of binding affinity. In order to verify this, we designed another ligand based on the biotin core as shown in Figure 6D. Compared with biotin, there is a lack of ureido group (-HNCONH-) in the modified ligand, we labeled it as “biotin-deuri”. As the initial ligand biotin-deuri is transformed to biotin, it involves the displacement of the two “high density hydrophilic waters” in region 10 as shown in Figure 6B. There is a significant change in the relative binding affinity as the ligand is transformed from biotin-deuri to biotin with ΔΔG = −7.36 kcal/mol as shown in Table 1, which is consistent with our previous discussion.

Ligands Binding to MUP

Finally, we consider another type of interfacial water that has been previously targeted by IST analysis²⁹ for purposes of ligand design which corresponds to “low density dry water” as shown in Table 3. The water at this position is much lower in density compared with bulk. Previously, it has been shown that the binding site of protein MUP is buried inside the protein so it is a classic example to study the effect of “dry regions” in the ligand binding affinity. Here, we studied the binding between MUP with two ligands: OC9 and F09 (structure shown in Figure 7B). Double decoupling calculations in Table 1 last row indicate the binding free energy difference to be small, ΔΔG = −0.75 kcal/mol. As the initial ligand OC9 changes to F09, it involves the displacement of one water molecule in region 11 as shown in Figure 7. Analysis of the thermodynamic signature of this displaced water in the last row of Table 2 reveals that it is a “low density dry water” with WT > 0 (ρ(x)/ρ(∞) = 0.04), u ≃ 0 and ω>0. In this example, the displacement of the “low density dry water” at a location which is “dewet” contributes a relatively small amount to the enhancement of binding affinity (ΔΔG = −0.75 kcal/mol) compared with the first three types of water signatures listed in Table 3.

Figure 7.

(A) Transforming the ligand OC9 to F09 causes the displacement of one water molecule in region 11 (B) Chemical structures from OC9 to F09

Discussion

In the IST analysis, several criteria have been proposed as thermodynamic signatures of the interfacial water positions that can be regarded as targets for ligand design. In the initial application of “WaterMap”, it was found that displacement of water molecules with highly restricted 1-body entropy leads to enhanced binding affinity²². In a further study of the relative binding affinity between congeneric ligand pairs using “WaterMap”, a more quantitative scoring function was proposed based on the following components: 1-body energy + 1-body entropy + 2-body energy^5,20. Later, scoring functions based on GIST which also involve 1-body energy, 1-body entropy, and 2-body energy terms were presented and it was further pointed out that the energy terms play a dominant role over the entropy term according to the fitted scoring function²⁶. In this work, we have developed an alternative approach rooted in end point DFT expressions which focuses on the effects of the direct and indirect PMF components of interfacial waters around the receptor on the binding free energy differences between the congeneric ligand pairs, binding to the same protein receptor. The indirect part of the PMF is equivalent to the sum of the 1-body energy + 1-body entropy terms in the IST expansion evaluated at fixed translational position and orientation of the interfacial water molecule which is displaced by a functional group of one of the congeneric ligands. Our analysis, which is based on the evaluation of both the direct and indirect components of the protein-solvent PMF, and therefore is limited to 1-body energy and 1-body entropy terms, appears to be balanced and provide physical insights, as the change in the binding free energies between congeneric ligands can be related to the thermodynamic signatures of individual water molecules that are displaced when a functional group is added to one of the congeneric ligand pairs.

The above examples illustrate the empirical correlation between ΔΔG_bind of congeneric ligand pairs and the magnitude of ω from the extra displaced water molecules. To visualize this relationship, we constructed a simple fitting function with two parameters based upon ω from the displaced water molecules to predict the standard binding free energy difference between a pair of congeneric ligands.

$$\mathrm{\Delta }\mathrm{\Delta }{\mathrm{G}}_{\text{bind}}=A\mid \sum _{i=1}^n{\omega }_i\mid +B$$ (9)

where ω_i is the indirect PMF from water molecule number i. Here, A and B are two fitting parameters determined by matching ΔΔG_predict with ΔΔG_DDM, which is the free energy difference from the double decoupling calculation. Using results from double decoupling calculations as reference values instead of experimental ones removes discrepancies from force field issue in the simulation. Based on the linear regression fitting, parameter A was −0.551 and parameter B was −0.432. The final ΔΔG_predict versus ΔΔG_DDM is plotted in Figure 8 with R² = 0.84. We emphasize that we are not proposing Equation 9 as a scoring function for ligand design, this subject is considered in the Appendix.

Figure 8.

ΔΔG_predict based on Equation 9 versus ΔΔG_DDM using double decoupling method from 12 congeneric ligand pairs.

To motivate the physical basis for the correlation shown in Figure 8, we refer to the Appendix which works through a thermodynamic cycle for the difference between the free energy of binding for two congeneric ligands in terms of the excess chemical potentials of all the species in the cycle. The result of this analysis, Equation A11, is a DFT based expression for ΔΔG_bind which is exact if all the terms are evaluated. The terms are of five kinds: (1) local integrals involving the solvent density and indirect PMF ω over small volumes (V^disp) at the protein-ligand receptor interface where one or a few waters are displaced during the process of an FEP type transformation from the smaller to the larger ligand of the congeneric pair; (2) the difference in the interaction of the congenic ligands with the protein; (3) local integrals of the solvent density and ω over V^disp around the unbound ligand; (4) a term arising from the difference in the DFT charging integrals between the congeneric ligands in solution, and a corresponding change between the complexes with the congeneric ligands bound; and (5) integrals from more distant regions (beyond V^disp) arising from the changes in the solvent density and ω between the two ligands or two complexes. The empirical relation Equation 9, suggests that a useful approximation to be applied to Equation A11 is to neglect the contribution to ΔΔG from changes in the solvent structure beyond V^disp and to neglect the the DFT charging terms; therefore to assume that the first two terms involving endpoint DFT expressions for the bound complex, along with the change in interaction term, make the most important contributions to ΔΔG_bind. If we make this assumption, it becomes apparent that when a “high density hydrophilic water” is displaced by a functional group which is added to a ligand core, the driving force for the more favorable binding of the larger ligand compared with smaller ligand is mainly from the interaction between the protein and the added functional group of the larger ligand, corresponding to the ΔU_pro-lig term in Equation A11. The first term in Equation A11 corresponds to the difference in solvent density, between the density at the location of the solvent molecule to be displaced, and the bulk. When the water to be displaced is “high density hydrophilic water”, the first term is positive and contributes unfavorably to ΔΔG_bind. Furthermore, when water has a “high density hydrophilic” thermodynamic signature, ω is positive and the second term is also unfavorable. Therefore, the favorable interactions between the protein and added functional group from the larger ligand will be opposed by the first and second terms in Equation A11. When ω is positive, this corresponds to an unfavorable interaction for the tagged water with the surrounding waters and a very favorable interaction with the protein (see Table 2). This suggests a ligand design strategy which adds a hydrophilic functional group to the original ligand core to replace the hydrophilic water and recover the favorable direct interaction between the tagged water and protein. Although the favorable interaction is weakened by the solvation effect from the first and second terms in Equation A11, ultimately, the added functional group can still drive the increased affinity through a favorable value of the ΔU_pro-lig term of Equation A11. This actually accentuates the importance of the competition between the direct and indirect terms in the DFT analysis approach for “high density hydrophilic water”. In the case of “high density hydrophobic water”, in contrast, the contribution from the change of interaction between the protein and larger ligand compared with smaller ligand is small. In this case, the first term in Equation A11 is still unfavorable due to the high density nature. On the other hand, the high density corresponding to large ρ(x) is strongly correlated with a negative ω, which makes the second term in Equation A11 favorable for the binding. Therefore, the first and second terms compensate partially against each other. For interfacial waters with thermodynamic signature “high density hydrophobic water”, the binding is driven by the second term; the displacement of water with negative ω contributes favorably to ΔΔG_bind. Finally, in the case of “low density dry water”, u ≈ 0 indicates that the contribution from ΔU_pro-lig term is also negligible in this case. However, the roles of the first and second terms in Equation A11 in determining the ΔΔG_bind are the inverse from the case of “high density hydrophobic water”. The first term in Equation A11 is favorable since ρ(x) is smaller than ρ₀, while ω > 0 implies that the second term in Equation A11 is unfavorable. There is still a competition between the first and second terms. But this time, the first term provides the driving force for more favorable binding when a “low density dry water” is displaced by a ligand functional group. Based on the analysis presented in the Appendix, it can be shown that the first term is larger in magnitude than the second, so that the effect of placing a ligand functional group at dry cavity which forms part of the protein binding site will be favorable, but the effect may be small as is the case in our example.

From an analysis of Equation A11, it should be clear that the sign of the indirect PMF cannot be used to determine the effect of water displacement on the strength of the ligand binding. Stated in another way, the sign of the first order contribution (1-body energy + 1-body entropy) of the IST solvation free energy of a solvent molecule displaced during the transformation of ligand to its congeneric pair, is not determinative of the sign of ΔΔG_bind. Instead, water locations with large absolute values of the indirect PMF ω, serve as targets for ligand design to enhance the binding affinity.

We note the fitting function, Equation 9, is greatly oversimplified. For one the density of the displaced solvent molecule does not appear explicitly. Furthermore, and most importantly, the difference in the binding affinity for a given pair of congeneric ligands with a protein receptor is not only determined by the displaced solvent. Changes in the interactions between protein and ligand pairs also make a contribution to the free energy difference as shown by ΔU_pro-lig term in Equation A11; this term is largely responsible for the gain in affinity when “high density hydrophilic water” is displaced by adding a functional group to a ligand core. Construction of more realistic scoring functions, like Equation A11, based on the analysis of the protein-solvent PMF and its direct and indirect components to predict ΔΔG_bind should also consider the change in the interactions between the protein and ligand in addition to the density weighted indirect PMF contribution. In order to construct scoring functions based on the spatially-resolved, end-point DFT framework, it will be necessary to develop a more automated procedure for calculating the solute-solvent PMF and its indirect part ω(x), as well as for calculating the charging integral (density functional) systematically throughout the protein-ligand binding interface. Work along these lines is underway in our groups.

Conclusion

Building upon the insights gained from the extensive prior analysis of the binding free energy between protein receptors (e.g. FXa and Streptavidin) and pairs of congeneric ligands^5,22,26, we describe an alternative approach based on the thermodynamic signatures of displaced water molecules at the interface of a protein receptor with a view towards aiding the design of more potent binding ligands with higher binding affinity. The idea of designing tight binding ligands by analyzing the thermodynamic signatures of solvent molecules around the target protein receptor has been described previously^{5,20–22,26–27}. The prior work is based on the IST framework which analyzes the thermodynamic signatures of interfacial water in terms of excess energies and entropies. In this work, we develop an alternative approach rooted in DFT which focuses on the effect of the indirect contribution to the solute-solvent PMF of interfacial waters around the receptor in governing the binding free energy changes when functional groups are added to a ligand core. We identified three types of interfacial water positions that can be regarded as targets for ligand design as summarized in Table 3: “bulk density hydrophilic water”, “high density hydrophilic water” and “high density hydrophobic water”. Considering the fourth type of interfacial water thermodynamic signature we studied, “low density dry” water, we found that for the one example we analyzed, the contribution to the binding affinity was small. While this result is consistent with an analytic argument we present in the Appendix concerning the relative contributions to ligand binding from the displacement of high density hydrophobic versus low density dry interfacial waters, more systematic study of this is required. Our major conclusion is that the displacement of a water molecule with an indirect solute-solvent PMF term which is large in magnitude, regardless of the sign, can make a significant contribution to tighter binding.

For the displacement of a “high density hydrophilic water” molecule with large positive ω(x), one goal in further design of ligands involves modification of the original ligand structure around a druggable site to mimic and enhance the favorable interaction between the displaced water and the receptor, which also disrupts the neighboring water structure to a smaller extent. In this case, the dominant effect in determining the relative binding affinity arises from the change in interaction term (ΔU_pro-lig) in Equation A11. Interfacial water locations which contribute favorably to the excess chemical potential of the solute (ω(x) > 0 in Equation 5) and locations which contribute unfavorably to the excess chemical potential of the solute (ω(x) < 0 in Equation 5) can both be targeted for displacement by adding a functional group to a reference ligand which will improve the binding affinity. Furthermore, we have found that a druggable site that can be targeted for further ligand design does not necessarily reside at positions where the solvent density is much higher than the bulk, which is usually required from the hydration site approach (HSA) in IST^5,22,31. In Table 2 row 1, we identified a type of “bulk density hydrophilic water” in region 1. From our end point DFT analysis approach, a water molecule in this region bears both large favorable direct interactions with the solute and unfavorable indirect contributions from surrounding solvent which almost completely cancel each other, resulting in a total PMF close to 0. Our analysis indicates that the displacement of such a bulk density hydrophilic water by adding a functional group to a ligand scaffold nearby can also result in a significant gain in the binding affinity.

APPENDIX

In this Appendix we highlight the roles of the indirect (solvent-mediated) part of the potential of mean force (PMF) in the statistical thermodynamics of protein-ligand binding. We base our formalism on the DFT expression of Equation 5 and discuss what information is carried by ω(x) for the difference in the binding free energy ΔΔG_bind between congeneric pairs of ligands. An approximate argument is presented, in particular, for the cases of “high density hydrophobic water” and “low density dry water”, for which the changes in the interactions between the protein and ligand are weak when an added functional group of a congeneric pair displaces interfacial water molecules, and the thermodynamic signature of the displaced waters is likely to be the key factor in the determination of ΔΔG_bind.

Consider a ligand S with smaller excluded volume and a ligand L with larger excluded volume binding to the same protein. The excess chemical potential of S in water is denoted as Δμ_S and the excess chemical potential of L in water is denoted as Δμ_L. The free energy of changing S to L in water is denoted as ΔG_wat,lig and the free energy of changing S to L in vacuum is denoted as ΔG_vac,lig. According to the thermodynamic cycle shown in Scheme 1A :

$$\mathrm{\Delta }{\mu }_{\mathrm{L}}-\mathrm{\Delta }{\mu }_{\mathrm{S}}=\mathrm{\Delta }{G}_{\text{wat},\text{lig}}-\mathrm{\Delta }{G}_{\text{vac},\text{lig}}$$ (A1)

Scheme 1.

Thermodynamic cycle for ΔΔG_bind by DFT analysis of displaced water (A) S change to L in vacuum and water (B) PS change to PL in vacuum and water

Label the complex between the protein and ligand S as PS and the complex between the protein and ligand L as PL. The excess chemical potentials of PS and PL in water are denoted as Δμ_PS and Δμ_PL respectively. The free energies of changing PS to PL in water and vacuum are denoted as ΔG_wat,com and ΔG_vac,com respectively. According to the thermodynamic cycle shown in Scheme 1B:

$$\mathrm{\Delta }{\mu }_{\text{PL}}-\mathrm{\Delta }{\mu }_{\text{PS}}=\mathrm{\Delta }{G}_{\text{wat},\text{com}}-\mathrm{\Delta }{G}_{\text{vac},\text{com}}$$ (A2)

Combining Equations A1 and A2 we obtain:

$$\mathrm{\Delta }{G}_{\text{wat},\text{com}}-\mathrm{\Delta }{G}_{\text{wat},\text{lig}}=(\mathrm{\Delta }{\mu }_{\text{PL}}-\mathrm{\Delta }{\mu }_{\text{PS}})-(\mathrm{\Delta }{\mu }_{\mathrm{L}}-\mathrm{\Delta }{\mu }_{\mathrm{S}})+(\mathrm{\Delta }{G}_{\text{vac},\text{com}}-\mathrm{\Delta }{G}_{\text{vac},\text{lig}})$$ (A3)

According to the thermodynamic cycle applied in FEP calculation shown in Scheme 2, the left-hand side of the above equation (ΔG_wat,com − ΔG_wat,lig) can be related to the relative binding free energy between the ligand pair S and L with the proteins in water:

$$\mathrm{\Delta }\mathrm{\Delta }{G}_{\text{bind}}=\mathrm{\Delta }{G}_{\text{bind}-\mathrm{L}}-\mathrm{\Delta }{G}_{\text{bind}-\mathrm{s}}=\mathrm{\Delta }{G}_{\text{wat},\text{com}}-\mathrm{\Delta }{G}_{\text{wat},\text{lig}}$$ (A4)

where ΔG_bind-L is the binding free energy between ligand L and protein and ΔG_bind-s is the binding free energy between ligand S and protein. Similarly, the last term of the right-hand side of Equation A3 (ΔG_vac,com −ΔG_vac,lig) can be expressed as ΔΔG_vac, which is the binding free energy difference between ligand pair L and S with protein in vacuum and it can be approximated by ΔU_pro-lig, the difference of the interaction between the protein and ligand as the binding ligand change from S to L, when the thermal motion of the protein and ligands are not considered. (We note that in the current work the thermal motion of the protein and ligands are not considered in the calculations involving direct and indirect PMF of displaced water, but they are included in the double decoupling free energy simulations to estimate ΔΔG_bind for a congeneric ligand pair.) Based on Equation A3 and A4:

$$\mathrm{\Delta }\mathrm{\Delta }{G}_{\text{bind}}=(\mathrm{\Delta }{\mu }_{\text{PL}}-\mathrm{\Delta }{\mu }_{\text{PS}})-(\mathrm{\Delta }{\mu }_{\mathrm{L}}-\mathrm{\Delta }{\mu }_{\mathrm{S}})+\mathrm{\Delta }{U}_{\text{pro}-\text{lig}}$$ (A5)

Scheme 2.

Thermodynamic cycle for ΔΔG_bind by FEP

This is the expression of ΔΔG_bind based on the difference of excess chemical potential, which can be evaluated based on DFT analysis. According to Equation 5 in the main text, Δμ_S can be expressed as:

$$\mathrm{\Delta }{\mu }_s=-k_{B}T\int d\mathbf{x}[{\rho }_s(\mathbf{x})-{\rho }_s(\infty )]-\int d\mathbf{x}{\rho }_s(\mathbf{x})[{\omega }_s(\mathbf{x})-{\omega }_s(\infty )]+\text{charging}\text{term}$$ (A6)

where ρ_S is the water density around S and ω_S is the indirect PMF derived from it. Similarly, Δμ_L can be expressed as:

$$\mathrm{\Delta }{\mu }_L=-k_{B}T\int d\mathbf{x}[{\rho }_L(\mathbf{x})-{\rho }_L(\infty )]-\int d\mathbf{x}{\rho }_L(\mathbf{x})[{\omega }_L(\mathbf{x})-{\omega }_L(\infty )]+\text{charging}\text{term}$$ (A7)

where ρ_L is the water density around L and ω_L is the indirect PMF derived from it. When the difference of Δμ_L from Δμ_S is dominated by those water molecules that are displaced when the ligand is grown from S to L, it can be expressed as:

$$\begin{gathered} \mathrm{\Delta }{\mu }_L-\mathrm{\Delta }{\mu }_s \\ =k_{B}T{\int }_{}^{V^{\mathit{disp}}}d\mathbf{x}[{\rho }_s(\mathbf{x})-{\rho }_s(\infty )]+k_{B}T{\rho }_0{V}^{\mathit{disp}}+{\int }_{}^{V^{\mathit{disp}}}d\mathbf{x}{\rho }_s(\mathbf{x})[{\omega }_s(\mathbf{x})-{\omega }_s(\infty )]+\text{change}\text{in}\text{charging}\text{term} \\ +\text{terms}\text{for}\text{the}\text{integration}\text{outside}{V}^{\mathit{disp}}\text{arising}\text{from}\text{the}\text{changes}\text{in}\rho \text{and}\omega \text{between}S\text{and}L \end{gathered}$$ (A8)

where the domain of integration is restricted to the region in which water is found in system S but not in system L. It is further assumed that the changes in the solvent density and indirect PMF are minor outside the domain of integration of V^disp, where water is not displaced and we express this part of contribution to the change in excess chemical potential as an integral over the volume V > V^disp. A similar expression holds for the protein-ligand complexes PS and PL:

$$\begin{gathered} \mathrm{\Delta }{\mu }_{PL}-\mathrm{\Delta }{\mu }_{PS} \\ =k_{B}T{\int }_{}^{V^{\mathit{disp}}}d\mathbf{x}[{\rho }_{PS}(\mathbf{x})-{\rho }_{PS}(\infty )]+k_{B}T{\rho }_0{V}^{\mathit{disp}}+{\int }_{}^{V^{\mathit{disp}}}d\mathbf{x}{\rho }_{PS}(\mathbf{x})[{\omega }_{PS}(\mathbf{x})-{\omega }_{PS}(\infty )] \\ +\text{change}\text{in}\text{charging}\text{term} \\ +\text{terms}\text{for}\text{the}\text{integration}\text{outside}{V}^{\mathit{disp}}\text{arising}\text{from}\text{the}\text{changes}\text{in}\rho \text{and}\omega \text{between}PS\text{and}PL \end{gathered}$$ (A9)

According to Equation A8 and A9:

$$\begin{gathered} (\mathrm{\Delta }{\mu }_{\text{PL}}-\mathrm{\Delta }{\mu }_{\text{PS}})-(\mathrm{\Delta }{\mu }_{\mathrm{L}}-\mathrm{\Delta }{\mu }_{\mathrm{S}}) \\ =k_{B}T{\int }_{}^{V^{\mathit{disp}}}d\mathbf{x}[{\rho }_{PS}(\mathbf{x})-{\rho }_{PS}(\infty )]+{\int }_{}^{V^{\mathit{disp}}}d\mathbf{x}{\rho }_{PS}(\mathbf{x})[{\omega }_{PS}(\mathbf{x})-{\omega }_{PS}(\infty )] \\ -k_{B}T{\int }_{}^{V^{\mathit{disp}}}d\mathbf{x}[{\rho }_s(\mathbf{x})-{\rho }_s(\infty )]-{\int }_{}^{V^{\mathit{disp}}}d\mathbf{x}{\rho }_s(\mathbf{x})[{\omega }_s(\mathbf{x})-{\omega }_s(\infty )] \\ +\text{change}\text{in}\text{charging}\text{term} \\ +\text{terms}\text{for}\text{the}\text{integration}\text{outside}{V}^{\mathit{disp}}\text{arising}\text{from}\text{the}\text{changes}\text{in}\rho \text{and}\omega \end{gathered}$$ (A10)

Combining Equation A5 and A10:

$$\begin{gathered} \mathrm{\Delta }\mathrm{\Delta }{\mathrm{G}}_{\text{bind}}=k_{B}T{\int }_{}^{V^{\mathit{disp}}}d\mathbf{x}[{\rho }_{PS}(\mathbf{x})-{\rho }_0]+{\int }_{}^{V^{\mathit{disp}}}d\mathbf{x}{\rho }_{PS}(\mathbf{x}){\omega }_{PS}(\mathbf{x})+\mathrm{\Delta }{U}_{\text{pro}-\text{lig}} \\ \{-k_{B}T{\int }_{}^{V^{\mathit{disp}}}d\mathbf{x}\left[{\rho }_s(\mathbf{x})-{\rho }_0\right]-{\int }_{}^{V^{\mathit{disp}}}d\mathbf{x}{\rho }_s(\mathbf{x}){\omega }_s(\mathbf{x})+\text{change}\text{in}\text{charging}\text{term} \\ +\text{terms}\text{for}\text{the}\text{integration}\text{outside}{V}^{\mathit{disp}}\text{arising}\text{from}\text{the}\text{changes}\text{in}\rho \text{and}\omega \} \end{gathered}$$ (A11)

where we have replaced the bulk values of water density and indirect PMF to the ones in the thermodynamic limit since the integration is done over the finite volume. The first three terms capture the thermodynamic effects of displacing interfacial waters closest to the protein, and changes in the protein-ligand interactions when a functional group is added to a ligand core of a congeneric pair; and in the following we focus on those terms. We further suppose that the functional group added to the ligand is polar when the water molecule to be displaced is of “high density hydrophilic” type and is nonpolar for a displacement of “high density hydrophobic water” or “low density dry water”.

For a “high density hydrophilic water”, ρ_PS(x) > ρ₀ and ω_PS(x) > 0. This means that the first two terms of Equation A11 contribute unfavorably to ΔΔG_bind. It is then suggested that the driving force for obtaining a favorable ΔΔG_bind is ΔU_pro-lig. ΔU_pro-lig needs to be a “strong” interaction to overturn the effect of the first two terms of Equation A11, and thus a functional group with a polar interaction is added to the ligand.

When the displaced water is “high density hydrophobic water” or “low density dry water”, its interaction with the complex of the protein with the reference ligand S is weak. This is rephrased as u≈0, and with our supposition, ΔU_pro-lig is further considered to be minor. The sum of the first to third terms of Equation A11 then reduces to

$$\begin{gathered} k_{B}T{\int }_{}^{V^{\mathit{disp}}}d\mathbf{x}[{\rho }_{PS}(\mathbf{x})-{\rho }_0]+{\int }_{}^{V^{\mathit{disp}}}d\mathbf{x}{\rho }_{PS}(\mathbf{x}){\omega }_{PS}(\mathbf{x}) \\ =k_{B}T{\int }_{}^{V^{\mathit{disp}}}d\mathbf{x}{\rho }_0[e^{-\beta u(\mathbf{x})-\beta {\omega }_{PS}(\mathbf{x})}-1+e^{-\beta u(\mathbf{x})-\beta {\omega }_{PS}(\mathbf{x})}\beta {\omega }_{PS}(\mathbf{x})] \\ \approx k_{B}T{\int }_{}^{V^{\mathit{disp}}}d\mathbf{x}{\rho }_0[e^{-\beta {\omega }_{PS}(\mathbf{x})}-1+e^{-\beta {\omega }_{PS}(\mathbf{x})}\beta {\omega }_{PS}(\mathbf{x})] \end{gathered}$$ (A12)

On the rightmost side, the integrand is always negative for a non-zero ω_PS, irrespective of its sign, and becomes larger in magnitude with |ω_PS| in both of the positive and negative regions of ω_PS. To prove this, let f(z) = exp(−z) − 1 + z exp(−z), where z corresponds to βω_PS in Equation A12. f(0) = 0 and df(z)/dz = −z exp(−z). This derivative is negative when z > 0, and is positive when z < 0. f(z) thus increases with z when z < 0 and decreases with z when z > 0, implying that f(z) < f(0) = 0 if z is not equal to 0. Therefore, in the case of “high density hydrophobic water” and “low density dry water” with u≈0, the sum of the first and second terms makes a favorable contribution to ΔΔG_bind according to Equation A12. We expect that these two terms can account for most of ΔΔG_bind a congeneric ligand pair involving the addition of a hydrophobic functional group which displaces a “high density hydrophobic” or “low density dry water”.

It is also possible to show that a “high density hydrophobic water” has a stronger effect than a “low density dry water”. To see this point, we note that f(∞) = −1. Thus, since f(z) is a decreasing function of z when z > 0, the rightmost side of Equation A12 satisfies

$$-k_{B}T{\rho }_0{V}^{\mathit{disp}}=-k_{B}T{\int }_{}^{V^{\mathit{disp}}}d\mathbf{x}{\rho }_0<k_{B}T{\int }_{}^{V^{\mathit{disp}}}d\mathbf{x}{\rho }_0\left[e^{-\beta {\omega }_{PS}(\mathbf{x})}-1+e^{-\beta {\omega }_{PS}(\mathbf{x})}\beta {\omega }_{PS}(\mathbf{x})\right]<0$$ (A13)

This equality shows that ω_PS of “low density dry water” (with ω_PS > 0) contributes to ΔΔG_bind in a range between 0 and −k_BT ρ₀V^disp. When V^disp is such that ρ₀V^disp is close to 1, the contribution is between 0 and −k_BT. Accordingly, the rightmost side of Equation A12 is more favorable (more negative) for a “high density hydrophobic water” (with ω_PS < 0) than for a “low density dry water” when

$$\langle {\omega }_{PS}\rangle <-k_{B}T$$ (A14)

holds, where 〈ω_PS 〉 is the average of ω_PS in the V^disp region introduced as

$$\langle {\omega }_{PS}\rangle =\frac{{\int }_{}^{V^{\mathit{disp}}}d\mathbf{x}{\rho }_{PS}(\mathbf{x}){\omega }_{PS}(\mathbf{x})}{{\int }_{}^{V^{\mathit{disp}}}d\mathbf{x}{\rho }_{PS}(\mathbf{x})}$$ (A15)

Equation A14 means that the average of ω_PS in the V^disp region is more negative than −k_BT, which is valid in Table 2. Therefore, a “high density hydrophobic water” can be a good target for ligand design, while a “low density dry water” may not be. We plan further analysis of this conjecture.

Finally, we remark on the numerical treatment of the first two terms of Equation A11. Let

$$N_{av}={\int }_{}^{V^{\mathit{disp}}}d\mathbf{x}{\rho }_{PS}(\mathbf{x})$$ (A16)

be the average number of water molecules in the V^disp region, in which the integration is taken over the space and over the orientation. This situation is common to Equation A15, where the spatial and orientational averaging is done. The first two terms of Equation A11 can then be rewritten as

$$k_{B}T{\int }_{}^{V^{\mathit{disp}}}d\mathbf{x}[{\rho }_{PS}(\mathbf{x})-{\rho }_0]+{\int }_{}^{V^{\mathit{disp}}}d\mathbf{x}{\rho }_{PS}(\mathbf{x}){\omega }_{PS}(\mathbf{x})=k_{B}T\left(N_{av}-{\rho }_0{V}_{\mathit{disp}}\right)+N_{av}\langle {\omega }_{PS}\rangle$$ (A17)

In MD, a finite sampling is possible for the water configuration x. When we sample many x_i within the V^disp region (i = 1,…, n), 〈ω_PS〉 is calculated as

$$\frac{1}{n}\sum _i{\omega }_{PS}({\mathbf{x}}_i)$$ (A18)

since x_i appears with a probability proportional to ρ_PS(x_i). The calculations performed in the present work correspond to n = 1, that this estimate is reasonable can be (semi-quantitatively) validated as follows. A “high density hydrophilic water” will be restrained in terms of the position and orientation, meaning that ρ_PS(x) has a sharp peak at the x sampled during the course of MD. Thus a single or a few snapshots (small n) can be representative and are expected to provide the average of Equation A15 without doing harm for semi-quantitative arguments like Figure 8. For a “high density hydrophobic water” or “low density dry water”, on the other hand, water can move rather freely and ρ_PS(x) is a broad distribution. This implies that since the direct interaction u is small, ω_PS does not depend strongly on x in the V^disp. Thus, 〈ω_PS〉 is considered to be close to ω_PS(x) sampled in MD, leading to sufficiency of small n in Equation A18. The dependence of a computed 〈ω_PS〉 on the number of samplings n is a subject of a forthcoming work, in which a predictive scheme for ΔΔG_bind is explored on the basis of Equation A11 that is derived through DFT.