Abstract
We describe a new analysis tool called Stratified unbinned Weighted Histogram Analysis Method (Stratified-UWHAM), which can be used to compute free energies and expectations from a multicanonical ensemble when a subset of the parallel simulations are far from being equilibrated because of barriers between free energy basins which are only rarely (or never) crossed at some states. The Stratified-UWHAM equations can be obtained in the form of UWHAM equations but with an expanded set of states. We also provide a stochastic solver, Stratified RE-SWHAM, for Stratified-UWHAM to remove its computational bottleneck. Stratified-UWHAM and Stratified RE-SWHAM are applied to study three test topics: the free energy landscape of alanine dipeptide, the binding affinity of a host-guest binding complex, and path sampling for a two dimensional double well potential. The examples show that when some of the parallel simulations are only locally equilibrated, the estimates of free energies and equilibrium distributions provided by the conventional UWHAM (or MBAR) solutions exhibit considerable biases, but the estimates provided by Stratified-UWHAM and Stratified RE-SWHAM agree with the benchmark very well. Lastly, we discuss features of the Stratified-UWHAM approach which is based on coarse-graining in relation to two other maximum likelihood-based methods which were proposed recently, that also coarse-grain the multicanonical data.
Graphical Abstract
1 Introduction
Atomistic molecular dynamics (MD) simulations are widely used to study biological systems today to understand how structural ensembles are connected with biological functions. However straightforward MD simulations cannot be used to study many biological problems since the timescales of transitions between functionally important states are much longer than the available simulation length determined by today’s computational resources.1–4 The desire to simulate structurally important transitions which occur on longer timescales has driven the development of simulation hardware and software.5–7 For example, the Anton supercomputer developed by D. E. Shaw research is able to perform millisecond-scale simulations for proteins in explicit solvent.7 The World Community Grid (WCG) projects of IBM (https://www.worldcommunitygrid.org) are able to combine the computational resources (~ 105 – 106 cpus) donated by volunteers all over the world to run molecular simulations whose goals are to develop therapies to fight cancer and AIDS. The same desire also encourages the development of enhanced sampling methods such as umbrella sampling,8–10 replica exchange (RE) techniques11–16 and others.17–25 Compared with straightforward MD simulations, those techniques show significantly better sampling efficiency on specific problems.
The Weighted Histogram Analysis Method (WHAM) is a powerful algorithm to compute free energies and expectations from multicanonical ensemble data.26–30 Along with the popularity of enhanced sampling methods running parallel simulations at multiple thermodynamic and/or Hamiltonian states, WHAM, which is a standard analysis tool associated with those methods, has been studied by many researchers.31–42 The most important improvement of WHAM is that a binless extension called the multistate Bennett acceptance ratio (MBAR) or unbinned WHAM (UWHAM) was introduced.31,34,36 To avoid the requirements of very large memory and computational power to solve the UWHAM equations when the input data ensemble is large, we developed stochastic solvers for the UWHAM equations based on resampling techniques.43,44
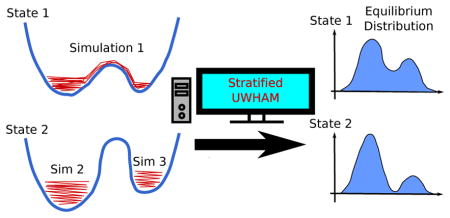
When WHAM or UWHAM is applied, it is assumed that the observations generated from each thermodynamic and/or Hamiltonian state are drawn from a distribution Pα that is close to equilibrium, where Pα is determined by the Hamiltonian and/or thermostat temperature used in the simulations. However, this assumption is not fulfilled if the simulations at some thermodynamic and/or Hamiltonian states are far away from convergence. For example, on massive but minimally communicating computational grids such as WCG, it is convenient to run multiple independent short MD simulations starting from different initial structures (which are not chosen from global equilibrium) at a single or multiple thermodynamic and/or Hamiltonian states. Here, our study focuses on how to obtain the optimal estimates of density of states, equilibrium distributions and free energy differences for multi-state simulations if the simulations at some thermodynamic and/or Hamiltonian state are far from convergence due to barrier(s) that are infrequently (or never) crossed at these states but frequently crossed at others. Simply combining all the observations of unconverged short simulations at a thermodynamic and/or Hamiltonian state as the input of that state for UWHAM introduces statistical biases even when the simulations at other thermodynamic and/or Hamiltonian states have already converged. To solve this problem, we introduce a powerful extension of UWHAM called Stratified-UWHAM. We also introduce the corresponding stochastic solver for the Stratified-UWHAM algorithm for cases where the input data ensemble is very large.
The remaining part of the paper proceeds as follows: First we review UWHAM (also called MBAR). Then we introduce Stratified-UWHAM and its stochastic solver Stratified RE-SWHAM. In the results and discussion section, we applied Stratified-UWHAM and Stratified RE-SWHAM to analyze the simulation data of three test systems — alanine dipeptide, a host-guest binding complex, and a Brownian particle in a two-dimensional double well potential. For the sake of simplicity, for the remainder of this paper, we refer to each of the thermodynamic and/or Hamiltonian states characterized by a specific combination of a Hamiltonian function and thermodynamic parameters, as a “λ-state”. We refer to each conformational structure of a biological or physical system as a “microstate” and to each free energy basin which is separated from other basins by free energy barriers as a “macrostate”. A macrostate cluster means a collection of one or more free energy basins that can be transversed in the simulations.
The idea underlying Stratified-UWHAM is to coarse-grain the configurational space into macrostate clusters and divide λ-states of parallel simulations into two groups based on how well-connected the coarse-grained network is at each λ-state. The first group includes the λ-states at which the simulations are “approximately” equilibrated among macrostate clusters, namely, the fully-connected λ-states. Notice that if a simulation at any λ-state is fully converged or fully globally equilibrated, running simulations at other λ-states additionally and applying UWHAM is redundant because the true density of states can be obtained from the fully converged simulation at that λ-state. In this study, the λ-states in the first group are those λ-states at which multiple transitions between macrostate clusters have been observed in simulations so that the coarse-grained state space is fully connected. The second group includes the λ-states at which the simulations are only locally equilibrated within each macrostate cluster, namely, the disconnected λ-states. They are also referred to as “locally equilibrated λ-states”.
2 Methods
2.1 Unbinned weighted histogram analysis method (UWHAM)
To illustrate basic ideas, we first review UWHAM36 (also called MBAR34). Suppose that Nα observations { } are independently drawn from the αth distribution Pα
| (1) |
where Zα is the partition function of the αth λ-state; xαi are the coordinates of the microstate ; and qα(xαi) is the unnormalized probability of observing the microstate at the αth λ-state. For example, qα(xγi) equals exp{−βαEα(xγi)} in the canonical ensemble, where xγi is the coordinates of the ith observation observed at the γth λ-state is the potential energy of the microstate at the αth λ-state and βα is the inverse temperature of the αth λ-state.
The likelihood of the simulated data is
| (2) |
where Ω(uαi) is the density of states of the reduced (energy) coordinate uαi of the microstate . The maximum likelihood estimates (MLEs) of the density of states Ω̂(uγi) and the corresponding MLEs Ẑα given the data satisfy the coupled equations
| (3) |
The UWHAM estimate of the probability of observing uγi at the αth λ-state is
| (4) |
2.2 Stratified-UWHAM
Our new method, called Stratified-UWHAM, is based on the following conditions: the λ-states are divided into two groups, (S1, S2), such that
simulations are approximately equilibrated among the macrostates for each of the λ-states in S1; or more generally, the coarse-grained set of macrostates form a connected network for each λ-state and together form a globally connected network;
simulations are locally equilibrated within each macrostate cluster (R1, …, RK) for each of the λ-states in S2, but may be far from equilibrated among the macrostates; or more generally, for each λ-state within S2 the coarse-grained set of macrostates forms a disconnected network.
These conditions can be captured by a stratified model, which assumes that the set of observations { } are independently drawn from Pα for each α ∈ S1, and the set of observations { , i = 1, …, Nα} are independently drawn from Pα restricted to macrostates Rk for each α ∈ S2, i.e.,
| (5) |
where qαk(x) = qα(x)δ{x ∈ Rk}, and δ{x ∈ A} denotes the indicator function for a macrostate A, and Zαk and Zα are the partition functions. In other words, the set of observations { } are stratified into macrostates (R1, …, RK) for each λ-state α in S2 such that simulations are only locally equilibrated, but are not stratified for each λ-state α in S1 where transitions between macrostates are enhanced. The likelihood of the simulated data from model (5) is
| (6) |
The method of nonparametric maximum likelihood31 can be used for estimating the density of states and subsequently free energies and expectations.
The estimating equations from the maximization of Eq.(6) can be obtained in the form of UWHAM equations Eq.(3), but with an expanded set of λ-states. The idea is to split the K disconnected macrostates of each λ-state in the S2 group into K λ-states. Suppose there is a new λ-state which is made of the kth macrostate of the γth λ-state. The Hamiltonian function of this new λ-state is set to be the same as the Hamiltonian function of the γth λ-state if the observation belongs to the kth macrostate and positive infinity if the observation does not. Then all the observations in the kth macrostate at the γth λ-state are treated as the observations observed at this new λ-state. This change of the Hamiltonian function and regrouping of the observations are equivalent to putting an infinite barrier covering the entire outside of the kth macrostate in the conformational space. Suppose there are M1 λ-states in the S1 group and M2 λ-states in the S2 group. After the expansion of λ-states, the total number of λ-states increases from M = M1 + M2 to , where Kα is the total number of macrostates at the αth λ-state in the S2 group. Then the MLEs of the density of states and free energy differences of Eq.(6) can be obtained by solving the UWHAM equations with an expanded set of λ-states
| (7) |
where the unnormalized probability of an observation uγi at a new λ-state is
| (8) |
for canonical ensembles. The population ratio between the mth and nth disconnected macrostate clusters of a locally equilibrated αth λ-state is estimated based on their free energy difference
| (9) |
2.3 Stratified Stochastic WHAM
There is a computational bottleneck in scaling up UWHAM. At minimum, numerical solution of the UWHAM equations (3) requires evaluating M unnormalized density functions q1(Xi), …, qM(Xi) at each observation Xi for i = 1, …, N. The total number of function evaluations is of order n̄M2, where n̄ = N/M is the average sample size per distribution. These unnormalized density values need to be either computed during every iteration of the numerical solution or pre-computed and stored in memory. Such a high computational cost presents a serious limitation on the use of UWHAM for large-scale simulations (for example, M = 240 and N = 3.5 × 107 in our recent work43,44). Although Stratified-UWHAM can be applied by directly using the UWHAM software package developed before, it can require much more memory and computational time to converge because the total number of λ-states can increase substantially.
To remove the computational bottleneck, we recently developed the RE-SWHAM algorithm which solves the UWHAM equations stochastically (See Ref.[43] for details). A straightforward way to solve the Stratified-UWHAM equations stochastically is by performing RE-SWHAM analyses as described in Ref.[43] for the corresponding UWHAM equations with an expanded set of λ-states. Note that the direct outputs of RE-SWHAM are the estimates of conformational equilibrium distributions at each λ-state. The estimates of free energy differences (and the population ratios) between macrostate clusters of a locally equilibrated λ-state can then be calculated using thermodynamic cycles similarly as shown in Fig. 2b and discussed in detail in Sec.3.1, while applying “free energy perturbation formula” (see Eq.(20) in Ref.[43])
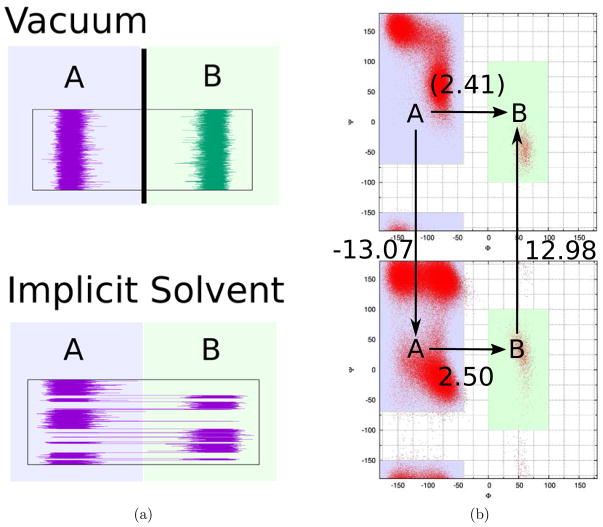
Figure 2.
Thermodynamic cycle of alanine dipeptide (AlaD) in vacuum and implicit solvent. (a) It is much more computationally time consuming to obtain the equilibrium distribution of AlaD in vacuum than AlaD in implicit solvent by brute force simulations. (b)The upper picture is the ramachandran plot of AlaD in vacuum, and the lower picture is the ramachandran plot of AlaD in implicit solvent. The free energy difference of the A and B macrostate clusters in vacuum equals to the sum of the other three legs.
We describe a different algorithm called Stratified RE-SWHAM to solve the Stratified-UWHAM equations stochastically by improving the above straightforward application of RE-SWHAM. In the original implementation of RE-SWHAM, every cycle consists of a move process and an exchange process, the same as replica exchange simulations. The move process for the next observation is chosen from the database of observations at each λ-state according to the probability 1/Nα, where nα is the number of observations generated at that λ-state. This move process in RE-SWHAM is analogous to the move process of an explicit RE simulation when the MD simulation period per cycle is so long that the initial and final configurations of the MD simulation period are largely uncorrelated. However, when the simulations at some λ-states are only locally equilibrated within macrostates and the coarse-graining results in a disconnected network of macrostates, the move process in RE-SWHAM at these λ-states needs to be adjusted accordingly as follows. In the stratified RE-SWHAM analysis, the next observation is chosen from the data elements in the same connected macrostate cluster (instead of all the macrostates) with equal probability for each of the λ-states in the stratified S2 group.
The procedure of running Stratified RE-SWHAM to analyze simulation data is as follows:
A database of observations is constructed for each λ-state using all the data elements observed at that λ-state. Each data element is tagged by the macrostate which it belongs to.
-
Then Stratified RE-SWHAM is run in cycles like replica exchange simulations:
Move: For each λ-state, one data element is selected from its database to associate with the replica at that λ-state. At the fully-connected λ-states, one of the data elements is chosen with equal probability; at the disconnected λ-states, one of the data elements which are in the same connected macrostate cluster as the data element previously associated with the replica at that λ-state is chosen with equal probability.
Exchange: Replica exchange attempts are examined according to the multicanonical exchange criterion. If an exchange attempt is accepted, the replicas are swapped, and the data elements associated with the replicas are also swapped to the database of the other λ-state.
At the end of the cycle, the data element associated with the replica at each λ-state is recorded as the output of that λ-state.
The output of each λ-state is the estimate of the equilibrium distribution of that λ-state. Further statistical analyses can be applied to the data ensembles generated by Stratified RE-SWHAM at those interested λ-states.
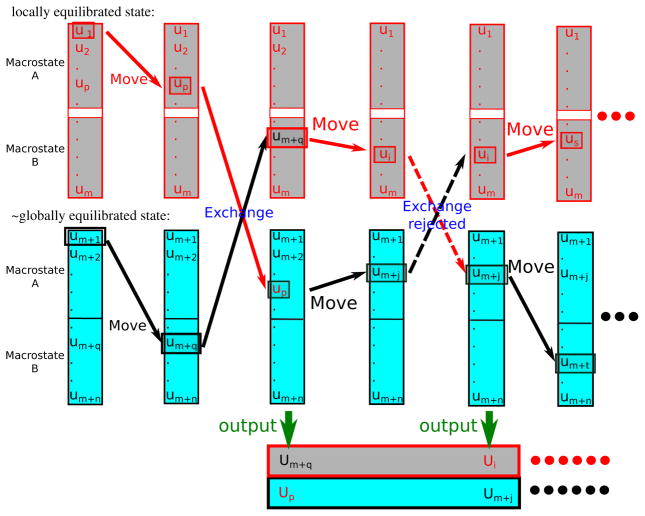
Fig. 1 illustrates the procedure of stratified RE-SWHAM.
Figure 1.
An illustration of the Stratified RE-SWHAM algorithm. This drawing shows two λ-states with “grey” or “cyan” color. Each λ-state has two macrostates A and B. The grey λ-state is locally equilibrated while the simulations at the cyan λ-state are approximately equilibrated among the macrostates. The white gap between macrostates at the grey λ-state represents an uncrossable barrier for the “move” procedure during the Stratified RE-SWHAM analysis. Beforehand, we construct each λ-state a database which contains all the observations obtained from that λ-state, and each observation is tagged by the macrostate which it belongs to. As shown in the picture, the observations are separated into two subgroups A and B. Then Stratified RE-SWHAM is run in cycles, which consists of a “move” procedure and an “exchange” procedure. In the move procedure, Stratified RE-SWHAM chooses an observation to associate with the replica at each λ-state. At the cyan λ-state, the next observation is chosen from the whole database of that λ-state with equal probability. However, at the grey λ-state, the next observation is chosen from the subgroup which the previous observation belongs to with equal probability. In the exchange procedure, if the exchange attempt is accepted, in addition to the swap of the replicas, the observations associated with the replicas are also swapped to the database of the other λ-state. At the end of each cycle, the observation associated with each replica is recorded as the output of Stratified RE-SWHAM.
Compared with RE-SWHAM with an expanded set of λ-states, Stratified RE-SWHAM does not split the λ-states in the S2 group into multiple new λ-states. In the Appendix, we show that, without the splitting of locally equilibrated λ-states, the output of Stratified RE-SWHAM at a locally equilibrated λ-state is the estimate of the equilibrium distribution of that λ-state. In particular, the population ratios can be estimated directly as those in the estimate of the equilibrium distribution of that λ-state from the output of Stratified RE-SWHAM, without explicitly invoking the thermodynamic cycle. Therefore, in addition to all of the advantages of RE-SWHAM over UWHAM discussed in Ref.[43], one more benefit of using Stratified RE-SWHAM to solve the Stratified-UWHAM equations is that the number of λ-states does not increase compared with the original system.
3 Results and Discussion
3.1 Example 1: Alanine Dipeptide
To illustrate the problem, first we study the free energy landscape of alanine dipeptide (AlaD) in vacuum and in implicit solvent. The ramachandran plots of an AlaD molecule are shown in Fig. 2b. In the picture, the A macrostate cluster contains the β/C5, C7eq and αR free energy basins on the left side of the plot, and the B macrostate cluster contains the αL and C7ax free energy basins on the right side of the plot. The simulation of AlaD in vacuum is ~ 6 time faster per step than the simulation of AlaD in implicit solvent (OBC GB model) using GROMACS.45,46 However, the free energy barriers between the A and B macrostate clusters are much higher for AlaD in vacuum than AlaD in implicit solvent because the electrostatic interaction screening of water is absent. Consequently, it turns out that it is much more computationally time consuming to obtain the equilibrium distribution of AlaD in vacuum by brute force simulations. The first passage times of AlaD in implicit solvent are τA→B = (78 ± 3) ns and τB→A = (1.33 ± 0.04) ns; and the first passage times of AlaD in vacuum are τA→B = (2.6 ± 0.2) μs and τB→A = (55 ± 4) ns. In this study, the equilibrium distribution of AlaD in implicit solvent was obtained by replica exchange simulations first. Then two independent simulations of AlaD in vacuum, one starting from the A macrostate cluster and the other from B were run. See Supporting Information for simulation details. For both simulations, no transitions between the A and B macrostate clusters were observed during the first 100 ns. The goal is to apply UWHAM to estimate the equilibrium distributions of AlaD in vacuum based on the data generated by two 100 ns long independent simulations of AlaD in vacuum and the previously obtained equilibrium distribution of AlaD in implicit solvent. The two λ-states of this model problem will be referred to as the implicit solvent (I) state and the vacuum (V) state.
Fig. 2b shows a typical thermodynamic cycle. To calculate the free energy difference between the A and B macrostate clusters at the vacuum state , the standard procedure is to calculate the two vertical legs, and using BAR (or UWHAM), and calculate the lower horizontal leg using the population percentages of the two macrostate clusters at the implicit solvent state obtained by simulations.47 Then the free energy difference presented by the upper horizontal leg can be calculated by
| (10) |
Given , the equilibrium distribution of AlaD in vacuum and the free energy difference between an AlaD molecule in vacuum and in implicit solvent can be estimated. The results obtained by using the thermodynamic cycle (Eq.(10)) serve as the benchmark for this model problem.
On the other hand, conventional UWHAM is inappropriate to be applied straightforwardly to estimate the density of states and free energy difference between an AlaD molecule in vacuum and in implicit solvent. As mentioned previously, the two simulations of AlaD in vacuum are far from converged in 100 ns because there have been no transitions between the two macrostate clusters (β/C5, C7eq, αR) and (αL, C7ax). Simply combining the two unconverged data sets at the same λ-state does not provide an ensemble drawn from the Boltzmann distribution of that λ-state. Therefore, the corresponding UWHAM results are not correct. The difference between the conventional UWHAM estimate of and the benchmark can be seen in table 1. However, Stratified-UWHAM can be used to process the same data to obtain an accurate estimate of the free energy surfaces. We split the vacuum state into two λ-states, and applied Stratified-UWHAM to obtain the density of states and free energy differences between λ-states for this new system with an expanded set of λ-states. The free energy difference between the A and B macrostate clusters at the vacuum state was calculated according to Eq.(9). As can be seen in table 1, estimated by Stratified-UWHAM agrees very well with the benchmark. And the Stratified RE-SWHAM estimate also matches the benchmark within statistical error.
Table 1.
Free energy difference between the A and B macrostate clusters of AlaD in vacuum estimated by thermodynamic cycle, the conventional UWHAM, Stratified-UWHAM and Stratified RE-SWHAM. Standard errors are estimated by the block bootstrap method.
| T Cycle | Stratified-UWHAM | Stratified RE-SWHAM | UWHAM | ||
|---|---|---|---|---|---|
|
|
2.41 ± 0.04 | 2.42 ± 0.04 | 2.45 ± 0.05 | 0.1060 ± 0.0007 |
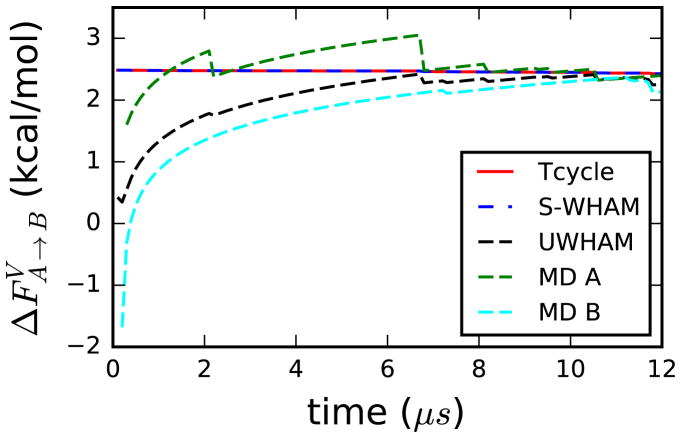
We continued running the two independent MD simulations at the vacuum states to obtain better converged raw data until the conventional UWHAM estimates also match the benchmark. The evolution of the conventional UWHAM and Stratified-UWHAM estimates are shown in Fig. 3. As can be seen, Stratified-UWHAM converges to the benchmark within statistical error from the first data point where the simulation time is 100 ns. On the contrary, it takes several microseconds simulation time of AlaD in vacuum for the conventional UWHAM estimate to reach a similar precision level as the Stratified-UWHAM estimate. Fig. 3 also shows the estimates of based on the independent MD simulations A and B. That converges on the same timescale when MD simulations A and B are UWHAMMed as when the simulations are considered individually reflects the fact that the macrostate clusters must be connected in simulations A and B before the two simulations can be UWHAMMed without bias. See more discussion about the convergence of Stratified-UWHAM estimates in the Supporting Information.
Figure 3.
Dependence of the conventional UWHAM and Stratified-UWHAM estimates of the free energy difference between the A and B macrostate clusters of AlaD in vacuum on the simulation length of the simulations of AlaD in vacuum. The red line is the benchmark — the estimates of thermodynamic cycle. The blue dash line is the estimates of Stratified-UWHAM when the vacuum state is split into two new λ-states. The black dash line is the estimates of the conventional UWHAM estimates when the data at the vacuum states are simply combined as the input of that λ-state. The green and cyan dash lines are the estimate based on the independent MD simulations starting from the A and B macrostate clusters respectively. It takes MD simulations lasting several microseconds of AlaD in vacuum for the conventional UWHAM estimates to match the benchmark compared with Stratified-UWHAM which converges within 100 ns. The Stratified-UWHAM estimates are visually identical with the benchmark.
3.2 Example 2: β-cyclodextrin Heptanoate complex
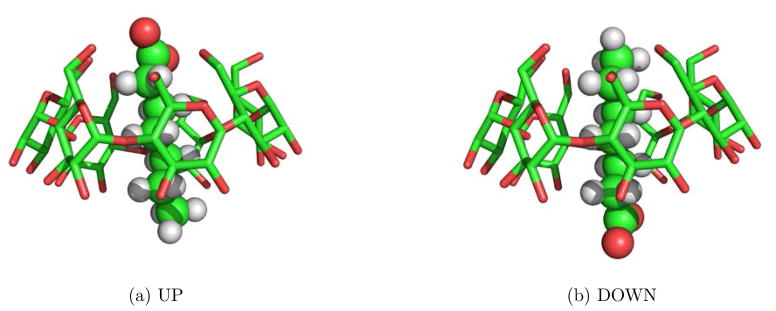
As the second example, we study the binding affinity of a host-guest system—β-Cyclodextrin Heptanoate complex. The host, β-Cyclodextrin (βCD), is a frustum-shaped molecule with a hydrophobic interior core. The narrow opening end of βCD is laced with 7 primary hydroxyls; and the wide opening end is laced with 14 secondary hydroxyls. Because of its chemical nature, βCD can bind with a number of ligands, therefore serves as a classic “host” for the study of molecular recognition phenomena. The guest molecule, heptanoate, consists of a hydrophilic carboxylate group and hydrophobic alkyl groups. As the hydrophobic alkyl groups of heptanoate is nested in the cavity of βCD, the carboxylate group of heptanoate can form hydrogen bonds with either the primary or the secondary hydroxyls of βCD depending on the orientation of the heptanoate molecule. As shown in Fig. 4, β-cyclodextrin heptanoate complex has two binding states, which will be referred to as the UP and DOWN macrostates. In our previous research,15,43 we have studied the binding affinity of this host-guest system by using BEDAM — a free energy method based on replica exchange simulations. In BEDAM simulations, an additional parameter λ is introduced to scale the interaction between the host and the guest molecules from none to full interaction. The features of β-Cyclodextrin heptanoate binding obtained using replica exchange serve as the benchmark for this test case where we employ Stratified-UWHAM to combine and analyze the results of independent (uncoupled) MD simulations at each of the λ Hamiltonian states.
Figure 4.
β-cyclodextrin Heptanoate binding complex. (a) UP macrostate. (b) DOWN macrostate.
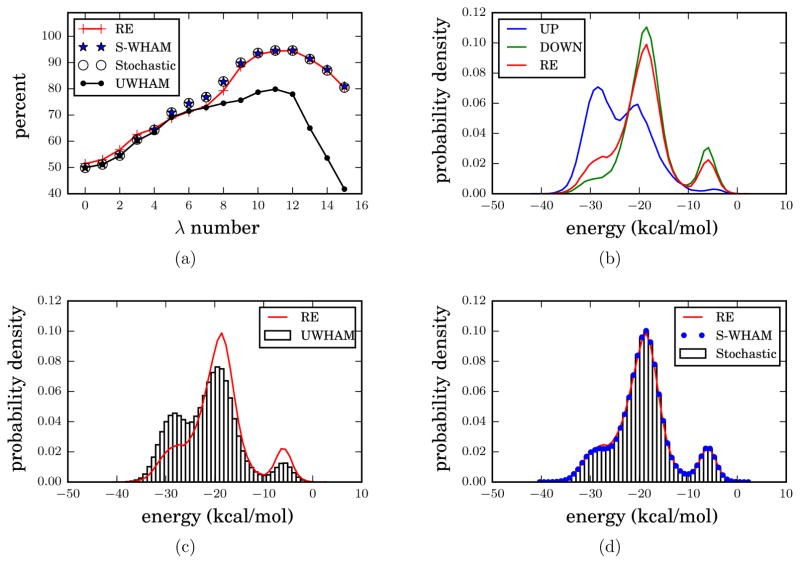
We ran two sets of 72 ns independent MD simulations at 300 K of the β-cyclodextrin Heptanoate complex in implicit solvent (AGBNP GB model48) at 16 λ-states: (0.0, 0.001, 0.002, 0.004, 0.01, 0.04, 0.07, 0.1, 0.2, 0.4, 0.6, 0.7, 0.8, 0.9, 0.95, 1.0). The λ-states are chosen to be the same as those in the previous BEDAM simulations.15,43 At the λ = 0.0 state, there is no interaction between the ligand and the receptor. And the interaction is fully turned on at the λ = 1.0 state. However, there is no replica exchange coupling among different λ-states. We note that simulations which use computational grids typically do not employ replica exchange; this observation serves to motivate example 2. One set of independent simulations was started from the UP macrostate; and the other set was started from the DOWN macrostate. The simulation details of this example can be found in Ref.[15]. At the seven λ-states with the largest λ values, because of the strong interaction between heptanoate and βCD molecules, it is difficult for the binding complex to switch between the UP and DOWN macrostates. During the 72 ns simulations, no transitions between the UP and DOWN macrostates were observed at the λ = 1.0, 0.95, 0.9 states; and only one or two transitions were observed at the λ = 0.8, 0.7, 0.6 states. However, when the interaction between the ligand and the receptor is further reduced (for λ values smaller or equal to 0.2), multiple transitions occurred. See the Supporting Information for the number of transitions between macrostates during each simulation. We applied conventional UWHAM, Stratified-UWHAM and Stratified RE-SWHAM to estimate the population percentage of each macrostate of the β-cyclodextrin Heptanoate complex. To compare the equilibrium conformational ensembles estimated by different analysis methods based on the raw data from the independent simulations at each of the λ-states, we also examined the probability density of the binding energies for each conformational ensemble.
The red line in Fig. 5a shows the equilibrium population percentages of the configurations in the DOWN macrostate at each λ-state as determined from the benchmark replica exchange data set. According to the benchmark, the population percentage of the DOWN macrostate starts from 50% at the λ = 0.0 state, and continues increasing to the highest value 94.5% at the λ = 0.8 state. Then the population percentage of the DOWN macrostate decreases to 80.3% at the λ = 1.0 state. The DOWN macrostate is more favorable at large λ values, this comes from the larger entropy when the carboxylate group of the heptanoate molecule is located in the wide opening of the βCD molecule. Fig. 5b shows the distributions of binding energy of the β-Cyclodextrin Heptanoate complex at the λ = 1.0 state. Although the UP macrostate is less favorable at λ = 1 state, heptanoate and βCD can form more hydrogen bonds, resulting in more favorable (i.e. more negative) binding energy in this macrostate, because of the flexibility of the primary hydroxyls at the narrow opening end of βCD which can interact with the heptanoate carboxylate of the UP macrostate. We combined the data generated at each λ-state from the two sets (UP and DOWN) of independent simulations and applied conventional UWHAM to estimate the population percentage of the DOWN macrostate. The results shown in Fig. 5a exhibit significant differences compared with the benchmark at all the λ-states whose λ value is larger than 0.2. At the λ = 1.0 state, the difference between the benchmark and the conventional UWHAM estimate is as large as 38.6%. Not surprisingly, Fig. 5c shows that the conventional UWHAM estimate (from the 32 independent simulations) of the distribution of the binding energies at the λ = 1.0 state does not agree with the benchmark either. Then we applied Stratified-UWHAM to analyze the data generated by the independent parallel MD simulations (Fig. 5a and Fig. 5d). In this case, the λ-states with the largest seven λ values are considered to be only locally equilibrated, and are split into 14 new λ-states. As can be seen in Fig. 5a and Fig. 5d, the Stratified-UWHAM estimates of the population percentage of the DOWN macrostate at each λ-state and the distribution of the binding energies at the λ = 1.0 state agree with the benchmark very well. And the estimates obtained by the stochastic RE-SWHAM analysis are indistinguishable from the Stratified-UWHAM estimates. In Supporting Information, we list the numerical results and uncertainties of the population percentages of the DOWN macrostate estimated by Stratified-UWHAM, Stratified RE-SWHAM, and the benchmark. We also show the comparisons of the probability density of binding energies estimated by Stratified-UWHAM, Stratified RE-SWHAM, and the benchmark at all λ-states.
Figure 5.
Population percentage of the configurations in the DOWN macrostates and probability density of binding energy at the λ = 1.0 state. The red line is the benchmark — the BEDAM (replica exchange simulation) results. (a) Comparison of the population percentages of the configurations in the DOWN macrostate estimated by Conventional UWHAM, Stratified-UWHAM, Stratified RE-SWHAM (based on the raw data generated by two sets of 72 ns independent MD simulations) and the benchmark. The blue stars are the Stratified-UWHAM estimates when the data at the largest seven λ-states are clustered into UP and DOWN macrostates. The black circles are the Stratified RE-SWHAM estimates; and the black line with dots are the conventional UWHAM estimates when the data at the unconverged λ-states are simply combined as the input of that λ-state. (b) the probability density of binding energy at the λ = 1.0 state obtained by replica exchange simulations. The blue line is the probability density of binding energy of the configurations in the UP macrostate; the green line is the probability density of binding energy of the configurations in the DOWN macrostate; and the red line is the overall probability density of binding energy at the λ = 1.0 state. (c) Comparison of the probability density of binding energy at the λ = 1.0 state estimated by conventional UWHAM to the 32 independent simulations and the benchmark. The bars show the UWHAM estimates. (d) Comparison of the probability density of binding energy at the λ = 1.0 state estimated by Stratified-UWHAM, Stratified RE-SWHAM and benchmark. The blue dots are the Stratified-UWHAM estimates. The bars are the Stratified RE-SWHAM estimates. As can be seen by comparing the four figures, only the Stratified-UWHAM and Stratified RE-SWHAM estimates agree with the benchmark.
3.3 Example 3: Dynamical Path Reweighting
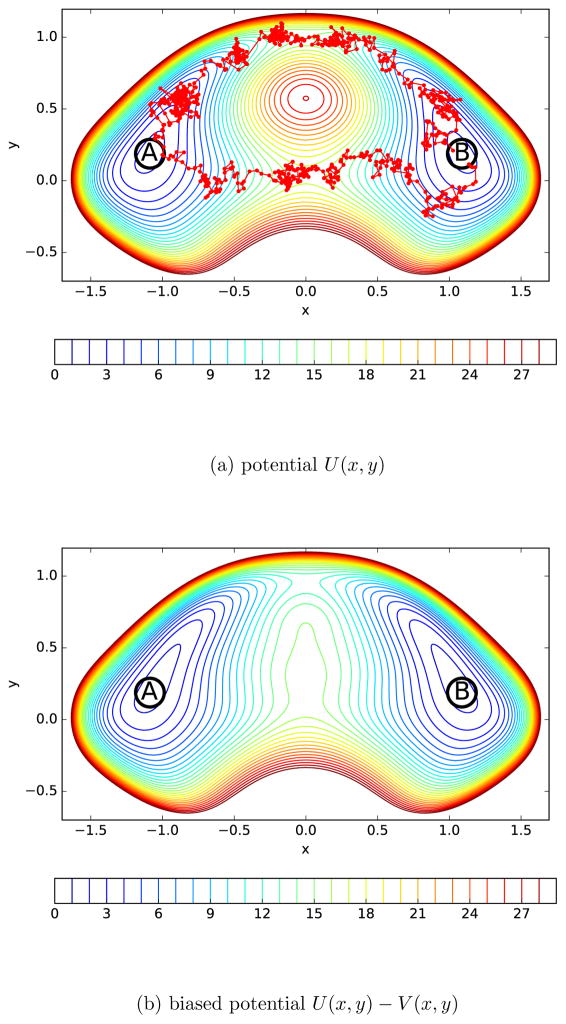
Lastly, we study the trajectories of a Brownian particle moving in a two dimensional double well potential. We apply UWHAM and Stratified-UWHAM to analyze the path ensembles generated by the transition path sampling method at different Hamiltonian states. Inspired by previous research,49,50 the two dimensional potential function is defined via
| (11) |
Fig.(6a) shows the contours of this potential. As can be seen, U(x, y)/kBT is symmetric with respect to a rotation about the y axis. The minimum of U(x, y) equals 1.698 kBT at (x = ±1.087, y = 0.188). To study the transition events between these two free energy basins, we define the region where
Figure 6.
Two dimensional double well potentials. (a) contours of the double well potential U(x, y) defined via Eq.(11). The red trajectories show two paths connecting the reactant (A) and product (B) regions. One goes through the UP channel and the other goes through the DOWN channel. (b) contours of the biased potential U(x, y) − V (x, y), where V (x, y) is defined via Eq.(14).
| (12) |
as the reactant (or A) region and
| (13) |
as the product (or B) region. The barrier between the reactant and product regions has two saddle points on the y axis. The upper saddle point is located at (x = 0.000, y = 1.000), where U(x, y) is 15.033 kBT; and the lower one is located at (x = 0.000, y = 0.039), where U(x, y) is 16.650 kBT. Along the y axis, the maximum potential between these two saddle points is located at (x = 0.000, y = 0.574), where U(x, y) is 27.024 kBT. See the supporting information for the cross-section of U(x, y) at x = 0. The pathways connecting the reactant and product regions are separated into two distinct channels by the peak around (x = 0.000, y = 0.574). To categorize paths according to the positions where they cross the barrier between the reactant and product regions, we examine the intersection points between the path and the y axis (xc = 0, yc). If a path crosses the y axis multiple times, the last intersection point is used. The paths with yc larger than 0.574 are tagged as in the UP channel; and the paths with yc smaller than 0.574 are tagged as in the DOWN channel. In Fig. 6a, we show two transition paths of a Brownian particle connecting the reactant and product regions. One transition path goes through the UP channel and the other goes through the DOWN channel.
The TPS method is applied to sample the path ensembles connecting the reactant and product regions. In TPS simulations, the trial paths are generated by the “shooting” algorithm. 18 As previous researchers found,49,51,52 like any conventional Monte Carlo (MC) simulations, TPS, which is a MC sampling in path space, can be trapped in local minima, namely channels. Possible solutions to this problem include combining the replica exchange algorithm with TPS,51–53 or applying different transition path sampling techniques.49 Notice that the path channels in this example are analogous to the macrostate clusters in the previous two examples. The goal is to estimate the population percentage of the paths in each channel.
Here we show how to overcome the “trapping” problem by running independent parallel TPS at different Hamiltonian states and reweighting paths by Stratified-UWHAM. First we introduce a biasing potential to remove the peak which separates transition paths into channels
| (14) |
In Fig. 6b the contours of the potential U(x, y) − λV (x, y) with λ = 1.0 are plotted. As can be seen, at the λ = 1.0 state the peak around (x = 0, y = 0.574) is removed and the two path channels are merged. See the supporting information for the cross-section of U(x, y) − V (x, y) at x = 0. Then two sets of independent TPS simulations were run at λ = (0.0, 0.2, 0.4, 0.6, 0.8, 1.0) states. The initial paths of the first set of simulations are in the UP channel and the initial paths of the second set are in the DOWN channel. Each TPS simulation generated 5 million paths connecting the reactant and product regions. At the λ = 0.0 state, no transitions of paths between the two channels were observed during the TPS simulations. In other words, at λ = 0.0 state, TPS simulations of paths started in the UP channel remain in the UP channel, while paths started in the DOWN channel remain there. The changes of yc during each TPS simulation are shown in the Supporting Information. Then we applied conventional UWHAM, Stratified-UWHAM and Stratified RE-SWHAM to estimate the probability percentage of the paths in the UP and DOWN channels. One of us (B.W.Z.) has applied the Weighted Ensemble (WE) algorithm to obtain the correct path ensemble for two dimensional potentials like the one shown in Fig. 6.49,50 The WE results are used as the benchmark for this test. The simulation details for Langevin dynamics, TPS and WE can be found in Ref.[54] and [23]
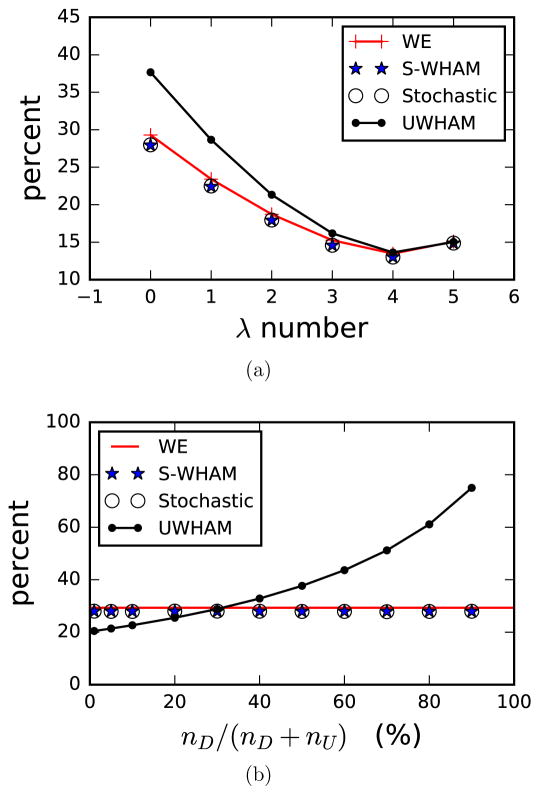
The red line in Fig. 7a shows the population percentages of the paths in the DOWN channel at different λ-states obtained by the WE simulations. At the λ = 0.0 state, the paths in the DOWN channel make up ~ 29.3% of the whole path ensemble. First we simply combined the data generated from the same λ-state and applied the conventional UWHAM to estimate the population percentage of the paths in each channel. It can be seen from Fig. 7a that the conventional UWHAM estimate of the population percentage of the DOWN channel shows significant differences compared with the benchmark at the smaller λ values. The difference is negligible at the λ = 1.0 state but increases to 9% at the λ = 0.0 states. Then we applied the Stratified-UWHAM to analyze the path ensembles. For this case, the λ = 0.0, λ = 0.2 and λ = 0.4 states are considered to be the locally equilibrated λ-states, and each is split into two new λ-states. As can be seen from Fig. 7a, the Stratified-UWHAM estimates of the population percentage of the paths in the DOWN channel at each λ-state agree with the WE results very well. The estimates obtained from the Stratified RE-SWHAM also match the benchmark results. In Supporting Information, we list the numerical results and uncertainties of the population percentages of the paths in the DOWN channel estimated by Stratified-UWHAM, Stratified RE-SWHAM, and the benchmark.
Figure 7.
Population percentage of the paths in the DOWN channel. The red line is the benchmark — the results obtained by weighted ensemble (WE) simulations. The blue stars are the Stratified-UWHAM estimates when the data at the smallest three λ-states are clustered into UP and DOWN states; the black circles are the Stratified RE-SWHAM estimates; and the black line with dots are the conventional UWHAM estimates when the data at the locally equilibrated λ-states are simply combined as the input of that λ-state. (a) Comparison of the population percentages of the paths in the DOWN channel at each λ-state estimated by conventional UWHAM, Stratified-UWHAM, Stratified RE-SWHAM and benchmark when the number of the paths in the UP and DOWN channels in the input path ensembles are equal. (b) Comparison of the population percentages of the paths in the DOWN channel at the λ = 0.0 state estimated by conventional UWHAM, Stratified-UWHAM, Stratified RE-SWHAM and benchmark when the population ratio nD/(nD + nU) changes from 1% to 90%, where nD is the number of paths in the DOWN channel at the λ = 0.0 state in the input path ensemble; and nU is the number of paths in the UP channel at the λ = 0.0 state in the input path ensemble. As can be seen by comparing the two figures, only the Stratified-UWHAM and Stratified RE-SWHAM estimates agree with the benchmark. And the conventional UWHAM estimate for the λ = 0.0 state strongly depends on the population ratio nD/(nD + nU).
When the simulations at the λ-states with a substantial barrier between the paths have not converged, the conventional UWHAM estimates of the probabilities of the UP and DOWN channel paths at these λ-states strongly depend on the number of UP and DOWN channel paths which are input to UWHAM because the conventional UWHAM always assumes the input data ensemble at each λ-state is independently drawn from the distribution described by Eq.(1) or Eq.(31). Therefore the difference between the conventional UWHAM estimates and the true values at the λ = 0.0 state can be much larger than the case that the numbers of paths in the UP and DOWN channels generated at the λ = 0.0 state are equal (as shown in Fig.(Fig. 7a)). To show this effect, we fixed the number of paths in the UP channel at the λ = 0.0 state in the input path ensemble nU but changed the number of paths in the DOWN channel at the λ = 0.0 state in the input path ensemble nD so that the population ratio nD/(nD + nU) ranges from 1% to 90%. Then these input path ensembles with different value of nD/(nD +nU) were fed to the conventional UWHAM, Stratified-UWHAM and Stratified RE-SWHAM to estimate the population percentage of the paths in each channel at the λ = 0.0 state. The results are shown in Fig. 7b. As expected, the conventional UWHAM estimates for the population percentage of the path in the DOWN channel at the λ = 0.0 state strongly depend on the ratio nD/(nD + nU), and changes from 20% to 75% when nD/(nD+nU) changes from 1% to 90% while the benchmark is ~ 29.3%. On the other hand, the Stratified-UWHAM and Stratified RE-SWHAM estimates are independent of the initial condition (i.e. the ratio nD/(nD + nU)), and agree with the benchmark.
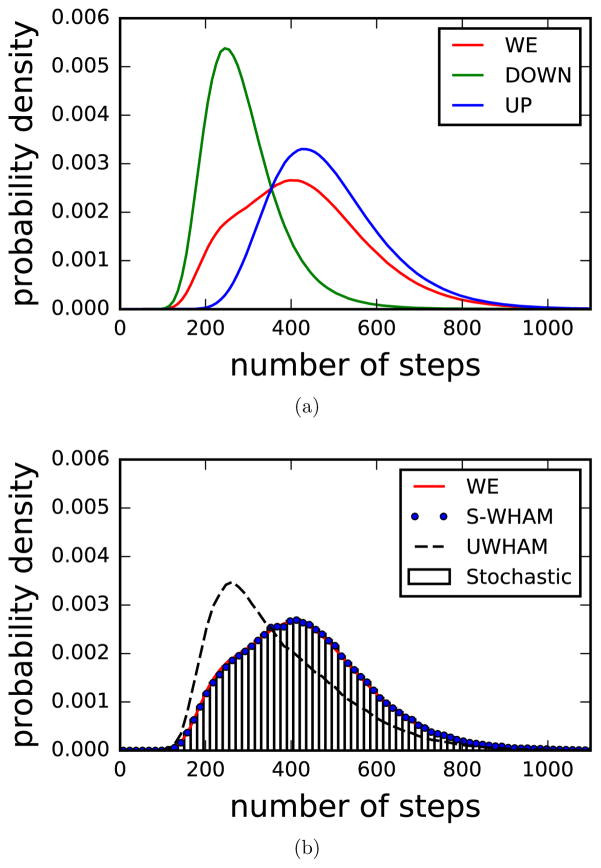
To further compare path ensembles, we also measured the probability density of transition-event durations for each path ensemble. The definition of transition-event durations is the number of Brownian steps between the Brownian particle last leaving the reactant region and first arriving in the product region, namely the path length.54–58 Fig. 8a shows the probability density of transition-event durations of paths in each channel and overall path ensemble at the λ = 0.0 states obtained by WE simulations. As can been seen, although the paths in the DOWN channel are less favorable compared with the paths in the UP channel, their average path length is shorter. This makes sense because if a pathway goes through a steeper barrier, namely a less favorable path channel, the Brownian particle has less freedom to wander along the optimal pathway, which ends in a shorter average path length.54 In Fig. 8b, we compare the probability densities of transition-event durations at the λ = 0.0 state estimated by the conventional UWHAM, Stratified-UWHAM and Stratified RE-SWHAM when the population ratio nD/(nD + nU) is 80%. As can be seen, the conventional UWHAM estimate shows a significant difference compared with the benchmark. However, the Stratified-UWHAM and Stratified RE-SWHAM estimates are indistinguishable and both agree with the benchmark very well, which confirms that both Stratified-UWHAM and Stratified RE-SWHAM correctly estimate the weight of each individual path following Eq.(4). In the supporting information, we show the comparisons of the probability density of transition-event durations estimated by Stratified-UWHAM, Stratified RE-SWHAM and the benchmark at all λ-states when the number of paths in the UP and DOWN channels in the input path ensemble are equal.
Figure 8.
probability densities of transition-event durations at the λ = 0.0 state. (a) the probability density of transition-event durations at the λ = 0.0 state obtained by WE simulations. The blue line is the probability density of transition-event durations of the paths in the UP channel; the green line is the probability density of transition-event durations of the paths in the DOWN channel; and the red line is the overall probability density of transition-event durations at the λ = 0.0 state. (b) Comparison of the probability density of transition-event durations at the λ = 0.0 state estimated by Stratified-UWHAM, Stratified RE-SWHAM and the benchmark when the population ratio nD/(nD + nU) is 80%. The blue dots are the Stratified-UWHAM estimates; the bars are the Stratified RE-SWHAM estimates and the dash line is the conventional UWHAM estimates. The conventional UWHAM estimates show a significant difference compared with the benchmark, while Stratified-UWHAM and Stratified RE-SWHAM estimates agree with the benchmark very well.
3.4 Discussion
Stratified-UWHAM requires that the conformational space be coarse-grained. This can be done based on preliminary simulations or from biophysical knowledge, but a more general and practical method is to partition the conformational space following procedures used to construct Markov States Models. MSMs are a natural choice for the preparation of Stratified-UWHAM for the following reasons: MSMs build up a network which coarse-grains the free energy landscape. The states in the MSM network are defined based on structural (order parameters) and kinetic criteria. Each state in an MSM corresponds to a cluster of conformations that constitute a basin (or collection of basins) in the free energy landscape, and the transition rates between states in an MSM reflect the properties of the corresponding (free) energy barriers. The stratified-UWHAM S1 and S2 groups of λ-states can be determined by the following procedure:
choose a set of λ-states as reference states to build the MSM using prior knowledge and/or run preliminary simulations, choosing for reference, those biased simulations where the relaxation between the slowly equilibrating basins are enhanced.
cluster the data from the other λ-states into MSM states using the same definition of MSMs used in the first step.
identify disconnected macrostates or macrostate clusters based on ergodicity analyses for each λ-state in each of the biased simulations. One macrostate cluster may contain one or many basins;
the biased λ-states whose macrostate clusters are fully connected are assigned to the S1 group; the λ-states which include disconnected macrostate clusters are assigned to the S2 group.
For some problems, the most straightforward applications of the Stratified-UWHAM algorithm will fail when metastable basins merge or separate as the Hamiltonian function and/or thermodynamic parameters of the λ-states change. To account for this it may be necessary to build into the UWHAM stratification procedure more detailed information about the correspondence between basins at different λ-states.
Two maximum likelihood-based methods, the dynamic histogram analysis method (DHAM) and the general transition-based reweighting analysis method (TRAM),59–62 were proposed recently to provide free energy estimates for multi-state simulations when the simulations at some λ-states are only locally equilibrated. As we propose for Stratified-UWHAM, both DHAM and TRAM require building MSMs first for further analyses. In addition to providing estimates of equilibrium distributions, both DHAM and TRAM analysis methods provide estimates of the transition rates between states of the MSMs which are not accessible by the Stratified-UWHAM analysis. Here we comment on the three methods and explain some possible advantages and drawbacks of Stratified-UWHAM for estimating equilibrium populations.
DHAM calculates the estimates of transition rates between states of MSMs first. Then the equilibrium distributions are obtained by solving the eigenvalue equation for the transition matrix. Suppose there are nb states in the MSM, then for the αth λ-state the transition matrix is T(α), where the element represents the probability of the system transitioning from the ith state to the jth state during lag time Δt. The log likelihood function of observing transitions from the ith state to the jth state at the αth λ-state during the simulation is59
| (15) |
DHAM supposes that the transition matrix element at the αth λ-states can be written as , where is a bias factor, Tij is the ijth elements of an unbiased transition matrix T, and is a normalization factor. With this assumption, DHAM maximizes the likelihood function , where L(α) is defined by Eq.(15). Notice that the transition probabilities at different λ-states are coupled by the bias factor. If the bias factors for the transition rates { } are known, DHAM provides better estimates of equilibrium populations than conventional UWHAM for multi-state simulations when the simulations at some λ-states are far from being equilibrated.59 However, the challenge of applying DHAM is that the bias factors { } are usually unknown and may be difficult to construct for arbitrary multi-state simulations. In contrast, the analogous quantities in Stratified-UWHAM — the probabilities of observing a microstate at different λ-states qα(uγi) in Eq.(3) — are more readily obtained from the Hamiltonian and Thermodynamic parameters of the multi-state simulations.
In the TRAM method, the estimates of equilibrium distributions and transition rates of MSMs are calculated simultaneously. The maximum likelihood function of TRAM is a product of the maximum likelihood functions of binless WHAM (population counts) and DHAM (transition counts).62 Unlike Stratified-UWHAM, TRAM stratifies every λ-state into configuration states (macrostates) of MSMs. The local free energy of each configuration state at each λ-state is calculated during each iteration of TRAM analysis: the free energy differences between the same configuration states at different λ-states are calculated in a binless manner; the free energy differences between configuration states at each λ-state are calculated based on the transition counts and the detailed balance condition. Those calculations form multiple thermodynamic cycles like the one shown in Fig. 2b. The optimal and consistent estimates of all the legs in the thermodynamic cycles, namely the free energy differences, and the transition rates are obtained simultaneously by maximizing the likelihood function. In Ref.[62] TRAM was applied to obtain the thermodynamic and kinetic information of a protein-ligand binding complex successfully while the MBAR/UWHAM or WHAM analysis was found to be unfeasible or less efficient.
Stratified-UWHAM and TRAM each have strength and weakness. Stratified-UWHAM is an algorithm that focuses on equilibrium populations, not kinetics. The transition counts observed during the multi-state simulations are not used to estimate the equilibrium distributions. And Stratified-UWHAM does not provide estimates for transition rates although there are methods which can infer transition rates from equilibrium distributions estimated from multicanonical simulations.63–67 When we solve the Stratified-UWHAM equations, the λ-states in the S1 group (fully-connected λ-states) are not split into new λ-states so that the density of states obtained by Stratified-UWHAM is global (or globally normalized). Therefore, the existence of at least one λ-state in the S1 group seems to be essential for applying Stratified-UWHAM. However, it is worth pointing out that this is not a requirement of Stratified-UWHAM. Suppose there is a system which has three macrostates. The simulations at one λ-state are approximately equilibrated between the first and the second macrostates; and the simulations at another λ-state are approximately equilibrated between the second and the third macrostates. If the sampled phase space of the second macrostate at these two λ-states are well overlapped,68,69 these two λ-states together are equivalent to one approximately globally equilibrated λ-state. For such cases, either Stratified-UWHAM or Stratified RE-SWHAM can be used to obtain the global density of states. A practical criterion to validate the application of Stratified-UWHAM is that if Stratified RE-SWHAM is used to analyze the raw data, each replica shall have resampled every macrostate of every λ-state during the analysis. In other words, in Stratified RE-SWHAM, which is a multicanonical resampling analysis analogous to multicanonical simulations such as replica exchange, all the macrostates need to be fully-connected when the data at all λ-states are combined in order to produce converged results.
On the other hand, as the name implies, TRAM is a transition-based reweighting analysis method. Because TRAM stratifies every λ-state, it does not depend on the population ratios of different states of the MSM at each λ-state, but approximately converged transition counts connecting states at each λ-state are essential for TRAM to obtain the global density of states. Note that unconverged transition counts can pollute the TRAM estimates, as unconverged population counts pollute the conventional UWHAM estimates as described previously in Sec.3. Because each transition matrix element at each λ-state is an unknown parameter to be determined by the maximum likelihood algorithm, TRAM has thousands more variables to solve than Stratified-UWHAM. Further work on TRAM and Stratified-UWHAM may benefit from the development of a “population-plus-transition-based” reweighting algorithm which inherits the strengths of both methods.
4 Conclusion
We have developed a new analysis tool called Stratified-UWHAM to compute the density of states and free energies for data ensembles generated by multi-state simulations when a subset of the simulations are only locally equilibrated, macrostate clusters may be disconnected at some λ-states, and their population estimates are far from equilibrium. To remove the computational bottleneck of Stratified-UWHAM, we developed a stochastic solver for the Stratified-UWHAM equations by extending the RE-SWHAM algorithm. As has been shown above, the Stratified-UWHAM equations can be solved in the form of UWHAM equations with an expanded set of λ-states; and the Stratified-UWHAM equations can be solved stochastically in the form of the original RE-SWHAM with a simple restraint introduced in the move procedure.
Stratified-UWHAM and Stratified RE-SWHAM have been applied to three model systems. First, we constructed the free energy surfaces of an alanine dipeptide molecule in vacuum by analyzing the data generated by two independent MD simulations of AlaD in vacuum starting from different macrostate clusters and the known equilibrium distributions of AlaD in implicit solvent which can be computed rapidly. Compared with Stratified-UWHAM and Stratified RE-SWHAM, the conventional UWHAM requires much longer MD simulations to produce estimates matching the benchmark within statistical error. Second, we studied the binding affinity of the β-cyclodextrin Heptanoate complex by running two set of independent MD simulations starting from different macrostates at 16 λ-states. Since the barrier between the “UP” and “DOWN” macrostates of this system is “infinitely” high at some λ-states, conventional UWHAM failed to estimate the equilibrium distribution at those λ-states correctly. However, the Stratified-UWHAM and Stratified RE-SWHAM estimates agree with the benchmark replica exchange simulation results very well. In the third example, we showed how to overcome the “trapping” problem of the transition path sampling algorithm by running TPS in a two dimensional double well potential at multiple λ-states independently and using Stratified-UWHAM and Stratified RE-SWHAM to analyze the path ensemble. As far as we know, this is the first time the Onsager-Machlup action-based path sampling algorithm has been combined with a UWHAM type analysis tool to study kinetics.
Stratified-UWHAM requires that the conformational space be coarse-grained. For the three examples we discussed above, the coarse-graining was done based on our preliminary knowledge about the system. For an arbitrary problem, we proposed that one can partition the conformational space using Markov States Models and suggested a procedure to identify locally equilibrated λ-states and macrostate clusters. Features of Stratified-UWHAM were compared with DHAM and TRAM. Compared with TRAM and DHAM, one drawback of the current version of Stratified-UWHAM is the requirement of manually determining locally equilibrated λ-states and macrostate clusters for each λ-state. However, this is necessary in order to avoid feeding UWHAM biased information which can pollute the estimates of the density of states. Algorithms to combine states of MSMs into macrostates and identify disconnected macrostate clusters based on raw simulation data can be automated.25 We proposed a criterion to validate the application of Stratified-UWHAM: if Stratified RE-SWHAM is used to analyze the raw data, each replica shall have resampled every macrostate of every λ-state during the analysis. Unlike DHAM or TRAM, Stratified-UWHAM does not require the bias factors for transition rates at different λ-states or approximately converged transition counts between states of MSMs to obtain equilibrium distributions. Last but not least, the stochastic version of Stratified-UWHAM, Stratified RE-SWHAM, provides a practical analysis tool for multi-state simulations on massive computational grids.14
Supplementary Material
Acknowledgments
This work was supported by NIH grant (GM30580), NSF grant (1665032) and by an NIH computer equipment grant OD020095. This work also used Extreme Science and Engineering Discovery Environment (XSEDE), which is supported by National Science Foundation (ACI-1053575).
Appendices
A Stratified RE-SWHAM
Stratified RE-SWHAM is a resampling technique we developed to solve the Stratified-UWHAM equations stochastically by using the replica exchange simulation protocol (See Fig. 1). Like RE simulations, at the end of each cycle, the observation associated with each replica is recorded as the output of Stratified RE-SWHAM. Here we use the alanine dipeptide problem as an example to show that the output of Stratified RE-SWHAM for a λ-state in the S2 set which contains disconnected macrostate clusters is the estimate of the equilibrium distribution of that λ-state. Therefore, the splits of locally equilibrated λ-states are not necessary.
In the AlaD problem, the implicit solvent state (I state) is a fully-connected λ-state; the vacuum state (V state) is a locally equilibrated λ-state with two disconnected macrostate clusters. Suppose the replica at the V state is resampling the observations of the A macrostate cluster by the move procedure. During Stratified RE-SWHAM, to switch the replica at the V state to resample the observations of the B macrostate cluster requires (i) the other replica at the I state is associated with an observation in the B macrostate cluster, (ii) an exchange attempt of these two replicas is accepted. Therefore the probability of switching the replica at the V state from resampling the A macrostate cluster to resampling the B macrostate cluster is
| (16) |
where is the probability that the observation associated with the replica at the I state belongs to the B macrostate cluster. and the potential energies of an observation of the “X” macrostate cluster at the V state and the I state respectively. Notice they are the energy values of the same microstate at different λ-states, and suppose the energies are in units of kBT. Ψ is the Metropolis function to determine the acceptance ratio70
| (17) |
The angle brackets and subscript V (A)I(B) represents the ensemble average when the observation associated with the replica at the V state belongs to the A macrostate cluster and the observation associated with the replica at the I state belongs to the B macrostate cluster.
Similarly, if the replica at the V state is resampling the B macrostate cluster, the probability of switching the replica to resample the A macrostate cluster is
| (18) |
Because of the requirement of detailed balance, the forward and backward currents of a replica moving between the A and B macrostate clusters at the V state are equal, which yields
| (19) |
where is the probability that the observation associated with the replica at the V state belongs to the “X” macrostate cluster.
The Metropolis exchange criterion in the Stratified RE-SWHAM analyses satisfies
| (20) |
Integrating the equation over the configuration space leads to
| (21) |
where is the canonical configurational integral of the “X” macrostate cluster at the “Y” λ-state,
| (22) |
Eq.[21] can be rewritten as
| (23) |
Namely, the log ratio of the acceptance probability over provides the estimate of the free energy difference between the two vertical legs in Fig. 2b.
Combining Eq.(19) and (23) yields
| (24) |
Eq[24] shows the ratio of over provides the estimate of the upper leg in Fig. 2b. Because at the end of each cycle, the observation associated with the replica at the V state is recorded as the output of Stratified RE-SWHAM at the V state (see Fig. 1), ( ) equals the population ratio of the A macrostate cluster over the B macrostate cluster in the output of the V state. In other words, the output of Stratified RE-SWHAM at the V state is the estimate of the equilibrium distribution of the V state.
There is another subtle difference between RE-SWHAM with an expanded set of λ-states and Stratified RE-SWHAM. During the analysis of RE-SWHAM with an expanded set of λ-states, an observation in a macrostate cluster of a locally equilibrated λ-state can possibly be exchanged only with an observation in the same macrostate cluster at another λ-state because of the infinite barrier covering the outside of that macrostate cluster at the corresponding expanded λ-state. Therefore, the number of observations in a macrostate cluster of a locally equilibrated λ-state stays as a constant. During the analysis of Stratified RE-SWHAM, because an observation in a macrostate cluster of a locally equilibrated λ-state is allowed to be exchanged with any observation at another λ-state if the exchange attempt is accepted (see Fig. 1), the number of observations in a macrostate cluster of a locally equilibrated λ-state fluctuates by ±1. However, if the total number of observations in each macrostate cluster at each λ-state is large, such fluctuations become negligible.
B Onsager-Machlup Action-based Path Ensemble
In Sec.3.3, we apply Stratified-UWHAM to analyze the path ensembles of a Brownian particle moving in a two dimensional double well potential. The stochastic dynamics of the Brownian particle in this two dimensional space is governed by the overdamped Langevin equation
| (25) |
where Fx and Fy are the forces acting on the particle; γ is the friction constant; and Rx(t) and Ry(t) are the thermal noise taken from Gaussian functions with zero mean and correlation
| (26) |
D = kBT/γ in Eq.(26) is the diffusion constant.
Given the two-dimensional potential U(x, y), the probability of a (N − 1)-steps path connecting the reactant region and the product region is
| (27) |
p(xi, xi+1; U) and p(yi, yi+1; U) in Eq.(27) are the single-step transition probabilities
| (28) |
where
| (29) |
and Δt is the time interval of a single step. By combining Eq.(27) and Eq.(28), the probability of a path can be written as a single exponential function
| (30) |
where A[x(t), y(t), U(x, y)] is called the Onsager-Machlup action “functional”.71 Compared with the probability of a microstate of a mechanical system governed by the canonical ensemble, the action functional of a path is analogous to the potential energy of a microstate. With this understanding, many enhanced sampling methods and analysis tools which have been developed to explore the conformational space such as replica exchange and UWHAM, can be applied straightforwardly to the transition path space.53,72,73 The transition path sampling (TPS) method is a MC simulation in the path space to draw pathway according to the distribution
| (31) |
where Zα is the normalizing constant (analogous to the partition function of a canonical ensemble) of the αth λ-state.17,18
Footnotes
Supporting Information Available
Simulation details of AlaD in vacuum and in implicit solvent. Convergence of Stratified-UWHAM estimates of the free energy difference between the A and B macrostate clusters of AlaD in vacuum. Orientation of heptanoate in each independent MD simulation. Population percentages of the DOWN macrostate of the β-cyclodextrin heptanoate complex at each λ-state estimated by Stratified-UWHAM, Stratified RE-SWHAM and RE simulations. Probability density of binding energies of the β-cyclodextrin Heptanoate complex at each λ-state estimated by Stratified-UWHAM, Stratified RE-SWHAM and RE simulations. Cross-section of the potential function (U(x, y) − λV (x, y)) at x = 0. Change of the intersection point (xc = 0, yc) in each TPS simulation. Population percentages of the paths in the DOWN channel estimated by Stratified-UWHAM, Stratified RE-SWHAM and WE simulations. Probability density of transition-event durations at each λ-state estimated by Stratified-UWHAM, Stratified RE-SWHAM and WE simulations. This material is available free of charge via the Internet at http://pubs.acs.org/.
References
- 1.Zwier MC, Chong LT. Reaching Biological Timescales with All-Atom Molecular Dynamics Simulations. Curr Opin Pharmacol. 2010;10:745–752. doi: 10.1016/j.coph.2010.09.008. [DOI] [PubMed] [Google Scholar]
- 2.Zuckerman DM. Equilibrium Sampling in Biomolecular Simulations. Annu Rev Bio-phys. 2011;40:41–62. doi: 10.1146/annurev-biophys-042910-155255. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Makarov DE. Single Molecule Science: Physical Principles and Models. Chapter 5. CRC Press; Boca Raton, Florida: 2015. p. 59. [Google Scholar]
- 4.Dai W, Sengupta AM, Levy RM. First Passage Times, Lifetimes, and Relaxation Times of Unfolded Proteins. Phys Rev Lett. 2015;115:048101. doi: 10.1103/PhysRevLett.115.048101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Shirts M, Pande VS. COMPUTING: Screen Savers of the World Unite! Science. 2000;290:1903–1904. doi: 10.1126/science.290.5498.1903. [DOI] [PubMed] [Google Scholar]
- 6.Anderson JA, Lorenz CD, Travesset A. General Purpose Molecular Dynamics Simulations Fully Implemented on Graphics Processing Units. J Comput Phys. 2008;227:5342–5359. [Google Scholar]
- 7.Lindorff-Larsen K, Piana S, Dror RO, Shaw DE. How Fast-Folding Proteins Fold. Science. 2011;334:517–520. doi: 10.1126/science.1208351. [DOI] [PubMed] [Google Scholar]
- 8.Torrie GM, Valleau JP. Nonphysical Sampling Distributions in Monte Carlo Free-Energy Estimation: Umbrella Sampling. J Comput Phys. 1977;23:187–199. [Google Scholar]
- 9.Northrup SH, Pear MR, Lee CY, McCammon JA, Karplus M. Dynamical Theory of Activated Processes in Globular Proteins. Proc Natl Acad Sci U S A. 1982;79:4035–4039. doi: 10.1073/pnas.79.13.4035. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Dickson A, Dinner AR. Enhanced Sampling of Nonequilibrium Steady States. Annu Rev Phys Chem. 2010;61:441–459. doi: 10.1146/annurev.physchem.012809.103433. [DOI] [PubMed] [Google Scholar]
- 11.Swendsen RH, Wang JS. Replica Monte Carlo Simulation of Spin-Glasses. Phys Rev Lett. 1986;57:2607–2609. doi: 10.1103/PhysRevLett.57.2607. [DOI] [PubMed] [Google Scholar]
- 12.Sugita Y, Okamoto Y. Replica-Exchange Molecular Dynamics Method for Protein Folding. Chem Phys Lett. 1999;314:141–151. [Google Scholar]
- 13.Zheng W, Andrec M, Gallicchio E, Levy RM. Simulating Replica Exchange Simulations of Protein Folding with a Kinetic Network Model. Proc Natl Acad Sci U S A. 2007;104:15340–15345. doi: 10.1073/pnas.0704418104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Xia J, Flynn WF, Gallicchio E, Zhang BW, He P, Tan Z, Levy RM. Large-Scale Asynchronous and Distributed Multidimensional Replica Exchange Molecular Simulations and Efficiency Analysis. J Comput Chem. 2015;36:1772–1785. doi: 10.1002/jcc.23996. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Zhang BW, Dai W, Gallicchio E, He P, Xia J, Tan Z, Levy RM. Simulating Replica Exchange: Markov State Models, Proposal Schemes, and the Infinite Swapping Limit. J Phys Chem B. 2016;120:8289–8301. doi: 10.1021/acs.jpcb.6b02015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Yu TQ, Lu J, Abrams CF, Vanden-Eijnden E. Multiscale Implementation of Infinite-Swap Replica Exchange Molecular Dynamics. Proc Natl Acad Sci U S A. 2016;42:11744–11749. doi: 10.1073/pnas.1605089113. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Pratt LR. A Statistical Method for Identifying Transition States in High Dimensional Problems. J Chem Phys. 1986;85:5045–5048. [Google Scholar]
- 18.Dellago C, Bolhuis PG, Chandler D. Efficient Transition Path Sampling: Application to Lennard-Jones Cluster Rearrangements. J Chem Phys. 1998;108:9236–9245. [Google Scholar]
- 19.Wang F, Landau D. Efficient, Multiple-Range Random Walk Algorithm to Calculate the Density of States. Phys Rev Lett. 2001;86:2050–2053. doi: 10.1103/PhysRevLett.86.2050. [DOI] [PubMed] [Google Scholar]
- 20.EW, Ren W, Vanden-Eijnden E. String Method for the Study of Rare Events. Phys Rev B. 2002;66:052301. doi: 10.1021/jp0455430. [DOI] [PubMed] [Google Scholar]
- 21.Laio A, Parrinello M. Escaping Free-Energy Minima. Proc Natl Acad Sci U S A. 2002;99:12562–12566. doi: 10.1073/pnas.202427399. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Liu P, Kim B, Friesner RA, Berne BJ. Replica Exchange with Solute Tempering: a Method for Sampling Biological Systems in Explicit Water. Proc Natl Acad Sci U S A. 2005;102:13749–13754. doi: 10.1073/pnas.0506346102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Zhang BW, Jasnow D, Zuckerman DM. Efficient and Verified Simulation of a Path Ensemble for Conformational Change in a United-Residue Model of Calmodulin. Proc Natl Acad Sci U S A. 2007;104:18043–18048. doi: 10.1073/pnas.0706349104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Zheng L, Chen M, Yang W. Random Walk in Orthogonal Space to Achieve Efficient Free-Energy Simulation of Complex Systems. Proc Natl Acad Sci U S A. 2008;105:20227–20232. doi: 10.1073/pnas.0810631106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Gregory R, Bowman FN, Pande VS, editors. An Introduction to Markov State Models and Their Application to Long Timescale Molecular Simulation (Advances in Experimental Medicine and Biology) Springer; Dordrecht Heidelberg New York London: 2013. [Google Scholar]
- 26.Ferrenberg A, Swendsen R. Optimized Monte Carlo Data Analysis. Phys Rev Lett. 1989;63:1195–1198. doi: 10.1103/PhysRevLett.63.1195. [DOI] [PubMed] [Google Scholar]
- 27.Kumar S, Rosenberg JM, Bouzida D, Swendsen RH, Kollman PA. The Weighted Histogram Analysis Method for Free-Energy Calculations on Biomolecules. I. The Method. J Comput Chem. 1992;13:1011–1021. [Google Scholar]
- 28.Kumar S, Rosenberg JM, Bouzida D, Swendsen RH, Kollman PA. Multidimensional Free-Energy Calculations Using the Weighted Histogram Analysis Method. J Comput Chem. 1995;16:1339–1350. [Google Scholar]
- 29.Roux B. The Calculation of the Potential of Mean Force Using Computer-simulations. Comput Phys Commun. 1995;91:275–282. [Google Scholar]
- 30.Bartels C, Karplus M. Multidimensional Adaptive Umbrella Sampling: Applications to Main Chain and Side Chain Peptide Conformations. J Comput Chem. 1997;18:1450–1462. [Google Scholar]
- 31.Tan Z. On a Likelihood Approach for Monte Carlo Integration. J Am Stat Assoc. 2004;99:1027–1036. [Google Scholar]
- 32.Gallicchio E, Andrec M, Felts AK, Levy RM. Temperature Weighted Histogram Analysis Method, Replica Exchange, and Transition Paths. J Phys Chem B. 2005;109:6722–6731. doi: 10.1021/jp045294f. [DOI] [PubMed] [Google Scholar]
- 33.Chodera JD, Swope WC, Pitera JW, Seok C, Dill KA. Use of the Weighted Histogram Analysis Method for the Analysis of Simulated and Parallel Tempering Simulations. J Chem Theory Comput. 2007;3:26–41. doi: 10.1021/ct0502864. [DOI] [PubMed] [Google Scholar]
- 34.Shirts MR, Chodera JD. Statistically Optimal Analysis of Samples from Multiple Equilibrium States. J Chem Phys. 2008;129:124105. doi: 10.1063/1.2978177. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Kim J, Keyes T, Straub JE. Communication: Iteration-Free, Weighted Histogram Analysis Method in Terms of Intensive Variables. J Chem Phys. 2011;135:061103. doi: 10.1063/1.3626150. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Tan Z, Gallicchio E, Lapelosa M, Levy RM. Theory of Binless Multi-State Free Energy Estimation with Applications to Protein-Ligand Binding. J Chem Phys. 2012;136:144102. doi: 10.1063/1.3701175. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Zhu F, Hummer G. Convergence and Error Estimation in Free Energy Calculations Using the Weighted Histogram Analysis Method. J Comput Chem. 2012;33:453–465. doi: 10.1002/jcc.21989. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Law SM, Ahlstrom LS, Panahi A, Brooks CL., III Hamiltonian Mapping Revisited: Calibrating Minimalist Models to Capture Molecular Recognition by Intrinsically Disordered Proteins. J Phys Chem Lett. 2014;5:3441–3444. doi: 10.1021/jz501811k. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Meng Y, Roux B. Efficient Determination of Free Energy Landscapes in Multiple Dimensions from Biased Umbrella Sampling Simulations Using Linear Regression. J Chem Theory Comput. 2015;11:3523–3529. doi: 10.1021/ct501130r. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Zhang C, Lai CL, Pettitt BM. Accelerating the Weighted Histogram Analysis Method by Direct Inversion in the Iterative Subspace. Mol Simul. 2016;42:1079–1089. doi: 10.1080/08927022.2015.1110583. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Thiede EH, Koten BV, Weare J, Dinner AR. Eigenvector Method for Umbrella Sampling Enables Error Analysis. J Chem Phys. 2016;145:084115. doi: 10.1063/1.4960649. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Ding X, Vilseck JZ, Hayes RL, Brooks CL., III Gibbs Sampler-Based λ-Dynamics and Rao-Blackwell Estimator for Alchemical Free Energy Calculation. J Chem Theory Comput. 2017;13:2501–2510. doi: 10.1021/acs.jctc.7b00204. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Zhang BW, Xia J, Tan Z, Levy RM. A Stochastic Solution to the Unbinned WHAM Equations. J Phys Chem Lett. 2015;6:3834–3840. doi: 10.1021/acs.jpclett.5b01771. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Tan Z, Xia J, Zhang BW, Levy RM. Locally Weighted Histogram Analysis and Stochastic Solution for Large-Scale Multi-State Free Energy Estimation. J Chem Phys. 2016;144:034107. doi: 10.1063/1.4939768. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Onufriev A, Bashford D, Case DA. Exploring Protein Native States and Large-Scale Conformational Changes with a Modified Generalized Born Model. Proteins: Struct, Funct Bioinf. 2004;55:383–394. doi: 10.1002/prot.20033. [DOI] [PubMed] [Google Scholar]
- 46.Abraham MJ, Murtola T, Schulz R, Páll S, Smith JC, Hess B, Lindahl E. GROMACS: High Performance Molecular Simulations through Multi-Level Parallelism from Laptops to Supercomputers. SoftwareX. 2015;1–2:19–25. [Google Scholar]
- 47.Deng N, Zhang BW, Levy RM. Connecting Free Energy Surfaces in Implicit and Explicit Solvent: An Efficient Method To Compute Conformational and Solvation Free Energies. J Chem Theory Comput. 2015;11:2868–2878. doi: 10.1021/acs.jctc.5b00264. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Gallicchio E, Levy RM. AGBNP: An Analytic Implicit Solvent Model Suitable for Molecular Dynamics Simulations and High-Resolution Modeling. J Comput Chem. 2004;25:479–499. doi: 10.1002/jcc.10400. [DOI] [PubMed] [Google Scholar]
- 49.Zhang BW, Jasnow D, Zuckerman DM. Weighted Ensemble Path Sampling for Multiple Reaction Channels. 2009 arXiv:0902.2772v1. [Google Scholar]
- 50.Zhang BW, Jasnow D, Zuckerman DM. The “Weighted Ensemble” Path Sampling Method is Statistically Exact for a Broad Class of Stochastic Processes and Binning Procedures. J Chem Phys. 2010;132:054107. doi: 10.1063/1.3306345. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Bolhuis PG. Rare Events via Multiple Reaction Channels Sampled by Path Replica Exchange. J Chem Phys. 2008;129:114108. doi: 10.1063/1.2976011. [DOI] [PubMed] [Google Scholar]
- 52.Fujisaki H, Shiga M, Kidera A. Onsager-Machlup Action-Based Path Sampling and Its Combination with Replica Exchange for Diffusive and Multiple Pathways. J Chem Phys. 2010;132:134101. doi: 10.1063/1.3372802. [DOI] [PubMed] [Google Scholar]
- 53.Vlugt TJH, Smit B. On the Efficient Sampling of Pathways in the Transition Path Ensemble. Phys Chem Comm. 2001;4:11. [Google Scholar]
- 54.Zhang BW, Jasnow D, Zuckerman DM. Transition-Event Durations in One-Dimensional Activated Processes. J Chem Phys. 2007;126:074504. doi: 10.1063/1.2434966. [DOI] [PubMed] [Google Scholar]
- 55.Chaudhury S, Makarov DE. A Harmonic Transition State Approximation for the Duration of Reactive Events in Complex Molecular Rearrangements. J Chem Phys. 2010;133:034118. doi: 10.1063/1.3459058. [DOI] [PubMed] [Google Scholar]
- 56.Hawk AT, Konda SSM, Makarov DE. Computation of Transit Times Using the Milestoning Method with Applications to Polymer Translocation. J Chem Phys. 2013;139:064101. doi: 10.1063/1.4817200. [DOI] [PubMed] [Google Scholar]
- 57.Makarov DE. Computational and Theoretical Insights into Protein and Peptide Translocation. Protein Pept Lett. 2014;21:217–226. doi: 10.2174/09298665113209990073. [DOI] [PubMed] [Google Scholar]
- 58.Pollak E. Transition Path Time Distribution and the Transition Path Free Energy Barrier. Phys Chem Chem Phys. 2016;18:28872–28882. doi: 10.1039/c6cp05052b. [DOI] [PubMed] [Google Scholar]
- 59.Rosta E, Hummer G. Free Energies from Dynamic Weighted Histogram Analysis Using Unbiased Markov State Model. J Chem Theory Comput. 2015;11:276–285. doi: 10.1021/ct500719p. [DOI] [PubMed] [Google Scholar]
- 60.Mey ASJS, Wu H, Noé F. xTRAM: Estimating Equilibrium Expectations from Time-Correlated Simulation Data at Multiple Thermodynamic States. Phys Rev X. 2014;4:041018. [Google Scholar]
- 61.Wu H, Mey ASJS, Rosta E, Noé F. Statistically Optimal Analysis of State-Discretized Trajectory Data from Multiple Thermodynamic States. J Chem Phys. 2014;141:214106. doi: 10.1063/1.4902240. [DOI] [PubMed] [Google Scholar]
- 62.Wu H, Paul F, Wehmeyer C, Noé F. Multiensemble Markov Models of Molecular Thermodynamics and Kinetics. Proc Natl Acad Sci U S A. 2016;113:3221–3230. doi: 10.1073/pnas.1525092113. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Zheng W, Gallicchio E, Deng N, Andrec M, Levy RM. Kinetic Network Study of the Diversity and Temperature Dependence of Trp-Cage Folding Pathways: Combining Transition Path Theory with Stochastic Simulations. J Phys Chem B. 2011;115:1512–1523. doi: 10.1021/jp1089596. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Deng N, Zheng W, Gallicchio E, Levy RM. Insights into the Dynamics of HIV-1 Protease: A Kinetic Network Model Constructed from Atomistic Simulations. J Am Chem Soc. 2011;133:9387–9394. doi: 10.1021/ja2008032. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65.Han W, Schulten K. Fibril Elongation by Aβ17-42: Kinetic Network Analysis of Hybrid-Resolution Molecular Dynamics Simulations. J Am Chem Soc. 2014;136:12450–12460. doi: 10.1021/ja507002p. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66.Dixit PD, Dill KA. Inferring Microscopic Kinetic Rates from Stationary State Distributions. J Chem Theory Comput. 2014;10:3002–3005. doi: 10.1021/ct5001389. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67.Dixit PD, Jain A, Stock G, Dill KA. Inferring Transition Rates of Networks from Populations in Continuous-Time Markov Processes. J Chem Theory Comput. 2015;11:5464–5472. doi: 10.1021/acs.jctc.5b00537. [DOI] [PubMed] [Google Scholar]
- 68.Wu D, Kofke DA. Phase-Space Overlap Measures. I. Fail-Safe Bias Detection in Free Energies Calculated by Molecular Simulation. J Chem Phys. 2005;123:054103. doi: 10.1063/1.1992483. [DOI] [PubMed] [Google Scholar]
- 69.Wu D, Kofke DA. Phase-Space Overlap Measures. II. Design and Implementation of Staging Methods for Free-Energy Calculations. J Chem Phys. 2005;123:084109. doi: 10.1063/1.2011391. [DOI] [PubMed] [Google Scholar]
- 70.Bennett CH. Efficient Estimation of Free Energy Differences from Monte Carlo Data. J Comput Phys. 1976;22:245–268. [Google Scholar]
- 71.Wiegel F. Introduction to Path-integral Methods in Physics and Polymer Science. World Scientific Publishing Co Pre Ltd; Singapore Philadelphia: 1986. [Google Scholar]
- 72.Minh DDL, Chodera JD. Optimal Estimators and Asymptotic Variances for Nonequilibrium Path-Ensemble Averages. J Chem Phys. 2009;131:134110. doi: 10.1063/1.3242285. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 73.Chodera JD, Swope WC, Noé F, Prinz JH, Shirts MR, Pande VS. Dynamical Reweighting: Improved Estimates of Dynamical Properties from Simulations at Multiple Temperatures. J Chem Phys. 2011;134:244107. doi: 10.1063/1.3592152. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.