Effects of Hollow Fiber Membrane Oscillation on an Artificial Lung

Abstract

Gas transfer through hollow fiber membranes (HFM) can be increased via fiber oscillation. Prior work, however, does not directly translate to present-day, full-scale artificial lungs. This in vitro study characterized the effects of HFM oscillations on oxygenation and hemolysis for a pediatric-sized HFM bundle. Effects of oscillation stroke length (2–10 mm) and frequency (1–25 Hz) on oxygen transfer were measured according to established standards. The normalized index of hemolysis was measured for select conditions. All measurements were performed at a 2.5 L min⁻¹ blood flow rate. A lumped parameter model was used to predict oscillation-induced blood flow and elucidate the effects of system parameters on oxygenation. Oxygen transfer increased during oscillations, reaching a maximum oxygenation efficiency of 510 mL min⁻¹ m⁻² (97% enhancement relative to no oscillation). Enhancement magnitudes matched well with model-predicted trends and were dependent on stroke length, frequency, and physical system parameters. A 40% oxygenation enhancement was achieved without significant hemolysis increase. At a constant enhancement magnitude, a larger oscillation frequency resulted in increased hemolysis. In conclusion, HFM oscillation is a feasible approach to increasing artificial lung gas transfer efficiency. The optimal design for maximizing efficiency at small fiber displacements should minimize bundle resistance and housing compliance.

INTRODUCTION

Current artificial lungs are primarily intended to provide respiratory support to lung failure patients as a bridge to lung recovery or transplantation.⁴ These devices use cylindrical (diameter of 200–400 μm) hollow fiber membranes (HFM) as the functional units to achieve gas exchange in blood. During use, sweep gas (typically oxygen) flows through the fiber lumen while blood flows over the fiber exterior. Oxygen and carbon dioxide transfer is achieved via diffusion of each gas through the microporous fiber wall along its respective concentration gradient. Full-scale devices incorporate thousands of fibers into a bundle with a total membrane surface area capable of the desired rate of gas transfer. Thus, the size of the HFM bundle for a given application is determined by the efficiency of the gas transfer process (i.e., gas transfer per unit membrane surface area). Since the HFM bundle typically represents the largest component of an artificial lung, a higher gas transfer efficiency enables a smaller overall device. Minimizing the size of artificial lungs is important because it more easily allows patients to ambulate while on support. Active rehabilitation during respiratory support can improve patient outcomes^14,17 but is difficult to enact due to the large and cumbersome nature of currently available devices. A reduction in the blood-contacting surface area of the device should also decrease the likelihood of adverse events related to clotting or infection. Thus, increased gas exchange efficiency is vital for the development of a more compact artificial lung capable of improved treatment.

The gas transfer efficiency of artificial lungs is limited by the blood-side mass transfer resistance. More specifically, the primary resistance for gas diffusing between the hollow fiber lumen and extraluminar flowing blood is that associated with the diffusional boundary layer at the blood-side HFM surface.^4,9 Blood velocities are reduced within the boundary layer due to viscous drag forces and thus gas transport within this region is primarily via diffusion. The blood-side gas transfer resistance is proportional to the thickness of the boundary layer.⁴ Both active and passive approaches have been taken towards mitigating the effects of the boundary layer on gas transfer resistance. Passive approaches involve modifications to the bundle geometry or HFM surface to utilize the energy of the flowing blood to increase mean flow velocities or induce secondary flows.⁹ Active approaches involve the application of external energy to the system to create additional relative motion between the blood and HFM surface.⁹

One previously proposed method for active boundary layer disruption is oscillatory movement of the HFM. In addition to increasing gas transfer efficiency, this approach has been noted for the potential added benefit of reducing intra-bundle fouling and clot formation.^9,12,13 The success of this approach was demonstrated as early as the 1970s when enhanced gas transfer was observed for torsional oscillations of a toroidal silicone membrane oxygenator.^1,2 Similarly, Krantz et al investigated the effect of axial oscillations of hollow silicone tubes (1.47-mm tube inner diameter, 0.25-mm wall thickness) on oxygen transfer to intraluminal water flow.⁹ This study used a scaled-down oxygenator apparatus (0.05 m² total surface area) to demonstrate that oxygen transfer to water could be increased by up to 58% via axial tube oscillations alone.⁹

More recent studies have examined the effects of HFM oscillation using fiber polymers and sizes more similar to those used in current-day devices. Kim et al evaluated the effects of oscillating polypropylene hollow fibers (380-μm inner diameter, 50-μm wall thickness) on gas transfer in an intravascular lung assist device.^5–8 In these studies, fibers were tied to a flexible beam which was oscillated using a piezoceramic multi-layer bending actuator. The oscillatory motion of the beam resulted in fiber oscillations perpendicular to both the fiber axis and direction of liquid (water or blood) flow. These studies demonstrated oxygen transfer rate enhancements up to approximately 60% in blood or 100% in water due to fiber oscillation.^5–8 Maximum enhancement was observed at a frequency corresponding to the resonant frequency of the beam.^5–8 It should be noted that neither the oscillation velocity or displacement (i.e., stroke length) of the fibers were measured in these studies. Additionally, the optimal frequency for maximum enhancement was simply a consequence of the specific geometry and material of the beam supporting the fibers. As such, these results provide limited insight into the broader topic of fiber oscillations within an artificial lung and are difficult to translate into useful design criteria.

Numerical modeling has also been used to investigate the effects of fiber oscillations within an artificial lung. Qamar et al performed Navier-Stokes and mass transfer computations to characterize blood flow and oxygen transfer around a single cylinder oscillating perpendicular to pulsatile blood flow.^12,13 The authors hypothesized that the gas exchange process in this setting is primarily governed by the evolving vortex field behind the fiber.¹³ Results showed that larger oscillatory velocity amplitudes and frequencies promoted vortex formation and shedding and thus could be capable of increasing gas exchange.^12,13 An important limitation of this study is that the analysis only considers a single fiber oscillating in unbounded flow. A full-scale device utilizes an array of thousands of closely packed fibers in which gas exchange will inevitably be affected by factors outside of those considered.

As evidenced by the discussed work, previous studies have demonstrated positive potential for the use of HFM oscillations to enhance gas transfer. The literature, however, lacks an evaluation in a setting that is directly applicable to current-day, full-scale artificial lungs. Design of an artificial lung that utilizes HFM oscillations will require an understanding of the fiber displacement and oscillation frequency that optimize artificial lung performance. Thus, the focus of this in vitro study is to characterize the effects of fiber oscillation parameters on oxygenation and hemolysis for a clinically relevant HFM bundle. A lumped parameter model was also used to elucidate the effects of system and oscillation parameters on oxygenation performance. Results were then used to establish clear design criteria for an artificial lung that uses HFM oscillation to enhance gas exchange.

MATERIALS AND METHODS

Experimental Apparatus

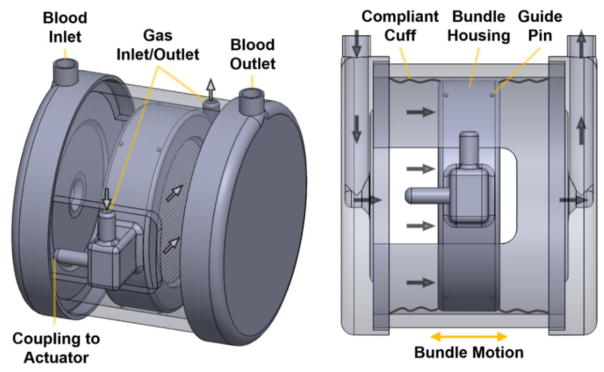
A schematic of the setup used for in vitro testing is shown in Figure 1.

Figure 1.

Simplified schematic of the bundle oscillation setup used during in vitro testing. The blood flow path is shown with solid arrows while the sweep gas pathway is shown with open arrows. Compliant cuffs were omitted in the left schematic for an unobstructed view of the device interior.

The device is comprised of two end caps (containing the blood inlet and outlet ports) connected to a rigid HFM bundle housing via compliant cuffs. The bundle housing contains the sweep gas inlet and outlet ports and is the point of coupling to an external actuator capable of oscillatory motion. The bundle housing is supported by small Teflon guide pins that protrude from its exterior and make contact with a solid outer cylindrical shell connected to the end caps. The use of compliant cuffs achieves a contained blood flow path while allowing the bundle housing a single degree of translational motion along the axis of the primary blood flow path (see Figure 1). Thus the direction of bundle oscillations was perpendicular to the axis of the fibers and parallel to the primary blood flow path. The rigid device housing components were modeled in SolidWorks^® CAD software (Dassault Systèmes, SolidWorks Corp., Waltham, MA) and machined from clear acrylic. The cylindrical, stacked-type HFM bundle has a circular cross section (6.48-cm diameter) and was manufactured from commercially available polypropylene hollow fiber sheets (CELGARD®, 50 fibers per inch, 300-μm fiber outer diameter, Membrana GmbH, Wuppertal, Germany) using previously described methods.¹⁰ The bundle is composed of 42 layers of stacked fiber sheets and has a thickness, porosity, and total membrane surface area of 1.4 cm, 0.5, and 0.25 m², respectively. The compliant cuffs attached to either side of the bundle housing were dip-casted from medical grade polyurethane (Tecoflex SG-85A, Lubrizol LifeSciences, Wickliffe, OH). Two different cuff designs were used during in vitro oxygenation evaluation. Initial testing utilized larger, more compliant cuffs with an approximate length of 3.8 cm and wall thickness of 200 μm. Following initial testing, a more optimized setup utilized shorter, less compliant cuffs with an approximate length of 1.9 cm and wall thickness of 300 μm. For both cuff types, some degree of folding or wrinkling in the cuff material was observed during oscillation when the bundle housing moved nearest to either end cap. The large-compliance and small-compliance cuffs will subsequently be referred to as the LC and SC cuffs, respectively.

Oscillatory bundle motion was induced by rigid attachment of the bundle housing to a rotary actuator via a scotch yoke coupling system. Oscillation frequency was specified via the rotational speed of the actuator. Oscillation stroke length was adjusted via the off-center distance of the eccentric connection to the actuator. Both the outer device housing and actuator were rigidly fixed to the work surface. An accelerometer (Model 352C22, PCB Piezotronics, Depew, NY) attached to the bundle housing was used during testing to verify oscillation frequency. The oscillation stroke length of the bundle housing was measured both before and after evaluation of each condition using a dial indicator.

In Vitro Oxygenation

Measurement of oxygen exchange rates was performed in bovine or porcine blood collected from a local slaughterhouse and used a previously described experimental protocol and circuit.¹⁰ Following collection, blood was filtered (40-μm filter, Pall Biomedical Inc., Fajardo, PR) and treated with heparin (15 IU mL⁻¹) and gentamicin (0.1 mg mL⁻¹). Blood flow through the circuit was maintained at 2.5 L min⁻¹ via a Biomedicus BP 80-X pump (Medtronic, Minneapolis, MN) and measured using an ultrasonic flow probe (Transonic Systems Inc., Ithaca, NY). Prior to oxygen transfer rate measurement, venous blood conditions (O₂ saturation = 65 ± 5%, pCO₂ = 45 ± 5 mmHg) were achieved via recirculation through a Medtronic Affinity NT oxygenator (Medtronic, Minneapolis, MN). A heated recirculator (Model 210, Polyscience Inc., Niles, IL) connected to the heat exchanger of the Affinity oxygenator was used to maintain a blood temperature of 37 ± 2 C. Oxygen transfer rates during varying oscillation conditions were measured for test setups utilizing each cuff type. Initial testing with the LC cuffs evaluated oscillation stroke lengths of 2, 6 and 10 mm at frequencies of 1 to 25 Hz. The SC cuffs were then used to evaluate stroke lengths of 2 and 6 mm over the same frequency range. Measurement of oxygen transfer rate for the no oscillation case was taken regularly during evaluation of the various oscillating conditions. Pure oxygen was used as the sweep gas and maintained at a constant gas flow rate of 12 L min⁻¹ using a GR series mass flow controller (Fathom Technologies, Georgetown, TX). Blood samples were taken at the inlet and outlet of the test device and analyzed using a RAPIDPoint 405 blood gas analyzer with co-oximetry (Siemens Healthcare Diagnostics Inc., Tarrytown, NY). Oxygen transfer rates were calculated and normalized to an inlet oxygen saturation of 65% using previously described methods.^3,10 The oxygen transfer rate enhancement induced by varying oscillation conditions was calculated as the percent increase in oxygen transfer rate from the no oscillation condition measured during the same experiment. Each condition was measured in triplicate.

Theoretical Analysis

The objective of the following analysis is to derive a relationship between oxygen transfer rate enhancement and oscillation/system parameters to elucidate the cause of trends observed within in vitro results. HFM oscillations are hypothesized to increase oxygen transfer primarily through increased blood flow velocities relative to the HFM surface. Based on a previously developed mass transfer correlation in HFM oxygenators,¹⁵ the expected relationship between oxygen transfer rate (V̇_O2, units of mL min⁻¹) and the superficial velocity of blood through the bundle (u, units of cm s⁻¹) is given by expression 1.

$${\stackrel{.}{V}}_{O_2}\propto u^{0.42}$$ (1)

Accordingly, the remaining analysis will focus on developing an expression describing the effective velocity of blood relative to the fibers as a function of oscillation/system parameters. Blood flow through the oscillating bundle can be represented by the sum of a steady flow component (due to bulk blood flow) and a sinusoidal component (due to oscillation-induced flow). To determine the relative magnitude of the sinusoidal component, steady flow will initially be ignored and analysis will consider flow through a bundle oscillating in stationary fluid. Flow will be considered from the reference frame of the moving bundle. From such a reference frame, a bundle oscillating in stationary fluid corresponds to sinusoidal flow through a static bundle with the form of equation 2.

$$Q=Q_{\mathit{amp}}sin(2\pi ft)$$ (2)

Where Q (units of mL s⁻¹) is the volumetric fluid flow through the bundle, Q_amp (units of mL s⁻¹) is the flow amplitude, f (units of Hz) is frequency, and t (units of s) is time. The frequency of the sinusoidal flow (f) is equal to the oscillation frequency. Q_amp will be dependent on the bundle geometry, oscillation frequency, and oscillation stroke length (L_stroke, units of cm). Stroke length is defined as the complete distance traveled by the bundle in a single direction during an oscillation. With each stroke of the actuator, the circular bundle will be displaced through a cylindrical volume of fluid with the cross sectional area of the bundle and a length of L_stroke. From the reference frame of the moving bundle, this same volume must equal the integral of equation 2 over half of the total oscillation period, resulting in equation 3.

$${\int }_0^{\frac{1}{2f}}{Q}_{\mathit{amp}}\mathit{sin}(2\pi ft)dt=\pi r_{\mathit{bundle}}^2{L}_{\mathit{stroke}}$$ (3)

Where r_bundle (units of cm) is the radius of the HFM bundle. From equation 3, an expression for Q_amp can be derived and is given by equation 4.

$$Q_{\mathit{amp}}={\pi }^{2}f{r}_{\mathit{bundle}}^2{L}_{\mathit{stroke}}$$ (4)

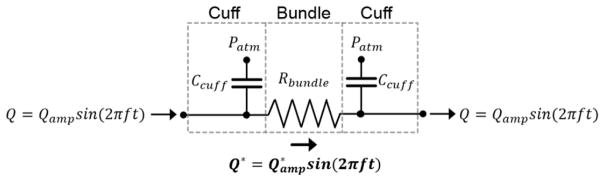
Based on Equation 4, the amplitudes of oscillation-induced bundle flow (i.e., Q_amp) calculated for the evaluated oscillation parameters are approximately 2.5–60 times greater than bulk blood flow. Considering this, intra-bundle flow velocities are expected to be primarily governed by oscillation-induced flow and the subsequent analysis will continue to ignore the steady flow component due to bulk blood flow. Equations 3 and 4 assume that the entire volume of fluid through which the bundle is displaced flows through the bundle. However, the combination of the bundle resistance and cuff compliance will have a frequency-dependent dampening effect on the volume of fluid forced through the bundle. Thus, the effective oscillation-induced flow through the bundle (Q^*, units of mL s⁻¹) is expected to be sinusoidal with a flow amplitude ( $Q_{\mathit{amp}}^{\ast }$, units of mL s⁻¹) less than Q_amp. The effects of bundle resistance and cuff compliance on $Q_{\mathit{amp}}^{\ast }$ can be described using the simplified lumped parameter model shown in Figure 2.

Figure 2.

Lumped parameter model representing the HFM bundle and surrounding compliant cuffs. C_cuff is the compliance of a single cuff, R_bundle is the bundle resistance to fluid flow, and P_atm represents atmospheric pressure.

In the analogous electrical circuit shown in Figure 2, the HFM bundle is represented by a resistor while the compliant cuffs are represented by capacitors. The impedances of the bundle (Z_bundle) and compliant cuff (Z_cuff) elements are given in equations 5 and 6.

$$Z_{\mathit{bundle}}=R_{\mathit{bundle}}$$ (5)

$$Z_{\mathit{cuff}}=\frac{1}{j2\pi f{C}_{\mathit{cuff}}}$$ (6)

Where R_bundle (units of mmHg s mL⁻¹) is the bundle resistance to blood flow, C_cuff (units of mL mmHg⁻¹) is the compliance of a single cuff, and $j=\sqrt{-1}$. Applying Kirchoff’s laws to the circuit shown in Figure 2 and using equations 4–6, an expression for $Q_{\mathit{amp}}^{\ast }$ can be derived and is given by equation 7.

$$Q_{\mathit{amp}}^{\ast }=\frac{{\pi }^2{r}_{\mathit{bundle}}^2{L}_{\mathit{stroke}}f}{\pi f{R}_{\mathit{bundle}}{C}_{\mathit{cuff}}+1}$$ (7)

Equation 7 can be used to describe the effects of the physical and oscillatory parameters of the bundle-cuff system on the predicted amplitude of oscillation-induced volumetric flow through the bundle. The amplitudes of the superficial velocity of blood through the bundle predicted by equation 4 (u_amp, units of cm s⁻¹) and equation 7 ( $u_{\mathit{amp}}^{\ast }$, units of cm s⁻¹) were used during analysis of in vitro oxygenation results.

Measurement of System Resistance and Compliance

The resistance of the HFM bundle to blood flow was measured using a carboxymethyl cellulose sodium salt (Sigma Aldrich, St. Louis, MO) solution (8.5 g L⁻¹) as a blood analog. The dynamic viscosity of the solution was verified to be 3.5 ± 0.2 cP immediately prior to testing using a capillary viscometer (Cannon Instrument Company, State College, PA). The experimental circuit consisted of the test apparatus, a Biomedicus BP 80-X pump, and an 800-mL compliant blood reservoir (Medtronic, Minneapolis, MN) connected with 3/8-inch inner diameter tubing. Pressures at the inlet and outlet plenums of the HFM bundle were measured at continuous flow rates of 0 to 4 L min⁻¹ using a Honeywell 143 PC03D transducer (Honeywell International Inc., Morris Plains, NJ). Flow rate was measured using an ultrasonic flow probe. Five repeated measurements were taken for each condition evaluated.

The static compliance of each cuff type was measured over the pressure range experienced during oxygenation testing. The blood inlet and outlet of the device were occluded while it was primed with water. Aliquots of water (2–10 mL) were then incrementally injected into the device to gradually distend the cuffs. After injection of each aliquot, the fluid pressure within each cuff was measured using a Honeywell 143 PC03D transducer. Pressure measurements were taken approximately 60 seconds after injection to allow pressure in the cuffs to equilibrate. At least two repeated measurements were taken for each cuff type.

In Vitro Hemolysis

The degree of blood damage sustained during varying bundle oscillation conditions was evaluated using bovine blood collected from a local slaughterhouse. Blood was filtered and treated as specified for oxygenation testing and diluted with native plasma to a hematocrit of 30%. The experimental circuit consisted of an 800-mL compliant blood reservoir, a Biomedicus BP 80-X pump, and the test apparatus connected with 3/8-inch inner diameter tubing. The compliant reservoir was submerged in a heated water bath to maintain a blood temperature of 37 ± 2 C. Two different oscillation conditions and the no oscillation case were evaluated at a blood flow rate of 2.5 L min⁻¹ using the SC cuffs. Oscillation stroke lengths of 2 and 6 mm were evaluated at the frequencies resulting in 40% enhancement of oxygen transfer rate from the no oscillation case. Specific frequency values for each stroke length were calculated via interpolation of oxygenation results. For each condition evaluated, blood was continuously circulated for a period of three hours during which blood samples were collected every 30 minutes. Plasma-free hemoglobin and hematocrit measurements were taken for each sample and used to calculate a normalized index of hemolysis (NIH). Further detail regarding the methods and equations used for NIH calculation have been previously published elsewhere.¹⁶ Three trials were conducted for each condition evaluated.

Statistics

SPSS 24 (IBM Corporation, Armonk, NY) was used to perform all statistical analysis. A two-sample t-test was used to determine the effect of cuff design on oxygen transfer rate for the no oscillation case. A repeated measures one-way analysis of variance was used to determine the significance of oscillation condition on NIH values. Post hoc tests using the Bonferroni correction were used to determine significant differences between groups.

RESULTS

System Resistance and Compliance

The pressure drop across the HFM bundle increased linearly with flow rate over the range of flows evaluated (R² = 0.99, data not shown). The measured resistance of the HFM bundle was 1.51 mmHg min L⁻¹. Regarding measurement of cuff compliance, pressure within the cuffs exhibited a linear relationship with internal fluid volume (R² > 0.95 for both cuffs types, data not shown). Since the polyurethane cuffs represent the only non-rigid portion of the device housing, the slope of internal fluid volume versus pressure can be interpreted as the total static compliance of the two cuffs acting in parallel. The compliances of a single LC and SC cuff were found to be 0.43 and 0.14 mL mmHg⁻¹, respectively. HFM bundle resistance and cuff compliance were then used in equation 7 to calculate predicted oscillation-induced flow amplitudes for varying test conditions.

In Vitro Oxygenation

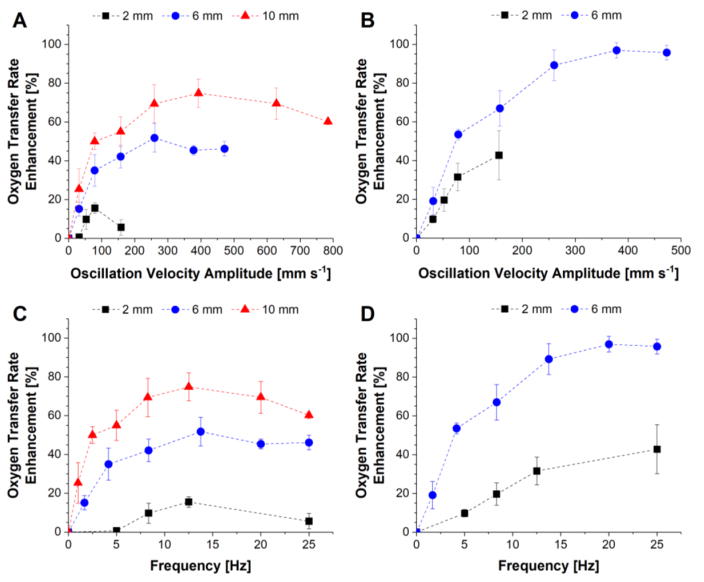
The normalized oxygen transfer rate for the no oscillation case was 62.8 ± 4.4 mL min⁻¹ and was not significantly different between the two cuff designs (62.2 ± 4.8 mL min⁻¹ for LC cuffs vs. 64.2 ± 3.2 mL min⁻¹ for SC cuffs). The oxygen transfer rate enhancements resulting from varying bundle oscillations are shown in Figure 3. Results for the LC and SC cuffs are presented as a function of oscillation velocity amplitude (calculated based on oscillation stroke length and frequency) in Figure 3 panels A and B, respectively. The same results are also presented as a function of oscillation frequency in Figure 3 panels C and D.

Figure 3.

Oxygen transfer rate enhancement as a function of bundle oscillation velocity amplitude at varying oscillation stroke lengths for the LC (A) and SC (B) cuff designs. The same enhancement results are also presented as a function of oscillation frequency for the LC (C) and SC (D) cuff designs.

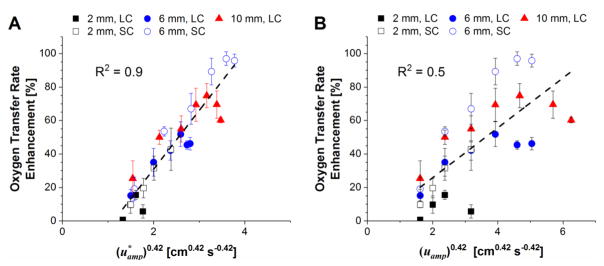
A maximum oxygen transfer rate of 127 mL min⁻¹ (corresponding to 97% enhancement) was achieved with the SC cuffs at an oscillation stroke length and frequency of 6 mm and 20 Hz, respectively. Enhancement at a given oscillation velocity amplitude increased with increasing stroke length (Figure 3 panels A and B). This effect is shown to be frequency-related with enhancement at any given stroke length generally increasing with increasing frequency until plateauing at frequencies between 12 and 25 Hz (Figure 3 panels C and D). The SC cuffs (compliance of 0.14 mL mmHg⁻¹) were able to achieve approximately twice the enhancement of the LC cuffs (compliance of 0.43 mL mmHg⁻¹) for a given stroke length and frequency. Figure 4 panels A and B show enhancement plotted as a function of ${(u_{\mathit{amp}}^{\ast })}^{0.42}$ and (u_amp)^0.42, respectively, calculated for each test condition. A linear trend line was fit to each data set to assess agreement between in vitro results and trends predicted via theoretical analysis. Ranges for average Reynolds and Strouhal numbers based on the flows predicted by Equation 7 were 8–90 and 0.5–9, respectively.

Figure 4.

Oxygen transfer rate enhancement as a function of oscillation-induced superficial blood velocity amplitudes predicted by equation 7 (A) and equation 4 (B). LC and SC denote results for the large-compliance and small-compliance cuff designs, respectively. A linear fit for each plot is given by the dotted line.

In Vitro Hemolysis

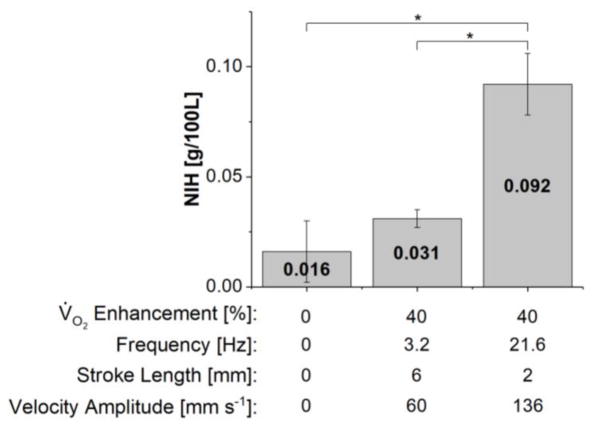
Plasma free hemoglobin increase over the 3-hour evaluation period exhibited a strong linear trend during all trials with an average R² value of 0.9 (data not shown). Calculated NIH values for varying oscillation conditions using the SC cuffs are shown in Figure 5. The oxygen transfer enhancement, oscillation frequency, stroke length, and oscillation velocity amplitude corresponding to each test condition are shown beneath the plot. The NIH for the 6-mm stroke length condition was not significantly different from that for the no oscillation case (p = 0.40). The NIH for the 2-mm condition was significantly larger than that for the no oscillation and 6-mm conditions (p < 0.05 for both cases).

Figure 5.

Normalized index of hemolysis (NIH) values for varying oscillation conditions for the setup utilizing the SC cuffs. The oxygen transfer enhancement as well as oscillation frequency, stroke length and velocity amplitude are shown below the bar graph for each condition evaluated. Statistically significant differences (p < 0.05) between groups are denoted by an asterisk.

DISCUSSION

HFM oscillations represent a means to increase the gas transfer efficiency of artificial lungs. Prior work has demonstrated the general feasibility of this approach in various settings. Yet the design of a clinically relevant artificial lung utilizing this approach requires a greater understanding of the oscillatory motion that will optimize device performance. The focus of this study was to evaluate the effects of varying oscillation stroke length and frequency on gas exchange enhancement and hemolysis in a full-scale artificial lung. In vitro results have shown that HFM oscillations can significantly increase gas transfer efficiency within a pediatric-sized HFM bundle. In this setting, the magnitude of enhancement is dependent on the oscillation stroke length and frequency as well as other physical system parameters such as housing compliance and bundle resistance. While oscillations resulted in some degree of additional blood damage, considerable oxygenation enhancement was achievable without significantly increased hemolysis. Oscillation-related hemolysis is also expected to be reduced via optimization of device design.

The effects of HFM oscillations on oxygen transfer were evaluated at the maximum blood flow rate typically used during pediatric respiratory support. Despite having a smaller HFM surface area than current pediatric oxygenators, the bundle used in this study was capable of meeting pediatric oxygenation needs (estimated at 118 mL min⁻¹ for a 25-kg child¹¹) during HFM oscillations. Oscillations were able to increase oxygen transfer by a factor of two and reached a maximum efficiency (i.e., oxygen transfer rate per unit fiber surface area) of approximately 510 mL min⁻¹ m⁻² at a blood flow rate of 2.5 L min⁻¹. To the best of the authors’ knowledge, this efficiency exceeds that of any other pediatric oxygenator in clinical use (200–260 mL min⁻¹ m⁻²)^19,20 or in the literature (maximum efficiency of 430 mL min⁻¹ m⁻² for the PediPL)¹⁸ at the same blood flow rate.

The magnitude of oxygen transfer enhancement was greatly affected by oscillation stroke length and frequency. The greatest enhancement for either cuff design was observed at the largest stroke length evaluated. This was expected due to the increase in oscillation velocity amplitude experienced by increasing stroke length for a given frequency range. Enhancement, however, was not dependent on oscillation velocity alone and exhibited a more complex relationship with oscillation frequency. Although oscillation velocity amplitude increases indefinitely with frequency for a given stroke length, enhancement plateaued at frequencies of 12 to 25 Hz. These effects can most likely be attributed to the effect of frequency on the impedance of the bundle-cuff system. As seen in equations 5 and 6, the impedance of the cuff elements decreases with increasing oscillation frequency while that of the bundle is independent of frequency. The compliant cuffs adjacent to the bundle are analogous to grounded capacitors that suppress high-frequency signals within a circuit. The implication of this on device function is that higher frequencies result in a greater fraction of the blood volume displaced by the oscillating bundle to flow into the compliant cuffs rather than through the bundle. Thus, the amplitude of the effective oscillation-induced flow through the bundle decreases with increasing frequency for a given oscillation velocity amplitude. As shown in equation 6, the impedance of the cuff elements increases with decreasing compliance. Consequently, the maximum enhancement achieved for a given stroke length was approximately doubled by decreasing cuff compliance by a factor of three. As shown in Figure 4 panel A, enhancement results for the varying test conditions collapse on to a single curve with reasonably good linearity (R² = 0.9) when plotted as a function of ${(u_{\mathit{amp}}^{\ast })}^{0.42}$. This indicates good agreement between in vitro results and the relationship predicted by theoretical analysis. By contrast, linearity is substantially decreased when results are plotted as a function of (u_amp)^0.42 where the effects of cuff compliance and bundle resistance are ignored (Figure 4 panel B, R² = 0.5). The linear fit in Figure 4 panel A indicates that enhancement begins to occur when oscillation-induced superficial blood velocity amplitude ( $u_{\mathit{amp}}^{\ast }$) exceeds 1.31 cm s⁻¹. The superficial blood velocity through the bundle due to continuous bulk blood flow at 2.5 L min⁻¹ (the flow rate used during testing) is 1.26 cm s⁻¹. Thus, these results are in agreement with previous work that predicts that enhancement occurs once oscillation-induced velocities exceed those due to bulk flow.⁶

The effects of HFM oscillations on blood damage were evaluated via measurement of the NIH using the test apparatus with the SC cuffs. Test conditions included the no oscillation case and stroke lengths of 2 and 6 mm at the frequencies corresponding to 40% oxygen transfer enhancement (the maximum common enhancement achieved for the two conditions). NIH was low for both the no oscillation and 6-mm condition, but increased for the 2-mm condition. Due to the previously discussed effect of frequency on oscillation-induced flow, the oscillation velocity required to achieve 40% enhancement for the 2-mm case is much larger than that for the 6-mm case. While oxygenation enhancement arises primarily from increased fluid velocities through the bundle, oscillation-induced blood damage likely has more varied sources. In addition to increased shear stresses at the HFM-blood interface, other dynamic system processes such as the repeated collapsing of the cuffs likely also contributed to blood damage in the current test setup. The additional motion associated with the higher oscillation velocity of the 2-mm case undoubtedly contributes to blood damage and may explain the increased NIH relative to the 6-mm case. A more optimized device that minimizes extraneous motion of blood contacting components should be used to further evaluate the hemolytic performance of this approach.

It is important to note that this work does not represent the characterization of a completely optimized, self-contained device, but rather aims to provide the preliminary analysis necessary to design one. The optimal artificial lung utilizing HFM oscillations would achieve significantly increased gas exchange efficiency via relatively small displacements while maintaining low blood damage. Although HFM oscillations in a variety of directions are possible, this work focused on oscillations parallel to blood flow due to its ease of implementation and ability to induce large relative motion between the fibers and blood. Small HFM displacements are ideal in order to minimize both device size as well as any potential inconvenience to the patient. Small displacements, however, require high frequencies to induce large oscillation velocities. This work has shown that, in this setting, high oscillation frequencies result in less efficient translation of fiber bundle motion to increased gas exchange. This inefficiency, however, can be minimized through modification of physical elements of the system. As shown via modeling and verified with in vitro results, reducing the compliance of the blood conduit immediately adjacent to the bundle significantly improves gas exchange enhancement. As shown in equations 5–7, similar effects can also be achieved by reducing bundle resistance. Thus, the optimal design using this approach should minimize both bundle resistance and conduit compliance to achieve maximal enhancement via small HFM displacements.

A potential concern with the HFM oscillation approach to creating a compact, lightweight artificial lung is the added weight and bulkiness of an actuator required to induce oscillations. However, a variety of oscillatory and vibrational actuators are available, many of which would add negligible weight and complexity to an artificial lung. This point only further highlights the need to determine the optimal oscillation displacements and frequencies in order to select the most appropriate actuator. A second concern may be the potential for mechanical deformation or failure of the hollow fibers under the added stress of oscillations. No such failures were observed during the repeated used of HFM bundles in the current work. However, fiber failure under longer-term continuous oscillation should be evaluated in future studies with the next generation device.

While this work provides valuable insight, it also has important limitations. First, the theoretical analysis in this work considers only the effect of blood velocity relative to the HFM surface in explaining the observed oxygenation trends. Other effects known to affect gas exchange such as the degree of spatial uniformity of intra-bundle blood flow are not considered in the analysis. The in vitro setup used in this early stage work was designed primarily to enable a large range of oscillation stroke lengths and was not necessarily optimized for spatially uniform intra-bundle blood flow. It is possible that bundle oscillations may enhance gas exchange by increasing the uniformity of intra-bundle blood flow compared to the no oscillation case. These effects would not be accounted for by the theoretical analysis and may contribute to differences between in vitro results and the predicted relationship. Second, the current test apparatus and results provide only a limited understanding of hemolysis during HFM oscillations. The current test setup allows for a large range of HFM oscillations but also results in a large degree of extraneous motion of blood contacting components outside of the bundle. A system specifically optimized for small scale oscillations could significantly reduce such motion and would likely reduce oscillation-related hemolysis. Thus, more rigorous evaluation of the effects of HFM oscillation on hemolysis should be a primary focus of future studies using a more optimized device.

In conclusion, HFM oscillations are a viable approach to increasing the gas exchange efficiency of artificial lungs. An increased efficiency will enable a smaller and more compact artificial lung design that has the potential to improve the morbidity and mortality associated with lung failure. This work has used both modeling and in vitro results to provide the insight necessary to begin to design a clinically relevant artificial lung that utilizes HFM oscillations. The current setup has demonstrated that sizable gas exchange enhancements can be achieved without significantly increased hemolysis, however further improvement is expected through optimization. Future work will use the design criteria established in this study to develop a highly efficient artificial lung that integrates a blood pump with an HFM bundle utilizing small-scale oscillations.