Manipulating nanoparticle transport within blood flow through external forces: an exemplar of mechanics in nanomedicine

Abstract

A large number of nanoparticles (NPs) have been raised for diverse biomedical applications and some of them have shown great potential in treatment and imaging of diseases. Design of NPs is essential for delivery efficacy due to a number of biophysical barriers, which prevents the circulation of NPs in vascular flow and their accumulation at tumour sites. The physiochemical properties of NPs, so-called ‘4S’ parameters, such as size, shape, stiffness and surface functionalization, play crucial roles in their life journey to be delivered to tumour sites. NPs can be modified in various ways to extend their blood circulation time and avoid their clearance by phagocytosis, and efficiently diffuse into tumour cells. However, it is difficult to overcome these barriers simultaneously by a simple combination of ‘4S’ parameters for NPs. At this moment, external triggerings are necessary to guide the movement of NPs, which include light, ultrasound, magnetic field, electrical field and chemical interaction. The delivery system can be constructed to be sensitive to these external stimuli which can reduce the non-specific toxicity and improve the efficacy of the drug-delivery system. From a mechanics point of view, we discuss how different forces play their roles in the margination of NPs in blood flow and tumour microvasculature.

1. Introduction

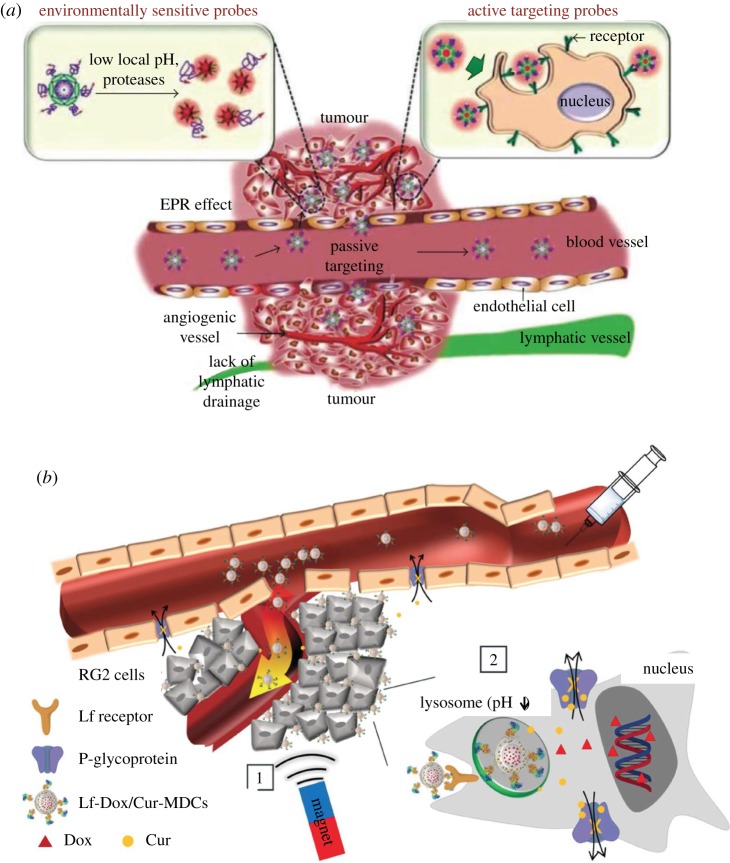
Recently, a large number of designed nanoparticles (NPs) have been raised for diverse biomedical applications and some of them have shown great potentials in the treatment and imaging of diseases [1–4]. Compared to freely administered drug molecules [3,5,6], the encapsulation of drug molecules and contrast agents into NPs can significantly improve their pharmacokinetics, biocompatibility and biodistribution. For intravenously administered NPs for cancer therapy, their journey to tumour sites follows four key steps [7,8] (cf. figure 1a): (i) transport and circulation in a complex vascular network with red blood cells (RBCs), white blood cells (WBCs) and many others; (ii) margination from the central stream of the blood flow to the vessel wall region and firm adhesion to the endothelium near the tumour site; (iii) diffusion into tumour tissues through leaky vasculatures; (iv) recognition and internalization by tumour cells. During this journey, the encapsulated drug molecules can be more efficiently delivered to the diseased tissue through the margination behaviours of NPs, which increase the NP’s interaction with the vascular wall. This allows the NPs to better ‘sense’ the biophysical and biological abnormalities, such as the presence of fenestrations or the expression of specific receptors, on the surface of endothelial cells. Afterwards, the NP can firmly adhere to the vessel wall under shear flow, if the hydrodynamic forces are balanced out by the interfacial adhesive interactions between the NP and vessel wall. Margination and the subsequent adhesion of NPs to the endothelium allow the NPs to transmigrate across the endothelial wall and enter a diseased area of tissue, eventually delivering the encapsulated drug molecules into tumour sites.

Figure 1.

Schematics of NP-mediated drug-delivery systems. (a) Passive targeting strategy depends on ‘4S’ parameters of NPs and local physiological properties of tumour microvasculature. (b) Magnetic field acts as an external triggering to guideNP-based drug carriers EPR, enhanced permeability and retention. (Reproduced with permission from (a): Bina et al. [9] (Copyright 2015 Hindawi Publishing Corporation) and (b): Fang et al. [10] (Copyright 2014 Wiley Online Library)). (Online version in colour.)

The margination propensity of NPs in blood depends on their size, shape, surface property and stiffness (‘4S’ parameters). Studies about their intrinsic properties, including experimental [11–13], theoretical [14] and numerical [15–17], have revealed the underlying physical mechanisms for the margination behaviours of NPs. A large number of studies [8,15,18] demonstrate that larger NPs readily marginate into the near vessel wall region, while smaller ones are trapped between RBCs and circulate with them in blood flow. The shape of NPs has also been identified as a key parameter in determining blood circulation time and vessel wall adhesion. Non-spherical NPs are found to exhibit efficient resistance to mononuclear phagocyte system (MPS) sequestration in blood circulation. More importantly, non-spherical NPs with higher aspect ratios can marginate more quickly than spherical NPs and establish firm adhesion to the vessel walls [19,20]. The surface of NPs is usually decorated by functional molecules, such as small targeting moieties (ligands), polymers and biomolecules to reduce their interactions with the immune system like serum proteins in blood flow, which can reduce the serum protein absorption and subsequent internalization by macrophages, thereby extending their blood circulation time [21,22]. Stiffness of NPs attracts relatively less attention compared to other key parameters. However, it also plays an important role in the blood circulation of NPs. For instance, Kumar et al. [23] found that stiff particles tend to marginate, while the soft particles accumulate near the centre of the blood vessel. As the aforementioned transport of NPs in blood flow relies on their intrinsic properties, we name these behaviours as ‘passive transport’.

The passive targeting strategies have certain limitations. The local physiological conditions of diseased sites may be different from patient to patient. Therefore, the efficacy of NP-based drug-delivery vehicles is difficult to predict a priori [24]. Besides, after intravenous injection, the transport of NP-based drug carriers within the vascular network cannot be easily controlled. To overcome these limitations, actively triggered systems are proposed to enhance the therapeutic efficacy of the drug-delivery platform. Lin et al. [25] presented that the release of anti-cancer drug molecules can be regulated precisely by manipulating external light such as changing irradiation wavelength, intensity and time. Additionally, Kagatani et al. [26] proposed a model for a pulsatile drug-delivery system, where electroresponsive polymer gels act as the drug carrier with loaded insulin. The transport of these drug carriers can be stimulated and guided by an externally applied electrical field, and have demonstrated the feasibility of this kind of delivery system through in vivo studies. Apart from these aspects, ultrasound [27], chemically triggered [28] and magnetic systems are largely used to control drug carriers. Among them, magnetic NPs have demonstrated great potential, due to the enhanced deposition at a specific anatomic site guided by external magnetic fields [29–32] (cf. figure 1b). For instance, Schleich et al. [31] have shown that intratumoural accumulation of injected poly-based NPs with loaded paclitaxel and iron oxides could be increased by placing a magnet above a tumour that guides the magnetic NPs to the diseased location. In particular, because of the excellent tissue penetration, magnetic fields have already been used in whole-body magnetic resonance imaging (MRI) [33]. Here we name the transport of these actively triggered systems in blood flow as ‘active transport’.

This review aims to thoroughly explore the forces and parameters governing NP transport behaviour and extravasation to tumours. In §2, we introduce the background on the transport of NPs in blood flow, including the fluid flow and influence of RBCs. Specifically, we emphasize individual force analysis, which can guide the motion of NPs in blood flow. In §3, the effect of physiochemical properties (‘4S’ parameters) of NPs are discussed. The shape, size, stiffness and surface functionality are considered to show how these intrinsic properties can influence motion of NPs in blood flow. In §3, we survey the application of external triggering in targeted drug delivery, by mainly focusing on magnetic triggering. Both experimental and numerical studies are discussed to illustrate the underlying physical mechanisms. In §4, concluding remarks are given. We also discuss the perspectives and key challenges in applying the external triggering strategies.

2. Background

(a). Blood flow in normal vasculature and tumour microenvironment

In large blood vessels, such as arteries near the heart, with diameters in the range of millimetres to centimetres, the inertial effects strongly influence the blood flow and the suspensions. Phenomena like pulsing, flow separation, instability, second flow and even turbulence may be present. While this situation changes in the microcirculation, such as the vein and capillary network. The Reynolds numbers (Re) of blood flow are typically much less than 1, so the inertial effects are negligible. Furthermore, the fluid flow can be approximately described by the Stokes equations as that of an incompressible fluid [34]. The drug carriers with encapsulated therapeutics are usually injected into vein, circulate with blood flow and then reach the tumour sites. Therefore, the effects relevant to inertial of flow are not considered in this review. It is suggested that people interested in this aspect read previous review articles [34–37].

Blood is a complex fluid and ensures transport of nutrients and oxygen throughout the body to support cell metabolism [34,38,39]. Blood mainly consists of plasma and formed elements. Plasma, composed of approximately 90% water, 7% proteins and other solutes, is usually considered a Newtonian fluid at physiological rates of shear. The formed elements include RBCs, WBCs and platelets occupying 40–45%, 1% and under 1% volume fraction of blood, respectively. Owing to the high volume fraction of RBCs, blood should be considered as a non-Newtonian fluid [40,41]. The rheological properties of blood are mainly determined by RBC properties and their dynamics [38]. An RBC is highly flexible, biconcave in shape and approximately 8μm in diameter under healthy conditions [42]. Deformation of RBCs serves to ensure the smooth circulation of RBCs along the whole blood vasculature, especially for capillaries in which the vessel diameter is smaller than a single RBC. More importantly, deformation of RBCs causes a cross-stream migration under the effect of the vessel wall. This leads to the formation of two phases in blood flow: an RBC-rich core region in the centre of the blood vessel and an RBC-depleted layer near the vessel wall. The RBC-depleted layer, also called cell-free layer (CFL) [38,43], has a lower viscosity compared to the core region. The CFL behaves like a lubrication layer and reduces the effective blood viscosity, which lowers the vascular resistance of blood flow [44].

The blood vessels in the vicinity of tumours exhibit irregular form and abnormal function. These irregularities result in the difference of blood flow and transport of nutrients and oxygen compared to the normal vessels. The tumour microenvironment comprises surrounding tissue cells and the extracellular matrix (ECM). Fibroblasts are the most abundant tissue cell in the tumour microenvironment that secretes the ECM molecules, which compose the tumour stroma. These structures will be altered by tumour cells and interactions with microenvironment [45], including growth-induced solid stresses, stiffened ECM, elevated fluid pressure and interstitial flow. Next to tumour cells, tissue cells are exposed to an elevated stress level, which triggers the release of growth factors, chemokines and proteases by fibroblasts, which can promote tumour growth and angiogenesis [46]. Stiffening of the ECM can assist cancer cell migration, which is known as a risk factor in breast cancer [47,48]. Increase of interstitial pressure inside tumours is a consequence of the leaky vasculature inside and surrounding the tumour. On the one hand, high pressure acts as a restriction to prevent the therapeutic agents from entering into tumour stroma [49]; on the other hand, it is found to stimulate proliferation and regulate the secretion of angiogenic factors [50]. The recent intra-vital microscopy (IVM) examinations of human tumour vasculature reveal that human tumour vessels are disorganized and tortuous, and 50% do not support blood flow [51]. More importantly, the vessel diameters of human tumour are larger than that predicted from immunohistochemistry or preclinical IVM, leading to lower wall shear stress. All these aspects can dramatically affect the efficacy of the drugs and cellular immunotherapies. The characteristics of blood flow near tumour sites are reviewed in detail by Koumoutsakos et al. [39].

(b). Essential forces for particle transport in blood flow

Particles (platelets, WBCs, RBCs and NPs) experience different kinds of forces [52,53]. Particle–particle collision force happens between the same or different kinds of particles when they move close to each other [23,54–56,56–58]. If particles are soft, they can deform under the shear stress of blood flow, and a lift force will be induced, which is perpendicular to the flow direction in the vicinity of the vessel wall [52,59–62]. When the shear flow is not uniform, i.e. shear gradient exists, particles will be subjected to lift force in the cross-stream direction, which depends on the Reynolds number of flow and location of particles in the flow field [52,63–71]. At the same time, other kinds of force, like Brownian force [72], thermal-induced buoyancy [73] and gravity force [74], will influence their motions under specific circumstances. Moreover, some external forces should be added on these particles under the external field we apply, such as electrical, chemical and magnetic fields. We will discuss the magnetic field in detail in the last part of this review.

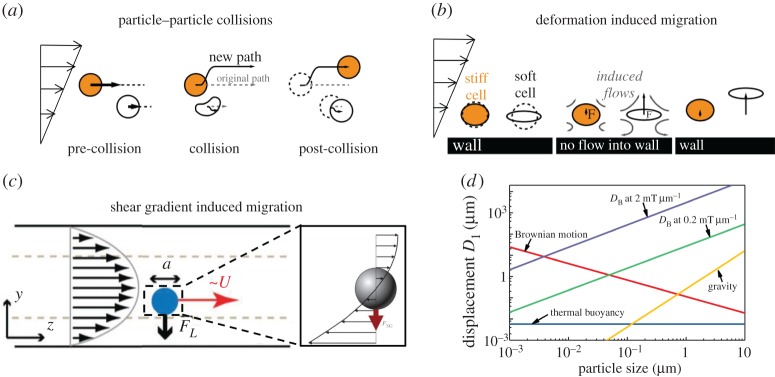
(i). Particle–particle collision

A large numbers of particles are located in and move along the blood flow. Thus, particle–particle collision is inevitable when they move close to each other, especially for blood flows with high haematocrit Ht (volume fraction of RBCs in blood flow). Owing to the complexity of collision between multiple particles, previous studies mainly focus on the pair collision, which can explain the collision-relevant phenomena in blood flow [23,54–58]. Figure 2a shows a simplified collision model including three processes: pre-collision, collision and post-collision. Owing to the collision effect and conservation of momentum, two particles will migrate to opposite directions, but both perpendicular to the flow direction. The migration distances depend on the particle properties, such as size, shape and stiffness. There is a simple phenomenological model developed by Phillips et al. [75] to predict the velocity of a particle arising from pair collision. In this model, the variation of the collision frequency over a distance has been expressed by $a\mathrm{\nabla }(\dot{\gamma }\varphi )$, where a is the radius of the particle and ϕ is the volume fraction of the particle in flow. Then, they assume that each of the collisions causes a displacement of O(a). This model has been further extended by Kumar & Graham [23] and used for a suspension of mixtures to obtain

$$\begin{array}{rl}{V}_{\mathrm{s}}^{\mathrm{p}}& =-a^2[Y_{\mathrm{ss}}\mathrm{\nabla }(\dot{\gamma }{\varphi }_{\mathrm{s}})+Y_{\mathrm{sf}}\mathrm{\nabla }(\dot{\gamma }{\varphi }_{\mathrm{f}})]\\ \text{and}{V}_{\mathrm{f}}^{\mathrm{p}}& =-a^2[Y_{\mathrm{fs}}\mathrm{\nabla }(\dot{\gamma }{\varphi }_{\mathrm{s}})+Y_{\mathrm{ff}}\mathrm{\nabla }(\dot{\gamma }{\varphi }_{\mathrm{f}})],\end{array}\}$$ 2.1

where V is the velocity; subscript s and f denote stiff and floppy (soft), respectively, and Y is the dimensionless constant which depends on the properties of particles. Here, we simply introduce two typical results: stiffness and shape dependence.

Figure 2.

Dominant forces in particle transport within blood flow. (a) Particle–particle collision; (b) deformation of particles induced migration behaviour; (c) shear gradient of flow-induced migration; (d) force order comparison under given parameters: density is 1 g cm⁻³ and viscosity is 0.78 Pa s. (Reproduced with permission from (a) and (b): Fay et al. [54] (Copyright 2016 National Acad Sciences). (c): Martel et al. [64] (Copyright 2014 Annual Reviews)). (Online version in colour.)

Kumar & Graham [23] conducted a series of simulations to isolate the pair collision contribution for the separation of elastic capsules with identical size but different stiffness in binary suspensions. In their study, the first consideration was the homogeneous collision (collision between particles with same stiffness). They found the velocity increased with increment of the stiffness, i.e. Y_ss>Y_ff. For the heterogeneous collision (collision between particles with different stiffness), simulation results showed stiff particles migrated faster than floppy particle (Y_sf>Y_fs), except that stiff particles had larger velocity than that in homogeneous collision (Y_sf>Y_ss), and at the same time, floppy particles possessed less migration velocity compared to that in homogeneous collision (Y_fs<Y_ff).

Recently, Sinha & Graham [57] investigated the margination and demargination behaviours of deformable capsules, which were modelled as blood cells and/or drug carriers in the microcirculation or in micro-fluidic devices. Again, pair collision was recognized as a critical factor in the movement of capsules. Simulation results for capsules with the same equatorial radius but different aspect ratio presented that, in homogeneous collision tests, an oblate particle had smaller migration velocity than a spherical particle (Y_oo>Y_ss), where o and s represent oblate and spherical, respectively; while for heterogeneous collision, an oblate particle outperformed a spherical particle. In general, the velocity order is: Y_so<Y_oo<Y_ss<Y_os. In addition, this trend continues also for the pair collision between spherical and prolate particles, where they found the order: Y_ps<Y_ss<Y_pp<Y_sp, where p denotes prolate. The details about the dependence of the aspect ratio on displacement in pair collision were described in [57].

(ii). Deformation-induced lift force

In the regime of Stokes flow, in which blood flow locates, reversibility precludes the lateral migration of rigid spheres without the help of inertia [76]. However, the deformation of particles breaks the reversibility and then particles can migrate away from the wall. This phenomenon has been investigated extensively for the case of a viscous drop [77,78], which is a kind of simple particle compared to complex particles such as RBCs, capsules and vesicles. Figure 2b provides a simplified model for migration of particles, including soft and stiff particles, in the presence of a wall under simple shear flow. The stiffness of a deformable particle is characterized by capillary number: $Ca=\mu \dot{\gamma }a/G_{\mathrm{s}}$, where μ is the viscosity of fluid, $\dot{\gamma }$ is the shear rate of flow and G_s is the shear modulus of the particle. A significant and detailed numerical discussion was carried out by Singh et al. [61]. They studied the lateral migration velocity of the deformable capsule, which was described by different membrane constitutive laws as a function of the stiffness of the capsule (Ca) and the distance away from the wall (h_w). A phenomenological formula for migration velocity is given by

$$\frac{V_d}{\dot{\gamma }a}=\{\begin{array}{ll}(0.65Ca+0.021){\left(\frac{a}{h_{\mathrm{w}}}\right)}^2,& Ca\le C{a}_{\mathrm{cr}}\\ {\frac{V_d}{\dot{\gamma }a}|}_{Ca=C{a}_{\mathrm{cr}}}+0.02{(Ca-C{a}_{\mathrm{cr}})}^{0.6}{\left(\frac{a}{h_{\mathrm{w}}}\right)}^{1.35},& Ca>C{a}_{\mathrm{cr}}.\end{array}$$ 2.2

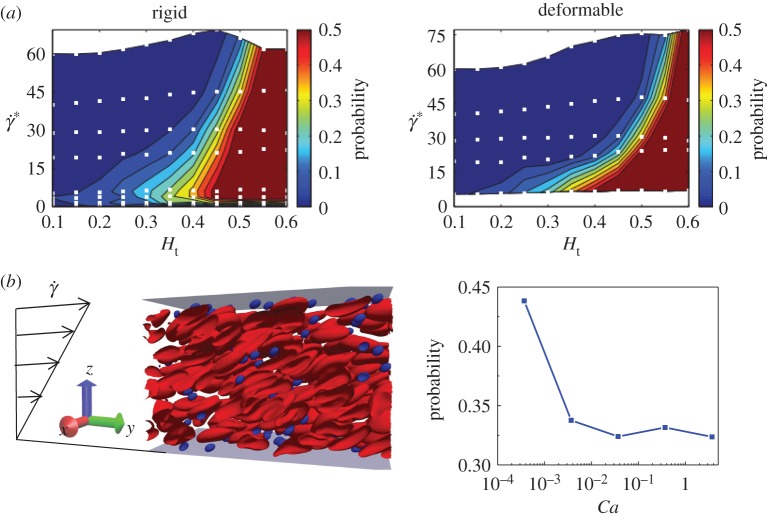
Simulation results pointed out a power law relation for the capsule velocity. There exists a critical stiffness, Ca_cr of the capsule. When Ca≤Ca_cr, the migration velocity is linearly proportional to Ca and related to h²_w, while when Ca>Ca_cr, the velocity has 0.6 and 1.35 power scalings with Ca and h_w, respectively.

Almost at the same time, Nix et al. [62] conducted the study of lateral migration of a particle in the presence of a rigid wall. They compared the numerical results for the capsule lift velocity with the far-field analytical solution for the lift velocity derived by Smart & Leighton [79]. The analytical solution was found invalid in the regime close to the wall. Besides, asymmetrical deformation of the capsule induced by the wall was correlated to a reduction in the lift velocity with respect to the lift velocity predicted by the analytical far-field solution. An increase in symmetrical deformation leads to an increase in lift velocity. Lastly, they found that, for large deformation, lift velocity was almost independent of Ca.

(iii). Shear gradient-induced lift force

A particle will experience a force due to the curvature of the velocity profile, i.e. shear gradient of the flow is non-zero. Poiseuille flow is the most common and typical flow owing to the curved velocity profile. Figure 2c [63–65] presents the velocity profile around a sphere in Poiseuille flow. Note that the velocities are relative to the velocity of the particle. It is obvious that the velocities on either side of the sphere have different magnitudes, and this difference should be compensated by the fluid flow, which will induce a force on the particle, directed towards the side of the particle with a higher relative velocity, in order to minimize the velocity difference. This shear gradient-induced lift force is independent of the rotation of the particle but highly dependent on the Reynolds number and particle position [64] as follows:

$$F_{\mathrm{s}}=\frac{C_{\mathrm{s}}\rho U_{\max }^2{a}^3}{D_{\mathrm{hydra}}},$$ 2.3

where ρ is the fluid density, $U_{max}$ is the maximum velocity of the shear flow and D_hydra is the hydraulic diameter of the channel which is defined as: D_hydra=2bw/(b+w). Here b and w are the height and width of the channel, respectively; C_s is the lift coefficient which depends on the Reynolds number and position of the particle in the flow channel. Here, as the blood flow belongs to the Stokes regime, we focus on the dependence of particle stiffness in Poiseuille flow [66]. Farutin & Misbah [52] adopted analytical and numerical methods to show a cross-streamline migration phenomenon in blood circulation. As particles are deformable and can adapt their shapes rapidly to the imposed flow profile, the migration behaviour largely depends on their location. For a high enough Ca number, particles initially placed away from the centre line of flow migrate towards the centre with an axisymmetric parachute shape. Lowering the Ca number leads to the same migration trend, but results in a lower symmetry shape. Further reducing the Ca number also makes the particle migrate towards the centre of the flow, but it never reaches it. For an extremely small Ca number, the particle would stop far away from the centre.

(iv). Evaluation of force orders

Owing to the complexity of blood flow and its intrinsic properties, particles can also experience some other kinds of forces, including Brownian, gravity, thermal buoyancy-induced and external forces. Brownian motion describes the random motion of small particles about or under 1 μm in diameter [72]. The force due to Brownian motion is dominated by a friction force f_b=Γv(t), where Γ is given by Stokes law Γ=6πηa. Gravitational force has the form $f_{\mathrm{g}}=\frac{1}{6}\pi {\rho }_s{a}^{3}g$ [74]; here ρ_s is the density of particle and g is the gravitational acceleration. Thermal buoyancy is caused by the pressure difference in thermal flow systems, and is independent of particle size [73]. Other forces induced by external fields such as the magnetic field [80] is crucial for guiding the motion of particles. Figure 2d presents the particle displacement in 1 s under various forces for different particle sizes. We find that the Brownian force decreases with increase in particle size, while gravitational force increases with increase in particle size; however, thermal buoyancy is independent of the particle size. For the magnetic force magnitude, D_B in this figure represents the space gradient of magnetic field B, and we will introduce this in detail in the last part of this review. For an NP-mediated drug-delivery system, the diameters of particles range from tens of nanometres to a few micrometres. From the figure 2d, we can see that when particle diameters are in tens to hundreds of nanometres, Brownian force plays an important role in the movement of particles, but an increase in particle size, the magnetic force becomes dominant. With further increase in particle size, gravitational force starts to play an important role [81].

3. Passive transport: physiochemical properties (‘4S’ parameters) of particles

As mentioned in the introduction, the initial concept of NP-mediated drug delivery is to use NPs as vehicles to protect drug molecules and deliver them into targeted diseased sites. To realize this kind of ultimate goal, NPs have to experience a tough ‘journey’ inside the human body. Firstly, the intravenously administrated NPs with loaded drug molecules need to circulate within the bloodstream. Under shear flow, RBCs tend to migrate away from vessel walls, creating a ‘CFL’ near the wall. By contrast, NPs which are much smaller than the RBCs, prefer to migrate into the ‘CFL’. Endothelial cells line together to form a monolayer, which forms the inner surface of vessel walls. By entering the ‘CFL’, NPs have a great probability of interacting with these endothelial cells. Endothelial cells near tumours are discontinuous, forming gaps of a few hundred nanometers between cells. It is unclear by which pathway the NPs extravasate and enter the tumour cellular matrix. The current view is that NPs are able to penetrate through these gaps and be retained in tumours because of the pressure created by poor lymphatic drainage, which is well known as the enhanced permeability and retention (EPR) effect [82–84], as shown in figure 1a. However, different arguments suggest that NPs could also extravasate via a transendothelial cell pathway [85]. Therefore, the margination of particles in blood flow plays a crucial role in enabling them to go through the leaky vessel wall under the EPR effect at the tumour site. As we have discussed in §2, the different forces related to margination behaviours of particles depend on their ‘4S’ parameters, as well as local physiological conditions, such as the shear rate of blood flow, vessel size and haematocrit, etc. In the following parts, we will discuss how the ‘4S’ parameters affect margination behaviours in blood flow.

(a). Size effect

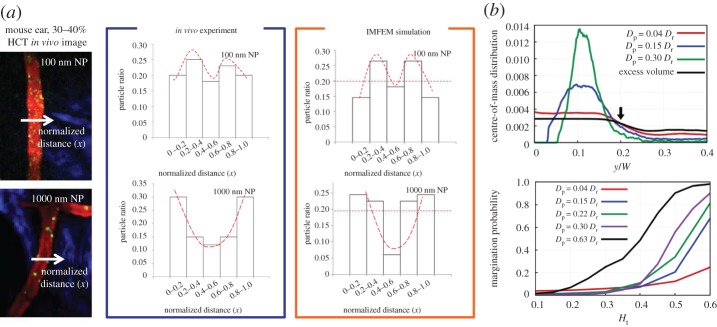
The size of particles (diameter D_p) plays a complex role in the drug-delivery system considering their intrinsic properties and surrounding physiological environment. In view of blood circulation time, experiments [18] demonstrated that liposomes with D_p<70 nm and D_p>300 nm showed a shorter circulation time than those with an intermediate size D_p≈150−200 nm. In consideration of the adhesion density to the vessel wall, spheres with a size of D_p=2 μm outperformed the particles with size D_p=200 and 500 nm [86]. With regard to physiological restriction, NPs with a size below 20–30 nm can be rapidly excreted through the kidneys [11], particles with D_p>3 μm are subjected to enhanced phagocytosis [87] and particles with D_p≈4 μm would be trapped in the smallest capillaries of the body [88]. Regarding the margination of particles, Lee et al. [16] and Li et al. [7] conducted in vivo experiments and immersed finite-element simulations which are shown in figure 3a. It was observed both in experiments and simulations that small NPs (D_p≤100 nm) moved with RBCs in blood flow with limited accumulation in the near-wall region, while large NPs (D_p∼100 nm) tended to accumulate next to the vessel walls. Following works done by Müller [15] provided systematic studies about the size effect on the margination behaviour. Figure 3b presents a typical distribution of particles with different sizes in the blood vessel. Here D_r refers to the corresponding RBC diameter defined as $D_{\mathrm{r}}=\sqrt{A/\pi }$, where A is the area of the RBC, W is the diameter of the vessel and y=0 denotes the location of the vessel wall. It shows that the larger particles are more favourable to accumulate in the near-wall region. Furthermore, they calculated the margination probability for particles with different sizes under different haematocrits, in which we can see that larger particles tend to marginate to the near-wall region to enable further near-wall adhesion. Therefore, if only considering the margination probability, large particles are better than smaller ones due to their collisions with RBCs in blood flow.

Figure 3.

Size effect of particles on their margination behaviour in blood flow. (a) Particle size with 100 nm and 1000 nm are compared. The first and second columns show the in vivo image and quantitative results, respectively. The third column gives the in silico result. (b) Systematic numerical study on the margination behaviour of particles with different sizes. (Reproduced with permission from (a): Li et al. [7] (Copyright 2014 Springer). (b): Müller et al. (Copyright 2014 Nature Publishing Group)). (Online version in colour.)

(b). Shape effect

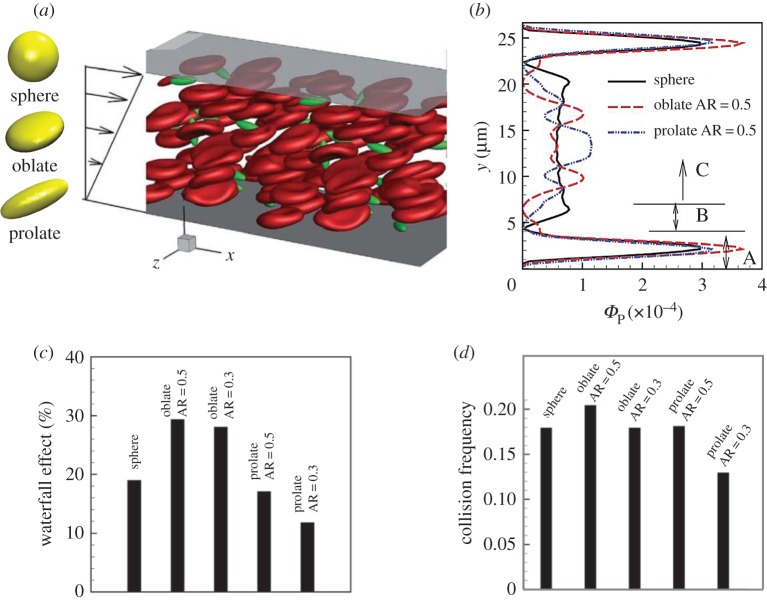
The shape of NPs has also been identified as a key parameter in determining blood circulation time and vessel wall adhesion [89–92]. Non-spherical NPs demonstrate more efficient resistance to MPS sequestration in the blood flow [93–95]. More importantly, non-spherical NPs with higher aspect ratios can marginate more readily than spherical NPs and establish firm adhesion to the vessel walls [96,97]. For instance, Gentile et al. [97] found that disc-shaped and hemispherical NPs outperformed their spherical counterparts in near-wall margination. Toy et al. [19] offered the experimental evidence that gold nanorods exhibited higher margination propensity than nanospheres. The effect of shape on drug carriers had been computationally investigated at different stages in the margination–adhesion cascade by Vahidkhah & Bagchi [20]. The motions, including transport, margination and adhesion for particles with different shapes (sphere, oblate and prolate) in blood flow represented by RBC suspension were studied, which is shown in figure 4a. Figure 4b is a typical distribution of particles with different shapes in the blood flow channel, where Φ_p is the volume fraction of particles at a specific position along height direction. A specific shape performing better in one sub-process over other shapes may not demonstrate a superior performance in another process. In near-wall accumulation, an oblate particle with a moderate aspect ratio stands out, followed by an oblate particle with small AR(AR=0.3), prolate particle with moderate AR(AR=0.5), spherical particle and the lowest for the elongated prolate particle (AR=0.3). This phenomenon is relevant to two mechanisms: the waterfall effect (figure 4c) and the collision with RBCs (figure 4d). In the particle–wall contact process, prolate particles are more likely to contact the wall than spherical and oblate particles due to their alignment along the vorticity axis and large angular fluctuations in blood flow. During the adhesion process, disc-like (oblate) particles perform the best, followed by prolate particles and spherical particles. Thus, the optimal shape of NP-based drug carriers should balance their performance in all the sub-processes of the margination–adhesion cascade.

Figure 4.

Numerical studies of shape effect on margination behaviour of particles. (a) Computational model. (b) Typical distribution of particles in blood flow channel. (c) Waterfall effect fraction for particles with different shapes. (d) Collision frequency between RBCs and particles with different shapes. (Reproduced with permission from Vahidkhah et al. [20] (Copyright 2015 Royal Society of Chemistry)). (Online version in colour.)

(c). Stiffness effect

Compared to rigid particles such as WBCs and platelets, deformable particles demonstrate more complex behaviours in blood flow due to deformation-induced hydrodynamic lift force, which results in their transverse motion. Many theraputic particles are considered to be designed as deformable particles, such as polymer particles and liposomes [98]. As deformable particles may drift away from the wall to the centre of the vessel, this behaviour can extend their circulation time in blood flow. However, compared to size, shape and surface functionalization, the stiffness of NPs receives relatively less attention [12,23,55,56,99–102]. The initial motivation to investigate NP stiffness originates from previous studies about the effect of elasticity on biological systems, such as varying a cell culture substrate’s elasticity to control cell fates and optimize cell growth [103,104]. On the nanoscale, Anselmo et al. [102] demonstrated that softer NPs (10 kPa) were better than stiffer NPs (3000 kPa) in blood circulation time and targeting specific sites both in vivo and in vitro, which also confirms that tuning NP stiffness can extend circulation time, reduce macrophage uptake and improve targeting. On the sub- and micro-scale, Merkel et al. [101] studied the effect of stiffness on circulation and biodistribution of RBC-like microparticles ranging 10–63.8 kPa. They found that an eight-fold decrease in modulus leads to an approximately 30-fold increase in the elimination half-life of NPs in vivo.

Figure 5a presents margination diagrams for rigid and deformable drug carriers with size (D_p=0.3D_r) [105] obtained from two-dimensional simulations. In this figure, non-dimensional shear rate is defined as: ${\dot{\gamma }}^{\ast }=\dot{\gamma }(\mu D_{\mathrm{r}}^3/\kappa )$, where $\dot{\gamma }$ is the shear rate of blood flow and κ is the bending rigidity of particle. In general, the rigid particles marginate better than the corresponding soft particles, and this is most significant at high shear rates, whereas, in a regime of low shear rate, the marginations for both rigid and deformable particles are comparable. This is because, at a low shear rate, the shear stresses are not strong enough to remarkably deform the soft particles. Additionally, we conducted two-dimensional simulations for studying margination behaviours of soft particles in a rectangular channel under simple shear flow. We found that, indeed, the margination probability decreases with increase in Ca (inverse proportional to stiffness), which confirms that rigid particles are more readily marginate than their soft counterparts.

Figure 5.

Stiffness effect on margination behaviour of particles. (a) Comparison of margination probabilities between rigid and deformable particles at different shear rates and haematocrits. (b) Numerical study of margination behaviour of particles in a rectangular channel with different stiffness. (Reproduced with permission from (a): Müller et al. [105] (Copyrigh 2016 Elsevier)). (Online version in colour.)

(d). Surface functionalization effect

Surface functionalization has been considered as one of the most important factors. To some extent, it can also be classified as an active targeting strategy. A large number of surface coatings are employed to promote the ligand–receptor binding process [22], which is a kind of active targeting probe as shown in figure 1a. However, another important application of surface functionalization is to avoid phagocytosis [106]. For instance, the biocompatible and hydrophilic polyethylene glycol (PEG) polymers have been widely used to decorate the surfaces of inorganic NPs. With a high grafting density, tethered PEG polymers form a brush on the surface of these NPs [107–109], and thus, they can be well dispersed in water. Also, due to the grafted PEG chains, the absorption of serum proteins has been dramatically reduced [110]. Therefore, PEGylated NPs demonstrate prolonged circulation time and high accumulation in tumour sites in vivo due to the EPR effect [106,111,112]. The readers interested in surface functionalization are suggested to read relevant review articles, such as [22,113–116].

Table 1 summarizes the influence of NPs’ 4S parameters on their margination behaviours. It should be noted that they may play different roles in the following adhesion process, which is not considered in this work. The table may provide the design principle to obtain high margination in the vicinity of a tumour site or long circulation time in normal blood flow.

Table 1.

Summary of influence of NPs’ 4S parameters on their margination behaviours.

parameter	key observations	key references
size	500 nm and larger diameter spherical NPs exhibit margination behaviour, while 200 nm and smaller ones do not significantly marginate	[16,19,86,97,117,118]
shape	non-spherical NPs with a higher aspect ratio marginate more readily than spherical ones	[19,96,117,119,120]
stiffness	stiff NPs outperform soft ones	[23,55,56,120,121]
surface	studies are too different to draw any meaningful conclusions	[22,106,122]

4. External triggering: magnetic system

Despite extensive efforts made by a large cadre of scientists and clinicians looking for effective cancer treatments, cancer still accounts for approximately 25% of annual deaths in the USA [123]. Nanomedicines are designed to alter the biodistribution and pharmacokinetic profile of small molecules and enable their selective delivery to diseased tissue. The most important pharmacokinetic principle for the delivery of macromolecules and NPs to solid tumours is the EPR effect resulting from the leaky vasculature of tumours, with a gap size of 400 nm to 4 μm between the blood vessel endothelial cells [124]. There are no functional lymphatic vessels inside solid tumours, and those in the tumour margin often display retrograde flow. As a result, macromolecules and NPs are retained in tumours longer than small molecules that can pass in and out easily [125]. A long residence of the NPs’ time in blood facilitates passive tumour accumulation through the EPR effect. However, the tumour accumulation of injected NPs is still relatively low. According to a recent review article [85], an average of only 0.7% of the injected dose through the nanocarriers is delivered to tumours. Improving the delivery efficiency may greatly enhance the impact of nanocarriers, and thereby shorten the timeline for developing nanomedicines for treating life-threatening diseases like cancer.

The therapeutic efficacy of NP-based drug carriers is determined by the proper concentration of drug molecules at the lesion site. NPs need to be delivered directly to the diseased tissues while minimizing their deposition/uptake by other tissues, thereby reducing the potential harm to healthy tissue. Considering the fact that NP concentration at the tumour site is relatively low under the passive targeting strategy, the nanocarriers that can be externally triggered to release encapsulated drug molecules at target tissues hold considerable promise for many diseases, by minimizing non-specific toxicity and enhancing the efficacy of therapy. To achieve the above goal, these drug carriers should be designed to be sensitive to a wide range of external stimuli, including light [25,126,127], ultrasound [27,128,129], electrical [26,130,131] and magnetic [10,24,33,132,133] fields. Then, the release of therapeutics by these nanocarriers can be triggered on-demand and remotely by a physician or patient. In this part, we will mainly focus on the magnetic field-guided NPs for drug delivery. Other external triggerings are described in detail in recent review papers by Wang et al. [24], and Gu and co-workers [134].

(a). Experimental observations

The magnetic field stands out among other external triggering factors due to its excellent tissue penetration [24]. It has been used in whole-body MRI [33]. Magnetic field triggers the release of drug molecules through either thermal or non-thermal ways. When an alternating magnetic field with high frequency is applied, the magnetic moments of magnetic particles (MPs) rotate and return to equilibrium by dissipating thermal energy through Néel (dipole rotation) and Brownian relaxation [135]. Thus, MPs can produce heat under an alternating magnetic field. This mechanism has been used to ablate tumours which is called hyperthermia treatment [132]. A magnetic field with low frequency can cause the mechanical deformation of the drug-delivery system, which induces the drug release. For instance, a low-frequency alternating magnetic field leads to mechanical disruption of liposomal membranes by the motion of MPs, and then the drug loaded in MP can be released [30,136]. Magnetic guidance is a process of enhancement on the deposition of injected magnetically responsive drug carriers at a specific site by applying a static magnetic field [31,32,137,138]. Under the external static magnetic field, drug molecules attached to magnetic materials can be directed to reach the disease location. The delivery systems using a magnetic field with different mechanisms are summarized in table 2. In the following, we will discuss two examples of magnetic field-guided drug delivery by using an external static magnetic field.

Table 2.

Application of an external magnetic field in drug-delivery systems with different mechanisms.

mechanism	frequency	drug-delivery system (magnetic particle)	key observations
heating [139]	220–260 kHz	poly(N-isopropylacrylamide)-based nanogels	on-demand drug release through on–off mechanism
heating [140]	200 kHz	hydrogels composed of magnetic particles	pulsatile release properties over multiple cycles and multiple days
mechanical deformation [30]	10 kHz	liposomes attached to chains of magnetic particles	defects on the liposomal walls trigger the release of encapsulated drugs
mechanical deformation [141]	0 Hz (static)	core–shell particle with grafted PAA-b-PPEGMA and encapsulated enzymes and therapeutic chemicals	shielded polymer brush barrier is overcome under a weak magnetic field, leading to the merge of enzyme and substrate, namely ‘magnetic field remotely controlled selective biocatalysis’
magnetic guidance [31]	0 Hz	poly(lactic-co-glycolic acid)-based nanoparticles loaded with paclitaxel	eight-fold increase in tumour accumulation and about twofold longer survival time
magnetic guidance [133]	0 Hz	iron oxide-coated phosphollipid-polyethylene glycol	disrupting endothelial adherens junctions
magnetic guidance [10]	0 Hz	lactoferrin-tethered magnetic double emulsion nanocapsules	high tumour accumulation and efficient suppressing of cancer growth

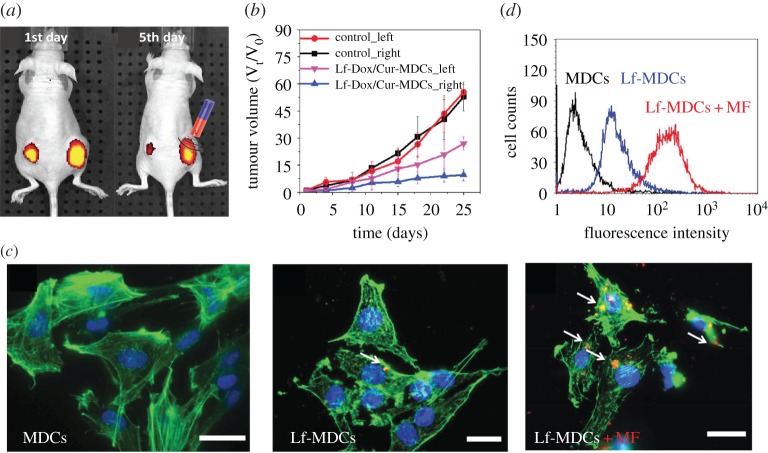
Fang et al. [10] studied the magnetic guidance on the accumulation of magnetic double emulsion nanocapsules (MDCs) and lactoferin (Lf)-tethered MDCs in brain tumour of mice and therapy on tumour volume, which is given in figure 6. After implanting cells to create tumours with specific volumes in each mouse, Lf-doxorubicin (Dox)/curcumin(Cur)-MDCs are injected via the tail vein, and an external magnetic field is placed on the right side, as shown in figure 6a. They found that the tumour cells treated under an external magnet were much smaller than those of the control group (cf. figure 6b). Simultaneously, the accumulation of MDCs/Lf-MDCs in brain tumour is examined. Each of them is loaded with red fluorescent quantum dots for tracking and imaging. The results, presented in figure 6c,d, demonstrated that magnetic guidance offered a higher accumulation in tumour cells, indicating that a magnetic field can improve the internalization efficiency and cellular uptake of MPs.

Figure 6.

Experimental results for magnetic guidance on accumulation of magnetic double emulsion nanocapsules (MDCs) and lactoferrin (Lf)-tethered MDCs (LF-MDCs) in brain tumour of mice and therapy on tumour volume. (a) Variation in fluorescence intensity of nude mice bearing two intravenously injected tumours after 1 and 5 d, with no magnetic treatment on the left tumour. (b) Effect of the treatment on tumour size. (c) Fluorescence microscopic images on cellular uptake of RG2 cells incubated with MDCs, Lf-MDCs and Lf-MDCs under a magnetic field. (d) Comparison of cellular uptake efficiency for difference cases in (c). (Reproduced with permission from Fang et al. [10] (Copyright 2014 Wiley Online Library)). (Online version in colour.)

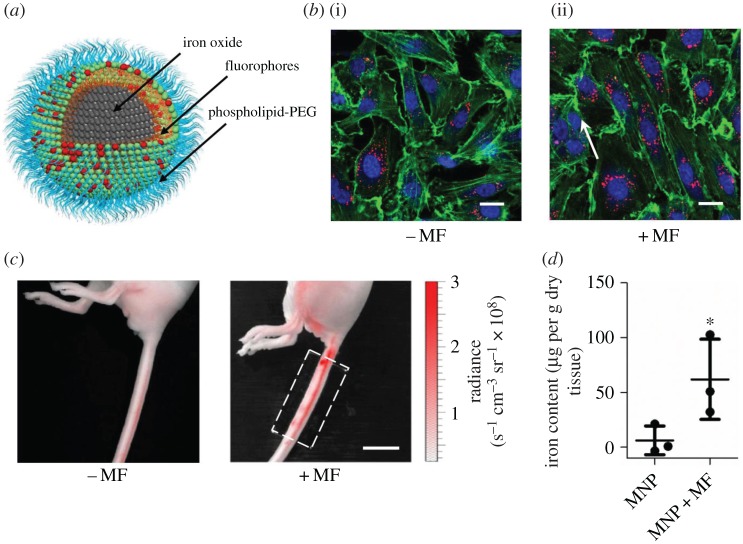
The vascular endothelium plays a selective role in the transport of drug carriers by only allowing specific solutes and molecules to permeate. Qiu et al. [133] demonstrated that the permeability of vascular endothelium can be increased by using an external magnetic field. The iron oxide NPs can temporarily disrupt endothelial adherens junctions under an external magnetic field. Thus, the enhancement of drug transport can rely on an external magnetic field rather than leaky vessels arising from disease states, which is uncertain and not easily controlled. In their study, MPs are water-dispersible and synthesized by coating the nanocrystals with phospholipid-poly(ethylene glycol), as shown in figure 7a. Magnetic force regulated MP uptake and actin dynamics were examined in static cell culture by applying a magnetic field, which was created using NdFeB magnets. The endothelial cells with MPs were incubated without (cf. figure 7b(i)) and with (cf. figure 7b(ii)) magnetic force. The fluorescent images showed that randomly distributed F-actin fibres in endothelial cells became aligned in the direction of the magnetic field, which suggests that magnetic force can regulate the motion of MPs in endothelial cells. Furthermore, they tested the control of vascular permeability using magnetic field in vivo in a mouse lateral tail vein (cf. figure 7c). MPs were injected into the distal end of a mouse lateral tail vein, and the opposite side of lateral tail vein was placed under the external magnetic field. Figure 7d indicates that the MPs in the tail subjected to an applied magnetic field accumulated significantly more than those without a magnetic field. These two results further confirm that, by using an external magnetic field, the permeability of the vascular endothelium can be effectively controlled without damaging its functions.

Figure 7.

Experimental results for enhanced permeability of vascular endothelium by an external magnetic field. (a) Schematic diagram of magnetic particle containing a magnetite nanocrystal and a phospholipid-polyethylene glycol (PEG) coating. (b) Endothelial cells containing magnetic particles incubated without and with magnetic field. (c) Particles with magnetism were injected into a mouse lateral tail vein, and the opposite lateral tail vein was placed under the external magnetic field. (d) Magnetic particles in the mouse tails quantified by a superconducting quantum interference device. (Reproduced with permission from Qiu et al. [133] (Copyright 2017 Nature Publishing Group)). (Online version in colour.)

(b). Computational study

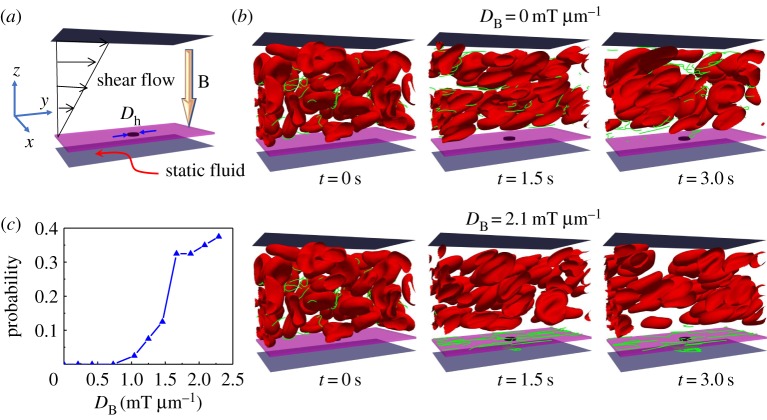
To understand the magnetic field-guided transport of NPs at a tumour site, we set up a computational model, as shown in figure 8a. As the blood flow has non-Newtonian effects, RBCs are explicitly considered in our computational model. The blood vessel is represented by a rectangular channel with width W=27 μm, length L=36 μm and height H=27 μm. The bottom plate of the channel is fixed, and the blood flow is driven by moving the upper plate with constant velocity. There is a static wall with a hole in the centre with diameter D_h=3 μm placed between two plates, and its position is z=3 μm. The wall with a hole is used to mimic the leaky vessel near the tumour site, considering the EPR effect. Simple linear shear flow of $\mathbf{\text{u}}=\{0,\dot{\gamma }z,0\}$ is considered and bounded by the upper plate and wall along the z-direction, thus the fluid between the wall and bottom plate is static. Here, $\dot{\gamma }$ is the shear rate and it remains constant at 200 s⁻¹ in our simulations. The flow direction is along the y-direction and x- and y-directions are applied with periodic boundary conditions. The haematocrit of blood flow is Ht=30% with 40 RBCs inside the channel. We investigate the margination and translocation of magnetic nanoworms under an external magnetic field within blood flow. There are 40 nanoworms inside the channel of 8 μm length. Each nanoworm consists of 32 consecutive MPs, which are connected by harmonic bonds. For the detailed computational methods the readers are referred to our recent studies [80,120].

Figure 8.

Computational study on translocation of nanoworms through ‘leaky’ vessel wall under an external magnetic field. (a) Schematic of the computation model. (b) Snapshots showing translocation of nanoworms without and with magnetic field guidance. (c) Translocation probability of nanoworms against an external magnetic field strength. (Online version in colour.)

The margination of nanoworms are examined by calculating the probability of their transferring into the static fluid layer (SFL) through the ‘leaky vessel’ (hole) in the wall, which is defined as: P=n_f(t)/N, where n_f(t) represents the number of nanoworms inside the SFL at time t and N is the total number of nanoworms in the channel. The external magnetic field B=D_B(0,0,z) is applied along the z-direction. Then only the z-directional magnetic force F^B_z is left non-zero due to its gradient D_B in space, $F_z^{\mathrm{B}}=m_z(\mathrm{\partial }{B}_z/\mathrm{\partial }z)=(V_c\chi /{\mu }^{\ast })D_{\mathrm{B}}^{2}z$. We set the channel in the space z≤0, which makes MPs experience negative magnetic force and marginate to the lower wall of the channel. The strength of the magnetic field B₀ ranges 0–55 mT, which ensures that the maximum value of magnetic strength in the flow field settles within the FDA-suggested range [142].

Figure 8b shows the snapshots of the magnetic nanoworms with and without an external magnetic field. Without the external magnetic field, we found that almost no nanoworms can move into the SFL from the blood flow through the ‘leaky wall’. Whereas under an external magnetic field with strength D_B=2.1 mT μm⁻¹, there are more and more nanoworms moving into the SFL as simulation processes. In addition, we plot the relationship of translocation probability of nanoworms against external magnetic strength in figure 8c. When the external magnetic field is relatively weak (D_B≤1.0 mT μm⁻¹), there is no nanoworms migrating into the SFL. Further increasing the magnetic field strength, the translocation probability drastically increases. Moreover, after the magnetic field strength exceeds approximately 1.71 mT μm⁻¹, the enhancement of the translocation probability of nanoworms is marginal. We can explain the phenomenon in the following way. As the fluid in the SFL is static, a large dragging force should be applied on the nanoworms if they have to move into the SFL to fight against the hydrodynamic static pressure. This is the reason why no nanoworms locate in the SFL when D_B≤1.0 mT μm⁻¹. However, stronger magnetic strength is not always better. Because when the magnetic field is very strong, the nanoworms can quickly marginate to the wall and probably adhere to the wall. Owing to the nearly zero velocity of fluid along the flow direction near the wall, the nanoworms can no longer move and stay there, as in the snapshots given in figure 8b. These adhered nanoworms could not translocate into the SFL any more. In conclusion, a moderate external magnetic field can maximize the probability for translocation of nanoworms into the SFL, considering the balance between the hydrodynamic force and external magnetic force.

5. Conclusion and perspective

In cancer treatment and imaging, the standard strategy for maximizing NP accumulation at a tumour site relies on the EPR effect. Tumour vessels tend to be discontinuous with fenestrations whose size depends on tumour type, stage and location. Sufficiently small NPs, sterically stabilized to have long circulation times (hours to days), passively exit tumour vessels at the fenestrations and generally reach peak accumulation 12–24 h after injection. However, it is currently unknown how the NPs enter the tumour tissue through the leaky vessel wall under the EPR effect. Therefore, in this work, we first discuss the relevant essential forces, which govern the vascular dynamics of drug carriers. Pair collision force, deformation-induced lift force and shear gradient force are three essential forces, determined by their intrinsic ‘4S’ properties and local physiological environment. These forces play different roles in different circumstances. For instance, in the blood flow with a high haematocrit, the pair collision forces due to frequent collisions between RBCs and drug carriers should be the dominant force. However, in the near-wall region without the appearance of RBCs, deformation of drug carriers induced lift force stands out. In addition, some external forces, such as magnetic force is introduced and compared with other NP size-relevant forces like Brownian force. After understanding these physical mechanisms, the effects of size, shape, stiffness and surface functionality of nanocarriers are discussed in detail, which serves as the ‘passive targeting’ strategy. Then, we use the magnetic field as an example to highlight the important role played by the external triggerings in nanomedicine. We name these external triggerings as ‘active targeting’ strategy in this study. Although extensive works have been done to understand the ‘passive targeting’ and ‘active targeting’ of nanocarriers as therapeutic or imaging agents, there are still many questions that remain to be answered.

• (i) Interplay between ‘4S’ parameters of NPs. The effects of size and surface (charge/ligand density) properties of spherical NPs on therapeutic and imaging efficacy have been extensively documented over the past two decades [106,143–145]. Owing to advances in nanofabrication strategies, different shaped NPs can be synthesized with precisely controlled size. This has fostered new theoretical and computational [8,95], as well as experimental (both in vitro and in vivo) studies that have confirmed the importance of shape in controlling the microcirculation, cellular uptake and organ accumulation of NPs. However, due to the interplay between 4S parameters of NPs, especially for the design of NPs with surface-tethered polymers, most experimental studies lead to ambiguous descriptions of NP shape effect. There are two reasons for this: (i) different-shaped NPs have different surface area-to-volume ratios, which makes distinguishing size effect from shape and surface effect difficult, especially when only a few different shapes are considered; and (ii) different-shaped NPs have different numbers of ligands per grafted chain due to their different surface curvatures [146]. These ‘4S’ parameters should be systematically addressed for rationally designing a novel class of NPs with preferential vascular accumulation.

• (ii) Tumour extravasation and accumulation of NPs. Although many computational studies have been done to understand the margination and adhesion of NPs in blood flow, we should emphasize that these computational works do not consider abnormal blood flow, such as seen in the tumour microvasculature. Only a few recent studies have considered the mathematical modelling of transport and extravasation of nanospheres at tumour sites [147,148]. An outlet pore on the vessel wall has been used to mimic the leaky vasculature, while the influence of RBCs has been ignored. Once the nanosphere enters the outlet pore, it is considered to be delivered into the tumour. Under the influence of blood pressure and Brownian motion, the extravasation and tumour accumulation of nanospheres is found to gradually increase with pore size of leaky vessel walls and decrease with particle size for tumours with high interstitial fluid pressure (IFP) [147,148]. These mathematical models provide initial guidance on how to utilize the EPR effect to improve tumour accumulation of nanocarriers during their blood circulation. However, the effects of RBCs and their molecular interactions with nanocarriers (such as particle–particle collision), which could play a predominate role as the RBCs occupy an approximately 20–50% volume fraction within the blood stream, have been ignored. Also, the extravasation of nanomaterials can be dramatically affected by their size, shape, stiffness, high tumour IFP as well as external magnetic dragging force. For instance, at what point will a magnetic dragging force be strong enough to enable nanocarriers to penetrate into the tumour site by overcoming the high tumour IFP? Considering the limitations of the previously mentioned studies a mathematical model taking into account the different physiological conditions between the normal blood flow and abnormal tumour microvasculature will be desired, which can provide a unique and accurate way to study the vascular dynamics and tumour extravasation of nanocarriers under realistic physiological conditions.

• (iii) External triggerings to overcome imbalance design of NPs. An optimal design of a drug carrier is always desired in nanomedicine. It requires the balance of different physiological properties. However, the optimal design of nanocarriers in one sub-process of the whole drug-delivery process may be the worst in another sub-process. For example, stiff particles demonstrate high margination probability in blood flow, while their adhesion probability is worse than soft particles. Thus, design only depending on intrinsic ‘4S’ parameters of particles needs to balance them according to specific processes and specific site/states. For example, some NPs used to treat cancer involving a single tumour grown in a small rodent may not reflect the clinical reality of the disease or its treatment. Moreover, the commonly used approaches in laboratory which works in small animals may not work in large animals, due to the different physiological conditions. With the help of external triggerings factor, some imbalance of NPs could be compensated to offer better efficacy in the drug-delivery system. For instance, the small NPs with long blood circulation time in normal vasculature cannot quickly marginate to the vessel wall and penetrate into tumour site through a leaky wall in the tumour microvasculature. With the help of an external magnetic field, the magnetic force can dramatically increase the probability of near-wall margination of these small NPs and enhance their tumour accumulation under the EPR effect. However, better efficacy, which usually means high loading, may not be the best. Within many trigger systems, the stimulus itself may be harmful to healthy cells. Higher external energy could help NPs to reach larger depths and high delivery efficacy or trigger less-sensitive systems, while it can introduce damage to ambient normal cells near the tumour site. Sometimes the damage is even permanent. We believe the next-generation nanomedicine should be the outcome of combining the intrinsic with external triggering together.

• (iv) Simulation-guided experimental design of NPs. The design of NP-based drug carriers traditionally relies on trial-and-error ‘Edisonian’ approaches, which is very slow and inefficient. Advances in multiscale and multiphysics modelling can foundationally accelerate the design process of novel nanocarriers. With the recently developed multiscale computational models at hand [7,8,80,120], the design process for NP carriers can be dramatically accelerated. The flexibility of the method allows for rapid computational prototyping and testing of drug-delivery complexes under realistic physiological conditions. This provides new insights into the interplay between molecular–scale interactions of intricate delivery vehicles and their transport through the microvasculature. By elucidating the different roles played by the ‘4S’ parameters of NPs, design paradigms for nanocarriers will be immediately available to guide the experimental design of next-generation NPs.

Data accessibility

This article has no additional data.

Authors' contributions

Y.L. and M.W. supervised and conceived this project. H.Y. conducted the simulations, collected and analysed the data, and wrote the manuscript. H.Y. and Z.S. collected and analysed the data for NP transport in blood flow. L.Y. collected experimental studies on magnetic drug-delivery systems. All of the authors commented on the manuscript.

Competing interests

We declare we have no competing interests.

Funding

Z.S., H.Y. and L.Y. acknowledge the partial financial support from the GE Fellowship for innovation.