Determinant Role of Electrogenerated Reactive Nucleophilic Species on Selectivity during Reduction of CO₂ Catalyzed by Metalloporphyrins

Abstract

This work provides insights to understand the selectivity during the reduction of CO₂ with metalloporphyrin (MP) catalysts. The attack of a nucleophile on the carbon of the CO₂ appears as an important event that triggers the catalytic reaction, and the nature of this nucleophile determines the selectivity between CO (or further reduced species) and HCOOH/HCOO^–. For MP, the possible electrogenerated nucleophiles are the reduced metal-center and the hydride donor species, metal-hydride and phlorin-hydride ligand. The reduced metal-center activates the CO₂ with the formation of the metal–carbon bond, which then gives rise to the formation of CO. The hydride donor species trigger the CO₂ reduction by the attack of the hydride on the carbon of the CO₂ (formation of a C–H bond), which results in the formation of HCOOH/HCOO^– (formation of the metal-bonded formate intermediate is not involved). The MP with the metals Ni, Cu, Zn, Pd, Ag, Cd, Ga, In, and Sn are predicted to only form the phlorin-hydride intermediate and are thus suitable to produce HCOOH/HCOO^–. This agrees well with the available experimental results. The MP with the metals Fe, Co, and Rh can form both the reduced-metal center and the hydride donor species (metal-hydride and phlorin-hydride), and thus are able to form both CO and HCOOH/HCOO^–. The production of CO for Fe and Co is indeed observed experimentally, but not for Rh, probably due to the presence of axial ligands that may hinder the formation of the metal-bonded intermediates and thus drive the CO2RR to HCOOH/HCOO^– via the phlorin intermediate.

Introduction

The efficient reductive conversion of CO₂ into fuels, using the energy gathered from sustainable resources, would imply a qualitative leap for modern society.¹ In this context, the reduction of CO₂ by electrochemical means could take advantage of the increasing share of renewable electricity in the global electric production.^2,3 Although considerable research efforts have been made in the last decades in the development of cheap, efficient and selective catalysts for the electrochemical reduction of CO₂, a large-scale viable achievement in this domain is still out of reach.^4,5

Among the classes of catalysts investigated, molecular catalysts (metal complexes),⁶⁻⁸ have the advantage to be easily tunable by the modification of the metal-center and the ligands. Recently, several experimental studies have shown that the modification of the metal center has a determinant impact on the selectivity of the CO2RR.⁹⁻¹¹ For metalloporphyrin (MP) catalysts, this allowed the identification of CO-producing and HCOOH/HCOO^–-producing MP catalysts depending on the metal-center. More precisely, MP with the metal centers Fe and Co, were shown to be particularly efficient to produce CO,⁹⁻¹² although minor products like HCOOH/HCOO^– and hydrocarbons can also be observed. For the series of metals, Rh, Ni, Pd, Cu, Ga, In, and Sn with protoporphyrin ligands, the main product of the CO2RR is HCOOH/HCOO^–.⁹ In this latter series, Rh, In, and Sn are noticeable examples since they can produce significant amounts of HCOOH/HCOO^– with faradaic efficiencies up to 70%.⁹ Yet, a full understanding of these encouraging results remains unclear and a more thorough description of these systems is required to tune them properly.

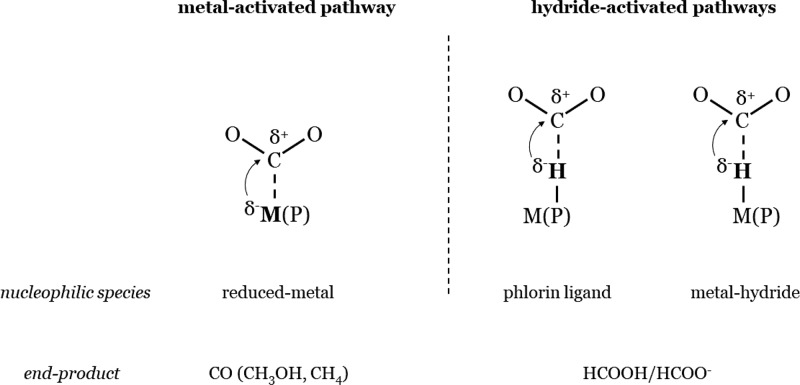
The present theoretical study aims to provide insights in the important impact of the metal center on the selectivity between CO and HCOOH/HCOO^– experimentally observed for the CO2RR with MP catalysts (note that other unwanted competing reactions involving CO₂ such as the carboxylation of the porphyrin ring can take place but are not considered in this work). For this purpose, MP with a porphine ligand (simplest porphyrin ligand without any substituent) and the metal-centers Fe, Co, Ni, Cu, Zn, Rh, Pd, Ag, Cd, Ga, In and Sn have been investigated. We will show that the distinction between metal-electroactive (by which we mean that after the reduction, the additional electron is mostly localized on the metal) and ligand-electroactive (by which we mean that additional electron localized on the ligand) MP, that was highlighted by the numerous experimental studies on the electrochemical behavior of MP,^13,14 is a relevant descriptor to understand the selectivity of the CO2RR with MP catalysts. In general, the metal-electroactive MP with Fe, Co, and Rh, are predicted to be suitable to produce CO (although HCOOH/HCOO^– is also possible, especially for Rh), whereas the ligand-electroactive MP with Ni, Cu, Zn, Pd, Ag, Cd, Ga, In, and Sn are suitable to produce HCOOH/HCOO^–. This general trend is based on two important results: (i) The metal-bonded carboxylato intermediate ([M(COOH)P]), which results in the formation of CO or further reduced species, can only form on the metal-electroactive MP and not on the ligand-electroactive MP. (ii) HCOOH/HCOO^– can be produced by all MP via the formation of hydride donor species, the hydridic phlorin ligand (protonation of the meso carbon of the macrocycle) and the metal-hydride. For this reaction, the intermolecular transfer of the hydride from the catalyst to the CO₂ allows the formation of the CH bond. The production of HCOOH/HCOO^– via metal-hydrides has already been observed or predicted for other catalysts^15,16 and the hydride donor capability of the phlorin ligand has been attracting careful attention for the HER recently.¹⁷⁻¹⁹ Our work here shows that the phlorin-type intermediates also deserve attention for the CO2RR. The significance of the model for the selectivity of the CO2RR developed in this paper, especially the importance of the reaction pathway involving the (phlorin-)hydride intermediate for the production of formic acid, is that it differs substantially from another model that is often assumed in the experimental and theoretical heterogeneous electrocatalysis literature.²⁰ Specifically, Yoo et al. have developed a theoretical model in which CO follows from the *COOH intermediate, with the C binding to the catalyst, and HCOOH follows from the *OOCH intermediate, with the oxygen binding to the catalyst. Both metal-bonded intermediates involve a concerted proton-coupled electron-transfer step in their formation.²¹ In our model, the relevant intermediates would rather be *CO₂^– and *H^–, i.e., formally negatively charged intermediates involving decoupled proton–electron transfer steps.^22,23 A fundamental picture is proposed herein to understand the selectivity of the CO2RR for MP catalysts. Namely, the attack of a nucleophile on the carbon of the CO₂ appears as the decisive event to trigger the CO2RR and the nature of this nucleophile is determinant for the selectivity of the reaction (cf. Scheme 1). In the case where the nucleophile is the reduced metal-center, the CO₂ is reduced to CO, whereas in the case where the nucleophile is a hydride (metal-hydride or phlorin-hydride for MP catalysts) the CO₂ is reduced to HCOOH/HCOO^–. In this context, the product spectrum observed for the CO2RR depends on the nature of the nucleophilic species that are generated upon the reduction of the catalyst. This picture should also be helpful to understand the selectivity of other classes of catalysts.

Scheme 1. Depiction of the Possible Ways of Activating CO₂ and its consequence on the Selectivity of the CO2RR.

Methodology and Computational Details

Methodology

The methodology used to elucidate the mechanisms of the CO2RR and the hydrogen evolution reaction HER, is based on the computation of the thermodynamics of the following chemical reactions (eqs 1–4). Many previous works have shown that thermodynamics-based studies work well for capturing trends, which is a consequence of the Bronsted–Evans–Polanyi relation according to which activation energies generally follow trends in free reaction energies.²⁴ In our computations, we calculate the free energies of the following proton-coupled electron transfer (PCET) reactions:

1

2

3

4

These reactions encompass the formation of the metal-bonded groups, carboxylate, formate, and hydride (eqs 1–3), and in addition, the formation of the phlorin ligand, for which the electron and proton are stored by the generation of a C–H bond on the porphyrin ligand (eq 4). If the proton and electron in eqs 1–4 transfer concertedly (concerted proton–electron transfer, CPET), then ΔG_CPET can be computed using the computational hydrogen electrode (CHE) method²⁵ in which the electrochemical potential for the proton–electron pair (H⁺ + e^–) is equal to the free energy of 1/2H₂ (g) = 0 (definition of the standard hydrogen electrode). The CHE method has been applied successfully to various classes of catalysts such as metallic surfaces and graphene porphyrin-like systems.²⁶⁻²⁸Equations 1–4 can be split in two or three separate events, electron transfer ET, coordination of the CO2 COOR, and proton transfer PT, as written explicitly for reaction 1:

1b

1c

1d

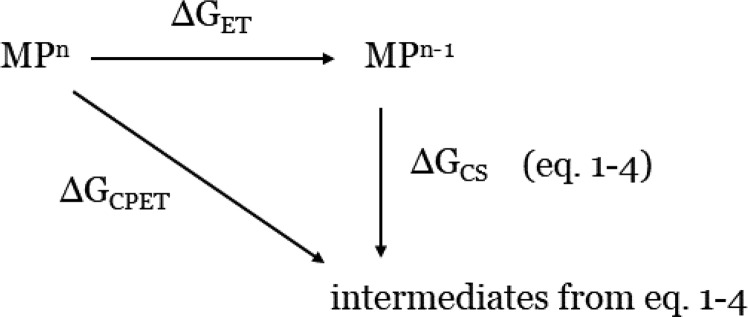
The driving force for the chemical step CS (ΔG_CS = ΔG_COOR + ΔG_PT, where ΔG_COOR is the binding energy of the CO₂ and ΔG_PT is the energy for the proton-transfer step) allows one to qualitatively evaluate the possible formation of each intermediate after the initial reduction step eq 1b. More precisely, a given intermediate can be formed if ΔG_CS is exothermic or moderately endothermic. To compute ΔG_CS, we make use of eq 5, where ET-related energy terms are involved (see also Scheme 2). The reduction step is likely to be outer sphere or noncatalytic (no strong coupling between the energy levels of the electrode and of the catalyst).

5

It is important to stress that these ET-related energy terms (ΔG_CPET and ΔG_ET) are computed to derive ΔG_CS, but the reactions corresponding to “CS” are not electrochemical. The use of the energy difference ΔG_CPET – ΔG_ET to compute ΔG_CS is equivalent to the direct computation of ΔG_CS but circumvent the use of free energy of the proton that is accounted for through the use of the CHE method. In addition, knowing ΔG_CPET and ΔG_ET allows us to derive at which potentials certain reactions would be thermodynamically favorable. We also computed ΔG_ET for some relevant intermediates (phlorin-hydride and metal-hydride; see later in the discussion of the results) and compared with ΔG_ET obtained for the initial reduction of the catalyst to derive some further information about the CO2RR and HER mechanisms.

Scheme 2. Thermodynamics Cycle, with the Relevant Thermodynamics Quantities Involved, Used to Compute ΔG_CS.

Computational Details

All density functional theory calculations were performed with the Amsterdam Density Functional (ADF) software²⁹ (version 2017).³⁰ We used an all-electron triple-ζ quality basis set with an additional polarization function for all atoms.³¹ The Perdew–Burke–Ernzerhof (PBE) functional,^32,33 based on the generalized-gradient approximation (GGA), was used to optimize all the structures. The same functional was used to perform frequency calculations to check that the structures obtained were actual minima, and to derive the zero-point energy and finite temperature corrections necessary to obtain the free energies. All calculations (optimization and frequencies) were performed using the implicit solvation model, COnductor-like Screening MOdel (COSMO),³⁴⁻³⁷ to compute the free energies in solution (water). In a previous work, microsolvation was shown to be necessary to correctly compute the pK_a for the anionic carboxylate intermediate on a cobalt protoporphyrin catalyst (formed following the sequence ET-ET-PT), but microsolvation had little impact on the neutral intermediate formed following the initial PCET.²³ Since in this work we focus on intermediates formed following the initial PCET, microsolvation is not expected to qualitatively modify the results obtained and thus it was not considered. All the energies presented in the discussion were obtained with PBE and correspond to the lowest energies spin state found with this functional. The energy of the lowest spin and higher spin configurations were computed for each metal and intermediates (Table S1 in the Supporting Information summarizes the multiplicity of the ground state found). In most cases, the ground state predicted is the lowest spin configuration except for Fe, Cu and Ag. We also tested the hybrid functionals B3LYP³⁸ and PBE0^39,40 to check if the formation energies (ΔG_CPET) and free energy for the reduction (ΔG_ET) were consistent. For the TM Fe, Co and Rh, ΔG_CPET values of some intermediates change drastically between PBE and the hybrid functionals, whereas for all the other metals all the functionals tested give rather consistent results (cf. Figures S1 and S2). The same trend is observed for the free energy of reduction ΔG_ET. It is known that the accurate computation of the energetics of the different spin states for MP with transition metals can be particularly challenging with DFT. Therefore, the calculation of formation energies that imply a change of the spin-state due to the electron transfer step, is probably impacted.^41,42 The details of the computation of the free energies for reduction ΔG_ET are reported in the Supporting Information together with the discussion on the comparison between the computed and experimental reduction potentials (cf. Table S2). The values obtained are in general in agreement with experiment as the average discrepancy is ∼0.20 eV, although for some metal-centers the discrepancy is larger (up to 0.4 eV). Despite the substantial errors for ΔG_ET in some cases, and probably also on ΔG_CPET, one should keep in mind that in the energy difference between these terms used to compute ΔG_CS (cf. eq 5), the error related to the change in the number of electrons is likely to partially cancel out. Furthermore, we will see in the discussion that the comparison between ΔG_ET for the initial reduction step of the ligand-electroactive MP (for which the expected errors are the largest in some cases, cf. Table S2) and ΔG_ET for the phlorin-hydride intermediates is clear-cut with energy differences larger than the expected errors on ΔG_ET.

Results and Discussion

The computed free energies ΔG_CPET and ΔG_ET, that are used to deduce ΔG_CS are reported in Figure 1. For the transition-metals (TM) and for the post-TM Zn and Cd, the neutral complex, [MP]⁰, was considered as the initial catalyst (+II is the common oxidation state for these metals in MP). Therefore, since we considered catalytic intermediates formed after a single electron transfer (via an overall proton-coupled electron transfer reaction, PCET), it is assumed that the CO2RR and HER can proceed at the reduction potential corresponding to the formation of the anionic catalyst, [MP]⁰ + e^– → [MP]⁻ (this point will be further discussed for CO producing MP as some experimental and theoretical evidence suggest that in some cases the formation of the dianionic catalyst is necessary to trigger the CO2RR). The common oxidation state for p-metals is higher, namely, +III for Ga and In, and +IV for Sn, and therefore, these metals usually display coordination of their axial sites, which can hinder the formation of the metal-bonded intermediates.⁴³⁻⁴⁶ We have considered the cationic complex [MP]⁺ without axial ligands as the initial state for Ga and In, and the cationic hydroxo-bonded complex, [M(OH)P]⁺ for the Sn due to its high affinity for axial ligation.⁴⁶ Therefore, only the formation of the phlorin was considered for Sn since the metal-site is blocked by a hydroxo ligand.

Figure 1.

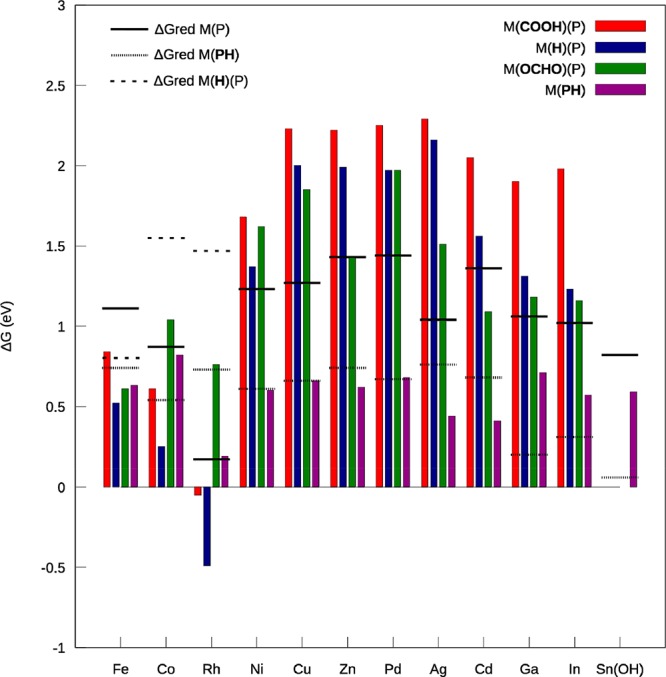
Formation energies of the possible intermediates, following a CPET mechanism according to reactions 1–4 in the text at pH = 0. The free energies for the reduction (ΔG_ET) of the initial catalyst, and the phlorin and metal-hydride (only for metal-electroactive MP) intermediates are displayed by horizontal lines.

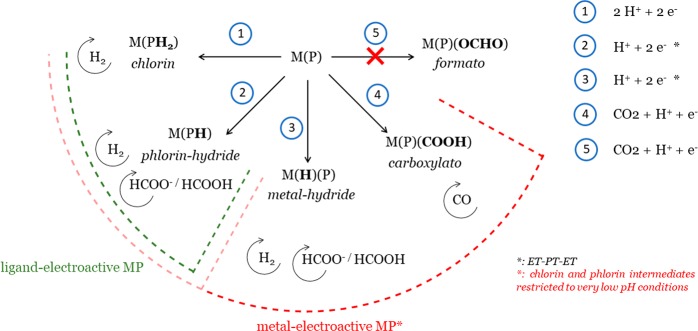
Regarding the metal-bonded intermediates, there is a clear distinction between MP with the metal-centers Fe, Co, and Rh on the one hand, and Ni, Cu, Zn, Pd, Ag, Cd, Ga, and In on the other hand, since their formation energies are in general much more exothermic for the former than for the latter (ΔG_CPET < 1 eV for the former and > 1 eV for the latter). By contrast, the formation energies for the phlorin ligand are in general similar and close to ∼0.5 eV for all the investigated MP. This result is obviously related to the passive role of the metal-center in the formation of the phlorin ligand. To simplify the following discussion of the results obtained, we first describe the results for the ligand-electroactive MP which encompass the metal-centers, Ni, Cu, Zn, Pd, Ag, Cd, Ga, In, and Sn, and next the metal-electroactive MP which encompass the metal centers Fe, Co, and Rh. The distinction between metal-electroactive and ligand-electroactive MP has been highlighted previously^13,14 and will be helpful for the discussion, because, as suggested by the trend described above, there is an apparent relation between this classification and the results obtained for the initial CPET. Scheme 3 summarizes the possible reaction pathways that can take place during CO2RR for the ligand-electroactive and metal-electroactive MP. The reaction pathways corresponding to the investigated intermediates (2–5 in Scheme 3) will be examined and described along the discussion.

Scheme 3. Depiction of the Possible Reaction Pathways That Can Take Place during the Electrocatalytic Reaction for MP Catalysts.

For each pathway, the specific determinant catalytic intermediate and the final reduction product(s) are displayed.

Ligand-Electroactive MP

The formation of the metal-bonded intermediates after the initial reduction of the catalyst (pathways 3–5 in Scheme 3) can be ruled out in most cases due to unfavorable thermodynamics since the computed free energies ΔG_CPET for the metal-bonded intermediates (red, blue, and green vertical bars in Figure 1) are more positive compared to the free energies ΔG_ET for the reduction of the initial catalyst (horizontal black lines in Figure 1), which implies ΔG_CS = ΔG_COOR + ΔG_PT > 0 (cf. computational details). By contrast, the formation of the phlorin ligand (dark purple bar in Figure 1, pathway 2 in Scheme 3) is favorable over a large pH range given the large negative values predicted for ΔG_PT at pH = 0 via the energy difference ΔG_CPET – ΔG_ET (pK_a between 10 and 16) except for the Sn, for which the phlorin is predicted to form in a narrower range of pH (pK_a ∼ 4). As a result, the phlorin ligand is the most likely product of the initial PCET step. For MP with Ga and In, the possible presence of axial ligands does not change this conclusion, since the metal-bonded intermediates cannot form on the bare complex [M(P)]⁺. For the Sn, on the bare [Sn(P)]²⁺ (not presented Figure 1), only the formation of the metal-hydride is predicted to be possible at very low pH (pK_a ∼ 2), therefore the presence of the axial ligands impacts the formation of the first intermediate by hindering the formation of metal-bonded intermediates and by shifting the reduction potential so that the formation of the phlorin becomes possible (ΔG_ET becomes more positive whereas the formation energies of the phlorin is impacted little). The more favorable formation of the phlorin compared to the metal-hydride predicted for ligand-electroactive MP, after the first reduction step, was discussed recently by Solis et al. for a MP complex with M = Ni.¹⁷ Our results suggest that this is a general trend among the ligand-electroactive MP. Interestingly, the phlorin intermediate is predicted to be easier to reduce than the starting catalyst (the computed free energy ΔG_ET for the reduction of the phlorin is lower than for the reduction of the initial catalyst as seen from the dotted lines being generally lower than the full lines in Figure 1). It follows that the reduced phlorin intermediate can be formed following an overall proton-coupled two-electron transfer reaction (PC2ET), with an ET-PT-ET sequence, at the reduction potential for the initial catalyst. As shown in Table 1, the hydride transfer from the reduced phlorin ligand to the CO₂, which eventually results in the formation of solvated formate (intermolecular hydride transfer), is favorable in all cases (for the Sn, it is slightly endothermic but surmountable at room temperature). Thus, the hydricity of the reduced intermediate is great enough to allow the hydrogen transfer and the formation of HCOOH/HCOO^–. It follows that the reduced phlorin intermediate is the key catalytic intermediate of the CO2RR to HCOOH/HCOO^–.

Table 1. Computed Free Energies (in eV) for the Formation of the Solvated Formate from the Reduced Phlorin [M(PH)]ⁿ⁻¹ or Reduced Metal-Hydride [M(H)P]ⁿ⁻¹ (Intermolecular Hydride Transfer), and for the Formation of the Metal-Bonded Formate Intermediate from the Reduced Phlorin (Intramolecular Hydride Transfer)^a.

metal	ΔG/eV for HCOO–sol from reduced phlorin [M(PH)]n−1	ΔG/eV for HCOO–sol from reduced metal-hydride [M(H)P]n−1	ΔG/eV for [M(OCHO)]P from reduced phlorin [M(PH)]n−1
Fe	–0.60	–0.55	–
Co	–0.59	–1.03	–
Rh	–0.15	–0.21	–
Ni	–0.44	–b	0.51
Cu	–0.55	–b	0.11 (−0.66)
Zn	–0.58	–b	–0.33 (−0.26)
Pd	–0.58	–b	1.77
Ag	–0.43	–b	0.17 (−0.60)
Cd	–0.33	–b	–0.40 (0.08)
Ga	–0.14	–b	–0.63 (0.49)
In	–0.11	–b	–0.67 (0.37)
Sn(OH)	0.12	–b	–

^aIn parentheses are reported the free energies for the desorption of the metal-bonded formate group (only for metals for which the formation of this intermediate is possible). n is the charge of the initial catalyst (n = 0 for TM and the post TM Cd and Zn, and n = +1 for p-metals).

^bThe metal-hydride does not form on ligand-electroactive MP (ΔG > 0).

The phlorin-hydride intermediate should also be involved in the HER reaction following a heterolytic mechanism in which the hydride reacts with a proton or a water molecule (H^– + H⁺ → H₂ or H^– + H₂O → H₂ + OH^–). Figure 2 summarizes the general reaction mechanism for the CO2RR and HER reactions with hydride donor species (pathways 2 and 3, Scheme 3).

Figure 2.

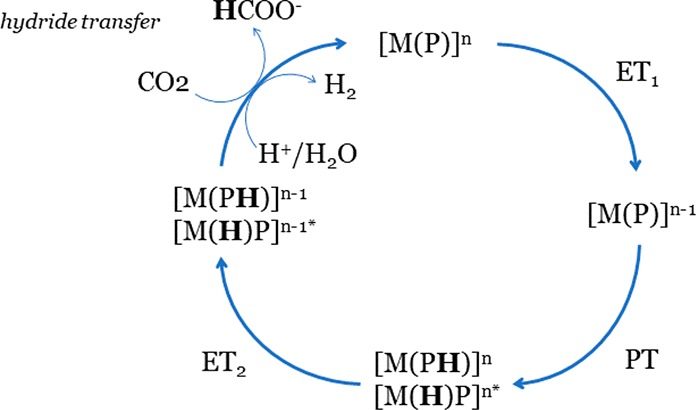
Reaction mechanisms for the CO2RR and HER via hydride donor species. n stands for the charge of the resting catalyst (n = 0 for MP with TM and post-TM Zn and Cd, n = +1 for Ga, In and Sn). Asterisk (*) shows that the formation of the metal-hydride is specific to the metal-electroactive MP and cannot form on ligand-electroactive MP.

It should be noticed that for all the metals, except Ni and Pd, the thermodynamics for the formation of the reduced metal-bonded formate intermediate, [M(OCHO)P]ⁿ⁻¹, following an intramolecular hydride transfer mechanism from the reduced phlorin ligand (concerted formation of the CH bond and metal–oxygen bond, [M(PH)]ⁿ⁻¹ + CO₂ → [M(OCHO)]ⁿ⁻¹), is possible based on thermodynamics (cfTable 1). For Ga and In, it is predicted to be even more favorable than the intermolecular mechanism. Hence, the metal-bonded formate group could form during the CO2RR on most metals, but it is important to stress that the key precursor in its formation remains the phlorin hydride (pathway 2, Scheme 3). It should be noticed that this mechanism for the formation of formic acid is in contrast with what is often assumed in theoretical studies (especially on metal surfaces), namely that the formation of the metal-bonded formate is achieved by the concerted formation of the metal–oxygen bond and the C–H bond with a proton (pathway 5, Scheme 3).²¹ Since the desorption of the metal-bonded formate from the MP is favorable for Cu, Zn, Ag and Cd, the formate intermediate should only be a transient species formed without significant impact on the catalytic reactions. However, the desorption of the metal-bonded formate group is predicted to be more difficult for Ga and In and may remain coordinated, especially at pH > ∼3.75, since under such pH conditions, even for the anionic complex, the protonation of the formate is not favorable and thus cannot facilitate its desorption. In any case, the formation of the metal-bonded formate does not prevent the formation of the phlorin ligand and thus the CO2RR to HCOOC/HCOO^–, but it may change the onset potential (shifted to more negative potentials upon the coordination of axial ligand).

The results obtained so far allow us to draw some conclusions regarding the selectivity of the CO2RR for ligand-electroactive MP. They suggest that these catalysts should be primarily HCOOH/HCOO^– producing via the formation of the phlorin-hydride intermediate, whereas they should not be particularly performant to produce CO, since the formation of the carboxylate intermediate is thermodynamically unfavorable. Experiments have shown that MP with P the protoporphyrin and M the investigated metal centers indeed produce formic acid instead of CO (i.e., M = Ni, Pd, Cu, Ga, In, and Sn).⁹ It is worth noting that other experimental results point out that MP catalysts with Cu and Zn can produce a significant amount of CO instead of HCOOH/HCOO^–, as expected from our results.^47,48 In the case of Cu, this selectivity was proposed to be due to the formation of small copper clusters and not to the molecular metal active site.⁴⁹ For the ZnP case, the redox-innocence of the metal-center during the electrocatalytic reaction is well-established and the protonation of the reduced ligand is likely to take place. The detailed mechanism for the CO2RR remains elusive, especially because it is not clear if the metal-bonded *CO₂ and *COOH intermediates are formed during the electrocatalytic reaction. According to our calculations, the formation of these intermediates is thermodynamically unfavorable for the investigated ligand-electroactive MP (thermodynamics for the binding of CO₂ is discussed later), but they may be stabilized by the interaction with surrounding functional groups borne by the substituents of the macrocycle (methyl groups in ref (43)). Furthermore, as for the CuP, instability of the metal center toward decoordination may also be responsible for the formation of CO. These considerations show that the propensity to form the phlorin-hydride intermediate is necessary for the formation of formic acid, but attention must be paid also to other factors that can considerably impact on the selectivity by promoting other competing pathways.

Among the ligand-electroactive MP whose activity for the CO2RR has been studied experimentally, In and Sn stand out from the rest since they produce significant amounts of formic acid at pH ≥ 3, with the remaining current going to the HER.⁹ The different hydricities that can be derived from Table 1 for the reduced phlorin intermediate, should not drastically influence the HER vs CO2RR competition since the free energies for the formation of the solvated formate or hydrogen should have a similar linear dependence on the hydricity. Instead, the different activities observed for the production of HCOOH/HCOO^– are probably due to the competition between the formation of the phlorin and the chlorin intermediates (chlorin is the doubly reduced porphyrin intermediate that allows the production of hydrogen by an elimination step but does not result in the reduction of CO₂, pathway 1 in Scheme 3).⁵⁰ Indeed, it was demonstrated that, in aqueous solutions, the formation of the chlorin tends to be favored over the formation of the phlorin, compared to organic solvents.⁵¹ Furthermore, low pH condition is also known to favor the formation of the chlorin over the phlorin.⁵¹ Therefore, given the experimental condition used for the comparison between the different metal-centers (aqueous solution, pH = 3),^9,12 which are very favorable for the formation of the chlorin ligand, it is not surprising that HER dominates for most of the investigated MP. The greater activity for the CO2RR obtained for MP with In and Sn is probably due to the strong electronegativity of these metals. This property is known to favor the formation of the phlorin over the chlorin by pulling the electron density toward the porphyrin core, and hence, it favors the protonation of the meso carbons.⁵¹ It is important to stress that with different experimental conditions and with an adequate choice of substituents for the macrocyle ring (electron withdrawing groups on meso carbons), all the investigated ligand-electroactive MP could in principle be relevant catalysts to produce HCOOH/HCOO^–. An intriguing point in the experimental results obtained for Sn and In is that the onset potential for the total current at pH > 3 exhibits a linear pH dependence on the NHE scale which is a characteristic feature for concerted proton–electron transfer.^9,21 Given the much more negative values for the experimental onset potentials at pH > 3 (E_onset < −1 V vs NHE)) compared to the theoretical equilibrium potentials predicted for the formation of the phlorin ligand following a CPET step (E_CPET ∼ −0.5 V vs SHE at pH = 0), it is very unlikely that the initial step in the experiment corresponds to the formation of the phlorin ligand following a concerted CPET step. Instead, the initial step could be the concerted reduction of the catalyst and protonation of an anionic axial ligand as this reaction has been observed for p-block MP, followed by dissociation from the complex.^44,45

Metal-Electroactive MP

The calculations clearly predict that the formation of the metal-bonded carboxylate and metal-hydride intermediates (pathways 3 and 4, Scheme 3) are much more favorable than on the ligand-electroactive MP, whereas the formation of the formate group is still unlikely for Co and Rh (for MP with Fe, the formation energy computed is probably largely underestimated due to the overstabilization of the formate intermediate which is in a high spin configuration, cf. Table S1). The favorable formation of the metal-bonded carboxylate group (ΔG_COOR + ΔG_PT < 0) implies that the catalysis of the CO2RR to CO or further reduced species, is possible following the initial proton-coupled electron transfer step (PCET) for metal-electroactive MP. This result was already demonstrated for Co in previous theoretical works^23,28 and agrees with experiment since CO or CH₄ are detected for MP with these metals.⁹ Yet, it has been also shown for Co MP that the CO2RR mechanism to CO is pH dependent as the pK_a for the neutral carboxylate intermediate is relatively low (pK_a[CoP(COOH)] ∼ 3.5).²³ At higher pH (pH > pK_a[CoP(COOH)]), the formation of the dianionic catalyst after two reduction steps is necessary to trigger CO2RR to CO. Regarding MP with Fe, experimental and theoretical evidence suggest that two reduction steps are necessary to trigger the CO2RR to CO (formation of the formal Fe(0) oxidation state).^8,52 The results obtained suggest that the formation of the carboxylate intermediate is possible at low pH for Fe (ΔG_CS < 0 at pH = 0), similarly to the Co, and thus CO2RR to CO is predicted to be possible at low pH, but two reduction steps (formation of the formal Fe(0)) should be necessary at higher pH. The accurate determination of the pK_a for the neutral and anionic carboxylate intermediates would be necessary to further address this point. Yet, we will see later that these observations do not change the conclusion that CO2RR to CO is specific to MP that form a reduced metal center whereas a hydride is necessary to form HCOOH/HCOO^–. For the Rh, CO has not been observed experimentally, in contrast with the theoretical prediction.⁹ This may be due to the presence of axial ligands for the initial catalyst which can hinder the efficient formation of the carboxylate intermediate. A strong affinity for axial ligation for the Rh has been observed experimentally and has been held responsible for its peculiar electrochemical behavior.^53,54 An indication for the presence of axial ligands in the experiment is the fact that the onset potential for the CO2RR at pH = 3 and higher (E < −1.2 V vs NHE), is substantially more negative than the computed reduction potential for the bare catalyst (E ≈ −0.2 V vs NHE). The presence of axial ligands is known to substantially shift the reduction potential toward more negative potentials (the reduction potential computed for the pentacoordinated hydroxo complex [Rh(III)P(OH)] is E ≈ −0.8 V vs NHE). Regarding the phlorin intermediate, its formation is predicted to be favorable over a large pH range for Fe but only at very low pH for Co and Rh (ΔG_PT ≈ 0 or pK_a ≈ 0 for MP with Co and Rh at pH = 0). Yet, as pointed out above, for the Rh, the possible presence of axial ligands may drastically shift the reduction potential of the initial catalyst toward more negative potential whereas the formation energy of the phlorin should be little impacted. It follows that the formation of the phlorin intermediate should be favorable over a much greater pH range for the axially bonded Rh MP catalyst compared to the bare MP catalyst. Since both the metal-hydride and the phlorin ligand can be formed for the investigated metal-electroactive MP, these catalysts can potentially catalyze the CO2RR to HCOOH/HCOO^– via the intermolecular hydride transfer mechanism. The formation of HCOO^– via the intermolecular hydride transfer mechanism is predicted to be favorable for all metals and from both the reduced metal-hydride and phlorin intermediates (cf. Table 1). As a result, the CO2RR to HCOOH/HCOO^– can be achieved following the mechanism with hydride-donor species as displayed in Figure 2 (pathways 2 and 3 in Scheme 3). Yet, it is important to note that for Co and Rh, these reaction pathways exhibit some restrictions compared to ligand-electroactive MP. Indeed, for Co and Rh, the metal-hydride is more difficult to reduce than the initial catalyst (ΔG_red M(H)(P) > ΔG_red M(P), cf. Figure 1), so the formation of HCOOH/HCOO^– via this intermediate should only take place at significant overpotential (conversely CO2RR to CO can proceed at the reduction potential of the initial catalyst). Furthermore, regarding the Rh, one should keep in mind that the possible presence of axial ligands can hinder the formation of the metal-hydride, and in such a case the production of HCOOH/HCOO^– is likely to mostly proceed via the phlorin intermediate for this metal. For the Co, as mentioned previously, the phlorin intermediate can only form at very low pH (pH ≈ 0). The small amount of formic acid detected for the Co MP (minority product for the CO2RR) at pH = 1, is probably produced via the phlorin intermediate.¹² For Fe, the calculations suggest that the formation of the reduced metal-hydride and phlorin intermediates can be achieved following an overall PC2ET mechanism, similar to the ligand-electroactive MP (M(H)P and M(PH) are easier to reduce than the initial catalyst). Yet, experimentally, no HCOOH/HCOO^– is detected for Fe at pH = 3,⁹ which indicates that the reduction pathway to this product may not be competitive compared to the HER or CO2RR to CO, but it is not clear why it is so. For Co and the axially bonded Rh MP, the PC2ET reduction mechanism via the phlorin intermediate is also possible. The reason why Rh produces a significant quantity of HCOOH/HCOO^– compared to H₂ is not clear but may be related to the competition between the formation of the phlorin and the chlorin intermediates, as for In and Sn.

Discussion

The results described above highlight the fact that the distinction between metal-electroactive and ligand-electroactive MP is a helpful descriptor to understand the selectivity and the reaction pathways that take place during the CO2RR for this class of catalysts. Ligand-electroactive MP tend to favor the formation of the phlorin-hydride intermediate suitable to produce formic acid, whereas the formation of the metal-bonded intermediates is more difficult on these catalysts and thus, they are less likely to produce CO (cf. Scheme 3). On the other hand, metal-electroactive MP tend to favor the formation of the metal-hydride and metal-carboxylate intermediates over the phlorin-hydride and thus they are more likely to produce CO than the ligand-electroactive MPs, although the production of HCOOH/HCOO^– is still possible via the metal-hydride intermediate (cf. Scheme 3). However, it should be kept in mind that other factors can considerably influence the selectivity, such as the strong interaction between the metal and coordinating species that can prevent the formation of metal-bonded intermediates (as proposed for the Rh), the presence of built-in functional groups, or the decoordination of the metal-center that may promote the formation of CO.

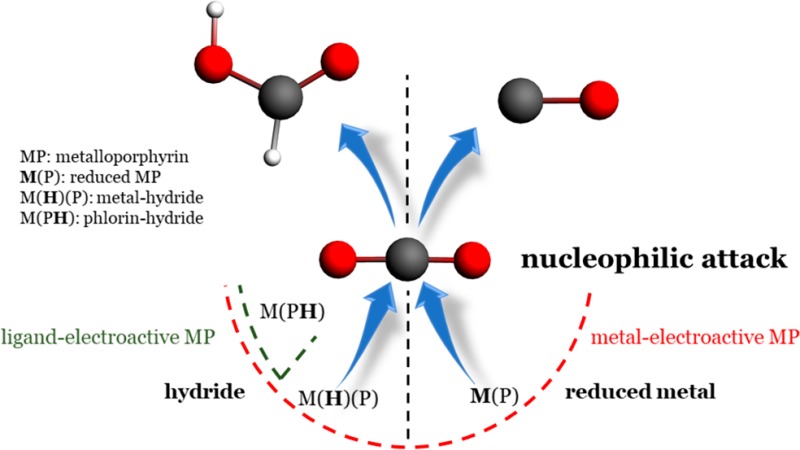
The investigation of the association step between the metal and the CO₂ provides insight in the underlying fundamental point corresponding to the ligand-electroactive vs metal-electroactive descriptor put forward in this paper. More precisely, we optimized the reduced CO₂ adducts, [MP-CO₂]ⁿ⁻¹ and [MP–OCO]ⁿ⁻¹, respectively, formed via the formation of the metal–carbon and the metal–oxygen bonds. The computed thermodynamics for the formation of these intermediates are reported in Table S3 in the Supporting Information. The formation of the reduced CO₂ adduct [M(CO₂)P]ⁿ⁻¹ is clearly more favorable on the metal-electroactive MP compared to the ligand-electroactive MP, for which [M (CO₂)P]ⁿ⁻¹ is not even stable in some cases (dissociation of the CO₂ during optimization). Furthermore, for the ligand-electroactive MP that can form the CO₂ adduct, the thermodynamics for the binding step is rather unfavorable (ΔG for binding CO₂ > ∼0.5 eV), and thus, this step may be hindered for these catalysts. The unfavorable formation of the metal–carbon bond for ligand-electroactive MP impedes the reaction pathway to CO. This corroborates what is obtained from the study of the initial PCET step. It is worth noting that, in the structure of [M(CO₂)P]ⁿ⁻¹, as observed in other works,²⁸ the backbone of the CO₂ is bent due to the activation of the substrate by the metal. The formation of the CO₂ adduct [M(OCO)P]ⁿ⁻¹ is predicted to be only possible for a few ligand-electroactive MP, and in the structure obtained the backbone of the CO₂ remains linear. Therefore, it seems that the activation of the CO₂ via the formation of the metal–oxygen bond is not possible (the metal–oxygen interaction is mostly electrostatic). This absence of activation indicates that for MP in general, the formation of the metal-bonded formate group is probably kinetically hindered. Furthermore, the fact that [M(OCO)P]ⁿ⁻¹ is not stable or difficult to form shows that, for all MP, the unfavorable formation of the metal–oxygen bond prevents the formation of the metal-bonded formate group following a PCET (pathway 5 on Scheme 3). This consideration further emphasizes that a local hydride source (phlorin-hydride or metal-hydride) is necessary to produce formic acid. To summarize, for MP catalysts, the attack by a reduced species with a strong nucleophilic character (hydride or reduced metal-center) on the carbon of the CO₂ appears as a key to initiate the CO2RR. From this viewpoint, the reduction pathway to CO and the reduction pathway to HCOOH/HCOO^– via the intermolecular hydride transfer share the same triggering event: the attack of a nucleophile on the carbon of the CO₂. In this context, as displayed in Scheme 1, the nature of the reactive nucleophile species generated upon the reduction of the catalyst governs the nature of the product observed. The metal-activated pathway, in which the reduced metal is the nucleophile, results in the formation of CO, whereas the hydride activated pathway, where the hydride is the nucleophile (metal-hydride or phlorin ligand for MP), results in the formation of HCOOH/HCOO^–. This picture allows one to understand in more detail the importance of the metal-electroactive vs ligand-electroactive descriptor put forward to clarify the selectivities observed for MP catalysts. Beyond the specificity of MP catalysts, the necessity to identify the possible reactive electrogenerated nucleophilic species may be useful to other classes of catalysts to understand the CO2RR.

Conclusion

This work provides insights in important mechanistic events that influence the selectivity of the CO2RR with metalloporphyrin (MP) catalysts. The attack of a nucleophile, generated upon the reduction of the catalyst, on the carbon of the CO₂, appears as an important requirement to trigger the CO2RR, and the nature of this nucleophile is determinant for the selectivity of the reaction. The proposed picture is not specific to MP and can be used to understand the selectivity of other catalysts. For MP, the nucleophile can be the reduced metal-center, or a hydride transferred from the metal-hydride group or from the phlorin ligand. In the case of the reduced metal-center, the metal–carbon bond can be formed and the reduction pathway results in the formation of CO or further reduced species, via the metal-bonded carboxylate intermediate. In the case of the hydride, the carbon–hydrogen bond is formed, and HCOOH/HCOO^– is the end-product of the CO2RR. It is worth noting that in the picture proposed, the formation of the metal–oxygen bond and the metal-bonded formate intermediate is not a requirement for the CO2RR to HCOOH/HCOO^–. In this context, the selectivity of a given MP for the CO2RR is determined by the identification of the potential nucleophilic species formed upon the reduction of the catalyst, and not by the relative stability of the initial catalytic intermediate formed (the carboxylate and the formate intermediates). The metal-electroactive MP with Fe, Co, and Rh metal-centers generate the reduced metal-center and are thus predicted to be suitable CO-producing MP. Yet, the formation of the hydride donor species, metal-hydride and phlorin ligand, is also possible for these metal-electroactive MP and may explain why a small amount of formic acid formation can be observed for these catalysts. Regarding Rh, the strong affinity of this metal for axial ligation can hinder the efficient formation of metal-bonded intermediates which can impact the production of CO and HCOOH/HCOO^– via the formation of the metal-hydride. For the ligand-electroactive MP, with Ni, Cu, Zn, Pd, Ag, Cd, Ga, In, or Sn metal center, the metal has a passive role and cannot bind any intermediates due to the lack of additional electron density on M during the reduction of the catalyst. The CO2RR takes place exclusively via the formation of the hydride donor phlorin ligand (nucleophilic species), and thus, these catalysts appear as good candidates for the selective production of HCOOH/HCOO^–, as observed in the experiment. The large discrepancy in the activity observed experimentally for the production of HCOOH/HCOO^– as compared to hydrogen evolution is deemed to be related to the competition between the formation of the phlorin and the chlorin intermediates, with this latter intermediate being inert for the CO2RR. The aspects covered in this work provide new guidelines for the design of efficient and selective catalysts for the CO2RR.

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/jacs.7b11267.

• Computed spin state of the ground state for all the optimized structures; free energy differences between the formation energies computed with PBE and PBE0/B3LYP; computation of absolute reduction potential and comparison with the experiment; computed thermodynamics for the association between CO₂ and the reduced catalyst (PDF)

The authors declare no competing financial interest.