Abstract
Culturally, people tend to abstain from alcohol intake during the weekdays and wait to consume in greater frequency and quantity during the weekends. The current research sought to empirically justify the days representing weekday versus weekend alcohol consumption. In study 1 (N = 419), item response theory was applied to a two-parameter (difficulty and discrimination) model that evaluated the days of drinking (frequency) during the typical 7-day week. Item characteristic curves were most similar for Monday, Tuesday, and Wednesday (prototypical weekday) and for Friday and Saturday (prototypical weekend). Thursday and Sunday, however, exhibited item characteristics that bordered the properties of weekday and weekend consumption. In study 2 (N = 403), confirmatory factor analysis was applied to test six hypothesized measurement structures representing drinks per day (quantity) during the typical week. The measurement model producing the strongest fit indices was a correlated two-factor structure involving separate weekday and weekend factors that permitted Thursday and Sunday to double load on both dimensions. The proper conceptualization and accurate measurement of the days demarcating the normative boundaries of “dry” weekdays and “wet” weekends are imperative to inform research and prevention efforts targeting temporal alcohol intake patterns.
Keywords: Alcohol, Weekend drinking, Weekday drinking, Item response theory, Confirmatory factor analysis
Diurnal fluctuations in alcohol use are attributed to socially and culturally acceptable normative practices. The flexible weekends, representing an interlude to the structured routine of the weekdays, are conducive to behavioral excess and vices (Wood et al. 2007). Commonly, weekends are viewed as a period to unwind, with these days exhibiting considerably higher rates of alcohol consumption than weekdays (Ekholm, Strandberg-Larsen, and Grønbæk 2011; Kuntsche and Cooper 2010; Studer et al. 2014). A common method to escape the predictability and stressors of weekday life is by imbibing alcoholic beverages during the end of the week (Orcutt and Harvey 1991). The elevated rate of alcohol intake upon arrival of the weekend coincides with an upsurge in public health consequences, including physical injuries and deaths attributed to motor vehicle accidents (Matzopoulos, Peden, Bradshaw, and Jordaan 2006) and the risk of fatality in general (Mørch, Johansen, Løkkegaard, Hundrup, and Grønbæk 2008).
Despite the variety of investigations examining disparities in risk factors and outcomes attributed to weekend and weekday alcohol consumption, a major gap persists in the literature regarding the optimal measurement representations of weekend and weekday alcohol use (Furr-Holden et al. 2011; Houwing and Twisk 2015; Palma et al. 2007). Furthermore, a number of studies have called for the development and implementation of interventions tailored to weekend drinkers and their intake behaviors due to the increased likelihood for detrimental consequences on these days (Kuntsche and Cooper 2010; Woodyard and Hallam 2010). Empirically understanding how the 7 days of the week should be conceptualized and categorized with regard to alcohol use is a crucial initial step to isolate and curtail risky usage patterns and to develop tailored prevention efforts.
Currently, no public consensus or widespread methodological standard exists regarding when alcohol intake commences and ceases during the weekdays and weekends. Ignoring the weekday versus weekend distinction entirely, some studies have consolidated the 7 days of drinking into a single index or factor to capture drinking behavior (Collins, Parks, and Marlatt 1985; Hummer, Labrie, Lac, Sessoms, and Cail 2012; Labrie, Lac, Kenney, and Mirza 2011). Technically, according to the Gregorian calendar, Monday to Friday constitute the weekdays and Saturday to Sunday the weekends. Previous investigations applying a 2-day weekend have adhered precisely to this division of dry and wet days (Hillbom and Kaste 1983; Matzopoulos et al. 2006). Other studies, however, have operationally defined weekend intake as the period involving Friday to Saturday (Bråthen, Brodtkorb, Sand, Helde, and Bovin 2000; Ekholm, Strandberg-Larsen, and Grønbæk 2011; Hoeppner et al. 2012), with participants found to be most resistant to the bottle on Monday and Tuesday (Argeriou 1975).
Aside from the conflicting 2-day weekend classifications, 3- and 4-day weekend conceptualizations also have been applied in the literature. Adopting a 3-day weekend paradigm, Mørch et al. (2008) determined that consuming at least seven alcoholic beverages during a Friday, Saturday, and Sunday weekend, but consuming just one beverage during a 4-day weekday (Monday to Thursday), heightened the risk of death. Lahaut, Jansen, van de Mheen, and Garretsen (2003) implemented the same conceptualization of weekends and weekdays to evaluate the statistical properties of different recall assessments of alcohol usage. Woodyard and Hallam (2010) expanded the categorization of weekends to the 4 days spanning Thursday to Sunday, a definition that doubles the days of intake by including drinkers and drinking behaviors excluded by 2-day weekend studies.
Further compounding measurement discrepancies in the literature, other investigations have assessed weekday use as occurring from Monday to Wednesday and weekend use as Friday to Saturday, leaving out Thursday and Sunday altogether (Cleveland and Almeida 2013; Turrisi et al. 2013). Research supports that Thursday drinkers are characteristically different from typical weekday and weekend users (Hoeppner et al. 2012; Paschall, Kypri, and Saltz 2006). Whereas this disagreement concerns the inclusion of Thursday as a weekday or weekend, most inconsistencies across research stem from whether to classify Sunday as a weekday or weekend, or to exclude Sunday altogether.
Sunday is an enigma when it comes to classifying drinking behavior. Does Sunday capture the typical habits of weekday or weekend consumption? A sociocultural distinction between these two temporal periods is that weekdays exhibit greater constancy whereas weekends are marked by more varied events and activities (Wood, Sher, and Rutledge 2007). Applying this logic, some people might perceive Sunday as a day of psychological and emotional transition in preparation for the upcoming week of work or school. Instead, if Sunday is perceived as part of the weekend, the day may be deemed as less predictable and a function of circumstances: Some people might be receptive to drinking if the opportunity arises. Thus, Sunday alcohol usage may be motivated by the perceived structure, or lack thereof, of the prototypical Sunday. As Cleveland and Almeida (2013) asserted, greater variations in alcohol intake patterns may be evidenced throughout the 7 days of the week than the simple dichotomy of the heavily organized weekdays and carefree weekends.
Regardless of the particular measurement variation in the research, the consensus is that weekends tend to foster greater prevalence of alcohol use than weekdays (Kuntsche and Cooper 2010; Studer et al. 2014). The vast majority of published studies comparing weekday to weekend drinking, however, apply arbitrary distinctions not based on empirical criteria. These investigations raise the question of whether the results obtained and the implications drawn would have been drastically different had the operational definitions of weekday and weekend included or excluded certain days. The central goal of the current research effort is to remedy this shortcoming by establishing an empirical rationale for the days constituting weekday versus weekend drinking. Findings are expected to confer theoretical and applied insights for future alcohol research. Conceptual and statistical clarifications of the boundaries that mark the weekend are essential for the appropriate measurement and interpretation of cyclical alcohol use patterns across the standard 7-day week (Kuntsche and Cooper 2010; Woodyard and Hallam 2010). From an applied standpoint, results should furnish prevention insights for designing programs and campaigns tailored to the temporal drinking habits of the public.
The demarcation of the weekdays and weekends with reference to alcohol intake was pursued by applying the framework of alcohol consumption frequency (drinking days) and quantity (drinks per day) during the typical week (Bloomfield, Hope, and Kraus 2013; Lahaut et al 2003). These two behaviors are conceptually distinct, yet related, as evidenced by a small to moderate correlation between frequency and quantity of drinking (Breslow and Graubard 2008; Stewart et al. 2006). Furthermore, alcohol frequency and quantity are not only predicted by different types of alcohol expectancies, but both constructs are correlated with increased incidences of alcohol-induced negative consequences (Stewart, Morris, Mellings, and Komar 2006). Two studies were conducted to understand prototypical weekday and weekend alcohol usage. Study 1, applying item response theory, served as an exploratory examination of the days (frequency) that people usually consumed alcohol during the week. The analysis permits comparing and contrasting the 7 days by evaluating and interpreting the parameters of item characteristic curves (Crano, Brewer, and Lac 2015). Study 2, applying confirmatory factor analysis, examined drinks per day (quantity) during the week by hypothesizing and testing six competing measurement models of weekday and weekend consumption. These factor structures were informed by the literature and specified differently in terms of the boundaries of weekdays and weekends. Fit indices of these models were scrutinized and compared to arrive at the best fitting measurement embodiment of weekday and weekend alcohol intake.
Study 1: Item Response Theory
Purpose
Analysis using item response theory was undertaken to evaluate the drinking days across the week. Each item represented whether or not participants typically drank on a particular day (e.g., Monday), and the underlying latent factor represented the propensity for daily drinking during the week. Item response theory, applying a single scale solution, was pursued because the items (7 days of alcohol usage) were presumed to be somewhat correlated. Results were expected to supply details regarding the extent that the item characteristic curves representing the 7 days of the week exhibited similar or different alcohol usage patterns.
Participants
The 419 participants ranged in age from 22 to 74 years (M = 33.78; SD = 11.54). Gender distribution was 43.7 % males and 56.3 % females. Racial identity of the sample was 75.9 % Caucasian, 4.8 % Latino, 8.4 % Black, 8.1 % Asian, and 2.9 % multiracial.
Procedure
Participants were recruited on Mechanical Turk (MTurk), a crowd sourcing website that permits the general public to participate in a variety of tasks (Crano et al. 2015). In comparison to traditional data collection methods, samples recruited through this source are more demographically representative and heterogeneous (Buhrmester, Kwang, and Gosling 2011; Goodman, Cryder, and Cheema 2013) and results are considered as reliable and valid (Rand 2012). Considering that the alcohol customs and laws vary across countries, participation was restricted to people residing in the USA. To ensure adequate quality of responses, the questionnaire was made available only to those in the system with at least a 90 % rating on previously completed tasks. Responses for all items were complete for this brief questionnaire. Due to the unique drinking habits of college students and those under the legal age of drinking, after the initial data collection of 508 participants, analyses were performed on the sample over 21 years of age (N = 419). Nominal compensation was offered for participation. The measures and procedures were approved by an institutional IRB.
Measures
Instructions defined a drink to be any beverage containing alcohol with examples listed (e.g., beer, wine, wine cooler, shot of liquor, cocktail). Next, participants were instructed to consider the “past month” as a frame of reference to help respond to questions about their usual drinking patterns during the typical week. They then read, “How much alcohol, on average (measured in number of drinks), do you drink on each day of a typical week?” This was followed by parallel variants for seven items that corresponded to each day of the week (e.g., “On a typical Monday, I have ___ drinks”). For each day, participants entered an open-ended quantitative response regarding the number of alcoholic beverages consumed. Items were based on a variant of the Daily Drinking Questionnaire (Collins, Parks, and Marlatt 1985), an inventory shown to exhibit adequate test-retest reliability (Neighbors, Dillard, Lewis, Bergstrom, and Neil 2006) and criterion validity (Kenney, Lac, Labrie, Hummer, and Pham 2013; Napper, Kenney, Lac, Lewis, and LaBrie 2014).
Analytic Plan
To examine the days of drinking, responses were recoded into whether participants drank alcohol (at least 1 drink) or not (0 drinks) on each day. The item response theory model was specified with EIRT (Valois et al. 2011), a program based on the formulas and procedures ofdetailed in Baker (2004). Initially, a three-parameter model (difficulty, discrimination, and guessing) was attempted (Crano et al. 2015; DeMars 2010; Edelen and Reeve 2007), but it was rejected based on the global test of model fit, χ2(70) = 646.71, p < .001. Thus, a two-parameter model (difficulty and discrimination) was estimated, which statistically corresponded to the data, χ2(70) = 7.56, ns. The assumption of local independence was satisfied, as none of the error terms for the items significantly correlated beyond p < .01.
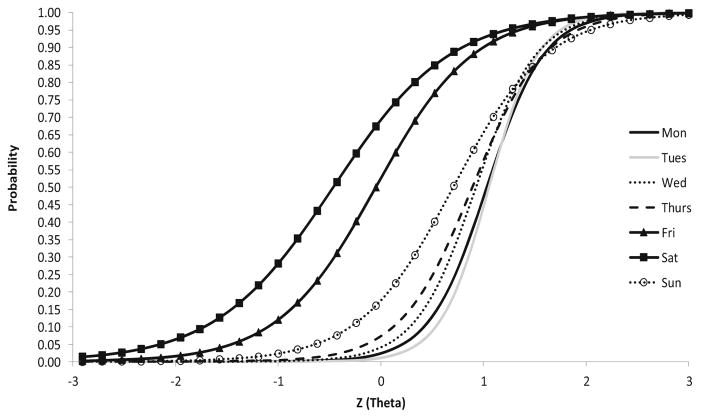
The parameter values for the item characteristic curves were tabled and graphed. In these graphs, the abscissa (x-axis) denotes the underlying latent factor of standardized scores (Z or theta or ability), interpreted as the propensity of daily drinking. The continuum of standardized values could be interpreted in terms of people with low (Z = −1), average (Z = 0), or high (Z = 1) daily drinking across the 7 days. The ordinate (y-axis) denotes the estimated probability of alcohol use on a particular day, as a function of participants’ standardized scores on the propensity to drink daily (x-axis).
A particular item’s difficulty (threshold) parameter is the point on the abscissa in which 50 % of participants consume alcohol on that day; a high positive index indicates a day in which only high daily drinkers were prone to consuming. An item’s discrimination (slope) parameter indicates its strength (in distinguishing among the spectrum of low to high daily drinking) across the latent factor. Items can be compared such that an item possessing a higher difficulty index signifies that people who have a greater likelihood of drinking daily (represented by the latent factor) are more likely to consume on that day. An item possessing a higher discrimination value is interpreted as being more successful in distinguishing across the latent factor of propensity for daily drinking. Furthermore, an item’s discrimination value also could be scrutinized as a function of a particular range of the latent factor.
Results
The percent of drinkers on each day was as follows: 17.2 % on Monday, 16.0 % on Tuesday, 19.8 % on Wednesday, 21.7 % on Thursday, 51.1 % on Friday, 62.8 % on Saturday, and 28.4 % on Sunday. Difficulty and discrimination parameters were evaluated to identify similar patterns (see Table 1 and Fig. 1). Difficulty values were highest for Monday, Tuesday, Wednesday, and Thursday, but lowest for Friday and Saturday. Thus, if the objective is to identify the days that alcohol is consumed only by high daily drinkers, the weekdays are ideally represented with Monday, Tuesday, Wednesday, and Thursday. In contrast, if the objective is to capture the days in which even the low daily drinkers are susceptible to consuming, the weekends are best represented by Friday and Saturday. The difficulty estimate for Sunday falls between weekdays and weekends, but it is somewhat closer to the estimate for weekdays.
Table 1.
Item response theory: estimates of difficulty and discrimination parameters for drinking days
| Item | Difficulty (location) | Discrimination (slope) |
|---|---|---|
| Monday | 1.03 | 3.58 |
| Tuesday | 1.05 | 4.23 |
| Wednesday | 0.93 | 3.41 |
| Thursday | 0.89 | 2.86 |
| Friday | −0.05 | 2.10 |
| Saturday | −0.46 | 1.75 |
| Sunday | 0.71 | 2.20 |
Fig. 1.
Item response theory: drinking days
Items possessing similar discrimination values were inspected, regardless of the item difficulty (Table 1 and Fig. 1). If classifying similar days based on item discrimination strength, then Monday, Tuesday, and Wednesday possess the strongest slopes and could be used to represent weekday consumption. On the other hand, if the focus is on the days with the weakest slopes, the conceptualization of weekend drinking is optimally captured using Friday, Saturday, and Sunday. Thursday’s discrimination index falls approximately between the parameter values for the days representing weekday and weekend intake.
The ranges of discrimination effectiveness were then interpreted as a function of the latent factor of drinking days (Fig. 1). Friday and Saturday were effective in discriminating among the continuum of low to high daily drinkers. Sunday discriminates somewhat in the range of low to moderate daily drinkers, but is more effective in separating moderate to high daily drinkers. Monday to Thursday were more discerning of the range of average to high (rather than low to average) daily drinkers.
Study 2: Confirmatory Factor Analysis
Purpose
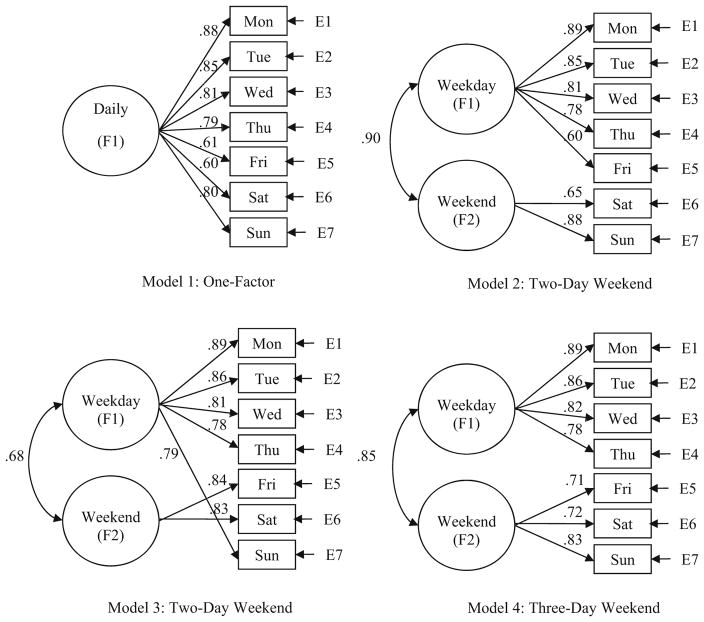
Extending upon the previous study, study 2 was designed to examine drinks per day across the week by testing hypothesized factor structures. Confirmatory factor analyses were undertaken on measurement models representing weekday and weekend drinking. The purposes of the study included determining whether two-factor structures (weekday versus weekend) were statistically superior in comparison to a one-factor structure (non-differentiation of weekday versus weekend) and identifying the optimal structure to capture quantity of drinks throughout the week. Six competing measurement models of quantity of alcohol intake per day across the week were tested and compared:
Model 1: one-factor structure encompassing all 7 days
Model 2: two-factor structure representing a 2-day weekend (Saturday and Sunday) and the remaining 5 days representing the weekdays
Model 3: two-factor structure representing another variant of a 2-day weekend (Friday and Saturday) and the remaining 5 days representing the weekdays
Model 4: two-factor structure representing a 3-day weekend (Friday, Saturday, and Sunday) and the remaining 4 days representing the weekdays
Model 5: two-factor structure representing a 4 -day weekend (Thursday, Friday, Saturday, and Sunday) and the remaining 3 days representing the weekdays
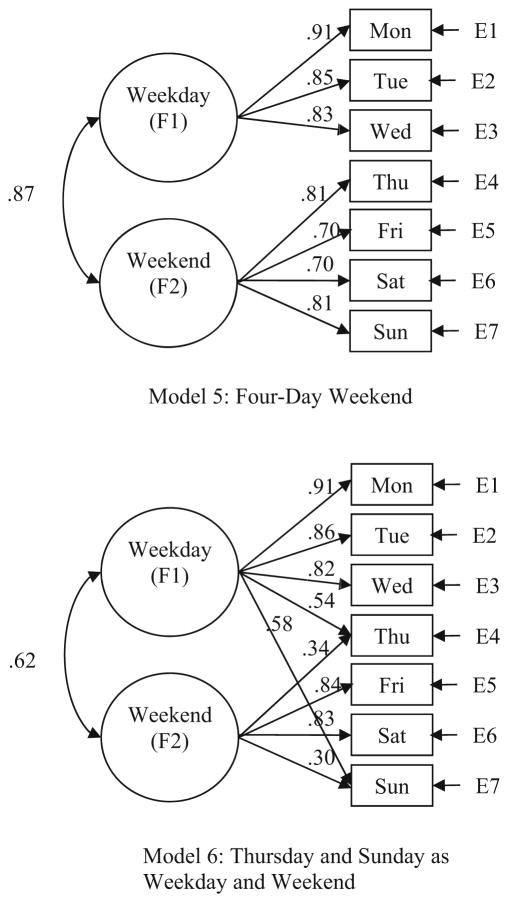
Model 6: two-factor structure with Thursday and Sunday each permitted to double load on the weekends (Friday and Saturday) and weekdays (Monday, Tuesday, and Wednesday)
Participants
The sample involved 403 participants ranging in age from 22 to 75 (M = 33.66, SD = 11.34) years. The gender distribution consisted of 46.2 % males and 53.8 % females. Racial composition was 72.5 % Caucasian, 5.0 % Latino, 7.7 % Black, 10.7 % Asian, and 4.2 % multiracial.
Procedure
The present study recruited a new sample. The same sampling procedures and measures of study 1 were followed.
Analytic Plan
The study focused on examining the quantity of drinks per day (across the 7 days of the week), so the original metrics of these open-ended quantitative items were retained. Confirmatory factor analyses were specified with the EQS 6.3 software (Bentler and Wu 2015). Items possessed the following positive skewness levels (Tabachnick and Fidell 2012): 4.10 (Monday), 3.63 (Tuesday), 3.53 (Wednesday), 2.99 (Thursday), 1.76 (Friday), 1.46 (Saturday), and 2.87 (Sunday). Thus, following recommendations for performing confirmatory factor analysis on items departing from normality (Hoyle 2012), the models were estimated with the robust maximum-likelihood procedure, to apply automatic corrections to fit indices and standard errors (Bentler 2006; Satorra and Bentler 1994). Advantages include that it is statistically superior to other latent-factor estimation approaches to account for non-normality and that the extent of adjustments is applied depending on the degree of normality violation. Alternative approaches include Poisson and negative binomial estimation, but these particular procedures necessitate stringent statistical assumptions that may be difficult to satisfy for all the variables (Gardner, Mulvey, and Shaw 1995; Ogasawara 1999; Zhou, Hannah, Dunson, and Carin 2012), given that the items representing Friday and Saturday were within reasonable boundaries of normality (Tabachnick and Fidell 2012).
Robust fit indices were interpreted to scrutinize the adequacy of each model. A non-significant chi-square test is desired and indicates that the model should not be rejected (Bollen 1989). The comparative fit index (CFI) and non-normed fit index (NNFI) range from 0.00 to 1.00, with a higher value, preferably above .95, indicative of a superior fitting model (Tabachnick and Fidell 2012; Ullman and Bentler 2003). The root mean square error of approximation (RMSEA) is appropriately sensitive in detecting model misspecifications, yields appropriate information about model quality, and produces confidence intervals around the index (MacCallum and Austin 2000). Values below.05 indicate close fit, between .05 and .08 indicate fair fit, between .08 and .10 indicate mediocre fit, and above .10 indicate poor fit (MacCallum, Browne, and Sugawara 1996). Akaike’s information criterion (AIC) balances the goodness of fit and the number of parameters estimated, with a lower value signifying a superior model (Bentler 2006). Acceptable models should generate statistically significant factor loadings, and interfactor correlations should not exceed a .80 or .85 cutoff to satisfy factor discriminant validity (Brown 2006). Finally, the scaled (robust) chi-square difference test was performed to determine whether nested models were statistically disparate (Bentler and Satorra 2010; Satorra and Bentler 2001).
Results
Model fit indices ranged from mediocre to excellent (Table 2). In all models, all standardized factor loadings and interfactor correlations were statistically significant, p < .001 (Figs. 2 and 3).
Table 2.
Confirmatory factor analysis: fit indices for drinks per day models
| Model | Model | χ2 | df | p value | CFI | NNFI | RMSEA (90 % CI) | AIC |
|---|---|---|---|---|---|---|---|---|
| 1 | F1 (Mon-Tue-Wed-Thurs-Fri-Sat-Sun) | 49.95 | 14 | <.001 | 0.85 | 0.78 | 0.08 (0.06, 0.10) | 21.95 |
| 2 | F1 (Mon-Tue-Wed-Thurs-Fri), F2 (Sat-Sun) | 45.99 | 13 | <.001 | 0.86 | 0.78 | 0.08 (0.06, 0.11) | 19.99 |
| 3 | F1 (Mon-Tue-Wed-Thurs-Sun), F2 (Fri-Sat) | 23.29 | 13 | .04 | 0.96 | 0.93 | 0.04 (0.01, 0.07) | −2.71 |
| 4 | F1 (Mon-Tue-Wed-Thurs), F2 (Fri-Sat-Sun) | 38.45 | 13 | <.001 | 0.89 | 0.83 | 0.07 (0.05, 0.10) | 12.45 |
| 5 | F1 (Mon-Tue-Wed), F2 (Thurs-Fri-Sat-Sun) | 38.73 | 13 | <.001 | 0.89 | 0.83 | 0.07 (0.05, 0.10) | 12.73 |
| 6 | F1 (Mon-Tue-Wed-Thurs-Sun), F2 (Thurs-Fri-Sat-Sun) | 7.98 | 11 | .71 (ns) | 1.00 | 1.00 | 0.00 (0.00, 0.04) | −14.02 |
Robust fit indices are reported. AIC with negative values are statistically plausible, with lower values denoting better model fit (Bentler and Wu 2015) F factor
Fig. 2.
Confirmatory factor analysis: drinks per day
Fig. 3.
Confirmatory factor analysis: drinks per day
The models were compared (Table 2 and Figs. 2 and 3) to identify the optimal factor structure. The measurement structure permitting the 7 days to be represented by one omnibus factor (model 1) generated the poorest fit indices overall. The 2-day weekend models for Saturday and Sunday (model 2) and Friday and Saturday (model 3) revealed better fit indices. The models for the 3-day weekend encompassing Friday, Saturday, and Sunday (model 4) and the protracted 4-day weekend involving Thursday, Friday, Saturday, and Sunday (model 5) revealed similar fit indices. The model permitting Thursday and Sunday to double load on weekday and weekend factors (model 6) emerged with the best fit indices. Specifically, model 6 produced the only non-significant model chi-square test, highest fit indices for the CFI and NNFI, and lowest residual values for the RMSEA. The items involving double loadings were expected to exhibit lower values, because of the competition in simultaneous explication by weekday and weekend factors (Brown 2006; Chen, Hayes, Carver, Laurenceau, and Zhang 2012) in the final model.
Nested models were compared to determine whether they were statistically different. Considering that it is possible to transition from one model to another by either incorporating or fixing parameters (Bentler and Satorra 2010), model 1 is nested with models 2 to 6 (Figs. 2 and 3). For instance, in model 2, forcing (fixing) a perfect (1.00) correlation between F1 and F2 and reestimating the model will accord a mathematically equivalent model to that of model 1. Chi-square difference tests revealed that the two-factor structures (models 2 to 6) each revealed statistically significant improvements over the one-factor structure, all p < .05. Models 3 through 5 are each nested with model 6. For instance, adding two paths to model 5 and reestimating the solution will produce model 6. Chi-square difference tests indicated that the final model was statistically superior to these other three models, all p < .001. The AIC, a fit index that does not require that models be nested (Ullman and Bentler 2003), corroborated that model 6 was the strongest fit to the data. In summary, the final model was superior compared to the other models across fit indices.
Discussion
Both studies underscored the importance of empirically delineating the temporal boundaries of weekday versus weekend alcohol ingestion. Throughout this discussion, findings in the current research support the reasonableness of referring to Monday, Tuesday, and Wednesday as prototypical of weekday drinking and referring to Friday and Saturday as prototypical of weekend drinking.
In study 1, item response theory offered insights regarding the particular days that people ingested alcohol throughout the week. Several notable findings were obtained from the analysis. Thursday and Sunday possessed similar statistical properties with both weekday and weekend intake. For Thursday, the difficulty parameter value resembled prototypical weekday usage, but the discrimination parameter was between that of weekdays and weekends. Sunday’s difficulty parameter was more similar to the weekdays, but the discrimination parameter was more reflective of the weekend. Findings discovered that people with a greater propensity for daily drinking were more inclined to drink during the weekdays. Although low daily drinkers rarely consumed on the weekdays, they were more susceptible to consuming during the weekend, which is considered a period for family events and social gatherings where alcohol is commonly supplied and readily available. The weekends (possessing the lowest difficulty parameter values) revealed higher discriminatory power among the wider range of low to high daily drinkers, but the weekdays discriminated primarily among average to high daily drinkers.
In study 2, several measurement models were specified and tested using confirmatory factor analyses to scrutinize drinking quantity per day throughout the typical week. The two-factor models rendered better fit than the single-factor solution positing that drinking quantity across the 7 days was undifferentiated. Thus, total alcohol consumption across the week is epitomized by a variant of the two-factor model of weekday versus weekend. The best fitting model indicated that Thursday and Sunday concurrently loaded on weekdays and weekends. Conceptually, this suggests the appropriateness of administering measures in which Thursday and Sunday are classified as part of the weekdays and the weekends. Both days revealed stronger loadings on the weekday relative to the weekend dimension. Although not ideal from a measurement perspective, if necessary to make a mutually exclusive classification decision, Thursday and Sunday are a better fit with weekday alcohol use. Taken together, the findings underscore the observation that Thursday and Sunday serve as transitional days for people to cyclically shift in and out of weekday and weekend use.
The proper conceptualization and accurate assessment of weekday versus weekend drinking are of utmost importance for designing prevention programs aimed at differential consumption habits during the week. If the days falling outside the temporal boundaries are included or excluded in either category, statistical comparisons may be conflated and results could generate misleading conclusions. In the scenario of the 4-day weekend representing Thursday through Sunday (Woodyard and Hallam 2010), different results might have emerged had these days been excluded from the weekend. Conversely, exclusively using a measure of Saturday and Sunday (Matzopoulos et al. 2006) and thereby leaving Friday out of the categorization may yield findings that are not reflective of weekend drinking.
Historically, troughs and crests in alcohol use, oscillating between weekday restraint and weekend over-indulgence, are motivated by an ethos of hedonic weekend inebriation (Measham 2006). Thus, the reasons for consuming alcohol may compel decisions regarding the appropriate days to consume alcohol (Cooper 1994). Research suggests that coping motives (i.e., to reduce negative internal states, such as to curtail anxiety and stress) prompt weekday drinking (Mohr et al. 2013; Studer et al 2014), whereas enhancement motives (i.e., to increase positive internal states, such as to facilitate positive feelings) foster weekend drinking. Based on these differing drinking motivations, prevention efforts targeting weekday use might design and deliver messages about alternative activities to self-soothe when managing stressful life situations, and efforts targeting weekend use might be more effective if offering alternative approaches to cultivate positive feelings and sensations.
Interpretation of the present research should take into consideration several limitations. Although prior methodological research supports that MTurk is demographically diverse (Buhrmester et al. 2011; Goodman et al. 2013) and yields reliable and valid measurements (Rand 2012), concerns about this medium of data collection should be acknowledged. Goodman et al. (2013) found that MTurk samples compared to traditional samples were “less emotionally stable” and possessed “lower self-esteem,” with both personal dispositions associated with greater alcohol use (Zeigler-Hill, Stubbs, and Madson 2013). This may affect external validity by introducing sampling bias of participants more prone to drinking. The underreporting of drinking behavior in self-report measures is a possibility, but this may be offset by the anonymity afforded in completing studies on the Internet (Crano et al. 2015). The current research sought to understand the alcohol habits of a population beyond undergraduate students and therefore recruited participants over the Internet. Future research might extend upon this line of investigation by evaluating potential moderating effects of participant age, gender, marital status, race/ethnicity, and college attendance status on drinking behaviors throughout the week, as differential drinking patterns may be exhibited across groups (Slutske 2005; LaBrie et al 2011). College students, for example, may be more vulnerable to drinking on Thursdays, as classes are less commonly offered the following day (i.e., Friday) at many campuses, so it is possible that the representativeness of Thursday as a weekend may be enhanced among this cohort.
In summary, both studies furnish insights about the social normative perimeters of weekday and weekend alcohol use. The literature commonly compares these two divisions, so the current research offers compelling evidence of the prototypical and non-prototypical days constituting weekday and weekend alcohol intake. This research provides statistical rationale for understanding weekday drinking as prototypically beginning on Monday and ending on Wednesday, whereas weekend drinking is optimally captured on Friday and Saturday. Thursday and Sunday consumption contains statistical properties of weekdays and weekends, so caution is warranted when assigning these particular days to a specific category. Findings emphasize that the conceptualization and operational definitions of alcohol behavioral patterns should be empirically justified.
Footnotes
Compliance with Ethnical Standards
Conflict of Interest The authors declare that they have no conflicts of interest.
Ethics All procedures performed in studies involving human participants were in accordance with the ethical standards of the institutional and/or national research committee and with the 1964 Helsinki Declaration and its later amendments or comparable ethical standards.
Consent Informed consent was obtained electronically from all individual participants included in the study.
References
- Argeriou M. Daily alcohol consumption patterns in Boston: Some findings and a partial test of the Tuesday hypothesis. Journal of Studies on Alcohol. 1975;36:1578–1583. doi: 10.15288/jsa.1975.36.1578. [DOI] [PubMed] [Google Scholar]
- Baker FB. Item response theory: Parameter estimation techniques. 2. New York: Marcel Dekker; 2004. [Google Scholar]
- Bentler PM. EQS 6 structural equations program manual. Encino: Multivariate Software; 2006. [Google Scholar]
- Bentler PM, Wu EJ. EQS 6.3 for windows. Encino, CA: Multivariate Software; 2015. [Google Scholar]
- Bentler PM, Satorra A. Testing model nesting and equivalence. Psychological Methods. 2010;15:111–123. doi: 10.1037/a0019625. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bloomfield K, Hope A, Kraus L. Alcohol survey measures for Europe: a literature review. Drugs: Dducation, Prevention and Policy. 2013;20:348–360. [Google Scholar]
- Bollen KA. Structural equations with latent variables. New York, NY: Wiley; 1989. [Google Scholar]
- Bråthen GG, Brodtkorb EE, Sand TT, Helde GG, Bovin GG. Weekday distribution of alcohol consumption in Norway: Influence on the occurrence of epileptic seizures and stroke? European Journal of Neurology. 2000;7:413–421. doi: 10.1046/j.1468-1331.2000.00097.x. [DOI] [PubMed] [Google Scholar]
- Breslow RA, Graubard BI. Prospective study of alcohol consumption in the United States: Quantity, frequency, and cause-specific mortality. Alcoholism: Clinical & Experimental Research. 2008;32:519. doi: 10.1111/j.1530-0277.2007.00595.x. [DOI] [PubMed] [Google Scholar]
- Brown TA. Confirmatory factor analysis for applied research. New York: Guilford Press; 2006. [Google Scholar]
- Buhrmester M, Kwang T, Gosling SD. Amazon’s mechanical Turk: a new source of inexpensive, yet high-quality, data? Perspectives on Psychological Science. 2011;6:3–5. doi: 10.1177/1745691610393980. [DOI] [PubMed] [Google Scholar]
- Chen FF, Hayes A, Carver CS, Laurenceau J, Zhang Z. Modeling general and specific variance in multifaceted constructs: A comparison of the bifactor model to other approaches. Journal Of Personality. 2012;80:219–251. doi: 10.1111/j.1467-6494.2011.00739.x. [DOI] [PubMed] [Google Scholar]
- Cooper ML. Motivations for alcohol use among adolescents: development and validation of a four-factor model. Psychological Assessment. 1994;6:117–128. doi: 10.1037/1040-3590.6.2.117. [DOI] [Google Scholar]
- Cleveland H, Almeida DM. A behavioral genetic investigation of weekend drinking among an adult sample. Substance Use & Misuse. 2013;48:359–370. doi: 10.3109/10826084.2013.763280. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Collins RL, Parks GA, Marlatt GA. Social determinants of alcohol consumption: The effects of social interaction and model status on the self-administration of alcohol. Journal of Consulting and Clinical Psychology. 1985;53:189–200. doi: 10.1037//0022-006x.53.2.189. [DOI] [PubMed] [Google Scholar]
- Crano WD, Brewer MB, Lac A. Principles and methods of social research. 3. New York, NY, US: Routledge; 2015. [Google Scholar]
- DeMars C. Item response theory. New York, NY, US: Oxford University Press; 2010. [Google Scholar]
- Edelen MO, Reeve BB. Applying item response theory (IRT) modeling to questionnaire development, evaluation, and refinement. Quality of Life Research. 2007;16:5–18. doi: 10.1007/s11136-007-9198-0. [DOI] [PubMed] [Google Scholar]
- Ekholm O, Strandberg-Larsen K, Grønbæk M. Influence of the recall period on a beverage-specific weekly drinking measure. European Journal of Clinical Nutrition. 2011;65:520–525. doi: 10.1038/ejcn.2011.1. [DOI] [PubMed] [Google Scholar]
- Furr-Holden CD, Voas RB, Lacey J, Romano E, Jones K. The prevalence of alcohol use disorders among night-time weekend drivers. Addiction. 2011;106:1251–1260. doi: 10.1111/j.1360-0443.2011.03408.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gardner W, Mulvey EP, Shaw EC. Regression analyses of counts and rates: Poisson, overdispersed poisson, and negative binomial models. Psychological Bulletin. 1995;118:392. doi: 10.1037/0033-2909.118.3.392. [DOI] [PubMed] [Google Scholar]
- Goodman JK, Cryder CE, Cheema A. Data collection in a flat world: the strengths and weaknesses of mechanical Turk samples. Journal of Behavioral Decision Making. 2013;26:213–224. doi: 10.1002/bdm.1753. [DOI] [Google Scholar]
- Hillbom M, Kaste M. Ethanol intoxication: a risk factor for ischemic brain infarction. Stroke. 1983;14:694–699. doi: 10.1161/01.str.14.5.694. [DOI] [PubMed] [Google Scholar]
- Hoeppner BB, Barnett NP, Jackson KM, Colby SM, Kahler CW, Monti PM, … Fingeret A. Daily college student drinking patterns across the first year college. Journal of Studies on Alcohol and Drugs. 2012;73:613–624. doi: 10.15288/jsad.2012.73.613. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Houwing S, Twisk D. Nothing good ever happens after midnight: Observed exposure and alcohol use during weekend nights among young male drivers carrying passengers in a late licensing country. Accident Analysis and Prevention. 2015;75:61–68. doi: 10.1016/j.aap.2014.11.014. [DOI] [PubMed] [Google Scholar]
- Hoyle RH. Handbook of structural equation modeling. New York, NY, US: Guilford Press; 2012. [Google Scholar]
- Hummer JF, LaBrie JW, Lac A, Sessoms A, Cail J. Estimates and influences of reflective opposite-sex norms on alcohol use among a high-risk sample of college students: Exploring Greek-affiliation and gender effects. Addictive Behaviors. 2012;37:596–604. doi: 10.1016/j.addbeh.2011.11.027. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kenney SR, Lac A, Labrie JW, Hummer JF, Pham A. Mental health, sleep quality, drinking motives, and alcohol-related consequences: a path-analytic model. Journal of Studies on Alcohol and Drugs. 2013;74:841–851. doi: 10.15288/jsad.2013.74.841. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kuntsche E, Cooper M. Drinking to have fun and to get drunk: Motives as predictors of weekend drinking over and above usual drinking habits. Drug and Alcohol Dependence. 2010;110:259–262. doi: 10.1016/j.drugalcdep.2010.02.021. [DOI] [PubMed] [Google Scholar]
- Lahaut VM, Jansen HA, van de Mheen D, Garretsen HF. Comparison of two formats of the weekly recall and quantity–frequency alcohol measures. Journal of Substance Use. 2003;8:164–169. [Google Scholar]
- Labrie JW, Lac A, Kenney SR, Mirza T. Protective behavioral strategies mediate the effect of drinking motives on alcohol use among heavy drinking college students: gender and race differences. Addictive Behaviors. 2011;36:354–361. doi: 10.1016/j.addbeh.2010.12.013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- MacCallum RC, Austin JT. Applications of structural equation modeling in psychological research. Annual Review of Psychology. 2000;51:201–226. doi: 10.1146/annurev.psych.51.1.201. [DOI] [PubMed] [Google Scholar]
- MacCallum RC, Browne MW, Sugawara HM. Power analysis and determination of sample size for covariance structure modeling. Psychological Methods. 1996;1:130–149. [Google Scholar]
- Matzopoulos R, Peden M, Bradshaw D, Jordaan E. Alcohol as a risk factor for unintentional rail injury fatalities during daylight hours. International Journal of Injury Control and Safety Promotion. 2006;13:81–88. doi: 10.1080/17457300500249582. [DOI] [PubMed] [Google Scholar]
- Measham FC. The new policy mix: Alcohol, harm minimisation and determined drunkenness in contemporary society. International Journal of Drug Policy. 2006;17:258–268. [Google Scholar]
- Mohr CD, Brannan D, Wendt S, Jacobs L, Wright R, Wang M. Daily mood–drinking slopes as predictors: a new take on drinking motives and related outcomes. Psychology of Addictive Behaviors. 2013;27:944–955. doi: 10.1037/a0032633. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mørch LS, Johansen D, Løkkegaard E, Hundrup YA, Grønbæk M. Drinking pattern and mortality in Danish nurses. European Journal of Clinical Nutrition. 2008;62:817–822. doi: 10.1038/sj.ejcn.1602799. [DOI] [PubMed] [Google Scholar]
- Napper LE, Kenney SR, Lac A, Lewis LJ, LaBrie JW. A cross-lagged panel model examining protective behavioral strategies: Are types of strategies differentially related to alcohol use and consequences? Addictive Behaviors. 2014;39:480–486. doi: 10.1016/j.addbeh.2013.10.020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Neighbors C, Dillard AJ, Lewis MA, Bergstrom RL, Neil TA. Normative misperceptions and temporal precedence of perceived norms and drinking. Journal of Studies on Alcohol. 2006;67:290–299. doi: 10.15288/jsa.2006.67.290. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ogasawara H. Negative binomial factor analysis. Behaviormetrika. 1999;26:235–250. [Google Scholar]
- Orcutt JD, Harvey LK. The temporal patterning of tension reduction: Stress and alcohol use on weekdays and weekends. Journal of Studies on Alcohol. 1991;52:415–424. doi: 10.15288/jsa.1991.52.415. [DOI] [PubMed] [Google Scholar]
- Palma S, Pardo-Crespo R, Mariscal M, Perez-Iglesias R, Llorca J, Delgado-Rodríguez M. Weekday but not weekend alcohol consumption before pregnancy influences alcohol cessation during pregnancy. European Journal of Public Health. 2007;17:394–399. doi: 10.1093/eurpub/ckl259. [DOI] [PubMed] [Google Scholar]
- Paschall MJ, Kypri K, Saltz RF. Friday class and heavy alcohol use in a sample of New Zealand college students. Journal of Studies On Alcohol. 2006;67:764–769. doi: 10.15288/jsa.2006.67.764. [DOI] [PubMed] [Google Scholar]
- Rand DG. The promise of mechanical Turk: How online labor markets can help theorists run behavioral experiments. Journal of Theoretical Biology. 2012;299:172–179. doi: 10.1016/j.jtbi.2011.03.004. [DOI] [PubMed] [Google Scholar]
- Satorra A, Bentler PM. Corrections to test statistics and standard errors in covariance structure analysis. In: von Eye A, Clogg CC, editors. Latent variable analysis: Applications for developmental research. Thousand Oaks: Sage; 1994. pp. 399–419. [Google Scholar]
- Satorra A, Bentler PM. A scaled difference chi-square test statistic for moment structure analysis. Psychomerika. 2001;66:507–514. doi: 10.1007/s11336-009-9135-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Slutske WS. Alcohol use disorders among US college students and their non-college-attending peers. Archives of General Psychiatry. 2005;62:321–327. doi: 10.1001/archpsyc.62.3.321. [DOI] [PubMed] [Google Scholar]
- Stewart SH, Morris E, Mellings T, Komar J. Relations of social anxiety variables to drinking motives, drinking quantity and frequency, and alcohol-related problems in undergraduates. Journal of Mental Health. 2006;15:671–682. [Google Scholar]
- Studer J, Baggio S, Mohler-Kuo M, Dermota P, Daeppen J-B, Gmel G. Differential association of drinking motives with alcohol use on weekdays and weekends. Psychology of Addictive Behaviors. 2014 Aug 18; doi: 10.1037/a0035668. Advance online publication. [DOI] [PubMed] [Google Scholar]
- Tabachnick BG, Fidell LS. Using multivariate statistics. 5. Boston, MA: Allyn & Bacon/Pearson Education; 2012. [Google Scholar]
- Ullman JB, Bentler PM. Structural equation modeling. In: Schinka JA, Velicer WF, editors. Handbook of psychology: Research methods in psychology. Vol. 2. Hoboken, NJ, US: Wiley; 2003. pp. 607–634. [Google Scholar]
- Valois P, Houssemand C, Germain S, Abdous B. A open source tool to verify the psycometric properties of an evaluation instrument. Procedia Social and Behavioral Sciences. 2011;15:552–556. [Google Scholar]
- Wood PK, Sher KJ, Rutledge PC. College student alcohol consumption, day of the week, and class schedule. Alcoholism: Clinical and Experimental Research. 2007;31:1195–1207. doi: 10.1111/j.1530-0277.2007.00402.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Turrisi R, Mallett KA, Cleveland MJ, Varvil-Weld L, Abar C, Scaglione N, Hultgren B. Evaluation of timing and dosage of a parent-based intervention to minimize college students’ alcohol consumption. Journal of Studies on Alcohol and Drugs. 2013;74:30–40. doi: 10.15288/jsad.2013.74.30. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Woodyard C, Hallam JS. Differences in college student typical drinking and celebration drinking. Journal of American College Health. 2010;58:533–538. doi: 10.1080/07448481003621734. [DOI] [PubMed] [Google Scholar]
- Zeigler-Hill V, Stubbs WJ, Madson MB. Fragile self-esteem and alcohol-related negative consequences among college student drinkers. Journal of Social and Clinical Psychology. 2013;32:546–567. doi: 10.1521/jscp.2013.32.5.546. [DOI] [Google Scholar]
- Zhou M, Hannah L, Dunson DB, Carin L. Beta-negative binomial process and Poisson factor analysis. Journal of Machine Learning Research: Workshop and Conference Proceedings. 2012;22:1462–1471. [Google Scholar]